Simulation Analysis and Experiment Research of Transformer Vibration Based on Electric–Magnetic–Mechanic Coupling
Abstract
1. Introduction
2. Theoretical Model for Vibration Analysis of Transformer Core and Winding
2.1. Theoretical Model for Transformer Core Vibration
2.2. Theoretical Model for Transformer Winding Vibration
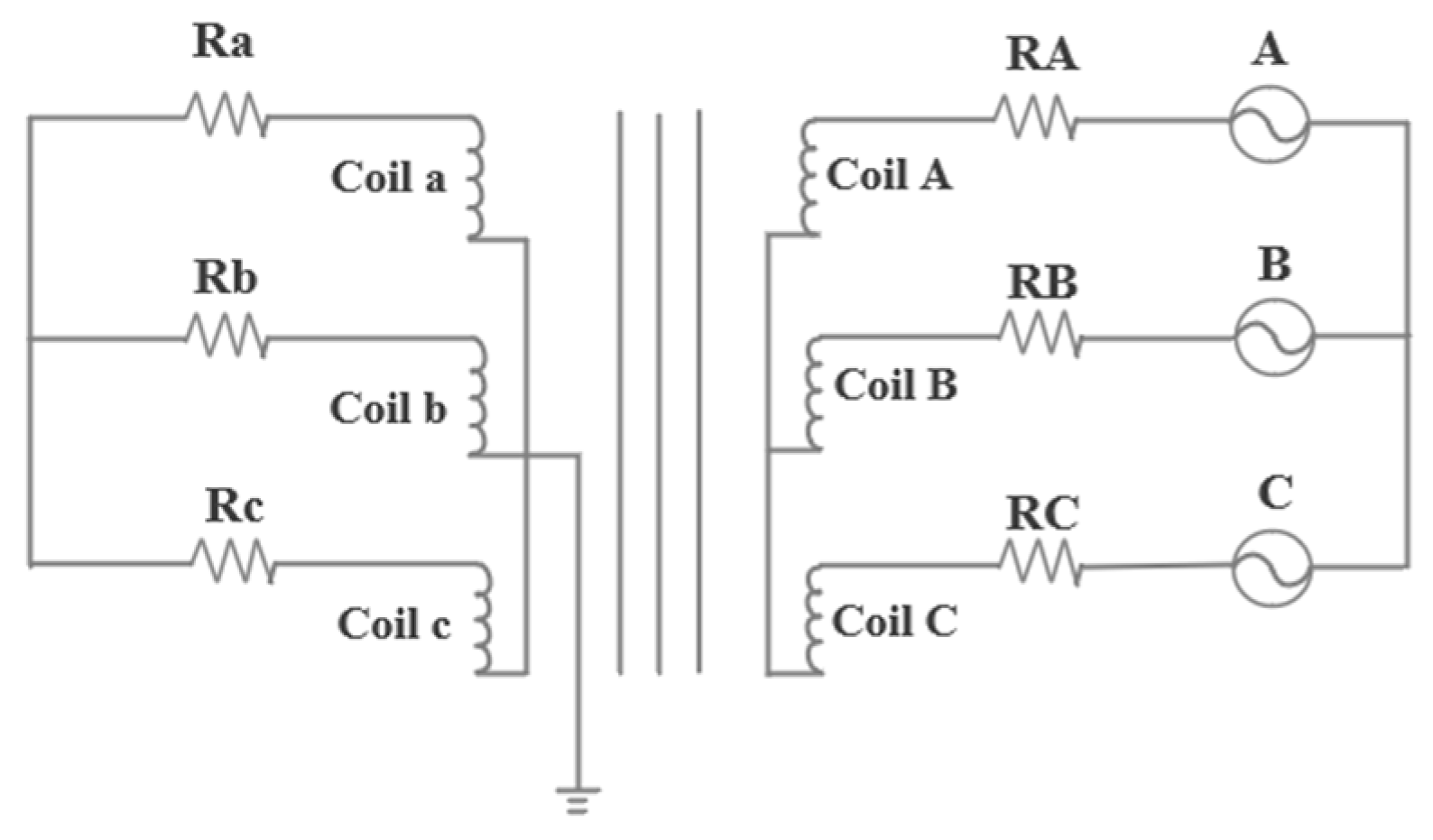
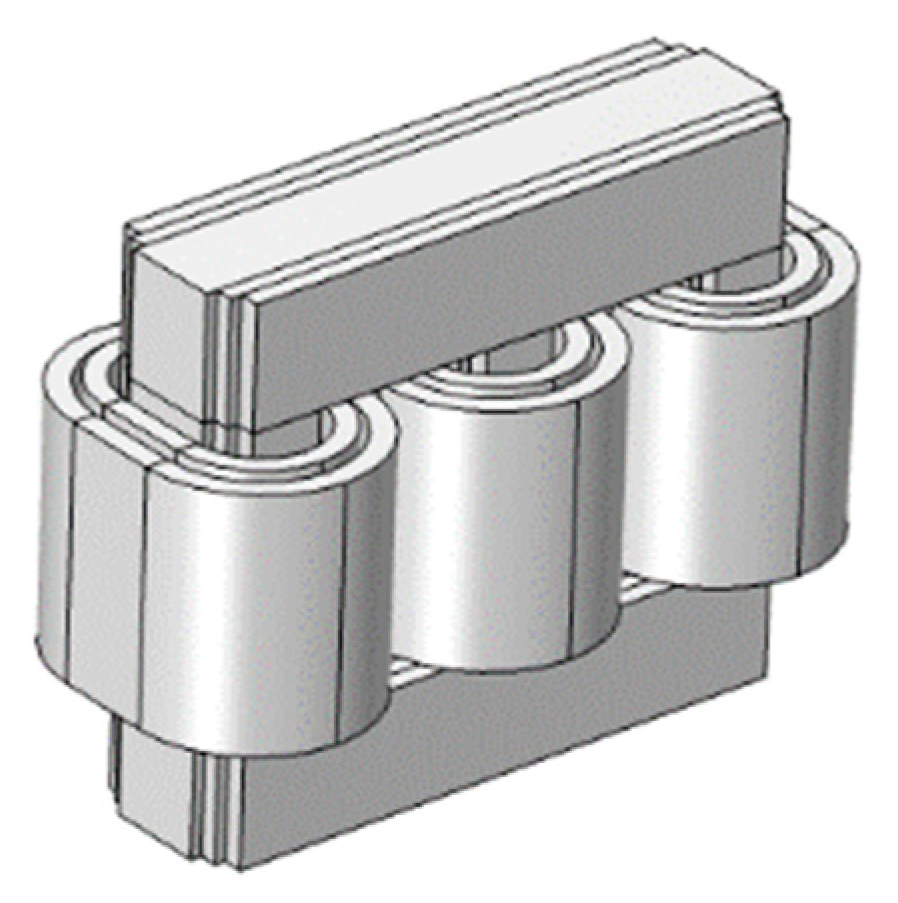
3. Simulation Model of Transformer Core and Winding Vibration Based on Multi-Physics Coupling
3.1. Simulation Analysis of Core Vibration Based on Multi-Physics Coupling
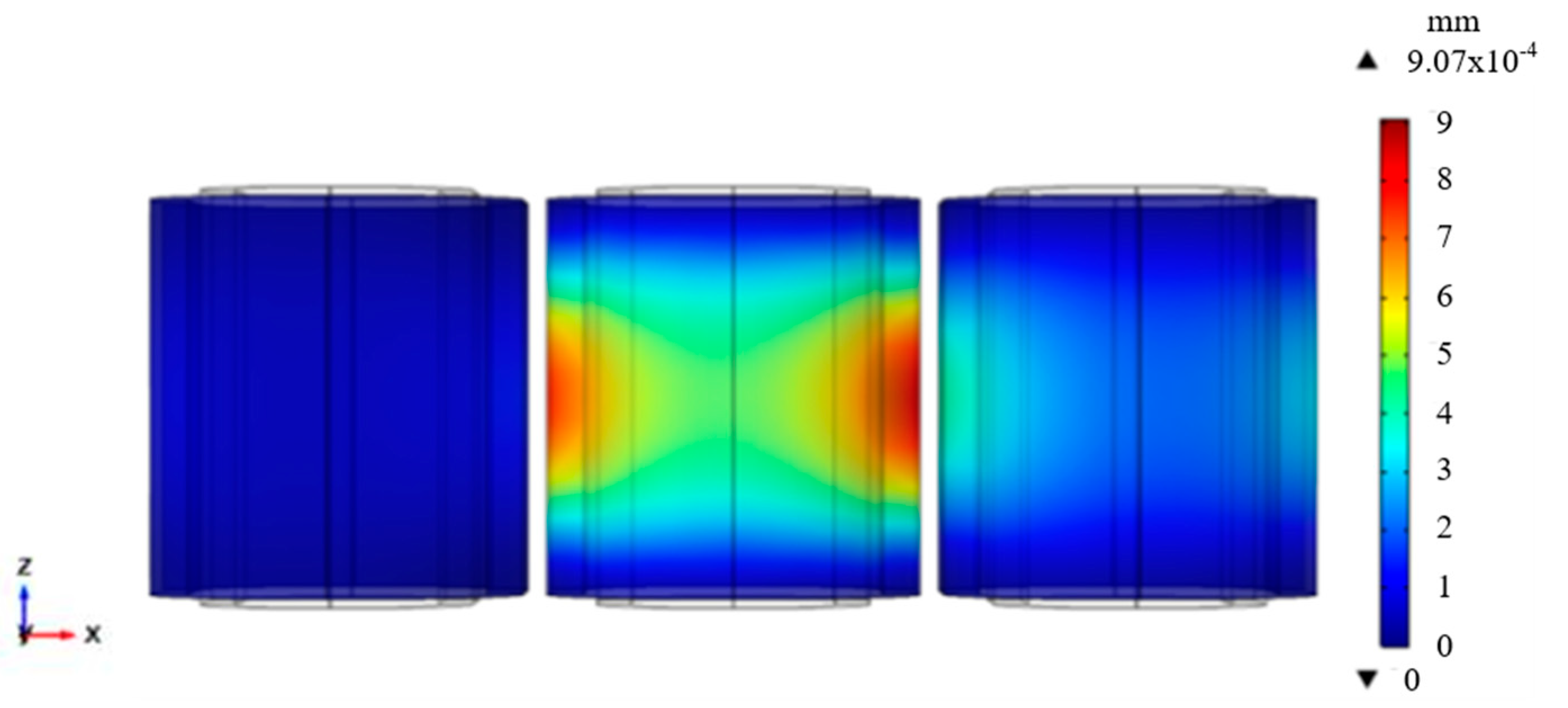
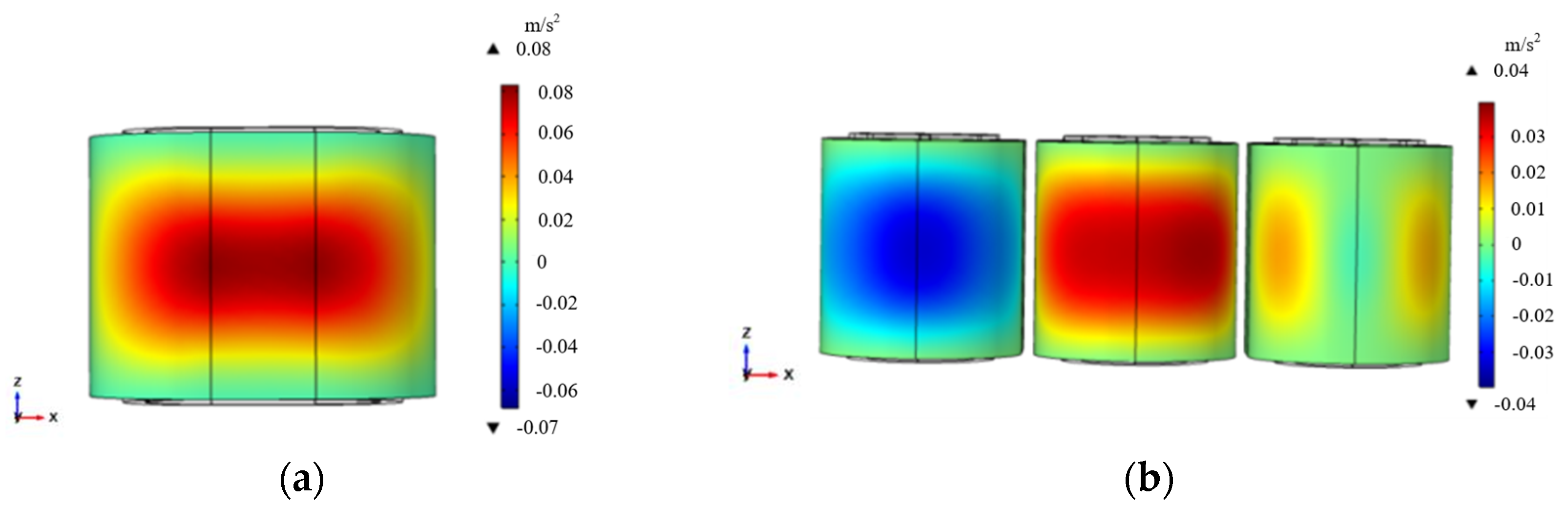
3.2. Simulation Analysis of Winding Vibration Based on Multi-Physics Coupling
4. Construction of Test Platform and Vibration Analysis of Transformer
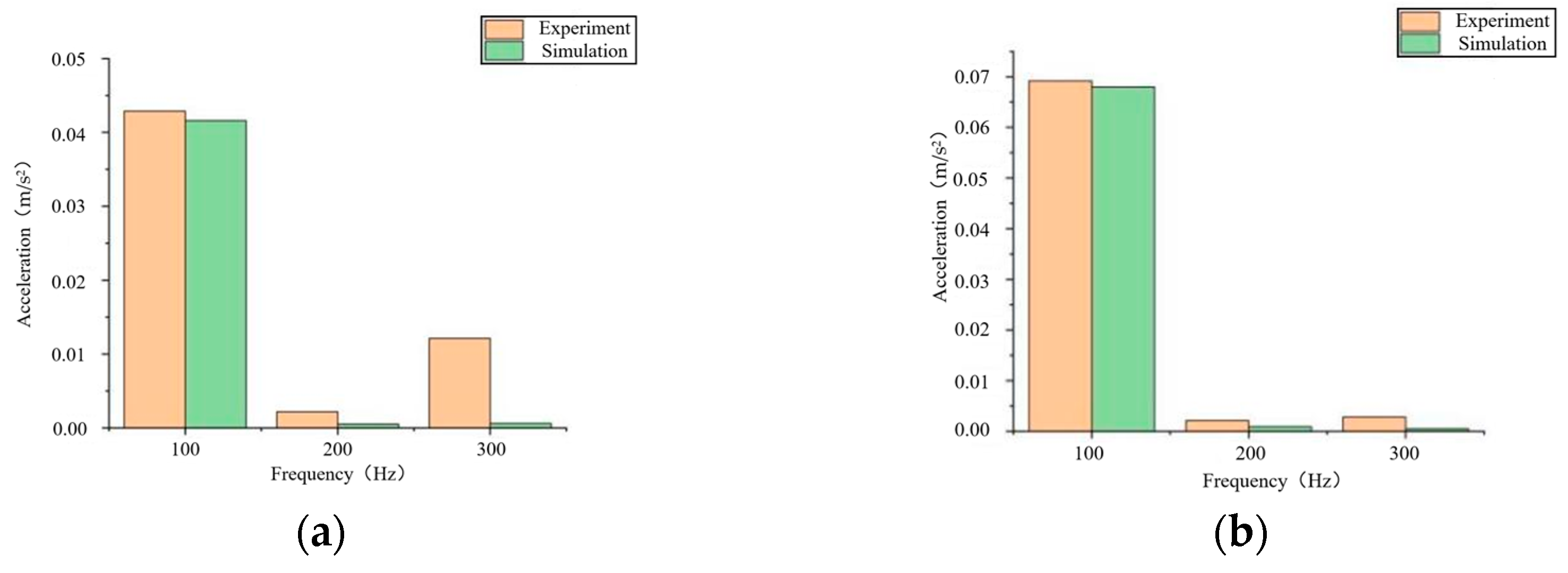
4.1. Construction of No-Load Test Platform and Vibration Analysis of Transformer Core
4.2. Construction of Load Test Platform and Vibration Analysis of Transformer Winding
5. Conclusions
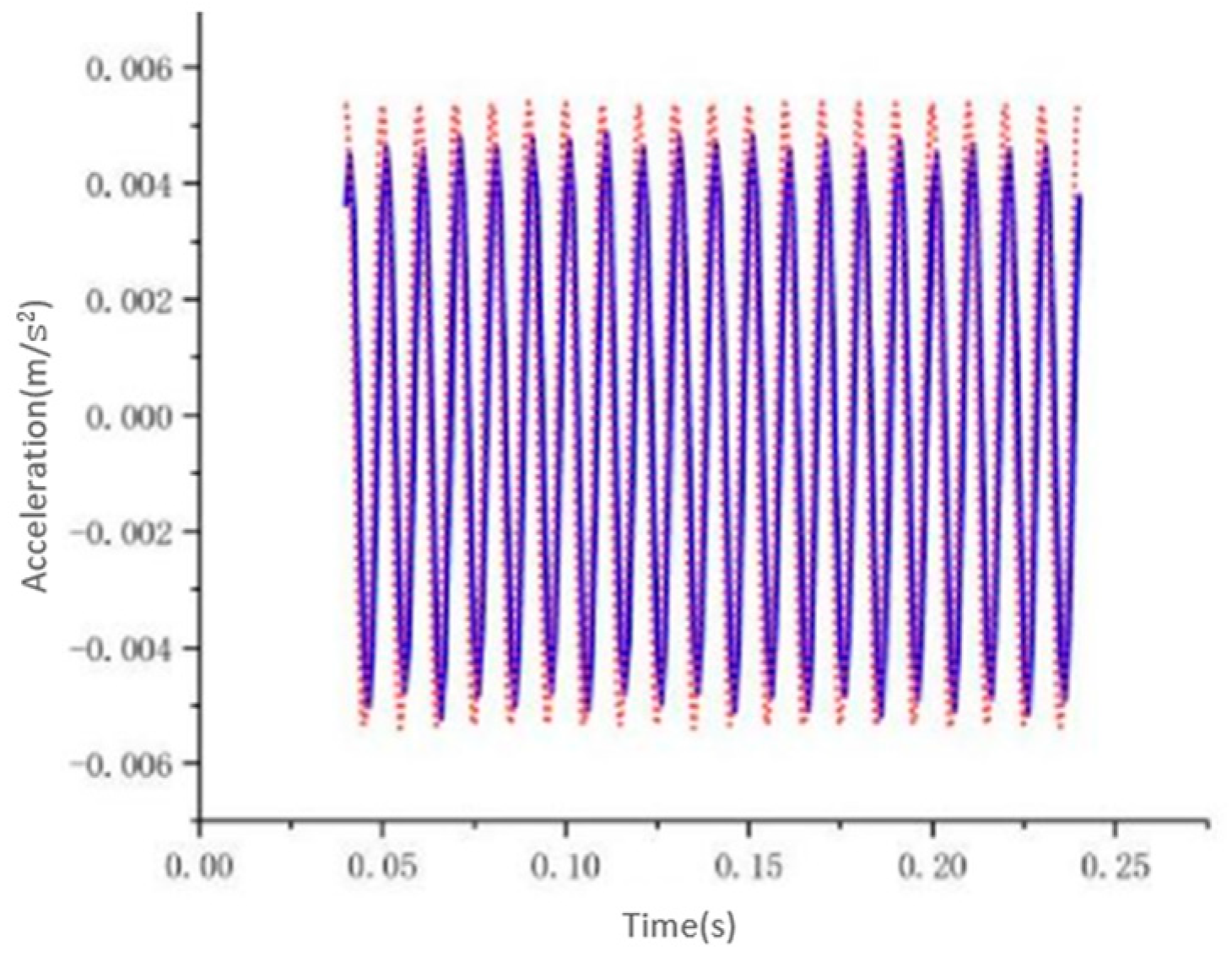
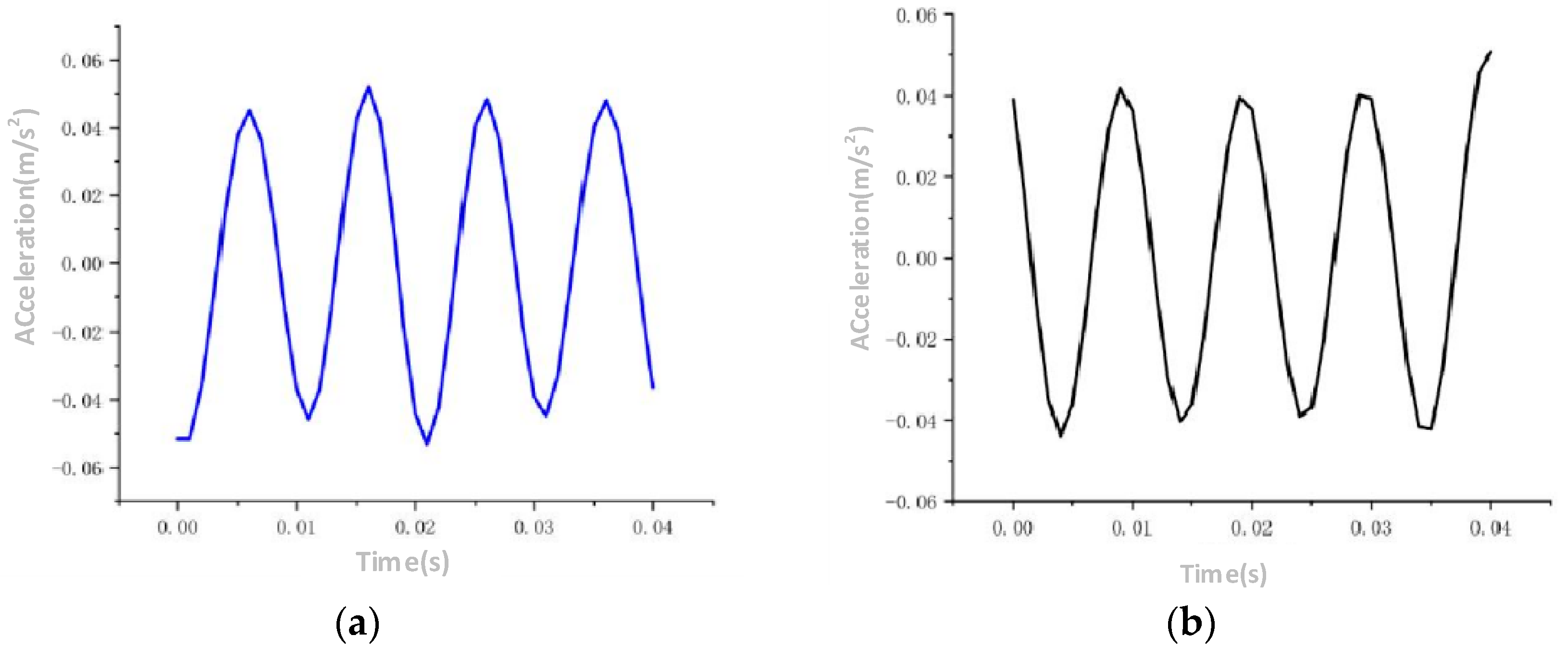
- A vibration simulation model of the transformer under no-load operation conditions was established, and the voltage waveform diagrams of the high-voltage side and the low-voltage side as well as the magnetic field distribution diagram of the core are obtained. The maximum value of the main magnetic flux of the transformer core is 1.79 T. The vibration of the core of the transformer is mainly at 100 Hz, and the vibration of the core exhibits a peak vibration acceleration of 0.005 m/s2 at 100 Hz under no-load condition. It uncovers a direct correlation between the input voltage squared and the acceleration of the vibrations in the core;
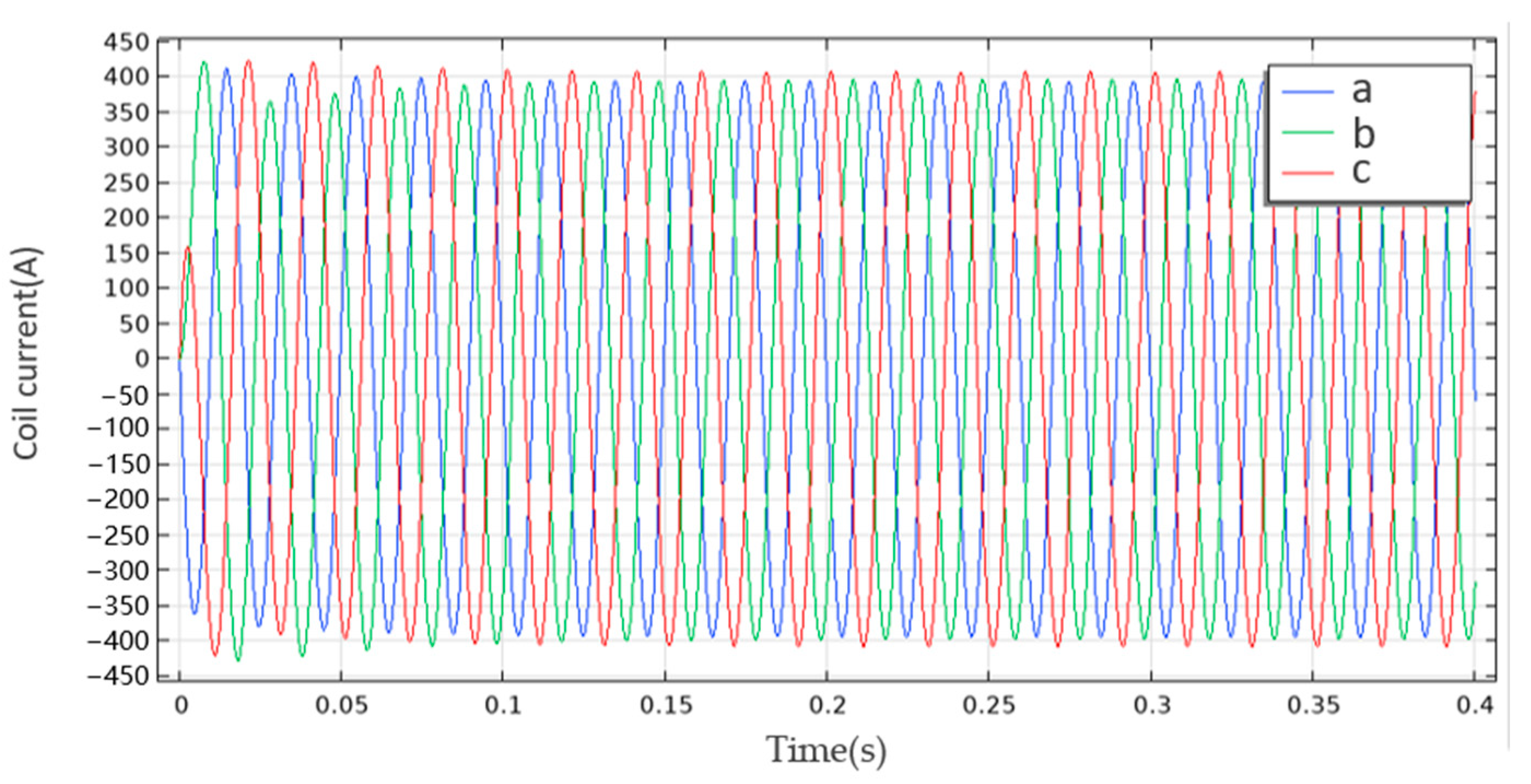
- A vibration model for load simulation is established, and the current waveform chart is derived. The vibration of the windings of the transformer is mainly at 100 Hz. The leakage magnetic field reaches 0.31 T, while the side vibration of the winding exhibits a peak vibration acceleration of 0.08 m/s2 and a maximum vibration acceleration of 0.04 m/s2. It uncovers that the electromagnetic force acting on the transformer winding is directly proportional to the current squared;
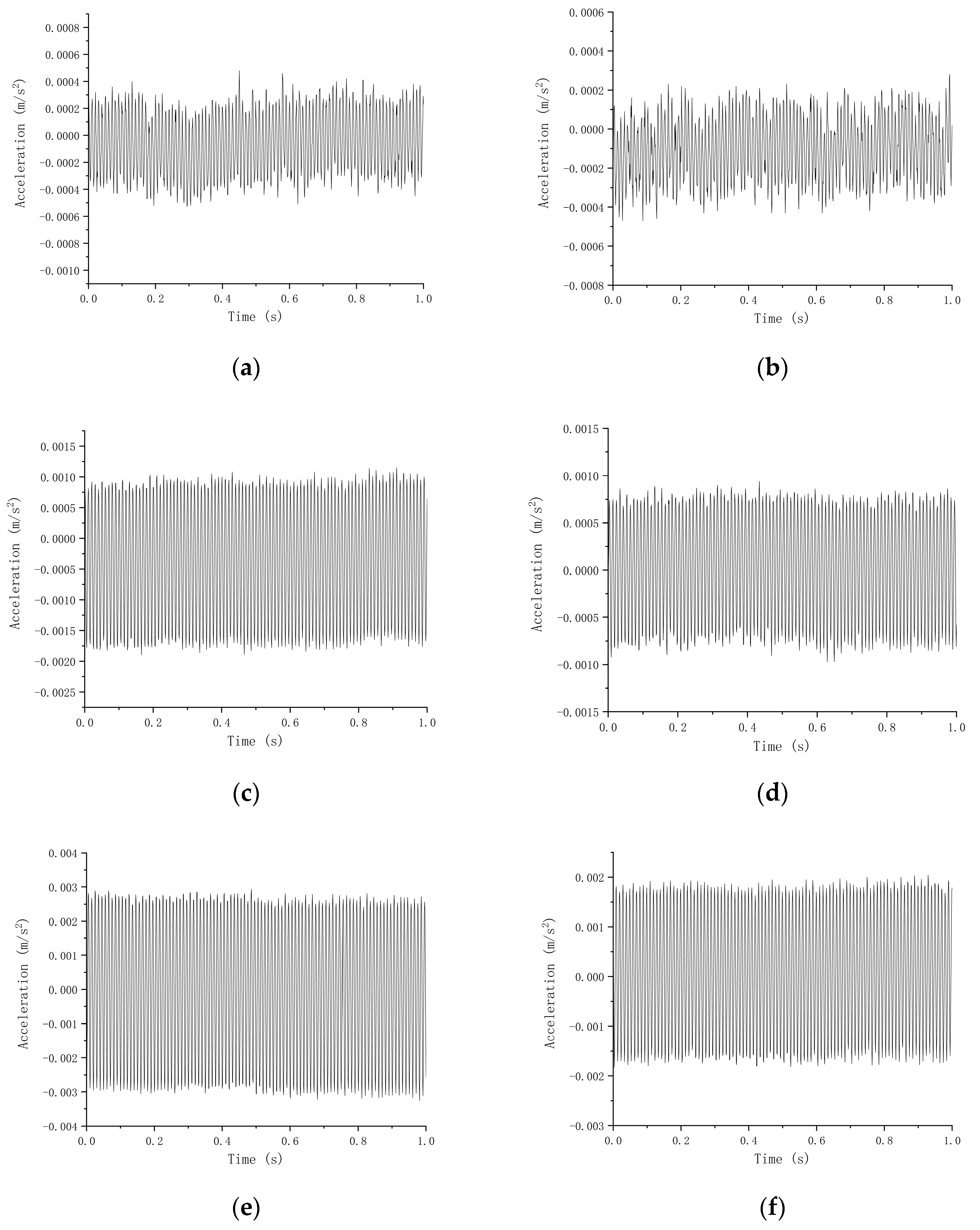
- The platform for collecting transformer vibration information was established, and no-load and load tests were conducted on the transformer under normal operating conditions. The experimental results uncover that the acceleration of core vibration in the transformer is 0.0047 m/s2, with a deviation of 6.38% from the simulation data. The maximum acceleration of winding vibration in phase A at the midpoint of its side and in phase B at the midpoint of its front are measured as 0.0714 m/s2 and 0.0416 m/s2, respectively, with errors of 2.1% and 3.3% compared to the simulation data. These findings demonstrate a consistent agreement between simulation and experiment, thus validating the reliability of both.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Komatowski, E. Amplitude detection of power transformer tank vibrations signal. In Proceedings of the 2016 International Conference on Signals and Electronic Systems (ICSES), Kraków, Poland, 5–7 September 2016; pp. 41–46. [Google Scholar]
- Qian, G. Research on spectrum eigenvalues of transformer vibration and its application on diagnosis. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 366–370. [Google Scholar]
- Gao, X.; Liu, Y. Nonlinear Research: Study Results from Beihang Universuty Broaden Understanding of Nonlinear Research (Research of giant magnetostrictive actuator’s nonlinear dynamic behaviors). J. Technol. Sci. 2018, 52, 864–872. [Google Scholar]
- Jin, M.; Pan, J. Vibration transmission from internal structures to the tank of an oil-filled power transformer. Appl. Acoust. 2016, 113, 1–6. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, J.; Huang, H. An experimental study of winding vibration of a single-phase power transformer using a laser Doppler vibrometer. Appl. Acoust. 2015, 87, 30–37. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Zhang, R. Real-time vibration-based fault diagnosis of power transformers using deep learning. Energies 2022, 15, 3678. [Google Scholar]
- Moses, A.J.; Anderson, P.I.; Phophongviwat, T. Localized Surface Vibration and Acoustic Noise Emitted from Laboratory-Scale Transformer Cores Assembled from Grain-Oriented Electrical Steel. IEEE Trans. Magn. 2016, 52, 1–15. [Google Scholar] [CrossRef]
- Cao, C.; Xu, B.W.; Li, X.B. Monitoring Method on Loosened State and Deformational Fault of Transformer Winding Based on Vibration and Reactance Information. IEEE Access 2020, 8, 215479–215492. [Google Scholar] [CrossRef]
- Zhou, Q.; Ding, G.; Wang, F. Edge computing-enabled real-time vibration monitoring for power transformers. IEEE Trans. Ind. Inform. 2023, 19, 6789–6800. [Google Scholar]
- Zhang, B.; Yan, N.; Du, J.; Wang, H.; Wei, X.; Zhou, C. A hybrid CNN-LSTM model for transformer winding fault diagnosis using vibration signals. Energies 2022, 15, 2985. [Google Scholar]
- Cao, C.; Xu, J.Y.; Lin, X.; Li, X. State diagnosis method of transformer winding deformation based on fusing vibration and reactance parameters. IET Electr. Power Appl. 2020, 14, 818–826. [Google Scholar]
- Jonghoek, K.; Sungyun, C. Robust and efficient WLS-based dynamic state estimation considering transformer core saturation. J. Frankl. Inst. 2020, 357, 12938–12959. [Google Scholar]
- Wang, Y.; Pan, J. Comparison of mechanically and electrically excited vibration frequency responses of a small distribution transformer. IEEE Trans. Power Deliv. 2015, 32, 1173–1180. [Google Scholar] [CrossRef]
- Li, D.; Yu, Z.; Zhao, J.; Zhang, L. Study on axial vibration characteristics of transformer winding. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1080–1083. [Google Scholar]
- Yu, Z.; Li, D.; Chen, L. Statistical analysis of vibration characteristics of power transformers with different voltage levels. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018; pp. 694–699. [Google Scholar]
- Hilgert, T.; Vandevelde, L.; Melkebeek, J. Comparison of magnetostriction models for use in calculations of vibrations in magneticcores. IEEE Trans. Magn. 2008, 44, 874–877. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, N.; Du, J.; Han, F.; Wang, H. A novel approach to investigate the core vibration in power transformers. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Q.; Ding, G.; Wu, X.; Wu, J.; Zhang, Y. Influence of magnetic state variation on transformer core vibration characteristics and its measurement. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Li, X.; Huang, X.; Zhou, Z.; Zhao, Y.; Chen, Y.; Song, X. Analysis of the measuring points selection of power transformer winding deformation though vibration test. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–5. [Google Scholar]
- Duan, X.; Zhao, T.; Liu, J.; Zhang, L.; Zou, L. Analysis of winding vibration characteristics of power transformers based on the finite-element method. Energies 2018, 11, 2404. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, Z.; Dong, Z.; Wu, Y.; Xiao, R.; Deng, J.; Pan, Z. Research on distribution characteristics of vibration signals of ± 500 kV HVDC converter transformer winding based on load test. Int. J. Electr. Power Energy Syst. 2021, 132, 107200. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Yu, X. Axial vibrations modal analysis and computation of power transformer windings under different levels of pre-compression. In Proceedings of the 2009 International Conference on Applied Superconductivity and Electromagnetic Devices, Chengdu, China, 25–27 September 2009; pp. 229–232. [Google Scholar]
- Peng, H.; Pan, Y.; Hu, J.; Yang, C.; Wang, Y.; Wu, K. The vibration analysis for transformer winding based on multi-field coupling. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing China, 25–26 March 2017; pp. 2003–2006. [Google Scholar]
- Wang, Z.; Liu, S.; Zhang, L. Analysis of vibration characteristics of dry-type transformer iron core and windings based on multi physical field. In Proceedings of the 2022 12th International Conference on Power and Energy Systems (ICPES), Guangzhou, China, 23–25 December 2022; pp. 52–56. [Google Scholar]
- Luo, B.; Wang, F.H. A tank vibration model for online monitoring of power transformer. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
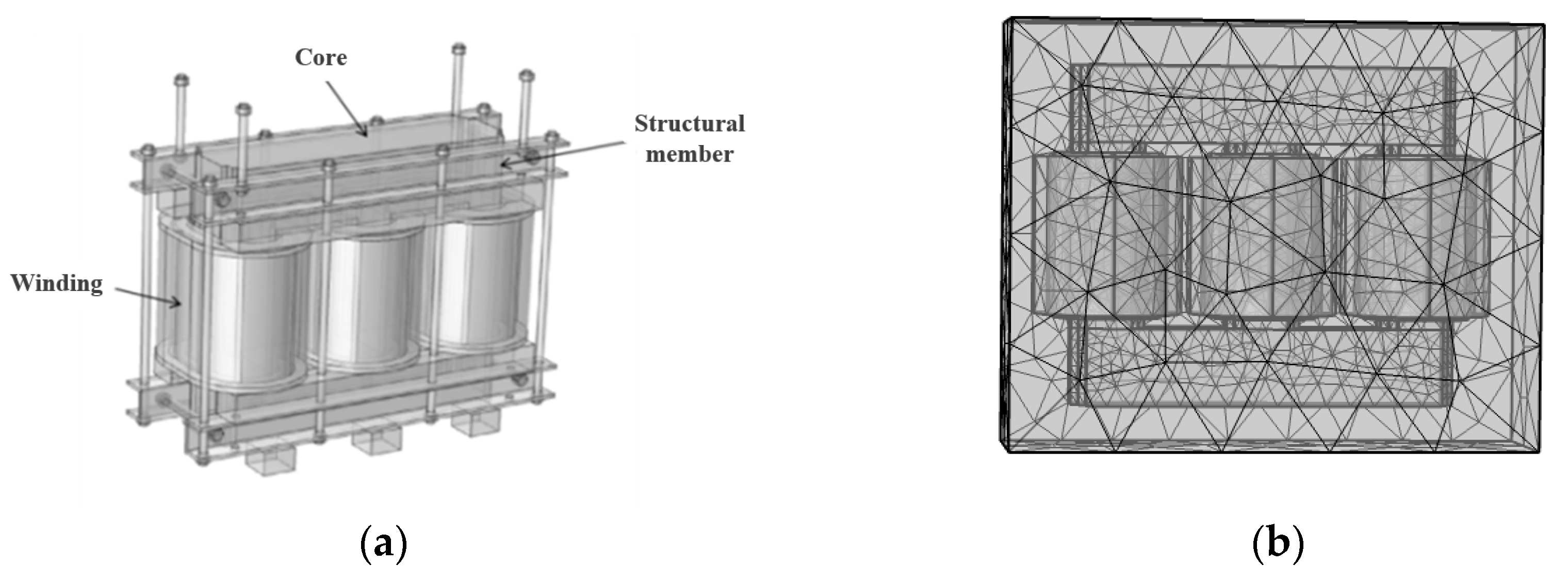
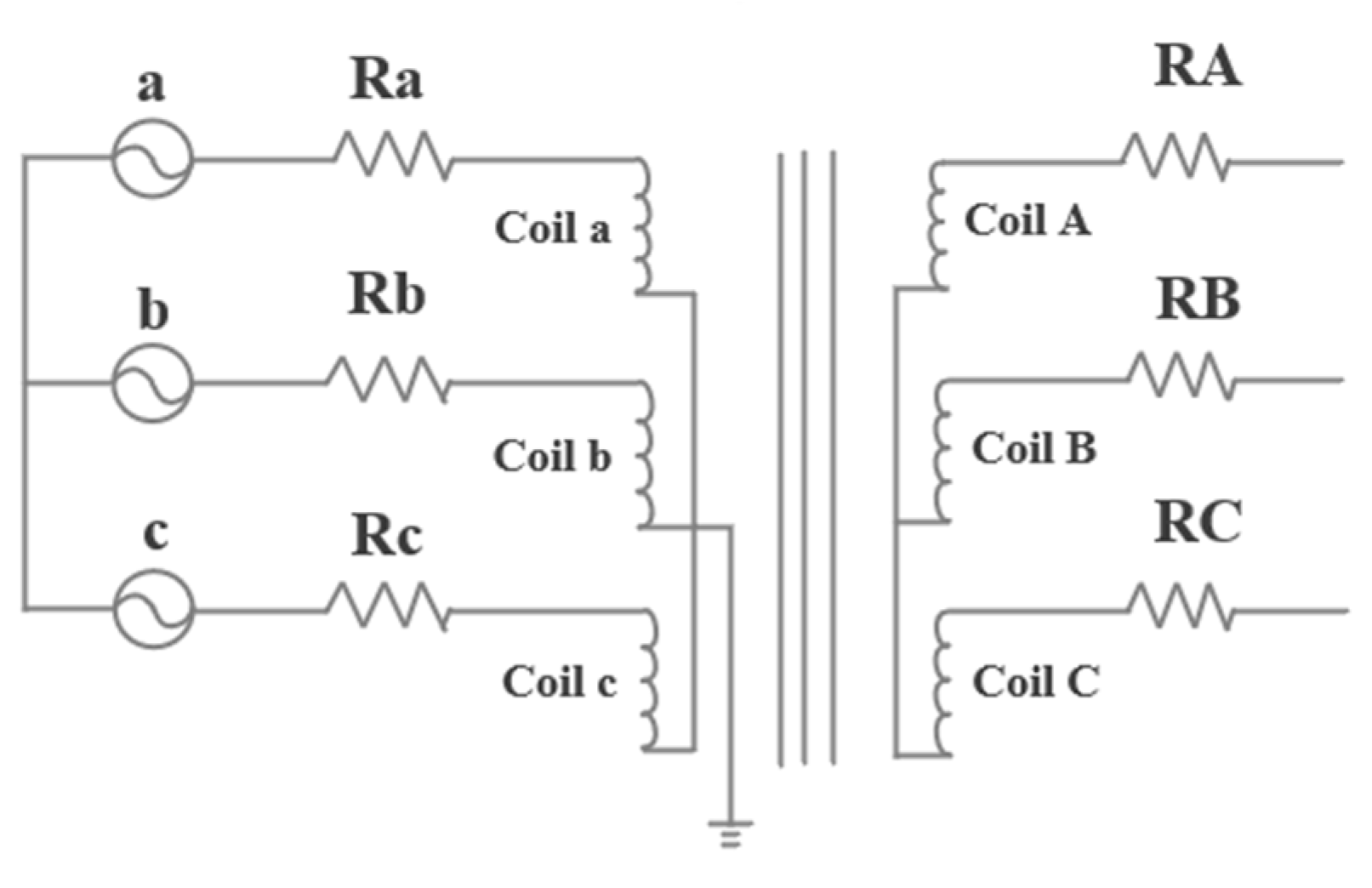
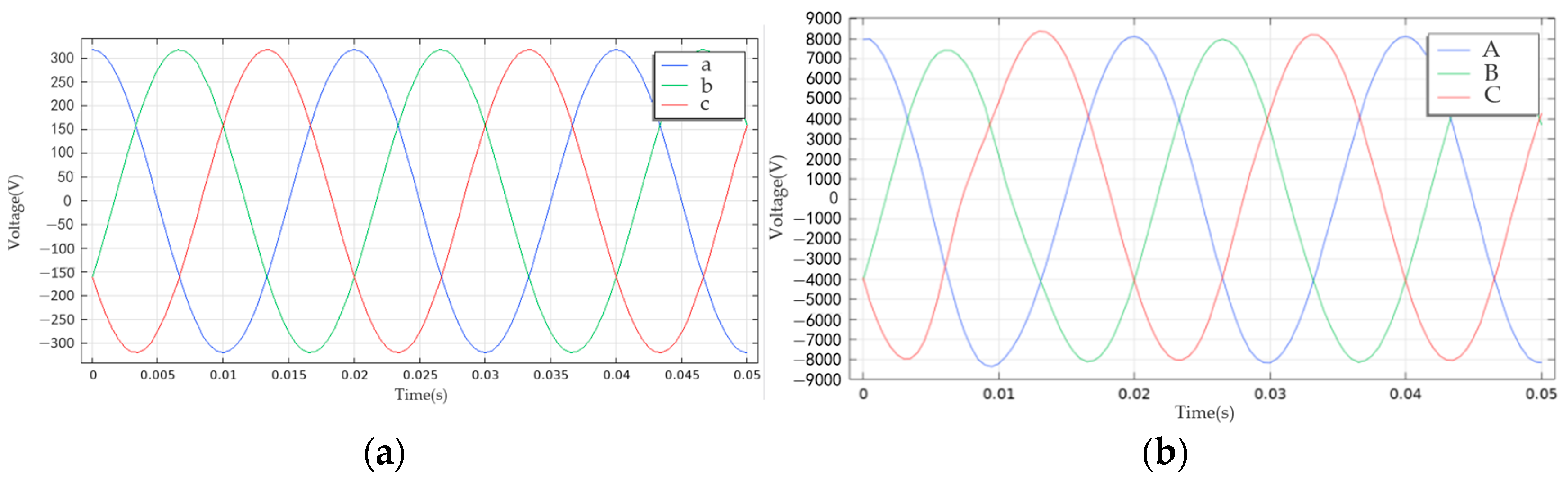

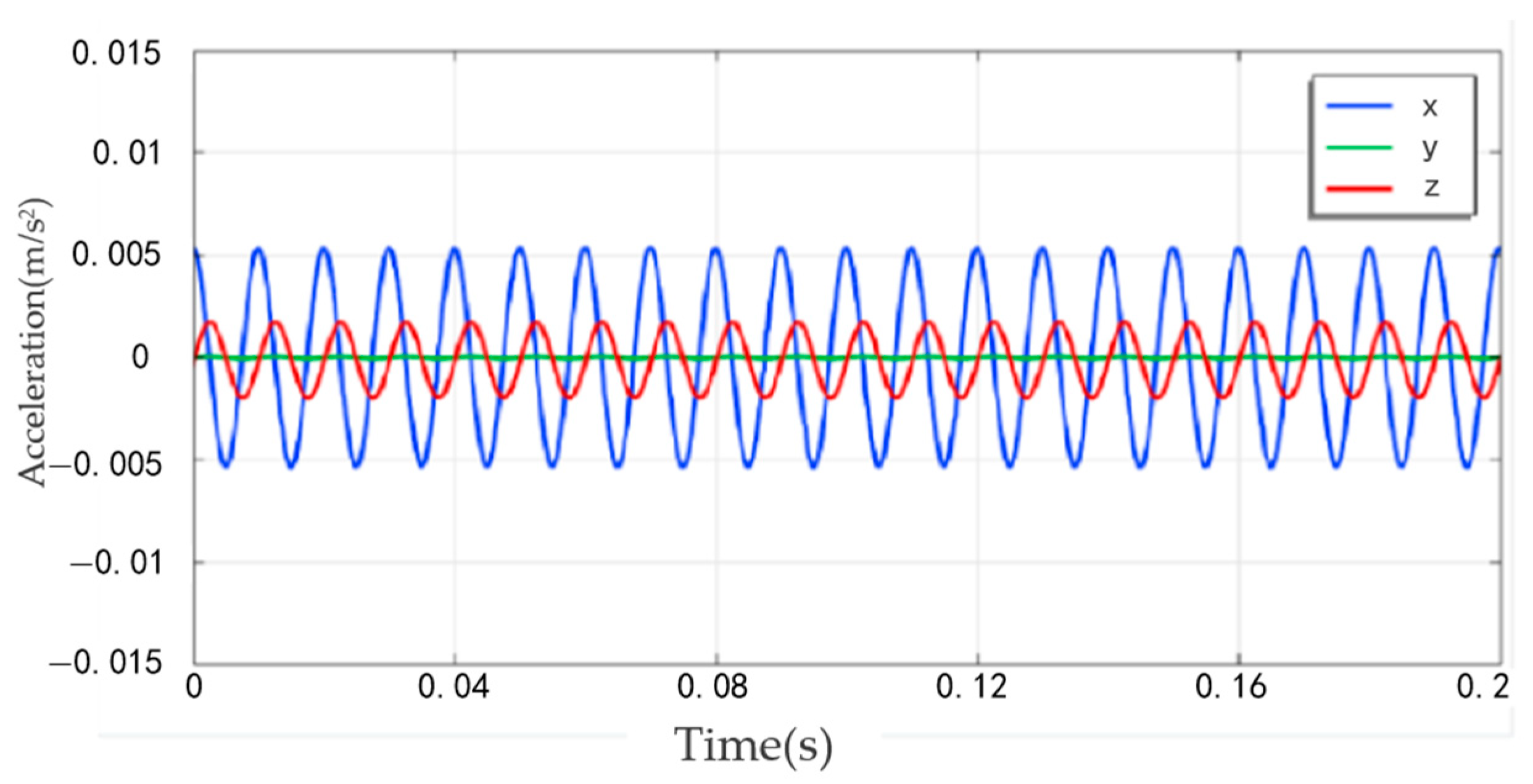






| Advantages | Limitations |
|---|---|
| It can directly measure vibration data, and the results are intuitive and reliable. | The core is only considered in terms of magnetostrictive mechanics. |
| High fault classification accuracy rate (95%), suitable for big data scenarios. | The multi-physics coupling effect has not been integrated, and the dynamic load adaptability is limited. |
| Materials | Density (kg/m3) | Modulus of Elasticity (Pa) | Poisson’s Ratio | Electric Conductivity (MS/m) |
|---|---|---|---|---|
| 30Q120 (core) | 7850 | 200e9 | 0.27 | 0 |
| Copper (winding) | 8700 | 126e9 | 0.4 | 59 |
| Parameter | Numerical Value |
|---|---|
| Transformer type | S11-M-200/10 kV |
| Rated capacity/kVA | 200 |
| Rated voltage/kV | 10/0.4 |
| Rated current/A | 11.55/288.7 |
| Connection group label | Yyn0 |
| Short-circuit impedance/% | 3.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Zhu, Y.; Liu, G.; Cao, C. Simulation Analysis and Experiment Research of Transformer Vibration Based on Electric–Magnetic–Mechanic Coupling. Energies 2025, 18, 2238. https://doi.org/10.3390/en18092238
He L, Zhu Y, Liu G, Cao C. Simulation Analysis and Experiment Research of Transformer Vibration Based on Electric–Magnetic–Mechanic Coupling. Energies. 2025; 18(9):2238. https://doi.org/10.3390/en18092238
Chicago/Turabian StyleHe, Long, Yongming Zhu, Gang Liu, and Chen Cao. 2025. "Simulation Analysis and Experiment Research of Transformer Vibration Based on Electric–Magnetic–Mechanic Coupling" Energies 18, no. 9: 2238. https://doi.org/10.3390/en18092238
APA StyleHe, L., Zhu, Y., Liu, G., & Cao, C. (2025). Simulation Analysis and Experiment Research of Transformer Vibration Based on Electric–Magnetic–Mechanic Coupling. Energies, 18(9), 2238. https://doi.org/10.3390/en18092238





