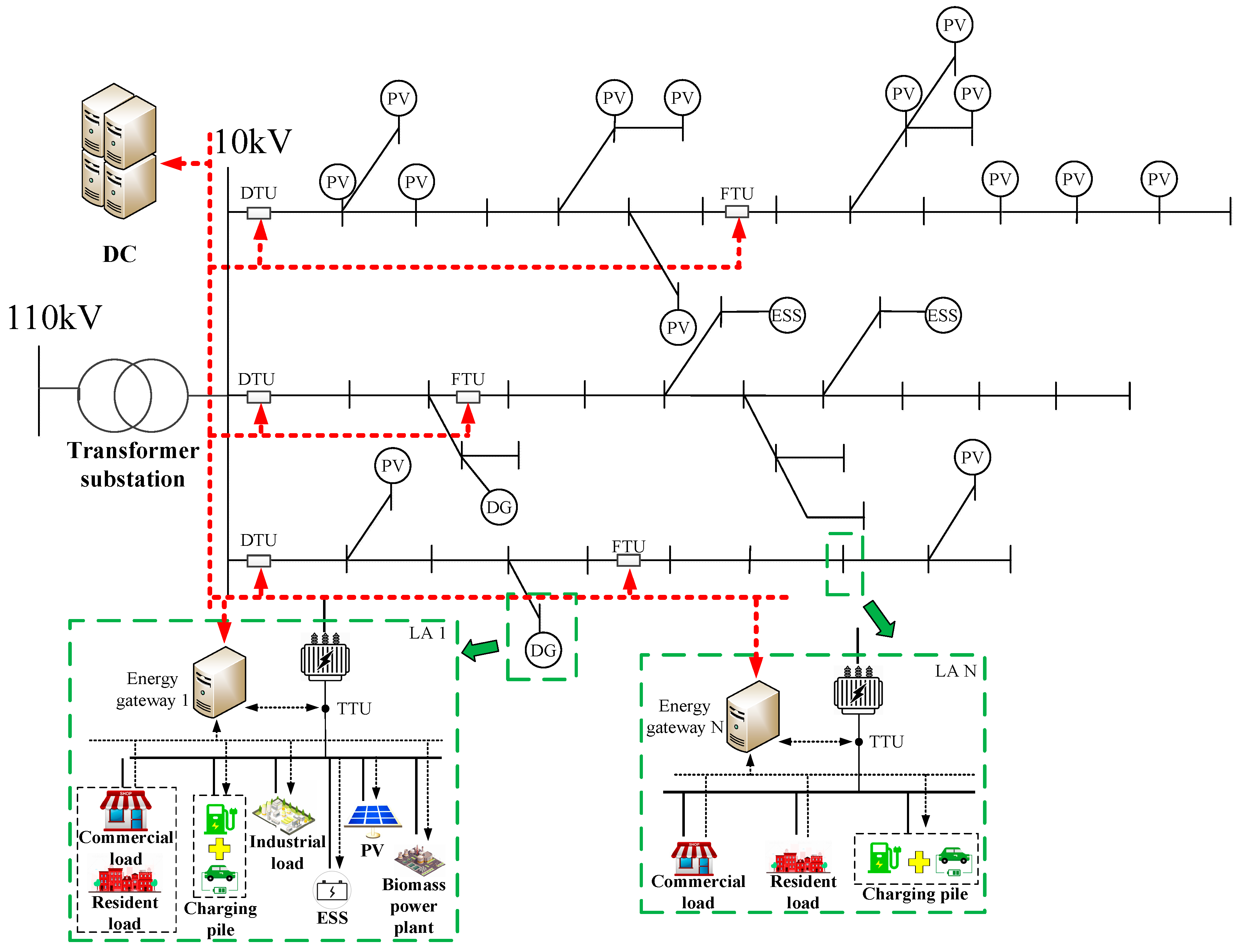
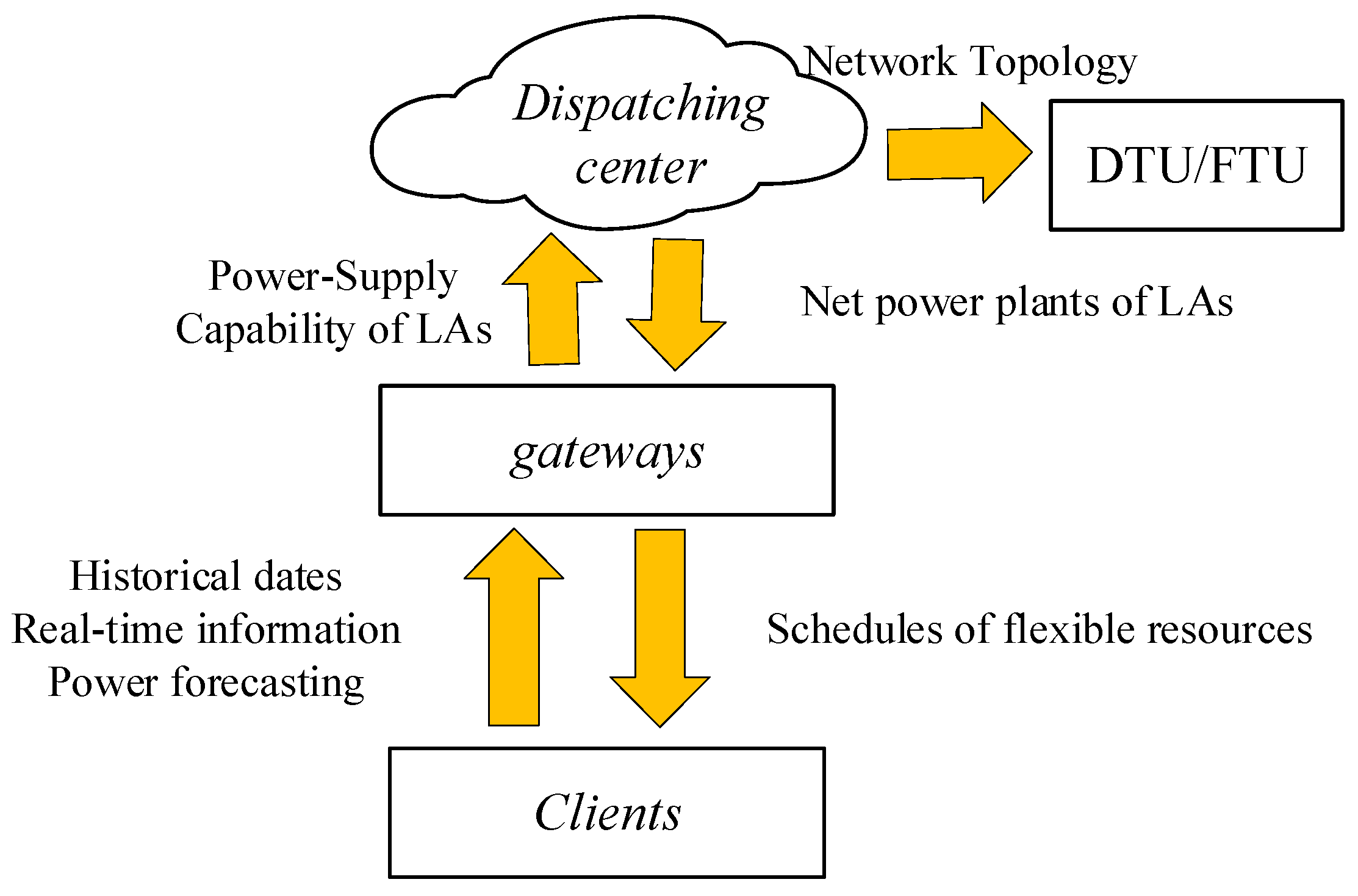
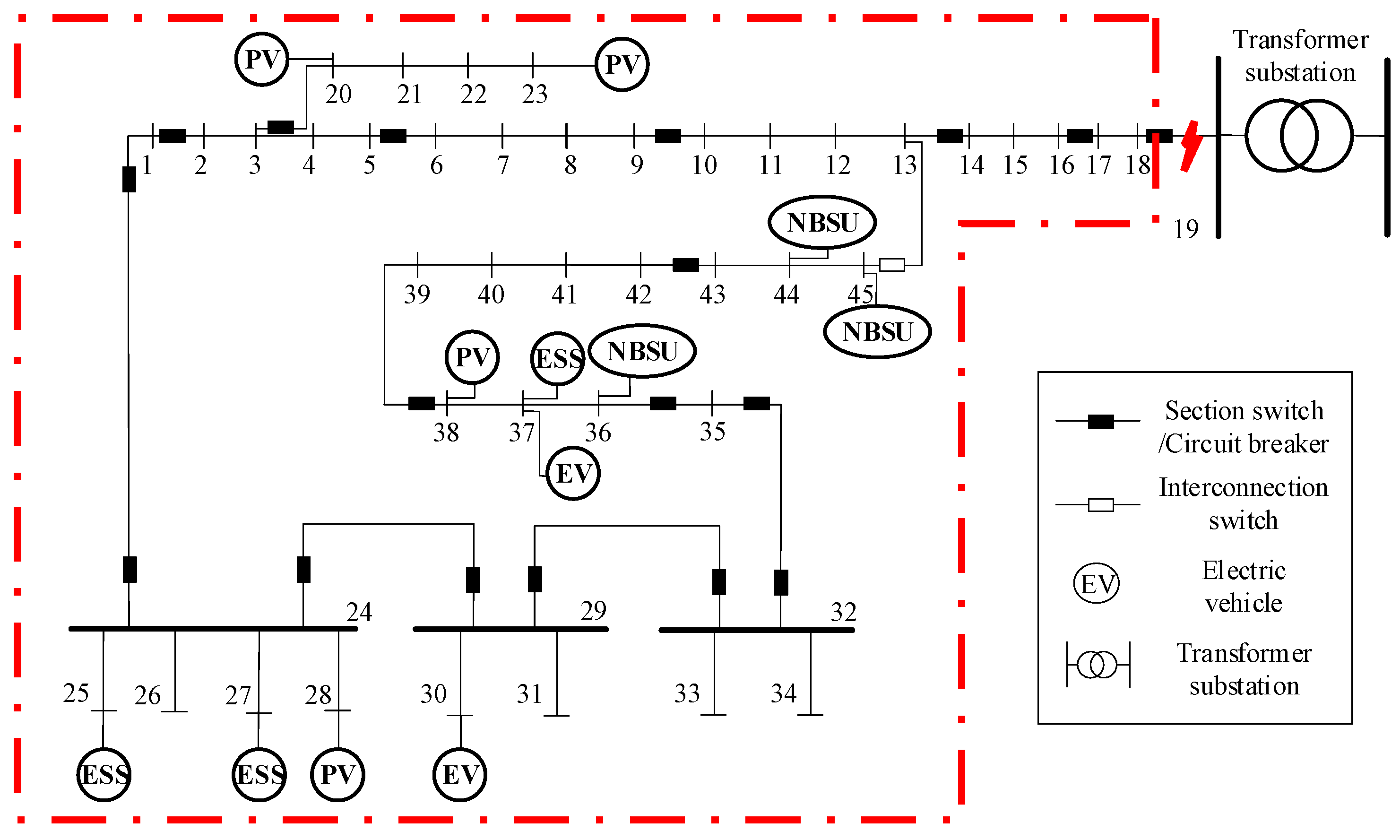
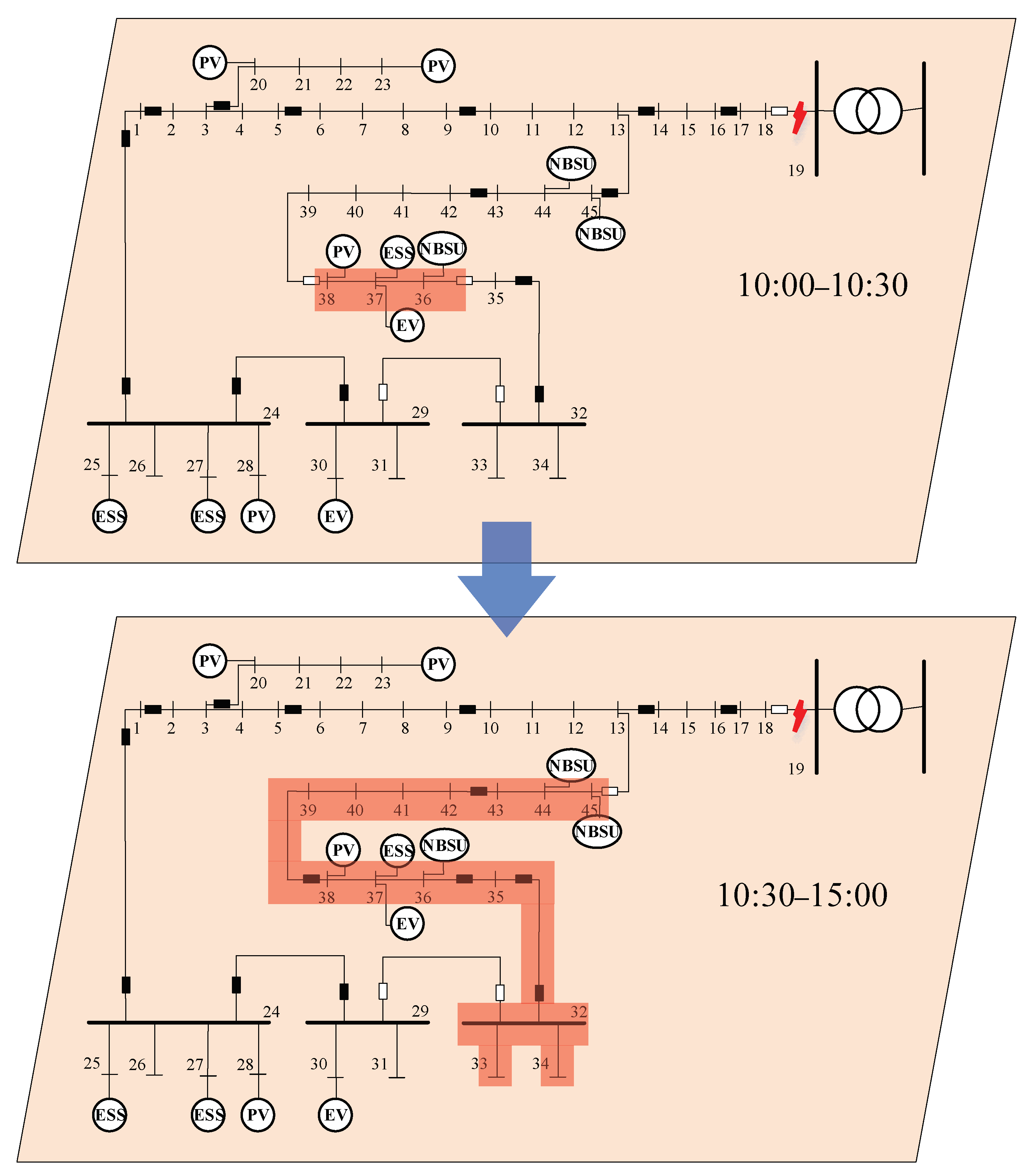
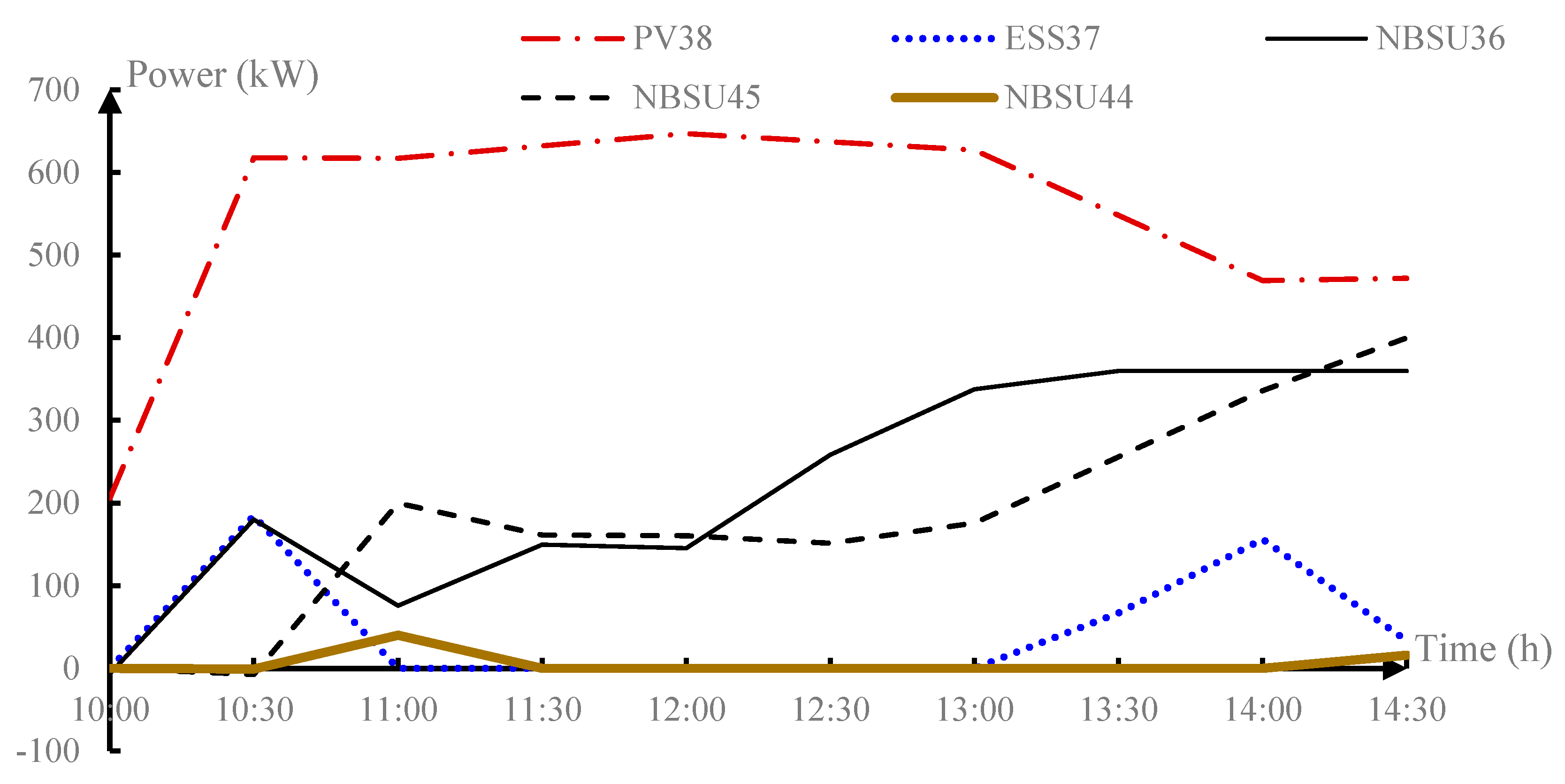
Appendix A.1. The Feasible Region of
When B = 2, the reactive power of the PV power stations is expressed as:
and
satisfy Equation (15), and given that
>
, the range of values for
derived using graphical methods is as follows:
When B > 2, the reactive power of the PV power stations is expressed as:
The condition for
is as follows:
satisfies Equation (15), and given that
>
, the range of values for
, which is equivalent to Equation (A2) in light of (5), derived using graphical methods is as follows:
Similarly, it can be derived that the ranges of values for
and
are as follows:
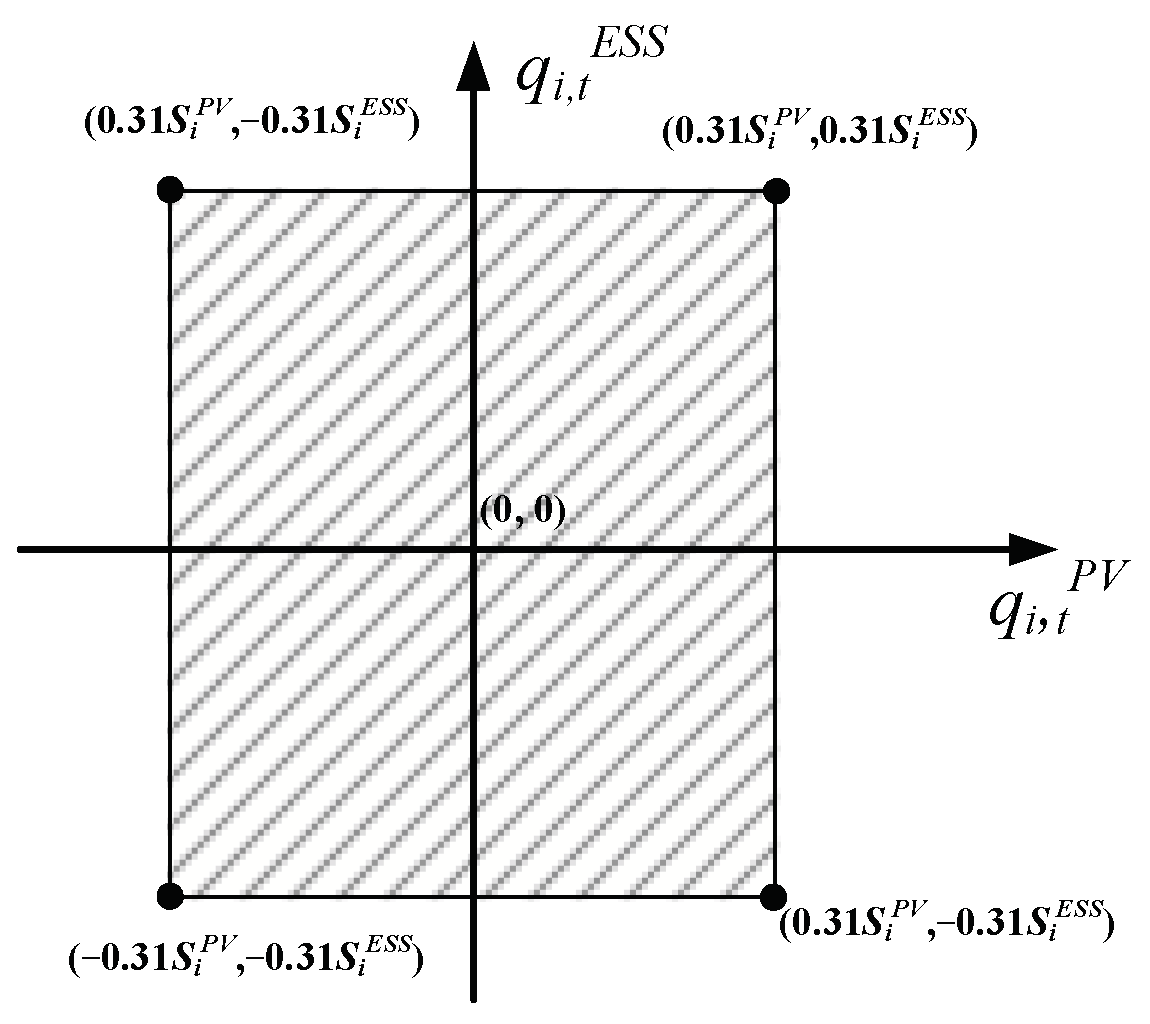
Using Equations (A5) and (A6), the feasible range of
is plotted on a Cartesian coordinate system, shown as the shaded area in
Figure A1.
Figure A1.
The feasible region of .
Figure A1.
The feasible region of .
The reactive power of PV power stations and ESSs is expressed as:
From the graphical representation in
Figure 3, the range of values for
is as follows:
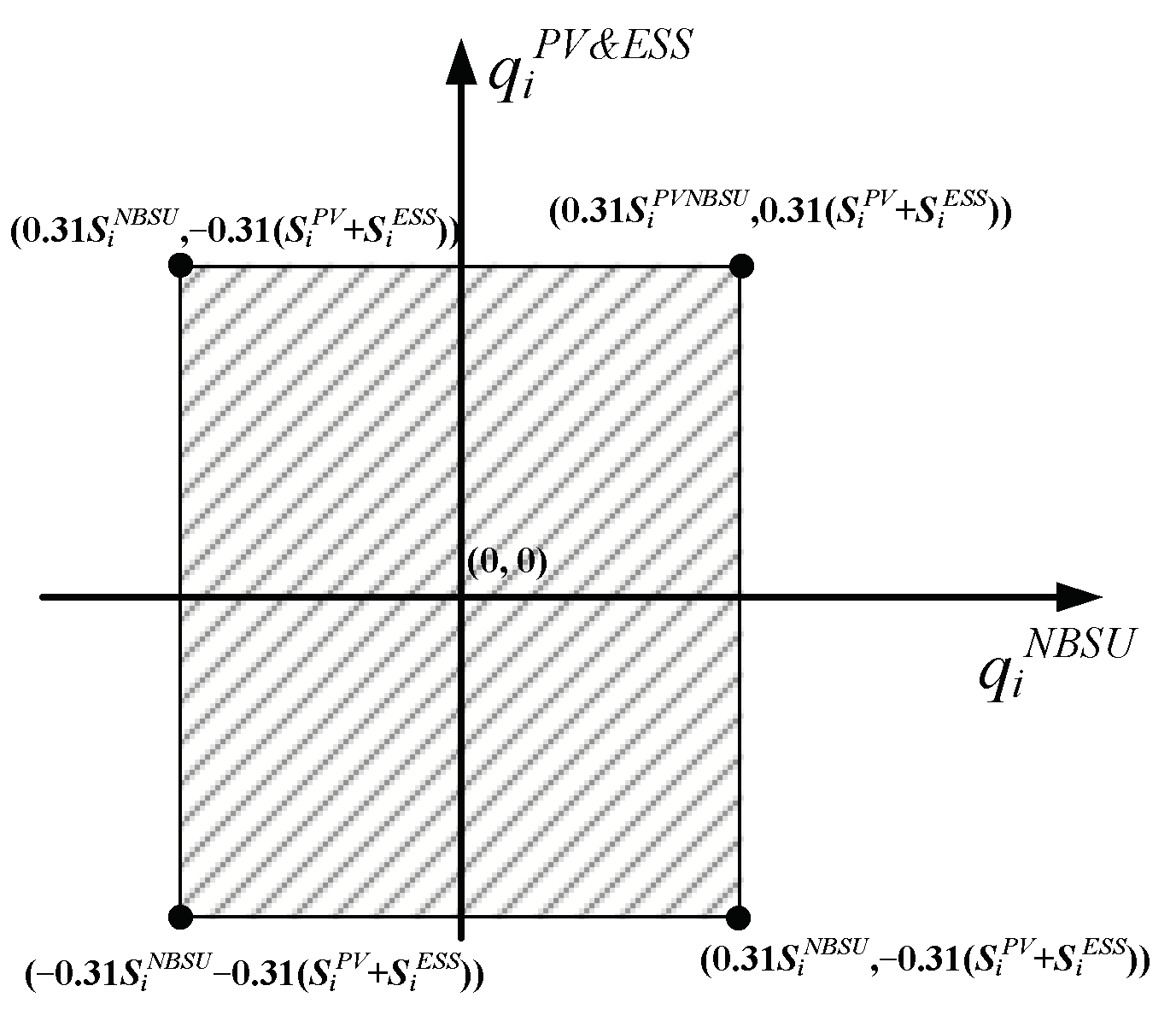
Based on Equations (A7) and (A8), the feasible region of
is plotted on a Cartesian coordinate system, as depicted by the shaded region in
Figure A2.
Figure A2.
The feasible region of .
Figure A2.
The feasible region of .
The equation for the net reactive power of LA i at time t is:
From the graphical representation in
Figure A2, the range of values for
, which is equivalent to Equation (13a), derived using graphical methods is as follows:
Appendix A.2. The Feasible Region of
When B = 2, the active power of the PV power stations is expressed as:
and
satisfy Equation (15), and given that
>
, the range of values for
derived using graphical methods is as follows:
Considering Equations (2) and (5), Equation (A13) is equivalent to Equation (13c).
When B > 2, the active power of the PV power stations is expressed as:
The condition for
is as follows:
When
satisfies Equation (15), and given that
>
, the range of values for
, which is equivalent to Equation (13c) in light of Equations (2) and (5), derived using graphical methods is as follows:
When C = 2, the active power of the ESSs is expressed as:
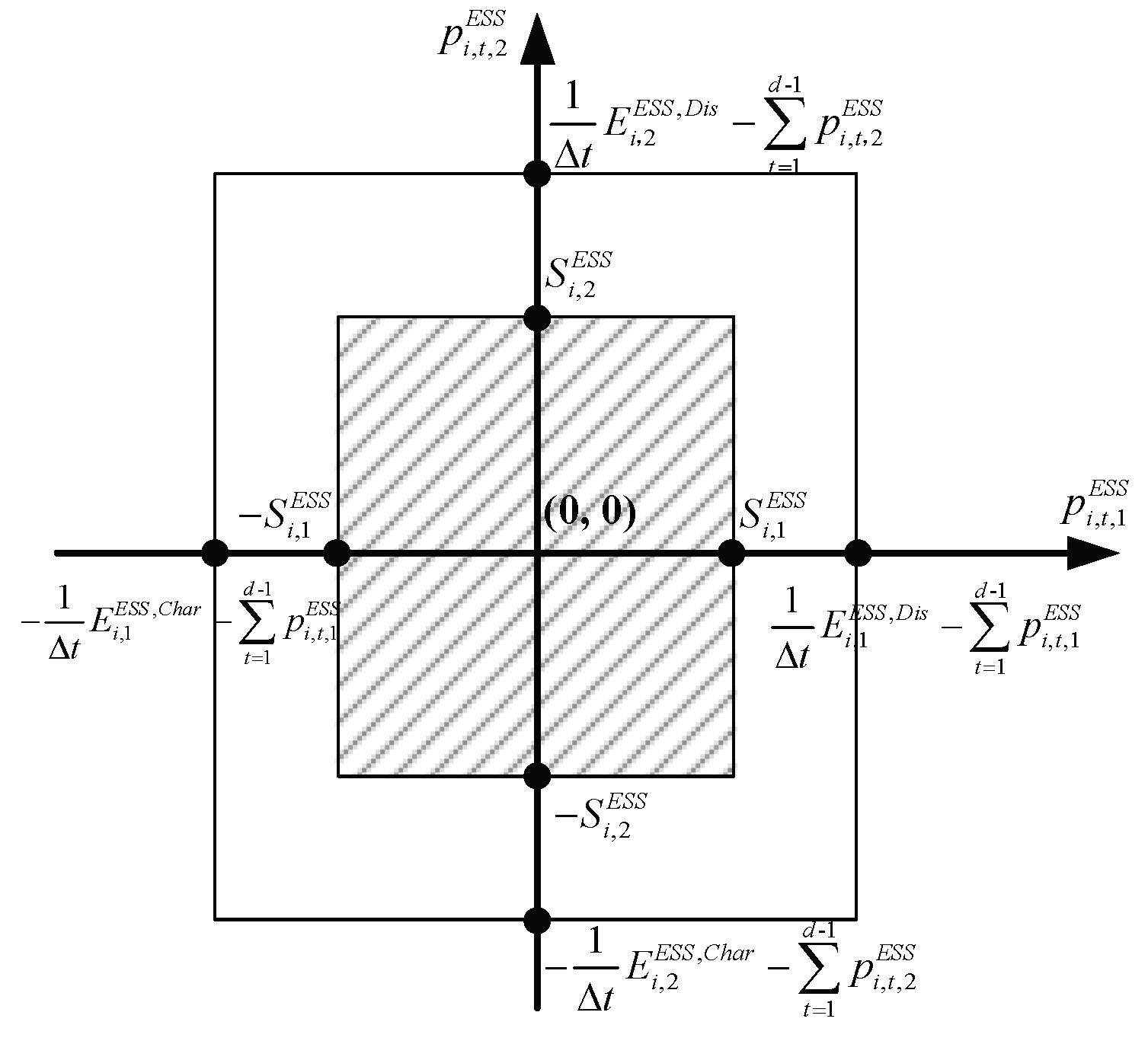
Using Equation (16), the feasible region of (
,
) is plotted on a Cartesian coordinate system, shown as the shaded area in
Figure A3. As t increases,
and
may decrease to values falling within the range of
, while
and
may be reduced to values within the range of
.
Figure A3.
The feasible region of .
Figure A3.
The feasible region of .
Based on the graphical representation in
Figure A1, the range of values for
derived using graphical methods is as follows:
where
,
,
, and
.
When we linearize Equation (A18), we obtain:
Considering Equations (3), (4) and (8), Equations (A19) and (A20) are equivalent to Equations (13d) and (13e). After linearization in Equations (A19) and (A20), the ESSs’ power capacities decrease, but their overall energy capacity remains unaffected.
When C > 2, the active power of the ESSs is expressed as:
Similarly, it can be derived that the range of values for
is as follows:
where
,
,
, and
.
When we linearize Equation (A22), we obtain:
Considering Equations (3), (4) and (8), Equations (A23) and (A24) are equivalent to Equations (13d) and (1e). After linearization in Equations (A23) and (A24), the ESSs’ power capacities decrease, but their overall energy capacity remains unaffected.
When E = 2, the active power of the ESSs is expressed as:
NBSUs start operating and producing energy simultaneously, maintaining
and
for dimensionality reduction. For various values of
and
, the range of
is presented in
Table A1 and
Table A2.
Table A1.
Upper limit change table for (E = 2).
Table A1.
Upper limit change table for (E = 2).
| | | |
|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | | |
| 1 | 1 | | |
Table A2.
Lower limit change table for (E = 2).
Table A2.
Lower limit change table for (E = 2).
| | | |
|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | | |
| 1 | 1 | | |
The range of values for variable
based on Equations (9)–(12) and
Table A1 and
Table A2 are defined as follows:
Equation (A26) is equal to Equation (13i), and Equation (A27) is equal to Equation (13j).
When E > 2, the active power of the ESSs is expressed as:
The NBSUs start operating and producing energy simultaneously, maintaining
and
for dimensionality reduction. For various values of
and
, the range of
is presented in
Table A3 and
Table A4.
Table A3.
Upper limit change table for (E > 2).
Table A3.
Upper limit change table for (E > 2).
| | | |
|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | | |
| 1 | 1 | | |
Table A4.
Lower limit change table for (E > 2).
Table A4.
Lower limit change table for (E > 2).
| | | |
|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | | |
| 1 | 1 | | |
Here, , , and .
The range of values for variable
based on Equations (9)–(12) and
Table A3 and
Table A4 are defined as follows:
Equation (A29) is equal to Equation (13i), and Equation (A30) is equal to Equation (13j).
In summary, Equation (13) is a sufficient condition for the set of Equations (14)~(17), which means and ensuring that all PSC-based net power plans are feasible for DG within LAs.