Energy Management Strategy for Fuel Cell Vehicles Based on Deep Transfer Reinforcement Learning
Abstract
1. Introduction
- Most studies that apply TL focus on the improvement in convergence speed it brings, while overlooking the optimization of energy distribution performance.
- Research on TL is not sufficiently in-depth. Because of differences between the source task and the target task, TL may introduce certain negative effects. How to avoid these issues and use TL appropriately is still an open problem.
- Combination of prioritized experience replay (PER) with the traditional DDPG algorithm to form the PER–DDPG algorithm, which is used for training EMS of fuel cell vehicles.
- Integration of DRL with TL by transferring the experience data saved from the source task when training the target task, aiming to accelerate model convergence and enhance the EMS’s energy distribution performance.
- Employment of two different strategies for comparison to explore more appropriate TL methods: transfer all parameters of the neural network or transfer only part of the neural network parameters.
2. Collection and Modeling for Fuel Cell Vehicles
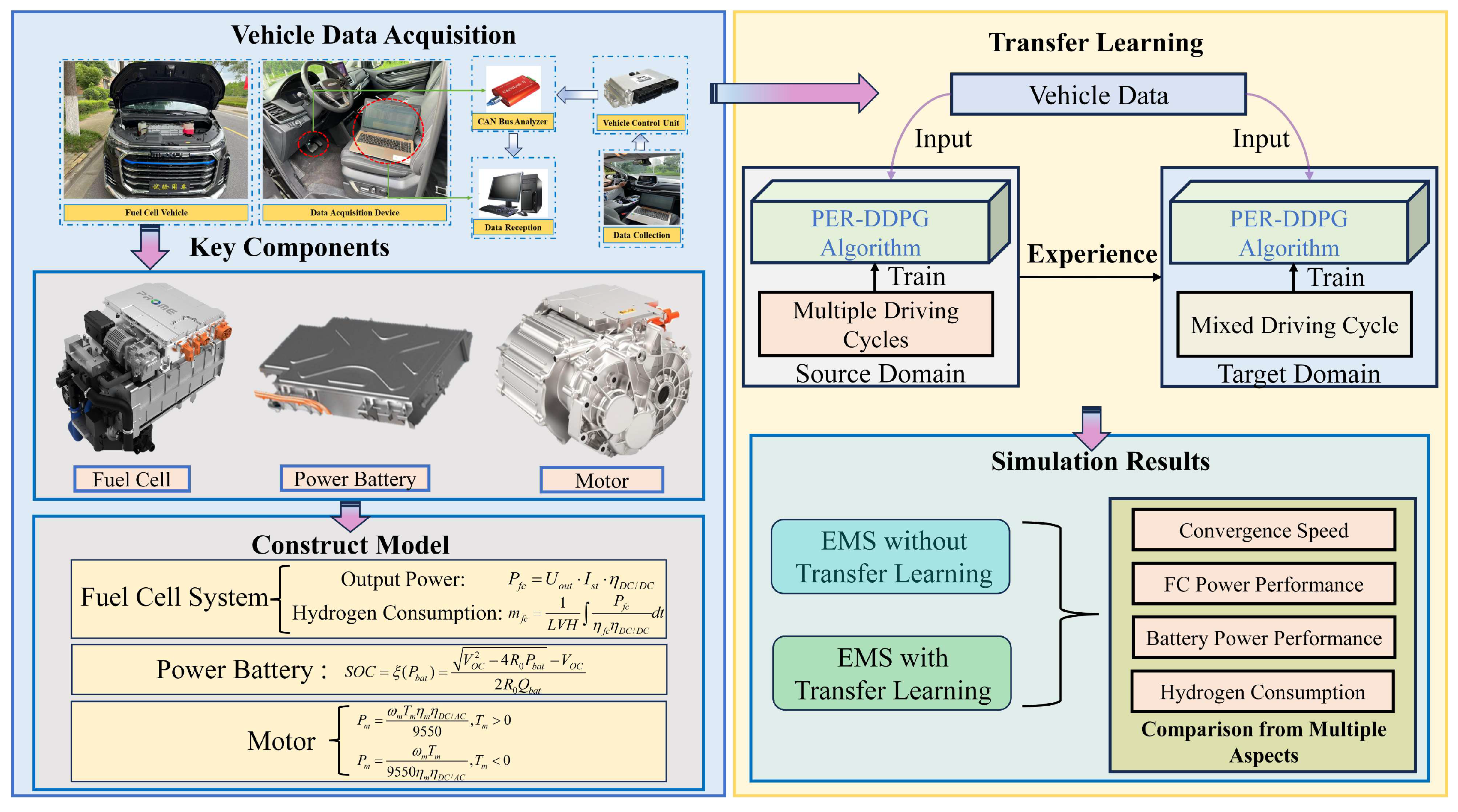
2.1. Data Collection
2.2. Fuel Cell Vehicle Structure
- Pure electric mode.
- Pure fuel cell mode.
- Hybrid mode.
- Regenerative braking mode.
2.3. Power System Model
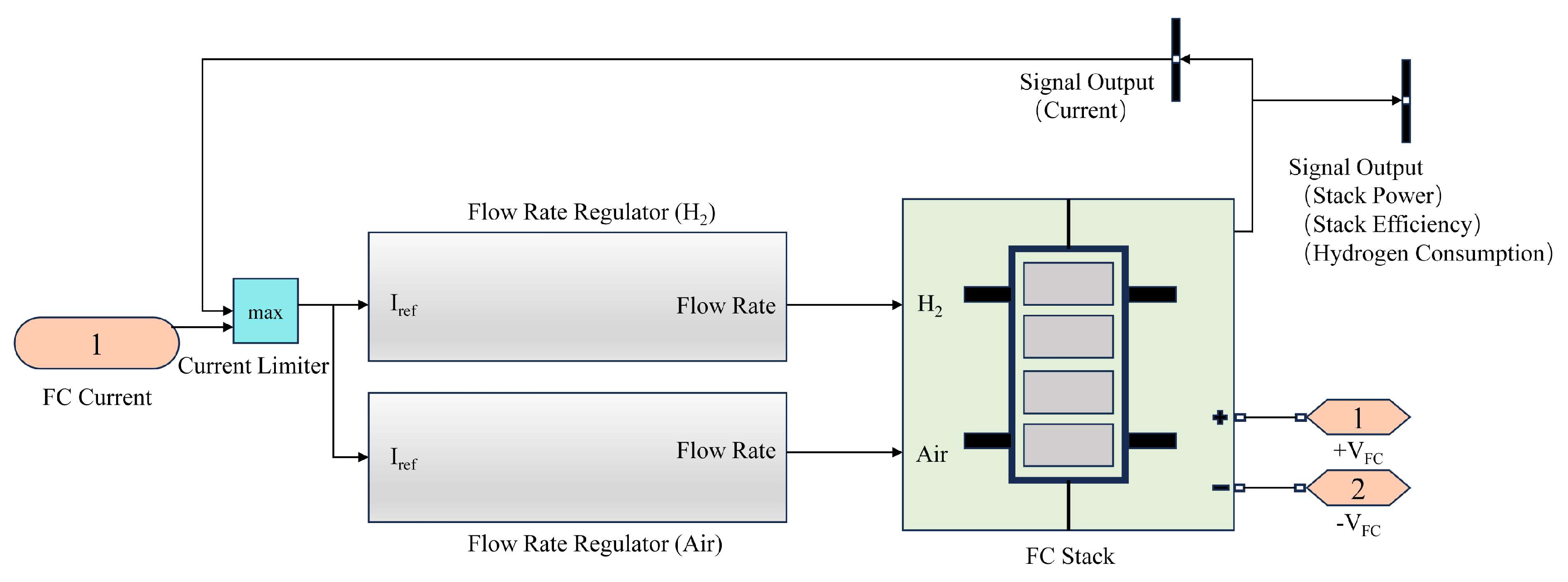
2.3.1. Fuel Cell Model
2.3.2. Traction Battery Model
2.3.3. Motor Model
3. Energy Management Strategies Based on PER–DDPG and Transfer Learning
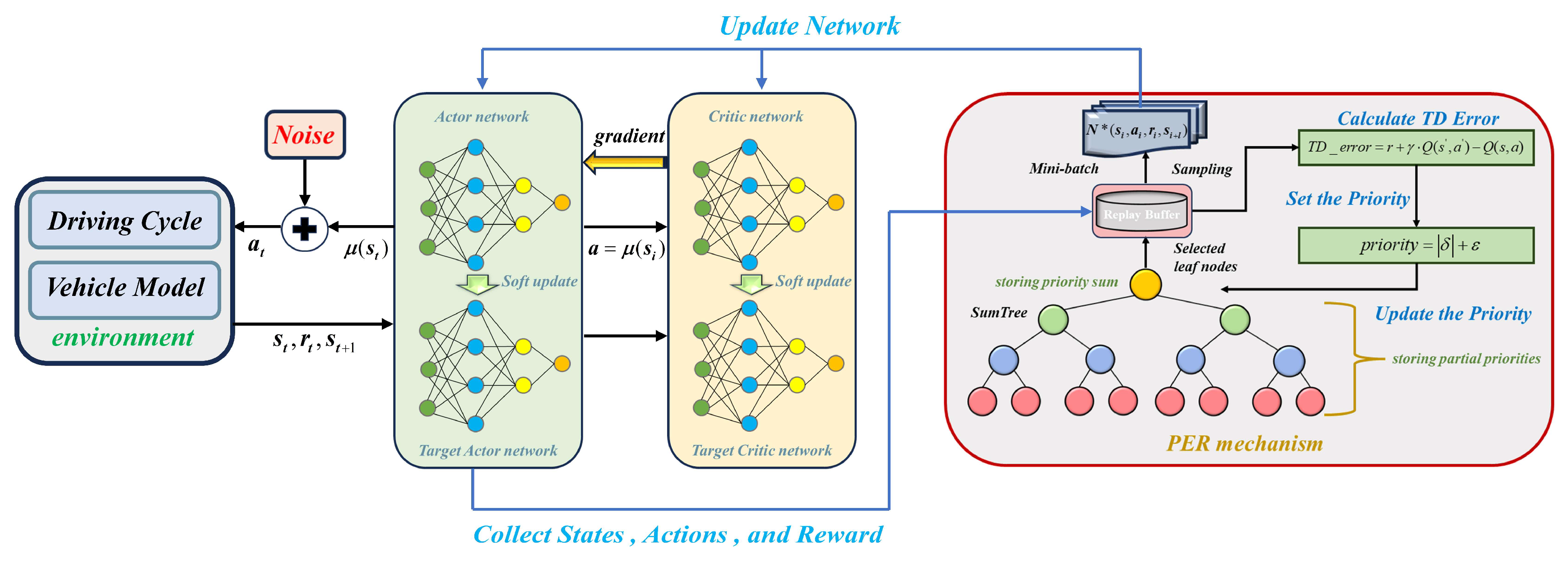
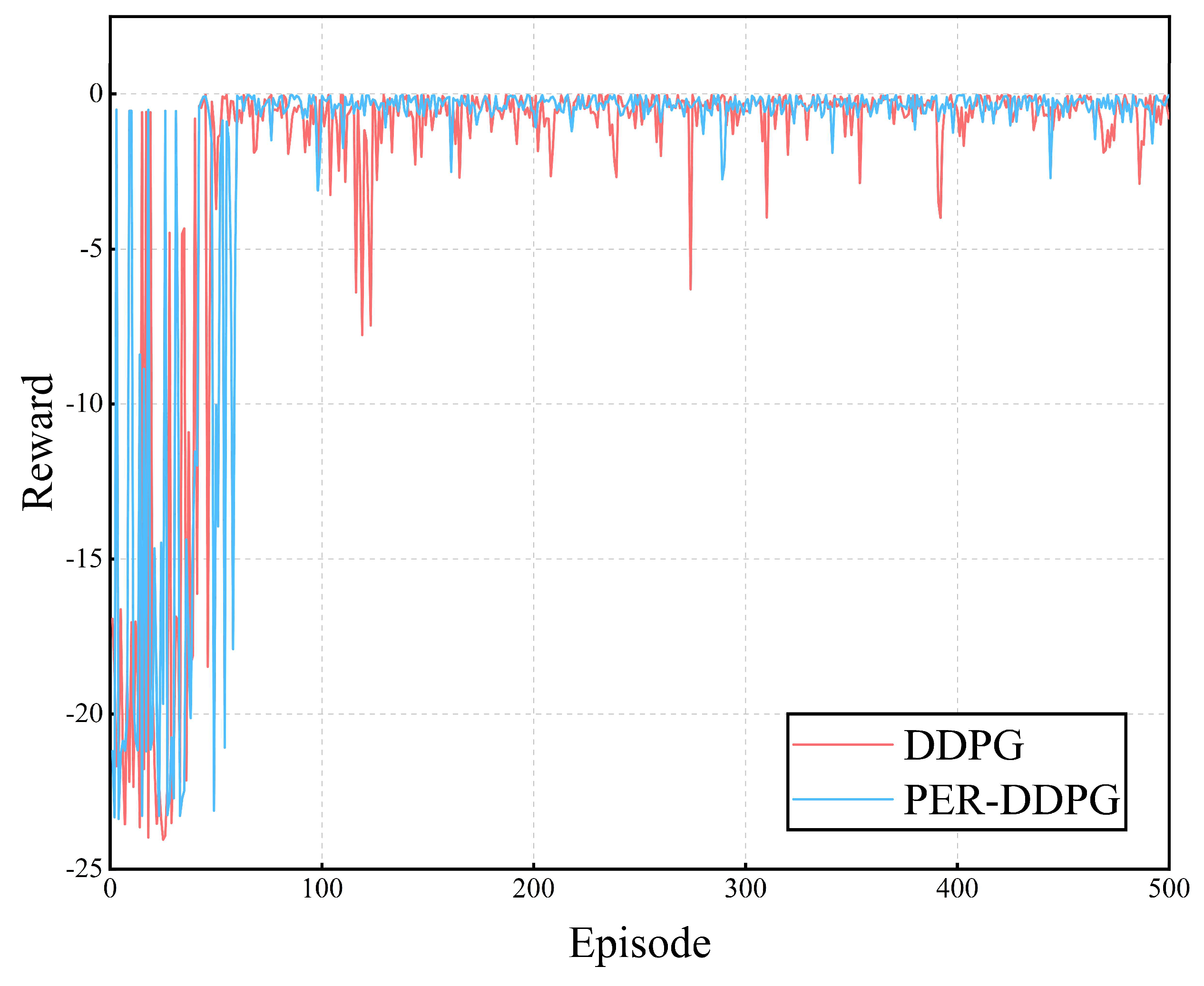
3.1. The PER–DDPG Algorithm
3.2. Algorithm Setting
3.3. Transfer Learning
4. Results and Discussion
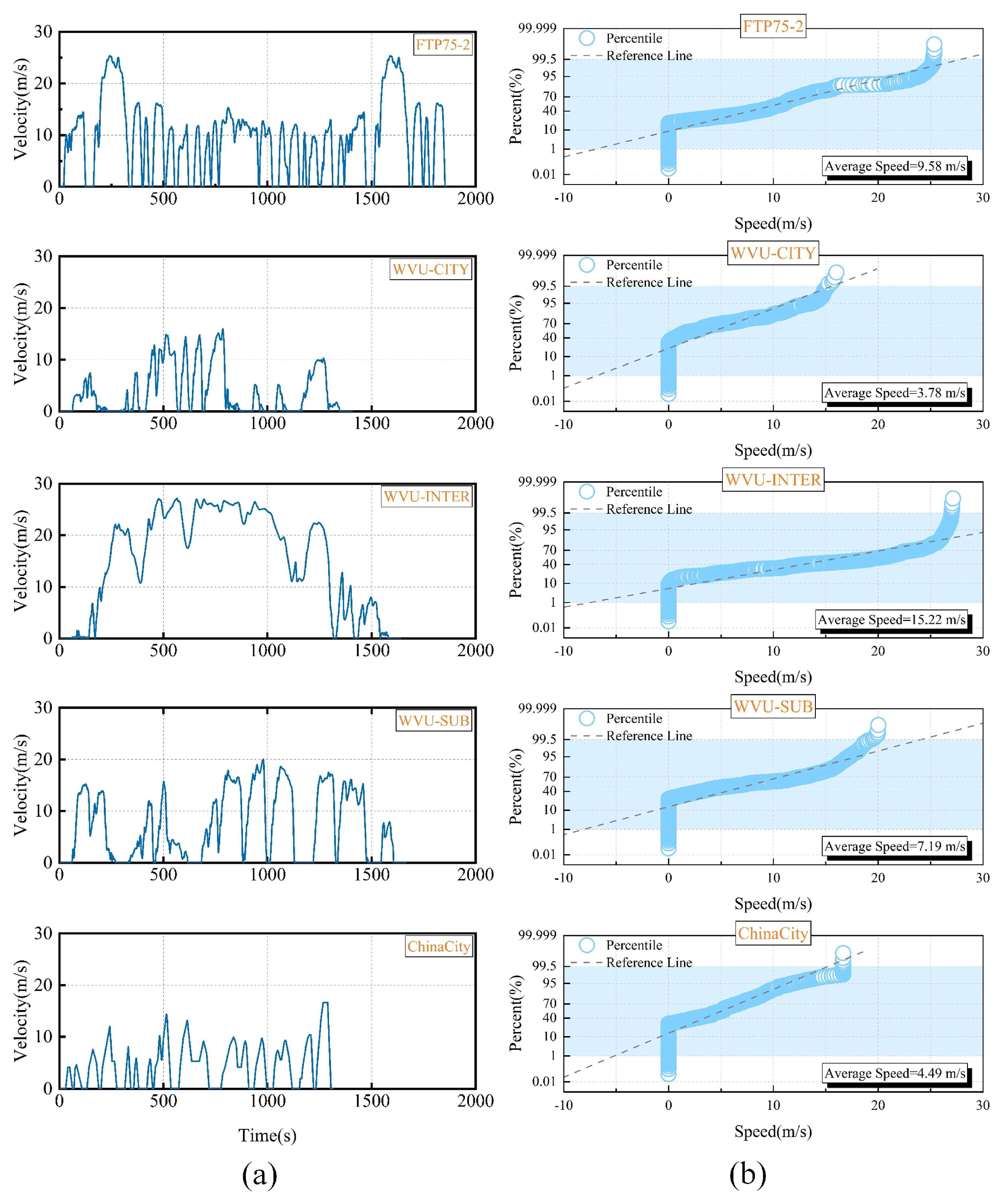
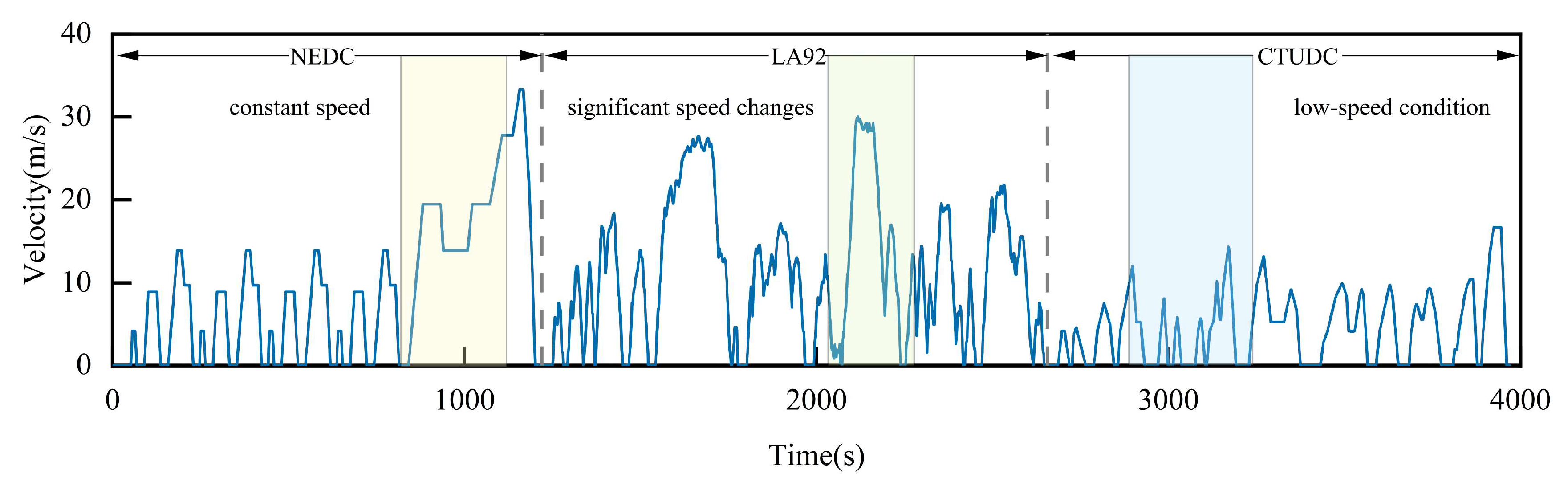
4.1. Driving Cycles
4.2. Training Conditions of the Source Domain
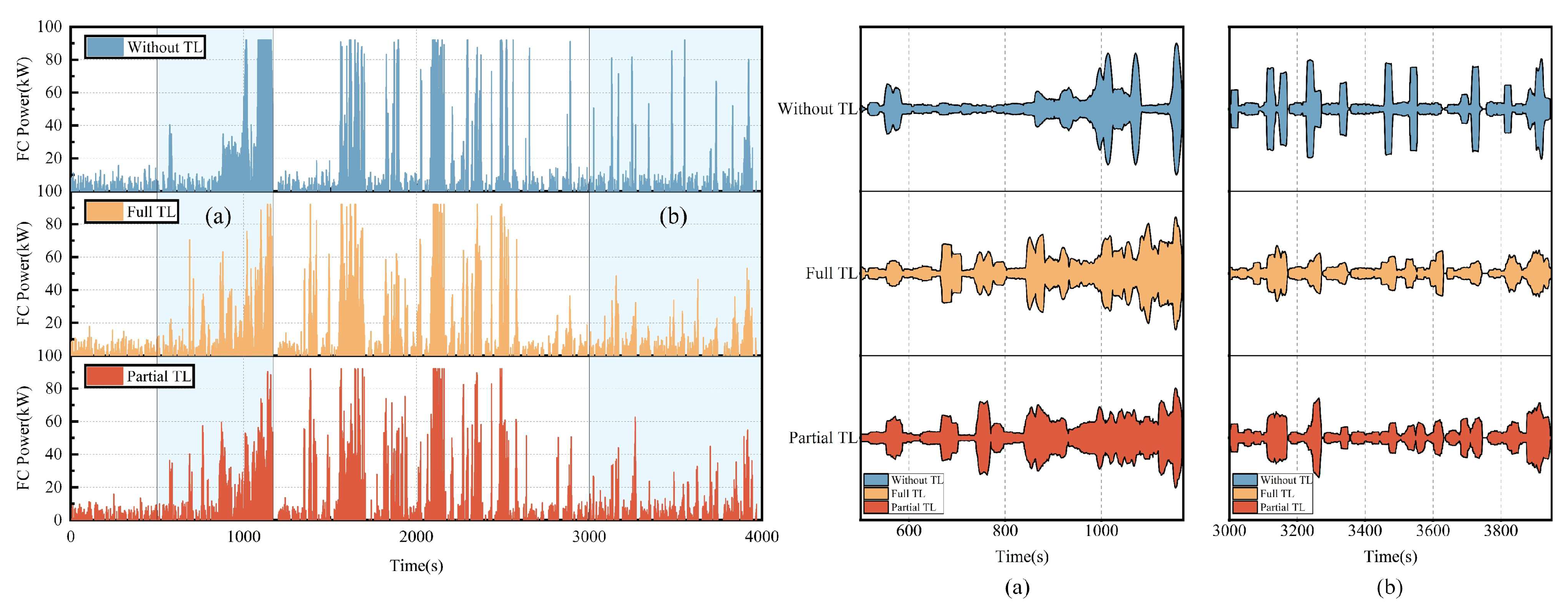
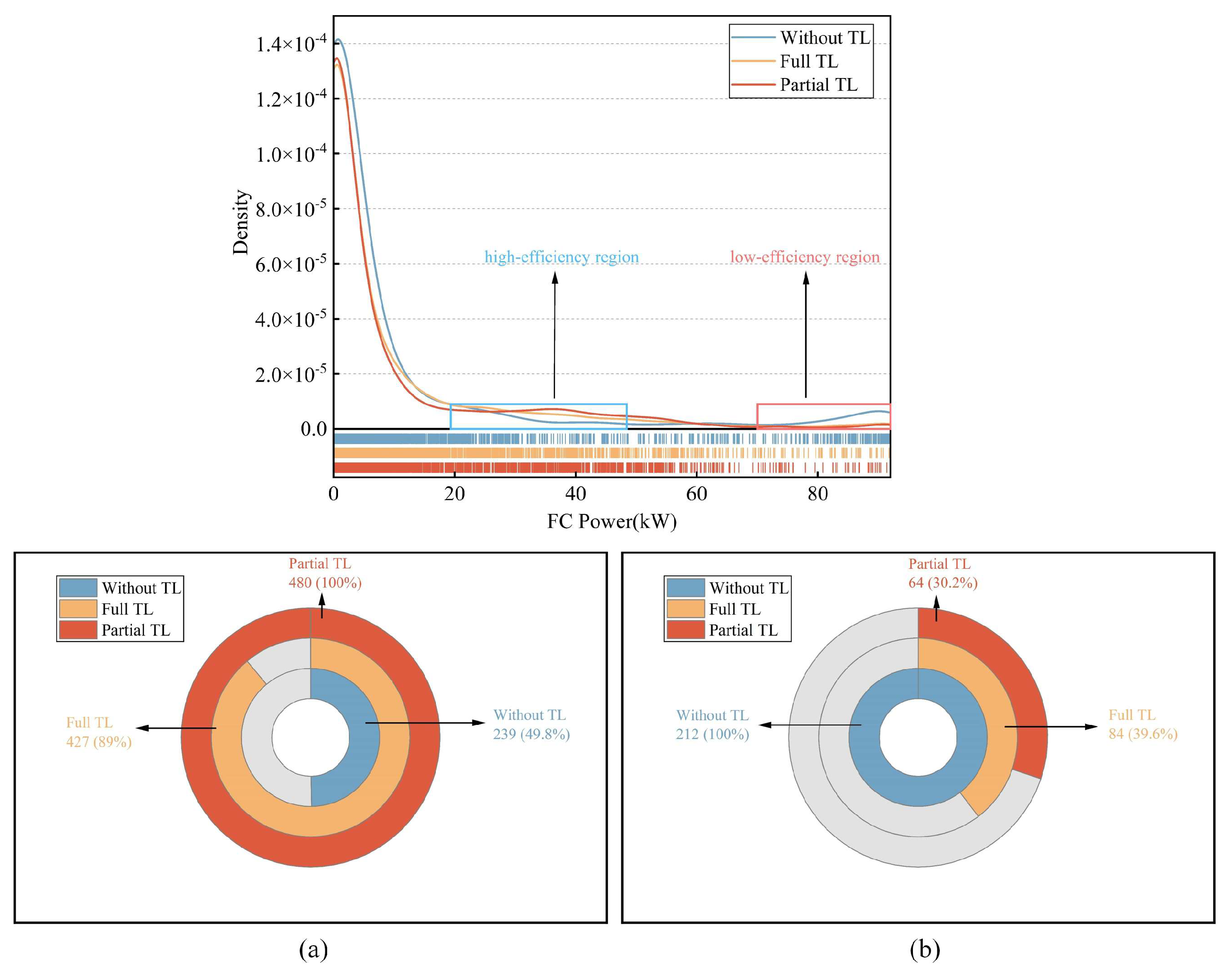
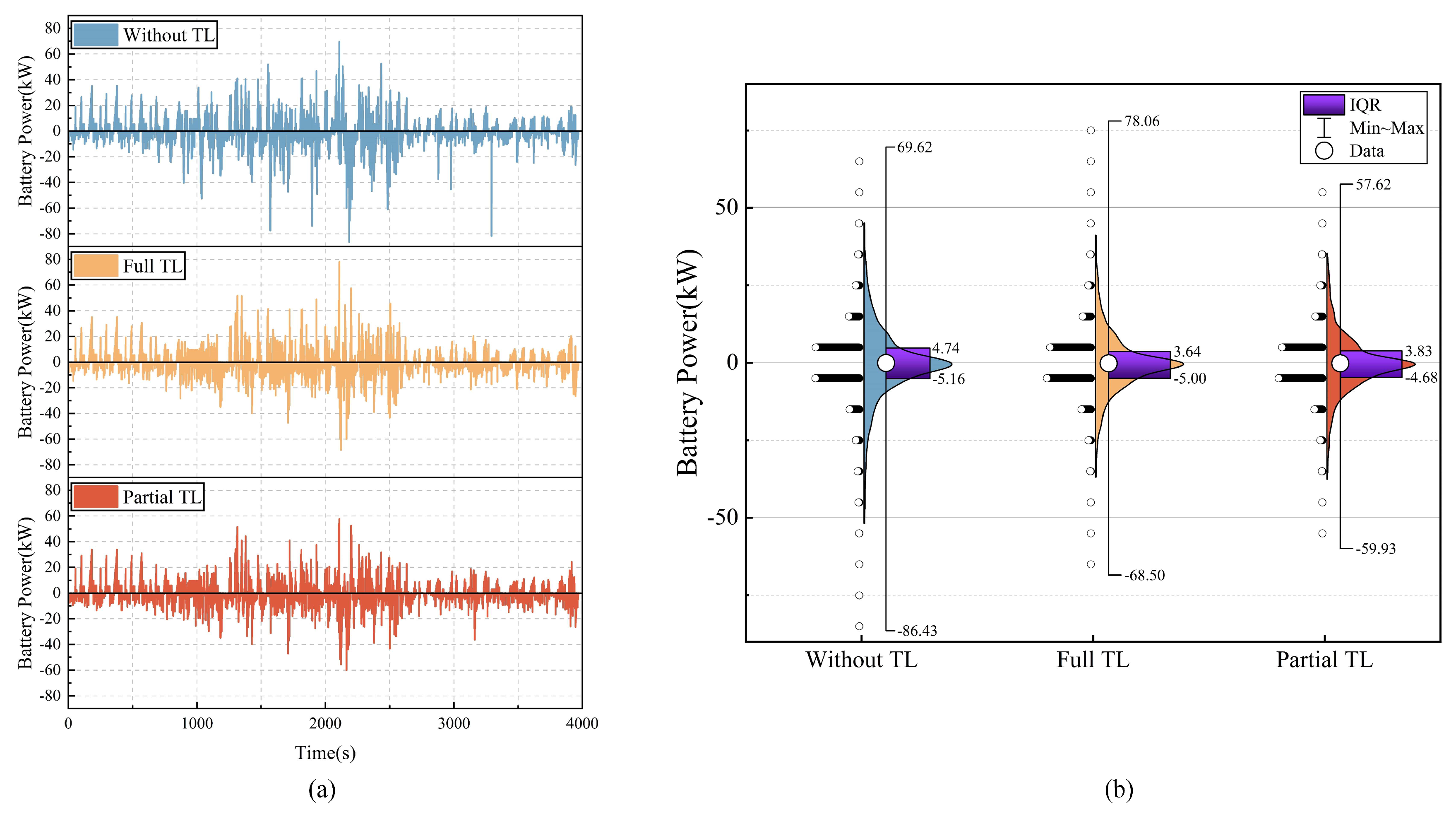
4.3. Power Distribution of Energy Sources in the Target Domain
4.4. SOC Maintenance Performance in the Target Domain
4.5. Model Training Efficiency and Hydrogen Consumption in the Target Domain
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pramuanjaroenkij, A.; Kakac, S. The fuel cell electric vehicles: The highlight review. Int. J. Hydrogen Energy 2023, 48, 9401–9425. [Google Scholar] [CrossRef]
- Song, H.; Liu, C.; Moradi Amani, A.; Gu, M.; Jalili, M.; Meegahapola, L.; Yu, X.; Dickeson, G. Smart optimization in battery energy storage systems: An overview. Energy AI 2024, 17, 100378. [Google Scholar] [CrossRef]
- Li, X.; Ye, T.; Meng, X.; He, D.; Li, L.; Song, K.; Jiang, J.; Sun, C. Advances in the Application of Sulfonated Poly(Ether Ether Ketone) (SPEEK) and Its Organic Composite Membranes for Proton Exchange Membrane Fuel Cells (PEMFCs). Polymers 2024, 16, 2840. [Google Scholar] [CrossRef] [PubMed]
- Deng, K.; Liu, Y.; Hai, D.; Peng, H.; Löwenstein, L.; Pischinger, S.; Hameyer, K. Deep reinforcement learning based energy management strategy of fuel cell hybrid railway vehicles considering fuel cell aging. Energy Convers. Manag. 2022, 251, 115030. [Google Scholar] [CrossRef]
- Luca, R.; Whiteley, M.; Neville, T.; Shearing, P.R.; Brett, D.J.L. Comparative study of energy management systems for a hybrid fuel cell electric vehicle- A novel mutative fuzzy logic controller to prolong fuel cell lifetime. Int. J. Hydrogen Energy 2022, 47, 24042–24058. [Google Scholar] [CrossRef]
- Chen, B.; Ma, R.; Zhou, Y.; Ma, R.; Jiang, W.; Yang, F. Co-optimization of speed planning and cost-optimal energy management for fuel cell trucks under vehicle-following scenarios. Energy Convers. Manag. 2024, 300, 117914. [Google Scholar] [CrossRef]
- Meng, X.; Sun, C.; Mei, J.; Tang, X.; Hasanien, H.M.; Jiang, J.; Fan, F.; Song, K. Fuel cell life prediction considering the recovery phenomenon of reversible voltage loss. J. Power Sources 2025, 625, 235634. [Google Scholar] [CrossRef]
- Sun, X.; Fu, J.; Yang, H.; Xie, M.; Liu, J. An energy management strategy for plug-in hybrid electric vehicles based on deep learning and improved model predictive control. Energy 2023, 269, 126772. [Google Scholar] [CrossRef]
- Lu, D.G.; Yi, F.Y.; Hu, D.H.; Li, J.W.; Yang, Q.Q.; Wang, J. Online optimization of energy management strategy for FCV control parameters considering dual power source lifespan decay synergy. Appl. Energy 2023, 348, 121516. [Google Scholar] [CrossRef]
- Dai-Duong, T.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar]
- Hou, S.; Gao, J.; Zhang, Y.; Chen, M.; Shi, J.; Chen, H. A comparison study of battery size optimization and an energy management strategy for FCHEVs based on dynamic programming and convex programming. Int. J. Hydrogen Energy 2020, 45, 21858–21872. [Google Scholar] [CrossRef]
- Oladosu, T.L.; Pasupuleti, J.; Kiong, T.S.; Koh, S.P.J.; Yusaf, T. Energy management strategies, control systems, and artificial intelligence-based algorithms development for hydrogen fuel cell-powered vehicles: A review. Int. J. Hydrogen Energy 2024, 61, 1380–1404. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Yuan, P.; Tian, H.; Shu, G. Optimizing hybrid electric vehicle coupling organic Rankine cycle energy management strategy via deep reinforcement learning. Energy AI 2024, 17, 100392. [Google Scholar] [CrossRef]
- Jia, C.C.; Zhou, J.M.; He, H.W.; Li, J.W.; Wei, Z.B.; Li, K.A. Health-conscious deep reinforcement learning energy management for fuel cell buses integrating environmental and look-ahead road information. Energy 2024, 290, 130146. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K.; Li, M. A novel deep reinforcement learning-based predictive energy management for fuel cell buses integrating speed and passenger prediction. Int. J. Hydrogen Energy 2025, 100, 456–465. [Google Scholar] [CrossRef]
- Lee, W.; Jeoung, H.; Park, D.; Kim, T.; Lee, H.; Kim, N. A Real-Time Intelligent Energy Management Strategy for Hybrid Electric Vehicles Using Reinforcement Learning. IEEE Access 2021, 9, 72759–72768. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Wu, J.; Peng, J.; Li, Y. Energy management based on reinforcement learning with double deep Q-learning for a hybrid electric tracked vehicle. Appl. Energy 2019, 254, 113708. [Google Scholar] [CrossRef]
- Du, G.; Zou, Y.; Zhang, X.; Guo, L.; Guo, N. Energy management for a hybrid electric vehicle based on prioritized deep reinforcement learning framework. Energy 2022, 241, 122523. [Google Scholar] [CrossRef]
- Zhang, J.; Jiao, X.; Yang, C. A Double-Deep Q-Network-Based Energy Management Strategy for Hybrid Electric Vehicles under Variable Driving Cycles. Energy Technol. 2021, 9, 2000770. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, H.; Peng, J.; Jiang, Z.; Wu, Y. Energy management of hybrid electric bus based on deep reinforcement learning in continuous state and action space. Energy Convers. Manag. 2019, 195, 548–560. [Google Scholar] [CrossRef]
- Hu, B.; Li, J. A Deployment-Efficient Energy Management Strategy for Connected Hybrid Electric Vehicle Based on Offline Reinforcement Learning. IEEE Trans. Ind. Electron. 2022, 69, 9644–9654. [Google Scholar] [CrossRef]
- Wu, J.D.; Wei, Z.B.; Li, W.H.; Wang, Y.; Li, Y.W.; Sauer, D.U. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus Based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 3751–3761. [Google Scholar] [CrossRef]
- Liu, R.; Wang, C.; Tang, A.H.; Zhang, Y.Z.; Yu, Q.Q. A twin delayed deep deterministic policy gradient-based energy management strategy for a battery-ultracapacitor electric vehicle considering driving condition recognition with learning vector quantization neural network. J. Energy Storage 2023, 71, 108147. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, H.; Jiang, Z.; Zheng, X.; Zhang, J.; Fan, W.; Deng, K.; Xu, K. Supplementary Learning Control for Energy Management Strategy of Hybrid Electric Vehicles at Scale. IEEE Trans. Veh. Technol. 2023, 72, 7290–7303. [Google Scholar] [CrossRef]
- Wu, C.C.; Ruan, J.G.; Cui, H.H.; Zhang, B.; Li, T.Y.; Zhang, K.X. The application of machine learning based energy management strategy in multi-mode plug-in hybrid electric vehicle, part I: Twin Delayed Deep Deterministic Policy Gradient algorithm design for hybrid mode. Energy 2023, 262, 125084. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Yan, M.; Wu, J.; Jin, L.; He, H. Data-driven bi-level predictive energy management strategy for fuel cell buses with algorithmics fusion. Energy Convers. Manag. X 2023, 20, 100414. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, J.; Xue, Y.; Liao, Y. Total travel costs minimization strategy of a dual-stack fuel cell logistics truck enhanced with artificial potential field and deep reinforcement learning. Energy 2022, 239, 121866. [Google Scholar] [CrossRef]
- Lee, H.; Song, C.; Kim, N.; Cha, S.W. Comparative Analysis of Energy Management Strategies for HEV: Dynamic Programming and Reinforcement Learning. IEEE Access 2020, 8, 67112–67123. [Google Scholar] [CrossRef]
- Wang, K.; Yang, R.; Zhou, Y.; Huang, W.; Zhang, S. Design and Improvement of SD3-Based Energy Management Strategy for a Hybrid Electric Urban Bus. Energies 2022, 15, 5878. [Google Scholar] [CrossRef]
- Lian, R.; Tan, H.; Peng, J.; Li, Q.; Wu, Y. Cross-Type Transfer for Deep Reinforcement Learning Based Hybrid Electric Vehicle Energy Management. IEEE Trans. Veh. Technol. 2020, 69, 8367–8380. [Google Scholar] [CrossRef]
- Lu, D.; Hu, D.; Wang, J.; Wei, W.; Zhang, X. A data-driven vehicle speed prediction transfer learning method with improved adaptability across working conditions for intelligent fuel cell vehicle. IEEE Trans. Intell. Transp. Syst. 2025; Early Access. [Google Scholar]
- Jouda, B.; Al-Mahasneh, A.J.; Abu Mallouh, M. Deep stochastic reinforcement learning-based energy management strategy for fuel cell hybrid electric vehicles. Energy Convers. Manag. 2024, 301, 117973. [Google Scholar] [CrossRef]
- Yan, M.; Li, G.; Li, M.; He, H.; Xu, H.; Liu, H. Hierarchical predictive energy management of fuel cell buses with launch control integrating traffic information. Energy Convers. Manag. 2022, 256, 115397. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K.; Shi, M. A novel energy management strategy for hybrid electric bus with fuel cell health and battery thermal- and health-constrained awareness. Energy 2023, 271, 127105. [Google Scholar] [CrossRef]
- Hu, D.; Wang, Y.; Li, J. Energy saving control of waste heat utilization subsystem for fuel cell vehicle. IEEE Trans. Transp. Electrif. 2023, 10, 3192–3205. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Xin, Z.; Brighton, J. Pontryagin’s Minimum Principle based model predictive control of energy management for a plug-in hybrid electric bus. Appl. Energy 2019, 236, 893–905. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Hu, S.; Fan, J. (Eds.) A Deep Reinforcement Learning Based Energy Management Strategy for Hybrid Electric Vehicles in Connected Traffic Environment. In Proceedings of the 6th IFAC Conference on Engine Powertrain Control, Simulation and Modeling (E-COSM), Tokyo, Japan, 23–25 August 2021. [Google Scholar]
- Zheng, C.; Zhang, D.; Xiao, Y.; Li, W. Reinforcement learning-based energy management strategies of fuel cell hybrid vehicles with multi-objective control. J. Power Sources 2022, 543, 231841. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, H.; Wang, F.; Wang, W.; Lin, X. Longevity-conscious energy management strategy of fuel cell hybrid electric Vehicle Based on deep reinforcement learning. Energy 2022, 238, 121593. [Google Scholar] [CrossRef]
- Gao, Z.; Gao, Y.; Hu, Y.; Jiang, Z.; Su, J. (Eds.) Application of Deep Q-Network in Portfolio Management. In Proceedings of the 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020. [Google Scholar]
- Zhu, Z.; Lin, K.; Jain, A.K.; Zhou, J. Transfer learning in deep reinforcement learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13344–13362. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H.; Yang, Z.; Feng, J.; Li, Y.; Yang, J.; Chen, Z. A transfer learning method for electric vehicles charging strategy based on deep reinforcement learning. Appl. Energy 2023, 343, 121186. [Google Scholar] [CrossRef]




| Items | Parameters | Value |
|---|---|---|
| Vehicle | Curb weight | 2650 kg |
| Tire radius | 0.35 m | |
| Frontal area | 3 m2 | |
| Rolling resistance coefficient | 0.013 | |
| Air resistance coefficient | 0.36 | |
| Final drive ratio | 9.5 |
| Parameter | Value | Unit |
|---|---|---|
| Uout | 256–320 | V |
| Ist | 0–360 | A |
| ηDC/DC | 0.94 | - |
| ηDC/AC | 0.95 | - |
| LVH | 120 | MJ/kg |
| Pfc | 0–92 | kW |
| ηfc | 0–0.64 | - |
| mfc | 0–1.8783 | g/s |
| VOC | 280.8–305.36 | V |
| R0 (discharging) | 0.2808–0.9768 | Ω |
| R0 (charging) | 0.3364–0.9884 | Ω |
| Qbat | 13 | kW·h |
| Pbat | 0–104 | kW |
| Tm | −310–310 | N·m |
| ωm | 0–16000 | r/min |
| ηm | 0.7–0.92 | - |
| Parameters | Source Domain | Target Domain |
|---|---|---|
| Episode | 500 | 100 |
| Replay buffer size | 50,000 | 50,000 |
| Learning rate of the actor network | 0.001 | 0.0009 |
| Learning rate of the critic network | 0.001 | 0.0009 |
| Reward discount | 0.9 | 0.9 |
| Batch size | 64 | 64 |
| Driving Cycles | Characteristics | Average Speed | Scenario |
|---|---|---|---|
| FTP75-2 | Frequent stops and starts | 9.58 m/s (34.49 km/h) | Urban peak traffic |
| WVU-CITY | More rapid acceleration | 3.78 m/s (13.61 km/h) | Urban driving |
| WVU-INTER | Smooth speed changes | 15.22 m/s (54.79 km/h) | Intercity driving condition |
| WVU-SUB | Stable speed, fewer stops | 7.19 m/s (25.88 km/h) | Suburban driving |
| ChinaCity | Low speed | 4.49 m/s (16.16 km/h) | Congested urban traffic |
| Strategy | STD | CV |
|---|---|---|
| Without TL | 21,450.7 | 2.22 |
| Full TL | 17,305.63 | 1.92 |
| Partial TL | 17,112.07 | 1.89 |
| Indicator | Without TL | Full TL | Partial TL | Full TL Improvement | Partial TL Improvement |
|---|---|---|---|---|---|
| MAE | 0.0116 | 0.0074 | 0.0070 | 36.21% | 39.66% |
| MSE | 0.00025 | 0.00019 | 0.00017 | 24.00% | 32.00% |
| RMSE | 0.0158 | 0.0138 | 0.0134 | 12.66% | 15.19% |
| MRE | 0.0187 | 0.0119 | 0.0111 | 36.36% | 40.64% |
| Bias | −0.0114 | −0.0073 | −0.0069 | 35.96% | 39.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; He, R.; Hu, D.; Lu, D. Energy Management Strategy for Fuel Cell Vehicles Based on Deep Transfer Reinforcement Learning. Energies 2025, 18, 2192. https://doi.org/10.3390/en18092192
Wang Z, He R, Hu D, Lu D. Energy Management Strategy for Fuel Cell Vehicles Based on Deep Transfer Reinforcement Learning. Energies. 2025; 18(9):2192. https://doi.org/10.3390/en18092192
Chicago/Turabian StyleWang, Ziye, Ren He, Donghai Hu, and Dagang Lu. 2025. "Energy Management Strategy for Fuel Cell Vehicles Based on Deep Transfer Reinforcement Learning" Energies 18, no. 9: 2192. https://doi.org/10.3390/en18092192
APA StyleWang, Z., He, R., Hu, D., & Lu, D. (2025). Energy Management Strategy for Fuel Cell Vehicles Based on Deep Transfer Reinforcement Learning. Energies, 18(9), 2192. https://doi.org/10.3390/en18092192






