Optimal Economic Dispatch Strategy for Cascade Hydropower Stations Considering Electric Energy and Peak Regulation Markets
Abstract
1. Introduction
- Introduction to the power market framework
- 2.
- Formulation of the objective function
- 3.
- Determine the solution method
- 4.
- Conduct simulation verification
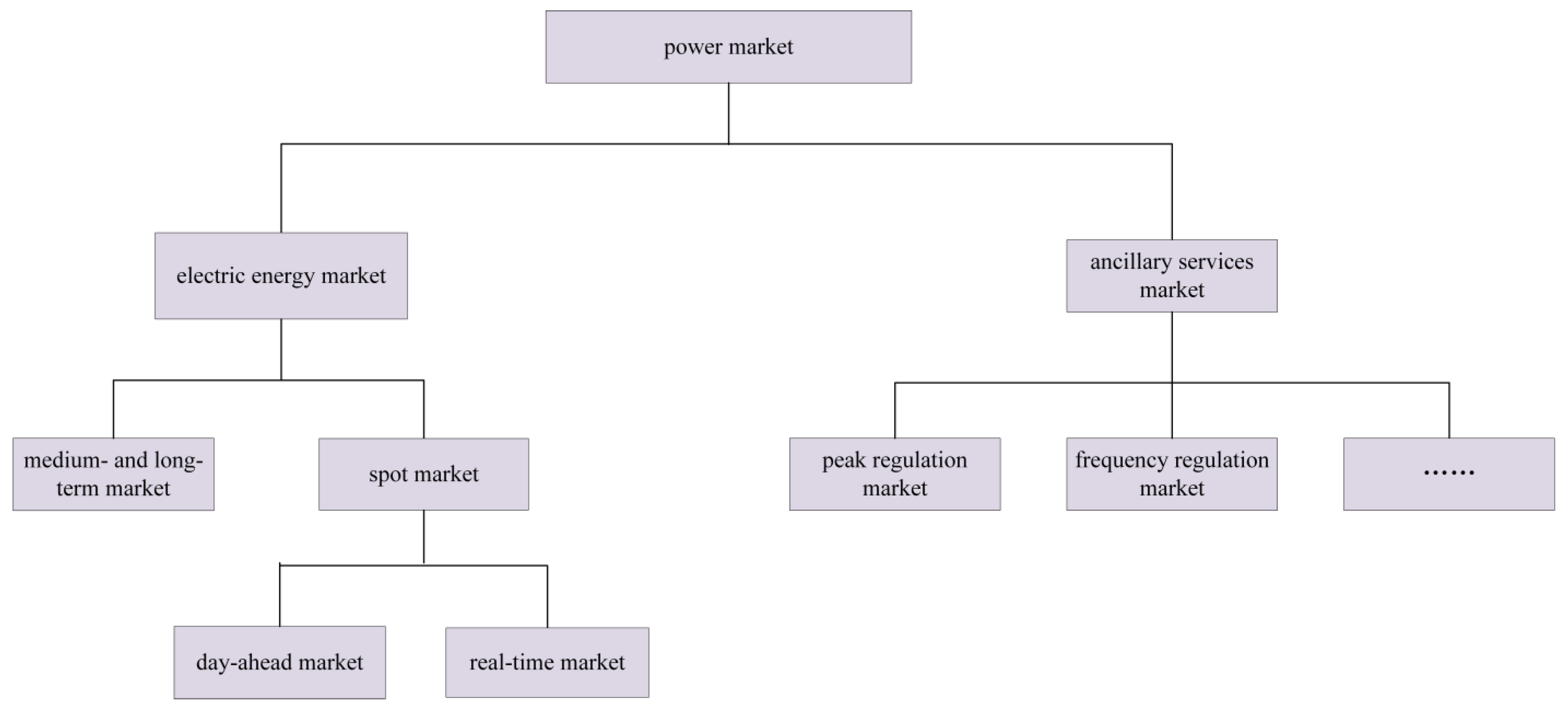
2. Theoretical Analysis of Cascade Hydropower Stations’ Participation in the EEM and PRM
2.1. Theoretical Analysis of Cascade Hydropower Stations’ Participation in the EEM
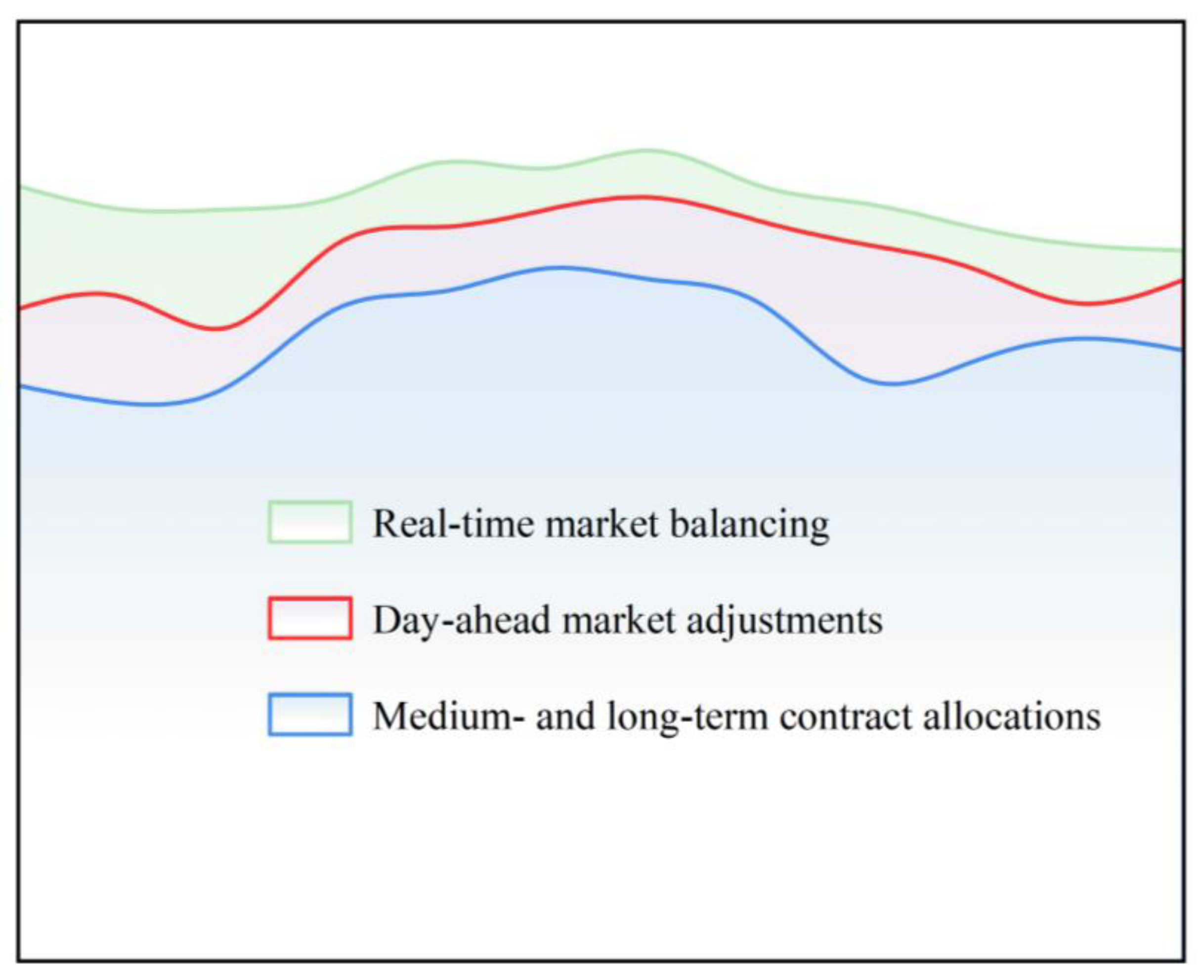
- Medium- and long-term contract allocations: These are based on energy sales agreements established through trading platforms, providing a foundational generation schedule.
- Day-ahead market adjustments: To align with real-time grid demands and supply conditions, adjustments are made in the day-ahead market, ensuring a balanced and responsive generation plan [23].
- Real-time market balancing: Any discrepancies between forecasted and actual loads are addressed in the real-time market, facilitating immediate market-based corrections to maintain system equilibrium [24].
2.2. Theoretical Analysis of Cascade Hydropower Stations’ Participation in the PRM
- Participating in deep peaking to earn compensation.
- Contributing to the shared costs when thermal power units engage in deep peaking.
3. Economic Dispatch Model for Cascade Hydropower Stations Considering the EEM and PRM
3.1. Objective Function
- (1)
- Medium- and long-term market returns:
- (2)
- Day-ahead market returns:
- (3)
- Real-time market returns:
3.2. Constraint Condition
- (1)
- Water level constraints:
- (2)
- Water balance constraints:
- (3)
- Transmission channel constraints:
- (4)
- Medium- and long-term contracted power decomposition constraints:
- (5)
- Hydropower plant output constraints at all levels:
- (6)
- Upper and lower limits of reservoir capacity and flow rate constraints for hydropower plants at all levels:
4. An Economic Dispatch Model Solution Based on the HHO Algorithm
4.1. Fundamentals of the HHO Algorithm
- (1)
- Global exploration phase
- (2)
- Transition phase
- (3)
- Development phase
- Soft Surrounding
- 2.
- Quick Dive Soft Wrap
- 3.
- Hard Surround
- 4.
- Rapid Dive Hard Surround
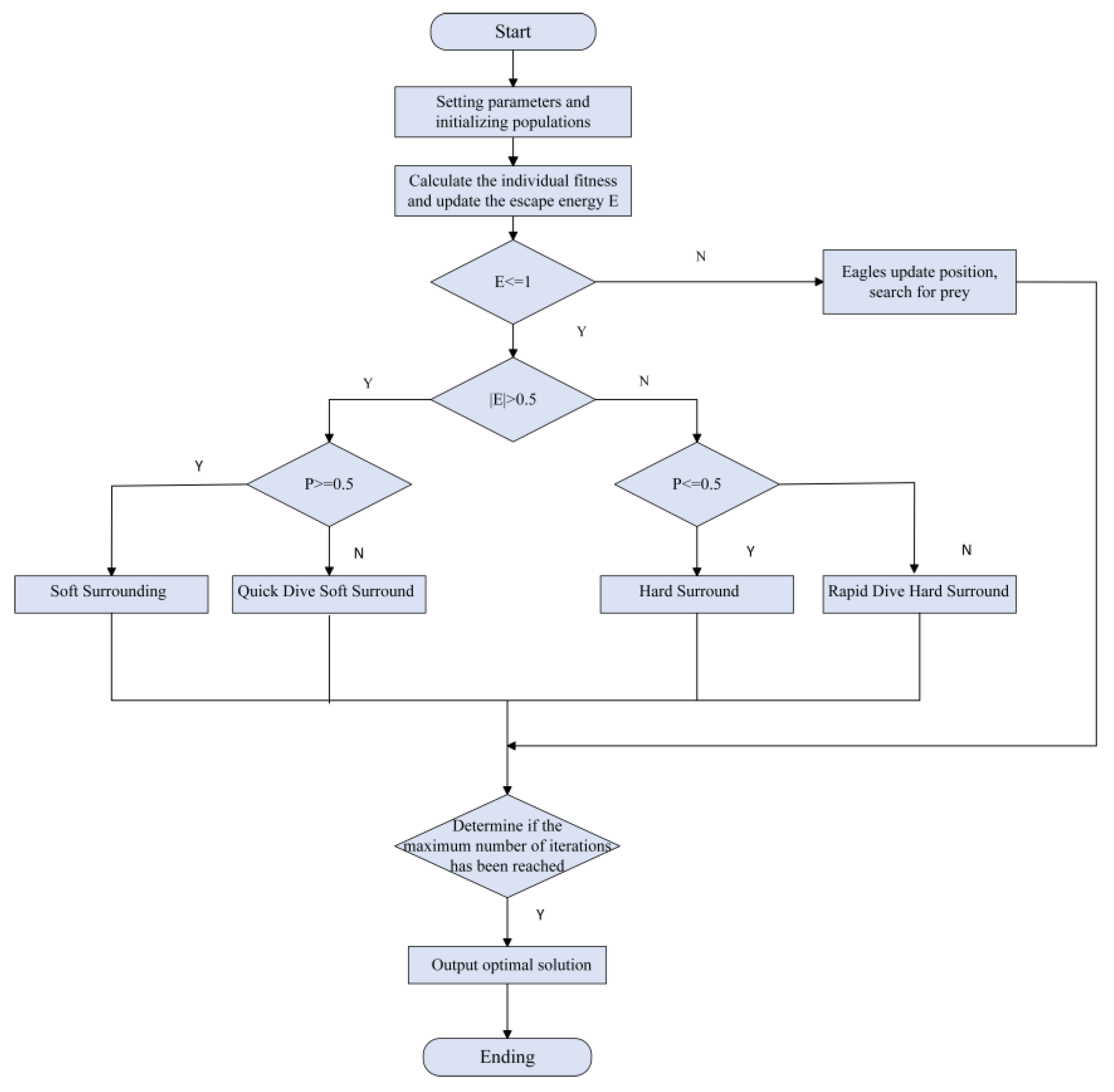
4.2. HHO Algorithm Solution Flow
- (1)
- Use the parameters of the cascade hydropower stations and the power grid as input data for the scheduling model; set the size of the hawk population and the total number of iterations.
- (2)
- Randomly initialize the population positions and calculate the fitness values of each hawk in the population.
- (3)
- Update the prey’s escape energy based on Equation (26).
- (4)
- Determine whether the hawks enter the exploration phase or the exploitation phase based on the prey’s escape energy.
- (5)
- When , the prey’s escape energy is high, so the population’s positions are updated according to Equation (24), and the hawks update their positions, entering the exploration phase.
- (6)
- When , the hawks update their positions, entering the exploitation phase.
- (7)
- When , the escape probability is used to determine whether to employ a soft encirclement or a progressive soft encirclement.
- 1.
- When , update the position based on Equation (27).
- 2.
- When , update the position based on Equation (28).
- (8)
- When , the escape probability is used to determine whether to employ a hard encirclement or a progressive hard encirclement.
- 3.
- When , update the position based on Equation (29).
- 4.
- When , update the position based on Equation (30).
- (9)
- Finally, check whether the maximum iteration count has been reached. If the maximum iteration count is reached, output the optimal solution; if not, return to step (3) and continue the iterations.
5. Simulation Verification
5.1. Initial Data for Simulation
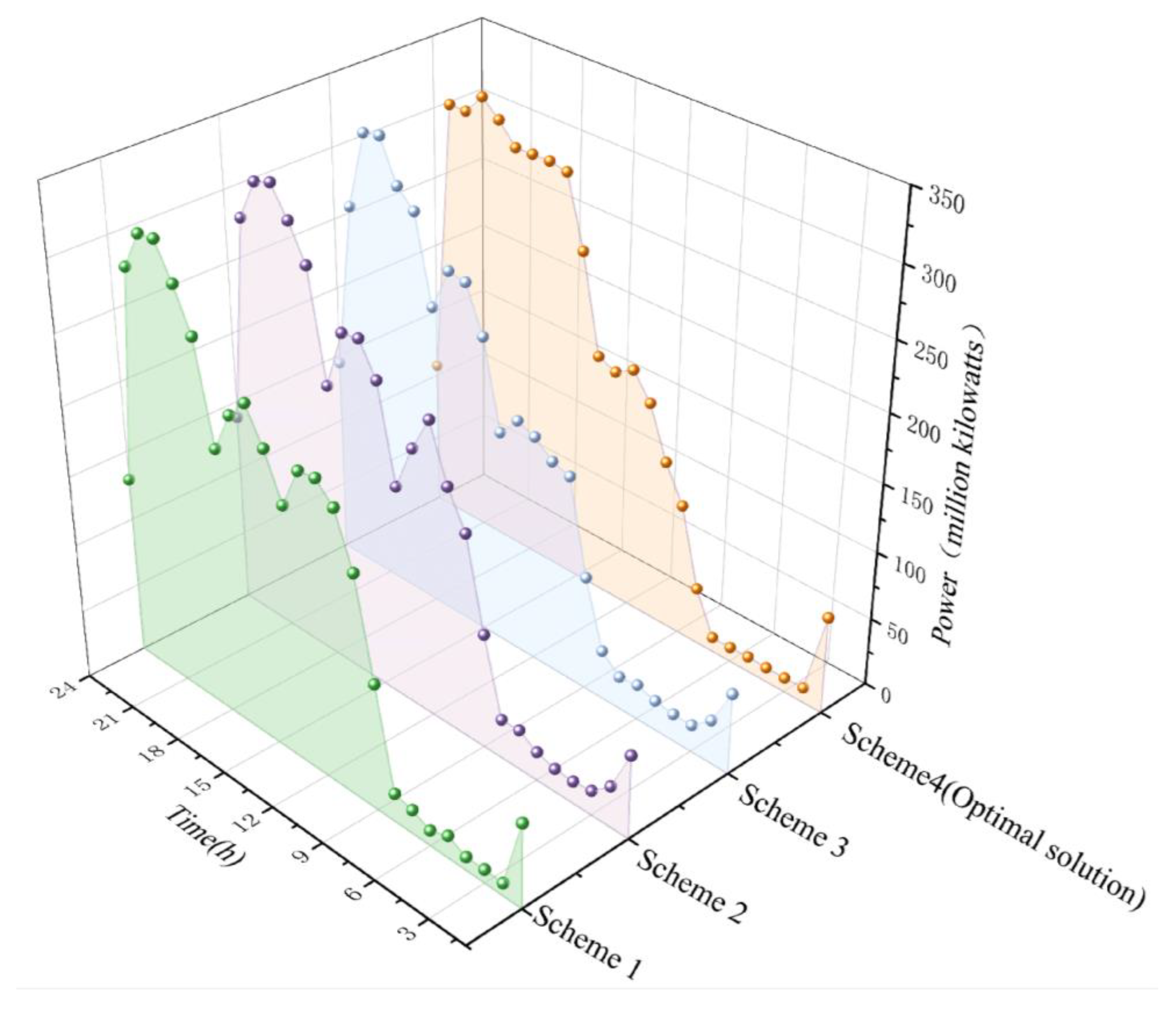
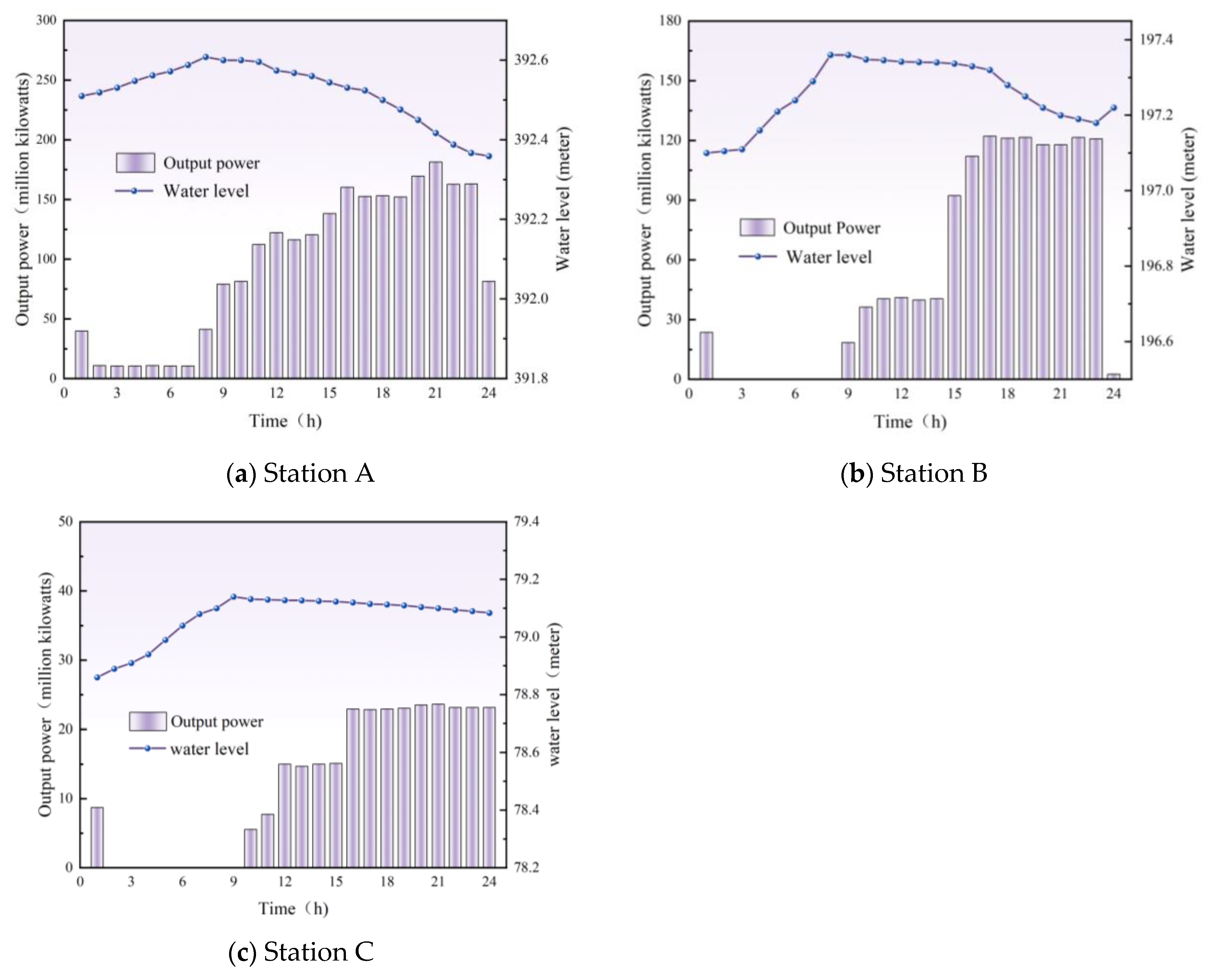
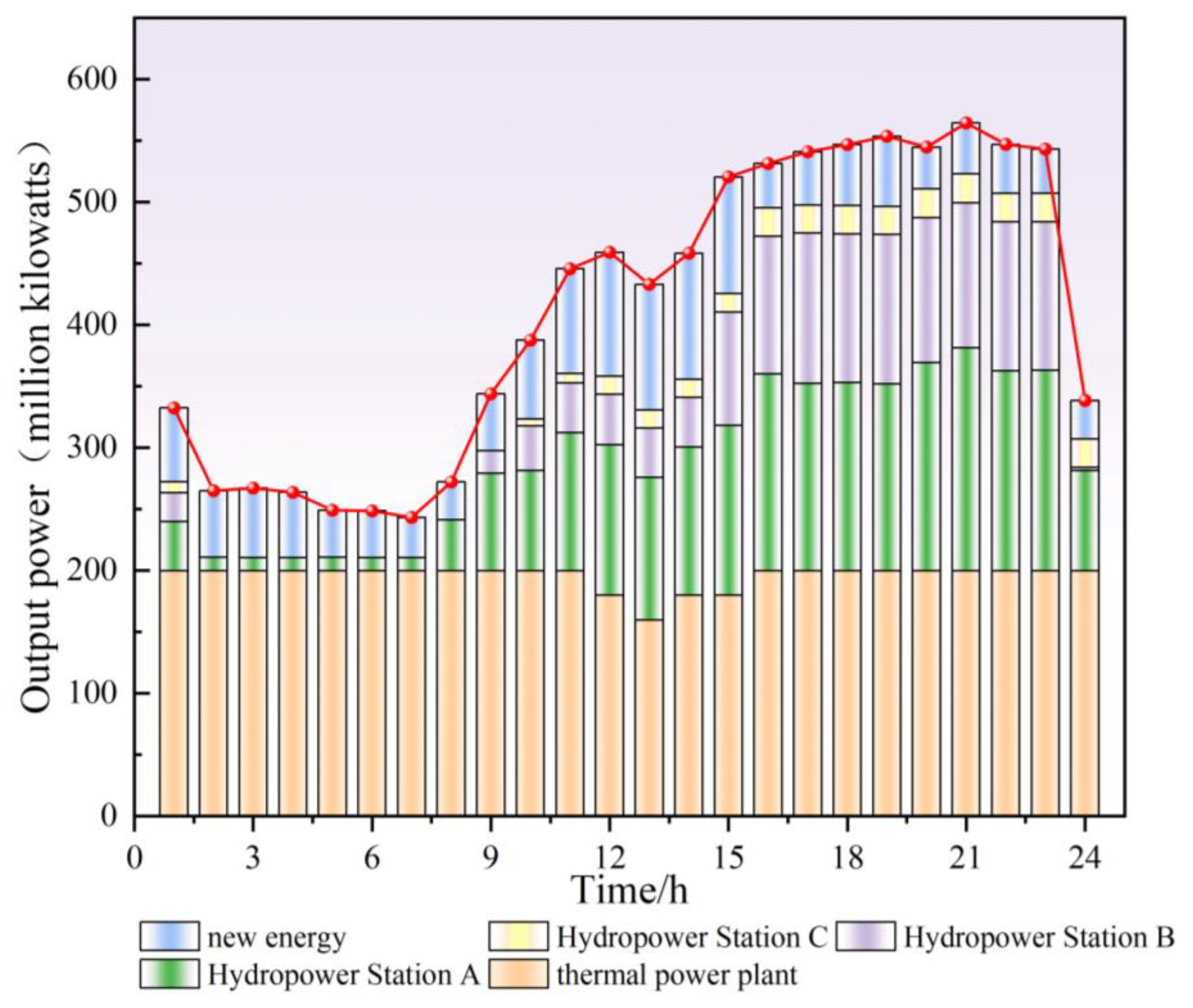
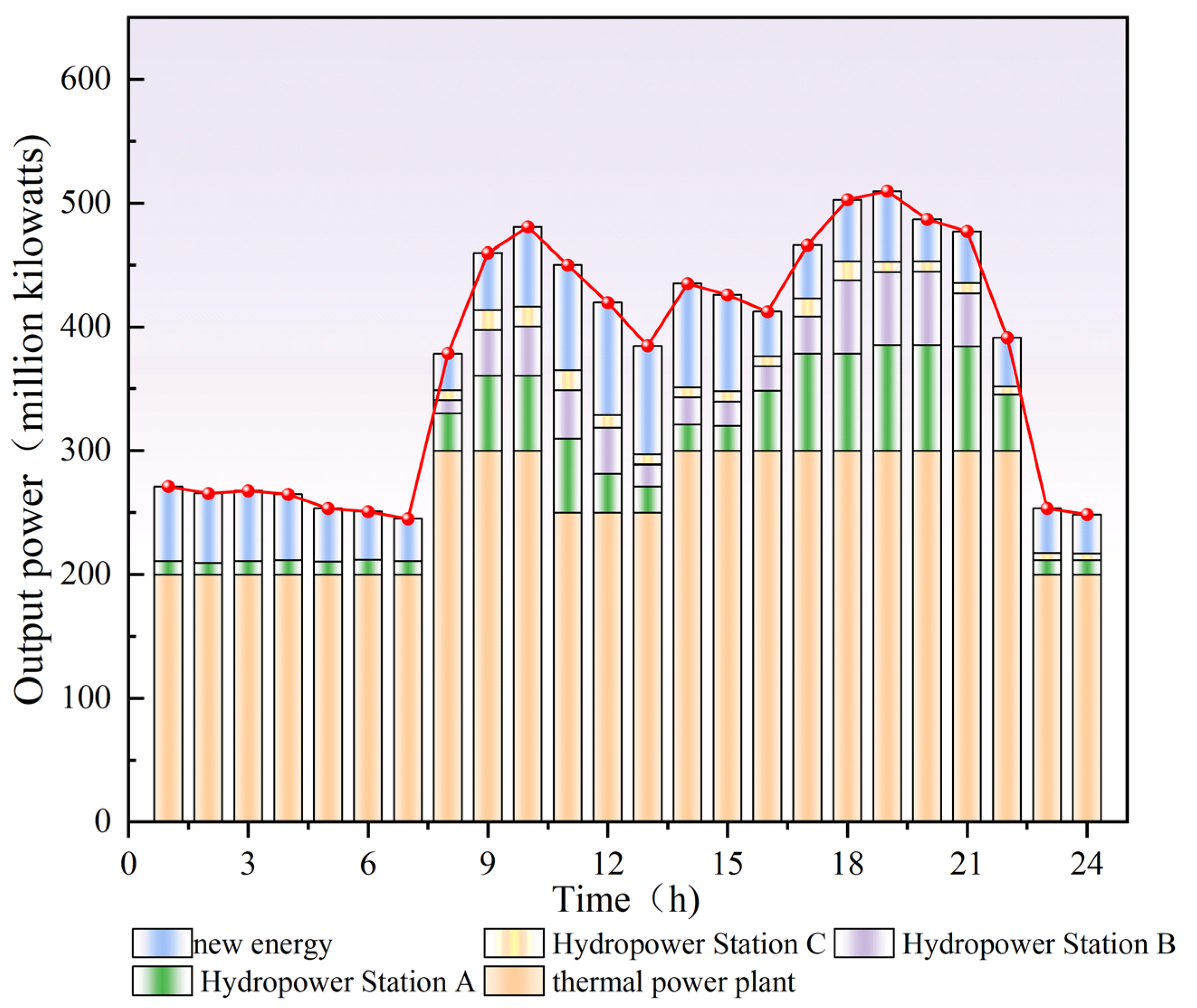
5.2. Simulation Results of Cascade Hydropower Stations Under the Wet Season
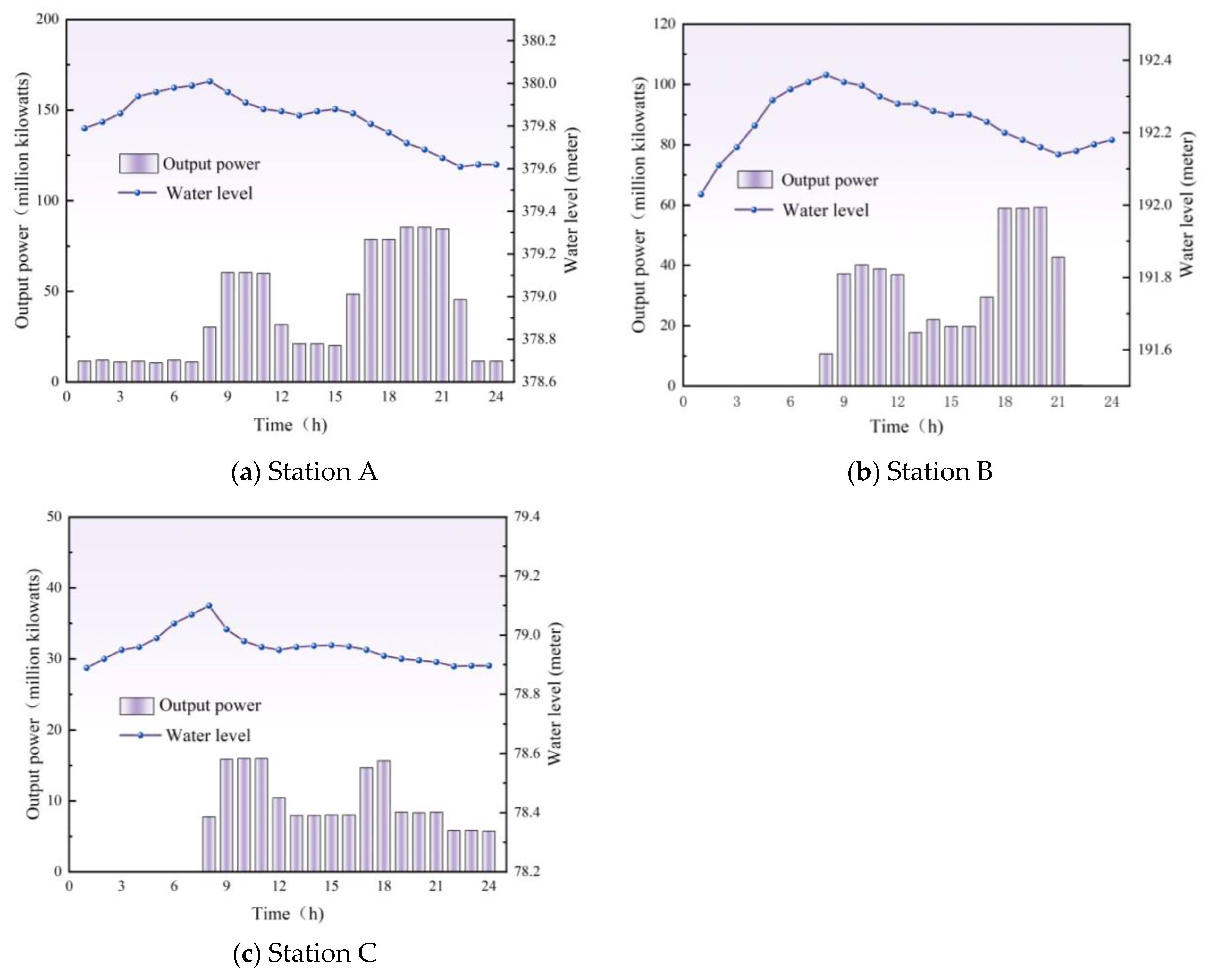
5.3. Simulation Results of Cascade Hydropower Stations Under the Dry Season
6. Conclusions
- (1)
- In short-term scheduling, renewable energy participation in the spot market causes fluctuations in day-ahead and real-time electricity prices. To maximize the economic benefits of cascade hydropower stations, they should increase power generation during high-price periods and store water during low-price periods. Incorporating the spot market’s influence into the EEM can significantly improve the profitability of hydropower generation.
- (2)
- When participating in the PRM, the losses incurred by cascade hydropower stations during deep-peak regulation are shared by other grid-connected power stations proportionally to their generation output. This mechanism prioritizes renewable energy integration, reducing wind and solar curtailment. Although participating in peak regulation may slightly reduce hydropower revenue in the EEM, it allows hydropower stations to earn additional compensation revenue from the PRM. Thus, participation in peak regulation enhances the overall profitability of cascade hydropower stations and incentivizes them to contribute to system flexibility actively.
- (3)
- Additionally, as thermal power plants serve as the primary peak regulation units, their peak regulation compensation is shared among other generating units. Therefore, reducing hydropower output during deep-peak regulation periods can lower the cost-sharing burden of cascade hydropower stations while creating more capacity for renewable energy generation. Furthermore, due to their clean and flexible characteristics, hydropower stations play a crucial role in peak shaving during periods of high electricity demand, thereby reducing the peak pressure on thermal power units.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| flow rate | |
| average net head | |
| power station work efficiency | |
| output of stations in the PRM | |
| PRM compensation price | |
| baseline electricity price | |
| fluctuating component of the price | |
| mean load | |
| average outputs of wind | |
| average outputs of PV | |
| average outputs of thermal power | |
| variation in power generation | |
| output of thermal power in the time period | |
| output of photovoltaic power in the time period | |
| output of wind power in the time period | |
| output of hydropower in the time period | |
| pressure output of thermal power to participate in peaking | |
| negotiated electricity price | |
| judgment matrix | |
| significance level of each target | |
| reservoir storage of hydropower station | |
| lower water level | |
| upper water level | |
| outflow from station | |
| minimum daily electricity generation. | |
| maximum transmission capacity | |
| lower power output | |
| , | minimum outflow |
| position of the prey | |
| average position of the population of hawks | |
| position of a randomly selected hawk | |
| , | upper and lower bounds of the search range |
| prey’s escape energy | |
| initial escape energy | |
| random jump strength | |
| actual location | |
| d-dimensional random vector | |
| Lévy flight strategy | |
| resulting position | |
| fitness function | |
| Abbreviations | |
| electric energy market | EEM |
| peak regulation market | PRM |
References
- Zheng, Y.; Li, Z.; Chai, J. Progress and prospects of international carbon peaking and carbon neutral research –based on bibliometric analysis (1991–2022). Front. Energy Res. 2023, 11, 1121639. [Google Scholar] [CrossRef]
- Wang, X.; Virguez, E.; Mei, Y.; Yao, H.; Patiño-Echeverri, D. Integrating wind and photovoltaic power with dual hydro-reservoir systems. Energy Convers. Manag. 2022, 257, 115425. [Google Scholar] [CrossRef]
- Guo, F.; Li, J.; Zhang, C.; Zhu, Y.; Yu, C.; Wang, Q.; Buja, G. Optimized Power and Capacity Configuration Strategy of a Grid-Side Energy Storage System for Peak Regulation. Energies 2023, 16, 5644. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Guo, P.; Li, C.; Wu, S. Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation. Energies 2024, 17, 2734. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.; Wang, X.; Chang, J.; Chen, Y.; Zhou, Y.; Guo, A. Flexibility evaluation of wind-PV-hydro multi-energy complementary base considering the compensation ability of cascade hydropower stations. Appl. Energy 2022, 315, 119024. [Google Scholar] [CrossRef]
- Ghaljehei, M.; Khorsand, M. Representation of Uncertainty in Electric Energy Market Models: Pricing Implication and Formulation. IEEE Syst. J. 2021, 15, 3703–3713. [Google Scholar] [CrossRef]
- Zhang, F.; Ma, G.; Yang, Z.; Xie, M.; Liu, Y.; Su, Y.; Zhang, Q. Research on the Collaborative Clearing Model of Ancillary Service and Electric Energy Market. J. Phys. Conf. Ser. 2021, 1974, 012009. [Google Scholar] [CrossRef]
- Liu, F.; Xu, Y.; Zhu, D.-D.; Wei, S.-M.; Tang, C.-P. Equilibrium Risk Decision Model for Bidding Electricity Quantity Deviation of Cascade Hydropower Stations. J. Electr. Eng. Technol. 2024, 19, 977–991. [Google Scholar] [CrossRef]
- Bojnec, Š. Electricity Markets, Electricity Prices and Green Energy Transition. Energies 2023, 16, 873. [Google Scholar] [CrossRef]
- Khodadadi, A.; Hesamzadeh, M.R.; Söder, L. Multimarket Trading Strategy of a Hydropower Producer Considering Active-Time Duration: A Distributional Regression Approach. IEEE Syst. J. 2023, 17, 3343–3353. [Google Scholar] [CrossRef]
- Tian, M.-W.; Yan, S.-R.; Tian, X.-X.; Nojavan, S.; Jermsittiparsert, K. Risk and profit-based bidding and offering strategies for pumped hydro storage in the energy market. J. Clean. Prod. 2020, 256, 120715. [Google Scholar] [CrossRef]
- Chazarra, M.; García-González, J.; Pérez-Díaz, J.I.; Arteseros, M. Stochastic optimization model for the weekly scheduling of a hydropower system in day-ahead and secondary regulation reserve markets. Electr. Power Syst. Res. 2016, 130, 67–77. [Google Scholar] [CrossRef]
- Sharafi Masouleh, M.; Salehi, F.; Raeisi, F.; Saleh, M.; Brahman, A.; Ahmadi, A. Mixed-integer Programming of Stochastic Hydro Self-scheduling Problem in Joint Energy and Reserves Markets. Electr. Power Compon. Syst. 2016, 44, 752–762. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Wilhelmi, J.R.; Arévalo, L.A. Optimal short-term operation schedule of a hydropower plant in a competitive electricity market. Energy Convers. Manag. 2010, 51, 2955–2966. [Google Scholar] [CrossRef]
- Chazarra, M.; Pérez-Díaz, J.I.; García-González, J. Deriving Optimal End of Day Storage for Pumped-Storage Power Plants in the Joint Energy and Reserve Day-Ahead Scheduling. Energies 2017, 10, 813. [Google Scholar] [CrossRef]
- Men, P.; Thun, V.; Yin, S.; Lebel, L. Benefit sharing from Kamchay and Lower Sesan 2 hydropower watersheds in Cambodia. Water Resour. Rural Dev. 2014, 4, 40–53. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, H.; Lu, Y.; Zhou, C.; Zhou, C.; Lu, Y. Multi-objective integrated decision method of cascade hydropower stations based on optimization algorithm and evaluation model. J. Hydrol. 2024, 638, 131533. [Google Scholar] [CrossRef]
- Tao, Y.; Mo, L.; Yang, Y.; Liu, Z.; Liu, Y.; Liu, T. Optimization of Cascade Reservoir Operation for Power Generation, Based on an Improved Lightning Search Algorithm. Water 2023, 15, 3417. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Y.; Tao, X.; Chen, S.; Huang, W.; Ma, G. A new clearing method for cascade hydropower spot market. Energy 2024, 289, 129937. [Google Scholar] [CrossRef]
- Lu, G.; Yang, Y.; Li, Z.; Tang, Y. Optimal energy portfolio allocation method for regulable hydropower plants considering the impact of new energy generation. Front. Energy Res. 2023, 11, 1114949. [Google Scholar] [CrossRef]
- Lu, G.; Yang, P.; Li, Z.; Yang, Y.; Tang, Y. Optimal energy portfolio method for regulable hydropower plants under the spot market. Front. Energy Res. 2023, 11, 1169935. [Google Scholar] [CrossRef]
- Xie, J.; Zheng, Y.; Pan, X.; Zheng, Y.; Zhang, L.; Zhan, Y. A Short-Term Optimal Scheduling Model for Wind-Solar-Hydro Hybrid Generation System With Cascade Hydropower Considering Regulation Reserve and Spinning Reserve Requirements. IEEE Access 2021, 9, 10765–10777. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, S.; Su, C.; Wu, Y.; Yan, D.; Wu, Z. Optimal scheduling of cascade hydropower plants in a portfolio electricity market considering the dynamic water delay. Energy 2022, 252, 124025. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Bao, Y.; Gao, D.W.; Fan, S.; Wang, Z. A risk-based procurement strategy for the charging station operator in electricity markets considering multiple uncertainties. Electr. Power Syst. Res. 2025, 241, 111381. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, M.; You, S. A Unified Trading Model Based on Robust Optimization for Day-Ahead and Real-Time Markets with Wind Power Integration. Energies 2017, 10, 554. [Google Scholar] [CrossRef]
- Zhang, Z.; Cong, W.; Liu, S.; Li, C.; Qi, S. Auxiliary Service Market Model Considering the Participation of Pumped-Storage Power Stations in Peak Shaving. Front. Energy Res. 2022, 10, 915125. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, P.; Pang, W.; Han, P. Research on deep peaking cost allocation mechanism considering peaking demand subject and thermal power unit. Energy Rep. 2024, 12, 158–172. [Google Scholar] [CrossRef]
- Shehab, M.; Mashal, I.; Momani, Z.; Shambour, M.K.Y.; Al-Badareen, A.; Al-Dabet, S.; Bataina, N.; Alsoud, A.R.; Abualigah, L. Harris Hawks Optimization Algorithm: Variants and Applications. Arch. Comput. Methods Eng. 2022, 29, 5579–5603. [Google Scholar] [CrossRef]
- Hussien, A.G.; Abualigah, L.; Abu Zitar, R.; Hashim, F.A.; Amin, M.; Saber, A.; Almotairi, K.H.; Gandomi, A.H. Recent Advances in Harris Hawks Optimization: A Comparative Study and Applications. Electronics 2022, 11, 1919. [Google Scholar] [CrossRef]
- Jia, D.; Wang, D. A Maximum Power Point Tracking (MPPT) Strategy Based on Harris Hawk Optimization (HHO) Algorithm. Actuators 2024, 13, 431. [Google Scholar] [CrossRef]

| Project | Hydropower Station A | Hydropower Station B | Hydropower Station C |
|---|---|---|---|
| Average annual runoff (billion m3) | 94.4 | 127 | 138 |
| Average annual flow (m3/s) | 299 | 403 | 436 |
| Normal storage level(m) | 400 | 200 | 80 |
| Dead water level (m) | 350 | 180 | 78 |
| Total reservoir capacity (billion m3) | 45.8 | 33.4 | 4.89 |
| Reservoir regulation performance | Multi-annual regulation | Annual regulation | Daily regulation |
| Installed capacity (MW) | 1840 | 1212 | 270 |
| Firm power (MW) | 308.3 | 241.9 | 77.4 |
| Maximum head (m) | 202 | 122 | 40 |
| Minimum head (m) | 147 | 80.7 | 22.3 |
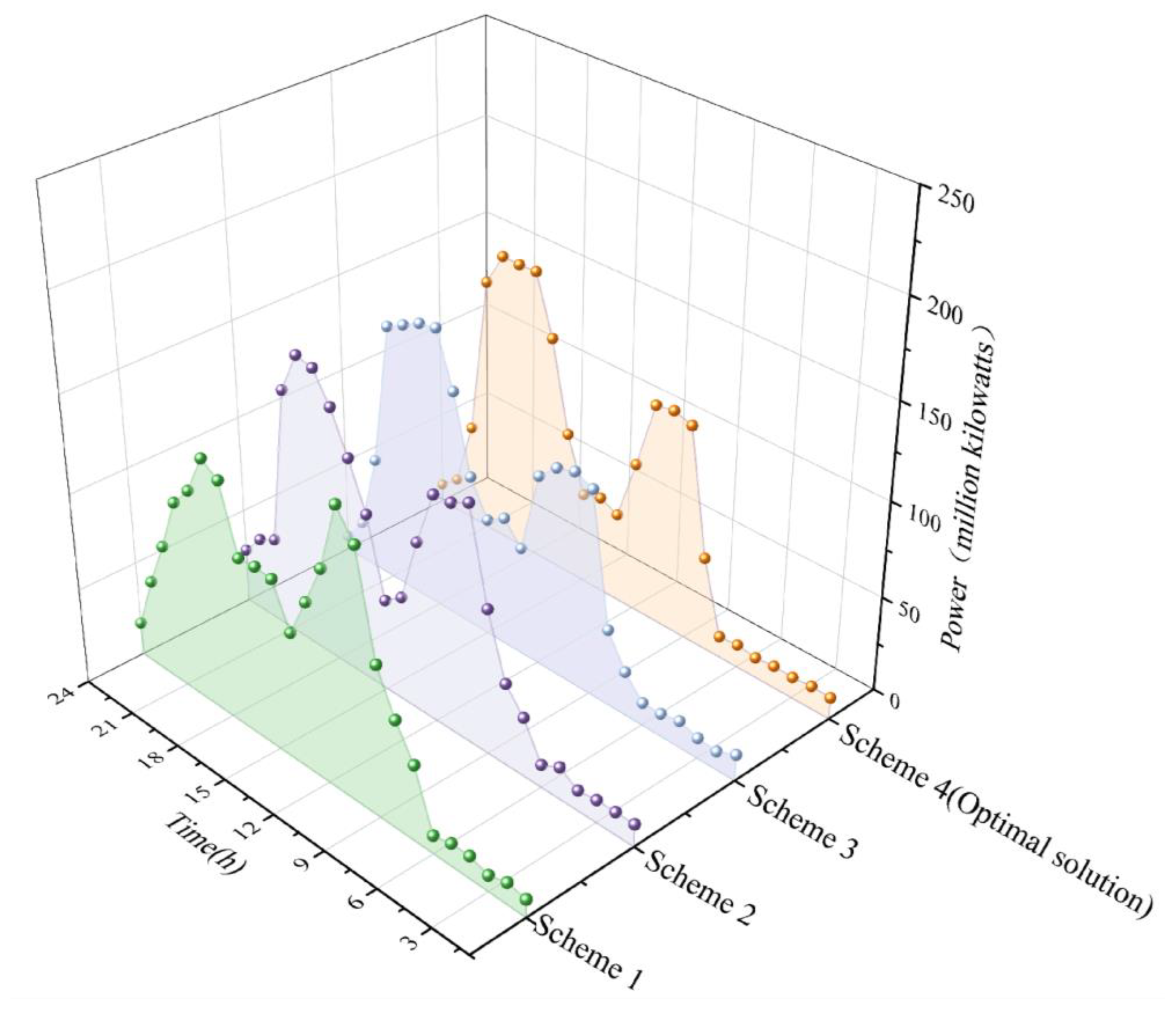
| Scheme | Revenue from EEM/CNY | Revenue from PRM/CNY | Total Revenue /CNY |
|---|---|---|---|
| Scheme 1 | 1376.45 | 0 | 1376.45 |
| Scheme 2 | 1389.34 | 0 | 1389.34 |
| Scheme 3 | 1332.89 | 66.34 | 1399.23 |
| Scheme 4 (optimal scheme) | 1321.23 | 81.52 | 1402.75 |
| Scheme | Revenue from EEM/CNY | Revenue from PRM/CNY | Total Revenue /CNY |
|---|---|---|---|
| Scheme 1 | 624.25 | 0 | 624.25 |
| Scheme 2 | 631.59 | 0 | 631.59 |
| Scheme 3 | 611.17 | 28.32 | 639.49 |
| Scheme 4 (optimal scheme) | 606.42 | 37.77 | 644.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Huang, W.; Ma, J.; He, J.; Lv, C.; Yang, Y. Optimal Economic Dispatch Strategy for Cascade Hydropower Stations Considering Electric Energy and Peak Regulation Markets. Energies 2025, 18, 1762. https://doi.org/10.3390/en18071762
Liu F, Huang W, Ma J, He J, Lv C, Yang Y. Optimal Economic Dispatch Strategy for Cascade Hydropower Stations Considering Electric Energy and Peak Regulation Markets. Energies. 2025; 18(7):1762. https://doi.org/10.3390/en18071762
Chicago/Turabian StyleLiu, Fan, Wentao Huang, Jingjing Ma, Jun He, Can Lv, and Yukun Yang. 2025. "Optimal Economic Dispatch Strategy for Cascade Hydropower Stations Considering Electric Energy and Peak Regulation Markets" Energies 18, no. 7: 1762. https://doi.org/10.3390/en18071762
APA StyleLiu, F., Huang, W., Ma, J., He, J., Lv, C., & Yang, Y. (2025). Optimal Economic Dispatch Strategy for Cascade Hydropower Stations Considering Electric Energy and Peak Regulation Markets. Energies, 18(7), 1762. https://doi.org/10.3390/en18071762





