Thermoelectric Energy Harvesting with a Stacked Configuration Using Porous Medium for Marine Applications
Abstract
1. Introduction
2. Numerical Method and Procedure
2.1. Numerical Model of the Stacked TEG
2.2. Porous Media Method
2.3. Numerical Method for Reflecting Multi-Physics Phenomena
2.4. Computational Process and Mesh Independent Test
3. Results and Discussion
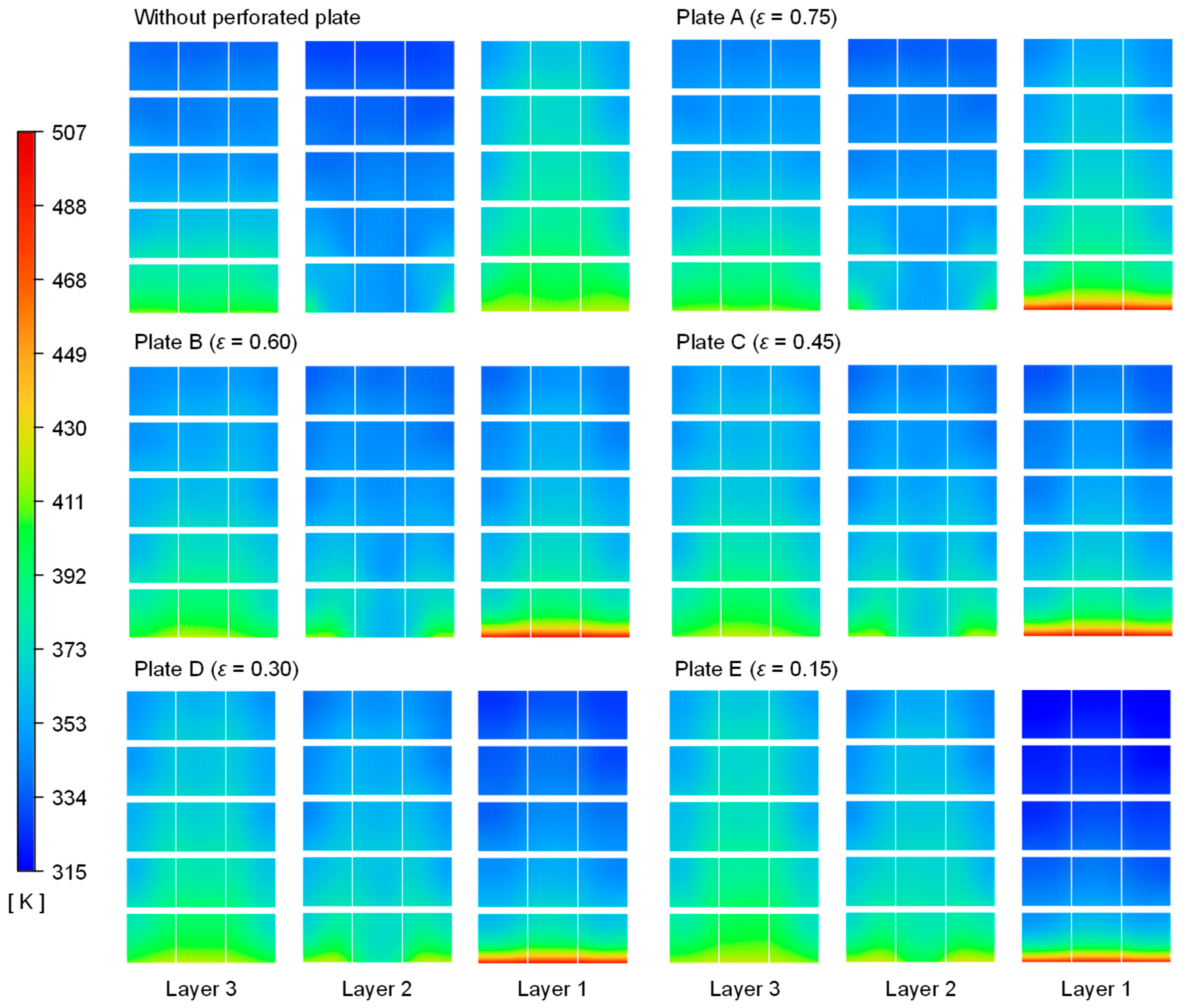
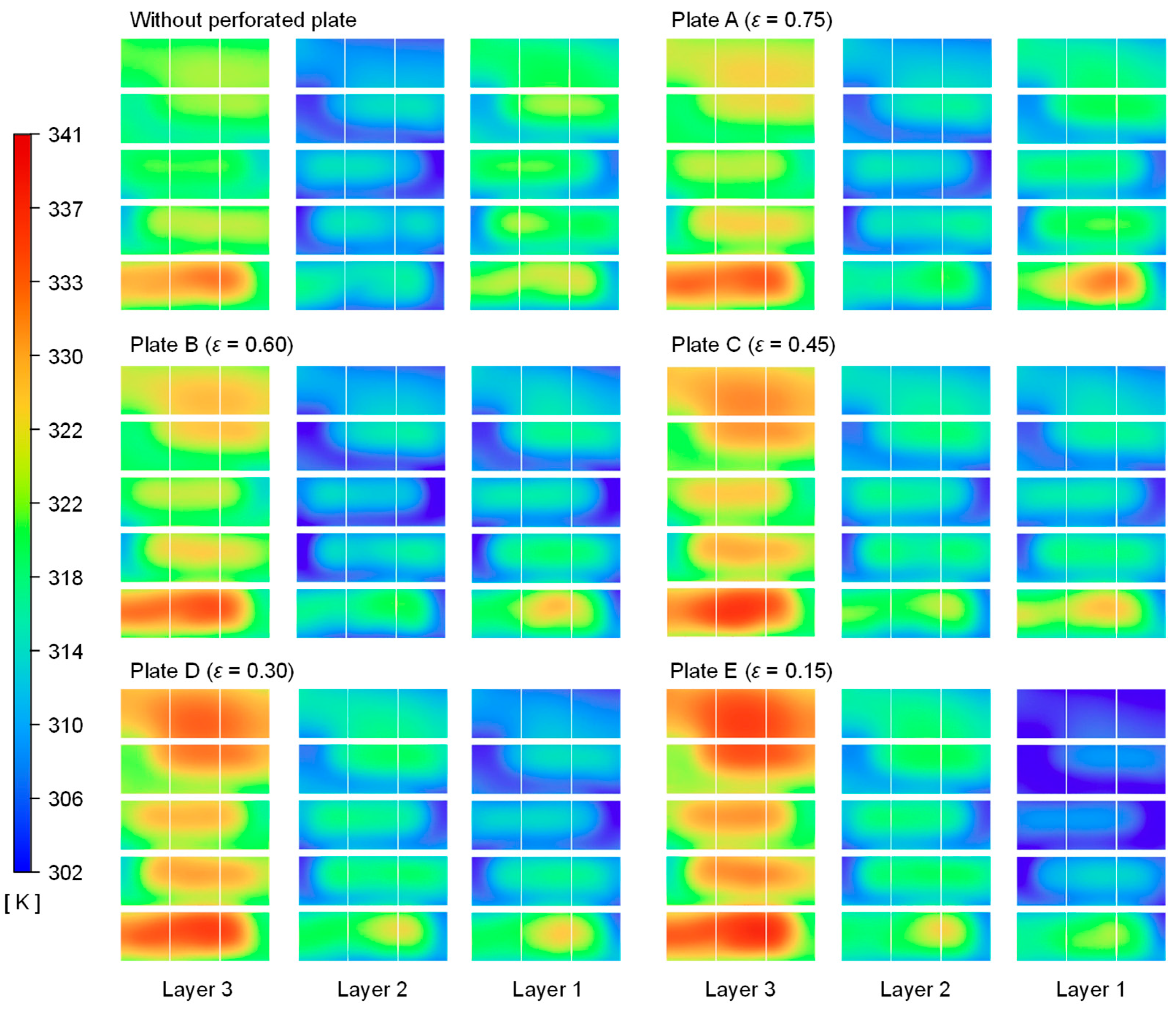
3.1. Velocity and Temperature Field Analysis
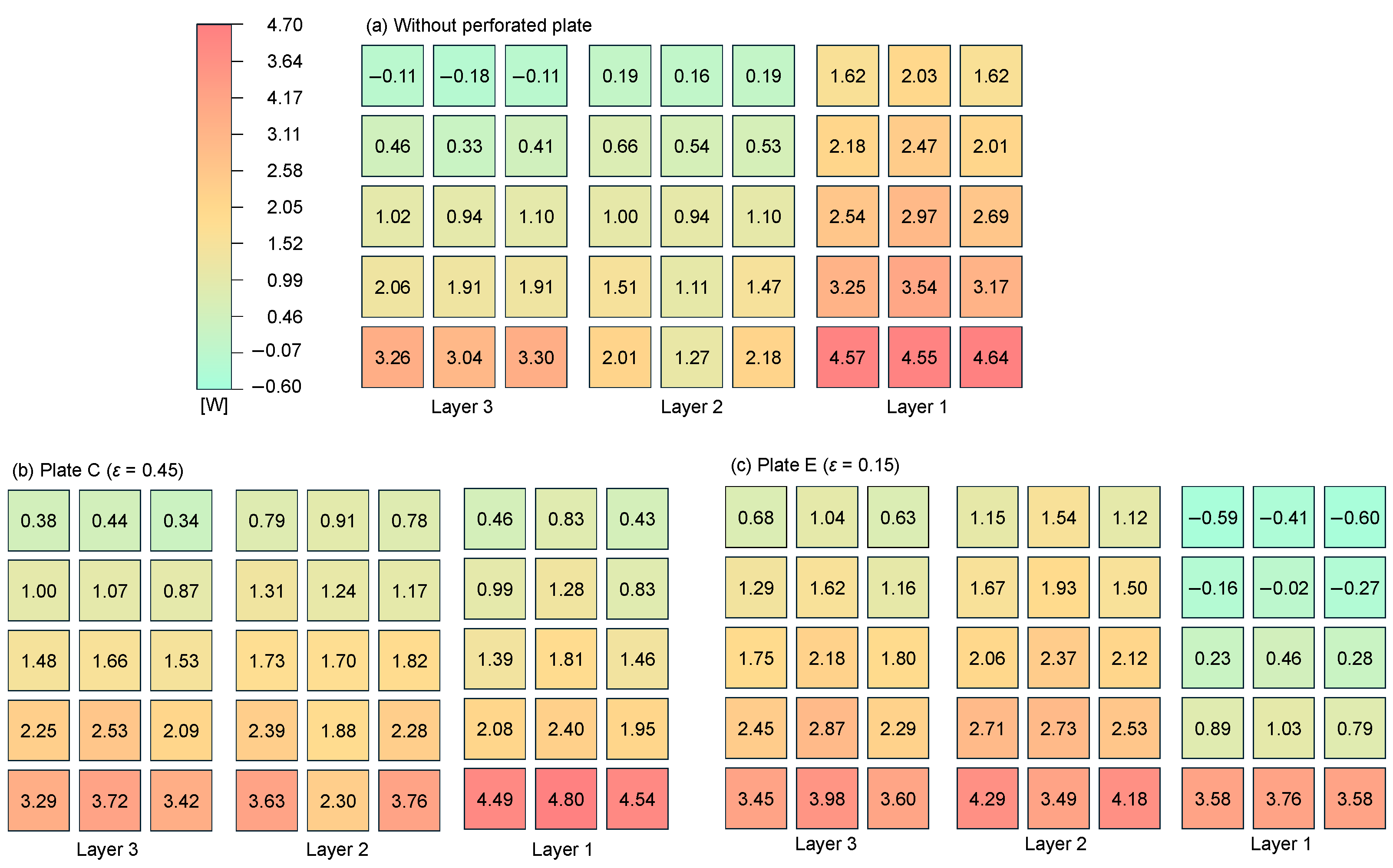
3.2. Module-Wise Output Power Analysis
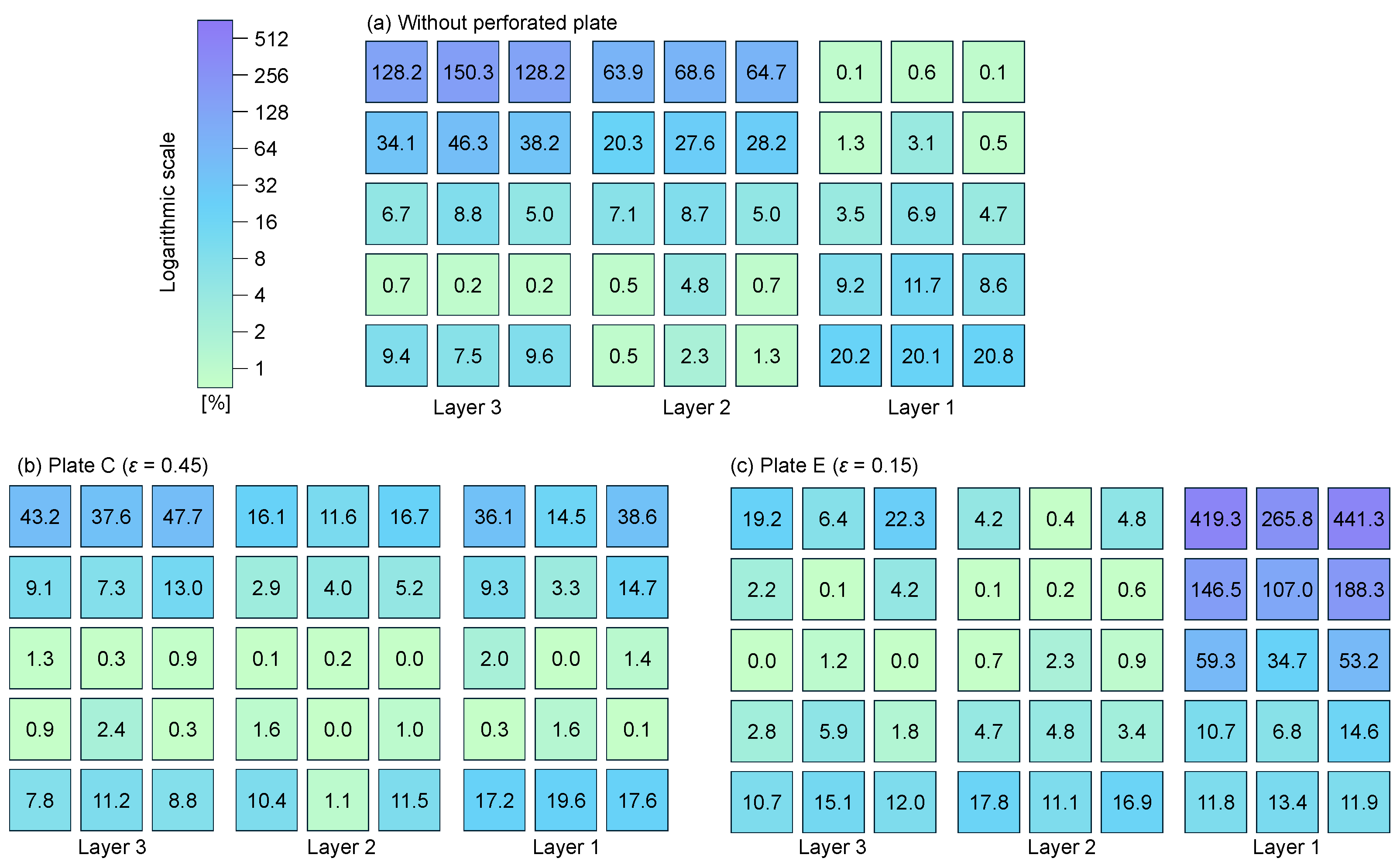
3.3. Module-Wise Electrical Loss Analysis
3.4. System-Level Output Power and Pressure Drop Analysis
3.5. System-Level Net Output Power and Energy Conversion Efficiency Analysis
4. Conclusions
- The effect of the flow distribution due to the perforated plate insertion on the module-wise output power and power loss was investigated. The insertion of a perforated plate of 0.15 porosity with a flow uniformity of 2.29 led to negative power generation of up to −0.6 W and 441.3% power loss in a TEM due to the non-uniform temperature across the TEMs. In contrast, a perforated plate of 0.45 porosity with a flow uniformity of 1.05 resulted in positive power generation across all TEMs, with a maximum power loss of 47.7%.
- The influence of the porosity of the perforated plate on the system-level output power and flow uniformity was systematically evaluated. The insertion of a perforated plate with 0.45 porosity significantly improved flow uniformity and output power, with a maximum of 167.1 W achieved, highlighting a 7.03% increase compared to the case without the perforated plate.
- The insertion of a perforated plate with 0.45 porosity resulted in a significant increase in electrical efficiency (91.1%) and conversion efficiency (3.41%), compared to the case without the perforated plate, where electrical efficiency (88.0%) and conversion efficiency (3.33%) were obtained. However, the perforated plate with 0.6 porosity increased the net output power by 6.2% compared to the case without the perforated plate, reaching a maximum of 136.6 W.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Abbreviations | |
| TEG | Thermoelectric generator |
| TEM | Thermoelectric module |
| UDF | User-defined function |
| Nomenclature | |
| Pore diameter (m) | |
| H | Height (m) |
| I | Current (A) |
| K | Thermal conductance (W/K) |
| L | Length (m) |
| P | Power (W) |
| Extracted thermal energy transfer rate (W) | |
| R | Electrical resistance (Ω) |
| S | Source term (kg/m2·s2) |
| T | Temperature (K) |
| t | Thickness (m) |
| U | Superficial velocity (m/s) |
| W | Width (m) |
| wo | Without |
| Greek symbols | |
| α | Seebeck coefficient (V/K); permeability (m2) |
| β | Inertial resistance (1/m) |
| δ | Electrical loss |
| Δp | Pressure drop (Pa) |
| ΔT | Temperature difference (K) |
| ε | Porosity |
| η | Efficiency |
| μ | Viscosity (kg/m·s) |
| ρ | Density (kg/m3) |
| Subscripts | |
| c | Cold side |
| conv | Conversion |
| el | Electrical |
| h | Hot side |
| out | Output |
| pump | Pumping |
| net | Net |
| system | System |
| udf | User-defined function |
References
- Islam Rony, Z.; Mofijur, M.; Hasan, M.M.; Rasul, M.G.; Jahirul, M.I.; Forruque Ahmed, S.; Kalam, M.A.; Anjum Badruddin, I.; Yunus Khan, T.M.; Show, P.-L. Alternative Fuels to Reduce Greenhouse Gas Emissions from Marine Transport and Promote UN Sustainable Development Goals. Fuel 2023, 338, 127220. [Google Scholar] [CrossRef]
- Nour Eddine, A.; Chalet, D.; Faure, X.; Aixala, L.; Chessé, P. Optimization and Characterization of a Thermoelectric Generator Prototype for Marine Engine Application. Energy 2018, 143, 682–695. [Google Scholar] [CrossRef]
- Saha, M.; Tregenza, O.; Twelftree, J.; Hulston, C. A Review of Thermoelectric Generators for Waste Heat Recovery in Marine Applications. Sustain. Energy Technol. Assess. 2023, 59, 103394. [Google Scholar] [CrossRef]
- Li, K.; Garrison, G.; Zhu, Y.; Moore, M.; Liu, C.; Hepper, J.; Bandt, L.; Horne, R.; Petty, S. Thermoelectric Power Generator: Field Test at Bottle Rock Geothermal Power Plant. J. Power Sources 2021, 485, 229266. [Google Scholar] [CrossRef]
- Børset, M.T.; Wilhelmsen, Ø.; Kjelstrup, S.; Burheim, O.S. Exploring the Potential for Waste Heat Recovery during Metal Casting with Thermoelectric Generators: On-Site Experiments and Mathematical Modeling. Energy 2017, 118, 865–875. [Google Scholar] [CrossRef]
- Konstantinou, G.; Kyratsi, T.; Louca, L.S. Design of a Thermoelectric Device for Power Generation through Waste Heat Recovery from Marine Internal Combustion Engines. Energies 2022, 15, 4075. [Google Scholar] [CrossRef]
- Luo, D.; Wang, R.; Yu, W.; Zhou, W. A Numerical Study on the Performance of a Converging Thermoelectric Generator System Used for Waste Heat Recovery. Appl. Energy 2020, 270, 115181. [Google Scholar] [CrossRef]
- Luo, D.; Yang, S.; Yan, Y.; Cao, J.; Yang, X.; Cao, B. Performance Improvement of the Automotive Thermoelectric Generator System with a Novel Heat Pipe Configuration. Energy 2024, 306, 132376. [Google Scholar] [CrossRef]
- Xie, H.; Gao, T.; Long, X.; Sun, L.; Wang, J.; Xia, E.; Li, S.; Li, B.; Li, C.; Gao, M.; et al. Design and Performance of a Modular 1 Kilowatt-Level Thermoelectric Generator for Geothermal Application at Medium-Low Temperature. Energy Convers. Manag. 2023, 298, 117782. [Google Scholar] [CrossRef]
- Zhu, X.; Zuo, Z.; Wang, W.; Zhang, M.; Yin, Q.; Liu, R.; Jia, B. Transient Modeling and Analysis of a Stepped-Configuration Thermoelectric Generator Considering Non-Uniform Temperature Distribution. Appl. Energy 2025, 383, 125360. [Google Scholar] [CrossRef]
- Georgopoulou, C.A.; Dimopoulos, G.G.; Kakalis, N.M.P. A Modular Dynamic Mathematical Model of Thermoelectric Elements for Marine Applications. Energy 2016, 94, 13–28. [Google Scholar] [CrossRef]
- Sheikh, R.; Gholampour, S.; Fallahsohi, H.; Goodarzi, M.; Mohammad Taheri, M.; Bagheri, M. Improving the Efficiency of an Exhaust Thermoelectric Generator Based on Changes in the Baffle Distribution of the Heat Exchanger. J. Therm. Anal. Calorim. 2021, 143, 523–533. [Google Scholar] [CrossRef]
- Yang, W.; Xie, C.; Jin, C.; Zhu, W.; Li, Y.; Tang, X. Simulation and Experimental Study of Thermoelectric Generators with an Axial Gradient Metal Foam Heat Exchanger. Renew. Energy 2024, 232, 121061. [Google Scholar] [CrossRef]
- Jun, F.; Zhang, Z.; Chen, W.; Mao, H.; Li, J. Computational fluid dynamics simulations of the flow field characteristics in a novel exhaust purification muffler of diesel engine. J. Low Freq. Noise Vib. Act. Control. 2018, 37, 816–833. [Google Scholar] [CrossRef]
- Sajjadi, H.; Mansouri, N.; Nabavi, S.N.; Amiri Delouei, A.; Atashafrooz, M. Sensitivity analysis of natural convection in a porous cavity filled with nanofluid and equipped with horizontal fins using various optimization methods and MRT-LB. Sci. Rep. 2024, 14, 9847. [Google Scholar] [CrossRef]
- Izadi, M.; Mohebbi, R.; Sajjadi, H.; Amiri Delouei, A. LTNE modeling of magneto-ferro natural convection inside a porous enclosure exposed to nonuniform magnetic field. Physica A Stat. Mech. Its Appl. 2019, 535, 122394. [Google Scholar] [CrossRef]
- Negash, A.A.; Choi, Y.; Kim, T.Y. Experimental Investigation of Optimal Location of Flow Straightener from the Aspects of Power Output and Pressure Drop Characteristics of a Thermoelectric Generator. Energy 2021, 219, 119565. [Google Scholar] [CrossRef]
- Niu, Z.; Liu, Q.; Zhang, L.; Chen, Z. Investigation and design optimization of exhaust-based thermoelectric generator system for internal combustion engine. Energy Convers. Manag. 2014, 85, 85–101. [Google Scholar] [CrossRef]
- Choi, Y.; Negash, A.; Kim, T.Y. Waste Heat Recovery of Diesel Engine Using Porous Medium-Assisted Thermoelectric Generator Equipped with Customized Thermoelectric Modules. Energy Convers. Manag. 2019, 197, 111902. [Google Scholar] [CrossRef]
- Guo, B.Y.; Zhang, Q.; Chen, Z.; Liu, L. Numerical modelling of the gas flow through perforated plates. Chem. Eng. Res. Des. 2013, 91, 403–408. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, T.Y. Development of a Multi-Physics Numerical Model for a Multi-Component Thermoelectric Generator with Discontinuous Porosity in the Exhaust Gas Channel. Appl. Therm. Eng. 2025, 260, 125043. [Google Scholar] [CrossRef]
- Choi, T.; Kim, T.Y. Three-Zone Numerical Modeling Method for Predicting System-Level Waste Heat Recovery Performance of Thermoelectric Generator with Various Electrical Array Configurations. Energy Convers. Manag. 2021, 240, 114270. [Google Scholar] [CrossRef]
- Choi, T.; Kim, T.Y. Layer-deepened current harmonized improvement method: An optimal electrical array configuration method for performance optimization of a thermoelectric generator. Appl. Therm. Eng. 2024, 248, 123143. [Google Scholar] [CrossRef]
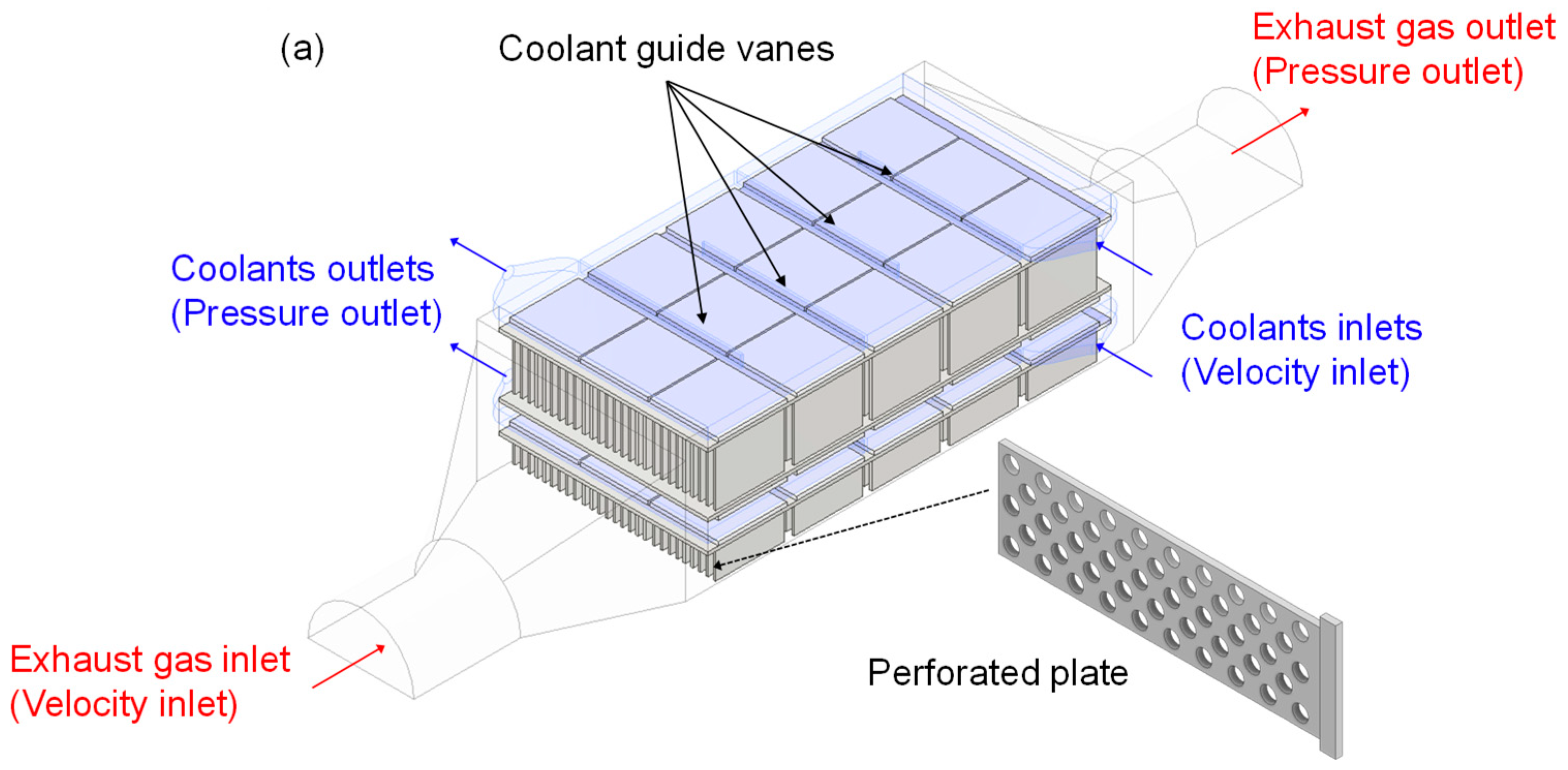
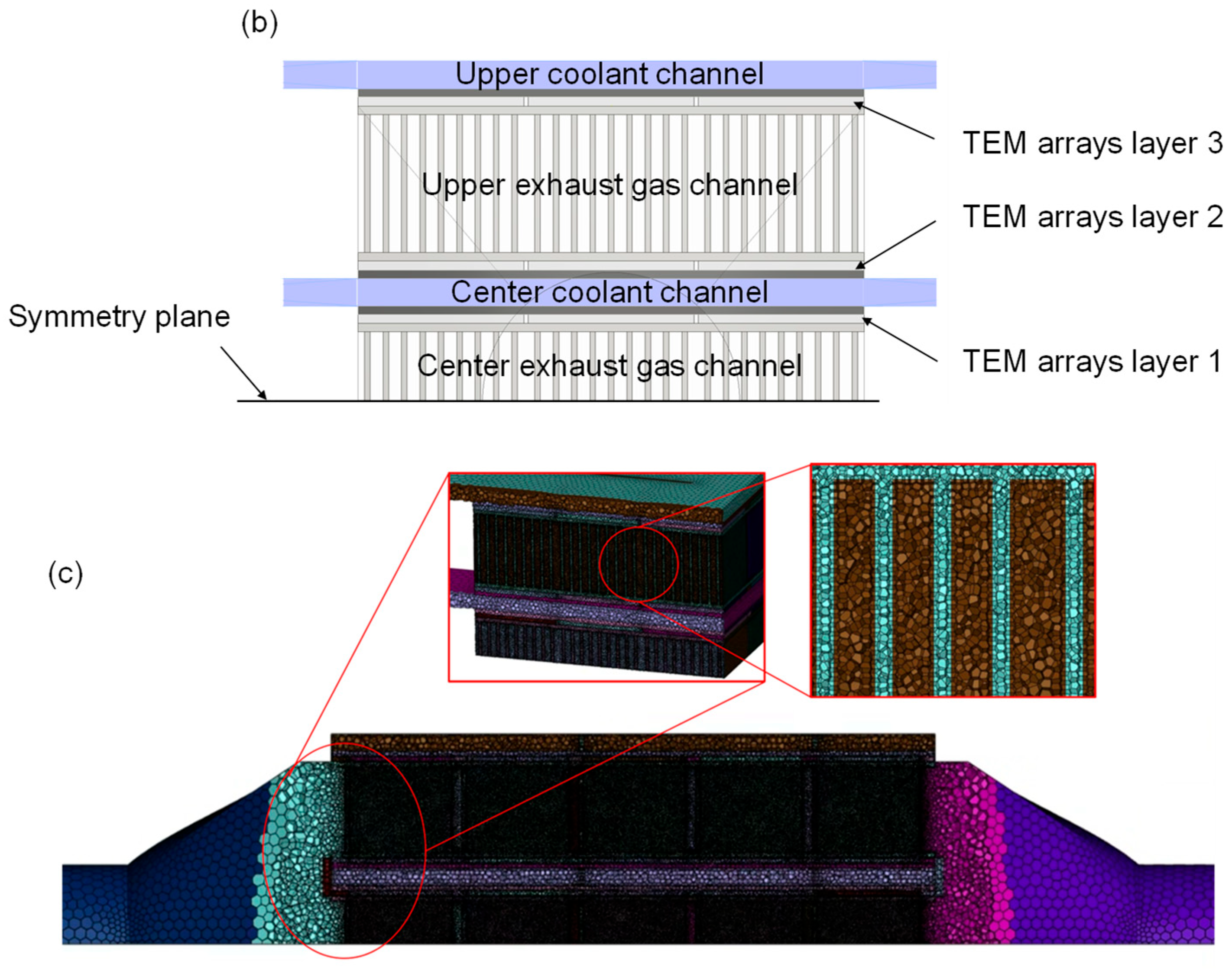
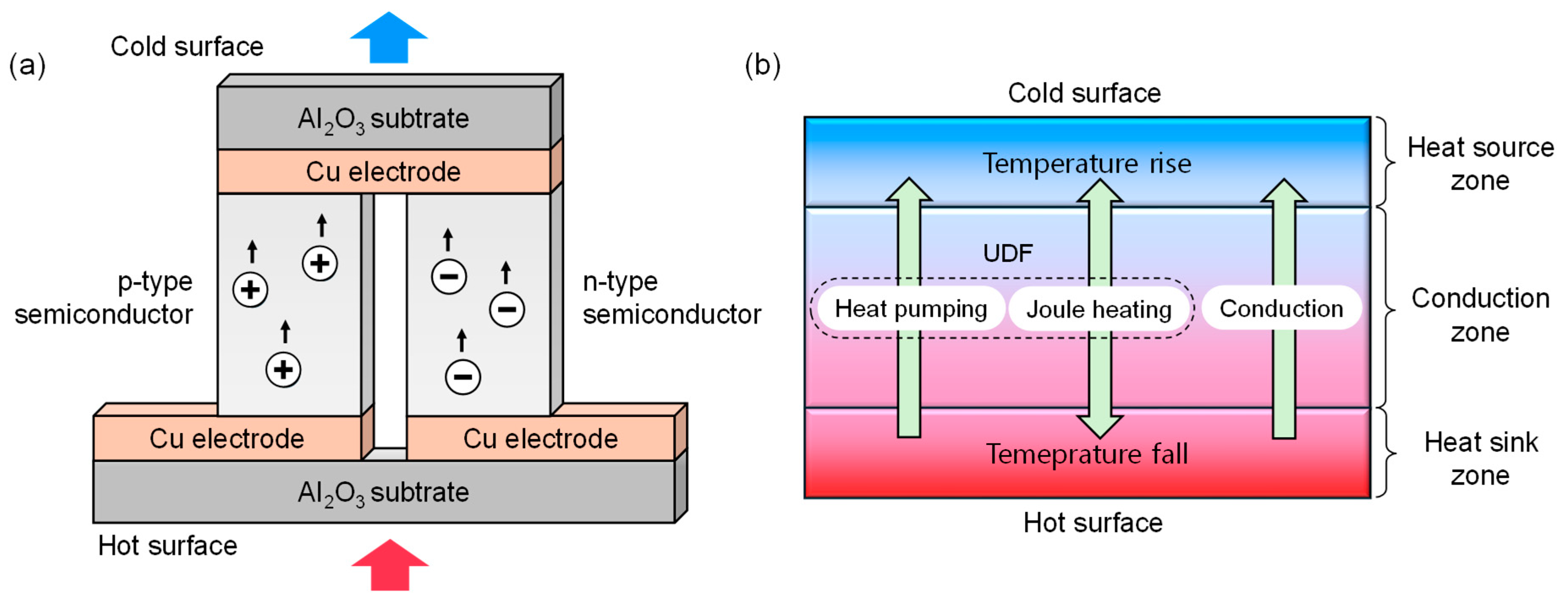
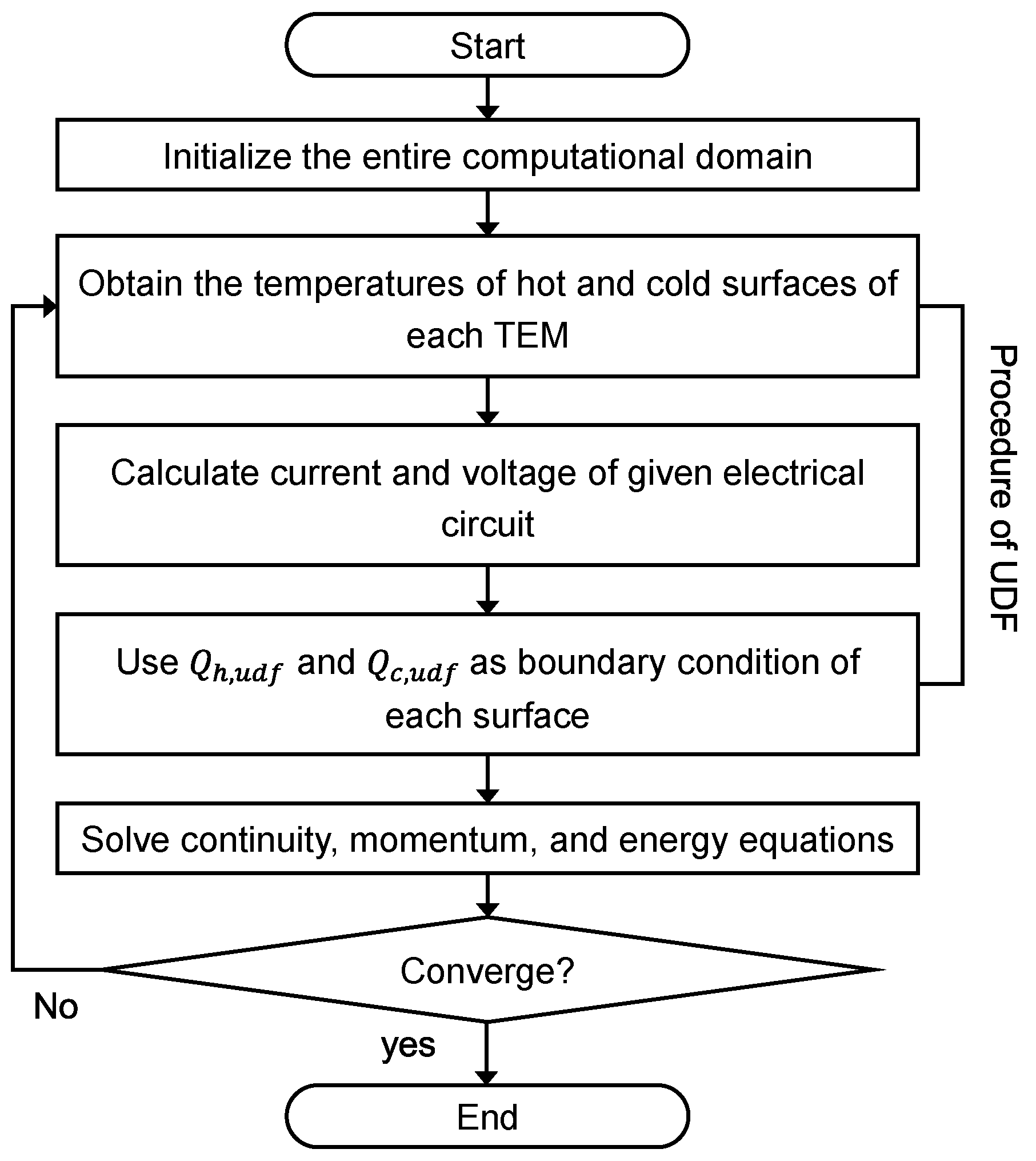




| Boundary Condition | Value | |
|---|---|---|
| Exhaust gas inlet | Temperature | 563 K |
| Velocity | 20 m/s | |
| Exhaust gas outlet | Pressure | 0 Pa (Gauge) |
| Coolant inlet | Temperature | 293 K |
| Velocity | 1.9 m/s (center), 0.95 m/s (upper) | |
| Coolant outlet | Pressure | 0 Pa (Gauge) |
| Perforated Plate | wo | A | B | C | D | E |
|---|---|---|---|---|---|---|
| ε | 1 | 0.75 | 0.60 | 0.45 | 0.30 | 0.15 |
| Dp (mm) | N/A | 5 | 5 | 5 | 5 | 5 |
| β (m−1) | N/A | 682 | 1429 | 2816 | 6122 | 20,309 |
| Number of Meshes (Million) | GCI (Output Power) | GCI (Pressure Drop) |
|---|---|---|
| 1.5 | N/A | N/A * |
| 3.5 | 6.95% | 5.22% |
| 6 | 2.21% | 4.22% |
| 9 | 0.21% | 3.27% |
| 18 | 0.21% | 0.22% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, T.; Lee, J.; Lee, J.; Kim, T.Y. Thermoelectric Energy Harvesting with a Stacked Configuration Using Porous Medium for Marine Applications. Energies 2025, 18, 1551. https://doi.org/10.3390/en18061551
Choi T, Lee J, Lee J, Kim TY. Thermoelectric Energy Harvesting with a Stacked Configuration Using Porous Medium for Marine Applications. Energies. 2025; 18(6):1551. https://doi.org/10.3390/en18061551
Chicago/Turabian StyleChoi, Taeho, Junghwan Lee, Junsu Lee, and Tae Young Kim. 2025. "Thermoelectric Energy Harvesting with a Stacked Configuration Using Porous Medium for Marine Applications" Energies 18, no. 6: 1551. https://doi.org/10.3390/en18061551
APA StyleChoi, T., Lee, J., Lee, J., & Kim, T. Y. (2025). Thermoelectric Energy Harvesting with a Stacked Configuration Using Porous Medium for Marine Applications. Energies, 18(6), 1551. https://doi.org/10.3390/en18061551







