Distributed Risk-Averse Optimization Scheduling of Hybrid Energy System with Complementary Renewable Energy Generation

Abstract

Large-scale penetration of renewable energy generation brings various challenges to the power system in terms of safety, reliability, economy and flexibility. The development of large-scale, high-security energy-storage technology can effectively address these challenges and improve the capabilities of power systems in power-supply guarantee and flexible adjustment. This paper proposes a novel distributed risk-averse optimization scheduling model of a hybrid wind–solar–storage system based on the adjustability of the storage system and the complementarity of renewable energy generation. The correlation of wind power and photovoltaic generation is quantified based on a Copula function. A risk-averse operation optimization model is proposed using conditional value at risk to quantify the uncertainty of renewable energy generation. A linear formulation of conditional value at risk under typical scenarios is developed by Gibbs sampling the joint distribution and Fuzzy C-Means clustering algorithm. A distributed solution algorithm based on an alternating-direction method of multipliers is developed to derive the optimal scheduling of hybrid wind–solar–storage system in a distributed manner. Numerical case studies based on IEEE 34-bus distribution network verify the effectiveness of the proposed model in reducing the uncertainty impact of renewable energy generation on an upstream grid (the overall amount of renewable energy generation sent back to the upstream grid has decreased about 80.6%) and ensuring the operational security of hybrid wind–solar–storage system (overall voltage deviation within 5.6%).

1. Introduction

With the rapid development of renewable energy generation (REG) technology, the penetration rate of renewable energy sources in the power system has increased significantly. The world’s newly installed capacity of renewable energy hit 510 GW in 2023, increasing nearly 50% from 2022, according to the market report Renewables 2023 released by the International Energy Agency [1]. It is predicted that by early 2025, renewables are expected to replace coal as the world’s main source of electricity. The increasing penetration of uncertain renewable energy sources has brought challenges to the power system pertaining to insufficient flexibility.

The wind–solar–storage multi-energy complementary system is an energy-supply system that comprehensively utilizes renewable energy and battery energy-storage technology to acquire a more stable and economical energy supply, since wind power and solar energy have naturally complementary characteristics [2]; that is, the solar irradiation is abandoned during the day, while the wind is strong during the night. In summer, there is sufficient solar irradiation and scare winds. While in winter and spring, there are stronger winds and insufficient solar irradiation. By utilizing the complementarity of wind and solar resources, the hybrid wind–solar–storage system can effectively reduce the intermittency of renewable generations, promote the renewable electricity consumption ability, improve energy utilization and system operation efficiency, and reduce carbon emission. In order to solve the fluctuation impact of REG on power systems, extensive studies have been carried out in recent years [3], which focus on the complementarity between renewable generations in different time scales, regions, and locations with various correlation quantification metrics [4]. A complementarity evaluation method is proposed in [5] for wind power, photovoltaic, and hydropower considering the complementarity in both fluctuation and ramp. Affected by climate conditions, the forecast errors of wind power in different geographic areas and different prediction horizons appear to be correlated [6]. In order to quantify and model the stochastic denpends between large-scale integration of wind power, Copula is utilized to ’couple’ one-dimensional marginal distributions into multivariate distribution functions [7]. Copulas are utilized in numerous studies to quantify and model the demands between REGs and weather data [8].

The HWSS system on the demand side (also called distributed HWSS in this paper) can be treated as a kind of ’microgrid’, which is considered an effective way to promote efficient use of REG. With the high penetration of REG and the fast development of electric vehicles, uncertainty on both sides of the power system intensifies the dilemma of insufficient flexible-adjustment capabilities [9]. Fluctuating REG and stochastic load-consuming behaviours challenge the safe and stable operation of local power grids. In order to reduce the uncertainty risk of energy shortage/surplus, energy-storage systems are usually utilized in microgrids [10]. Numerous studies focusing on scheduling under both the grid-connected modes and island modes have been carried out [11,12], whereas uncertainty is ignored in these papers. Considering the uncertainty of REG and the possible forecast error, a hierarchical energy-management strategy with three layers is proposed in [13] for grid-connected microgrid. High intermittency of REG is considered by updating shorter-term and more accurate forecast data. In [14], the day-ahead scheduling of microgrid energy-storage systems considering the uncertainty of unscheduled islanding events is formulated as a multi-objective stochastic optimization model with both the cost under grid-connected mode and the reliability under island mode. A convex model of a bi-directional converter for the economic dispatch of hybrid AC/DC micro-grid is proposed in [15]. These articles focus on more sophisticated modeling of microgrid-scheduling optimization in terms of multiple time scale or multi-objective function to deal with uncertainty risks.

The operation optimization problem of a wind–solar–storage multi-energy complementary system considering the uncertainty of REG is a typical uncertain optimization problem [16]. The general modeling methods to deal with uncertain optimization problems include stochastic programming [17], robust optimization [18], and distributionally robust optimization (DRO) [19], etc. Robust optimization solves the decision-making problem under the worst scenario by setting the fluctuation range of random parameters called an ’uncertainty set’, and its robustness setting is often conservative [20]. The day-ahead scheduling of a hybrid thermal–hydrowind–solar system is formulated as a multistage robust optimization in [21], including uncertainties of REG. In [22], a dispatch model of the large-scale hybrid wind/photovoltaic/hydro/thermal power system is formulated as a robust optimization with an adjustable-uncertainty budget dispatch model without a specific quantification of the uncertainty of REG. A short-term reliable–economic equilibrium operation model of the hydro–wind–solar energy systems is proposed in [23] using DRO based on Wasserstein metric. Since DRO assumes that the true distribution lies in an ambiguity set, DRO can compromise the robustness of robust optimization and the economy of stochastic programming [24], whereas the geographical distance and physical connections of multiple types of REG are not focused on in these studies, since these models are highly complex and it is difficult to include network constraints. The probability distribution of random variables is assumed in stochastic programming. Then, the uncertainty problem can be transformed into a deterministic problem under multiple scenarios that are extracted based on probability distribution. At present, the stochastic programming method based on scenario analysis has been widely used in optimal power-flow problems and economic dispatch problems involving intermittent REG.

Since the distributed hybrid wind–solar–storage (HWSS) system necessitates that the geographical distance between the access points for wind and solar power generation remains within a specific range (e.g., 10 km), the spatial correlation of REGs in HWSS system can no longer be ignored. However, less attention has been paid to integrate the complementarity of wind power and photovoltaic into optimizing the daily operation strategy of distributed HWSS system to improve the reliability of battery energy-storage system decisions and reduce the uncertainty risk faced by distributed HWSS system. Considering the system’s natural complementary characteristics among internal resources and their ability to cope with uncertainty, a novel distributed risk-averse operation optimization model of a HWSS system is proposed in this paper to overcome the uncertainty impact of renewable energy generation on an upstream grid. The complementarity of wind power and solar generation is analysed based on the Frank copula function, by which the joint probability distribution is constructed. The uncertainty risk of renewable generation is quantified by a parameterized linear function using conditional value at risk (CVaR). Then, a risk-averse operation optimization model is established, compromising the operation cost and the potential uncertainty risk loss. A linear formulation of CVaR based on typical scenarios is utilized here to reformulate the parameterized linear objective function. Gibbs sampling method is used to sample the joint distribution to generate typical scenes and scenarios reduction is realized using the clustering method. A distributed algorithm is designed based on the alternating direction method of multipliers (ADMM) to solve the risk-aversion operation optimization model. Finally, a simulation and analysis are carried out based on the IEEE 34-bus radial network to demonstrate the effectiveness of the risk-averse operation model of the HWSS system. Studies on handling the uncertainty risks brought by REG in the hybrid energy system can be divided into planning-based methods [25], scheduling-based methods [26], and control-based methods [27] according to the different time scope focused on by the researchers. In the studies using planning-based methods, seasonally adjustable resources can be applied to mitigate the impact of REG uncertainties on the annual time scale. In the studies using scheduling-based methods, hourly adjustable resources such as battery energy storage and demand response are utilized to reduce the uncertainty risk of daily operation, while control-based methods can deal with uncertainty risk in real time through control methods such as model predict control and adaptive control, etc. A detailed comparison between the proposed method and the the state of the art is reported in

Table 1. A comparison between the proposed method with the state of the art.

Ref.	Operational Stage	Resources	Distribution Network	REG Correlation	Uncertainty Model	Approah	Solution
[28]	Planning	WGs, PVs, ESS	Graph theory	No	No	NLP	PSO
[29]	Planning	WGs, PVs	Distflow	No	No	NLP	PSO
[30]	Planning	WGs, PVs, ES, CHP, ect.	No	Frank Copula	Stochastic Programming	NLP	PSO
[25]	Planning	WGs, PVs, hydrogen storage	No	No	No	MILP	Yalmip+Gurobi
[31]	Daily operation	WGs, PVs, ES, EV, heater, etc.	No	No	Robust Optimization	MILP	Yalmip+CPLEX
[32]	Daily operation	WGs, PVs, Diesel Engines, Fuel Cells	Standard Model	No	Interval Optimization	Non-convex NLP	Group Search Optimizer
[33]	Daily operation	WGs, PVs, ESS, DR	Standard Model	No	Stochastic Programming	MINLP	Benders Decomposition + CPLEX + CONOPT
[34]	Daily operation	WGs, PVs, ESS, DR, Fuel Gen	No	No	Robust Optimization	Convex	Dual decomposition
This paper	Daily operation	WGs, PVs, ESS	Branch flow model	Frank Copula	Stochastic Programming	Convex QP	ADMM

.

The main contributions of this paper are summarized as:

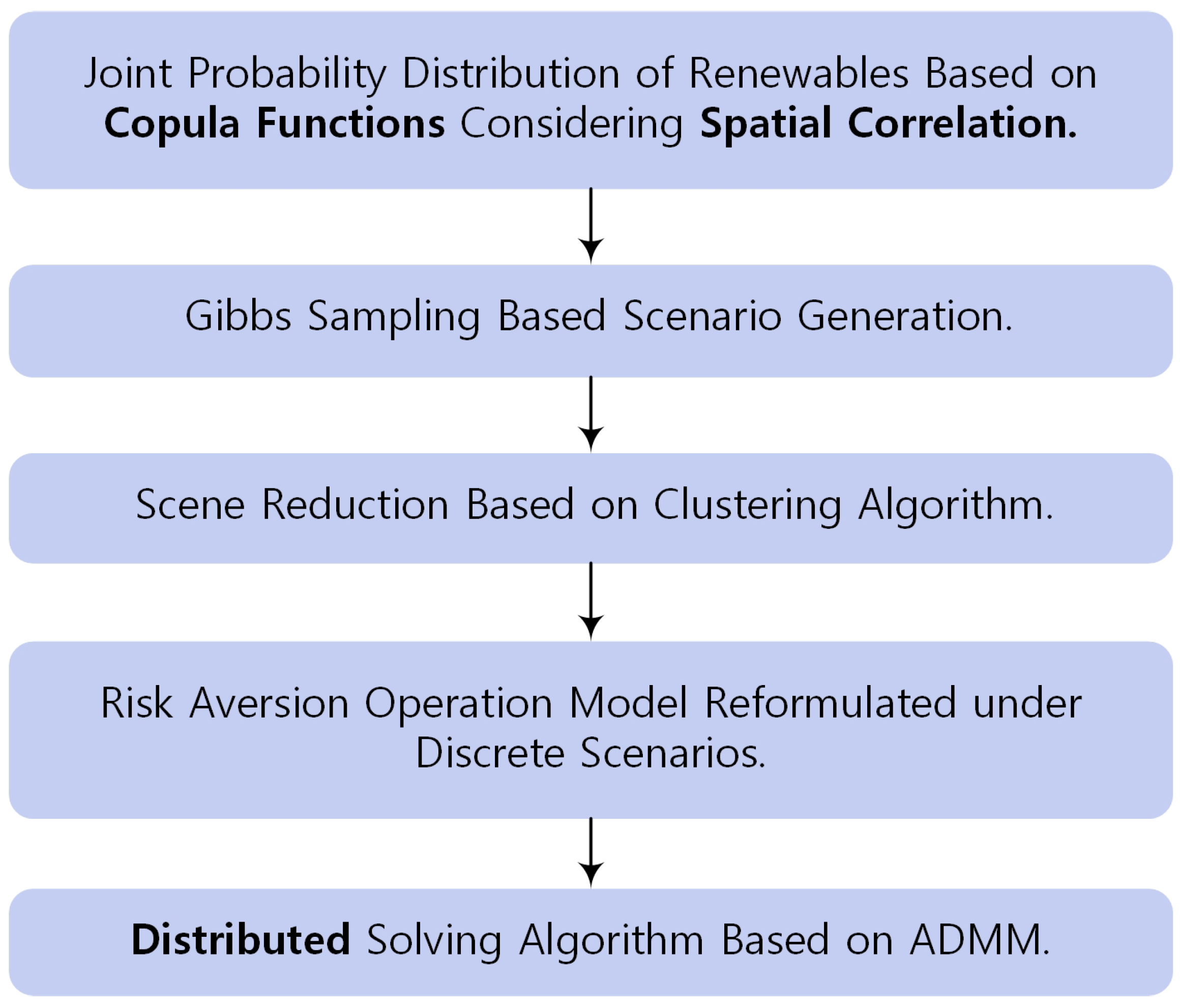
• The complementarity and relevance of wind and solar generations in HWSS is analyzed and quantified based on the Frank copula, by which the cumulative distribution function of joint probability distribution is derived.
• The uncertainty of REG is quantified by CVaR which is modelled into the cost function of risk-averse operation optimization problem of HWSS based on a parameterized linear function of CVaR.
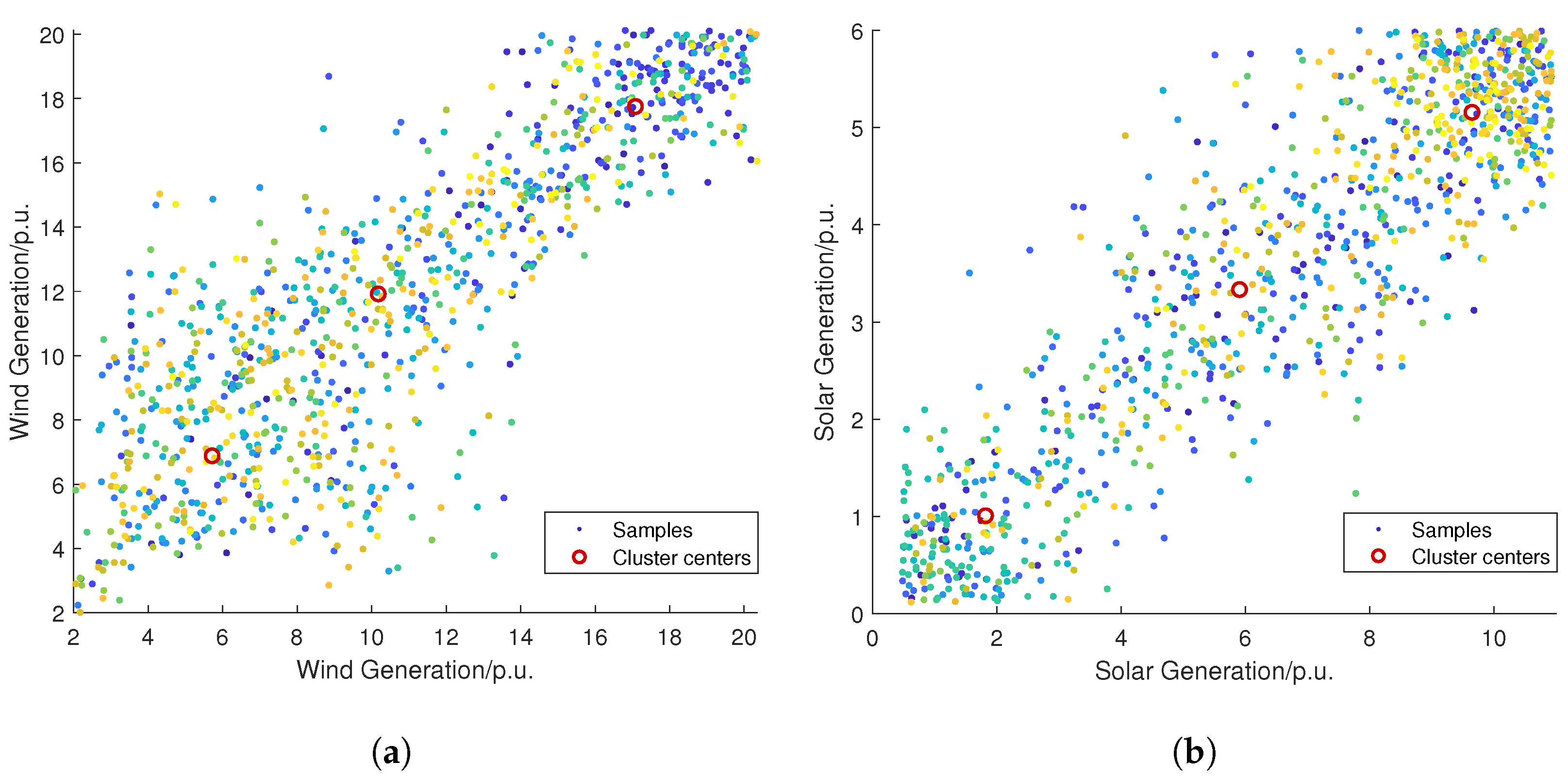
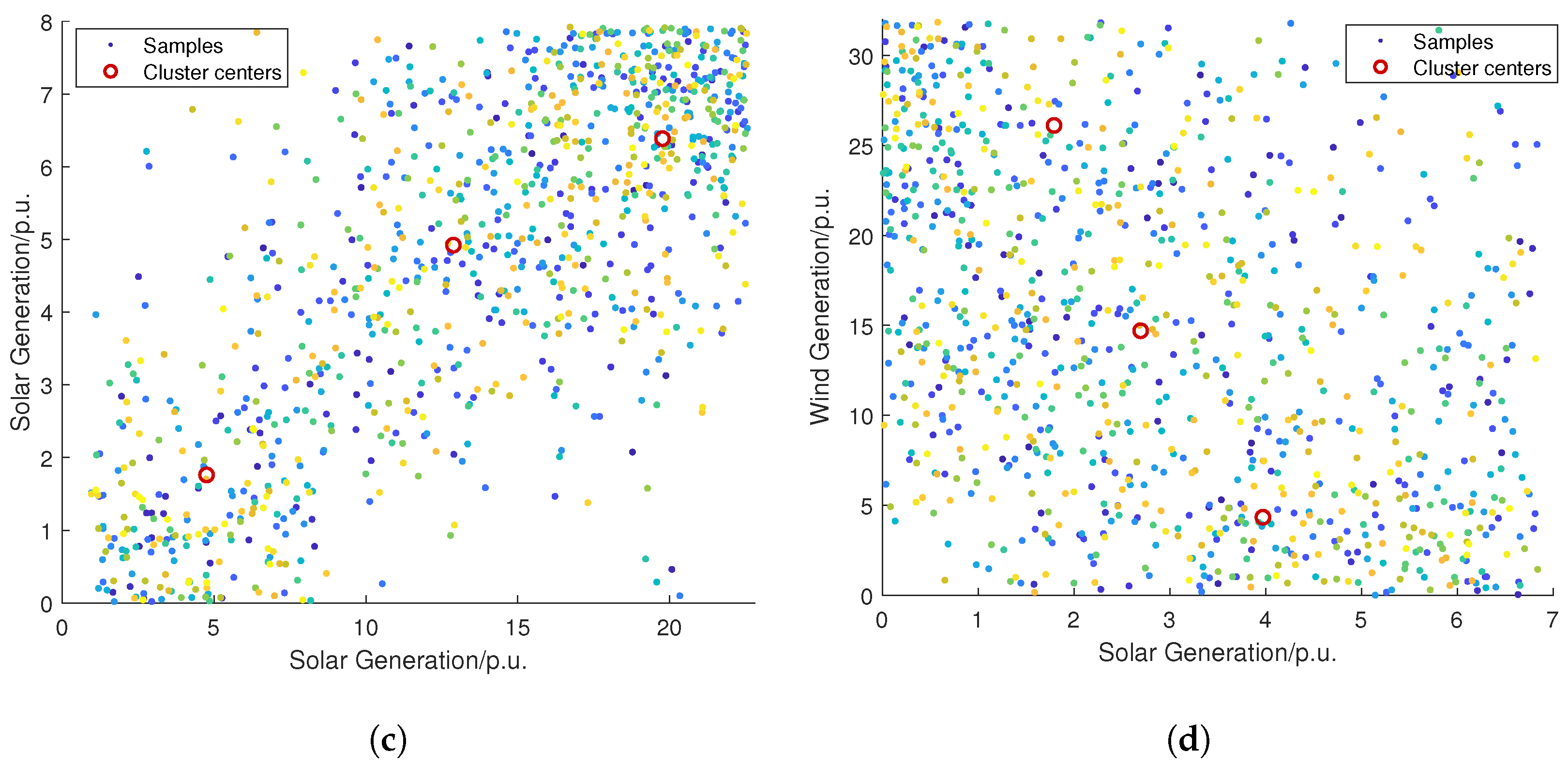
• A linear formulation of CVaR under typical scenarios is utilized to transform the risk-averse operation optimization model of HWSS into a deterministic optimization problem. Typical scenarios are selected based on Gibbs sampling and Fuzzy C-Means algorithm.
• A distributed algorithm based on ADMM is developed to solve the risk-averse operation optimization problem in distributed manner with limited variables exchanged.

The main content of this paper is organized as follows. Section 2 presents the mathematical model of components in the HWSS system. In Section 3, the uncertainty of joint output of wind and solar generation is quantified by CVaR and a risk-averse operation optimization model is proposed based on a parameterized linear function of CVaR for the safe and economic operation of the HWSS system. Section 4 describes the scenario generation-based uncertainty problem reformulation and the distributed algorithm used to solve the risk-averse operation optimization problem. Numerical studies and analyses are demonstrated in Section 5. A discussion is detailed in Section 6.

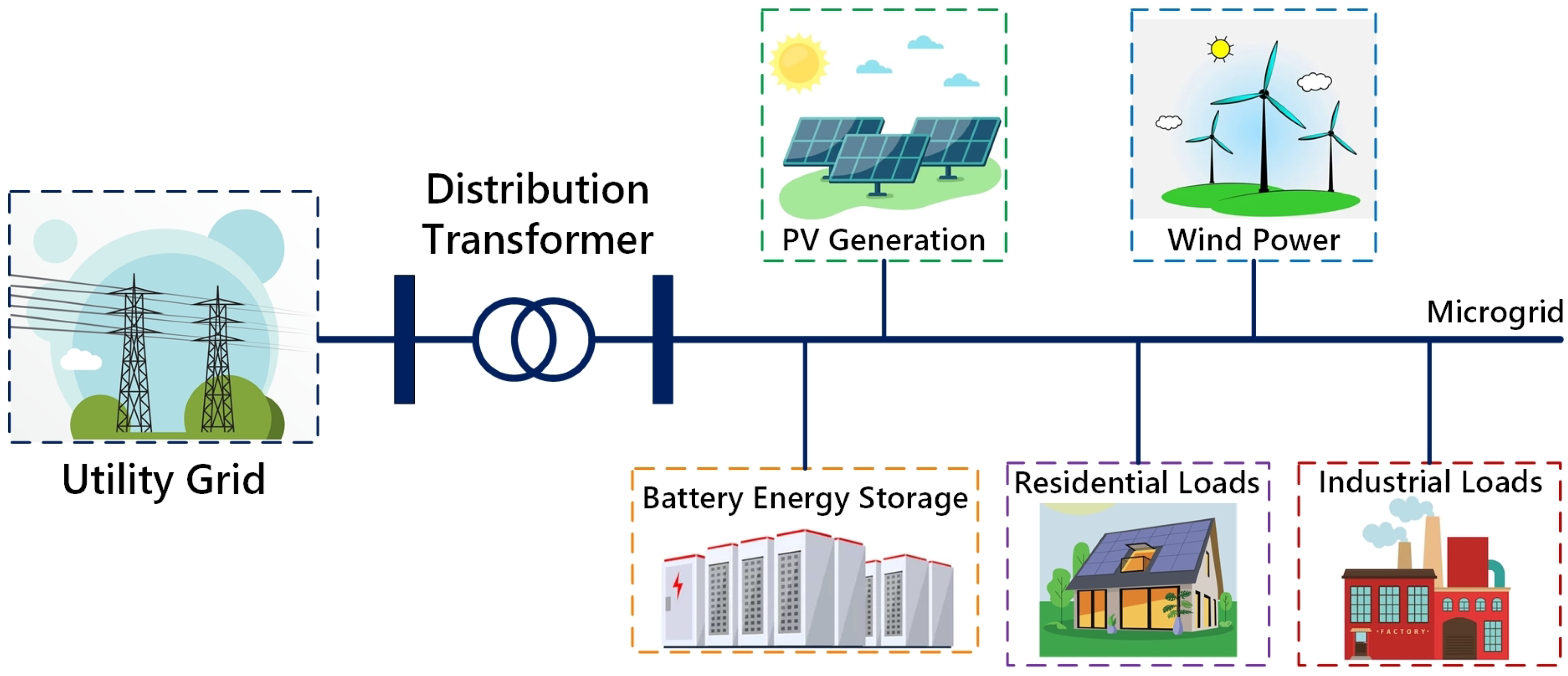
2. Hybrid Renewable Energy System Model

The HWSS system proposed in this paper is constructed from wind-power generation, PV generation, shared energy storage, consumer-side energy storage, and loads connected by a grid-connected microgrid. The detailed structure of the HWSS system is shown in Figure 1. The entire system is optimized to meet the local load demand at a low cost while reducing the impact of fluctuated REG output on the upstream grid.

2.1. Network Model

In this paper, a branch flow model [35] is utilized to formulate the radial network of HWSS system denoted as $\mathbb{M}:=\{\mathbb{N},\mathbb{B}\}$, $\mathbb{N}:=\{0,1,\dots ,N-1\}$. Each bus $i\in \mathbb{N}$ except the root bus has an unique ancestor bus $A_i$ and a set of children buses ${\mathbb{C}}_i$. Hence, each branch $b\in \mathbb{B}$ can be uniquely labeled by its endpoints i and $A_i$, in other words, the branch points from bus i to the ancestor bus $A_i$ is labeled as branch i. Let ${\mathrm{z}}_i={\mathrm{r}}_i+\mathbf{i}·{\mathrm{x}}_i$ represent the complex impedance for each branch i. The branch flow model for microgrid $\mathbb{M}$ is described as follows:

$$\begin{array}{cc}\hfill P_i& =\sum _{j\in {\mathbb{C}}_i}{P}_j+p_i\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill Q_i& =\sum _{j\in {\mathbb{C}}_i}{Q}_j+q_i\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill v_{A_i}& -v_i+2({\mathrm{r}}_i·P_i+{\mathrm{x}}_i·Q_i)=0\hfill \end{array}$$

(3)

where $v_i=\left|{\left(V_i\right)}^2\right|$ represents the squared magnitude of a complex voltage of bus i; $p_i$ and $q_i$ denote the active and reactive power injection at bus i, respectively; $P_i$ and $Q_i$ represent the active and reactive power flow on branch i, respectively. The voltage of bus i is restricted by the following constraints:

$$\begin{array}{c}\hfill v_{min}\le v_i\le v_{max},i\in \mathbb{N}\end{array}$$

(4)

where $v_{min}$ defines the lower bound of volatge at bus $i\in \mathbb{N}$; and $v_{max}$ describes the upper bound of volatge at bus $i\in \mathbb{N}$.

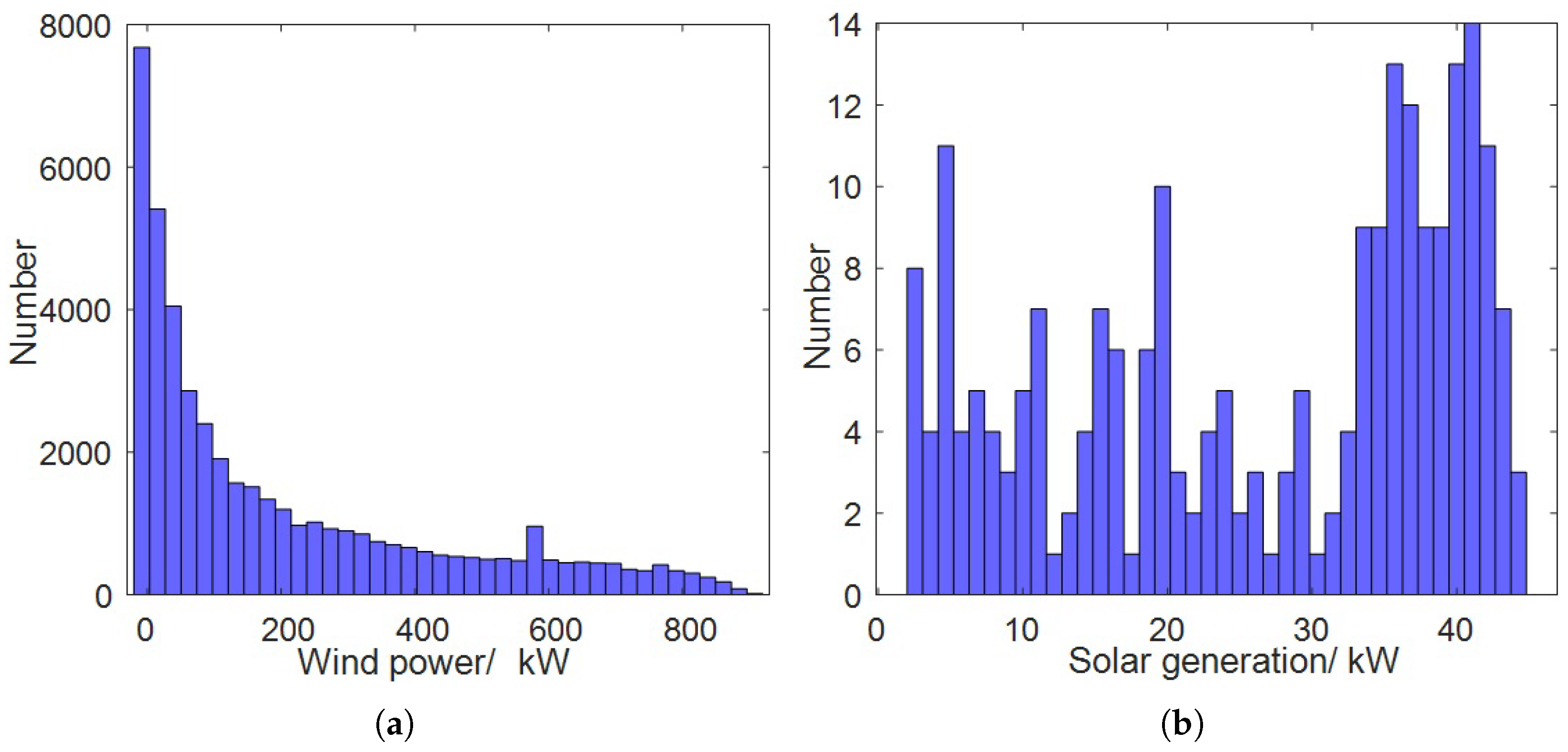
2.2. Wind–Photovoltaic Correlation Model

The probabilistic prediction model based on parameterized assumptions can obtain the probability distribution of REG based on historical data directly [36]. It is assumed that probability density functions (PDF) of wind power and photovoltaic generation can be obtained based on parametric probabilistic prediction methods. Let $p^{\mathrm{wind}}$ and $p^{\mathrm{pv}}$ denote the wind-power generation and photovoltaic generation, respectively. Then, the accordance PDF can be described as $f\left(p^{\mathrm{wind}}\right)$ and $f\left(p^{\mathrm{pv}}\right)$, respectively.

The correlation among wind-power generation and photovoltaic generation are described by a function called copula. Copulas are considered as functions that join or couple the multivariate distribution functions to their one-dimensional marginal distribution functions [37,38]. Sklar’s theorem gives the relationship between a joint probability distribution and marginal distribution functions. For a two-dimensional distribution function denoted as $H(x_1,x_2)$, the accordance marginal distribution functions are represented as $F_1\left(x_1\right)$ and $F_2\left(x_2\right)$, respectively. Then, there exists a copula C which satisfies:

$$\begin{array}{c}\hfill H(x_1,x_2)=C(F_1\left(x_1\right),F_2\left(x_2\right))\end{array}$$

(5)

The elliptical copulas family (normal copula, t-copula) and Archimedean copulas family (Frank copula, Gumbel copula, Clayton copula) are the most commonly used copulas in research [39]. Figure 2 demonstrates the asymmetrical characteristics in probability distributions of wind power and solar generation by histograms. Considering the complementary and asymmetry characteristics in probability distributions of wind and solar power generation, one of the Archimedean family copulas called the ’Frank-Copula’ is utilized to describe the inter-correlation between wind and solar-power generation. Compared with other copula functions, Frank-Copula achieves better performance in describing the correlation of wind and solar outputs [30].

The cumulative distribution function (CDF) and probability density function (PDF) of the Frank copula are described as follows:

$$\begin{array}{c}\hfill C^{\mathrm{Frank}}(h,g;\theta )=-{\displaystyle \frac{1}{\theta }}ln(1+{\displaystyle \frac{(e^{-\theta ·h}-1)(e^{-\theta ·g}-1)}{e^{-\theta }-1}})\end{array}$$

(6)

$$\begin{array}{c}\hfill c^{\mathrm{Frank}}(h,g;\theta )={\displaystyle \frac{-\theta (e^{-\theta }-1)e^{-\theta (h+g)}}{{[(e^{-\theta }-1)+(e^{-\theta ·h}-1)(e^{-\theta ·g}-1)]}^2}}\end{array}$$

(7)

where $h=F_1\left(x_1\right)$ and $g=F_2\left(x_2\right)$ denote the marginal distribution functions of wind power and solar generation. Then, the CDF of joint probability distribution can be obtained by substituting the CDF of the Frank copula (6) into Equation (5).

2.3. Battery Energy Storage Model

The battery energy-storage system (BESS) in the HWSS system can be shared energy storage, which is constructed and possessed by the third-party utility or consumer-side energy storage which is owned by individual. The BESS model in the HWSS system at bus i for $\forall t\in \mathbb{T}:=\{1,2,\dots ,T\}$ is formulated as:

$$\begin{array}{cc}\hfill & 0\le p_{i,t}^{\mathrm{ch}}\le \overline{p_{i,t}^{\mathrm{ch}}}\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill & 0\le p_{i,t}^{\mathrm{dis}}\le \overline{p_{i,t}^{\mathrm{dis}}}\hfill \end{array}$$

(8b)

$$\begin{array}{cc}\hfill & p_{i,t}^{\mathrm{ch}}·p_{i,t}^{\mathrm{dis}}=0\hfill \end{array}$$

(8c)

$$\begin{array}{cc}\hfill & \underline{E_{i,t}}\le \sum _{\tau =1}^t\Delta \tau ·({\eta }^{\mathrm{ch}}·p_{i,\tau }^{\mathrm{ch}}-{\displaystyle \frac{p_{i,\tau }^{\mathrm{dis}}}{{\eta }^{\mathrm{dis}}}})+E_{i,0}\le \overline{E_{i,t}}\hfill \end{array}$$

(8d)

where $p_{i,t}^{\mathrm{ch}}$ and $p_{i,t}^{\mathrm{dis}}$ denote the charging and discharging power of the BESS connected to bus i at time slot t, respectively; ${\eta }^{\mathrm{ch}}$ and ${\eta }^{\mathrm{dis}}$ represent the charging efficiency and discharging efficiency of the BESS, respectively; boundary constraints (8a)–(8b) describe the upper and lower bound of charging and discharging power of BESS, respectively; constraint (8c) ensures the BESS to be either charged or discharged at a single time slot; constraint (8d) indicates the stored energy of the BESS at time slot t within the allowable upper bound and lower bound, $E_{i,0}$ denotes the initial energy amount stored in the BESS.

3. Risk-Averse Operation Optimization Model

Conditional value at risk (CVaR) is a method used to measure the risk of financial assets or investment portfolios. It provides a more comprehensive risk assessment than the traditional value at risk. CVaR describes the average loss of a portfolio when the loss exceeds a given value at risk, which is the maximum amount of loss expected at a given confidence level and holding period. For any given confidence level $\alpha$, CVaR can be used to measure the uncertainty risk brought by the volatility of REG.

$$\begin{array}{c}\hfill {\mathrm{CVaR}}_{1-\alpha }=\mathbb{E}(-c_x|-c_x\ge {\mathrm{VaR}}_{\alpha })\end{array}$$

(9)

where $c_x$ represent the random loss brought by intermittent REG; $Va{R}_{\alpha }$ denotes the value at risk with confidence level $\alpha$; and $\mathbb{E}(·)$ is the function of mathematic expectation. In this paper, a parameterized linear function [40] is used to describe the proportion of the potential uncertainty risk loss in contrast with the operation cost, where CVaR is used to quantify the uncertainty risk loss caused by REG,

$$\begin{array}{c}\hfill C^{\mathrm{RA}}=\mathbb{E}\left(c\right)+\varphi {\mathrm{CVaR}}_{\alpha }\left(c\right)\end{array}$$

(10)

where $C^{\mathrm{RA}}$ denotes the risk-averse operation cost of HWSS system; c defines the entire operation cost under the uncertainty of REG; $\varphi$ represents the risk preference of system operator, a larger $\varphi$ means the system operator is more risk-averse; and $\alpha \in (0,1)$ is the confidence level of CVaR.

The entire operation cost of HWSS system for a single time slot is described as:

$$\begin{array}{c}\hfill c_t=\sum _{i\in \mathbb{N}}[{\sigma }_i^{\mathrm{deg}}·(p_{i,t}^{\mathrm{ch}}+p_{i,t}^{\mathrm{dis}})]+{\eta }^{\mathrm{up}}(P_{0,t},\pi )\end{array}$$

(11)

where the first item of the operation cost (11) describes the depreciation cost of BESS, ${\sigma }_i^{\mathrm{deg}}$ denotes the degradation rate of BESS; the second item ${\eta }^{\mathrm{up}}(P_{0,t},\pi )$ describes the entire penalty cost of the HWSS system in exchanging energy with upstream grid, which is utilized to facilitate the self-consumption of the HWSS system.

The entire energy-exchange penalty of the HWSS system with an upstream grid is described by a quadratic function:

$$\begin{array}{c}\hfill {\eta }^{\mathrm{up}}(P_{0,t},\pi )=\pi ·{\left(P_{0,t}\right)}^2\end{array}$$

(12)

where $\pi$ denotes the penalty coefficient for the HWSS system to exchange energy with the upstream grid; the power injection from root bus 0 to the upstream grid can be detailed as:

$$\begin{array}{c}\hfill P_{0,t}=\sum _{i\in \mathbb{N}}(p_i^{\mathrm{wind}}+p_i^{\mathrm{pv}}+p_i^{\mathrm{dis}}-p_i^{\mathrm{ch}}-p_i^{\mathrm{d}})-p_{0,t}^{\mathrm{ch},\omega }+p_{0,t}^{\mathrm{dis},\omega }.\end{array}$$

(13)

where $p_{i,t}^{\mathrm{d}}$ denotes the power demand at time slot t under bus i. Then, the risk-averse operation model of HWSS system can be formulated as:

$$\begin{array}{cc}\hfill & \underset{p_{i,t}^{\mathrm{ch}},p_{i,t}^{\mathrm{dis}}}{min}\mathbb{E}\left[\sum _{t\in \mathbb{T}}{c}_t\right]+\varphi {\mathrm{CVaR}}_{\alpha }\left[\sum _{t\in \mathbb{T}}{c}_t\right]\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill s.t.& \left(1\right)–\left(3\right)\mathrm{and}\left(4\right),i\in \mathbb{N},t\in \mathbb{T}\hfill \end{array}$$

(14b)

$$\begin{array}{cc}\hfill & \left(\text{8a})–(\text{8d}\right),i\in \mathbb{N},t\in \mathbb{T}\hfill \end{array}$$

(14c)

$$\begin{array}{cc}\hfill p_{i,t}=& p_{i,t}^{\mathrm{wind}}+p_{i,t}^{\mathrm{pv}}+p_{i,t}^{\mathrm{dis}}-p_{i,t}^{\mathrm{d}}-p_{i,t}^{\mathrm{ch}},i\in \mathbb{N},t\in \mathbb{T}\hfill \end{array}$$

(14d)

4. Solution Methodology

4.1. Typical Scenario-Based Problem Reformulation

Gibbs sampling is a kind of Markov-Chain Monte Carlo which is used to generate samples from high-dimensional joint probability distributions. It gradually approaches the target joint distribution by repeatedly extracting conditional distribution samples of each variable. Gibbs sampling is widely used in multi-dimensional distribution sampling. Thus, in this paper, the Gibbs sampling method is used to sample the joint distribution and generate typical scenes to solve the risk-averse operation problem (14) of the HWSS system. After the scenario generation by Gibbs sampling, scenario reduction is realized using the clustering method based on the Fuzzy C-Means (FCM) algorithm. The detailed framework for solution methods of the risk-averse operation problem (14) is shown in Figure 3.

The Fuzzy C-Means clustering algorithm is a classic fuzzy clustering algorithm used for data-cluster analysis in unsupervised learning. Different from the traditional hard clustering algorithm, data may belong to all the cluster classes at the same time with a certain fuzzy membership degree in the FCM method [41]. FCM obtains cluster centers by minimizing the objective function, essentially the sum of the distances from each point to each class. Let $\{c_1,c_2,\dots ,c_C\}$ represent the set of cluster centers; the objective of FCM can be described as follows:

$$\begin{array}{cc}\hfill & J(U,C)=\sum _{i=1}^N\sum _{j=1}^k{u}_{ij}^m{d}_{ij}^2\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \sum _{j=1}^C{u}_{ij}=1,u_{ij}\in [0,1]\hfill \end{array}$$

(16)

where $u_{ij}$ denotes the membership degree of sample $x_i$ to the cluster center $c_j$; $d_{ij}$ represents the distance between sample $x_i$ and the cluster center $c_j$; $m>1$ denotes the ambiguity index; $c_j$ is the cluster center. The detailed expression of membership degree $u_{ij}$ and cluster center $c_j$ is as follows:

$$\begin{array}{cc}\hfill u_{ij}& ={\displaystyle \frac{1}{{\sum }_{k=1}^C{\left(\frac{d_{ij}}{d_{ik}}\right)}^{\frac{2}{m-1}}}}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill c_j& ={\displaystyle \frac{{\sum }_{i=1}^N{u}_{ij}^m{x}_i}{{\sum }_{i=1}^N{u}_{ij}^m}}\hfill \end{array}$$

(18)

The basic process of FCM is depicted in Algorithm 1. Since ${\mathrm{CVaR}}_{\alpha }$ represents the expectation of cost that exceeds the VaR at the given confidence level $\alpha$, which can be approximately calculated by the expected cost of the $(1-\alpha )100\%$ scenarios with a cost greater than VaR. A linear formulation of CVaR is proposed in [42], which is utilized here to transform the parameterized linear objective function. Let $\omega \in \mathsf{\Omega }$ denote the typical scenarios selected by the Gibbs method, the ${\mathrm{CVaR}}_{\alpha }\left(\xi \right)$ can be calculated by solving the following optimization problem [26,43]:

$$\begin{array}{cc}\hfill \underset{\xi ,\beta \left(\omega \right)}{min}\xi +{\displaystyle \frac{1}{1-\alpha }}\sum _{\omega \in \mathsf{\Omega }}\psi \left(\omega \right)·& \beta \left(\omega \right)\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill s.t.F_{loss}\left(\omega \right)-\xi -\beta \left(\omega \right)& \le 0;\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(19b)

$$\begin{array}{cc}\hfill \beta \left(\omega \right)& \ge 0;\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(19c)

where the optimal solution of (19) denoted as $\widehat{\xi }$ is the optimal value at risk (VaR). $\beta \left(\omega \right)$ denotes the difference between the cost of scenario $\omega$ and VaR $\widehat{\xi }$; $F_{loss}\left(\omega \right)$ denotes the discrete cost distribution. Then, the problem (14) under discrete scenarios can be reformulated as:

$$\begin{array}{cc}\hfill min& \sum _{\omega \in \mathsf{\Omega }}\psi \left(\omega \right)\sum _{t\in \mathbb{T}}{c}_t\left(\omega \right)+\varphi [\xi +{\displaystyle \frac{1}{1-\alpha }}\sum _{\omega \in \mathsf{\Omega }}\psi \left(\omega \right)\beta \left(\omega \right)]\hfill \end{array}$$

(20a)

$$\begin{array}{cc}\hfill s.t.& \left(1\right)–\left(3\right)\mathrm{and}\left(4\right),i\in \mathbb{N},t\in \mathbb{T},\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(20b)

$$\begin{array}{cc}\hfill & \left(\text{8a})–(\text{8d}\right),i\in \mathbb{N},t\in \mathbb{T},\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(20c)

$$\begin{array}{cc}\hfill & \sum _{t\in \mathbb{T}}{c}_t\left(\omega \right)-\xi -\beta \left(\omega \right)\le 0,\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(20d)

$$\begin{array}{cc}\hfill & \beta \left(\omega \right)\ge 0,\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(20e)

$$\begin{array}{cc}\hfill p_{i,t}^{\omega }& =p_{i,t}^{\mathrm{wind},\omega }+p_{i,t}^{\mathrm{pv},\omega }+p_{i,t}^{\mathrm{dis},\omega }-p_{i,t}^{\mathrm{d}}-p_{i,t}^{\mathrm{ch},\omega },i\in \mathbb{N},t\in \mathbb{T},\forall \omega \in \mathsf{\Omega }\hfill \end{array}$$

(20f)

where $\psi \left(\omega \right)$ denotes the probability of scenario $\omega \in \mathsf{\Omega }$, $\beta \left(\omega \right)$ describes the difference between the cost of scenario $\omega$ and VaR. $c_t\left(\omega \right)$ represents the entire operation cost of the HWSS system of time slot t under scenario $\omega \in \mathsf{\Omega }$, which is detailed as follows:

$$c_t\left(\omega \right)=\pi ·{(\sum _{i\in \mathbb{N}}{p}_{i,t}^{\omega }-p_{0,t}^{\mathrm{ch},\omega }+p_{0,t}^{\mathrm{dis},\omega })}^2+\sum _{i\in \mathbb{N}}\left[{\sigma }_i^{\mathrm{deg}}(p_{i,t}^{\mathrm{ch},\omega }+p_{i,t}^{\mathrm{dis},\omega })\right]$$

(21)

Algorithm 1: Basic process of FCM

Initialize parameters 1: Initialize the number of cluster centers C, the ambiguity index m, the membership degree matrix $U_0\in [0,1]$ Iterative calculation 2: do 3:    Calculate cluster center $c_j$ according to (18). 4:    Update membership-degree matrix U according to (17). 5: until $\parallel J^h-J^{h-1}\parallel \le ϵ$, $h=h+1$ denotes the iterative index.

4.2. ADMM-Based Distribution Algorithm

Since the objective function of the risk-averse problem under discrete scenarios (20) is quadratic and $\pi \ge 0$. The quadratic inequality constraints (20d) have a convex quadratic form (the Hessian matrix of the quadratic inequality constraints (20d) is positive semidefinite [44]). Therefore, the risk-averse problem under discrete scenarios (20) is a typical convex optimization problem which can be solved directly using commercial solvers, such as Cplex, Gurobi, etc. However, considering the dispersion of renewable generation locations and the complexity of optimization problems under multiple scenarios, centralized optimization requires a hybrid dispatching platform of the HWSS system. With the expansion of the network scale, solving optimization problems will face greater computational pressure. The risk-aversion operation optimization problem of the distributed HWSS system (14) is a typical convex optimization problem. As the number of scenarios increases, the size of the problem will expand significantly. Besides, the REG, BESS, and load in distributed HWSS system may belong to a different investment entity and the sites are physically far apart. Centralized optimization requires a unified dispatch management platform collecting data and information from all parties, bringing challenge to communication process and massive data encryption. The alternating direction method of multipliers (ADMM) is widely used to solve distributed convex optimization, taking the form of a decomposition–coordination procedure. The ADMM algorithm finds the solution to a large global problem by coordinating the solutions to small local subproblems [45]. Therefore, the ADMM algorithm is used to solve this problem to optimize operation strategy with limited information exchange and achieve better scalability. Then, problem (20) is reformulated into a standard compact matrix as follows:

$$\begin{array}{cc}\hfill & \underset{{\mathit{x}}_i,{\mathit{z}}_i}{min}\sum _{i\in \mathbb{N}}f\left({\mathit{x}}_i\right)+g\left({\mathit{z}}_i\right)\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill s.t.& {\mathit{x}}_j-{\mathit{z}}_{ji}=0,j\in N,i\in \mathbb{N}\hfill \end{array}$$

(22b)

$$\begin{array}{cc}\hfill & \sum _{j\in \mathbb{N}}{K}_{ij}·{\mathit{z}}_{ji}=0,i\in \mathbb{N}\hfill \end{array}$$

(22c)

$$\begin{array}{cc}\hfill & {\mathit{x}}_i\in {\mathcal{X}}_i,i\in \mathbb{N}\hfill \end{array}$$

(22d)

where ${\mathit{x}}_i:=\left\{[p_{i,t}^{\omega },p_{i,t}^{\mathrm{ch},\omega },p_{i,t}^{\mathrm{dis},\omega },v_{i,t}^{\omega },P_{i,t}^{\omega },Q_{i,t}^{\omega }|t\in \mathbb{T}]\right|\omega \in \mathsf{\Omega }\}$ denotes the variables to be solved. Specifically, variables under the root bus are global variables which are denoted as ${\mathit{x}}_0:=\left\{{\beta }_x\left(\omega \right)\right|\omega \in \mathsf{\Omega },{\xi }_x\}$. ${\mathit{z}}_i:=\{{\mathit{p}}_{ii},{\mathit{q}}_{ii},{\mathit{v}}_{ii},{\mathit{v}}_{A_{i}i},[P_{ji},Q_{ji}]|j\in {\mathbb{C}}_i\}$ are auxiliary variables included at bus i to formulate the problem (20) into a standard compact matrix; ${\mathit{z}}_{ji}$ represents the duplicate of variables ${\mathit{x}}_j$ at bus j obtained by bus i; $\mathit{z}:=\left\{{\mathit{z}}_i\right|i\in \mathbb{N},{\beta }_z\left(\omega \right)|\omega \in \mathsf{\Omega },{\xi }_z\}$; ${\sum }_{j\in \mathbb{N}}{K}_{ij}·{\mathit{z}}_{ji}=0$ represents equation constraints (1)–(3); ${\mathcal{X}}_i$ denotes the feasible region of variables ${\mathit{x}}_i$ described by constraints (4), (8a)–(8d), and (20d)–(20e).

The objective of risk-aversion operation optimization problem (14d) is divided into two parts, the first part is the function of BESS and network variables:

$$f\left({\mathit{x}}_i\right)=\sum _{\omega \in \mathsf{\Omega }}\psi \left(\omega \right)\sum _{t\in \mathbb{T}}[\sum _{i\in \mathbb{N}}{\sigma }_i^{\mathrm{deg}}(p_{i,t}^{\mathrm{ch},\omega }+p_{i,t}^{\mathrm{dis},\omega })+\pi {\left(P_{0,t}\right)}^2]$$

(23)

The second part is the function of CVaR variables:

$$\begin{array}{c}\hfill g\left({\mathit{z}}_i\right)=\varphi \left[\xi +{\displaystyle \frac{1}{1-\alpha }}\sum _{\omega \in \mathsf{\Omega }}\psi \left(\omega \right)\beta \left(\omega \right)\right].\end{array}$$

(24)

Then, the scaled augmented Lagrangian of problem (22) is detailed as:

$$\begin{array}{c}\hfill L_{\rho }=\sum _{i\in \mathbb{N}}f\left({\mathit{x}}_i\right)+g\left({\mathit{z}}_i\right)+\sum _{i\in \mathbb{N}}\sum _{j\in N_i}{\displaystyle \frac{\rho }{2}}{\parallel {\mathit{x}}_i-{\mathit{z}}_{ij}+{\mathit{y}}_{ij}\parallel }_2^2\end{array}$$

(25)

where ${\mathit{y}}_{ji}$ denotes the Lagrange multiplier of consensus constraint ${\mathit{x}}_j-{\mathit{z}}_{ji}=0$. Therefore, the ADMM components in each iteration is represented as:

$$\begin{array}{cc}\hfill {\mathit{x}}_i^{\mathrm{k}+1}& =arg\underset{{\mathit{x}}_i\in \mathcal{X}}{min}\left[f\left({\mathit{x}}_i\right)+\sum _{j\in N_i}{\displaystyle \frac{\rho }{2}}{\parallel {\mathit{x}}_i-{\mathit{z}}_{ij}^{\mathrm{k}}+{\mathit{y}}_{ij}^{\mathrm{k}}\parallel }_2^2\right]\hfill \end{array}$$

(26a)

$$\begin{array}{cc}\hfill {\mathit{z}}_i^{\mathrm{k}+1}& =arg\underset{{\mathit{z}}_i\in \mathcal{Z}}{min}\left[g\left({\mathit{z}}_i\right)+\sum _{j\in N_i}{\displaystyle \frac{\rho }{2}}{\parallel {\mathit{x}}_j^{\mathrm{k}+1}-{\mathit{z}}_{ij}+{\mathit{y}}_{ji}^{\mathrm{k}}\parallel }_2^2\right]\hfill \end{array}$$

(26b)

$$\begin{array}{cc}\hfill {\mathit{y}}_{ji}^{\mathrm{k}+1}& ={\mathit{y}}_{ji}^k+{\mathit{x}}_j^{\mathrm{k}+1}-{\mathit{z}}_{ji}^{\mathrm{k}+1}\hfill \end{array}$$

(26c)

where $\mathcal{Z}:=\left\{{\mathit{z}}_i|{\sum }_{j\in \mathbb{N}}{K}_{ij}{\mathit{z}}_{ji}=0,i\in \mathbb{N}\right\}$ represents the feasible region of auxiliary variable ${\mathit{z}}_i$. The stopping criteria of ADMM iterations is as follows:

$$\begin{array}{cc}\hfill {\epsilon }_{pri}& =\sqrt{H}·{ϵ}_{abs}+{max\{\parallel \mathit{x}\parallel }_2^{\mathrm{k}}{,\parallel \mathit{z}\parallel }_2^{\mathrm{k}}\}·{ϵ}_{rel}\hfill \end{array}$$

(27a)

$$\begin{array}{cc}\hfill {\epsilon }_{dual}& =\sqrt{H}·{ϵ}_{abs}+{max\{\parallel \mathit{y}\parallel }_2^{\mathrm{k}}\}·{ϵ}_{rel}\hfill \end{array}$$

(27b)

where $H=\mathrm{rank}\mathit{x}$, ${ϵ}_{abs}$ denotes the absolute tolerance and ${ϵ}_{rel}$ represent the relative tolerance.

The objective function of the update process for the z-variable (26b) is a convex quadratic function of ${\mathit{z}}_i$, which is constrained only by equations ${\mathit{z}}_i|{\sum }_{j\in \mathbb{N}}{K}_{ij}{\mathit{z}}_{ji}=0$. Then, the update process of ${\mathit{z}}_i$ can be reformulated as follows:

$$\begin{array}{cc}\hfill & \underset{{\mathit{z}}_i\in \mathcal{Z}}{min}\varphi \xi +{\displaystyle \frac{\varphi }{1-\alpha }}\sum _{\omega \in \mathsf{\Omega }}\psi \left(\omega \right)\beta \left(\omega \right)+\sum _{j\in N_i}{\displaystyle \frac{\rho }{2}}{\parallel {\mathit{x}}_j^{\mathrm{k}+1}-{\mathit{z}}_{ij}+{\mathit{y}}_{ji}^{\mathrm{k}}\parallel }_2^2\hfill \end{array}$$

(28a)

$$\begin{array}{cc}\hfill & s.t.\sum _{j\in \mathbb{N}}{K}_{ij}·{\mathit{z}}_{ji}=0\hfill \end{array}$$

(28b)

Transform problem (28) into a general form:

$$\begin{array}{cc}\hfill & \underset{{\mathit{z}}_i}{min}{\displaystyle \frac{1}{2}}{\mathit{z}}_i^T\mathit{M}{\mathit{z}}_i+c^T{\mathit{y}}_i\hfill \end{array}$$

(29a)

$$\begin{array}{cc}\hfill & s.t.\mathit{K}{\mathit{z}}_i=0\hfill \end{array}$$

(29b)

The closed-form solution can be derived by [46]:

$$\begin{array}{c}\hfill {\mathit{z}}_i=({\mathit{M}}^{-1}{\mathit{K}}^T{\left(\mathit{K}{\left(\mathit{M}\right)}^{-1}{\mathit{K}}^T\right)}^{-1}\mathit{K}{\left(\mathit{M}\right)}^{-1}-{\left(\mathit{M}\right)}^{-1})c\end{array}$$

(30)

The entire pseudo code of the distributed algorithm used to slove the risk-aversion operation optimization problem of the HWSS system is described in Algorithm 2.

Algorithm 2: Distributed algorithm for risk-aversion operation optimization problem of the HWSS system

Initialize variables 1: Initialize all ${\mathit{x}}_i$, ${\mathit{z}}_i$, ${\mathit{y}}_i$. Particularly, ${\mathit{x}}_i^0$ is calculated using the historical data of renewable energy generation and power-flow calculation. 2: Initialize iteration index $k=0$ Iterative calculation 3: do 4:    Each bus i updates ${\mathit{x}}_i$ according to (26a). 5:    Each bus i updates ${\mathit{z}}_i$ according to (26b). 6:    Each bus i updates ${\mathit{y}}_i$ according to (26c). 7:    Update iteration index $k=k+1$. 8: until $\parallel {\mathit{x}}^{\mathrm{k}+1}-{\mathit{z}}^{\mathrm{k}+1}\parallel \le {ϵ}_{pri}$ and $\rho \parallel {\mathit{y}}^{\mathrm{k}+1}-{\mathit{y}}^{\mathrm{k}}\parallel \le {ϵ}_{dual}$

5. Case Study

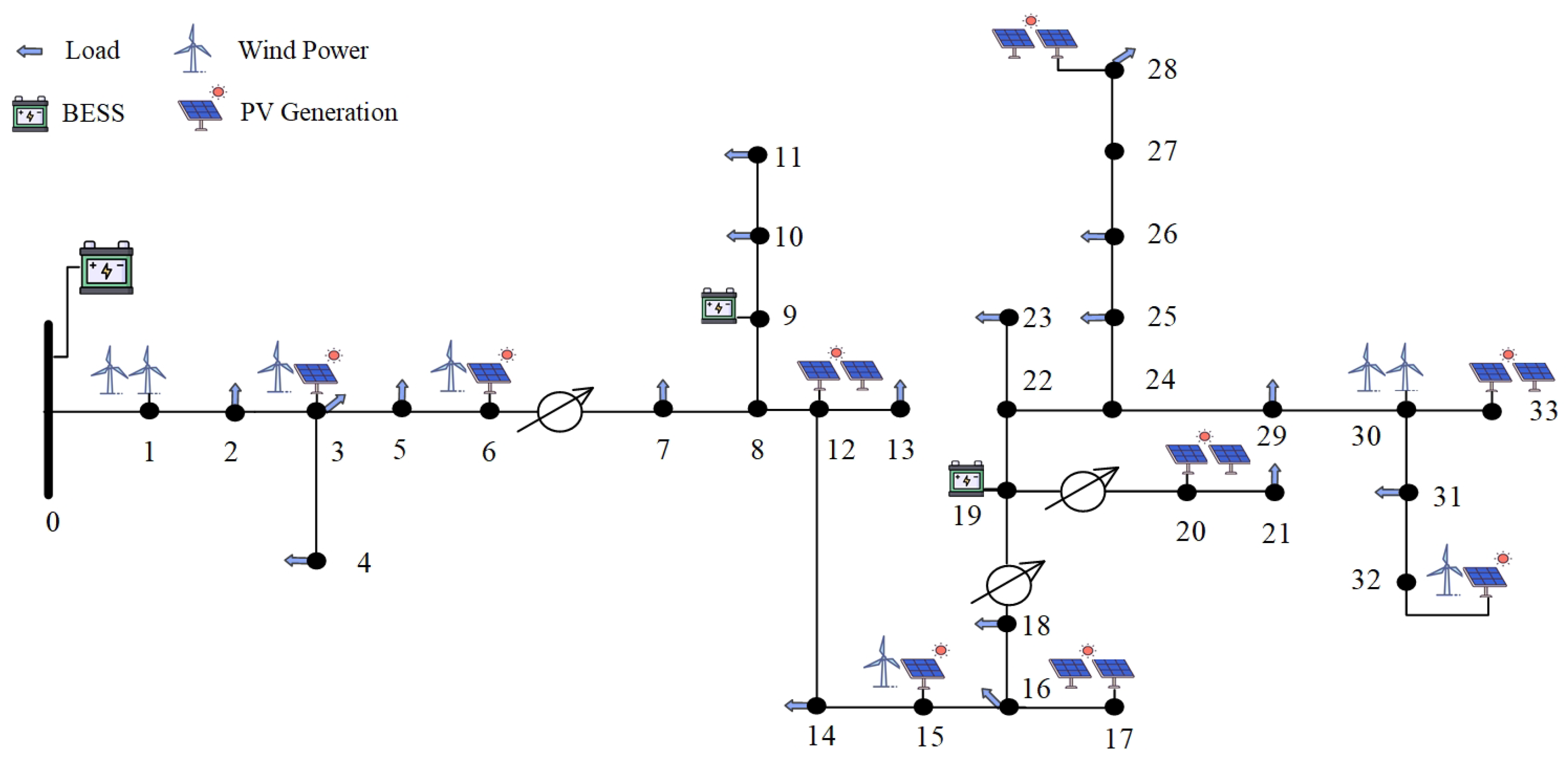
5.1. System Configuration

The proposed risk-averse operation model of the HWSS system is tested under a 24.9 kV modified IEEE 34-bus radial network, which is shown in Figure 4. Simulations are carried out on a desktop with Inter core i7-1260P, 2.10 GHz, 16 GB RAM using MATLAB 2023. The configuration of wind and solar-power generation is as shown in Figure 3. There are 8 instances of wind generation and 14 instances of roof-top solar generation in total. Overall, the renewable generation installed in HWSS is about 2 MW. The 15 min wind-power and PV generation data are based on real data from South China. As depicted in Figure 4, the root bus is equipped with a 40 kW/80 kWh battery storage system; bus 9 and bus 19 are fitted with 10 kW/20 kWh battery storage systems. The total installed energy-storage capacity is 20% of the renewable generation’s installed capacity in the HWSS system. The lower bound of the stored energy for the battery storage system is ${\underline{E}}_0=$ 0.4 kWh for the BESS located under the root bus, $\underline{E}=0.1$ kWh for others. The initial state of charge for the battery storage system at the start of the day is set at 50% of its total capacity. The degradation coefficient for the battery storage system is defined as ${\sigma }_i^{\mathrm{deg}}=$ 0.06. Other parameters are established as follows: the voltage limits are $\underline{v}=0.{93}^2$, $\overline{v}=1.{07}^2$, the penalty coefficient is $\pi =$ 0.25, the risk preference coefficient is $\varphi =$ 0.5, and the absolute and relative convergence tolerances are set to ${ϵ}_{abs}={10}^{-4}$ and ${ϵ}_{rel}={10}^{-4}$, respectively.

5.2. Correlation Analysis

The correlation between wind and solar-power generation when geographically close to each other is analyzed in this paper to quantify the uncertainty of REG more accurately. Partial correlation analysis results are demonstrated in Figure 5. In the simulation, 1000 initial scenarios are generated by Gibbs sampling and three of them are selected as typical scenarios according to the distribution of the initial samples using Fuzzy C-Means (FCM) algorithm. The cluster centers are represented by the small red circle. As shown in Figure 5, the typical scenarios can effectively preserve the distribution characteristics of the original samples. The correlations are also quantified using Kendall rank correlation, and the corresponding Kendall’s tau coefficient is demonstrated in

Table 2. Kendall rank correlation coefficient of REG.

Item	Bus 1	Bus 12	Bus 2	Bus 32
t = 14	0.8470	0.5669	0.4807	−0.2221
t = 15	0.8012	0.6657	0.4929	−0.3164

. It can be observed that there is a strong positive correlation between wind-power plants that are geographically close to each other, the Kendall rank correlation coefficient of which is over $\tau =$ 0.8. The same is true for photovoltaic power generations that are geographically close to each other. In addition, a weak negative correlation is observed between wind and solar-power generation.

5.3. Performance on Uncertainty Risk Aversion

Figure 6 depicts the power injection results from the root bus of the HWSS system to the upstream grid. Since there is a shared energy storage at root bus 0, it is hereafter referred to as BESS0. As shown in Figure 6, the blue line denotes power injection into upstream grid after the optimization of BESS charging power. Compared with the original power injection denoted by the red dotted line, it can be observed that power fluctuations caused by REG can be effectively smoothed through the charging and discharging of BESS0. When there is excess renewable power generation in the HWSS system, BESS is charged to prevent excess renewable power generation from being sent back to the upstream grid. The overall amount of REG sent back to the upstream grid has decreased by about 80.6% due to the proposed model. BESS is discharged when there is an energy shortage in the HWSS system; the load peak is reduced up to 41.8% at t = 21. Obviously, the ability of smoothing power fluctuations for the HWSS system is limited by the capacity of BESS. Figure 7 depicts the power injection results under various scenarios. Compared with power injection result under a single scenario, the average value of multiple scenarios could consider the impact of uncertainty REG on the upstream grid more comprehensively, which illustrates the effectiveness of proposed risk-aversion operation optimization model on uncertain risk aversion of REG.

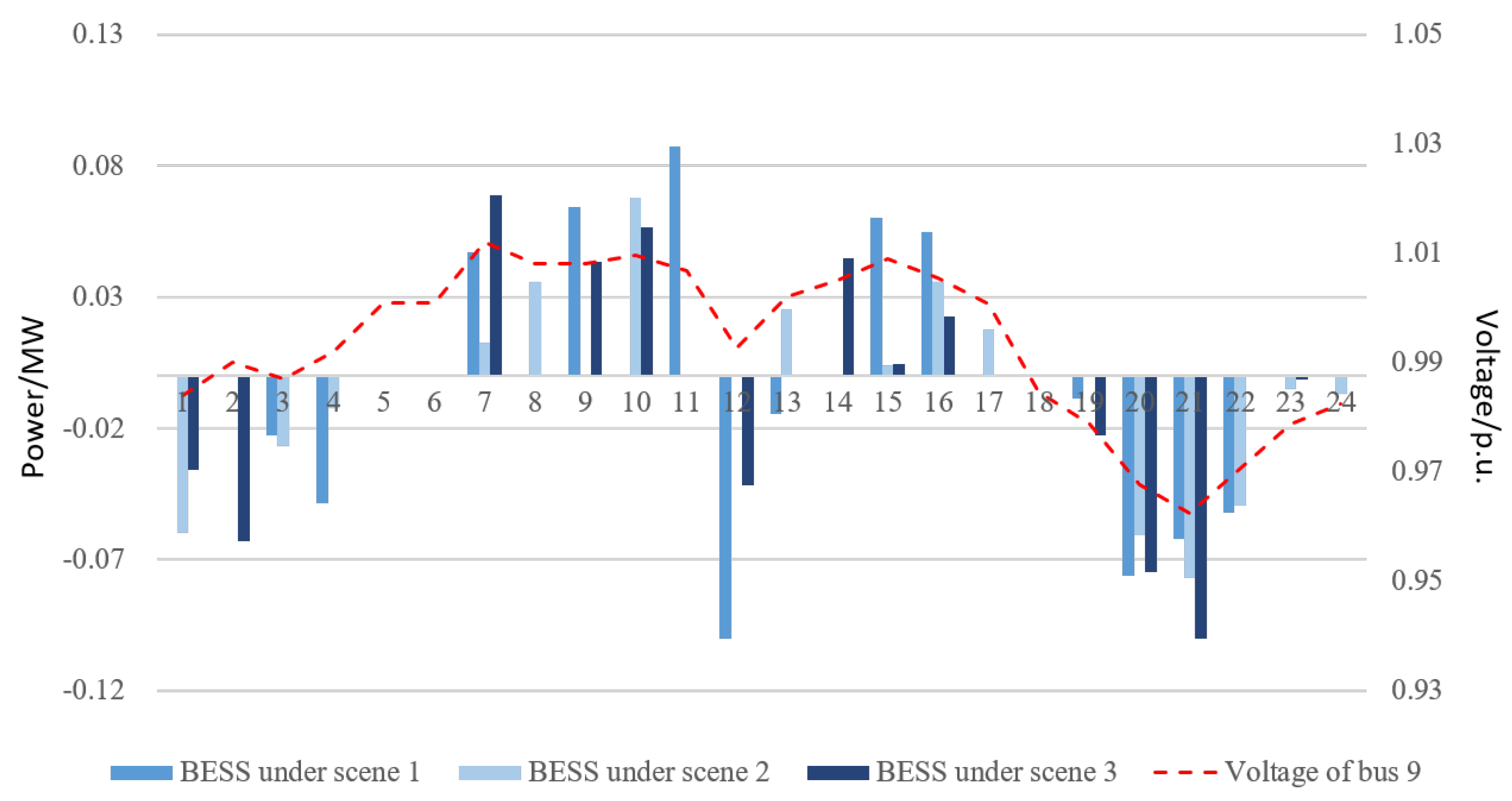
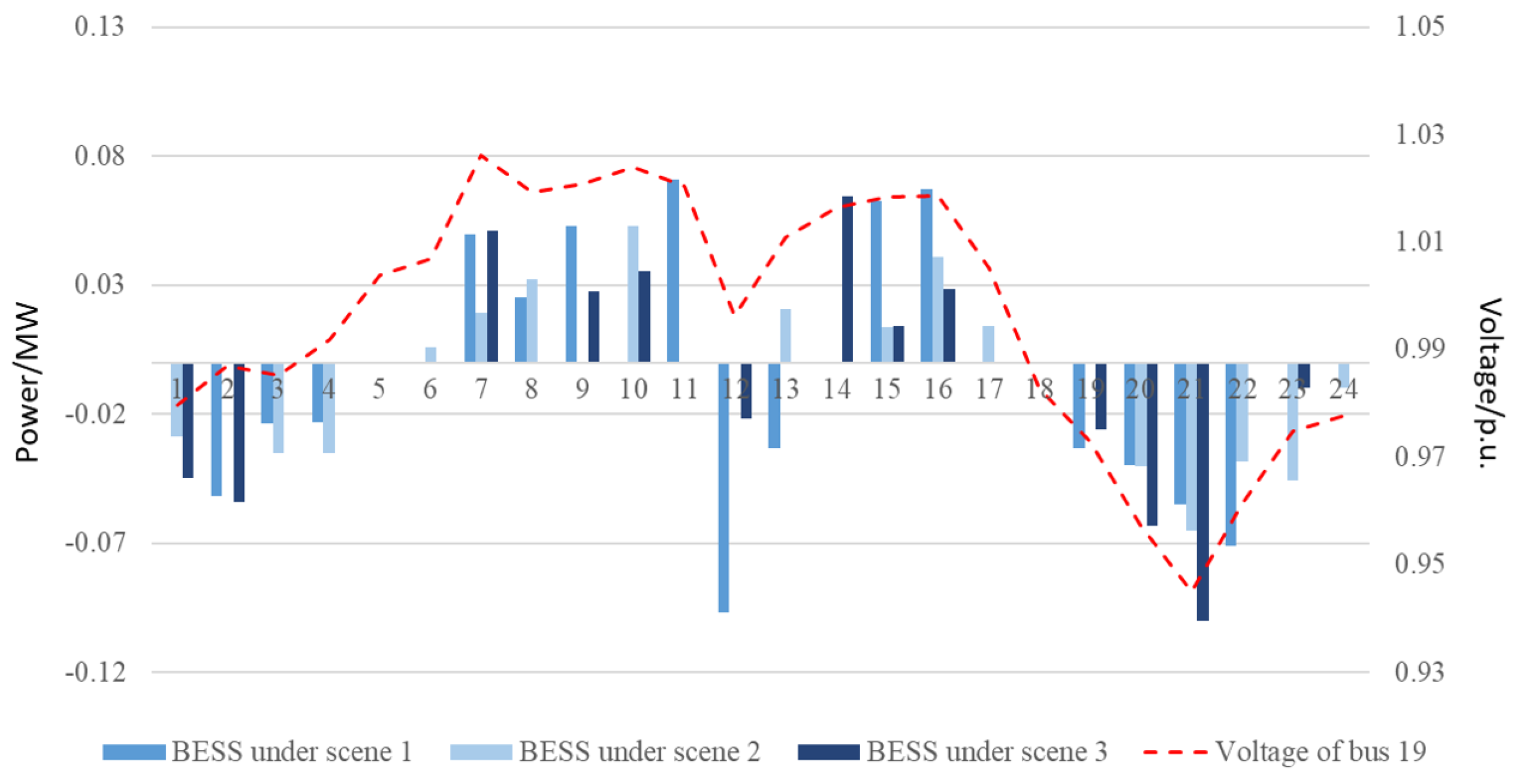
5.4. Voltage Regulation Effectiveness

The operation of HWSS system may face volatge violation problems at the peak of REG and peak load. Thus, the bus voltage constraints are introduced into the risk-aversion operation optimization model to ensure safe operation of the HWSS system. Figure 8 shows the bus voltage of the HWSS system except the root bus. As depicted in Figure 8, voltage drops during load peak at night (t = 21), especially at the end-load bus of the radial network, where the minimum voltage is 0.9436 p.u. with a volatge deviation about 5.6%. The charging and discharging of energy storage on the consumer side and the accordance bus voltage is depicted in Figure 9 and Figure 10. Due to the voltage constraints, the main function of consumer-side energy storage is to participate in peak load regulation within the HWSS system, reducing overall system operating costs about 37.2% by shaving peaks and filling valleys.

5.5. Sensitivity Analysis

There are several coefficients utilized in the parameterized linear-loss function of the risk-aversion operation optimization model (10). In order to analyze the impact of these parameters on the simulation results of the risk-aversion operation optimization model, a sensitivity analysis on the penalty coefficient $\pi$, the risk preference coefficient $\varphi$, and the confidence level $\alpha$ is carried out in this section.

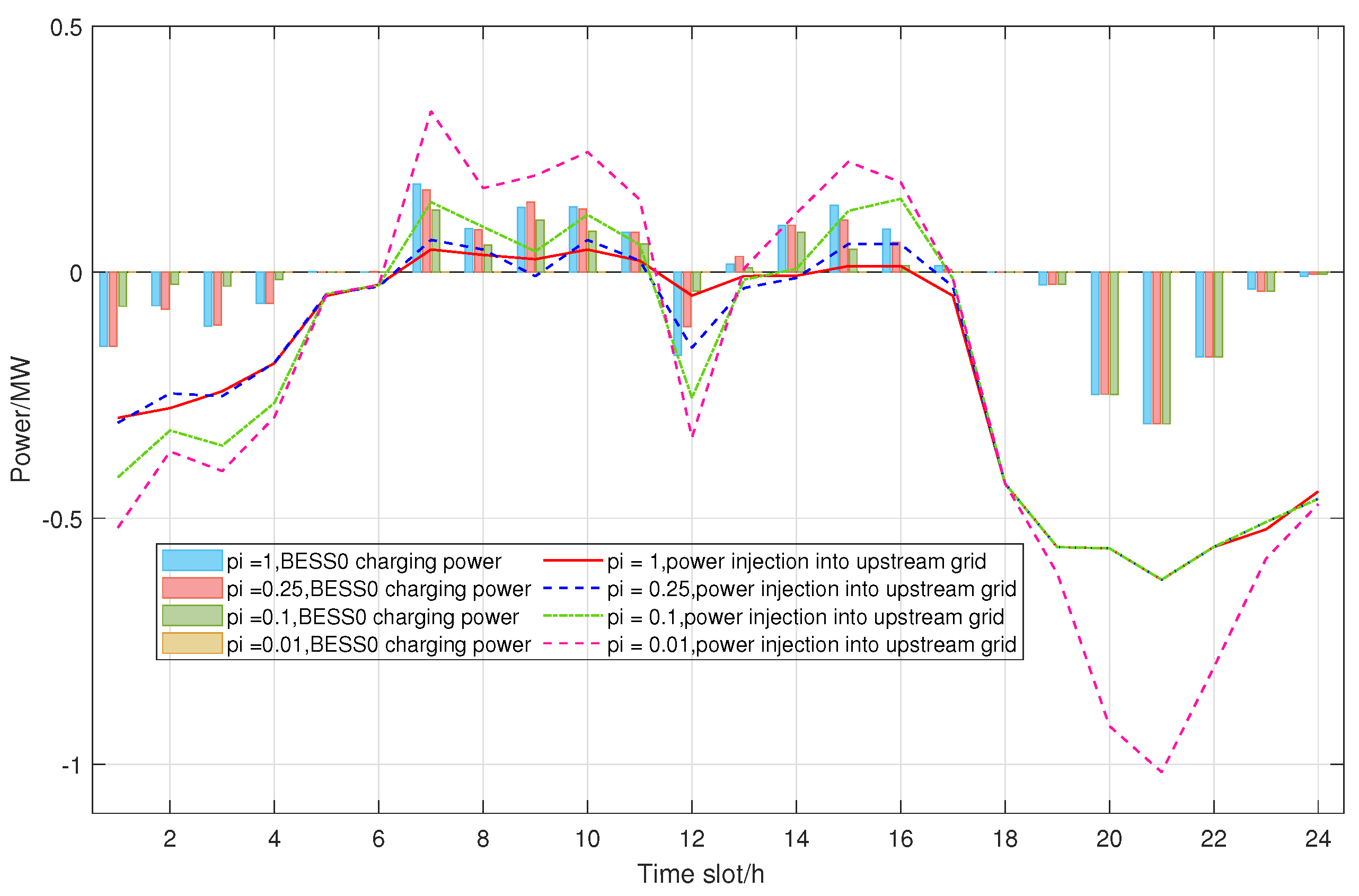
5.5.1. Penalty Coefficient $\pi$ for Exchanging Energy with Upstream Grid

Figure 11 gives the sensitivity analysis result of penalty coefficient $\pi$. As the penalty coefficient increases, the HWSS system has a better effect in smoothing the fluctuation of power injected into the upstream grid. When the penalty coefficient is small enough (in this case $\pi =$ 0.01), there is not enough motivation for BESS0 at the root bus to charge or discharge considering the depreciation cost. When the penalty coefficient is greater than a certain value, there will be no significant improvement in the incentive effect for volatility smoothing (e.g., $\pi =$ 1 represented by red line compared with $\pi =$ 0.25 denoted by the blue dotted line), but it will result in higher operation costs (the risk-averse operation cost for $\pi =$ 1 is about 3.2 times the cost for $\pi =$ 0.25).

5.5.2. The Risk-Preference Coefficient $\varphi$ of HWSS System

The risk-averse operation cost of HWSS with a different risk-preference coefficient $\varphi$ is demonstrated in Figure 12 to illustrate the impact of $\varphi$ on the risk-averse performance. As the risk preference coefficient $\varphi$ grows, the operation cost will increase linearly, which complies with the parameterized linear function (10), indicating that the value of the risk-preference coefficient $\varphi$ has little impact on the system operation optimization results. This is because that the optimal dispatch decision of the minimum CVaR problem (19) under discrete scenarios is consistent with the optimal decision of the HWSS system obtained by minimizing the expected total loss of the system ($\mathbb{E}\left({\sum }_t^{\mathbb{T}}{c}_t\right)$), since the decision variables under each scenario are decoupled from each other.

5.5.3. The Confidence Level $\alpha$ of CVaR

As shown in Figure 13, the confidence level $\alpha$ will influence the value of VaR and CVaR. A larger $\alpha$ means most losses will not exceed VaR, indicating a larger value of VaR and CVaR.

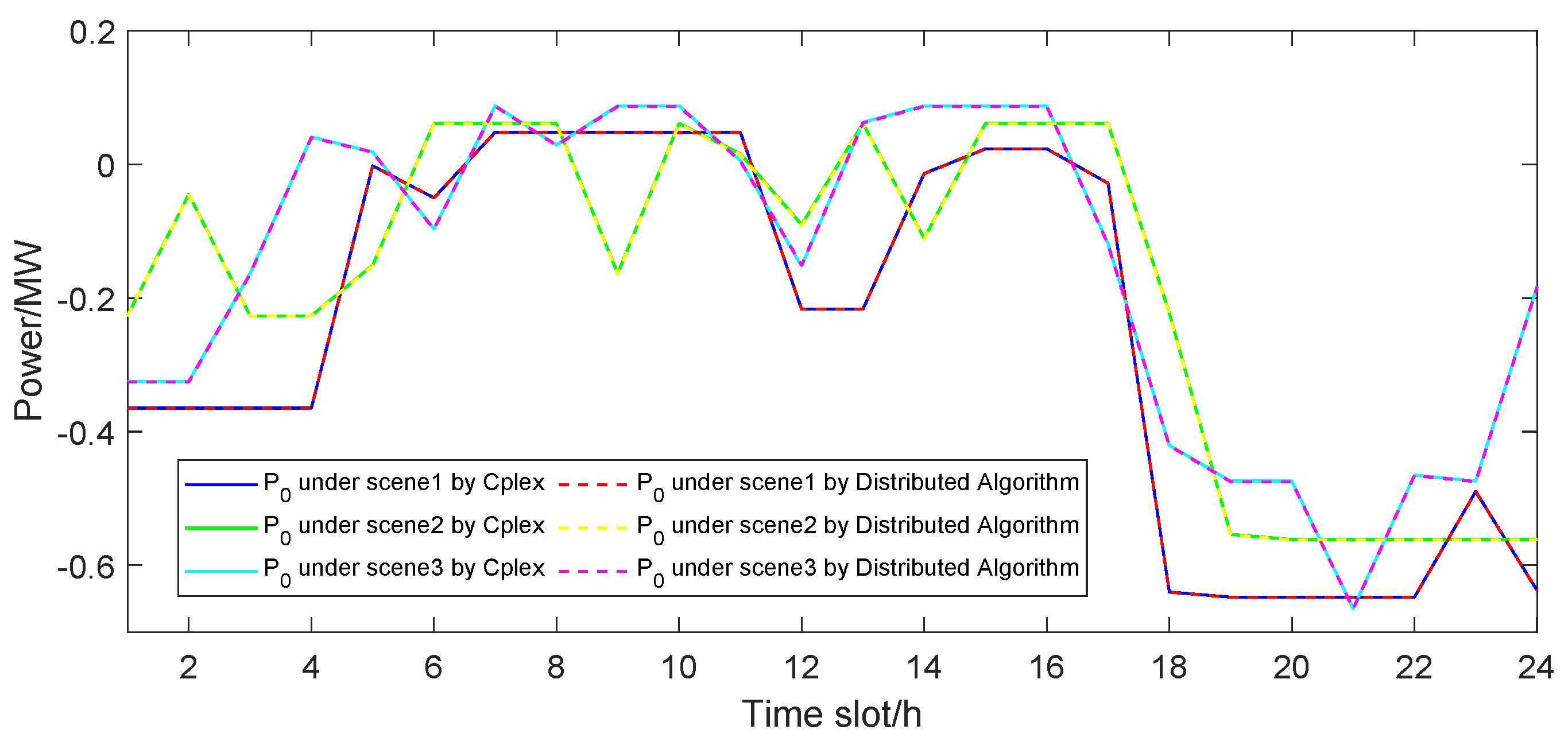
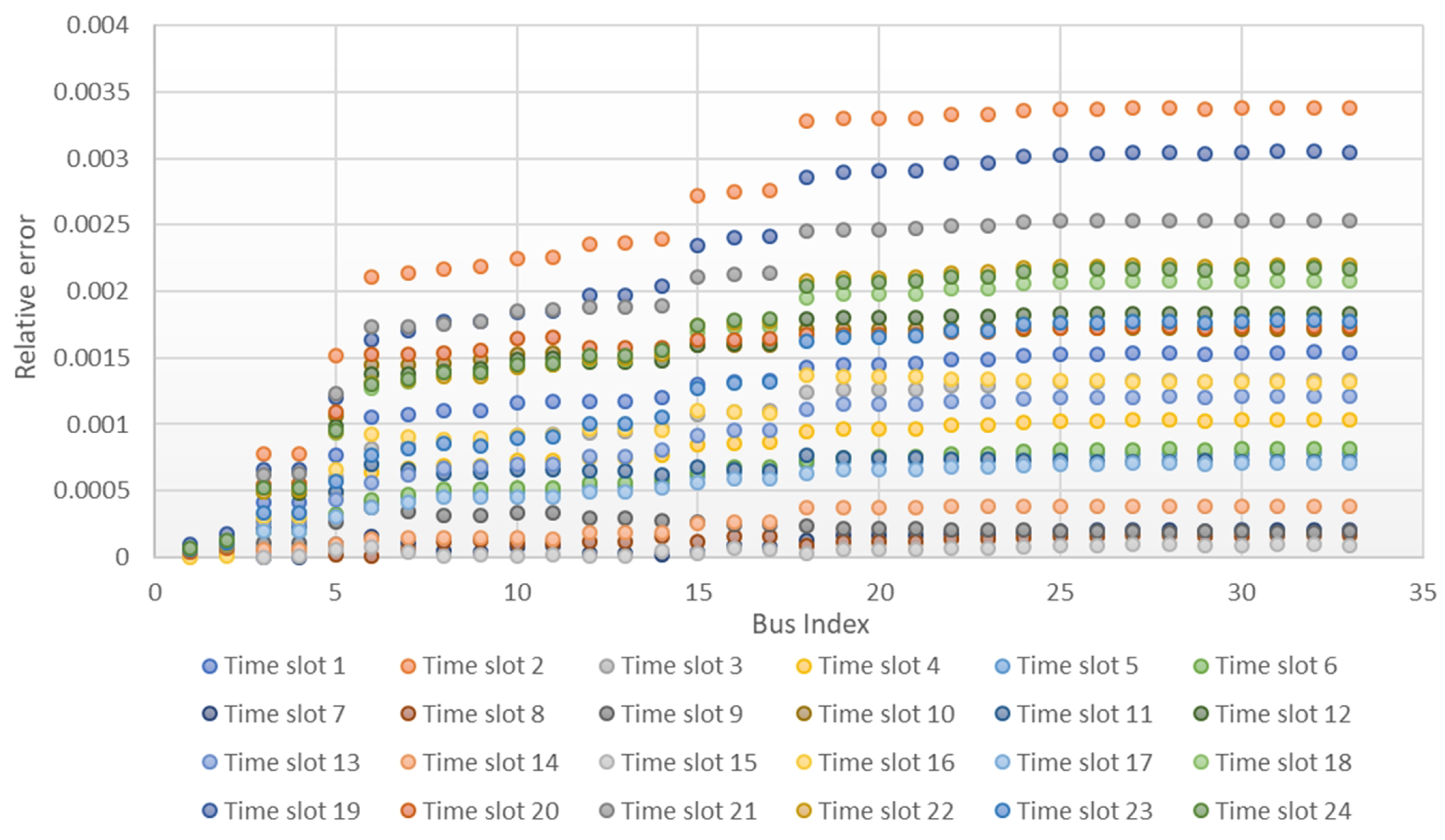
5.6. Effectiveness of Distributed Algorithm

Figure 14 shows the convergence results of the risk-averse operation optimization problem under the 34-bus distribution network using the proposed distributed algorithm based on ADMM. It takes about 2200 iterations for the problem to converge into the allowable tolerance. The calculation time for each iteration is around 6s, since the closed-form solution is derived for the z-update process. Each bus of HWSS optimizes local variables in parallel by only exchanging limit information. The objective function converge to the nearby of the optimal value after around 2000 iterations, as shown in Figure 14b. The proposed model can be scaled to a larger-scale network without influencing the solution time for a single iteration dramatically. Compared with the centralized solution, the average relative error of using the proposed distributed algorithm to solve the bus voltage is about 0.108% and the maximum relative error is about 0.347%, which illustrates the effectiveness and scalability of the proposed distributed risk-averse operation model.

To validate the accuracy of the ADMM-based distribution algorithm in solving the risk-averse operation model (20), the solution calculated by the ADMM-based distribution algorithm is compared with results solved in centralized by a commercial solver called Cplex. Let $P_0$ denote power injection from the root bus to the upstream grid; a comparison of the root-bus power injection results is demonstrated in Figure 15. The average relative error of $P_0$ is about $1.02\%$ of all time slots $\mathbb{T}$ under three typical scenarios. The relative error of the bus voltage calculation using the distribution algorithm compared with results by Cplex is depicted in Figure 16. As shown in Figure 16, since the calculation error of the bus voltage will gradually accumulate to the end bus, it can be observed that the terminal bus of the grid has a larger voltage calculation error than their ancestor bus. The average relative error of bus voltage is about $0.11\%$ and the maximum relative error of the bus voltage is $0.34\%$, which illustrates the calculation accuracy of the proposed distributed algorithm.

6. Discussion

With the increasing penetration of uncertainty REG, the power system is facing a dilemma of insufficient flexibility which brings challenges regarding operation security. The hybrid wind, solar, and storage system can effectively solve the above issues, promoting the local consumption of REG and comprehensively improve the system operation efficiency. In this paper, a novel distributed risk-averse optimization scheduling model of the HWSS system is proposed to effectively smooth the fluctuations in renewable energy output by the complementarity of REG and flexibility of BESS. The Frank copula and CVaR is utilized to quantify the uncertainty of REG described by the joint distribution of wind and solar-power generation. The potential operational uncertainty risk of HWSS is formulated based on a parameterized linear function of CVaR. The risk-averse operation optimization problem is transformed into a deterministic optimization problem under typical scenarios generated by Gibbs sampling and Fuzzy C-Means algorithm to facilitate the quick solving of the problem in a distributed manner.

Comprehensive studies illustrate the effectiveness of proposed model in reducing the uncertainty impact of renewable energy generation on the upstream grid and ensuring the operational security of HWSS system. The overall amount of renewable energy generation sent back to the upstream grid has decreased by about 80.6% and the overall voltage deviation is limited to 5.6%. The proposed model can reduce overall system-operating costs by about 37.2% by shaving peaks and filling valleys through BESS. The ADMM calculation time for each iteration is around 6 s. The proposed model can be scaled to a larger-scale network without influencing the solution time for a single iteration dramatically, since the closed-form solution is derived for the z-update process with network constraints. However, it may take more iterations to converge as the scale of the network increases, which can be further improved in future studies.

Several aspects of the operation of a hybrid renewable-energy-distribution system, including modeling the time/seasonal correlation of renewable energy generation and coordinating the operation of multiple types of energy-storage systems (e.g., thermal/hydrogen storage system), deserve further investigation.