State-of-Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy Features and Fusion Interpretable Deep Learning Framework
Abstract
1. Introduction
- (1)
- This study proposes a novel deep learning framework called CGMA-Net (Convolutional Gated Multi-Attention Network), which enables flexible estimation of battery SOH under three different temperatures in this dataset.
- (2)
- In this study, an ensemble model strategy is employed to automatically extract impedance features from multiple modules and track feature variations for information mining. Without the need for complex manual feature engineering, valuable electrochemical information can be extracted from EIS data.
- (3)
- Comprehensive experiments were conducted to compare the proposed framework with advanced models based on impedance feature–battery SOH estimation research, evaluating its robustness and effectiveness.
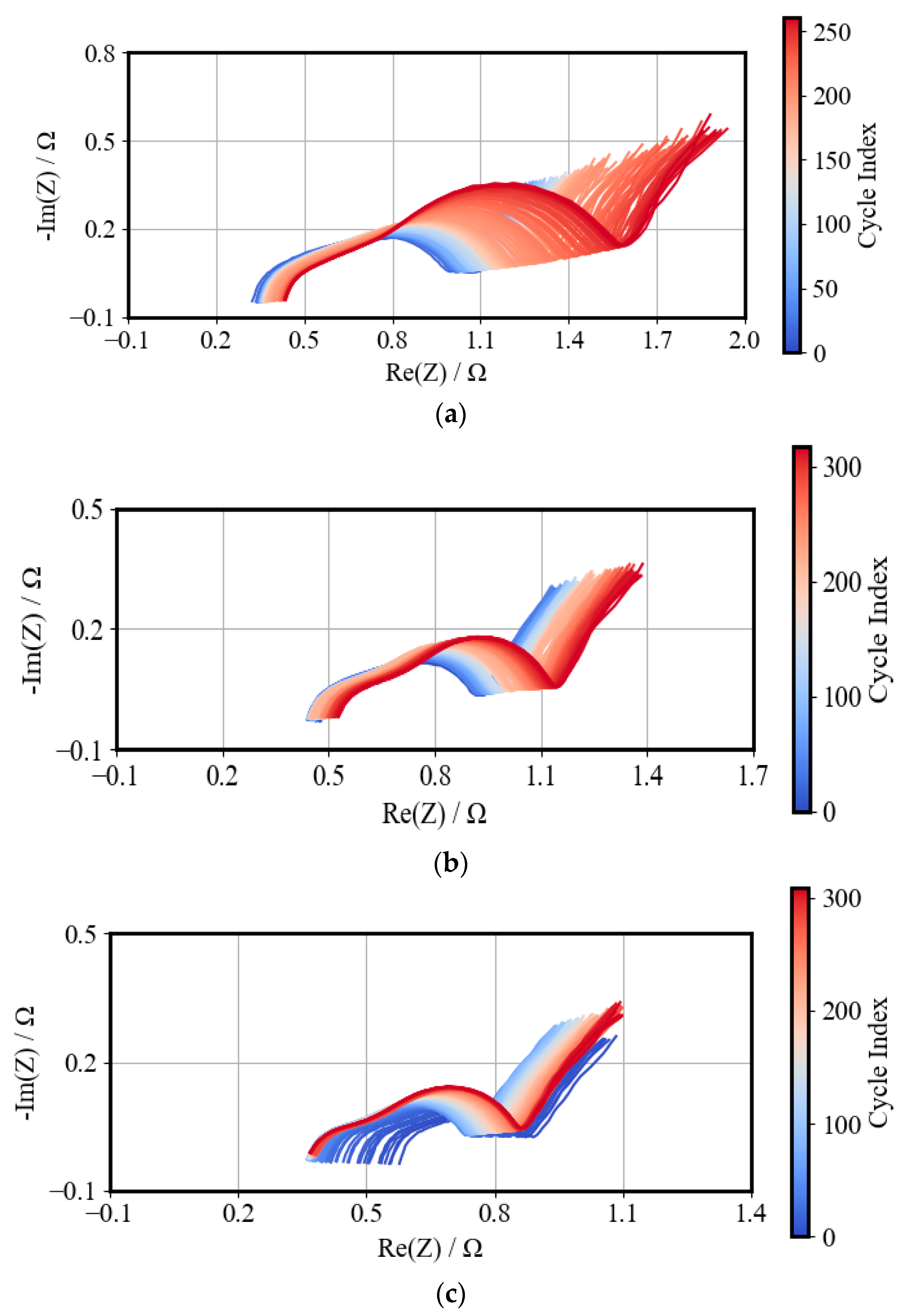
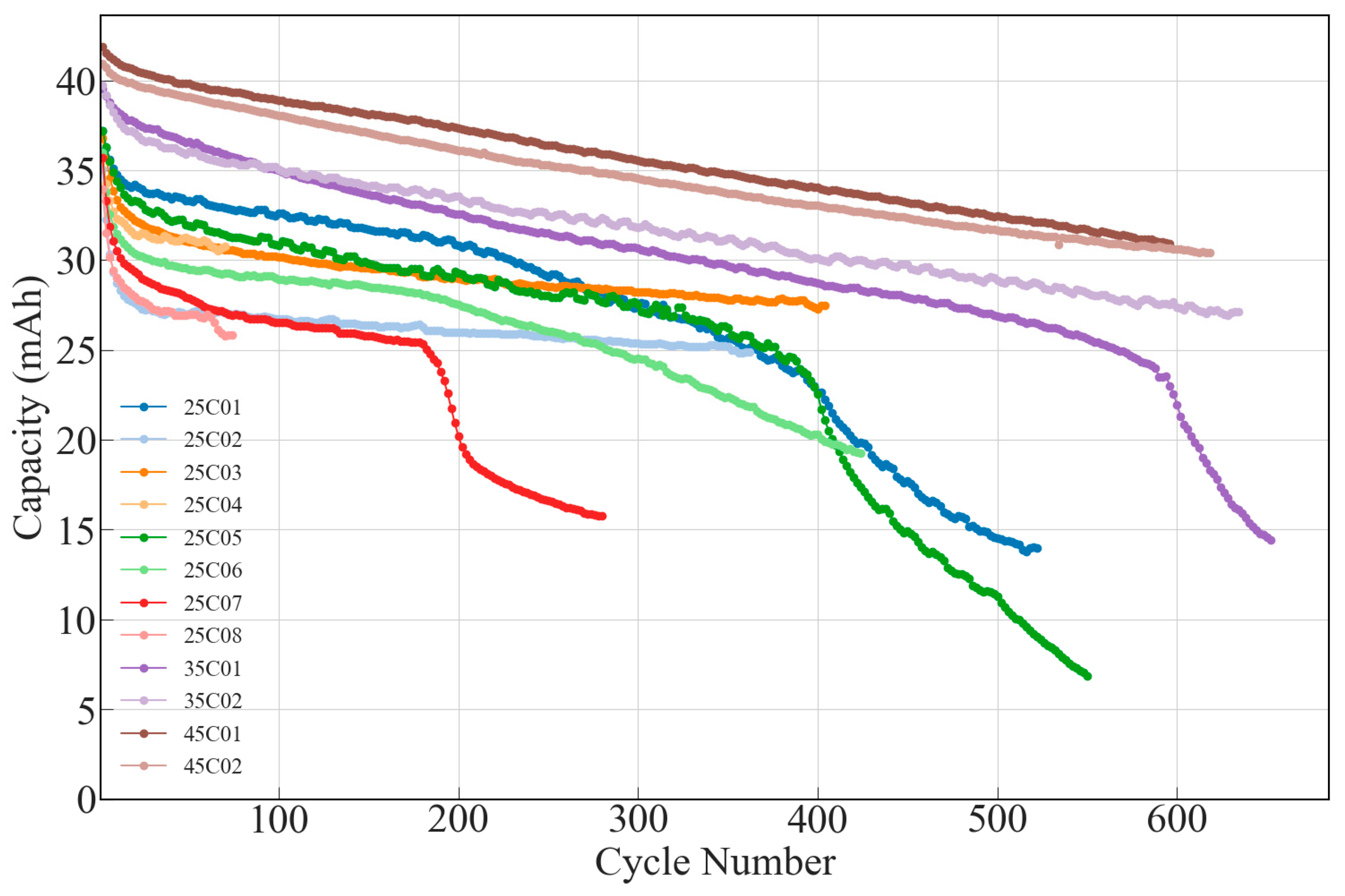
2. Dataset Analysis and Data Pre-Processing
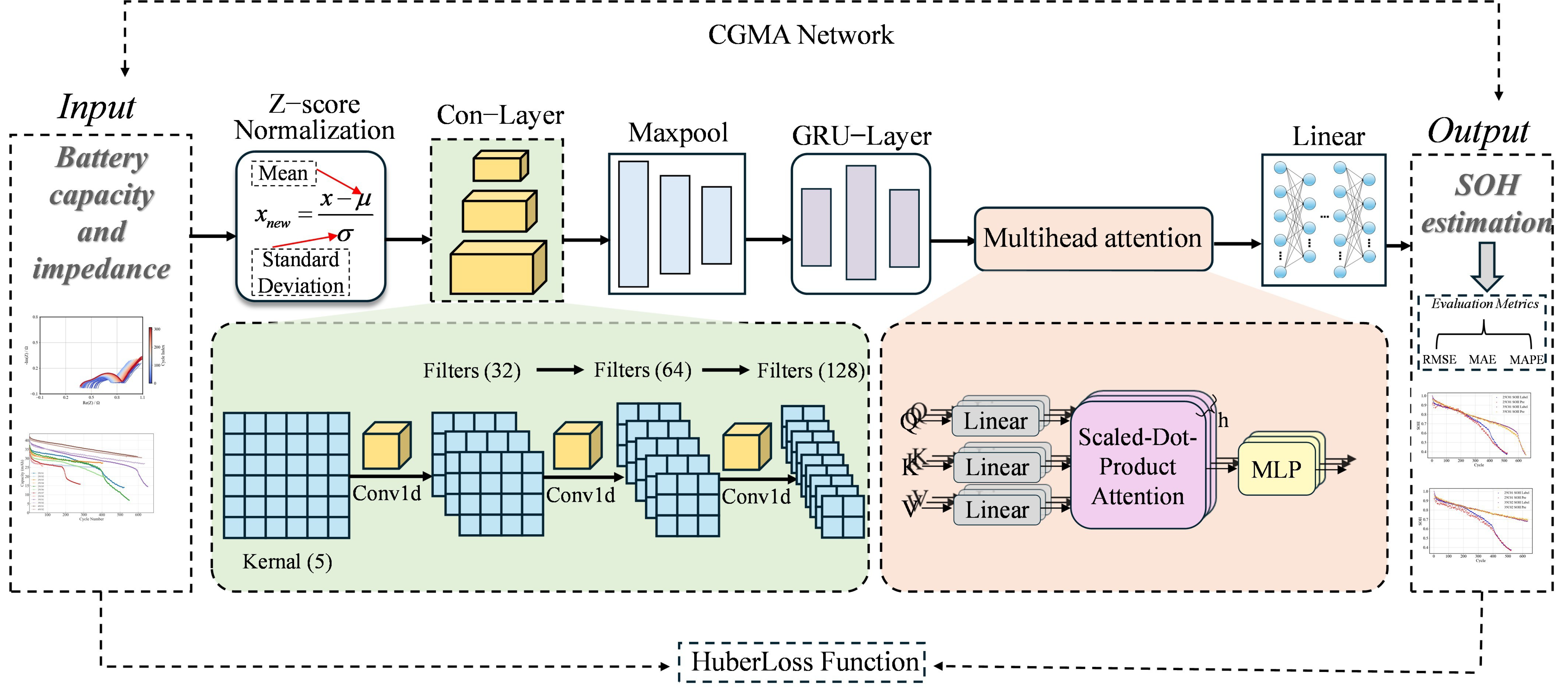
3. Methodology
3.1. Convolutional Neural Network
3.2. Gated Recurrent Unit Network
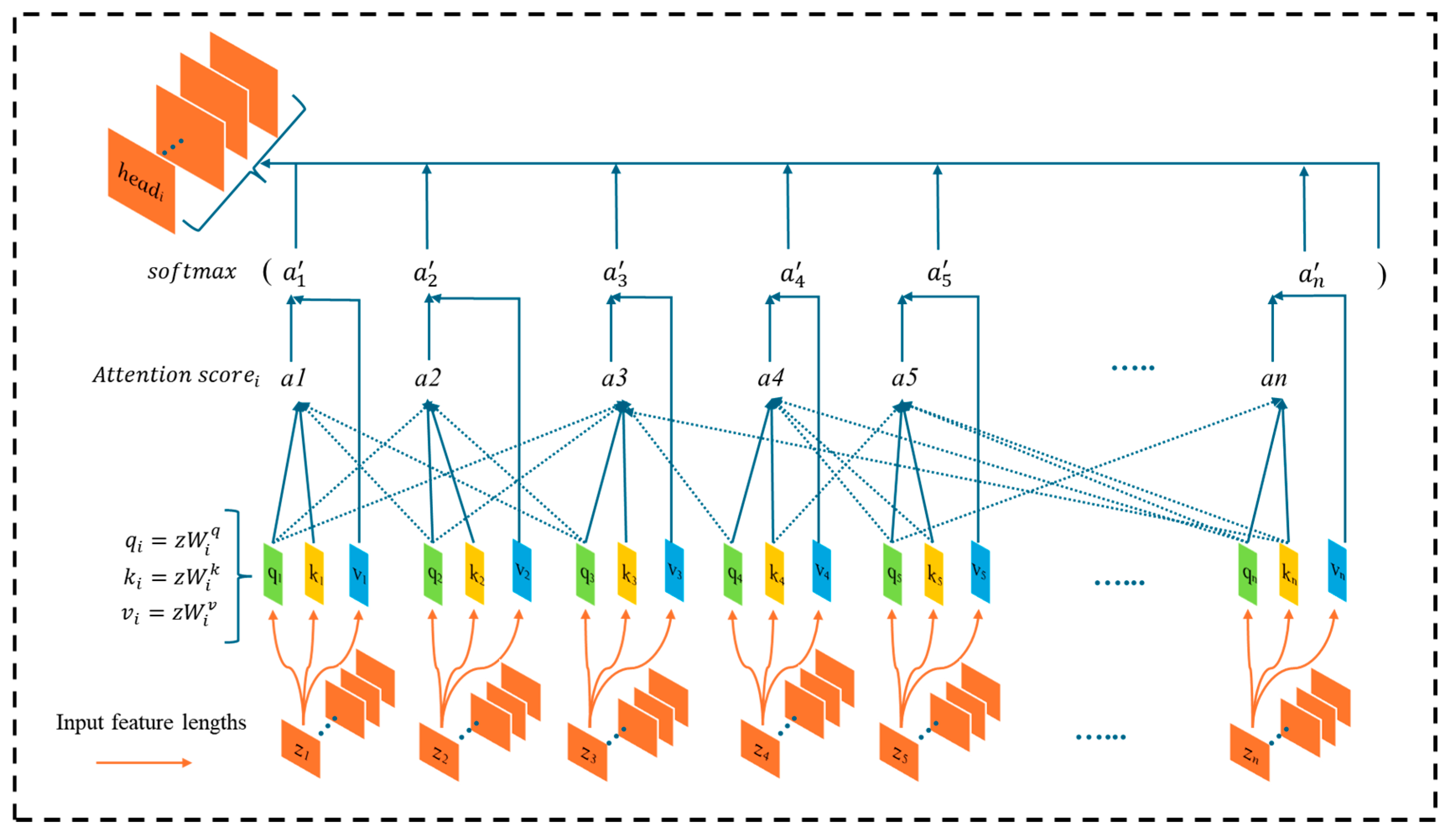
3.3. Multi-Head Attention in Model Architecture
- (1)
- Linear Mapping: the input feature is mapped through , , and values, as shown in the following Equation (7),
- (2)
- Calculating Similarity Scores: for each head, the similarity score between the query and all keys is calculated as shown in Equation (8):
- (3)
- Normalizing Weights: to transform the scores into a probability distribution, the function is applied to the scores of each query, ensuring that all weights sum to 1, as shown in Equation (9):
- (4)
- Weighted Sum: the normalized weights are applied to the values to obtain the weighted output for each head, as shown in Equation (10),
- (5)
- Output Combination: the outputs from each head are combined and processed through a linear layer to generate the final result as follows:
3.4. Model Framework
4. Results and Discussion
4.1. Dataset Division
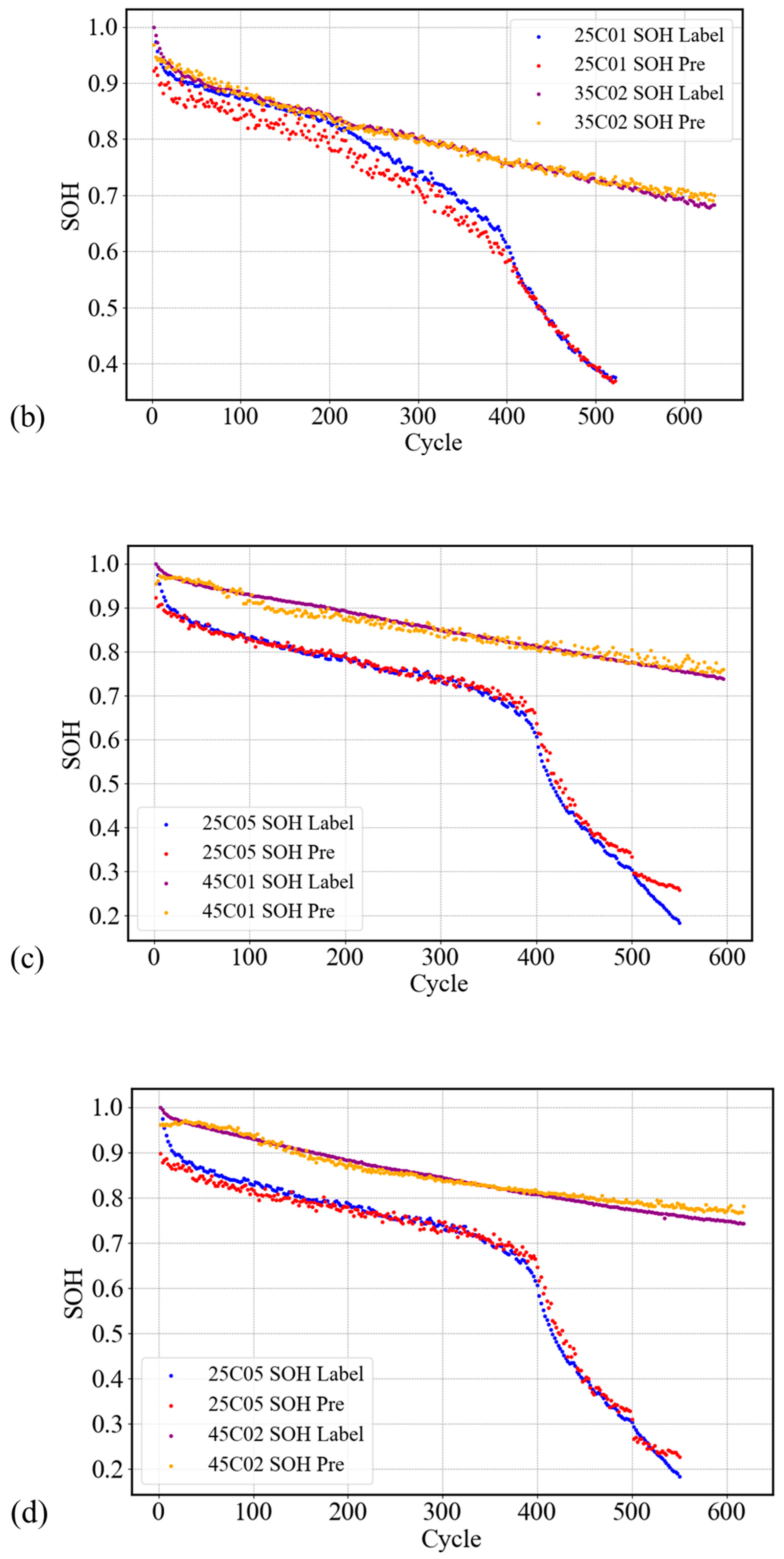
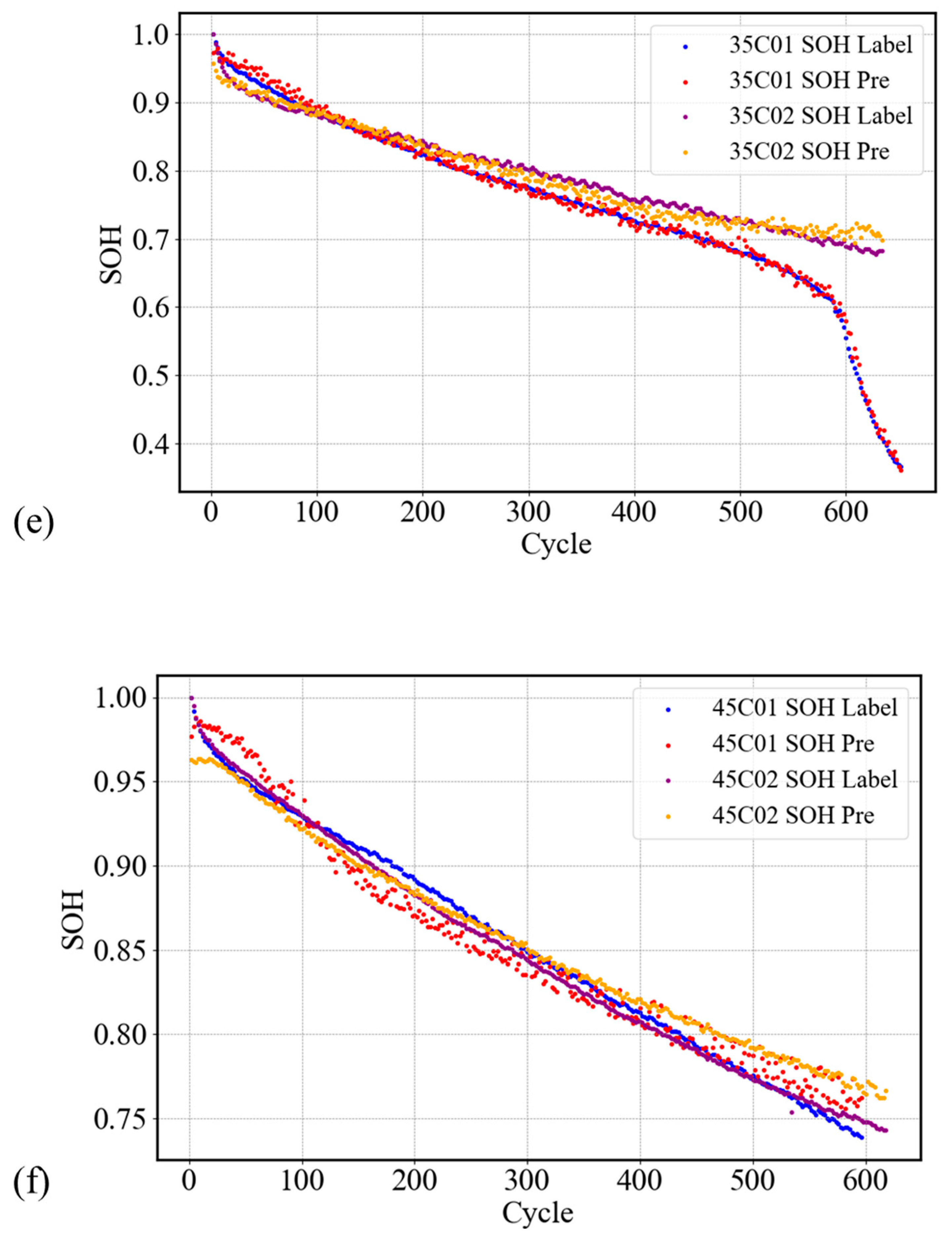
4.2. Analysis of Cross-Validation Results
4.3. Ablation Experiments
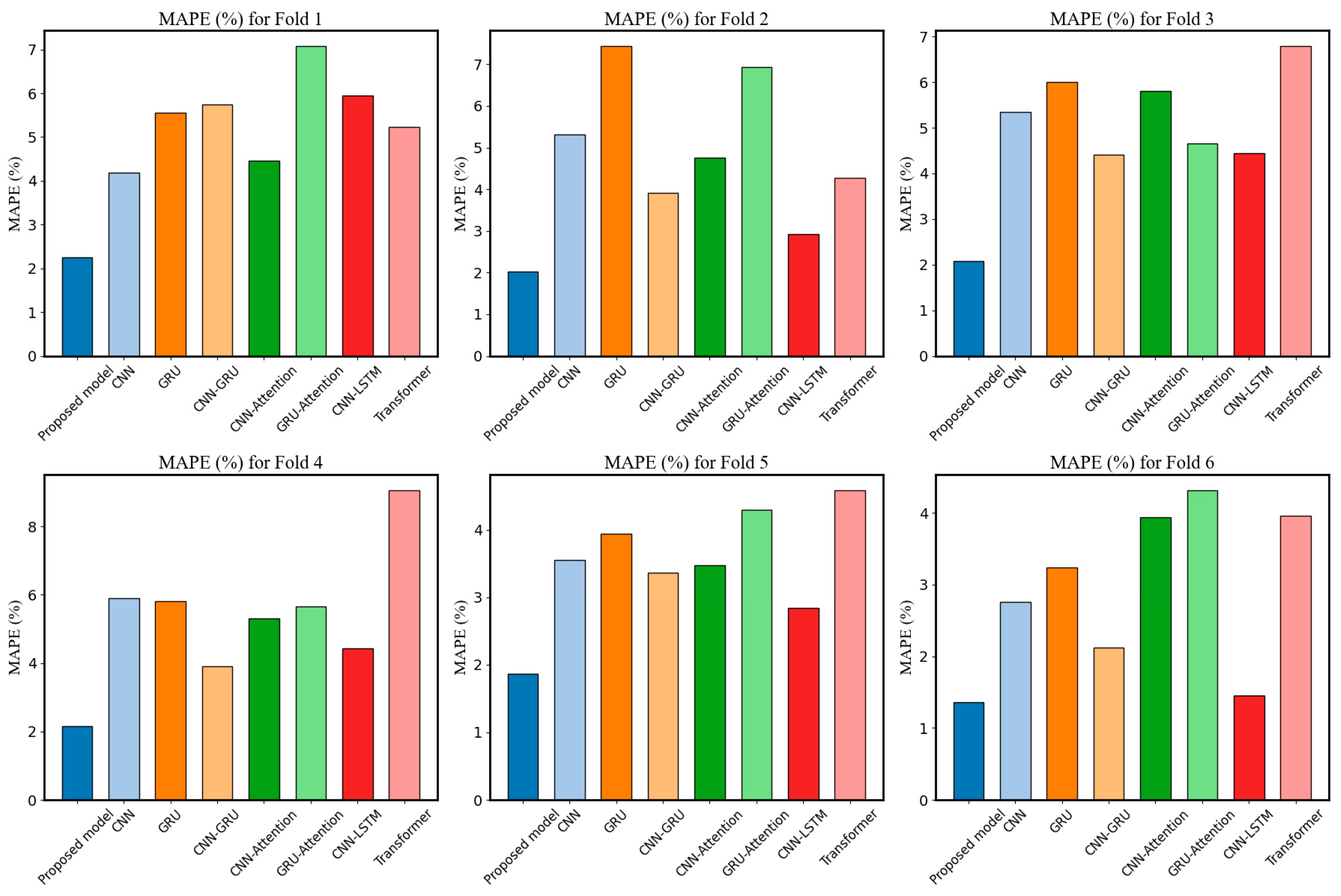
4.4. Comparison of the Advanced Models
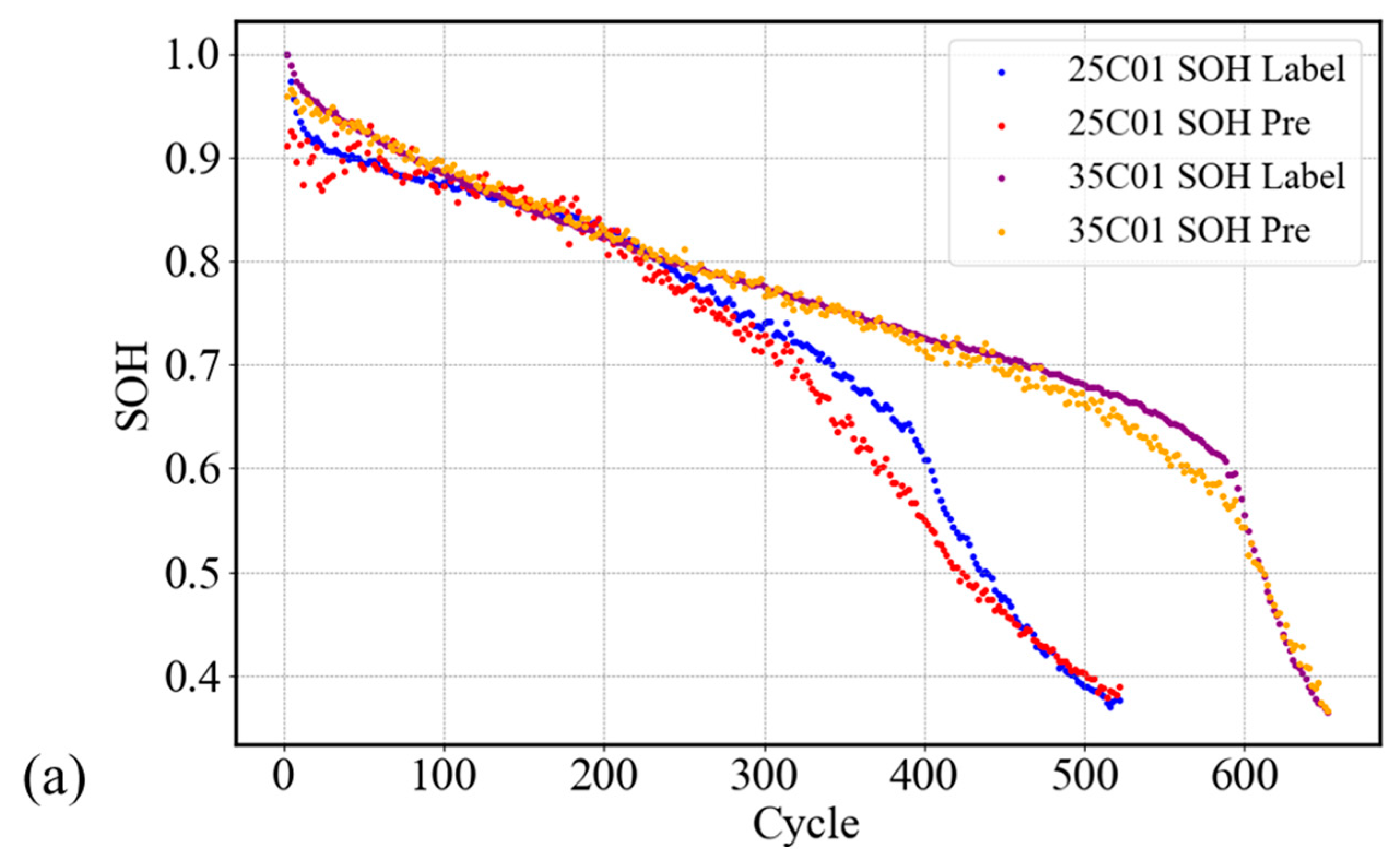
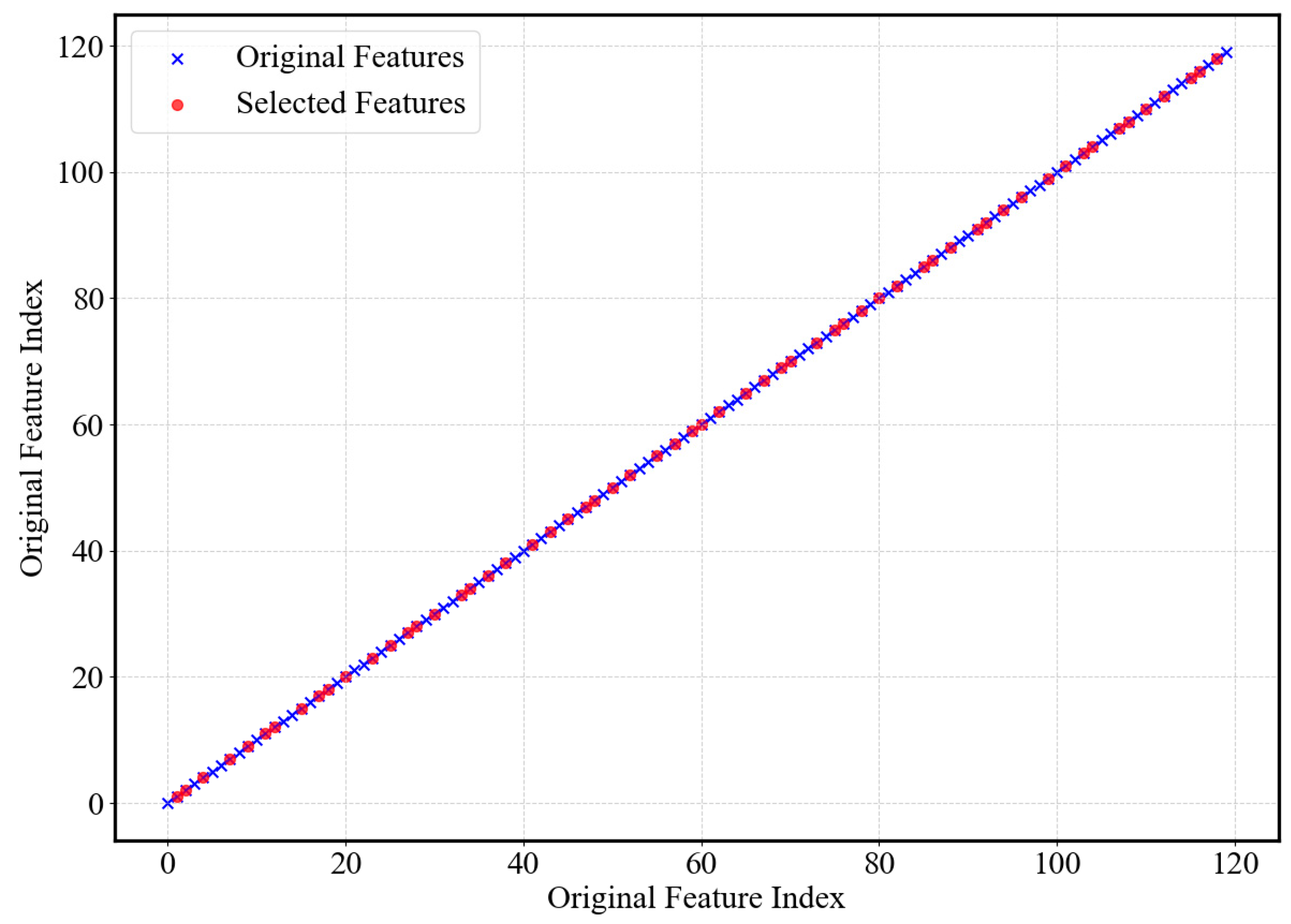
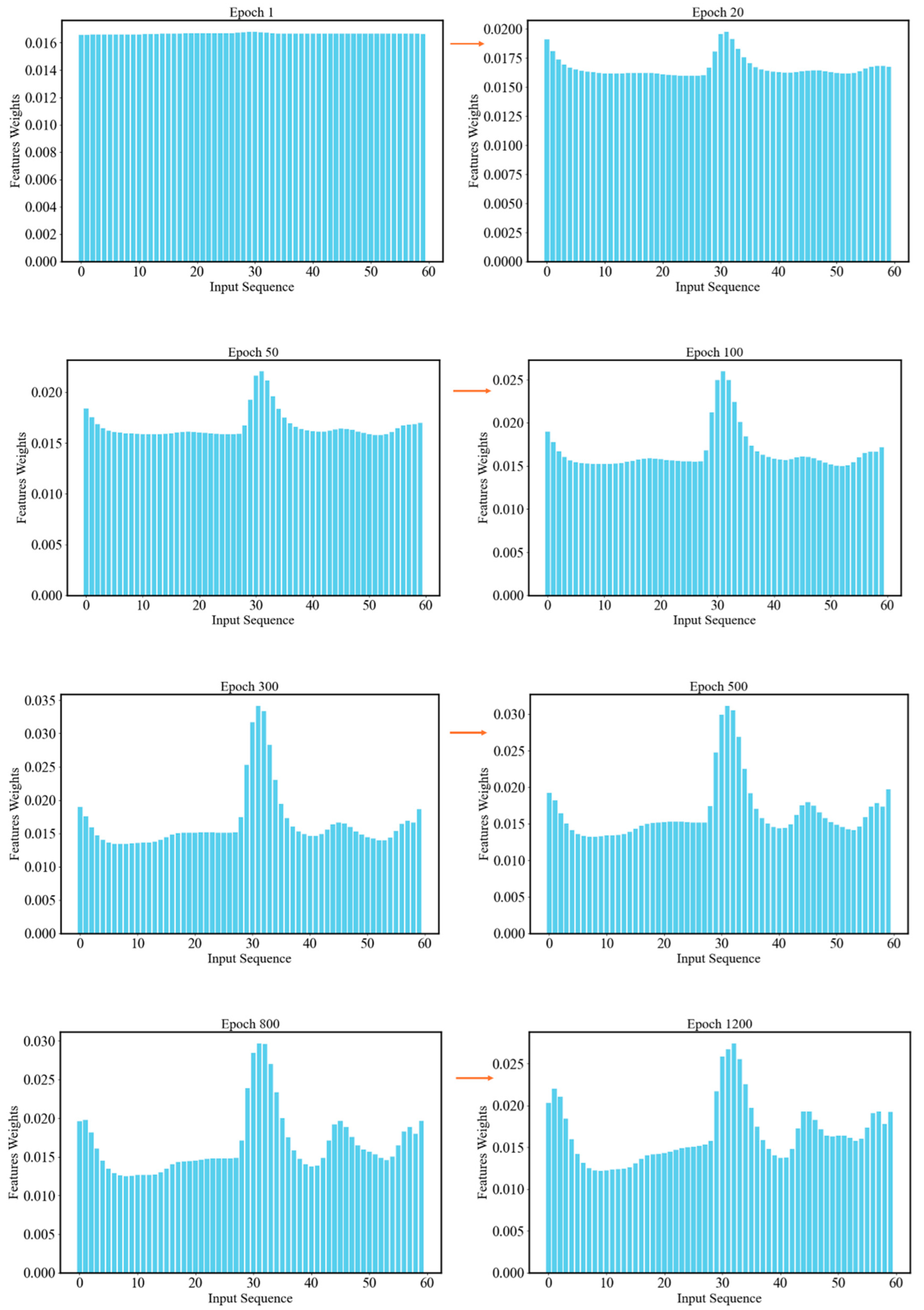
4.5. Interpretability Analysis Based on Attention Mechanism
4.6. Future Research Directions and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rajaeifar, M.A.; Ghadimi, P.; Raugei, M.; Wu, Y.; Heidrich, O. Challenges and recent developments in supply and value chains of electric vehicle batteries: A sustainability perspective. Resour. Conserv. Recycl. 2022, 180, 106144. [Google Scholar] [CrossRef]
- Grey, C.P.; Hall, D.S. Prospects for lithium-ion batteries and beyond—A 2030 vision. Nat. Commun. 2020, 11, 6279. [Google Scholar] [CrossRef] [PubMed]
- Habib, A.A.; Hasan, M.K.; Issa, G.F.; Singh, D.; Islam, S.; Ghazal, T.M. Lithium-ion battery management system for electric vehicles: Constraints, challenges, and recommendations. Batteries 2023, 9, 152. [Google Scholar] [CrossRef]
- Zhou, L.; Lai, X.; Li, B.; Yao, Y.; Yuan, M.; Weng, J.; Zheng, Y. State estimation models of lithium-ion batteries for battery management system: Status, challenges, and future trends. Batteries 2023, 9, 131. [Google Scholar] [CrossRef]
- Nuroldayeva, G.; Serik, Y.; Adair, D.; Uzakbaiuly, B.; Bakenov, Z. State of health estimation methods for Lithium-ion batteries. Int. J. Energy Res. 2023, 2023, 4297545. [Google Scholar] [CrossRef]
- You, H.; Wang, X.; Zhu, J.; Jiang, B.; Han, G.; Wei, X.; Dai, H. Investigation of lithium-ion battery nonlinear degradation by experiments and model-based simulation. Energy Storage Mater. 2024, 65, 103083. [Google Scholar] [CrossRef]
- Arora, P.; White, R.E.; Doyle, M. Capacity fade mechanisms and side reactions in lithium-ion batteries. J. Electrochem. Soc. 1998, 145, 3647. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part I. Cycling performance. J. Power Sources 2002, 112, 606–613. [Google Scholar] [CrossRef]
- Xia, L.; Najafi, E.; Bergveld, H.J.; Donkers, M.C.F. A computationally efficient implementation of an electrochemistry-based model for Lithium-ion batteries. IFAC PapersOnLine 2017, 50, 2169–2174. [Google Scholar] [CrossRef]
- Li, J.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model for lithium-ion batteries with electrolyte and stress-enhanced diffusion physics. J. Electrochem. Soc. 2017, 164, A874. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, D.; Cheng, J.; Wang, B.; Luk, P.C.K. An improved Thevenin model of lithium-ion battery with high accuracy for electric vehicles. Appl. Energy 2019, 254, 113615. [Google Scholar] [CrossRef]
- Liu, X.; Li, W.; Zhou, A. PNGV equivalent circuit model and SOC estimation algorithm for lithium battery pack adopted in AGV vehicle. IEEE Access 2018, 6, 23639–23647. [Google Scholar] [CrossRef]
- Luo, W.; Syed, A.U.; Nicholls, J.R.; Gray, S. An SVM-based health classifier for offline Li-ion batteries by using EIS technology. J. Electrochem. Soc. 2023, 170, 030532. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; Van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelghafar, A.A.; Soudan, B.; Alami, A.H.; Semeraro, C.; Al Radi, M.; Al-Murisi, M.; Abdelkareem, M.A. Artificial neural network driven prognosis and estimation of Lithium-Ion battery states: Current insights and future perspectives. Ain Shams Eng. J. 2023, 15, 102429. [Google Scholar] [CrossRef]
- Qu, J.; Liu, F.; Ma, Y.; Fan, J. A neural-network-based method for RUL prediction and SOH monitoring of lithium-ion battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Sun, H.; Sun, J.; Zhao, K.; Wang, L.; Wang, K. Data-driven ICA-Bi-LSTM-combined lithium battery SOH estimation. Math. Probl. Eng. 2022, 2022, 9645892. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Rong, Y.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, H.; Zhang, Y.; Shen, S.; Shen, J.; Liu, Y. State of health estimation for lithium-ion batteries based on temperature prediction and gated recurrent unit neural network. J. Power Sources 2022, 521, 230892. [Google Scholar] [CrossRef]
- Li, Y.; Tao, J. CNN and transfer learning based online SOH estimation for lithium-ion battery. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 5489–5494. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Zhang, P.; Schmidt, C.; Gomadam, P.; Gorka, T. Data-driven method based on particle swarm optimization and k-nearest neighbor regression for estimating capacity of lithium-ion battery. Appl. Energy 2014, 129, 49–55. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A deep learning method for online capacity estimation of lithium-ion batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Liu, X.; Wang, Y.; Zhang, L. Lithium-ion battery capacity estimation—A pruned convolutional neural network approach assisted with transfer learning. Appl. Energy 2021, 285, 116410. [Google Scholar] [CrossRef]
- Zhang, Y.; Wik, T.; Bergström, J.; Pecht, M.; Zou, C. A machine learning-based framework for online prediction of battery ageing trajectory and lifetime using histogram data. J. Power Sources 2022, 526, 231110. [Google Scholar] [CrossRef]
- Li, C.; Yang, L.; Li, Q.; Zhang, Q.; Zhou, Z.; Meng, Y.; Zhao, X.; Wang, L.; Zhang, S.; Li, Y.; et al. SOH estimation method for lithium-ion batteries based on an improved equivalent circuit model via electrochemical impedance spectroscopy. J. Energy Storage 2024, 86, 111167. [Google Scholar] [CrossRef]
- Li, D.; Yang, D.; Li, L.; Wang, L.; Wang, K. Electrochemical impedance spectroscopy based on the state of health estimation for lithium-ion batteries. Energies 2022, 15, 6665. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Obregon, J.; Han, Y.R.; Ho, C.W.; Mouraliraman, D.; Lee, C.W.; Jung, J.Y. Convolutional autoencoder-based SOH estimation of lithium-ion batteries using electrochemical impedance spectroscopy. J. Energy Storage 2023, 60, 106680. [Google Scholar] [CrossRef]
- Lin, Y.H.; Ruan, S.J.; Chen, Y.X.; Li, Y.F. Physics-informed deep learning for lithium-ion battery diagnostics using electrochemical impedance spectroscopy. Renew. Sustain. Energy Rev. 2023, 188, 113807. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.F.; Zhang, Y. Bioinspired spiking spatiotemporal attention framework for lithium-ion batteries state-of-health estimation. Renew. Sustain. Energy Rev. 2023, 188, 113728. [Google Scholar] [CrossRef]
- Luo, K.; Zheng, H.; Shi, Z. A simple feature extraction method for estimating the whole life cycle state of health of lithium-ion batteries using transformer-based neural network. J. Power Sources 2023, 576, 233139. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Zou, C.; Yao, K.; Xia, Y.; Gao, F. A novel framework for Lithium-ion battery modeling considering uncertainties of temperature and aging. Energy Convers. Manag. 2019, 180, 162–170. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.M.; Pecht, M. Effect of temperature on the aging rate of Li ion battery operating above room temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium-ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef] [PubMed]
- Lazanas, A.C.; Prodromidis, M.I. Electrochemical impedance spectroscopy—A tutorial. ACS Meas. Sci. Au 2023, 3, 162–193. [Google Scholar] [CrossRef]
- Mc Carthy, K.; Gullapalli, H.; Ryan, K.M.; Kennedy, T. Use of impedance spectroscopy for the estimation of Li-ion battery state of charge, state of health and internal temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar] [CrossRef]
- Zhao, B.; Lu, H.; Chen, S.; Liu, J.; Wu, D. Convolutional neural networks for time series classification. J. Syst. Eng. Electron. 2017, 28, 162–169. [Google Scholar] [CrossRef]
- Canizo, M.; Triguero, I.; Conde, A.; Onieva, E. Multi-head CNN–RNN for multi-time series anomaly detection: An industrial case study. Neurocomputing 2019, 363, 246–260. [Google Scholar] [CrossRef]
- Liu, S.; Ji, H.; Wang, M.C. Nonpooling convolutional neural network forecasting for seasonal time series with trends. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2879–2888. [Google Scholar] [CrossRef]
- Liu, C.L.; Hsaio, W.H.; Tu, Y.C. Time series classification with multivariate convolutional neural network. IEEE Trans. Ind. Electron. 2018, 66, 4788–4797. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent neural networks for time series forecasting: Current status and future directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, C.; Yang, L.; Chen, Y. DSTP-RNN: A dual-stage two-phase attention-based recurrent neural network for long-term and multivariate time series prediction. Expert Syst. Appl. 2020, 143, 113082. [Google Scholar] [CrossRef]
- Guo, T.; Xu, Z.; Yao, X.; Chen, H.; Aberer, K.; Funaya, K. Robust online time series prediction with recurrent neural networks. In Proceedings of the 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Montreal, QC, Canada, 17–19 October 2016; pp. 816–825. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Pradyumna, T.K.; Cho, K.; Kim, M.; Choi, W. Capacity estimation of lithium-ion batteries using convolutional neural network and impedance spectra. J. Power Electron. 2022, 22, 850–858. [Google Scholar] [CrossRef]
| Input Feature | Model Classification | Specific Methods | Ref. |
|---|---|---|---|
| DFN | [9] | ||
| Physical model | DP | [11] | |
| PNGV | [13] | ||
| LSTM-PSO | [17] | ||
| CNN-RF | [18] | ||
| Based on charging/ discharging curve | AST-LSTM NN | [20] | |
| Data-driven | GRU | [21] | |
| KNN-PSO | [23] | ||
| FRA-CNN | [25] | ||
| ECMC-GPR | [27] | ||
| ECM | [28] | ||
| CAE-DNN | [30] | ||
| EIS data | PIDL | [31] | |
| SSA-Net | [32] | ||
| Transformer | [33] |
| Layer | Other Parameters | |
|---|---|---|
| Conv1d—1 (1, 32) BatchNorm1d (32) LeakyReLU () | Kernel—1 (5) | Loss function (Huber) |
| Conv1d—2 (32, 64) BatchNorm1d (64) LeakyReLU () | Kernel—2 (5) | Optimize (SGD) |
| Conv1d—3 (64, 128) BatchNorm1d (128) LeakyReLU () Maxpool (2) | Kernel—3 (5) | |
| GRU—1 (128, 256) Dropout (0.3) | ||
| GRU—2 (256, 128) Dropout (0.1) | ||
| Multihead-attention (128) Dropout (0.1) | Num heads (4) | |
| Linear (128, 64) Linear (64, 1) |
| Cross Validation | Fold1 | Fold2 | Fold3 | Fold4 | Fold5 | Fold6 |
|---|---|---|---|---|---|---|
| Cell ID | 25C01 | 25C01 | 25C05 | 25C05 | 35C01 | 45C01 |
| 35C01 | 35C02 | 45C01 | 45C02 | 35C02 | 45C02 |
| Model | Cross Validation | Cell ID | RMSE (mAh) | MAE (mAh) | MAPE (%) |
|---|---|---|---|---|---|
| CGMA-Net | Fold 1 | 25C01 35C01 Average | 1.0217 0.5634 0.7926 | 0.7574 0.4013 0.5794 | 2.99 1.49 2.24 |
| Fold 2 | 25C01 35C02 Average | 1.0919 0.3266 0.7093 | 0.9378 0.2412 0.5895 | 3.27 0.77 2.02 | |
| Fold 3 | 25C05 45C01 Average | 0.8258 0.5876 0.7067 | 0.5663 0.4747 0.5205 | 2.81 1.33 2.07 | |
| Fold 4 | 25C05 45C02 Average | 0.8073 0.5341 0.6707 | 0.5985 0.4373 0.5179 | 2.99 1.30 2.15 | |
| Fold 5 | 35C01 35C02 Average | 0.3345 0.4869 0.4107 | 0.2525 0.3778 0.3156 | 2.41 1.31 1.86 | |
| Fold 6 | 45C01 45C02 Average | 0.5727 0.5308 0.5516 | 0.4895 0.4488 0.4692 | 1.36 1.34 1.35 |
| Cross Validation | Metrics | CGMA-Net | CNN | GRU | CNN-GRU | CNN-Attention | GRU-Attention | CNN-LSTM | Transformer | |
|---|---|---|---|---|---|---|---|---|---|---|
| Fold1 | 25C01 | MAE | 0.7574 | 1.1032 | 1.0536 | 1.7649 | 1.3162 | 2.1073 | 1.5336 | 1.5671 |
| RMSE | 1.0217 | 1.3960 | 1.1505 | 1.9633 | 1.6336 | 2.1438 | 1.6997 | 1.8548 | ||
| MAPE | 2.99 | 4.89 | 4.18 | 6.66 | 4.93 | 8.45 | 5.95 | 6.42 | ||
| 35C01 | MAE | 0.4013 | 0.9270 | 1.8104 | 1.2442 | 1.1186 | 1.4328 | 1.6023 | 1.1790 | |
| RMSE | 0.5634 | 1.3403 | 2.1833 | 1.6641 | 1.2435 | 1.7668 | 1.8142 | 1.5145 | ||
| MAPE | 1.49 | 3.47 | 6.92 | 4.80 | 3.98 | 5.70 | 5.93 | 4.05 | ||
| Average | MAE RMSE MAPE | 0.5794 0.7926 2.24 | 1.0151 1.3682 4.18 | 1.4320 1.6667 5.55 | 1.4956 1.8137 5.73 | 1.2174 1.4386 4.45 | 1.7700 1.9553 7.07 | 1.5679 1.7569 5.94 | 1.3730 1.6846 5.23 | |
| Fold2 | 25C01 | MAE | 0.9378 | 2.2811 | 3.3675 | 1.5786 | 1.8490 | 3.0064 | 0.8402 | 1.1989 |
| RMSE | 1.0919 | 2.4838 | 3.7431 | 1.6951 | 2.0318 | 3.3559 | 0.9333 | 1.6072 | ||
| MAPE | 3.27 | 8.48 | 11.97 | 5.79 | 6.85 | 10.79 | 3.16 | 4.83 | ||
| 35C02 | MAE | 0.2412 | 0.6823 | 0.9022 | 0.6299 | 0.8565 | 0.9598 | 0.8748 | 1.1673 | |
| RMSE | 0.3266 | 0.7519 | 0.9332 | 0.7001 | 1.0192 | 0.9882 | 1.0256 | 1.3964 | ||
| MAPE | 0.77 | 2.15 | 2.89 | 2.04 | 2.65 | 3.07 | 2.68 | 3.73 | ||
| Average | MAE RMSE MAPE | 0.5895 0.7093 2.02 | 1.4817 1.6179 5.32 | 2.1349 2.3382 7.43 | 1.1043 1.1976 3.91 | 1.3527 1.5255 4.75 | 1.9831 2.1721 6.93 | 0.8575 0.9795 2.92 | 1.1831 1.5018 4.28 | |
| Fold3 | 25C05 | MAE | 0.5663 | 1.0634 | 0.8404 | 1.1455 | 1.4675 | 0.5944 | 1.2033 | 2.1234 |
| RMSE | 0.8258 | 1.2323 | 1.1818 | 1.5297 | 1.6850 | 1.0950 | 1.4363 | 2.7911 | ||
| MAPE | 2.81 | 5.62 | 5.87 | 7.65 | 7.13 | 4.90 | 7.36 | 10.76 | ||
| 45C01 | MAE | 0.4747 | 1.8426 | 2.1769 | 0.4246 | 1.5927 | 1.5634 | 0.5540 | 1.0446 | |
| RMSE | 0.5876 | 2.2685 | 2.3353 | 0.5156 | 1.8769 | 1.7664 | 0.6632 | 1.2845 | ||
| MAPE | 1.33 | 5.07 | 6.13 | 1.15 | 4.47 | 4.39 | 1.51 | 2.81 | ||
| Average | MAE RMSE MAPE | 0.5205 0.7067 2.07 | 1.4530 1.7504 5.34 | 1.5087 1.7586 6.00 | 0.7850 1.0226 4.40 | 1.5301 1.7809 5.80 | 1.0789 1.4037 4.65 | 0.8786 1.0497 4.43 | 1.5840 2.0378 6.79 | |
| Fold4 | 25C05 | MAE | 0.5985 | 1.9677 | 1.6948 | 0.9784 | 1.3104 | 1.2250 | 1.0235 | 2.4121 |
| RMSE | 0.8073 | 2.1827 | 2.0172 | 1.2712 | 1.6652 | 1.6711 | 1.5149 | 3.0633 | ||
| MAPE | 2.99 | 8.93 | 9.17 | 6.23 | 8.45 | 8.49 | 7.35 | 14.01 | ||
| 45C02 | MAE | 0.4373 | 0.9533 | 0.8212 | 0.5405 | 0.6954 | 0.9552 | 0.4983 | 1.3870 | |
| RMSE | 0.5341 | 1.1153 | 0.9036 | 0.6570 | 1.1120 | 1.0754 | 0.6657 | 1.6495 | ||
| MAPE | 1.30 | 2.87 | 2.43 | 1.59 | 2.14 | 2.81 | 1.50 | 4.13 | ||
| Average | MAE RMSE MAPE | 0.5179 0.6707 2.15 | 1.4605 1.6490 5.90 | 1.2580 1.4604 5.80 | 0.7594 0.9641 3.91 | 1.0029 1.3886 5.30 | 1.0901 1.3732 5.65 | 0.7609 1.0903 4.42 | 1.8995 2.3564 9.07 | |
| Fold5 | 35C01 | MAE | 0.2525 | 1.1867 | 1.7578 | 1.2736 | 0.8134 | 1.8474 | 0.9964 | 1.2641 |
| RMSE | 0.3345 | 1.3648 | 1.8663 | 1.4067 | 0.9909 | 2.0332 | 1.0752 | 1.7900 | ||
| MAPE | 2.41 | 4.52 | 6.56 | 4.29 | 2.90 | 6.99 | 3.65 | 4.77 | ||
| 35C02 | MAE | 0.3778 | 0.8006 | 0.4282 | 0.7344 | 1.2130 | 0.5120 | 0.6451 | 1.3652 | |
| RMSE | 0.4869 | 0.8480 | 0.5038 | 0.9388 | 1.4198 | 0.5663 | 0.7299 | 1.6493 | ||
| MAPE | 1.31 | 2.59 | 1.31 | 2.42 | 4.05 | 1.58 | 2.02 | 4.41 | ||
| Average | MAE RMSE MAPE | 0.3156 0.4107 1.86 | 0.9936 1.1064 3.55 | 1.0930 1.1851 3.93 | 1.0040 1.1727 3.36 | 1.0132 1.2053 3.47 | 1.1797 1.2998 4.29 | 0.8207 0.9026 2.83 | 1.3146 1.7196 4.59 | |
| Fold6 | 45C01 | MAE | 0.4895 | 1.0895 | 1.6596 | 0.8339 | 1.6693 | 2.4081 | 0.3537 | 2.0117 |
| RMSE | 0.5727 | 1.2415 | 1.7658 | 1.1916 | 2.4035 | 2.8839 | 0.5288 | 2.3453 | ||
| MAPE | 1.36 | 3.02 | 4.60 | 2.22 | 4.64 | 6.55 | 0.98 | 5.64 | ||
| 45C02 | MAE | 0.4488 | 0.8207 | 0.6787 | 0.6926 | 1.0958 | 0.7546 | 0.6475 | 0.8200 | |
| RMSE | 0.5308 | 0.9770 | 0.8094 | 0.7389 | 1.2233 | 0.9133 | 0.7467 | 1.0717 | ||
| MAPE | 1.34 | 2.50 | 1.87 | 2.02 | 3.22 | 2.07 | 1.92 | 2.29 | ||
| Average | MAE RMSE MAPE | 0.4692 0.5516 1.35 | 1.3151 1.1092 2.76 | 1.1692 1.2876 3.24 | 0.7633 0.9633 2.12 | 1.3825 1.1834 3.93 | 1.5814 1.8986 4.31 | 0.5006 0.6377 1.45 | 1.4158 1.7085 3.96 |
| Model Size | Total Parameters | Average Training Time | Average Testing Time | |
|---|---|---|---|---|
| GRU | 1751 kb | 446,849 | 285.84 s | <0.1 s |
| CNN-GRU | 1986 kb | 505,025 | 1008.82 s | <0.2 s |
| CGMA-Net | 2242 kb | 571,073 | 1159.29 s | <0.2 s |
| CNN-LSTM | 2560 kb | 653,249 | 1239.52 s | <0.2 s |
| Transformer | 3072 kb | 783,953 | 1373.25 s | <0.2 s |
| Temperature | Model | RMSE | R2 | References |
|---|---|---|---|---|
| 25 °C | ECMC-GPR | 0.0207 | - | [27] |
| ECM | 0.0537 | 0.9374 | [28] | |
| PIDL | 0.0636 | 0.9500 | [31] | |
| SSA-Net | 0.0257 | 0.3828 | [32] | |
| CGMA-Net | 0.0275 | 0.9731 | - | |
| 35 °C | ECMC-GPR | 0.0131 | - | [27] |
| ECM | 0.0691 | 0.9453 | [28] | |
| CAE-DNN | 0.0129 | 0.9657 | [30] | |
| SSA-Net | 0.0262 | 0.8711 | [32] | |
| Transformer | 0.6400 | 0.9400 | [33] | |
| CGMA-Net | 0.0105 | 0.9908 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, B.; Zhong, J.; Tian, J.; Li, Y.; Chen, X.; Dou, W.; Liao, Q.; Lai, C.; Lu, T.; Xie, J. State-of-Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy Features and Fusion Interpretable Deep Learning Framework. Energies 2025, 18, 1385. https://doi.org/10.3390/en18061385
Shao B, Zhong J, Tian J, Li Y, Chen X, Dou W, Liao Q, Lai C, Lu T, Xie J. State-of-Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy Features and Fusion Interpretable Deep Learning Framework. Energies. 2025; 18(6):1385. https://doi.org/10.3390/en18061385
Chicago/Turabian StyleShao, Bohan, Jun Zhong, Jie Tian, Yan Li, Xiyu Chen, Weilin Dou, Qiangqiang Liao, Chunyan Lai, Taolin Lu, and Jingying Xie. 2025. "State-of-Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy Features and Fusion Interpretable Deep Learning Framework" Energies 18, no. 6: 1385. https://doi.org/10.3390/en18061385
APA StyleShao, B., Zhong, J., Tian, J., Li, Y., Chen, X., Dou, W., Liao, Q., Lai, C., Lu, T., & Xie, J. (2025). State-of-Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy Features and Fusion Interpretable Deep Learning Framework. Energies, 18(6), 1385. https://doi.org/10.3390/en18061385






