Analysis of the Mechanical Stability of Power Transformer Windings Considering the Influence of Temperature Field
Abstract
1. Introduction
2. Theoretical Model of Transformer Windings
2.1. Theoretical Modeling of Transformer Electromagnetic Fields
2.2. Theoretical Modeling of Transformer Heat-Flow Field
3. Transformer Mechanical Stability Analysis
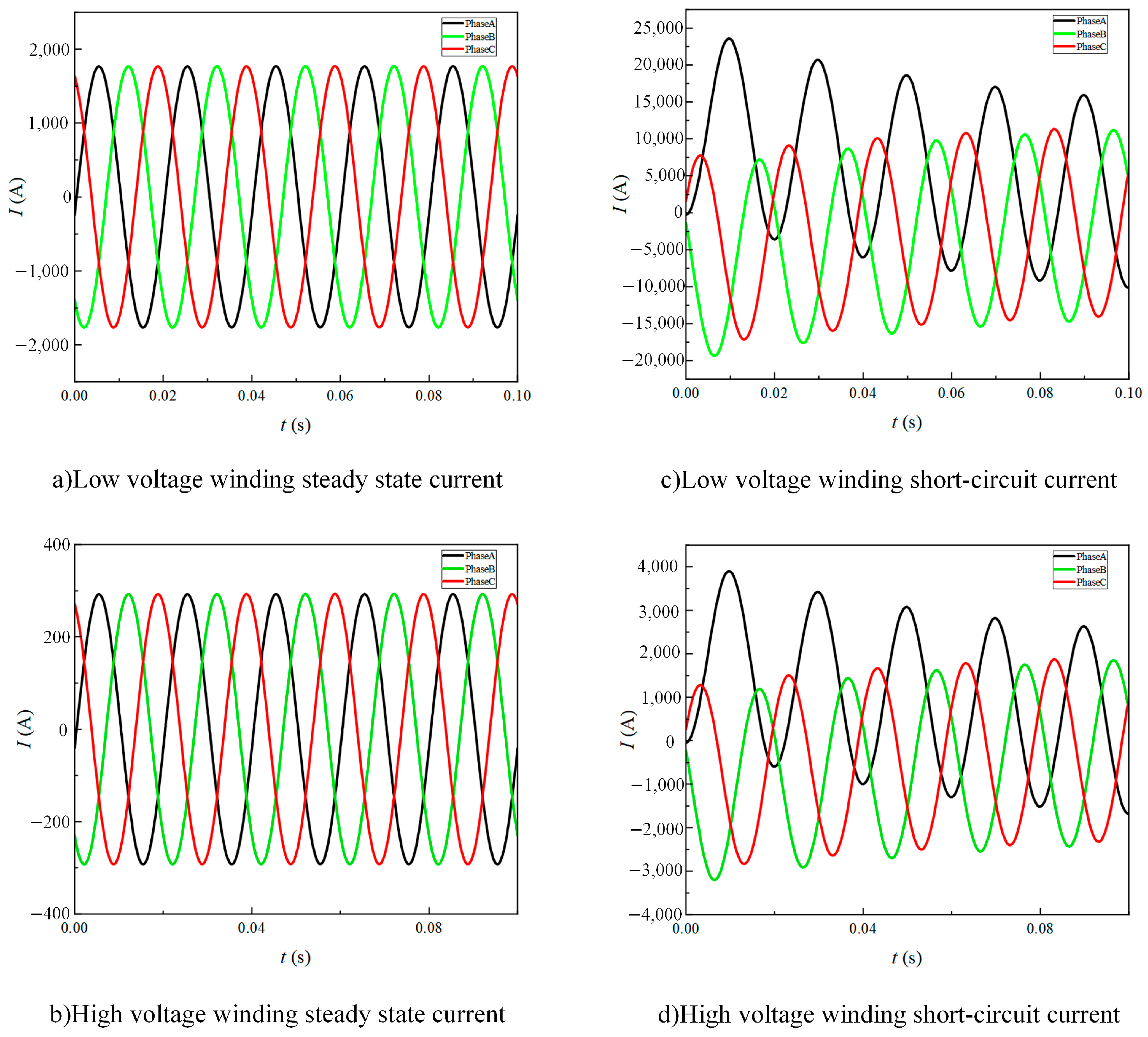
3.1. Transformer Winding Current Calculation Model
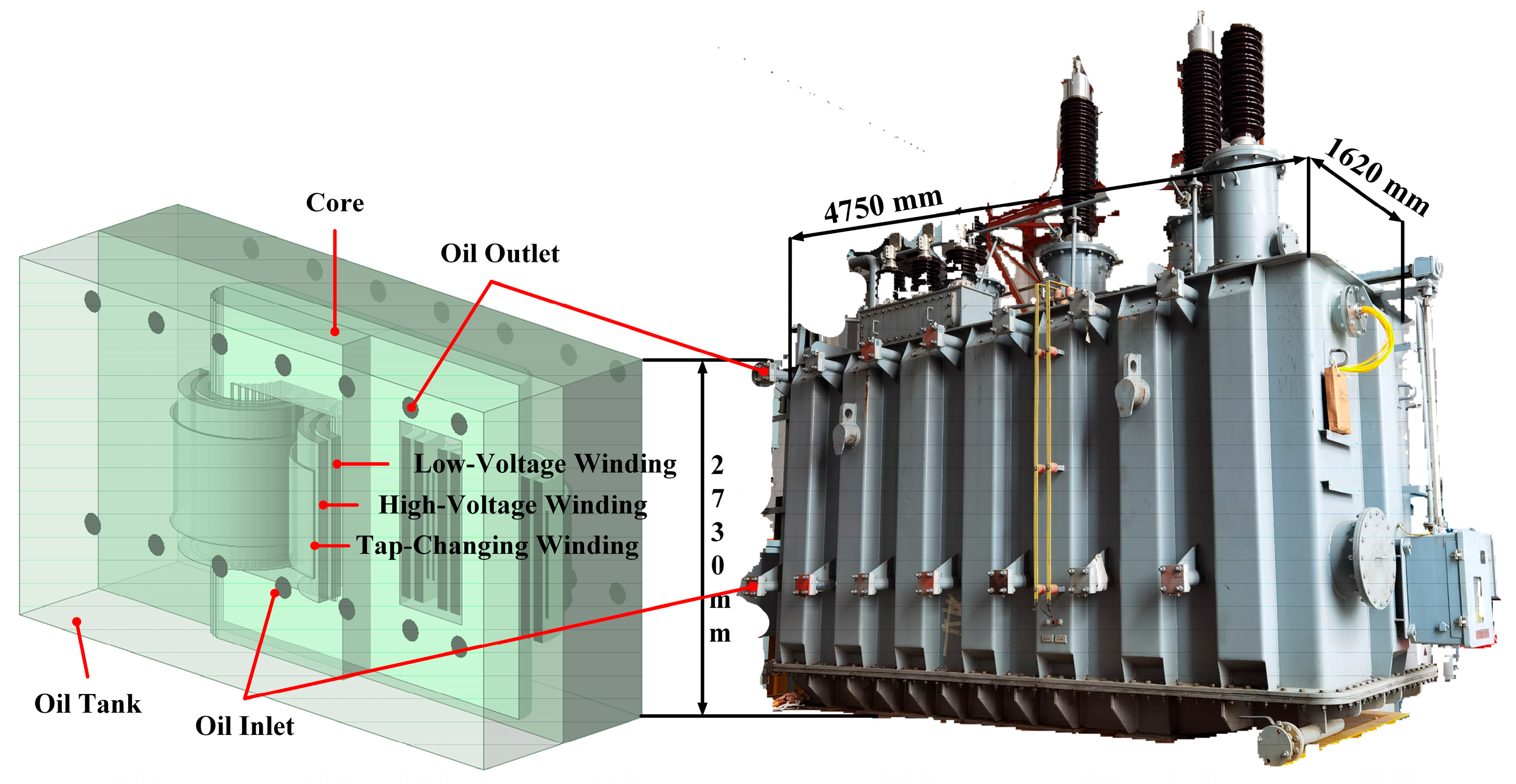
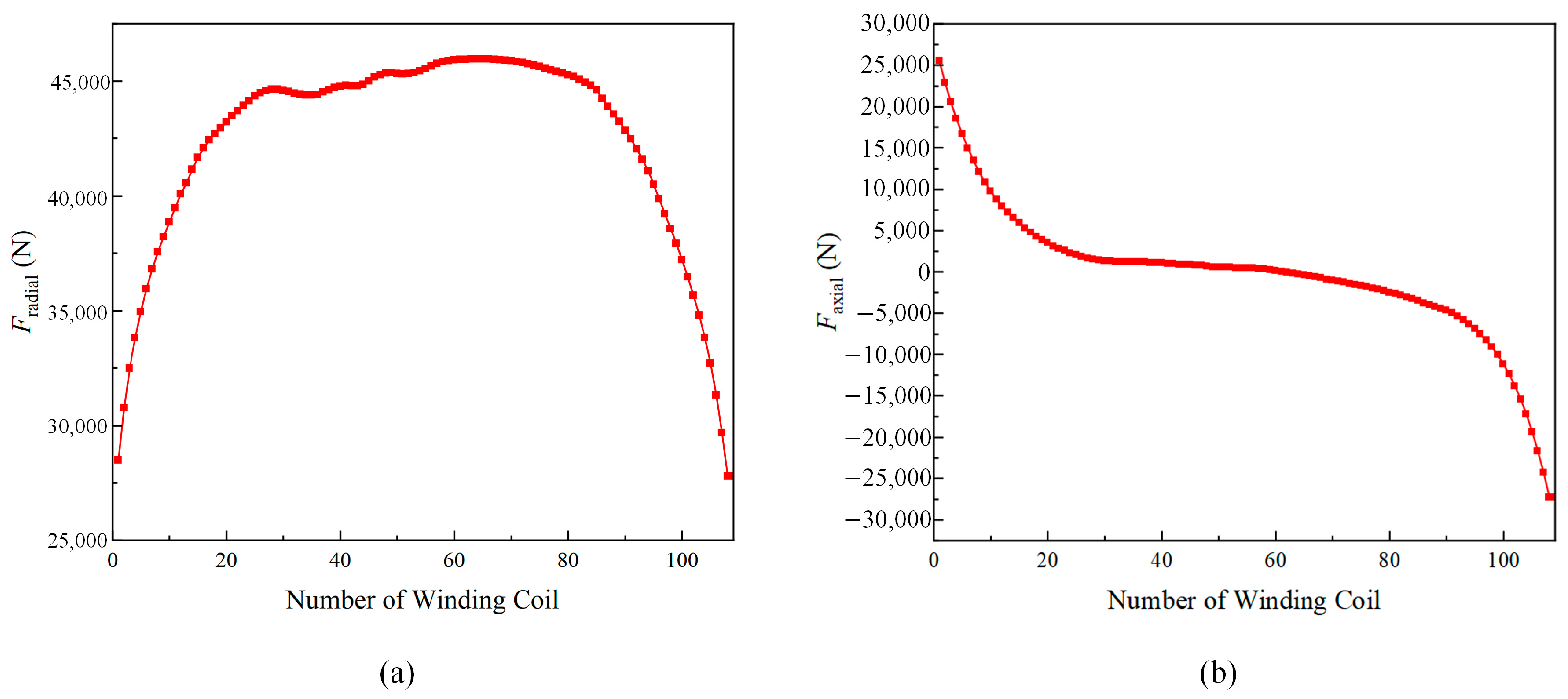
3.2. Finite Element Modeling and Analysis of Transformer Electromagnetic Force Fields
- (1)
- The model retains only the core, windings, and tank structure.
- (2)
- The oil ducts between the windings are neglected, and each phase winding is simplified to a hollow cylindrical structure.
- (3)
- The cooling fin structures are ignored, with only the oil inlet and outlet retained. Other components on the surface of the tank are neglected, as well as the thickness of the tank walls.
- (4)
- The core is treated as a whole, disregarding its laminated silicon steel structure.
3.3. Mechanical Stability of Transformers
- (1)
- Mean hoop compressive stress
- (2)
- Radial bending stress
- (3)
- Free buckling critical stress
- (4)
- Compressive stress on radial spacers
- (5)
- Axial bending stress
4. Mechanical Stability Analysis of Power Transformer Windings by Counting and Temperature Field
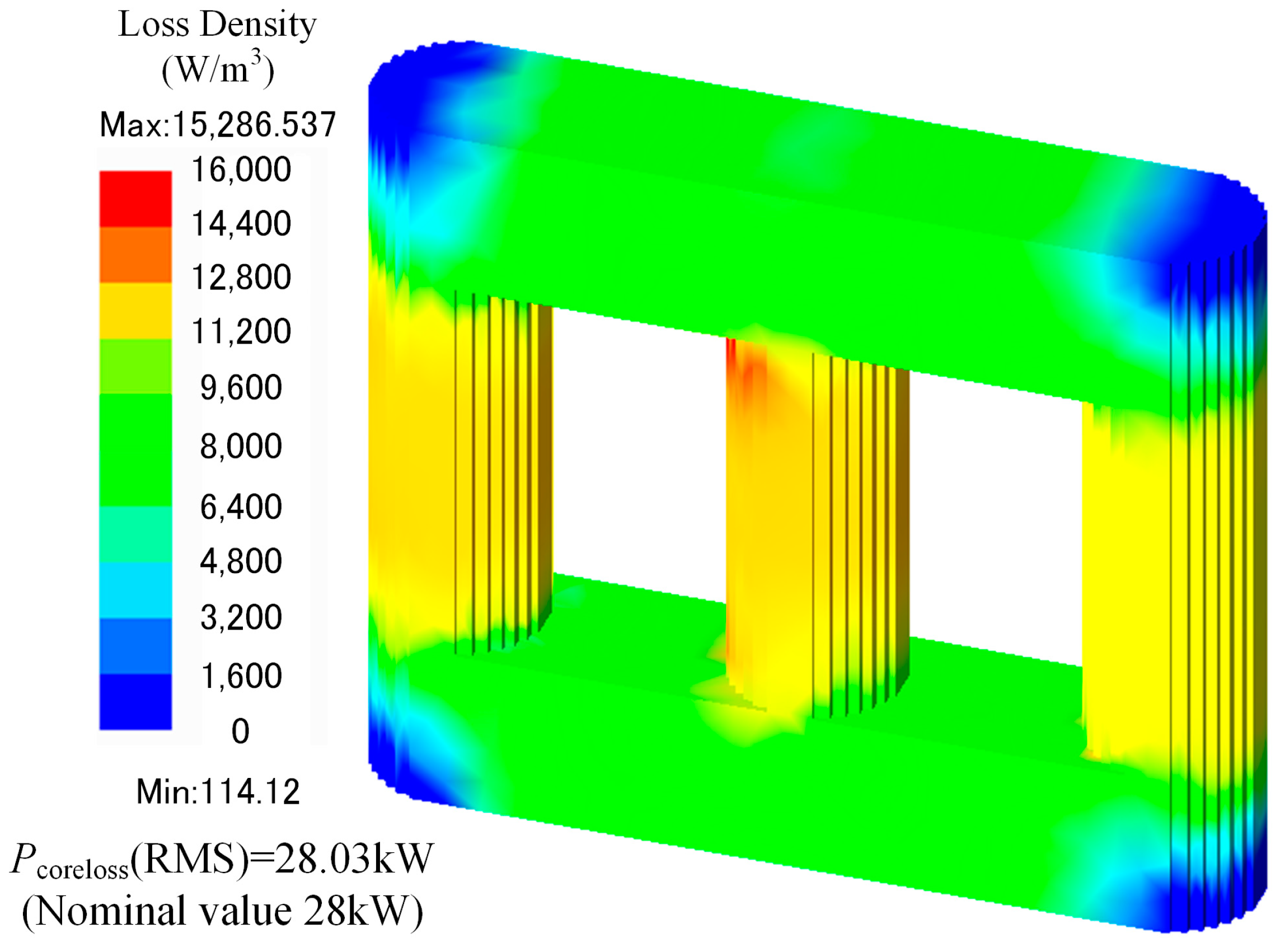
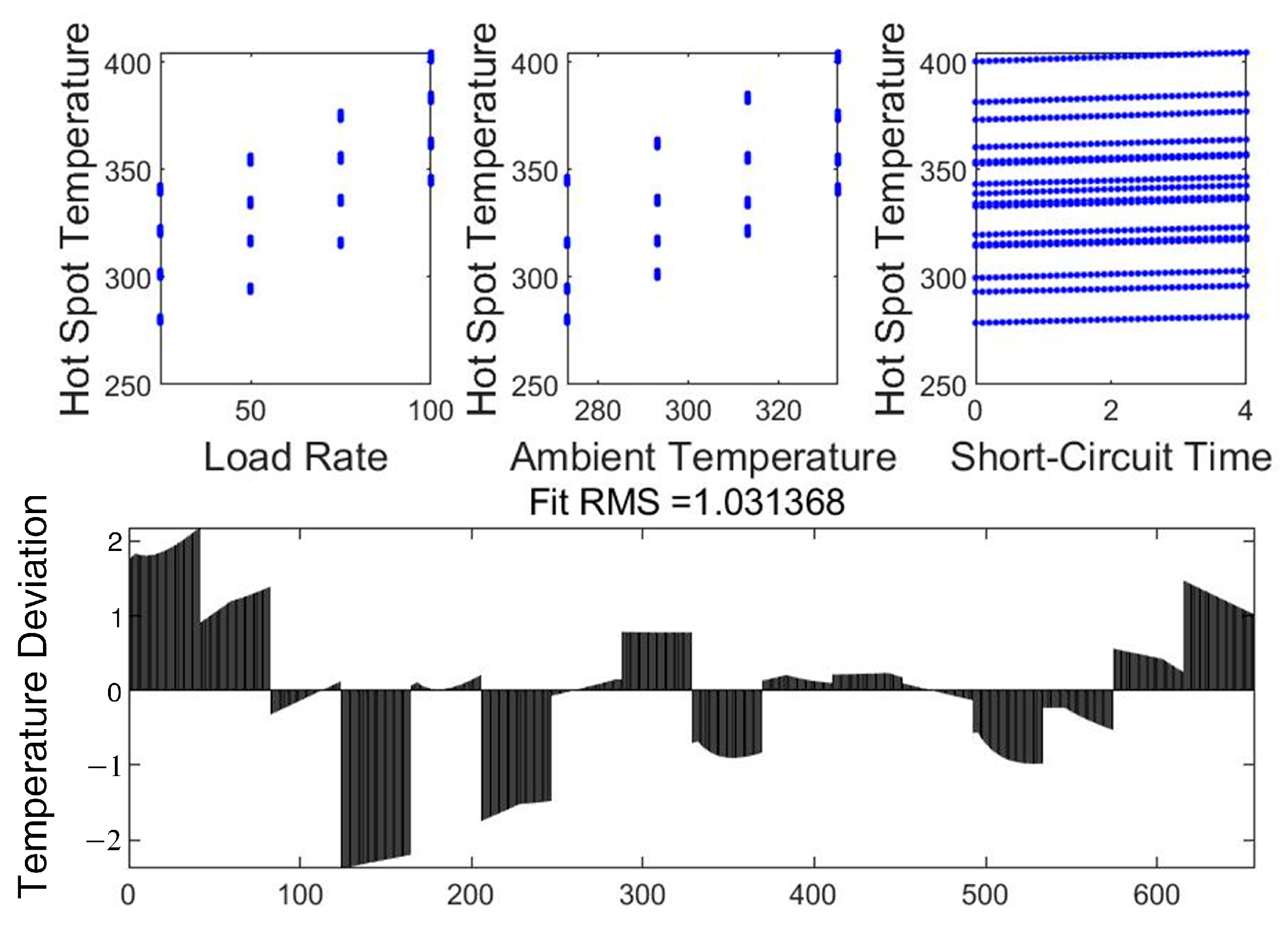
4.1. Transformer Heat-Flow Steady-State Field Calculations and Their Experimental Validation
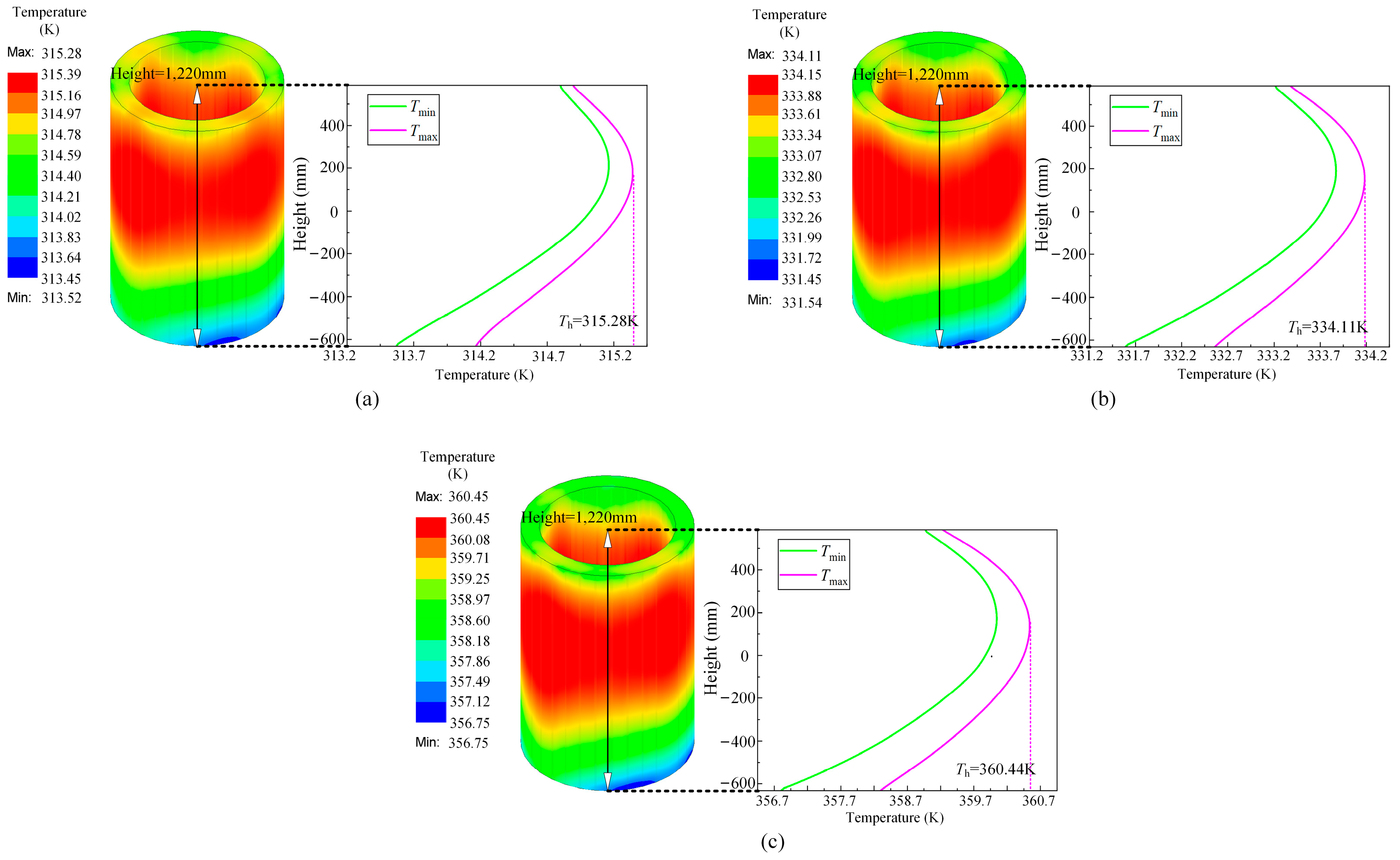
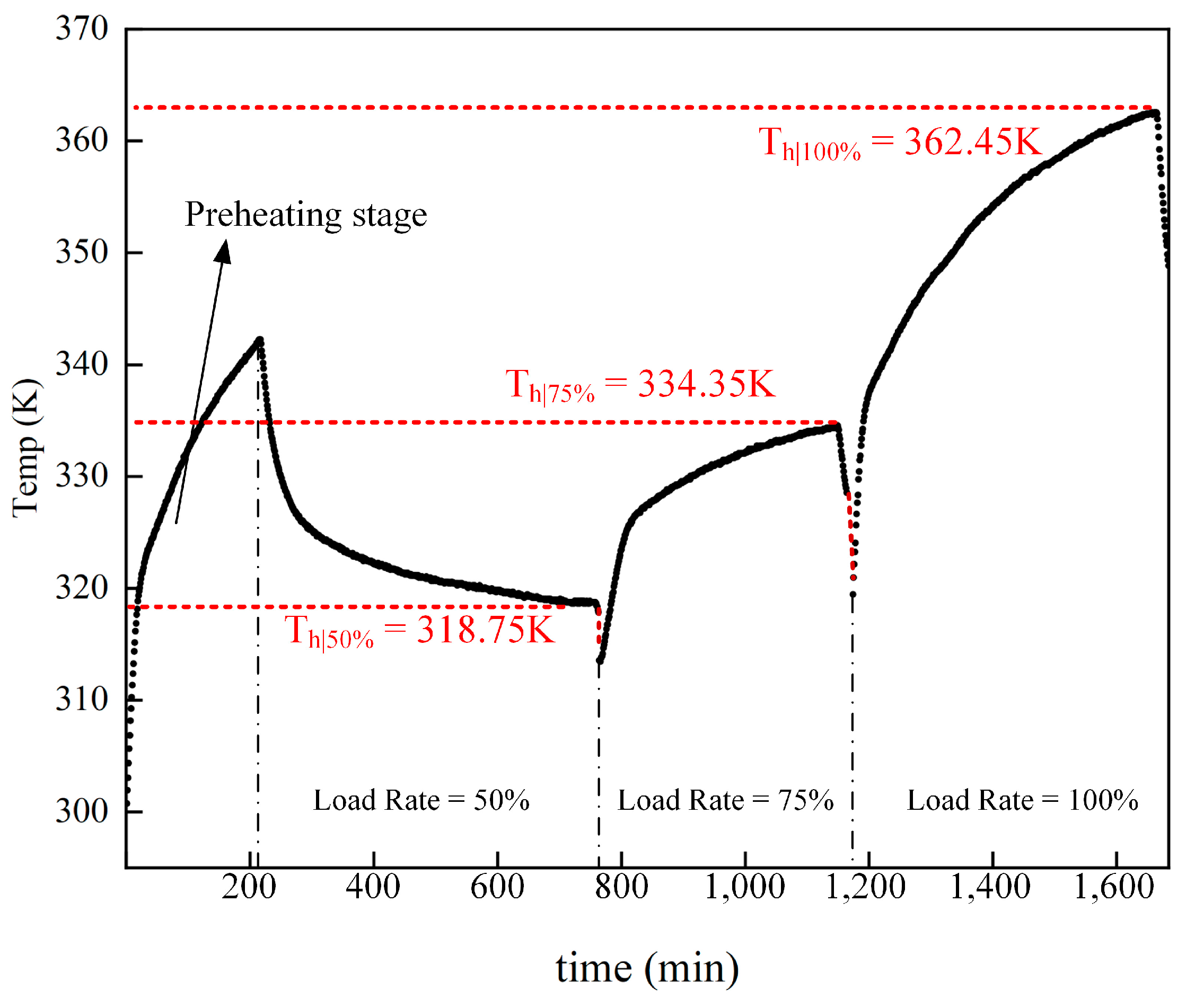
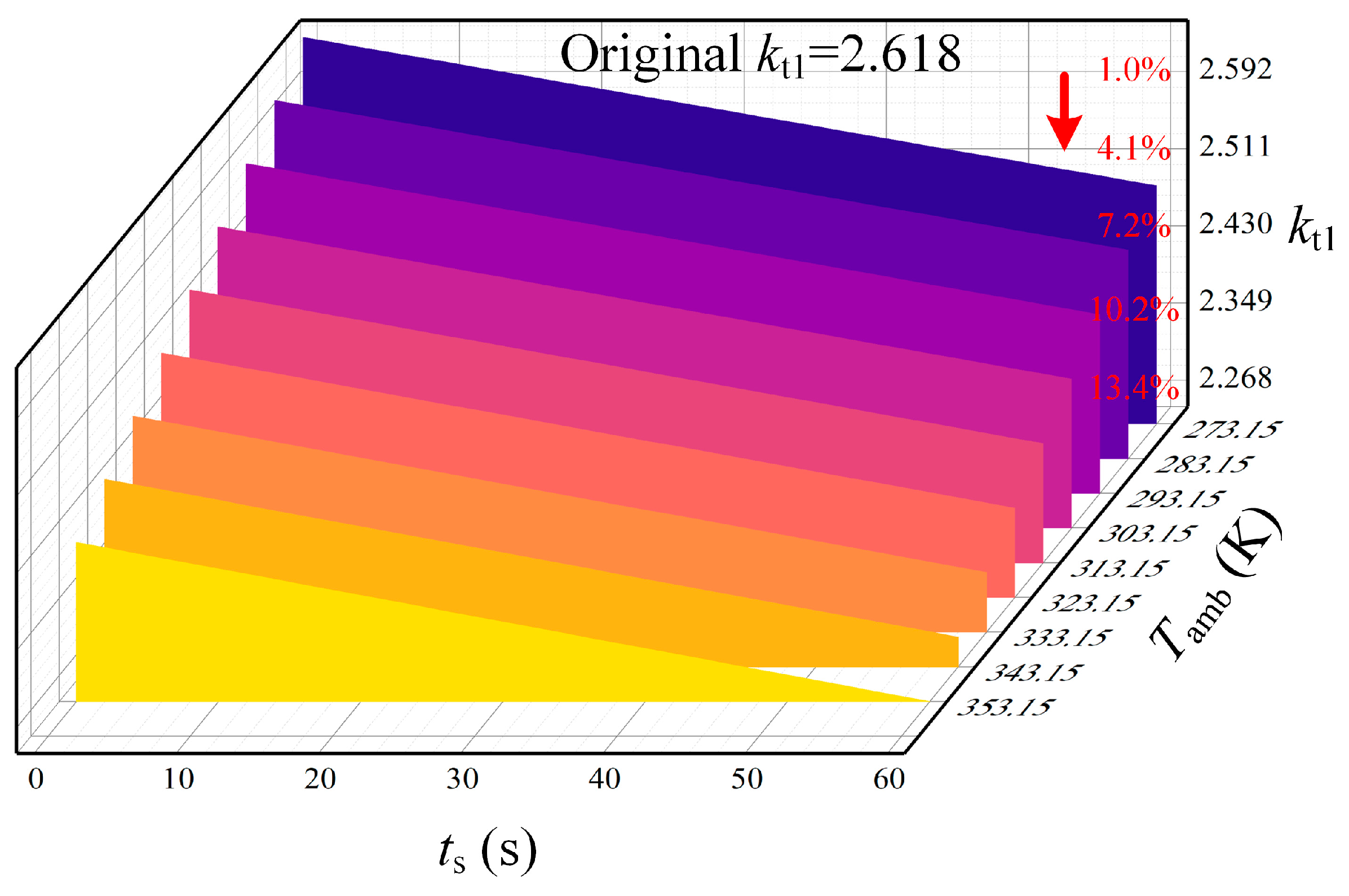
4.2. Transformer Heat-Flow Transient Field Calculations and Winding Hot Spot Temperature Fitting
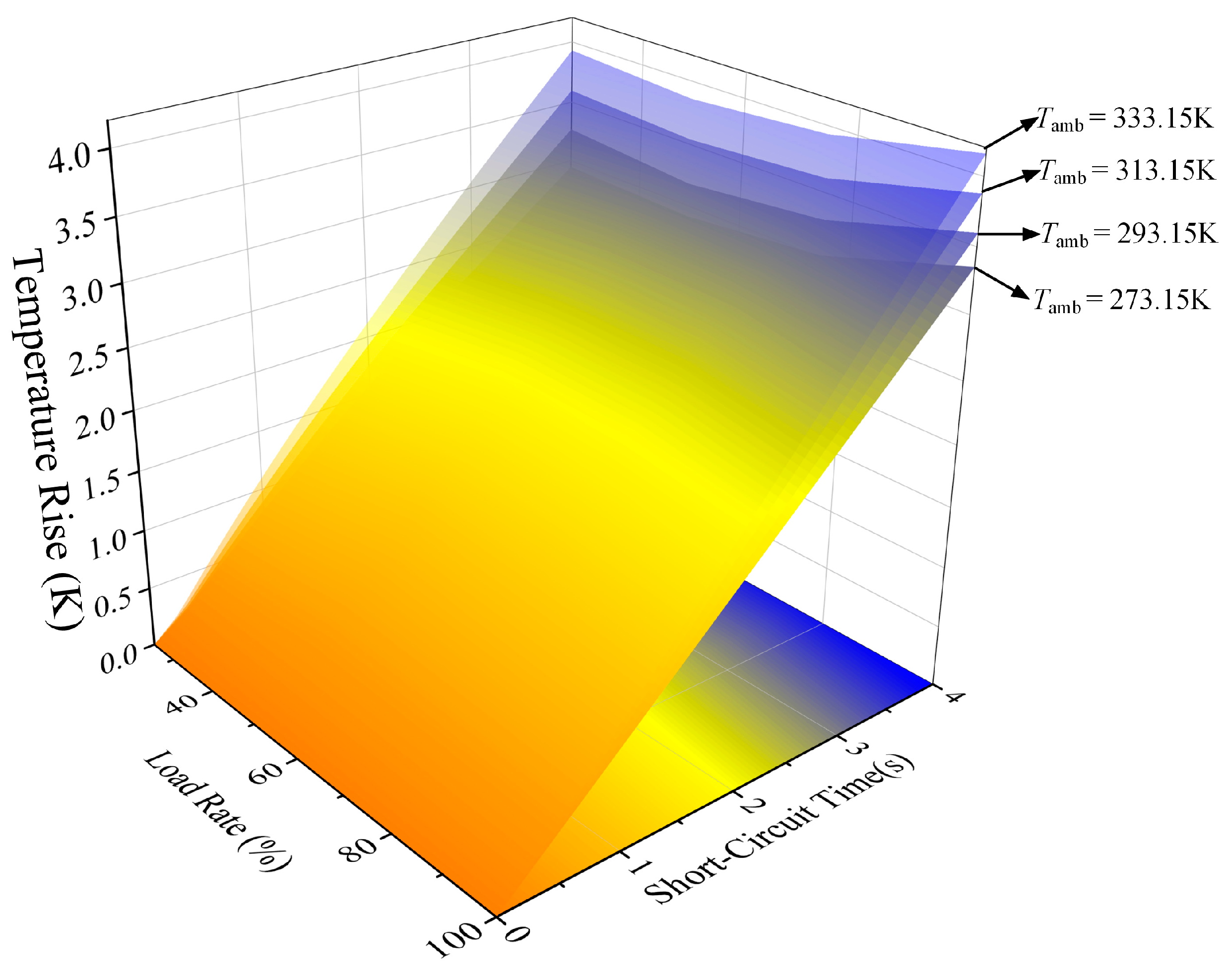
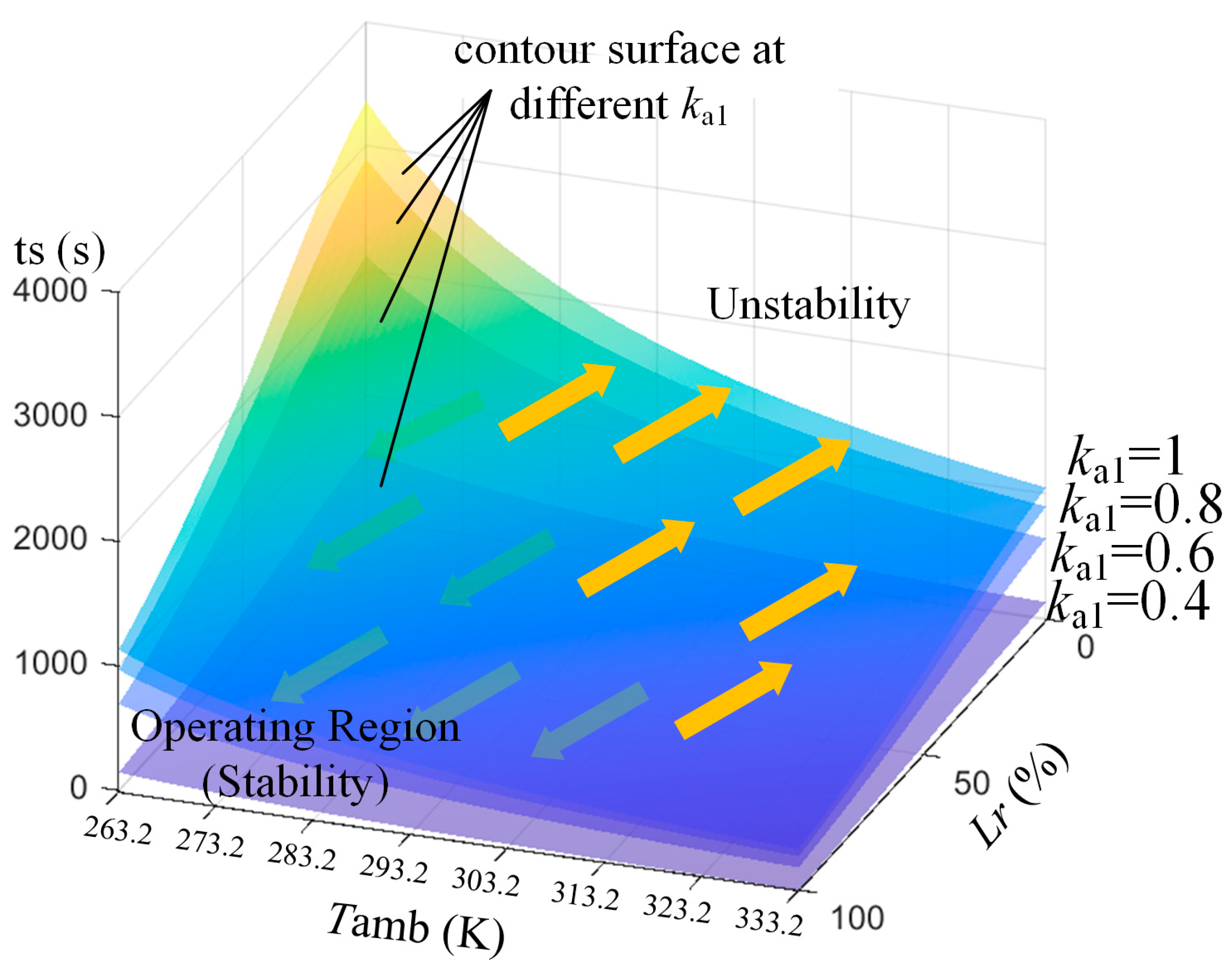
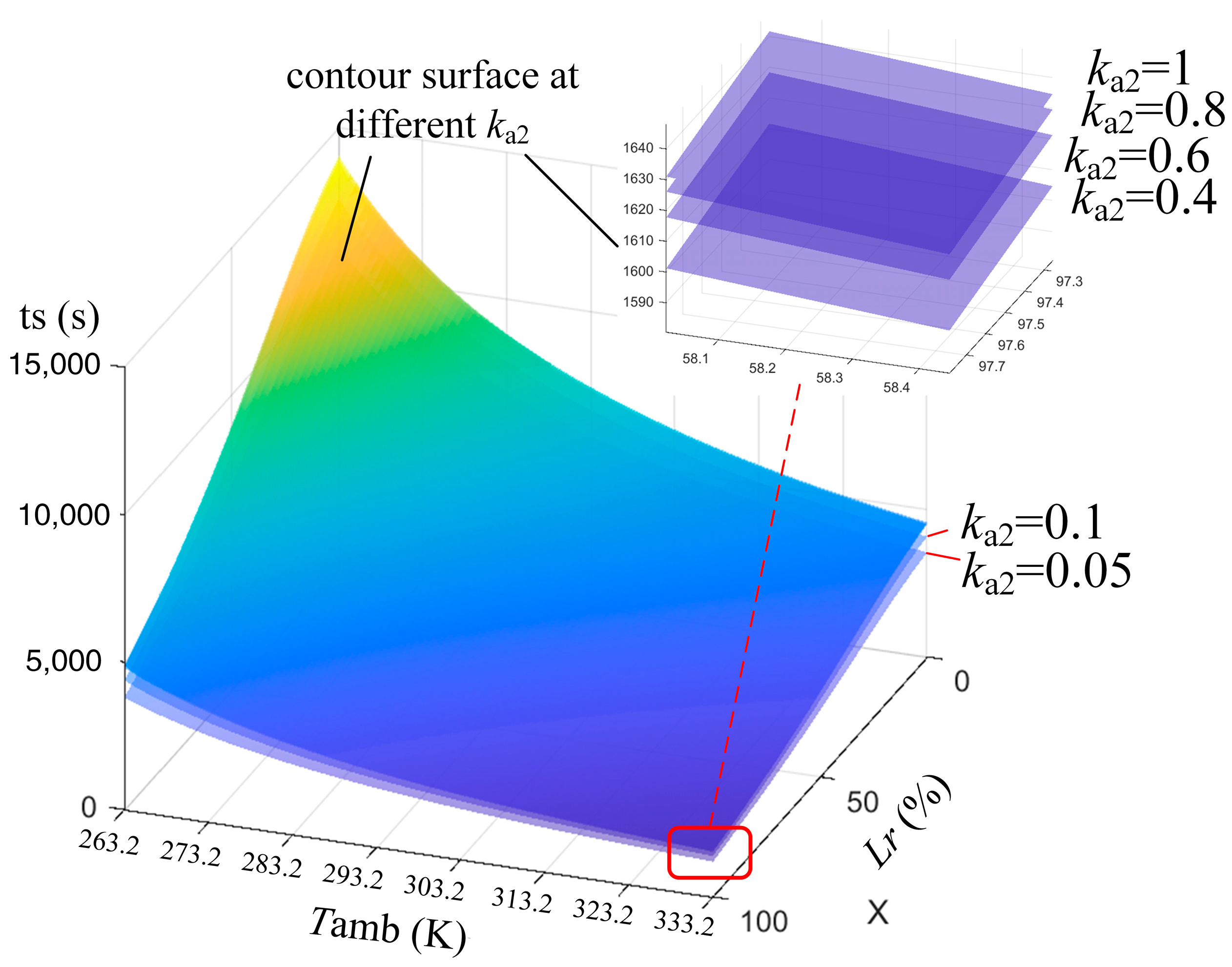
4.3. Calculation and Analysis of Mechanical Stability Margins of Power Transformer Windings Taking into Account Temperature Field
5. Conclusions
- Design more experimental conditions to verify the model more comprehensively and universally. Specifically, increase more load rates and carry out related experiments at various ambient temperatures.
- Design a reasonable method for a transient temperature rise test of transformer windings. Due to the short transient time and small transient temperature change, there is no low-cost and high-precision method to measure the transient temperature rise in transformer windings. This is an urgent problem to be solved to study the influence of transformer short-circuit temperature rise on the mechanical stability of transformer windings.
- Accurately measure the influence of temperature on the yield strength and elastic modulus of transformer windings. Subject to the experimental conditions of material mechanics, the relationship among winding yield strength, elastic modulus, and temperature used in this paper refers to the existing articles. In the future, targeted measurements should be carried out for the target transformer used to more accurately evaluate the influence of temperature on winding mechanical stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Yan, N.; Ma, S.; Wang, H. Buckling Strength Analysis of Transformer Windings Based on Electromagnetic Thermal Structural Coupling Method. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Meško, N.; Ćućić, B.; Žarko, D. Short-Circuit Stress Calculation in Oval Windings. Procedia Eng. 2017, 202, 319–326. [Google Scholar] [CrossRef]
- Wang, J. Research on Anti-Short Circuit Ability of Power Transformer Considering Heat Accumulation Effect. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2023. [Google Scholar]
- Ou, Q. Investigation on Evaluation of Mechanical Damage and Cumulative Effect for Power Transformer Windings Under Short Circuit Impact. Ph.D. Thesis, Hunan University, Changsha, China, 2023. [Google Scholar]
- GB 1094.5-2008; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Pepublic of China. Power Transformer-Part 5: Ability to Withstand Short Circuit. China Standard Press: Beijing, China, 2008.
- IEC 60076-5; Power Transformer-Part 5: Ability to Withstand Short Circuit. International Electrotechnical Commission: Geneva, Switzerland, 2006.
- Li, K. Study on Calibration Models and Evaluation Technology for Short Circuit Withstand Ability of Power Transformer. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. [Google Scholar]
- Ou, Q.; Luo, L.; Li, Y.; Li, Y.; Xiang, J. Buckling Strength Investigation for Power Transformer Winding Under Short Circuit Impact Considering Manufacture and Operation. IEEE Access 2023, 11, 7850–7859. [Google Scholar] [CrossRef]
- Bakshi, A.; Kulkarni, S.V. Analysis of Buckling Strength of Inner Windings in Transformers Under Radial Short-Circuit Forces. IEEE Trans. Power Deliv. 2014, 29, 241–245. [Google Scholar] [CrossRef]
- Cotas, C.; Santos, R.J.; Gonçalves, N.D.; Quintela, M.; Couto, S.; Campelo, H.; Dias, M.M.; Lopes, J.C.B. Numerical Study of Transient Flow Dynamics in a Core-Type Transformer Windings. Electr. Power Syst. Res. 2020, 187, 106423. [Google Scholar] [CrossRef]
- Zhang, Y.; Ho, S.-L.; Fu, W.; Yang, X.; Wu, H. Numerical Study on Natural Convective Heat Transfer of Nanofluids in Disc-Type Transformer Windings. IEEE Access 2019, 7, 51267–51275. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Liu, Q. Prediction of Pressure Drop and Flow Distribution in Disc-Type Transformer Windings in an OD Cooling Mode. IEEE Trans. Power Deliv. 2017, 32, 1655–1664. [Google Scholar] [CrossRef]
- Tsili, M.A.; Amoiralis, E.I.; Kladas, A.G.; Souflaris, A.T. Power Transformer Thermal Analysis by Using an Advanced Coupled 3D Heat Transfer and Fluid Flow FEM Model. Int. J. Therm. Sci. 2012, 53, 188–201. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Z.; Hao, Y.; Zhao, H.; Liu, X. Method for Measuring Thermal Flow Field Distribution in Oil-Immersed Transformer Using Dynamic Heat Transfer Coefficient. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Z.; Yang, Y.; Xiao, J.; Chen, J. A Dynamic Monitoring Method of Temperature Distribution for Cable Joints Based on Thermal Knowledge and Conditional Generative Adversarial Network. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Liu, G.; Rong, S.; Wu, W.; Wang, X.; Li, L. A Two-Dimensional Transient Fluid-Thermal Coupling Method for Temperature Rising Calculation of Transformer Winding Based on Finite Element Method. AIP Adv. 2020, 10, 035325. [Google Scholar] [CrossRef]
- Liu, G.; Jin, Y.J.; Ma, Y.Q.; Sun, L.; Chi, C. 2-D transient temperature field simulation of oil-immersed transformer based on hybrid method. High Volt. Appar. 2019, 55, 82–89. [Google Scholar] [CrossRef]
- Hayt, W.H.; Buck, J.A. Engineering Electromagnetics, 9th ed.; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Liu, F.; Li, D.; Wang, Y.; Li, Y.; Zhao, Z.; Yang, Q. Analysis of Magnetizing Process Using the Discharge Current of Capacitor by T-Ω Method. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Nagsarkar, T.K.; Sukhija, M.S. Power System Analysis; Oxford University Press: New Delhi, India, 2014. [Google Scholar]
- Ma, J. Power System Analysis and Control Theory; John Wiley & Sons, Ltd.: Singapore, 2018. [Google Scholar]
- Ceraolo, M.; Poli, D. Fundamentals of Electric Power Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kebriti, R.; Hossieni, S.M.H. 3D Modeling of Winding Hot Spot Temperature in Oil-Immersed Transformers. Electr. Eng. 2022, 104, 3325–3338. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Li, H.; Liu, Y.; Wang, J.; Zhang, W.; Sui, Y.; Fan, X. Analysis and test verification of dynamic thermal model of oil-immersed distribution transformer. Proc. CSEE 2023, 43, 389–399. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Xu, M.; Guo, Z.; Wang, B. Study on optimization model control method of light and temperature coordination of greenhouse crops with benefit priority. Comput. Electron. Agric. 2023, 210, 107892. [Google Scholar] [CrossRef]
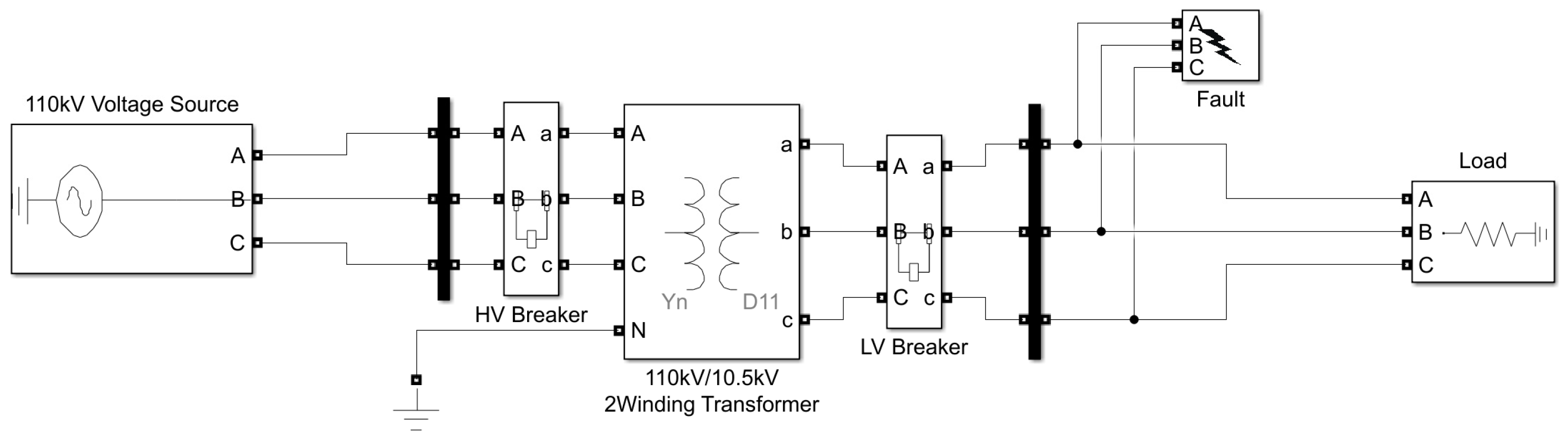



| Components | Parameters | Value |
|---|---|---|
| 110 Kv Voltage Source | Nominal voltage | 110 kV |
| Nominal frequency | 50 Hz | |
| Connection type | Yg | |
| SFZ-40000/110 Transformer | Nominal voltage | 110/10.5 |
| Nominal frequency | 50 Hz | |
| Connection type | YNd11 | |
| Nominal capacity | 40 MVA | |
| LV winding R | 0.010032 Ω | |
| LV winding L | 9.212 × 10−4 H | |
| HV winding R | 0.50364 Ω | |
| HV winding L | 0.1011 H | |
| Excitation R | 4,321,42.86 Ω | |
| Excitation L | 481.44 H | |
| Load | Nominal voltage | 10.5 kV |
| Nominal frequency | 50 Hz | |
| Connection type | Yg | |
| Nominal active power | 40 MVar | |
| Nominal reactive power | 0 | |
| Circuit-Breaker | Breaker resistance | 0 Ω |
| Snubber resistance | 1 × 106 Ω | |
| Fault | Fault resistance | 0.001Ω |
| Snubber resistance | 1 × 106 Ω |
| Num | Parameters | Configuration |
|---|---|---|
| 1 | Connection group | YNd11 |
| 2 | Nominal voltage | 110 kV/10.5 kV |
| 3 | Nominal frequency | 50 Hz |
| 4 | Nominal capacity | 40 MVA |
| 5 | No-load loss | 28 kW |
| 6 | No-load current percentage | 0.2 |
| 7 | Wire diameter (HV/LV) | 86.5 mm/90 mm |
| 8 | Winding height | 1220 mm |
| 9 | Tank (length × width × height) | 4750 mm × 1620 mm × 2730 mm |
| Num | Stress | Criteria |
|---|---|---|
| 1 | mean hoop compressive stress | σt1 ≤ 0.35 Rp0.2 |
| 2 | radial bending stress | σbr ≤ 0.7 Rp0.2 |
| 3 | free buckling critical stress | σt1 ≤ σcr |
| 4 | compressive stress on radial spacers | σact ≤ 80 MPa |
| 5 | axial bending stress | σAL ≤ 0.9 Rp0.2 |
| Num | Calculated Value (MPa) | Critical Value (MPa) |
|---|---|---|
| 1 | σt1 = 21.43 | ≤56 |
| 2 | σbr = 2.24 | ≤112 |
| 3 | σcr = 1800 | ≥21.43 |
| 4 | σact = 3.39 | ≤80 MPa |
| 5 | σba = 15.22 | ≤144 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, Z.; Gao, Z.; Wu, J. Analysis of the Mechanical Stability of Power Transformer Windings Considering the Influence of Temperature Field. Energies 2025, 18, 1374. https://doi.org/10.3390/en18061374
Chen J, Zhang Z, Gao Z, Wu J. Analysis of the Mechanical Stability of Power Transformer Windings Considering the Influence of Temperature Field. Energies. 2025; 18(6):1374. https://doi.org/10.3390/en18061374
Chicago/Turabian StyleChen, Junxin, Zhanlong Zhang, Zhihao Gao, and Jinbo Wu. 2025. "Analysis of the Mechanical Stability of Power Transformer Windings Considering the Influence of Temperature Field" Energies 18, no. 6: 1374. https://doi.org/10.3390/en18061374
APA StyleChen, J., Zhang, Z., Gao, Z., & Wu, J. (2025). Analysis of the Mechanical Stability of Power Transformer Windings Considering the Influence of Temperature Field. Energies, 18(6), 1374. https://doi.org/10.3390/en18061374















