Influence of Conductor Temperature on the Voltage–Current Characteristic of Corona Discharge in a Coaxial Arrangement—Experiments and Simulation
Abstract
1. Introduction
2. Corona Discharges and Temperature Effects
2.1. Corona Voltage–Current Characteristics
2.2. Influence of Conductor Temperature on Corona
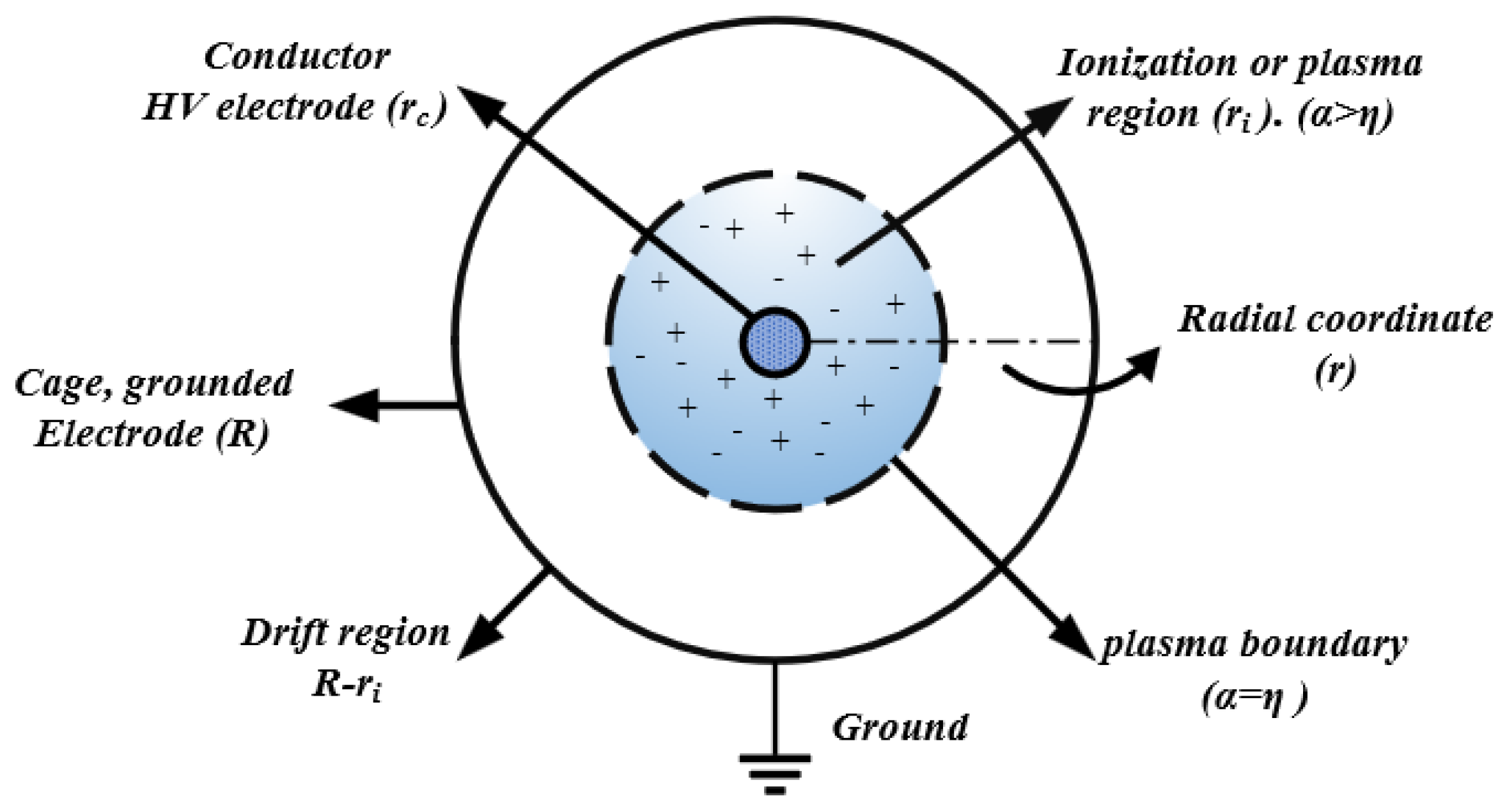
3. Simulation Model and Results
3.1. Governing Equation
3.1.1. Boundary Conditions and Initial Conditions
3.1.2. Plasma Air Chemistry
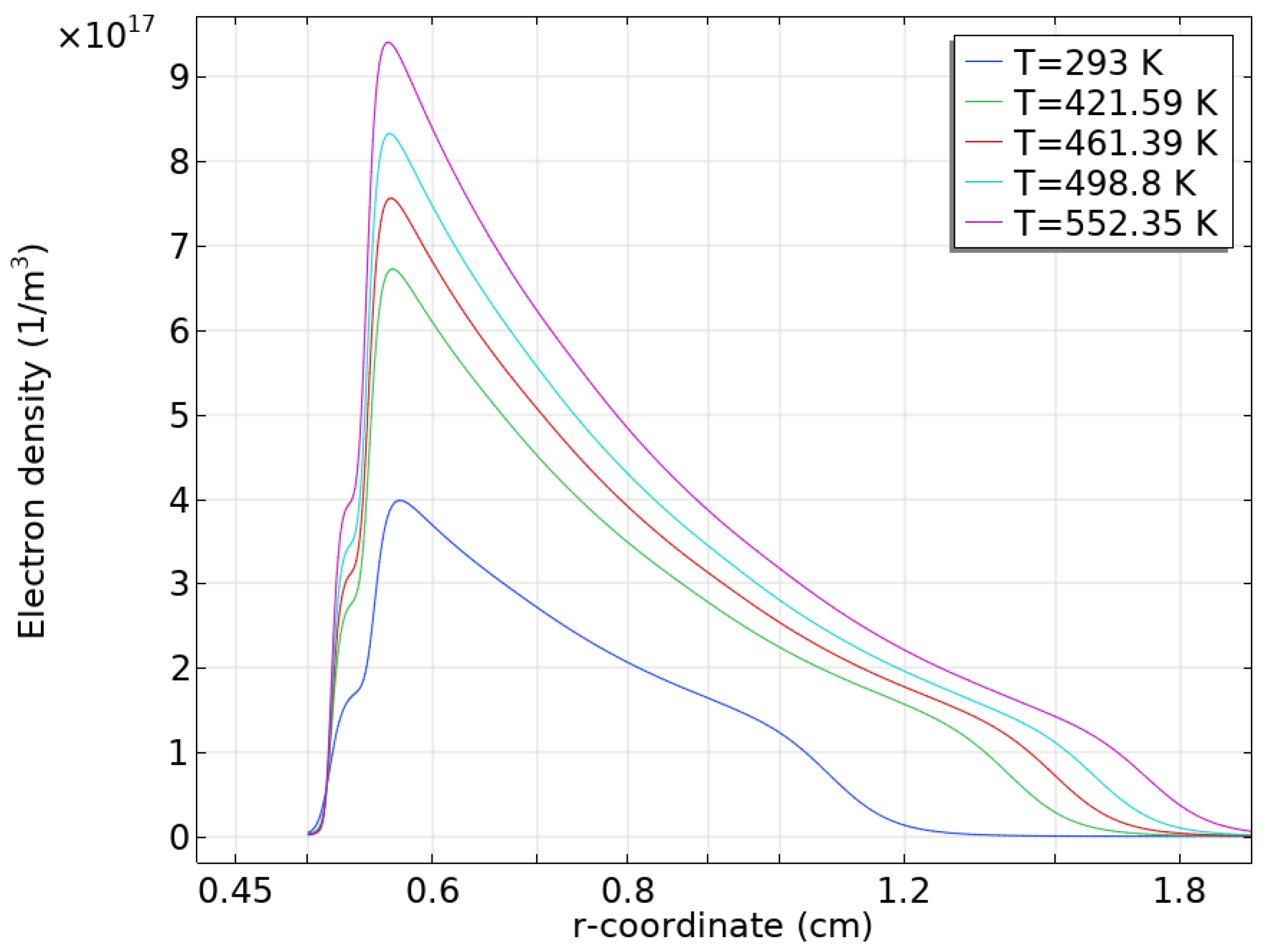
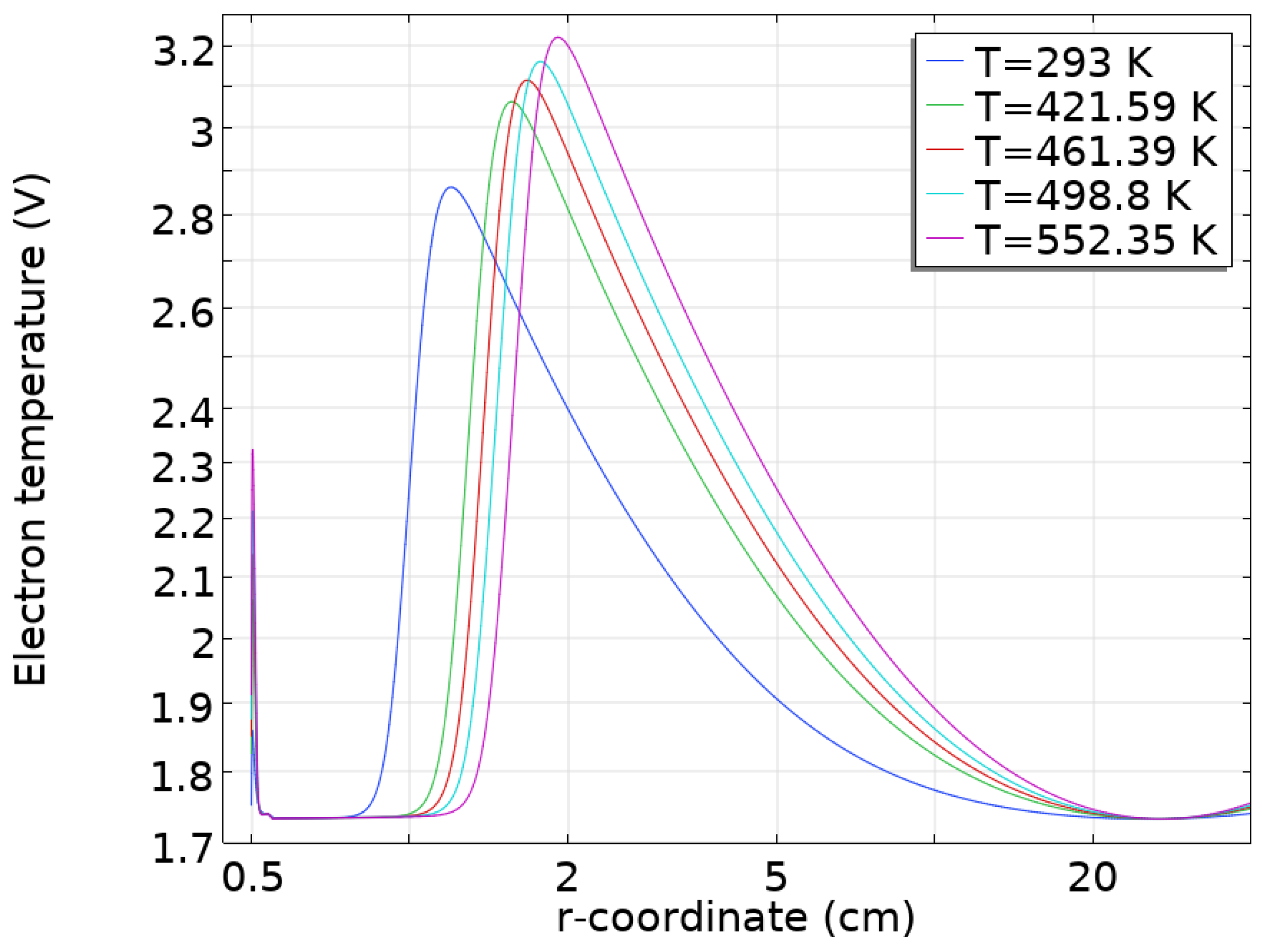
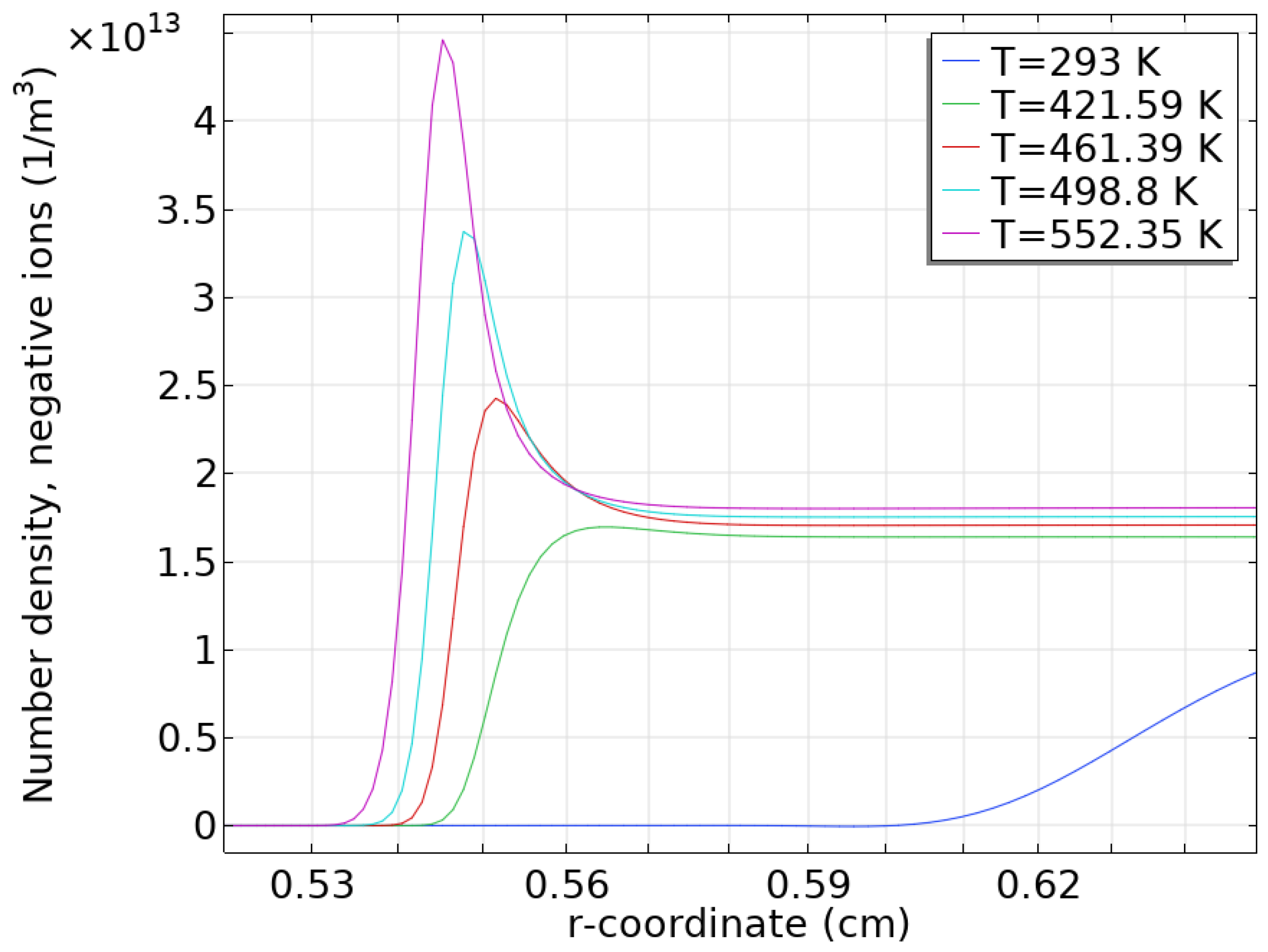
3.2. Simulation Results
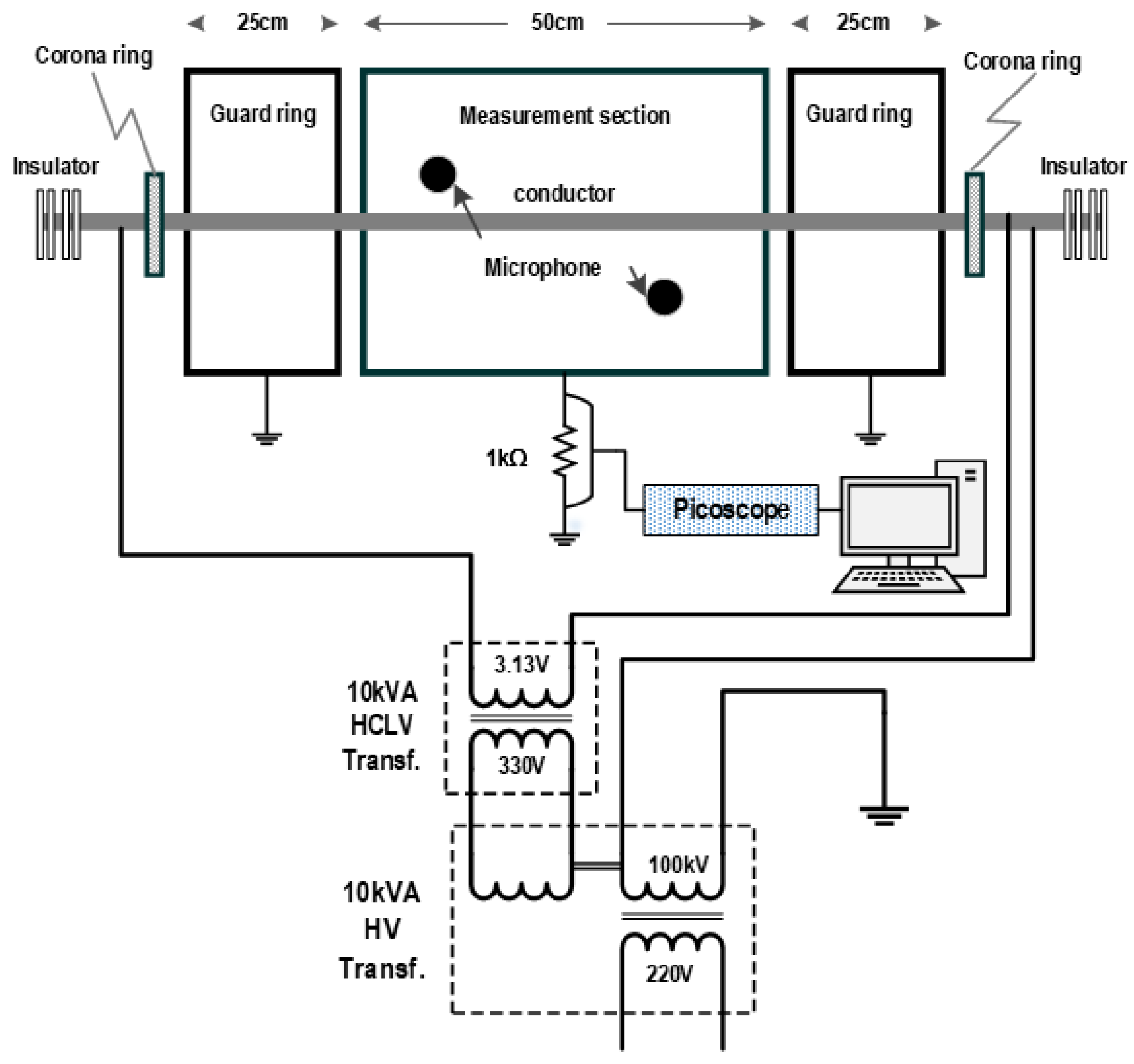
4. Experimental Measurement and Results
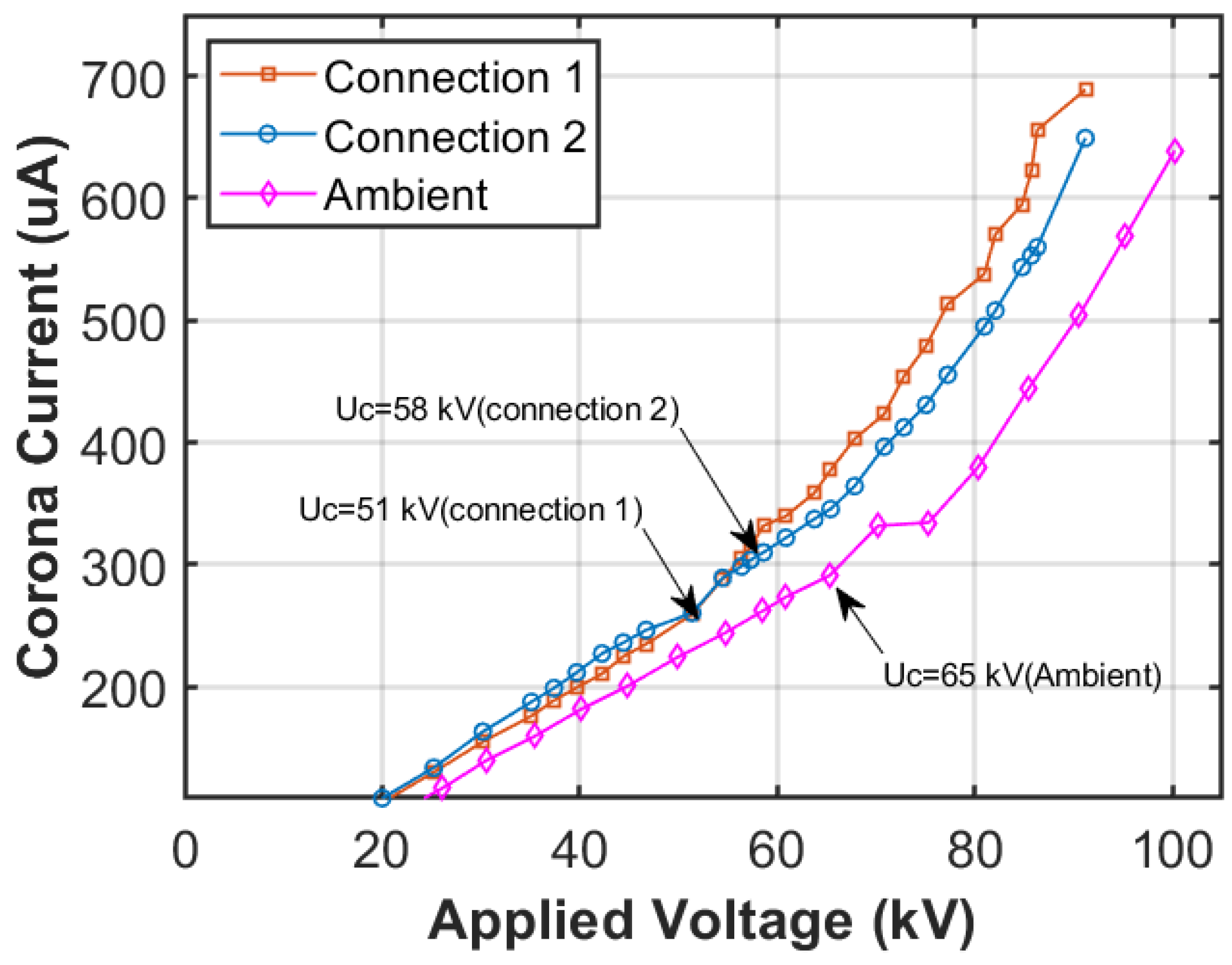
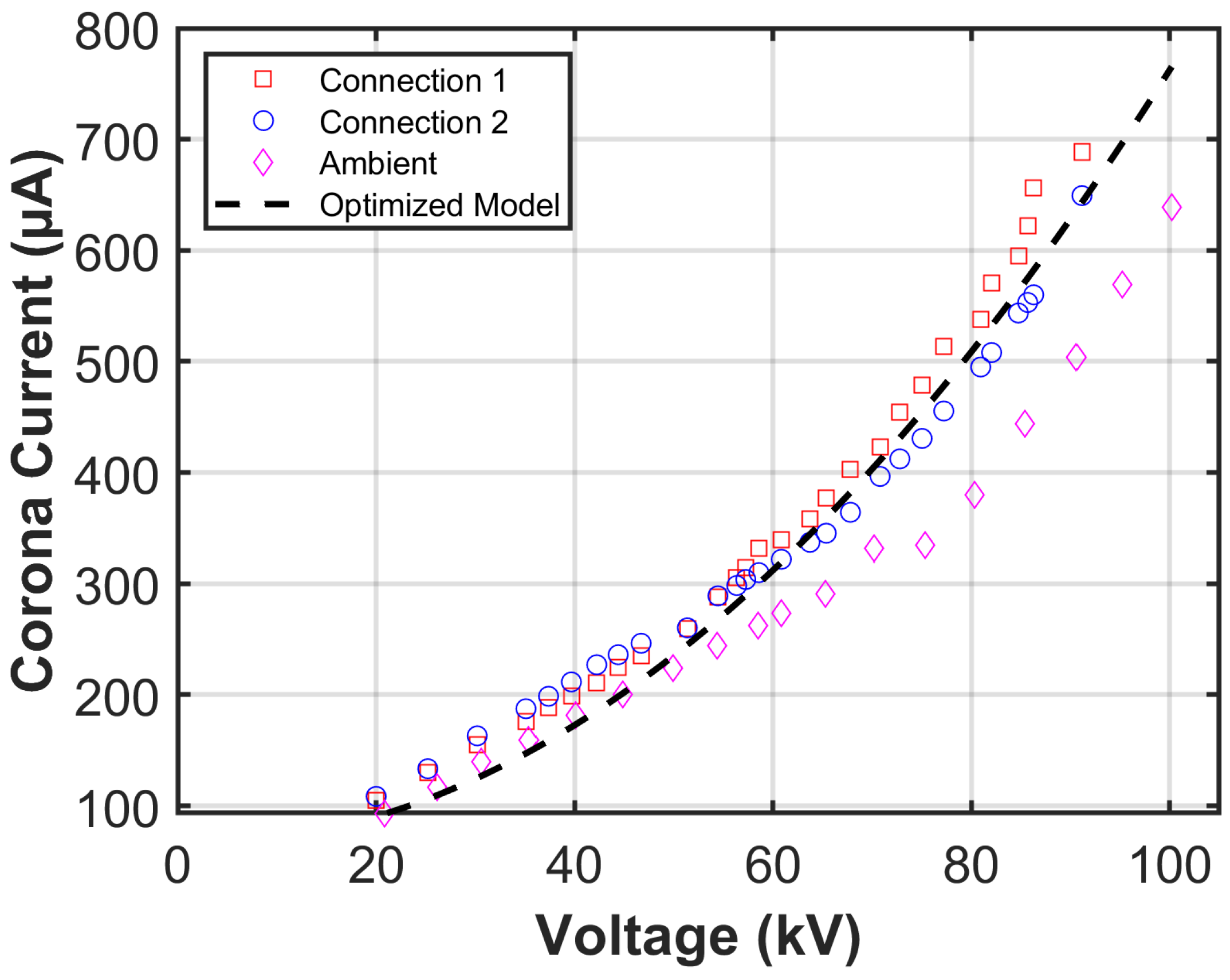
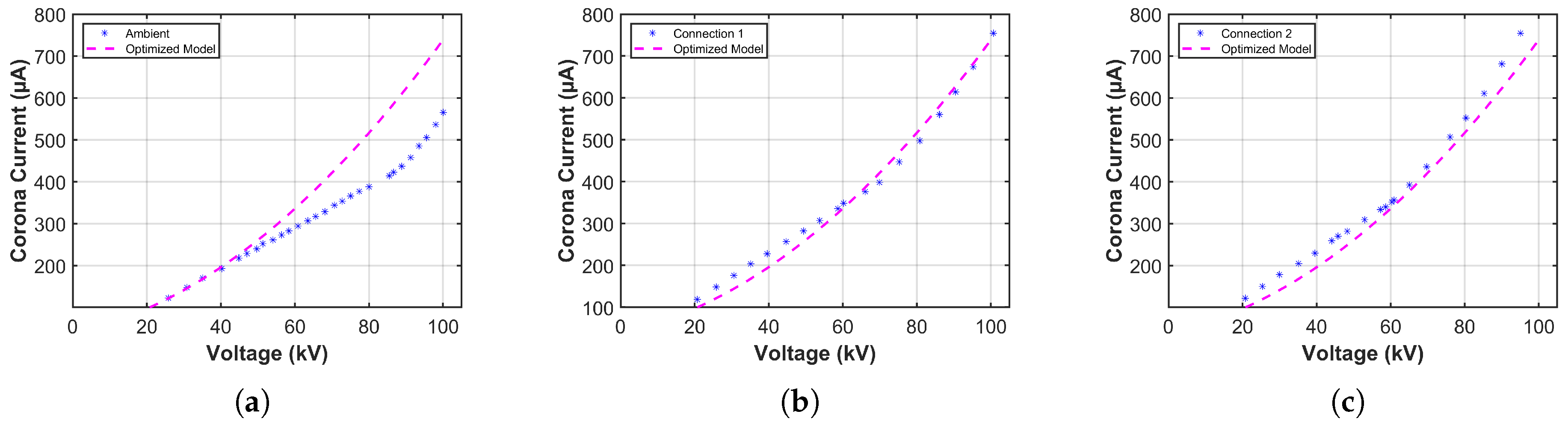
4.1. Experimental Results and Discussion
4.1.1. Results of Copper Tubes in the 75 cm Corona Cage
4.1.2. Results of Copper Tubes in the 25 cm Corona Cage
5. Conclusions
- To identify the most suitable materials for high-temperature operation with minimal corona-induced power losses.
- To introduce new considerations in bundle configuration optimization of HTLS conductors as they are designed to operate at elevated temperatures. Since corona discharge depends highly on conductor surface conditions and temperature, studying how different bundle arrangements influence corona activity at high temperatures is critical for efficient transmission line design.
- To develop temperature-dependent transmission line design guidelines for corona discharge effects and electromagnetic interference (EMI).
- To investigate and develop computational models on the impact of elevated temperatures on radio interference (RI) and Audible Noise (NA).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nawi, Z.M.; Ab Kadir, M.; Azis, N.; Ahmad, W.W.; Rawi, I.M.; Amirulddin, U.U.; Nordin, F. Comparative analysis of ACSR and ACCC conductors on corona effect for lightning surge studies. In Proceedings of the 2019 11th Asia-Pacific International Conference on Lightning (APL), Hong Kong, China, 12–14 June 2019; pp. 1–5. [Google Scholar]
- Baumann, R.; Novak, P. Efficient computation and experimental validation of ACSR overhead line conductors under tension and bending. CIGRE Sci. Eng. 2017, 9, 5–16. [Google Scholar]
- Kubelwa, Y.; Loubser, R.; Moodley, P. Experimental investigations of bending stresses of ACSR conductors due to aeolian vibrations. CIGRE Sci. Eng. 2017, 9, 17–26. [Google Scholar]
- Riba, J.R.; Bogarra, S.; Gómez-Pau, Á.; Moreno-Eguilaz, M. Uprating of transmission lines by means of HTLS conductors for a sustainable growth: Challenges, opportunities, and research needs. Renew. Sustain. Energy Rev. 2020, 134, 110334. [Google Scholar] [CrossRef]
- Mitra, G. Investigations on high temperature low sag (HTLS) conductors. IEEE Trans. Power Deliv. 2019, 35, 1716–1724. [Google Scholar]
- Stengel, D.; Bardl, R.; Kühnel, C.; Großmannn, S.; Kiewitt, W. Accelerated electrical and mechanical ageing tests of high temperature low sag (HTLS) conductors. In Proceedings of the 2017 12th International Conference on Live Maintenance (ICOLIM), Strasbourg, France, 26–28 April 2017; pp. 1–6. [Google Scholar]
- Vermeulen, G.R.H.; Reid, G. Effects of conductor temperature on corona inception. In Proceedings of the 2014 49th International Universities Power Engineering Conference, Cluj-Napoca, Romania, 2–5 September 2014. [Google Scholar]
- Bologa, A.; Paur, H.; Seifert, H.; Woletz, K. Influence of gas composition, temperature and pressure on corona discharge characteristics. Int. J. Plasma Environ. Sci. Technol. 2011, 5, 110–116. [Google Scholar]
- Xue, W.; Huang, S.; Mao, J.; Yan, X.; Song, C.; Liu, Y. Experimental and theoretical study on the influence of bundle number on corona loss characteristics of ultra high voltage corona cage positive/negative DC conductors at high altitude. Electr. Power Syst. Res. 2024, 232, 110370. [Google Scholar] [CrossRef]
- Javadi, H.; Farzaneh, M. Measuring of corona discharge inception voltage to determine electric field over the non-homogenous electrodes in the air insulation. In Proceedings of the 19th International Power System Conference, Tehran, Iran, 22 November 2004. [Google Scholar]
- Xu, P.; Zhang, B.; He, J.; Chen, S. Influence of humidity on the characteristics of negative corona discharge in air. Phys. Plasmas 2015, 22, 093514. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, B.; Chen, S.; He, J. Influence of humidity on the characteristics of positive corona discharge in air. Phys. Plasmas 2016, 23, 063511. [Google Scholar] [CrossRef]
- Feng, N.; Ma, T.; Chen, C.; Yao, B.; Gao, W. Simulation and study of DC corona discharge characteristics of bar-plate gap. Energies 2022, 15, 6431. [Google Scholar] [CrossRef]
- Liang, H.; Du, B.; Li, J.; Du, Q. Numerical simulation on the surface charge accumulation process of epoxy insulator under needle-plane corona discharge in air. IET Sci. Meas. Technol. 2018, 12, 9–16. [Google Scholar] [CrossRef]
- Liu, K.L.; Liao, R.J.; Zhao, X.T. Numerical simulation of the characteristics of electrons in bar-plate DC negative corona discharge based on a plasma chemical model. J. Electr. Eng. Technol. 2015, 10, 1804–1814. [Google Scholar] [CrossRef]
- Durbin, P.; Turyn, L. Analysis of the positive DC corona between coaxial cylinders. J. Phys. D Appl. Phys. 1987, 20, 1490. [Google Scholar] [CrossRef]
- Stearns, R.G. The positive corona in air: A simplified analytic approach. J. Appl. Phys. 1989, 66, 2899–2913. [Google Scholar] [CrossRef]
- Monrolin, N.; Praud, O.; Plouraboué, F. Revisiting the positive DC corona discharge theory: Beyond Peek’s and Townsend’s law. Phys. Plasmas 2018, 25, 063503. [Google Scholar] [CrossRef]
- Allen, N.; Abdel-Salam, M.; Cotton, I. Effects of temperature and pressure change on positive corona and sparkover under direct voltage in short airgaps. IET Sci. Meas. Technol. 2007, 1, 210–215. [Google Scholar] [CrossRef]
- Allen, N.; Kong, J. Positive corona inception in air at elevated temperatures. IEE Proc. Sci. Meas. Technol. 2006, 153, 31–38. [Google Scholar] [CrossRef]
- Ilunga, K.G.; Swanson, A.G.; Ijumba, N.; Stephen, R. Experimental Investigation of the Effect of Conductor Temperature on Corona Performance in Overhead Transmission Lines. IEEE Access 2024, 12, 122114–122125. [Google Scholar] [CrossRef]
- Kulumbaev, E.; Lelevkin, V.; Niyazaliev, I.; Tokarev, A. Characteristics of a corona discharge with a hot corona electrode. Plasma Phys. Rep. 2011, 37, 707–714. [Google Scholar] [CrossRef]
- Awad, M.; Castle, G. Ozone generation in an electrostatic precipitator with a heated corona wire. J. Air Pollut. Control. Assoc. 1975, 25, 369–374. [Google Scholar] [CrossRef]
- Holtzhausen, J.; Pieterse, P.; Vermeulen, H. Investigation of the effect of conductor temperature on AC power line corona. In Proceedings of the 2010 International Conference on High Voltage Engineering and Application, New Orleans, LA, USA, 11–14 October 2010; pp. 96–99. [Google Scholar]
- Pieterse, P. Corona measurement in an inverted coaxial geometry to evaluate the effect of conductor temperature. In Proceedings of the 23rd Southern African Universities Power Engineering Conference, Johannesburg, South Africa, 28–30 January 2015. [Google Scholar]
- Awad, M.; Castle, G. Breakdown streamers in coronas with heated discharge electrode. In Proceedings of the 1976 IEEE International Conference on Electrical Insulation, Montreal, QC, Canada, 14–16 June 1977; pp. 234–236. [Google Scholar]
- Chartier, V.; Stearns, R. Examination of Grizzly Mountain database to determine effects of relative air density and conductor temperature on HVDC corona phenomena. IEEE Trans. Power Deliv. 1990, 5, 1575–1582. [Google Scholar] [CrossRef]
- Bousiou, E.I.; Mikropoulos, P.N.; Zagkanas, V.N. Corona Activity on Single-circuit Overhead Transmission Lines under Variable Altitude. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–5. [Google Scholar]
- Chartier, V.; Stearns, R.; Burns, A. Electrical environment of the uprated pacific NW/SW HVDC intertie. IEEE Trans. Power Deliv. 1989, 4, 1305–1317. [Google Scholar] [CrossRef]
- Maskell, B. The Effect of Humidity on a Corona Discharge in Air; Technical Report; Royal Aircraft Establishment: Farnborough, UK, 1970. [Google Scholar]
- Hu, Q.; Shu, L.; Jiang, X.; Sun, C.; Zhang, S.; Shang, Y. Effects of air pressure and humidity on the corona onset voltage of bundle conductors. IET Gener. Transm. Distrib. 2011, 5, 621–629. [Google Scholar] [CrossRef]
- Chen, S.; Li, K.; Wang, F.; Sun, Q.; Zhong, L. Effect of humidity and air pressure on the discharge modes transition characteristics of negative DC corona. IET Sci. Meas. Technol. 2019, 13, 1212–1218. [Google Scholar] [CrossRef]
- Chen, Q.; Fang, M.; Cen, J.; Liu, J. Characteristics of negative DC discharge in a wire–cylinder configuration under coal pyrolysis gas components at high temperatures. RSC Adv. 2018, 8, 22737–22747. [Google Scholar] [CrossRef]
- Aleksandrov, N.; Bazelyan, E. Ionization processes in spark discharge plasmas. Plasma Sources Sci. Technol. 1999, 8, 285. [Google Scholar] [CrossRef]
- Ashraf, Y. Assessment of the Ionization Region in the Positive DC Coronas. Int. J. Plasma Environ. Sci. Technol. 2008, 2, 82–88. [Google Scholar]
- Yehia, A.; Mizuno, A.; Takashima, K. On the characteristics of the corona discharge in a wire-duct reactor. J. Phys. D Appl. Phys. 2000, 33, 2807. [Google Scholar] [CrossRef]
- Urban, R.G.; Reader, H.C.; Holtzhausen, J.P. Small corona cage for wideband HVac radio noise studies: Rationale and critical design. IEEE Trans. Power Deliv. 2008, 23, 1150–1157. [Google Scholar] [CrossRef]
- Kuffel, J.; Kuffel, P. High Voltage Engineering Fundamentals; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Liu, L.; Guo, J.; Li, J.; Sheng, L. The effect of wire heating and configuration on ozone emission in a negative ion generator. J. Electrost. 2000, 48, 81–91. [Google Scholar] [CrossRef]
- Wais, S.I.; Mohammed, P.A. Influence of Magnetic Field on Characteristics of Corona Discharge in Wire-Cylinder Electrodes Configuration. Plasma 2021, 4, 764–779. [Google Scholar] [CrossRef]
- Grosu, F.; Bologa, A.M.; Bologa, M.; Motorin, O. On temperature dependence of the parameters of corona discharge current-voltage characteristics. Surf. Eng. Appl. Electrochem. 2016, 52, 85–91. [Google Scholar] [CrossRef]
- Zhang, L.; Sheng, G.; Hou, H.; Zhou, N.; Song, H.; Jiang, X. Effect of temperature on current pulse characteristics of negative corona discharge based on numerical model. IEEE Trans. Plasma Sci. 2022, 51, 15–25. [Google Scholar] [CrossRef]
- Cobine, J.D. Gaseous Conductors: Theory and Engineering Applications; Dove Publication: Macclesfield, UK, 1958; pp. 205–289. [Google Scholar]
- Chen, X.; Lan, L.; Lu, H.; Wang, Y.; Wen, X.; Du, X.; He, W. Numerical simulation of Trichel pulses of negative DC corona discharge based on a plasma chemical model. J. Phys. D Appl. Phys. 2017, 50, 395202. [Google Scholar] [CrossRef]
- Wang, X.; Qu, L.; Yang, Y.; Liao, M.; Liao, Y.; Chen, H. The effect of Atmospheric Pressure and Temperature on corona discharge process at lightning rod tip. In Proceedings of the 2023 IEEE Sustainable Power and Energy Conference (iSPEC), Chongqing, China, 29–30 November 2023; pp. 1–8. [Google Scholar]

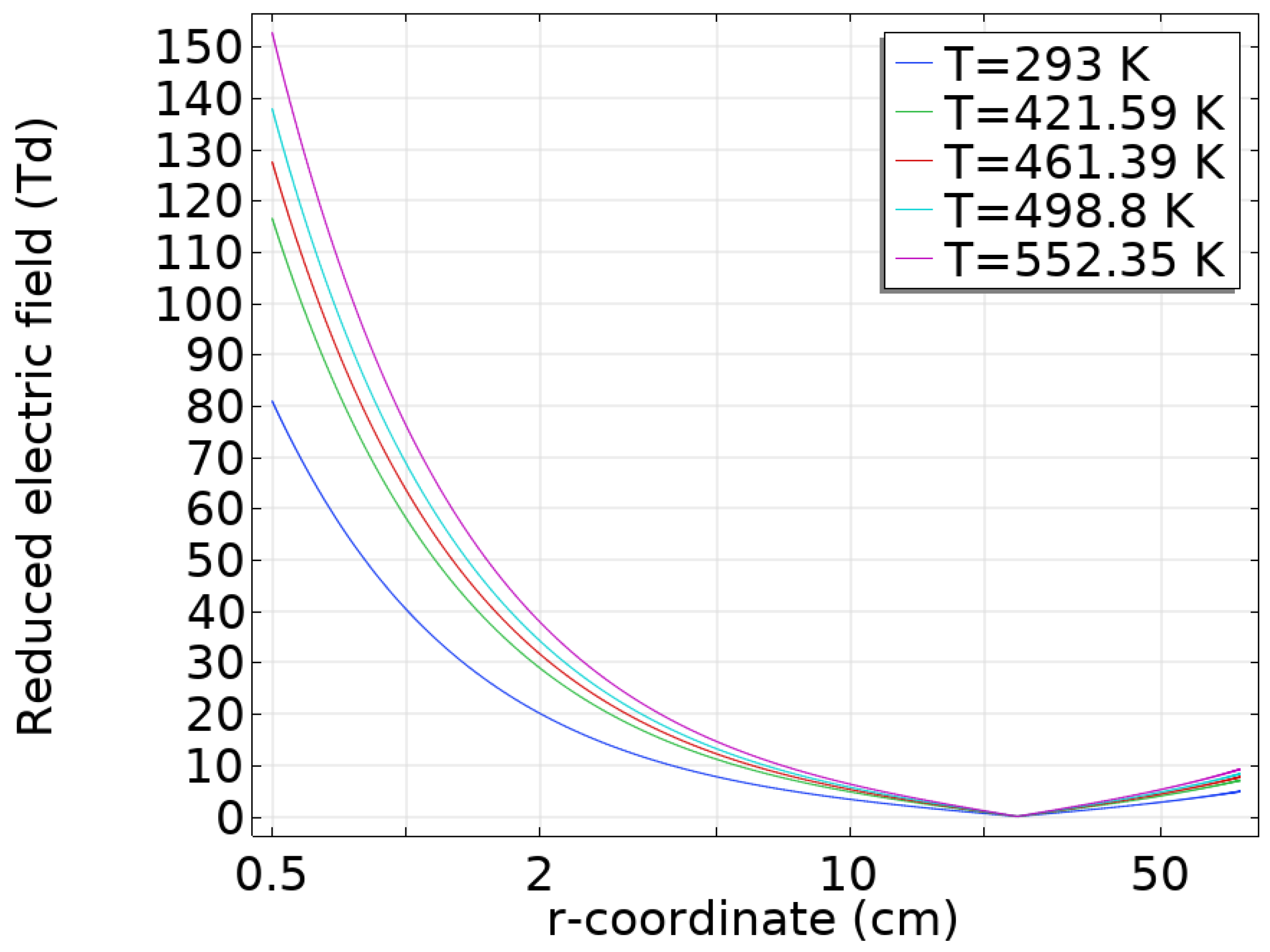
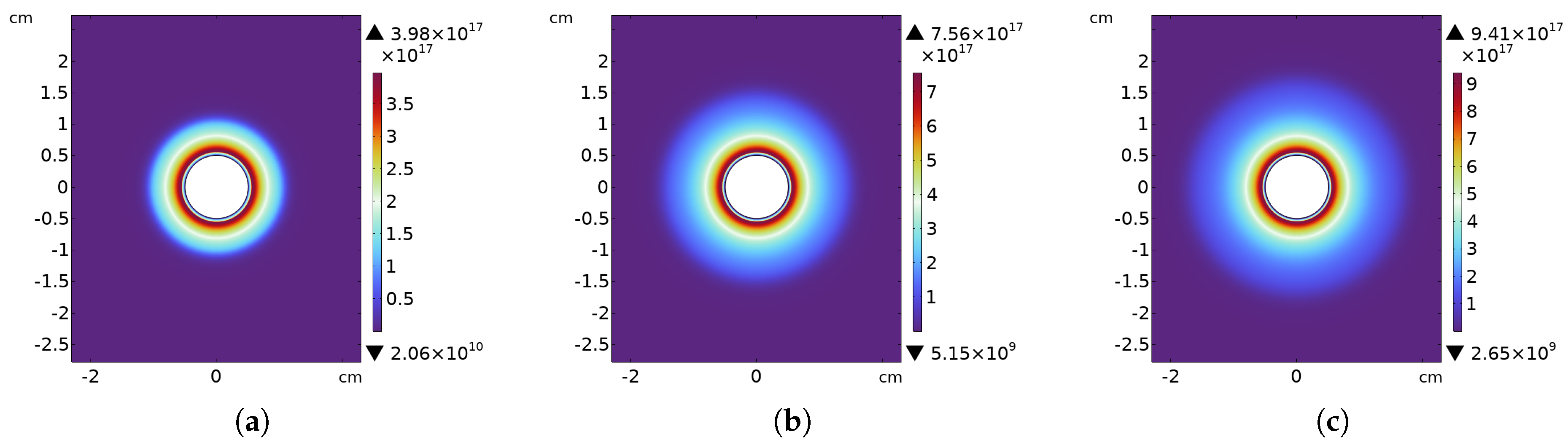
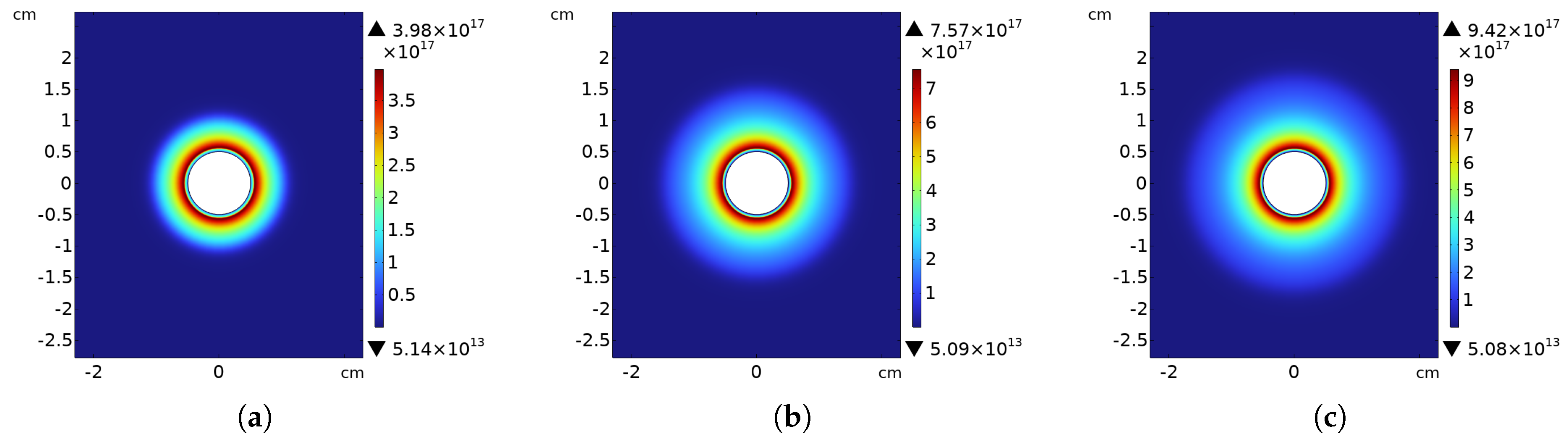

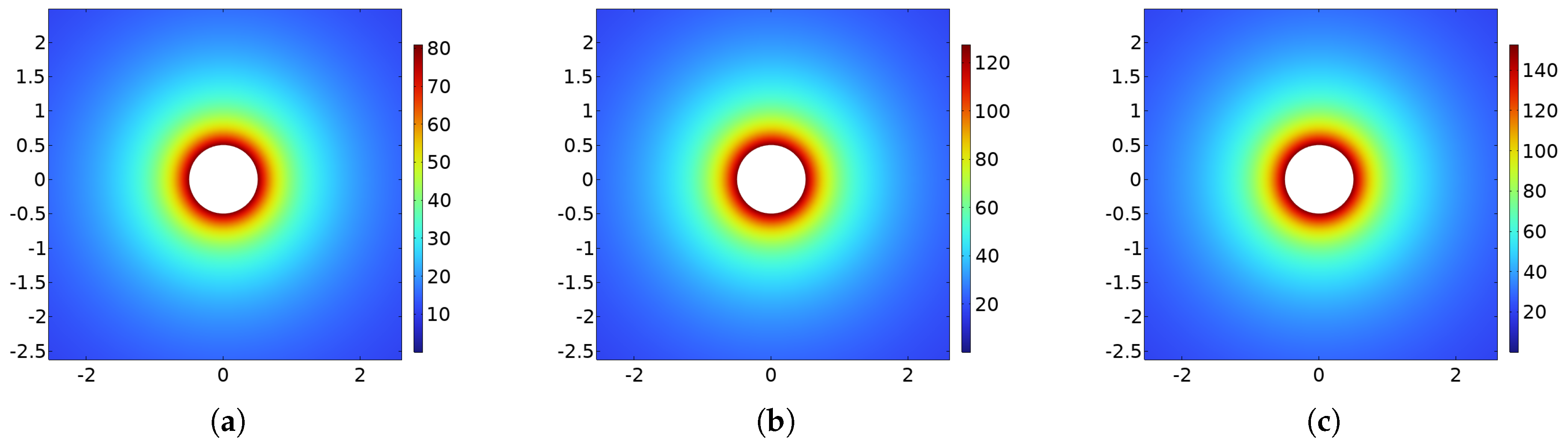


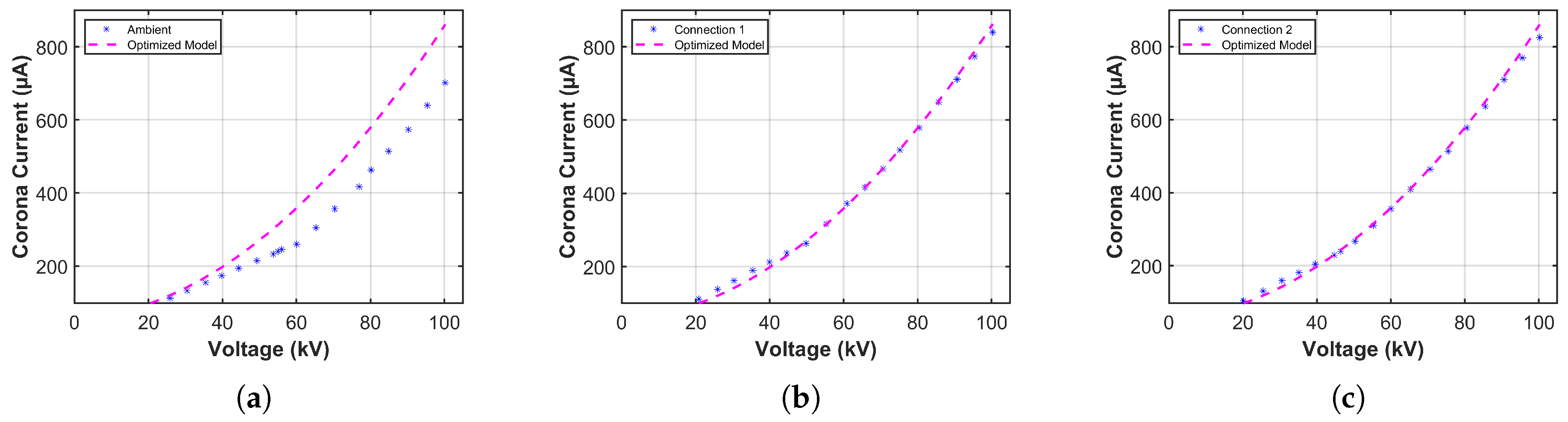
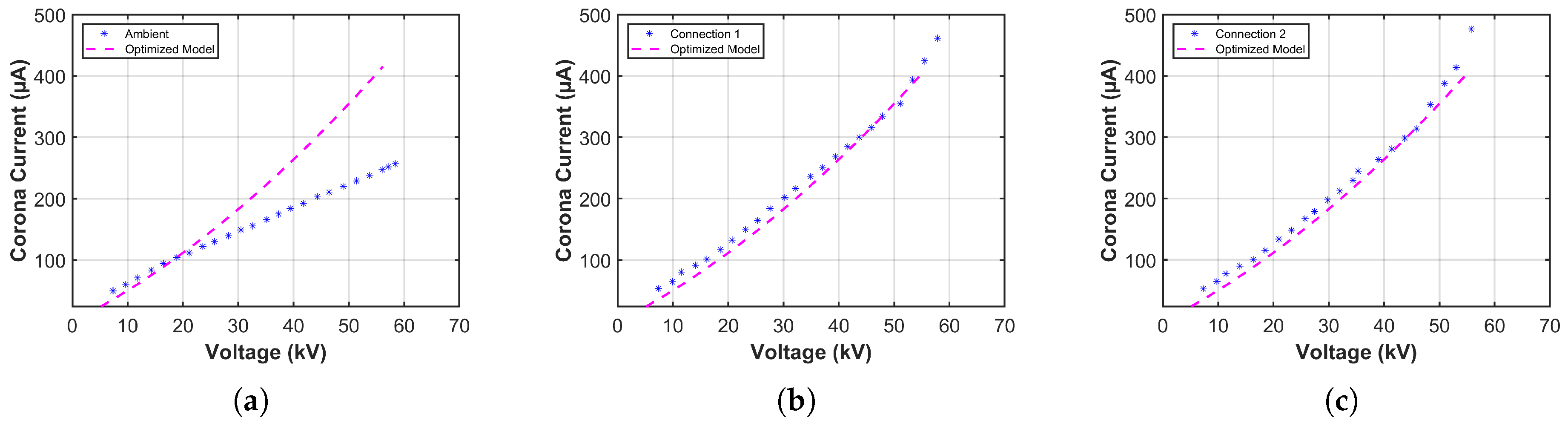
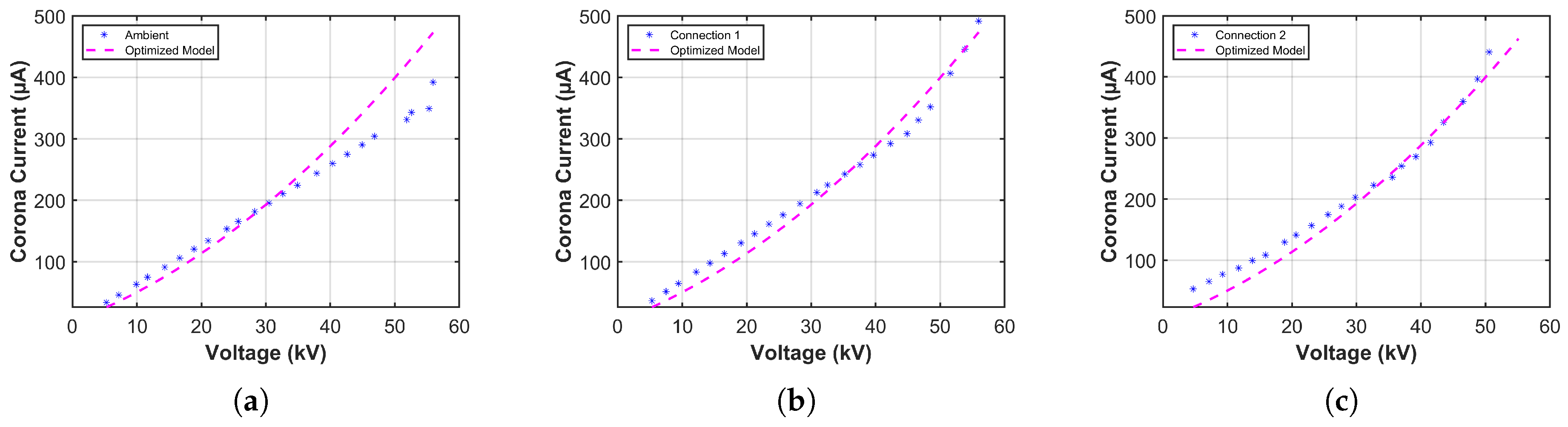
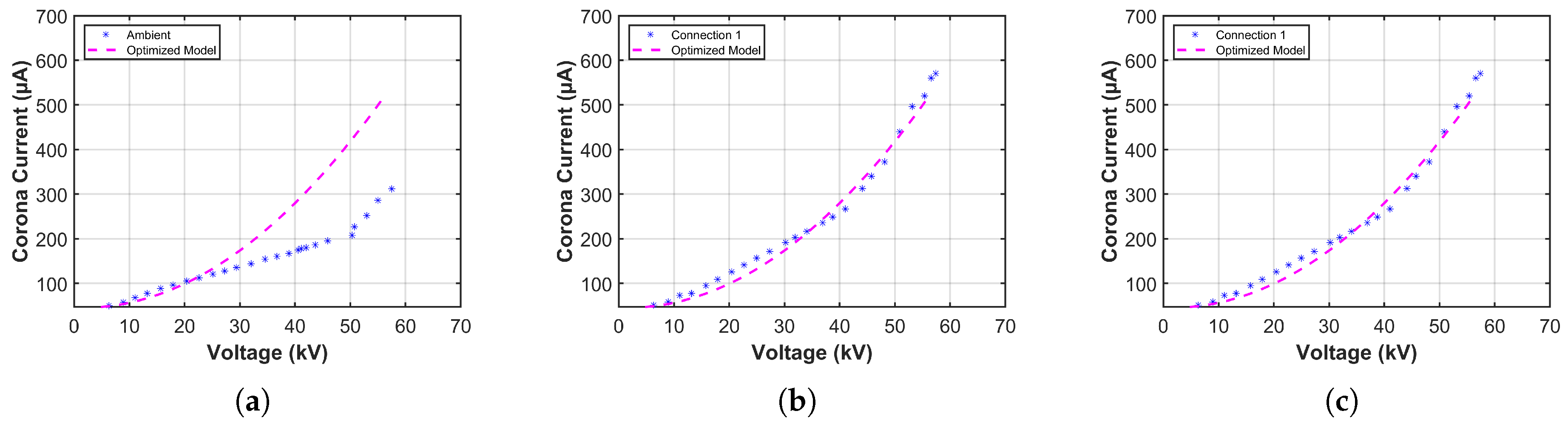
| Connection | Inception Voltage (kV) | Corona Current (mA) | Audible Noise (dbA) | Low Voltage (V) |
|---|---|---|---|---|
| Ambient | 65.25 | 290.7 | 39.6 | 140 |
| Connection 1 | 51.36 | 259.2 | 39.6 | 110 |
| Connection 2 | 56.35 | 298.6 | 39 | 120 |
| RMSE | ||||
|---|---|---|---|---|
| 0.071458 | −1.1716 | 118.5694 | 0.968 | 25.136 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilunga, K.G.; Swanson, A.G.; Ijumba, N.; Stephen, R. Influence of Conductor Temperature on the Voltage–Current Characteristic of Corona Discharge in a Coaxial Arrangement—Experiments and Simulation. Energies 2025, 18, 1303. https://doi.org/10.3390/en18051303
Ilunga KG, Swanson AG, Ijumba N, Stephen R. Influence of Conductor Temperature on the Voltage–Current Characteristic of Corona Discharge in a Coaxial Arrangement—Experiments and Simulation. Energies. 2025; 18(5):1303. https://doi.org/10.3390/en18051303
Chicago/Turabian StyleIlunga, Kayumba Grace, Andrew Graham Swanson, Nelson Ijumba, and Robert Stephen. 2025. "Influence of Conductor Temperature on the Voltage–Current Characteristic of Corona Discharge in a Coaxial Arrangement—Experiments and Simulation" Energies 18, no. 5: 1303. https://doi.org/10.3390/en18051303
APA StyleIlunga, K. G., Swanson, A. G., Ijumba, N., & Stephen, R. (2025). Influence of Conductor Temperature on the Voltage–Current Characteristic of Corona Discharge in a Coaxial Arrangement—Experiments and Simulation. Energies, 18(5), 1303. https://doi.org/10.3390/en18051303






