China’s Energy Stock Price Index Prediction Based on VECM–BiLSTM Model
Abstract
1. Introduction
2. Literature Review
3. Method and Data
3.1. VECM Model
3.2. Standardization with Z-Score
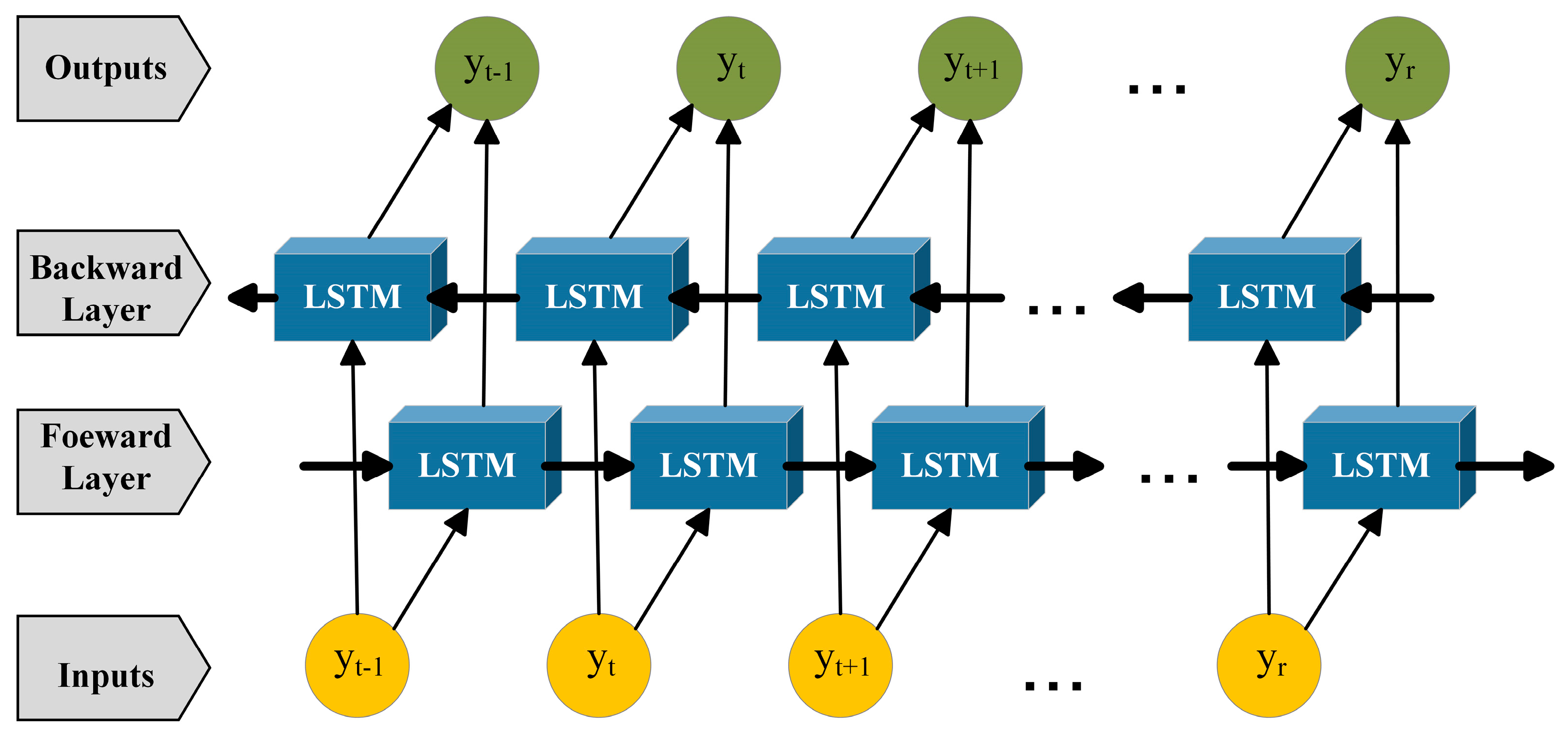
3.3. BiLSTM Model
3.4. Data and Descriptions
3.5. Parameter Tuning
4. Empirical Evidence
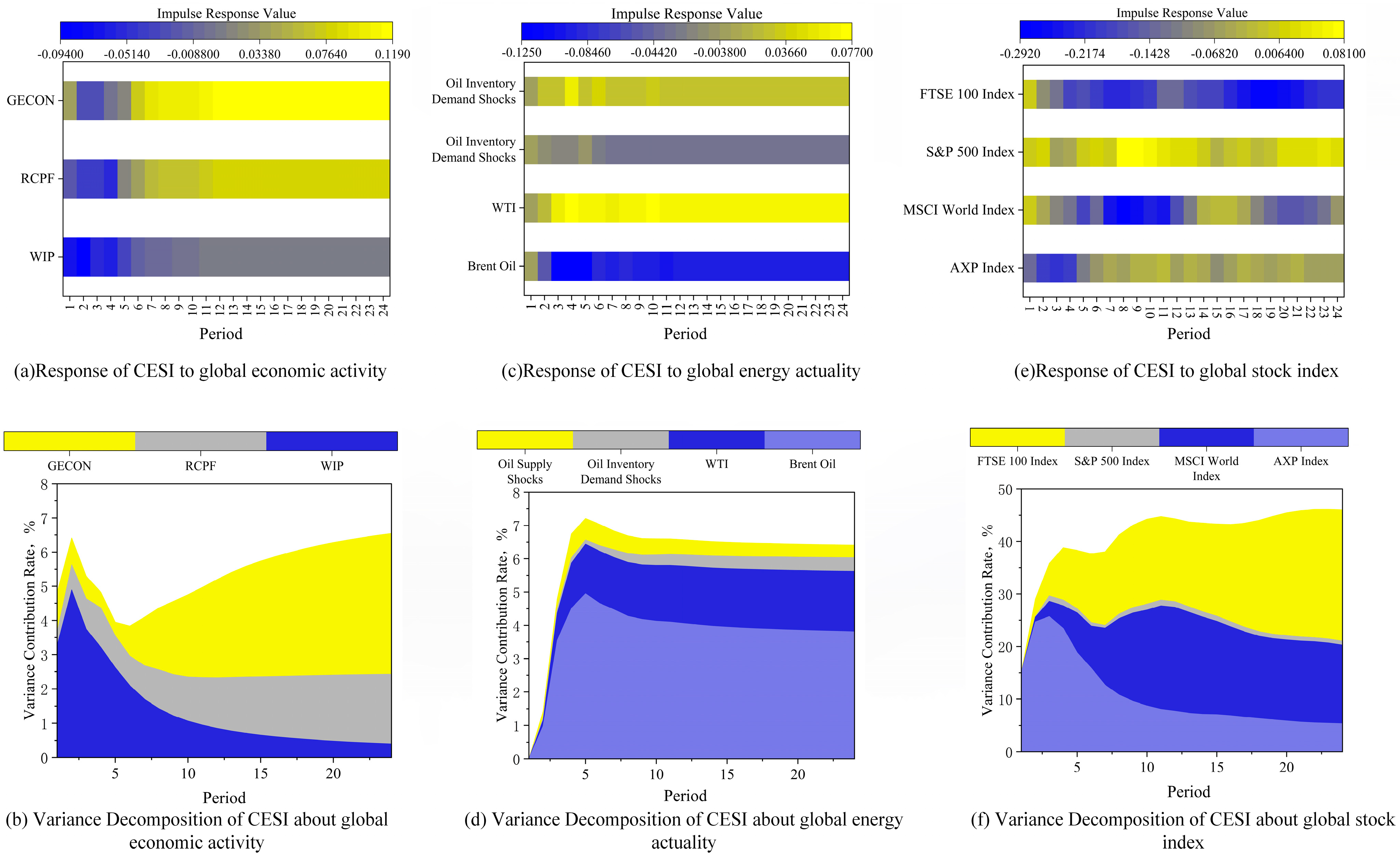
4.1. Spillover Analysis
4.1.1. Global Economic Activity
4.1.2. Global Energy Actuality
4.1.3. Global Stock Index
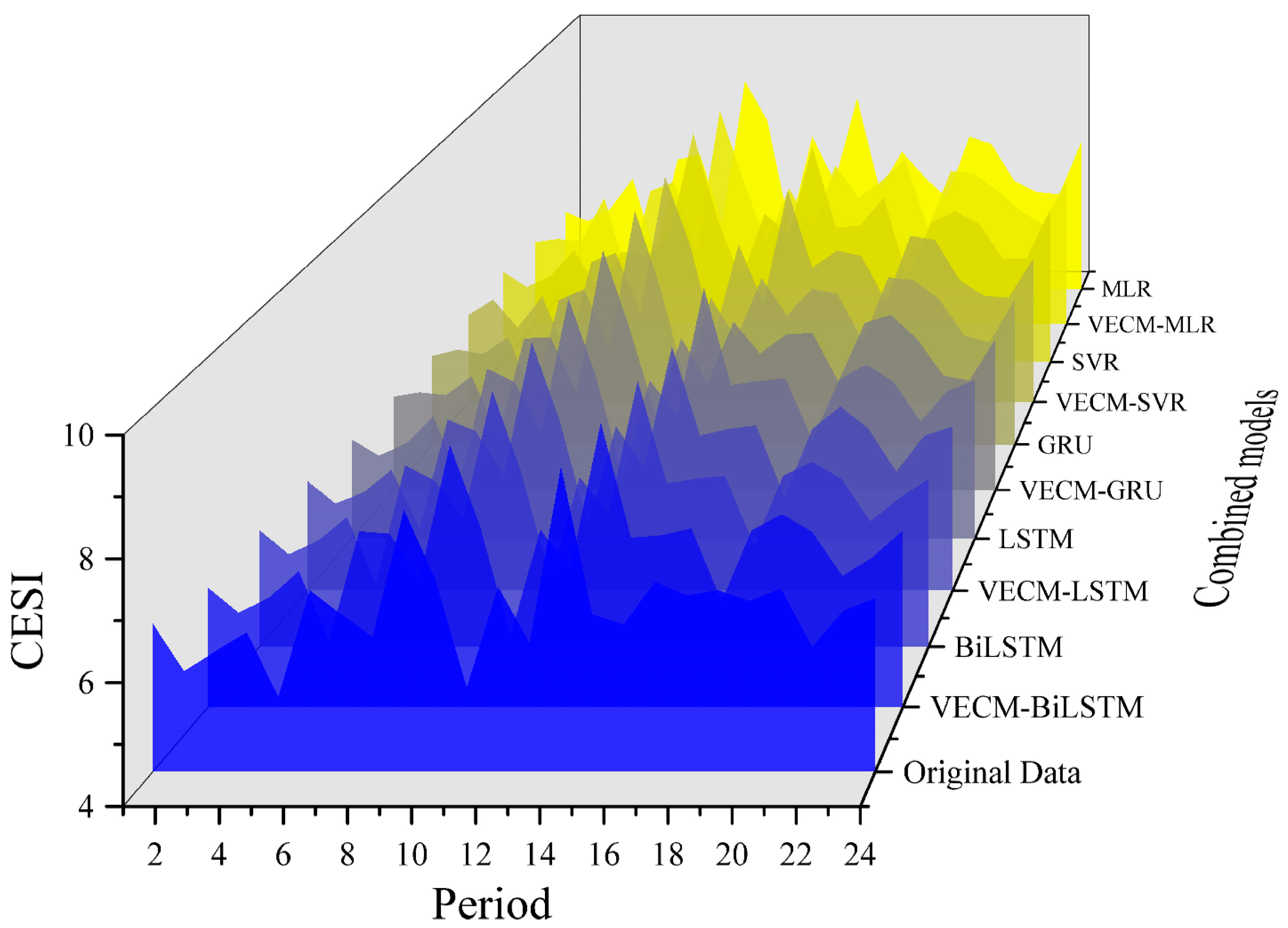
4.2. Chinese Energy Stock Price Index Predication
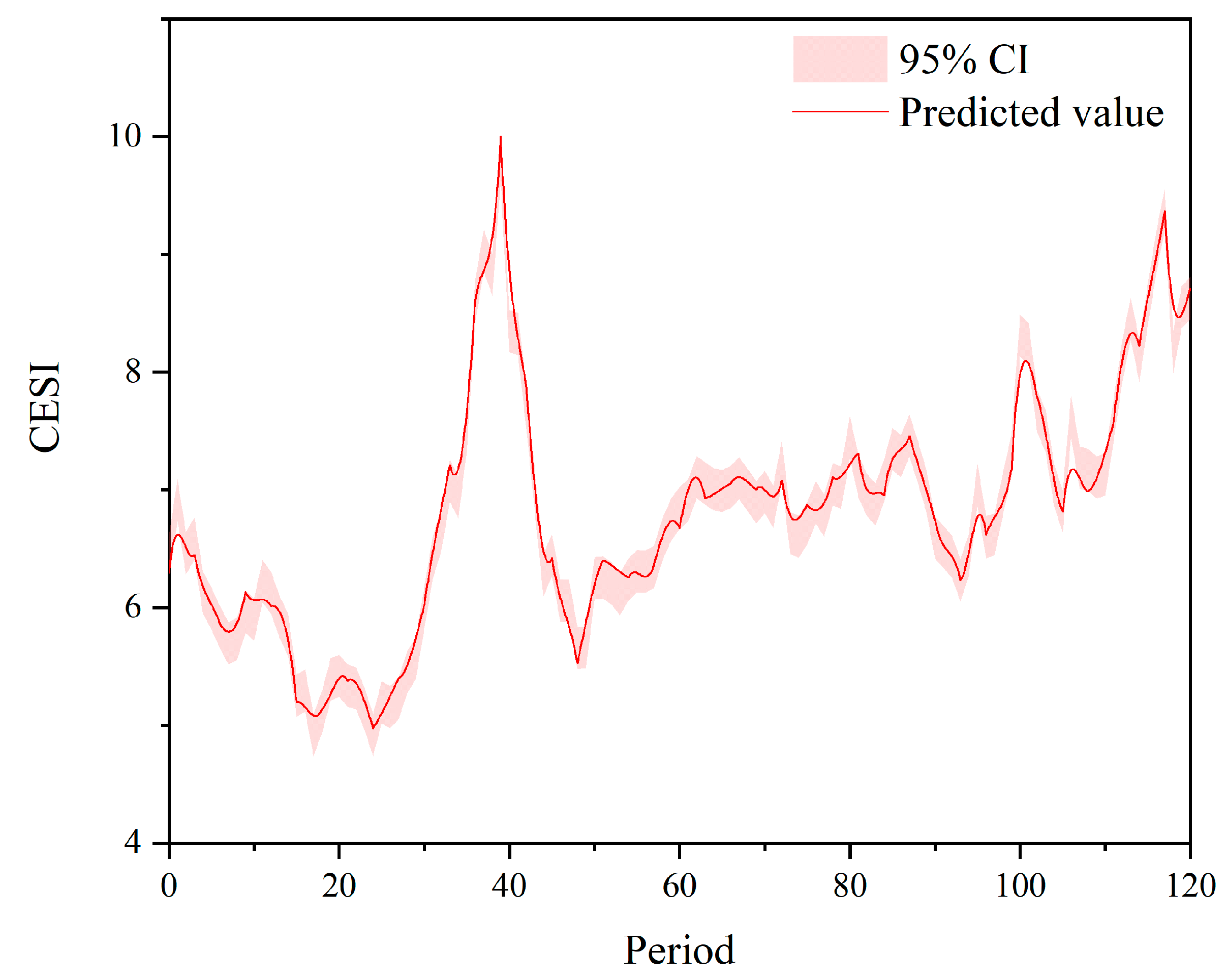
4.2.1. Stock Price Index Prediction Results
4.2.2. Market Stability Scenario Discussion
5. Discussion
5.1. Predictive Efficiency of the Model
5.2. Evaluation of Key Impact Indicators
5.3. Limitations
6. Conclusions and Policy Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Y.; Lu, Q.; Tan, B.; Yu, Y. Forecasting energy prices using a novel hybrid model with variational mode decomposition. Energy 2022, 246, 123366. [Google Scholar] [CrossRef]
- Atems, B.; Mette, J.; Lin, G.; Madraki, G. Estimating and forecasting the impact of nonrenewable energy prices on US renewable energy consumption. Energy Policy 2023, 173, 113374. [Google Scholar] [CrossRef]
- Maghyereh, A.; Boulanouar, Z.; Essid, L. The dynamics of green innovation and environmental policy stringency in energy transition investments. J. Clean Prod. 2025, 487, 144649. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y. China mainland new energy index price forecasting with the neural network. Energy Nexus. 2023, 10, 100210. [Google Scholar] [CrossRef]
- Xia, D.; Yang, N.; Jian, S.; Hu, Y.; Li, H. SW-BiLSTM: A Spark-based weighted BiLSTM model for traffic flow forecasting. Multimed. Tools Appl. 2022, 81, 23589–23614. [Google Scholar] [CrossRef]
- Ju, K.; Su, B.; Zhou, D.; Wu, J. Does energy-price regulation benefit China's economy and environment? Evidence from energy-price distortions. Energy Policy 2017, 105, 108–119. [Google Scholar] [CrossRef]
- Chen, Z.-M.; Chen, P.-L.; Ma, Z.; Xu, S.; Hayat, T.; Alsaedi, A. Inflationary and distributional effects of fossil energy price fluctuation on the Chinese economy. Energy 2019, 187, 115974. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Du, X. Impact of oil price uncertainty shocks on China’s macro-economy. Resour. Policy 2022, 79, 103080. [Google Scholar] [CrossRef]
- Nonejad, N. Forecasting crude oil price volatility out-of-sample using news-based geopolitical risk index: What forms of nonlinearity help improve forecast accuracy the most? Financ. Res. Lett. 2022, 46, 102310. [Google Scholar] [CrossRef]
- Ashfaq, S.; Tang, Y.; Maqbool, R. Volatility spillover impact of world oil prices on leading Asian energy exporting and importing economies’ stock returns. Energy 2019, 188, 116002. [Google Scholar] [CrossRef]
- Jia, Z.; Wen, S.; Lin, B. The effects and reacts of COVID-19 pandemic and international oil price on energy, economy, and environment in China. Appl. Energy 2021, 302, 117612. [Google Scholar] [CrossRef]
- Sadorsky, P. Forecasting solar stock prices using tree-based machine learning classification: How important are silver prices? N. Am. J. Econ. Financ. 2022, 61, 101705. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L.; Peng, L.; Luo, K. Measuring the response of clean energy stock price volatility to extreme shocks. Renew. Energy 2023, 206, 1289–1300. [Google Scholar] [CrossRef]
- Li, J.; Umar, M.; Huo, J. The spillover effect between Chinese crude oil futures market and Chinese green energy stock market. Energy Econ. 2023, 119, 106568. [Google Scholar] [CrossRef]
- Meng, A.; Wang, P.; Zhai, G.; Zeng, C.; Chen, S.; Yang, X.; Yin, H. Electricity price forecasting with high penetration of renewable energy using attention-based LSTM network trained by crisscross optimization. Energy 2022, 254, 124212. [Google Scholar] [CrossRef]
- Wang, K.; Yu, M.; Niu, D.; Liang, Y.; Peng, S.; Xu, X. Short-term electricity price forecasting based on similarity day screening, two-layer decomposition technique and Bi-LSTM neural network. Appl. Soft Comput. 2023, 136, 110018. [Google Scholar] [CrossRef]
- Iwabuchi, K.; Kato, K.; Watari, D.; Taniguchi, I.; Catthoor, F.; Shirazi, E.; Onoye, T. Flexible electricity price forecasting by switching mother wavelets based on wavelet transform and Long Short-Term Memory. Energy AI 2022, 10, 100192. [Google Scholar] [CrossRef]
- Xiong, X.; Qing, G. A hybrid day-ahead electricity price forecasting framework based on time series. Energy 2023, 264, 126099. [Google Scholar] [CrossRef]
- de Oliveira, E.M.; Cyrino Oliveira, F.L. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Fan, D.; Sun, H.; Yao, J.; Zhang, K.; Yan, X.; Sun, Z. Well production forecasting based on ARIMA-LSTM model considering manual operations. Energy 2021, 220, 119708. [Google Scholar] [CrossRef]
- Wang, X. Research on the prediction of per capita coal consumption based on the ARIMA–BP combined model. Energy Rep. 2022, 8, 285–294. [Google Scholar] [CrossRef]
- Chiu, F.-P.; Hsu, C.-S.; Ho, A.; Chen, C.-C. Modeling the price relationships between crude oil, energy crops and biofuels. Energy 2016, 109, 845–857. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, X.; Wang, S. Assessing Potentiality of Support Vector Machine Method in Crude Oil Price Forecasting. EURASIA J. Math. Sci. Technol. Educ. 2017, 13, 7893–7904. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hu, Y.; Yan, L.-Z.; Chang, C.-P. Volatility spillover and hedging strategies between the European carbon emissions and energy markets. Energy Strategy Rev. 2023, 46, 101058. [Google Scholar] [CrossRef]
- Singh, S.; Bansal, P.; Hosen, M.; Bansal, S.K. Forecasting annual natural gas consumption in USA: Application of machine learning techniques-ANN and SVM. Resour. Policy 2023, 80, 103159. [Google Scholar] [CrossRef]
- Bristone, M.; Prasad, R.; Abubakar, A.A. CPPCNDL: Crude oil price prediction using complex network and deep learning algorithms. Petroleum 2020, 6, 353–361. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, W.; Xiao, L.; Dong, Y. A decomposition ensemble based deep learning approach for crude oil price forecasting. Resour. Policy 2022, 78, 102855. [Google Scholar] [CrossRef]
- Zargarnezhad, S.; Dashti, R.; Ahmadi, R. Predicting vehicle fuel consumption in energy distribution companies using ANNs. Transp. Res. Part D Transp. Environ. 2019, 74, 174–188. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Z.; Sun, J.; Sun, S. Multi-perspective crude oil price forecasting with a new decomposition-ensemble framework. Resour. Policy 2022, 77, 102737. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Nie, R.; Chi, P.; He, X.; Zhang, L. A novel fractional grey forecasting model with variable weighted buffer operator and its application in forecasting China's crude oil consumption. Petroleum 2022, 8, 139–157. [Google Scholar] [CrossRef]
- Wu, C.; Wang, J.; Hao, Y. Deterministic and uncertainty crude oil price forecasting based on outlier detection and modified multi-objective optimization algorithm. Resour. Policy 2022, 77, 102780. [Google Scholar] [CrossRef]
- Busari, G.A.; Lim, D.H. Crude oil price prediction: A comparison between AdaBoost-LSTM and AdaBoost-GRU for improving forecasting performance. Comput. Chem. Eng. 2021, 155, 107513. [Google Scholar] [CrossRef]
- Wang, L.; Wu, J.; Cao, Y.; Hong, Y. Forecasting renewable energy stock volatility using short and long-term Markov switching GARCH-MIDAS models: Either, neither or both? Energy Econ. 2022, 111, 106056. [Google Scholar] [CrossRef]
- Ying, C.; Wang, W.; Yu, J.; Li, Q.; Yu, D.; Liu, J. Deep learning for renewable energy forecasting: A taxonomy, and systematic literature review. J. Clean. Prod. 2023, 384, 135414. [Google Scholar] [CrossRef]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Zhong, B. Deep learning integration optimization of electric energy load forecasting and market price based on the ANN–LSTM–transformer method. Front. Energy Res. 2023, 11, 1292204. [Google Scholar] [CrossRef]
- Zhang, X.; Zong, Y.; Du, P.; Wang, S.; Wang, J. Framework for multivariate carbon price forecasting: A novel hybrid model. J. Environ. Manag. 2024, 369, 122275. [Google Scholar] [CrossRef]
- Ghallabi, F.; Souissi, B.; Du, A.M.; Ali, S. ESG stock markets and clean energy prices prediction: Insights from advanced machine learning. Int. Rev. Financ. Anal. 2025, 97, 103889. [Google Scholar] [CrossRef]
- Wang, J.; Hou, R.; Wang, C.; Shen, L. Improved v-Support vector regression model based on variable selection and brain storm optimization for stock price forecasting. Appl. Soft Comput. 2016, 49, 164–178. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, Y.; Chen, J. Risk spread in multiple energy markets: Extreme volatility spillover network analysis before and during the COVID-19 pandemic. Energy 2022, 256, 124580. [Google Scholar] [CrossRef]
- Gong, X.; Shi, R.; Xu, J.; Lin, B. Analyzing spillover effects between carbon and fossil energy markets from a time-varying perspective. Appl. Energy 2021, 285, 116384. [Google Scholar] [CrossRef]
- Inoue, A.; Kilian, L. Joint Bayesian inference about impulse responses in VAR models. J. Econom. 2022, 231, 457–476. [Google Scholar] [CrossRef]
- Urolagin, S.; Sharma, N.; Datta, T.K. A combined architecture of multivariate LSTM with Mahalanobis and Z-Score transformations for oil price forecasting. Energy 2021, 231, 120963. [Google Scholar] [CrossRef]
- Min, Y.; Shuzhen, Z.; Wuwei, L. Carbon price prediction based on multi-factor MEEMD-LSTM model. Heliyon 2022, 8, e12562. [Google Scholar] [CrossRef] [PubMed]
- Yildirim, O. A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Comput. Biol. Med. 2018, 96, 189–202. [Google Scholar] [CrossRef]
- Zeng, Y.-R.; Zeng, Y.; Choi, B.; Wang, L. Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network. Energy 2017, 127, 381–396. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, F.; Li, H.; Lai, X. Oil price volatility predictability based on global economic conditions. Int. Rev. Financ. Anal. 2022, 82, 102195. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Wang, J.-L. Do high-frequency stock market data help forecast crude oil prices? Evidence from the MIDAS models. Energy Econ. 2019, 78, 192–201. [Google Scholar] [CrossRef]
- Li, J.; Liu, R.; Yao, Y.; Xie, Q. Time-frequency volatility spillovers across the international crude oil market and Chinese major energy futures markets: Evidence from COVID-19. Resour. Policy 2022, 77, 102646. [Google Scholar] [CrossRef]
- Sadeghi, A.; Roudari, S. Heterogeneous effects of oil structure and oil shocks on stock prices in different regimes: Evidence from oil-exporting and oil-importing countries. Resour. Policy 2022, 76, 102596. [Google Scholar] [CrossRef]
- Pan, X.-Z.; Ma, X.-R.; Wang, L.-N.; Lu, Y.-C.; Dai, J.-Q.; Li, X. Spillover of international crude oil prices on China’s refined oil wholesale prices and price forecasting: Daily-frequency data of private enterprises and local refineries. Pet. Sci. 2022, 19, 1433–1442. [Google Scholar] [CrossRef]


| MAPE (%) | Prediction Classes |
|---|---|
| 10% | High accuracy |
| 10% < MAPE < 20% | Good |
| 20% < MAPE < 50% | Reasonable |
| >50% | Inaccurate |
| Indicator Category | Indicator | Minimum | Maximum | Mean | Standard Error | Skewness | Kurtosis | ADF |
|---|---|---|---|---|---|---|---|---|
| Global Economic Activity | WIP | 83.4000 | 107.30 | 100.9125 | 3.8220 | −1.134 | 3.406 | 0.0932 * |
| RCPF | −0.8072 | 0.9271 | 0.0043 | 0.3590 | 0.0920 | −0.3930 | 0.0000 * | |
| GECON | −4.2357 | 1.3616 | 0.0108 | 0.5767 | −4.6280 | 31.7030 | 0.0000 * | |
| Global Energy Actuality | Oil Supply Shocks | −10.6261 | 3.1544 | −0.1099 | 1.5027 | −2.8290 | 19.4220 | 0.0000 * |
| Oil Inventory Demand Shocks | −2.0091 | 2.6931 | 0.3462 | 1.1089 | 0.0550 | −0.5370 | 0.0000 * | |
| WTI | 8.6200 | 107.7700 | 64.9357 | 23.4412 | 0.1400 | −0.6750 | 0.2236 * | |
| Brent Oil | 22.7400 | 122.8800 | 72.2966 | 25.6152 | 0.4290 | −0.9960 | 0.5893 * | |
| Global Stock Index | S&P 500 Index | 1310.3300 | 4766.1800 | 2477.8241 | 829.1314 | 0.8850 | 0.3190 | 0.1373 * |
| MSCI World Index | 26.9400 | 664.8800 | 163.0448 | 161.1320 | 1.5390 | 1.5900 | 0.9822 * | |
| FTSE 100 Index | 5320.8600 | 7748.7600 | 6715.2183 | 582.4066 | −0.3030 | −0.7950 | 0.3371 * | |
| AXP Index | 50.1400 | 173.7800 | 92.2218 | 28.7330 | 1.0280 | 0.8070 | 0.0721 * | |
| China‘s Energy Actuality | Diesel Output | 1179.3000 | 1686.2000 | 1436.1342 | 94.4273 | −0.3240 | 0.4080 | 0.0010 * |
| Crude Output | 1517.6000 | 1832.3000 | 1670.2633 | 80.8207 | 0.2100 | −0.9570 | 0.9304 * | |
| Gasoline Output | 692.0000 | 1374.2000 | 1038.9183 | 169.1628 | −0.3240 | −0.7310 | 0.1850 * | |
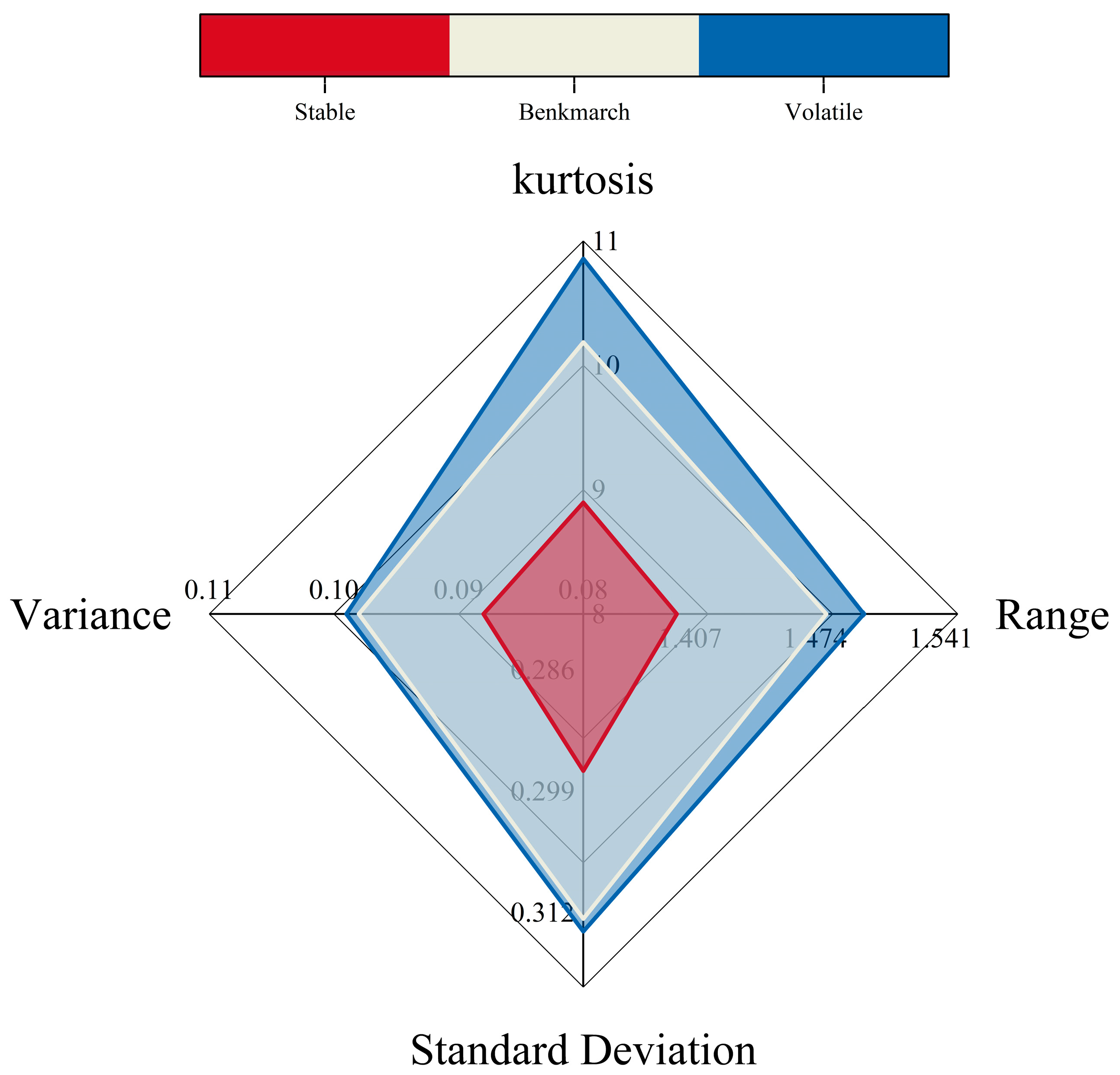
| CESI | 4.91750 | 9.80250 | 6.7946 | 1.0065 | 0.477 | 0.209 | 0.4493 * | |
| 0 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.0733 | 0.3663 | 0.2198 | 0.0733 | 0.0733 | 0.2198 | 0.0733 | 0.0733 | 0.0733 | 0.2930 |
| 4 | 0.1465 | 0.0000 | 0.0733 | 0.1465 | 0.2198 | 0.1465 | 0.1465 | 0.1465 | 0.1465 | 0.0733 |
| 6 | 0.5128 | 0.0733 | 0.5128 | 0.5128 | 0.4396 | 0.5128 | 0.2930 | 0.0733 | 0.5128 | 0.5128 |
| 8 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.2198 | 0.0733 | 0.0733 |
| 10 | 0.2930 | 0.1465 | 0.2930 | 0.2930 | 0.2930 | 0.2930 | 0.2930 | 0.2930 | 0.2930 | 0.2930 |
| 12 | 0.0733 | 0.0733 | 0.0000 | 0.1465 | 0.0733 | 0.0000 | 0.0733 | 0.0000 | 0.0733 | 0.0000 |
| 14 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0000 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 |
| 16 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 0.0733 |
| 18 | 0.0733 | 6.0073 | 0.0733 | 0.0733 | 0.0733 | 0.0733 | 1.1722 | 0.0733 | 0.0733 | 0.0733 |
| 20 | 0.6593 | 10.5495 | 1.0989 | 0.0733 | 1.0256 | 6.3004 | 5.9341 | 0.0733 | 1.1722 | 0.0733 |
| 22 | 10.4762 | 6.7399 | 6.1538 | 1.1722 | 6.8864 | 1.1722 | 6.7399 | 1.7582 | 0.0733 | 10.1832 |
| 24 | 10.3297 | 9.6703 | 1.0256 | 10.2564 | 9.9634 | 9.8168 | 9.9634 | 10.5495 | 10.6227 | 9.5238 |
| 26 | 9.9634 | 10.6227 | 10.6227 | 10.5495 | 10.0366 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 |
| 28 | 10.5495 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 |
| 30 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 | 10.6227 |
| Hypothesized No. of CE(s) | Eigenvalue | Trace | Maximum Eigenvalue | ||||
|---|---|---|---|---|---|---|---|
| Trace Statistic | 0.05 Critical Value | Prob. ** | Max-Eigen Statistic | 0.05 Critical Value | Prob. ** | ||
| None * | 0.313407 | 73.56230 | 47.85613 | 0.0000 | 43.9935 | 27.5843 | 0.0002 |
| At most 1 | 0.120782 | 29.56875 | 29.79707 | 0.0531 | 15.0604 | 21.1316 | 0.2847 |
| At most 2 | 0.106791 | 14.50826 | 15.49471 | 0.0700 | 13.2133 | 14.2646 | 0.0728 |
| At most 3 | 0.011006 | 1.294881 | 3.841465 | 0.2551 | 1.2948 | 3.8414 | 0.2551 |
| Hypothesized No. of CE(s) | Eigenvalue | Trace | Maximum Eigenvalue | ||||
|---|---|---|---|---|---|---|---|
| Trace Statistic | 0.05 Critical Value | Prob. ** | Max-Eigen Statistic | 0.05 Critical Value | Prob. ** | ||
| None * | 0.400745 | 121.9333 | 69.81889 | 0.0000 | 59.91193 | 33.87687 | 0.0000 |
| At most 1 * | 0.256203 | 62.02135 | 47.85613 | 0.0014 | 34.63047 | 27.58434 | 0.0053 |
| At most 2 | 0.143787 | 27.39088 | 29.79707 | 0.0924 | 18.16258 | 21.13162 | 0.1239 |
| At most 3 | 0.055426 | 9.228293 | 15.49471 | 0.3447 | 6.671451 | 14.26460 | 0.5287 |
| At most 4 | 0.021616 | 2.556842 | 3.841465 | 0.1098 | 2.556842 | 3.841465 | 0.1098 |
| Hypothesized No. of CE(s) | Eigenvalue | Trace | Maximum Eigenvalue | ||||
|---|---|---|---|---|---|---|---|
| Trace Statistic | 0.05 Critical Value | Prob. ** | Max-Eigen Statistic | 0.05 Critical Value | Prob. ** | ||
| None * | 0.304742 | 86.99072 | 69.81889 | 0.0012 | 40.70887 | 33.87687 | 0.0066 |
| At most 1 | 0.158249 | 46.28185 | 47.85613 | 0.0698 | 19.29436 | 27.58434 | 0.3921 |
| At most 2 | 0.134916 | 26.98749 | 29.79707 | 0.1019 | 16.23202 | 21.13162 | 0.2116 |
| At most 3 | 0.064984 | 10.75547 | 15.49471 | 0.2270 | 7.525459 | 14.26460 | 0.4290 |
| At most 4 | 0.028427 | 3.230011 | 3.841465 | 0.0723 | 3.230011 | 3.841465 | 0.0723 |
| Model | MAE | MAPE | RMSE |
|---|---|---|---|
| BiLSTM | 0.2204 | 3.2864 | 0.3238 |
| LSTM | 0.2451 | 3.6876 | 0.3342 |
| GRU | 0.3442 | 4.9668 | 0.4995 |
| SVR | 0.3625 | 5.4421 | 0.4372 |
| MLR | 0.4441 | 6.5698 | 0.4995 |
| VECM-BiLSTM | 0.2069 | 3.1265 | 0.3147 |
| VECM-LSTM | 0.2422 | 3.5704 | 0.3529 |
| VECM-GRU | 0.3218 | 4.6004 | 0.4882 |
| VECM-SVR | 0.3537 | 5.2783 | 0.4209 |
| VECM-MLR | 0.4188 | 6.1578 | 0.5289 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Zhang, X.; Gao, Y.; Xu, M.; Wang, X. China’s Energy Stock Price Index Prediction Based on VECM–BiLSTM Model. Energies 2025, 18, 1242. https://doi.org/10.3390/en18051242
Liu B, Zhang X, Gao Y, Xu M, Wang X. China’s Energy Stock Price Index Prediction Based on VECM–BiLSTM Model. Energies. 2025; 18(5):1242. https://doi.org/10.3390/en18051242
Chicago/Turabian StyleLiu, Bingchun, Xia Zhang, Yuan Gao, Minghui Xu, and Xiaobo Wang. 2025. "China’s Energy Stock Price Index Prediction Based on VECM–BiLSTM Model" Energies 18, no. 5: 1242. https://doi.org/10.3390/en18051242
APA StyleLiu, B., Zhang, X., Gao, Y., Xu, M., & Wang, X. (2025). China’s Energy Stock Price Index Prediction Based on VECM–BiLSTM Model. Energies, 18(5), 1242. https://doi.org/10.3390/en18051242






