Numerical Simulation on Aerodynamic Noise of (K)TS Control Valves in Natural Gas Transmission and Distribution Stations in Southwest China
Abstract
1. Introduction
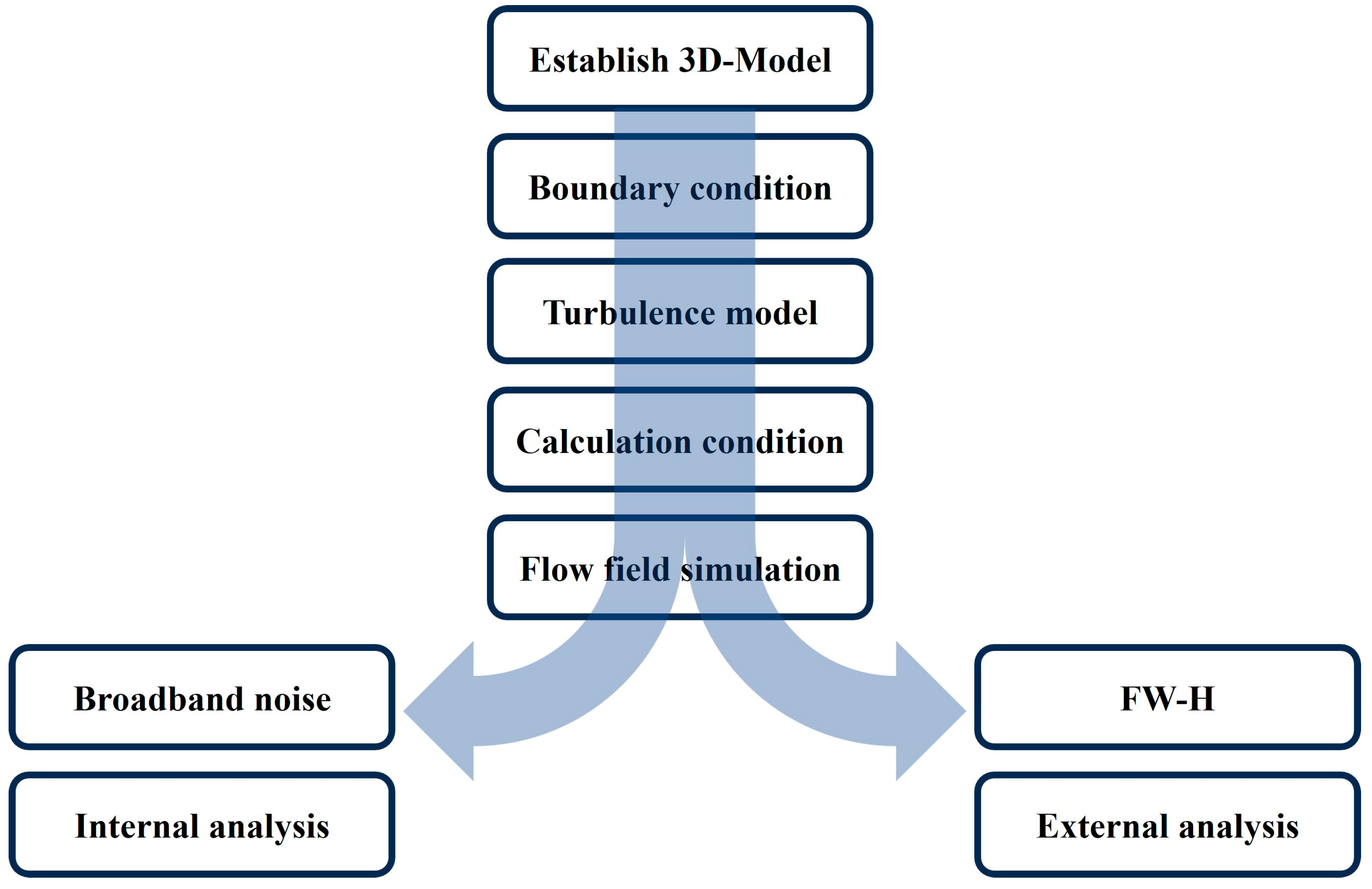
2. Theoretical Basis
2.1. Control Equations
2.2. Turbulence Model
2.3. Broadband Noise Model
2.4. FW-H Acoustic Analogy Method
3. Geometric Model Establishment
3.1. Establishment of the Geometric Model
3.2. Simulation Method Settings
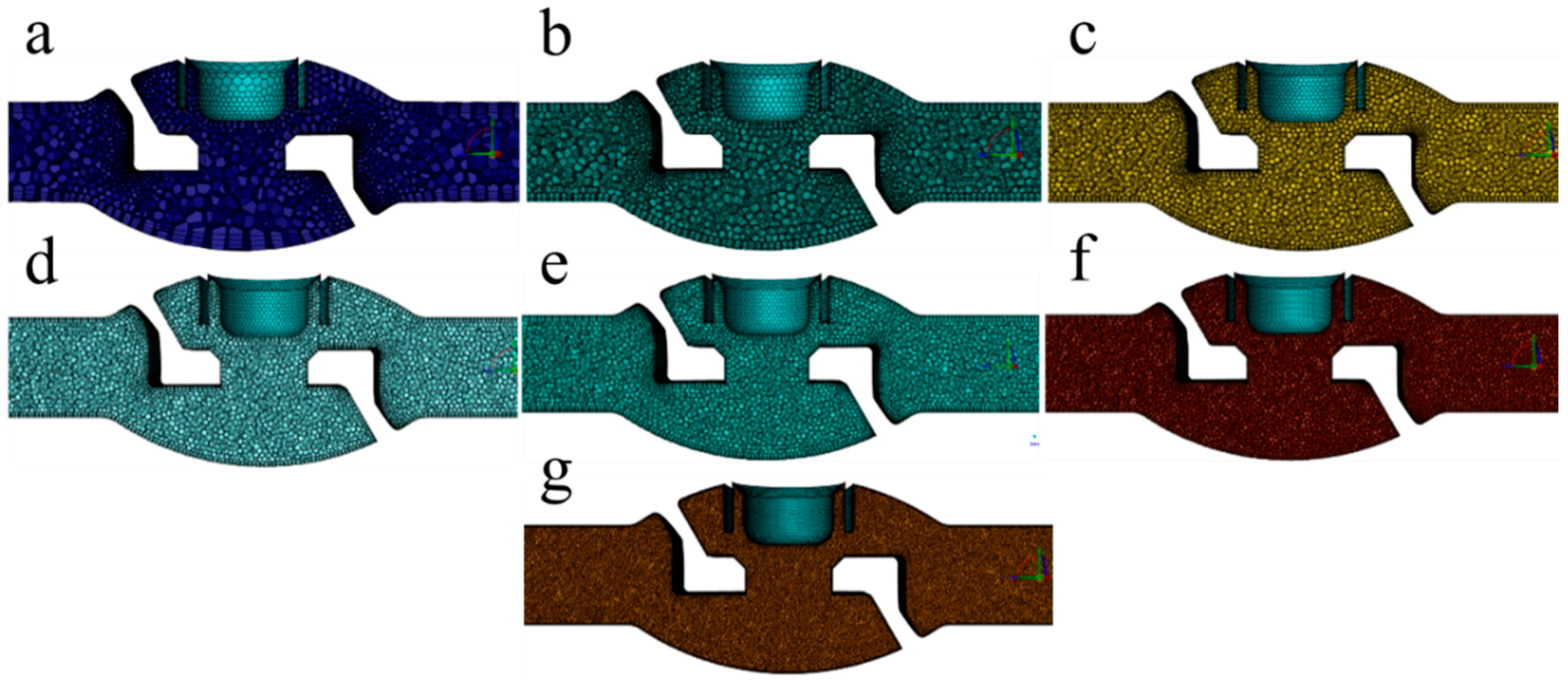
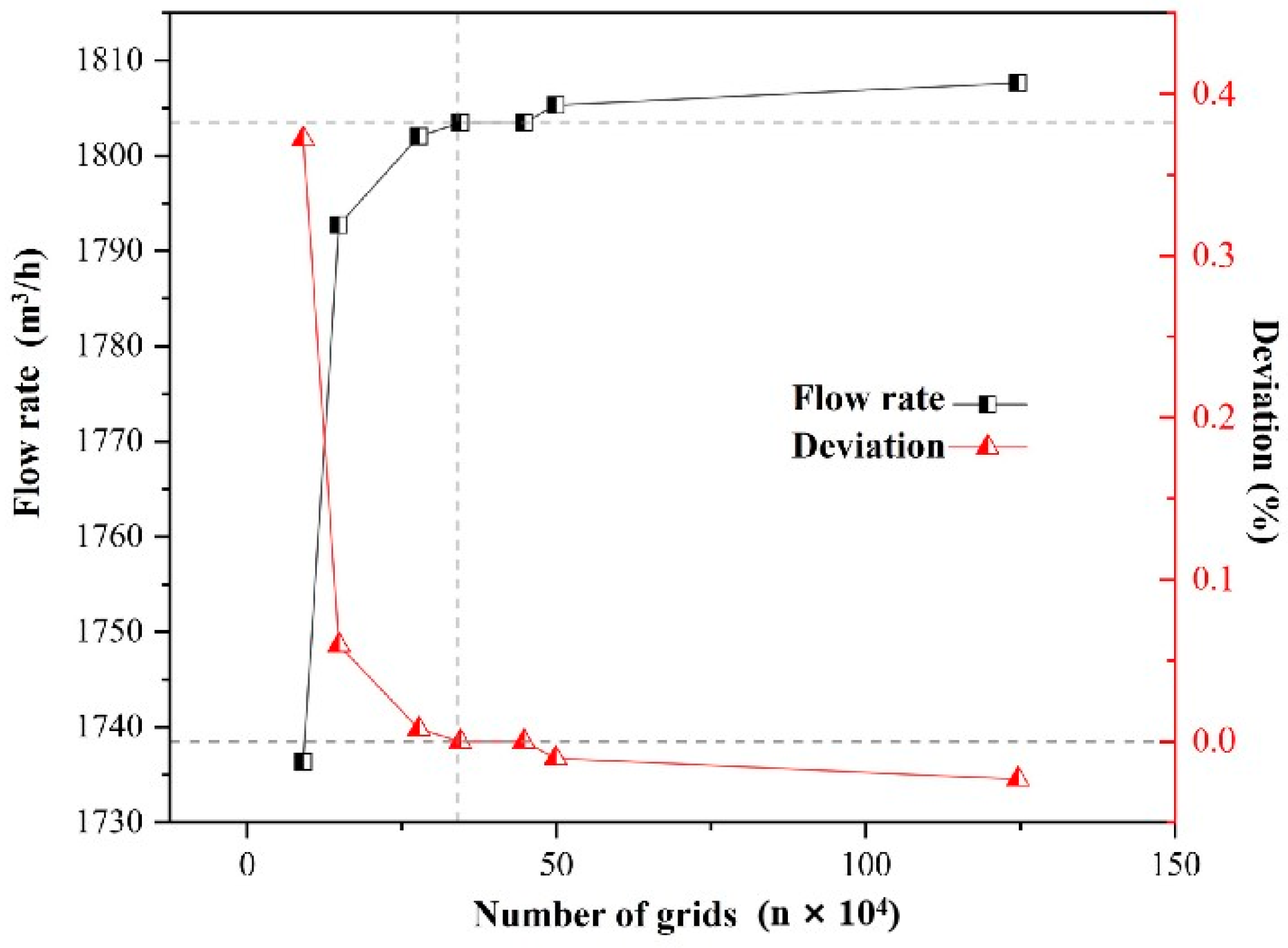
3.3. Grid Independence Verification
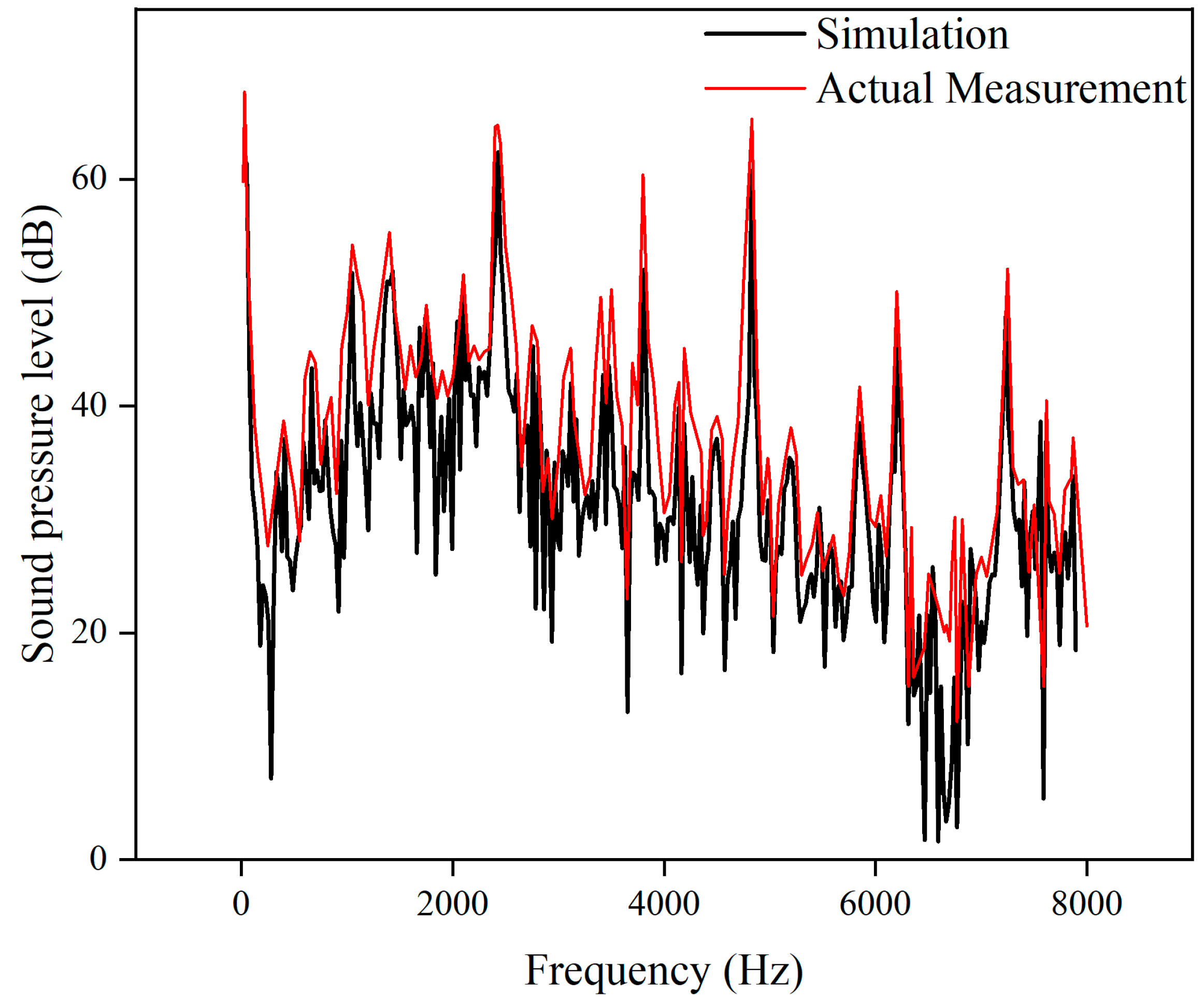
3.4. Model Validation
4. Results and Analysis
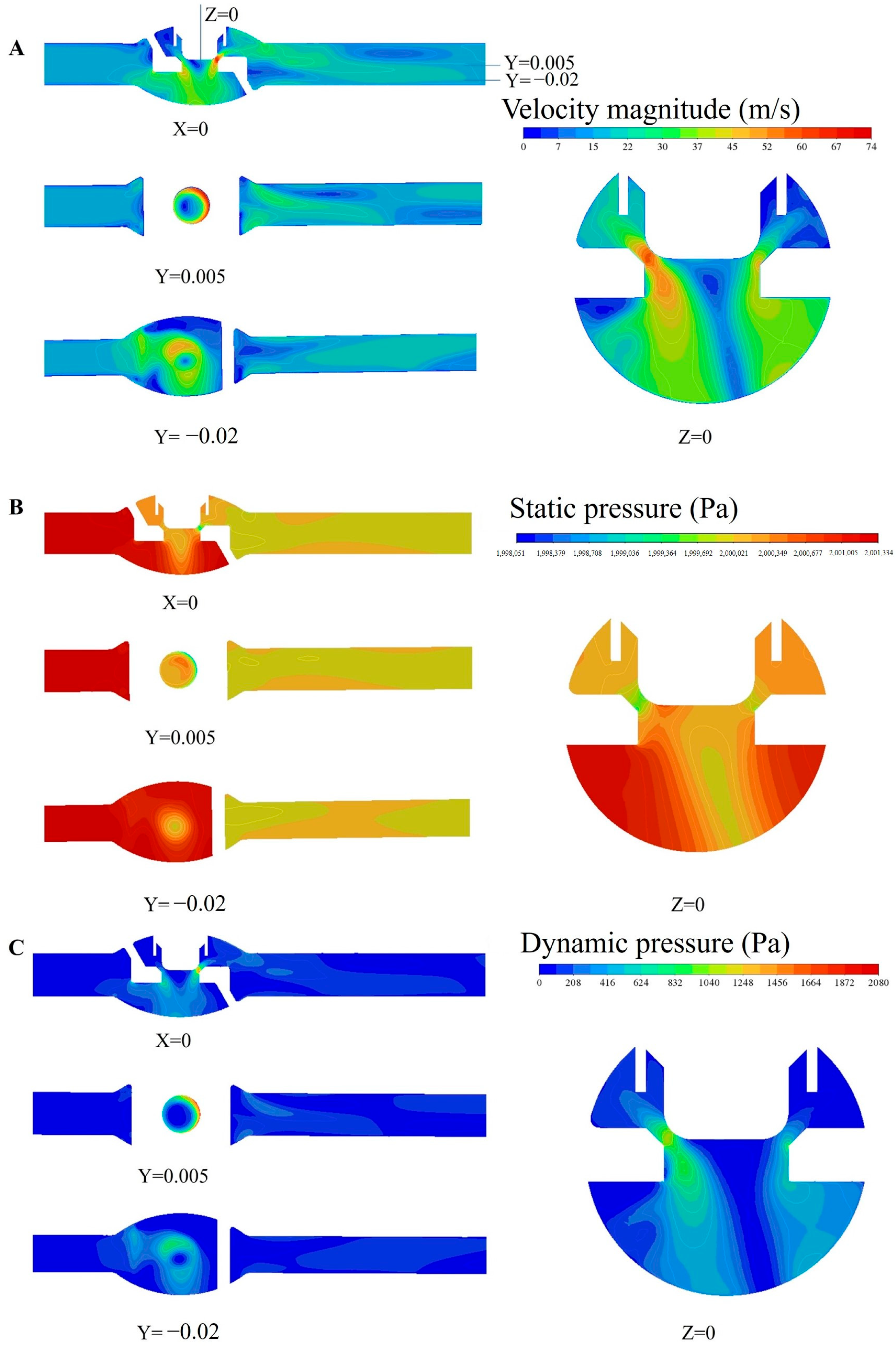
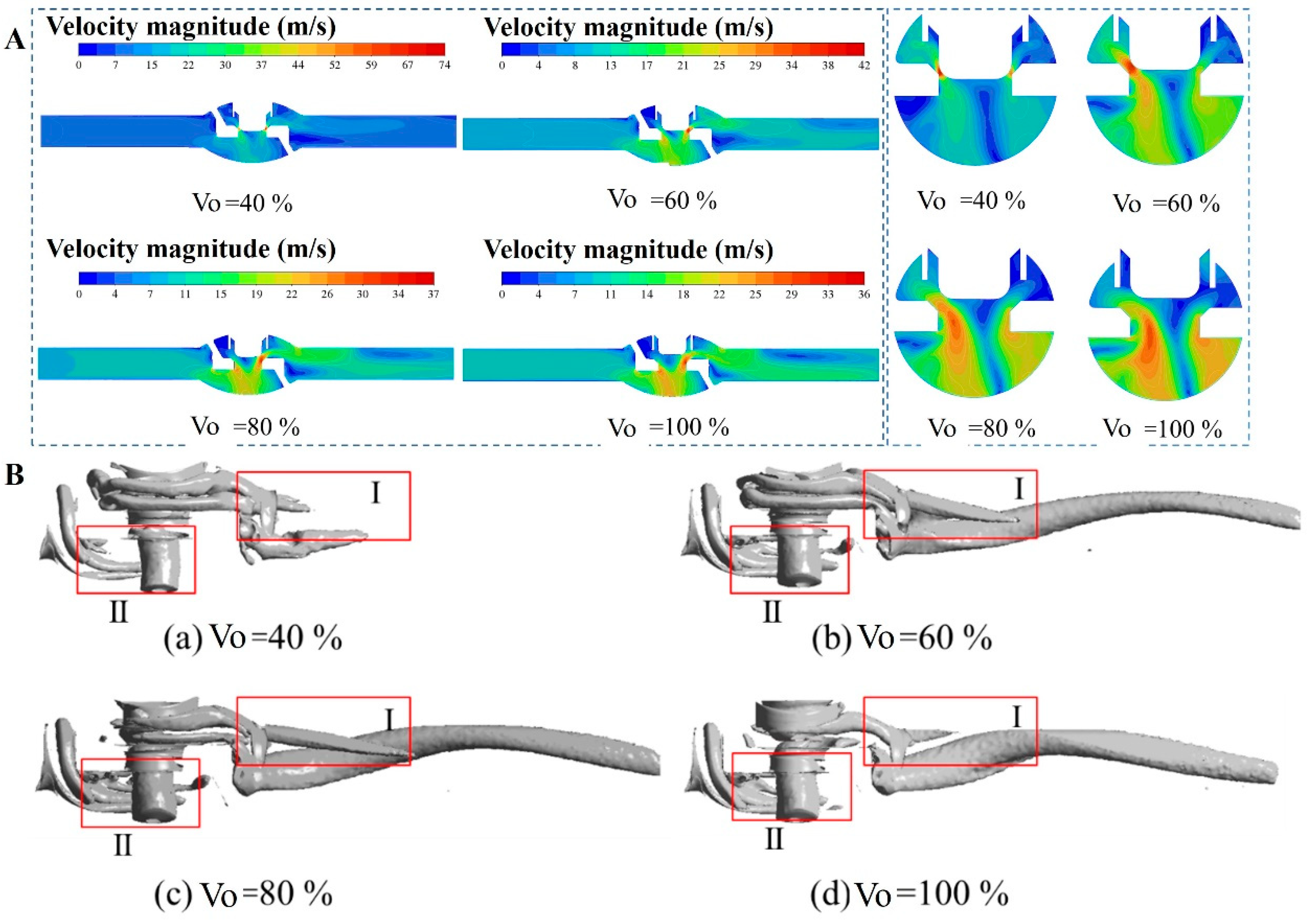
4.1. Flow Field Simulation Calculation
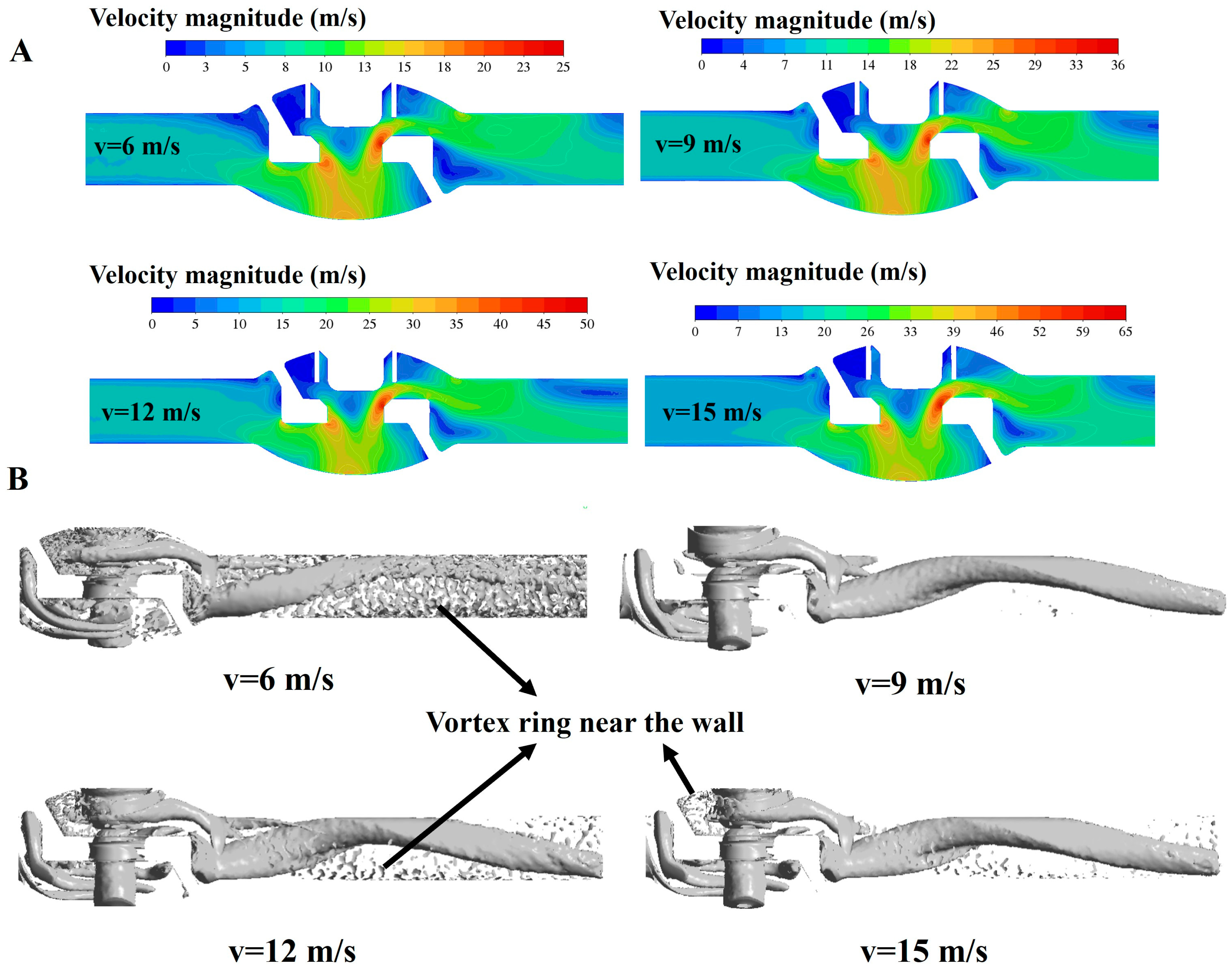
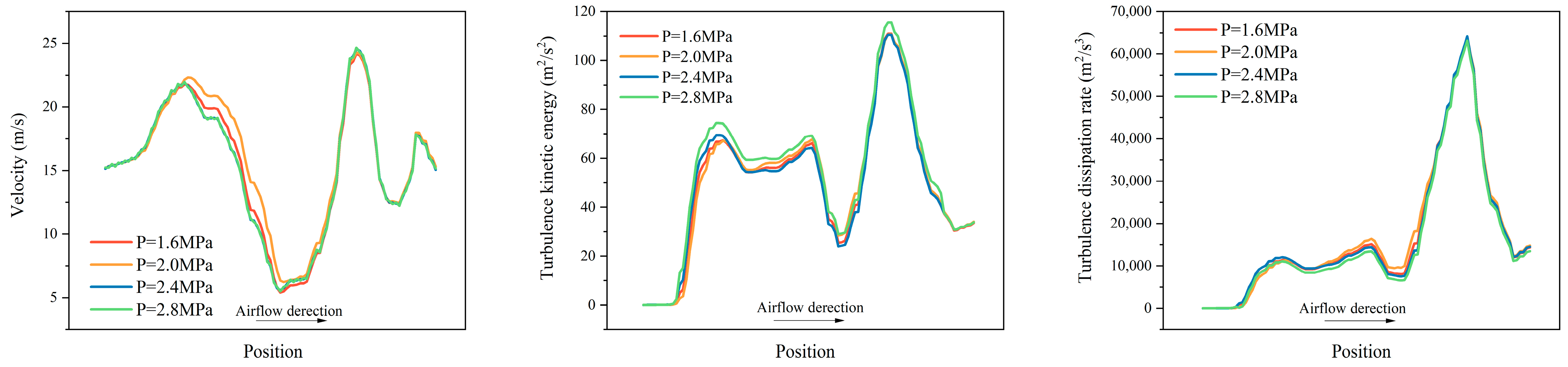
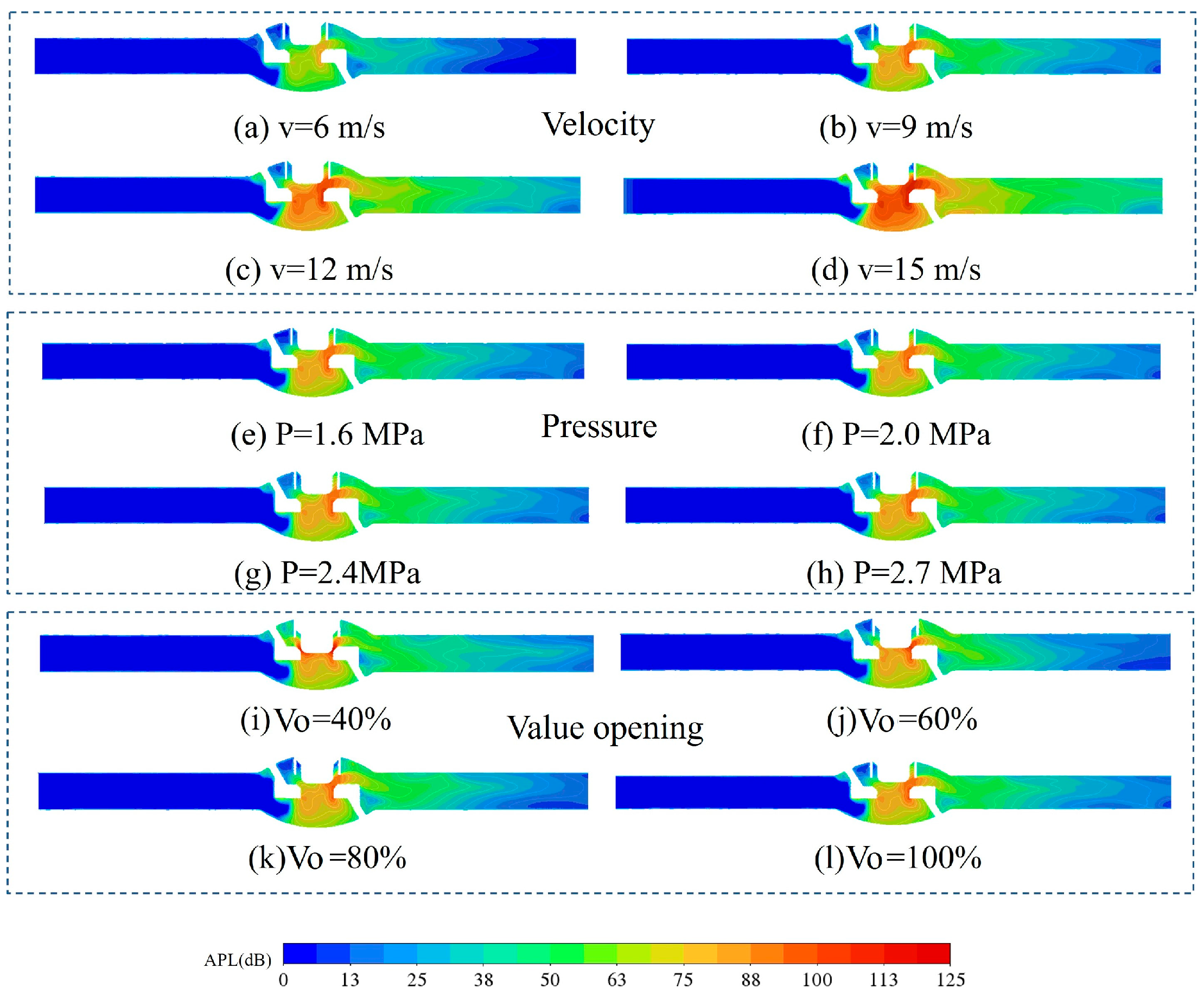
4.2. The Influencing Factors of Aerodynamic Noise Generation
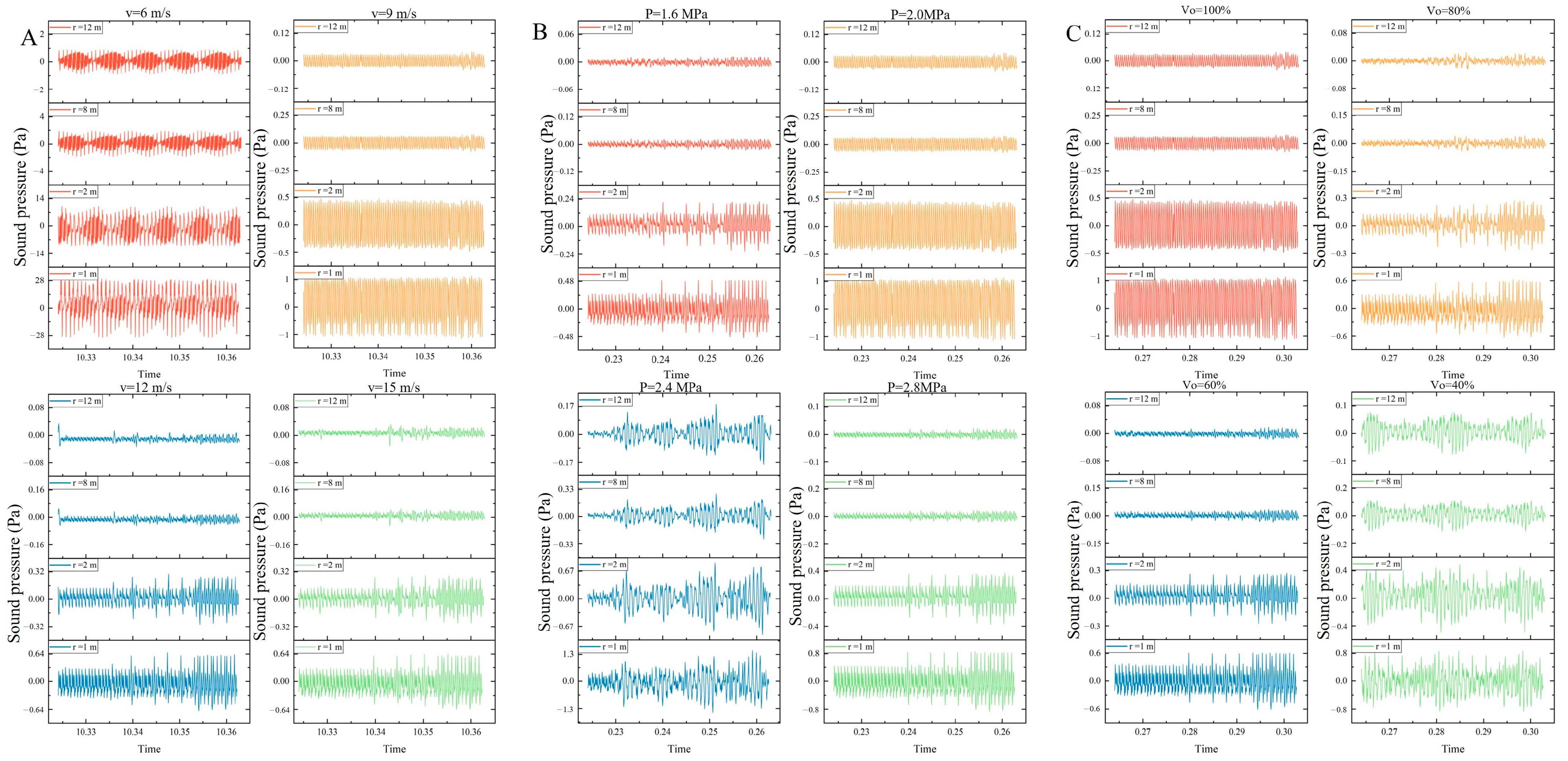
4.3. Acoustic Simulation
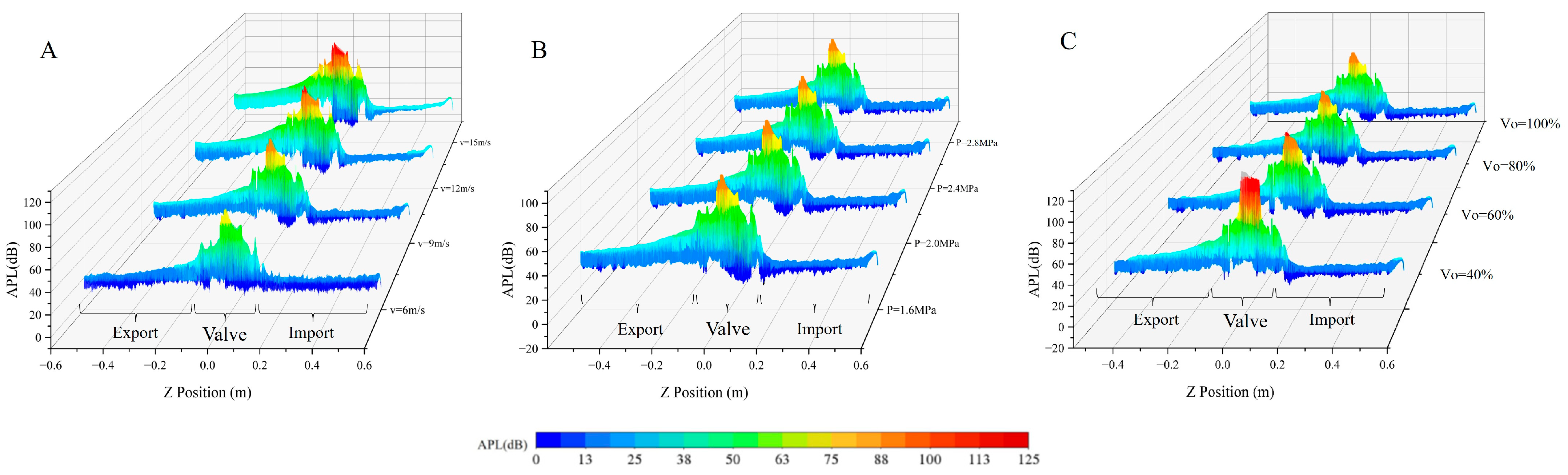
4.4. The Characteristics of Propagation of Noise Outside the Valve
4.5. Directional Analysis of Aerodynamic Noise
5. Conclusions
- (1)
- A grid cell size of 3.6 mm and boundary layer of 3 were used to ensure the accuracy of the 3D valve model calculations. The spectral curves of the measured aerodynamic noise data closely matched the simulation results, thus validating the effectiveness of the model.
- (2)
- Increasing the pipeline inlet flow velocity leads to more intense turbulence and faster energy dissipation inside the valve, whereas the outlet pressure minimally affects the flow field characteristics. The valve opening primarily affected the size of the vortex rings at the valve chamber and throttle outlet.
- (3)
- High flow velocity gradients, strong turbulence intensity, and rapid turbulent energy dissipation, along with vortex formation and shedding, were the primary causes of aerodynamic noise generated inside the valve. Noise-generating regions were primarily concentrated at the throttle port, valve chamber, and valve inlet.
- (4)
- Under different operating conditions, the directional noise distribution was similar, exhibiting symmetry along the central axis of the flow channel, resembling six-leaf or four-leaf flower shapes. The aerodynamic noise of the valve propagated along the pipeline. However, with increasing distance, it became more concentrated in the vertical direction of the valve.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomson, H.; Corbett, J.J.; Winebrake, J.J. Natural gas as a marine fuel. Energy Policy 2015, 87, 153–167. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Wu, Y.S. A study of the similarity relationship in hydrodynamic noise. J. ACTA Acust. 2002, 27, 373–378. [Google Scholar]
- Hays, J.; McCawley, M.; Shonkoff, S.B.C. Public Health Implications of Environmental Noise Associated with Unconventional Oil and Gas Development. Sci. Total Environ. 2017, 580, 448–456. [Google Scholar] [CrossRef] [PubMed]
- Cinto, M.E.; McClure, C.J.W.; Barber, J.R. Large-scale Manipulation of the Acoustic Environment Can Alter the Abundance of Breeding Birds: Evidence from a Phantom Natural Gas Field. J. Appl. Ecol. 2019, 56, 2091–2101. [Google Scholar] [CrossRef]
- Alzamzam, W.S.; Alfaghi, W.B. Noise Evaluation in Oil and Gas Fields and Associated Risk Assessment. Euro-Mediterr. J. Environ. Integrat. 2021, 6, 78. [Google Scholar] [CrossRef]
- Liu, E.B.; Yan, S.K.; Peng, S.B.; Huang, L.Y.; Jiang, Y. Noise Silencing Technology for Manifold Fow Noise Based on ANSYS Fluent. J. Nat. Gas Sci. Eng. 2016, 29, 322–328. [Google Scholar] [CrossRef]
- Su, Z.Y.; Liu, E.B.; Xu, Y.W.; Xie, P.; Shang, C.; Zhu, Q.Y. Flow Field and Noise Characteristics of Manifold in Natural Gas Station. Oil Gas Sci. Technol. 2019, 74, 70. [Google Scholar] [CrossRef]
- Ma, D.Y.; Li, P.Z.; Dai, G.H.; Wang, H.Y. Pressure Dependence of Turbulent Jet Noise. Acta Phys. Sin. Ed. 1978, 2, 122–125. [Google Scholar]
- Ma, D.; Li, P.; Dai, G.; Wang, H. Shock Associated Noise From Choked Jets. Acta Acust. 1980, 3, 172–182. [Google Scholar]
- Zhao, M.; Liu, D.; Hou, J.; Zhang, X.; Li, S. Numerical Simulation of Inverted Bucket Steam Valve Noise Based on Multiband Analysis. J. Appl. Fluid Mech. 2024, 17, 1002–1014. [Google Scholar]
- Shi, H.; Zhou, X.; Zhou, A.M.; Zhang, B.H.; Li, S.X. Numerical Simulation of Fluid-Solid Coupling Noise in Marine Three-Way Control Valve. J. Appl. Acoust. 2024, 43, 142–150. [Google Scholar]
- Han, N.; Mak, C.M. Estimation of Breakout Sound Power Level due to Turbulence Caused by an In-Duct Element. Tech. Acoust. 2007, 5, 653–657. [Google Scholar]
- Williams, J.E.F.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philos. Trans. R. Soc. A 1969, 264, 321–342. [Google Scholar]
- Li, Y.A.; Cui, W.Z.; Jiang, X.F.; Li, L.J.; Liu, J.F. Numerical Study of Thermal and Resistance Characteristics in the Vortex-Enhanced Tube. Energies 2025, 18, 13. [Google Scholar] [CrossRef]
- Yan, S.K.; Li, C.J.; Xia, Y.F.; Li, G.L. Analysis and Prediction of Natural Gas Noise in a Metering Station Based on CFD. Eng. Fail Anal. 2020, 108, 104296. [Google Scholar] [CrossRef]
- Zhang, N.; Xie, H.; Wang, X.; Wu, B.S. Computation of Vortical Flow and Flow Induced Noise by Large Eddy Simulation with FW-H Acoustic Analogy and Powell Vortex Sound Theory. J. Hydrodyn. 2016, 28, 255–266. [Google Scholar] [CrossRef]
- Tan, J.; Dong, P.; Gao, J.; Wang, C.; Zhang, L. Coupling Bionic Design and Numerical Simulation of the Wavy Leading-Edge and Seagull Airfoil of Axial Flow Blade for Air-Conditioner. J. Appl. Fluid Mech. 2023, 16, 1316–1330. [Google Scholar]
- Hou, J.J.; Li, S.X.; Yang, L.X.; Liu, D.; Zhao, Q. Numerical Simulation and Reduction of Balance Valve Noise Based on Considering Quadrupole and Dipole in Different Frequency Bands. Appl. Acoust. 2023, 211, 109504. [Google Scholar] [CrossRef]
- Li, S.X.; Hou, J.J.; Pan, W.L.; Wang, Z.H.; Kang, Y.X. Study on Aerodynamic Noise Numerical Simulation and Characteristics of Safety Valve Based on Dipole and Quadrupole. Acoust. Aust. 2020, 48, 441–454. [Google Scholar] [CrossRef]
- Huang, J.Y.; Zhang, K.; Li, H.Y.; Wang, A.R.; Yang, M.Y. Numerical Simulation of Aerodynamic Noise and Noise Reduction of Range Hood. Appl. Acoust. 2021, 175, 107806. [Google Scholar] [CrossRef]
- Sun, L.H.; Zhe, C.T.; Guo, C.; Cheng, S.; He, S.Y.; Gao, M. Numerical Simulation Regarding Flow-Induced Noise in Variable Cross-Section Pipelines Based on Large Eddy Simulations and Ffowcs Williams—Hawkings Methods. AIP Adv. 2021, 11, 065118. [Google Scholar] [CrossRef]
- Jia, J.B.; Shi, Y.; Meng, X.Y.; Zhang, B.; Li, D.M. Pneumatic Noise Study of Multi-Stage Sleeve Control Valve. Processes 2023, 11, 2544. [Google Scholar] [CrossRef]
- Guo, G.; Zhu, L.; Xing, B.Y. Density Distribution Characteristics of Fluid Inside Vortex in Supersonic Mixing Layer. Acta Phys. Sin. 2020, 69, 144701–144715. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, M.; Jin, Z.J.; Chen, L.L. Numerical Analysis of Aerodynamic Noise in a High Parameter Pressure Reducing Valve. Appl. Mech. Mater. 2013, 397–400, 274–277. [Google Scholar] [CrossRef]
- Xu, W.W.; Wang, Q.G.; Wu, D.Z.; Li, Q. Simulation and Design Improvement of a Low Noise Control Valve in Autonomous Underwater Vehicles. Appl. Acoust. 2019, 146, 23–30. [Google Scholar] [CrossRef]
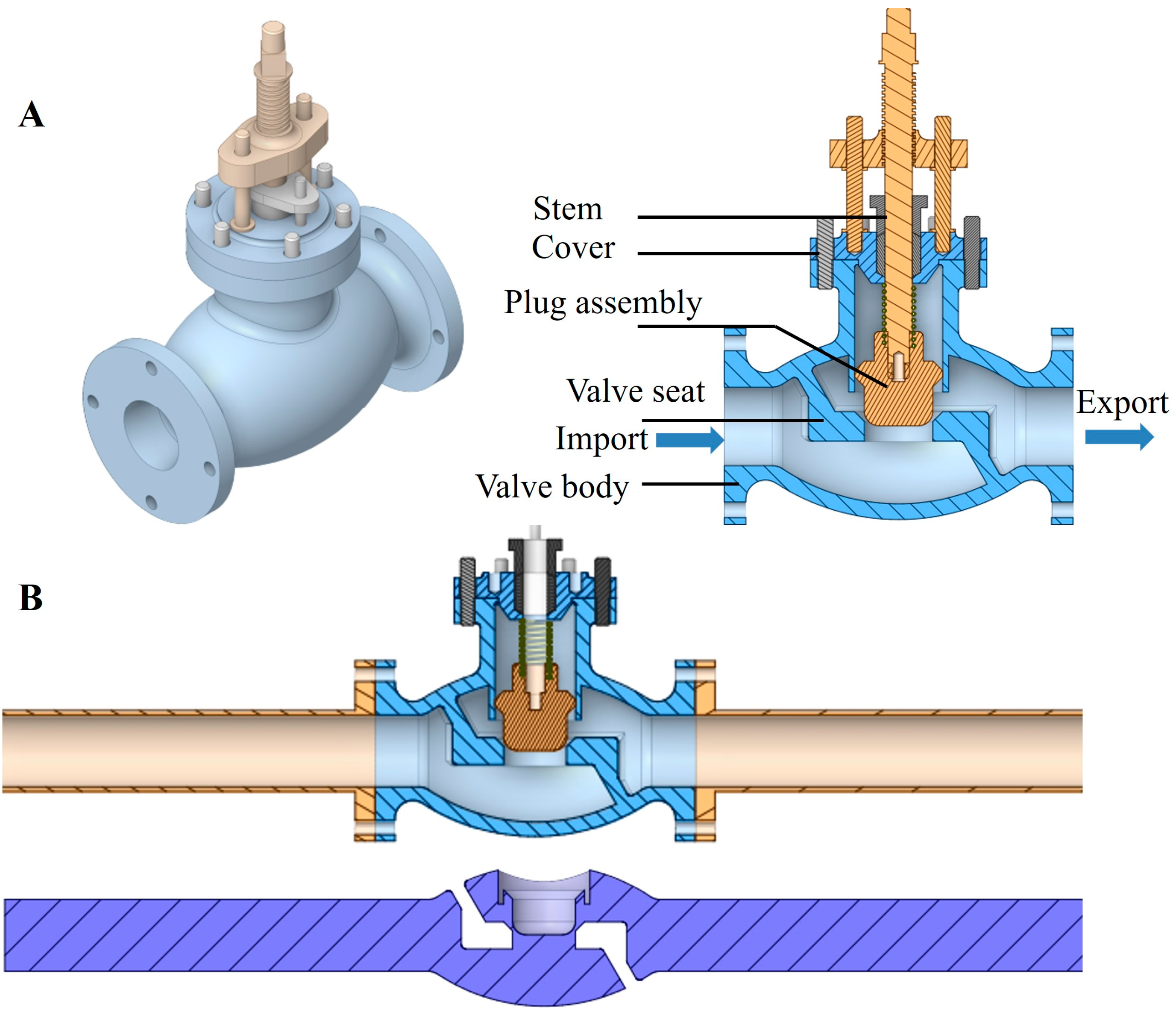



| Parameter | Value |
|---|---|
| Nominal diameter | 80 mm |
| Nominal pressure grade | 6.3 MPa |
| Valve body material | WCB |
| Valve cover material | Forged steel |
| Piston and valve seat materials | S30408 (Stainless steel) |
| No. | Maximum Unit Size (m) | Boundary Layers (n) | Number of Grids | Minimum Orthogonal Mass |
|---|---|---|---|---|
| 1 | 0.0400 | 3 | 9 × 104 | 0.21 |
| 2 | 0.0060 | 3 | 1.4 × 105 | 0.21 |
| 3 | 0.0040 | 3 | 2.8 × 105 | 0.21 |
| 4 | 0.0036 | 3 | 3.4 × 105 | 0.20 |
| 5 | 0.0036 | 5 | 4.4 × 105 | 0.21 |
| 6 | 0.0030 | 3 | 5.0 × 105 | 0.20 |
| 7 | 0.0020 | 3 | 1.2 × 106 | 0.20 |
| Parameters | Inlet Velocities v (m/s) | Outlet Pressure P (Pa) | Valve Opening Vo (%) |
|---|---|---|---|
| Value | 6, 9 *, 12, 15 | 1.6, 2.0 *, 2.4, 2.8 | 40, 60, 80, 100 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Yu, L.; Cao, H.; Zhang, L.; Pei, Y.; Wu, J.; Yang, W.; Gao, J. Numerical Simulation on Aerodynamic Noise of (K)TS Control Valves in Natural Gas Transmission and Distribution Stations in Southwest China. Energies 2025, 18, 968. https://doi.org/10.3390/en18040968
Feng X, Yu L, Cao H, Zhang L, Pei Y, Wu J, Yang W, Gao J. Numerical Simulation on Aerodynamic Noise of (K)TS Control Valves in Natural Gas Transmission and Distribution Stations in Southwest China. Energies. 2025; 18(4):968. https://doi.org/10.3390/en18040968
Chicago/Turabian StyleFeng, Xiaobo, Lu Yu, Hui Cao, Ling Zhang, Yizhi Pei, Jingchen Wu, Wenhao Yang, and Junmin Gao. 2025. "Numerical Simulation on Aerodynamic Noise of (K)TS Control Valves in Natural Gas Transmission and Distribution Stations in Southwest China" Energies 18, no. 4: 968. https://doi.org/10.3390/en18040968
APA StyleFeng, X., Yu, L., Cao, H., Zhang, L., Pei, Y., Wu, J., Yang, W., & Gao, J. (2025). Numerical Simulation on Aerodynamic Noise of (K)TS Control Valves in Natural Gas Transmission and Distribution Stations in Southwest China. Energies, 18(4), 968. https://doi.org/10.3390/en18040968





