Research on the Mechanism of Thermal Power of an Interior Permanent Magnet Eddy Current Heater Driven by Wind
Abstract
1. Introduction
- Different structures models of IPMECHs are established, and the formulas for calculating the electromagnetic field, thermal power, and electromagnetic torque of IPMECHs are derived;
- The characteristics of air gap and stator MFD distributions are analyzed for different structural IPMECHs, as well as the effects of the quantity and size of copper strips on the MFD distribution;
- The effect of the quantity and size of copper strips on the thermal power and electromagnetic torque of open/closed slots is analyzed using the finite element method;
- The operating characteristics of closed-slot and open-slot heater prototypes are experimentally explored and the accuracy and reliability of the simulation results are verified.
2. Methods and Experimental
2.1. IPMECH
2.2. Theoretical Model
- Ampere–Maxwell law:
- Gauss’s law for magnetism:
- Faraday’s law of induction:
- Gauss’s law:
2.3. Independence Verification
2.4. Experimental
2.4.1. Experimental Setup
2.4.2. Experimental Procedure
2.4.3. Analysis of Uncertainty
3. Results and Discussion
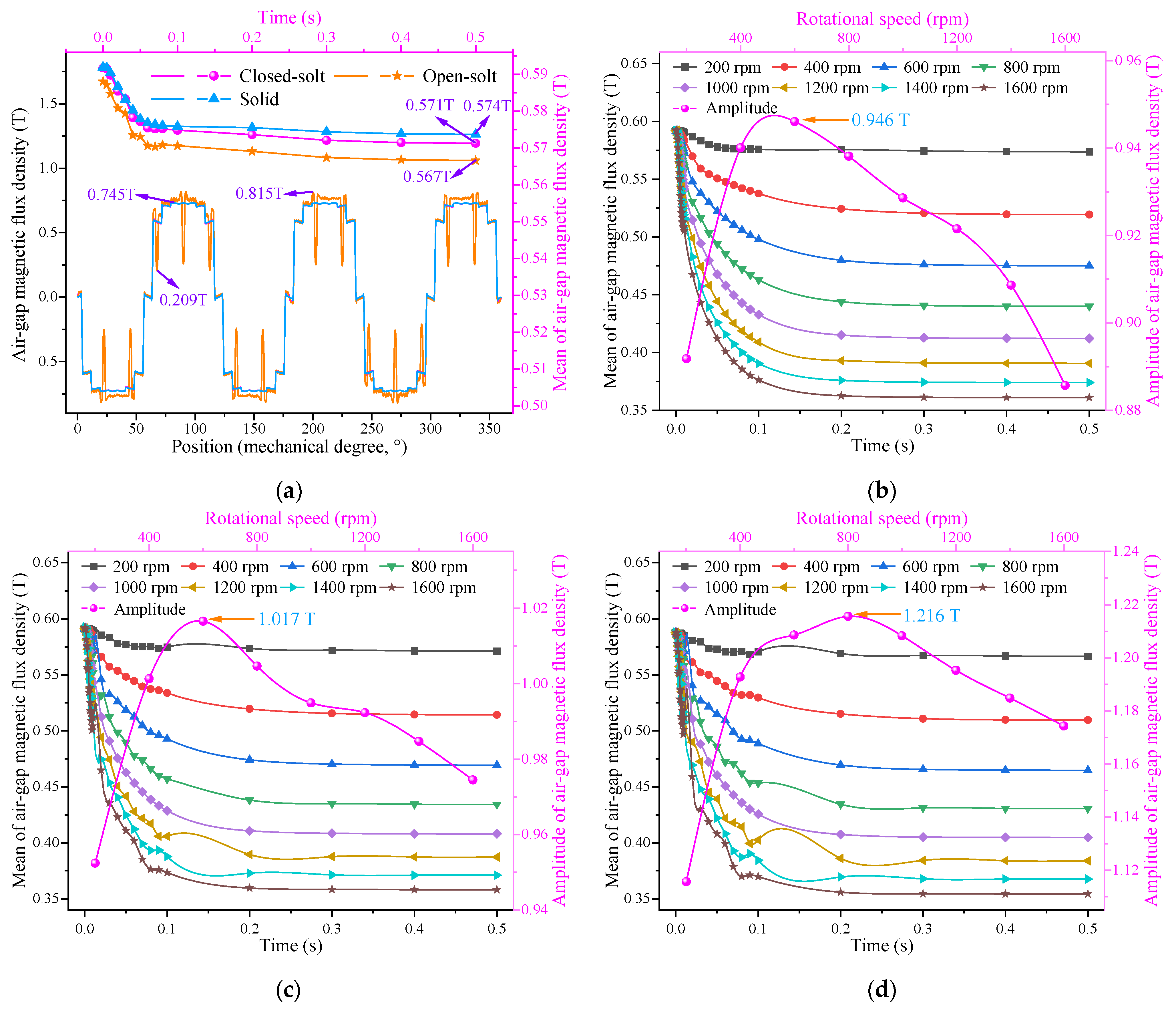
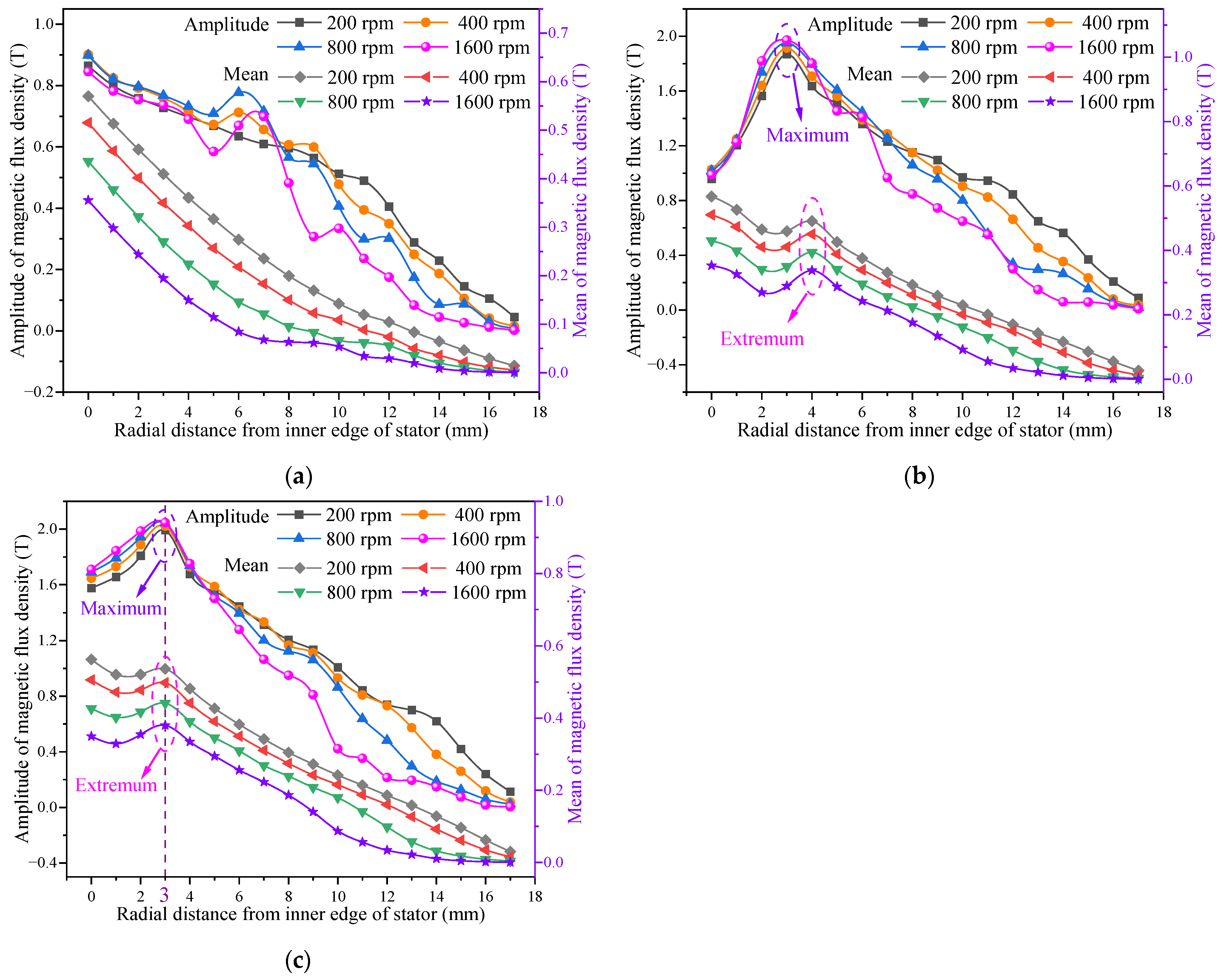
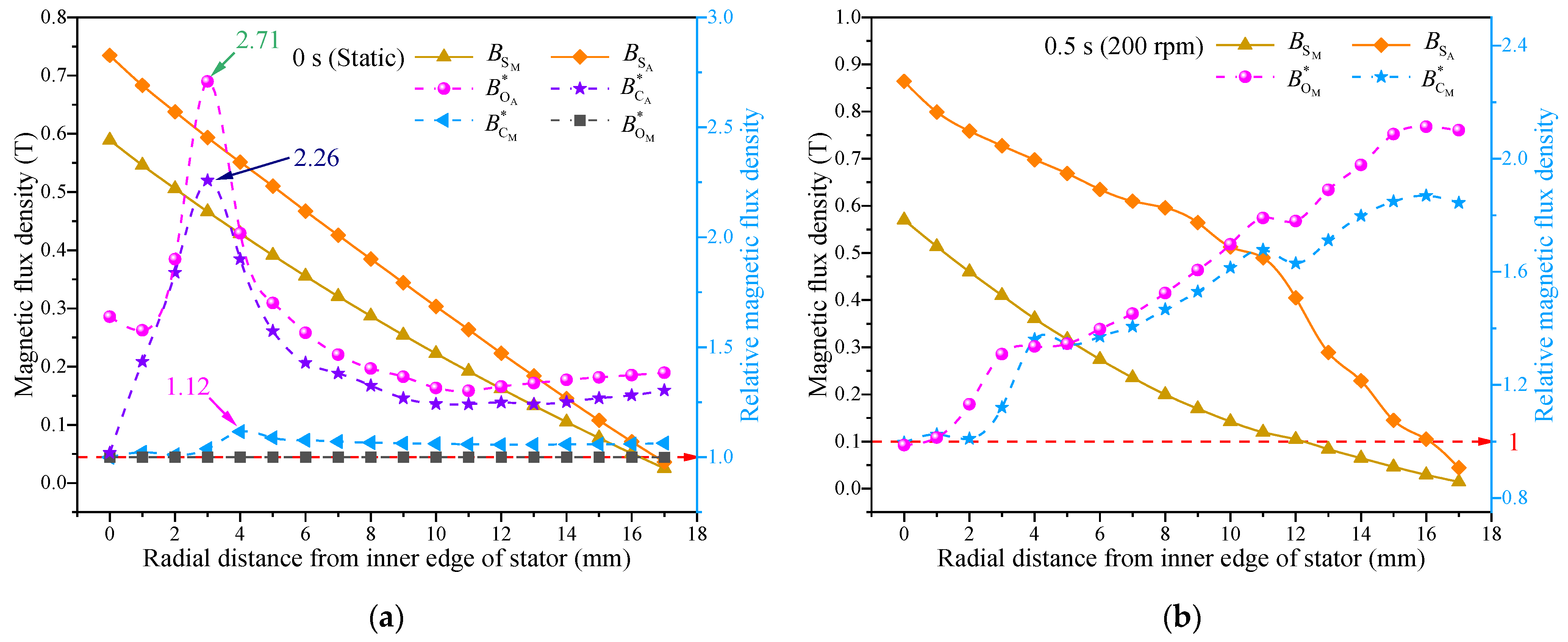
3.1. Electromagnetic Field Characteristics of IPMECH
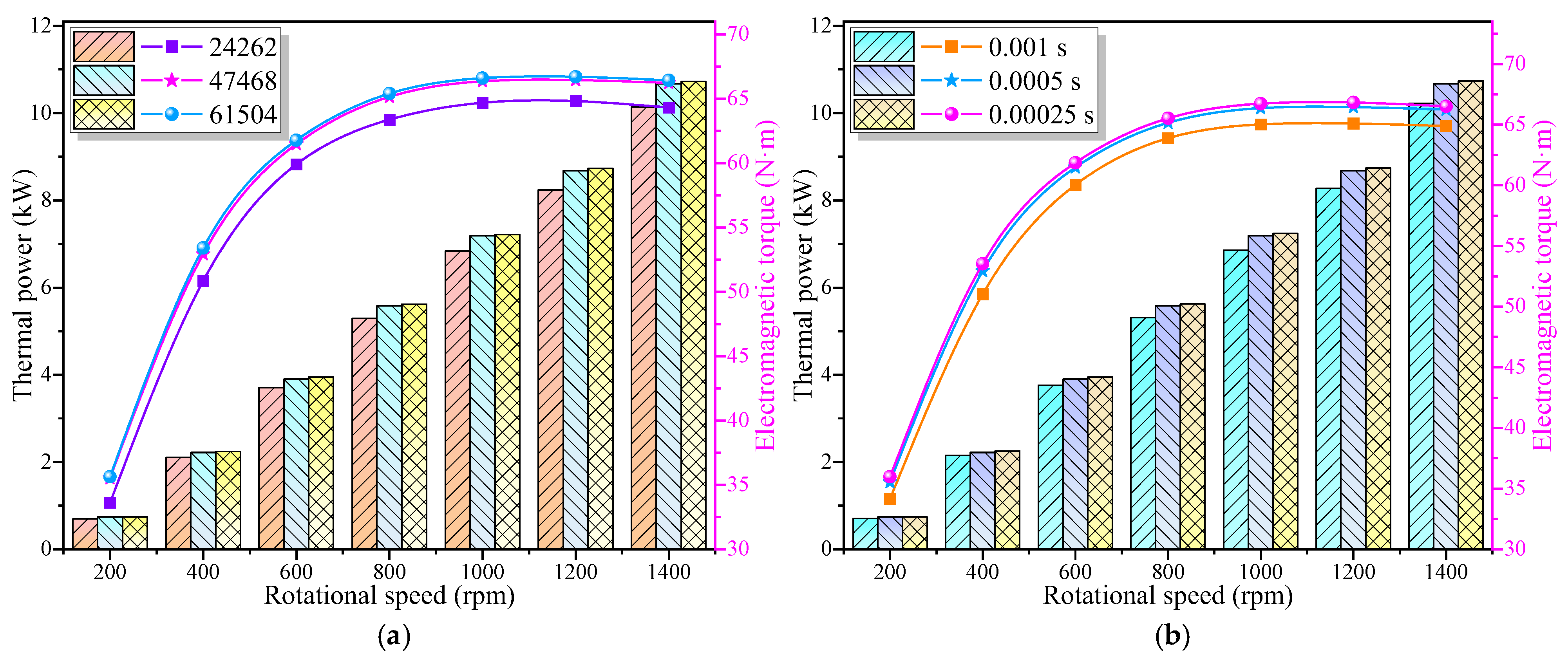
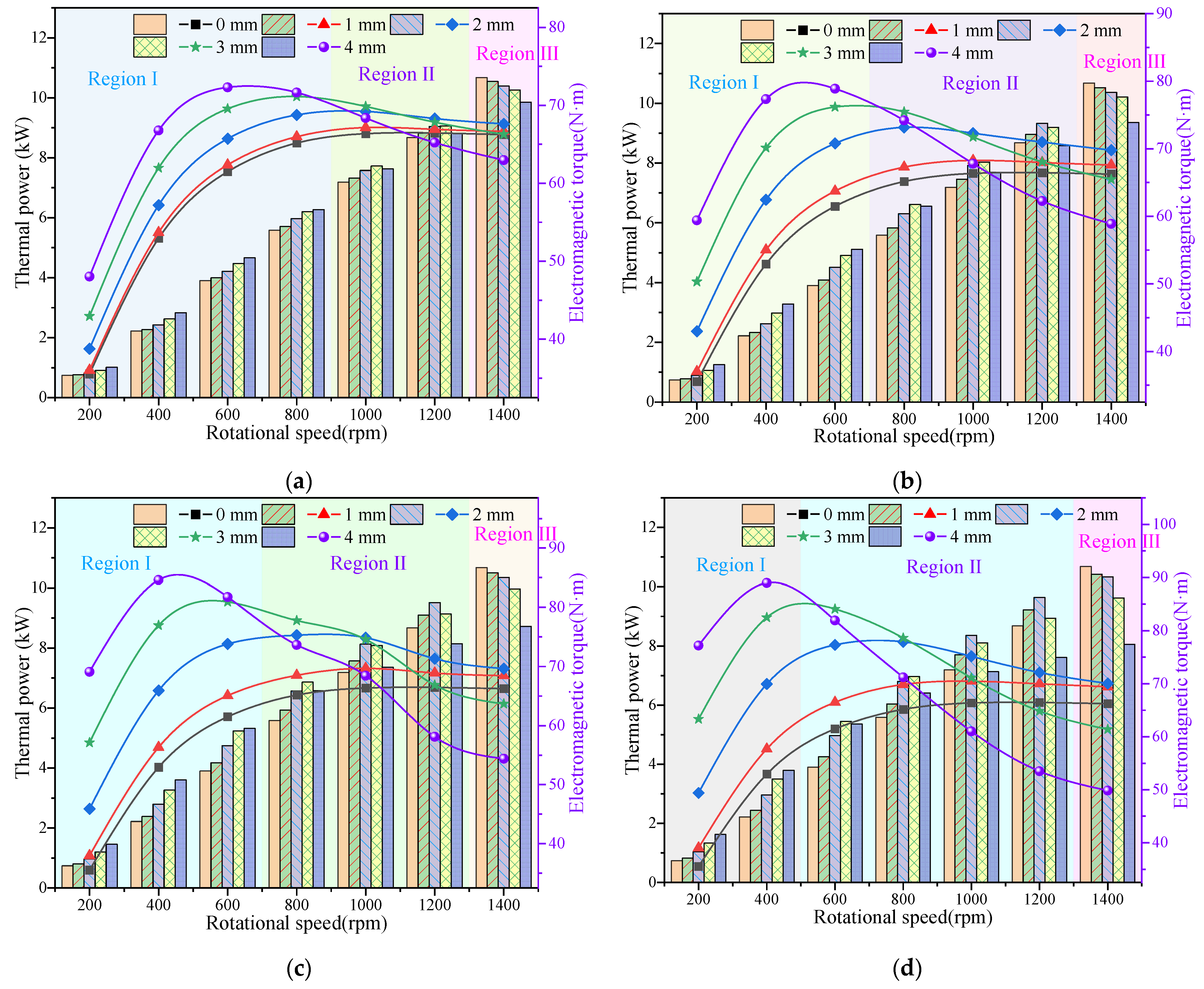
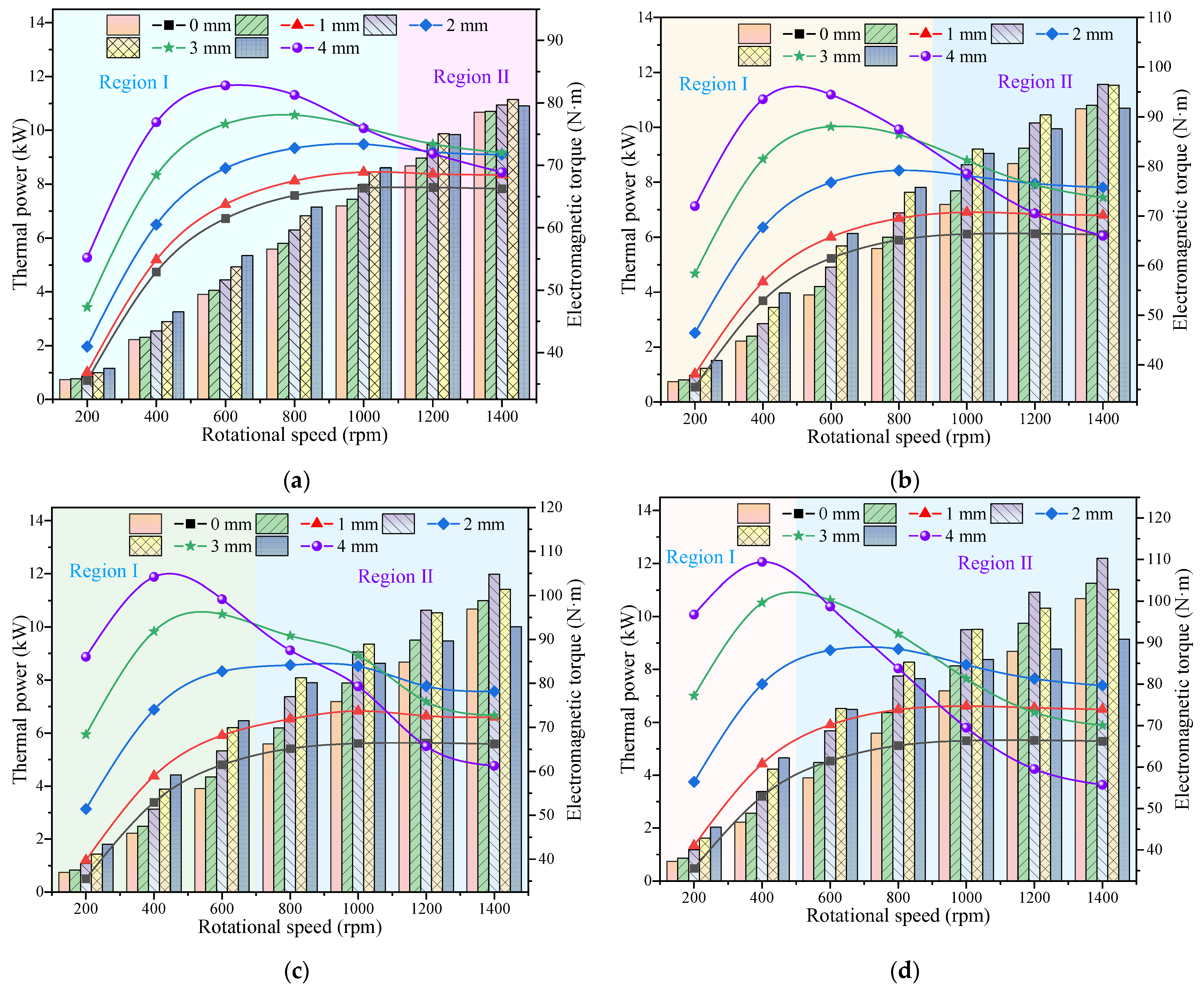
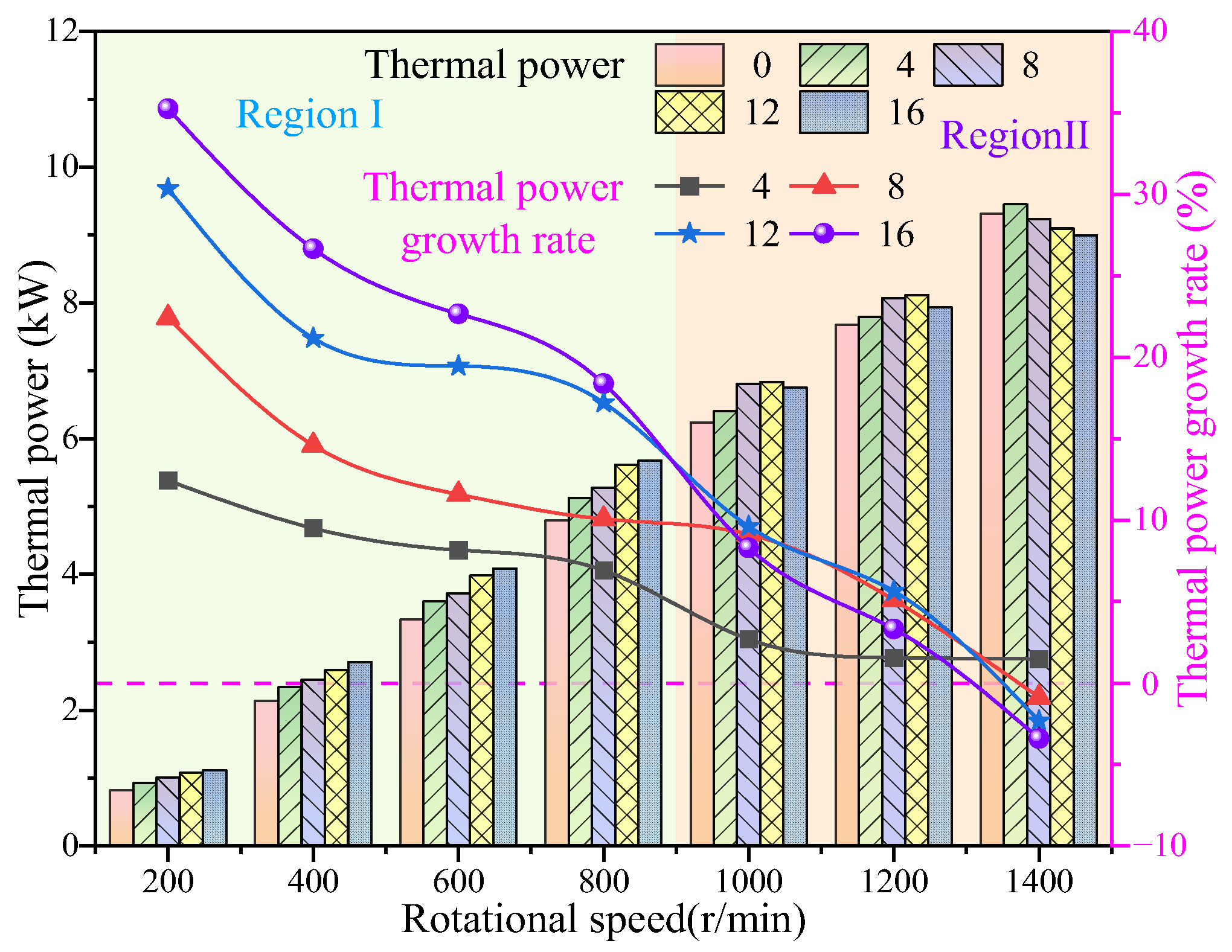
3.2. Thermal Power and Electromagnetic Torque Characteristics of IPMECH
3.3. Experiment of Prototypes
4. Conclusions
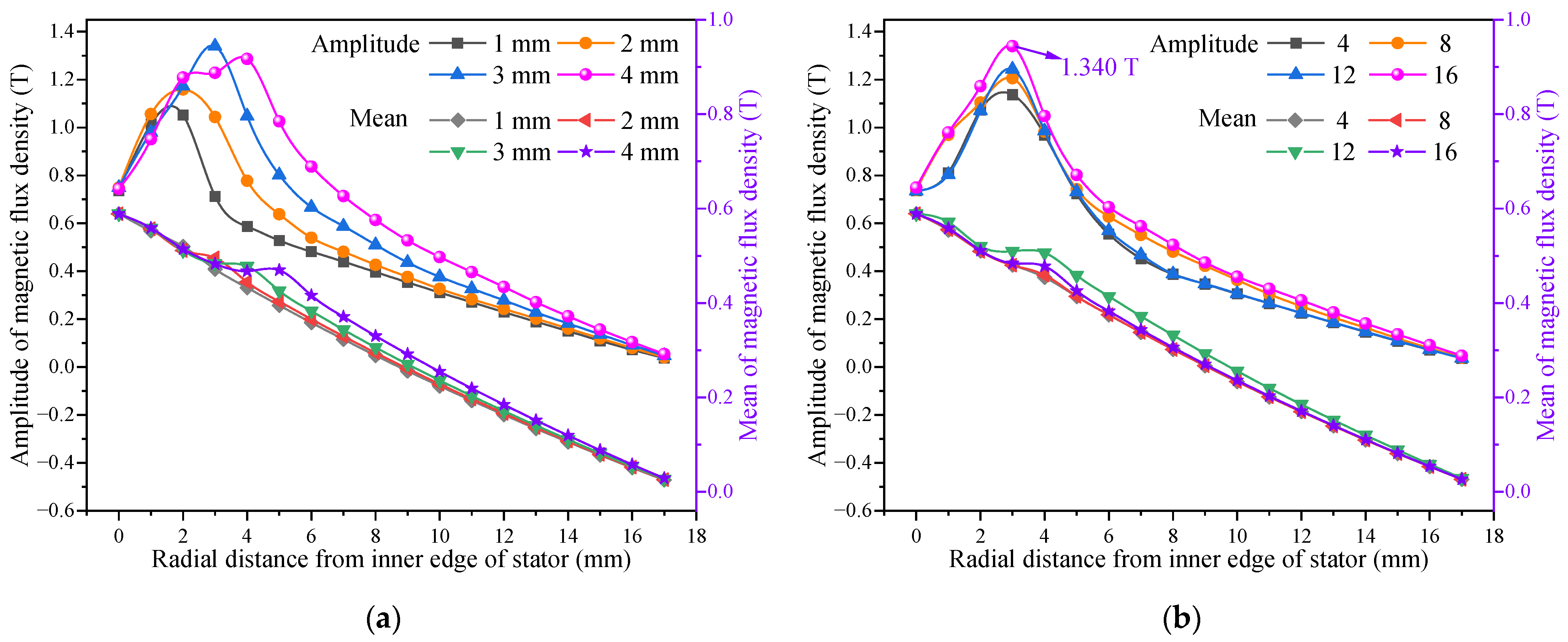
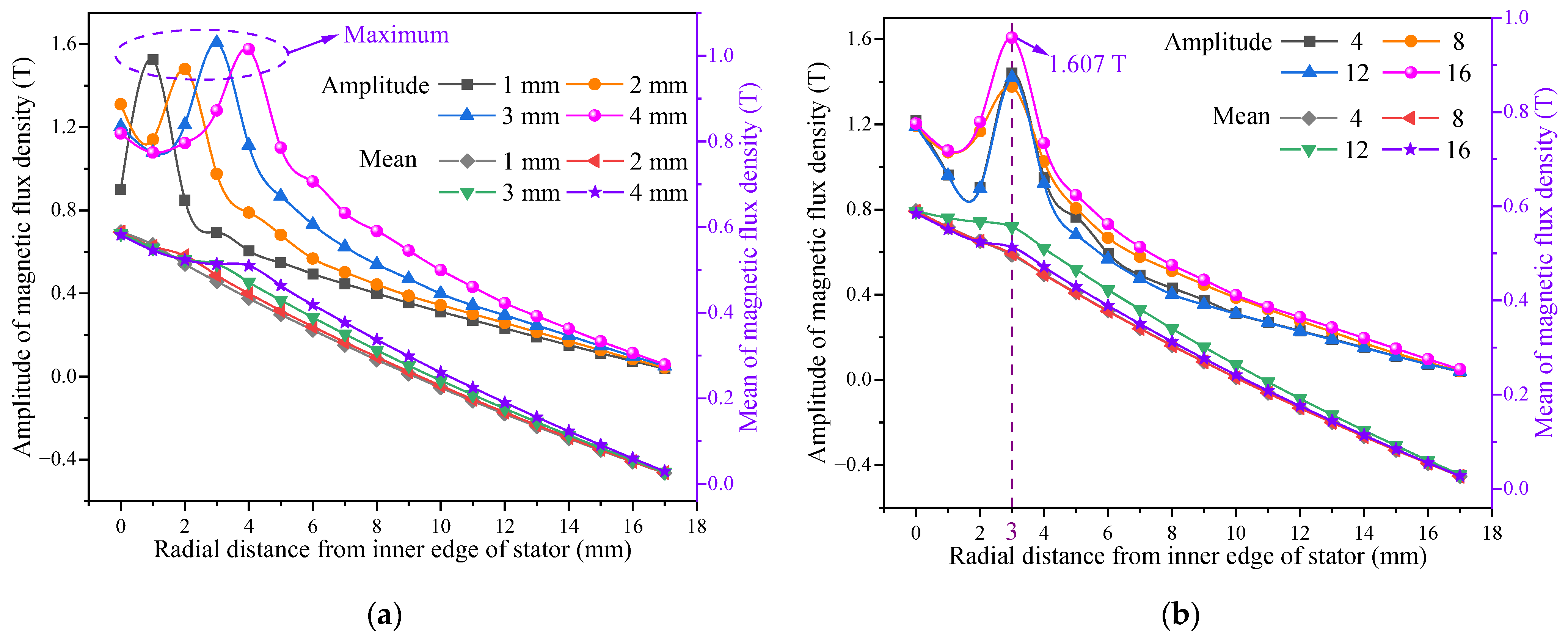
- Compared with the solid IPMECH, the closed-slot and open-slot IPMECHs can improve the heaters’ stator MFD, and the stator static MFD amplitudes of closed-slot and open-slot IPMECHs with 16 3 mm copper strips are 1.340 and 1.607 T, respectively.
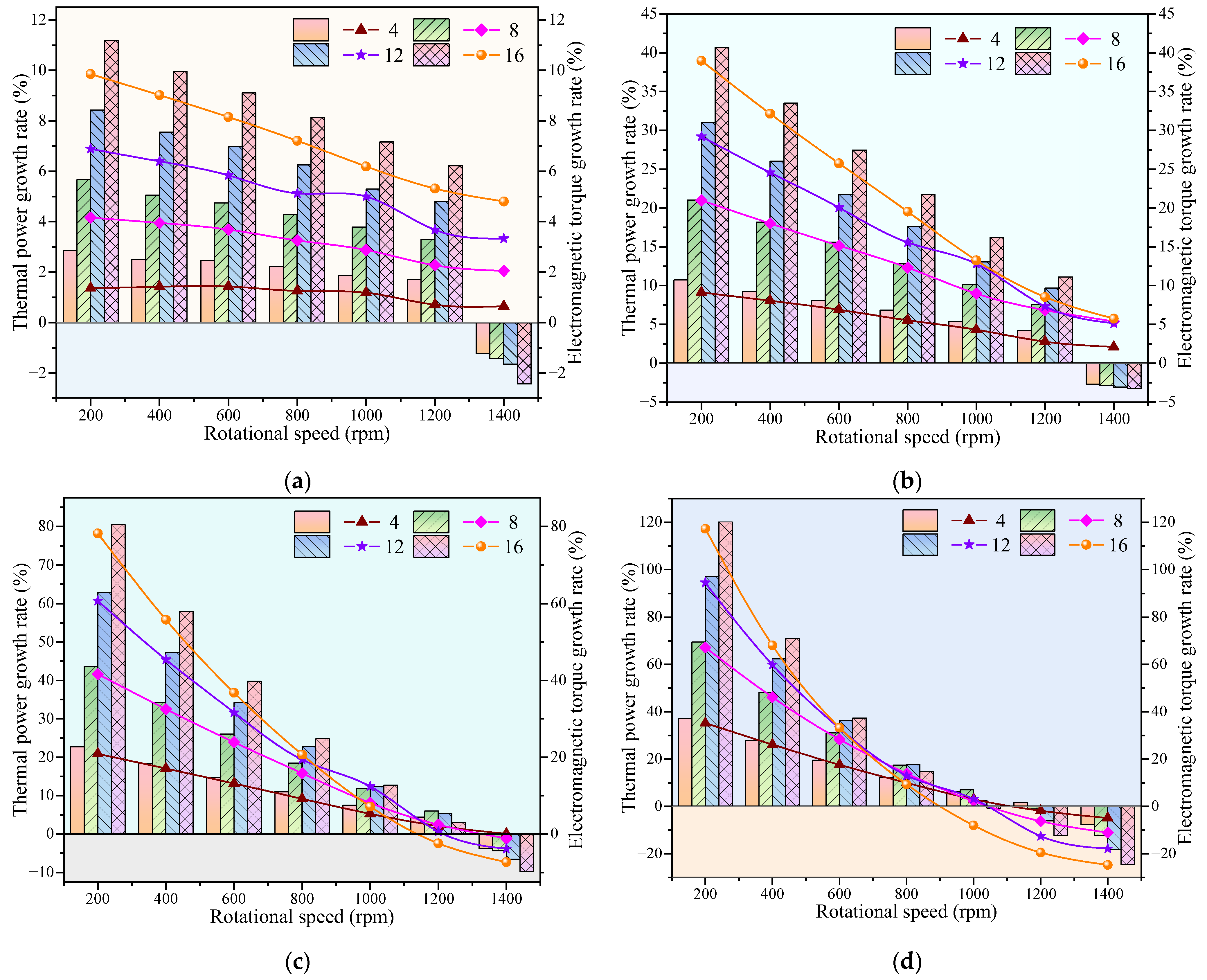
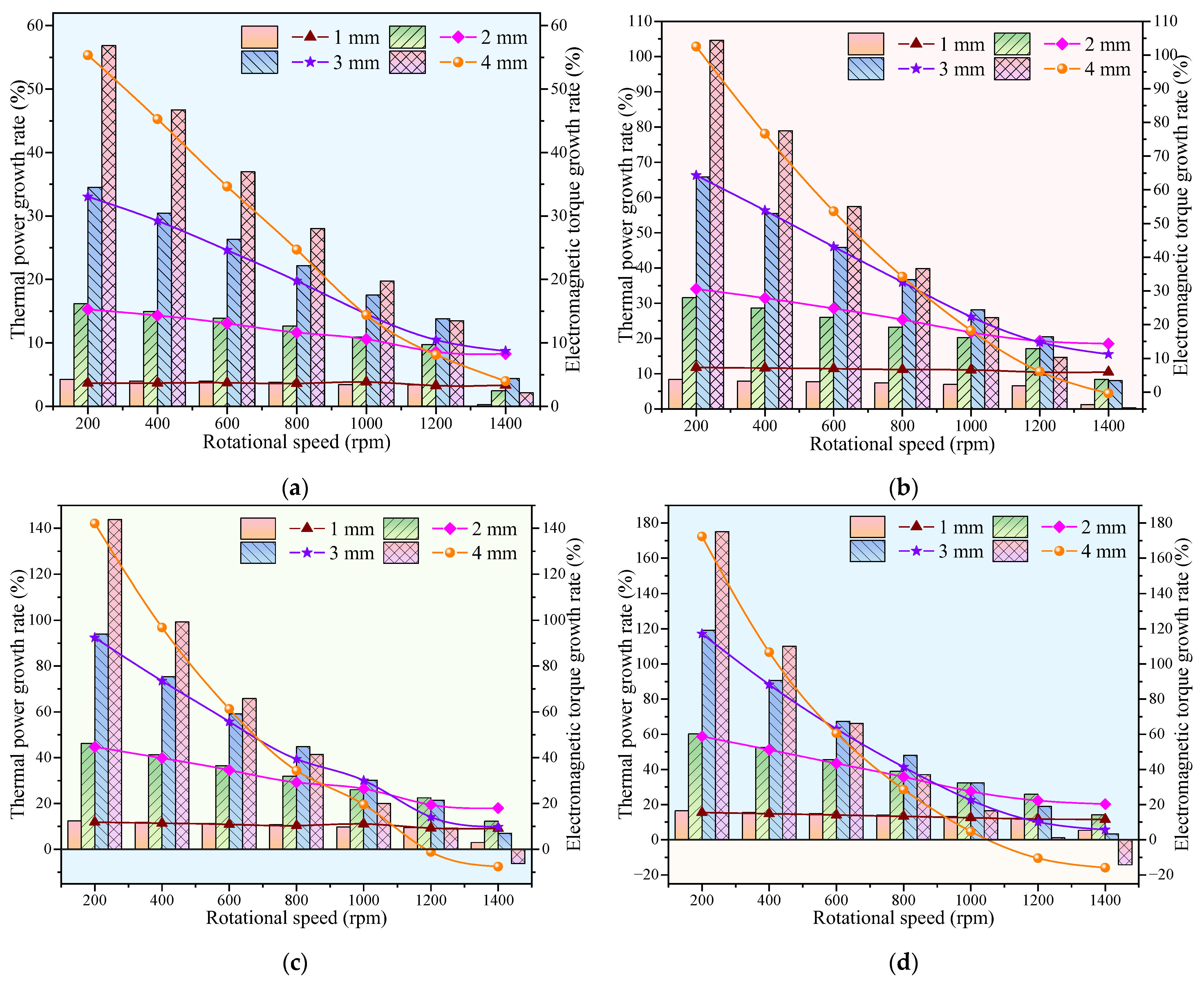
- Compared with the solid IPMECH, the thermal power and electromagnetic torque of the closed-slot IPMECH can be enhance in Region Ⅰ, while it can be reduced in Region II. The TPGRs of the closed-slot IPMECH with 16 3 mm copper strips at 200 and 1400 rpm are 80.46% and −9.84%, respectively, while the ETGRs are 78.22% and −7.31%, respectively.
- Enhancement of thermal power and electromagnetic torque by the open-slot IPMECH is more significant. The TPGRs of the open-slot IPMECH with 16 3 mm copper strips at 200 and 1400 rpm are 119.10% and 3.32%, respectively, while the ETGRs are 117.17% and 5.69%, respectively.
- At 200 rpm, the TPGRs of the closed-slot prototype with four, eight, twelve, and sixteen copper strips are 12.43%, 22.42%, 30.34%, and 35.24%, respectively, while the TPGRs of the open-slot prototype are 26.17%, 38.79%, 51.17%, and 61.09%, respectively. The experimental results verify the accuracy and reliability of the simulation results.
- End effects and temperature effects on the physical properties of the material are neglected during numerical simulations in this paper. In the future, magnetic–thermal coupling analysis will be performed on the heat generator to further optimize it.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMECH | Permanent magnet eddy current heater |
| IPMECH | Interior permanent magnet eddy current heater |
| MFD | Magnetic flux density |
| AMFD | Air gap magnetic flux density |
| TPGR | Thermal power growth rate |
| ETGR | Electromagnetic torque growth rate |
| Symbols | |
| The electric field (V/m) | |
| The magnetic flux density (MFD) (T) | |
| The magnetic field intensity (A/m) | |
| The current density (A/m2) | |
| The electric displacement (C/m2) | |
| The charge density (C/m3) | |
| The permittivity | |
| The permeability (H/m) | |
| The conductivity (S/m) | |
| The vacuum permittivity | |
| The vacuum permeability (H/m) | |
| The relative permeability | |
| The angular velocity of magnetic field variation (rad/s) | |
| The phase angle of the solution point (°) | |
| The rotational speed (rpm) | |
| The amplitude of external magnetic field strength (A/m) | |
| The thermal power of IPMECH | |
| The specific heat capacity of water (mm) | |
| The quality of water in the experiment (kg) | |
| The water temperature in the water tank at the end of the experiment (°C) | |
| The water temperature in the water tank at the beginning of the experiment (°C) | |
| The operating time of IPMECH (s) |
Appendix A
| Structural | rpm | Parameter | Measurement | Unit | Accuracy | Relative Uncertainty |
|---|---|---|---|---|---|---|
| solid | 200 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | |
| 30 | kg | ±1 g | ||||
| 7.9 | °C | 0.2% | ||||
| 400 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 10.2 | °C | 0.2% | ||||
| 600 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 16.4 | °C | 0.2% | ||||
| 800 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 22.9 | °C | 0.2% | ||||
| 1000 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 29.8 | °C | 0.2% | ||||
| 1200 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 36.7 | °C | 0.2% | ||||
| 1400 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 44.5 | °C | 0.2% |
| Structural | rpm | Parameter | Measurement | Unit | Accuracy | Relative Uncertainty |
|---|---|---|---|---|---|---|
| solid | 200 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | |
| 30 | kg | ±1 g | ||||
| 10.6 | °C | 0.2% | ||||
| 400 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 12.9 | °C | 0.2% | ||||
| 600 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 19.5 | °C | 0.2% | ||||
| 800 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 27.1 | °C | 0.2% | ||||
| 1000 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 32.3 | °C | 0.2% | ||||
| 1200 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 37.9 | °C | 0.2% | ||||
| 1400 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 43.0 | °C | 0.2% |
| Structural | rpm | Parameter | Measurement | Unit | Accuracy | Relative Uncertainty |
|---|---|---|---|---|---|---|
| solid | 200 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | |
| 30 | kg | ±1 g | ||||
| 12.4 | °C | 0.2% | ||||
| 400 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 13.5 | °C | 0.2% | ||||
| 600 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 19.6 | °C | 0.2% | ||||
| 800 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 27.0 | °C | 0.2% | ||||
| 1000 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 33.5 | °C | 0.2% | ||||
| 1200 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 39.3 | °C | 0.2% | ||||
| 1400 | 4.183 | kJ/kg/°C | 0.3% | 0.36% | ||
| 60 | kg | ±1 g | ||||
| 44.5 | °C | 0.2% |
References
- Zhou, G.; Bahn, G.; Lao, J.; Zhang, Y. COP28 Targets for Mobilizing Private Investment in Fossil Fuels Extraction Industry to Cope with the Climate Change. Resour. Policy 2024, 97, 105285. [Google Scholar] [CrossRef]
- Acen, C.; Bamisile, O.; Cai, D.; Ukwuoma, C.C.; Obiora, S.; Huang, Q.; Uzun Ozsahin, D.; Adun, H. The Complementary Role of Carbon Dioxide Removal: A Catalyst for Advancing the COP28 Pledges towards the 1.5 °C Paris Agreement Target. Sci. Total Environ. 2024, 947, 174302. [Google Scholar] [CrossRef] [PubMed]
- IEA. Energy System Buildings Overview. World Energy Outlook 2024-Event-IEA. Available online: https://www.iea.org/energy-system/buildings/ (accessed on 29 December 2024).
- He, Y.; Zhu, C.; Cao, C. A Wind Power Ramp Prediction Method Based on Value-at-Risk. Energy Convers. Manag. 2024, 315, 118767. [Google Scholar] [CrossRef]
- GWEC. Global Wind Report 2024; Global Wind Energy Council: Gewest, Belgium, 2024; p. 75. Available online: https://www.gwec.net/reports/globalwindreport (accessed on 7 December 2024).
- You, G.D.; Chang, Z.C.; Li, X.Y.; Liu, Z.F.; Xiao, Z.Y.; Lu, Y.R.; Zhao, S. Using Enhanced Variational Modal Decomposition and Dung Beetle Optimization Algorithm Optimization-Kernel Extreme Learning Machine Model to Forecast Short-Term Wind Power. Electr. Power Syst. Res. 2024, 236, 110904. [Google Scholar] [CrossRef]
- Li, J.; Meng, F.; Zhang, Z.; Zhang, Y. Prediction of Wind Power Ramp Events via a Self-Attention Based Deep Learning Approach. Energy Rep. 2024, 12, 1488–1502. [Google Scholar] [CrossRef]
- Miao, Q.; Wang, D.; Xia, Z.; Xu, C.; Zhan, J. Exploring Spatio-Temporal Dynamics for Enhanced Wind Turbine Condition Monitoring. Mech. Syst. Signal Process 2025, 223, 111841. [Google Scholar] [CrossRef]
- Fang, Y.; Fan, R.; Shao, Z.; Yue, Y.; Liu, Z. Research on the Cost Allocation Mechanism of Wind Power Heating in China from a Cost-Benefit Perspective. Energy Rep. 2024, 11, 4622–4630. [Google Scholar] [CrossRef]
- Wang, W.; Dong, Z. Economic Benefits Assessment of Urban Wind Power Central Heating Demonstration Project Considering the Quantification of Environmental Benefits: A Case from Northern China. Energy 2021, 225, 120246. [Google Scholar] [CrossRef]
- Mu, Y.; Li, H.; Yu, X.; Jia, H.; Wang, M.; Hou, K.; Wang, Z. A Scenario-Based Optimal Dispatch for Joint Operation of Wind Farms and Combined Heat and Power Plants Considering Energy Flexibilities in Heating Networks. Electr. Power Syst. Res. 2022, 204, 107683. [Google Scholar] [CrossRef]
- Lei, Z.; Wang, G.; Li, T.; Cheng, S.; Yang, J.; Cui, J. Strategy Analysis about the Active Curtailed Wind Accommodation of Heat Storage Electric Boiler Heating. Energy Rep. 2021, 7, 65–71. [Google Scholar] [CrossRef]
- Nourollahi, R.; Zare, K.; Mohammadi-Ivatloo, B.; Vahidinasab, V.; Moghadam, A.A. Continuous-Time Optimization of Integrated Networks of Electricity and District Heating under Wind Power Uncertainty. Appl. Therm. Eng. 2023, 225, 119926. [Google Scholar] [CrossRef]
- Cheng, W.L.; Han, B.C.; Nian, Y.L.; Han, B.B. Theoretical Analysis of a Wind Heating Conversion and Long Distance Transmission System. Energy Convers. Manag. 2017, 137, 21–33. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, S.; Cheng, H.; Liu, L.; Zhang, J.; Zhang, X. Reducing Wind Power Curtailment by Risk-Based Transmission Expansion Planning. Int. J. Electr. Power Energy Syst. 2021, 124, 106349. [Google Scholar] [CrossRef]
- Zheng, J.; Zhou, Z.; Zhao, J.; Wang, J. Effects of the Operation Regulation Modes of District Heating System on an Integrated Heat and Power Dispatch System for Wind Power Integration. Appl. Energy 2018, 230, 1126–1139. [Google Scholar] [CrossRef]
- Javed, M.H.; Duan, X. Experimental Study of Kinetic to Thermal Energy Conversion with Fluid Agitation for a Wind-Powered Heat Generator. Energies 2024, 17, 4246. [Google Scholar] [CrossRef]
- Liu, X.; Sun, X.; He, J.; Wang, D.; Qiu, X.; Bi, S.; Cao, Y. Study on the Influence of Working-Fluid’s Thermophysical Properties on the Stirring-Heating. Energies 2022, 15, 4835. [Google Scholar] [CrossRef]
- Serov, A.F.; Nazarov, A.D.; Mamonov, V.N.; Terekhov, V.I. Experimental Investigation of Energy Dissipation in the Multi-Cylinder Couette-Taylor System with Independently Rotating Cylinders. Appl. Energy 2019, 251, 113362. [Google Scholar] [CrossRef]
- Iyer, K.R.; Roozbahani, H.; Alizadeh, M.; Handroos, H. A Novel Approach for Direct Conversion of Wind Energy to Heat Utilizing a Hydraulic Medium for Domestic Heating Applications. Energy Rep. 2022, 8, 11139–11150. [Google Scholar] [CrossRef]
- Zdankus, T.; Cerneckiene, J.; Jonynas, R.; Stelmokaitis, G.; Fokaides, P.A. Experimental Investigation of a Wind to Thermal Energy Hydraulic System. Renew. Energy 2020, 159, 140–150. [Google Scholar] [CrossRef]
- Chen, L.; Pei, Y.; Chai, F.; Cheng, S. Investigation of a Novel Mechanical to Thermal Energy Converter Based on the Inverse Problem of Electric Machines. Energies 2016, 9, 518. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, Q.; Ding, Y.; Wang, L.; Yang, G. Optimization Design and Heat Performance Analysis of a Cylindrical Wind-Magnetic Eddy Current Heater. Int. J. Therm. Sci. 2025, 210, 109606. [Google Scholar] [CrossRef]
- Chen, Y.-C.B. Direct Wind-to-Heat Energy Systems Integrated with Storage for Electricity and Heat Generation. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2021. [Google Scholar]
- Hadadi, S.; Kang, S.; Park, G.; Lee, J.H. Analysis of the Eddy Current of Water Heating Device to Convert Wind Energy Directly into Heat: Case Study Maldo Island, South Korea. Appl. Energy 2024, 376, 124192. [Google Scholar] [CrossRef]
- Cao, K.K.; Nitto, A.N.; Sperber, E.; Thess, A. Expanding the Horizons of Power-to-Heat: Cost Assessment for New Space Heating Concepts with Wind Powered Thermal Energy Systems. Energy 2018, 164, 925–936. [Google Scholar] [CrossRef]
- Sobor, I.; Chicuic, A.; Ciuperca, R.; Rachier, V. Concerning the Conversion Efficiency Increase of the Available Wind Potential. Ann. Univ. Craiova Electr. Eng. Ser. 2011, 35, 122–127. [Google Scholar]
- Liu, X.H.; Chen, C.C.; Yu, H.D.; Wei, G.D.; Tian, Z. De The Study of the Heat Device in Wind-Magnetic Water Heater. Adv. Mat. Res. 2011, 201–203, 460–464. [Google Scholar] [CrossRef]
- Du, H.; Qu, Y.; Cheng, S. A Novel Dynamic Electromagnetic Heating-Magnetizing Device Used for Reverse Osmosis System. Adv. Mater. Res. 2012, 562–564, 913–916. [Google Scholar] [CrossRef]
- Du, H.; Qu, Y. Research on Loss and Temperature Rise of a Novel Dynamic Electromagnetic Induction Heater. Adv. Mater. Res. 2012, 468–471, 3108–3112. [Google Scholar] [CrossRef]
- Du, H.; Li, J.; Qu, Y. Mathematical Modeling of Eddy-Current Loss for a New Induction Heating Device. Math. Probl. Eng. 2014, 2014, 923745. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, L.; Hou, Y.; Zhao, W.; Lei, T. Fundamental Research on Flameless Electromagnetic Heater Based on the Reverse Problem of Temperature Rise and Loss in Electrical Machines. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar]
- Chu, J. Mathematic Model Based on Rotating Electromagnetic Theory Used in Building a Thermal Circuit Used in Food Heater. Carpathian J. Food Sci. Technol. 2016, 8, 106–113. [Google Scholar]
- Lu, H.; Zhang, L.; Hong, W. Thermal Power Calculation of Interior Permanent Magnet Eddy Current Heater Using Analytical Method. Processes 2024, 12, 1457. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Yang, Z.; Cai, Y.; Lei, G.; Zhu, J.; Lee, C.H.T. Design Optimization of a Spoke-Type Axial-Flux PM Machine for In-Wheel Drive Operation. IEEE Trans. Transp. Electrif. 2024, 10, 3770–3781. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Lei, G.; Tian, X.; Guo, Y.; Zhu, J. Multiobjective Optimization of a Five-Phase Bearingless Permanent Magnet Motor Considering Winding Area. IEEE/ASME Trans. Mechatron. 2022, 27, 2657–2666. [Google Scholar] [CrossRef]
- Sun, X.; Xu, N.; Yao, M. Sequential Subspace Optimization Design of a Dual Three-Phase Permanent Magnet Synchronous Hub Motor Based on NSGA III. IEEE Trans. Transp. Electrif. 2023, 9, 622–630. [Google Scholar] [CrossRef]
- Tudorache, T.; Popescu, M. FEM Optimal Design of Wind Energy-Based Heater. Acta Polytech. Hung. 2009, 6, 55–70. [Google Scholar]
- Fireeanu, V.; Nebi, O. Finite element electromagnetic 2d model of an eddy current heater with rotating permanent magnets. Ann. Univ. Craiova Electr. Eng. Ser. 2008, 32, 62–67. [Google Scholar]
- Yuan, J.; Liu, N.; Zhang, W.; Peng, B.; Dong, W. Study on the Effect of Changing Stator Structure on Wind Permanent Magnet Eddy Current Heating Device. Energy Rep. 2022, 8, 592–600. [Google Scholar] [CrossRef]
- Dirba, I.; Kleperis, J. Practical Application of Eddy Currents Generated by Wind. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2011; Volume 23. [Google Scholar]
- Lu, H.; Zhou, C.; Hong, W.; Ding, H. Research on the Mechanism of Thermal Power Enhancement in an Interior Permanent Magnet Eddy Current Heater Driven by Wind. Processes 2024, 12, 2390. [Google Scholar] [CrossRef]
- Khanjari, A.; Kang, S.; Lee, D.; Jung, D.Y.; Lee, J.H. Studying Four Different Permanent Magnet Eddy Currents Heaters with Different Magnet Areas and Numbers to Produce Heat Directly from a Vertical Axis Wind Turbine. Energies 2022, 15, 275. [Google Scholar] [CrossRef]
- Khanjari, A.; Kang, S.; Lee, S.I.; Lee, J.H.; Kim, Y.S. Direct Heat Energy Harvesting from Wind by a Permanent Magnet Eddy Currents Heater with Different Magnet Arrangements. Energy Sci. Eng. 2023, 11, 929–951. [Google Scholar] [CrossRef]
- Sobor, I.; Rachier, V.; Chicuic, A.; Ciuperca, R. Small Wind Energy System with Permanent Magnet Eddy Current Heater. Bull. Polytech. Inst. Jassy Elechtrotech. Energetics Electron. Sect. 2013, 13, 143–150. [Google Scholar]
- Tudorache, T.; Melcescu, L.; Bostan, V.; Colț, G.; Popescu, M.; Predescu, M. Electromagnetic analysis of a hybrid permanent magnet generator. Rev. Roum. des Sci. Tech. Ser. Electrotech. Energ. 2018, 63, 33–37. [Google Scholar]
- Tudorache, T.; Melcescu, L.; Predescu, M. Analysis of a Permanent Magnet Eddy Current Heater Driven by a Wind Turbine. Adv. Electr. Comput. Eng. 2015, 15, 53–58. [Google Scholar] [CrossRef]
- Tudorache, T.; Melcescu, L. Outer Rotor Eddy Current Heater for Wind Turbines. Renew. Energy Environ. Sustain. 2016, 1, 25. [Google Scholar] [CrossRef][Green Version]
- Song Zhihao, Y.W.W. Modeling of Interior PMSM Based on Normal Canonical Form Under Low Carrier Ratio. Proc. CSEE 2023, 43, 4779–4788. [Google Scholar]
- Liu, F.; Wang, X.; Xing, Z.; Yu, A.; Li, C. Reduction of Cogging Torque and Electromagnetic Vibration Based on Different Combination of Pole Arc Coefficient for Interior Permanent Magnet Synchronous Machine. CES Trans. Electr. Mach. Syst. 2021, 5, 291–300. [Google Scholar] [CrossRef]
- Karakoc, K.; Park, E.J.; Suleman, A. Improved Braking Torque Generation Capacity of an Eddy Current Brake with Time Varying Magnetic Fields: A Numerical Study. Finite Elem. Anal. Des. 2012, 59, 66–75. [Google Scholar] [CrossRef]
- Gu, G.; Chen, F.; Ma, T.; Xu, F.; Yang, D. Electromagnetic and Mechanical Properties of Soft Magnetic Cement Composite for Airport Runway Induction Heating: Experimental and Simulation Analyses. J. Clean. Prod. 2022, 332, 130141. [Google Scholar] [CrossRef]
- Li, F.; Li, X.; Wang, T.; Rong, Y.; Liang, S.Y. In-Process Residual Stresses Regulation during Grinding through Induction Heating with Magnetic Flux Concentrator. Int. J. Mech. Sci. 2020, 172, 105393. [Google Scholar] [CrossRef]
- Lu, H.; Zhou, C.; Hong, W.; Ding, H. Thermal Power and the Structural Parameters of a Wind Turbine Permanent Magnet Eddy Current Heater. Processes 2024, 12, 2398. [Google Scholar] [CrossRef]
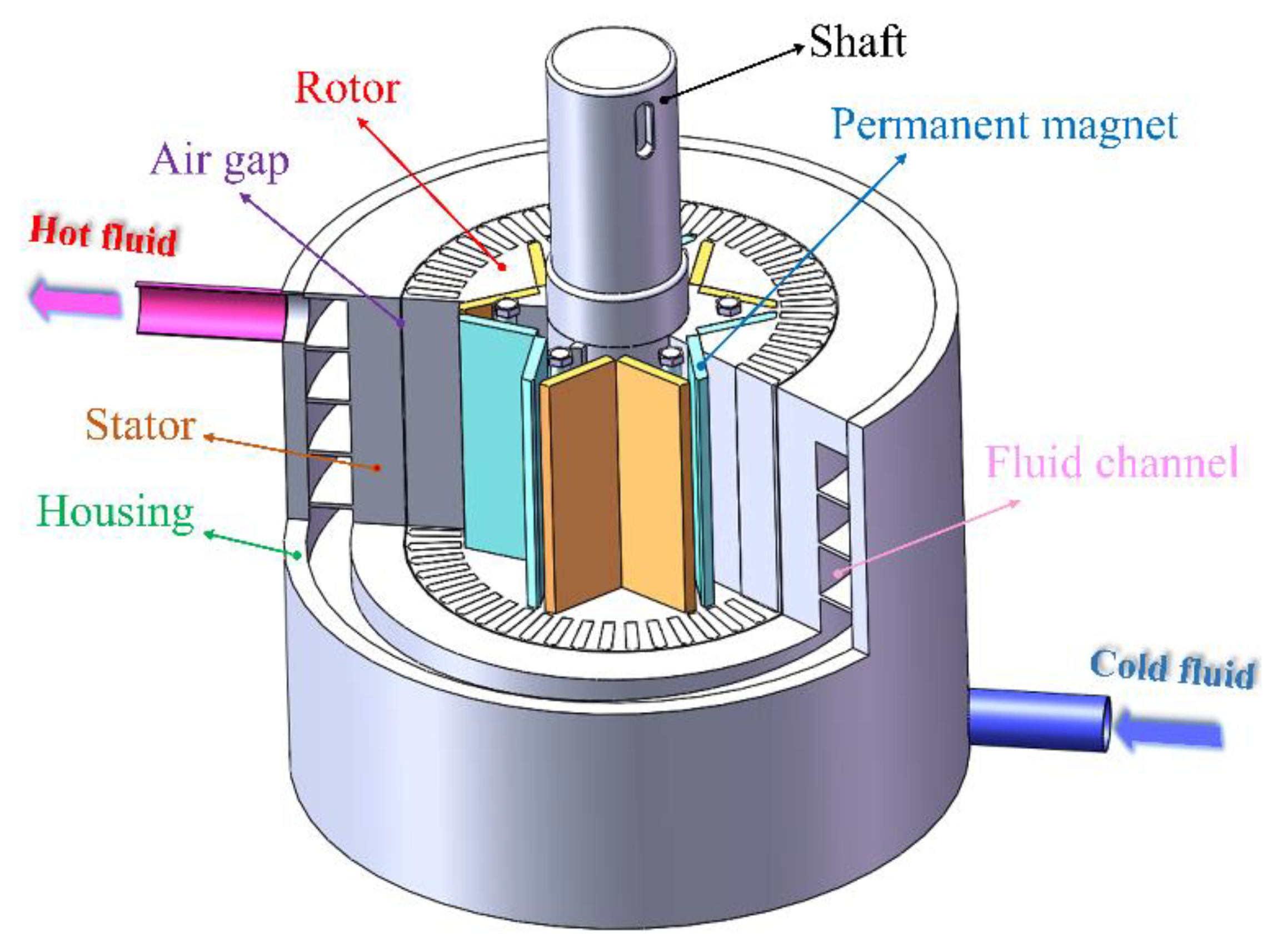
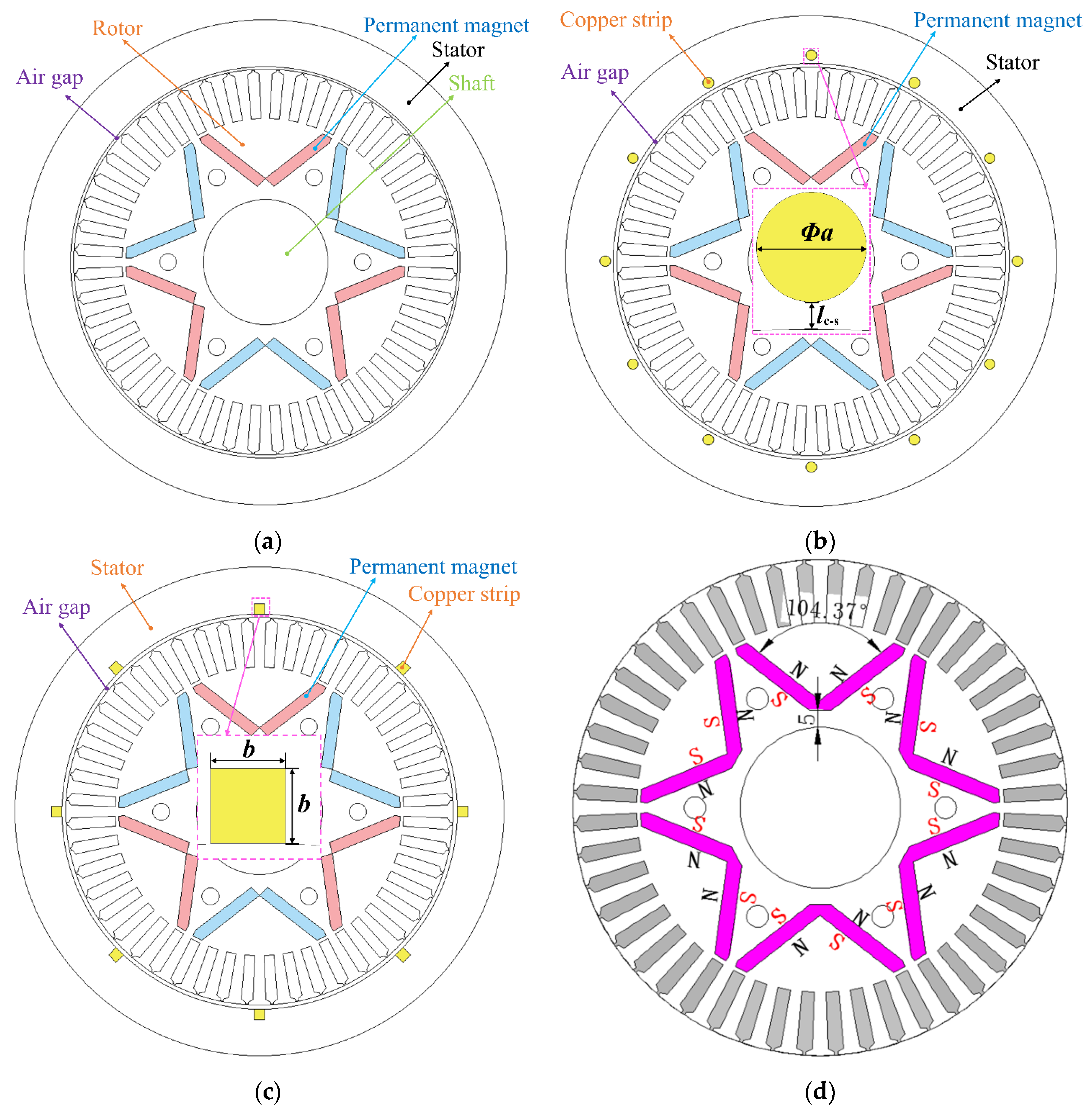







| Parameters | Steel-1010 | Aluminum | Copper | Parameters | NdFe35 |
|---|---|---|---|---|---|
| Density (kg/m3) | 7872 | 2689 | 8933 | Density (kg/m3) | 7400 |
| Relative permeability | B-H curve | 1.000021 | 0.999983 | Coercive force (A/m) | 890,000 |
| Conductivity (S/m) | 2 × 106 | 3.33 × 107 | 5.55 × 107 | Remanence (T) | 1.2884956 |
| Structural Parameters | Dimensions |
|---|---|
| Rotor outer diameter (mm) | 148 |
| Stator inner diameter (mm) | 149 |
| Length of air gap (mm) | 0.5 |
| Stator outer diameter (mm) | 185 |
| Thickness of permanent magnets (mm) | 4 |
| Width of permanent magnets (mm) | 27.7 |
| Number of pole pairs | 6 |
| Axial length of IPMECH (mm) | 175 |
| Structural Parameters | Solid | Closed-Slot | Open-Slot |
|---|---|---|---|
| Rotor outer diameter (mm) | 148 | 148 | 148 |
| Stator inner diameter (mm) | 149 | 149 | 149 |
| Stator outer diameter (mm) | 185 | 185 | 185 |
| Thickness of permanent magnets (mm) | 4 | 4 | 4 |
| Width of permanent magnets (mm) | 27.7 | 27.7 | 27.7 |
| The thickness of the air gap (mm) | 0.5 | 0.5 | 0.5 |
| Conductor strips size (mm) | — | Φ = 3 | b = 3 |
| Number of poles | 6 | 6 | 6 |
| Axial length of stator and rotor (mm) | 175 | 175 | 175 |
| Equipment | Measure Range | Characteristics/Accuracy |
|---|---|---|
| Electronic balance | 0–100 kg | ±1 g |
| Temperature transmitter | 0–100 °C | 0.2% |
| Flowmeter | 0.15–1.5 m3/h | 0.2% |
| Data acquisition unit | — | Data collection and storage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Hong, W. Research on the Mechanism of Thermal Power of an Interior Permanent Magnet Eddy Current Heater Driven by Wind. Energies 2025, 18, 932. https://doi.org/10.3390/en18040932
Lu H, Hong W. Research on the Mechanism of Thermal Power of an Interior Permanent Magnet Eddy Current Heater Driven by Wind. Energies. 2025; 18(4):932. https://doi.org/10.3390/en18040932
Chicago/Turabian StyleLu, Honglei, and Wenpeng Hong. 2025. "Research on the Mechanism of Thermal Power of an Interior Permanent Magnet Eddy Current Heater Driven by Wind" Energies 18, no. 4: 932. https://doi.org/10.3390/en18040932
APA StyleLu, H., & Hong, W. (2025). Research on the Mechanism of Thermal Power of an Interior Permanent Magnet Eddy Current Heater Driven by Wind. Energies, 18(4), 932. https://doi.org/10.3390/en18040932





