Influence of Chemical Kinetics on Tulip Flame Formation in Highly Reactive (H₂/Air) and Low Reactive (CH₄/Air) Mixtures

Abstract

The early stages of hydrogen–air and methane–air flame dynamics and the development and evolution of tulip flames in closed tubes of various aspect ratios and in a semi-open tube are studied by solving the fully compressible reactive Navier–Stokes equations using a high-order numerical method coupled to detailed chemical models for stoichiometric hydrogen/air and methane/air mixtures. The use of adaptive mesh refinement (AMR) provides adequate resolution of the flame reaction zone, pressure waves, and flame–pressure wave interactions. The purpose of this study is to gain a deeper insight into the influence of chemical kinetics on the combustion regimes leading to the formation of a tulip flame and its subsequent evolution. The simulations highlight the effect of the flame thickness, flame velocity, and reaction order on the intensity of the rarefaction wave generated by the flame during the deceleration phase, which is the principal physical mechanism of tulip flame formation. The obtained results explain most of the experimentally observed features of tulip flame formation, e.g., faster tulip flame formation with a deeper tulip shape for faster flames compared to slower flames.

1. Introduction

The burning of fossil fuels is believed to significantly increase the amount of carbon dioxide in the atmosphere, leading to climate change and global warming. A natural way to reduce carbon dioxide emissions and avoid these problems is the production of clean energy through the use of hydrogen. However, hydrogen leaks easily and is highly flammable, which complicates its use because of its explosive nature [1]. A possible solution to this problem, which has been the subject of intensive experimental and numerical studies in recent years, is the use of carbon or ammonia fuels mixed with hydrogen [2,3,4,5]. An effective way to improve combustion in the power industry is to inject hydrogen into natural gas. Carbon emissions can be reduced and energy efficiency increased by blending hydrogen with natural gas. The addition of hydrogen can improve the combustion of hydrocarbon fuel due to its low ignition energy, high reactivity, and fast combustion rate, making hydrogen-enriched natural gas a promising alternative fuel. The ignition delay time, which is important for industrial applications, such as direct injection engines [6] or diesel engines [7], can be significantly reduced depending on the percentage of hydrogen added to methane or ammonia. For this reason, extensive experimental and numerical studies on the combustion of premixed methane, hydrogen, and air mixtures in closed or half-open tubes are currently being carried out, with the aim of better understanding the different combustion modes and efficiency levels, cf. for example [5,6,7,8]. Using a two-dimensional laminar combustion model and simplified reaction mechanisms derived from the one-step methane/air reaction model, the effect of laminar flame velocity on flame dynamics was investigated by Deng et al. [9]. The effect of the reaction order on flame propagation has been studied by Qi et al. [10] using numerical models with three single-step reaction mechanisms.

Flame propagation in tubes is important for industrial and technological applications, as well as for the understanding of combustion processes in confined spaces, such as explosions and safety issues. It offers an essential physicochemical platform to analyze more complex engineering and process problems and to develop appropriate analytical methods and numerical models. Therefore, an understanding of the structure and acceleration of premixed flames in tubes is of primary interest to the combustion community.

It is well known that when a flame is ignited near the closed end of a tube and propagates to the opposite closed or open end, it suddenly slows down and the shape of the flame front rapidly changes from a convex shape with the tip pointing forward to a concave shape with the tip pointing backward. This phenomenon has been first investigated and photographed by Ellis [11] and later named “Tulip Flame” (TF). Subsequent experimental studies have shown that tulip flame formation is remarkably robust across combustible highly or slowly reactive mixtures and downstream conditions, such as open or closed tube ends and tube shapes, tube wall roughness, and obstructed tubes [12,13]. In the numerical study [14], it has been shown that the formation of the tulip flame is similar for the adiabatic and the isothermal wall boundary conditions. The geometry of the ignition source has also been shown [15,16] not to be critical for flame dynamics and tulip flame formation. The transition to a tulip flame always occurs in tubes with a sufficiently large aspect ratio L/D > 4 for laminar and turbulent flames. Only with a relatively strong breaking of the initial symmetry, e.g., with sufficiently strong perturbations of the initial flame front, the formation of a tulip flame does not take place. Thus, the formation of a tulip flame can be regarded as one of the most fundamental phenomena in the physics of combustion.

A flame front reversal may occur due to a number of different processes, such as a flame collision with a shock or pressure wave or due to different instabilities inherent to the propagating flame, such as the Darrieus–Landau (DL), Thermal-diffusion (TD), or Rayleigh–Taylor (RT) instabilities. This makes the concept of tulip flame formation somewhat ambiguous, which has led to a variety of different scenarios being investigated to explain the physical mechanism of tulip flame formation. Flame collision with a shock wave [17], flame front instabilities, such as DL instability [18], and RT instability [19,20] have been considered as possible mechanisms of tulip flame formation. Flame–vortex interactions have been considered by many researchers [21,22,23,24,25] as an apparently plausible scenario for flame front inversion and tulip flame formation, although no evidence has been provided that this is actually the case. For references to numerous studies on the physical mechanisms associated with tulip flame formation, the reader is referred to the reviews [12,13]. Until recently, however, the physical mechanism of tulip flame formation remained one of the fundamental unsolved problems in combustion science, as numerous theoretical, computational, and experimental studies have failed to provide a convincing and experimentally consistent explanation.

The tulip flame considered in this study is the rapid inversion of the flame front from the convex to the concave shape with the flame tip pointing toward the burned combustion products, which occurs during the deceleration phase associated with the reduction of the flame surface area when the lateral parts of the finger-shaped flame contact the tube sidewalls. Recent work by Liberman et al. [26] has demonstrated for the first time that the rarefaction waveform generated by the flame during the deceleration phase is the key process for tulip flame formation. This mechanism of the tulip flame formation explains various phenomena observed in experimental studies and numerical simulations, such as reverse flow, adverse pressure gradient, etc. This also implies that tulip flame formation is a purely hydrodynamic phenomenon, since it occurs much faster than the time required for flame front instabilities to develop, which is consistent with the experimental study of tulip flame formation by Ponizy et al. [27].

Recent experimental and numerical studies [6,7,8,28,29,30] have revived interest in the physical mechanism of tulip flame formation with various methane/hydrogen/air mixtures. The purpose of the present work is to gain a deeper insight into the influence of chemical kinetics on the combustion regimes leading to the formation of a tulip flame and its subsequent evolution for a flame in the highly reactive H₂/air mixture compared to a flame in the slowly reactive CH₄/air mixture. To do this, we compare and contrast unsteady, fully compressible high-accuracy solutions of the Navier–Stokes equations coupled with the multistep detailed chemical models for hydrogen–air flames with the solutions for methane–air flames. Based on these two limiting cases, pure H₂/air flame and pure CH₄/air flame, it is easy to understand the hydrogen/methane/air flame dynamics for different percentages of the hydrogen admixture.

We show that the faster hydrogen–air flames generate stronger pressure waves during the finger flame acceleration phase compared to a slower methane–air flame. We also show that the magnitude of the deceleration of hydrogen–air flames during the phase when the flame skirt touches the sidewalls of the tube is significantly greater than the deceleration of a slower methane–air flame. Thus, the intensity of the rarefaction wave produced by the decelerating hydrogen–air flame is significantly greater than the intensity of the rarefaction wave produced by the methane–air flame. This results in a faster and deeper tulip flame formation by a hydrogen–air flame as compared to a methane–air flame.

The paper is organized as follows. In Section 2, the details of the numerical simulation, chemical models, and boundary conditions are presented. In Section 3.1, Section 3.2 and Section 3.3 we present the results from a series of two-dimensional simulations of H₂/air and CH₄/air flame propagation in closed tubes of various aspect ratios and in a half-open tube. The results of these simulations are analyzed and compared with experimental studies of H₂/air and CH₄/air flame propagation in closed and half-open tubes. In Section 4, “Summary and Discussion”, we show that instabilities inherent to the propagating flame, such as Darrieus–Landau, Thermal-diffusion, and Rayleigh–Taylor (RT) instabilities, do not play a role in tulip flame formation.

2. Numerical Models

2.1. Two-Dimensional DNS

In our previous studies [16,26], we have shown that the flame dynamics obtained from 2D modeling are qualitatively very similar to those observed in experimental studies. However, it should be emphasized that 3D flames accelerate and decelerate much faster than 2D flames. Two-dimensional modeling provides a good qualitative but not a quantitative, agreement with the experimental data.

In the present work, the two-dimensional computational domains are modeled using high-resolution DNS of the fully compressible reactive Navier–Stokes equations coupled to detailed multistep chemical models for the combustion of stoichiometric hydrogen/air and methane/air mixtures. A detailed chemical kinetic model for a stoichiometric hydrogen/air mixture consisting of 21 reactions and 9 species developed by Li et al. [31] was implemented and used in the simulations. The multistep detailed chemistry for stoichiometric methane/air is the reduced detailed mechanism 15S-26R in [32], which consists of 15 species and 26 reversible reaction steps. This reduced mechanism has been calibrated using a freely propagating laminar flame with an adiabatic boundary. The laminar flame velocities, mass fractions of target species, and heat release obtained via the 15S-26R mechanism agree well with those obtained using the more complex detailed chemical model DRM-19 [33] and GRI 1.2 [34]. In our previous paper [35], we have shown that the results obtained by using DRM-19 are very close to those using GRI 3.0 [36] and experimental data, such that the reduced mechanism 15S-26R is considered the smallest chemical model that can produce the correct important properties of the flame, such as laminar flame velocities, the mass fraction of species, etc., and it is employed in the simulations of CH₄/air in this paper.

The considered 2D computational domains are rectangular channels of width $D=1 \mathrm{cm}$ with both ends closed and aspect ratios of $L/D=6,12$ and a rectangular channel of width $D=1 \mathrm{cm}$ with an open right end. Formally, a semi-open channel can be thought of as a channel with an infinitely large aspect ratio. From a physical point of view, the main characteristic of a semi-open channel is the absence of reflected pressure waves. In Section 3.3, we will show that without reflected pressure waves, flame shape evolution and tulip flame formation in a semi-open channel take longer and proceeds more smoothly than in a channel with closed ends.

The numerical simulations solve the 2D time-dependent, reactive compressible Navier–Stokes equations, including the molecular diffusion, thermal conduction, viscosity, and detailed chemical kinetics. The governing equations are

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial (\rho u_i)}{\partial x_i}}=0$$

(1)

$${\displaystyle \frac{\partial (\rho u_i)}{\partial t}}+{\displaystyle \frac{\partial (P{\delta }_{ij}+{\rho u_i}^2)}{\partial x_j}}={\displaystyle \frac{\partial {\sigma }_{ij}}{\partial x_j}}$$

(2)

$${\displaystyle \frac{\partial (\rho E)}{\partial t}}+{\displaystyle \frac{\partial \left[(\rho E+P)u_i\right]}{\partial x_i}}={\displaystyle \frac{\partial ({\sigma }_{ij}{u}_i)}{\partial x_i}}-{\displaystyle \frac{\partial q_i}{\partial x_i}}$$

(3)

$${\displaystyle \frac{\partial \rho Y_k}{\partial t}}+{\displaystyle \frac{\partial \rho u_i{Y}_k}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_i}}\left(\rho V_{ik}{Y}_k\right)+{\dot{\omega }}_k$$

(4)

$$P=\rho R_{B}T\left({\displaystyle {\sum }_{i=1}^{N_s}\frac{Y_i}{W_i}}\right)$$

(5)

$${\sigma }_{ij}={\displaystyle \frac{4}{3}}\mu \left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)-{\displaystyle \frac{2}{3}}\mu {\displaystyle \frac{\partial u_i}{\partial x_i}}{\delta }_{ij}$$

(6)

$$q_i=-\kappa {\displaystyle \frac{\partial T}{\partial x_i}}$$

(7)

The quantities $\rho$, $u_i$, $T$, $P$, $E$, ${\sigma }_{ij}$, and $q_i$ are density, velocity components, temperature, pressure, specific total energy, viscosity stress tensor, and the heat fluxes. $R_B$ is the universal gas constant; $Y_i,W_i,V_{i,j}$ are the mass fraction, molar mass, and diffusion velocity of species $i$. The viscosity, thermal conduction and diffusion coefficients of the mixture are calculated using the method presented in [37]. The reaction rate of species $k$ is determined as

$${\dot{\omega }}_k=W_k{\displaystyle \sum _{j=1}^{N_r}({v^{″}}_{js}-{v^{\prime }}_{js})}\cdot \left(k_{f,j}{\displaystyle \prod _{s=1}^{N_s}{\left(\frac{\rho Y_s}{W_s}\right)}^{{v^{\prime }}_{js}}}-k_{b,j}{\displaystyle \prod _{s=1}^{N_s}{\left(\frac{\rho Y_s}{W_s}\right)}^{{v^{″}}_{js}}}\right)$$

(8)

where ${v^{\prime }}_{js}$ and ${v^{″}}_{js}$ are stoichiometric coefficients of species $s$ of the reactant and product sides of reaction $j$. $k_{f,j}$ and $k_{b,j}$ are the forward and backward reaction rates of reaction $j$, which are calculated using the Arrhenius equation.

The governing equations are solved using open-source code AMReX-Combustion PeleC [38], which is a load-balanced Adaptive Mesh Refinement (AMR) compressible reacting flow solver. The convection terms are discretized by the classical 5th order WENO-JS scheme of Jiang and Shu [39]. The 2nd order centered difference method is used to calculate the diffusion terms. The time integral method is based on a spectral deferred correction approach [40]. The integrator of chemical source terms is the explicit Runge–Kutta methods in the ARKODE packages of SUNDIALS [41].

An adaptive mesh refinement (AMR) method was used to reduce the computational time required for the numerical simulations with detailed chemistry for H₂/air and CH₄/air flames. The criterion for grid adaptation was a mass fraction of HO₂ in the computational domain. The AMR method in PeleC is based on the AMReX framework [42], which supports massively parallel, block-structured adaptive mesh refinement. A more detailed discussion of grid resolution and convergence is presented in Appendix A. The non-reflecting outflow boundary condition [43] was used to calculate the subsonic outflow.

The reliable modeling of reactive flows requires adequate resolution of the internal structure of the flame. Since the thickness of a laminar flame decreases with increasing pressure, higher resolution is required to determine the flame structure at an elevated pressure. For a hydrogen/air flame, the reaction order is $n=2$, which means that the hydrogen/air flame velocity does not depend on pressure since $U_f\propto P^{{\displaystyle \frac{n}{2}}-1}$ [44]. The method used to calculate the reaction order is described in Appendix B. For the flame thickness we obtain

$$L_f\approx \nu /U_f\propto P^{-n/2}$$

(9)

where $\nu$ is kinematic viscosity. Therefore, the flame thickness decreases with pressure as $L_f\propto 1/P$. The reaction order of methane/air flame is $n\approx 1.1$. In the same way for the methane/air flame, we obtain $U_f\propto 1/P^{1/2}$, $L_f\propto 1/P^{0.55}$. The maximum pressure during tulip flame formation in a channel with closed ends and aspect ratio $\alpha =6$ is about 2 atm for a hydrogen/air flame, resulting in a reduction in the flame front thickness from $L_f=350 \mathsf{\mu }\mathrm{m}$ to $L_f\simeq 100 \mathsf{\mu }\mathrm{m}$.

The uniform coarse grid resolution of 40 μm was used. With each refinement, the grid size is halved, allowing for a maximum of two refinements. As a result, the grid resolution near the flame front reaches 10 μm corresponding to 10 grid points per flame front, which is sufficient to predict the correct laminar flame structure and the flame velocity. Thorough resolution and convergence (grid independence) tests have been performed in our previous publications [16,26] by varying the value of the computational grid size $\mathsf{\Delta }x$ to ensure that the resolution is sufficient to capture details of the problem in question and to avoid computational artifacts. The reader is referred to [16,26] for details of the convergence and resolution tests.

2.2. Boundary and Initial Conditions: Modeling Parameters

The flame is ignited by a small (3 mm) semi-circular pocket of burned gas at an adiabatic flame temperature, ${\mathrm{T}}_{\mathrm{b}}=2350 \mathrm{K}$ for H₂/air and ${\mathrm{T}}_{\mathrm{b}}=2231 \mathrm{K}$ for CH₄/air, near the left closed end. The initial conditions are $P_0=1 \mathrm{atm}$, $T_0=298 \mathrm{K}$. The center of the ignition spot is on the mid-plane of the channel near the left closed end.

The adiabatic, no-slip reflective boundary conditions at the channel walls are

$$u_x=0,\partial T/\partial \overrightarrow{n}=\partial Y_k/\partial \overrightarrow{n}=0$$

(10)

where $\overrightarrow{n}$ is the normal to the wall. The $x$ coordinate is taken along the channel walls, $y=0$ is the mid-plane coordinate, and the sidewalls are at $y=\pm D/2$.

During tulip flame formation, symmetry boundary conditions can be applied at the mid-plane, $y=0$, between the plane sidewalls

$${\left.{\displaystyle \frac{\partial \overrightarrow{u}}{\partial y}}\right|}_{y=0}=0,{\left.{\displaystyle \frac{\partial T}{\partial y}}\right|}_{y=0}=0,{\left.{\displaystyle \frac{\partial Y_k}{\partial y}}\right|}_{y=0}=0$$

(11)

The symmetric formulation of the problem is justified by the fact that the formation of a tulip flame symmetrical with respect to the axis of the tube has been observed in many experimental studies, see, e.g., [6,8,24]. Depending on the experimental conditions, the gravitational buoyancy effect can cause an asymmetric shape of the tulip flame. However, the characteristic time for the buoyancy is usually larger than the time of a tulip flame formation even for methane/air flames.

The model parameters used in the simulations are shown in

Table 1. Model parameters for simulating a stoichiometric hydrogen–air flame.

Initial pressure	$P_0$	1.0 atm
Initial temperature	$T_0$	298 K
Initial density	${\mathsf{\rho }}_0$	$8.5\times {10}^{-4} {\mathrm{g}/\mathrm{cm}}^3$
Laminar flame velocity	$U_f$	2.43 m/s
Laminar flame thickness	$L_f$	0.0325 cm
Adiabatic flame temperature	$T_b$	2503 K
Expansion coefficient (${\mathsf{\rho }}_u/{\mathsf{\rho }}_b$)	$\mathrm{\Theta }$	8.34
Specific heat ratio	$\mathsf{\gamma }=C_P/C_V$	1.399
Sound speed	${\mathrm{a}}_{\mathrm{s}}$	$408.77 \mathrm{m}/\mathrm{s}$

for a hydrogen/air mixture and in

Table 2. Model parameters for simulating a stoichiometric methane–air flame.

Initial pressure	$P_0$	1.0 atm
Initial temperature	$T_0$	298 K
Initial density	${\mathsf{\rho }}_0$	1.1 × 10−3 g/cm3
Laminar flame velocity	$U_f$	0.3803 m/s
Laminar flame thickness	$L_f$	451 μm
Adiabatic flame temperature	$T_b$	2231 K
Expansion coefficient (${\mathsf{\rho }}_u/{\mathsf{\rho }}_b$)	$\mathrm{\Theta }$	7.2
Specific heat ratio	$\mathsf{\gamma }=C_P/C_V$	1.38
Sound speed	${\mathrm{a}}_{\mathrm{s}}$	332 m/s

for a methane/air mixture.

3. Results and Discussions

In Section 3.1, Section 3.2 and Section 3.3, we use 2D simulations to compare the flame dynamics leading to the flame front inversion and tulip flame formation in a highly reactive H₂/air mixture and a slowly reactive CH₄/air mixture in channels of different aspect ratios and in a semi-open channel. In a previous study [26], the primary physical process leading to flame front inversion and tulip flame formation was shown to be the rarefaction wave generated by the flame during the flame deceleration phase. It is useful to recall the underlying physics of flame front inversion, which is surprisingly simple considering a theoretical thin-flame model [44,45] where the flame is considered a discontinuous surface separating unburned and burned gases. During the acceleration phase, the flame acts as a semi-transparent accelerating piston, generating pressure waves for which the amplitude increases with the acceleration of the flame (piston). The first rarefaction wave is generated by the flame as the flame skirt touches the sidewalls of the tube, resulting in a reduction in the flame surface area and a subsequent reduction in the flame velocity. In the reference frame of the unburned flow, the decelerating flame is similar to the piston that begins to move with acceleration out of the tube (to the left). It is well known [46] that such a piston generates a simple rarefaction wave, for which the “head” propagates forward (to the right) with the sound speed, creating a reverse flow of the unburned gas between the piston and the head of the rarefaction wave. The velocity of the reverse flow of unburned gas is maximum (equal to the piston velocity) in the vicinity of the piston surface and tends to be zero towards the head of the rarefaction wave. It is important to recall that in the classical problem of a rarefaction wave initiated by a flat piston (one-dimensional problem) [46], the reverse flow velocity is uniform. On the contrary, the reverse flow velocity generated by a convex piston is not uniform: close to the piston surface (the flame front), the axial velocity of the reverse flow is maximum at the tube axis and decreases towards the side walls. The resulting flow in the unburned gas is a superposition of the unburned gas flow created by the flame during the acceleration phases and the reverse flow created by the rarefaction wave. It is obvious that in the immediate vicinity of the flame front, the unburned gas flow acquires a mirror tulip-shaped profile of axial velocity. In the thin flame model, the velocity of each point on the flame front is equal to the sum of the laminar flame velocity at which the small portion of the flame is propagating relative to the unburned gas and the velocity of the unburned gas immediately ahead of that portion of the flame front at which the unburned gas is entraining that portion of the flame front. This means that the mirror tulip velocity profile formed in the unburned gas in the immediate vicinity ahead of the flame front will lead to the inversion of the flame front and the formation of a tulip flame. In closed tubes, the collision of a flame with a pressure wave reflected from the opposite end of the tube will also cause the flame to decelerate, thereby increasing the effect of the first rarefaction wave or leading to a distorted tulip flame if the deceleration caused by the flame collisions with pressure waves is sufficient for the RT instability to develop.

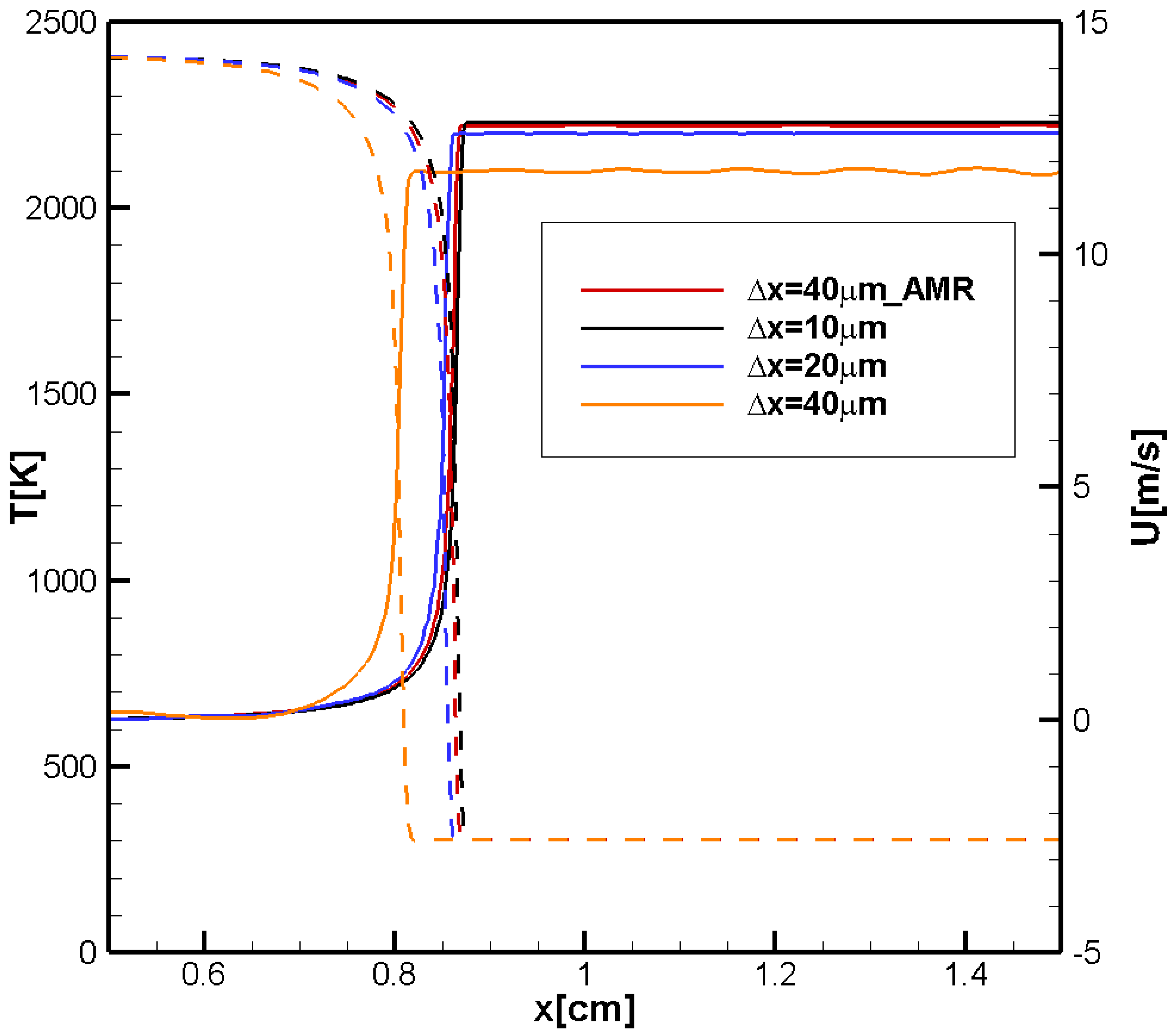
3.1. 2D Channel with Both Ends Closed and Aspect Ratio $\alpha =L/D=6$

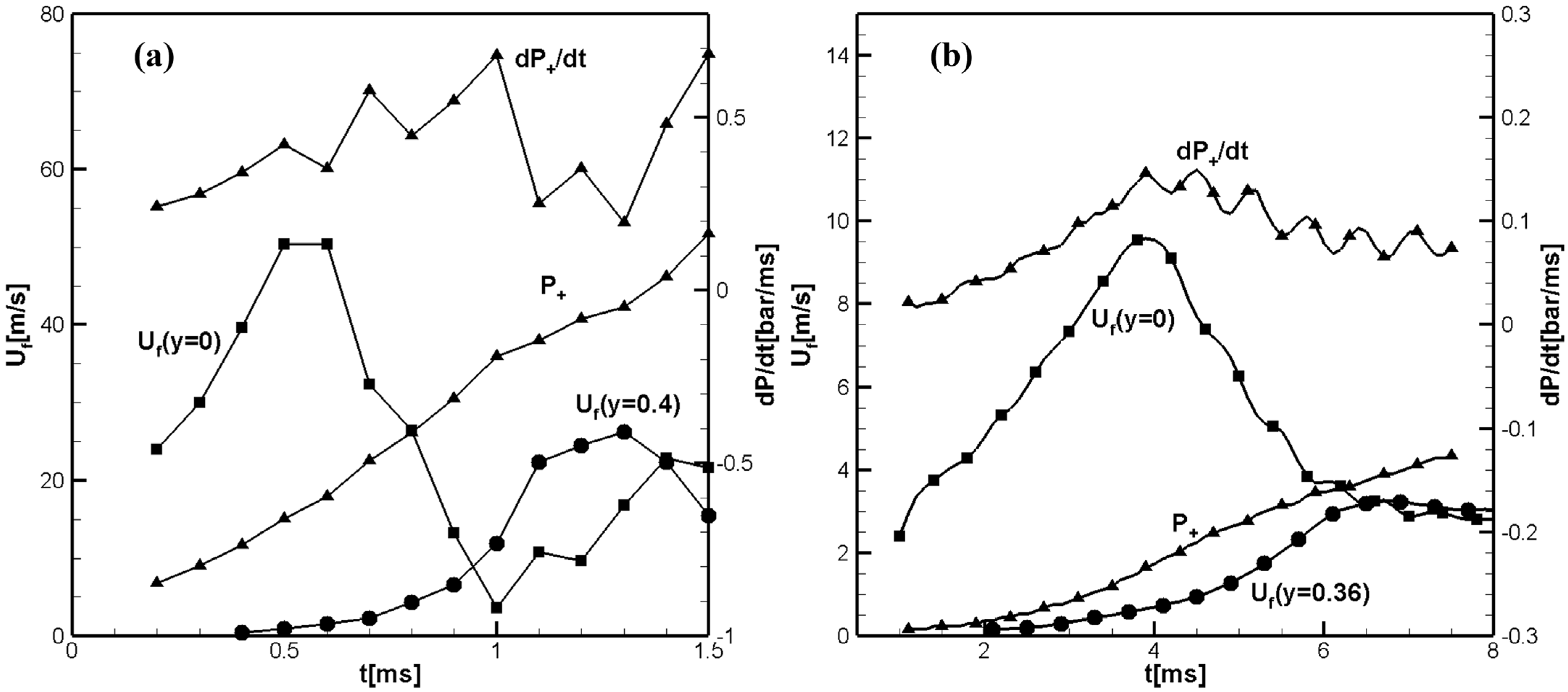
In this section, we will compare the results of modeling the dynamics of a hydrogen/air flame with the dynamics of a methane/air flame in a 2D channel with both ends closed and an aspect ratio $\alpha =6$. Figure 1a shows the time evolution of the flame front velocities along the channel axis, $U_f(y=0)$ and the flame velocity close to the sidewall, $U_f(y=0.4 \mathrm{cm})$ calculated for the hydrogen/air flame. Figure 1b shows the calculated time evolution of the flame front velocities along the tube axis, $U_f(y=0)$, and near the side wall, $U_f(y=0.38 \mathrm{cm})$, calculated for the methane/air flame. Both figures also show the pressure increase $P_{+}$ and the pressure growth rate $d{P}_{+}/dt$ at the centerline just ahead of the flame front. The pressure growth rate shows the location of the reflected pressure waves immediately before their collisions with the flame.

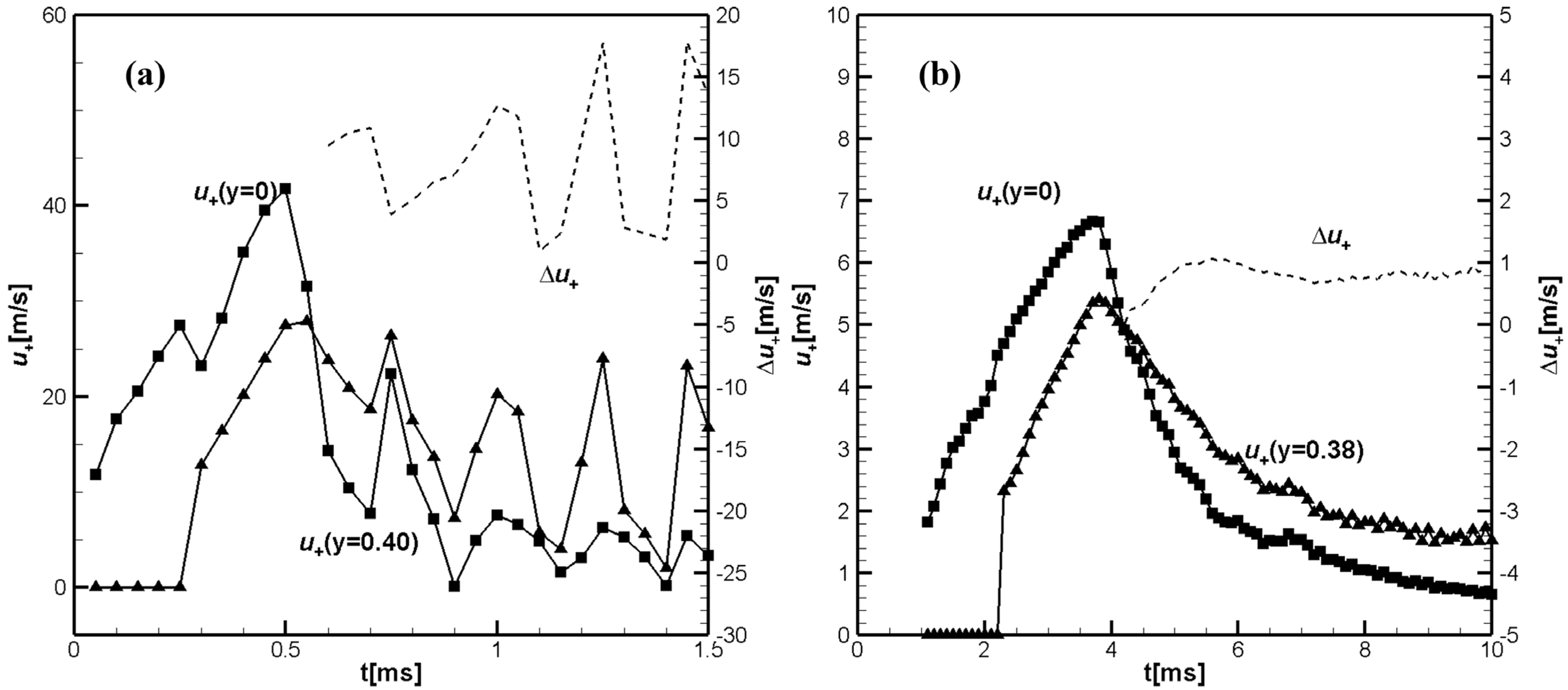
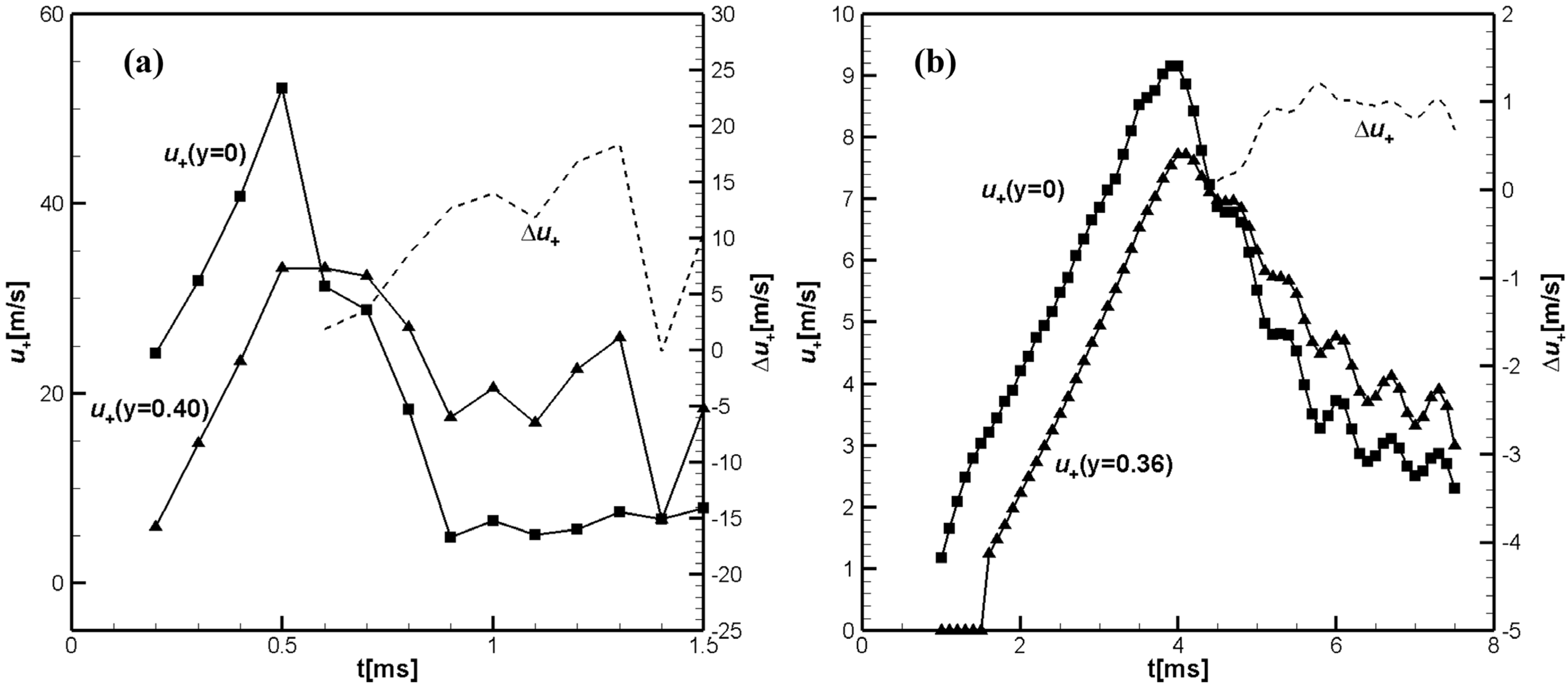
Figure 2 shows temporal evolution of the unburned flow velocities at the tube axis, $u_{+}(y=0)$, and near the sidewall, at $y=0.4 \mathrm{cm}$, calculated closely ahead of the flame front, at $Y_{H{O}_2}<{10}^{-8}$, for hydrogen/air flame (a) and similar values $u_{+}(y=0)$ and $u_{+}(y=0.38 \mathrm{cm})$ for CH₄/air.

Dashed lines in Figure 2a,b show the differences $\mathsf{\Delta }{u}_{+}=u_{+}(y=0.4 \mathrm{cm})-u_{+}(y=0)$ in Figure 2a and $\mathsf{\Delta }{u}_{+}=u_{+}(y=0.38 \mathrm{cm})-u_{+}(y=0)$ in Figure 2b. It can be seen that for hydrogen/air, the velocity in the unburned gas near the sidewall exceeds the unburned gas velocity at the channel axis (mid-plane), $\mathsf{\Delta }{u}_{+}>0$ at $t\approx 0.57 \mathrm{ms}$. Shortly thereafter, the axial velocity profile in the unburned gas begins to take on a tulip-shape, which leads to the inversion of the flame front and the formation of a tulip shape flame, as can be seen in Figure 3a.

In general, the scenario for the formation of the tulip flame in the methane/air mixture shown in Figure 2b is similar to that for the hydrogen/air flame shown in Figure 2a. The main difference is that the tulip flame formation for hydrogen/air flame occurs about ten times faster than for the methane/air flame due to the much larger value of the negative acceleration of the hydrogen–air flame during the first deceleration phase, which causes a much more intense initial rarefaction wave and, consequently, much faster formation of the tulip flame. Another difference is the greater acceleration of the hydrogen–air flame during the finger stage, just prior to the deceleration phase. Therefore, during this phase, the accelerating hydrogen–air flame generates strong pressure waves, which can be seen as the pressure growth rate $d{P}_{+}/dt$ in Figure 1a. The amplitude of the pressure waves generated by accelerating the hydrogen/air flame is much greater than the amplitude of pressure waves generated by the methane/air flame. The strong pressure waves reflect from the opposite closed end of the channel travelling back and forth. They first enhance the effect of the initial rarefaction wave. Later, their collisions with the tulip flame slowdown the flame and can cause a sufficiently large negative acceleration of the flame to induce Rayleigh–Taylor instability leading to the formation of a distorted tulip flame [24,25]. This can be seen in Figure 3a at $t=1.3 \mathrm{ms}$. On the contrary, in case of a methane/air flame, the pressure waves are very weak and do not cause the flame velocity oscillations seen in Figure 1a and Figure 2a or flame instability, which can be seen in Figure 3a.

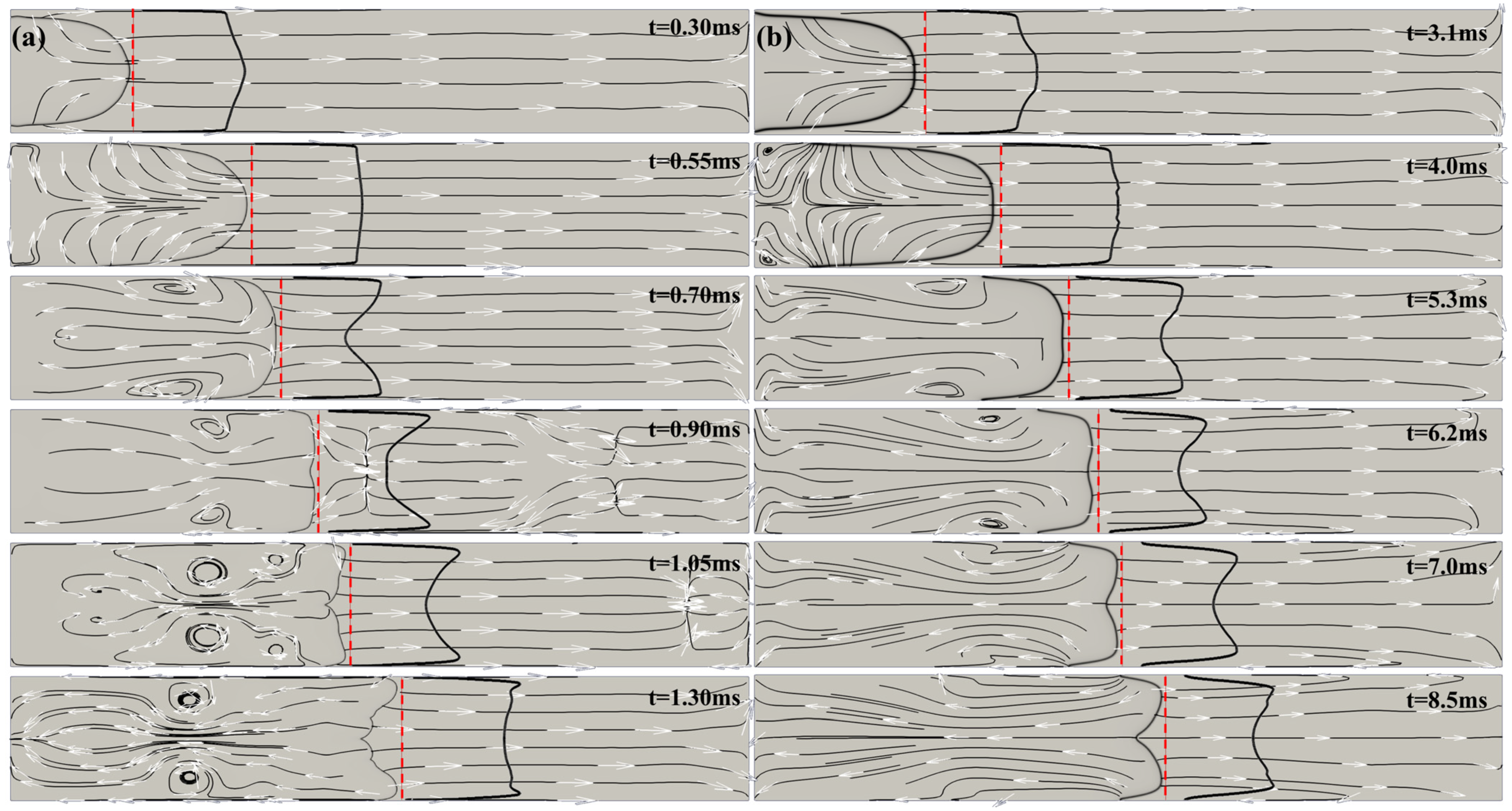
Figure 3 shows computed schlieren images and streamlines for the H₂/air flame (a) and for the CH₄/air flame (b) for selected times during tulip flame formation. The red dashed lines in the figures show the location of the unburned gas axial velocity profile at 0.5 mm ahead of the flame front, where it was measured.

Below, in Section 4 we will show that the magnitude of flame acceleration/deceleration is strongly dependent on the flame velocity. The greater the flame velocity, the greater the magnitudes of flame acceleration and deceleration. Since the intensity of the rarefaction wave generated by the decelerating flame is characterized by the magnitude of the flame deceleration, a faster flame will produce a stronger rarefaction wave. Therefore, the difference between the unburned gas velocity immediately ahead of the flame at the tube axis and the axial velocity closer to the sidewalls is greater for a faster flame than for a slower flame. This means that a higher velocity flame will transition to a tulip flame with a deeper tulip (longer tulip petals) and more quickly than a lower-velocity flame. This can be clearly seen by comparing images (a) and (b) in Figure 3. On the contrary, in the case of a methane/air flame, the pressure waves are very weak and do not cause the flame velocity oscillations seen in Figure 1a and Figure 2a or the flame instability seen in Figure 3a. Figure 3b shows that the methane/air flame is formed smoothly, without oscillations or instabilities.

3.2. 2D Channel with Both Ends Closed and Aspect Ratio $\alpha =12$

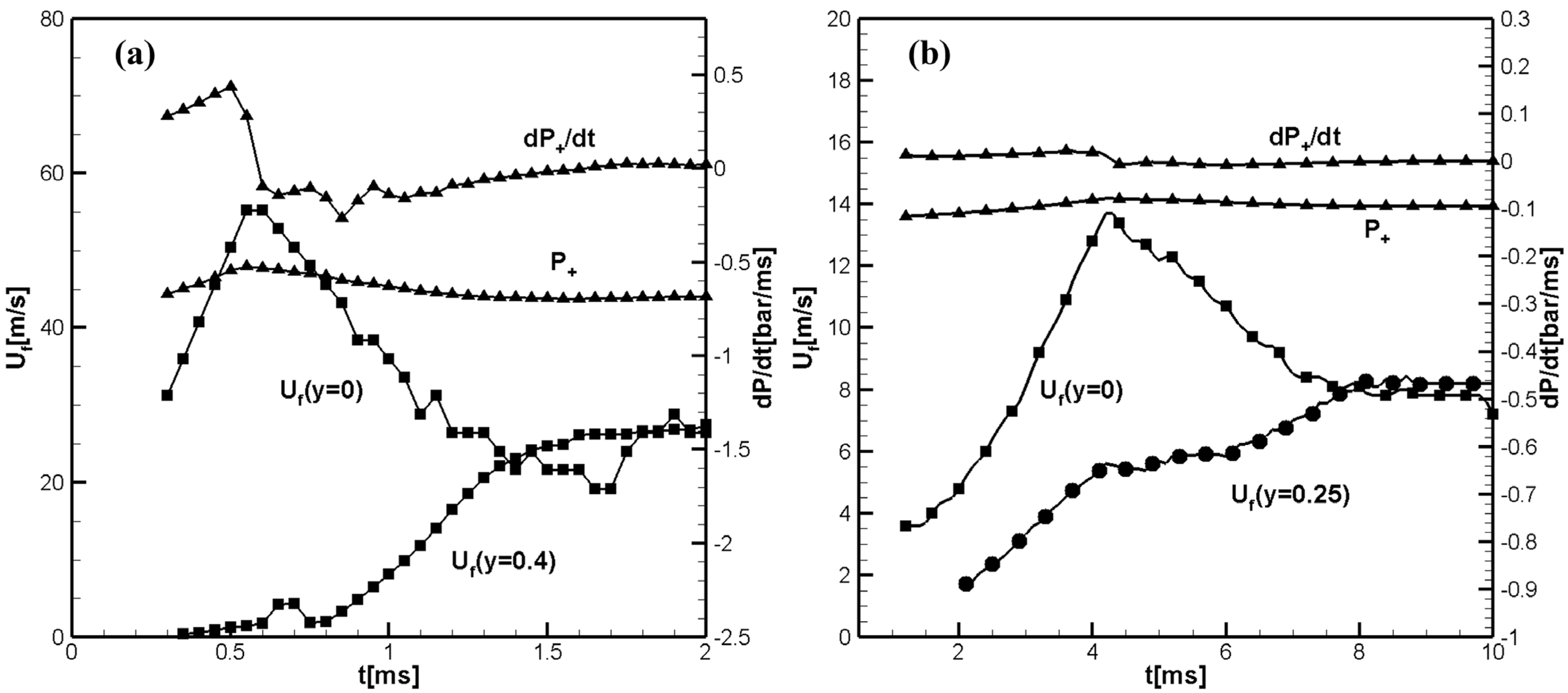
Figure 4a,b show the temporal evolution of the flame front velocities along the mid-plane of the channel and near the sidewall, the pressure rise, $P_{+}$, and the pressure growth rate $d{P}_{+}/dt$ at the centerline ahead of the flame front calculated for the hydrogen/air (Figure 4a) and methane/air (Figure 4b) flames propagating in a 2D channel with an aspect ratio $\alpha =12$.

It can be seen in Figure 4a that there are fewer reflected pressure waves colliding with the flame compared to the shorter channel with an aspect ratio $\alpha =6$ shown in Figure 1a. Figure 1a shows that the collision of the flame with the reflected pressure wave at 0.25 ms results in a lower maximum flame front velocity $U_f(y=0)=45 \mathrm{m}/\mathrm{s}$, while in Figure 4a, the maximum flame front velocity along the center line is $U_f(y=0)=50 \mathrm{m}/\mathrm{s}$. A comparison of Figure 3a with similar figure for larger aspect ratio shows that in the longer channel, flame collisions with reflected pressure waves, if they can lead to the formation of a distorted tulip flame, do so at a later time than in a shorter channel. The laminar velocity of methane/air flame is small, and therefore, the scenario of tulip flame formation is practically the same for channels with an aspect ratio $\alpha =6$ and $\alpha =12$.

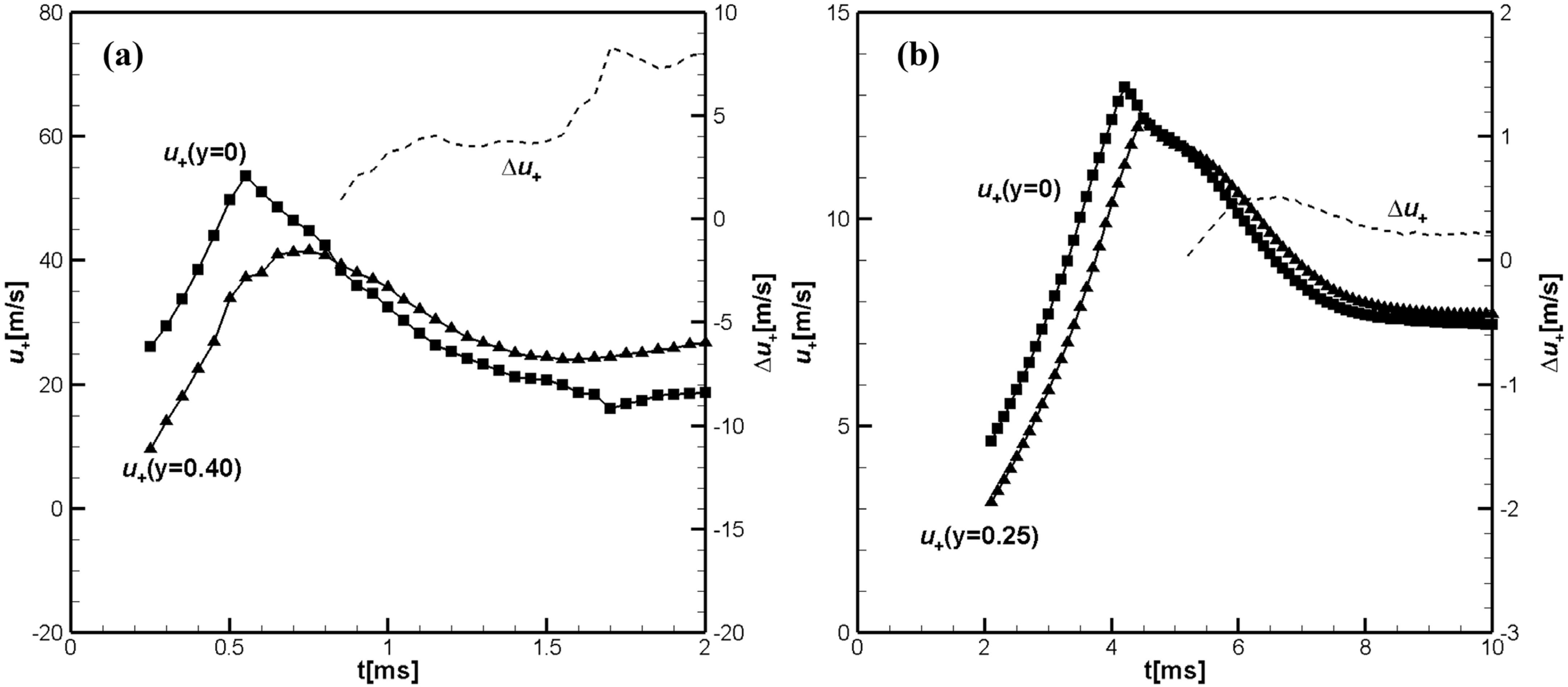
Figure 5a,b show (a) the temporal evolution of the unburned gas velocities just ahead of the flame front for hydrogen/air and (b) the same for the methane/air flame. A higher unburned flow velocity along the centerline $u_{+}(y=0)$ compared to that in the shorter channel shown in Figure 1a is the result of a higher flame front velocity $U_f(y=0).$ Due to the reduced number of collisions with the reflected pressure wave, the distorted tulip flame may develop at a later time, if at all. Except for small fluctuations in unburned flow velocities $u_{+}(y=0)$ and $u_{+}(y=0.36 \mathrm{cm})$ caused by weak pressure waves, the whole scenario of tulip flame formation in CH₄/air is very similar to that in the shorter channel $\alpha =6$.

Figure 6a,b shows computed schlieren images and streamlines during tulip flame formation in (a) H₂/air and (b) CH₄/air mixtures in the long channel with an aspect ratio $\alpha =12$. The red dashed lines in the figures show the location of the unburned gas flow velocity profile measured just ahead of the flame front.

3.3. 2D Semi-Open Channel

A semi-open channel can be considered as a limiting case of a channel with a very large aspect ratio, such that the pressure waves reflected from the opposite end have no time to reach and collide with the flame. In a semi-open channel, there is no reflected pressure waves and the pressure is almost constant. Without reflected pressure waves, which in a closed channel amplify the effect of the initial rarefaction wave and can initiate the RT instability leading to a distorted tulip flame, tulip flame formation in a semi-open channel takes longer time and proceeds smoothly.

Figure 7a,b show the temporal evolution of the flame front velocities along the centerline and near the sidewall, the overpressure $P_{+}$, and the pressure growth rate calculated for the hydrogen/air (Figure 7a) and methane/air flames (Figure 7b). The weak changes in the pressure growth rate and small oscillations of the flame front velocity seen in Figure 7a are related to the moment when the flame skirt touches the sidewall, which causes a weak expansion wave propagating towards the channel centerline and reflecting from the sidewalls. They are much weaker for the methane/air flame in Figure 7b. The temporal evolutions of the unburned gas velocities $u_{+}(y=0)$, $u_{+}(y=0.4 \mathrm{cm})$, and $u_{+}(y=0.25 \mathrm{cm})$ measured just ahead of the flame front are shown in Figure 8a,b, and it is seen that they also proceed more smoothly than for a channel with closed ends.

Figure 9a,b show sequences of computed schlieren images with streamlines during tulip flame formation in a half-open tube. It can be seen that in both cases, for the fast hydrogen/air flame and for the slow methane/air flame, the tulip flame formation in a semi-open channel takes longer than in a closed channel, but it is much faster for the hydrogen/air flame than for the methane/air flame. The red dashed lines in the figures show the location of the unburned gas flow velocity profile just ahead of the flame front.

4. Summary and Discussions

It has been found that 2D simulations provide good qualitative agreement with experimentally observed flame dynamics, tulip and distorted tulip flame evolution in the highly reactive hydrogen/air and low reactive methane/air flames, in particular the dependence on the channel aspect ratio [30,47,48]. It was shown that the magnitude of laminar flame velocity strongly affects flame dynamics in the early stages of flame propagation, in agreement with numerical simulations by Deng et al. [9], which used a one-step chemical model. The effect of the reaction order was studied by Qi et al. [10]. The present study shows that the reaction order has little effect on the formation of tulip flames but may be important in later stages during the formation of distorted flames.

One of the important conclusions of this study is that laminar flame velocity and flame acceleration are the main factors responsible for the formation of the tulip flame. In particular, the ratio of the tulip flame formation times for H₂/air and for CH₄/air mixtures is approximately equal to the ratio of their laminar flame velocities, ${\tau }_{tulip}(H_2)/{\tau }_{tulip}(C{H}_4)\approx U_{fL}(H_2)/U_{fL}(C{H}_4)\approx 6.3$.

Clanet and Searby [19] identified four characteristic times of the earlier stages of flame propagation in a tube: the time of transition from a spherical flame to a finger-shape flame ${\tau }_{spher}$; the time when the flame skirt of the finger shape flame touches the sidewall ${\tau }_{wall}$; the time when flame inversion is initiated and the plane flame is formed ${\tau }_{inv}$; the time of tulip flame formation ${\tau }_{tulip}$. It should be emphasized that the hydrodynamic processes in 3D flames proceed considerably faster than those in 2D flames [26,48]. Therefore, the characteristic times ${\tau }_{inv}$ and ${\tau }_{tulip}$ are longer for 2D flames than for 3D flames [26]. This explains the discrepancy between the theoretical prediction of the characteristic times ${\tau }_{inv}$ and ${\tau }_{tulip}$ obtained using a simple 2D model and the experimental times ${\tau }_{inv}$ and ${\tau }_{tulip}$ measured in [24,49].

Using a geometric model by Clanet and Searby [19], we can write the equation for the flame tip velocity during the finger flame phase as

$${\displaystyle \frac{d{X}_{tip}}{dt}}=4\mathrm{\Theta }{\displaystyle \frac{U_{fL}}{D}}{X}_{tip}$$

(12)

where $X_{tip}$ is the coordinate of the finger flame tip, $\mathrm{\Theta }={\rho }_u/{\rho }_b$ is the expansion factor, $D$ is the channel width, and $U_{fL}$ is the laminar flame velocity. Differentiating Equation (12) with respect to time gives the dependence of flame acceleration on the laminar flame velocity

$$d^2{X}_{tip}/d{t}^2={(4\mathrm{\Theta }{U}_{fL}/D)}^2{X}_{tip}$$

(13)

Equation (13) shows that the flame acceleration increases significantly as the flame velocity $U_{fL}$ increases. Since the amplitude of the pressure waves generated by the accelerating piston (flame front) is greater at higher piston accelerations, this means that a higher-velocity flame generates stronger pressure waves than a lower-velocity flame. It should be noted that in the phase of flame deceleration, when the flame skirt begins to touch the sidewalls of the tube, the main part of the finger flame skirt is almost parallel to the sidewalls of the tube, and it is larger for higher-velocity flames. This also results in a large difference in the deceleration values of a high-speed flame compared to the deceleration of a lower-speed flame. For example, the numerical values of the flame accelerations ($a_{+}$) and deceleration ($a_{-}$) for the 2D channel considered in Section 3.1 are as follows: for H₂/air flame $a_{+}\simeq 1.5\times {10}^5{ \mathrm{m}/\mathrm{s}}^2$ and $a_{-}\simeq -3\times {10}^5{ \mathrm{m}/\mathrm{s}}^2$; for CH₄/air flame $a_{+}\simeq 3\times {10}^3{ \mathrm{m}/\mathrm{s}}^2$ and $a_{-}\simeq -6\times {10}^3{ \mathrm{m}/\mathrm{s}}^2$.

In a recent paper by Lei et al. [50], it was assumed that effect of self-induced turbulence of burning velocity and the flame wrinkling induced by DL instability is the main mechanism of tulip flame formation: “Darrieus-Landau instability and thermal-diffusive (TD) instabilities are the main reason for the formation of tulip flames, and the DL instability played a dominant role”. However, no evidence has been provided that this is actually the case. The fact that tulip flame formation occurs faster than the characteristic time of the DL instability was established in numerical simulations a long time ago by Gonzalez et al. [51] and Dunn–Rankin and Sawyer [52].

Here we show that the tulip flame formation due to the rarefaction wave takes much less time than the characteristic times of the Darrieus–Landau (DL) and thermal-diffusive (TD) instabilities. The time of the DL instability development can be estimated as ${\tau }_{DL}=1/{\sigma }_{DL}$, where ${\sigma }_{DL}=k{U}_{fL}{\displaystyle \frac{\mathrm{\Theta }}{\mathrm{\Theta }+1}}\left(\sqrt{\mathrm{\Theta }+1-1/\mathrm{\Theta }}-1\right)\approx k{U}_{fL}\sqrt{\mathrm{\Theta }}$ is the increment of the DL instability, $U_{fL}$ is the laminar flame speed, $\mathrm{\Theta }={\rho }_u/{\rho }_b$ is expansion coefficient, the ratio of unburned to burned gas densities, and $k$ is the wave number. The time of establishing the reverse flow by a rarefaction wave can be estimated as

$${\tau }_{RW}\approx D/a_s$$

(14)

where $a_s$ is a speed of sound. Considering that the perturbation wavelength of the DL instability, which could be responsible for the flame front inversion, is about the channel width, $\lambda \sim D$, we obtain

$${\tau }_{RW}/{\tau }_{DL}\approx \pi \sqrt{\mathrm{\Theta }}\left({\displaystyle \frac{U_{fL}}{a_s}}\right)<<1$$

(15)

Since the laminar flame velocity is much less than the sound velocity, $U_{fL}/a_s\sim {10}^{-3}-{10}^{-4}$, the inequality (15) holds for all flammable gas mixtures. In the same way, assuming for simplicity a unity Lewis number, it can be shown that the ratio of the characteristic time of the rarefaction wave ${\tau }_{RW}$ to the characteristic time of the thermal-diffusive instability ${\tau }_{TD}$ for $\lambda \sim D$ is

$${\tau }_{RW}/{\tau }_{TD}\approx {\displaystyle \frac{L_f}{D}}\left({\displaystyle \frac{U_{fL}}{a_s}}\right)<<1$$

(16)

This means that, in agreement with the experimental studies of Ponizy et al. [27], Darrieus–Landau or thermally diffusive flame front instabilities are not involved in flame front inversion and tulip flame formation.

A decelerating flame front can be distorted by Rayleigh–Taylor instability if small perturbation can grow significantly during the deceleration time $\mathsf{\Delta }t$. This occurs if the increment of the RT instability, ${\sigma }_{RT}=\sqrt{Akg}$, is sufficiently large to satisfy the condition ${\sigma }_{RT}\mathsf{\Delta }t>>1$. Here $A=({\rho }_u-{\rho }_b)/({\rho }_u+{\rho }_b)=(\mathrm{\Theta }-1)/(\mathrm{\Theta }+1)\approx 1$ is the Attwood number, and $k=2\pi /\lambda$ is the wave number.

A necessary condition for the development of RT instability is negative flame acceleration. Negative flame acceleration first appears at the flame deceleration phase, caused by a decrease in the flame front surface area, when lateral parts of the flame skirt touch and collapse on the channel sidewalls. Negative flame acceleration can also be caused by the flame collision with reflected pressure waves. In the first case, calculating the flame acceleration $g$ during the flame front inversion, we find that for a perturbation with wavelength $\lambda \sim D$, which could be a possible candidate for flame front inversion, ${\sigma }_{RT}\mathsf{\Delta }t<1$.

The effects of flame collisions with reflected pressure waves have been studied by Qian and Liberman [53]. It was shown that the flame collisions with reflected pressure waves play an important role in the formation of the tulip flame and its further evolution to a distorted tulip flame. In particular, flame collisions with pressure waves enhance the effect of the first rarefaction wave generated by the decelerating flame in the unburned gas when it touches the tube sidewalls. This explains the more pronounced tulip flame formation in closed tubes compared to a semi-open tube observed in experiments and numerical simulations. In the later stages, the flame collisions with the reflected pressure waves can result in a much greater flame deceleration to meet the condition ${\sigma }_{RT}\mathsf{\Delta }t>>1$. It was shown that considering a finite thickness of the flame front, $L_f$, the maximum growth rate of the RT instability corresponds to perturbation $k{L}_f\approx 0.3$ [54], so the wavelength of the fastest growing mode of the RT instability is

$${\lambda }_{\max }={\displaystyle \frac{2\pi }{0.3}}{L}_F\approx 0.2 \mathrm{cm}$$

(17)

The value ${\lambda }_{\max }\approx 0.2 \mathrm{cm}$ agrees well with the size of the bulges developed at the tulip flame front in numerical and experimental studies of the distorted tulips in a closed duct [24,25]; see schlieren images at t = 1.3 ms in Figure 3a.

Since the intensity of the rarefaction wave is characterized by the flame acceleration after the flame skirt touches the sidewall, the times of flame front inversion and tulip flame formation are determined by the magnitude of the flame acceleration, which in turn depends strongly on the laminar flame velocity. Therefore, another conclusion is that at sufficiently low laminar flame velocities, the intensity of the rarefaction wave may be so small that a tulip flame formation takes a relatively long time. In this case, possible phenomena that may prevent tulip flame formation at low laminar flame velocities are the buoyancy effect resulting in faster development of the upper or lower lip or sufficient time for flame instabilities to develop. This conclusion is consistent with the evolution of CH₄/H₂/air flames at different inhibitor percentages and hence different laminar flame velocities shown in Figure 3 and with the experimental study of methane/hydrogen/air flames by Zhang et al. [55].

A faster flame produces a stronger rarefaction wave during the finger phase of flame propagation. Therefore, for a faster flame, the difference between the unburned gas velocity at the tube axis and the axial (along the tube) velocity closer to the sidewalls is greater than for a flame with a slower velocity. This explains the deeper shape of the tulip formed by faster flames than that formed by slower flames.