Issues Related to Water Hammer in Francis-Turbine Hydropower Schemes: A Review

Abstract

This paper reviews key parameters which may cause unacceptable water hammer loads in Francis-turbine hydropower schemes. Water hammer control strategies are presented for this context including operational scenarios (closing and opening laws), surge control devices, redesign of the pipeline components, or limitation of operating conditions. Theoretical water hammer models and solutions are outlined and discussed. Case studies include simple and complex new and refurbished hydropower systems including headrace and tailrace tunnels, surge tanks of various designs, and different penstock layouts. The case studies in this paper cover the application of both commercial and in-house software packages for hydraulic transient analysis. Two-stage guide vane closing law, increased unit inertia and surge tank(s) are used in the cases considered to keep the water hammer within the prescribed limits. Typical values for the maximum pressure head at the turbine inlet and the maximum unit speed rise during normal transient regimes were in the range of 10 to 35% of the maximum gross head and 35 to 50% above the nominal speed, respectively. The agreement between computational results using both software packages, and field test results is well within the limits of ±5% accepted in hydropower engineering practice.

1. Introduction

Modern hydropower plants play essential role in renewable energy systems and contribute to stability of large electrical grids [1,2,3]. The hydropower systems are characterized by efficient and flexible operation and large energy storage [4]. Refurbishment and upgrading of aging hydropower plants is an environmentally friendly means to enhance the output and flexible response of hydropower plants [5]. An increase in hydraulic turbine discharge results in higher dynamic loads on the plant components during rapid load changes induced by water hammer effects [6,7]. The consequences of transients can cause damage to turbine and hydromechanical equipment, to segments of the flow system, or disruptions in operation [8]. For owners and operators of hydropower plants, this means high costs in the form of expensive repairs, more frequent maintenance, and reduced electricity production. Unwanted large water hammer loads in hydropower plants should be kept within the prescribed limits [9,10]. Stability issues related to small load variations [11,12] are not the subject of this paper.

This article reviews essential parameters that can cause unacceptable water hammer loads in Francis-turbine hydroelectric power plants [13]. In the first part of the article, we focus on critical operating modes and methods for mitigating the negative consequences of water hammer with an additional review of the theoretical models used and a description of the Francis turbine as a hydraulic turbine machine. Water hammer suppression strategies include control of operational regimes (closing and opening laws of devices), surge control devices (surge tank, pressure regulating valve), redesign of the pipeline components (change in dimensions), or limitation of operating conditions (reduced output). In the second part, we present the practical use of in-house and commercial computer programs and a comparison between calculated and measured values of hydrodynamic quantities. Distinct case studies include simple and complex new and refurbished hydropower systems. It should be noted that the rehabilitation process offers the advantage of allowing comparative water hammer tests in the plant before and after the rehabilitation. On the other hand, design of a new plant is based on gained knowledge and good engineering practice.

2. Water Hammer Phenomena in Hydropower Plants

The main cause of water hammer phenomena in hydroelectric power plants is operation of the Francis turbine to the required load changes. In a stationary state, the turbine load is the same as the generator load, so the turbine governor must respond to any change in load, otherwise the rotational speed, flow and pressure in the system will change. After each maneuver, however, the disturbances in the system persist for some time after the establishment of a new equilibrium state as oscillations that are dampened by friction. Extreme pressure pulsations in the flow system and the turbine speed must be mitigated, which is achieved by appropriate operating maneuvers (opening and closing the turbine guide vanes) and the installation of surge protective equipment [10].

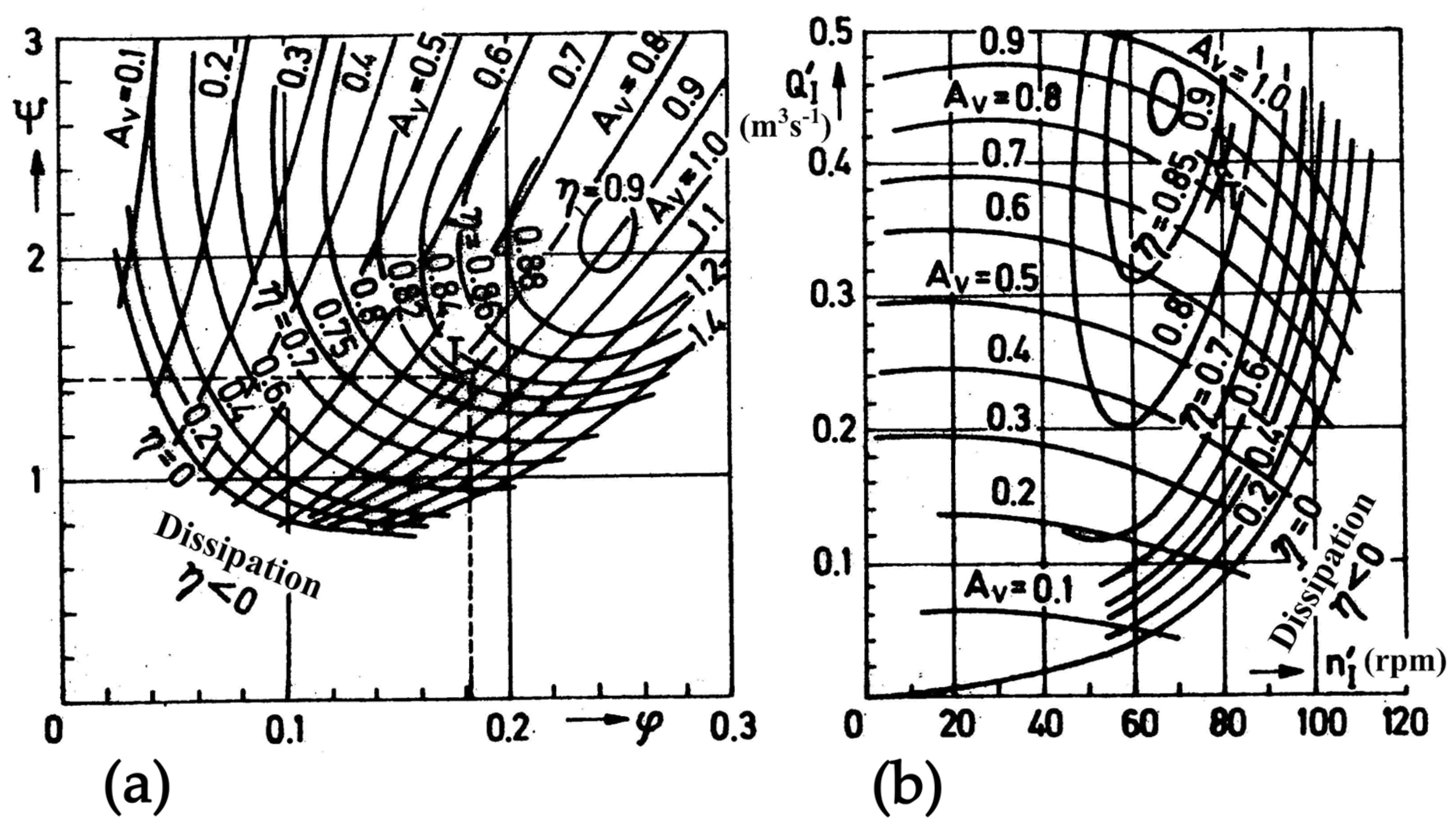
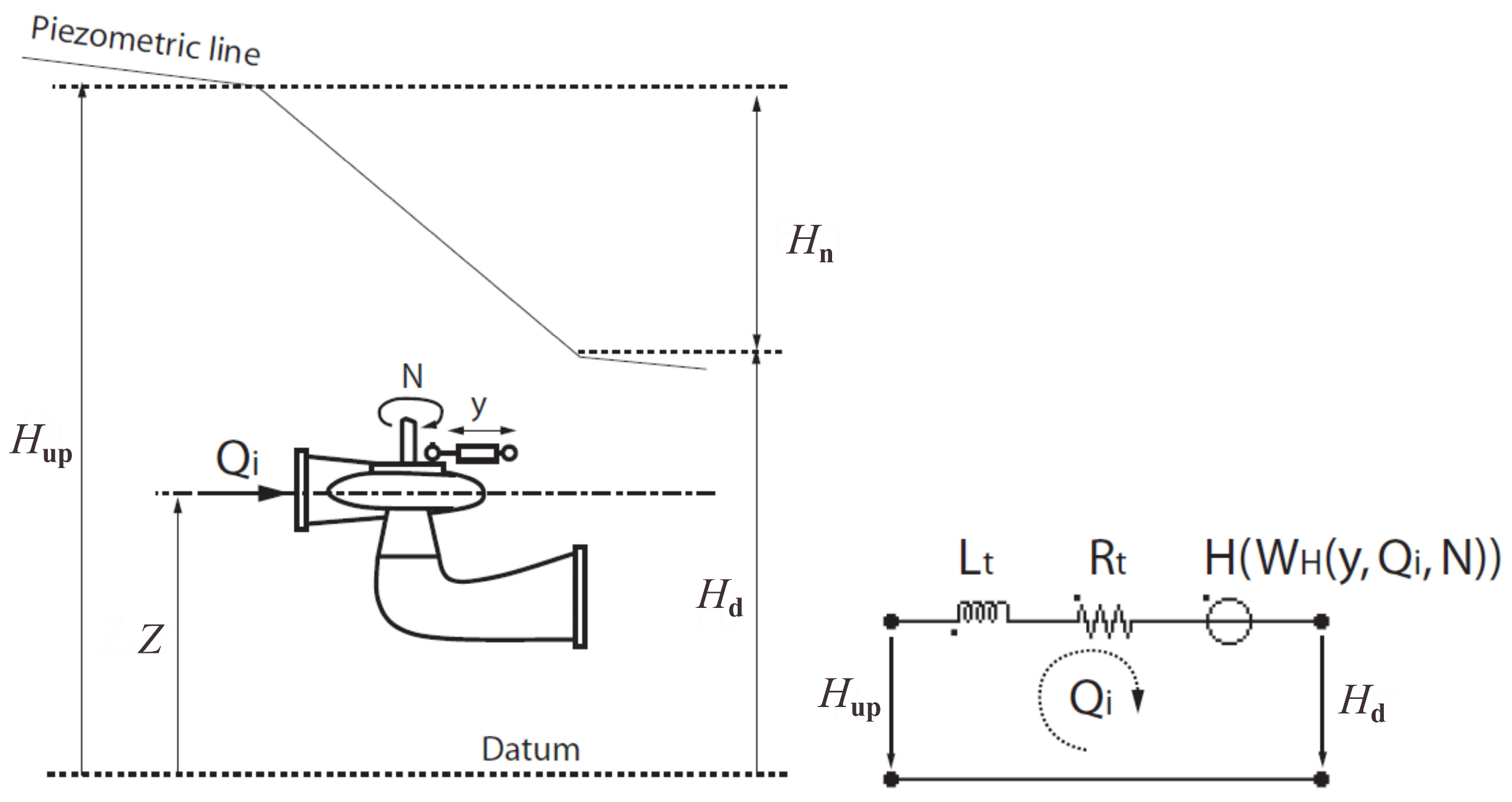
2.1. Note on Hydraulic Turbines

Hydraulic turbines are the power units of hydroelectric power plants, whose task is to harness water energy to produce electricity. The most suitable type of hydraulic turbine machine is determined based on the hydrological and geomorphological characteristics of the location, economic aspects of production, operating dynamics, maintenance costs, and safety. The following common types of hydraulic turbines are used: Pelton, Francis, Kaplan, and tubular turbines. The Francis turbine is suitable for a wide operating range of head and flow rates; that is why this type of turbine is the most used turbine in hydropower plants [14]. The Francis turbine is a radial–axial turbine in which water enters the runner in the radial direction and leaves it in the axial direction. Not all the potential energy of the water is converted into kinetic energy, which is why Francis turbines are classified as reaction turbines. The design can be horizontal or vertical, with a horizontal design having a single or double runner. The efficiency and flexibility of the Francis turbine can be enhanced by variable speed operation [15]. This paper deals with Francis turbines operating at constant (synchronous) speed.

The turbine head and torque characteristics are traditionally measured on a turbine model in a hydraulic laboratory and represented in the form of a hill chart [14,16]. The laws of model similarity play an extremely important role in the theory of hydraulic turbines, as they enable comparisons of turbines of different types and sizes. With their help, the properties of the prototype of the installed turbine can be predicted from the experimental results on the turbine model. The turbine is uniquely defined and described in terms of form using the specific rotational speed n_q:

$$n_q={\displaystyle \frac{n\sqrt{Q}}{\sqrt[4]{{H_n}^3}}}$$

(1)

Herein all symbols are defined in Nomenclature. The specific turbine speed is a constant value and is defined at the optimum operating point of the turbine (the point of highest efficiency). The influence of the specific speed on the selection of a suitable reaction turbine is shown in Figure 1.

The Francis-turbine hill chart traditionally includes the measured discharge and torque characteristics. Steady-state turbine characteristics are used for water hammer analysis [17]. There are some discrepancies between the steady and unsteady performance characteristics due to unsteady flow effects at off-design conditions and when the turbine operates in cavitating region [18]. Hydraulic transient events in hydropower plants are relatively slow; therefore, the unsteadiness should not affect the turbine characteristics significantly. Figure 2 presents typical hill chart for medium-head Francis turbine [19]. The specific rotational speed for this turbine is 45 rpm. The turbine characteristics can be represented in dimensionless ψ − φ (Figure 2a) or unit numbers Q_I′ − n_I′ (Figure 2b).

The turbine characteristics dimensionless and unit numbers are defined by the following equations:

$${n_{\mathrm{I}}}^{\prime }={\displaystyle \frac{n·D_1}{\sqrt{H_n}}}; {Q_{\mathrm{I}}}^{\prime }={\displaystyle \frac{Q}{{D_1}^2·\sqrt{H_n}}} ;n \mathrm{i}\mathrm{n} (\mathrm{r}\mathrm{p}\mathrm{m})$$

(2)

$$\phi ={\displaystyle \frac{Q}{\frac{{\pi }^2}{4}·n·{D_2}^3}}; \psi ={\displaystyle \frac{g·H_n}{\frac{{\pi }^2}{4}·n^2·{D_2}^2}} ;n \mathrm{i}\mathrm{n} (\mathrm{r}\mathrm{p}\mathrm{s})$$

(3)

The turbine characteristics can be further transformed into a form suitable for computer programming [7,20].

2.2. Critical Operating Modes

The loads resulting from hydraulic transients arise due to different operating modes. They are divided according to the level of danger to the flow system of the hydropower plant equipped with Francis turbines [7,20,21]:

(i)

Normal operating regimes

All safety elements in the system operate appropriately according to their designed functions. These regimes include hydropower plant start-up and connection to the grid, load acceptance and reduction, load rejection under governor control and emergency shutdown [22].

(ii)

Safety operating modes

In this case, one of the safety elements fails, which can cause partial turbine runaway and closing of the turbine inlet butterfly or ball valve [23].

(iii)

Exceptional operating modes

In a hydroelectric power plant, several safety elements fail in the most unfavorable way. This yields a full turbine runaway [24] or closing of the surge tank safety valve under maximum discharge.

In addition, the turbine unit can operate in synchronous compensation mode. Water hammer analysis should include cases with extreme values of head and discharge when either one unit or all units operate, cases with malfunction of one of the devices (inoperative guide vane apparatus or pressure regulating valve) and cases with unwanted sets of events (malfunction of several devices).

3. Safety and Mitigation Measures

Safety elements and measures to mitigate the unwanted water hammer effects should meet the following conditions [9]:

(i)

Ensure the highest possible level of safety of the hydroelectric power plant for all intended operating modes;

(ii)

Determine and observe appropriate limit values for specific operating parameters;

(iii)

Identify the most unfavorable operating modes and ensure that the limit values of the operating parameters are not exceeded.

When choosing surge protection strategy against the undesirable effects of water hammer, operational, safety and economic factors are decisive. Most often the best solution is the simultaneous use of the following approaches [10,21]:

(i)

Alteration of operational regimes;

(ii)

Installation of water hammer control devices in hydropower flow-passage system;

(iii)

Redesign of hydropower plant waterway system;

(iv)

Limitation of operating conditions.

It should be noted that relevant water hammer constants can give an initial guess on how to select water hammer control means in preliminary stage of the project [6,7,25]. The two common water hammer constants are the water starting time T_w and mechanical acceleration time T_m:

$$T_w={\displaystyle \frac{L·v_0}{g·H_0}}; T_m={\displaystyle \frac{I·{\omega }^2}{P_0}}$$

(4)

Đorđević [6] suggested that no surge tank and pressure regulating valve are needed for T_w < {3 to 4 s}. For {3 to 4 s} < T_w < {10 to 12 s}, he recommended installation of the pressure regulating valve; surge tank is an option. Finally, for T_w > {10 to 12 s}, a surge tank is foreseen as an adequate solution.

3.1. Alteration of Operating Regimes

This includes appropriate control of the guide vane maneuvers, and shutoff valve and pressure regulating valve closing/opening times. A two-speed guide vane closing time function with an added cushioning stroke is recommended [26]. Alteration of operating regime is the most efficient method for water hammer control in hydropower plants due to the low cost of the work involved.

3.2. Installation of Water Hammer Control Devices in the Hydropower Plant Flow-Passage System

Water hammer control devices can be installed along the flow-passage system of a hydroelectric power plant. These devices change the characteristics of the system (shorten the active length of the conduit, reduce the effects of fluid compressibility, increase the inertia of the hydraulic turbine). The following devices can be installed in the Francis-turbine hydropower system:

(i)

Increased Francis-turbine unit inertia (adding flywheel to small units, increasing the generator inertia);

(ii)

Resistors (to absorb excessive power);

(iii)

Surge tank in the headrace and/or tailrace waterway (shortens the active conduit length, reduces unit starting time, improves governing stability) [27] or an air-cushion surge chamber (ventilation type with standpipe [28], or compressed air cushion type [29]);

(iv)

Pressure-regulating valve (operates synchronously with the turbine guide vane mechanism) [30];

(v)

Pressure-relief valve (opens at a set pressure, for small units);

(vi)

Rupture disk (bursts at a set pressure, for small units);

(vii)

Aeration pipe (attenuates unwanted transient air-water flow effects) or air valve (attenuates water column separation effects, removes trapped air) [31]; both release unwanted air from the water-conveyance system (tunnel, penstock).

Installation of water hammer control devices is appropriate in the construction of the new hydroelectric power plants and to a lesser extent in the renovation of the existing power plants.

3.3. Redesign of Hydropower Plant Flow-Passage System

Redesign of hydropower plant flow-passage system may include the following:

(i)

Change in the tunnel or penstock profile (high point), dimensions (diameter, pipe-wall thickness, length) and material (steel and plastic) [32];

(ii)

Re-arrangement of the placement of the surge protective elements along the waterway system (valve, surge tank, air valve).

Redesign is the most appropriate method for mitigating water hammers early in new hydropower plant developments, while severe cost constraints often limit the redesign of the existing waterway system layout (expensive and time-consuming civil works).

3.4. Limitation of Operating Conditions

Limitation of operating conditions narrows the hydropower plant operating range, and consequently the plant flexibility to grid demands. This may include the following:

(i)

Limiting maximum operating discharge;

(ii)

Limiting maximum and minimum gross heads;

(iii)

Limiting maximum and minimum unit power.

4. Modern Approach to Treatment

Due to the flexible operation of a hydroelectric power plant, the presence of water hammer phenomena is inevitable. Disturbances in operation, start-ups, shutdowns, or load changes are present throughout the entire operating period. The tasks of the engineer responsible for the analysis of transient phenomena are to identify and address operating regimes that may pose a threat to safe operation and to prepare a solution. From the stated scope of critical operating regimes (Section 2.2) and the possible use of water hammer control devices (Section 3), it follows that the engineering analyst must have a broad interdisciplinary knowledge in various fields:

(i)

Civil engineering (hydrology, hydraulics, and hydraulic structures);

(ii)

Mechanical engineering (fluid mechanics, hydraulic turbines, hydromechanical and auxiliary equipment, turbine governor);

(iii)

Electrical engineering (generators, electrical power control, and electrical distribution systems).

The scope of the analysis depends on the specific requirements of the client, the type of hydraulic turbine, the complexity of the flow system and the design phase. The client can determine the scope of the analysis according to the intended operation of the hydropower plant. The type of the installed turbine determines the use of turbine characteristics and the complexity of the flow system. Sensitivity analysis to uncertain parameters (wave speed, friction factor, valve closure time, etc.) may be required [33,34,35].

In practice the two most important guaranteed quantities are (i) the maximum and/or minimum pressure (pressure head) at the turbine inlet and/or outlet and (ii) the maximum unit rotational speed rise. These two items are defined by IEC 60545:1976 [36], IEC 60805:1985 [37], IEC 60041:1991 [38] and IEC 60308:2005 [39]. Both IEC 61362:1998 [40] and IEC 60308:2005 [39] recommend the performance of the following safety tests: (i) unit trip (rapid shutdown), (ii) emergency shutdown, (iii) testing of over-speed safety device, and (iv) checking interlocks. IEC 60545:1976 [36] describes the importance and extent of adequate performance of water hammer tests in the phase of commissioning, operation and maintenance. Load rejection tests should be performed at successively higher loads up to the maximum expected load. IEC 62006:2010 [41] recommends that the emergency shutdown of the unit should be performed first due to safety reasons.

Hydropower plants with built-in Francis turbines generally have more complex flow systems (tunnels, pipelines, water levels, additional inlets, etc.). In the early design phase (conceptual design, preliminary design), the analysis can be performed using simplified analytical models based on experience, guidelines and regulations [6,7,10,20]. At this stage, we can already select appropriate safety elements and procedures to mitigate the negative consequences of water hammer phenomena, particularly the change in the longitudinal profile of the flow system, the location and basic parameters of the water hammer control devices. In the later phase (project for implementation), we use commercial or proprietary, i.e., in-house software packages to determine critical operating modes and final parameters and location of the safety elements. The operating regimes at extreme flows and heads for the operation of one or more units simultaneously, the failure of one or more safety elements, and an unfavorable sequence of events should be investigated. These results represent the basis for the development of a risk analysis [42,43,44,45]. The hydropower components must be designed to withstand water hammer loads during the entire design period of the plant. Fatigue damage of the plant components is the most significant failure type of the plant components [46]. Fatigue-relevant water hammer events may include turbine start-up, emergency shutdown, load rejection, load increase and decrease, and runaway. These events are defined by case-by-case events basis depending on the role of the hydropower plant in the electrical grid system [47]. The two most important fatigue-prone components that should be investigated by the structural engineer are the Francis-turbine runner [48,49] and the penstock [50]. The relevant load cases are agreed between the manufacturer and the utility owner. The fatigue analysis of the five case studies in Section 6 has been performed based on the expected load events during the entire period of the plant operation. During the commissioning tests, the engineer responsible provides support to the field team with additional analyses in case the boundary conditions on the field differ from those in the design for implementation. The fatigue analysis is beyond the scope of this paper; however, the water hammer analyst should provide water hammer loads (maximum and minimum pressures in the system, maximum turbine unit rotational speed rise) to the structural engineer. Finally, it should be noted that a new standard for fatigue assessment of hydraulic turbine runners should be published in the coming days [47].

5. Water Hammer Modeling

Joukowsky [51] developed a simple formula (Joukowsky equation) for a pressure head rise caused by a rapid closure of the valve at the downstream end of the pipe in a time t_c less or equal to than the reflection time t_r = 2L/a:

$$\Delta h={\displaystyle \frac{a}{g}}{v}_0$$

(5)

For a linear reduction in flow in time larger than t_r a formula for reduced water hammer pressure head rise can be used [33]:

$$\Delta h={\displaystyle \frac{2L{v}_0}{g{t}_c}}$$

(6)

Using the above two equations, one can calculate the maximum pressure head in simple pipelines with a slightly compressible liquid in which no cavitation occurs during the water hammer event. In practice, however, we are mostly interested in the examination of the entire dynamic history of pressure head pulsations. This is due to the superposition of pressure waves occurring in complex systems [52] that can strongly affect the safety of the entire system [53]. Water hammer in hydropower plants can be calculated using either elastic or rigid water hammer theory [7,20].

5.1. Elastic Water Column Model

The elastic water column model is used for the systems with relatively long tunnels and penstocks, and systems with rapid transients. Slightly compressible liquid and elastic pipe walls are assumed in the elastic column model. Elastic water hammer describes propagation of pressure waves in liquid-filled pipelines. Unsteady flow in closed conduits is described by two one-dimensional (1D) hyperbolic partial differential equations; the continuity equation and the equation of motion [7,20]:

$${\displaystyle \frac{\partial H}{\partial t}}+v{\displaystyle \frac{\partial H}{\partial x}}-v\sin \theta +{\displaystyle \frac{a^2}{g}}{\displaystyle \frac{\partial v}{\partial x}}=0$$

(7)

$$g{\displaystyle \frac{\partial H}{\partial x}}+{\displaystyle \frac{\partial v}{\partial t}}+v{\displaystyle \frac{\partial v}{\partial x}}+f{\displaystyle \frac{v\left|v\right|}{2D}}=0$$

(8)

The flow in the pipe is assumed to be one-dimensional (cross-sectional averaged velocity and pressure distributions), the pressure is higher than the liquid vapor pressure (no column separation), the pipe wall and liquid behave linearly elastically, unsteady friction losses are approximated as steady friction losses, the amount of free gas in the liquid is negligible and fluid–structure coupling is weak (the pipe does not move) [54,55]. For most engineering applications, the transport terms v($\partial H/\partial x$), v($\partial v/\partial x$) and v·sinθ, are very small compared to the other terms and may be neglected [7,20]. A simplified form of Equations (7) and (8) using the discharge Q = vA instead of the flow velocity v is expressed as follows:

$${\displaystyle \frac{\partial H}{\partial t}}+{\displaystyle \frac{a^2}{gA}}{\displaystyle \frac{\partial Q}{\partial x}}=0$$

(9)

$${\displaystyle \frac{\partial H}{\partial x}}+{\displaystyle \frac{1}{gA}}{\displaystyle \frac{\partial Q}{\partial t}}+f{\displaystyle \frac{Q\left|Q\right|}{2gD{A}^2}}=0$$

(10)

5.2. Rigid Water Hammer Model

Run-of-river hydropower plants comprise relatively short inlet and outlet conduits. The length of the conduit is of the same order of magnitude as its cross-sectional dimensions. The standard one-dimensional elastic water hammer model cannot accurately predict the wave physics [56]. The rigid water hammer model is recommended to be used for this case [17]. In addition, Parmakian [57] recommends that the rigid water can be used only when the closing time (t_c) is larger than L/305.

The rigid water hammer is described by the one-dimensional equation of motion for unsteady flow assuming incompressible liquid and rigid pipe walls [20]:

$${\displaystyle \frac{\partial H}{\partial x}}+{\displaystyle \frac{fQ\left|Q\right|}{2gD{A}^2}}+{\displaystyle \frac{1}{gA}}{\displaystyle \frac{dQ}{dt}}=0$$

(11)

5.3. Methods of Solution for Water Hammer Equations

Elastic and rigid column equations are solved simultaneously with the boundary condition equations (turbine, valve, surge tank, reservoir, etc.) [7,20,58]. Water hammer equations can be solved analytically or numerically (graphical by hand and computer based).

5.3.1. Analytical Methods

Analytical solutions of elastic water hammer Equations (9) and (10) for frictionless simple pipe systems and for systems with consideration of quasi-steady friction have been developed by Rich [59]. There also exists a set of semi-analytical solutions for simple reservoir-pipe-valve systems that account for unsteady friction [60]. Similar analytical solutions exist for rigid water hammer Equation (10) [17,20,58]. Analytical methods are useful for quick estimation of water hammer pressure head amplitudes induced by linear opening or closing of the valve approximating linear closure of Francis-turbine guide vanes. In addition, semi-analytical approximate solutions based on combined theoretical and empirical methods are available for initial estimation of pressure head and rotational speed amplitude during turbine closure or opening events [6,7,17,61,62,63,64].

5.3.2. Numerical Methods

The following methods based on the numerical grid can be used for solution of water hammer equations [20,65,66,67,68]:

(i)

Graphical method [20,69];

(ii)

Method of characteristics (MOC) [7,20];

(iii)

Finite difference method (FDM) [70,71,72,73];

(iv)

Wave characteristic method (WCM) [74];

(v)

Weighted residual methods (WRM) [75,76].

In the group of WRM, the solution can be approximated in the whole range or segmentally in an analytical manner. The WRM group numerical solutions currently include the following:

(v-i)

Finite volume method (FVM) [77,78,79];

(v-ii)

Galerkin finite element method (FEM) [80,81,82].

Traditionally, the hyperbolic set of Equations (9) and (10) is solved by the method of characteristics (MOC) [7,20]. The MOC interprets the physical essence of the transient flow phenomenon. It is characterized by fast convergence, ease of accounting for various boundary conditions, and high accuracy of calculation results. For hydraulic transient analysis of coupled problems including hydraulic, electrical, and mechanical systems, the electrical-analogy-based finite difference method can be used [70,71]. The rigid water hammer Equation (11) can be solved numerically by using the finite difference method [17]. Elastic and rigid column equations are solved simultaneously with the boundary condition equations (Francis turbine, valve, surge tank, reservoir, etc.) [7,20].

Method of Characteristics

The method of characteristics (MOC) transformation of the simplified Equations (9) and (10) produces the water hammer compatibility equations which are valid along the characteristic lines. The compatibility equations in finite-difference form are numerically stable unless the friction is large and the computational grid is coarse and, when written for the computational section i (marked with circle in Figure 3), are [20]:

-

Along the C⁺ characteristic line (Δx/Δt = a),

$$H_{i,t}-H_{i-1,t-\Delta t}+{\displaystyle \frac{a}{gA}}\left({\left(Q_{up}\right)}_{i,t}-{\left(Q_d\right)}_{i-1,t-\Delta t}\right)+{\displaystyle \frac{f\Delta x}{2gD{A}^2}}{\left(Q_{up}\right)}_{i,t}\left|{\left(Q_d\right)}_{i-1,t-\Delta t}\right|=0$$

(12)

-

Along the C⁻ characteristic line (Δx/Δt = −a),

$$H_{i,t}-H_{i+1,t-\Delta t}-{\displaystyle \frac{a}{gA}}\left({\left(Q_d\right)}_{i,t}-{\left(Q_{up}\right)}_{i+1,t-\Delta t}\right)-{\displaystyle \frac{f\Delta x}{2gD{A}^2}}{\left(Q_d\right)}_{i,t}\left|{\left(Q_{up}\right)}_{i+1,t-\Delta t}\right|=0$$

(13)

The discharge at the upstream side of the computational section i ((Q_up)_i) and the discharge at the downstream side of the section ((Q_d)_i) are identical for pure unsteady liquid pipe flow [83]. The staggered grid in applying the method of characteristics [20] is the most efficient and stable MOC scheme.

At a boundary (reservoir, valve, Francis turbine, surge tank, etc.), a device-specific equation replaces one of the water hammer compatibility equations [7,20]. The Francis-turbine boundary condition will be briefly described herein. The Francis turbine may undergo several transient operating regimes (see Section 2.2). The dynamic behavior of a governed turbine is described by (i) the turbine head balance equation, (ii) the dynamic equation of rotating masses), (iii) the governor dynamic equation which relates the turbine rotational speed change to the position of the regulating mechanism(s), and (iv) the pipeline equations (water hammer and column separation equations) [7,20,84,85]. The relationship among influential variables is presented in the form of the experimentally predicted turbine characteristics (see Section 2.1). It should be noted that approximate turbine characteristics can be used for preliminary analysis [86,87,88,89]. The complete set of the hydraulic turbomachine–governor–pipeline equations should be used for the case of load reduction in which the turbine speed is regulated by the governor. The governor equations are omitted in analysis for the case of turbine shutdown in which the unit speed change is controlled by the net torque only. Boundary condition defining the shutdown of the Francis turbine, which is incorporated into the staggered grid of the MOC, is described by the following equations (no column separation is allowed at the Francis turbine inlet and outlet):

-

Water hammer compatibility Equations (9) and (10)

-

Head balance equation:

$$H_{up}-H_r\left({\left({\displaystyle \frac{n}{n_r}}\right)}^2+{\left({\displaystyle \frac{Q}{Q_r}}\right)}^2\right)W_H\left(y\left(t\right),x\right)-H_d=0$$

(14)

-

Dynamic equation of the turbine unit rotating masses:

$$\left({\left({\displaystyle \frac{n}{n_r}}\right)}^2+{\left({\displaystyle \frac{Q}{Q_r}}\right)}^2\right)\hspace{0.33em}{W}_T\left(y\left(t\right),x\right)+{\left({\displaystyle \frac{T}{T_r}}\right)}_{t-2\Delta t}-I{\displaystyle \frac{\pi }{30}}{\displaystyle \frac{n_r}{T_r}}{\displaystyle \frac{1}{\Delta t}}\left(\left({\displaystyle \frac{n}{n_r}}\right)-{\left({\displaystyle \frac{n}{n_r}}\right)}_{t-2\Delta t}\right)=0$$

(15)

For ease of coding, the turbine characteristics in Equations (14) and (15) are represented as dimensionless head (W_H) and torque (W_T) characteristics along the rectangular abscissa x = π + tan⁻¹((Q/Q_r)/(n/n_r)) [20].

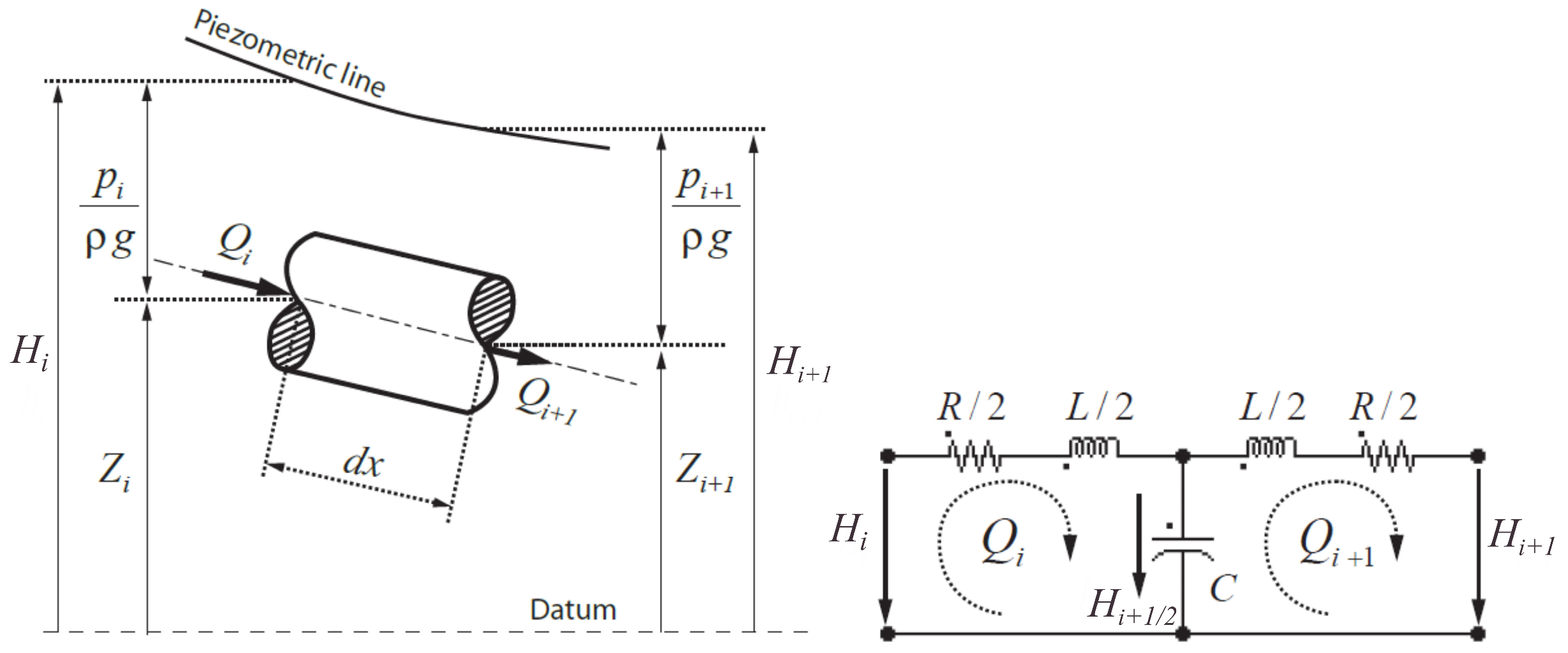
Electrical-Analogy-Based Finite Difference Method

Hydraulic elements are modeled using the impedance method [90] based on an RLC electrical circuit, where the variables piezometric head H at the node and flow rate Q through an individual element correspond to the electrical voltage U and the electrical current i in the equivalent electrical circuit.

Using the continuity (9) and momentum (10) equations and electrical analogy of modeling the propagation of pressure head waves in pipeline and modeling the propagation of voltage waves in conductors allows the introduction of a lineic hydraulic resistance R′, a lineic hydraulic inductance L′ and a lineic hydraulic capacitance C′ (lineic hydroacoustic parameters) [71] as follows:

$${\displaystyle \frac{\partial H}{\partial t}}+{\displaystyle \frac{1}{C\prime }}{\displaystyle \frac{\partial Q}{\partial x}}=0$$

(16)

$${\displaystyle \frac{\partial H}{\partial x}}+L\prime {\displaystyle \frac{\partial Q}{\partial t}}+R\prime Q=0$$

(17)

The system of hyperbolic partial differential Equations (16) and (17) is solved using the finite difference method [71]. The results of the method are ordinary differential equations that are represented as a T-shaped equivalent scheme as shown in Figure 4. The RLC parameters of the equivalent scheme are calculated as follows:

$$R={\displaystyle \frac{f\left|Q\right|}{2gD{A}^2}}dx, L={\displaystyle \frac{1}{gA}}dx, C={\displaystyle \frac{gA}{a^2}}dx$$

(18)

The set of Equations (16) and (17) can now be formulated according to Figure 4 as follows:

$$\left[\begin{array}{ccc}C& 0& 0\\ 0& L/2& 0\\ 0& 0& L/2\end{array}\right]\cdot {\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{H}_{i+1/2}\\ Q_i\\ Q_{i+1}\end{array}\right]+\left[\begin{array}{ccc}0& -1& 1\\ 1& R/2& 0\\ -1& 0& R/2\end{array}\right]\cdot \left[\begin{array}{c}{H}_{i+1/2}\\ Q_i\\ Q_{i+1}\end{array}\right]=\left[\begin{array}{c}0\\ H_i\\ -H_{i+1}\end{array}\right]$$

(19)

The set of Equation (19) is extended to the whole pipe and solved by the fourth order Runge–Kutta method [71]. In a pipe with a length dx, the hydroacoustic capacitance C is related to storage effect due to pressure increase and it is a function of the wave speed; hydroacoustic inductance L is related to inertia effect of the liquid; hydroacoustic resistance R is related to the pressure head losses through the pipe.

The Francis-turbine model is based on an electrical analogy as well. It allows modeling of a hydraulic component as a set of RLC elements—see Figure 5. If the transition between two operating points of a turbine corresponds to a succession of steady-state points, the transient behavior of a hydraulic machine can be modeled using steady-state characteristics (hill chart).

The complete hydropower system comprises objects, each representing a specific element of the system. A global set of differential equations is generated and solved by the fourth order Runge–Kutta procedure [71].

5.4. Note on Multidimensional Water Hammer Modeling

One-dimensional numerical models cannot accurately predict some high-frequency transient effects in pipelines (unsteady skin friction) or hydraulic turbines (draft tube vortex, rotor–stator interaction). Flow instabilities during water hammer events are not yet fully understood [91]. The accuracy of 1D model, traditionally used for water hammer analysis in hydropower plants, can be increased by introducing terms that account for multidimensional effects [92]. For direct treatment of 3D effects [93,94], either coupled 1D-3D (global-local) [29,95,96,97,98] or full 3D (global) water hammer models have been developed [24,99,100,101,102,103]. The 3D unsteady flow models are computationally intensive and defining the right boundary conditions in hydropower structures is not an easy task. Certain approximations in water hammer modeling [104,105] may have a negligible influence in some applications but may introduce significant systematic errors in other circumstances. Field measurements are needed to validate water hammer models and adequacy of design strategies. Validation studies of 1D water hammer models traditionally used by practicing engineers are presented in Section 6 of this paper. Multidimensional water hammer models are subject of intensive research elsewhere and their treatment is beyond the scope of this paper.

6. Validation and Discussion of 1D Water Hammer Models Applied to Hydropower Systems

In this Section, we present and discuss the practical use of in-house and commercial computer programs [21,54,70] and a comparison between calculated and measured values of hydrodynamic quantities. Five distinct case studies investigated by the industrial authors of this paper include simple and complex new and refurbished hydropower systems in which different water hammer control methods have been applied. Readers of this paper can find additional water hammer case studies in Francis-turbine hydropower systems in a number of professional textbooks [7,17,19,20,69,90] and technical papers [8,13,25,30,42,43,64,66,70], just to mention a few.

The software packages have been selected based on their availability and capabilities to model hydropower systems with different boundary conditions (types of surge tank, consideration of electrical grid systems) and requirements by the clients. For the very same boundary conditions and relevant input data, the selected in-house and the commercial software packages produce the same results.

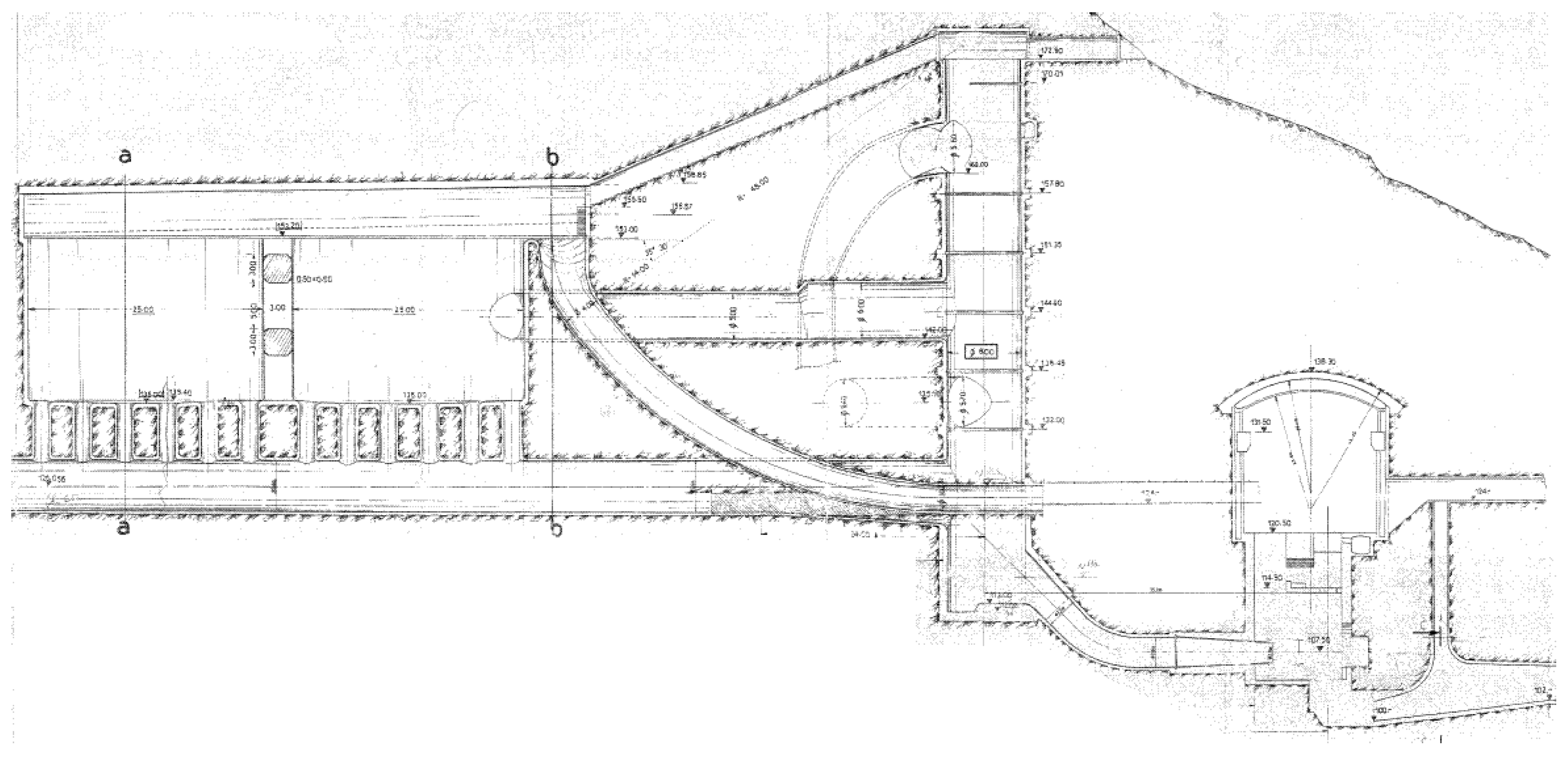
6.1. Plužna Small Hydropower Plant

Plužna small hydropower plant (SHPP) is in the north-western part of Slovenia. The plant was built in 1931 and upgraded in 1995. Two old horizontal-shaft Francis turbines (output 2 × 0.55 MW) were replaced by one new horizontal-shaft Francis turbine (output 1.87 MW). The total discharge in the existing penstock was increased from 2.2 m³/s to 3.3 m³/s; however, the permissible maximum pressure head at the turbine inlet h_sc,max,all = 85.8 m remained the same [106].

The plant comprises an upstream Gljun Creek reservoir, penstock of diameter D = 0.85 m and length L = 121.2 m, horizontal-shaft 1.87 MW Francis turbine and tailwater reservoir (see Figure 6). The water level in the upstream reservoir is in the range of 420.0 m.a.s.l. to 421.5 m.a.s.l. and the level in the tailwater reservoir is 352.1 m.a.s.l. The maximum gross head is H_g,max = 63 m and maximum discharge Q_max = 3.3 m³/s. The rotational speed of the turbine is n = 750 rpm and the polar moment of inertia of the unit rotating parts is I = 8.86 × 10³ kg·m² (after adding a flywheel of 7.70 × 10³ kg·m²).

Several operating regimes were investigated during commissioning tests, including turbine start-up, load acceptance, load reduction, load rejection, and emergency shutdown of the turbine unit. The resulting water hammer was controlled by appropriate adjustment of the guide vane closing and opening times, and increased unit inertia by adding a flywheel—see Figure 7. The in-house MOC numerical model was used for computational analysis.

Emergency Shutdown of the Turbine from Full Load

Emergency shutdown of the turbine from full load is the most severe transient regime occurring under normal operating conditions [7]. The turbine was disconnected from the electrical grid followed by the full closure of the guide vanes. A two-stroke guide vane closing law was applied—see Figure 8a.

The maximum pressure in the scroll case and maximum turbine rotational speed are two important parameters in turbine design (see Section 4). The turbine rotational speed n and the pressure head in the scroll case at the turbine inlet h_sc (datum level Z = 353.95 m.a.s.l.) are depicted in Figure 8b and Figure 8c, respectively. There is very good match between simulated and experimental results. The computed maximum head h_sc,max,c = 83.9 m matches the measured maximum head h_sc,max,m = 83.9 m perfectly. The computed maximum turbine rotational speed n_max,c = 1036 rpm is slightly higher than the measured speed n_max,m = 1030 rpm. The maximum head is less than the maximum permissible head h_sc,max,all = 85.8 m. The computed maximum turbine rotational speed rise Δn_max,c = n_max,c/n₀ × 100 − 100 = 38% is within the permissible limits Δn_max,all = 40% too.

Computed envelopes of the maximum and minimum piezometric heads along the concave-shaped penstock profile are shown in Figure 8d. This diagram is important for pipeline design engineers to construct a safe and economic waterway system. The envelope of the minimum head (H_min) indicates the danger of liquid column separation [83] when the pressure drops below the penstock profile. In this instance, the computed minimum head is well above the penstock profile.

6.2. Toro II Hydropower Plant

A high-head hydropower plant Toro II is in the province of Alajuela, Costa Rica. It is the second stage of a cascade on the Toro River catchment area and was put into operation in 1995 [107]. The flow-passage system comprises an upstream end Toro River storage basin, steel penstock with a length of L = 1577.3 m and an equivalent diameter [7] D_e = 2.23 m feeding the water to two vertical-shaft 34 MW Francis turbines and a downstream end reservoir—see Figure 9. The water level in the upstream end reservoir is in the range from 1069.5 m.a.s.l. to 1075.0 m.a.s.l.; the level in the downstream end reservoir is from 689.7 m.a.s.l. to 690.5 m.a.s.l. The two turbine units operate at maximum gross head H_g,max = 385.3 m and maximum turbine discharge Q_max = 10.0 m³/s. The rated speed of the turbine is n = 720 rpm, and the polar inertia of the unit rotating parts is I = 47.2 × 10³ kg·m².

Hydraulic transient tests included operation with one or two turbines. Water hammer was controlled by appropriate adjustment of the guide vane closing/opening laws only. Simultaneous shutdown of the two units from the full load was considered as an extreme case within the normal operating transient regimes, and the computational and field test results are presented in this paper. Computational analysis was performed using the MOC-based in-house software package.

Simultaneous Emergency Shutdown of Two Turbine Units from Full Load

Computed and measured results for simultaneous emergency shutdown of two turbine units from full load are presented in this paper [107]. Initially, the electromagnetic torque of the generator drops to zero instantaneously, consequently the rotational turbine speed of the units increases. The closure of the guide vanes reduces the hydraulic torque, limiting the maximum rotational speed. In the presented transient event, after disconnection from the electrical grid, the guide vanes fully close—see Figure 10a. The measured and calculated results for turbine rotational speed (n) and pressure head at the turbine inlet (h_sc) (datum level Z = 685.0 m.a.s.l.) are depicted in Figure 10b and Figure 10c, respectively. There is a reasonable agreement between the results of computation and measurement. The computed maximum head h_sc,max,c = 504.2 m is slightly higher than the measured one h_sc,max,m = 501.0 m. The maximum head is less than the permissible head h_sc,max,all = 515.0 m. The computed maximum turbine rotational speed n_max,c = 1075 rpm is slightly lower than the measured speed n_max,m = 1082 rpm. The computed maximum turbine rotational speed rise Δn_max,c = n_max,c/n₀ × 100 − 100 = 49.3% is within the permissible limits Δn_max,all = 55%. The same holds for the measured speed increase i.e., Δn_max,m = n_max,m/n₀ × 100 − 100 = 50.3%. One may observe that discrepancies between the measured and calculated results increase at small guide wane openings.

Figure 10d depicts the envelopes of maximum and minimum piezometric heads along the penstock profile H_min and H_max, respectively. As pointed out in Section 6.1, this diagram is important for design engineers to ensure the construction of a safe and economical pipeline system. In our case study the envelope H_min is well above the penstock profile which is of convex-shaped longitudinal profile. This type of profile is more sensitive to low pressure heads as the concave-shaped profile (compare Figure 8d and Figure 10d).

6.3. Moste Hydropower Plant

The Moste hydroelectric power plant has been operating as the first upstream power plant on the Sava River in the north-west of Slovenia since 1952. The Moste HPP is a storage hydroelectric power plant for peak energy production and, together with a separate unit that exploits the energy potential of the Završnica Creek, forms a single energy system, as shown in Figure 11. The storage basin enables weekly flow balancing.

Three vertical-shaft 5.5 MW Francis turbine units were originally installed in the Moste power plant powerhouse, and the fourth 8.1 MW Francis-type pump-turbine unit was later installed in Moste powerhouse with a separate connection to the Završnica supply pipeline [108]. In the pumping mode, this unit was intended to pump Sava water into the higher-lying Završnica basin. Due to the pollution of the Sava River, the pumping regime was abandoned in 1982, and the unit operated only as a classical type Francis turbine. Growing geological problems and the need for modernization of the three old Francis turbine units resulted in a decision to replace the old units and reinforce the powerhouse structure to reduce unwanted deformations. In the period 2009–2010, two old 5.5 MW Francis units were replaced by new 7.5 MW units, and the space of the third 5.5 MW unit was intended for the construction of reinforcements of the power plant powerhouse structure.

In this paper, we consider water hammer in the flow-passage system of the Sava River—see Figure 11 [109], which includes: a supply tunnel with a length of L = 840 m and an internal diameter D = 3.0 m, cylindrical surge tank of diameter D = 7.5 m with lower and upper side galleries, and penstock with a length L = 154.5 m and a diameter D = 2.6 m feeding two 7.5 MW vertical-shaft Francis turbines—see Figure 11. The two turbines are connected to a common tailrace tunnel, measuring L = 1500 m in length and D = 4.0 m in diameter, and a downstream end reservoir. The water level in the upstream end reservoir is in the range from 510.0 m.a.s.l. to 524.75 m.a.s.l.; the level in the downstream end reservoir is in the range from 454.28 m.a.s.l. to 457.53 m.a.s.l. The two units operate at maximum gross head H_g,max = 70.47 m and maximum turbine discharge Q_max = 13.0 m³/s. The rated speed of the turbine is n = 500 rpm, and the polar inertia of the unit rotating parts is I = 20.0 × 10³ kg·m².

Water hammer in the considered Moste HPP was controlled by appropriate adjustment of the guide vane closing and opening laws, and surge tank with galleries. The transient effects in the Sava River tailwater system are negligible and neglected in water hammer analysis. The results of the analysis for simultaneous load rejection of the two Francis turbines are presented and discussed. Computational analysis was performed by using an electrical-analogy-based software package SIMSEN-Hydro v1.5 [110].

Simultaneous Full-Load Rejection of Two Turbines

Simultaneous full-load rejection of two Francis turbines is the most severe transient regime which occurs at normal operating conditions. After initial disconnection from the electrical grid, the guide vanes do not fully close. The turbine governor sets the unit rotational speed to the initial value. The two units are operating at speed-no-load conditions and are ready for load acceptance. This analysis considers the initial state when the two units are operating at generator power P_gen = 6.7 MW and at a headwater level Z_up = 524.75 m.a.s.l. Figure 12 shows the relative guide vane servomotor stroke (y_gv/y_gv,max), the pressure head at the turbine inlet valve coupled to the spiral case (h_sc) and the turbine rotational speed (n).

The calculated and measured servomotor strokes are the same (Figure 12a). The calculated maximum pressure head h_sc,max,c = 87.3 m is higher than the measured head h_sc,max,m = 81.5 m (Figure 12c; datum level Z = 457.53 m.a.s.l.). The maximum computed pressure head exhibits a peak value during the guide vanes cushioning stroke; there is no such peak at measured results. The maximum head h_sc,max,c = 87.3 m is less than the maximum permissible head h_sc,max,all = 91.9 m. Figure 12d shows the pressure head oscillations over a longer time period. One may visualize the effect of surge tank with galleries on pressure oscillations in the penstock. The characteristic shape of the pressure oscillation in the pipeline shows that the water level in the surge tank reaches the upper chamber and after approximately T = 180 s drops back into the vertical shaft. The calculated maximum turbine rotational speed n_max,c = 711.5 rpm is higher than the measured turbine rotational speed n_max,m = 696.2 rpm (Figure 12b). The computed maximum turbine rotational speed rise Δn_max,c = n_max,c/n₀ × 100 − 100 = 42.3% is within the permissible limits Δn_max,all = 50%. The discrepancies between measured and calculated results may be attributed to the model turbine characteristics that are difficult to measure at small guide vane openings.

6.4. Doblar I Hydropower Plant

The Doblar I hydroelectric power plant is a combined storage/run-of-river hydroelectric power plant on the Soča River in the north-west of Slovenia. The plant was put into operation in 1939. Initially, the plant was equipped with three Francis turbines each operating with a maximum output of 11.6 MW producing electricity for the Italian network with a network frequency of 42 Hz. In 1950, the hydropower plant changed the state ownership and, together with the rest of the Slovenian grid, changed to a grid frequency of 50 Hz. In 2023, the old three turbines were replaced by new upgraded turbine units, each operating at a maximum output of 13.6 MW.

The flow-passage system comprises an upstream end Soča River storage Basin, headrace tunnel with a length L = 3735 m and a diameter D = 5.6 m, complex surge tank system with an ellipse-shaped surge tank and cylindrical shape surge shaft, three parallel penstocks with a length L = 46 m and a diameter D = 3.0 m, three vertical-shaft Francis-turbine units each with a rated power of P_r = 9.5 MW (maximum 13.6 MW) and connected to its own downstream end horizontal horseshoe-shaped surge tank of horizontal-cross-sectional area A = 78.5 m², tailrace tunnel of a length L = 111.4 m and a dimeter D = 4.2 m, and a downstream end reservoir—see Figure 13. The water level in the upstream reservoir is in the range from 145.0 m.a.s.l. to 153.0 m.a.s.l.; the level in the downstream reservoir ranges from 104.5 m.a.s.l. to 106.87 m.a.s.l. The two units operate at maximum gross head H_g,max = 48.5 m and maximum turbine discharge Q_max = 33.0 m³/s. The rated speed of the turbine is n = 300 rpm, and the polar inertia of the unit rotating parts is I = 84.7 × 10³ kg·m².

The configuration of the upstream end surge tank system in Doblar I HPP flow-passage system needs further explanation (Figure 13 and Figure 14) [111]. The surge tank system comprises two connected surge tanks. The first surge tank is built of two ellipse-shaped orifice surge tanks. The combined cross-sectional area of the two chambers is A = 880 m². There are 12 orifices at the bottom of the two chambers with an orifice diameter D = 1.6 m and a length L = 5.84 m. The second surge tank (surge shaft) is located L = 46 m downstream of the first surge tank and is of a cylindrical shape with an inner diameter D = 8.0 m. The two surge tanks are coupled with a L = 46.0 m long tunnel of a variable inner diameter from 5.0 to 6.0 m.

Water hammer in Doblar I HPP is controlled through appropriate adjustment of the guide vane closing and opening laws, the surge tank system in the headrace tunnel and the surge tanks in the three tailrace tunnels. Due to the age of the hydropower power plant and the historical context (change in the country ownership after the Second World War), one of the main obstacles in water hammer analysis was the lack of documentation for the completed works of the flow and upstream water level system. Subsequent geodetic measurements provided a clear picture of the situation, necessary for appropriate modeling and calibration of the computational model. Limited availability of existing documentation in cases of reconstruction can cause delays, inaccurate modeling and additional costs. The responsibility of the hydropower power plant owner (client of the analysis) is to provide access to necessary documentation. The results of the analysis for simultaneous load rejection of the three Francis turbines are presented and discussed. Computational analysis was performed by using an electrical-analogy-based software package SIMSEN-Hydro v1.5 [110].

Simultaneous Load Rejection of Three Turbine Units

Simultaneous full-load rejection of three Francis turbines is the most severe transient regime which occurs at normal operating conditions. This analysis considers the initial state when the three units are operating at generator power P_gen,1 = 11.0 MW, P_gen,2 = 12.0 MW and P_gen,3 = 10.2 MW, and at a headwater level Z_up = 152.4 m.a.s.l. The computed and measured results for the relative guide vane servomotor stroke (y_gv/y_gv,max), the turbine rotational speed (n), the pressure head at the turbine inlet valve coupled to the spiral case (h_sc) and the pressure head at the draft tube inlet (h_dt) are shown in Figure 15 and apply to the unit 3 (P_gen,3 = 10.2 MW).

The computed and experimental servomotor strokes are the same (Figure 15a). The calculated maximum turbine rotational speed n_max,c = 405.5 rpm is higher than the measured turbine rotational speed n_max,m = 391.5 rpm (Figure 15b). The computed maximum turbine rotational speed rise Δn_max,c = n_max,c/n₀ × 100 − 100 = 35.2% is within the permissible limits Δn_max,all = 40%. The discrepancies between measured and calculated results may be attributed to the model turbine characteristics that are difficult to measure at small guide vane openings.

The calculated maximum pressure head in the scroll case during the guide vanes closure h_sc,max,c = 44.2 m is higher than the measured head h_sc,max,m = 42.9 m (Figure 15c; datum level Z = 107.25 m.a.s.l.). The maximum computed pressure head exhibits a peak value during the guide vanes closure and soon after that starts to grow due to the response of the headrace surge tank system. Investigation of head history in an extended time frame of 2000 s (Figure 16a) shows that the maximum computed head h_sc,max,c = 46.1 m is lower than the measured head h_sc,max,m = 47.5 m and occurs about 100 s after the start of the transient event. However, the maximum measured turbine inlet head h_sc,max,m = 47.5 m is much lower than the maximum permissible head h_sc,max,all = 54.6 m. Figure 16b shows the comparison between the measured and calculated water level oscillations in the cylindrical shaft of the surge tank system (Figure 14). The maximum computed water level in the shaft Z_st,max,c = 154.8 m.a.s.l. is slightly higher than the measured one Z_st,max,m = 154.7 m.a.s.l. The results reveal excellent damping properties of the surge tank system. The deviation between the calculated and measured values of the turbine inlet pressure heads in the penstock and water level oscillations in the surge tank system are attributed to the simplified modeling of the headrace surge tank system and the uncertain data for the ellipsoidal camber inflow/outflow orifice head losses.

The simulated maximum draft tube pressure head h_dt,max,c = 3.9 m is higher than the measured h_dt,max,m = 1.9 m (average of the pressure head peaks)—see Figure 15d. The calculated minimum pressure head is h_sc,min,c = −2.0 m is slightly lower than the measured h_sc,min,m = −1.6 m (average of the pressure peaks). The minimum draft tube head is well above the vapor pressure head of −10 m; therefore, there is no danger of water column separation [83]. Observation of draft tube head oscillations reveal beneficial effect of the tailrace surge tank on low head oscillations in the tailrace system. In addition, during the guide vane closure and operation at speed-no-load conditions, high-frequency pulsations are present in the draft tube pressure head measurements. These pulsations can be attributed to complex local flow behavior in the draft tube entrance. The 1D numerical model cannot accurately capture multidimensional multiphase flow effects under the Francis turbine runner.

6.5. Lomščica Small Hydropower Plant

Lomščica small hydropower plant (SHPP) is in the northern part of Slovenia. The plant was put into operation in 1991. It comprises an upstream end Lomščica Creek reservoir, intake gate, penstock, turbine inlet butterfly valve, horizontal-shaft 2.1 MW Francis turbine equipped with a pressure regulating valve, and a tailrace, as shown in Figure 17. The total length of the penstock system is L = 715.5 m, and the diameter is D = 1.0 m. The water level in the upstream end reservoir ranges from 645.5 m.a.s.l. to 658.5 m.a.s.l.; the level in the downstream end reservoir is 540.0 m.a.s.l. The turbine unit operates at maximum gross head H_g,max = 118.5 m and maximum turbine discharge Q_max = 2.0 m³/s. The rated speed of the turbine is n = 1000 rpm and the polar inertia of the unit rotating parts is I = 0.88 × 10³ kg·m².

This Subsection presents results given for the closure of the turbine inlet butterfly valve of diameter D = 0.7 m under the discharge conditions. The turbine inlet valve is a shutoff type valve which is either in fully open or fully closed position. Shutoff valves (butterfly, spherical) proved to be one of the key elements regarding safe and economic operation of the hydropower plant [112,113]. Their main function is to close in emergency conditions such as pipe rupture and turbine runaway. The turbine inlet valve installed in Lomščica SHPP is equipped with a passive actuator. A self-closing type of the valve actuator (passive actuator) comprises an external weight, hydraulic servomotor and release mechanism proved to be simple and reliable in operation of the valve. Because the torque acting on the valve disk is highly dependent on flow conditions, the valve closing time varies significantly for different flow velocities. Computational analysis was performed using the MOC-based in-house software package.

Figure 18 presents measured and calculated pressure heads at the upstream end of the inlet butterfly valve and valve openings during the closure from the full and half load operation of the Francis turbine. The maximum calculated pressure head of h_v,up,max,c = 129.8 m at the upstream end of the valve (datum level Z = 541.3 m.a.s.l.) at full load operation of the plant is slightly higher than the measured head of h_v,up,max,m = 127.6 m (Figure 18b), respectively. Similar results were obtained for the case of half-load plant operation. The maximum calculated and measured heads are h_v,up,max,c = 127.7 m and h_v,up,max,m = 127.0 m (Figure 18d). The discrepancies in amplitude and phase shift are larger at small valve openings (complex flow structure downstream the valve). The maximum measured and calculated heads are less than the prescribed maximum head h_v,up,max,all = 130 m. The valve closure time is much longer for the case of half-load plant operation (t_c = 196 s, Figure 18c) than for the case of full-load operation (t_c = 127.7 s, Figure 18a). Unsteady hydraulic torque acting on the self-closing butterfly valve disk significantly affects the valve closing time [114].

6.6. Computational Error Analysis

For quantifying the results of the water hammer analysis presented in the above Section 6.1, Section 6.2, Section 6.3, Section 6.4 and Section 6.5, a uniform error metric is introduced. The computed and measured values of the maximum spiral case pressure head and the maximum turbine rotational speed are quantified by the maximum spiral case pressure head error h_sc,max,Err and the maximum turbine speed error n_max,Err as follows:

$$h_{sc,max,Err}=\left({\displaystyle \frac{h_{sc,max,c}}{h_{sc,max,m}}}-1\right)·100$$

(20)

$$n_{max,Err}=\left({\displaystyle \frac{n_{max,c}}{n_{max,m}}}-1\right)·100$$

(21)

The resulting values of the error analysis for the considered five water hammer cases are presented in

Table 1. Error analysis of maximum values of parameters h_sc (h_v) and n.

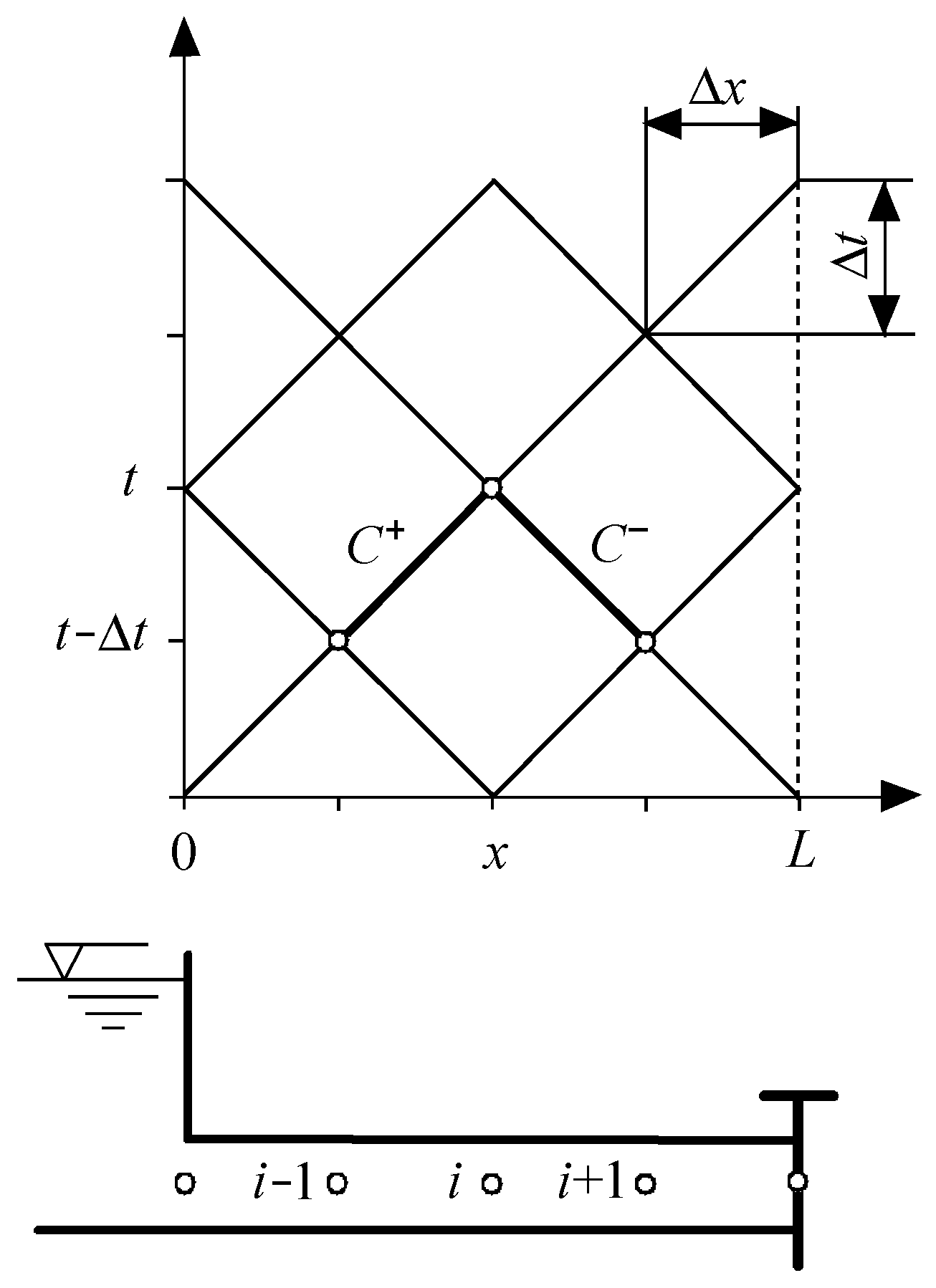
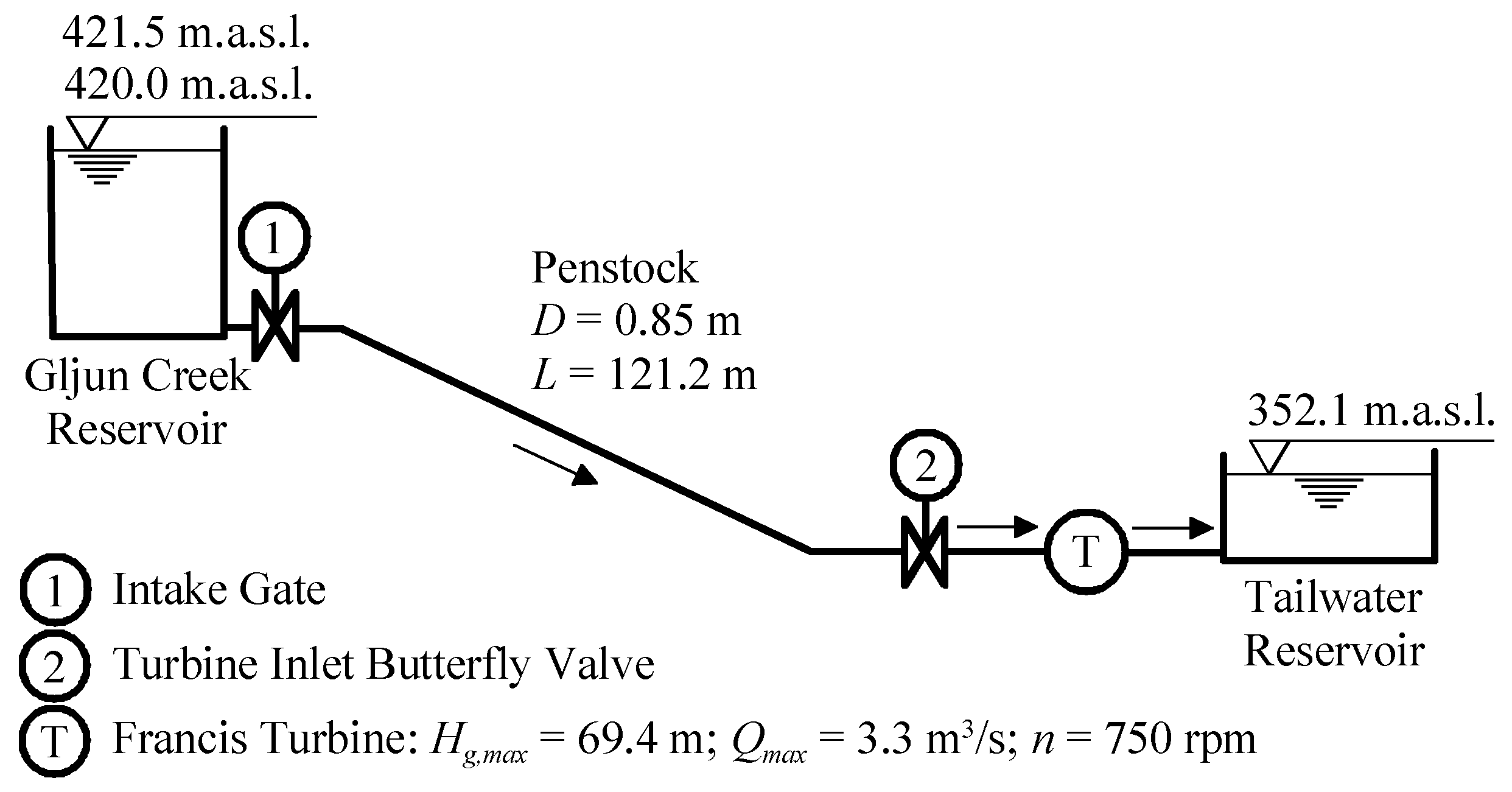
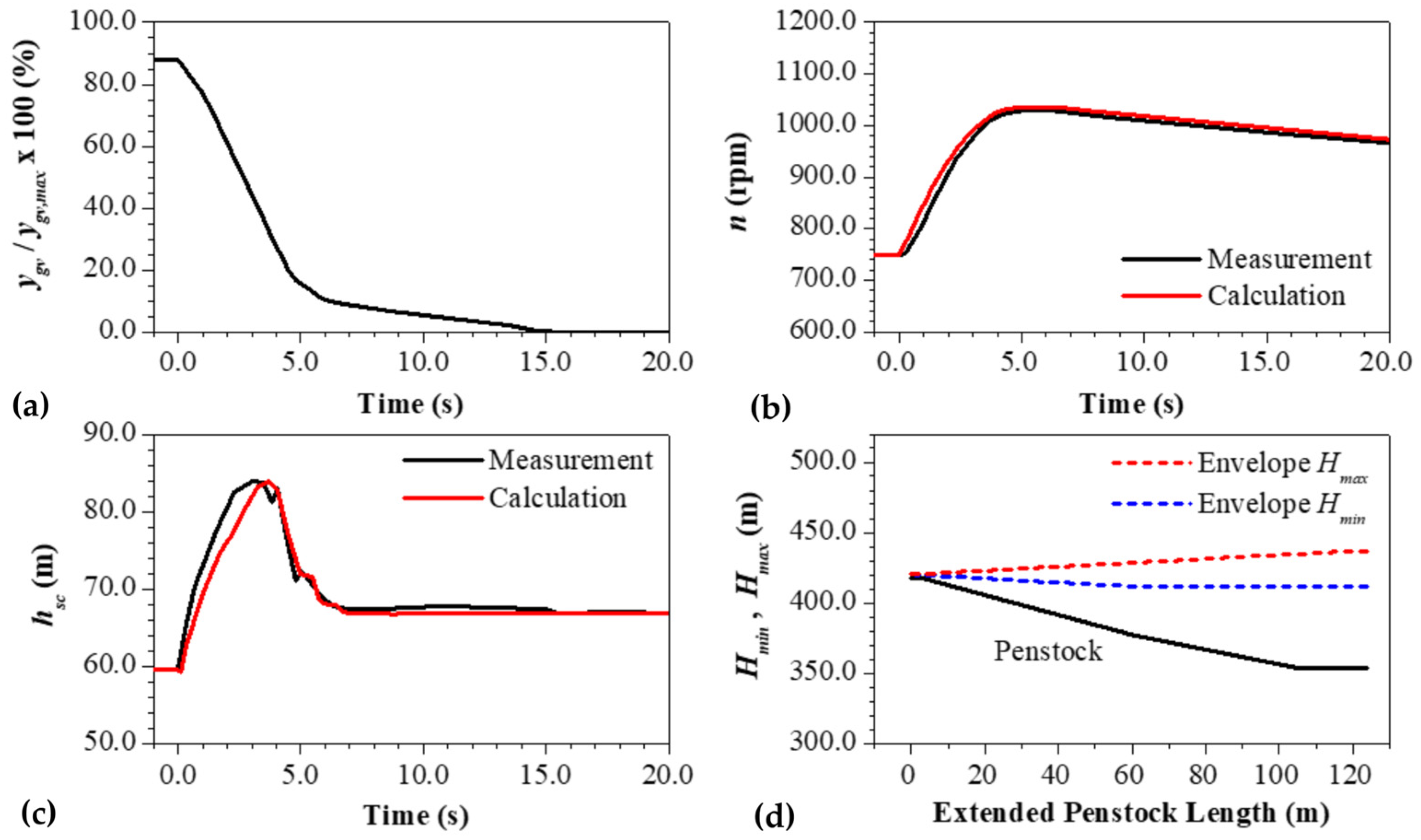
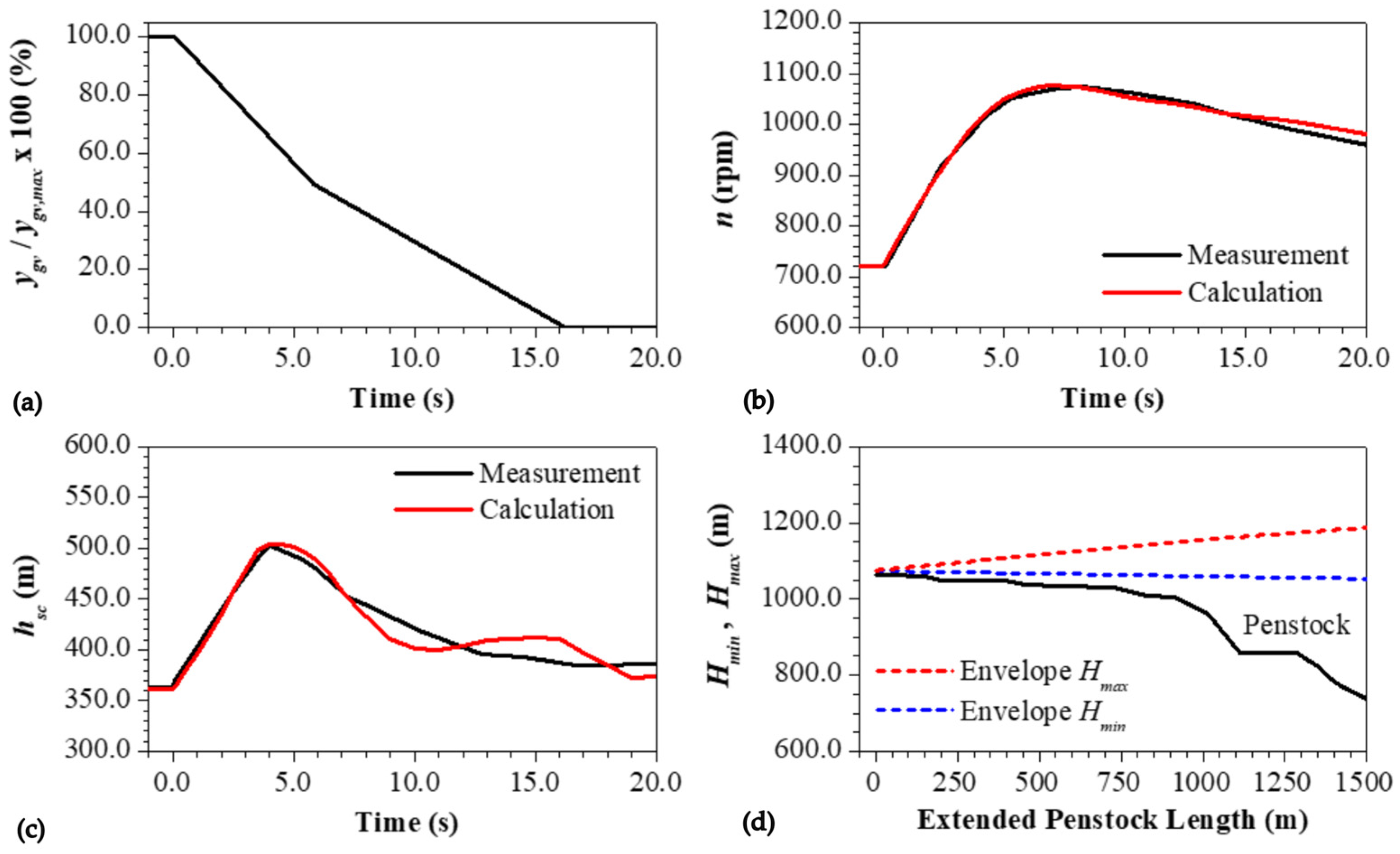
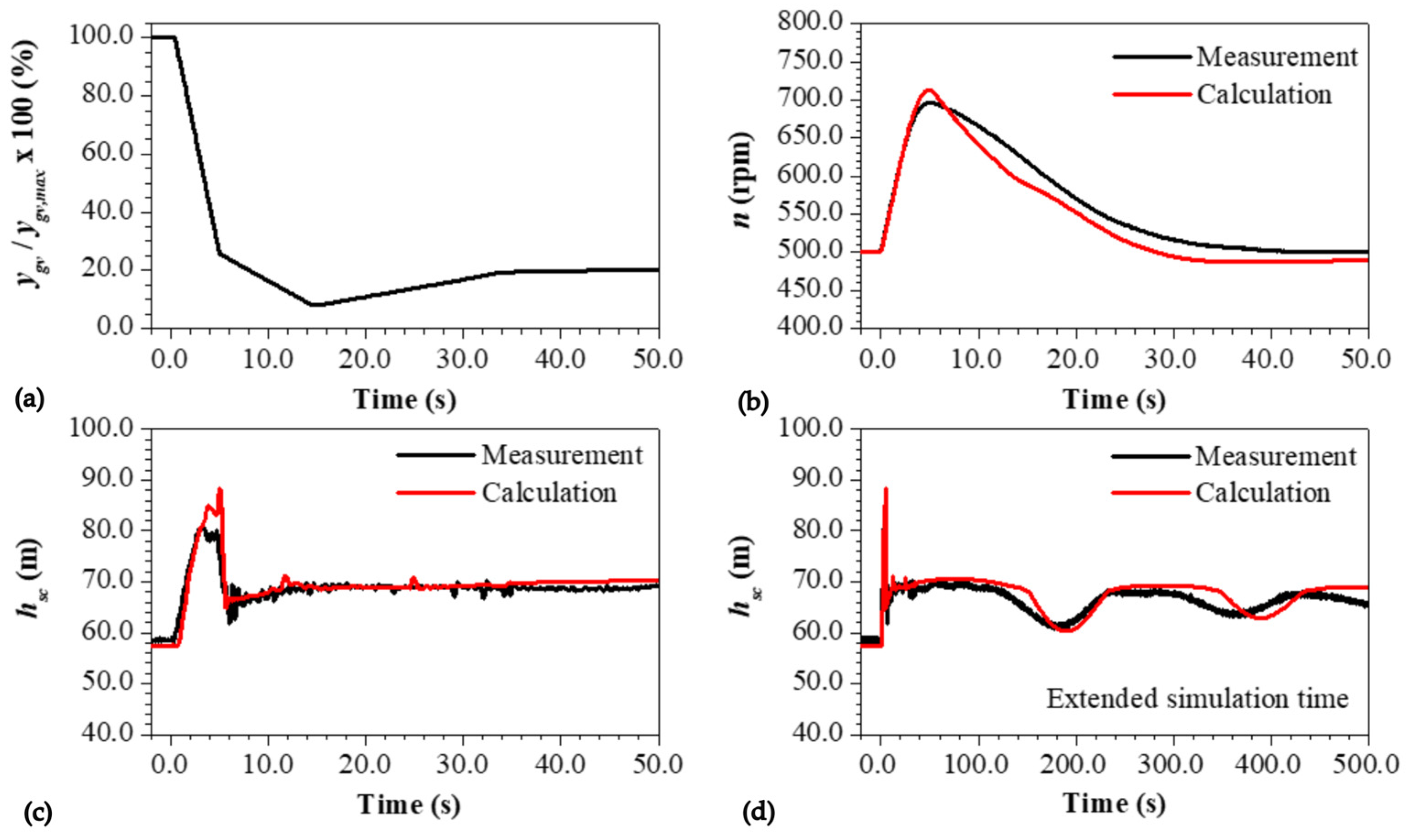
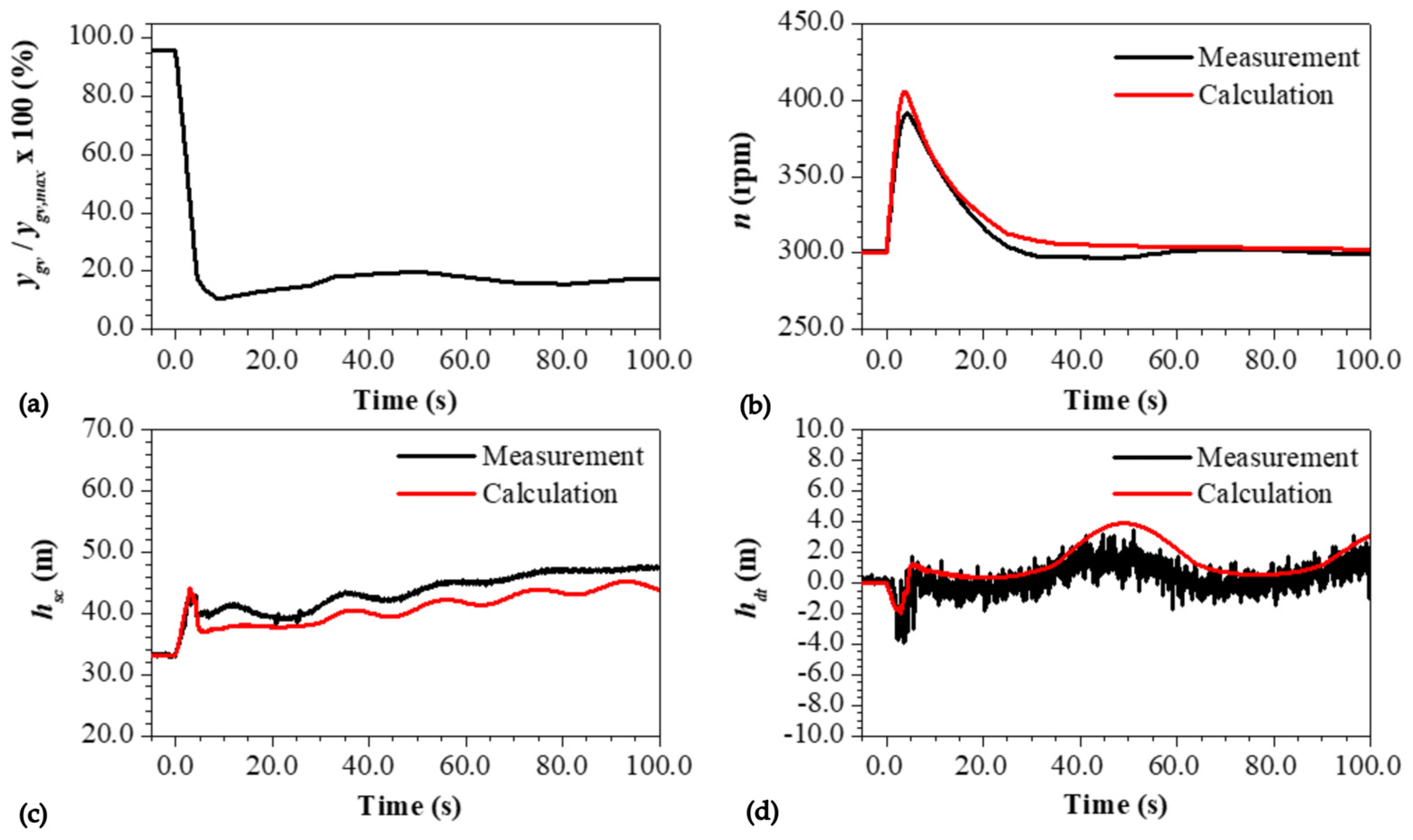
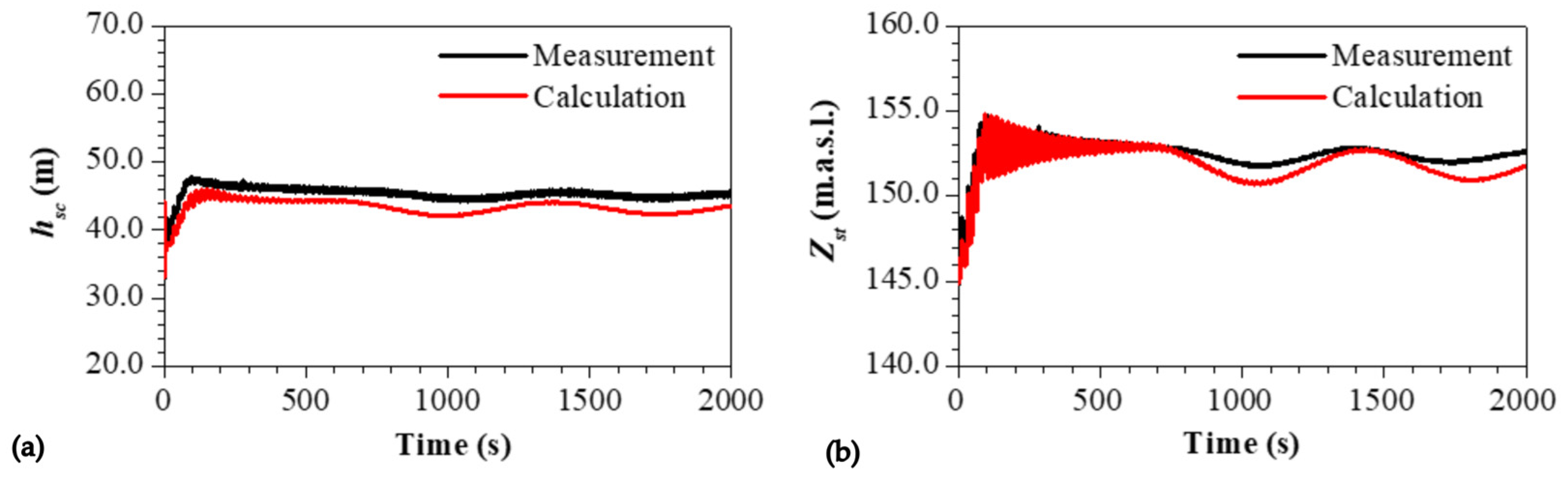
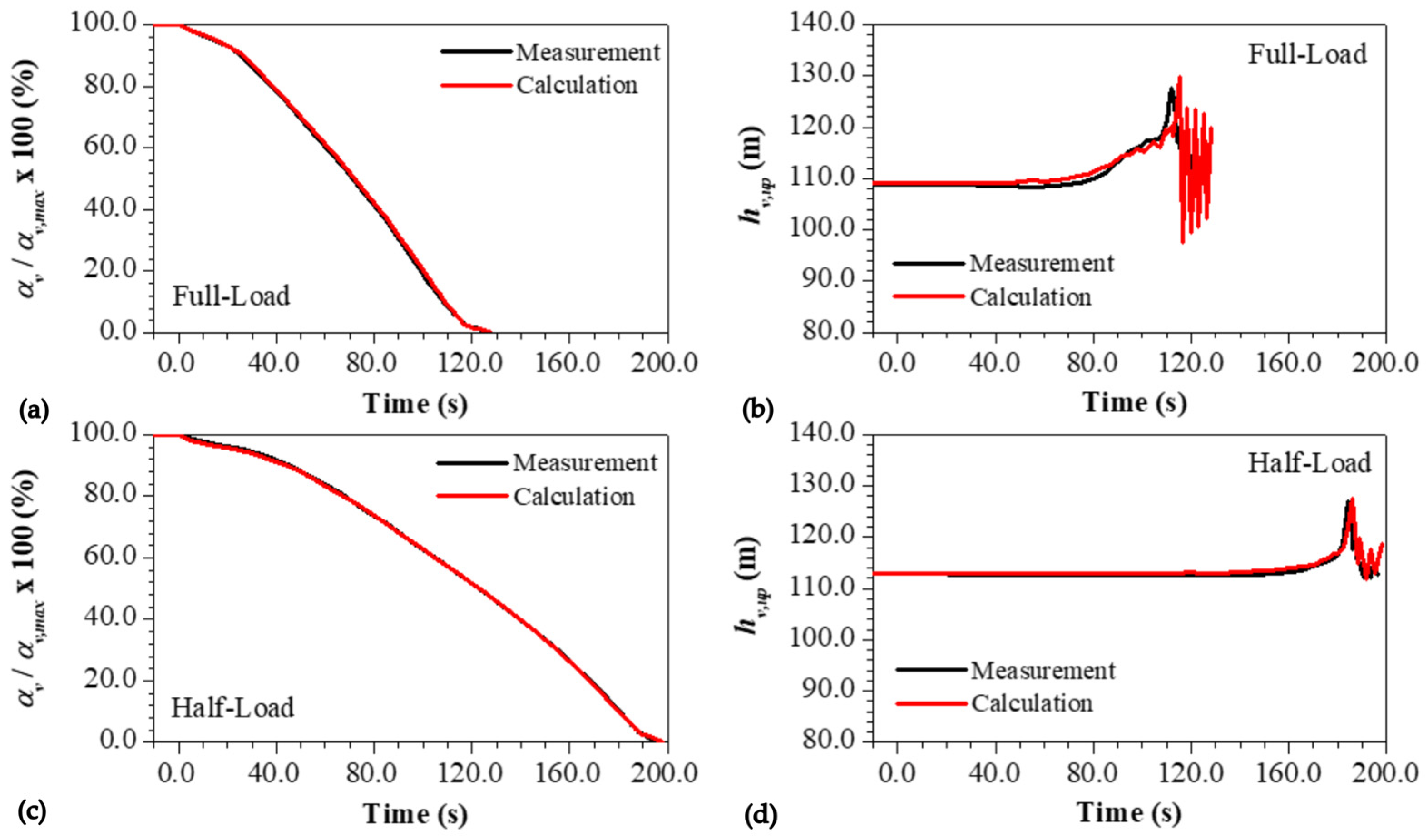
Subsection	hsc,max,c (m)	hsc,max,m (m)	hsc,max,Err (%)	nmax,c (m)	nmax,m (m)	nmax,Err (%)
6.1.	83.9	83.9	0	1036	1030	+0.6
6.2.	504.2	501.0	+0.6	1075	1082	−0.6
6.3.	87.3	81.5	+7.1	711.5	696.2	+2.2
6.4.	44.2	42.9	+3.0	405.5	391.5	+3.6
Subsection	hv,up,c (m)	hv,up,m (m)	hv,up,Err (%)	-	-	-
6.5.	129.8	127.6	1.7

.

Error analysis shows that 1D comparisons between the calculated and measured results are within the limits ±5% accepted in daily engineering practice. The discrepancies are larger for complex hydropower schemes due to difficulties both in measurements and simulations [104,105]. Most importantly, all the simulated and field test results are within the prescribed design limits as stated in the relevant sections.

7. Conclusions

The issues related to water hammer in new, renovated, and upgraded Francis-turbine hydroelectric power plants with simple and complex flow systems are reviewed and discussed in this paper. The engineers should be able to identify critical transient operating regimes during flexible operation of the power plant. Methods for mitigating the unwanted consequences of water hammer effects include operational scenarios (closing and opening laws), surge control devices, redesigning the pipeline components or limitation of operating conditions. A review of theoretical methods reveals that 1D modeling is widely used for water hammer analysis in engineering practice. Two numerical methods are traditionally used in hydropower industry due to their computational efficiency and flexibility: (1) method of characteristics and (2) electrical-analogy-based finite difference method. The two methods are successfully validated against field measurements in five distinct hydroelectric power plants including simple and complex, new and refurbished power plant systems. Naturally, the rehabilitation process offers the advantage of allowing comparative water hammer tests in the plant before and after the rehabilitation. On the other hand, design of a new plant is based on gained knowledge and good engineering practice. Investigation of water hammer control methods of five distinct case studies shows that the two-stage closing law of the guide vanes is the first choice to control water hammer. Additional control means (flywheel, surge tank(s)) may be required due to client demands and increasing complexity of the systems. The agreement between 1D calculated and measured results for the five test cases is acceptable from the engineering point of view. Finally, future developments are sought in development of computationally effective, robust and accurate multidimensional methods that will capture secondary high-frequency flow instabilities during the low-frequency water hammer events.