1. Introduction
The systemic crises of recent decades have progressively shifted the attention of policy makers from a primary focus on energy system affordability toward a more comprehensive set of requirements accounting for its resilience, security, and sustainability [
1,
2,
3]. Within this context, bioeconomy has emerged as a potential solution, this being an economic model “where the basic building blocks for materials, chemicals and energy are derived from renewable biological resources” [
1,
2,
4,
5]. Within this framework, bioenergy derives from the valorization and conversion of biomass and has gained significant attention as a renewable energy source (RES) due to its potential to reduce greenhouse gas (GHG) emissions and contribute to sustainable energy production. Differently from the other RESs, bioenergy is not subject to intermittency issues and offers the chance of unlocking a continuous, tunable, and clean generation of electrical and thermal energy, as well as a fuel for transport [
4,
5]. Going beyond biomass combustion, prominent studies have explored the potentialities of modern bioenergy, encompassing the conversion of biomass into energy through various processes, including combustion, gasification, and anaerobic digestion [
6,
7,
8,
9,
10]. In particular, the development of Bioenergy with Carbon Capture and Storage (BECCS) has emerged as a critical technology for mitigating climate change by enabling negative emissions. Prominent works by Azar et al. [
11], Smith et al. [
5], and Hayat et al. [
2] have assessed the feasibility and implications of BECCS systems in achieving global climate targets. Together, these studies highlight the dual role of biomass as both an RES and a tool for carbon sequestration, forming the foundation for ongoing research and innovation in the field of bioenergy. According to the 2024 Global Status Report of the CCS Institute, there are five operational BECCS plants, all located in the United States and providing a comprehensive capture capacity of roughly 2 Mtpa of CO
2, though their number is expected to substantially increase in the coming years [
12].
However, further research is required to enhance the design of such plants, with a particular emphasis on biomass-to-energy conversion processes. Among the different pathways to obtain bioenergy, gasification is a thermochemical conversion process occurring at a high temperature (in the range 750–900 °C) and in the presence of a gasifying agent (this being either air, oxygen, steam, or a mixture of them) that reacts with biomass [
7,
10,
13]. The product gas, also referred to as syngas, is mostly composed of hydrogen (H2), carbon monoxide (CO), carbon dioxide (CO
2), and methane (CH
4), along with traces of solid products (char), inorganic contaminants, and organic contaminants (tar) [
13,
14,
15].
The efficacy of a gasifier depends on a series of interconnected phenomena, the complexity and inherent variability of which render performance prediction challenging. Therefore, research on the design and modelling of biomass gasification has been critical for the optimization of the biomass conversion and process thermal efficiency [
14,
15,
16,
17,
18]. Modelling and simulation tools are valuable for exploring different operating conditions and optimizing the process, as they help in predicting process performance and providing a comprehensive representation of the chemical and physical phenomena, thus facilitating the scale up from laboratory- to pilot-scale equipment through kinetic, thermodynamic, and Computational Fluid Dynamic (CFD) models [
14,
15,
16]. Early models primarily focused on the thermodynamic and kinetic aspects of the gasification process, aiming to predict key parameters such as temperature, gas composition, and reaction rates [
18,
19,
20,
21,
22]. Thermodynamic models predict syngas composition based on the assumption that reactants react in a fully mixed condition for an infinite time [
21,
22]. The advantage of these models is their independence from gasifier design, allowing them to describe a wide range of plants without specific restrictions; on the other hand, thermodynamic equilibrium cannot be achieved in “real” gasifiers under a wide range of operating conditions [
16,
17]. Kinetic models predict syngas yield and composition over time or volume in a flowing medium, but their applicability is limited to specific reactor configurations, with increasing complexity as reactor design becomes more intricate, and they require the experimental measurement of physico-chemical parameters, limiting their generalizability and deeper understanding of process trends [
18,
19,
20]. CFD and multiphase flow modelling provide detailed insights into gas–solid–liquid interactions in gasifiers, enabling accurate predictions of syngas composition, temperature profiles, and species concentrations—particularly in fluidized bed reactors—and the supporting optimization of gasifier design, operating conditions, and biomass feedstock variability. However, the drawbacks include a high computational effort and limited extendibility, as the results are tied to specific geometries [
21,
22,
23,
24].
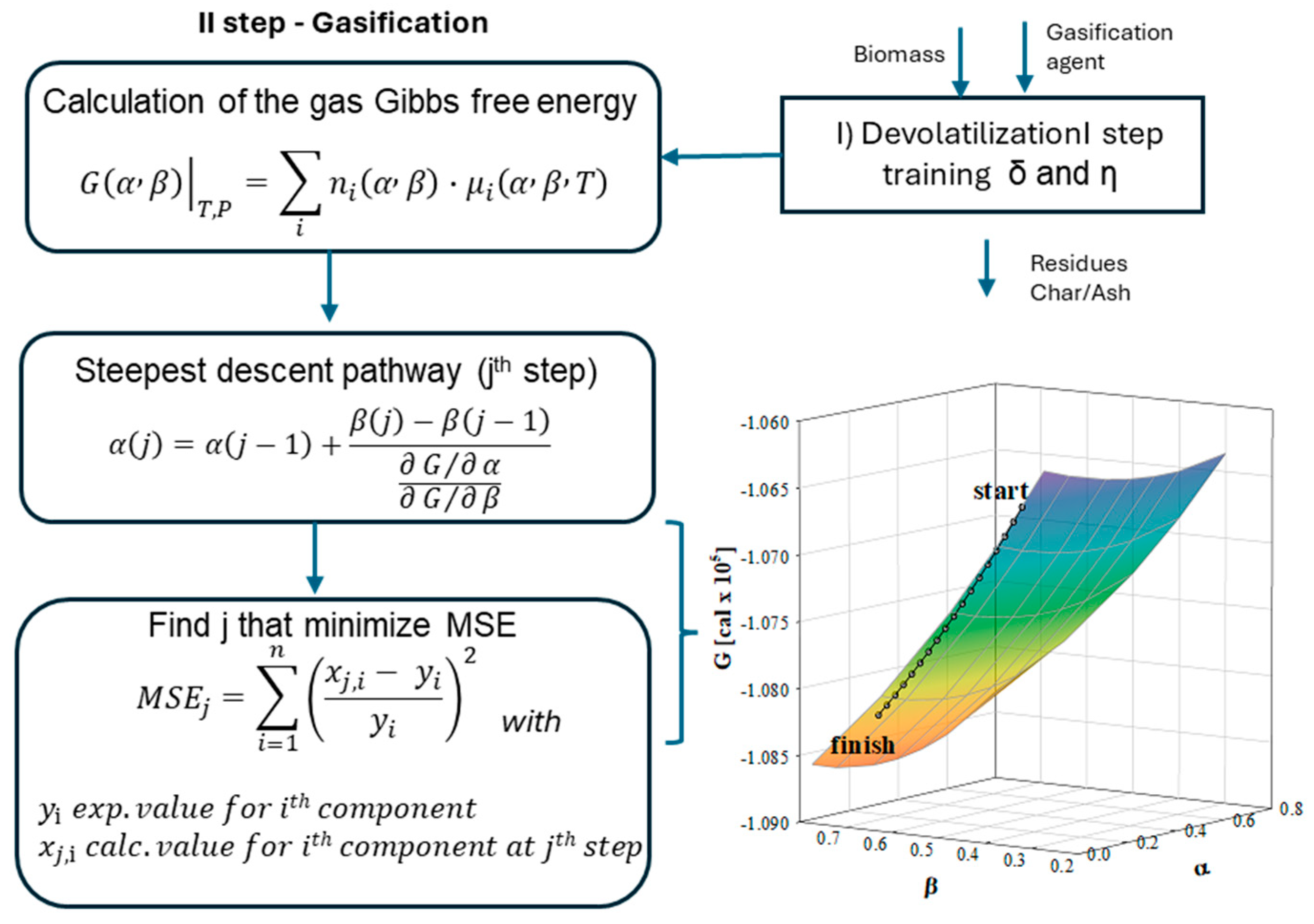
There is an increasing demand for short-cut models that can reliably predict gasifier design and optimization, while minimizing computational effort and the need for many experimental inputs. Once trained and validated on experimental data, these models can be integrated into commercial process simulators or used for comprehensive techno-economic analyses. The Gibbs Free Energy Gradient Method (GMM), originally proposed by this research group in 2011 [
25,
26], has been successfully applied in numerous gasification contexts. It represents a short-cut modelling approach, capable of providing rapid and reliable predictions of gasifier performance for design and optimization purposes. On the other hand, this model does not involve black-box approaches or empirical formulas but relies on rigorous non-equilibrium training. GMM training ensures a strong physical basis in the calibration phase; once trained, it becomes a versatile and computationally efficient tool, easily adaptable to different feedstocks, operating conditions, and reactor geometries. Previous studies have demonstrated its capability to reproduce experimental data obtained with different biomasses and waste-derived fuels and unreacted carbon residues, as well as its applicability for scaling up a rotary kiln gasifier operation [
25,
26,
27].
The present study extends the GMM to different reactor geometries and gasifying agents, applying it to residual biomass, particularly agricultural residues and forestry by-products. In Italy, forests cover 9.6 million hectares (about 32% of the national territory), and timber stocks have increased by 54% over the past two decades, reaching 5.2% of EU stocks [
28,
29]. Despite this, woody biomass remains underutilized due to its fragmented ownership, difficult terrain, and limited infrastructure [
30]. Additional biomass sources include agri-food residues, such as olive pomace, grape marc, rice husks, and canning by-products. Valorizing these resources is thus key to advancing a bio-based circular economy in line with the Italian Bioeconomy Action Plan [
31,
32]. Poplar wood (POP) and olive pomace (OP) briquettes were selected for their proven ability to produce syngas with a higher energy density [
33] and availability (~2.3 Gton for OP) [
31]. From a techno-scientific perspective, the refinement and validation of the model with experimental data from a commercial downdraft gasifier operating on air allow for the accurate prediction of syngas composition under realistic conditions. Moreover, by integrating model validation with a systematic sensitivity analysis, the study offers valuable insights into the role of operating parameters, particularly temperature and air flow, in regulating the hydrogen yield, calorific value, and process efficiency. These outcomes are intended not only to advance the methodological robustness of the GMM but also to support the wider deployment of biomass gasification plants, facilitating the sustainable valorization of agricultural and forestry residues.
3. Results and Discussion
The experimental tests were carried out on both POP and OP feedstocks, under four distinct temperature regimes. The two campaigns differ in average temperature; while the OP average temperature in the gasifier is around 851 °C, the values for POP experiments were higher, with an average temperature of 918 °C. The measurements (for each feedstock and temperature level) were repeated for at least three consecutive measurements taken over ~15 min, once the system had reached steady-state conditions. The average volume percentage of the experimental campaign is reported for each gaseous component in
Figure 3. The standard deviation for each gaseous component is 6.35 × 10
−3 (CH
4); 7.51 × 10
−3 (CO); 3.39 × 10
−3 (H
2O); 3.81 × 10
−3 (H
2); 3.47 × 10
−3 (CO
2); and 8.75 × 10
−3 (N
2).
The purpose of this work is to use the GMM for predictive purposes. However, since the model had already been tested on other reactor geometries and feedstocks, an initial training phase was required. Nearly half of the gathered experimental data was used to calibrate the model and determine the optimal values for the independent adaptive parameters. Before implementing GMM for predictions, the model was trained to reproduce the experimental dataset by adjusting the independent adaptive parameters. Using as inputs the operating temperature, system pressure, and ultimate analysis of the biomasses, the GMM algorithm iteratively determined the
α and
β coordinates, thereby following the Gibbs free energy descent trajectory. The iterative procedure was designed to stop before full equilibrium was reached, converging instead at the point where the mean squared deviation between experimental and simulated syngas compositions was minimized. This approach ensured that the model calibration remained consistent with the finite residence time and incomplete conversion observed under realistic operating conditions. The resulting correlations, with temperature expressed in °C, are reported in Equations (17)–(20).
These correlations were obtained with an R
2 of 0.74–0.84. The mean values of these variables, calculated for both POP and OP at four nominal temperature levels, are presented in
Figure 4, together with the results obtained in our previous works [
25,
26].
Figure 4a illustrates the first-step training values for
η and
δ, whereas
Figure 4b shows the results for
α and
β, which describe the behaviour of the second step. The regression lines from our previous works are shown only for comparative purposes. A good correspondence is observed, even though the mean values obtained in this work deviate slightly from the previous linear correlations—higher deviations for the values of
α and
δ—while remaining consistent at lower temperatures. It is important to note that the preceding datasets were derived under differing operating conditions, involving wood and waste gasification in reactors of various scales and geometries [
25,
26]. These deviations prove that the GMM cannot be applied to all possible experimental or industrial configurations without prior calibration. However, the close agreement of the temperature-dependent trends supports the robustness of the model structure and the suitability of the adopted simplifications and independent parameters.
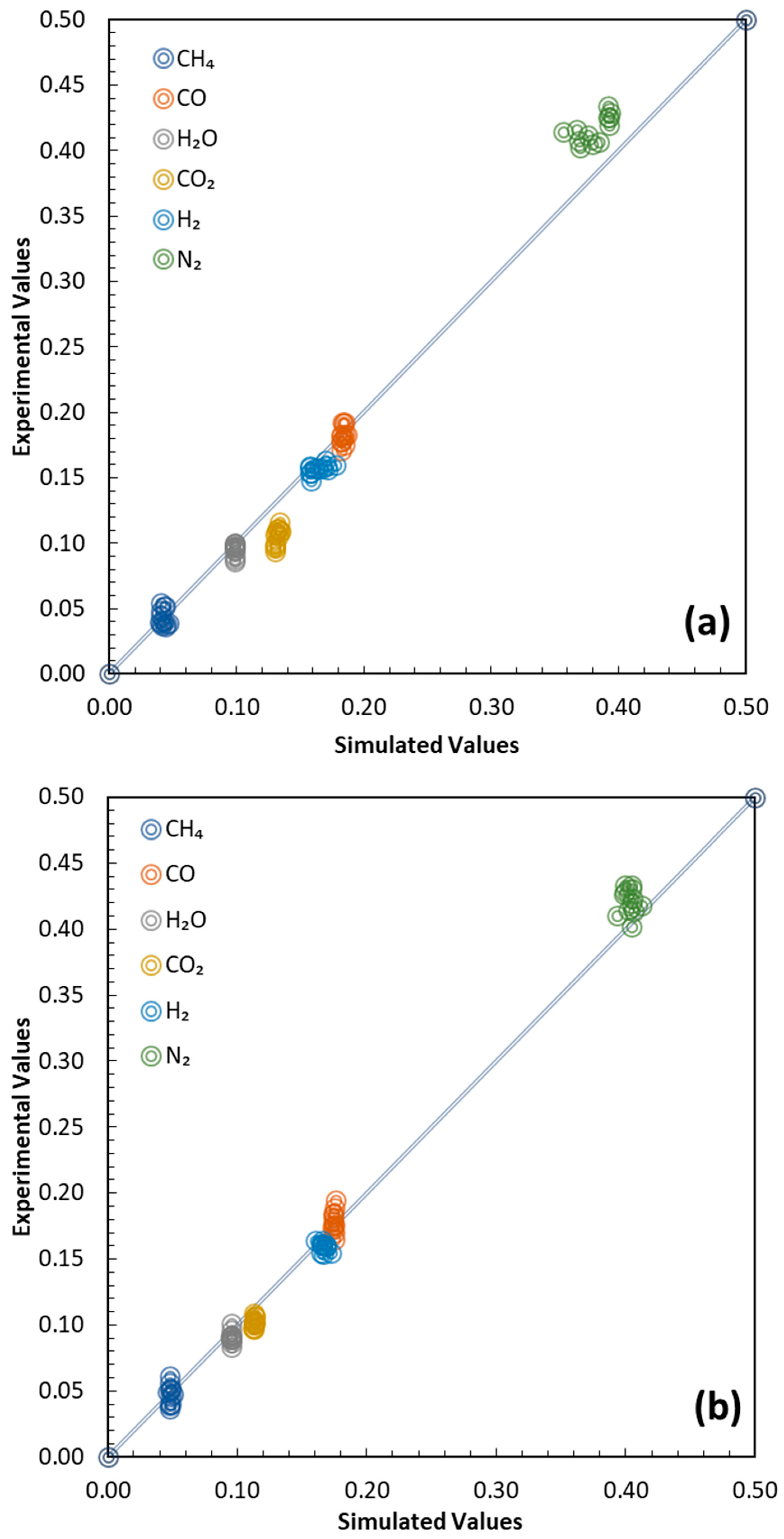
Once the model has been trained, it can be used to simulate all experimental data and perform predictive analyses.
Figure 5 shows all the results, in terms of gas mole fraction, for overall validation. The simulated syngas compositions are compared with experimental data using parity diagrams.
Figure 5a refers to POP gasification, while
Figure 5b corresponds to OP. The agreement between the predicted and measured molar fractions of the main gaseous species was generally very good, with an average deviation below 7%, and only limited discrepancies exceeding 10% for specific components. Overall, it can be observed that the GMM simulator in predictive mode slightly overestimates the CO
2 mole fraction. The MSE for the POP simulation is 3.87 × 10
−4, while for OP it is 1.37 × 10
−4. This may be directly dependent on the observed scattering in the adaptive parameter values, especially delta. On the other hand, the level of accuracy confirms the robustness of the GMM calibration and its ability to reliably reproduce syngas compositions across different biomass feedstocks and operating conditions, extending the previous validation [
25,
26] across various reactor configurations, different plant scales and capacities, with both air and steam as gasifying agents, and employing a range of biomass feedstocks.
The next results are related to energy performance evaluation. First, the thermo-chemical conversion efficiency will be calculated, and finally the overall biomass-to-electricity efficiency, which has a direct industrial impact on the obtainable electrical power of the overall process described in
Figure 1.
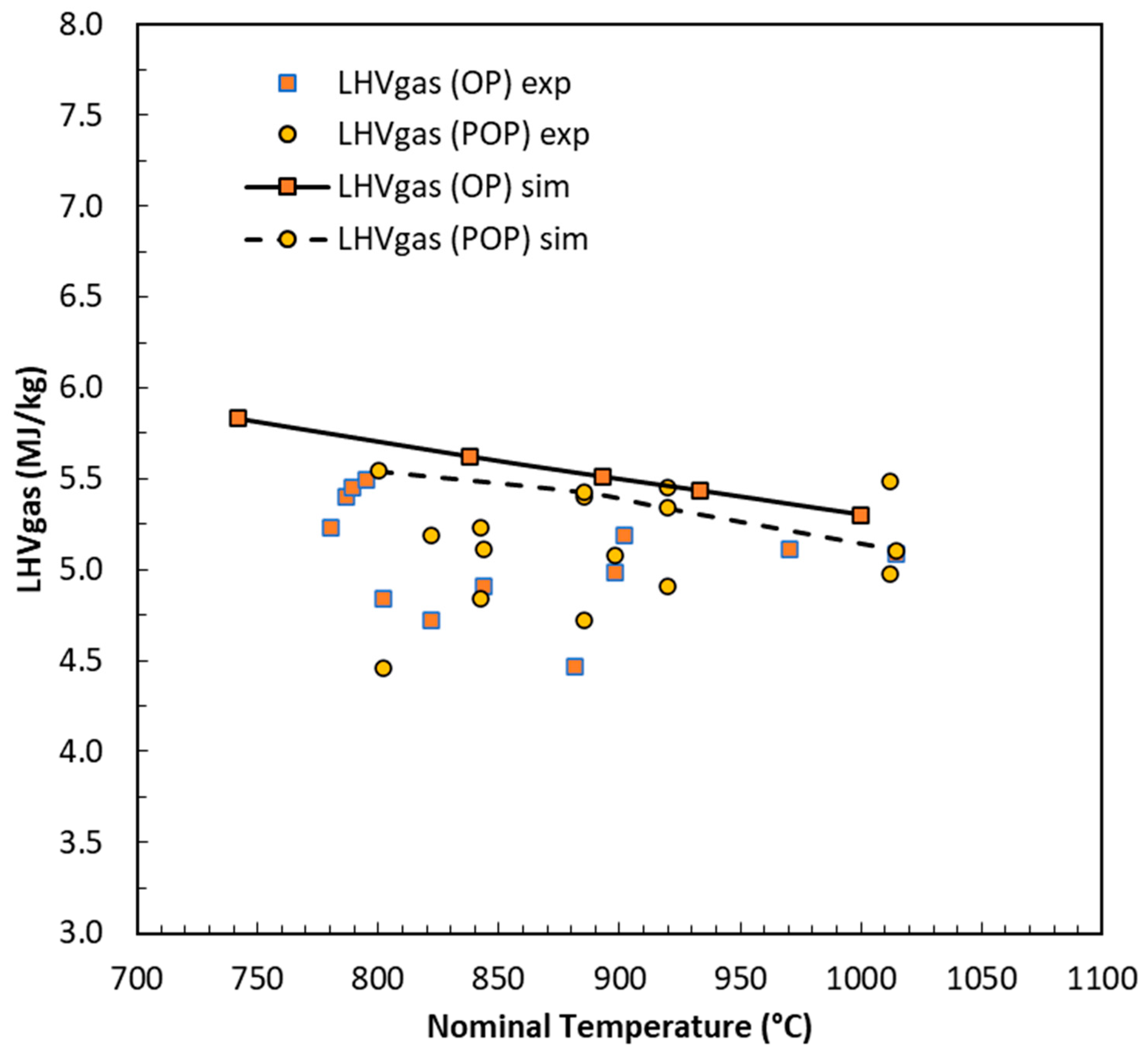
Figure 6 reports the obtained values of the lower heating value (LHV) for both POP- and OP-derived syngas, with average values of 5.1 MJ/kg for both.
The model reproduces the calorific value of gas reliably, although it shows a slightly decreasing trend with temperature, while the experimental data are distributed almost independently of the T variable. However, the slight training flaw in step 1 translates into lower gas production; in fact, the model tends to overestimate char production and underestimate gas yield. The final result will still be conservative. To demonstrate this, we can analyze the overall energy performance.
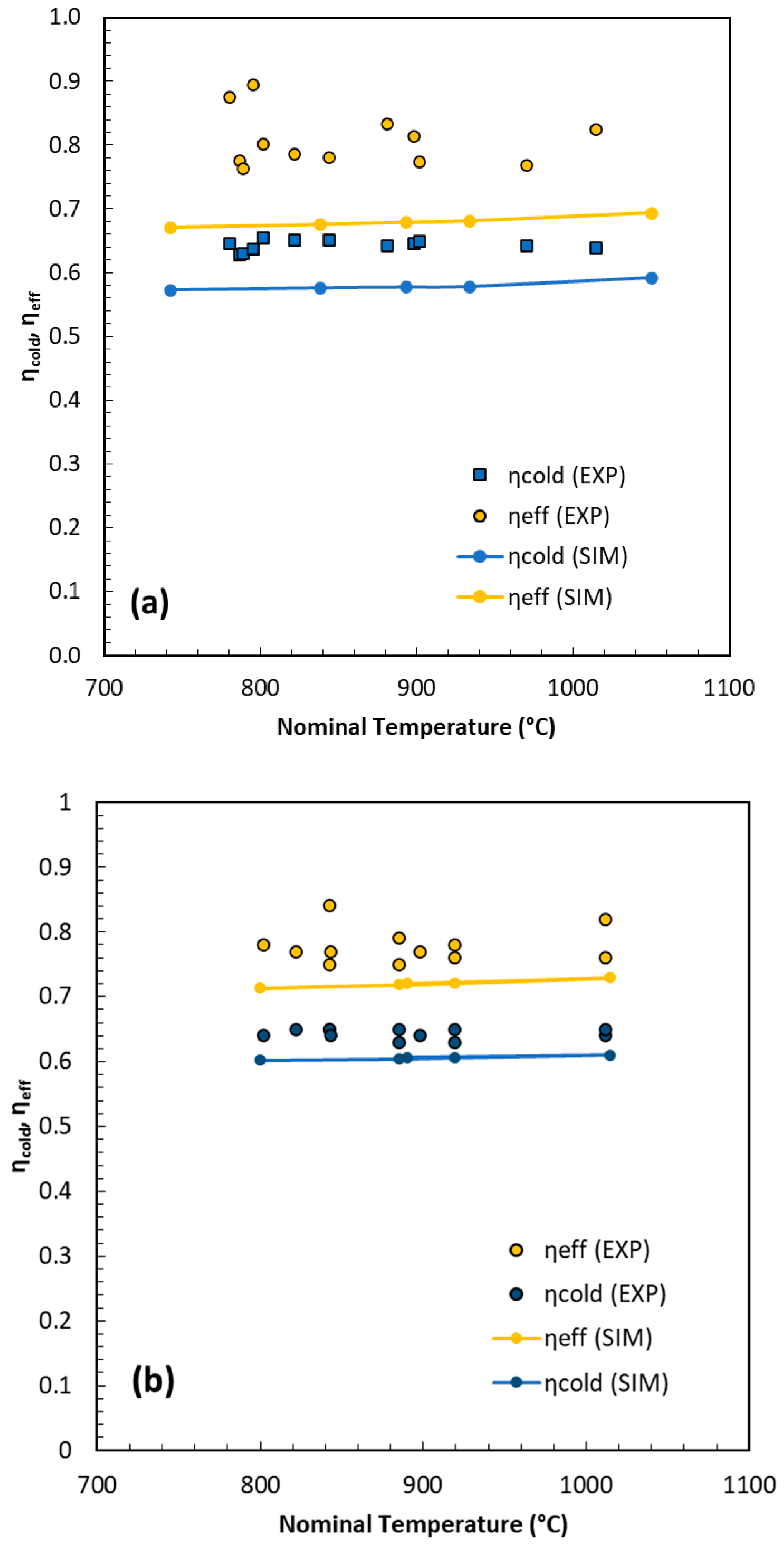
Figure 7 depicts the trends of the efficiencies, computed according to Equations (13) and (14), for OP (a) and POP (b). The experimental results indicate that, from a thermodynamic standpoint, the gasification of POP briquettes performs better than OP, with both cold and effective thermal efficiencies being approximately 7–8% higher. The experimental trends are accurately reproduced by the GMM simulations, although the calculated efficiencies are systematically 2–5 percentage points lower. This deviation originates mainly from uncertainties in the first simulation step, which involves the formation of char and the initial gas mixture. It should be noted that, in order to construct a short-cut GMM model, a parameter function dependent solely on temperature was employed. Although this simplification is consistent with previous studies, it inevitably introduces some approximation. A finer tuning, though at the expense of model simplicity, could consider the specific characteristics of the biomass or reactor geometry and residence time. Overall, the results remain consistent with the literature data, and the model behaves conservatively, slightly overestimating char formation and consequently underestimating gas yield and overall efficiency.
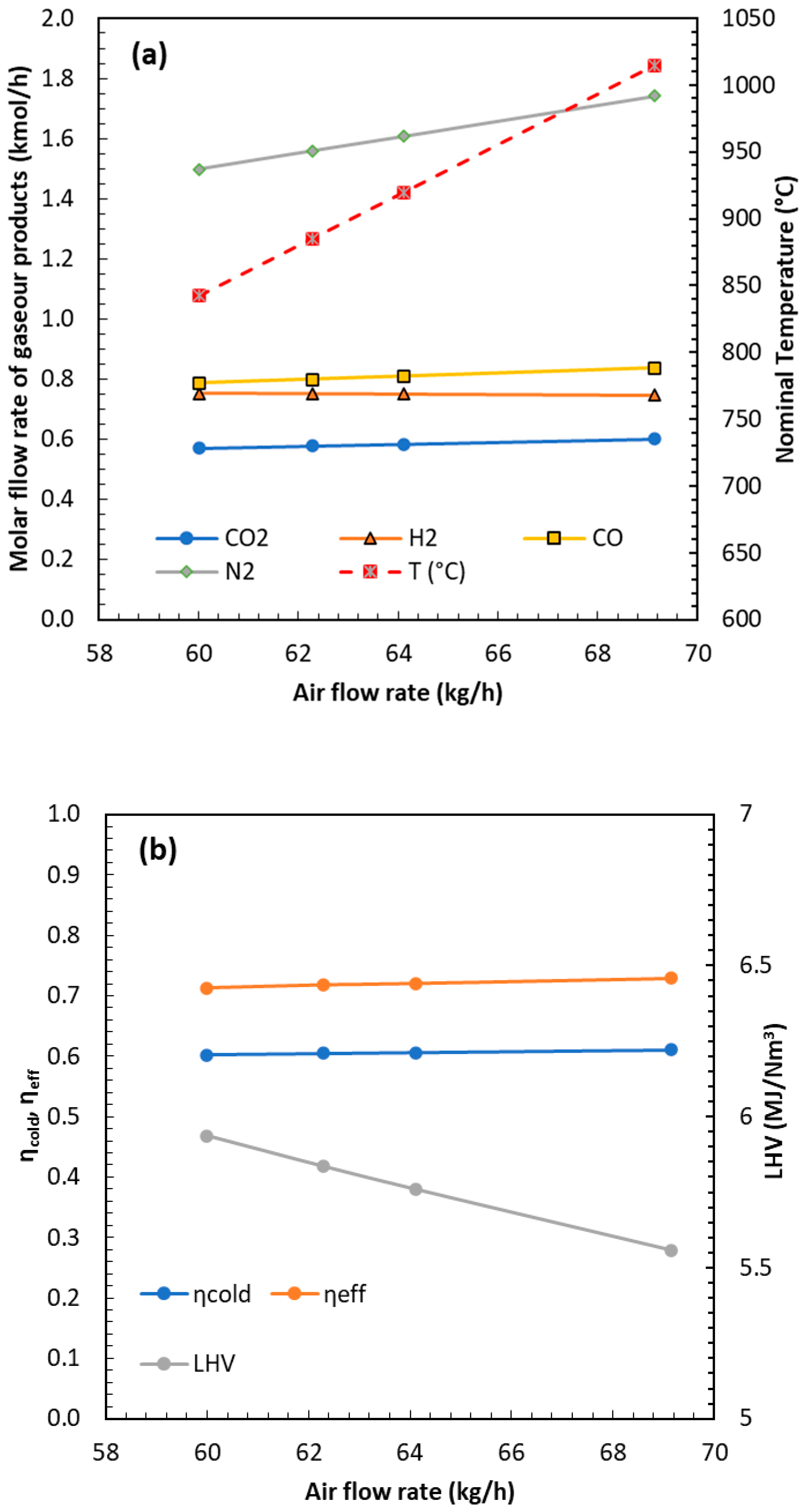
Once the simulator is ready, sensitivity analysis, optimization studies, and the process of scaling up can be generated. In the present work, the effect of the Equivalence Ratio (ER) was investigated by varying the air flow rate (ranging from 60 to 75 kg/h) at a constant biomass feed (50 kg/h for both POP and OP). The effect of the ER was investigated under the same range of temperatures as the testing conditions.
Figure 8 shows the representative simulation results obtained for the POP fuel. The figure also reports the variation in temperature with an increasing air flow rate. As the air flow increases, exothermic reactions become more prominent, resulting in a modest rise in temperature and a corresponding increase in CO
2 formation. Simultaneously, gas dilution due to the higher CO
2 molar flow reduces the calorific value of the syngas. Overall, the influence of the air flow rate, and thus of the ER, is slightly positive, as reflected in the increase in both cold gas and effective efficiencies. A decrease in the CH
4 concentration was observed with increasing temperature, consistent with the enhanced extent of the steam-reforming reaction, which also promotes higher H
2 and CO yields. A slight reduction in char production was detected, with average rates of approximately 3.3 kg/h for POP and 8 kg/h for OP. Although higher temperatures and H
2 yields lead to a minor decrease in syngas LHV due to dilution, this is compensated by an increased total syngas flow rate. Consequently, the overall deliverable energy remains nearly constant across the tested ER values and operating temperatures, while the higher-temperature conditions are beneficial in reducing both char and tar formation.
The main results relating to energy performance are reported in
Table 3. From an energy standpoint, the gasification of POP briquettes yields an energy output comparable to that obtained with OP, indicating that POP gasification is globally more efficient. Nevertheless, OP briquettes can achieve similar results under milder operating conditions, as their gasification requires lower temperatures. From an exergetic perspective, the efficiency was found to be slightly higher than the electrical one, because it accounts for the export of second-kind energy (i.e., thermal energy recovered in cogeneration mode) through the correction factors defined in Equation (16).
A woody biomass such as POP is generally more abundant and economically accessible across the national territory [
30,
31,
32], which further strengthens its technical and logistical advantages. On the other hand, from a circular economy standpoint, the valorisation of agricultural residues such as OP represents an environmentally preferable option, contributing to waste reduction and local resource recovery. For this reason, the use of OP as a feedstock may be particularly advantageous in Central and Southern Italy, where this residue is widely available, and its supply chain can be efficiently integrated into existing agro-industrial activities.
Building on these considerations, the trained GMM model has been applied to a preliminary techno-economic assessment of a scaled-up commercial unit (200 kW downdraft gasifier) to be potentially installed in these regions. The simulations were carried out assuming the reactor operates 80% of the time with POP briquettes and 20% with POP briquettes, reflecting their respective local availability. Using an average gasification temperature representative of the optimal range for both feedstocks and an annual operating time of approximately 7200 h (i.e., a capacity factor of nearly 0.83), the estimated electricity production cost is around EUR 200 per MWh. The calculated capital expenditure (CAPEX) is slightly above EUR 1 million, with an expected payback period of about 10 years, while operating costs (OPEX) are estimated at EUR 220,000 per year.
These results confirm that the GMM model can effectively support pre-feasibility and scaling analyses, providing a computationally efficient tool for evaluating the economic viability of biomass gasification systems under different regional and feedstock scenarios.
4. Conclusions
The present study validated and extended the Gibbs Free Energy Gradient Method (GMM) as a predictive tool for biomass gasification, using experimental data from a commercial downdraft pilot gasifier provided by RESET S.r.l. and applying it to poplar wood and olive pomace briquettes. By refining the model parameters against experimental observations, the GMM reproduced syngas compositions with an average error below 8%, confirming its robustness across different feedstocks and operating conditions. Energy performance indicators were also reliably captured, with deviations in enthalpy balances of approximately 6%, demonstrating the consistency of the model in predicting process efficiency.
In terms of syngas composition, the mean squared error (MSE) between simulated and measured data was 3.87 × 10−4 and 1.37 × 10−4 for poplar (POP) and olive pomace (OP), respectively, demonstrating a strong convergence and statistical reliability. The predicted gas mixtures showed average molar fractions of approximately 16% for H2 (standard deviation 3.81 × 10−3), 17–18% for CO (standard deviation 7.51 × 10−3), 10–12% for CO2 (standard deviation 3.47 × 10−3), 5–6% for CH4 (standard deviation 6.35 × 10−3), and 39–42% is N2 (standard deviation 8.75 × 10−3), in line with experimental measurements. From an energy perspective, the cold gas efficiency ranged between 56 and 61%, while the effective thermal efficiency was between 66 and 72%, depending on the feedstock and temperature. On average, POP gasification exhibited efficiencies 7–8% higher than OP, consistent with its lower moisture content and higher reactivity. The electrical efficiency of the integrated system was approximately 14–15%, and the exergetic efficiency reached 16–18%, confirming the reliability of the energy balance and the conservative nature of the model predictions.
These outcomes align with literature benchmarks, wherein woody feedstocks typically yield higher conversion efficiencies, while agro-industrial residues contribute to higher syngas energy density due to their intrinsic composition. The sensitivity analysis highlighted the central roles of operating temperature and air flow in governing syngas quality, hydrogen yield, and char conversion. Specifically, higher temperatures promoted methane conversion, improving hydrogen yield, although air dilution partially offset the gains in syngas concentration. These findings are consistent with the thermochemical benchmarks reported for downdraft gasifiers in the 800–1000 °C range, supporting the validity of the approach.
From a broader perspective, the integration of experimental validation with advanced modelling establishes the GMM as a scalable, predictive tool that bridges the gap between laboratory-scale research and commercial plant deployment. Unlike purely equilibrium or kinetic models, the GMM is trained with a rigorous thermodynamic framework to predict non-equilibrium compositions due to finite residence time and incomplete conversion phenomena. On the other hand, in the prediction mode, the model offers a user-friendly short-cut methodology.
Moreover, both experimental and modelling results confirm that residual biomass streams such as olive pomace can be effectively valorized for energy generation, complementing more conventional forestry resources. The systematic exploitation of such underutilized residues aligns with the objectives of the EU Bioeconomy Strategy and the Italian Bioeconomy Action Plan, strengthening energy security while reducing the environmental impacts associated with waste disposal.
The main limitation of the GMM model is the neglection of tar formation, since it is based on the hypothesis that operating at higher temperature might hinder its formation. The tar made from heavy organic compounds could represent a highly viscous liquid fraction, capable of causing filter clogging, circuit fouling, and malfunctions to downstream equipment [
35,
36]. As outlined by a recent investigation of Safarian et al. [
14], while updraft and fluidized bed gasifiers featured tar yields up to 12 wt.% and 15 wt.%, respectively, downdraft gasifiers can achieve yields lower than 1 wt.% by operating at temperatures higher than 800–900 °C.
Overall, the GMM can be considered a reliable and conservative predictive tool for high-temperature, steady-state downdraft gasification systems. Its scalability to other configurations (e.g., fluidized bed or dual-stage reactors) requires dedicated recalibration, given the different thermal regimes, residence times, and mixing conditions. Within these defined boundaries, the GMM effectively balances physical rigour and computational simplicity, offering a practical short-cut methodology for process design, optimization, and preliminary techno-economic evaluation. Future research should expand the GMM framework by incorporating tar formation and cracking kinetics, and by validating the model (with a focus on the first devolatilization step) under alternative reactor configurations, such as fluidized bed and dual-stage gasifiers, which dominate industrial-scale applications.