Performance Enhancement of a Novel Compression/Ejection Trans-Critical CO₂ Heat Pump System Coupled with Composite Heat Sources

Abstract

The efficient utilization of renewable heat sources is important for the performance enhancement of trans-critical CO₂ heat pump systems and for promoting the transformation of energy structures. A composite-heat-source matching ratio is introduced in this article to assess the impact of a high-temperature heat source and low-temperature heat source on the performance of a novel compression/ejection trans-critical CO₂ heat pump (CTHP) system coupled with the use of composite heat sources theoretically. The research results show that the maximum reduction in the optimum gas cooler outlet pressure (P_opt,out,gc) is 3.13% with the increase in evaporating temperature (T_e), and the maximum reduction is 1.67% with the rise in the composite-heat-source matching ratio, which means that the composite-heat-source matching ratio is equally significant on the optimum high-pressure side compared to the T_e. The correlations of optimum high pressure and other optimum cycle parameters for the CTHP system, considering the composite-heat-source matching ratio, were obtained, which provide useful guidelines for optimizing the system design and selecting the appropriate operating conditions. Overall, this article will be helpful for the further development and optimization of the CTHP system, which is of great importance for increasing the utilization rate of renewable heat sources such as geothermal or air-source for urban buildings and accelerating the electrification and low-carbon transformation of terminal energy consumption.

1. Introduction

In current society, the proportion of heating, hot water supply, and refrigeration in building energy consumption has been rapidly increasing, and the amount of energy used by buildings worldwide accounts for 40% of all energy consumption [1]. As efficient energy-saving equipment, heat pumps can convert waste heat or low-quality heat in the environment into high-quality heat energy [2], which play important roles in energy saving and carbon reduction, and have been widely adopted in the fields of energy and building, etc. [3,4]. While heat pump technology can significantly lower CO₂ emissions, the use of synthetic refrigerants, such as chlorofluorocarbons (CFCs) and hydrochlorofluorocarbons (HCFCs), has a detrimental effect on the ozone layer [5]. Carbon dioxide (CO₂) is a natural refrigerant with great environmental friendliness, good safety characteristics (including non-flammability, non-toxicity, and chemical stability) [6], and peculiar thermodynamic and thermophysical properties, which include the following aspects: CO₂ has a high critical pressure of 73.8 bar and a comparatively low critical temperature of 31.1 °C [7]; CO₂ in the supercritical state has small flow resistance and large latent heat due to high density and low viscosity, and the temperature change in CO₂ and water can produce good slip, resulting in significant heat rejection [8]. Therefore, CO₂ has low ambient temperature adaptability and high-temperature heating ability, which is mainly used in trans-critical thermodynamic cycles [9]. Compared to the sub-critical heat pump system using traditional refrigerants, the trans-critical CO₂ heat pump (TCHP) cycle has better advantages in its environmental protection, high efficiency, and wide temperature range, and has broader application prospects in the fields of building and energy, etc.

The trans-critical CO₂ cycle was first applied to the automotive air conditioning system by Lorentzen [10]. In recent years, substantial research has been conducted on the performance and optimization of basic TCHP systems. Qin [11] experimentally investigated the performance of the system under the condition of compressor frequency conversion and determined the correlation of the optimum discharge pressure (P_opt,dis) using Buckingham PI analysis. Yang [12] conducted a numerical analysis of a trans-critical CO₂ heating system’s energetic and exergetic performance in cold regions. Findings reveal that ambient temperature and gas cooler CO₂ outlet conditions significantly impact system performance. In addition, the design of TCHP systems has been enhanced by researchers. Incorporating an internal heat exchanger (IHX) effectively lowers the temperature prior to expansion valve entry and simultaneously boosts the compressor’s suction superheat. Furthermore, the integration of an internal heat exchanger (IHX) can augment the heating capacity by enhancing the enthalpy difference within the gas cooler [2]. Yang [13] further investigated the impact of the outlet state of CO₂ in the gas cooler and the inlet water temperature on system performance as the compressor frequency increases. Based on these findings, they proposed a novel operational strategy to optimize system performance. In addition, the mechanical subcooling technology is another effective approach to enhance system performance, which was verified by Song [14] with a space-heating-using TCHP system and demonstrated by Chowdhury [15] with a two-stage vapor compression system.

More significantly, the influence of expansion work recovery cannot be disregarded during system optimization, given the substantial throttling losses involved. The most common methods of recovering expansion work are mainly the use of expanders or ejectors. The expander suffers from high-pressure leaks and is limited by its manufacturing cost. Compared with the expander, the ejector has a simple structure and low manufacturing cost, which is considered to be one of the most promising ways to realize expansion work recovery. Research on the application of two-phase ejectors in the trans-critical CO₂ cycle began in early 2000. Zhu [16] found that, compared with the basic system, the addition of ejectors can effectively generate high-temperature hot water. Specifically, when the outlet water temperature reaches 70 °C, the system’s COP is elevated by 10.3%. Wang [17] integrated an ejector and an internal heat exchanger into the TCHP system. Theoretical analysis revealed that these modifications led to a 7.38% increase in the COP and an 86.80% reduction in exergy destruction at the throttle valve. In summary, existing research on CO₂ heat pumps with an ejector has achieved COP values improved by more than 5% up to 30%.

Notably, although the TCHP cycle system with an ejector can recover part of the expansion power and reduce the compressor power consumption, the ejector is likely to deviate from the design condition in actual operation and may cause the system to fail to heat or cool. Furthermore, its operating temperature range will be limited by the environment if it is only an air source, and multi-source heat pumps have increasingly attracted significant research attention [18,19]. The combined system of carbon dioxide heat pumps and ground-source heat pumps can effectively reduce heating costs, achieving a highest return on investment of 13.27% per year, with a payback period of approximately 6.8 years, which not only significantly reduces reliance on the power grid but also improves heating efficiency and environmental benefits [20]. In fact, the advantage of heat pumps is that they can integrate renewable energy or waste heat sources. The application of a composite heat source can compensate for the deficiencies of a single heat source and can make full use of renewable energy sources such as air and geothermal energy. Consequently, further research on TCHP systems with an ejector and composite heat source is receiving increased attention because of the dual-carbon objective.

Nevertheless, as a potential method, the CTHP system with composite heat sources is rarely debated. Our research group has been engaging with TCHP systems for the past few years [21,22,23]. The CTHP system was proposed by Qin [24]. The main difference between the CTHP system and the TCHP system lies in the fact that not only an ejector has been added, but also a new water source evaporator (WSE) has been incorporated. The water source and the air source evaporator, respectively, serve as two different heat sources of the CTHP system. Subsequently, Zhang [25] carried out an experimental investigation into the performance of the innovative system and demonstrated that it was superior to the basic system. Next, it is necessary to further study the control strategy and the selection of operating parameters with the CTHP system.

As is known to all, due to the unique isotherm of CO₂, the TCHP system exhibits an optimal high-pressure value that corresponds to the maximum COP, which is difficult to estimate and depends on a number of parameters. Many scholars have searched for the optimum high pressure by analyzing and fitting simulation or experimental results [24,26], or through a model-free extreme seeking control method [27] and online optimization control method [2]. In fact, the P_opt,dis correlations proposed by scholars are different due to their independent variables [28], which are hardly competent to the different CO₂ heat pump cycles. However, the existing simulation and experimental research mainly focus on the basic TCHP system, while research on the TCHP system with a composite heat source is lacking. Furthermore, a more thorough investigation is needed since the intricate layout of heat pump systems may result in a rise in influencing factors that determine the P_opt,dis.

To address the effect of the composite heat source, the composite-heat-source matching ratio ($\phi$) is proposed. To the best of the authors’ knowledge, no study has yet developed correlations for P_opt,dis that account for $\phi$ in an ejector-enhanced CTHP system. Therefore, investigating the optimal pressure in CTHP systems under the influence of $\phi$ is of significant value.

In this paper, the impact of the composite-heat-source matching ratio on CTHP performance is systematically evaluated, and correlations for key optimization parameters are developed. The correlations of the P_opt,out,gc and the corresponding optimum COP, ejector entrainment coefficient, pressure lift ratio, compressor pressure ratio with the system operating conditions, namely T_e, T_{gc, out}, and the composite heat source matching ratio in the CTHP system were obtained through multivariate nonlinear regression analysis. These correlations provide valuable insights for the optimized design and operational condition selection of CTHP systems with composite heat sources.

2. Numerical Model

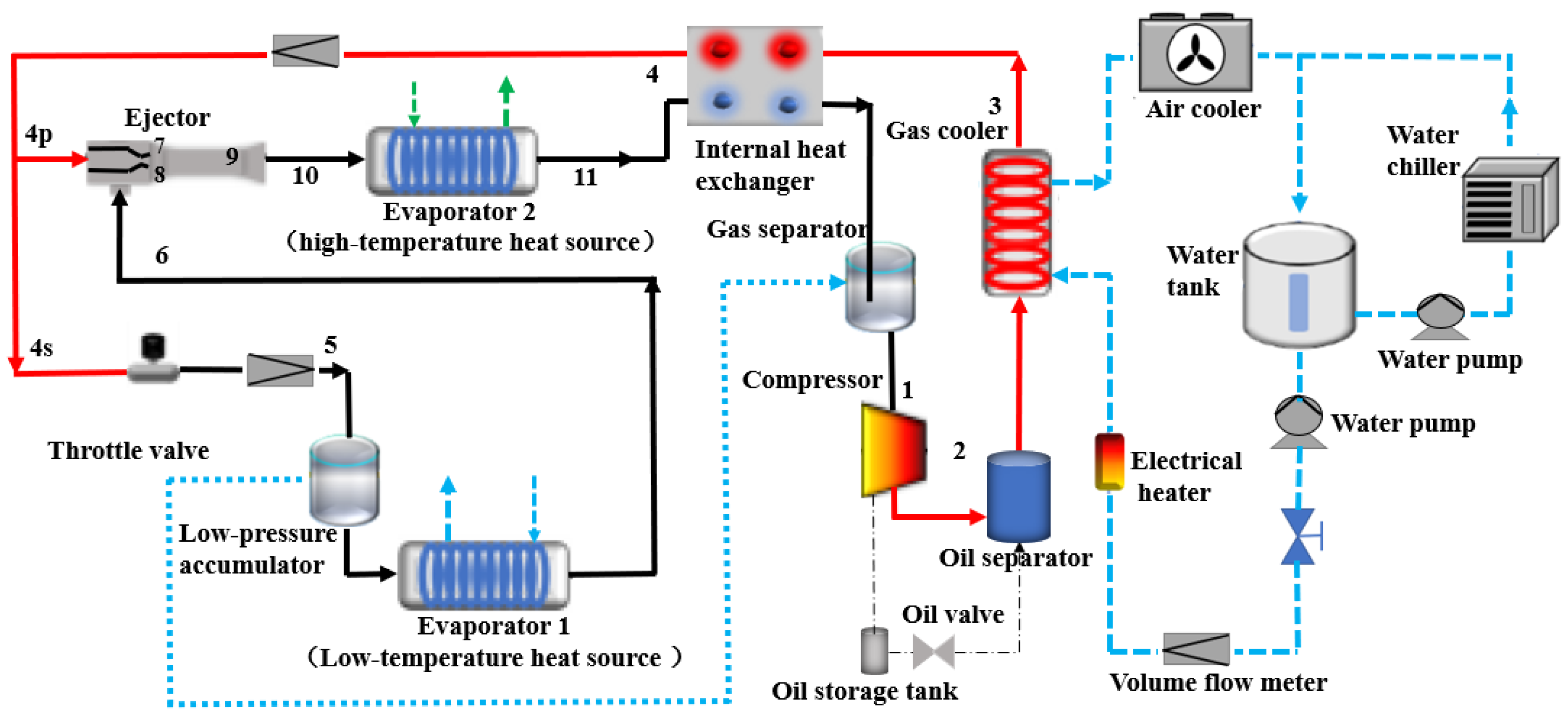
2.1. System Description

The schematic and P-h diagram of the CTHP system with composite heat sources are displayed in Figure 1 and Figure 2. The CTHP system is described as follows: 1–2, non-isentropic compression process in the compressor; 2–3, exothermic process in the gas cooler; 3–4, re-exothermic process in the internal heat exchanger; 4–5, isenthalpic throttling process in the expansion valves; 5–6, endothermic process in the low-temperature evaporator; 4–10, the low-pressure refrigerant exiting from the low-temperature evaporator is propelled into the ejector by the high-pressure refrigerant originating from the high-pressure side of the internal heat exchanger, and then mixed and diffused into the high-temperature evaporator; 10–11, endothermic process in the high-temperature evaporator; 11–1, endothermic process in the internal heat exchanger and gas–liquid separation process in the gas–liquid separator.

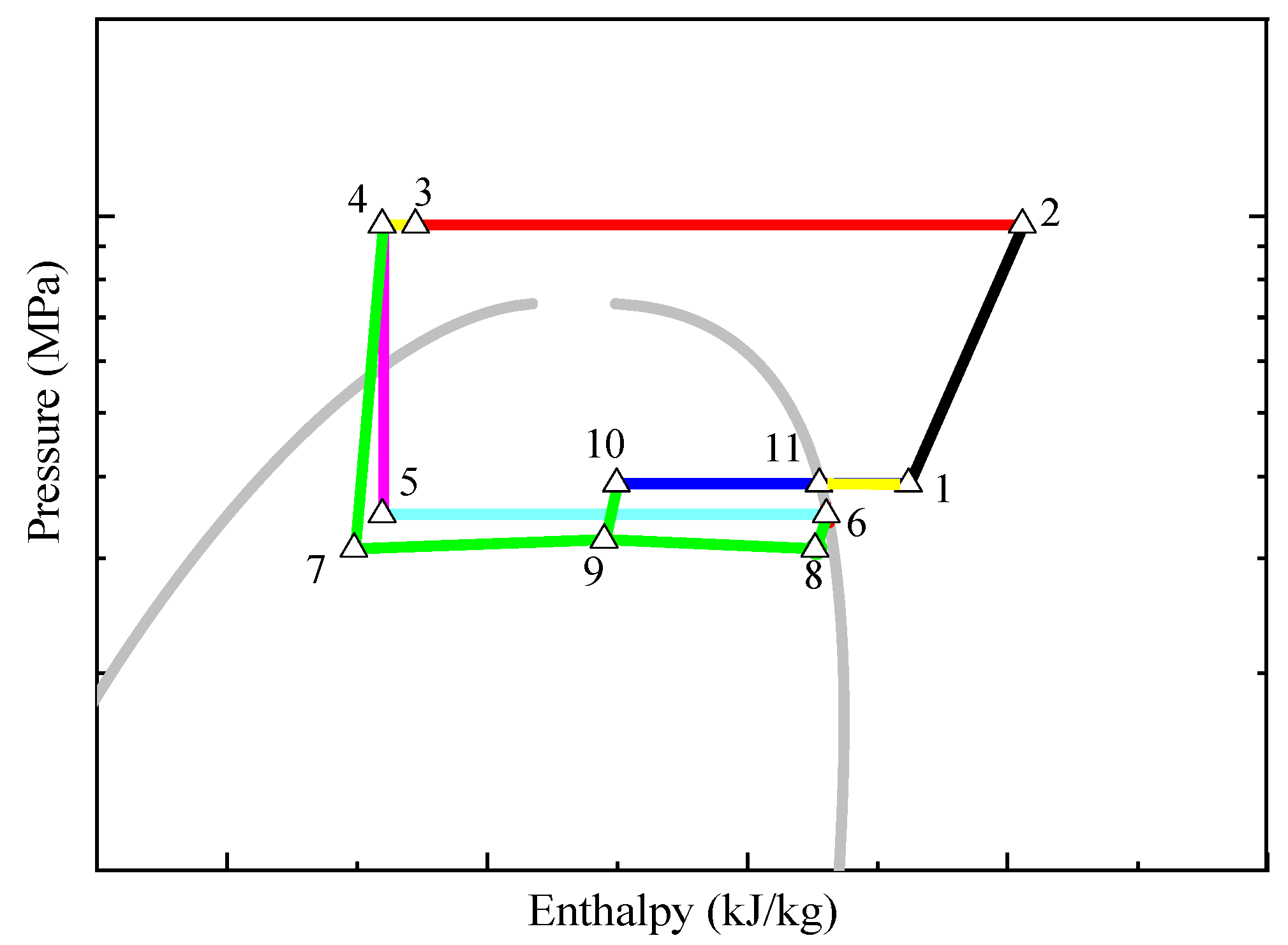
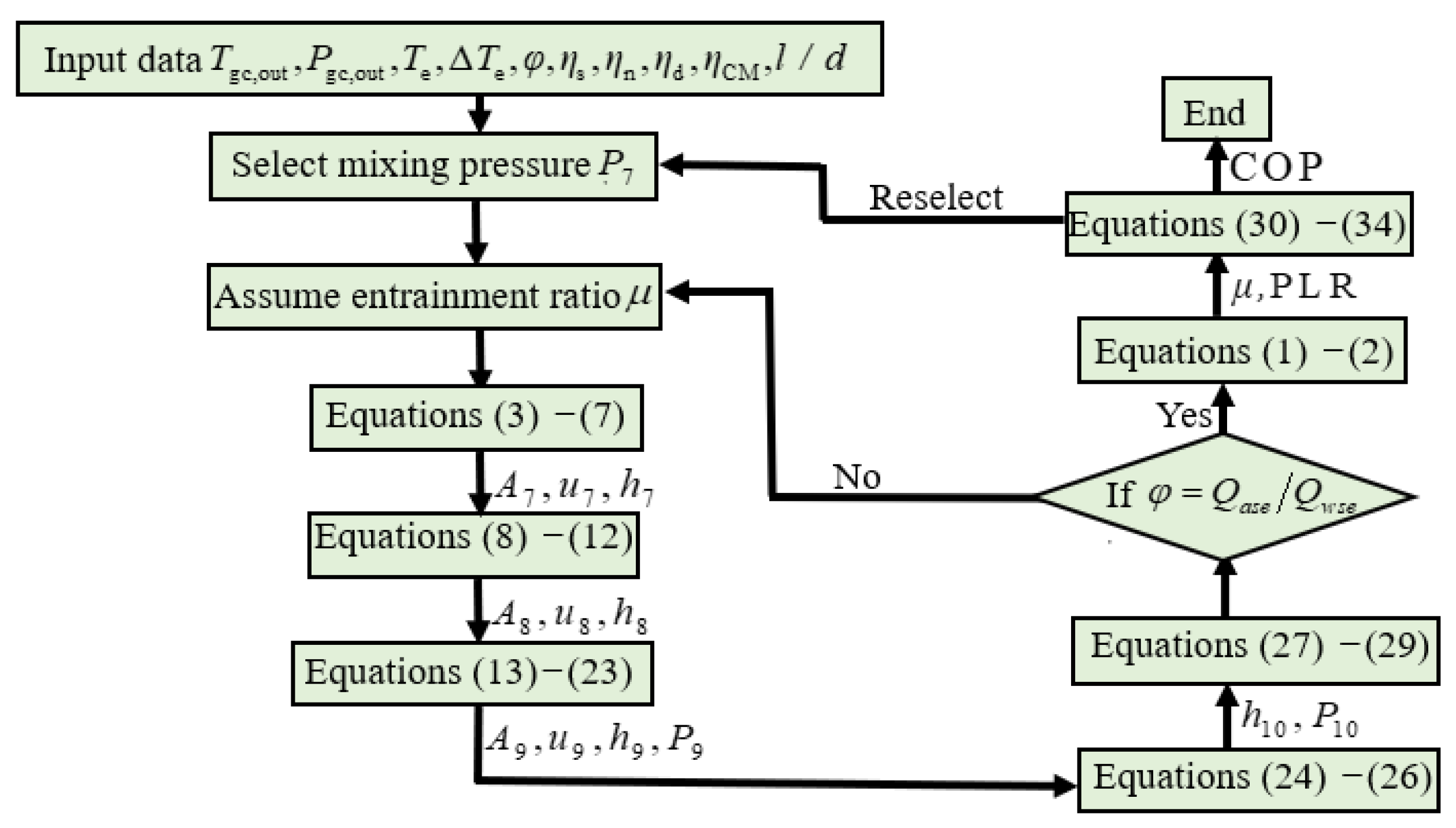
2.2. Mathematical Modeling and Simulation

Figure 3 illustrates the structural diagram of the two-phase ejector utilized in the CTHP system. For the purpose of simplifying the theoretical model, the following assumptions are adopted in the thermodynamic analysis of the CTHP cycle:

Disregard the system and environment’s heat transmission.

Pressure drop in the heat-exchange equipment and connecting tubes is disregarded.

The kinetic energy of the CO₂ working medium at the inlet and outlet of the ejector is ignored.

The throttling of the expansion valve is an isenthalpic process.

The flow within the primary nozzle, secondary chamber, and diffuser chamber of the ejector, except in the mixing chamber, is one-dimensional and uniform.

An equal area mixing model is employed, meaning that the cross-sectional area remains constant during the mixing process of the primary and secondary flows within the mixing chamber.

The two fluids commence the mixing process at the inlet section of the mixing chamber, and at this very moment, the pressures of the primary flow and secondary flow are equal.

Based on the above assumptions [29], the calculation models of each part of the system are established from the perspective of mass conservation, momentum conservation, and energy conservation [30]. In all calculations, the isentropic efficiency of the primary nozzle, secondary nozzle, and diffuser chamber are expressed by ${\eta }_{\mathrm{p}}$, ${\eta }_{\mathrm{s}}$, and ${\eta }_d$, respectively, (${\eta }_{\mathrm{p}}$ = 0.85, ${\eta }_{\mathrm{s}}$ = 0.85, and ${\eta }_d$ = 0.85) [4,29]. The ejector performance is expressed by the ejector entrainment coefficient and pressure lift ratio [31,32,33]. Its formula is as follows [34]:

$$\mu ={\displaystyle \frac{{\dot{m}}_{\mathrm{s}}}{{\dot{m}}_{\mathrm{p}}}}$$

(1)

$$PLR={\displaystyle \frac{P_{10}}{P_6}}$$

(2)

According to the primary nozzle inlet state of 4p, outlet pressure $P_7$ and constant entropy efficiency (${\eta }_{\mathrm{p}}$), the velocity ($u_7$), enthalpy ($h_7$), and density (${\rho }_7$) of the working medium at the outlet of the primary nozzle and the outlet cross-sectional area ($A_7$) of the primary nozzle are calculated. The mathematical model is as follows:

$$h_{4\mathrm{p},\mathrm{is}}=f(P_7,s_{4\mathrm{p}})$$

(3)

$$u_7=\sqrt{2{\eta }_{\mathrm{p}}(h_{4\mathrm{p}}-h_{7,\mathrm{is}})}$$

(4)

$${\eta }_{\mathrm{p}}={\displaystyle \frac{h_{4\mathrm{p}}-h_7}{h_{4\mathrm{p}}-h_{7,\mathrm{is}}}}$$

(5)

$${\displaystyle \frac{1}{{\rho }_7}}={\displaystyle \frac{1}{{\rho }_{7,\mathrm{l}}}}+x_7({\displaystyle \frac{1}{{\rho }_{7,\mathrm{g}}}}-{\displaystyle \frac{1}{{\rho }_{7,\mathrm{l}}}})$$

(6)

$$A_7={\displaystyle \frac{{\dot{m}}_{\mathrm{p}}}{{\rho }_7{u}_7}}$$

(7)

The secondary fluid expands in the secondary chamber due to the pressure reduction. The velocity ($u_8$), enthalpy ($h_8$), and density (${\rho }_8$) of the outlet of the secondary nozzle and the outlet cross-sectional area ($A_8$) of the primary nozzle are calculated according to the inlet state 6 and the outlet pressure ($P_8$) ($P_8$ = $P_7$) of the secondary fluid. The mathematical model is as follows:

$$h_{8,\mathrm{is}}=f(P_8,s_6)$$

(8)

$$u_8=\sqrt{2{\eta }_{\mathrm{s}}(h_6-h_{8,\mathrm{is}})}$$

(9)

$${\eta }_{\mathrm{s}}={\displaystyle \frac{h_6-h_8}{h_6-h_{8,\mathrm{is}}}}$$

(10)

$${\displaystyle \frac{1}{{\rho }_8}}={\displaystyle \frac{1}{{\rho }_{8,\mathrm{l}}}}+x_8({\displaystyle \frac{1}{{\rho }_{8,\mathrm{g}}}}-{\displaystyle \frac{1}{{\rho }_{8,\mathrm{l}}}})$$

(11)

$$A_8={\displaystyle \frac{{\dot{m}}_{\mathrm{s}}}{{\rho }_8{u}_8}}$$

(12)

In the mixing chamber, the two flows are thoroughly combined. Based on the equal area mixing theory of the ejector, the velocity ($u_9$), enthalpy ($h_9$), pressure ($p_9$), and density (${\rho }_9$) at the mixing chamber outlet are calculated.

$$A_9=A_7+A_8$$

(13)

$$u_9={\displaystyle \frac{{\dot{m}}_{\mathrm{p}}+{\dot{m}}_{\mathrm{s}}}{{\rho }_9{A}_9}}$$

(14)

$$h_9={\displaystyle \frac{{\dot{m}}_{\mathrm{p}}{h}_{4\mathrm{m}}+{\dot{m}}_{\mathrm{s}}{h}_6}{{\dot{m}}_{\mathrm{p}}+{\dot{m}}_{\mathrm{s}}}}-{\displaystyle \frac{1}{2}}{u}_9^2$$

(15)

$$P_9={\displaystyle \frac{({\dot{m}}_{\mathrm{p}}{u}_7+{\dot{m}}_{\mathrm{s}}{u}_8)-u_9({\dot{m}}_{\mathrm{p}}+{\dot{m}}_{\mathrm{s}})(1+\frac{f_{\mathrm{m}}}{2}\frac{l}{d})}{A_9}}+P_7$$

(16)

$${\displaystyle \frac{1}{{\rho }_9}}={\displaystyle \frac{1}{{\rho }_{9,\mathrm{l}}}}+x_9({\displaystyle \frac{1}{{\rho }_{9,\mathrm{g}}}}-{\displaystyle \frac{1}{{\rho }_{9,\mathrm{l}}}})$$

(17)

The mixing chamber is in a turbulent state, and the formula for calculating the friction resistance coefficient [35] is as follows. To obtain more accurate results, $f_m$ is evaluated by taking the average value of the friction resistance coefficient at the inlet and outlet of the mixing chamber.

$${\displaystyle \frac{1}{\sqrt{f_{\mathrm{m}}}}}=2\lg (\mathrm{Re}\sqrt{f_{\mathrm{m}}})-0.8$$

(18)

The fluid in the mixing chamber is in a state of gas–liquid coexistence. At this time, the sound velocity of the fluid is far less than that in the single-phase state, and shock waves can occur. The physical parameters of the fluid on the wave front, such as stress, temperature, and density, change dramatically. Therefore, it is necessary to determine whether shock waves will be generated in the mixing chamber. The following is the formula for calculating the sound velocity in the gas–liquid two-phase state. If the velocity is higher than the sound velocity, shock waves will be generated in the supersonic state, and the state of the fluid will change after the generation of shock waves. Assuming the state after the change is state 9, the formula is as follows according to the conservation of momentum:

The sound velocity is calculated as outlined below:

$$a_v={\displaystyle \frac{1}{1+\frac{1-x}{x}\frac{{\rho }_g}{{\rho }_l}}}$$

(19)

$$c=k{R}_{g}T({a_v}^2+{\displaystyle \frac{a_v(1-a_v)\rho l}{{\rho }_g}}{)}^{-1}$$

(20)

The parameters of changed state are calculated as follows:

$${\rho }_9{u}_9={\rho }_{9^{\prime }}{u}_{9^{\prime }}$$

(21)

$${\rho }_9{u}_9^2+p_6={\rho }_{9^{\prime }}{u}_{9^{\prime }}^2+p_{6^{\prime }}$$

(22)

$$h_9+{\displaystyle \frac{1}{2}}{u}_9^2={\displaystyle \frac{1}{2}}{u}_{9^{\prime }}^2+h_{9^{\prime }}$$

(23)

In the diffuser chamber of the ejector, the velocity of the mixed fluid decelerates while the pressure rises. According to the inlet state 9 and constant entropy efficiency (${\eta }_d$) of the diffuser, the enthalpy ($h_{10}$), and pressure ($p_{10}$) of the outlet of the diffuser are calculated. The mathematical model is as follows:

$$h_{10}=h_{9^{\prime }}+{\displaystyle \frac{{u_{9\prime }}^2}{2}}$$

(24)

$${\eta }_d={\displaystyle \frac{h_{10,is}-h_{9^{\prime }}}{h_{10}-h_{9^{\prime }}}}$$

(25)

$$p_{10}=f(h_{10,is},s_{9^{\prime }})$$

(26)

The cooling capacity of the two evaporators are calculated as follows, respectively:

$${\dot{Q}}_{\mathrm{h}\mathrm{e}}=({\dot{m}}_{\mathrm{s}}+{\dot{m}}_{\mathrm{p}})(h_{10}-h_{11})$$

(27)

$${\dot{Q}}_{\mathrm{l}e}={\dot{m}}_{\mathrm{s}}(h_5-h_6)$$

(28)

To make better use of the composite heat source, the composite-heat-source matching ratio ($\phi$) is introduced to analyze the comprehensive influence of the low-temperature and high-temperature heat sources on the system performance of the CTHP system. In addition, considering that the two heat sources are greatly affected by flow and temperature, and there is an ejector between the two evaporators. The matching ratio of the composite heat source is also affected by the entrainment coefficient of the ejector, so the matching ratio of the composite heat source is defined as the ratio of the cooling capacity of the high-temperature evaporator to that of the low-temperature evaporator, as shown in Equation (29).

$$\phi ={\displaystyle \frac{{\dot{Q}}_{\mathrm{he}}}{{\dot{Q}}_{\mathrm{le}}}}$$

(29)

Compressor power consumption and compressor pressure ratio:

$${\dot{W}}_{\mathrm{cm}}=({\dot{m}}_{\mathrm{s}}+{\dot{m}}_{\mathrm{p}})(h_2-h_1)=({\dot{m}}_{\mathrm{s}}+{\dot{m}}_{\mathrm{p}}){\displaystyle \frac{(h_{1,\mathrm{is}}-h_1)}{{\eta }_{\mathrm{cm}}}}$$

(30)

$$\gamma ={\displaystyle \frac{P_2}{P_1}}$$

(31)

The isentropic efficiency of the compressor is connected to the pressure ratio, using the following empirical formula [36]:

$${\eta }_{\mathrm{cm}}=0.815+0.022\left({\displaystyle \frac{P_2}{P_1}}\right)-0.0041{\left({\displaystyle \frac{P_2}{P_1}}\right)}^2+0.0001{\left({\displaystyle \frac{P_2}{P_1}}\right)}^3$$

(32)

Performance coefficient of the heat pump system (cooling and heating) is as follows:

$$\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{c}}={\displaystyle \frac{{\dot{Q}}_{\mathrm{he}}+{\dot{Q}}_{\mathrm{l}\mathrm{e}}}{{\dot{W}}_{\mathrm{c}\mathrm{m}}}}$$

(33)

$$\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{h}}={\displaystyle \frac{h_2-h_3}{{\dot{W}}_{\mathrm{cm}}}}$$

(34)

From the P-h diagram of the CTHP system, the discharge pressure is equal to the P_gc,out in the previously assumed conditions of this paper. Under the known conditions—T_gc,out, T_e, and ΔT_e of the low-temperature evaporator, the matching ratio of the composite heat source, isentropic efficiency of the primary nozzle, secondary nozzle, the diffuser chamber of the two-phase ejector, and a mixing chamber length-to-diameter ratio of 10—the mixing pressure of the ejector was selected in order to obtain the maximum system performance coefficient, then the ejector entrainment coefficient was assumed. In conditions of optimum mixing pressure and the total cooling capacity of the water and high-temperature evaporator remaining unchanged, the optimum COP of the system performance and the corresponding gas cooler outlet pressure (P_gc,out), the ejector entrainment coefficient, and other parameters are calculated in MATLAB R2019b. The mathematical model solution process is shown in Figure 4.

(1)

The parameters of state 7 can be calculated by Equations (3)–(7), and the parameters of state 8 can be obtained by Equations (8)–(12). Then, the mixing chamber outlet state 9 can be calculated from Equations (13)–(23). According to Equations (24)–(26), state 10 of the diffuser outlet state can be obtained.

(2)

According to Equations (27)–(29), the cooling capacity of the heat pump and the utilization ratio of the composite heat source are calculated, and whether the matching ratio of the composite heat source is the same as the input value is checked. If they are different, the ejector entrainment coefficient is reselected for calculation until the convergence error is satisfied.

(3)

The compressor power consumption, mass flow rate, and performance coefficient of the CTHP system can be calculated using Equations (30)–(34). The optimum mixing pressure under different working conditions is obtained.

(4)

The optimum system performance coefficient and corresponding P_opt,out,gc are found using the same optimization. To achieve the optimum system performance, the results under the optimum mixing pressure corresponding to different T_e are adopted. In this numerical model, the convergence errors of density and matching ratio of the composite heat source are both 10⁻³.

(5)

The maximum COP of the system was obtained by changing the outlet pressure of the gas cooler, and the step size was 1 kPa. For CTHP systems, the system COP can be expressed as $\mathrm{C}\mathrm{O}{\mathrm{P}}_{\mathrm{CTHP}}=f(T_{gc,out,}{T}_{\mathrm{e},}\phi )$.

2.3. Sensitivity Analysis of Ejector Efficiency

In the simulation of the CTHP system, the isentropic efficiencies of the primary nozzle, secondary nozzle, and diffuser chamber are assumed to be a constant value of 0.85. However, in reality, this efficiency is subject to variation due to changes in operating conditions and geometric tolerances. To quantify the impact of this uncertainty on system performance, the sensitivity analysis of the ejector efficiency is shown in Figure 5.

As can be seen from Figure 5, the influence of the isentropic efficiency of the primary nozzle, secondary nozzle, and diffuser chamber decreases in that order, with the impact of the isentropic efficiency of the diffuser chamber being the smallest and negligible. The isentropic efficiency of the nozzle has the greatest influence. An increase in the isentropic efficiency of the ejector will reduce internal losses and enhance the ejector entrainment coefficient and pressure lift ratio, thereby improving the COP of the CTHP system. When the isentropic efficiency of the ejector nozzle increases from 85% to 95%, the change in system COP is the most significant, with a maximum increase of 1.79%.

3. Experimental Setup and Model Verification

3.1. Experimental System

As shown in Figure 6, the experimental platform of the CTHP system was established by modifying the conventional TCHP system in our previous studies. The information on the primary equipment in the CTHP system is not listed in this section but are not presented for simplicity, which can be found in previous publications [24]. The data acquisition devices used in this experiment are listed in

Table 1. The data acquisition devices.

Instrument	Description	Range	Accuracy
Digital vortex flowmeter	LWYC-15	0~6 ${\mathrm{m}}^3\cdot {\mathrm{h}}^{-1}$	±0.5%
Temperature sensor	PT100 type	−50~200 °C	±0.15%
Electromagnetic flowmeter	HXLD-25	0~15 ${\mathrm{m}}^3\cdot {\mathrm{h}}^{-1}$	±0.5%
Pressure transducer	HSTL-800	0~160 kPa	±0.25%
Voltage	INVT GD200A	0~380 V	±1%

. The maximum uncertainty for the system COP was 0.5417% [24].

3.2. Test Procedure

In the experimental setup, the compressor frequency was adjusted to 25 Hz using an inverter. The inlet water temperatures for the gas cooler and the low-temperature evaporator were maintained at 11 °C and 30 °C, respectively, which were controlled by a water chilling unit. An electromagnetic flowmeter was employed to measure the water flow rates entering the gas cooler and the low-temperature evaporator, which were manually set at 0.5 m³/h and 1 m³/h, respectively. The ambient temperature was 30 °C, and the air inlet speed of the high-temperature evaporator was 11 m∙s⁻¹. The discharge pressure was controlled from 7500 kPa to 10,000 kPa by two expansion valves that were connected in parallel. The CO₂ refrigerant flow was measured by a Coriolis flowmeter transmitter. Each measurement was obtained after the experiment had run for at least 15 to 20 min to establish steady-state conditions.

In unchanged inlet conditions of the gas cooler, gas cooler outlet pressure is changed by adjusting the expansion valve. The CO₂ outlet temperature and pressure of the ejector, gas cooler, low-temperature evaporator, and high-temperature evaporator are measured experimentally, and then the low-temperature evaporator outlet superheat, as well as the cooling capacities of the low- and high-temperature evaporators, are calculated by the measured temperature, pressure, and flow of CO₂, which are the input conditions for numerical simulation experiment verification. Composite-heat-source matching ratio φ is calculated by Equation (29). The input parameters for model validation using the experimental data are shown in

Table 2. Input parameters for model validation using experimental data.

Input Parameters	#1	#2	#3	#4	#5
Gas cooler outlet pressure (kPa)	7840	7900	7980	8200	8380
Gas cooler outlet temperature (°C)	32.2	32.5	31.8	28.2	27.7
Low-temperature evaporator inlet temperature (°C)	22.43	22.36	21.58	19.56	19.17
Low-temperature evaporator Outlet superheat (°C)	1.09	1.04	1.22	1.24	1.21
Cooling capacity of high-temperature evaporator (kW)	36.21	35.10	34.76	33.02	32.02
Cooling capacity of low-temperature evaporator (kW)	7.73	7.34	7.20	7.28	7.17

. Based on the thermophysical property data from NIST Refprop 9.1, the enthalpy values at the inlet and outlet of the gas cooler are calculated using the corresponding pressure and temperature measurements. The compressor power consumption is recorded, and the system’s heating COP is then determined using Equation (34).

3.3. Model Verification

To verify the accuracy of the model, some simulation results were first obtained under the above input conditions, and Figure 7 shows the comparison results between experimental values and simulated values. Through the comparison, it was found that the maximum relative error of the heating COP was within 8.49%, indicating that the established model can effectively predict the system performance.

4. Results and Discussion

The COP of the CTHP system under different P_gc,out was first investigated with different T_e (−10 °C to 10 °C), T_gc,out (30 °C to 50 °C), and composite-heat-source matching ratio (1–2). The optimum COP of the system and the corresponding P_opt,out,gc, ejector entrainment coefficient, pressure ratio, ejector efficiency, and compressor pressure ratio were found.

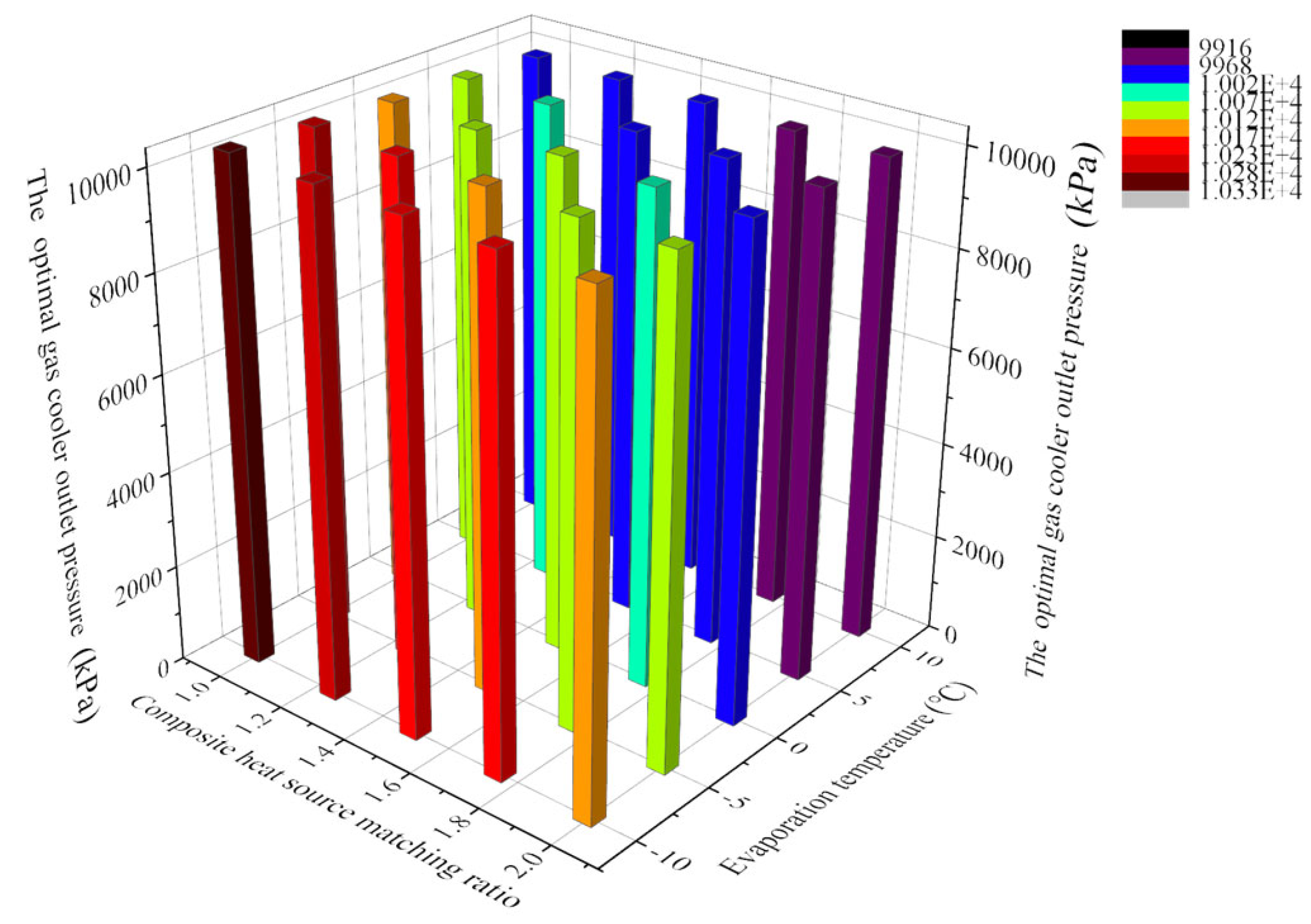
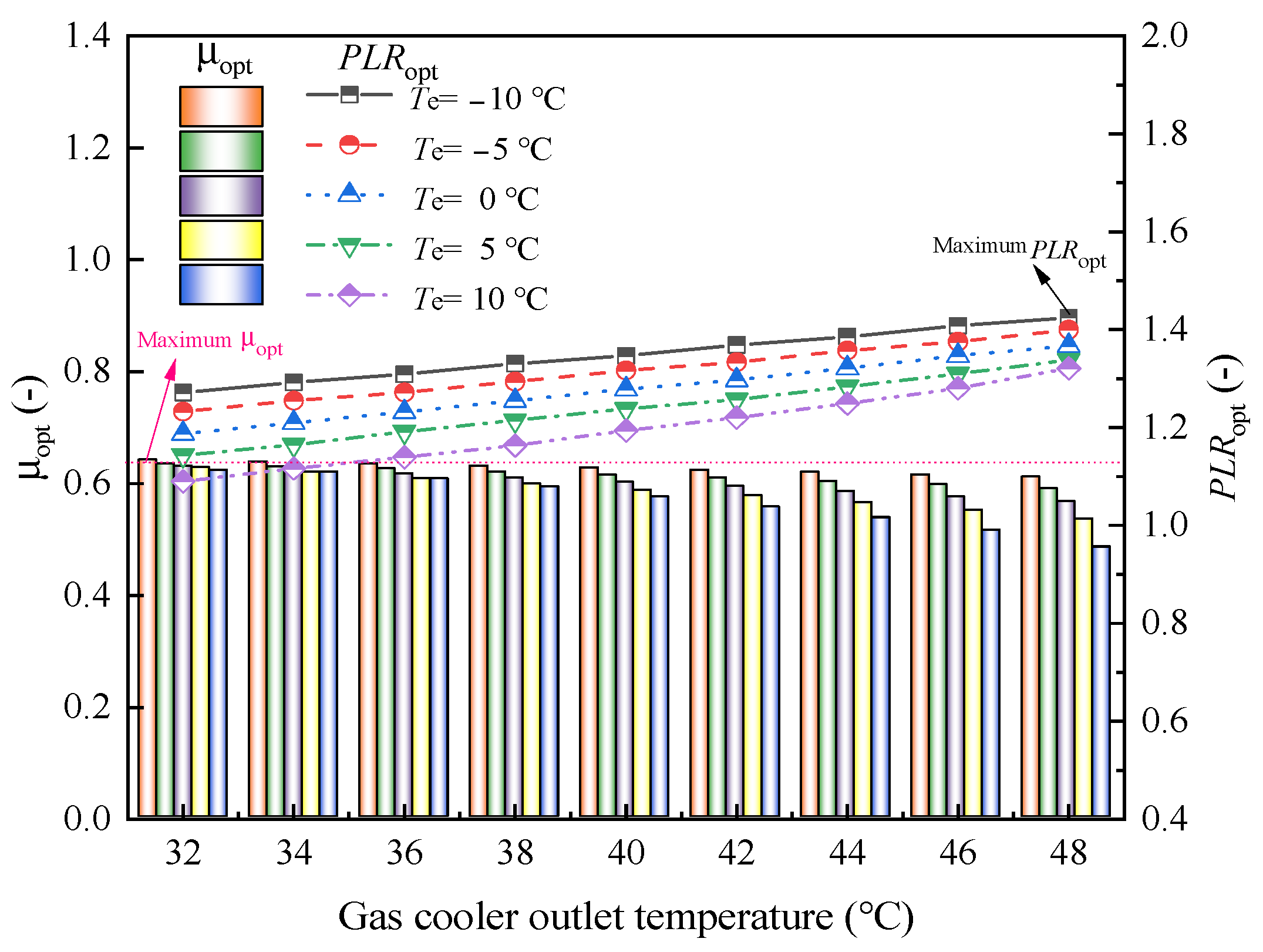
4.1. Gas Cooler Outlet Pressure

The control and optimization of gas cooler outlet pressure is crucial to improve the performance of the CTHP system. The gas cooler outlet pressure (P_gc,out) corresponding to the peak COP is called the P_opt,out,gc. The variations in the P_opt,out,gc are shown in Figure 8, where T_e is −10–10 °C, T_gc,out is 30–50 °C, and the composite-heat-source matching ratio is 1.5. In the range of working conditions, the P_opt,out,gc rises significantly, and the maximum increase is 59.21% with the rise in T_gc,out. P_opt,out,gc decreased slowly and the maximum decrease is 2.72% with the increase in T_e. It can be seen that the effect of T_e is much smaller than that of T_e; in addition, it can be seen that the effect of Te is much smaller than that of Tgc,out, which was also obtained in the study of Bahman [37]. When T_gc,out is higher than 40 °C, P_opt,out,gc is above 10,000 kPa.

Figure 9 displays the variations in the P_opt,out,gc with the composite-heat-source matching ratio (φ) and evaporation temperature (T_e), where T_e is −10 °C to 10 °C, φ is 1–2, and T_gc,out is 40 °C. It can be seen from the figures that the maximum reduction in the P_opt,out,gc is 3.13% with the increase in the T_e, and the maximum reduction in P_opt,out,gc is 1.67% with the increase in the composite-heat-source matching ratio. It presents that T_gc,out has the greatest influence on the P_opt,out,gc, and the effect of the composite-heat-source matching ratio is close to that of T_e. It is beneficial to find the P_opt,out,gc corresponding to the optimum COP under different working conditions in order to better control the optimum pressure on the high-pressure side of the system when selecting the operating parameters.

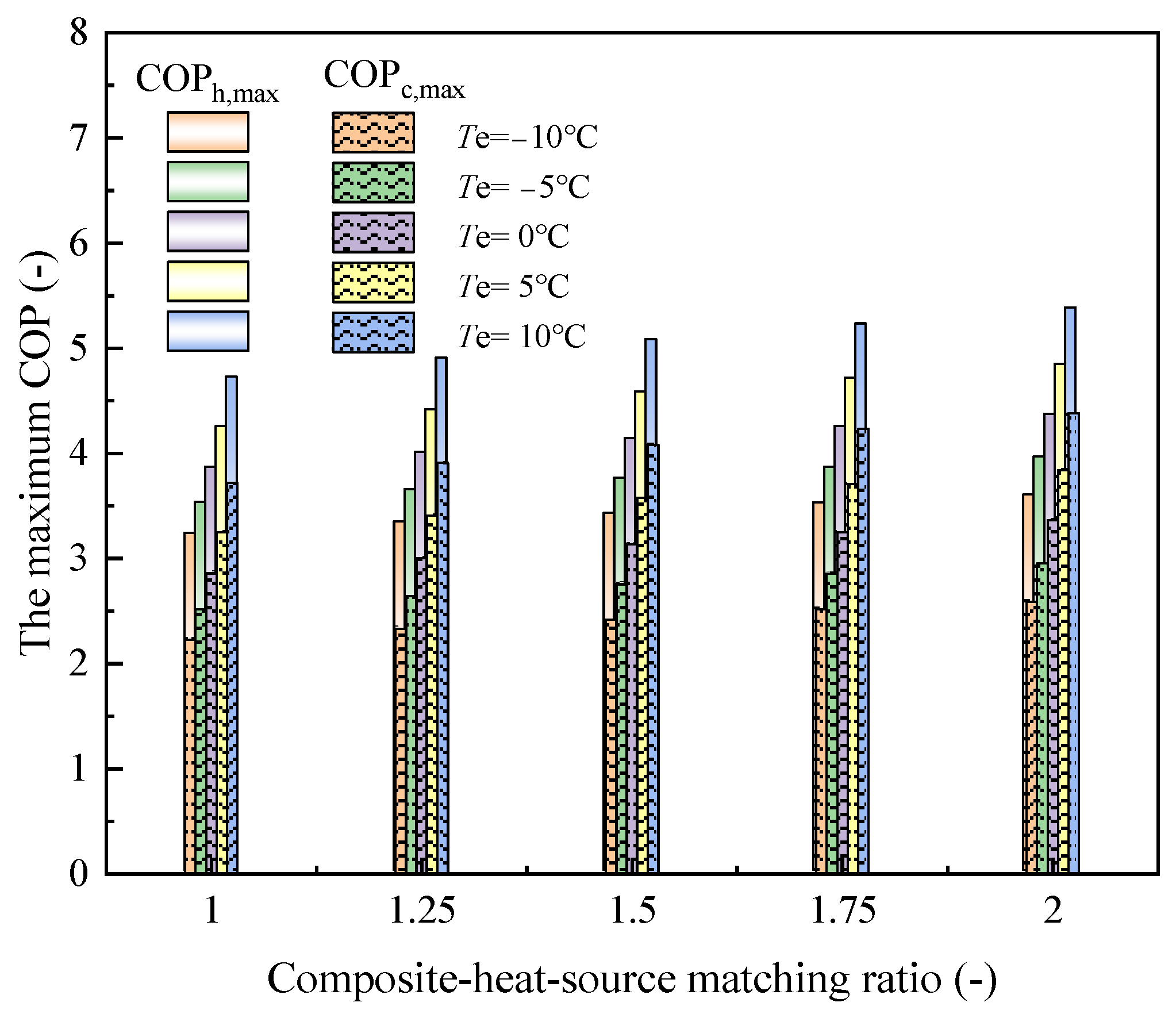
4.2. System Performance Coefficient

Owing to the unique physical characteristics of carbon dioxide, the COP of the CTHP system has a peak as the gas cooler outlet pressure (P_gc,out) rises. The maximum COP of the CTHP is found by changing the P_gc,out, and the variation trends of maximum system heating and cooling COP (COP_c,max and COP_h,max) with T_gc,out and T_e under the optimal gas cooler outlet pressure are shown in Figure 10, where evaporation temperature (T_e) ranges from −10 °C to 10 °C and gas cooler outlet temperature (T_gc,out) ranges from 30 °C to 50 °C and the composite-heat-source matching ratio (φ) is 1.5. The variation clearly shows that the COP_c,max and COP_h,max of the CTHP system increase as T_e increases and T_gc,out decreases. When T_e rises from −10 °C to 10 °C and T_gc,out drops from 48 °C to 32 °C, the COP_c,max and COP_h,max of the system increase from 1.864 and 2.862 to 6.246 and 7.235, respectively. This is because the discharge pressure increases with the rising T_e, leading to a decrease in the pressure ratio, decreased compressor power, and an increase in the optimum COP. When T_gc,out is higher, the amount of flash gas produced increases, the enthalpy difference that can be used for cooling or heating decreases, and the COP decreases. COP_h,max is 15.83–53.56% larger than COP_c,max under the same working conditions. Consequently, both the heating and cooling COP advantages of the CHTP system are enhanced under higher evaporation temperatures and a lower gas cooler outlet temperature, while the heating superiority is more significant.

Variations in COP_c,max and COP_h,max under the operating conditions of composite-heat-source matching ratio φ (1–2), evaporation temperature T_e (−10 °C to 10 °C), and gas cooler outlet temperature T_gc,out (40 °C) at P_opt,out,gc are shown in Figure 11. It can be seen that the COP_c,max and COP_h,max of the CTHP system increase as the T_e and φ increase. It can be seen that the COP_c,max and COP_h,max of the system vary from 2.226 to 4.383 and 3.225 to 5.53, respectively. As T_e increases, the maximum improvement ratios of COP_h,max and COP_c,max are 49.80% and 69.26%, respectively, and are 14.01% and 18.26% with the increase in the composite-heat-source matching ratio. Furthermore, it should be noted that when T_e rises from −10 °C to 10 °C and φ varies from 1 to 2, the heating performance improvement ratio of the CTHP system over that of the cooling performance increases from 66.68% to 96.90%. This implies that it is better to seek optimum system performance by changing the combination of main operation parameters, and the effects of the composite-heat-source matching ratio on CTHP system performance cannot be ignored.

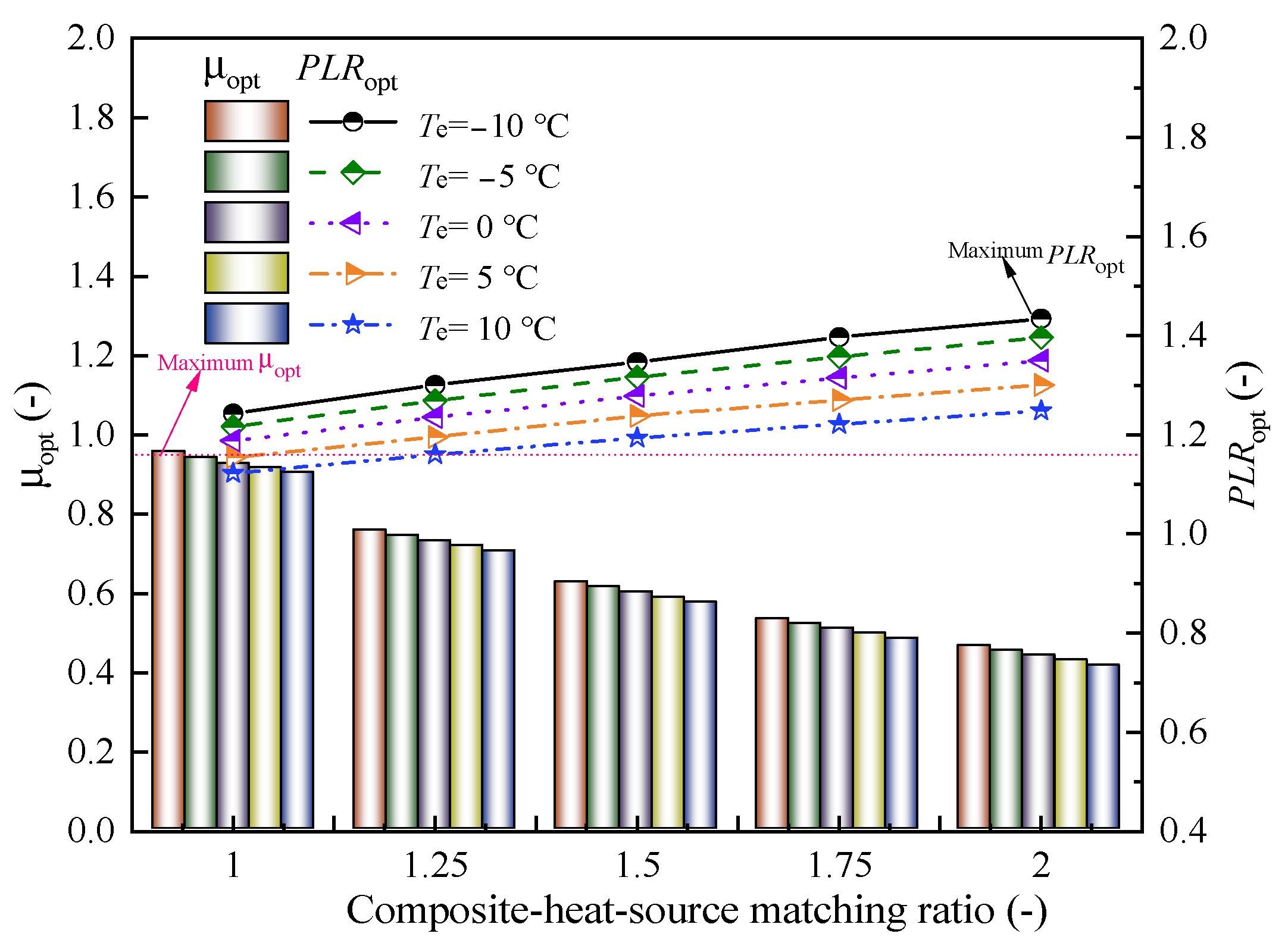
4.3. Ejector Performance

The entrainment coefficient (μ) and the pressure lift ratio (PLR) are both the main performance parameters of the ejector. The variations in the μ and PLR under the optimum COP (μ_opt and PLR_opt) at different T_gc,out and T_e are presented in Figure 12. The composite-heat-source matching ratio is set at 1.5. As shown, as the T_gc,out increases from 32 °C to 48 °C, the μ_opt tends to reduce and PLR_opt shows an upward trend. The μ_opt decrement and increment of PLR_opt are mainly attributed to the increments in the fluid enthalpy at the primary nozzle inlet and the corresponding fluid velocity at the primary nozzle caused by increasing the gas cooler outlet temperature, which subsequently leads to an increase in the velocity difference between the primary and secondary flows at the inlet of the mixing chamber. It also appears that the μ_opt decreases and the PLR_opt presents a decreasing trend with T_e increasing from −10 °C to 10 °C; this is mainly due to the fact that the P_gc,out decreases as the T_e increases and that the nozzle pressure drop corresponding to the optimum mixing pressure continuously increases with increasing T_e, which can give the reduction in the ejector outlet pressure and, hence, the pressure lift ratio of the ejector decreases. As T_e increases, the enthalpy of the steam at the inlet of the secondary chamber and the velocity of the secondary flow near the working nozzle outlet decrease, resulting in a downward trend in the entrainment ratio.

To be conclusive from Figure 12, the maximum improvement ratio of μ_opt is 4.99% with the increase in T_gc,out when T_e is −10 °C, and the maximum improvement ratio of μ_opt is only 2.88% with the increase in T_e when T_gc,out is 32 °C, which indicates that the μ_opt yields a tiny variation amplitude by adjusting T_e or T_gc,out when T_gc,out or T_e is lower. This minor change indicates a low sensitivity and also demonstrates the robustness of the ejector within the range of the working conditions. The maximum improvement ratio of μ_opt is 32.14% with decreasing T_gc,out and T_e, and the maximum improvement ratio of PLR_opt is 30.69% with the increase in T_gc,out and the decrease in T_e.

The μ_opt and PLR_opt, with different composite-heat-source matching ratios and evaporation temperatures, are shown in Figure 13, where T_e is −10 °C−10 °C, φ is 1–2, and T_gc,out is 40 °C. As shown, the entrainment coefficient under the optimum COP is mainly distributed in the range of 0.41–0.95, and the pressure lift ratio under the optimum COP of the ejector ranges from 1.12 to 1.43. It is also observed that the μ_opt decreases and PLR_opt increases as φ increases from 1 to 2, and the maximum improvement ratio of μ_opt and PLR_opt are 54.09% and 15.40%, respectively. Finding μ and PLR corresponding to the optimum COP system under different working conditions can provide a reference for improving the design parameters of the system ejector.

4.4. Compressor Pressure Ratio

The compressor pressure ratio (γ) is an important index to evaluate compressor efficiency. The variation in the compressor pressure ratio under the optimum COP (γ_opt) with the different T_gc,out and T_e is shown in Figure 14. It can be seen that the γ_opt tends to reduce as the T_gc,out decreases. The γ_opt decrement is mainly attributed to the decrements in the P_gc,out and the compressor suction pressure with the decrease in T_gc,out. It also appears that the γ_opt decreases with rising T_e; this is because the outlet pressure and a specific enthalpy of evaporator increase with increasing T_e, leading to an increase in the suction pressure in the compressor, and a decrease in the compressor compression ratio. The maximum improvement ratio of γ_opt is 52.55% by increasing T_e and decreasing T_gc,out.

The variations in the compressor pressure ratio at the optimum performance coefficient for different evaporator temperatures and composite-heat-source matching ratios are depicted in Figure 15. The γ_opt decreases with the decrease in T_e and increase in φ. In the range of working conditions, the maximum reduction in the compressor pressure ratio under the optimum COP is 36.91% with the increase in T_e, and the maximum reduction is 14.80% with the rise in the composite-heat-source matching ratio. The maximum improvement ratio of γ_opt is 43.78% by increasing T_e and φ. So, finding the compressor pressure ratio corresponding to the optimum COP under different working conditions can provide a reference for the adjustment of system operating parameters.

From the above analysis, it can be seen that the composite-heat-source matching ratio significantly affects the CTHP system’s performance coefficient, P_gc,out, compressor pressure ratio, and other factors. The CTHP system’s overall performance is greatly impacted by the appropriate matching of its high- and low-temperature heat sources. The effect of the composite-heat-source matching ratio should be considered in the process of optimization of system operating parameters.

4.5. Regression Analysis of Parameters

In order to obtain the matching relationship between the P_opt,out,gc and the working condition parameters of the CTHP heat pump system, while considering the influence of the composite-heat-source matching ratio, an orthogonal test is designed to simulate the P_opt,out,gc under the different working conditions, valid for the ranges of the T_gc,out from 30 °C to 50 °C, T_e from −10 °C to 10 °C, and composite-heat-source matching ratio from 1 to 2. The multivariate nonlinear regression analysis is performed by the comprehensive optimization analysis and calculation software 1stOpt V15.0, and the optimization calculation is performed by the Levenberg–Marquardt method and general global optimization method. As shown in Equations (35)–(40), the following relationships for the CTHP have been established to predict P_opt,out,gc in bar (R² = 99.92%), the maximum system COP (R² = 99.02%), the optimum entrainment ratio (R² = 97.47%), the optimum pressure lift ratio (R² = 95.33%), and the corresponding optimum compressor pressure ratio (R² = 98.71%), which can provide reference for the optimum design of the system and the selection of operating parameters. To evaluate the effectiveness of the regression model, the goodness-of-fit indicators for the models are shown in

Table 3. Goodness-of-fit indicators for models.

Parameters	Popt,out,gc	COPc,max	COPh,max	μopt	PLRopt	γopt
Root Mean Square Error	52.3598	0.1076	0.1111	0.0275	0.0273	0.0555
Sum of Squared Residuals	68,538.72	0.2893	0.3084	0.0189	0.0186	0.0770
Correlation Coefficient	0.9997	0.9954	0.9951	0.9872	0.9764	0.9935
Chi-square	3.4362	0.0371	0.0308	0.0179	0.0075	0.0174
F-statistic	3767.2451	265.5271	244.9293	93.4033	49.8385	186.0757

.

$$\begin{array}{ll}{P}_{\mathrm{opt},\mathrm{out},\mathrm{gc}}=& 28884.808\exp (0.0113T_{\mathrm{gc},out}-0.000682T_{\mathrm{e}}-0.0210\phi )-208.411T_{\mathrm{gc},\mathrm{out}}\\ & +18.419T_{\mathrm{e}}+918.156\phi -27030.107\end{array}$$

(35)

$$\begin{array}{ll}{\mathrm{COP}}_{\mathrm{c},\max }=& 100.679\exp (-0.130T_{\mathrm{gc},\mathrm{out}}+0.0578T_{\mathrm{e}}-0.264\phi )-0.0671T_{\mathrm{gc},\mathrm{out}}\\ & +0.0505T_{\mathrm{e}}+0.423\phi +4.784\end{array}$$

(36)

$$\begin{array}{ll}{\mathrm{COP}}_{\mathrm{h},\max }=& 116.170\exp (-0.135T_{\mathrm{gc},\mathrm{out}}+0.0592T_{\mathrm{e}}-0.302\phi )-0.0689T_{\mathrm{gc},\mathrm{out}}\\ & +0.0512T_{\mathrm{e}}+0.424\phi +5.881\end{array}$$

(37)

$$\begin{array}{ll}{\mu }_{\mathrm{opt}}=& 0.0423\exp (-0.0123T_{\mathrm{gc},\mathrm{out}}-0.0221T_{\mathrm{e}}+1.716\phi )-0.00177T_{\mathrm{gc},\mathrm{out}}\\ & +0.00347T_{\mathrm{e}}-1.082\phi +1.929\end{array}$$

(38)

$$\begin{array}{ll}PL{R}_{\mathrm{opt}}=& -24.292\exp (0.00492T_{\mathrm{gc},\mathrm{out}}-0.00406T_{\mathrm{e}}-0.0481\phi )+0.148T_{\mathrm{gc},\mathrm{out}}\\ & -0.119T_{\mathrm{e}}-1.197\phi +24.678\end{array}$$

(39)

$$\begin{array}{ll}{\gamma }_{\mathrm{opt}}=& 0.463\exp (0.0373T_{\mathrm{gc},\mathrm{out}}-0.0398T_{\mathrm{e}}-0.229\phi )-0.0122T_{\mathrm{gc},\mathrm{out}}\\ & +0.0109T_{\mathrm{e}}+0.110\phi +1.094\end{array}$$

(40)

5. Conclusions

In this paper, the collaborative influence of the operating parameters of a composite-heat-source CTHP system has been studied by considering the composite-heat-source matching ratio and other factors. The main conclusions are as follows:

(1)

The maximum increase in the P_opt,out,gc was 59.21% with the increase in the T_gc,out, and the maximum decrease in the P_opt,out,gc was 3.13% with the increase in the T_e, and the maximum decrease was 1.67% with the increase in the composite-heat-source matching ratio. The results showed that the T_gc,out had the greatest influence on the P_gc,out, and the effect of the composite-heat-source matching ratio was equally significant on the P_opt,out,gc compared with the T_e.

(2)

When designing or operating the CTHP system, a higher evaporator temperature, lower T_gc,out, and higher composite-heat-source matching ratio were found to be more successful in achieving both a lower optimum high-pressure side and maximum system COP. The maximum improvement ratio of the μ_opt is 32.14% with decreasing T_gc,out and T_e, and that of the PLR_opt is 30.69% with the increase in T_gc,out and the decrease in T_e. The μ_opt decreases and PLR_opt increases as the composite-heat-source matching ratio increases, and the maximum improvement ratios of μ_opt and PLR_opt are 54.09% and 15.40%, respectively. The optimum high-pressure side governing equation of the CTHP system and the expressions for optimum cycle parameters of the CTHP system were obtained by multivariate nonlinear regression analysis.

(3)

The in-depth research on the reasonable matching of the high-temperature heat source and low-temperature heat source will be helpful for further development and optimization of the CTHP system, which is of great significance for the comprehensive utilization of renewable heat sources such as geothermal or air-source and the promotion of efficiency, environmental protection, and sustainable development in the fields of building and energy, etc. Future research may consider more factors, integrating performance parameters, cost parameters, and attempting to maximize performance as well as minimize costs, using an optimization method, such as machine learning or a genetic algorithm, to reduce the cost and improve the efficiency of energy utilization.