Assessing the Effectiveness of an Intelligent Algorithms-Based PII2 Controller in Enhancing the Quality of Power Output from a DFIG-Based Power System
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Research Gaps and Contributions
- The development of effective control strategies is imperative, and these strategies must take into account a realistic MRT model based on DFIG and the parametric variations. The implementation of these strategies will help improve stability problems.
- A substantial opportunity exists for enhancing the PQ of an MRT system through the exploration of control strategies and system operational performance through simulation experiments.
- It is imperative to augment the implementation of the DPC strategy with enhanced robustness and flexibility to regulate the integrated DFIG power in an MRT system.
- It is conceivable that the RTO strategy could be leveraged to refine the outcomes of the modified DPC strategy.
- It is imperative to ascertain which control algorithm (GA or RTO) is more efficacious, as it is essential to rely on it in the future to adjust the gains of an MRT system.
- Providing a suitable and effective solution to the drawback of low PQ in energy systems using MRTs, through the analytical design of the PII2 smart controller, which is easy to implement and ensures high compatibility with industrial systems.
- Develop a robust regulator capable of reducing power and current fluctuations under various operating conditions while enhancing operational performance.
- Design a command algorithm that maintains high performance under parameter uncertainty.
- Demonstrate that the intelligent PII2 regulator based on the RTO algorithm outperforms other regulators in terms of reducing overshoot, improving settling time, and SSE.
- Use the Integral of Time-weighted Absolute Error (ITAE)-based performance index to enhance the overall efficiency of the studied system by improving dynamic response and reducing oscillations.
- Despite the existence of numerous control systems, a prevailing challenge in the extant literature pertains to achieving an optimal balance between operational performance, robustness, ease of realization and application, and ease of control. Additionally, the enhancement of power and current quality in MRT-based power systems has not been sufficiently addressed. The present study is the first to address the PII2 regulator using intelligent algorithms in MRT systems, distinguishing itself as a pioneering work in this field.
- In this research, the gain values of the PII2 regulator were determined using two different strategies: the GA and the RTO algorithms. These algorithms have been demonstrated to offer high performance and robustness, leveraging the ITAE to ascertain the optimal values.
- The evaluation of the proposed regulator was conducted in order to ascertain its efficacy in power control under a variety of operating conditions. These conditions included parameter changes, and the regulator was compared with a conventional approach based on a PI regulator. The findings indicate the efficacy of the RTO algorithm-based PII2 regulator in comparison to alternative regulators and substantiate the feasibility of this proposed approach in real-time systems.
1.4. Organization
2. Materials and Methods
2.1. MRT Model
2.2. Designed Intelligent PII2 Regulator
2.3. New DPC-PWM Technique
- The elimination of hysteresis comparators is imperative.
- The provision of a smoother command is accompanied by lower current and energy fluctuations.
- The utilization of the PWM technique is contingent upon a constant switching frequency.
- Parameter sensitivity.
- Variable switching frequency.
- Poor performance under faults or at low speed.
- Flux estimation errors.
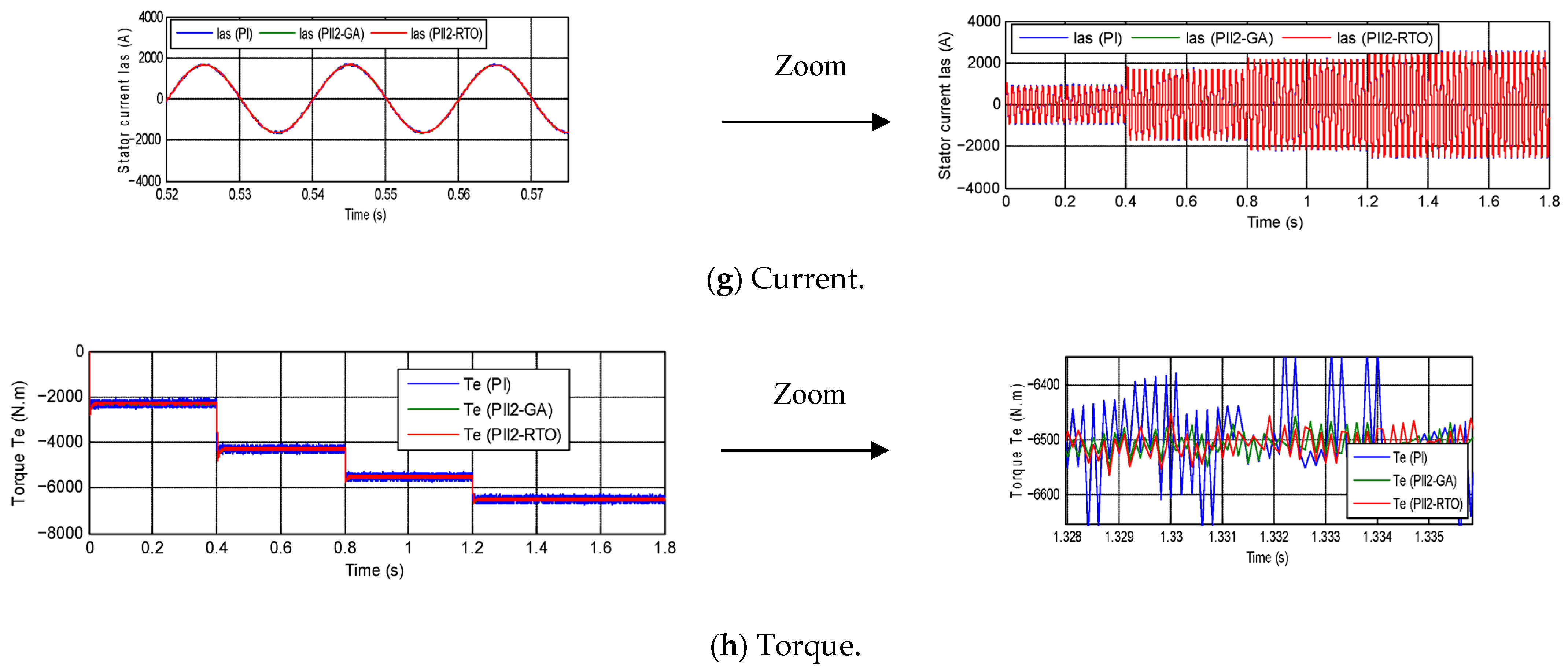
3. Results
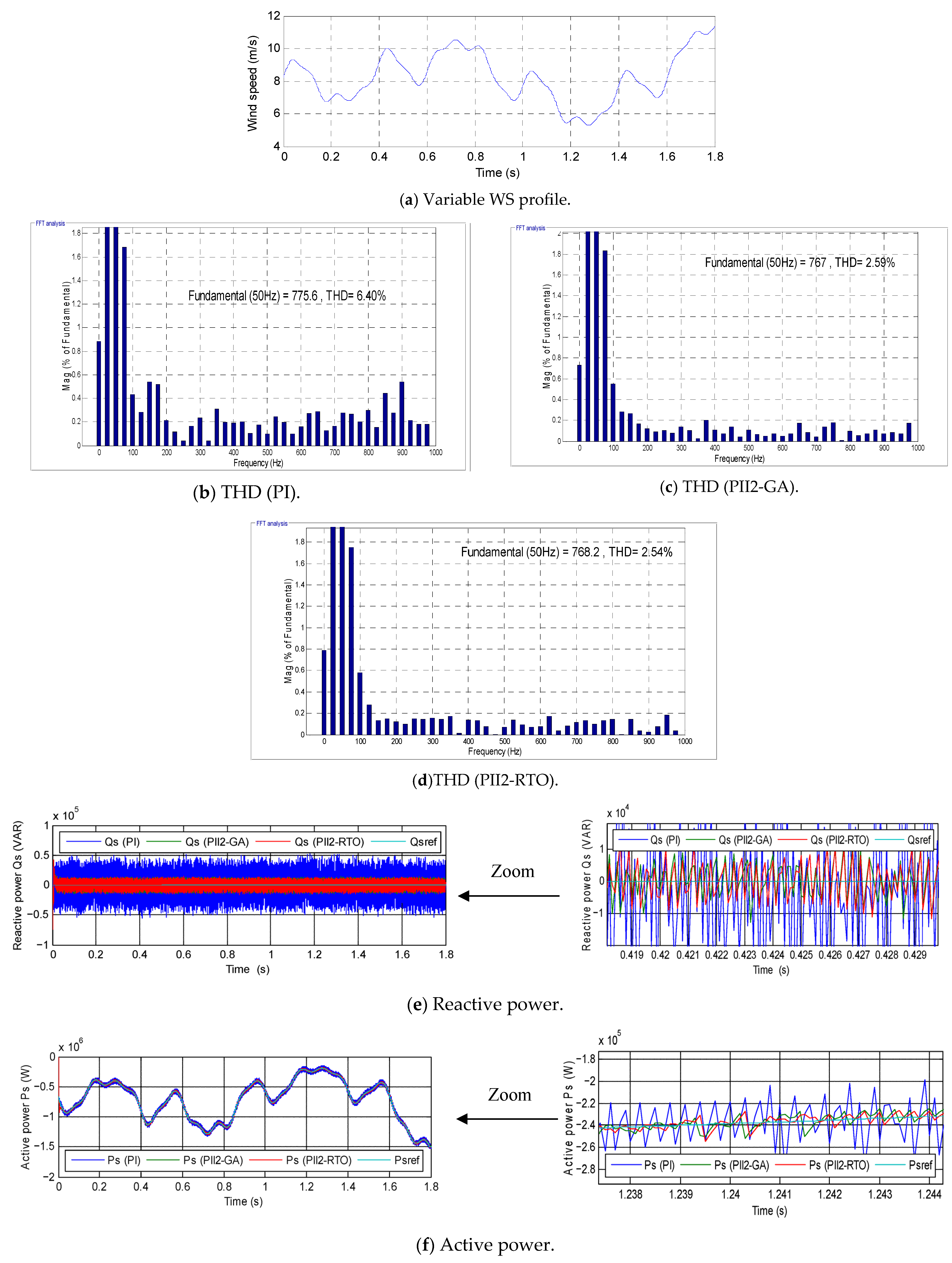
3.1. The First Test
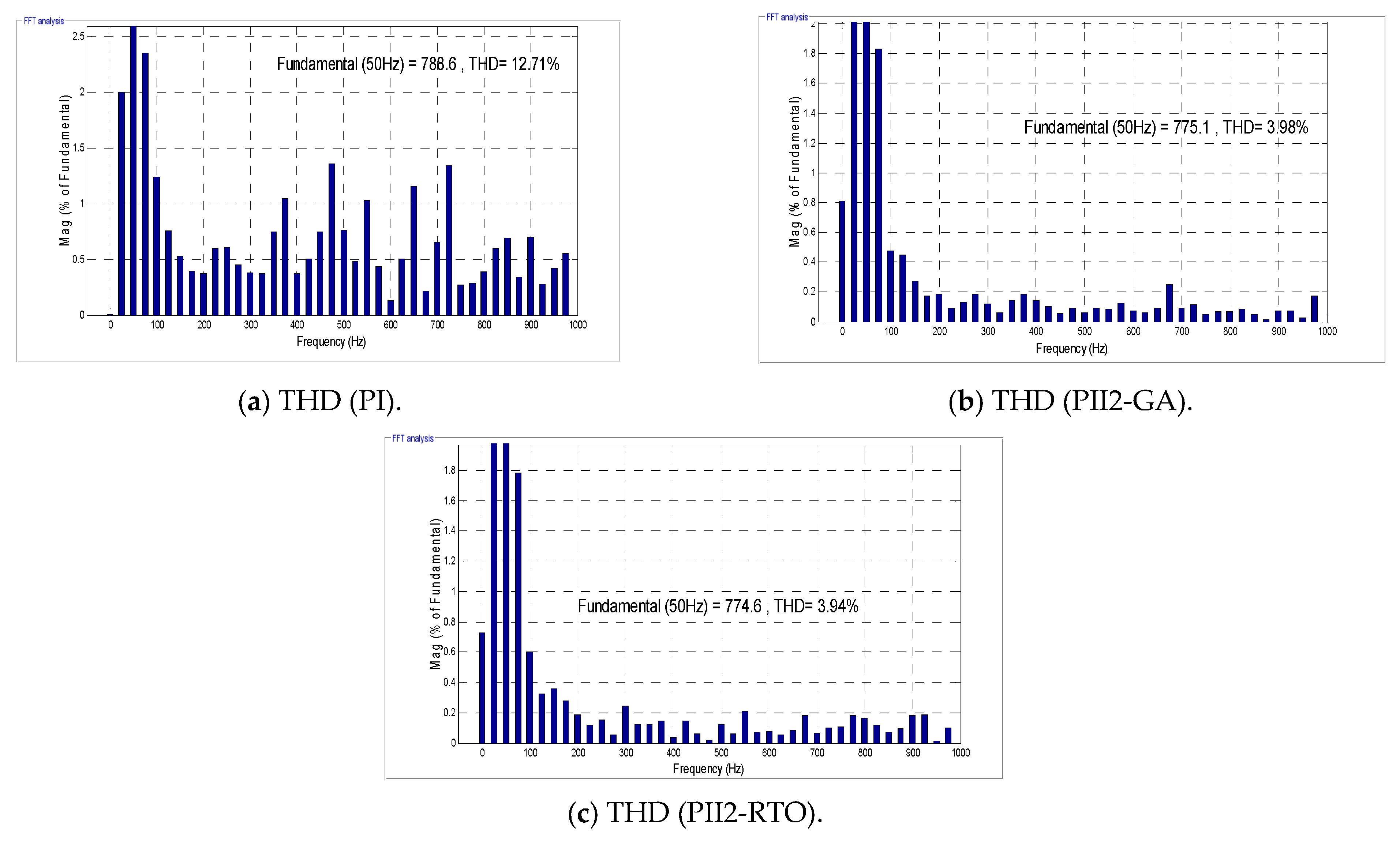
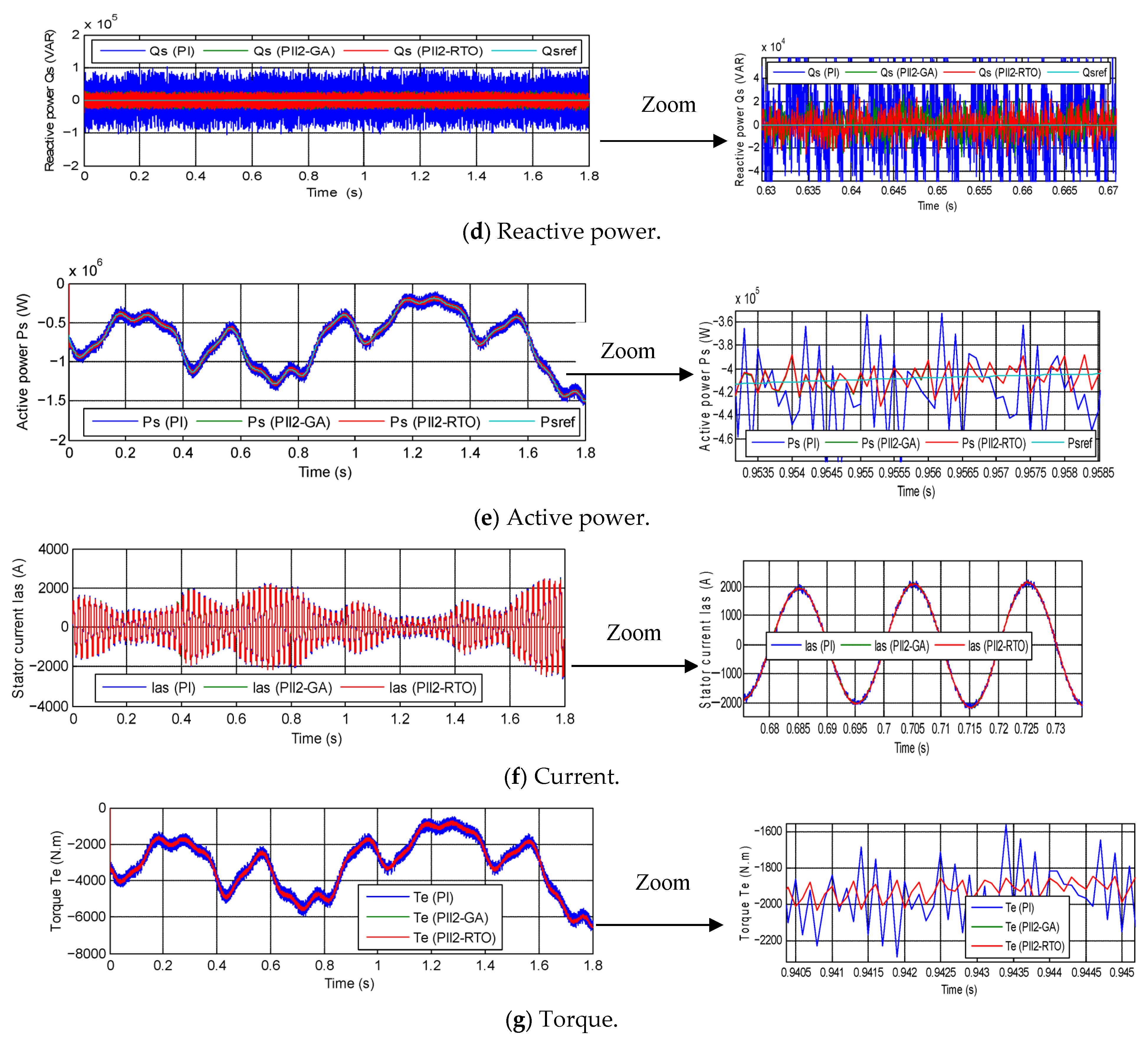
3.2. The Second Test
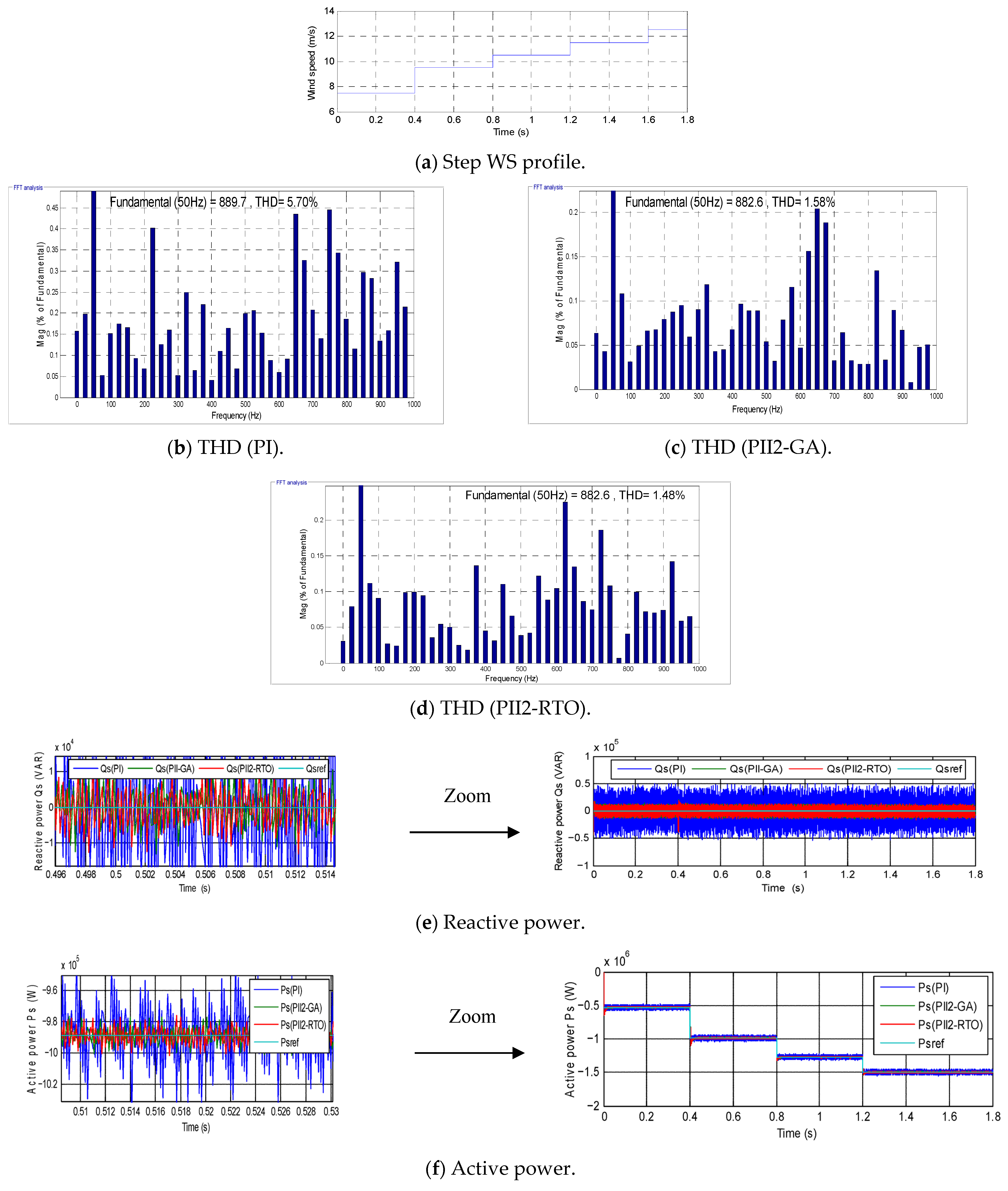
3.3. The Third Test
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PII2 | Proportional-integral plus second-order integral regulator |
| RTO | Rooted tree optimization |
| MPPT | Maximum power point tracking |
| DFIG | Doubly fed induction generator |
| WP | Wind power |
| PQ | Power quality |
| MRT | Multi-rotor turbine |
| DPC | Direct power control |
| GA | Genetic algorithm |
| THD | Total harmonic distortion |
| WS | Wind speed |
| GWO | Grew wolf optimization |
| ITAE | Integral time-weighted absolute error |
| SSE | Steady-state error |
| RES | Renewable energy source |
References
- Von, J.A.; Agamloh, E.; Yokochi, A. A Review of Offshore Renewable Energy for Advancing the Clean Energy Transition. Energies 2025, 18, 4798. [Google Scholar] [CrossRef]
- Ahmed, F.A.; Montaser, A.; Hamdi, A.M. Negative Effects and Processing Methods Review of Renewable Energy Sources on Modern Power System: A Review. Int. J. Renew. Energy Res. 2024, 14, 385–394. [Google Scholar] [CrossRef]
- Sarah, K.; Roland, U.; Kenneth, O. Harnessing Solar and Wind Power for Hybrid Stand-alone Energy System: The Case of Coastline Communities in Delta State of Southern Nigeria. Int. J. Smart Grid 2023, 7, 25–37. [Google Scholar]
- Asad, M.; Sánchez-Fernández, J.Á. Frequency Regulation Provided by Doubly Fed Induction Generator Based Variable-Speed Wind Turbines Using Inertial Emulation and Droop Control in Hybrid Wind–Diesel Power Systems. Appl. Sci. 2025, 15, 5633. [Google Scholar] [CrossRef]
- Abdirahman, S.H.; Neha, C.; Rainer, G.; Terence, M. Multi-Rotor Wind Turbines: A Review of Modern Research Efforts and Challenges. Renew. Sustain. Energy Rev. 2026, 226 Pt A, 116252. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Noura, A.N.A.; Ahmed, M.A.; Walid, S.E.A. A Fuzzy Logic-based MPPT Technique for PMSG Wind Generation System. Int. J. Renew. Energy Res. 2019, 99, 1751–1760. [Google Scholar] [CrossRef]
- Caglayan, R.Z.; Kayisli, K.; Zhakiyev, N.; Harrouz, A.; Colak, I. A Review of Hybrid Renewable Energy Systems and MPPT Methods. Int. J. Smart Grid 2022, 6, 72–78. [Google Scholar] [CrossRef]
- Raghvendraprasad, D. Power Quality Analysis of Electrical Distribution Systems with Asynchronous Generators. Int. J. Renew. Energy Res. 2018, 8, 2210–2217. [Google Scholar] [CrossRef]
- Da, X.; Ziyi, B.; Tao, W.; Zhibin, W.; Ke, Z. An energy-based control scheme for optimal power quality management in 12-pulse rectifier integrated distribution systems. Int. J. Electr. Power Energy Syst. 2023, 145, 108707. [Google Scholar] [CrossRef]
- Habib, B. A direct power control of the doubly fed induction generator based on the three-level NSVPWM technique. Int. J. Smart Grid 2019, 3, 216–225. [Google Scholar] [CrossRef]
- Seyed, M.T.; Mohammad, A.P.; Mohammad, R.Z. Comparison between Different DPC Methods Applied to DFIG Wind Turbines. Int. J. Renew. Energy Res. 2013, 3, 446–452. [Google Scholar]
- Habib, B.; Hamza, G.; Nicu, B. Direct reactive and active power regulation of DFIG using an intelligent modified sliding-mode control approach. Int. J. Smart Grid 2022, 6, 157–171. [Google Scholar] [CrossRef]
- Habib, B. Application of five-level NPC inverter in DPC-ANN of doubly fed induction generator for wind power generation systems. Int. J. Smart Grid 2019, 3, 128–137. [Google Scholar] [CrossRef]
- Harun, F.A.; Murtaza, F. Power Quality Analysis of a Hybrid MATLAB/Simulink Using a DSTATCOM and Comparison with a Real Plant. Int. J. Renew. Energy Res. 2024, 14, 503–515. [Google Scholar] [CrossRef]
- Reza, G.; Ali, M.; Alireza, D.S. A New Control Algorithm Method Based on DPC to Improve Power Quality of DFIG in Unbalance Grid Voltage Conditions. Int. J. Renew. Energy Res. 2018, 8, 2228–2238. [Google Scholar] [CrossRef]
- Farida, M.; Sebti, B.; Ilhami, C. DPC- SVM of DFIG Using Fuzzy Second Order Sliding Mode Approach. Int. J. Smart Grid 2021, 5, 174–182. [Google Scholar] [CrossRef]
- Lunardi, A.; Conde, E.R.; Rocha, N.; Sguarezi Filho, A.J. Direct power control for DFIG systems under distorted voltage using predictive repetitive control. Int. J. Electr. Power Energy Syst. 2025, 165, 110465. [Google Scholar] [CrossRef]
- Ahmed, B.; Houari, K.; Boubaker, B. Parallel model predictive direct power control of DFIG for wind energy conversion. Int. J. Electr. Power Energy Syst. 2021, 125, 106453. [Google Scholar] [CrossRef]
- Farida, M.; Sebti, B.; Ilhami, C.; Said, D.; Youcef, H. Adaptive direct power control for double fed induction generator used in wind turbine. Int. J. Electr. Power Energy Syst. 2020, 114, 105395. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Colak, I.; Bizon, N. Backstepping control of multilevel modified SVM inverter in variable speed DFIG-based dual-rotor wind power system. Trans. Inst. Meas. Control 2024, 47, 1917–1930. [Google Scholar] [CrossRef]
- Khedher, A.; Khemiri, N.; Mimouni, M.F. Wind Energy Conversion System Using DFIG Controlled by Backstepping and Sliding Mode Strategies. Int. J. Renew. Energy Res. 2012, 2, 421–430. [Google Scholar]
- Habib, B. Direct power control of a DFIG fed by a seven-level inverter using SVM strategy. Int. J. Smart Grid 2019, 3, 54–62. [Google Scholar] [CrossRef]
- Dardabi, C.; Álvarez, S.C.; Djebli, A. An Artificial-Neural-Network-Based Direct Power Control Approach for Doubly Fed Induction Generators in Wind Power Systems. Energies 2025, 18, 1989. [Google Scholar] [CrossRef]
- Karim, F.S.; Salah, T.; Djamel, Z.; Nabil, B.; Sofia, L.B.; Youcef, B. Real-time fuzzy logic-based direct power control for wind energy systems. Eng. Appl. Artif. Intell. 2025, 154, 110968. [Google Scholar] [CrossRef]
- Mohammad, J.Z.; Abolfazl, V. Modeling and improvement of direct power control of DFIG under unbalanced grid voltage condition. Int. J. Electr. Power Energy Syst. 2014, 59, 58–65. [Google Scholar] [CrossRef]
- Wenshao, B.; Leilei, X. Direct Power Control Strategy of PWM Rectifier Based on Improved Virtual Flux-Linkage Observer. J. Control Sci. Eng. 2017, 2017, 9376735. [Google Scholar] [CrossRef]
- Sumanth, Y.; Sambasiva, R.G.; Dharani, K.N. Optimized FoPID Controller for Doubly-Fed Induction Generator based Wind Turbine using Root Tree Optimization Algorithm. Int. J. Renew. Energy Res. 2025, 15, 373–383. [Google Scholar] [CrossRef]
- Sumanth Yampara, L.A.; Lakshminarasimman, L.; Sambasiva, R.G. Optimal design of FoPID controller for DFIG based wind energy conversion system using Grey-Wolf optimization algorithm. Int. J. Renew. Energy Res. 2022, 12, 2111–2120. [Google Scholar] [CrossRef]
- Youcef, B.; Djilani, B.A. Comparison Study Between SVM and PWM Inverter in Sliding Mode Control of Active and Reactive Power Control of a DFIG for Variable Speed Wind Energy. Int. J. Renew. Energy Res. 2012, 2, 471–476. [Google Scholar]
- Itouchene, H.; Amrane, F.; Boudries, Z.; Mekhilef, S.; Benbouhenni, H.; Bizon, N. Enhancing the performance of grid-connected DFIG systems using prescribed convergence law. Sci. Rep. 2025, 15, 28550. [Google Scholar] [CrossRef]
- Echiheb, F.; Ihedrane, Y.; Bossoufi, B.; Bouderbala, M.; Motahhir, S.; Masud, M.; Aljahdali, S.; ElGhamrasni, M. Robust sliding-Backstepping mode control of a wind system based on the DFIG generator. Sci. Rep. 2022, 12, 11782. [Google Scholar] [CrossRef]
- Xiong, L.; Li, P.; Li, H.; Wang, J. Sliding Mode Control of DFIG Wind Turbines with a Fast Exponential Reaching Law. Energies 2017, 10, 1788. [Google Scholar] [CrossRef]
- Chojaa, H.; Derouich, A.; Chehaidia, S.E.; Zamzoum, O.; Taoussi, M.; Benbouhenni, H.; Mahfoud, S. Enhancement of Direct Power Control by Using Artificial Neural Network for a Doubly Fed Induction Generator-Based WECS: An Experimental Validation. Electronics 2022, 11, 4106. [Google Scholar] [CrossRef]
- Pura, P.; Iwański, G. Rotor Current Feedback Based Direct Power Control of a Doubly Fed Induction Generator Operating with Unbalanced Grid. Energies 2021, 14, 3289. [Google Scholar] [CrossRef]
- Cheng, P.; Wu, C.; Ning, F.; He, J. Voltage Modulated DPC Strategy of DFIG Using Extended Power Theory under Unbalanced Grid Voltage Conditions. Energies 2020, 13, 6077. [Google Scholar] [CrossRef]
- Mazen Alhato, M.; Bouallègue, S.; Rezk, H. Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach. Mathematics 2020, 8, 2012. [Google Scholar] [CrossRef]
- Mossa, A.M.; Echeikh, H.; Diab, A.A.Z.; Quynh, N.V. Effective Direct Power Control for a Sensor-Less Doubly Fed Induction Generator with a Losses Minimization Criterion. Electronics 2020, 9, 1269. [Google Scholar] [CrossRef]
- Han, Y.; Ma, R. Adaptive-Gain Second-Order Sliding Mode Direct Power Control for Wind-Turbine-Driven DFIG under Balanced and Unbalanced Grid Voltage. Energies 2019, 12, 3886. [Google Scholar] [CrossRef]
- Yousefi-Talouki, A.; Zalzar, S.; Pouresmaeil, E. Direct Power Control of Matrix Converter-Fed DFIG with Fixed Switching Frequency. Sustainability 2019, 11, 2604. [Google Scholar] [CrossRef]
- Amira, E.; Amr, I.; Abdellatif, A.; Shaaban, S. Aerodynamic Performance and Structural Design of 5 MW Multi Rotor System (MRS) Wind Turbines. Int. J. Renew. Energy Res. 2022, 12, 1495–1505. [Google Scholar] [CrossRef]
- Ercan, E.; Selim, S.; Fevzi, C.B. Analysis Model of a Small Scale Counter-Rotating Dual Rotor Wind Turbine with Double Rotational Generator Armature. Int. J. Renew. Energy Res. 2018, 8, 1849–1858. [Google Scholar] [CrossRef]
- Elkodama, A.; Abdellatif, A.; Shaaban, S.; Rushdi, M.A.; Yoshida, S.; Ismaiel, A. Investigation into the Yaw Control of a Twin-Rotor 10 MW Wind Turbine. Appl. Sci. 2024, 14, 9810. [Google Scholar] [CrossRef]
- Berdugo-Parada, I.; Servan-Camas, B.; Garcia-Espinosa, J. Numerical Framework for the Coupled Analysis of Floating Offshore Multi-Wind Turbines. J. Mar. Sci. Eng. 2024, 12, 85. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, X.; Lin, S.; Wang, Y.; Guo, X. CFD Simulation of Co-Planar Multi-Rotor Wind Turbine Aerodynamic Performance Based on ALM Method. Energies 2022, 15, 6422. [Google Scholar] [CrossRef]
- Adil, Y.; Abdelkadir, B.D.; Elhadj, B.; Habib, B. Using neural network super-twisting sliding mode to improve power control of a dual-rotor wind turbine system in normal and unbalanced grid fault modes. Int. J. Circuit Theory Appl. 2024, 52, 4323–4347. [Google Scholar] [CrossRef]
- Yahdou, A.; Habib, B.; Colak, I.; Bizon, N. Application of Backstepping Control with Nonsingular Terminal Sliding Mode Surface Technique to Improve the Robustness of Stator Power Control of Asynchronous Generator-Based Multi-Rotor Wind Turbine System. Electr. Power Compon. Syst. 2024, 1–29. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Mosaad, M.I.; Colak, I.; Bizon, N.; Gasmi, H.; Aljohani, M.; Abdelkarim, E. Fractional-Order Synergetic Control of the Asynchronous Generator-Based Variable-Speed Multi-Rotor Wind Power Systems. IEEE Access 2023, 11, 133490–133508. [Google Scholar] [CrossRef]
- Bekhada, H.; Mamadou, L.D.; Mohamed, B.; Azeddine, D.; Hicham, C.; Mustapha, B. Comparative Study of PI, RST, Sliding Mode and Fuzzy Supervisory Controllers for DFIG based Wind Energy Conversion System. Int. J. Renew. Energy Res. 2015, 5, 1174–1185. [Google Scholar] [CrossRef]
- Mohamed, N.; Ahmed, E.; Tamou, N. Comparative Analysis between PI & Backstepping Control Strategies of DFIG Driven by Wind Turbine. Int. J. Renew. Energy Res. 2021, 7, 1307–1316. [Google Scholar] [CrossRef]
- Asma, D.; Jihed, H.; Messaoud, A.; Manel, C.; Hafedh, T. Robust Fractional PI Controller Design for Stand-Alone Microgrid under Load Variation: An Optimization-Based Approach. Int. J. Renew. Energy Res. 2023, 13, 1526–1537. [Google Scholar] [CrossRef]
- Sabzevari, K.; Khosravi, N.; Abdelghany, M.B.; Belkhier, Y.; Tostado-Véliz, M.; Kotb, H.; Govender, S. Low-voltage ride-through capability in a DFIG using FO-PID and RCO techniques under symmetrical and asymmetrical faults. Sci. Rep. 2023, 13, 17534. [Google Scholar] [CrossRef] [PubMed]
- Habib, B.; Nicu, B. A new direct power control method of the DFIG-DRWT system using neural PI controllers and four-level neural modified SVM technique. J. Appl. Res. Technol. 2023, 21, 36–55. [Google Scholar] [CrossRef]
- Kanasottu, A.N.; Chandra, P.G.; Eugene, F. Design and implementation of interval type-2 fuzzy logic-PI based adaptive controller for DFIG based wind energy system. Int. J. Electr. Power Energy Syst. 2020, 115, 105468. [Google Scholar] [CrossRef]
- Linyun, X.; Penghan, L.; Jie, W. High-order sliding mode control of DFIG under unbalanced grid voltage conditions. Int. J. Electr. Power Energy Syst. 2020, 117, 105608. [Google Scholar] [CrossRef]
- Mishra, V.; Rishabh, D.S.; Premnath, G. An approach towards Application of Semiconductor Electronics Converter in Autonomous DFIM based Wind Energy Generation System: A Review. Int. J. Smart Grid 2019, 3, 152–162. [Google Scholar] [CrossRef]
- Habib, B.; Hamza, G. Comparative Study of Synergetic Controller with Super Twisting Algorithm for Rotor Side Inverter of DFIG. Int. J. Smart Grid 2022, 6, 144–156. [Google Scholar]
- Xiong, P.; Sun, D. Backstepping-Based DPC Strategy of a Wind Turbine-Driven DFIG Under Normal and Harmonic Grid Voltage. IEEE Trans. Power Electron. 2016, 31, 4216–4225. [Google Scholar] [CrossRef]
- Yusoff, N.A.; Razali, A.M.; Karim, K.A.; Sutikno, T.; Jidin, A. A concept of virtual-flux direct power control of three-phase AC-DC converter. Int. J. Power Electron. Drive Syst. 2017, 8, 1776–1784. [Google Scholar] [CrossRef]
- Said, M.; Derouich, A.; El Ouanjli, N.; El Mahfoud, M. Enhancement of the Direct Torque Control by using Artificial Neuron Network for a Doubly Fed Induction Motor. Intell. Syst. Appl. 2022, 13, 200060. [Google Scholar] [CrossRef]
- El Ouanjli, N.; Aziz, D.; El Ghzizal, A.; Mohammed, T.; Youness, E.; Khalid, M.; Badre, B. Direct torque control of doubly fed induction motor using three-level NPC inverter. Prot. Control Mod. Power Syst. 2019, 4, 17. [Google Scholar] [CrossRef]
- Quan, Y.; Hang, L.; He, Y.; Zhang, Y. Multi-Resonant-Based Sliding Mode Control of DFIG-Based Wind System under Unbalanced and Harmonic Network Conditions. Appl. Sci. 2019, 9, 1124. [Google Scholar] [CrossRef]
- Ayrira, W.; Ourahoua, M.; El Hassounia, B.; Haddib, A. Direct torque control improvement of a variable speed DFIG based on a fuzzy inference system. Math. Comput. Simul. 2020, 167, 308–324. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; Iqbal, A.; El Ouanjli, N. Ant-Colony optimization-direct torque control for a doubly fed induction motor: An experimental validation. Energy Rep. 2022, 8, 81–98. [Google Scholar] [CrossRef]
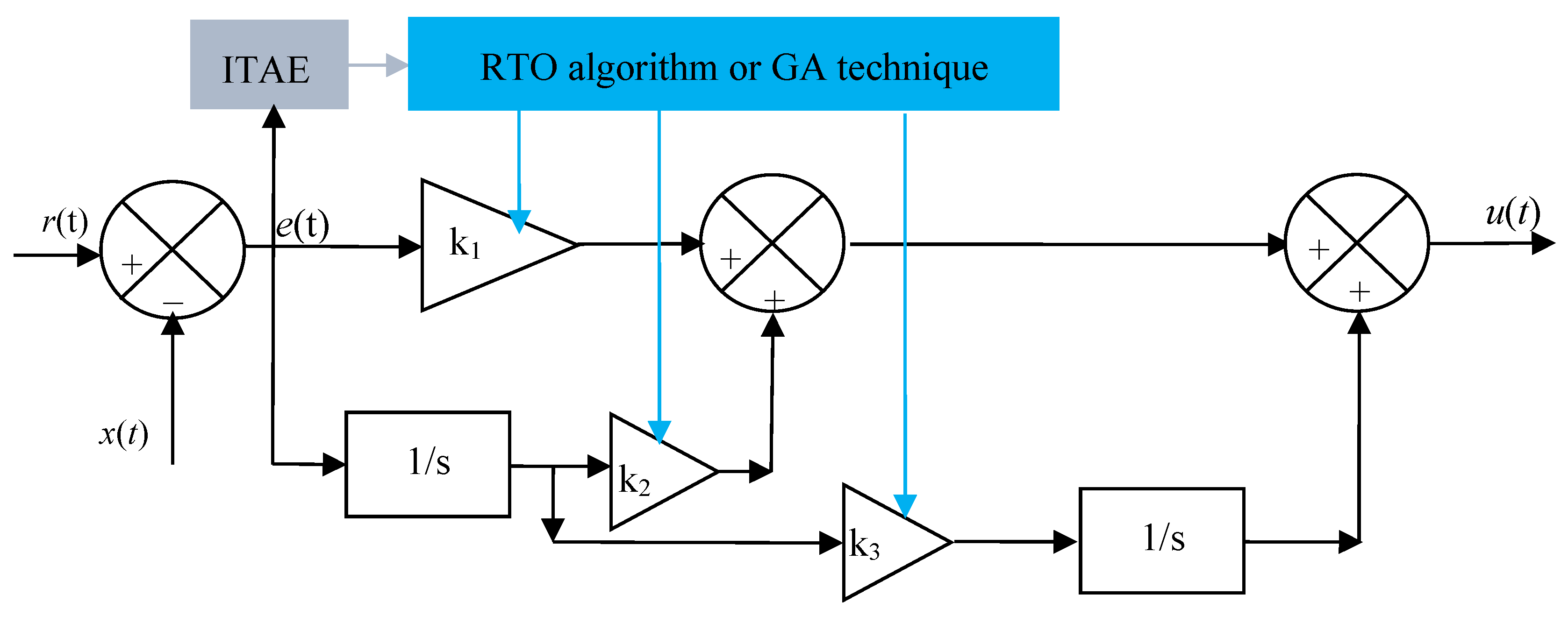

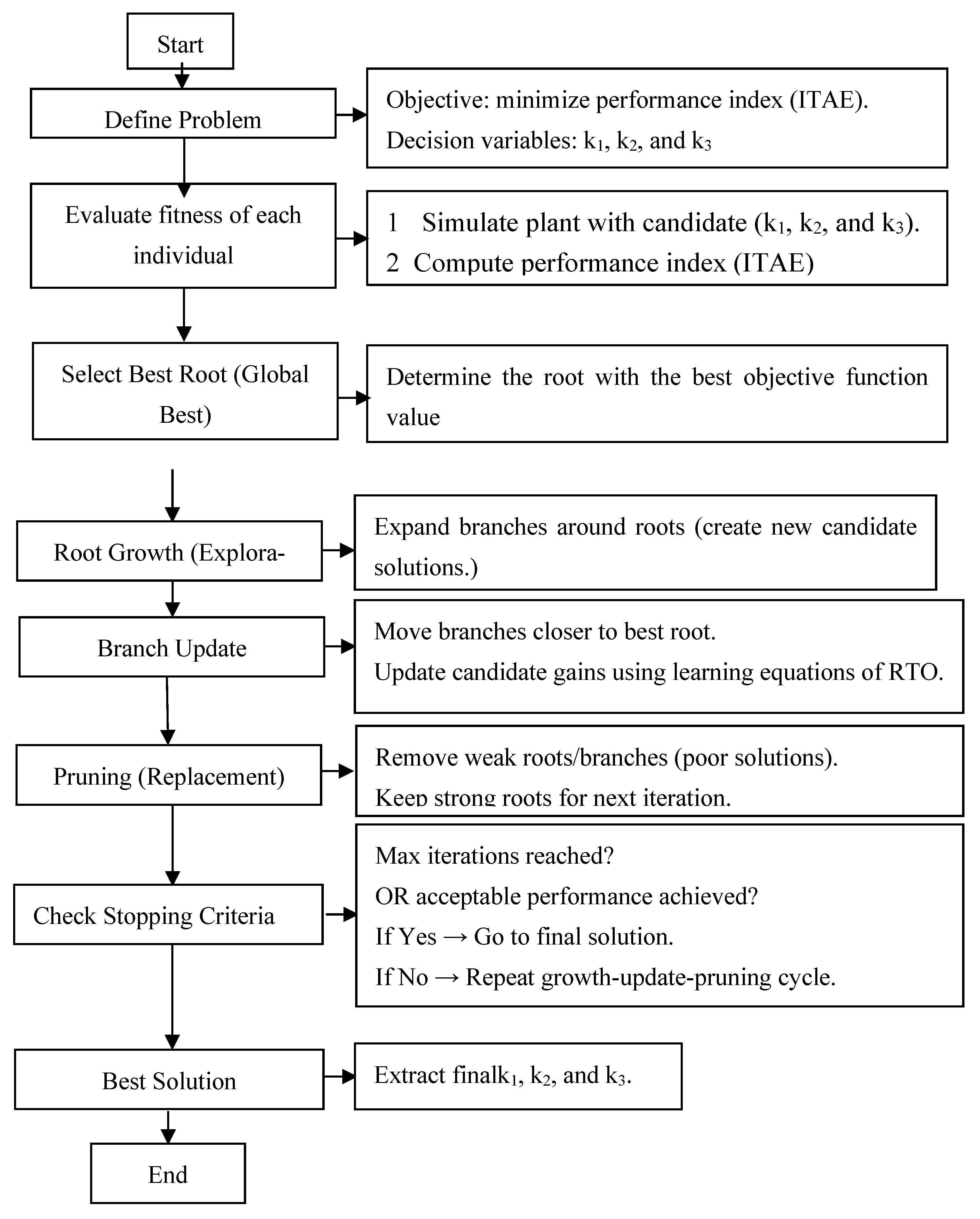
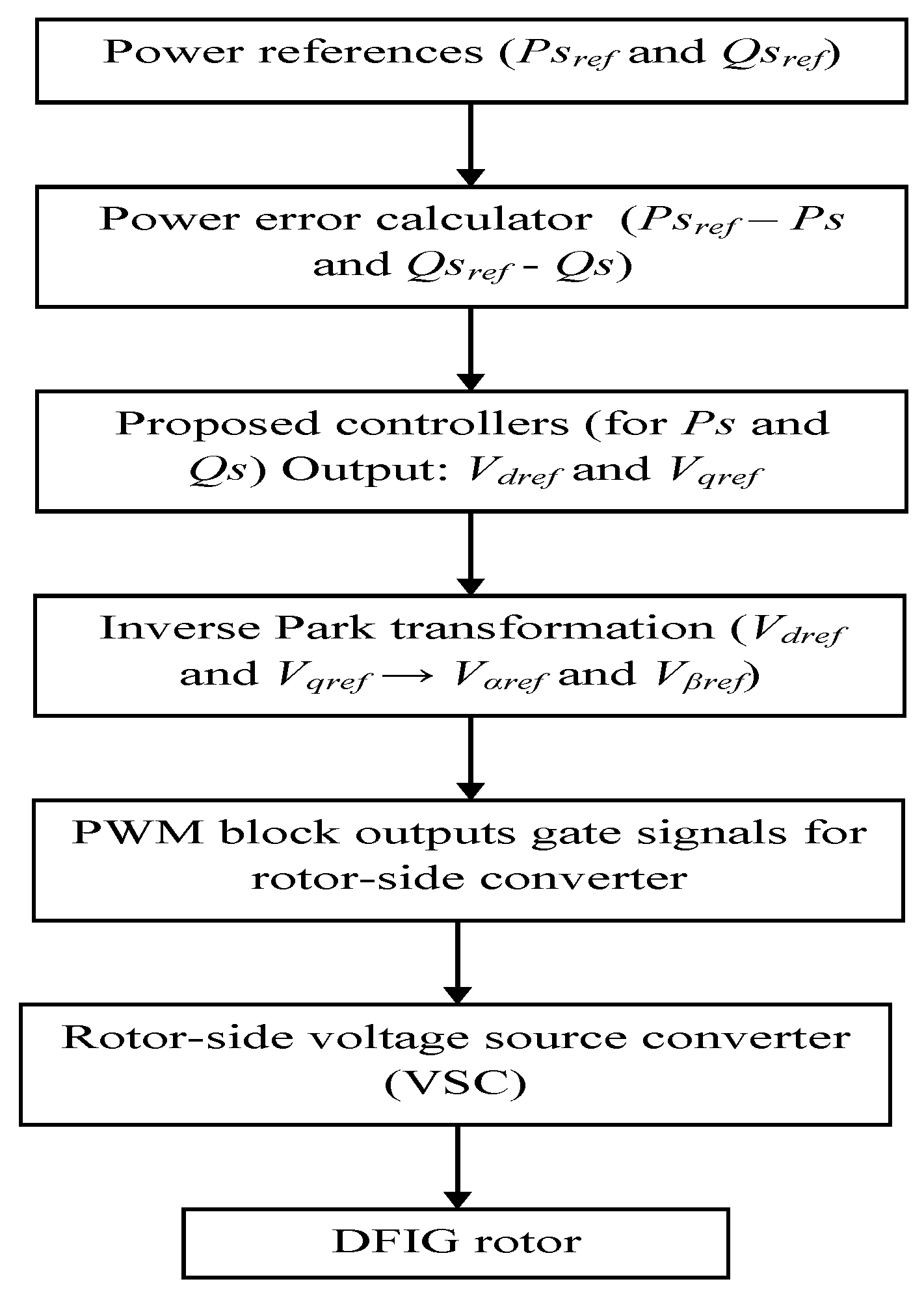
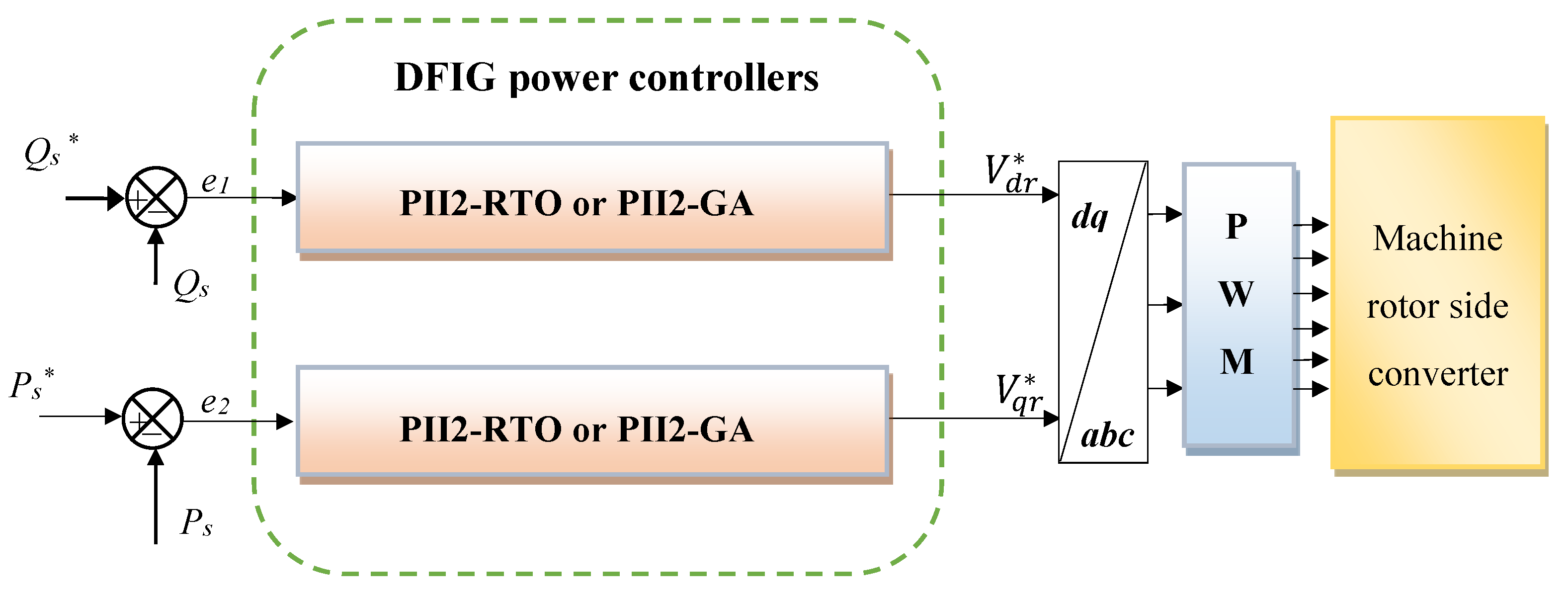


| Limitations | Issue | Consequence |
|---|---|---|
| Current and energy fluctuations | The use of hysteresis controllers causes torque and current ripples. | This can lead to increased mechanical stress on the wind turbine components and increased acoustic noise. |
| Switching frequency variation | DPC often uses a switching table (similar to direct torque control), which can lead to variable switching frequency. | This makes the design of filters more complex and may increase electromagnetic interference. |
| Sensitivity to parameter changes | DPC performance is sensitive to machine parameter changes, especially rotor resistance and stator/rotor inductance. | Variations (due to temperature, aging, etc.) can degrade control performance. |
| Difficulty in multivariable optimization | DPC typically targets instantaneous power control and may not optimize efficiency, thermal limits, or other secondary objectives. | This can reduce overall system performance or energy yield. |
| Complexity in realization | The real-time implementation of DPC requires fast processing and precise estimation of stator flux and power. | This increases the computational burden and may require high-performance DSPs or FPGAs. |
| Lack of standardization | Unlike vector control, DPC techniques lack a universal or standardized structure. | Implementation may vary widely, affecting reliability and reproducibility. |
| Limited low-speed operation | At low rotor speeds, the back-EMF is small, making it difficult to accurately estimate stator flux. | This affects power control accuracy and dynamic performance. |
| Grid code compliance | DPC may struggle to meet strict grid code requirements, such as Low Voltage Ride Through (LVRT) or reactive power support during faults. | Additional control layers may be needed to satisfy grid codes. |
| Improvement | Description | Positive | Negatives |
|---|---|---|---|
| Model predictive control [18] | Uses a predictive model to determine the optimal switching state that minimizes a cost function. |
|
|
| DPC with adaptive control [19] | Introduces adaptive laws to modify DPC parameters in real-time based on system behavior. |
|
|
| Space vector modulation (SVM) [20]. | Replaces the switching table and hysteresis controllers with space vector modulation. |
|
|
| Sliding mode control (SMC) [21] | Robust nonlinear control that enhances DPC under uncertainties and disturbances |
|
|
| Hybrid DPC (combining DPC with field-oriented control (FOC) or scalar control) [22] | Merges DPC with other control strategies to balance performance and complexity. |
|
|
| Artificial Intelligence-based DPC (e.g., neural networks, fuzzy logic) [23,24] | Integrates AI to enhance switching logic or estimate system parameters. |
|
|
| DPC with dynamic reference frame (DRF-DPC) [25] | Utilizes rotating reference frames for control variables instead of stationary frames. |
|
|
| DPC with observer-based flux estimation [26] | Uses observers like Kalman Filters or Luenberger observers to improve flux estimation |
|
|
| Features | Controllers | |||||
|---|---|---|---|---|---|---|
| PID | PI | SMC | PII2 | MPC | Synergetic Controller | |
| Control type | Linear | Linear | Nonlinear | Linear (high order) | Predictive model-based) | Nonlinear |
| Robustness | Moderate | Low to moderate | Very high | Moderate to high | High | Very high |
| Order of integration | 1 | 1 | Discontinuous logic | 2 (double integration) | Varies with prediction horizon | Custom-defined via macrovars |
| Chattering | None | None | High | None | None | None |
| Noise sensitivity | Low | High (due to derivative) | Low | Low | Moderate | Low |
| Implementation ease | Moderate | Moderate | Moderateto hard | Moderate | Hard (requires full model) | Moderate |
| Steady-state accuracy | Moderate | High | High | Very high | Very high | Very high |
| Suitability for DPC | Basic | Better than PI | Very good | Good | Excellent | Excellent |
| Feature | DPC | Neural DPC | SMC-DPC | Proposed Technique |
|---|---|---|---|---|
| Power & Torque Ripple | High | Low | Moderate | Low |
| Dynamic Response | Fast | Fast | Very fast | Fast |
| Robustness to Parameter Variations | Low | High | Very high | Very high |
| Switching Frequency | Variable | Variable/Flexible | Variable | Fixed |
| Implementation Complexity | Low | High | High | Moderate |
| Grid Fault Performance (e.g., LVRT) | Poor | High | High | Moderate to high |
| Flux Estimation Accuracy | Low (needs sensors) | Moderate | Moderate | High |
| Computational Burden | Low | High | High | Moderate |
| Suitability for Real-time Control | Excellent | Good | Good | Good |
| Sensor Dependence | High | Low to moderate | Moderate | Low |
| Techniques | Criteria | Ps (W) | Qs (VAR) | |
|---|---|---|---|---|
| DPC-PI | ITAE | 17,720 | - | |
| Ripples | 60,000 | 106,742 | ||
| Overshoot | 21,740 | 8220 | ||
| Response time (ms) | 1.27 | 0.069 | ||
| SSE | 29,000 | 41,128 | ||
| PII2-GA | ITAE | 5617 | - | |
| Ripples | 22,610 | 21,863 | ||
| Overshoot | 196,440 | 1900 | ||
| Response time (ms) | 3.58 | 4.50 | ||
| SSE | 1000 | 7569.94 | ||
| PII2-RTO | ITAE | 5636 | - | |
| Ripples | 10,870 | 23,546 | ||
| Overshoot | 217,370 | 3952.70 | ||
| Response time (ms) | 3.56 | 4.50 | ||
| SSE | 7400 | 12,683 | ||
| Ratios (%) | ITAE | PII2-RTO/PI | 68.19 | - |
| PII2-GA/PI | 68.30 | - | ||
| PII2-RTO/PII2-GA | −0.33 | - | ||
| Ripples | PII2-RTO/PI | 81.88 | 77.94 | |
| PII2-GA/PI | 62.31 | 79.51 | ||
| PII2-RTO/PII2-GA | 51.92 | −7.14 | ||
| Overshoot | PII2-RTO/PI | −89.99 | 51.91 | |
| PII2-GA/PI | −88.93 | 76.88 | ||
| PII2-RTO/PII2-GA | −9.62 | −51.93 | ||
| Response time (ms) | PII2-RTO/PI | −64.32 | −98.46 | |
| PII2-GA/PI | −64.52 | −98.46 | ||
| PII2-RTO/PII2-GA | 0.5 | 0 | ||
| SSE | PII2-RTO/PI | 74.48 | 69.16 | |
| PII2-GA/PI | 96.55 | 81.59 | ||
| PII2/RTO/PII2-GA | −86.48 | −40.31 | ||
| Techniques | Criteria | Ps (W) | Qs (VAR) | |
|---|---|---|---|---|
| DPC-PI | ITAE | 36,080 | - | |
| Ripples | 165,000 | 200,000 | ||
| Overshoot | 36,630 | 15,875 | ||
| Response time (ms) | 0.66 | 0.070 | ||
| SSE | 36,000 | 100,000 | ||
| PII2-GA | ITAE | 10,510 | - | |
| Ripples | 34,440 | 50,000 | ||
| Overshoot | 95,900 | 3804 | ||
| Response time (ms) | 1.99 | 2.17 | ||
| SSE | 4000 | 15,000 | ||
| PII2-RTO | ITAE | 10,580 | - | |
| Ripples | 45,000 | 50,000 | ||
| Overshoot | 127,200 | 3804 | ||
| Response time (ms) | 1.99 | 2.17 | ||
| SSE | 12,900 | 20,000 | ||
| Ratios (%) | ITAE | PII2-RTO/PI | 70.67 | - |
| PII2-GA/PI | 70.87 | - | ||
| PII2-RTO/PII2-GA | −0.6 | - | ||
| Ripples | PII2-RTO/PI | 72.72 | 75 | |
| PII2-GA/PI | 79.12 | 75 | ||
| PII2-RTO/PII2-GA | −23.46 | 0 | ||
| Overshoot | PII2-RTO/PI | −71.20 | 76.03 | |
| PII2-GA/PI | −61.80 | 76.03 | ||
| PII2-RTO/PII2-GA | −24.60 | 0 | ||
| Response time (ms) | PII2-RTO/PI | −66.83 | −96.77 | |
| PII2-GA/PI | −66.83 | −96.77 | ||
| PII2-RTO/PII2-GA | 0 | 0 | ||
| SSE | PII2-RTO/PI | 64.16 | 80 | |
| PII2-GA/PI | 88.88 | 85 | ||
| PII2/RTO/PII2-GA | −68.99 | −25 | ||
| Approaches | Criteria | Ps (W) | Qs (VAR) | |
|---|---|---|---|---|
| DPC-PI | ITAE | 17,670 | - | |
| Ripples | 77,870 | 100,000 | ||
| Overshoot | 4200 | 8219 | ||
| Response time (ms) | 0.95 | 0.068 | ||
| SSE | 30,000 | 12,700 | ||
| PII2-GA | ITAE | 6567 | - | |
| Ripples | 22,100 | 7757.40 | ||
| Overshoot | 110,400 | 12,356 | ||
| Response time (ms) | 2.55 | 3.04 | ||
| SSE | 8200 | 7181.18 | ||
| PII2-RTO | ITAE | 6563 | - | |
| Ripples | 9600 | 6000 | ||
| Overshoot | 129,860 | 12,500 | ||
| Response time (ms) | 2.55 | 3.04 | ||
| SSE | 12,000 | 6774.40 | ||
| Ratios (%) | ITAE | PII2-RTO/PI | 62.85 | - |
| PII2-GA/PI | 62.83 | - | ||
| PII2-RTO/PII2-GA | 0.06 | - | ||
| Ripples | PII2-RTO/PI | 87.67 | 94 | |
| PII2-GA/PI | 71.61 | 92.24 | ||
| PII2-RTO/PII2-GA | 56.56 | 22.65 | ||
| Overshoot | PII2-RTO/PI | −96.76 | −34.24 | |
| PII2-GA/PI | −96.19 | −33.48 | ||
| PII2-RTO/PII2-GA | −14.98 | −1.15 | ||
| Response time (ms) | PII2-RTO/PI | −62.74 | −97.76 | |
| PII2-GA/PI | −62.74 | −97.76 | ||
| PII2-RTO/PII2-GA | 0 | 0 | ||
| SSE | PII2-RTO/PI | 60 | 46.65 | |
| PII2-GA/PI | 72.66 | 43.45 | ||
| PII2/RTO/PII2-GA | −31.66 | 5.66 | ||
| Techniques | THD | ITAE | Maximum Value | Minimum Value | Average Value | Standard Deviation | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| THD | ITAE | THD | ITAE | THD | ITAE | THD | ITAE | ||||
| PI | Test 1 | 6.40% | 17,720 | 12.71% | 36,080 A | 5.70% | 17,670 A | 8.27% | 23,823.33 A | 3.15% | 8667.37 A |
| Test 2 | 12.71% | 36,080 | |||||||||
| Test 3 | 5.70% | 17,670 | |||||||||
| PII2-GA | Test 1 | 2.59% | 5617 | 3.98% | 10,510 A | 1.58% | 5617 A | 2.71% | 7254.33 A | 0.98% | 2141.11 A |
| Test 2 | 3.98% | 10,510 | |||||||||
| Test 3 | 1.58% | 6567 | |||||||||
| PII2-RTO | Test 1 | 2.54% | 5636 | 3.94% | 10,580 A | 1.48% | 5636 A | 2.65% | 7593 A | 1.02% | 2145.76 A |
| Test 2 | 3.94% | 10,580 A | |||||||||
| Test 3 | 1.48% | 6563 A | |||||||||
| Algorithms | THD (%) | References | |
|---|---|---|---|
| DPC-backstepping controller | With harmonics suppression strategy | 4.59 | [57] |
| Without harmonics suppression strategy | 18.51 | ||
| DPC | 4.88 | [58] | |
| Virtual-Flux DPC | 4.19 | ||
| DTC | 7.83 | [59] | |
| 2-level DTC | 8.75 | [60] | |
| Integral SMC | 9.71 | [61] | |
| DTC | 6.70 | [62] | |
| DTC-PI | 12 | [63] | |
| Ant-colony optimization-based DTC | 7.19 | ||
| PII2-GA | 2.59 | Proposed regulators | |
| PII2-RTO | 2.54 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benbouhenni, H.; Bizon, N. Assessing the Effectiveness of an Intelligent Algorithms-Based PII2 Controller in Enhancing the Quality of Power Output from a DFIG-Based Power System. Energies 2025, 18, 5566. https://doi.org/10.3390/en18215566
Benbouhenni H, Bizon N. Assessing the Effectiveness of an Intelligent Algorithms-Based PII2 Controller in Enhancing the Quality of Power Output from a DFIG-Based Power System. Energies. 2025; 18(21):5566. https://doi.org/10.3390/en18215566
Chicago/Turabian StyleBenbouhenni, Habib, and Nicu Bizon. 2025. "Assessing the Effectiveness of an Intelligent Algorithms-Based PII2 Controller in Enhancing the Quality of Power Output from a DFIG-Based Power System" Energies 18, no. 21: 5566. https://doi.org/10.3390/en18215566
APA StyleBenbouhenni, H., & Bizon, N. (2025). Assessing the Effectiveness of an Intelligent Algorithms-Based PII2 Controller in Enhancing the Quality of Power Output from a DFIG-Based Power System. Energies, 18(21), 5566. https://doi.org/10.3390/en18215566











