Electricity Demand Forecasting and Risk Assessment for Campus Energy Management
Abstract
1. Introduction
2. Grey–Markov Model
2.1. GM (1, 1) Model
2.2. Markov Chain
2.3. Grey–Markov Model
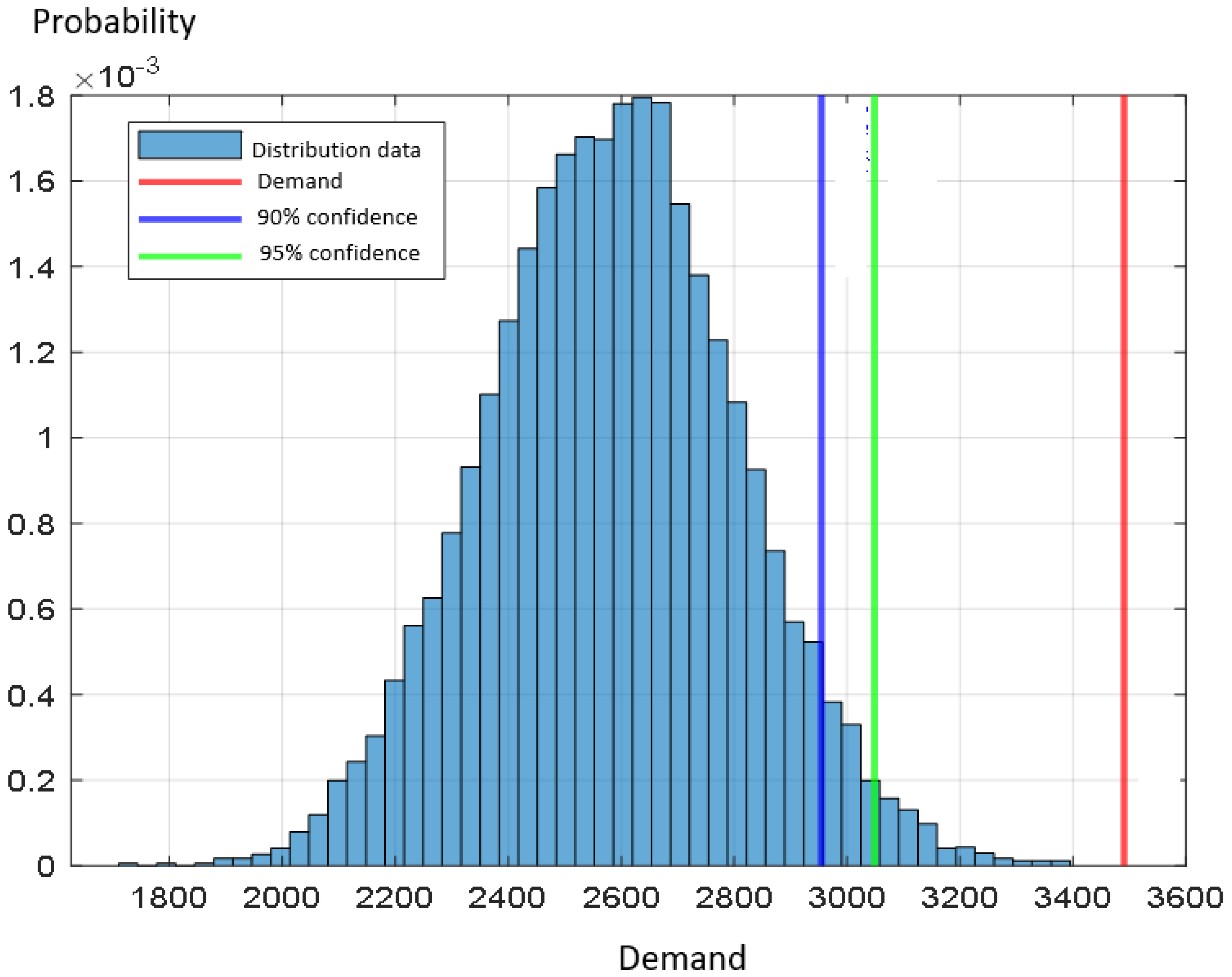
3. Enhanced Monte Carlo
4. Case Study
4.1. Demand Consumption Prediction
4.2. Risk Assessment of Demand Consumption
5. Conclusions
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| EMC | Enhanced Monte Carlo |
| EMS | Energy Management System |
| EV | Electric Vehicles |
| GDE | Grey Differential Equation |
| GM | Grey Model |
| GMM | Grey–Markov Model |
| MC | Monte Carlo |
| TOU | Time-of-Use |
References
- Chen, M.; Xie, Z.; Sun, Y.; Zheng, S. The predictive management in campus heating system based on deep reinforcement learning and probabilistic heat demands forecasting. Appl. Energy 2023, 350, 121710. [Google Scholar] [CrossRef]
- Alsamraee, S.A.; Khanna, S. High-resolution energy consumption forecasting of a university campus power plant based on advanced machine learning techniques. Energy Strategy Rev. 2025, 60, 101769. [Google Scholar] [CrossRef]
- Zhakiyev, N.; Satan, A.; Akhmetkanova, G.; Medeshova, A.; Omirgaliyev, R.; Bracco, S. Energy Management System for the Campus Microgrid Using an Internet of Things as a Service (IoTaaS) with Day-ahead Forecasting. Procedia Comput. Sci. 2024, 241, 488–493. [Google Scholar] [CrossRef]
- Taiwan Power Company. The Electricity Tariff Structure of TPC. Available online: http://taipower.com.tw/tc/indexaspx (accessed on 1 July 2024).
- Fernandez, M.A.; Zorita, A.L.; Escudero, L.A.; Duque, O.; Morinigo, D.; Riesco, M. Cost optimization of electrical contracted capacity for large customers. Int. Electr. Power Energy Syst. 2013, 46, 123–131. [Google Scholar] [CrossRef]
- Yang, S.H. Demand Forecasting Method Based Contract Capacity Optimization. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2013. [Google Scholar]
- Falasca, S.; Zinzi, M.; Siani, A.M.; Curci, G.; Ding, L.; Santamouris, M. Investigating the effects of the greenery increase on air temperature, ventilation and cooling energy demand in Melbourne with the Weather Research and Forecasting model and Local Climate Zones. Sci. Total Environ. 2024, 953, 176016. [Google Scholar] [CrossRef] [PubMed]
- Hansen, T.V.A.; Nielsen, J.P. Risk-based sampling for surveillance of medicinal residues in carcasses of pigs and cattle: A scoping review. Prev. Vet. Med. 2025, 243, 106602. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, Y.; Headley, J.V.; Huang, R. Sample preparation, analytical characterization, monitoring, risk assessment and treatment of naphthenic acids in industrial wastewater and surrounding water impacted by unconventional petroleum production. Sci. Total Environ. 2024, 913, 169636. [Google Scholar] [CrossRef]
- Popławski, T. Long-Term Forecast of Peak Power Demand for Poland—Construction and Use of Simplified Forecasting Models. Energies 2025, 18, 3472. [Google Scholar] [CrossRef]
- Shao, Z.; Fu, C.; Yang, S.L.; Zhou, K.L. A review of the decomposition methodology for extracting and identifying the fluctuation characteristics in electricity demand forecasting. Renew. Sustain. Energy Rev. 2017, 75, 123–136. [Google Scholar] [CrossRef]
- Köse, E.; Kaynar, S.K. Energy Demand Forecasting and Policy Development in Turkey. Energies 2025, 18, 3301. [Google Scholar] [CrossRef]
- Mu, Y.; Tan, H.; Jia, Y.; Wang, X.; Zhao, H.; Zhao, Y. Research on the Optimal Design of Seasonal Time-of-Use Tariff Based on the Price Elasticity of Electricity Demand. Energies 2023, 16, 1625. [Google Scholar] [CrossRef]
- Chou, J.H.; Nguyen, H.M. Simulating long-term energy consumption prediction in campus buildings through enhanced data augmentation and metaheuristic-optimized artificial intelligence. Energy Build. 2024, 312, 114191. [Google Scholar] [CrossRef]
- Kolokotsa, D.; Yang, J.; Eang, L. Energy management in university campuses. Ref. Modul. Earth Syst. Environ. Sci. 2025, 9, 614–632. [Google Scholar] [CrossRef]
- Grandón, A.T.G.; Schwenzer, J.; Steens, T.; Breuing, J. Electricity demand forecasting with hybrid classical statistical and machine learning algorithms: Case study of Ukraine. Appl. Energy 2024, 355, 122249. [Google Scholar] [CrossRef]
- Mahmud, M.; Abedin, T.; Rahman, M.; Shoishob, S.A.; Kiong, T.S.; Nur-E-Alam, M. Integrating demand forecasting and deep reinforcement learning for real-time electric vehicle charging price optimization. Util. Policy 2025, 96, 102038. [Google Scholar] [CrossRef]
- Lei, X.; Zhong, J.; Chen, Y.; Shao, Z.; Jian, L. Grid integration of electric vehicles within electricity and carbon markets: A comprehensive overview. eTransportation 2025, 25, 100435. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, K.; Li, J.; Wei, Z. A performance degradation prediction model for PEMFC based on bi-directional long short-term memory and multi-head self-attention mechanism. Int. J. Hydrogen Energy 2024, 60, 133–146. [Google Scholar] [CrossRef]
- Zhou, J.; Shu, X.; Zhang, J.; Yi, F.; Jia, C.; Zhang, C.; Kong, X.; Zhang, J.; Wu, G. A deep learning method based on CNN-BiGRU and attention mechanism for proton exchange membrane fuel cell performance degradation prediction. Int. J. Hydrogen Energy 2024, 94, 394–405. [Google Scholar] [CrossRef]
- Dong, X.; Guo, W.; Zhou, C.; Luo, Y.; Tian, Z.; Zhang, L.; Wu, X.; Liu, B. Hybrid model for robust and accurate forecasting building electricity demand combining physical and data-driven methods. Energy 2024, 311, 133309. [Google Scholar] [CrossRef]
- Al-Abri, A.; Okedu, K. Overview of the Global Electricity System in Oman Considering Energy Demand Model Forecast. Energy Eng. 2022, 120, 409–423. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, D.; Zhou, Y.; Hua, K. Energy Risks Zoning and Demand Forecasting in Jiangsu rovince. Energy Procedia 2011, 5, 813–817. [Google Scholar] [CrossRef][Green Version]
- Choi, T.M.; Ren, S. Intelligent demand forecasting supported risk management systems for fast fashion inventory management. In Information Systems for the Fashion and Apparel Industry; Woodhead Publishing: Cambridge, UK, 2016; pp. 263–271. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, M.; Huang, Z. A new adaptive grey prediction model and its application. Alex. Eng. J. 2025, 120, 515–522. [Google Scholar] [CrossRef]
- Tjakra, J.; Bao, J.; Hudon, N.; Yang, R. Modeling collective dynamics of particulate systems under time-varying operating conditions based on Markov chains. Adv. Powder Technol. 2013, 24, 451–458. [Google Scholar] [CrossRef]
- Zhang, F.; Xiao, X.; Gao, M. An extended neural ordinary differential equation network with grey system and its applications. Neurocomputing 2024, 576, 127343. [Google Scholar] [CrossRef]
- Tsay, M.T.; Lin, W.M.; Lee, J.L. Optimal contracts decision of industrial customers. Int. J. Electr. Power Energy Syst. 2001, 23, 795–803. [Google Scholar] [CrossRef]
- Aluigi, A.; Corradini, M.; Gheno, A. Chapman–Kolmogorov lattice method for derivatives pricing. Appl. Math. Comput. 2014, 226, 606–614. [Google Scholar] [CrossRef]
- Caralis, G.; Diakoulaki, D.; Yang, P.; Gao, Z.; Zervos, A.; Rados, K. Profitability of wind energy investments in China using a Monte Carlo approach for the treatment of uncertainties. Renew. Sustain. Energy Rev. 2014, 40, 224–236. [Google Scholar] [CrossRef]
- Antonio, C. Risk Management Tools and Analysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Marrison, C. Fundamentals of Risk Measurement; McGraw-Hill Companies, Inc.: Chicago, IL, USA, 2002. [Google Scholar]
- Energy Management System of Cheng-Shiu University. Available online: http://120.118.246.40:8080/ECOA/index.jsp (accessed on 2 July 2024).

| MAPE Value | <10% | 10%~20% | 20%~50% | >50% |
|---|---|---|---|---|
| prediction ability | High accuracy | Good | Reasonable | Inaccuracy |
| Type | Demand Charge (NT$/KW) | |
|---|---|---|
| Summer Month | Non-Summer Month | |
| Peak contract | 236.2 | 173.2 |
| Semi-peak contract | 173.2 | 173.2 |
| Saturday Semi-peak contract | 47.2 | 34.6 |
| Off-peak contract | 47.2 | 34.6 |
| 2023 | GM | GDE | GMM | |||
|---|---|---|---|---|---|---|
| Month | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3028.52 | 13.2316 | 3150.65 | 9.73255 | 3286.6 | 5.83752 |
| 6 | 2896.56 | 12.0482 | 2925.65 | 11.1649 | 2969.54 | 9.83224 |
| 7 | 2399.15 | 11.2724 | 2456.23 | 9.16141 | 2463.13 | 8.90623 |
| 8 | 2501.23 | 10.4234 | 2564.23 | 8.16716 | 2605.61 | 6.68522 |
| 9 | 3179.71 | 8.2999 | 3089.23 | 10.9093 | 3105.73 | 10.4334 |
| 10 | 3214.09 | 7.49995 | 3219.23 | 7.35202 | 3289.56 | 5.32796 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 |
| MAPE | 10.46258 | 9.414556 | 7.837098 | |||
| 2023 | GM | GDE | GMM | |||
|---|---|---|---|---|---|---|
| Month | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) |
| 1 | 2165.56 | 9.492285 | 2180.53 | 8.866627 | 2523.4 | 5.46333 |
| 2 | 1986.32 | 14.93276 | 2001.52 | 14.2818 | 2450.23 | 4.934904 |
| 3 | 2406.36 | 8.058045 | 2566.33 | 1.945928 | 2777.45 | 6.120523 |
| 4 | 2818.63 | 8.610364 | 3015.14 | 2.238837 | 3278.95 | 6.314786 |
| 5 | 3985.32 | 8.746574 | 3828.26 | 12.34284 | 3979.82 | 8.87251 |
| 6 | 3659.25 | 11.20071 | 3578.1 | 13.16998 | 3896.56 | 5.441891 |
| 7 | 2875.63 | 15.00567 | 2898.52 | 14.32912 | 3169.86 | 6.309187 |
| 8 | 2665.5 | 10.96719 | 2660.2 | 11.14422 | 3038.69 | 1.498076 |
| 9 | 3896.36 | 10.19563 | 3986.32 | 8.122211 | 4031.97 | 7.070058 |
| 10 | 4117.57 | 5.293361 | 4190.22 | 3.622367 | 4268.23 | 1.828089 |
| 11 | 2694.56 | 12.8431 | 2647.76 | 14.35687 | 3230.99 | 4.507993 |
| 12 | 2811.61 | 6.579546 | 2711.13 | 9.918163 | 3051.26 | 1.383227 |
| MAPE | 10.16044 | 9.528247 | 4.978714 | |||
| 2023 | GM | GDE | GMM | |||
|---|---|---|---|---|---|---|
| Month | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) |
| 1 | 1589.36 | 12.2612 | 1466.45 | 3.57968 | 1522.34 | 7.52735 |
| 2 | 1051.73 | 7.14103 | 993.56 | 12.277 | 1127.53 | 0.44852 |
| 3 | 1635.36 | 12.454 | 1518.7 | 18.6991 | 1789.56 | 4.19914 |
| 4 | 1791.61 | 14.433 | 1896.36 | 9.43018 | 2201.45 | 5.14087 |
| 5 | 2098.56 | 14.9468 | 2159.42 | 12.4802 | 2650.37 | 7.41767 |
| 6 | 2275.3 | 13.6404 | 2387.44 | 9.38406 | 2616.25 | 0.69952 |
| 7 | 2242.14 | 3.65114 | 2070.85 | 4.26737 | 2249.27 | 3.98075 |
| 8 | 1720.56 | 10.1132 | 1783.19 | 6.84119 | 2046.59 | 6.91956 |
| 9 | 2539.65 | 8.44809 | 2673.12 | 3.63663 | 2837.77 | 2.29885 |
| 10 | 2478.55 | 10.8355 | 2453.15 | 11.7493 | 2972.46 | 6.93264 |
| 11 | 2045.56 | 17.294 | 2189.56 | 11.4718 | 2729.67 | 10.3659 |
| 12 | 2087.56 | 13.2965 | 2084.48 | 13.4244 | 2521.26 | 4.71653 |
| MAPE | 11.54289 | 9.77007 | 5.053946 | |||
| 2023 | GM | GDE | GMM | |||
|---|---|---|---|---|---|---|
| Month | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) | Prediction value (kW) | error (%) |
| 1 | 907.6 | 5.12231 | 911.23 | 4.74284 | 922.36 | 3.57934 |
| 2 | 1356.25 | 14.0363 | 1398.56 | 11.3545 | 1456.25 | 7.69791 |
| 3 | 1580.58 | 10.6219 | 1602.35 | 9.39087 | 1632.58 | 7.68143 |
| 4 | 1836.82 | 11.8570 | 1869.45 | 10.2912 | 1898.72 | 8.88666 |
| 5 | 2145.36 | 9.03131 | 2204.35 | 6.52999 | 2245.78 | 4.77325 |
| 6 | 1986.25 | 10.7400 | 2047.36 | 7.99374 | 2089.56 | 6.09732 |
| 7 | 1536.25 | 15.9136 | 1587.23 | 13.1232 | 1701.05 | 6.89331 |
| 8 | 1425.68 | 11.8138 | 1523.12 | 5.78659 | 1473.6 | 8.84967 |
| 9 | 1989.56 | 15.0817 | 2145.89 | 8.4092 | 2119.45 | 9.53771 |
| 10 | 2019.58 | 13.9784 | 2133.41 | 9.12998 | 2215.26 | 5.64368 |
| 11 | 1869.56 | 10.5015 | 1967.49 | 5.8135 | 1979.08 | 5.25867 |
| 12 | 1798.56 | 11.5548 | 1812.45 | 10.8717 | 1898.51 | 6.63969 |
| MAPE | 11.68772 | 8.619784 | 6.794887 | |||
| GM | GDE | GMM | |
|---|---|---|---|
| The MAPE of peak demand (%) | 10.46258 | 9.414556 | 7.837098 |
| The MAPE of semi-peak demand (%) | 10.16044 | 9.528247 | 4.978714 |
| The MAPE of Saturday semi-peak demand (%) | 11.54289 | 9.77007 | 5.053946 |
| The MAPE of off-peak demand (%) | 11.68772 | 8.619784 | 6.794887 |
| Average MAPE (%) | 10.96341 | 9.333164 | 6.560526 |
| 2023 | Risk Probability (%) | 90% Confidence Level | 95% Confidence Level | |||
|---|---|---|---|---|---|---|
| Month | Actual Value (kW) | Risk Margin (kW) | Error (%) | Risk Margin (kW) | Error (%) | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3490.35 | 24.38 | 2955.12 | 16.57 | 3155.16 | 10.37 |
| 6 | 3293.35 | 2.39 | 3234.08 | 1.83 | 3324.03 | 0.95 |
| 7 | 2703.95 | 22.42 | 2278.40 | 13.17 | 2380.52 | 10.01 |
| 8 | 2792.28 | 7.08 | 2463.51 | 10.18 | 2686.44 | 3.28 |
| 9 | 3467.51 | 2.83 | 3357.25 | 3.41 | 3528.93 | 1.90 |
| 10 | 3474.69 | 12.74 | 3128.89 | 10.70 | 3290.92 | 5.69 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 |
| MAPE | 11.97 | 9.31 | 5.37 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, Y.-H.; Tsai, M.-T. Electricity Demand Forecasting and Risk Assessment for Campus Energy Management. Energies 2025, 18, 5521. https://doi.org/10.3390/en18205521
Tsai Y-H, Tsai M-T. Electricity Demand Forecasting and Risk Assessment for Campus Energy Management. Energies. 2025; 18(20):5521. https://doi.org/10.3390/en18205521
Chicago/Turabian StyleTsai, Yon-Hon, and Ming-Tang Tsai. 2025. "Electricity Demand Forecasting and Risk Assessment for Campus Energy Management" Energies 18, no. 20: 5521. https://doi.org/10.3390/en18205521
APA StyleTsai, Y.-H., & Tsai, M.-T. (2025). Electricity Demand Forecasting and Risk Assessment for Campus Energy Management. Energies, 18(20), 5521. https://doi.org/10.3390/en18205521






