A Matrix-Based Analytical Approach for Reliability Assessment of Mesh Distribution Networks
Abstract
1. Introduction
- (1)
- A network configuration and operation control strategy centered on SOP is established. This configuration enables flexible power flow control among multiple feeders and rapid fault transfer, providing a structural foundation for reliability modeling and analysis of mesh ADN.
- (2)
- A fault incidence matrix (FIM)-based analytical calculation method is proposed, utilizing spatial topology. By classifying the restoration states of load nodes under different branch fault scenarios, three types of FIMs are constructed. Through algebraic computation between the FIMs and reliability parameters, explicit analytical expressions of reliability indices are derived for mesh distribution networks. This approach eliminates the redundant fault impact range traversal required by existing reliability assessment algorithms and significantly improves computational efficiency.
2. Characteristics and Structural Advantages of Mesh Distribution Networks
2.1. Network Configuration of Mesh Distribution Networks
2.2. Control and Protection Strategies of Mesh Distribution Networks
2.3. Core Features of Mesh Distribution Networks
2.3.1. Support for Dynamic Power Flow Regulation Among Multiple Feeders
2.3.2. Adaptive Local Energy Balancing with Source-Load-Storage Coordination
2.3.3. High Scalability for Flexible Planning and Iterative Upgrading
3. Typical Component Modeling of Mesh Distribution Networks
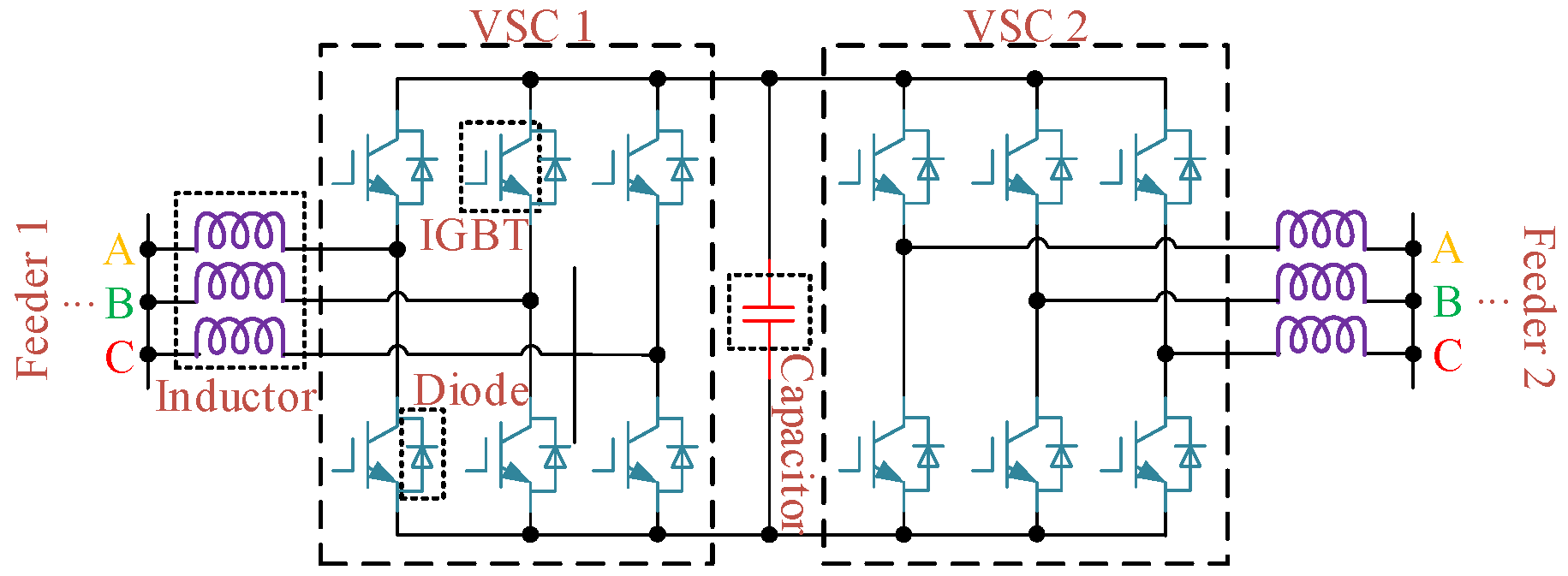
3.1. Soft Open Point Model
3.2. Wind Turbine Output Model
3.3. Photovoltaic Output Model
4. Analytical Calculation Method for Reliability Indices of Mesh Distribution Networks Based on FIMs
4.1. Generation Method of Fault Incidence Matrix
- (1)
- Load nodes that cannot be immediately restored by SOP and can only be restored after fault repair on the faulted branch. Their outage duration depends on the fault repair time.
- (2)
- Load nodes that are immediately restored by the main power source after fault isolation. Their outage duration depends on the time required for isolating the faulted line using switches.
- (3)
- Load nodes that are restored via SOP after fault isolation. Their outage duration depends on the time for fault isolation and the switching time of the SOP to the Vf mode for load restoration.
- (1)
- Fault incidence matrix Awhere Ψl,A represents the set of nodes that cannot be immediately restored via the SOP after a fault occurs on branch l.
- (2)
- Fault incidence matrix Bwhere Ψl,B represents the set of nodes that are restored by the main power source after a fault occurs on branch l.
- (3)
- Fault incidence matrix Cwhere Ψl,C represents the set of nodes that are restored via the SOP after a fault occurs on branch l.
- (1)
- When the faulty branch lies upstream of a node’s power supply path, the impact type depends on whether an alternative supply path is available after the fault. If there is no sectionalizing switch between the faulted branch and the affected node, and the node cannot be effectively isolated from the fault area, its power supply will be completely interrupted and can only be restored after the fault is repaired; this is categorized as a type-a impact. If a sectionalizing switch is installed between the faulted branch and the node, and an SOP is deployed downstream of the node’s branch, the SOP can quickly restore the power supply after fault isolation, and the node is classified as experiencing a type-c impact.
- (2)
- When the faulted branch is not on the original power supply path of the node, the impact type is determined by both the isolation conditions and the availability of supply paths. If there is no sectionalizing switch isolating the node from the faulted branch, the node loses its ability to recover power supply and is categorized as a type-a impact. If a sectionalizing switch exists to isolate the node from the faulted branch and the node has a direct path to be restored from the main power source, then the node can be quickly resupplied after isolation, corresponding to a type-b impact.
4.2. Node Reliability Index Calculation Method
- (1)
- Average interruption frequency
- (2)
- Average interruption duration
- (3)
- Expected energy not supplied
4.3. System Reliability Index Calculation Method
4.4. Reliability Analysis Method for Mesh Distribution Networks with Soft Open Points
- (1)
- Input the parameters of the distribution network and DG, the access location and capacity of the SOP, the average number of faults per branch, operation time of components, and other initial values;
- (2)
- Solve the load restoration model of the active distribution network based on SOP to obtain the load restoration status of each load node under different branch fault scenarios, including: restored only after faulted branch repair, immediately restored by the main power source, and restored via SOP;
- (3)
- Based on the load restoration status of each load node, classify the outage nodes and generate the fault incidence matrix;
- (4)
- Based on the FIMs, calculate the reliability indices of each load node using the reliability index calculation method for active distribution networks, and further calculate the system-level reliability indices;
- (5)
- Based on the calculated reliability indices, evaluate the power supply reliability of the meshed distribution networks.
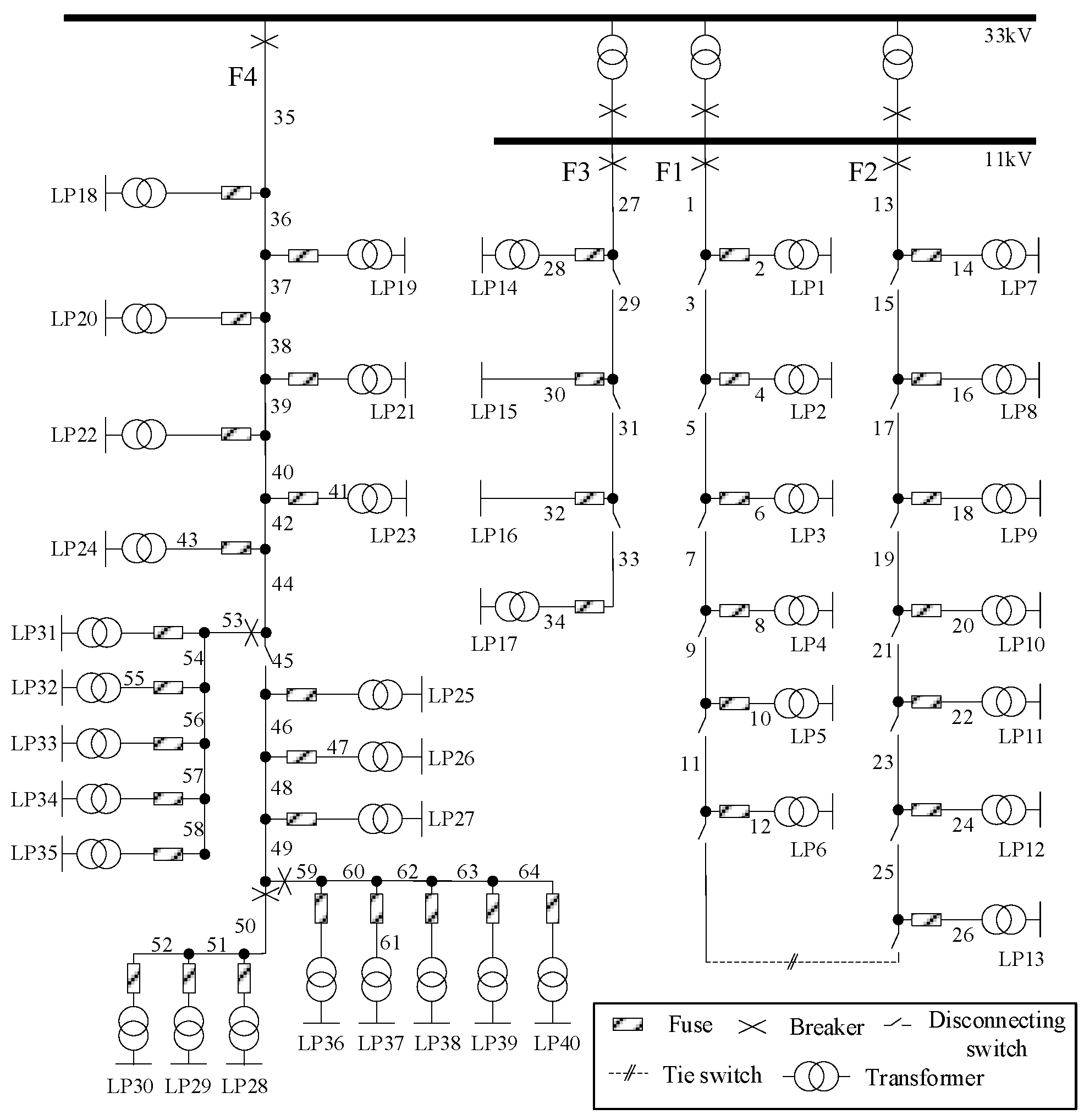
5. Case Study
5.1. Algorithm Correctness Verification and Comparison of Computational Efficiency
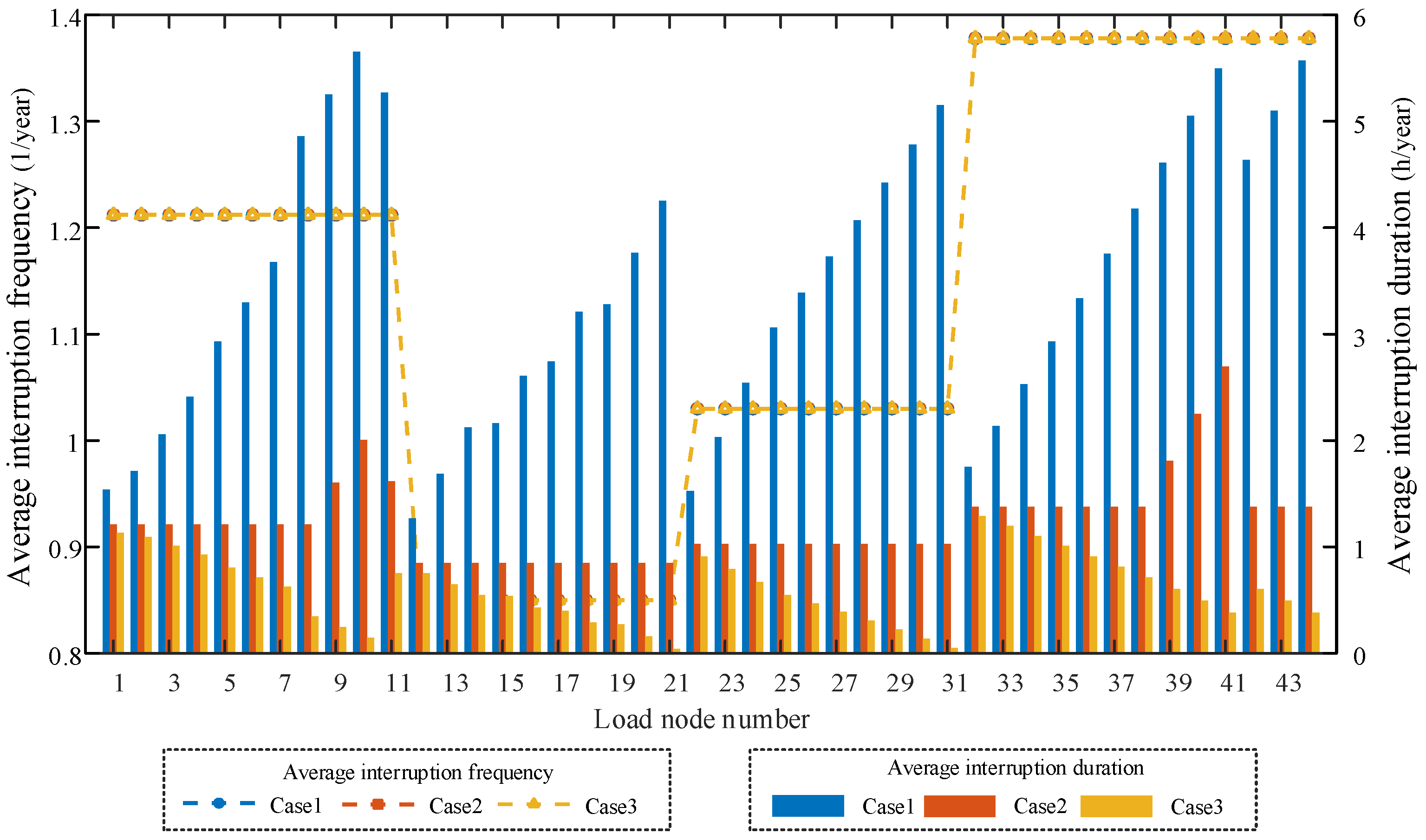
5.2. Reliability Evaluation
6. Conclusions
- (1)
- By constructing three types of FIMs, explicit analytical expressions for both system-level and node-level reliability indices are achieved. Case studies based on the IEEE RBTS Bus-6 system and the modified 44-bus Taiwan system verify the effectiveness of the proposed method.
- (2)
- The proposed method avoids fault scenario enumeration and iterative computation required in conventional reliability assessment methods, thereby significantly improving computational efficiency while maintaining accuracy. Its advantages are particularly evident in large-scale networks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, P.; Ji, J.; Ji, H.R.; Song, G.Y.; Zhao, J.L.; Wang, C.S. Multi-stage expansion planning of energy storage integrated soft open points considering tie-line reconstruction. Prot. Control Mod. Power Syst. 2022, 7, 45. [Google Scholar] [CrossRef]
- Hu, D.; Sun, L.; Ding, M. Integrated Planning of an active distribution network and DG integration in clusters considering a novel formulation for reliability assessment. CSEE J. Power Energy Syst. 2023, 9, 561–576. [Google Scholar]
- Guo, J.; Liu, W.X.; Syed, F.R.; Zhang, J.H. Reliability assessment of a cyber physical microgrid system in island mode. CSEE J. Power Energy Syst. 2019, 5, 46–55. [Google Scholar] [CrossRef]
- Wangdee, W.; Billinton, R. Reliability assessment of bulk electric systems containing large wind farms. Int. J. Electr. Power Energy Syst. 2007, 29, 759–766. [Google Scholar] [CrossRef]
- Billinton, R.; Wang, P. Teaching distribution system reliability evaluation using Monte Carlo simulation. IEEE Trans. Power Syst. 1999, 14, 397–403. [Google Scholar] [CrossRef]
- Li, G.F.; Bie, Z.H.; Xie, H.P.; Lin, Y.L. Customer satisfaction based reliability evaluation of active distribution networks. Appl. Energy 2016, 162, 1571–1578. [Google Scholar] [CrossRef]
- Brown, R.E.; Gupta, S.; Christie, R.D.; Venkata, S.S.; Fletcher, R. Distribution system reliability assessment: Momentary interruptions and storms. IEEE Trans. Power Deliv. 1997, 12, 1569–1575. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F. Reliability evaluation for distribution system with renewable distributed generation during islanded mode of operation. IEEE Trans. Power Syst. 2009, 24, 572–581. [Google Scholar] [CrossRef]
- Bie, Z.H.; Zhang, P.; Li, G.F.; Hua, B.W.; Meehan, M.; Wang, X.F. Reliability Evaluation of Active Distribution Systems Including Microgrids. IEEE Trans. Power Syst. 2012, 27, 2342–2350. [Google Scholar] [CrossRef]
- Billinton, R.; Jonnavithula, S. A test system for teaching overall power system reliability assessment. IEEE Trans. Power Syst. 1996, 11, 1670–1676. [Google Scholar] [CrossRef]
- Billinton, R.; Wang, P. Reliability-network-equivalent approach to distribution-system-reliability evaluation. IEE Proc. Gener. Transm. Distrib. 1998, 145, 149–153. [Google Scholar] [CrossRef]
- Jia, H.P.; Ding, Y.; Song, Y.H.; Singh, C.N.; Li, M.Z. Operating Reliability Evaluation of Power Systems Considering Flexible Reserve Provider in Demand Side. IEEE Trans. Smart Grid 2019, 10, 3452–3464. [Google Scholar] [CrossRef]
- Li, W.X.; Wang, P.; Li, Z.M.; Liu, Y.C. Reliability evaluation of complex radial distribution systems considering restoration sequence and network constraints. IEEE Trans. Power Deliv. 2004, 19, 753–758. [Google Scholar] [CrossRef]
- Al-Muhaini, M.; Heydt, G.T. A novel method for evaluating future power distribution system reliability. IEEE Trans. Power Syst. 2013, 28, 3018–3027. [Google Scholar] [CrossRef]
- Lin, Y.-K. System Reliability Evaluation for a Multistate Supply Chain Network With Failure Nodes Using Minimal Paths. IEEE Trans. Reliab. 2009, 58, 34–40. [Google Scholar] [CrossRef]
- Chen, J.; Yu, T.; Xu, Y.; Cheng, X. Analytic method for power supply reliability assessment of electricity-gas coupled energy system. Autom. Electr. Power Syst. 2018, 42, 59–66. [Google Scholar]
- Liu, H.J.; Huang, J.G. Reliability Evaluation for Complex Distribution System Based on the Simplified Zone Model and the Minimal Path. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 May 2011; pp. 1–4. [Google Scholar]
- Xie, K.; Zhou, J.; Billinton, R. Reliability evaluation algorithm for complex medium voltage electrical distribution networks based on the shortest path. IEE Proc. Gener. Transm. Distrib. 2004, 150, 686–690. [Google Scholar] [CrossRef]
- Wang, C.S.; Zhang, T.Y.; Luo, F.Z.; Li, P.; Yao, L.Z. Fault Incidence Matrix Based Reliability Evaluation Method for Complex Distribution System. IEEE Trans. Power Syst. 2018, 33, 6736–6745. [Google Scholar] [CrossRef]
- Chiou, J.P.; Chang, C.F.; Su, C.T. Variable scaling hybrid differential evolution for solving network reconfiguration of distribution systems. IEEE Trans. Power Syst. 2005, 20, 668–674. [Google Scholar] [CrossRef]



| Reliability Indices | Reference [10] | This Paper |
|---|---|---|
| SAIFI (1/year) | 1.0067 | 1.006649 |
| SAIDI (h/year) | 6.669 | 6.668781 |
| ASAI | 0.99924 | 0.999238 |
| EENS (MWh/year) | 72.81 | 72.815310 |
| Load Number | Reference [10] | This Paper | ||
|---|---|---|---|---|
| SAIFI (1/Year) | SAIDI (h/Year) | SAIFI (1/Year) | SAIDI (h/Year) | |
| 1 | 0.3303 | 3.67 | 0.3303 | 3.666 |
| 4 | 0.3303 | 3.67 | 0.3303 | 3.666 |
| 8 | 0.3725 | 3.76 | 0.3725 | 3.761 |
| 12 | 0.3595 | 3.70 | 0.3595 | 3.696 |
| 16 | 0.2405 | 1.01 | 0.2405 | 1.008 |
| 18 | 1.6725 | 8.40 | 1.6725 | 8.402 |
| 23 | 1.7115 | 8.60 | 1.7115 | 8.597 |
| 26 | 1.7115 | 11.48 | 1.7115 | 11.483 |
| 32 | 2.5890 | 12.98 | 2.5890 | 12.984 |
| 37 | 2.5595 | 15.72 | 2.5595 | 15.724 |
| 40 | 2.5110 | 15.48 | 2.5110 | 15.480 |
| 85-Node | 137-Node | 417-Node | 1080-Node | |
|---|---|---|---|---|
| Reference [19] | 0.061 | 0.145 | 1.003 | 8.862 |
| This paper | 0.010 | 0.019 | 0.092 | 0.591 |
| Tie Switch | DG | SOP | |
| Case 1 | × | × | × |
| Case 2 | √ | × | × |
| Case 3 | √ | √ | √ |
| SAIFI (1/Year) | SAIDI (h/Year) | EENS (MWh/Year) | |
|---|---|---|---|
| Case 1 | 1.1374 | 3.4443 | 37.2208 |
| Case 2 | 1.1374 | 1.2332 | 14.3298 |
| Case 3 | 1.1374 | 0.6257 | 7.0129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Lin, L.; Chen, Y.; Xu, C.; Zhang, C.; Zhang, Y.; Luo, F.; Fo, J. A Matrix-Based Analytical Approach for Reliability Assessment of Mesh Distribution Networks. Energies 2025, 18, 5508. https://doi.org/10.3390/en18205508
Li S, Lin L, Chen Y, Xu C, Zhang C, Zhang Y, Luo F, Fo J. A Matrix-Based Analytical Approach for Reliability Assessment of Mesh Distribution Networks. Energies. 2025; 18(20):5508. https://doi.org/10.3390/en18205508
Chicago/Turabian StyleLi, Shuitian, Lixiang Lin, Ya Chen, Chang Xu, Chenxi Zhang, Yuanliang Zhang, Fengzhang Luo, and Jiacheng Fo. 2025. "A Matrix-Based Analytical Approach for Reliability Assessment of Mesh Distribution Networks" Energies 18, no. 20: 5508. https://doi.org/10.3390/en18205508
APA StyleLi, S., Lin, L., Chen, Y., Xu, C., Zhang, C., Zhang, Y., Luo, F., & Fo, J. (2025). A Matrix-Based Analytical Approach for Reliability Assessment of Mesh Distribution Networks. Energies, 18(20), 5508. https://doi.org/10.3390/en18205508








