Probabilistic State of Health Prediction for Lithium-Ion Batteries Based on Incremental Capacity and Differential Voltage Curves
Abstract
1. Introduction
- (1)
- IC and DV curves are utilized as core degradation descriptors, enabling precise feature extraction that reflects internal aging behavior while maintaining generalizability across cycles and conditions.
- (2)
- A BiLSTM model incorporating the WOA is proposed for automatically fine-tuning key neural network hyperparameters to effectively improve prediction accuracy and convergence stability.
- (3)
- A Bootstrap-based uncertainty quantification scheme is introduced to provide confidence-aware SOH forecasts, facilitating risk identification in battery management systems.
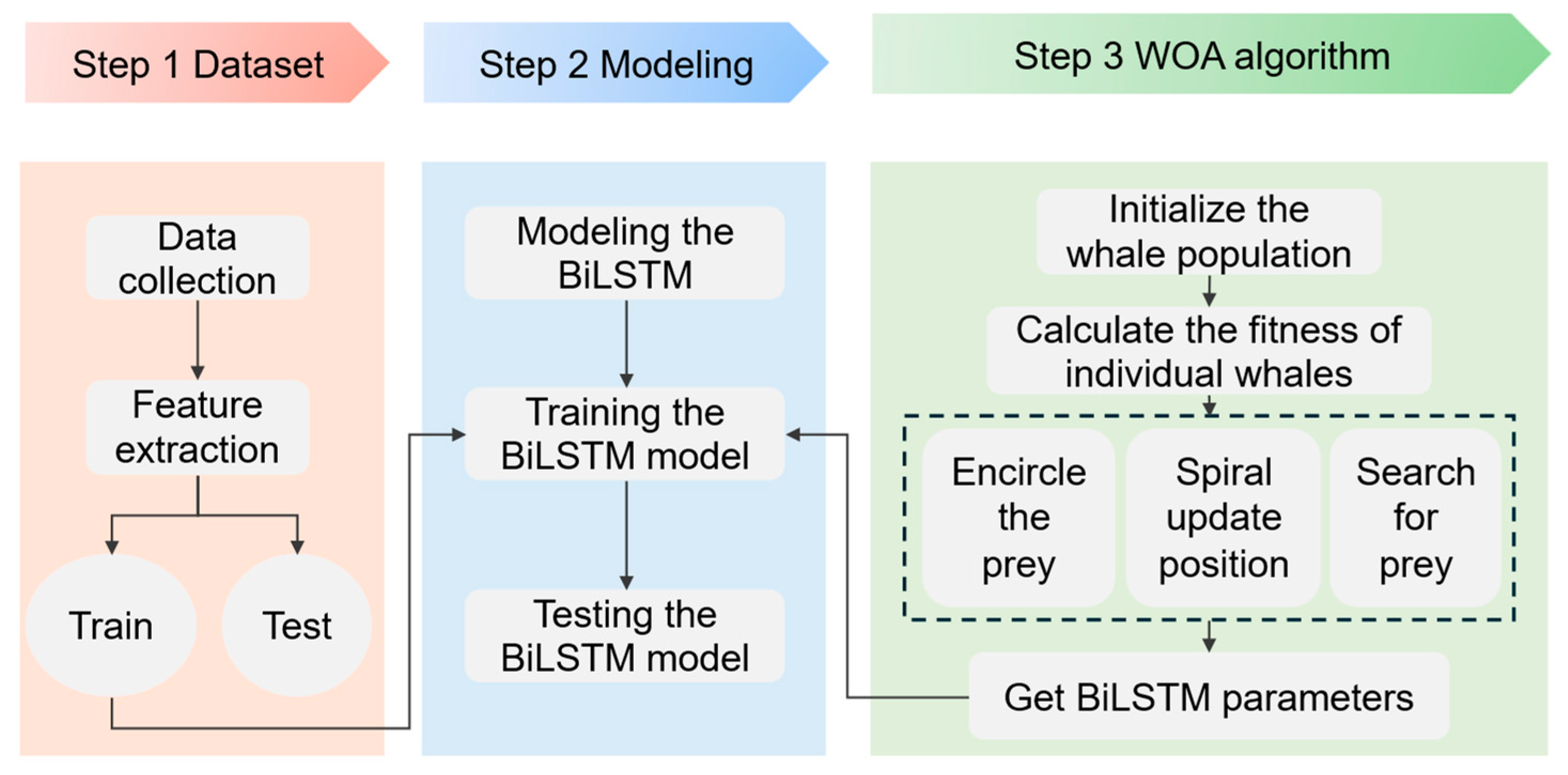
2. Methodology
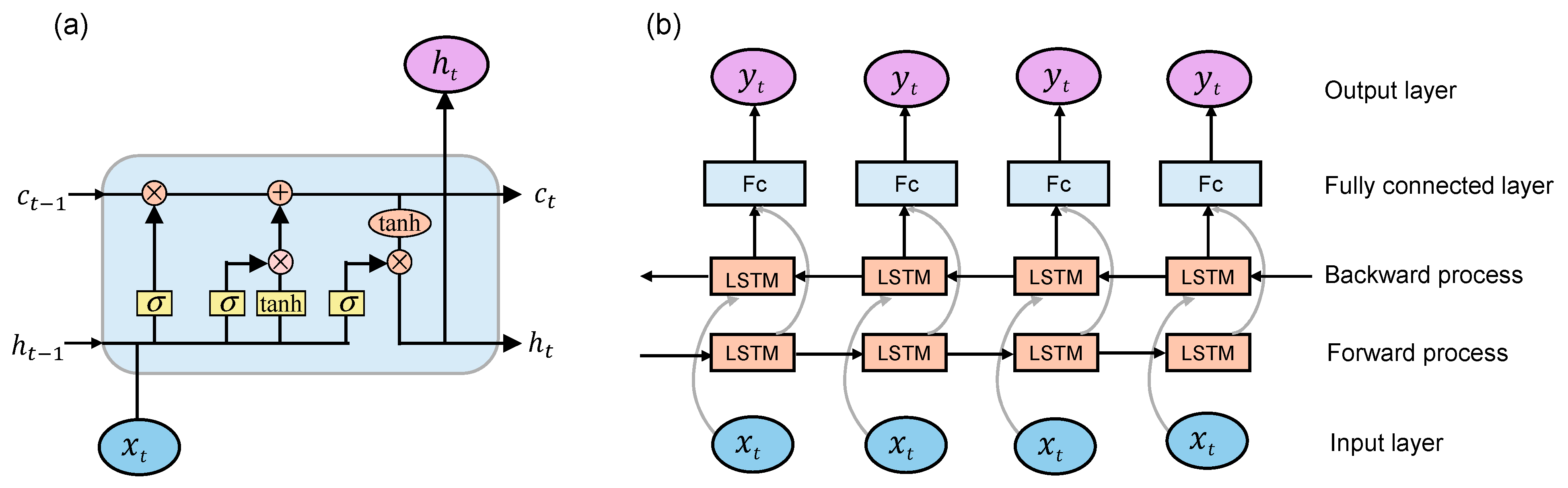
2.1. BiLSTM Model
2.2. Parameter Optimization Based on WOA Algorithm
2.3. Probabilistic Interval Prediction Using Bootstrap
3. Experimental Data and Feature Extraction
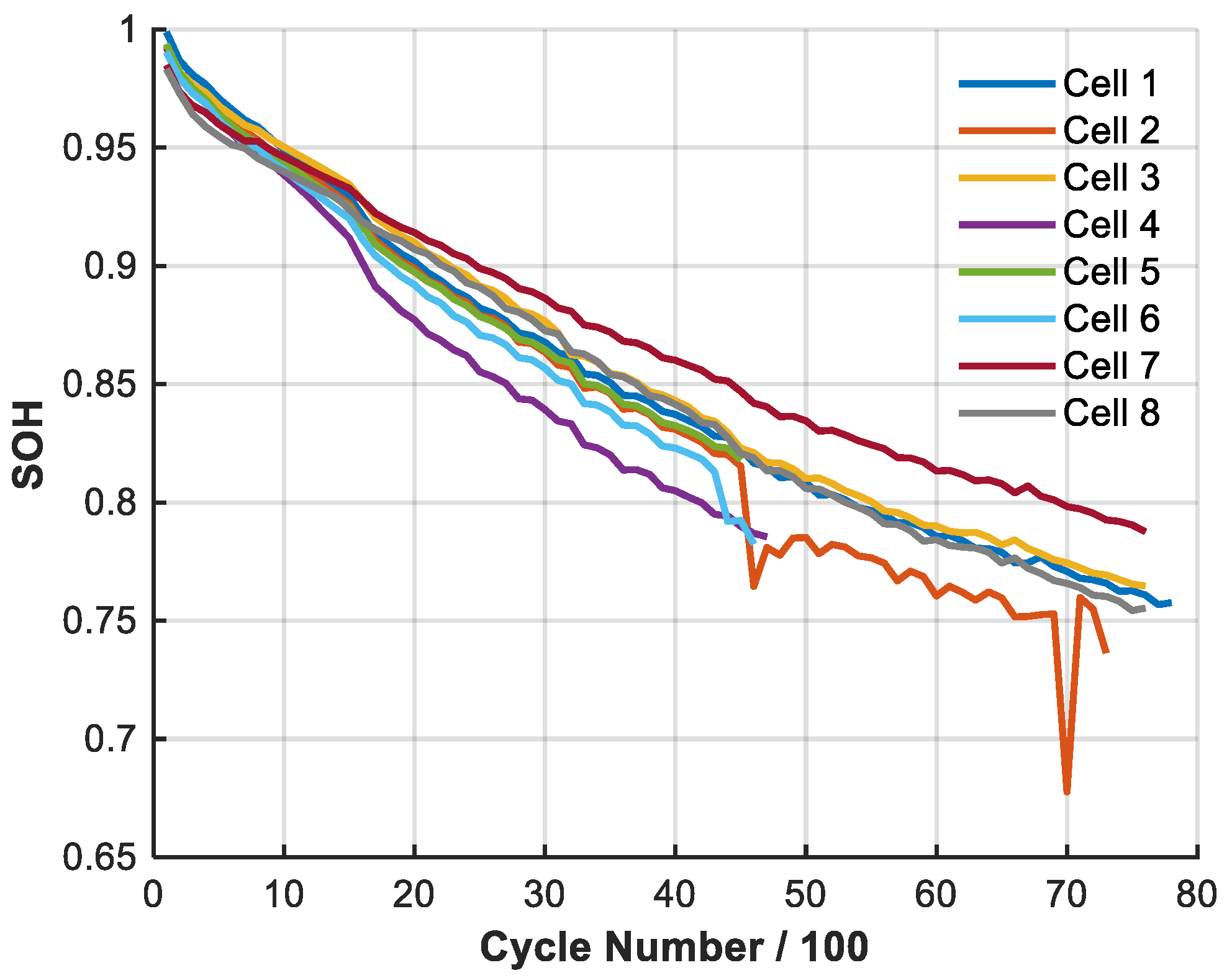
3.1. Oxford Dataset
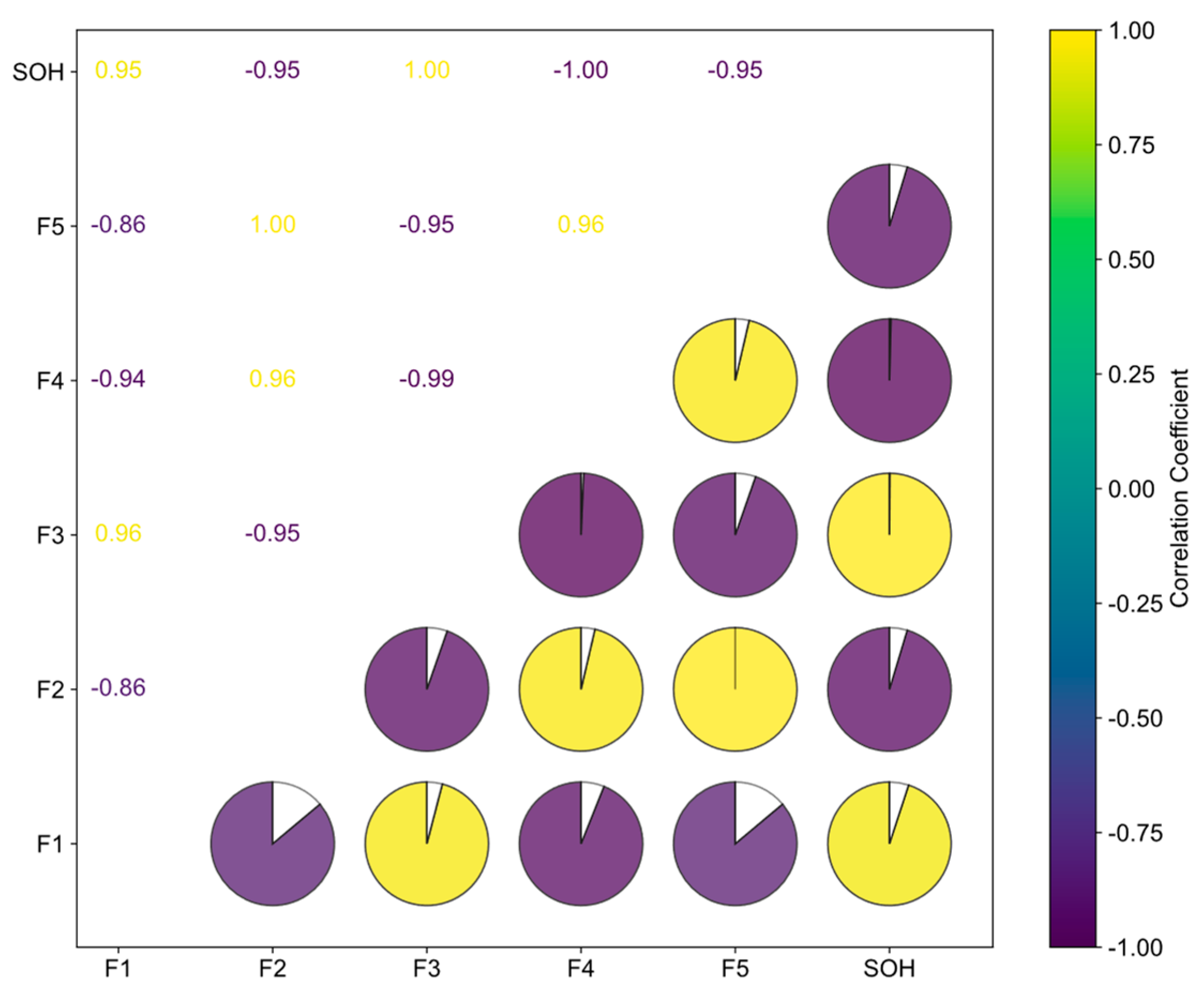
3.2. IC and DV Curves
3.3. Evaluation Metrics
4. Results and Discussion
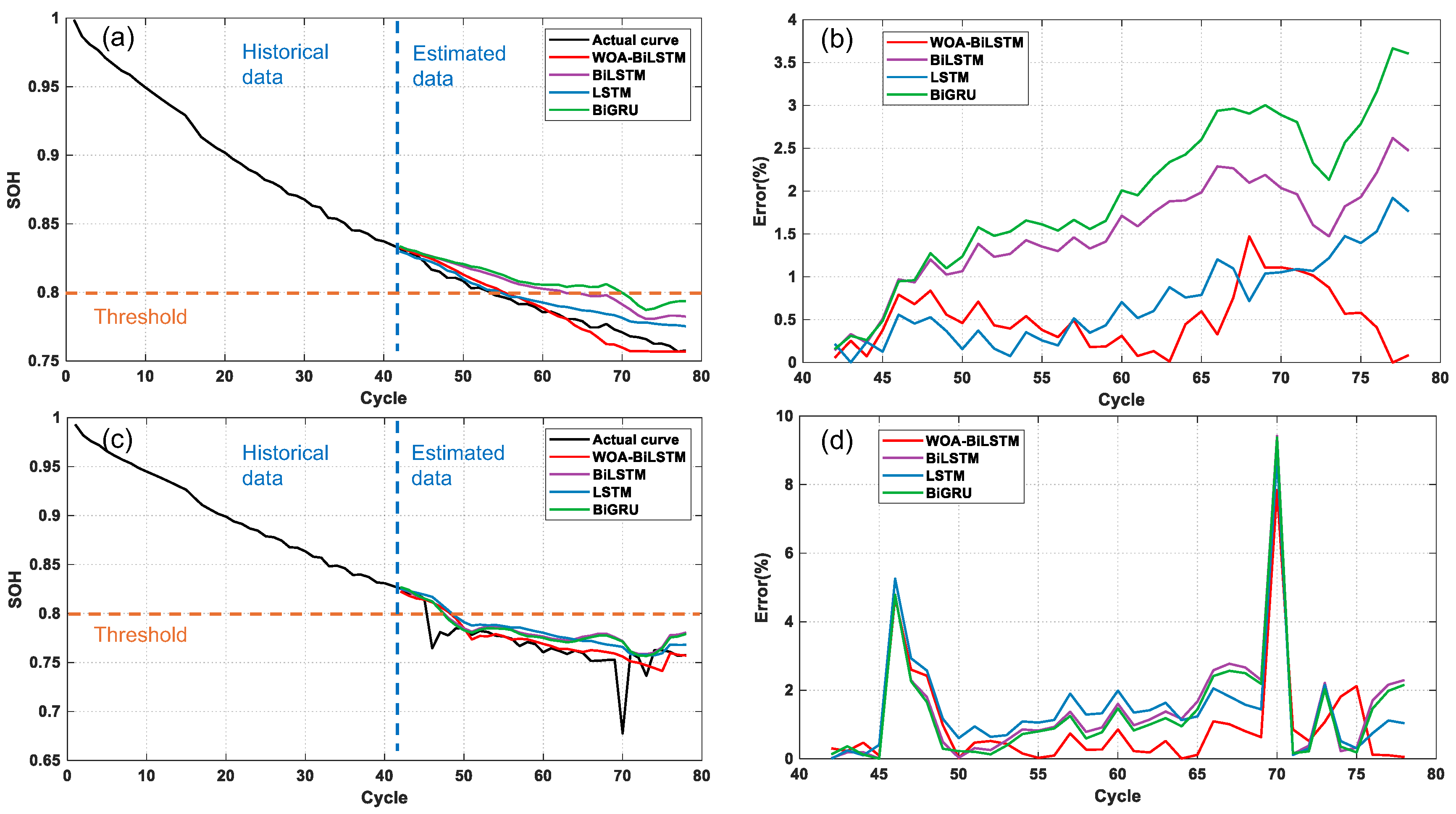
4.1. Deterministic Prediction Results
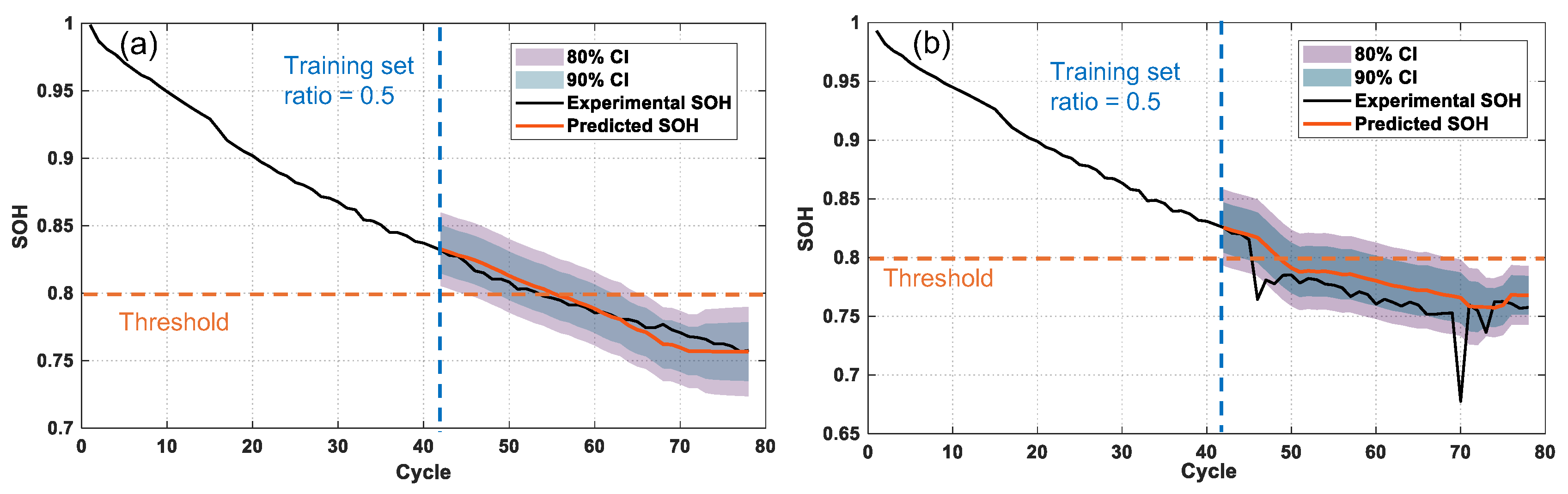
4.2. Probabilistic Prediction Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, S.; Ma, L. A Comparative Study of Different Deep Learning Algorithms for Lithium-Ion Batteries on State-of-Charge Estimation. Energy 2023, 263, 125872. [Google Scholar] [CrossRef]
- Vennam, G.; Sahoo, A.; Ahmed, S. A Survey on Lithium-Ion Battery Internal and External Degradation Modeling and State of Health Estimation. J. Energy Storage 2022, 52, 104720. [Google Scholar] [CrossRef]
- Ng, M.F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Whittingham, M.S. History, Evolution, and Future Status of Energy Storage. Proc. IEEE 2012, 100, 1518–1534. [Google Scholar] [CrossRef]
- Feng, X.; Pan, Y.; He, X.; Wang, L.; Ouyang, M. Detecting the Internal Short Circuit in Large-Format Lithium-Ion Battery Using Model-Based Fault-Diagnosis Algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, L.; Cheng, L. Review on State Estimation and Remaining Useful Life Prediction Methods for Lithium-Ion Battery. Power Gener. Technol. 2023, 44, 1–17. [Google Scholar] [CrossRef]
- Sun, T.; Xu, B.; Cui, Y.; Feng, X.; Han, X.; Zheng, Y. A Sequential Capacity Estimation for the Lithium-Ion Batteries Combining Incremental Capacity Curve and Discrete Arrhenius Fading Model. J. Power Sources 2021, 484, 229248. [Google Scholar] [CrossRef]
- Han, X.; Wang, Z.; Wei, Z. A Novel Approach for Health Management Online-Monitoring of Lithium-Ion Batteries Based on Model-Data Fusion. Appl. Energy 2021, 302, 117511. [Google Scholar] [CrossRef]
- Xia, F.; Wang, K.; Chen, J. State of Health and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on a Disturbance-Free Incremental Capacity and Differential Voltage Analysis Method. J. Energy Storage 2023, 64, 107161. [Google Scholar] [CrossRef]
- Lin, M.; Wu, D.; Meng, J.; Wu, J.; Wu, H. A Multi-Feature-Based Multi-Model Fusion Method for State of Health Estimation of Lithium-Ion Batteries. J. Power Sources 2022, 518, 230774. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, B. Battery Health Prognosis Using Improved Temporal Convolutional Network Modeling. J. Energy Storage 2022, 51, 104480. [Google Scholar] [CrossRef]
- Torai, S.; Nakagomi, M.; Yoshitake, S.; Yamaguchi, S.; Oyama, N. State-of-Health Estimation of LiFePO4/Graphite Batteries Based on a Model Using Differential Capacity. J. Power Sources 2016, 306, 62–69. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Habibi, S. Estimating Battery State of Health Using Electrochemical Impedance Spectroscopy and the Relaxation Effect. J. Energy Storage 2021, 43, 103210. [Google Scholar] [CrossRef]
- Huang, Z.; Best, M.; Knowles, J.; Fly, A. Adaptive Piecewise Equivalent Circuit Model With SOC/SOH Estimation Based on Extended Kalman Filter. IEEE Trans. Energy Convers. 2023, 38, 959–970. [Google Scholar] [CrossRef]
- Vennam, G.; Sahoo, A. A Dynamic SOH-Coupled Lithium-Ion Cell Model for State and Parameter Estimation. IEEE Trans. Energy Convers. 2023, 38, 1186–1196. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of Model-Based Online State-of-Charge Estimation Using Kalman Filter Family for Lithium-Ion Batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.; Cheng, G.; Wang, J. State-of-Charge Estimation of Lithium-Ion Batteries Based on Fractional-Order Modeling and Adaptive Square-Root Cubature Kalman Filter. Energy 2023, 271, 127007. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Li, H. A Novel Data-Driven Method for Mining Battery Open-Circuit Voltage Characterization. Green Energy Intell. Transp. 2022, 1, 100001. [Google Scholar] [CrossRef]
- Meng, H.; Geng, M.; Han, T. Long Short-Term Memory Network with Bayesian Optimization for Health Prognostics of Lithium-Ion Batteries Based on Partial Incremental Capacity Analysis. Reliab. Eng. Syst. Saf. 2023, 236, 109288. [Google Scholar] [CrossRef]
- He, J.; Bian, X.; Liu, L.; Wei, Z.; Yan, F. Comparative Study of Curve Determination Methods for Incremental Capacity Analysis and State of Health Estimation of Lithium-Ion Battery. J. Energy Storage 2020, 29, 101400. [Google Scholar] [CrossRef]
- Zhou, Q.; Anderson, D.; Sun, J. State of Health Estimation for Battery Modules with Parallel-Connected Cells under Cell-to-Cell Variations. eTransportation 2024, 22, 100346. [Google Scholar] [CrossRef]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-Board State of Health Estimation of LiFePO4 Battery Pack through Differential Voltage Analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A Quick On-Line State of Health Estimation Method for Li-Ion Battery with Incremental Capacity Curves Processed by Gaussian Filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A Support Vector Machine-Based State-of-Health Estimation Method for Lithium-Ion Batteries under Electric Vehicle Operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Lin, C.; Xu, J.; Jiang, D.; Hou, J.; Liang, Y.; Zou, Z.; Mei, X. Multi-Model Ensemble Learning for Battery State-of-Health Estimation: Recent Advances and Perspectives. J. Energy Chem. 2025, 100, 739–759. [Google Scholar] [CrossRef]
- Thelen, A.; Huan, X.; Paulson, N.; Onori, S.; Hu, Z.; Hu, C. Probabilistic Machine Learning for Battery Health Diagnostics and Prognostics—Review and Perspectives. npj Mater. Sustain. 2024, 2, 14. [Google Scholar] [CrossRef]
- Bamati, S.; Chaoui, H. Lithium-Ion Batteries Long Horizon Health Prognostic Using Machine Learning. IEEE Trans. Energy Convers. 2022, 37, 1176–1186. [Google Scholar] [CrossRef]
- Tang, A.; Huang, Y.; Xu, Y.; Hu, Y.; Yan, F.; Tan, Y.; Jin, X.; Yu, Q. Data-Physics-Driven Estimation of Battery State of Charge and Capacity. Energy 2024, 294, 130776. [Google Scholar] [CrossRef]
- Jia, C.; Tian, Y.; Shi, Y.; Jia, J.; Wen, J.; Zeng, J. State of Health Prediction of Lithium-Ion Batteries Based on Bidirectional Gated Recurrent Unit and Transformer. Energy 2023, 285, 129401. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; He, Y.; Zhang, S.; Cai, Y. Edge–Cloud Collaborative Estimation Lithium-Ion Battery SOH Based on MEWOA-VMD and Transformer. J. Energy Storage 2024, 99, 113388. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. Prognostics Methods for Battery Health Monitoring Using a Bayesian Framework. IEEE Trans. Instrum. Meas. 2009, 58, 291–296. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2021, 68, 3170–3180. [Google Scholar] [CrossRef]
- Lin, Y.H.; Li, G.H. A Bayesian Deep Learning Framework for RUL Prediction Incorporating Uncertainty Quantification and Calibration. IEEE Trans. Ind. Inform. 2022, 18, 7274–7284. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Cao, L.; Liu, J.; You, P.; Gopaluni, B.; Cao, Y. A Generalizable Method for Capacity Estimation and RUL Prediction in Lithium-Ion Batteries. Ind. Eng. Chem. Res. 2024, 63, 345–357. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Feng, X. State-of-Health Estimation and Remaining-Useful-Life Prediction for Lithium-Ion Battery Using a Hybrid Data-Driven Method. IEEE Trans. Veh. Technol. 2020, 69, 10854–10867. [Google Scholar] [CrossRef]
- Lin, C.P.; Cabrera, J.; Yang, F.; Ling, M.H.; Tsui, K.L.; Bae, S.J. Battery State of Health Modeling and Remaining Useful Life Prediction through Time Series Model. Appl. Energy 2020, 275, 115338. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Z.; Zhu, Z.; Jiang, W.; Ma, Y.; Sang, X.; Yang, S. A Framework of Joint SOC and SOH Estimation for Lithium-Ion Batteries: Using BiLSTM as a Battery Model. J. Power Sources 2025, 635, 236342. [Google Scholar] [CrossRef]
- Li, J.; Ye, M.; Wang, Y.; Wang, Q.; Wei, M. A Hybrid Framework for Predicting the Remaining Useful Life of Battery Using Gaussian Process Regression. J. Energy Storage 2023, 66, 107513. [Google Scholar] [CrossRef]
- Nasiri, J.; Khiyabani, F.M. A Whale Optimization Algorithm (WOA) Approach for Clustering. Cogent Math. Stat. 2018, 5, 1483565. [Google Scholar] [CrossRef]
- Schmitt, C.; Kopljar, D.; Friedrich, K.A. Detailed Investigation of Degradation Modes and Mechanisms of a Cylindrical High-Energy Li-Ion Cell Cycled at Different Temperatures. J. Energy Storage 2025, 120, 116486. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A Rapid Online Calculation Method for State of Health of Lithium-Ion Battery Based on Coulomb Counting Method and Differential Voltage Analysis. J. Power Sources 2020, 479, 228740. [Google Scholar] [CrossRef]



| Cell Type | Electrode Material | Rated Capacity/Ah | Discharge Cut-Off Voltage/V | Charge Cut-Off Voltage/V | Temperature |
|---|---|---|---|---|---|
| Pouch | LCO, NCO | 0.74 | 2.7 | 4.2 | 40 °C |
| Feature | Source Curve | Definition |
|---|---|---|
| F1 | IC | Peak value of IC curve |
| F2 | IC | Voltage corresponding to IC curve peak |
| F3 | IC | Integrated area under the peak region |
| F4 | DV | Valley value of DV curve |
| F5 | DV | Voltage corresponding to DV curve valley |
| Battery No. | Model | RMSE/% | MAE/% | MAPE/% |
|---|---|---|---|---|
| Cell 1 | WOA-BiLSTM | 0.62 | 0.50 | 0.64 |
| BiLSTM | 1.64 | 1.52 | 1.95 | |
| LSTM | 0.86 | 0.71 | 0.91 | |
| BiGRU | 2.15 | 1.95 | 2.50 | |
| Cell 2 | WOA-BiLSTM | 1.75 | 0.94 | 1.26 |
| BiLSTM | 2.22 | 1.45 | 1.95 | |
| LSTM | 2.13 | 1.46 | 1.95 | |
| BiGRU | 2.15 | 1.35 | 1.82 | |
| Cell 3 | WOA-BiLSTM | 0.44 | 0.34 | 0.43 |
| BiLSTM | 0.78 | 0.63 | 0.76 | |
| LSTM | 1.03 | 0.94 | 1.20 | |
| BiGRU | 1.20 | 0.96 | 1.23 | |
| Cell 4 | WOA-BiLSTM | 0.48 | 0.36 | 0.45 |
| BiLSTM | 1.34 | 1.46 | 1.37 | |
| LSTM | 1.06 | 0.98 | 1.21 | |
| BiGRU | 2.71 | 2.38 | 2.96 | |
| Cell 5 | WOA-BiLSTM | 0.25 | 0.20 | 0.23 |
| BiLSTM | 0.65 | 0.56 | 0.67 | |
| LSTM | 1.22 | 1.03 | 1.17 | |
| BiGRU | 1.83 | 1.46 | 1.75 | |
| Cell 6 | WOA-BiLSTM | 0.64 | 0.43 | 0.52 |
| BiLSTM | 0.79 | 0.73 | 0.88 | |
| LSTM | 0.71 | 0.62 | 0.75 | |
| BiGRU | 1.01 | 0.54 | 0.76 | |
| Cell 7 | WOA-BiLSTM | 0.41 | 0.31 | 0.38 |
| BiLSTM | 0.82 | 0.75 | 0.93 | |
| LSTM | 1.52 | 1.33 | 1.71 | |
| BiGRU | 1.58 | 1.35 | 1.67 | |
| Cell 8 | WOA-BiLSTM | 0.43 | 0.36 | 0.46 |
| BiLSTM | 0.20 | 0.15 | 0.19 | |
| LSTM | 0.73 | 0.62 | 0.79 | |
| BiGRU | 1.72 | 1.51 | 1.94 |
| Battery No. | PICP | PINAW | CWC | |||
|---|---|---|---|---|---|---|
| 90% | 80% | 90% | 80% | 90% | 80% | |
| Cell 1 | 0.95 | 1 | 0.41 | 0.47 | 0.41 | 0.47 |
| Cell 2 | 0.86 | 1 | 0.31 | 0.37 | 0.31 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Yan, H.; Wang, Y.; Yang, Y.; Liu, X.; Zhu, Z.; Huang, G.; Huang, Z. Probabilistic State of Health Prediction for Lithium-Ion Batteries Based on Incremental Capacity and Differential Voltage Curves. Energies 2025, 18, 5450. https://doi.org/10.3390/en18205450
Wang Q, Yan H, Wang Y, Yang Y, Liu X, Zhu Z, Huang G, Huang Z. Probabilistic State of Health Prediction for Lithium-Ion Batteries Based on Incremental Capacity and Differential Voltage Curves. Energies. 2025; 18(20):5450. https://doi.org/10.3390/en18205450
Chicago/Turabian StyleWang, Qingbin, Hangang Yan, Yuxi Wang, Yun Yang, Xiaoguang Liu, Zhuoqi Zhu, Gancai Huang, and Zheng Huang. 2025. "Probabilistic State of Health Prediction for Lithium-Ion Batteries Based on Incremental Capacity and Differential Voltage Curves" Energies 18, no. 20: 5450. https://doi.org/10.3390/en18205450
APA StyleWang, Q., Yan, H., Wang, Y., Yang, Y., Liu, X., Zhu, Z., Huang, G., & Huang, Z. (2025). Probabilistic State of Health Prediction for Lithium-Ion Batteries Based on Incremental Capacity and Differential Voltage Curves. Energies, 18(20), 5450. https://doi.org/10.3390/en18205450




