Physics-Informed Neural Networks in Grid-Connected Inverters: A Review

Abstract

Physics-Informed Neural Networks (PINNs) have emerged as a powerful tool for modeling and controlling complex energy systems by embedding physical laws into deep learning architectures. This review paper highlights the application of PINNs in grid-connected inverter systems (GCISs), categorizing them by key tasks: parameter estimation, state estimation, control strategies, fault diagnosis and detection, and system identification. Particular focus is given to the use of PINNs in enabling accurate parameter estimation for aging and degradation monitoring. Studies show that PINN-based approaches can outperform purely data-driven models and traditional methods in both computational efficiency and accuracy. However, challenges remain, mainly related to high training costs and limited uncertainty quantification. To address these, emerging strategies such as advanced PINN frameworks are explored. The paper also explores emerging solutions and outlines future research directions to support the integration of PINNs into practical inverter design and operation.

1. Introduction

Rapid integration of renewable energy sources (RESs) such as wind and solar requires a growing number of electronic power converters to interface these resources with the grid [1,2]. It is noted that by 2050, RESs can establish most of the generation, increasing dependence on inverters with fast dynamics and low inertia [2]. This evolution presents challenges to traditional simulation and control approaches; purely data-driven models often lack physical interpretability, while electromagnetic transient (EMT) models are computationally intensive [3]. PINNs overcome these limitations by implementing governing equations into neural network training [1]. The accurate modeling and real-time estimation of these systems are critical for stable operation, especially under dynamic grid conditions such as voltage sags, frequency deviations, and fault events [3,4,5].

As the share of inverter-based resources increases, traditional model-based methods, often dependent on offline parameter tuning and detailed knowledge of system dynamics, struggle to provide robust performance across varying operational situations. To address these challenges, PINNs are considered a promising model. PINNs combine the governing physical laws, typically stated as partial differential equations (PDEs) or ordinary differential equations (ODEs), directly into training neural networks [6,7,8]. This enables them to learn system dynamics from noisy or sparse data while preserving physical consistency, yielding more generalizable and accurate models than black-box neural networks. PINNs are particularly powerful for GCIs because they can learn converter dynamics under varying conditions, perceive parameter drifts, and speed up simulations for real-time control [9,10]. Unlike purely data-driven models, PINNs do not require large labeled datasets and are inherently more interpretable due to their embedded physics constraints [11]. A wide range of tasks, including parameter estimation [12,13], state estimation [14,15,16], enhancement of control strategy [17,18], fault detection [4,19,20], optimization of efficiency [17], and system identification [21,22], have been addressed using PINNs. These applications validate not only the flexibility of PINNs but also their role in enabling more robust, data-efficient, and physically grounded intelligence in GCISs. The combination of domain knowledge and machine learning through PINNs marks an important step forward in the realization of smart, adaptive, and self-diagnosing power electronics in the era of renewable energy and smart grids.

This paper reviews the state of the art of PINN applications for GCIs. In particular, it focuses on parameter and state estimation, efficiency improvement, control strategies, fault detection and diagnosis, and limitations with a path forward. Unlike previous related review papers on PINNs for general power systems or machine learning, this review paper focuses primarily on GCISs and their incorporation with PINNs. The paper provides a targeted understanding of how PINNs make modeling more accurate, enhance reliability, and improve control under uncertainties. In addition, this review paper classifies PINN applications in GCISs into several core areas: parameter estimation, state estimation, control approaches, fault detection and diagnosis, and system identification, highlighting their practical importance in real-world GCI operations. Moreover, the paper compares PINN approaches against traditional model-based methods (Kalman filtering, EMT simulations, MPC) and purely data-driven models (RNNs, CNNs, GCNNs). This review emphasizes how PINNs surpass limitations in data efficiency, physical interpretability, and noise robustness. Finally, this review paper explains the need for real-time implementations using PINNs and supports inverter-tied renewable integration. The paper also outlines key limitations, including hyperparameter tuning, computational cost, lack of standardized benchmarks, and scalability for large-scale systems.

The remainder of this paper is organized as follows. In Section 2, we provide an overview of grid-connected inverters (GCIs). The data-driven approaches for GCIs are discussed in Section 3. Next, the architecture and various applications of PINNs in GCIs are presented in Section 4. In Section 5, we discuss the limitations and in Section 6, we conclude the paper.

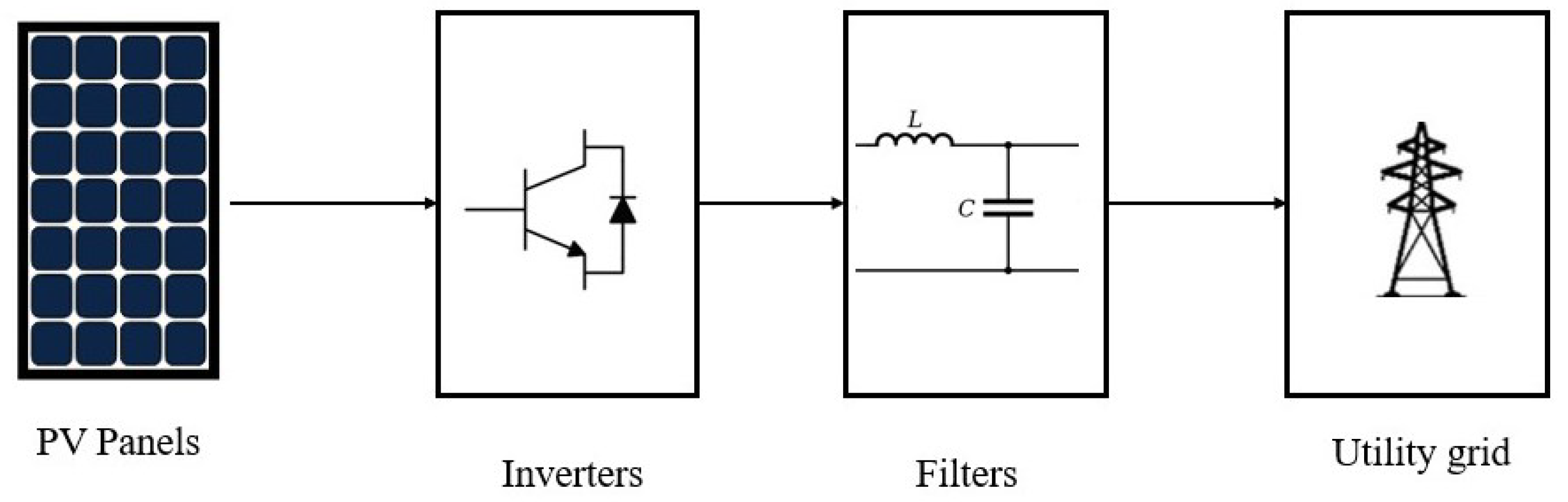
2. An Overview to Grid-Connected Inverters

GCIs act as crucial power electronic interfaces between renewable energy sources and the utility grid. Their main function is to convert direct current (DC) into synchronized alternating current (AC) and inject it into the grid with proper frequency and voltage. These inverters are responsible for supporting grid stability and maintaining power quality, not only for active and reactive power control [2,13,23]. Modern GCIs often include LC filters, control, and various feedback mechanisms to ensure robust and accurate operation under dynamic grid conditions [2,13]. However, the performance and reliability of GCIs are increasingly challenged by the high penetration of distributed energy resources (DERs), variations in grid impedance, component degradation, and transient phenomena [3,4,5]. Conventional control and estimation approaches based either purely on physical models or data-driven black-box methods suffer from limitations such as modeling inaccuracies or poor generalization across conditions [6,7,11].

In this context, PINNs offer a compelling solution by embedding known physical laws into neural network training, thus offering a hybrid paradigm that leverages both model-driven and data-driven strengths [8,11]. Their application to GCIs allows improved parameter and state estimation, fault diagnostics and detection, and model-based control, all while reducing the dependency on large datasets or exhaustive measurements [2,9,10].

Figure 1 shows a schematic of a three-phase grid-connected inverter. PINNs can leverage the known circuit equations of the inverter ([14]).

3. Data-Driven Approaches for Grid-Connected Inverter Systems

In recent years, GCISs have become central to modern power systems, allowing the integration of RESs like photovoltaic (PV) systems into the power grid. Monitoring, control, and fault detection are necessary for ensuring reliable and stable operation. In this context, data-driven methods have gained prominence due to their ability to model complex nonlinear dynamics and capture system behavior from observed data without requiring a complete physical model. Among traditional data-driven approaches, Sparse Extreme Learning Machines (SELMs) reduce computational complexity and offer fast training. Ref. [24] introduced SELMs for optimal power flow in power systems, highlighting their adaptability and superior training speed compared to deep learning models, although acknowledging limited generalization in complex unseen scenarios. Similarly, Convolutional Neural Networks (CNNs) have been effectively used for fault detection in inverter systems under variable operating conditions, resulting in strong classification performance across diverse fault modes [25]. In another study, ref. [26] proposed a CNN-based method to diagnose faults in shipboard inverter systems, using one-dimensional convolution and global pooling to achieve high accuracy and noise resilience. However, such architectures are sensitive to sensor noise and require large training datasets. Another method is Graph Convolutional Neural Networks (GCNNs), which have shown strong potential in modeling and analyzing distributed power systems by leveraging the inherent graph structure of the electrical grid. Ref. [27] demonstrates that GCNNs have high accuracy, generalization, and computational efficiency. However, GCNNs remain purely data-driven and do not embed the physical laws of the system, which limits their performance in low-data regimes. Ref. [28] introduced an ANN-based harmonic distortion prediction model for grid-connected PV inverters (GCPIs) that estimates the total harmonic distortion (THDI) using measured inputs, such as irradiance and ambient temperature. The Multilayer Perceptron Neural Network (MLPNN) model achieved high predictive accuracy and noise resilience over long-term data. Although it is effective for waveform forecasting, it lacks embedded physics and does not generalize well under changing grid dynamics. In [29], a Recurrent Neural Network (RNN) was used for fault detection in PV inverters by learning the temporal dependencies in voltage waveforms, achieving better detection performance under varying irradiance and temperature conditions. Moreover, RNNs have been successfully integrated with forecasting tasks such as short-term load prediction and frequency estimation. However, despite their ability to capture time-series patterns, RNNs often suffer from vanishing gradient issues during long sequences, leading to performance degradation in deep architectures or when modeling long-range dependencies.

Among these developments, (PINNs) and their variants such as (ePINNs) have emerged as a transformative solution for parameter estimation and control of GCISs. Unlike previous approaches, PINNs incorporate the governing differential equations of the inverters into the loss function, enabling them to generalize well even with limited data. In [13], it is emphasized that PINNs accurately estimated RLC filter parameters in a three-phase GCI with fewer data points and better robustness.

In

Table 1. Comparison of data-driven methods for GCIS applications. ( ✓ = included; ✗ = not included).

Aspects	SELM	CNN	MLP	RNN	GCNN	PINN
Small datasets	✗	✗	✗	✗	✗	✓
Dynamic estimation	✗	✗	✗	✓	✓	✓
System physics integration	✗	✗	✗	✗	✗	✓
Scalability for large systems	✓	✗	✗	✗	✓	✗
Robustness to noise/cyber-attacks	✗	✗	✓	✗	✓	✓

, we present a summary comparison of the various data-driven approaches discussed above and their use in grid-connected inverters. Table 1 summarizes the strengths of several data-driven approaches used in (GCIS). PINNs stand out for their ability to work well with small datasets, perform dynamic estimation, integrate system physics, and remain robust to noise and cyber-attacks. RNNs and GCNNs also handle dynamic estimation effectively, while GCNNs and SELMs scale better in large systems. MLPs offer moderate robustness, but most other models struggle with small data and lack physical interpretability. Overall, PINNs provide a balanced advantage across critical aspects of GCIS monitoring and control.

As emphasized in Table 1, the PINN method outperforms other data-driven approaches for GCISs because it combines data efficiency, physical consistency, and noise robustness. Unlike other methods (e.g., CNNs, RNNs), which need large labeled datasets and struggle with unnoticed operating conditions, PINNs embed physical laws and system dynamics directly into the learning process. This method allows accurate parameter and state estimation with limited measurements, while also ensuring resilience and interpretability. Therefore, PINNs are more reliable than purely data-driven approaches in real-time monitoring and control of GCIs.

4. Architecture and Applications of Physics-Informed Neural Networks in Grid-Connected Inverters

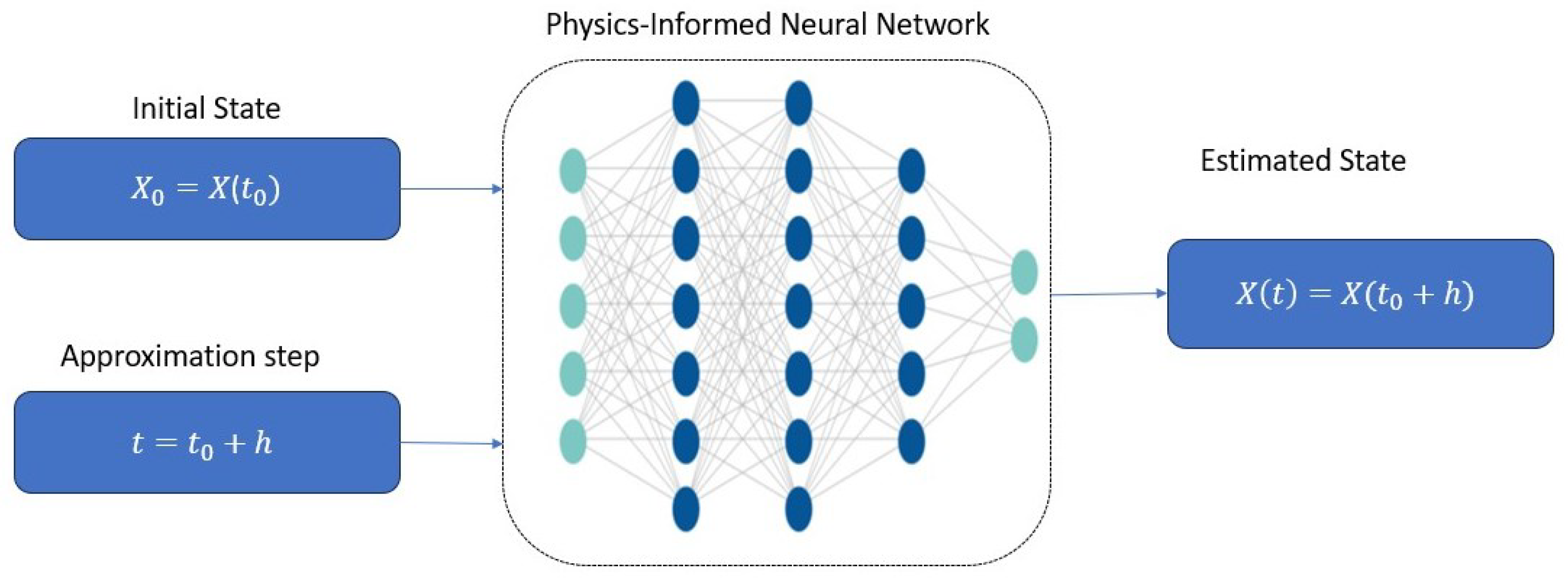
4.1. Architecture of PINN

The architecture of PINNs is designed to embed governing physical laws directly into the training process of deep neural networks, thus combining physics-based modeling with the flexibility of data-driven methods. In its standard form, a PINN includes a feedforward neural network trained on a composite loss function that includes multiple components: data loss, residuals of the governing equations (typically ODEs or PDEs), and initial or boundary conditions [6]. Within GCISs, these governing laws are derived from circuit-level principles such as Kirchhoff’s voltage and current laws, dynamic filter equations, and grid synchronization constraints [9,13]. This physics-based structure enables accurate modeling and estimation with minimal data and no requirement for full-state observation.

Many architectural improvements have been suggested to improve the convergence, scalability, and robustness of PINNs in power electronic applications. For example, gradient-enhanced PINNs (gPINNs) integrate higher-order derivative information directly into the loss function, stabilizing training in stiff systems like those found in power electronics [8]. Automatic PINN frameworks, such as the balanced adaptive PINN, introduced by [30], dynamically adjust loss weighting to handle typical transient behaviors in inverter operation. Causality-conforming PINNs restructure the input and loss computation flow to enforce the temporal sequence of inverter dynamics, leading to enhanced generalization and prediction accuracy in state estimation tasks [1].

Bayesian PINNs (BPINNs) extend conventional PINN methods by incorporating uncertainty quantification through probabilistic layers. This is particularly valuable in inverter-dominated grid environments, where model assurance and reliability are critical for real-time operation [22]. For large-scale systems, distributed or multi-network PINN methods are increasingly implemented to moderate computational burden and improve scalability, as seen in applications involving wide-area grid identification and dynamics learning [22].

A (PINN) begins by normalizing inputs to a standard range to improve training stability. The inputs feed into a deep neural network (DNN) that predicts the desired physical fields (e.g., voltages, currents) at each point. Significantly, automatic differentiation is applied to the network outputs to compute the exact spatial and temporal derivatives required by the governing equations [8]. The structure of the (PINN) is shown in Figure 2, where the core idea is to enforce physics-informed constraints: the loss function includes a term for the residual of the governing PDE (computed from these derivatives) as well as terms for initial and boundary conditions. In practice, the total loss is a weighted sum of:

(i)

a data loss: mean-squared error between predicted and measured values, if any

$${\mathrm{MSE}}_i={\displaystyle \frac{1}{N_i}}\sum _{i=1}^{N_i}{\left|u_{\mathrm{pred}}\left(x_i^{\mathrm{ini}},0;\theta \right)-g\left(x_i^{\mathrm{ini}},0\right)\right|}^2$$

(ii)

PDE loss: MSE of the PDE residual at collocation points

$${\mathrm{MSE}}_b={\displaystyle \frac{1}{N_b}}\sum _{i=1}^{N_b}{\left|u_{\mathrm{pred}}\left(0,t_i^b;\theta \right)-\phi \left(0,t_i^b\right)\right|}^2$$

(iii)

a boundary/initial-condition loss

$${\mathrm{MSE}}_f={\displaystyle \frac{1}{N_f}}\sum _{i=1}^{N_f}{\left|\lambda {\displaystyle \frac{{\partial }^n{u}_{\mathrm{pred}}\left(x_i^f,t_i^f;\theta \right)}{\partial x^n}}+f\left(x_i^f,t_i^f\right)\right|}^2$$

The loss function ${\mathrm{MSE}}_{\mathrm{total}}$ is then determined by:

$${\mathrm{MSE}}_{\mathrm{total}}={\mathrm{MSE}}_i+{\mathrm{MSE}}_b+{\mathrm{MSE}}_f$$

where ${\mathrm{MSE}}_i$, ${\mathrm{MSE}}_b$, and ${\mathrm{MSE}}_f$ are the mean square errors (MSE) of the residuals of the initial condition, boundary condition, and governing equation, respectively. ${\mathrm{N}}_i$ and ${\mathrm{N}}_b$ are the numbers of sampling points for the initial and boundary conditions, respectively. ${\mathrm{N}}_f$ is the number of collocation points randomly sampled in the equation domain. The network and any latent parameters are then trained by gradient-based optimization such as Adam.

The computational graph for all terms is automatically built, so gradients of the total loss with respect to the network weights are computed efficiently [8]. Training proceeds iteratively over epochs until convergence, yielding a substitute model that fits the data while also satisfying the physics constraints.

In GCISs, this general PINN framework has been enhanced in several ways for tasks like parameter and state estimation, control strategies, and system identification. For example, ref. [10] treats unknown grid inertia and damping as latent network parameters: the PINN includes these physical constants as trainable variables alongside the weights, so that minimizing the combined data and physics loss yields estimates of the inverter dynamics. In control-oriented PINNs, ref. [31] introduces a variant called Physics-Informed Neural Nets for Control (PINC) that adds control inputs to the network architecture and allows flexible long-horizon simulation for model-predictive control of power converters. In another case, ref. [3] applies a PINN to grid-tie converters by deriving converter-specific equations from the voltage-source converter (VSC) control model and including them as a physics-informed loss term [3]. This hybrid approach, which combines measured data with determined domain equations in the loss, allows accurate multi-point impedance identification with very limited test data. In each example, the PINN core relies on a normalized-input DNN with a multi-term loss, but the physics block is customized to exploit the inverter application [21].

In the control field, PINNs have been combined with learning-based and model predictive control frameworks. The paper [2] confirmed that a hybrid PINN-based controller for a buck converter surpasses conventional PI control in response time and robustness to load variation. Similarly, ref. [31] presented a control-oriented variant known as Physics-Informed Neural Control (PINC), which embeds control variables into the network architecture for improved long-term route prediction and simulation.

Moreover, hybrid PINN approaches have been used to improve fault detection and diagnosis in inverter-based systems. These methods combine data-driven features with physics-informed constraints to improve detection sensitivity under noisy or limited measurement conditions [13]. The impact of network architecture, such as collocation point density, activation function type, and depth, on PINN performance has also been studied extensively. For example, refs. [9,13] achieved accurate LC parameter estimation in three-phase and DC–DC inverters using carefully designed PINNs trained on small datasets.

Recent studies, such as [30], have shown that PINNs can also be employed as fast, reliable surrogates for electromagnetic transient (EMT) simulation, offering over 100× speedup compared to traditional EMT software while maintaining high fidelity. These advancements highlight that strategic architectural choices are fundamental to maximizing PINN effectiveness in inverter control, system identification, and real-time fault management.

4.2. Applications of PINN in GCISs

The ability of PINNs to embed system dynamics directly into the learning process enables accurate estimation and control with limited data. For example, PINNs have been used for parameter estimation in DC–DC and three-phase inverters, achieving high precision in identifying inductance and capacitance values without requiring complete system observability [14,15]. In the domain of state estimation, PINNs can reconstruct hidden internal states of complex inverter models from divergent measurements [13,32,33]. For control strategies, hybrid frameworks that incorporate PINNs into adaptive controllers have established superior dynamic performance compared to classical PI control [2,5,34], while system identification tasks exploit PINNs’ ability to replicate inverter behavior for real-time electromagnetic transient simulation [21,34]. Furthermore, fault detection methods that integrate data and physical constraints demonstrate improved sensitivity and robustness in anomaly identification [4,19,20]. These applications validate PINNs’ effectiveness and adaptability in various real-time and predictive tasks critical to next-generation smart inverters.

4.2.1. Parameter Estimation

By embedding physical laws into neural network architectures, Physics-Informed Machine Learning (PIML) overcomes key limitations of traditional data-driven models, including the need for large labeled datasets, poor extrapolation to unseen conditions, high computational cost, and limited physical interpretability [34,35].

Recent studies emphasize the effectiveness of PINNs in estimating critical parameters such as resistance, inductance, capacitance, damping, and inertia. For instance, ref. [13] applied a standard PINN to a three-phase full-bridge inverter for estimating DC-link capacitance and AC-side inductance. Their model, trained on only 360 samples per phase and without additional sensors, achieved maximum errors of $5.2\%$ and $14.7\%$, respectively. Furthermore, ref. [36] discusses how PINNs solve ordinary differential equations related to electrical equipment in microgrids, enabling dynamic time-domain predictions and the estimation of unknown parameters. The method has been validated through modeling and verification in real-time digital simulation systems, showcasing its effectiveness and potential for broader applications in microgrid scenarios where traditional numerical methods may struggle.

In the same direction, ref. [32] shows that PINNs are capable of handling strong nonlinearities and perform well in systems with standard or fast dynamics. However, their computational complexity, slow execution time, and significant accuracy issues with slow dynamics and larger systems limit their practical applicability for real-time power grid parameter estimation compared to more efficient methods like Sparse Identification of Nonlinear Dynamics (SINDy).

Similarly, ref. [37] presents parameter estimation using PINNs in a buck converter. The performance was analyzed through simulation, and the training loss landscape was examined. The results show that parameters such as inductance, capacitance, and load resistance are accurately estimated with low variation and high accuracy across different operating conditions. In simulation, these parameters (L, C, R, $R_C$) achieved high accuracy, with median errors below $3\%$ and stable estimations with standard deviations below $2\%$. In addition, parameters such as the diode forward voltage ($V_F$), inductor resistance ($R_L$), and MOSFET on-state resistance ($R_{dson}$) could not be reliably estimated under the given problem formulation. These parameters exhibited lower accuracy, with a maximum error of $148\%$, as well as greater variation, with a maximum standard deviation of $65\%$ in simulations.

The accuracy of parameter estimation in PINNs is further influenced by various factors, including the sensitivity of the parameters to the system equations, the amount of training data across several operating conditions, and the level of measurement noise. Additionally, coupling between parameters within the model equations can obscure their individual effects, making simultaneous estimation more difficult. Overall, parameters that strongly govern the system’s energy exchange and appear linearly in the state equations are inherently easier to estimate, while weakly coupled or nonlinear parameters require more advanced formulations, such as multi-frequency excitation or hybrid PINN data-driven methods, to improve accuracy and identifiability.

To address these challenges, ref. [16] proposed the PINC architecture that learns both latent system states and physical parameters. While this method improves convergence and reduces training complexity, it can slightly compromise accuracy for parameters with minimal dynamic influence, such as small resistances.

Advanced PINN variants continue to improve estimation robustness. The paper [22] introduced a BPINN with transfer learning to estimate dynamic system parameters. This approach achieved lower errors compared to SINDy, and also quantified uncertainty via confidence intervals. Similarly, ref. [38] used a standard PINN to estimate system inertia in inverter-based distributed generation, validated in MATLAB/Simulink simulations.

Comparative studies reinforce the superiority of PINNs. Ref. [21] show their PINN-based model achieved relative errors below $1\%$ when estimating damping and inertia, outperforming Unscented Kalman Filter (UKF) approaches. Meanwhile, ref. [39] demonstrates a hybrid PINN with pretraining and a distance function to estimate converter parameters, achieving an average accuracy of $98.76\%$ even under grid disturbances.

Non-invasive parameter estimation, which avoids the need for hardware modification or signal injection, is a major advantage of PINNs. Ref. [33] demonstrated the use of ANNs to estimate grid impedance, filter elements, and control parameters based solely on measurable voltage and current signals.

Recent works also emphasize real-time deployment. Ref. [40] estimated inverter system parameters using instantaneous voltage and frequency measurements from reduced-order IEEE test systems. Ref. [3] developed a hybrid PINN incorporating domain equations for modeling grid-forming inverters, achieving extremely low impedance estimation errors ($8.6\times {10}^{-47}$), while maintaining high simulation fidelity and scalability.

Estimating parameters accurately and reliably remains a challenge. In order to overcome this challenge, the paper [41] suggests an improved PINN, called the Uniform Physics-Informed Neural Network (UPINN). The outcome of this paper emphasizes that the performance of UPINN surpassed other neural network approaches with respect to accuracy and reliability.

In summary, PINNs offer a physics-consistent and data-efficient solution for parameter estimation in power electronic systems. They demonstrate superior generalization and interpretability compared to conventional methods, especially when enhanced through hybrid architectures, transfer learning, or Bayesian inference. Parameters like inductance and capacitance are more reliably estimated due to their stronger influence on system dynamics, while resistances and thermal parameters remain challenging. Despite issues such as sensitivity to noise, low-impact parameter modeling, and real-time scalability, PINNs continue to evolve into a powerful tool for accurate, non-invasive, and robust estimation in inverter-based power systems.

4.2.2. State Estimation

State estimation refers to the process of deducing the internal, time-varying states of inverters or power grids based on limited or indirect measurements. Within the framework of PINNs, this task is naturally formulated as solving the governing differential equations of the system, with the hidden or latent state trajectories being inferred as part of the solution.

Several recent works validate the potential of PINNs for this purpose in both grid-level and inverter-level systems. The paper [15] presented a graph-based PINN architecture (GNN-PINN) tailored for state estimation in power grids. By explicitly incorporating the grid’s topological structure into the learning process, the model accurately predicted voltage phasors across IEEE 14-bus and 57-bus systems, achieving over $20\%$ lower mean squared error (MSE) compared to conventional estimators. This highlights how physical laws and structural priors can be effectively leveraged in complex, interconnected systems. Moreover, ref. [42] highlights the application of PINNs in estimating system inertia in inverter-dominated distribution grids. It presents a method for real-time inertia estimation, addressing challenges posed by virtual inertia from inverter-coupled resources (ICRs). The proposed approach utilizes a modified loss function with adaptive weighting in a recurrent PINN, demonstrating its effectiveness on a 14-bus medium-voltage distribution grid model with nonlinear characteristics.

Focusing on inverter dynamics, ref. [1] applied PINNs to a detailed grid-forming inverter model with 17 internal states. Without any labeled state trajectories and using only initial and boundary condition data, their method successfully reconstructed the full internal state vector. This was made possible through a carefully formulated composite loss function and adaptive network architecture. Despite the absence of supervised data, the model was able to recover the latent dynamics, although training required large neural networks and was sensitive to system stiffness and multi-scale behavior.

Similarly, ref. [21] proposed a hybrid framework where measurement data were combined with physical constraints to estimate both parameters and states instantaneously. Applied to reduced-order IEEE grid models, this technique achieved precise state forecasting from sparse voltage and frequency data. While the results are promising, they were validated only in simulation and lack real-time deployment.

The authors in [43] emphasize the use of PINNs for accelerating power system state estimation, highlighting their integration with physical laws for improved accuracy and efficiency. The results show notable improvements, including an $11\%$ increase in accuracy, a $30\%$ faster convergence rate, and a $75\%$ reduction in standard deviation.

Figure 3 shows the general architecture of PINNs applied to state estimation. Given the state of the system at an initial time $t_0$ and a target prediction time $t_0+h$, the PINN uses governing equations to infer the trajectory of the state $x\left(t\right)$. This method allows simultaneous compliance with measurement data and physical constraints, which is particularly beneficial when reconstructing hidden states in inverter and grid models with sparse measurements.

Furthermore, the reviewed report emphasizes the potential of PINNs in handling unmeasured states in grid-connected inverters (GCIs), particularly in nonlinear dynamics and fault scenarios. The report presents a case where PINNs were able to reconstruct both observable and hidden states from limited voltage/current data by embedding Kirchhoff’s laws and differential models into the learning pipeline. This aligns with the larger goal of enhancing observability in GCIs, especially when sensor data are scarce or noisy.

Although PINNs demonstrate promise in simulation for power system state estimation, the transition to hardware demonstrations is hindered by computational difficulties for large systems, the practical challenges of acquiring high-quality and comprehensive real-world data, and the complexities of validating performance under dynamic and uncertain operational situations essential in GCISs.

Overall, these studies demonstrate that PINNs offer a promising pathway for reconstructing hidden dynamic states in power systems and inverter dynamics. The main challenges include handling high-dimensional, stiff models, achieving stable convergence, and scaling solutions for real-time or embedded applications. Nevertheless, the ability to infer complete state trajectories without explicit supervision sets PINNs apart, making them highly attractive for future smart, inverter-based power systems.

4.2.3. Control Strategies

Advanced control of power converters and GCIs is gradually shifting toward learning-based approaches, driven by the need for more intelligent and adaptable systems. Among these, PINNs have emerged as a compelling hybrid solution, combining model-based and data-driven methods to deliver robust and adaptive control.

In [2], a PINN-based control framework was introduced for grid-forming inverters operating within microgrids. This method starts by integrating physics-aware learning with adaptive control laws, enabling the controller to maintain effective performance even in the presence of load disturbances. By embedding physical equations into the learning process, the PINN module ensures that the system dynamics are faithfully represented while adjusting to real-time variations. This results in improved noise robustness and resilience to unmodeled dynamics compared to traditional control approaches.

In [16], the use of PINNs within a nonlinear model predictive control (NMPC) framework was explored, specifically for tracking control in multi-link robotic manipulators. The PINNs were employed as replacements for traditional time-integration schemes, providing a faster yet sufficiently accurate representation of nonlinear system dynamics. This significantly reduced computational time and enabled real-time control of systems with fast dynamics. However, the method is not without limitations. Accuracy heavily relies on the quality of training data, and tuning the network for highly nonlinear or time-varying systems remains challenging, often requiring extensive hyperparameter optimization.

Similarly, ref. [44] suggested a control method for uncertain networked microgrids. Their approach integrates PINNs with Lyapunov-based stability certification, ensuring that the learned control laws align with both the physical dynamics and stability constraints of the microgrid. This method demonstrated strong robustness against parameter uncertainties and topology changes while maintaining transient stability margins, making it highly relevant for inverter-dominated and weak-grid scenarios.

Extending PINNs into the power electronics domain, ref. [39] applied them to GCI control by embedding governing physical equations into the neural network’s training process. Their results verified that PINNs reached a prediction accuracy of $98.76\%$ using only 3000 datapoints, significantly reducing computational effort compared to conventional neural networks. The method proved robust under various grid disturbances and was confirmed experimentally. Nevertheless, limitations arose in estimating boundary conditions, particularly with reactive power compliance, which introduced complexities that affected dynamic stability. Furthermore, selecting suitable loss function weights proved critical for effective harmonic suppression and transient control, underscoring the sensitivity of PINN training to hyperparameter tuning.

The study in [45] expanded on the potential of PIML in inverter control, emphasizing the role of physical constraints in enhancing model robustness and generalization. By incorporating physical laws into the learning process, the PIML-based controller achieved improved tracking performance and superior stability margins, especially in grid-connected scenarios where operating conditions are highly variable. However, limitations persisted in optimizing the trade-off between physical fidelity and computational efficiency through carefully designed loss functions. Moreover, ensuring the real-time adaptability of such models in dynamic environments remains an open area for research, specifically regarding adaptive weight balancing and uncertainty quantification.

From a theoretical perspective, ref. [31] introduced the concept of PINC, a generalized extension of PINNs for closed-loop control systems. PINC explicitly incorporates control inputs into the network architecture, enabling simulation of control-dependent dynamics over extended time horizons. Although focused on classical nonlinear systems, this work lays the foundation for integrating PINNs with advanced control frameworks such as model predictive control (MPC) and reinforcement learning (RL), particularly in highly nonlinear and uncertain environments.

These advances highlight the growing role of PINNs in control applications, providing reduced dependence on exhaustive system identification, compatibility with existing paradigms such as MPC and RL, and enhanced robustness under uncertainty. As inverter-based systems become more complex and interact with variable renewable sources, PINN-based control emerges as a viable solution for adaptive, physics-consistent smart controllers.

Embedded deployment of PINN-based controllers is increasingly feasible. Lightweight variants, such as pruned, quantized, or distilled networks, reduce computational load, while hardware acceleration using FPGAs or edge AI chips enables real-time inference. Hybrid approaches, combining offline training with online fine-tuning, further mitigate runtime demands. Ongoing work on efficient architectures and embedded ML frameworks continues to improve deployability, making real-time embedded PINN control a realistic near-term goal.

4.2.4. Fault Detection and Diagnosis

Fault detection and diagnosis in GCIs are important for ensuring system reliability, especially in dynamic environments where components such as capacitors and inductors may degrade over time due to installation variability and temperature fluctuations. PINNs have shown significant promise in this domain by leveraging system physics to infer hidden states and estimate drifting parameters, which are critical for early fault detection and predictive maintenance.

For example, the study in [3] investigates the use of PINNs to reconstruct the impedance of voltage source converters (VSCs). Their model required only sparse data to accurately learn the converter’s impedance, thus facilitating fast stability assessments without exhaustive measurement campaigns. This efficiency in training and evaluation has direct implications for grid stability assessment in converter-dense networks. The ability to detect unexpected impedance changes from limited measurements allows the identification of incipient converter faults. Together, these studies illustrate that PINNs can support fault-related modeling by combining physical insight with data-driven estimation.

Beyond PINNs, hybrid artificial intelligence methods are gaining traction for real-time fault detection. In [19], several deep learning models, such as CNN-RNN, CNN-GRU, and CNN-LSTM, are assessed for fault prediction in smart grids. The CNN-GRU model emerges as the most effective in terms of prediction accuracy and mean error. While these approaches offer high fault sensitivity and improved system resilience, they require large, high-quality datasets and struggle to generalize to unseen or evolving fault scenarios.

One of the key motivations behind the use of PINNs in inverter-dominated power systems is their potential to enhance computational and operational efficiency. Traditional electromagnetic transient (EMT) simulations using tools like PSCAD and EMTP are computationally intensive, particularly when simulating large or high-order systems over finite time steps. To address this, [1] applies enhanced physics-informed neural networks (PINNs) to analyze the transient dynamics of synchronous generators, demonstrating their effectiveness in modeling complex power system behaviors. Their work shows that PINNs can maintain high modeling accuracy while drastically reducing computation time, supporting fast, high-fidelity simulations for stability analysis.

The paper [30] advanced this concept with their “AI-Inverter,” which uses a balanced-loss PINN for EMT simulation of grid-forming inverters. Their model delivered performance comparable to traditional EMT tools, such as PSCAD, but with over a 100× speedup. This demonstrates the feasibility of using PINNs to partially replace traditional simulation pipelines, enabling rapid design iterations and real-time simulation capabilities.

In a more hardware-oriented context, ref. [20] introduces a fault detection method for Neutral Point Clamped (NPC) converters, which avoids direct gate feedback or voltage measurement by relying solely on clamp-diode and load current data. This method validates accurate and fast detection of short- and open-circuit faults, although it introduces cost implications due to the added sensing requirements, such as Rogowski coils.

To address sensor-level problems, ref. [16] suggests a fault-tolerant method that compensates for current sensor offset faults using average current reconstruction. Experimental outcomes demonstrate that this method improves fault diagnosis and maintains inverter stability under such faults, though it remains limited to predefined fault types and struggles with complex multi-fault scenarios.

A decentralized control framework is presented in [5] for inverter-based resources (IBRs), combining parameter estimation with adaptive control to support real-time fault prediction and power restructuring. While this framework excels under fault conditions, its dependence on real-time optimization introduces latency risks, and the stability of decentralized strategies under line constraints warrants further investigation.

Focusing specifically on high-impedance faults (HIFs), ref. [40] presents a Physics-Informed Convolutional Autoencoder (PICAE) that leverages voltage-current trajectory features for unsupervised fault detection in distribution grids. The model achieves high accuracy even in noisy environments and does not require labeled fault data. Despite its robustness, the method relies on adequate phasor measurement unit (PMU) coverage and periodic retraining to accommodate system changes.

Likewise, ref. [45] recommends a machine learning technique to detect interturn short-circuit faults (ISCFs) in induction motors controlled via model predictive control (MPC). By leveraging inverter switching statistics for learning, the model achieves ultra-fast detection in 0.1 s with an AUROC of $0.9950$. However, the model’s sensitivity diminishes at higher motor speeds, highlighting the trade-offs between speed, accuracy, and operating range.

While many of the approaches above leverage data-driven or physics-regularized neural networks, few studies explicitly apply PINNs to inverter fault detection. As noted in [4], the FaultNet-ML model integrates ANNs and CNNs for fault detection in microgrid inverters but does not incorporate physical equations. Similarly, the physics-regularized model proposed by [40] for high-impedance fault (HIF) detection in distribution lines shares theoretical similarities with PINNs, yet it is not directly applied to inverter fault diagnosis.

Despite the strengths of PINNs, they are still rarely applied for fault detection in GCISs. The main challenge lies in the nature of inverter faults, which often manifest as switching irregularities, discontinuities, or rapid waveform distortions that violate the smooth differential equation assumptions underlying standard PINNs. Consequently, direct application is difficult, as PINNs are better suited for modeling continuous dynamics rather than discrete fault events. Moreover, sensitivity to network design and high computational burden further hinder their real-time deployment in embedded fault detection.

Recent studies in rotating machinery have shown that novel inverse PINNs can effectively address limitations such as sample imbalance and limited fault data. For instance, ref. [46] proposed an inverse PINN that embeds bearing dynamics into a neural network, with boundary and truth losses incorporated to align with frequency-domain data and accelerate convergence. When combined with a digital-twin-based data generation approach, this method produced synthetic fault signals that significantly improved detection under imbalanced operating conditions.

Building on this idea, inverse or hybrid PINN frameworks could be adapted for fault detection in GCISs, where discontinuities, infrequent fault events, and class imbalance are major challenges. In this context, inverse PINNs could estimate difficult-to-measure or hidden system parameters by embedding inverter dynamics directly into the training process, while hybrid PINNs could combine physics-based modeling with data-driven enhancements such as dedicated fault classifiers or digital-twin augmentation. These adaptations offer a promising path to improving the robustness and reliability of fault detection in GCISs. Future research should focus on extending PINNs to handle non-smooth events, potentially by embedding latent anomaly states or adopting hybrid architectures that integrate physics-based modeling with irregularity detection logic.

4.2.5. System Identification

System identification is used to construct accurate models of inverters or power grids from input–output data, enabling simulation, control, and analysis without requiring full system specifications. PINNs support this task by learning system behavior constrained by its underlying differential equations. Instead of purely fitting input–output patterns like black-box models, PINNs enforce the known physics of the system, making them well suited for identifying nonlinear and time-varying dynamics in power electronic systems.

This paper [47] contributes to the field by offering a more accurate and robust impedance modeling method for GCIs, especially those with unknown internal characteristics. By combining neural networks with physical information and measured data, it provides a valuable tool for analyzing and ensuring the stability of modern power grids, which are increasingly reliant on inverter-based resources.

The authors in [22] utilize Bayesian Physics-Informed Neural Networks, which combine the advantages of Physics-Informed Neural Networks for inverse problem applicability with Bayesian approaches for uncertainty quantification, to estimate power system dynamics under uncertainty from inverter-based resources. The paper explores methods to accelerate BPINN training, including pretraining and transfer learning, which can reduce training time by up to 80% while achieving significantly lower errors compared to conventional system identification methods like SINDy and standard PINNs.

The paper [48] discusses the use of PINNs for identifying inverter nonlinearity compensation values, thereby enhancing system identification in GCIs. This method reduces identification time and complexity, effectively predicting compensation voltages across various working conditions using minimal experimental data.

The authors in [49] discuss PINNs for dynamical system identification and estimation, leveraging physics-based principles to enhance machine learning, and demonstrate their efficiency in state and parameter estimation with uncertainty quantification. They also state that PINNs provide more accurate and generalizable system identification compared to traditional methods.

In another study, ref. [3] focused on impedance modeling for voltage source converters (VSCs) in high-voltage direct current (HVDC) systems. They trained a PINN to learn the mapping between converter states and the impedance seen by the surrounding grid. The resulting model enabled fast stability evaluation of the grid under fluctuating load or control conditions, supporting real-time impedance tracking without extensive offline characterization.

These comparisons show that PINN-based methods often outperform purely data-driven or traditional approaches in simulation speed, parameter accuracy, and robustness. For example, ref. [30] reports that their PINN solver surpasses legacy EMT programs in speed while maintaining comparable fidelity. Ref. [22] finds that BPINNs significantly outperform sparse identification techniques under noisy conditions. In control tasks, ref. [2] demonstrates that embedding physics into the controller enables better handling of disturbances compared to model-free RL. A summary of key studies and their comparative findings is shown in

Table 2. Comparisons of PINN-based methods in renewable energy systems.

Ref.	Application	Task	Efficiency	Data Required	Validation	Limitations
[50]	Power Systems (Nonlinear Dynamics)	System Identification	Captured nonlinear dynamics; good qualitative match	Small time-domain datasets	Simulation	No hardware validation; model simplifications
[21]	Power System Dynamics	System Identification	Accurate dynamic reconstruction	Voltage/angle data	Simulation	Sensitive to complexity of equations
[30]	Grid-Connected Inverter (EMT)	System Identification	$>100$× faster than PSCAD	Moderate	Simulation	Needs real-world validation
[22]	Inverter-Dominated Grids	System Identification	Orders-of-magnitude error reduction vs. SINDy	Synthetic	IEEE Test Cases	Sensitive to priors; high cost
[13]	3-Phase Inverter (LC)	Parameter Estimation	$5.2\%$ (C), $14.7\%$ (L)	360 samples/phase	Simulation and Hardware	ADC quantization/sync issues
[10]	Buck Converter	Parameter Estimation	Median errors <5%	Moderate	Simulation	Accuracy-speed trade-off
[15]	Power Grid	State Estimation	$20\%$ lower MSE vs. baseline	Bus-wise data	IEEE Test Cases	Not inverter-level states
[1]	High-Order Inverter	State Estimation	All states recovered; no labels	Initial/ boundary vals	Simulation	Ill-conditioning in stiff systems
[3]	HVDC Back-to-Back VSC	System Identification/ State Estimation	Accurate grid stability estimation	Simulation data	Simulation	No real-world validation
[37]	Power System Operation	Control Support	Improved convergence	Partial + boundary	Simulation	Not real-time ready
[2]	Buck Inverter	Control	Settling time 1.5–2.1 ms; < 1.2 V overshoot	Live measurements	Hardware	Needs manual tuning
[31]	General Nonlinear	Control	Long-horizon accuracy	Low	Standard simulation models	Not yet applied to switching systems
[40]	High-Impedance Faults	Fault Detection	Unlabeled fault detection	Unlabeled data	Simulation	Focused on distribution lines

.

Overall, PINN-based methods for GCIs show great promise across diverse tasks. Ref. [13] consistently achieves high accuracy with limited data by enforcing physics. Experimental results validate their practical feasibility. Key challenges include training complexity, especially for high-order models, sensitivity to noise or sampling, and the need for careful network design. As illustrated in Table 2, many recent studies advance the state of the art, ranging from concrete hardware demonstrations to large-grid identification. However, common open issues remain (e.g., estimating multiple parameters simultaneously, embedding discontinuities, scaling to large networks). Future work will likely combine PINNs with model reduction, Bayesian inference, or control-theoretic guarantees to further improve their applicability to inverter systems.

5. Limitations

Despite their potential, PINNs face numerous challenges in practical inverter applications. First, training PINNs can be sensitive to hyperparameters and computationally expensive. Balancing data-fitting and physics-based loss terms often requires manual tuning, and convergence can be slow for stiff or high-frequency dynamics common in power electronics. Researchers address this by using adaptive weighting schemes or gradient-enhanced PINN variants to accelerate training [1].

Second, traditional PINNs do not quantify uncertainty in their estimates. In grid applications where safety is critical, this is a drawback. Bayesian PINNs (BPINNs) have been proposed for system identification under uncertainty [22]. The study [22] demonstrates that a BPINN yields orders-of-magnitude lower error in frequency dynamics estimation compared to PINN or SINDy when inverter-based resources dominate the grid. Such probabilistic PINNs can provide confidence bounds on estimations, representing an important direction for future research.

Finally, data availability and scalability remain concerns. Large-scale power systems involve numerous dynamics, and training a single PINN to capture all of them may be impractical. Transfer learning and domain decomposition offer possible solutions: a PINN trained on one operating condition or system can be fine-tuned for another, as suggested by pretraining methods [22]. Furthermore, hybrid digital twin frameworks could pair a PINN with real-time measurements to continuously refine the model, mitigating model mismatch over time [13].

To standardize future evaluations and facilitate direct comparison of PINN methods in GCISs, it is advisable to adopt established benchmark systems such as IEEE test cases (e.g., 14-bus, 57-bus) and CIGRE models for microgrids. Furthermore, open-source EMT simulation datasets from tools like PSCAD/EMTDC or OPAL-RT, alongside public datasets from NASA or NREL adapted for inverters, and standardized inverter topologies with published parameters, would provide consistent and accessible benchmarks for comparative research. Addressing these challenges through improved training methods, uncertainty quantification, scalable architectures, and standardized benchmarks will be crucial for advancing the practical deployment of PINNs in real-world GCISs.

6. Conclusions and Future Works

PINNs offer a compelling fusion of physics-based modeling and machine learning, making them well suited for modern inverter-dominated power systems. This review confirms that PINNs can significantly improve system efficiency by accelerating inverter simulations and control design, enhancing fault detection through precise parameter estimation, and supporting robust control strategies in the presence of system uncertainties. Recent studies highlight substantial improvements in accuracy and computational speed, often by orders of magnitude compared to conventional methods.

The advances in PINNs underscore their potential to improve the modeling, monitoring, and control of GCISs. Despite these advantages, several limitations remain in their application to real-world systems. Many studies rely on simplified models, which restrict the ability to capture complex dynamics. Sensitivity to measurement noise, training stability, and the absence of standardized benchmarks further challenge widespread implementation.

In the near term, research should focus on validating PINNs on hardware-in-the-loop testbeds, prioritizing stabilizing training approaches, and refining hybrid data–physics loss formulations. In the longer term, key challenges include achieving real-time deployment in complex GCISs, embedding PINNs into large-scale system-level optimization and control frameworks, and developing generalizable models across different converter topologies. Addressing these challenges will be crucial to realizing the full potential of PINNs in next-generation GCISs.