A Comparative Study of Electricity Sales Forecasting Models Based on Different Feature Decomposition Methods
Abstract
1. Introduction
- We design 15 forecasting models by combining three feature decomposition methods (X13, DWT, and EMD) with three predictive models (ADL, SARIMAX, and LSTM), enabling comparisons across both decomposition techniques and model types.
- Without using decomposition, we incorporate abnormal temperature and holiday effects as exogenous variables into the ADL and SARIMAX models, expanding the set of direct forecasting models and enhancing comparison scope.
- In alignment with the requirement from the State Grid Corporation of China that annual forecasting error must not exceed 2%, we propose a model selection criterion based on 12 rolling monthly forecasts per year, each satisfying the ≤2% error threshold. This provides a clearer and more actionable standard for future model selection in practice.
2. Literature Review
3. Materials and Methods
3.1. Data Description and Preprocessing
3.2. Feature Decomposition Methods
- Identify all local extreme points in the time series s(t).
- Based on the local extreme points, define the upper and lower envelopes U(t) and L(t) using cubic spline interpolation.
- Compute the mean envelope m(t) = [U(t) + L(t)]/2.
- Subtract m(t) from the original signal to obtain a new sequence .
- If meets the two conditions of IMF, the resulting sequence is considered the first IMF, which represents the highest-frequency component . Then is updated by the residual R(t) = s(t) − .
- The original signal X(t) is decomposed into several IMFs and a trend component.
3.3. Prediction Models
3.4. Forecasting Requirements and Evaluation Criteria
4. Results and Discussion
4.1. Comparison of Electricity Sales Forecasting Results Using ADL Model with Different Feature Decomposition Methods
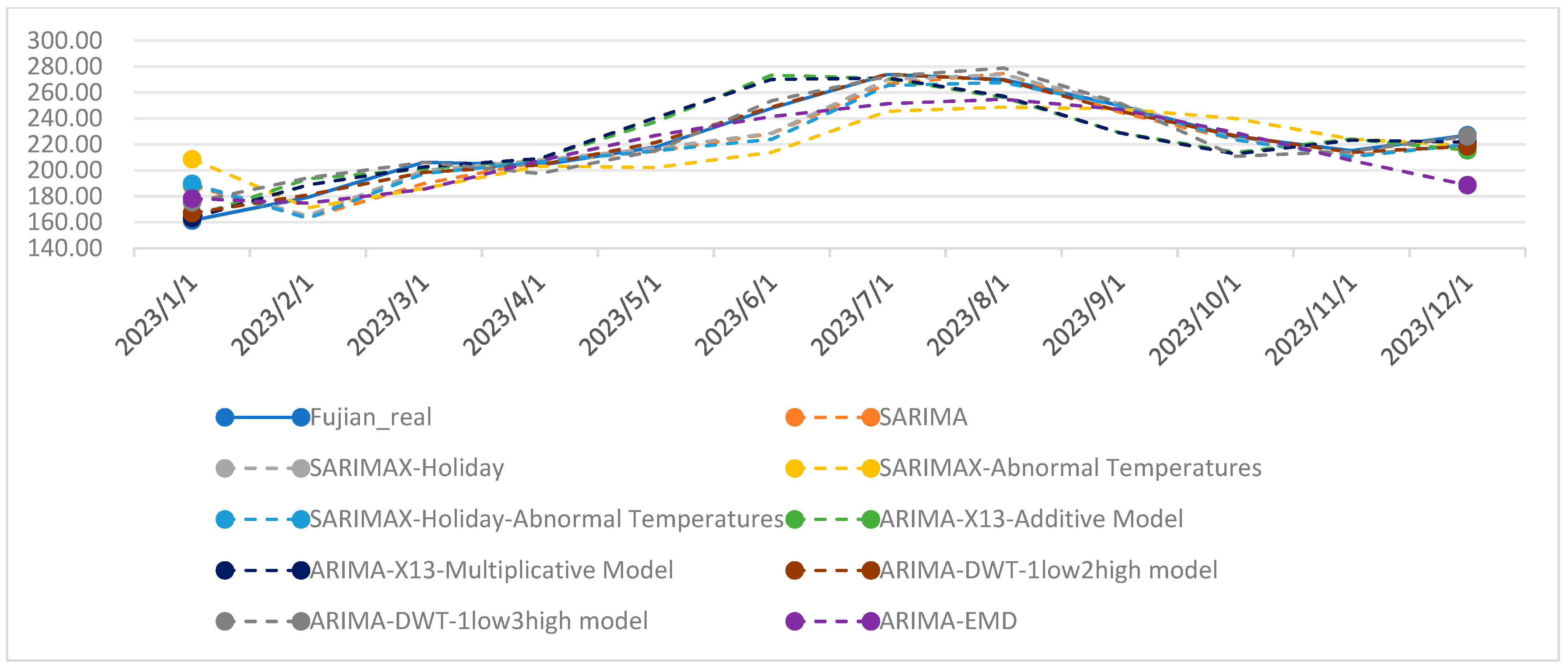
4.2. Comparison of Electricity Sales Forecasting Results Using SARIMAX Model with Different Feature Decomposition Methods
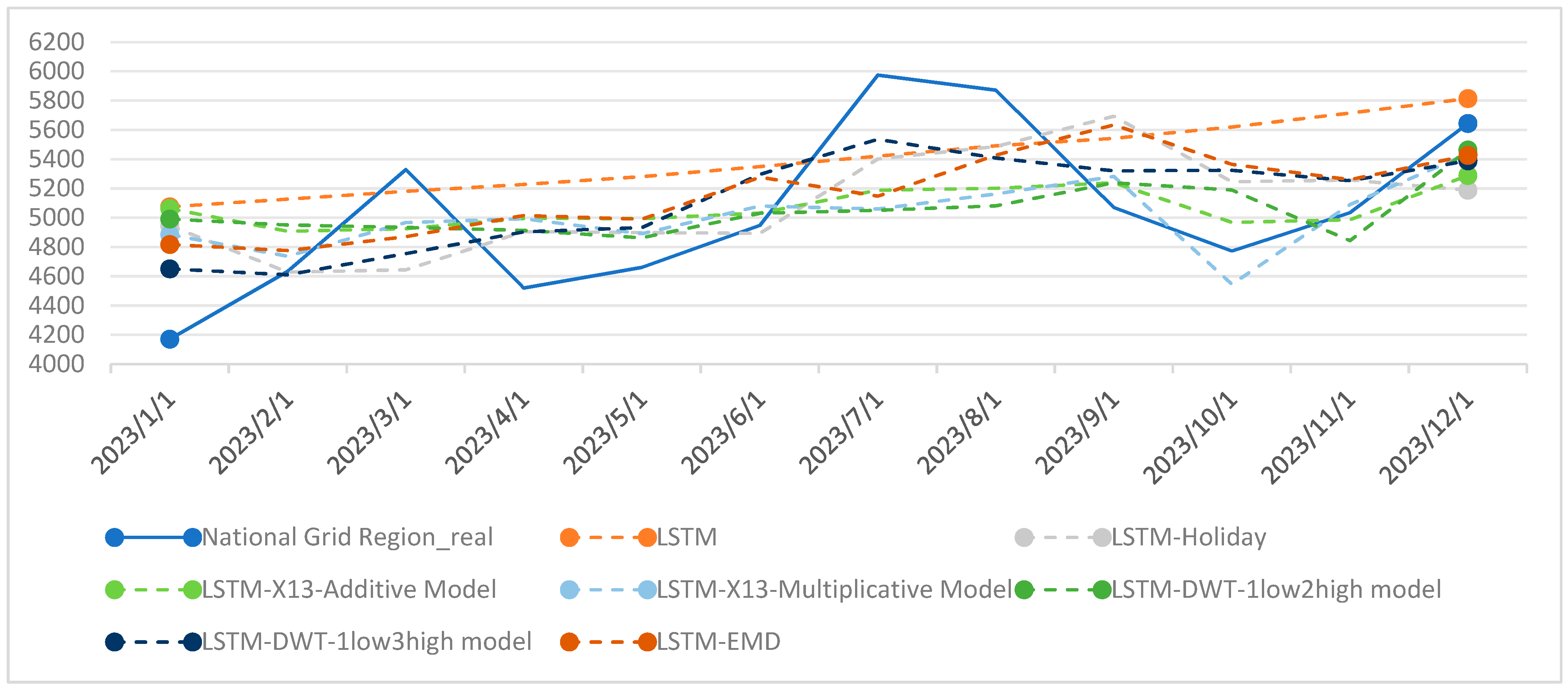
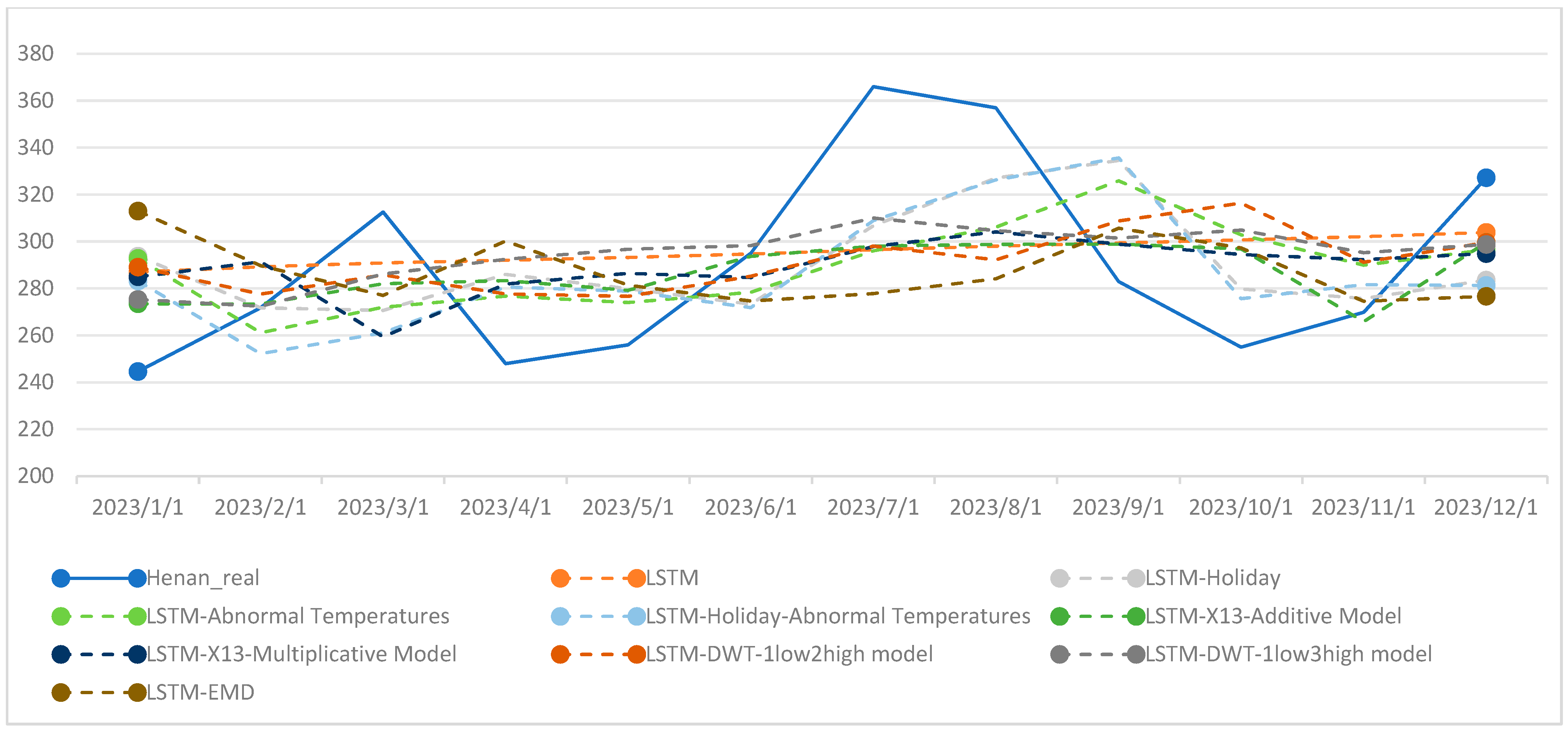
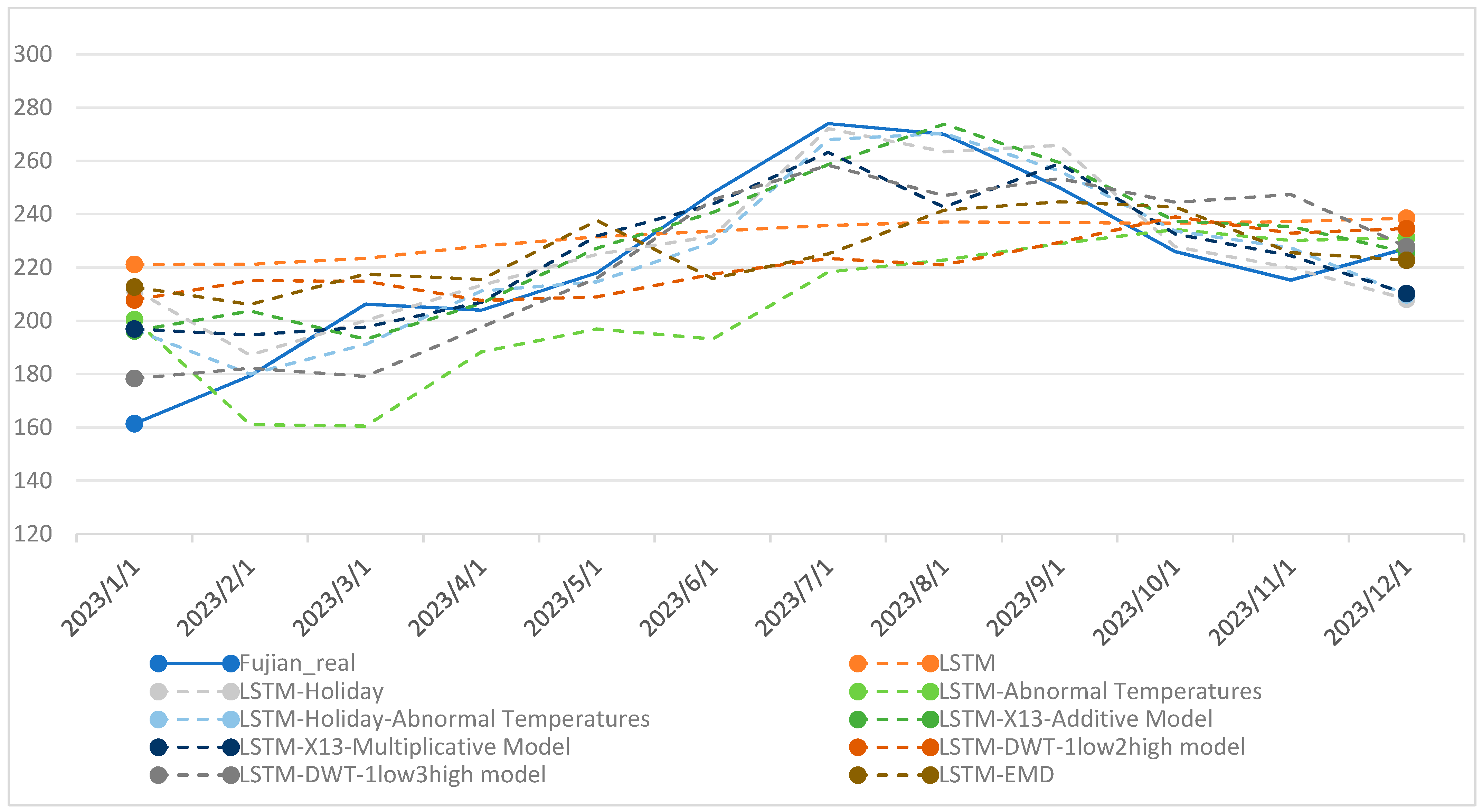
4.3. Comparison of Electricity Sales Forecasting Results Using LSTM Model with Different Feature Decomposition Methods
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Full Term | Definition |
| X13 | X-13-ARIMA-SEATS | Seasonal adjustment method combining X-11 and SEATS with TRAMO-style preprocessing; decomposes a series into Trend, Cycle, Seasonal, and Irregular components. |
| X-11 | X-11 Seasonal Adjustment | Classic seasonal adjustment filter; a core module within X13. |
| SEATS | Signal Extraction in ARIMA Time Series | ARIMA-based signal extraction seasonal adjustment method used within X13. |
| TRAMO/TRAMOS | Time Series Regression with ARIMA Noise, Missing Observations and Outliers | Pre-adjustment approach (regression with ARIMA noise) for outliers and missing values, used by X13. |
| RegARIMA | Regression with ARIMA Errors | Regression model with ARIMA error structure used in X13 preprocessing to remove deterministic effects. |
| EMD | Empirical Mode Decomposition | Adaptive decomposition of a signal into several Intrinsic Mode Functions (IMFs) and a residual trend. |
| IMF/IMFs | Intrinsic Mode Function(s) | Oscillatory components produced by EMD that capture different characteristic scales. |
| DWT | Discrete Wavelet Transform | Multi-scale wavelet decomposition into low-frequency (trend) and high-frequency (detail/noise) components. |
| ADL | Autoregressive Distributed Lag | Time-series regression with lags of the dependent variable and current/lagged exogenous variables. |
| ARIMA | Autoregressive Integrated Moving Average | Classical time-series model combining AR, differencing (I), and MA components. |
| SARIMA | Seasonal ARIMA | ARIMA with seasonal terms; seasonal parameters are P (SAR), D (seasonal differencing), Q (SMA), and S (seasonal period). |
| SARIMAX | Seasonal ARIMA with eXogenous Regressors | SARIMA model extended to include exogenous variables X. |
| LSTM | Long Short-Term Memory | Recurrent neural network architecture designed to capture long-term temporal dependencies. |
| RNN | Recurrent Neural Network | Neural network class for sequence modeling with recurrent connections. |
| ReLU | Rectified Linear Unit | Activation function max(0, x) commonly used to mitigate vanishing gradients. |
| TC | Trend–Cycle | Combined trend and cycle component (often denoted TC in X13 outputs). |
| T/C/S/I | Trend/Cycle/Seasonal/Irregular | Four components of seasonal adjustment decomposition. |
| SI | Seasonal differencing order | Order of seasonal differencing in SARIMA/SARIMAX. |
| NOAA | National Oceanic and Atmospheric Administration | US federal agency providing meteorological data (temperature series source in the paper). |
| GM(1,1) | Grey Model (1,1) | Univariate first-order grey forecasting model. |
| RBF (NN) | Radial Basis Function Neural Network | Neural network using radial basis functions as activation units. |
| BP (NN) | Backpropagation Neural Network | Feedforward neural network trained via backpropagation. |
| LSSVM | Least Squares Support Vector Machine | LS-SVM variant using least squares cost for regression/classification. |
| SD | Standard Deviation (EMD stopping criterion) | Stopping criterion in EMD sifting (e.g., SD ≤ 0.2–0.3). |
| HW | Holt–Winters | Seasonal exponential smoothing model (mentioned as a comparative method). |
References
- Gao, L.; Liang, S.; Chen, S.; Li, S. Short-term load forecasting method for distribution networks based on multi-level load clustering and decoupling mechanisms. Power Syst. Its Autom. J. 2021, 33, e0300229. [Google Scholar]
- Zhuang, J.; Li, K.; Liu, Z.; Cheng, X. Research on monthly electricity sales forecasting based on seasonal adjustment and regression analysis. Econ. Res. Guide 2018, 19, 181–186. [Google Scholar]
- Zhuang, J.; Li, K.; Liu, Z.; Liu, R. Study of monthly electricity sales forecasting based on seasonal adjustment and multi-factor correction method. In Proceedings of the 30th Chinese Control and Decision Conference, Shenyang, China, 9–11 June 2018; pp. 1–6. [Google Scholar]
- Liu, J.; Zhao, J.; Chen, Y.; Fang, X.; Liu, Y.; Wang, S.; Chen, Y.; Ou, H. Correction method for electricity sales forecasting results considering the impact of the Spring Festival. In 2018 Power Industry Informationization Annual Conference Proceedings; China Electric Power Engineering Society: Beijing, China, 2018; pp. 424–425. [Google Scholar]
- Lang, J.; Jin, J.; Li, R.; Wang, Y.; Shen, B. Analysis of the impact of special events on monthly electricity sales and its forecasting. Power Big Data 2018, 21, 43–48. [Google Scholar]
- Qi, Z. Research on electricity sales forecasting based on LSTM deep network. China New Technol. New Prod. 2023, 23, 133–135. [Google Scholar] [CrossRef]
- Klyuev, R.V.; Morgoev, I.D.; Morgoeva, A.D.; Gavrina, O.A.; Martyushev, N.V.; Efremenkov, E.A.; Mengxu, Q. Methods of forecasting electric energy consumption: A literature review. Energies 2022, 15, 8919. [Google Scholar] [CrossRef]
- Salkuti, S.R. Short-term electrical load forecasting using radial basis function neural networks considering weather factors. Electr. Eng. 2018, 100, 1985–1995. [Google Scholar] [CrossRef]
- Deng, F.; Si, J.; Deng, Z.; Yu, B.; Li, H.; Jin, M. QPSO-LSTM Based Electricity Sales Forecasting Model. In Proceedings of the 2024 6th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 March 2024; pp. 1347–1352. [Google Scholar] [CrossRef]
- Gnatyuk, V.I.; Kivchun, O.R.; Morozov, D.G. Electric consumption predictions of socio-economic systems based on the ranked values. Mar. Intellect. Technol. 2020, 4, 107–111. [Google Scholar]
- Li, W.; Li, X.; Fan, P.; Zhang, H. Regional electricity sales forecasting based on multi-head self-attention mechanism and LSTM network. Power Demand Side Manag. 2025, 27, 67–73. [Google Scholar]
- Yang, L.; Wu, Y.; Zhang, C.; Liu, C.; Jiang, B.; Zhang, P. Improved least squares support vector machine electricity forecasting algorithm. Power Grid Clean Energy 2017, 33, 71–76. [Google Scholar]
- Sun, W.; Liu, X.; He, Q. Monthly industry electricity sales forecasting based on similar months and Elman neural network. Power Demand Side Manag. 2022, 24, 53–58. [Google Scholar]
- Ma, X.; Sun, C.; Wang, W.; Zhao, R.; Chen, P.; Wu, B. Research on proxy electricity purchase forecasting considering meteorological and special event impacts. Power Inf. Commun. Technol. 2025, 23, 25–32. [Google Scholar] [CrossRef]
- Wei, T.; Tang, K. Classification and monthly electricity forecasting based on BP neural network and regression analysis. Electr. Ind. 2023, 11, 74–78. [Google Scholar]
- Zhang, L.; Ji, T.; Liu, J. Monthly electricity forecasting considering sub-sectors and multiple influencing factors. Guangdong Electr. Power 2023, 36, 30–39. [Google Scholar]
- Yao, L.X.; Liu, X.Q. Monthly load combination forecasting based on wavelet analysis. Power Syst. Technol. 2007, 31, 65–68. [Google Scholar]
- Zhang, T.; Zhu, J. Wavelet regression analysis method in short-term power system load forecasting. J. Harbin Univ. Sci. Technol. 2008, 1, 74–76. [Google Scholar]
- Meng, M.; Niu, D.; Sun, W. Forecasting monthly electric energy consumption using feature extraction. Energies 2011, 4, 1495–1507. [Google Scholar] [CrossRef]
- Fan, J.; Feng, H.; Niu, D. Monthly electricity sales forecasting based on wavelet analysis and GM-ARIMA model. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2015, 42, 101–105. [Google Scholar]
- Asadpour, M.; Pourhaji, N.; Ahmadian, A. Electricity price and load demand forecasting using an adaptive hybrid BiLSTM model based on wavelet transform technique and Pareto optimization: An application in the smart cities. J. Energy Manag. Technol. 2024, 8, 178–195. [Google Scholar]
- Buratto, W.G.; Muniz, R.N.; Nied, A.; Barros, C.F.d.O.; Cardoso, R.; Gonzalez, G.V. Wavelet CNN-LSTM time series forecasting of electricity power generation considering biomass thermal systems. IET Gener. Transm. Distrib. 2024, 18, 3654–3663. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, J. Impact of Coiflet Wavelet Decomposition on Forecasting Accuracy: Shifts in ARIMA and Exponential Smoothing Performance. Metall. Mater. Eng. 2025, 31, 177–192. [Google Scholar] [CrossRef]
- Yan, W.; Cheng, C.; Xue, B.; Li, D.; Chen, F.; Wang, S. Monthly electricity sales forecasting method combining X12 multiplicative model and ARIMA model. Power Syst. Its Autom. J. 2016, 28, 74–80. [Google Scholar]
- Wang, A.; Wang, D.; Ye, J. Monthly electricity sales forecasting model based on factorization machine. J. Tianjin Vocat. Tech. Norm. Univ. 2020, 30, 42–47. [Google Scholar] [CrossRef]
- Mei, X.; Cao, W.; Wang, J. Monthly electricity sales forecasting method for large power customers based on empirical mode decomposition and ARIMA model. Autom. Technol. Appl. 2025, 44, 13–17. Available online: http://kns.cnki.net/kcms/detail/23.1474.TP.20241218.0957.008.html (accessed on 18 December 2024). [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In 35th Conference on Neural Information Processing Systems (NeurIPS 2021); Curran Associates Inc.: Red Hook, NY, USA, 2021. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Li, C.; Huang, X.; Wang, J.; Long, M. Timer: Generative Pre-trained Transformers Are Large Time Series Models. arXiv 2024, arXiv:2402.02368. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, G.; Huang, X.; Wang, J.; Long, M. Timer-XL: Long-Context Transformers for Unified Time Series Forecasting. arXiv 2025, arXiv:2410.04803. [Google Scholar] [CrossRef]
- Guo, Y. Application of wavelet transform in signal denoising based on LabVIEW. Intern. Combust. Engine Parts 2017, 18, 144–145. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Chen, L.; Chi, Y.; Guan, Y.; Fan, J. A hybrid attention-based EMD-LSTM model for financial time series prediction. In Proceedings of the 2019 International Conference on Artificial Intelligence and Big Data, Chengdu, China, 25–28 May 2019; pp. 113–118. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Shi, J.; Tang, H.; Zhou, Q.; Han, L.; Hao, R. High frequency measurement of carbon emissions based on power big data: A case study of Chinese Qinghai province. Sci. Total Environ. 2023, 902, 166075. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
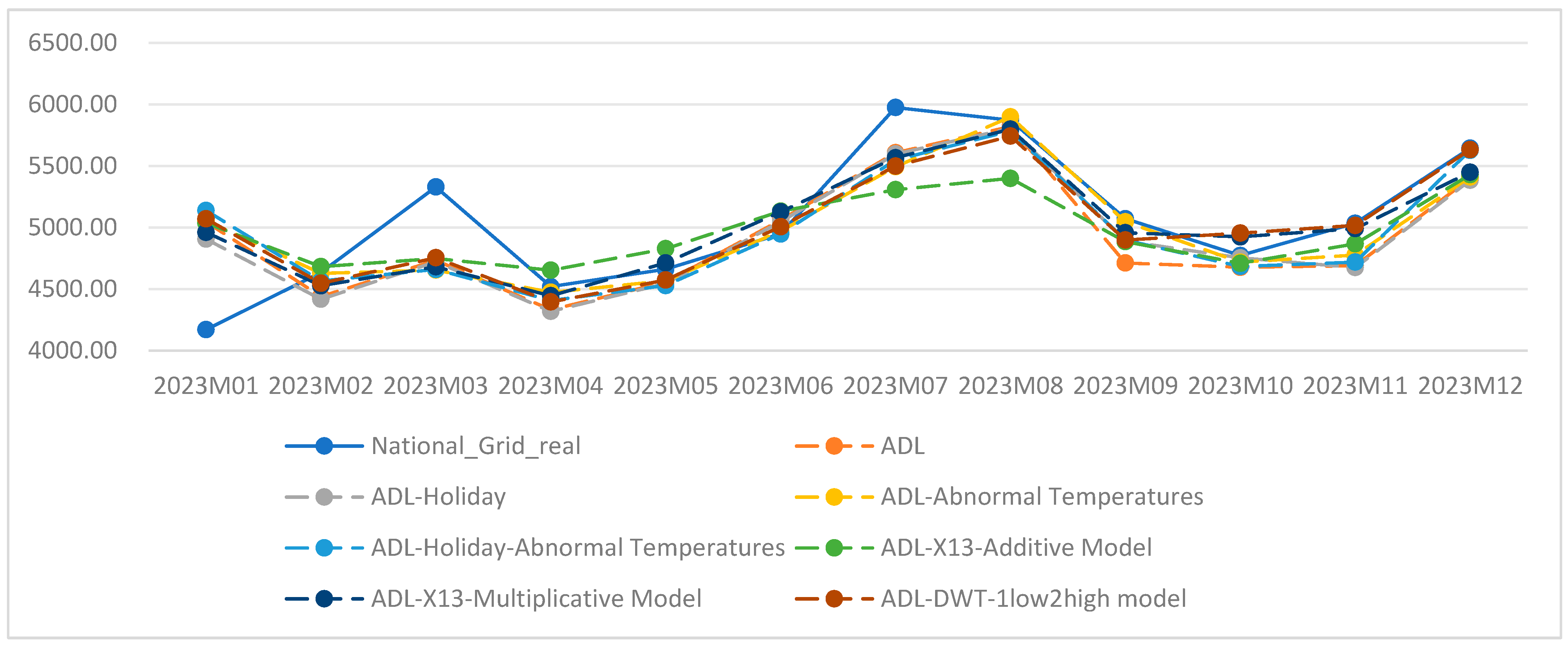
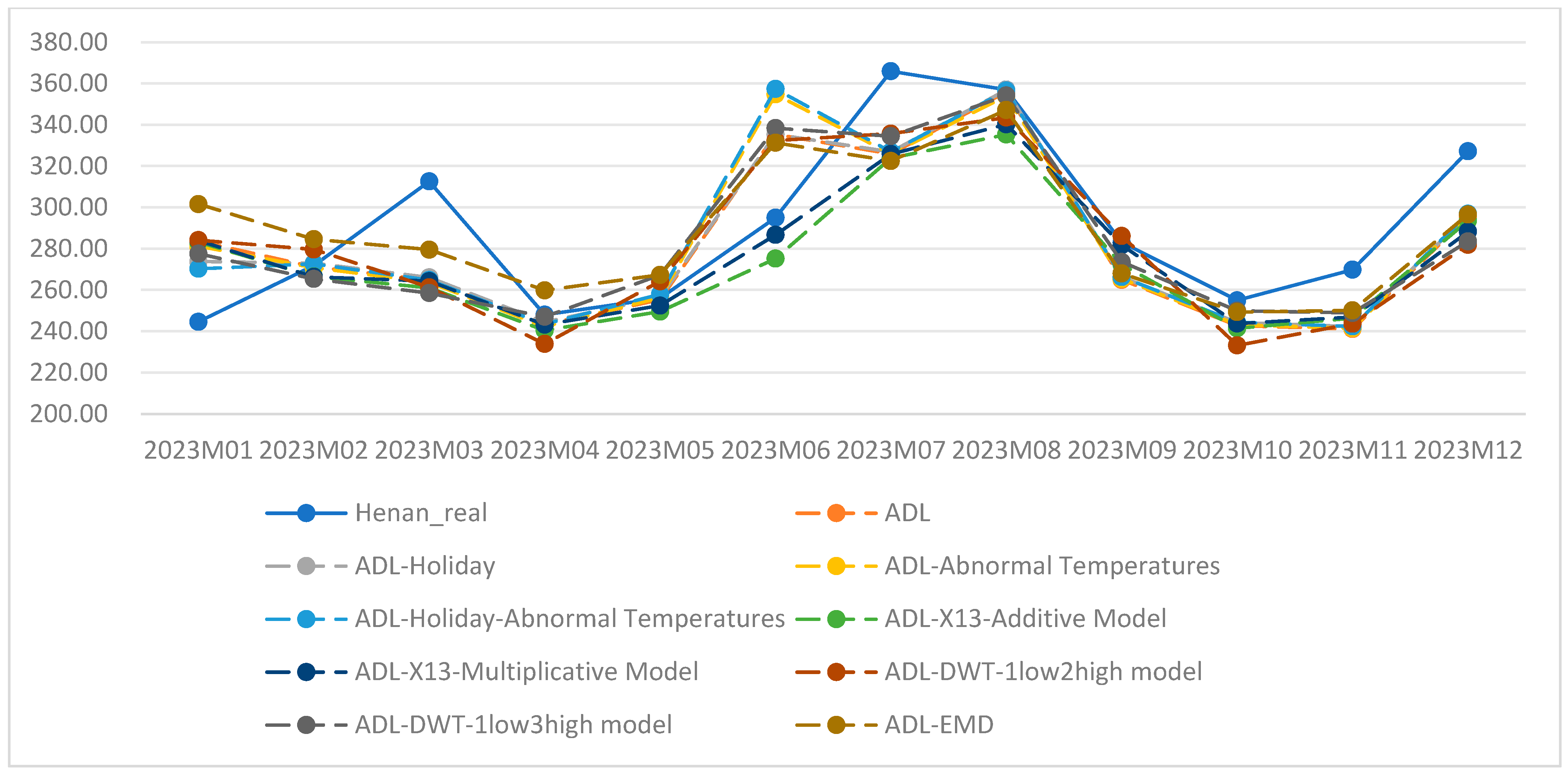
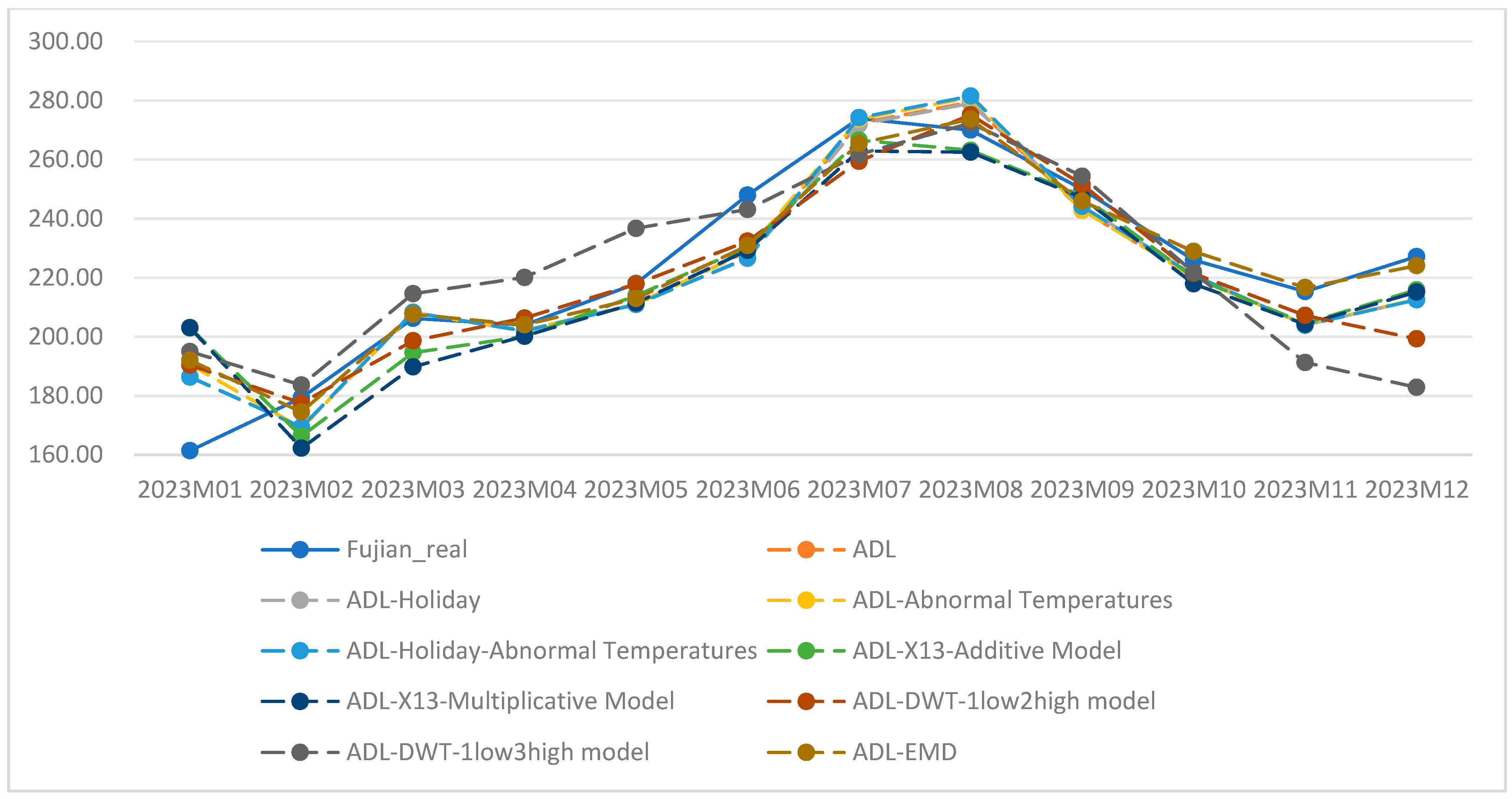
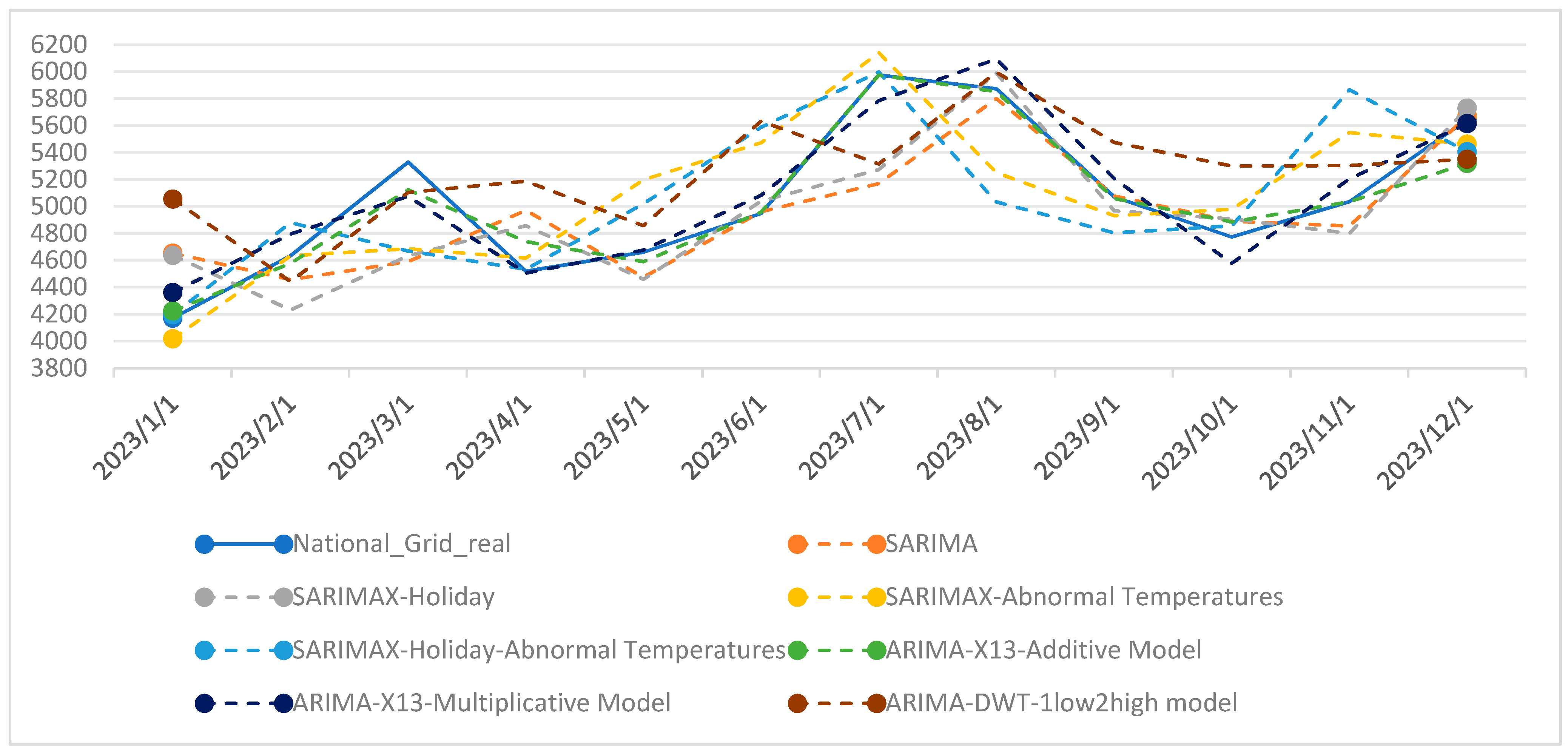


| Forecast Horizon | ADL | ADL-Holiday | ADL-Abnormal Temperatures | ADL-Holiday-Abnormal Temperatures | ADL-X13-Additive Model | ADL-X13-Multiplicative Model | ADL-DWT-1low2high Model | ADL-DWT-1low3high Model | ADL-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 2.62% | 2.76% | N/A | N/A | 1.57% | 2.01% | 1.53% | 1.04% | 0.72% |
| 11 | 3.03% | 3.07% | N/A | N/A | 1.65% | 2.10% | 1.71% | 1.10% | 0.83% |
| 10 | 2.97% | 3.00% | N/A | N/A | 1.66% | 2.09% | 1.77% | 1.07% | 0.84% |
| 9 | 2.77% | 2.79% | N/A | N/A | 1.61% | 2.02% | 1.75% | 0.97% | 0.80% |
| 8 | 2.72% | 2.74% | N/A | N/A | 1.61% | 1.98% | 1.76% | 0.92% | 0.80% |
| 7 | 2.70% | 2.71% | N/A | N/A | 1.60% | 1.95% | 1.76% | 0.87% | 0.81% |
| 6 | 2.73% | 2.74% | N/A | N/A | 1.60% | 1.93% | 1.75% | 0.84% | 0.84% |
| 5 | 2.63% | 2.64% | N/A | N/A | 1.58% | 1.90% | 1.68% | 0.80% | 0.86% |
| 4 | 2.62% | 2.63% | N/A | N/A | 1.57% | 1.89% | 1.66% | 0.81% | 0.87% |
| 3 | 2.59% | 2.61% | N/A | N/A | 1.56% | 1.87% | 1.61% | 0.81% | 0.87% |
| 2 | 2.58% | 2.61% | N/A | N/A | 1.56% | 1.87% | 1.60% | 0.82% | 0.89% |
| 1 | 2.57% | 2.60% | N/A | N/A | 1.55% | 1.86% | 1.58% | 0.81% | 0.89% |
| Number of Errors Exceeding 2% | 12 | 12 | N/A | N/A | 0 | 4 | 0 | 0 | 0 |
| Forecast Horizon | ADL | ADL-Holiday | ADL-Abnormal Temperatures | ADL-Holiday-Abnormal Temperatures | ADL-X13-Additive Model | ADL-X13-Multiplicative Model | ADL-DWT-1low2high Model | ADL-DWT-1low3high Model | ADL-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 2.99% | 3.07% | 2.47% | 2.39% | 6.05% | 4.84% | 3.07% | 2.85% | 0.12% |
| 11 | 3.25% | 3.20% | 2.60% | 2.42% | 6.09% | 4.93% | 3.23% | 2.84% | 0.34% |
| 10 | 3.25% | 3.21% | 2.60% | 2.42% | 6.06% | 4.90% | 3.27% | 2.79% | 0.41% |
| 9 | 3.04% | 3.00% | 2.45% | 2.27% | 5.94% | 4.80% | 3.19% | 2.69% | 0.44% |
| 8 | 3.02% | 2.99% | 2.44% | 2.26% | 5.91% | 4.77% | 3.14% | 2.64% | 0.52% |
| 7 | 3.02% | 2.99% | 2.44% | 2.27% | 5.88% | 4.76% | 3.10% | 2.64% | 0.59% |
| 6 | 3.24% | 3.17% | 2.81% | 2.67% | 5.81% | 4.74% | 3.10% | 2.68% | 0.69% |
| 5 | 3.09% | 3.01% | 2.65% | 2.52% | 5.76% | 4.71% | 3.12% | 2.63% | 0.74% |
| 4 | 3.08% | 3.01% | 2.65% | 2.52% | 5.73% | 4.70% | 3.14% | 2.60% | 0.92% |
| 3 | 3.07% | 2.99% | 2.63% | 2.49% | 5.70% | 4.69% | 3.09% | 2.59% | 0.85% |
| 2 | 3.06% | 2.99% | 2.62% | 2.49% | 5.67% | 4.67% | 3.08% | 2.55% | 0.81% |
| 1 | 3.05% | 2.98% | 2.60% | 2.47% | 5.66% | 4.66% | 3.05% | 2.51% | 0.81% |
| Number of Errors Exceeding 2% | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 0 |
| Forecast Horizon | ADL | ADL-Holiday | ADL-Abnormal Temperatures | ADL-Holiday-Abnormal Temperatures | ADL-X13-Additive Model | ADL-X13-Multiplicative Model | ADL-DWT-1low2high Model | ADL-DWT-1low3high Model | ADL-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 1.42% | 1.62% | 1.40% | 1.55% | 2.22% | 3.26% | 1.62% | −0.29% | −0.20% |
| 11 | 1.63% | 1.79% | 1.56% | 1.67% | 2.26% | 3.28% | 1.72% | −0.11% | −0.09% |
| 10 | 1.58% | 1.74% | 1.50% | 1.62% | 2.26% | 3.18% | 1.73% | 0.01% | −0.01% |
| 9 | 1.59% | 1.76% | 1.52% | 1.63% | 2.24% | 3.05% | 1.70% | 0.07% | 0.03% |
| 8 | 1.58% | 1.75% | 1.51% | 1.62% | 2.19% | 2.97% | 1.66% | 0.14% | 0.08% |
| 7 | 1.54% | 1.71% | 1.48% | 1.59% | 2.13% | 2.91% | 1.65% | 0.18% | 0.11% |
| 6 | 1.42% | 1.61% | 1.32% | 1.45% | 2.09% | 2.85% | 1.62% | 0.18% | 0.08% |
| 5 | 1.41% | 1.59% | 1.31% | 1.45% | 2.06% | 2.81% | 1.60% | 0.18% | 0.05% |
| 4 | 1.45% | 1.63% | 1.34% | 1.48% | 2.03% | 2.79% | 1.61% | 0.18% | 0.07% |
| 3 | 1.43% | 1.62% | 1.32% | 1.46% | 2.00% | 2.76% | 1.61% | 0.21% | 0.08% |
| 2 | 1.42% | 1.61% | 1.31% | 1.45% | 1.99% | 2.75% | 1.59% | 0.16% | 0.09% |
| 1 | 1.42% | 1.61% | 1.31% | 1.45% | 1.98% | 2.74% | 1.57% | 0.07% | 0.10% |
| Number of Errors Exceeding 2% | 0 | 0 | 0 | 0 | 10 | 12 | 0 | 0 | 0 |
| Forecast Horizon | SARIMA | SARIMAX-Holiday | SARIMAX-Abnormal Temperatures | SARIMAX-Holiday-Abnormal Temperatures | ARIMA-X13-Additive Model | ARIMA-X13-Multiplicative Model | ARIMA-DWT-1low2high Model | ARIMA-DWT-1low3high Model | ARIMA-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | −3.64% | −4.08% | N/A | N/A | −12.07% | −3.31% | −3.18% | 0.52% | 4.03% |
| 11 | −5.09% | −5.83% | N/A | N/A | −5.99% | −1.86% | −4.60% | 1.70% | 6.50% |
| 10 | −4.71% | −4.64% | N/A | N/A | 1.02% | −0.71% | −4.94% | 0.09% | −0.18% |
| 9 | −2.70% | −2.55% | N/A | N/A | 0.75% | −0.27% | −2.63% | 0.09% | 2.20% |
| 8 | −3.83% | −3.40% | N/A | N/A | 0.63% | 0.01% | −1.96% | −0.01% | 3.72% |
| 7 | −3.41% | −2.93% | N/A | N/A | −0.90% | 0.04% | −1.68% | 0.24% | 4.22% |
| 6 | −3.44% | −3.13% | N/A | N/A | 2.50% | 0.42% | −0.15% | 0.49% | 4.64% |
| 5 | −1.89% | −1.83% | N/A | N/A | 1.16% | 0.37% | −0.99% | 0.42% | 3.60% |
| 4 | −1.78% | −2.01% | N/A | N/A | 0.66% | 0.27% | −1.15% | 0.32% | 3.61% |
| 3 | −1.78% | −1.88% | N/A | N/A | 0.39% | 0.21% | −0.37% | 0.25% | 4.15% |
| 2 | −1.91% | −2.03% | N/A | N/A | 0.44% | 0.43% | −0.70% | 0.36% | 4.10% |
| 1 | −1.76% | −1.83% | N/A | N/A | 0.50% | 0.35% | −0.49% | 0.57% | 3.93% |
| Number of Errors Exceeding 2% | 7 | 9 | N/A | N/A | 3 | 1 | 4 | 0 | 11 |
| Forecast Horizon | SARIMA | SARIMAX-Holiday | SARIMAX-Abnormal Temperatures | SARIMAX-Holiday-Abnormal Temperatures | ARIMA-X13-Additive Model | ARIMA-X13-Multiplicative Model | ARIMA-DWT-1low2high Model | ARIMA-DWT-1low3high Model | ARIMA-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | −0.47% | −0.38% | −4.04% | −1.58% | −2.15% | −2.86% | −0.08% | 1.50% | 1.21% |
| 11 | −2.49% | −3.05% | −6.87% | −3.61% | −2.23% | −3.12% | −5.38% | 2.34% | 1.47% |
| 10 | −3.13% | −3.29% | −5.80% | −3.97% | −1.76% | −2.44% | −6.13% | 2.43% | 0.65% |
| 9 | −0.28% | −0.02% | −2.83% | −0.94% | −0.02% | −2.69% | −2.76% | 1.53% | 0.23% |
| 8 | −1.44% | −1.24% | −5.31% | −2.07% | −0.44% | −1.54% | −3.39% | 1.34% | −0.28% |
| 7 | −1.60% | −1.28% | −5.60% | −1.92% | −0.87% | −2.42% | −1.97% | 0.49% | −0.92% |
| 6 | −2.11% | −1.68% | −4.90% | −2.01% | 0.05% | −0.95% | 0.30% | 0.22% | −1.12% |
| 5 | −0.23% | 0.10% | −2.51% | −0.97% | −0.46% | −1.82% | −1.58% | 0.52% | −1.62% |
| 4 | −0.26% | −0.06% | −0.56% | −0.53% | −0.16% | −1.40% | −1.13% | −0.04% | −2.13% |
| 3 | −0.69% | −0.58% | −1.47% | −0.09% | −0.08% | −1.18% | −0.43% | −0.10% | −2.16% |
| 2 | −0.80% | −0.64% | −2.17% | −1.00% | 0.00% | −1.11% | −0.53% | 0.11% | −1.98% |
| 1 | −0.72% | −0.58% | −2.18% | −0.94% | 0.07% | −1.05% | −0.62% | 0.88% | −1.56% |
| Number of Errors Exceeding 2% | 3 | 2 | 10 | 4 | 2 | 5 | 4 | 2 | 2 |
| Forecast Horizon | SARIMA | SARIMAX-Holiday | SARIMAX-Abnormal Temperatures | SARIMAX-Holiday-Abnormal Temperatures | ARIMA-X13-Additive Model | ARIMA-X13-Multiplicative Model | ARIMA-DWT-1low2high Model | ARIMA-DWT-1low3high Model | ARIMA-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | −2.20% | −0.80% | −7.41% | −3.08% | −5.80% | −6.67% | −1.97% | −0.78% | −3.92% |
| 11 | −3.65% | −2.54% | −13.87% | −3.49% | −3.94% | −3.67% | −4.11% | −0.15% | −3.78% |
| 10 | −3.04% | −1.45% | −12.81% | −3.10% | −2.58% | −1.90% | −6.03% | 0.86% | −3.87% |
| 9 | −2.39% | −1.23% | −10.48% | −2.88% | −0.88% | −0.69% | −2.72% | 0.95% | −4.19% |
| 8 | −2.50% | −1.36% | −10.42% | −2.93% | −0.35% | −0.42% | −1.69% | 1.12% | −4.17% |
| 7 | −2.28% | −1.34% | −8.88% | −2.87% | 0.10% | −0.25% | −1.82% | 1.62% | −4.16% |
| 6 | −1.63% | −0.78% | −5.80% | −2.12% | 0.87% | 0.73% | 0.91% | 1.18% | −4.08% |
| 5 | −1.47% | −0.69% | −3.51% | −1.93% | 0.64% | 0.53% | −1.27% | 1.88% | −3.66% |
| 4 | −1.90% | −0.78% | −1.84% | −1.85% | 0.21% | 0.08% | −2.72% | 1.00% | −3.32% |
| 3 | −1.99% | −0.82% | −1.67% | −1.85% | 0.19% | 0.08% | −0.90% | −0.57% | −3.27% |
| 2 | −1.75% | −0.79% | −2.32% | −1.79% | 0.30% | 0.32% | −0.83% | 0.24% | −3.21% |
| 1 | −1.73% | −0.73% | −2.55% | −1.72% | 0.32% | 0.40% | −0.35% | 0.69% | −3.19% |
| Number of Errors Exceeding 2% | 6 | 1 | 10 | 7 | 3 | 2 | 4 | 0 | 12 |
| Forecast Horizon | LSTM | LSTM-Holiday | LSTM-Abnormal Temperatures | LSTM-Holiday-Abnormal Temperatures | LSTM-X13-Additive Model | LSTM-X13-Multiplicative Model | LSTM-DWT-1low2high Model | LSTM-DWT-1low3high Model | LSTM-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 0.30% | −8.34% | N/A | N/A | 5.20% | 0.50% | 3.80% | −3.10% | 0.10% |
| 11 | 0.83% | 7.12% | N/A | N/A | −2.10% | −1.60% | −0.20% | −1.00% | 2.60% |
| 10 | 1.02% | −3.83% | N/A | N/A | 0.40% | 1.20% | 0.40% | −0.10% | 3.80% |
| 9 | 1.23% | −1.72% | N/A | N/A | 1.30% | −0.70% | −0.50% | −0.10% | 2.70% |
| 8 | 1.40% | −3.62% | N/A | N/A | 0.40% | −2.50% | −1.90% | −1.20% | 2.00% |
| 7 | 1.83% | −3.35% | N/A | N/A | 0.90% | 0.50% | 0.10% | 1.50% | 4.50% |
| 6 | 2.76% | 13.26% | N/A | N/A | 1.30% | −0.70% | −0.70% | 2.70% | 1.10% |
| 5 | 3.62% | 3.11% | N/A | N/A | 0.80% | 0.20% | −0.10% | 1.00% | 2.60% |
| 4 | 4.55% | 3.64% | N/A | N/A | 1.00% | 0.60% | 0.80% | 0.70% | 3.80% |
| 3 | 5.16% | 1.16% | N/A | N/A | −0.10% | −3.30% | 0.20% | 1.00% | 2.40% |
| 2 | 6.25% | 1.12% | N/A | N/A | −0.10% | −1.30% | −1.10% | 0.90% | 2.00% |
| 1 | 6.95% | 0.92% | N/A | N/A | 0.30% | −0.80% | −0.10% | 1.20% | 2.30% |
| Number of Errors Exceeding 2% | 6 | 8 | N/A | N/A | 2 | 2 | 1 | 2 | 10 |
| Forecast Horizon | LSTM | LSTM-Holiday | LSTM-Abnormal Temperatures | LSTM-Holiday-Abnormal Temperatures | LSTM-X13-Additive Model | LSTM-X13-Multiplicative Model | LSTM-DWT-1low2high Model | LSTM-DWT-1low3high Model | LSTM-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | −0.38% | −2.71% | 2.69% | 3.58% | −8.70% | 1.60% | 6.90% | 2.90% | 7.70% |
| 11 | −0.21% | −38.08% | −2.58% | −26.96% | −5.90% | 0.50% | −0.30% | −5.40% | 1.70% |
| 10 | −0.12% | −3.17% | −6.16% | −7.05% | −2.10% | −5.40% | −0.30% | −0.50% | −3.90% |
| 9 | −0.22% | 2.07% | −4.75% | −2.88% | −1.50% | −1.20% | −2.30% | 2.00% | 2.40% |
| 8 | −0.60% | −5.27% | −4.76% | −6.33% | −3.00% | −1.10% | −3.30% | 0.30% | −2.40% |
| 7 | −0.46% | −5.49% | −4.50% | −6.12% | −0.20% | −0.90% | −1.80% | 1.10% | −2.30% |
| 6 | −0.10% | 4.95% | −0.49% | 16.82% | −0.50% | −0.10% | −0.50% | 0.40% | −2.60% |
| 5 | 0.57% | 0.47% | 1.51% | 0.93% | −0.20% | −0.50% | −0.60% | 0.30% | −2.00% |
| 4 | 0.86% | 3.94% | 1.99% | 1.49% | −0.10% | −0.20% | 0.90% | 2.00% | −1.20% |
| 3 | 1.05% | −0.80% | 0.08% | −1.63% | −0.20% | −0.20% | 1.70% | 2.30% | 0.30% |
| 2 | 1.71% | −0.10% | −0.58% | −1.12% | −1.80% | −0.40% | 0.20% | 1.60% | −1.00% |
| 1 | 1.77% | −0.09% | −0.39% | −1.40% | −1.20% | −0.40% | 0.40% | 1.40% | −1.00% |
| Number of Errors Exceeding 2% | 0 | 8 | 6 | 7 | 4 | 1 | 3 | 5 | 7 |
| Forecast Horizon | LSTM | LSTM-Holiday | LSTM-Abnormal Temperatures | LSTM-Holiday-Abnormal Temperatures | LSTM-X13-Additive Model | LSTM-X13-Multiplicative Model | LSTM-DWT-1low2high Model | LSTM-DWT-1low3high Model | LSTM-EMD |
|---|---|---|---|---|---|---|---|---|---|
| 12 | −0.49% | −0.42% | −10.10% | −6.58% | −0.20% | −0.10% | −1.80% | −4.80% | 5.20% |
| 11 | −0.47% | 56.65% | −36.84% | 61.83% | −3.00% | −5.70% | −0.30% | −5.10% | 5.00% |
| 10 | −0.69% | −4.05% | −31.65% | −1.80% | 0.50% | 1.60% | 2.60% | −5.80% | 3.70% |
| 9 | −0.26% | −0.18% | −20.05% | −1.00% | 0.00% | 1.60% | −3.80% | −5.70% | 2.20% |
| 8 | −0.25% | −5.68% | −13.55% | −5.50% | 2.30% | 3.60% | −4.90% | −2.50% | 4.80% |
| 7 | 0.14% | −0.98% | −15.52% | −5.95% | 1.90% | 2.80% | −3.10% | −1.40% | −2.30% |
| 6 | 0.65% | 9.81% | −9.24% | 13.25% | 1.30% | 3.60% | −2.90% | 0.20% | −0.60% |
| 5 | 1.31% | 3.84% | −8.50% | 2.07% | 3.10% | 1.60% | −2.90% | −2.60% | 1.30% |
| 4 | 2.07% | 4.03% | −8.59% | 1.97% | 2.60% | 1.40% | −1.90% | 0.50% | 0.00% |
| 3 | 2.89% | 1.59% | −7.48% | −0.16% | 3.30% | 1.90% | −0.40% | 0.10% | 2.20% |
| 2 | 3.23% | 1.64% | −7.97% | 0.50% | 3.10% | 0.90% | −1.00% | 0.60% | 0.90% |
| 1 | 3.80% | 1.75% | −7.96% | 0.34% | 2.90% | 0.90% | −1.00% | −0.10% | 1.10% |
| Number of Errors Exceeding 2% | 4 | 6 | 12 | 6 | 7 | 4 | 6 | 6 | 7 |
| ADL | SARIMAX | LSTM | Total | |||||
|---|---|---|---|---|---|---|---|---|
| Total Number of Models | Number of Models That Meet the Requirements | Total Number of Models | Number of Models That Meet the Requirements | Total Number of Models | Number of Models That Meet the Requirements | Total Number of Models | Number of Models That Meet the Requirements | |
| National Grid Region | 9 | 4 | 9 | 1 | 9 | 0 | 27 | 5 |
| Henan Province | 9 | 1 | 9 | 0 | 9 | 1 | 27 | 2 |
| Fujian Province | 9 | 7 | 9 | 1 | 9 | 0 | 27 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Zhang, Y.; Ma, X.; Yang, X.; Shi, J.; Ji, H. A Comparative Study of Electricity Sales Forecasting Models Based on Different Feature Decomposition Methods. Energies 2025, 18, 5352. https://doi.org/10.3390/en18205352
Chen S, Zhang Y, Ma X, Yang X, Shi J, Ji H. A Comparative Study of Electricity Sales Forecasting Models Based on Different Feature Decomposition Methods. Energies. 2025; 18(20):5352. https://doi.org/10.3390/en18205352
Chicago/Turabian StyleChen, Shichong, Yushu Zhang, Xiaoteng Ma, Xu Yang, Junyi Shi, and Haoyang Ji. 2025. "A Comparative Study of Electricity Sales Forecasting Models Based on Different Feature Decomposition Methods" Energies 18, no. 20: 5352. https://doi.org/10.3390/en18205352
APA StyleChen, S., Zhang, Y., Ma, X., Yang, X., Shi, J., & Ji, H. (2025). A Comparative Study of Electricity Sales Forecasting Models Based on Different Feature Decomposition Methods. Energies, 18(20), 5352. https://doi.org/10.3390/en18205352






