Research on Wellhead Uplift Prediction for Underground Gas Storage Wells
Abstract
1. Introduction
2. Analysis of Wellhead Uplift Causes in Underground Gas Storage Wells
3. Prediction Method for Wellhead Uplift in Underground Gas Storage Wells
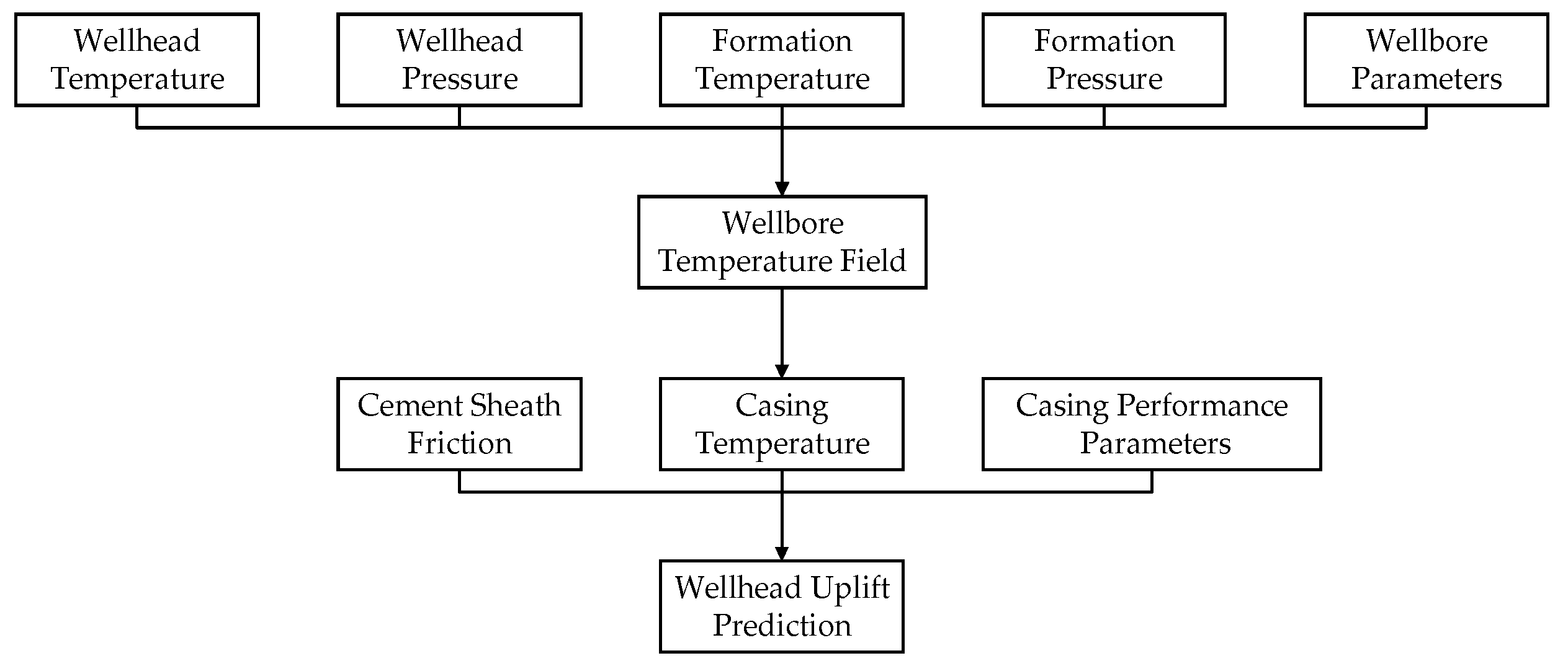
3.1. Methodological Framework
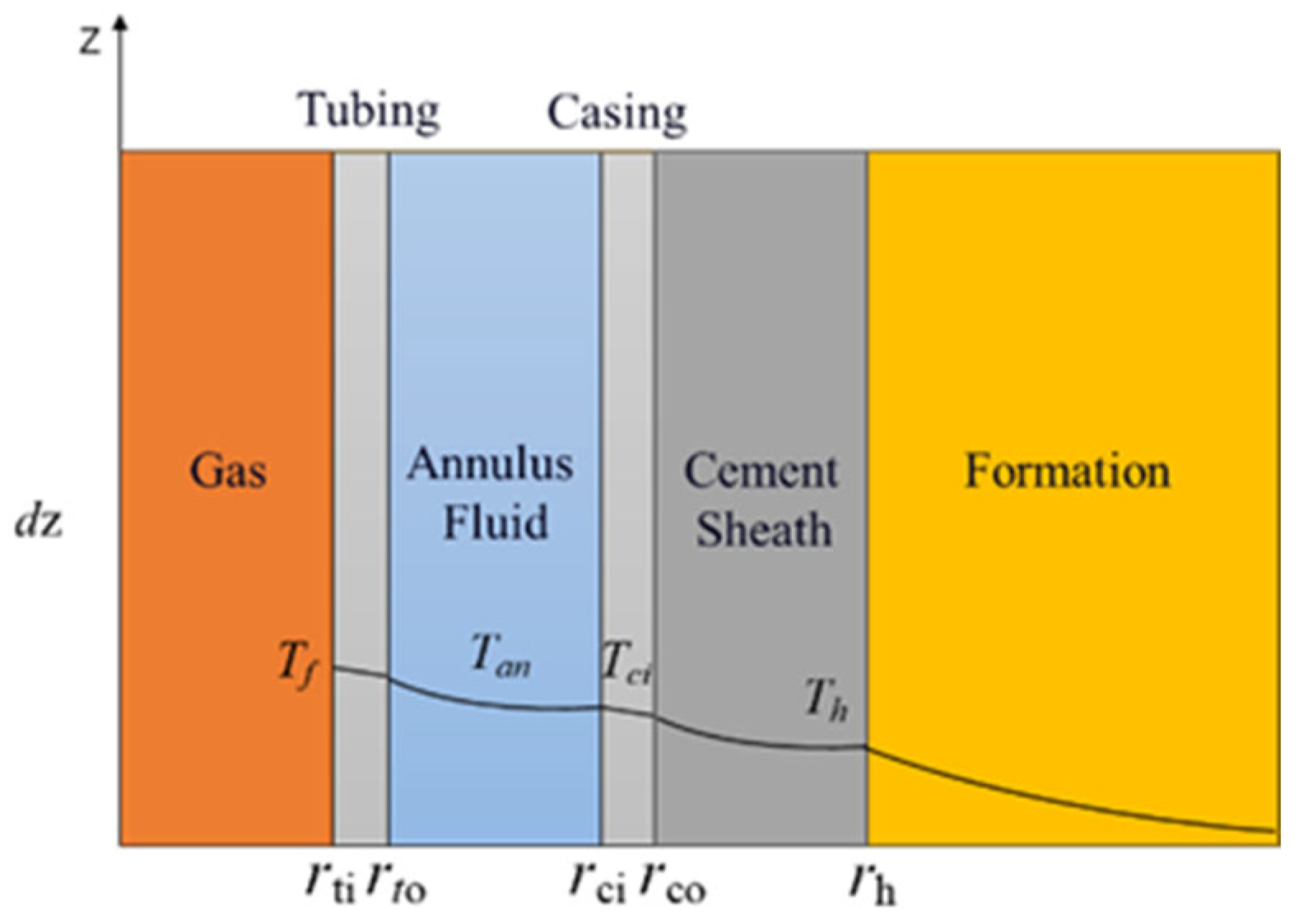
3.2. Analytical Model for Injection–Production Temperature Field
- (1)
- Model Assumptions
- (a)
- Heat transfer from the gas in the tubing to the outer edge of the cement sheath (wellbore section) is considered steady-state, while heat transfer in the formation is transient.
- (b)
- Heat is primarily conducted radially from the tubing to the formation, with radial heat flux significantly exceeding axial heat flux.
- (c)
- The tubing, casings, and cement sheath are concentric cylinders.
- (d)
- Gas flows in a one-dimensional steady manner within the wellbore, meaning flow parameters in the tubing are time-invariant and uniformly distributed across any cross-sectional area, varying only along the flow direction [18].
- (2)
- Analysis of Heat Transfer Model
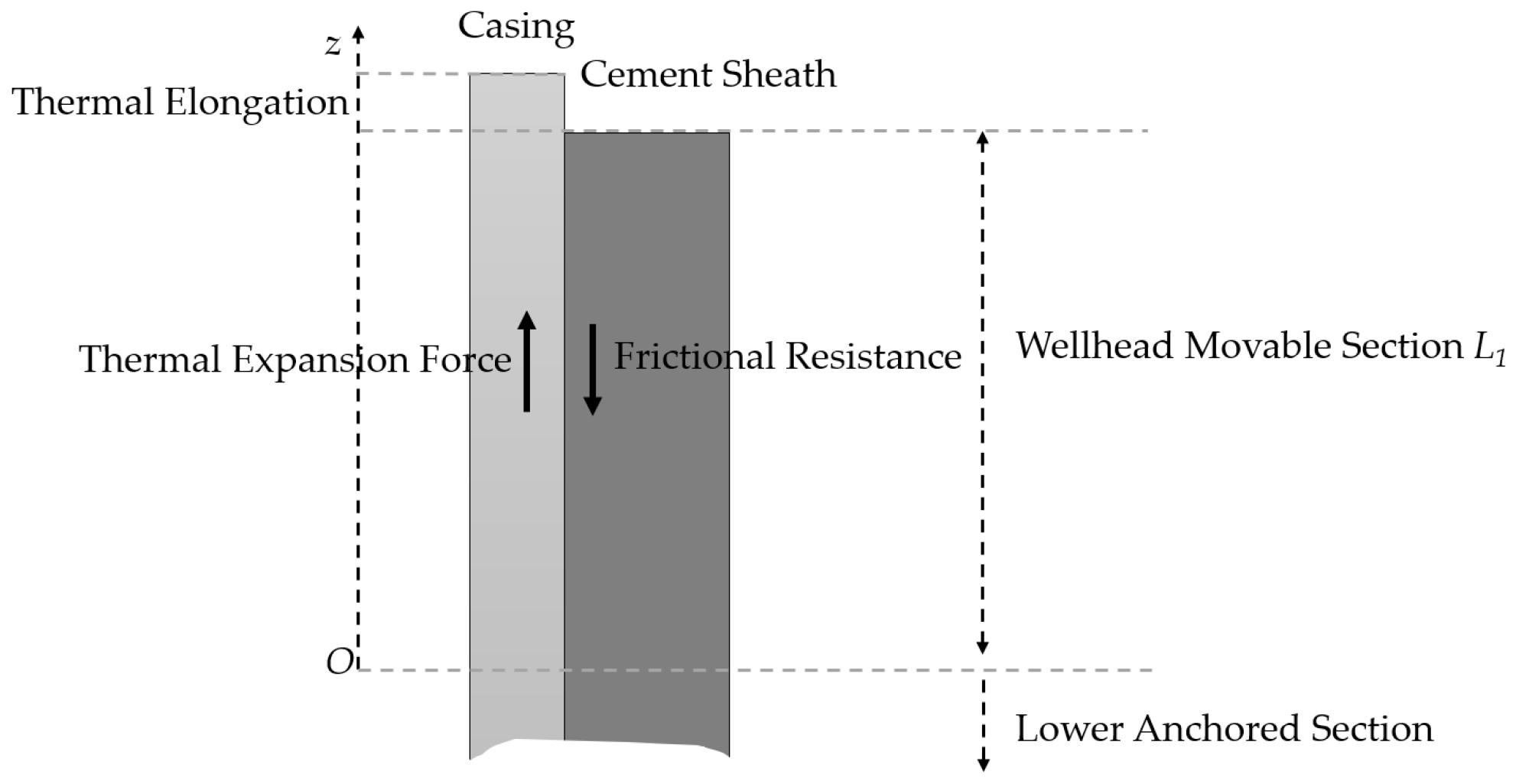
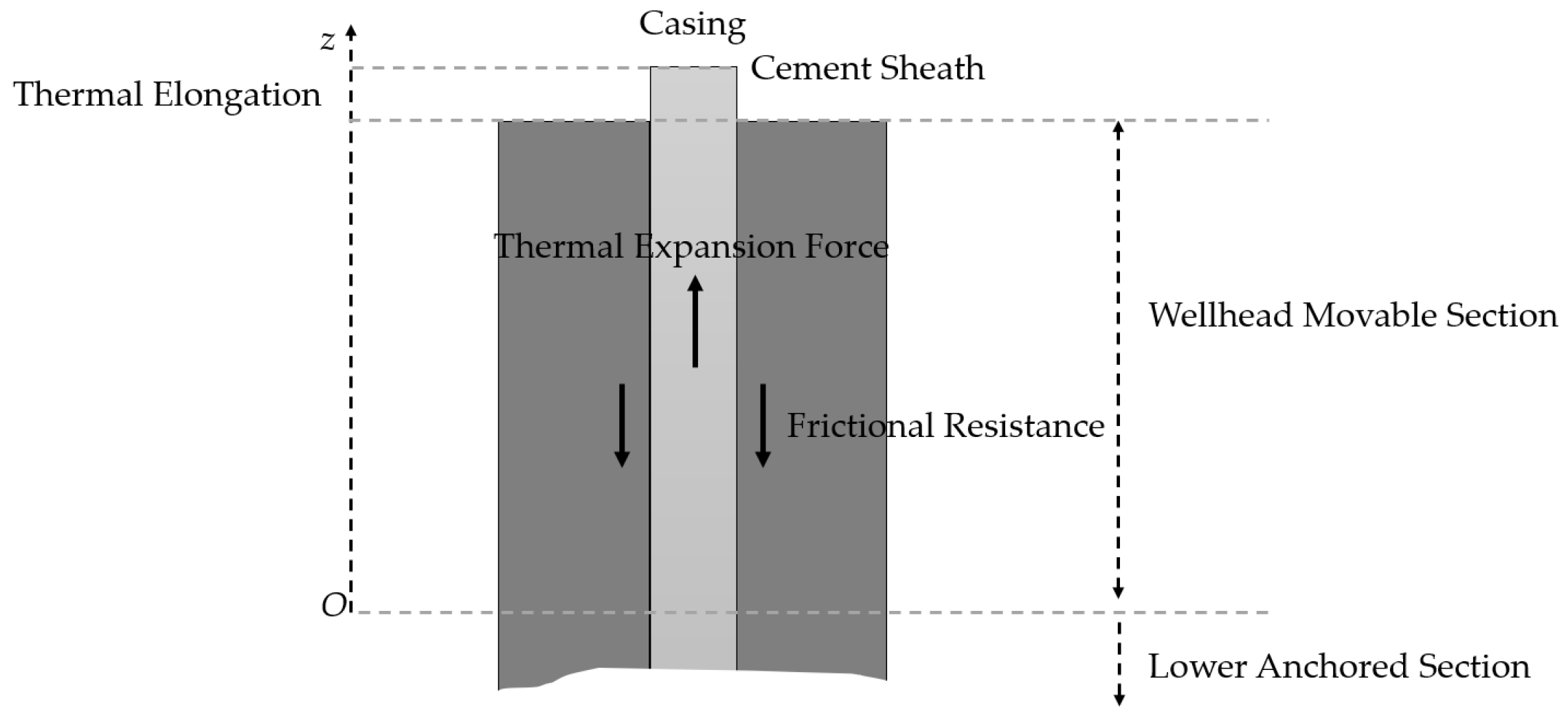
3.3. Wellhead Uplift Calculation Model
- (1)
- The casing maintains good circularity and centralization;
- (2)
- The cement sheath and casing body remain intact without significant damage or deformation;
- (3)
- The casing–cement sheath composite system is radially continuous without gaps.
4. Engineering Case Study
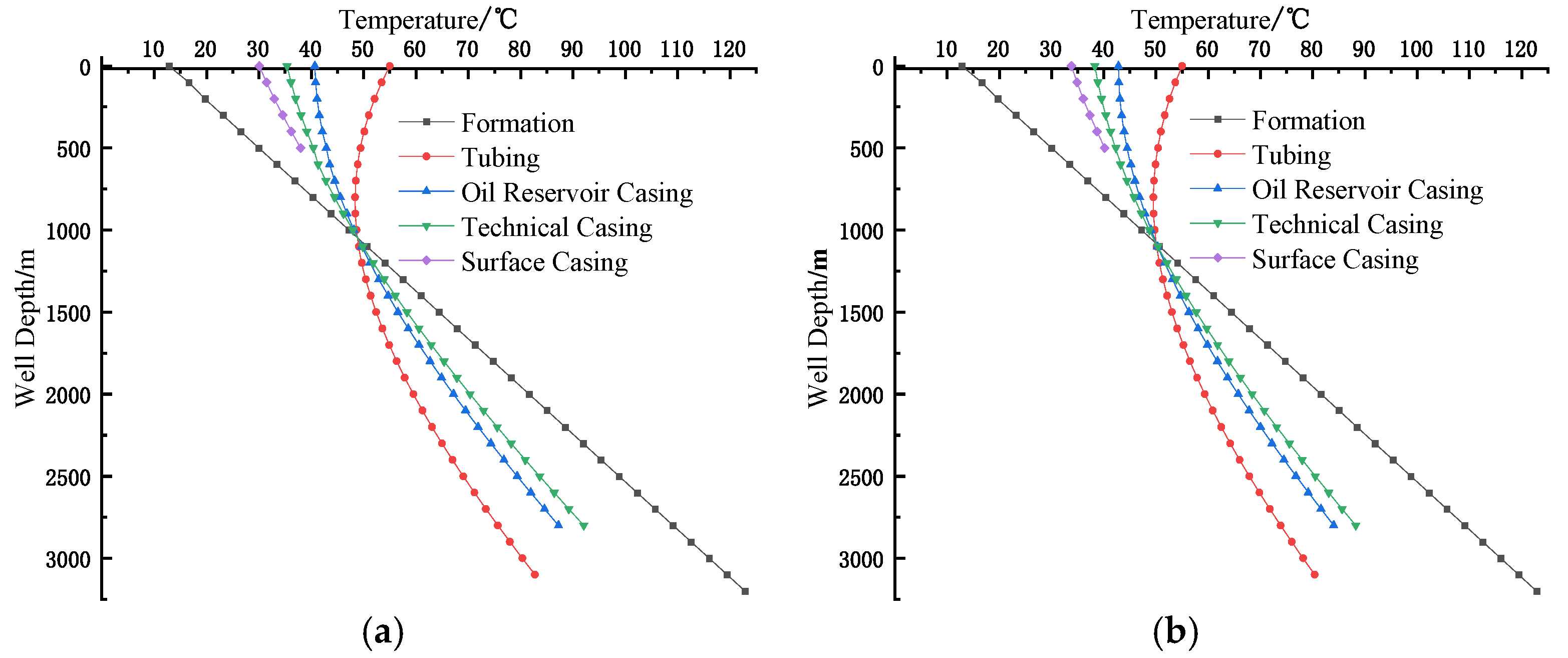
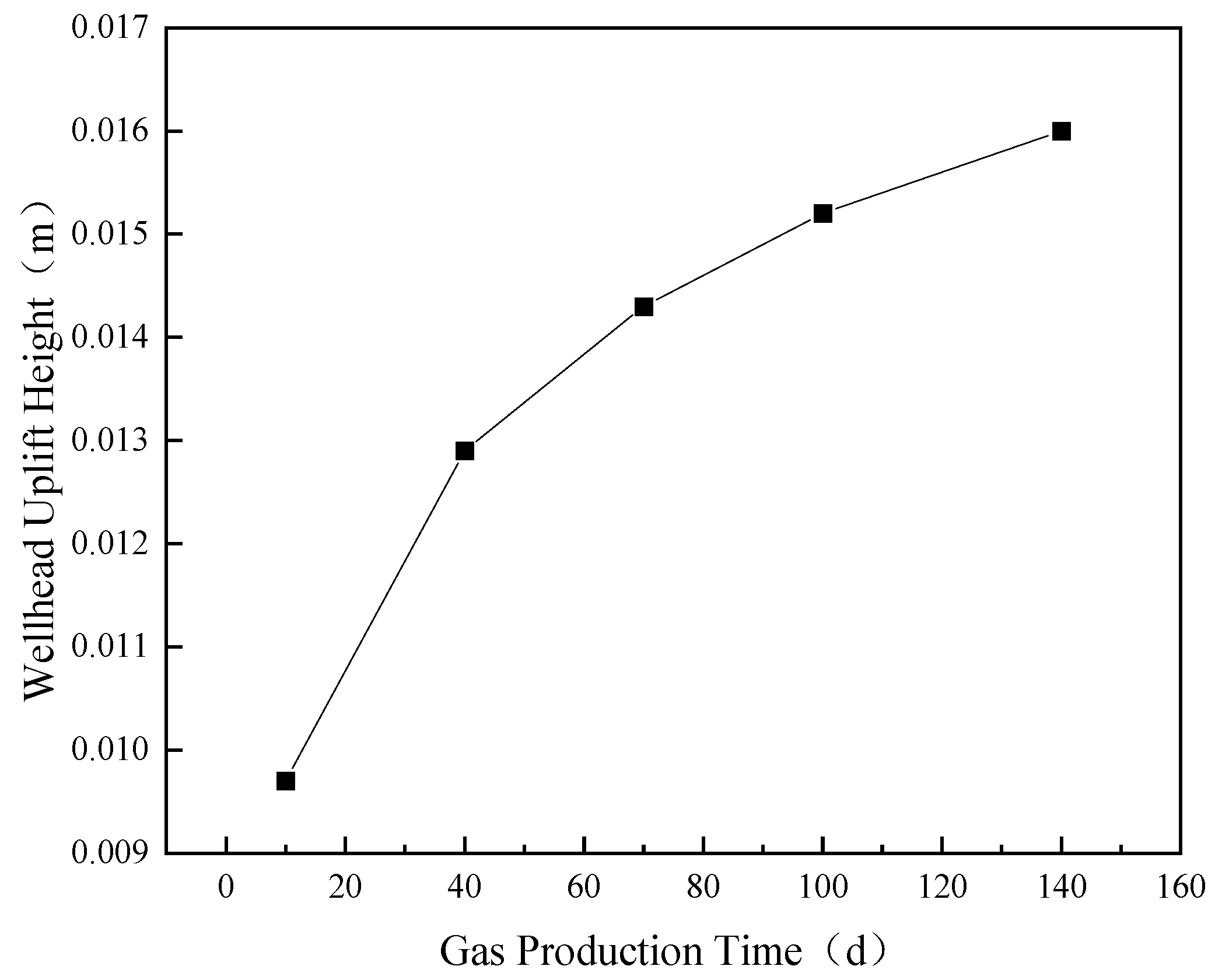
4.1. Field Measurement Comparison
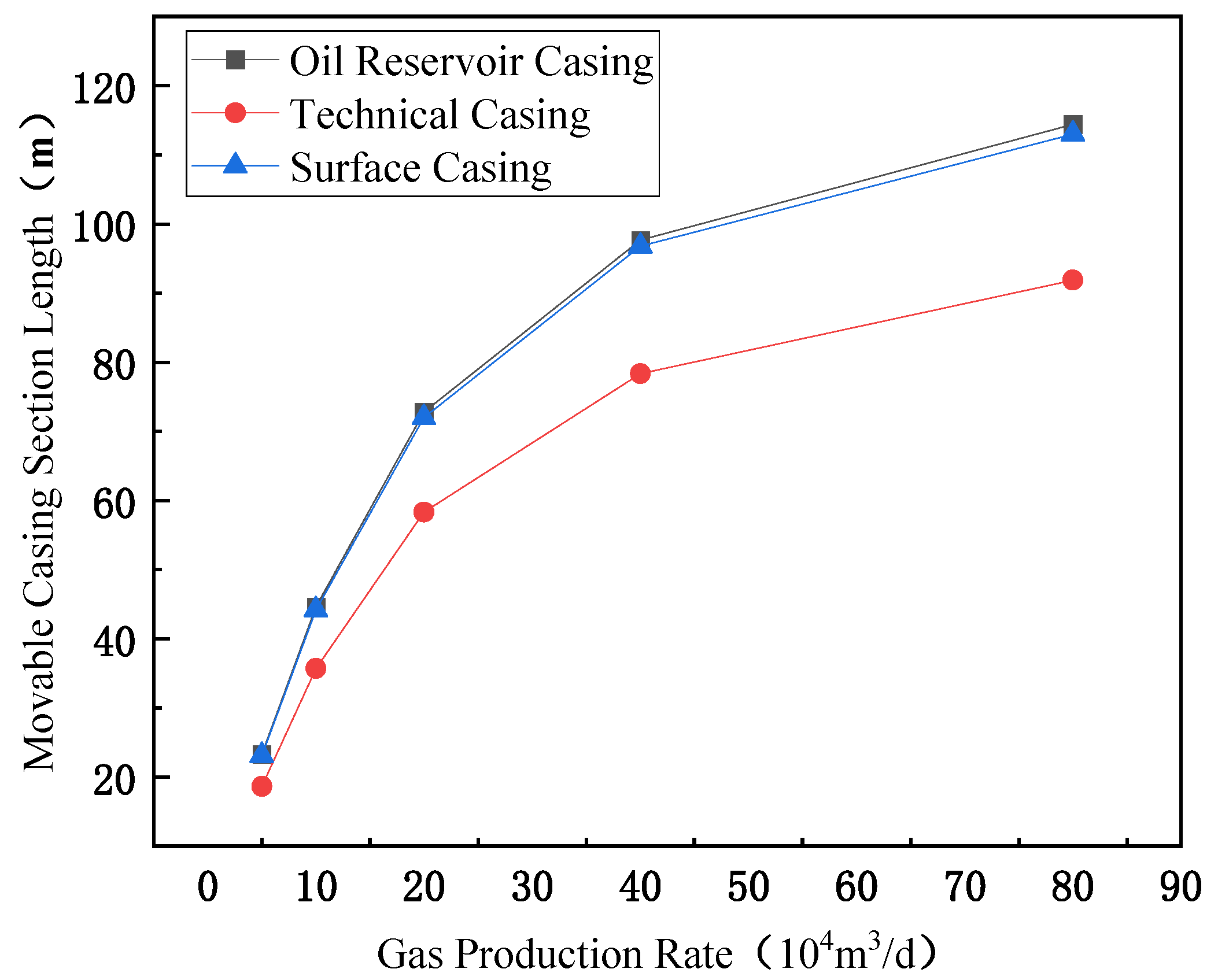
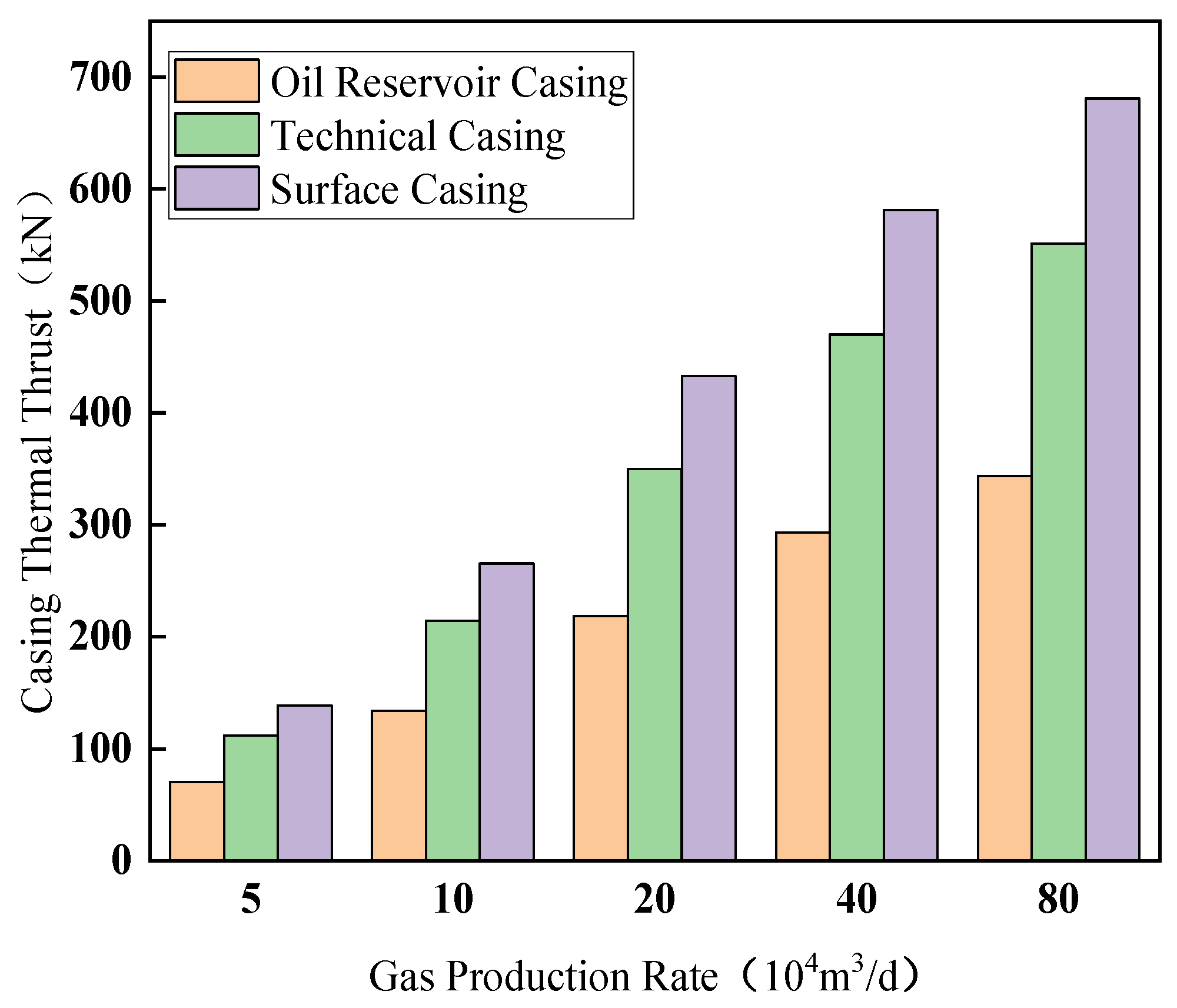
4.2. Influence Analysis of Injection–Production Parameters
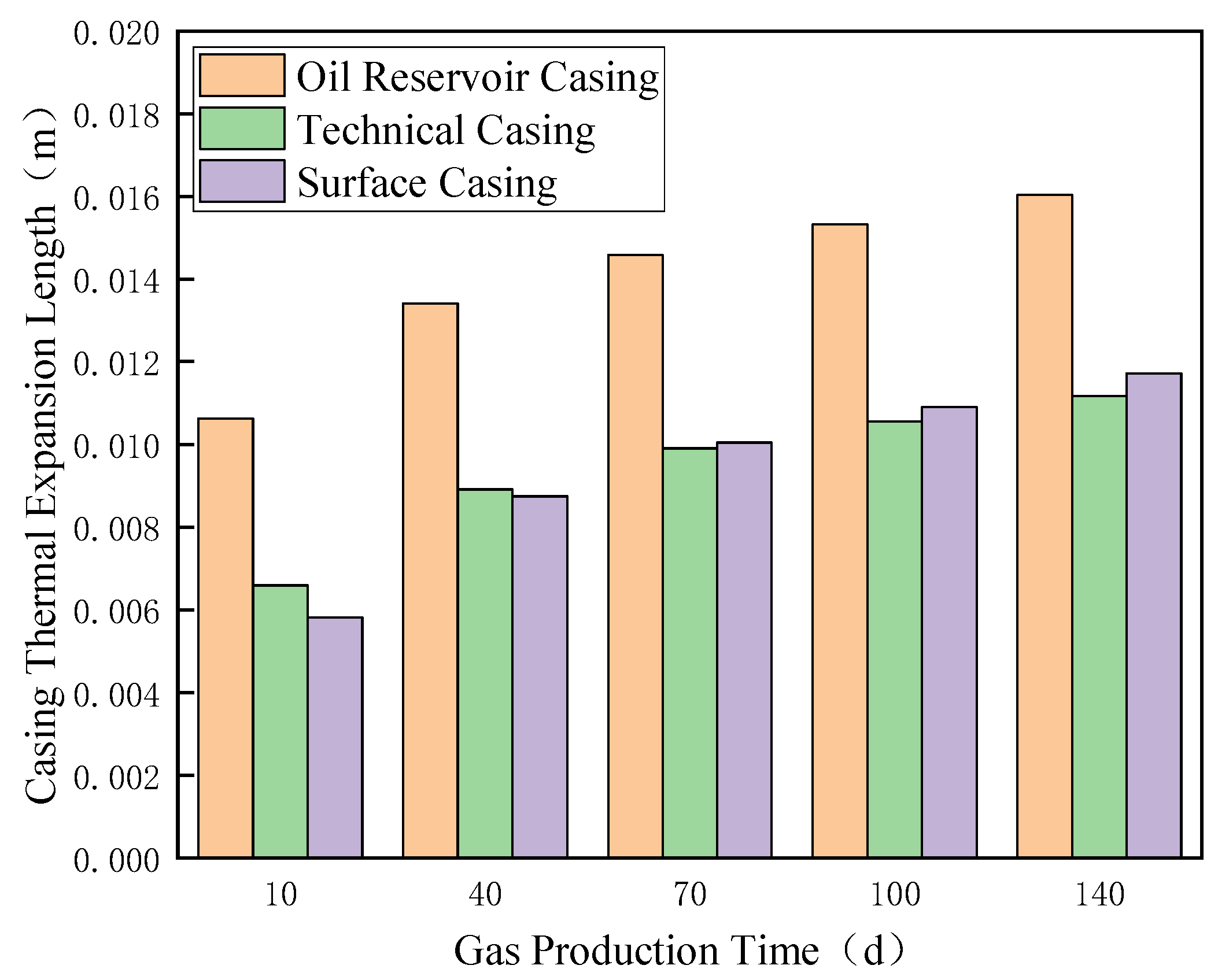
4.2.1. Production Phase Analysis
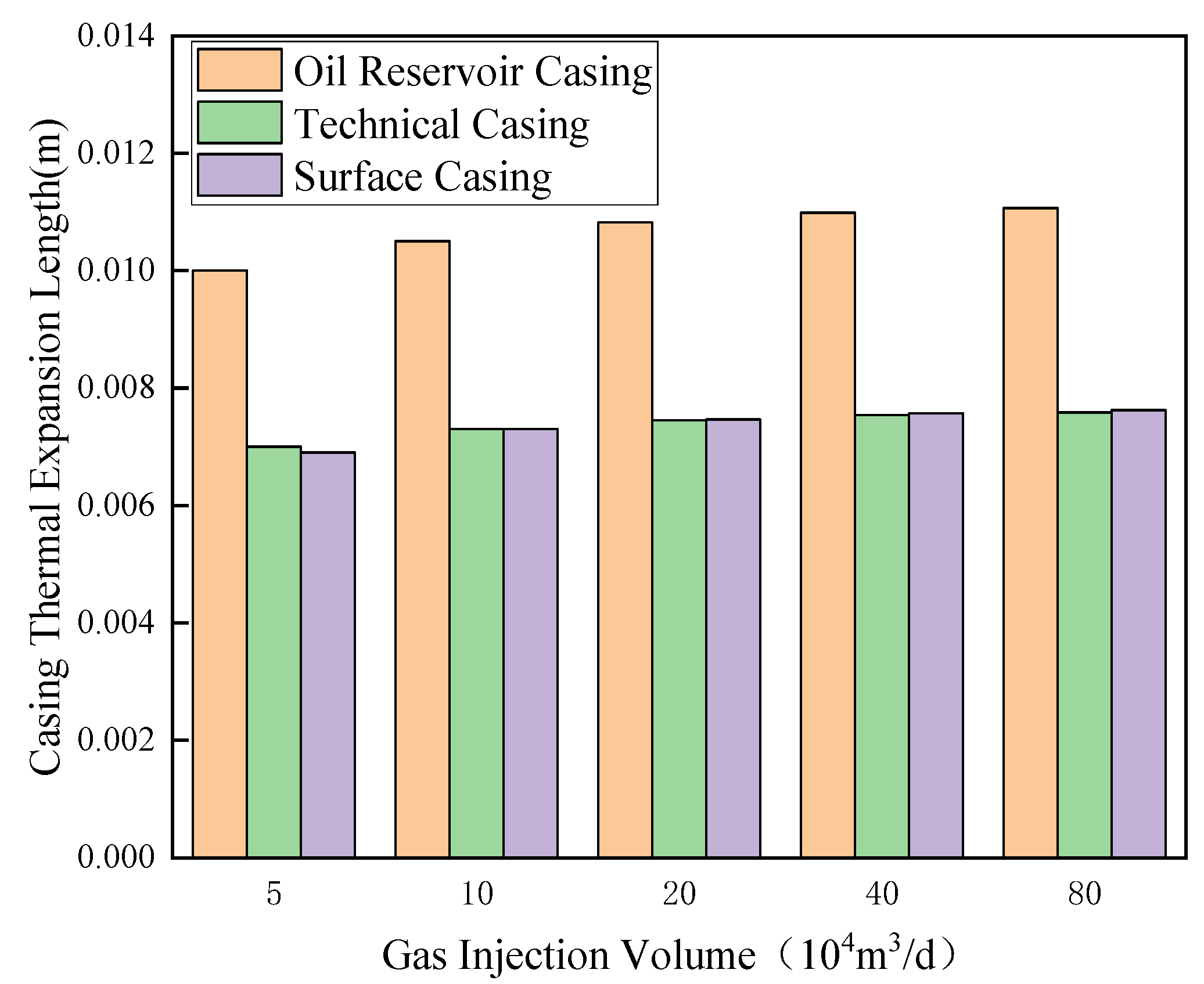
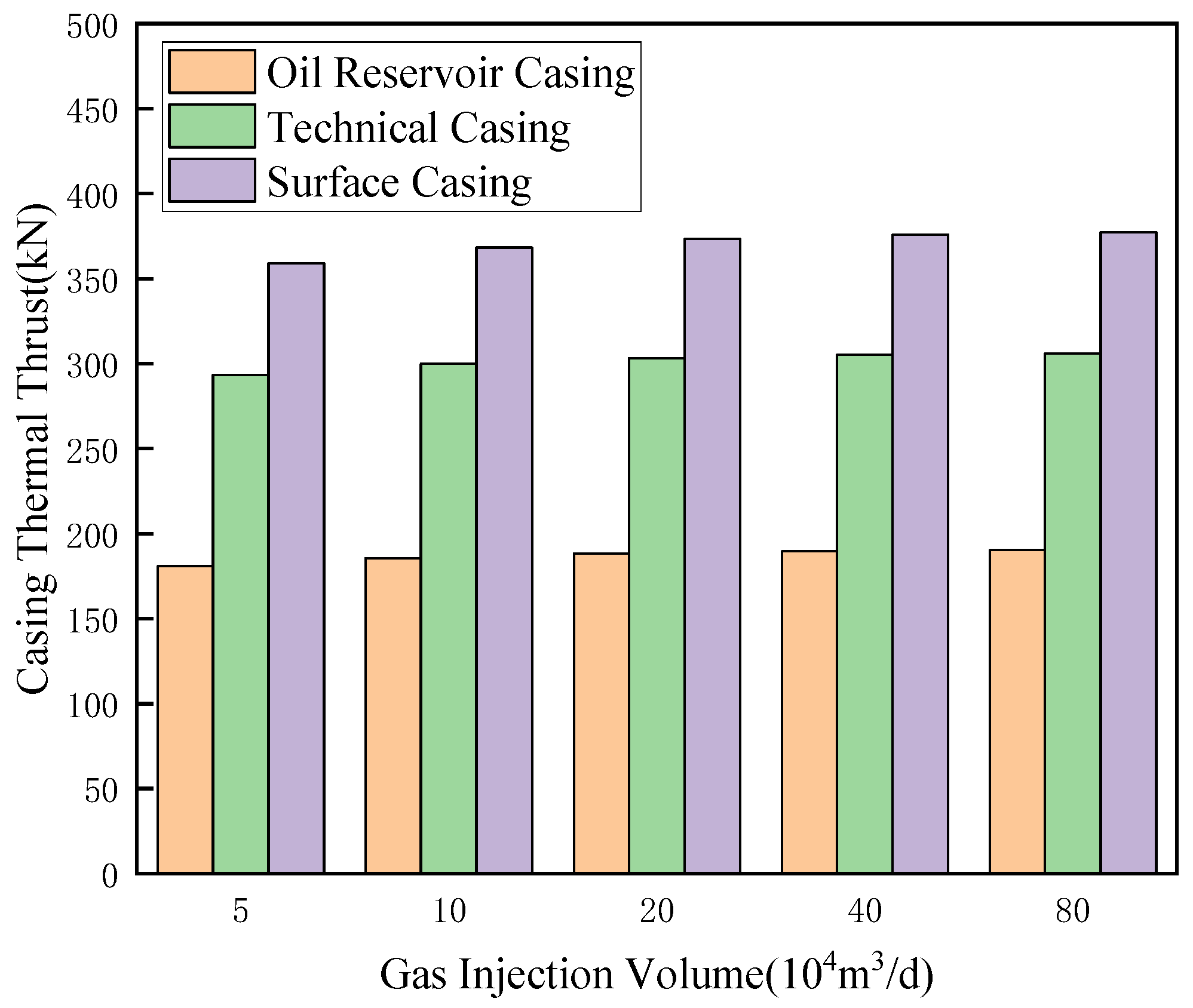
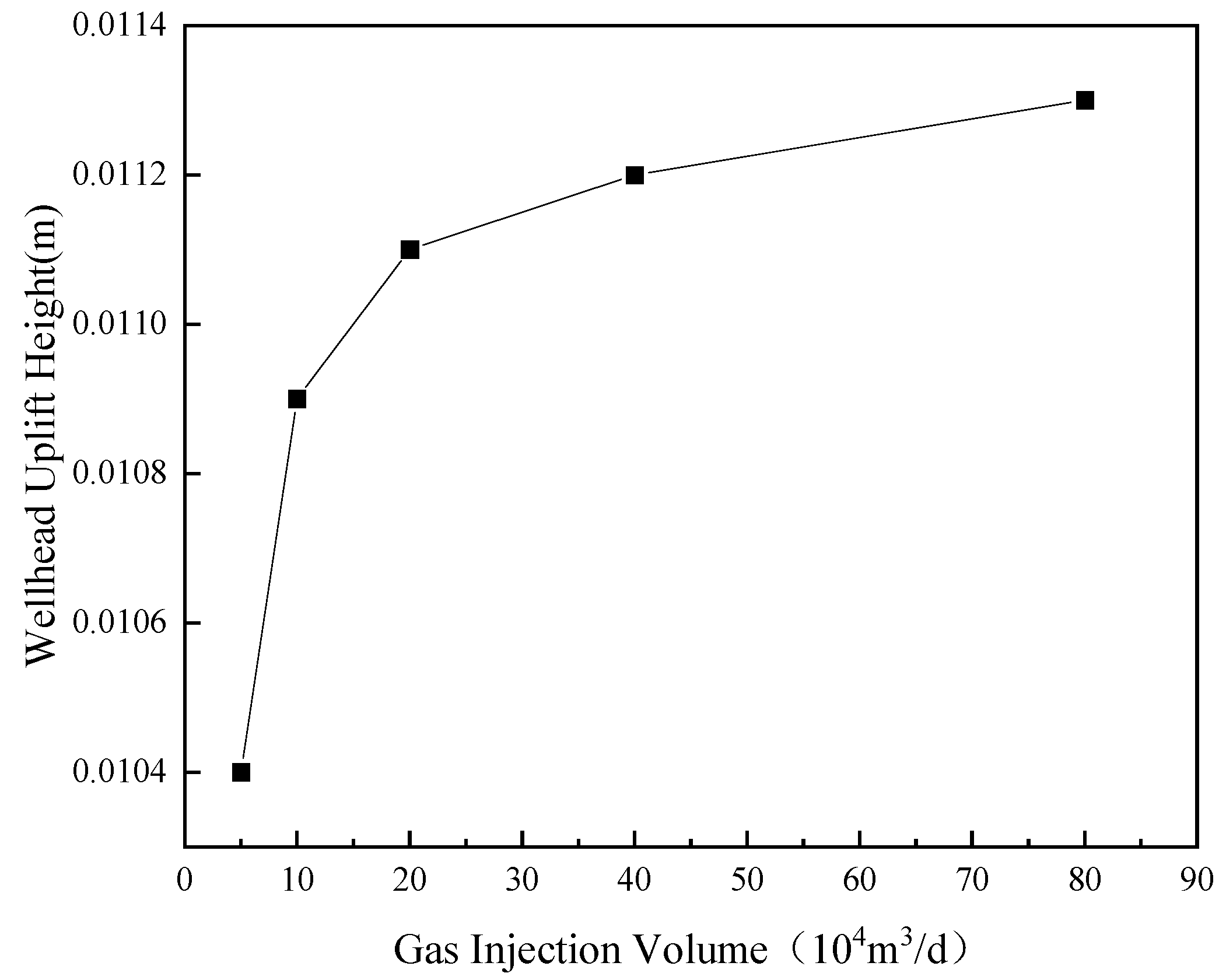
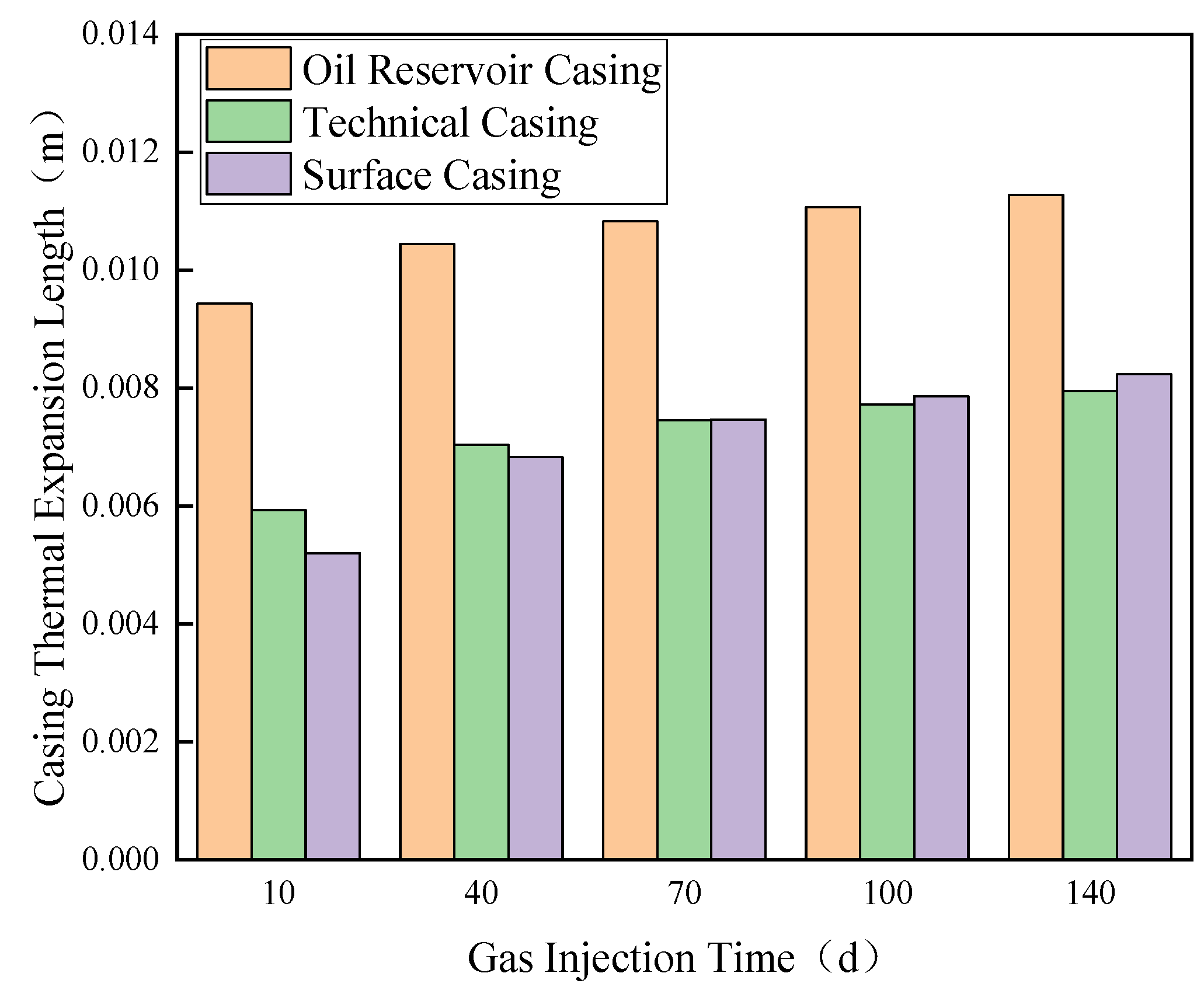
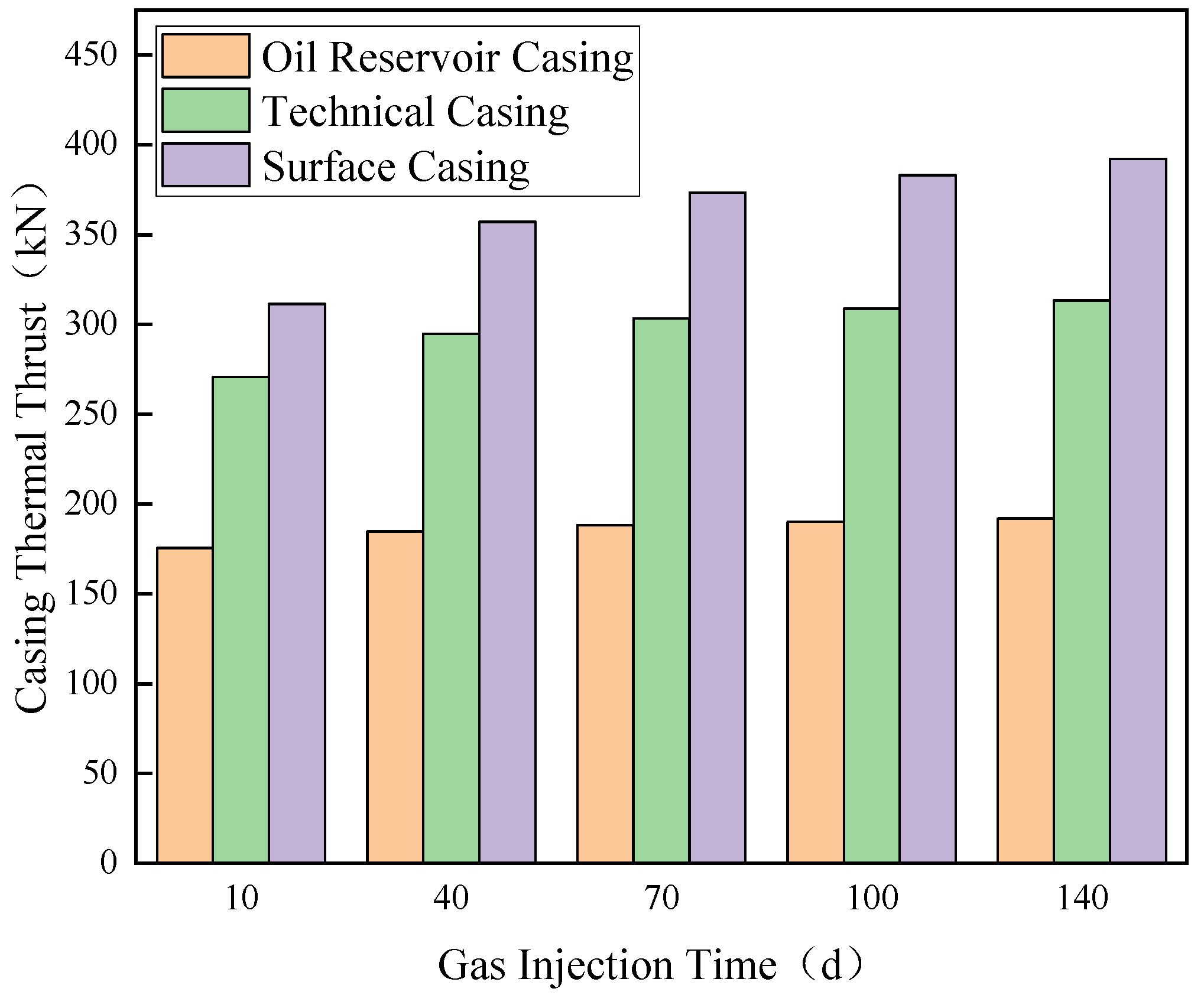
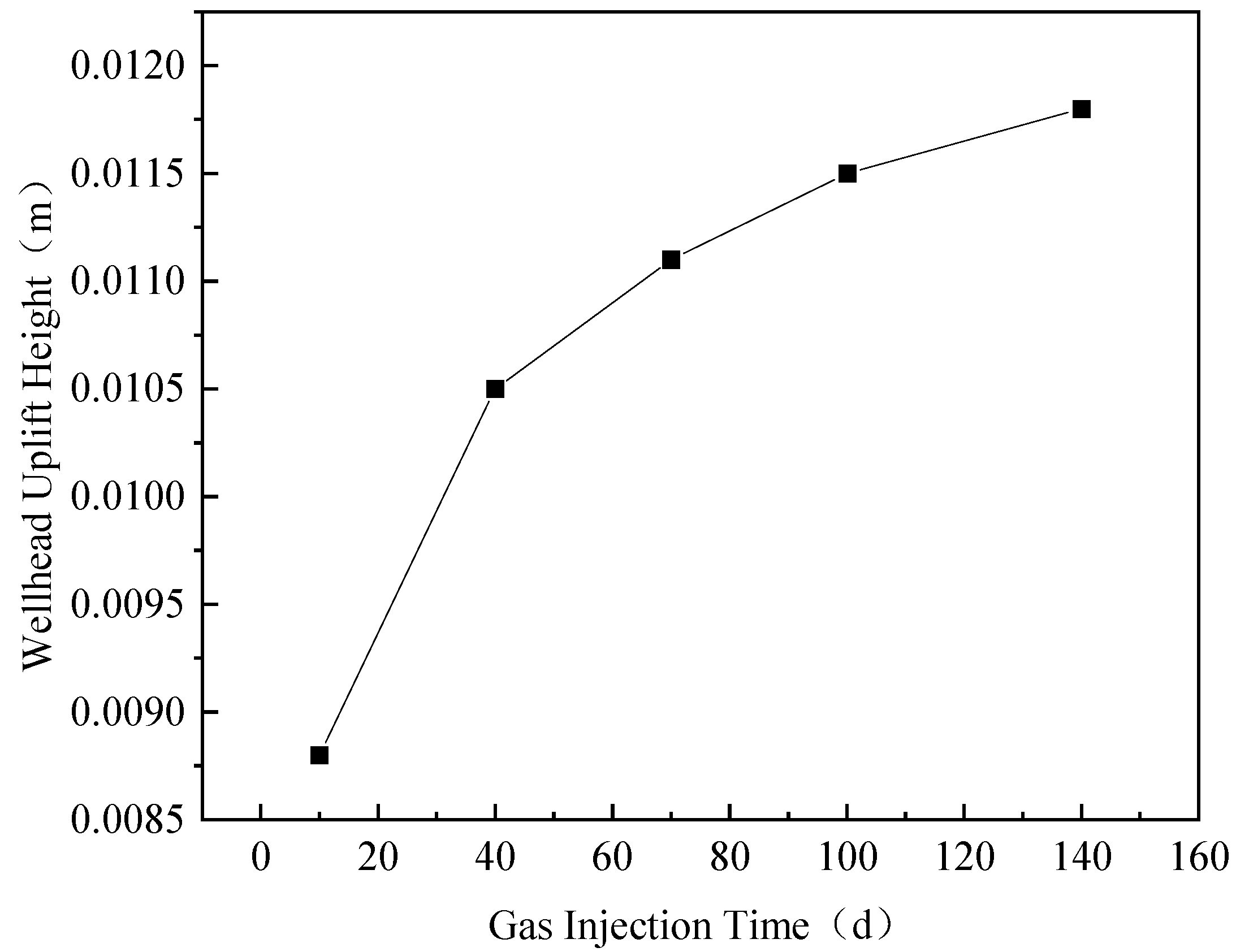
4.2.2. Gas Injection Phase
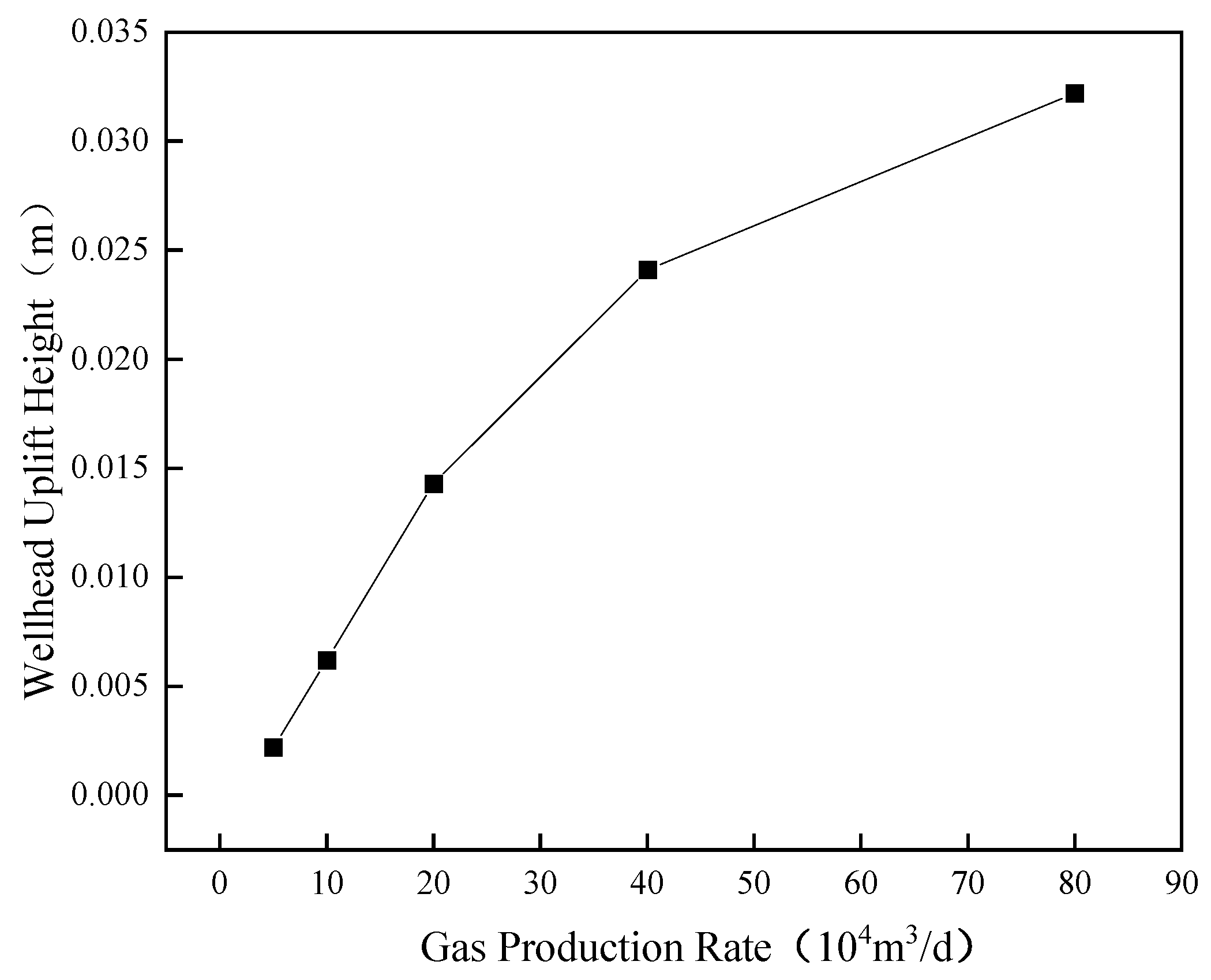
4.3. Prediction of Wellhead Elevation Under Different Operating Conditions
4.3.1. Normal Condition Analysis
4.3.2. Extreme Condition Analysis
5. Conclusions
- (1)
- During gas injection, the elevated temperature of injected gas near the wellhead compared to the formation temperature leads to an increase in casing temperature. As formation depth increases, the formation temperature gradually rises. When the formation temperature exceeds the temperature of the gas inside the tubing, the wellbore temperature field begins to decrease.
- (2)
- Based on the wellbore temperature field calculation model and the wellhead elevation prediction model, the wellhead elevation during the gas injection phase of well A-6 is calculated. The model is validated using field data, providing a reference for predicting wellhead elevation in practical applications.
- (3)
- By analyzing dynamic parameters such as gas production time, production rate, gas injection time, and injection rate, key factors influencing wellhead elevation are identified. Wellhead elevations under normal and extreme production conditions are predicted.
- (4)
- Based on the prediction of wellhead uplift height and in consideration of enterprise production requirements, production rates should be appropriately reduced when the calculated uplift height is relatively high, ensuring the stable and safe operation of injection and production wells.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miao, J.; Qin, H.Y.; Dai, J.; Jiang, X.D.; Shi, J. Analysis of influencing factors and countermeasures for wellhead uplift in deepwater gas fields. Offshore Oil 2023, 43, 94–98. [Google Scholar]
- Zheng, S.J.; Xie, R.J.; Huang, Z.Q.; Wang, C.; Wu, Z.Q. Study on prediction of wellhead uplift caused by deepwater high-temperature and high-pressure oil and gas production. China Offshore Oil Gas 2021, 33, 126–134. [Google Scholar]
- Ramey, H.J.J. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Holst, P.H.; Flock, D.L. Wellbore Behaviour During Saturated Steam Injection. J. Can. Pet. Technol. 1966, 5, 184–193. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Heat Transfer During Two-Phase Flow in Wellbores; Part I—Formation Temperature. In Proceedings of the 66th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Dallas, TX, USA, 6–9 October 1991. [Google Scholar]
- Hasan, A.R.; Kabir, C.S. Aspects of Wellbore Heat Transfer During Two-Phase Flow (includes associated papers 30226 and 30970). SPE Prod. Facil. 1994, 9, 211–216. [Google Scholar] [CrossRef]
- Aasen, J.A.; Aadnøy, B.S. Multistring analysis of well growth. In Proceedings of the Society of Petroleum Engineers, Kuala Lumpur, Malaysia, 13–15 September 2004. [Google Scholar]
- Gjonnes, M.; Myhre, I.G. High Angle HPHT Wells. In Proceedings of the Society of Petroleum Engineers, Rio de Janeiro, Brazil, 20–23 June 2005. [Google Scholar]
- Mcspadden, A.R.; Glover, S. Analysis of complex wellhead load events for conductor and surface casing strings. In Proceedings of the Society of Petroleum Engineers, Amsterdam, The Netherlands, 17–19 March 2009. [Google Scholar]
- Jing, J.; Shan, H.; Zhu, X.; Luo, H.; Sun, H.; Eryue, X. 2023. Analysis of wellhead growth mechanism and influencing factors of offshore gas wells based on gas-liquid two-phase. Geoenergy Sci. Eng. 2023, 223, 211541. [Google Scholar]
- Zhao, J.Z. Key engineering technologies of Wen 23 underground gas storage. Pet. Drill. Technol. 2019, 47, 18–24. [Google Scholar]
- Wei, S.Q.; Rong, W.; Yang, X.; Pan, Z.; Liu, L.; Yang, K.; Zhang, Y.; Li, H. Safety Evaluation and Treatment of Annular Pressure in Injection-Production Wells of Suqiao Gas Storage; China University of Petroleum: Beijing, China, 2022. [Google Scholar]
- Yuan, G.J.; Zhang, H.; Jin, G.T.; Xia, Y. Current status and development suggestions of drilling and completion technologies for underground gas storage in China. Pet. Drill. Tech. 2020, 48, 1–7. [Google Scholar]
- Gong, N.; Li, J.; Chen, Y.; Jia, L.; Xu, T. Analysis of causes and countermeasures for wellhead uplift in offshore oilfield production wells. China Pet. Mach. 2017, 45, 51–55. [Google Scholar]
- Pang, D.H. Wellhead uplift and sensitivity analysis of deepwater subsea wells. China Pet. Chem. Stand. Qual. 2022, 42, 135–137. [Google Scholar]
- Wang, X.Q. Research and application of solutions for wellhead uplift in Bohai A oilfield. Tianjin Chem. Ind. 2023, 37, 50–53. [Google Scholar]
- Guo, X.; Song, G. Prediction of Temperature and Pressure in Gas Wellbore; Science Press: Beijing, China, 2016. [Google Scholar]
- Wang, J.J.; Zeng, X.J.; Jia, S.P.; Sui, X.F.; Zhang, Y.X.; He, H.J. Prediction and analysis of influencing factors of wellbore temperature field in gas storage injection-production wells. Sci. Technol. Eng. 2022, 22, 7890–7902. [Google Scholar]
- Xiao, X.J.; Jiang, H.Q.; Liu, Y.W.; Zhang, J.; Wan, Y.; Wang, X.; Ouyang, W. Calculation method of wellbore temperature for high-temperature and high-pressure gas wells with complex wellbore structures. Sci. Technol. Rev. 2011, 29, 32–37. [Google Scholar]
- Zhang, H.; Shen, R.C.; Liang, Q.M.; Dong, W.T. Coupled analysis of temperature and pressure in injection-production wells of underground gas storage. Sci. Technol. Eng. 2017, 17, 66–73. [Google Scholar]
- Li, J.; Wang, H.; Zhang, H.; Zheng, G.W.; Liu, S.J.; Sun, T.F. Study on prediction of wellhead uplift distance for heavy oil thermal recovery wells in Bohai Sea. J. Eng. Thermophys. 2019, 40, 599–604. [Google Scholar]
- Liu, C.M. Research on optimization of wellhead uplift calculation for offshore high-temperature gas wells. Pet. Ind. Technol. Superv. 2024, 40, 42–45, 65. [Google Scholar]





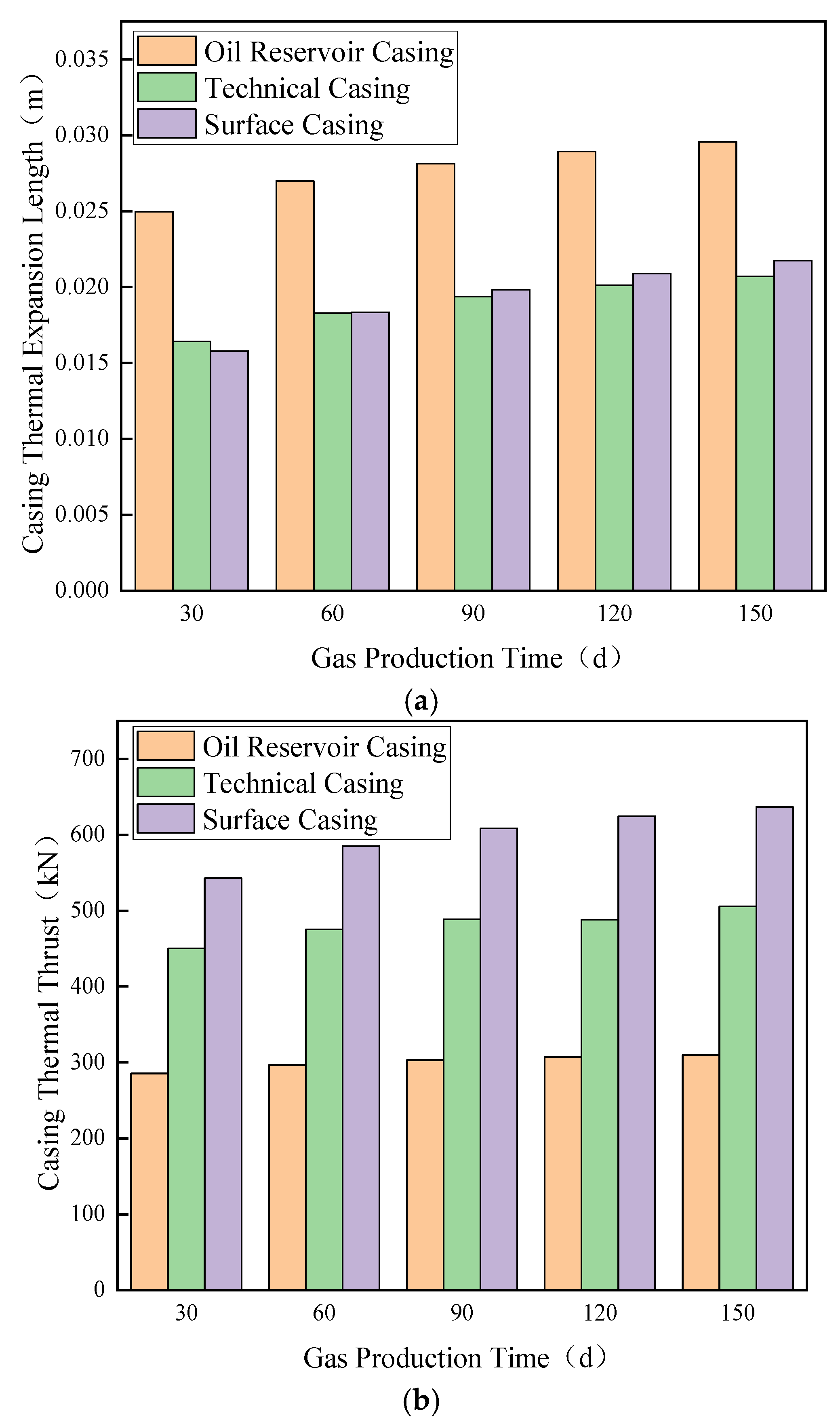

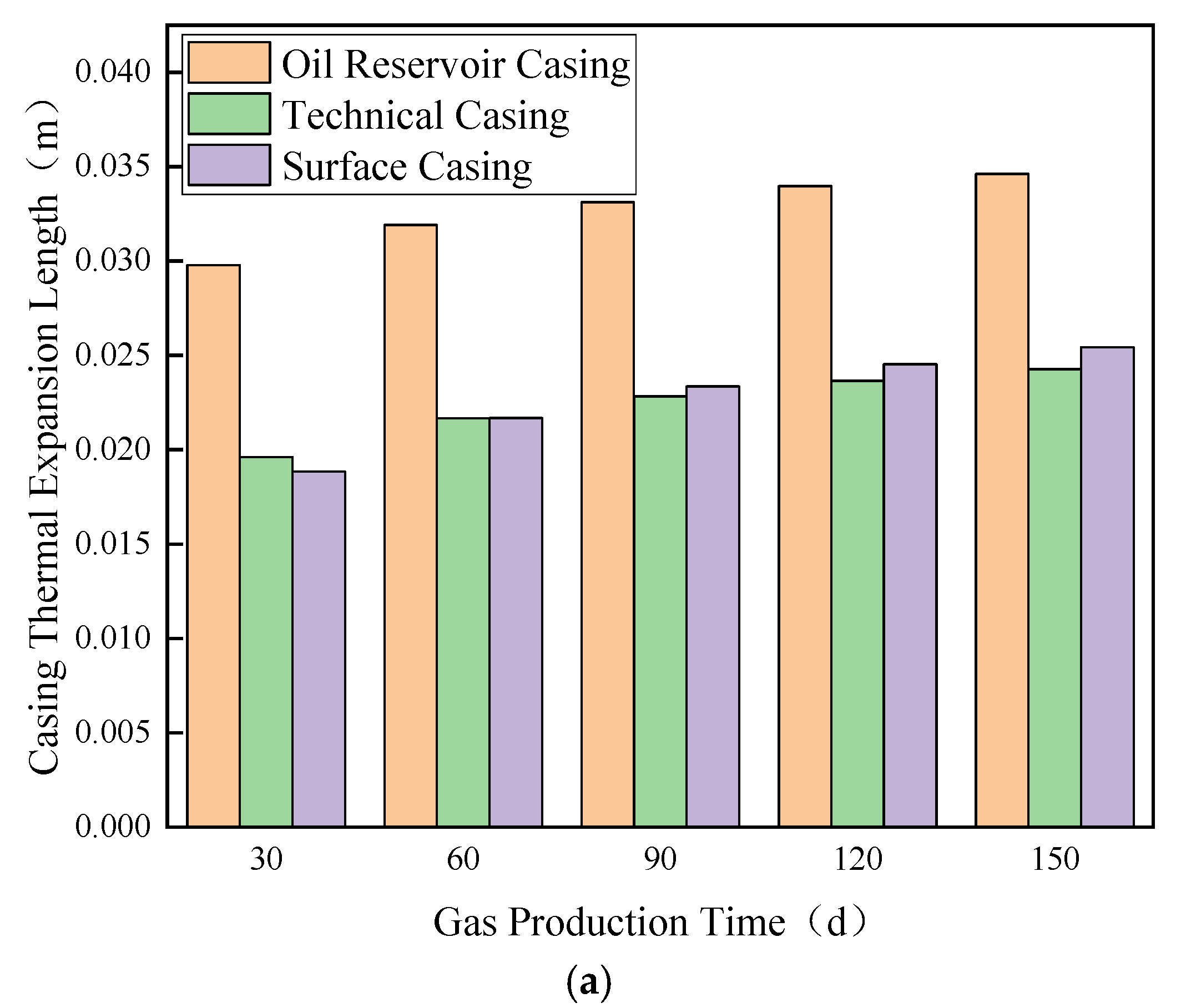
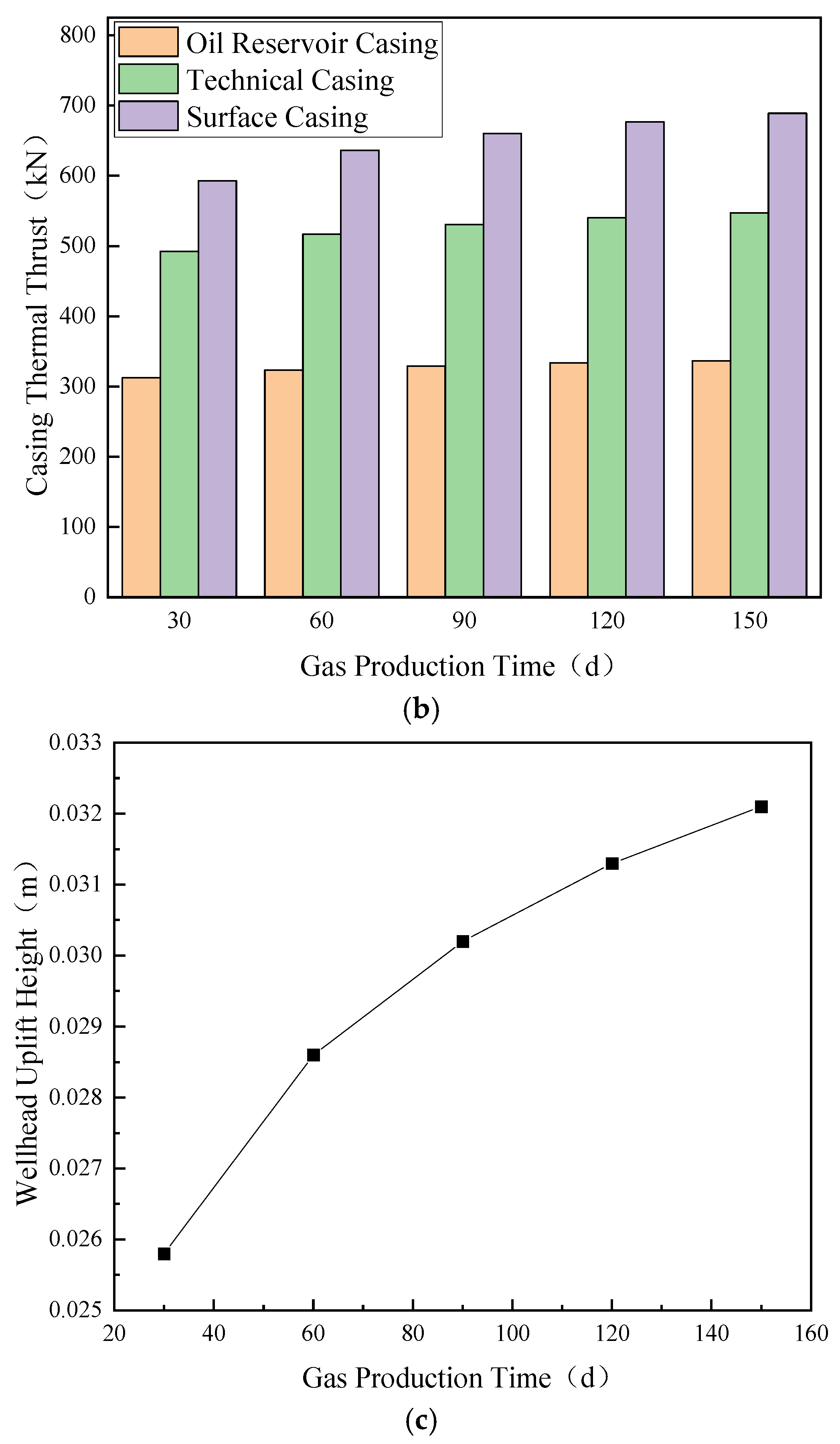
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Well depth | 3200 m | Average gas injection rate | 21.4 × 104 m3/d |
| Packer position | 2800 m | Gas injection time | 10 d/80 d |
| Outer diameter of oil layer casing | 88.9 mm | Formation temperature | 114.3 °C |
| Outer diameter of technical casing | 177.8 mm | Geothermal gradient | 3.44 °C/100 m |
| Outer diameter of surface casing | 273.1 mm | Steel grade | P110 |
| Ground thermal conductivity | 2.06/[W·(m·°C)−1] | Cement ring thermal conductivity | 0.98/[W·(m·°C)−1] |
| Ground thermal diffusivity | 0.0037/(m2·h−1) | Oil and casing pipe thermal conductivity | 45.35/[W·(m·°C)−1] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Wang, J.; Zhao, G.; Guan, F.; Cao, J.; Jia, S. Research on Wellhead Uplift Prediction for Underground Gas Storage Wells. Energies 2025, 18, 5331. https://doi.org/10.3390/en18205331
Shen Z, Wang J, Zhao G, Guan F, Cao J, Jia S. Research on Wellhead Uplift Prediction for Underground Gas Storage Wells. Energies. 2025; 18(20):5331. https://doi.org/10.3390/en18205331
Chicago/Turabian StyleShen, Zhaoxi, Jianjun Wang, Gang Zhao, Fatian Guan, Junfeng Cao, and Shanpo Jia. 2025. "Research on Wellhead Uplift Prediction for Underground Gas Storage Wells" Energies 18, no. 20: 5331. https://doi.org/10.3390/en18205331
APA StyleShen, Z., Wang, J., Zhao, G., Guan, F., Cao, J., & Jia, S. (2025). Research on Wellhead Uplift Prediction for Underground Gas Storage Wells. Energies, 18(20), 5331. https://doi.org/10.3390/en18205331






