Testing Method for Non-Isothermal Radial Wall Jets from Ceiling Diffusers Used in Building Ventilation
Abstract
1. Introduction
2. Methods
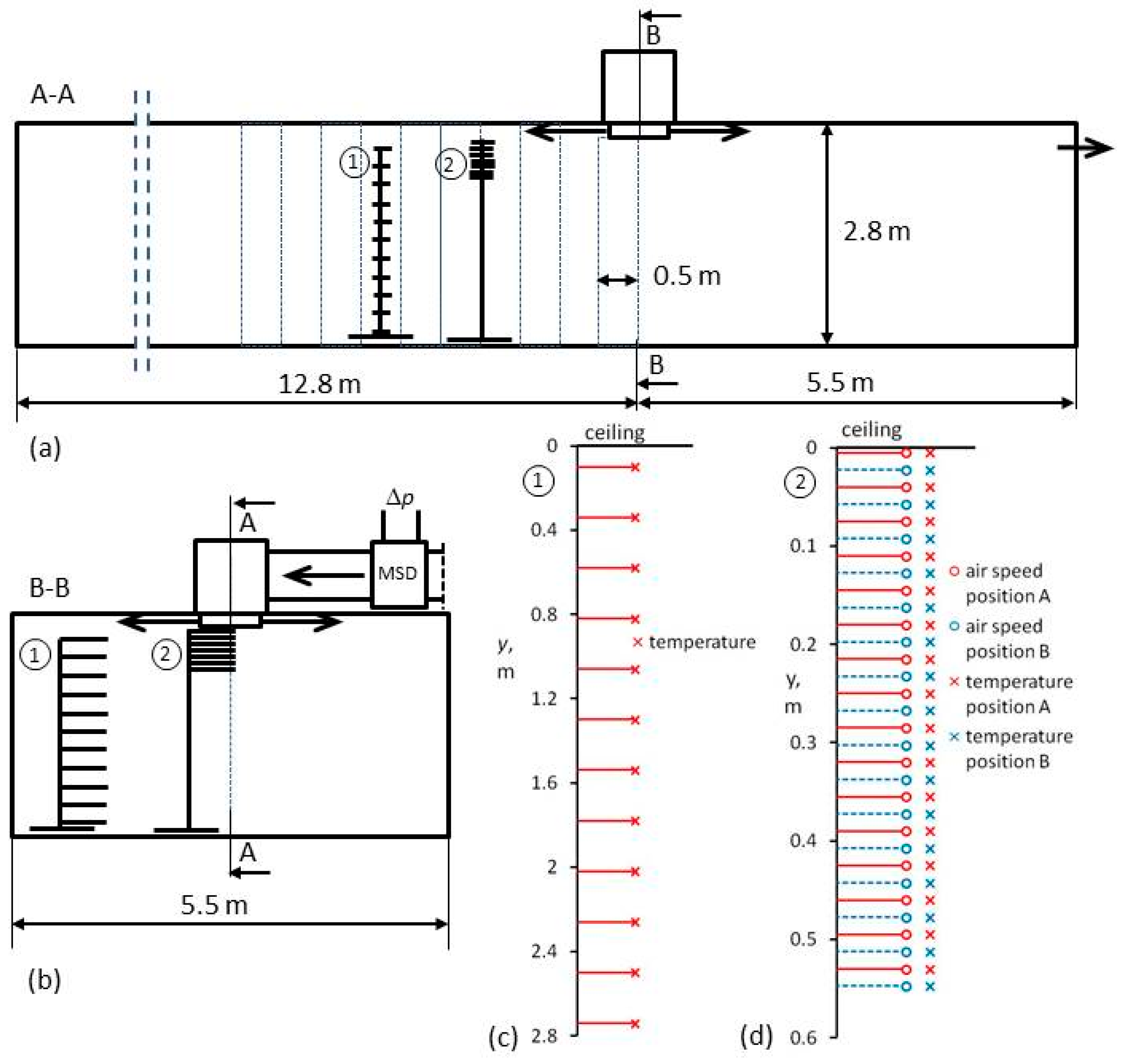
2.1. Measurement Method
- ▪
- The average air temperature in the room was determined based on the readings of thermocouples placed on a vertical stand; the supply air temperature was set depending on the assumed temperature difference in a given measurement series;
- ▪
- The supply and exhaust air flow rates were varied using fan inverters; the flow rate was measured using a circular MSD air flow unit, which was calibrated using the TSI 8710 measuring capture hood shown in Figure 4; and the pressure difference across the MSD air flow unit was measured using a precision manometer from Furness Controls;
- ▪
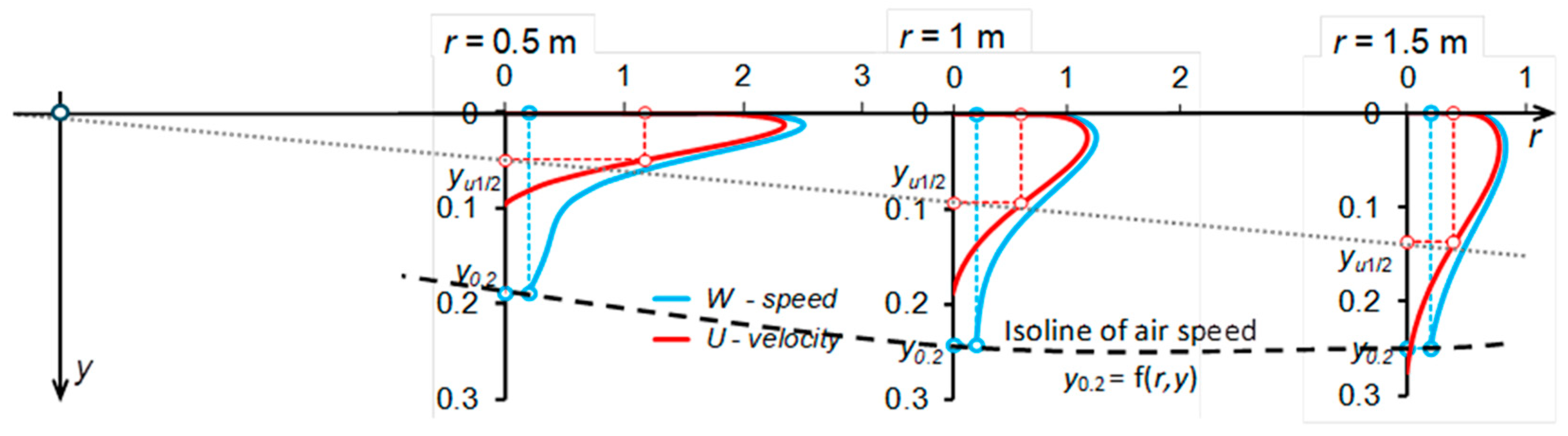
- Air velocity measurements in the jet were performed using hot-sphere anemometric sensors positioned horizontally, Figure 2. The distance between the air speed sensors was 0.035 m; during the measurement, the rack with anemometric transducers and thermocouples, marked as (2) in Figure 3d, was moved down 0.0175 m from the starting position A to position B to be the same distance from diffuser, r, and air speed and temperature were measured in 32 points. Measurements started at a distance of 0.5 m from the center of the diffuser, and then sensors were moved every 0.5 m; the average time was 360 s;
- ▪
- Measurements were carried out up to a radial distance at which all the anemometer sensors showed a speed value lower than 0.2 m/s.
2.2. Envelopes of Isothermal RWJs
2.3. Envelopes of Non-Isothermal RWJs
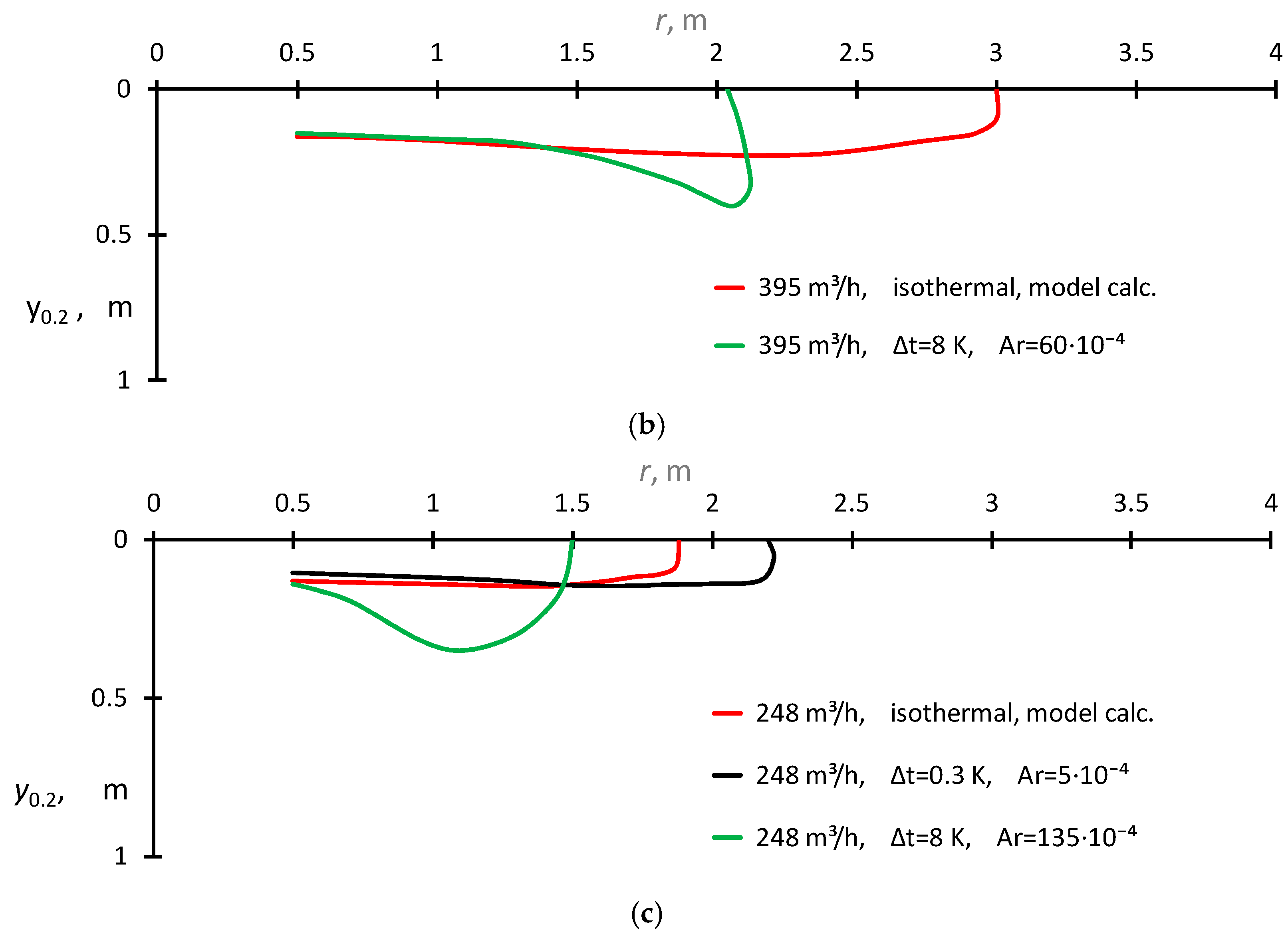
3. Results and Discussion
4. Conclusions
- -
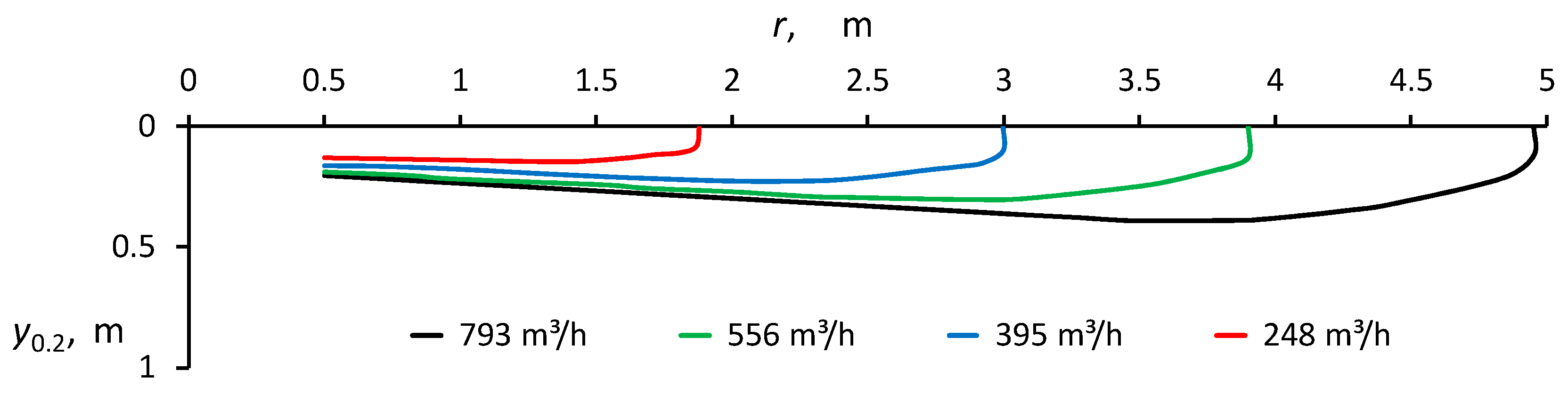
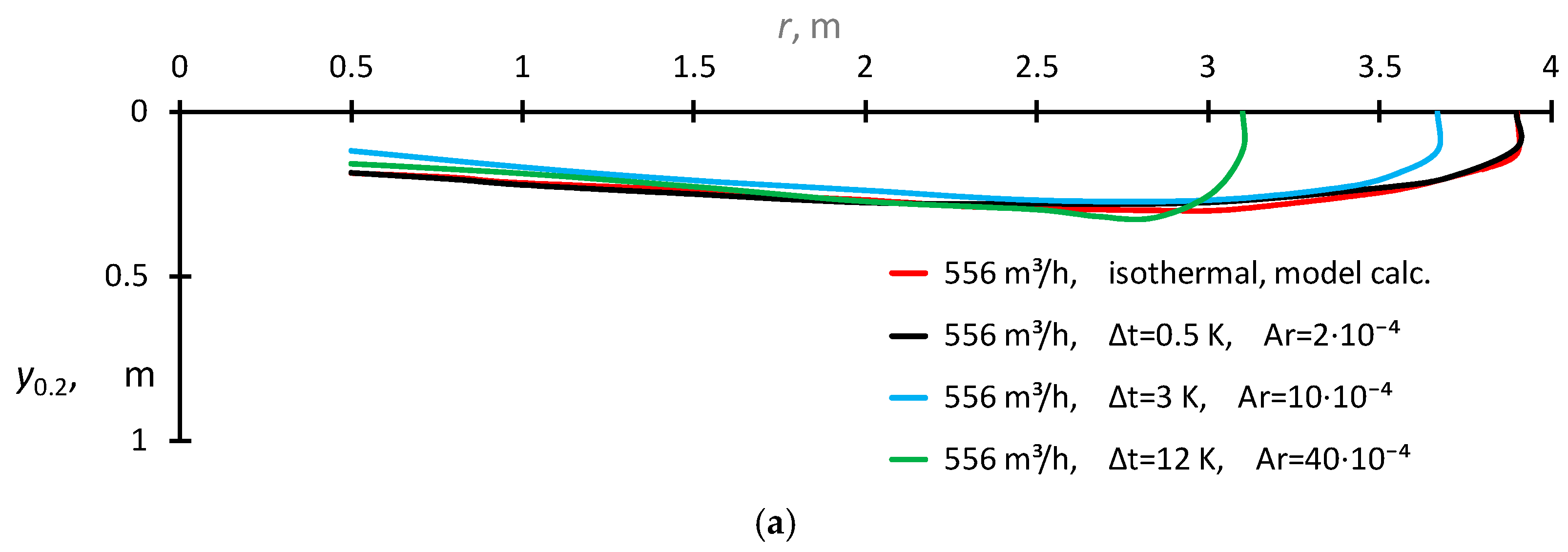
- A comparison of the measured speed envelope, determined using the assumed terminal value of the speed, e.g., W = 0.2 m/s, with the calculated envelope for the isothermal radial wall jet obtained using the proposed model;-
- -
- The value of the boundary Aro number used as a criterion for the jet dumping risk assessment;
- -
- The test results which showed that the risk of jet dumping increases significantly for Aro numbers higher than approximately 50 × 10−4.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area, m2 |
| a | coefficient |
| Ar | Archimedes number |
| g | acceleration due to gravity, m/s2 |
| K | velocity decay coefficient |
| L | throw length, m |
| M | mean motion momentum flux, kg · m/s2 |
| n | exponent |
| r | radial distance, m |
| Re | Reynolds number, |
| RMS | root mean square, m/s |
| T | temperature, °C |
| U | velocity, m/s |
| V | volume flux, m3/s |
| W | mean speed, m/s |
| y | distance normal to the ceiling, m |
| β | air volume expansion coefficient, 1/K |
| ρ | density, kg/m3 |
| η | dimensionless distance from the wall |
| ν | kinematic viscosity of air, m2/s |
| Subscripts | |
| M | momentum flux |
| i | indoor |
| m | maximum |
| o | outlet |
| u | velocity |
References
- Ratajczak, K.; Amanowicz, Ł.; Pałaszyńska, K.; Pawlak, F.; Sinacka, J. Recent Achievements in Research on Thermal Comfort and Ventilation in the Aspect of Providing People with Appropriate Conditions in Different Types of Buildings—Semi-Systematic Review. Energies 2023, 16, 6254. [Google Scholar] [CrossRef]
- Introducing High Performance Air System. An AMCA International White Paper. Available online: www.krueger-hvac.com/files/white%20papers/white_paper_amca_hpas.pdf (accessed on 27 November 2024).
- Amanowicz, Ł.; Ratajczak, K.; Dudkiewicz, E. Recent Advancements in Ventilation Systems Used to Decrease Energy Consumption in Buildings—Literature Review. Energies 2023, 16, 1853. [Google Scholar] [CrossRef]
- Hydeman, M.; Taylor, S.; Stein, J.; Kolderup, E.; Hong, T. Advanced Variable Air Volume System Design Guide; California Energy Commission, Energy Design Resour: Sacramento, CA, USA, 2003. [Google Scholar]
- Okochi, G.S.; Yao, Y. A Review of Recent Developments and Technological Advancements of Variable-Air-Volume (VAV) Air-Conditioning Systems. Renew. Sustain. Energy Rev. 2016, 59, 784–817. [Google Scholar] [CrossRef]
- Kang, S.-H.; Kim, H.-J.; Cho, Y.-H. A Study on the Control Method of Single Duct VAV Terminal Unit through the Determination of Proper Minimum Air Flow. Energy Build. 2014, 69, 464–472. [Google Scholar] [CrossRef]
- Nassif, N.; Tahmasebi, M.; Ridwana, I.; Ebrahimi, P. New Optimal Supply Air Temperature and Minimum Zone Air Flow Resetting Strategies for VAV Systems. Buildings 2022, 12, 348. [Google Scholar] [CrossRef]
- Hurnik, M. Novel Cylindrical Induction Controller and Its Application in VAV Air Conditioning System in an Office Building. Energy Build. 2016, 130, 341–349. [Google Scholar] [CrossRef]
- Herzog, K.; Sullens, W.; Ivanovich, M.; Perez, H. Achieving High Satisfaction in High Performance Buildings. In Proceedings of the Conference: ACEEE Summer Study on Energy Efficiency in Buildings, Portland, Oregon, 12–15 August 2019. [Google Scholar]
- Awbi, H.B. Ventilation of Buildings, 2nd ed.; Spoon Press: London, UK; New York, NY, USA, 2002. [Google Scholar]
- Szczepanik-Scislo, N.; Schnotale, J. An Air Terminal Device with a Changing Geometry to Improve Indoor Air Quality for VAV Ventilation Systems. Energies 2020, 13, 4947. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Brambley, M.R.; Futrell, B. Performance Simulation and Analysis of Occupancy-Based Control for Office Buildings with Variable-Air-Volume Systems. Energies 2020, 13, 3756. [Google Scholar] [CrossRef]
- Melikov, A.; Yordanova, B.; Bozkhov, L.; Zboril, V.; Kosonen, R. Human Response to Thermal Environment in Rooms with Chilled Beams. In Proceedings of the CLIMA, 2007, Helsinki, Finland, 10–14 June 2007; 2007; pp. 10–14. [Google Scholar]
- Arens, E.; Zhang, H.; Hoyt, T.; Kaam, S.; Goins, J.; Bauman, F.; Zhai, Y.; Webster, T.; West, B.; Paliaga, G.; et al. Thermal and Air Quality Acceptability in Buildings That Reduce Energy by Reducing Minimun Airflow from Overhead Diffusers. 2012. Available online: https://core.ac.uk/download/pdf/13801478.pdf (accessed on 5 January 2025).
- Arens, E.; Zhang, H.; Hoyt, T.; Kaam, S.; Bauman, F.; Zhai, Y.; Paliaga, G.; Stein, J.; Seidl, R.; Tully, B.; et al. Effects of Diffuser Airflow Minima on Occupant Comfort, Air Mixing, and Building Energy Use (RP-1515). Sci. Technol. Built Environ. 2015, 21, 1075–1090. [Google Scholar] [CrossRef]
- Saheb, Y.; Becirspahic, S.; Simon, J. Effect of the Certification on Chillers Energy Efficiency. In Proceedings of the IEECB’06, Frankfurt, Germany, 26–27 April 2006; p. 137. [Google Scholar]
- Wu, Y.; Mustakallio, P.; Kosonen, R.; Kaukola, T.; Chen, J.; Liu, H.; Li, B. Experimental Study of Five Different VAV Air Terminal Devices under Variable Heat Gain Conditions in Simulated Office and Meeting Rooms. Build. Environ. 2022, 209, 108641. [Google Scholar] [CrossRef]
- Rajaratnam, N. Turbulent Jets; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands; Oxford, UK; New York, NY, USA, 1976. [Google Scholar]
- Beltaos, S.; Rajaratnam, N. Impinging Circular Turbulent Jets. J. Hydr. Div. 1974, 100, 1313–1328. [Google Scholar] [CrossRef]
- Poreh, M.; Tsuei, Y.G.; Cermak, J.E. Investigation of a Turbulent Radial Wall Jet. J. Appl. Mech. 1967, 34, 457–463. [Google Scholar] [CrossRef]
- Tanaka, T.; Tanaka, E. Experimental Studies of a Radial Turbulent Jet: 2nd Report, Wall Jet on a Flat Smooth Plate. Bull. JSME 1977, 20, 209–215. [Google Scholar] [CrossRef]
- Mierzwinski, S.; Popiolek, Z. Anemometria i Jej Zastosowanie w Badaniach Modelowych Procesów Odpylania i Wentylacji; Zakład Narodowy Imienia Osolinskich; Wydawnictwo Polskiej Akademii Nauk: Wrocław, Poland, 1980; Available online: https://delibra.bg.polsl.pl/Content/25922/BCPS_29531_1980_Anemometria-i-jej-za.pdf (accessed on 14 January 2025).
- Hargrave, G.K.; Williams, T.C.; Anandarajah, K.; Halliwell, N.A. The 3D Velocity Field of an Impacting Turbulent Jet. J. Phys. Conf. Ser. 2006, 45, 162. [Google Scholar] [CrossRef]
- Shademan, M.; Balachandar, R.; Roussinova, V.; Barron, R. Round Impinging Jets with Relatively Large Stand-off Distance. Phys. Fluids 2016, 28, 075107. [Google Scholar] [CrossRef]
- Tummers, M.J.; Jacobse, J.; Voorbrood, S.G.J. Turbulent Flow in the near Field of a Round Impinging Jet. Int. J. Heat Mass Transf. 2011, 54, 4939–4948. [Google Scholar] [CrossRef]
- Hurnik, M.; Kaczmarczyk, J.; Popiolek, Z. Study of Radial Wall Jets from Ceiling Diffusers at Variable Air Volume. Energies 2021, 14, 240. [Google Scholar] [CrossRef]
- Yadav, H.; Agrawal, A. Self-Similar Behavior of Turbulent Impinging Jet Based upon Outer Scaling and Dynamics of Secondary Peak in Heat Transfer. Int. J. Heat Fluid Flow 2018, 72, 123–142. [Google Scholar] [CrossRef]
- Van Hout, R.; Rinsky, V.; Grobman, Y.G. Experimental Study of a Round Jet Impinging on a Flat Surface: Flow Field and Vortex Characteristics in the Wall Jet. Int. J. Heat Fluid Flow 2018, 70, 41–58. [Google Scholar] [CrossRef]
- EN 12238; Ventilation for Buildings—Air Terminal Devices-Aerodynamic Testing and Rating for Mixed Flow Application. European Standard: Luxembourg, 2001.




| Measuring Instrument | Uncertainty |
|---|---|
| TSI 8710 capture hood, TSI Incorporated, Shoreview, Minnesota, USA | 3% of reading |
| Precision micro-manometer of Furness Controls Limited, Bexhill-on-Sea, England | 0.005 + 0.005 Δp Pa |
| MTT-302 Multichannel thermocouple type T thermometer, Sensor Electronic, Gliwice, Poland | 0.3 K |
| AirDistSys 5000 16 channel air speed measurement system, Sensor Electronic, Gliwice, Poland | 0.03 + 0.02 · W m/s |
| - | 0.906 | |
| ro | m | −0.05 |
| Ao | m2 | 0.0356 |
| Ao0.5 | m | 0.189 |
| - | −0.00122 | |
| - | 1.71 |
| Vo | m3/h | 793 | 556 | 395 | 248 |
| Vo | m3/s | 0.220 | 0.154 | 0.1097 | 0.0689 |
| Mo/p | m4/s2 | 1.363 | 0.670 | 0.338 | 0.133 |
| Uo | m/s | 6.19 | 4.34 | 3.08 | 1.94 |
| Series | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Vo, m3/h | 793 | 556 | 556 | 556 | 556 | 395 | 395 | 248 | 248 | 248 |
| ∆to, K | isotherm | isotherm | 0.5 | 3 | 12 | isotherm | 8 | isotherm | 0.3 | 8 |
| Ar | 0 | 0 | 2 × 10−4 | 10 × 10−4 | 40 × 10−4 | 0 | 60 × 10−4 | 0 | 5 × 10−4 | 135 × 10−4 |
| L0.2, m | 4.9 | 3.9 | 3.9 | 3.7 | 3.1 | 3.0 | 2.1 | 2.0 | 2.2 | 1.5 |
| ymax, m | 0.39 | 0.30 | 0.28 | 0.27 | 0.33 | 0.23 | 0.4 | 0.15 | 0.15 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hurnik, M. Testing Method for Non-Isothermal Radial Wall Jets from Ceiling Diffusers Used in Building Ventilation. Energies 2025, 18, 411. https://doi.org/10.3390/en18020411
Hurnik M. Testing Method for Non-Isothermal Radial Wall Jets from Ceiling Diffusers Used in Building Ventilation. Energies. 2025; 18(2):411. https://doi.org/10.3390/en18020411
Chicago/Turabian StyleHurnik, Maria. 2025. "Testing Method for Non-Isothermal Radial Wall Jets from Ceiling Diffusers Used in Building Ventilation" Energies 18, no. 2: 411. https://doi.org/10.3390/en18020411
APA StyleHurnik, M. (2025). Testing Method for Non-Isothermal Radial Wall Jets from Ceiling Diffusers Used in Building Ventilation. Energies, 18(2), 411. https://doi.org/10.3390/en18020411






