Optimal µPMU Placement Considering Node Importance and Multiple Deployed Monitoring Devices in Distribution Networks
Abstract
1. Introduction
- (1)
- The number of μPMUs required to realize the global observability of the DN is large and the cost of placement is high. The number of PMUs required to realize the global observability of a DN is significantly higher than that of transmission networks due to the small number of lines connected to a single node, and, under the same circumstances, only 1/4 of the number of nodes of PMUs are required to realize the global observability of transmission grids, while 1/3 of the number of PMUs are required for the DN [10]; meanwhile, the larger number of nodes of DN further raises the requirement of the number of μPMUs. Although the above studies [10,11,12,18] reduced the number of configured μPMUs by combining PMUs with existing devices, they all consider only one type of measurement device and do not sufficiently combine multiple measurement devices that exist in the DN, and there is still a large potential to reduce the number of μPMU placements. There is an urgent need to study the μPMU placement scheme for the synergistic optimization of multiple monitoring devices.
- (2)
- It is still difficult to simultaneously balance the number of PMUs and the observability of the system in the event of line breaks [19,20], PMU failures [18,21], and topology changes [22,23] (“special cases” is used to indicate these faults below). First, Refs. [13,14] include single special cases such as line break and μPMU faults in the consideration of μPMU placement, and give the corresponding constraints, which theoretically can guarantee the observation performance of the system if there are enough constraints involved. However, it is undoubtedly difficult to consider a wide variety of DN fault forms, and more general strategies that can ensure observation performance need to be considered. Ref. [5] establishes a joint fault probability of the μPMU placement model, but it needs to collect the occurrence probability of various faults through historical data statistics, which is too idealized and difficult to achieve. Second, some of the methods obtained with second-order observability as a constraint [16,17], which can guarantee system observability in any special case, require more PMUs (about 1.5–2 times), which cannot meet the economy. Some researchers have partly considered the above two points by considering the maximization of measurement redundancy in the objective function [10], which improves the observability of the system under special cases by preferentially placing PMUs at nodes with a higher number of connected branches and increasing the overall number of observations at system nodes. However, this measurement redundancy only considers the overall number of system observations and focuses on placing μPMUs at a few nodes with high measurement redundancy, while neglecting the consideration of the remaining nodes, which does not guarantee the observability of the system under special cases. A typical example is that, in the case of topology transformation, some of the neighboring nodes with open lines have a high risk of losing observability, which should also be prioritized for the placement of μPMUs. Nowadays, supporting the global observability of the system in normal and special cases with a small number of PMUs is still an urgent problem.
- (1)
- To address the issue of the large number of μPMUs required to realize global observability in existing DNs, the observation performance provided by the existing measurement devices for the system is fully utilized, so that they can provide higher observability performance for the system. The number of PMUs required to realize global observability in active DNs is reduced as a result.
- (2)
- We aim in this study at the problem of insufficient observability of the existing μPMU placement scheme in special cases such as line fault and topology change. The observation stability of each node in the DN is analyzed under special cases, and the μPMUs are preferentially placed at critical nodes in the DN that are more relevant to the observation stability, and the observation performance of the system is thus improved.
2. Analysis of DN Observability
- (1)
- The network topology of the power system only considers the electrical topology of the system without considering large-scale geographic distribution or geographic barriers, and the parameters need to be known. This is because the analysis of the observability of the system is built based on reasoning about the power network, due to the limited number of measurement devices, which is not sufficient to install measurement devices at each node. The nodes of the system that are not placed with measurement devices need to be deduced from the data collected by existing measurement devices and the network topology parameters. The above-simplified topology parameters and structure can often be obtained from power operators.
- (2)
- Each measurement device can operate normally, and can correctly measure the required electrical parameters, and ensure that the measurement error is maintained in a certain acceptable range. This is because the essence of the measurement placement problem is a process of reasoning the unknown measurement data through the existing measurement data; to ensure the measurement accuracy of the existing measurement is the premise of deducing the global state of the power system. This assumption is also the premise to meet the stable operation of the power system.
- (3)
- Communication and data transmission assume that data transfer between systems is either latency-free or that the latency is small enough not to affect the real-time performance of the system. It is also required that the communication channel is highly reliable and does not suffer from severe packet loss or loss of data. This is because extrapolating an unknown system state using known gauge data requires that all data be analyzed simultaneously. This communication and data transmission problem corresponds to another specialized research area in power systems and is not the focus of this paper.
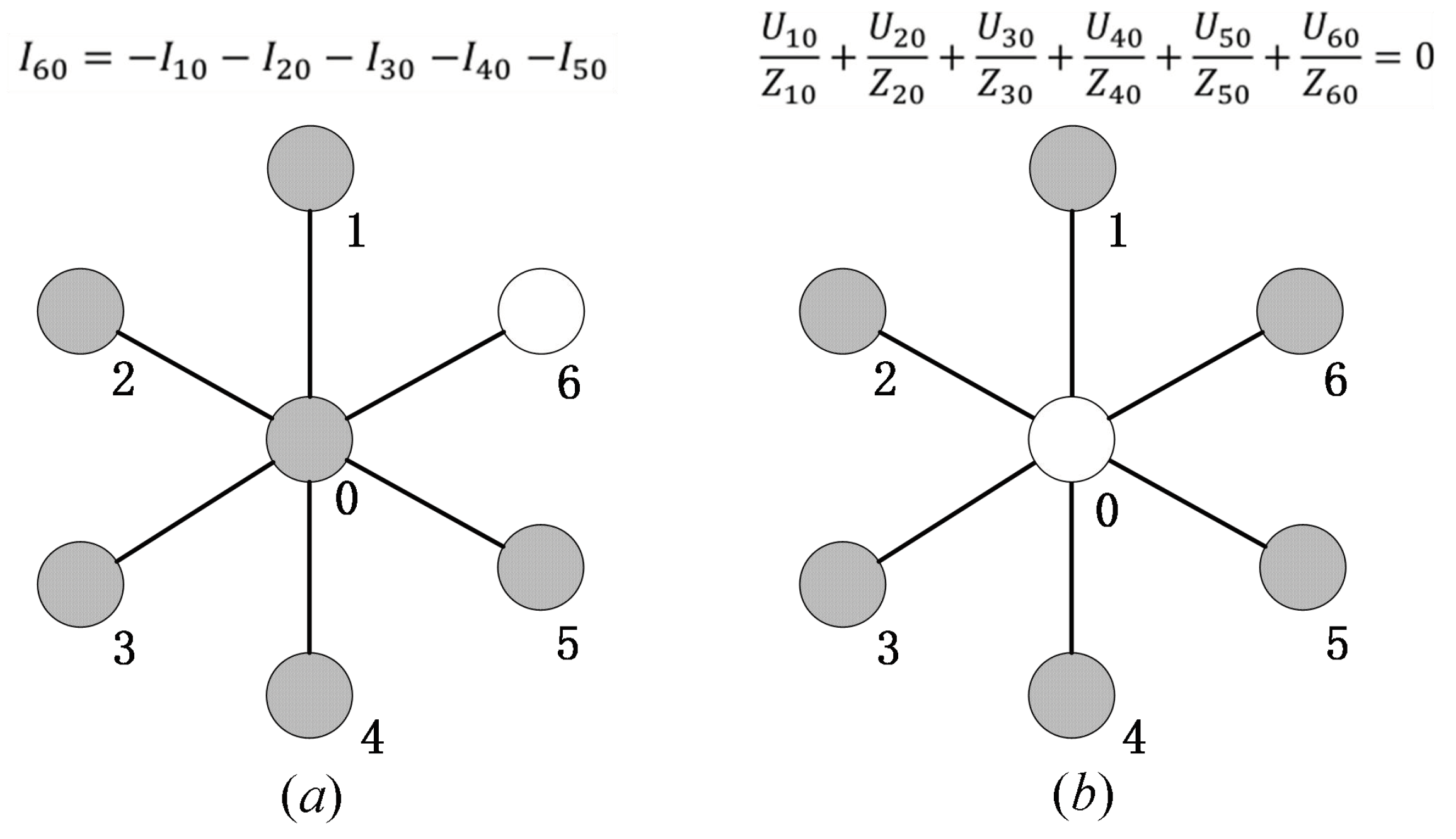
2.1. Observability Considering PMUs
2.2. Observability Considering ZIBs and Meters
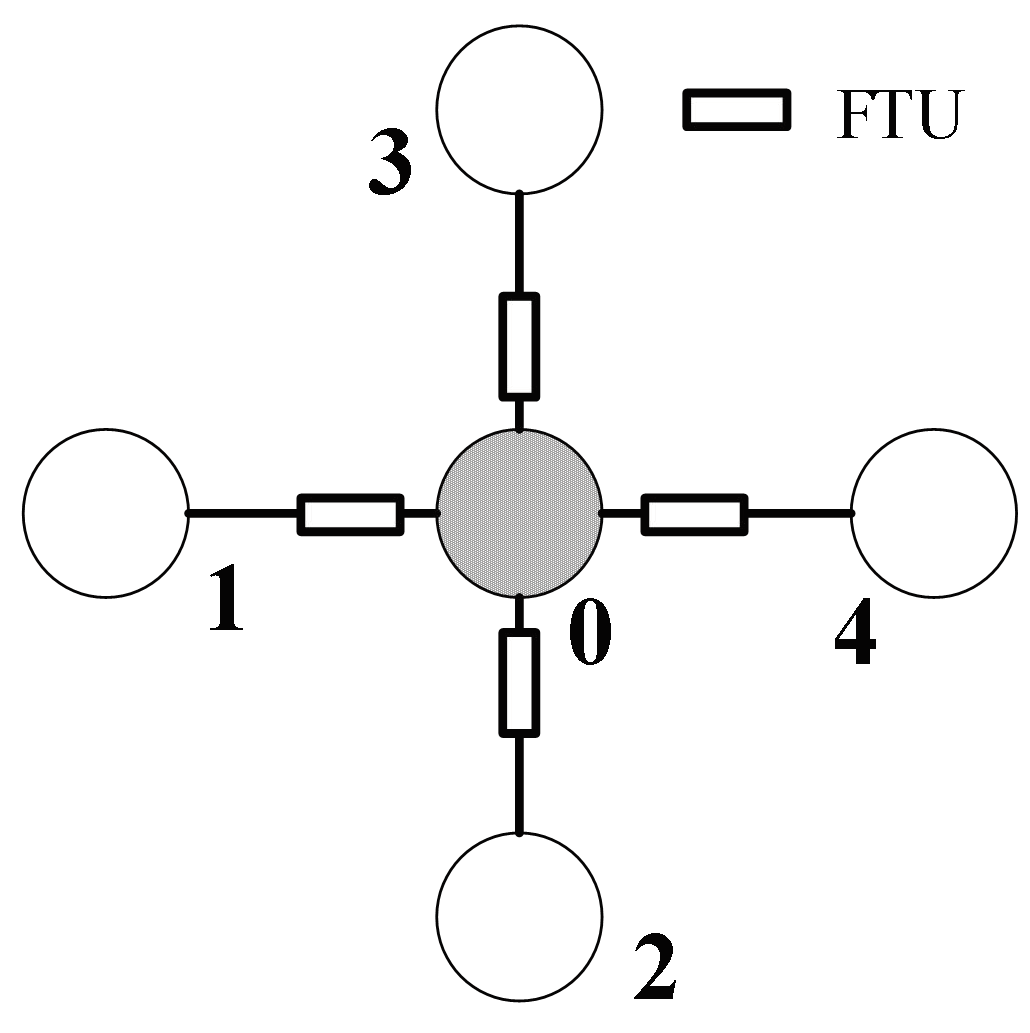
2.3. Observability Considering FTUs
2.4. Observability Constraint
- (1)
- Nodes are directly observable if PMUs are placed, and indirectly observable if they are topologically connected to nodes with PMUs placed;
- (2)
- If the node is a ZIB or placed with a meter, and m-1 of the m nodes connected to the node are either directly observable or indirectly observable, then the remaining nodes are indirectly observable;
- (3)
- FTUs are placed on the line connecting the two nodes, and when any one node is directly or indirectly observable, the other node is indirectly observable.
3. μPMU Placement Optimization
3.1. Cost of μPMU Placement
3.2. Assessment of Critical Node
3.3. μPMU Placement at Critical Nodes
4. μPMU Placements Optimization Model
4.1. Model Establishment
4.2. Model Solution
5. Simulation and Analysis
5.1. Validation of Algorithm
5.2. μPMU Placement Scheme Considering Existing Monitoring Devices
5.2.1. Rationality Verification
5.2.2. Effectiveness Verification
5.3. Effect on μPMUs Placement Considering Node Importance
5.3.1. The Impact of Node Importance on Placement Schemes
5.3.2. The Effectiveness of Prioritizing the Placement of μPMUs at Critical Nodes
6. Conclusions
- (1)
- In response to the problem of many μPMUs required for global observability in existing DNs, the layout of μPMUs fully utilizes the observation performance provided by existing measurement devices for the system, reducing the number of PMUs required for achieving global observability. Among them, the number of PMUs required for global observability in IEEE33, IEEE34, and P&G69 systems is less than existing methods, and more μ PMUs are saved as the system grows.
- (2)
- Aiming at the problem of insufficient observability of existing μPMU placement schemes in special cases such as line fault and topology changes. In this paper, the placing μPMUs at critical nodes in the DN that are more related to the observation stability (e.g., high-observable redundant nodes, adjacent nodes of frequently disconnected lines), which improves the observation performance of the system in the case of disconnected faults and μPMU fault, and greatly reduces the unobservable risk of the system caused by topology changes in the DN. Higher monitoring stability of the system is ensured with a smaller number of μPMUs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |||
| DER | distributed energy resources | FTU | feeder terminal unit |
| DN | distribution network | OPP | optimal µPMU placement |
| μPMUs | micro phasor measurement units | ZIB | zero-injection bus |
| Symbol | |||
| A | the system adjacency matrix in n × n dimensions | Z | the set of ZIBs |
| X | the PMU placement matrix in n × 1 dimensions | M | the total cost of the placement scheme |
| B | the matrix with all elements equal to 1 in n × 1 dimensions | FC | the unit cost of the voltage measuring device |
| the elements in the ith row and jth column of matrix A | CCH | the unit of the current measuring device | |
| the nth element in matrix X | the importance of node i | ||
| n | the number of nodes | the importance of node j observed by node i | |
| a 1 × n matrix of observability of adjacent nodes of the ZIB | the topological importance of node j | ||
| the number of nodes except the ith node that is observable among the nodes connected to the ZIB | the importance of the electrical distance of node j | ||
| the zth row of the adjacency matrix A | the importance of node j which considers the DGs and frequent disconnection of line joint points | ||
| the value of non-zero elements in the matrix (AX) is set to 1 | the DG coefficient of node j | ||
| the number of nodes connected to the zth ZIB | whether the ith node has a µPMU placed or not | ||
| the indirect observable matrix representing the ZIB z | the self-impedance of node i or j | ||
| the nth element in the matrix | the mutual impedance between nodes i and j | ||
| the line matrix of FTUs placed in n × n dimensions | the equivalent mutual impedance between nodes i and j | ||
| the elements in the ith row and jth column of the matrix | the DG coefficient of node j | ||
| D | the indirect observability matrix of FTUs in n × 1 dimensions | , , | the constant coefficients of the importance of the nodes |
| z | ZIB | the weight coefficient | |
Appendix A

| Algorithm A1. Weighting coefficient simulated annealing a algorithm. |
| Step 1: Randomly generate a binary-encoded target vector with the length of the number of nodes to represent the installation of PMUs, where 1 indicates the system nodes with PMUs installed. Step 2: Determine whether the current objective vector satisfies the mixed observation constraint, if so turn to step 3 and record the current objective function value as the optimal value, otherwise turn to step 1. Step 3: Update the target vector by randomly using any of the following strategies: ① Descending strategy: randomly select an element in the vector with value 1 and set it to 0. The number of elements set to 0 follows a normal distribution with a mean of 1 and a standard deviation of 1 (absolute value, rounding). ② Ascending strategy: randomly select an element in the vector with value 0 and set it to 1. The number of elements set to 1 is fixed at 1. ③ Changing strategy: randomly exchange the positions of two elements in the target vector, including interpolation, exchange, and reverse. Step 4: Check if the mixed observation constraints are satisfied. If they are, move to step 5 and record the current objective function value; otherwise, go back to step 3 to update the target vector. Step 5: Compare the objective value with the optimal value. If the former is smaller, replace the target vector; otherwise, there is a chance to update the target vector based on the difference between the optimal and the objective values. Step 6: Update the factors in the descending and changing strategies based on the number of elements equaling 1 in the target vector. Check if the termination condition is met; if yes, output the target vector; otherwise, go back to step 3. |
References
- Wu, Z.; Yu, X.; Dong, X.; Liu, Z.; Chen, L.; Li, P. Real-time Situation Awareness and Evaluation of Distribution Network Based on State Estimation. Proc. CSU-EPSA 2018, 30, 140–145. [Google Scholar]
- Bai, L. PMU Application Prospect in the Distribution and the Optimized Allocation of Research. Master’s Thesis, North China Electric Power University, Beijing, China, 2009. [Google Scholar]
- Mallikarjuna, B.; Gopakumar, P.; Jaya Bharata Reddy, M.; Mohanta, D.K. A case study on optimal phasor measurement unit placement for emerging Indian national smart grid. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016. [Google Scholar]
- Li, Q.; Cui, T.; Weng, Y.; Negi, R.; Franchetti, F.; Ilic, M.D. An information-theoretic approach to PMU placement in electric power systems. IEEE Trans. Smart Grid 2012, 4, 446–456. [Google Scholar] [CrossRef]
- Aminifar, F.; Lucas, C.; Khodaei, A.; Fotuhi-Firuzabad, M. Optimal placement of phasor measurement units using immunity genetic algorithm. IEEE Trans. Power Deliv. 2009, 24, 1014–1020. [Google Scholar] [CrossRef]
- Cho, K.-S.; Shin, J.-R.; Hyun, S.H. Optimal placement of phasor measurement units with GPS receiver. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting Conference Proceedings (Cat No 01CH37194), Columbus, OH, USA, 28 January–1 February 2001. [Google Scholar]
- Manoharan, H.; Srikrishna, S.; Sivarajan, G.; Manoharan, A. Economical placement of PMUs considering observability and voltage stability using binary coded ant lion optimization. Int. Trans. Electr. Energy Syst. 2018, 28, e2591. [Google Scholar] [CrossRef]
- Zhang, J.L.; Gao, Z.J.; Wang, Z.Y.; Sun, X.R. Fault Location Method for Active Distribution Based on Finite μPMU. Power Syst. Technol. 2020, 44, 2722–2731. [Google Scholar]
- Milosevic, B.; Begovic, M. Nondominated sorting genetic algo-rithm for optimal phasor measurement placement. IEEE Trans. Power Syst. 2003, 18, 69–75. [Google Scholar] [CrossRef]
- Gou, B. Generalized integer linear programming formulation for optimal PMU placement. IEEE Trans. Power Syst. 2008, 23, 1099–1104. [Google Scholar] [CrossRef]
- Xu, B.; Abur, A. Observability analysis and measurement placement for systems with PMUs. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004. [Google Scholar]
- Dubey, R.; Popov, M.; Muro, J.D.J.C. Cost effective wide area measurement systems for smart power network. IEEE Power Energy Technol. Syst. J. 2018, 5, 85–93. [Google Scholar] [CrossRef]
- Abdelkader, M.; Selim, A.; Kamel, S.; Jurado, F. Optimal placement of phasor measurement units for state estimation of electrical power systems. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019. [Google Scholar]
- Rather, Z.H.; Chen, Z.; Thøgersen, P.; Lund, P.; Kirby, B. Realistic approach for phasor measurement unit placement: Consideration of practical hidden costs. IEEE Trans. Power Deliv. 2014, 30, 3–15. [Google Scholar] [CrossRef]
- Huang, Y.; Li, S.; Li, J.; Hou, W.; Zhang, Y.; Yang, K. A multi-objective model for PMU placement considering redundancy in the presence of line outages. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration, Changsha, China, 8–10 November 2019. [Google Scholar]
- Du, X. Optimal Placement of Micro-PMU in Distribution System. Master’s Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Guo, X.-C.; Liao, C.-S.; Chu, C.-C. Probabilistic Optimal PMU Placements Under Limited Observability Propagations. IEEE Syst. J. 2022, 16, 767–776. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, Q.; Cao, Y. Optimal PMU placement to guarantee observability under N − 1 condition. Proc. CSEE 2009, 29, 47–51. [Google Scholar]
- Arpanahi, M.K.; Alhelou, H.H.; Siano, P. A novel multiobjective OPP for power system small signal stability assessment considering WAMS uncertainties. IEEE Trans. Ind. Inform. 2019, 16, 3039–3050. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, H.; Zhang, C.; Dai, Q. Optimal placement of PMUs using adaptive genetic algorithm considering measurement redundancy. Int. J. Reliab. Qual. Saf. Eng. 2016, 23, 1640001. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-Firuzabad, M.; Safdarian, A.; Shahidehpour, M. Observability of hybrid AC/DC power systems with variable-cost PMUs. IEEE Trans. Power Deliv. 2014, 29, 345–352. [Google Scholar] [CrossRef]
- Almunif, A.; Fan, L. Optimal PMU placement for modeling power grid observability with mathematical programming methods. Int. Trans. Electr. Energy Syst. 2020, 30, e12182. [Google Scholar] [CrossRef]
- Bi, G. Research on the Influence of Distributed Generation on Distribution Network. Master’s Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Tan, Y.; Li, X.; Cai, Y.; Zhang, Y.D. Critical node identification for complex power grid based on electrical distance. Proc. CSEE 2014, 34, 146–152. [Google Scholar]
- Fu, J.C.; Lu, Q.S. Fault sections location of distribution network based on bat algorithm. Power Syst. Prot. Control 2015, 43, 100–105. [Google Scholar]
- Gong, M.; Xu, Z.; Xie, Y.; Pan, J.; Li, R. Fault-section location of distribution network containing distributed generation based on the multiple-population genetic algorithm of chaotic optimization. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Chakrabarti, S.; Kyriakides, E. Optimal placement of phasor measurement units for power system observability. IEEE Trans. Power Syst. 2008, 23, 1433–1440. [Google Scholar] [CrossRef]
- Kong, X.; Wang, Y.; Yuan, X. Optimal configuration of PMU based on customized genetic algorithm and considering observability of multiple topologies of distribution network. Electr. Power Autom. Equip. 2020, 40, 66–72. [Google Scholar]
- Chen, X.; Chen, T.; Tseng, K.J.; Sun, Y.; Amaratunga, G. Customized optimal μPMU Placement method for distribution networks. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 135–140. [Google Scholar] [CrossRef]
- Kumar, V.S.S.; Thukaram, D. Approach for multistage place-ment of phasor measurement units based on stability criteria. IEEE Trans. Power Syst. 2015, 31, 2714–2725. [Google Scholar] [CrossRef]
- Abdelsalam, H.A.; Abdelaziz, A.Y.; Osama, R.A.; Salem, R.H. Impact of distribution system reconfiguration on optimal placement of phasor measurement units. In Proceedings of the 2014 Clemson University Power Systems Conference, Clemson, SC, USA, 11–14 March 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, P.; Liu, M. PMU placement method based on improved integer programming method combined with zero injection nodes. Power Syst. Prot. Control 2021, 49, 143–150. [Google Scholar]
- Do Coutto Filho, M.B.; de Souza, J.C.S.; Tafur, J.E.V. Quanti-fying observability in state estimation. IEEE Trans. Power Syst. 2013, 28, 2897–2906. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y. Dynamic Reconfiguration of Dis-tribution Network Based on Optimal Fuzzy C-means Cluster-ing and Improved Chemical Reaction Optimization. Proc. CSEE 2014, 34, 1682–1691. [Google Scholar]







| Parameters | Value | [10,11] | [12] | [18] | Ours | [13] | [14] | [10] | Ours |
|---|---|---|---|---|---|---|---|---|---|
| Consideration of existing measurement devices | ZIB | √ | √ | ||||||
| Meter | √ | √ | |||||||
| FTU | √ | √ | |||||||
| Considerations of observation Stability | μPMU failure | √ | √ | √ | |||||
| line failure | √ | √ | √ | ||||||
| Topology Change | √ |
| Parameters | Value |
|---|---|
| Niter | 1000 |
| T0 | 1 |
| 0.9995 |
| Number of PMU | Observability | Nodes with PMU Placed |
|---|---|---|
| 11 | observable | 2, 4, 6, 9, 13, 14, 17, 21, 24, 29, 32 |
| With Measurement or Not | Number of PMU | Nodes with PMU Placed |
|---|---|---|
| No | 11 | 2, 4, 6, 9, 13, 14, 17, 21, 24, 29, 32 |
| Yes | 9 | 2, 5, 9, 13, 17, 21, 24, 29, 32 |
| With Measurement or Not | IEEE 33 | IEEE 34 | PG&E 69 |
|---|---|---|---|
| Ours | 11 | 11 | 19 |
| [28] | 11 | 11 | 23 |
| [29] | 11 | 13 | 25 |
| [30] | 13 | 15 | 25 |
| [31] | 14 | 14 | 27 |
| Scheme | Nodes with μPMUs Placed | Importance Factor |
|---|---|---|
| 1 | 2, 4, 6, 9, 13, 14, 17, 21, 24, 29, 32 | 1.254 |
| 2 | 2, 5, 9, 12, 14, 17, 21, 24, 27, 30, 32 | 1.222 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Lu, J.; Chen, Y.; Gao, Y.; Gan, K.; Li, M.; Wei, C.; Huang, R.; Xiao, F.; Che, L. Optimal µPMU Placement Considering Node Importance and Multiple Deployed Monitoring Devices in Distribution Networks. Energies 2025, 18, 395. https://doi.org/10.3390/en18020395
Zhao R, Lu J, Chen Y, Gao Y, Gan K, Li M, Wei C, Huang R, Xiao F, Che L. Optimal µPMU Placement Considering Node Importance and Multiple Deployed Monitoring Devices in Distribution Networks. Energies. 2025; 18(2):395. https://doi.org/10.3390/en18020395
Chicago/Turabian StyleZhao, Ruifeng, Jiangang Lu, Yizhe Chen, Yifan Gao, Kai Gan, Ming Li, Chengzhi Wei, Runhong Huang, Fan Xiao, and Liang Che. 2025. "Optimal µPMU Placement Considering Node Importance and Multiple Deployed Monitoring Devices in Distribution Networks" Energies 18, no. 2: 395. https://doi.org/10.3390/en18020395
APA StyleZhao, R., Lu, J., Chen, Y., Gao, Y., Gan, K., Li, M., Wei, C., Huang, R., Xiao, F., & Che, L. (2025). Optimal µPMU Placement Considering Node Importance and Multiple Deployed Monitoring Devices in Distribution Networks. Energies, 18(2), 395. https://doi.org/10.3390/en18020395





