Abstract
With the widespread adoption of renewable energy sources like wind power and photovoltaic (PV) power, uncertainties in the renewable energy output and the battery-swapping demand for electric heavy-duty trucks make it challenging for battery-swapping stations to optimize battery-charging management centrally. Uncoordinated large-scale charging behavior can increase operation costs for battery-swapping stations and even affect the stability of the power grid. To mitigate this, this paper proposes a multi-timescale battery-charging optimization for electric heavy-duty truck battery-swapping stations, taking into account the source–load–storage uncertainty. First, a model incorporating uncertainties in renewable energy output, time-of-use pricing, and grid load fluctuations is developed for the battery-swapping station. Second, based on day-ahead and intra-day timescales, the optimization problem for battery-charging strategies at battery-swapping stations is decomposed into day-ahead and intra-day optimization problems. We propose a day-ahead charging strategy optimization algorithm based on intra-day optimization feedback information-gap decision theory (IGDT) and an improved grasshopper algorithm for intra-day charging strategy optimization. The key contributions include the following: (1) the development of a battery-charging model for electric heavy-duty truck battery-swapping stations that accounts for the uncertainty in the power output of energy sources, loads, and storage; (2) the proposal of a day-ahead battery-charging optimization algorithm based on intra-day-optimization feedback information-gap decision theory (IGDT), which allows for dynamic adjustment of risk preferences; (3) the proposal of an intra-day battery-charging optimization algorithm based on an improved grasshopper optimization algorithm, which enhances algorithm convergence speed and stability, avoiding local optima. Finally, simulation comparisons confirm the success of the proposed approach. The simulation results demonstrate that the proposed method reduces charging costs by 4.26% and 6.03% compared with the two baseline algorithms, respectively, and improves grid stability, highlighting its effectiveness for managing battery-swapping stations under uncertainty.
1. Introduction
Due to advantages such as energy savings, environmental protection, and high efficiency, electric heavy-duty trucks, as a type of vehicle utilizing clean energy, have attracted widespread attention [1,2]. However, the large battery capacity of electric heavy-duty trucks results in long recharging times, affecting operational efficiency [3]. Battery swapping offers a solution by providing quick and safe energy replenishment, enhancing truck operation efficiency by replacing depleted batteries with fully charged ones without waiting for recharging. This process significantly improves the operation efficiency of electric heavy-duty trucks [4]. With the widespread deployment of renewable energy sources like wind power and photovoltaic (PV) power, uncertainty in the power output and fluctuating battery-swapping demand complicate optimal battery-charging management at swapping stations [5]. Uncoordinated large-scale charging behaviors can increase operation costs for battery-swapping stations and even affect grid stability. Therefore, optimizing battery-charging scheduling for electric heavy-duty truck battery-swapping stations is crucial.
Currently, numerous scholars have conducted studies on battery-charging behavior modeling for battery-swapping stations. In [6], Wu et al. proposed a constant voltage/current battery-charging model for battery-swapping stations. The optimization objectives were to maximize the swapping frequency and to minimize the swapping costs. As a result, the stations’ efficiency and economic viability were enhanced. In [7], Ko et al. considered real-time electricity prices and swapping demand in battery-swapping stations, aiming to maximize the station’s profit while ensuring battery replacement efficiency. A linear programming approach was employed to determine the optimal battery-charging approach. In [8], Esmaeili et al. introduced a joint optimization model for the management of battery-swapping stations and microgrids, which was solved using the alternating direction method of multipliers. In [9], Jin et al. proposed an optimal operation model for battery-swapping stations that accounts for factors such as user arrival times, grid power constraints, electricity price fluctuations, user waiting times, and battery degradation costs. However, the aforementioned models for battery-charging behavior in battery-swapping stations largely overlook the uncertainties in renewable energy output and fluctuations in the grid load, which creates a gap between the models and the real operation environment of the grid.
Due to the highly random and unpredictable nature of electric heavy-duty truck operations, battery-swapping stations find it difficult to accurately forecast swapping demands. These forecasting deviations have a significant negative impact on battery-charging optimization. Currently, methods to address uncertainty primarily rely on a multi-timescale optimization framework, where day-ahead optimization provides scheduling references for intra-day optimization, while the latter adjusts the day-ahead strategies based on updated forecasting information. Regarding day-ahead optimization, Davari et al. proposed a day-ahead energy management system that considers forecasting deviations [10]. Information-gap decision theory (IGDT) is employed to quantify system uncertainty in the absence of known probability distributions, with both robustness and economic efficiency being ensured. In [11], Gazijahani et al. introduced a two-level decision model that addresses renewable energy output uncertainty using IGDT, resulting in a decision-making model with enhanced robustness. However, these methods treat uncertainty as a negative factor, overlooking its potential beneficial effects on optimizing battery charging in electric heavy-duty truck battery-swapping stations.
In terms of intra-day optimization, the increasing demand for battery swapping in electric heavy-duty trucks has made the battery-charging model for battery-swapping stations increasingly complex. The solution process often encounters challenges such as high-dimensional variables, large variable quantities, and closely interrelated variables. As swarm intelligence algorithms have shown certain advantages in solving complex high-dimensional functions, they have been widely applied to optimize battery-charging strategies for battery-swapping stations. In [12], Jamian et al. used an artificial bee colony algorithm to address the battery-charging optimization problem, taking into account the impact of various DC charging facilities on battery-charging performance. In [13], Fang et al. applied a hybrid particle swarm and genetic algorithm to minimize battery-charging costs. However, uncertainties in the renewable energy output, time-of-use pricing, and fluctuations in the grid load add complexity to the dimensions of the charging strategy optimization. As a result, these works suffer from problems such as low convergence speed and accuracy, making them prone to becoming trapped in local optima.
Despite the progress made in optimizing battery-charging strategies for electric heavy-duty truck battery-swapping stations, several challenges remain. First, existing research has not fully integrated the uncertainties of renewable energy output, time-of-use pricing mechanisms, and grid-load fluctuations. This gap between theoretical models and the actual operation environment of the grid leads to poor accuracy. Second, current day-ahead battery-charging strategies for electric truck charging stations typically rely on robust planning methods, which often treat the uncertainties in energy sources, loads, and storage as negative factors. The potential beneficial effects of these uncertainties are overlooked, leading to overly conservative charging strategies and a degradation in economic performance. Finally, existing optimization methods struggle to achieve intra-day optimization of battery-charging strategies under uncertain conditions. The increased dimensionality caused by uncertainties in the renewable energy output, time-of-use pricing, and grid-load fluctuations lead to slow convergence speeds, low accuracy, and a tendency to get stuck in local optima.
To address the aforementioned challenges, we propose a multi-timescale battery-charging optimization algorithm for electric heavy-duty truck battery-swapping stations, considering source–load–storage uncertainty. First, a model of the electric heavy-duty truck battery-swapping station is constructed, incorporating the uncertainties of energy sources, loads, and storage. Second, based on two optimization timescales, i.e., day-ahead and intra-day, the optimization problem is decomposed into day-ahead and intra-day battery-charging strategies. Next, a day-ahead battery-charging strategy optimization algorithm based on intra-day optimization feedback IGDT is proposed, along with an intra-day battery-charging strategy optimization algorithm based on an improved grasshopper optimization algorithm. Finally, simulations are conducted to evaluate and compare the effectiveness of the proposed algorithm. The key contributions of this paper are outlined below:
- (1)
- A battery-charging model for electric heavy-duty truck battery-swapping stations is developed, accounting for the variability in the power output of energy sources, loads, and storage. Under the time-of-use pricing mechanism, the model comprehensively accounts for the uncertainties of renewable energy sources like PV and wind power, as well as the impact of grid-load fluctuations on battery-charging behaviors. It simulates the complexity of the battery-swapping station’s operation under real-world conditions, such as seasonal climate changes and variations in user electricity consumption behavior, enhancing the modeling accuracy.
- (2)
- A day-ahead battery-charging optimization algorithm for electric heavy-duty truck battery-swapping stations based on intra-day optimization feedback IGDT is proposed. The algorithm solves the day-ahead charging strategy optimization problem with the uncertainties in energy sources, loads, and storage, using both robust optimization and opportunistic optimization models. The former treats uncertainty as a negative factor and provides risk-averse strategies, while the latter views uncertainty as a favorable condition, optimizing decisions to pursue higher returns. This allows decision-makers to create different day-ahead scheduling strategies based on varying risk preferences. Additionally, the algorithm adjusts the day-ahead robust and opportunistic factors dynamically based on feedback from intra-day optimization results, allowing the day-ahead optimization risk attitude to be fine-tuned in response to real-time conditions.
- (3)
- An intra-day battery-charging optimization algorithm based on an improved grasshopper optimization algorithm is proposed. The algorithm uses chaotic sequences for population initialization, ensuring a more even spread of the population across the search space, thus improving the population quality, accelerating the iteration speed, and enhancing stability. Moreover, an elite opposition-based learning strategy is employed to select elite grasshoppers and to assign appropriate influence weights to the individuals, enabling them to collaboratively identify an elite leader. This leader guides the population’s position updates, helping avoid local optima when solving high-dimensional optimization problems.
In conclusion, this study aims to optimize battery-charging management at electric heavy-duty truck battery-swapping stations amidst uncertainties in renewable energy output and battery-swapping demand. We employ a multi-timescale optimization approach, leveraging IGDT for day-ahead strategies and an enhanced grasshopper optimization algorithm for intra-day adjustments. Our results show significant reductions in charging costs and improvements in grid stability, validating the effectiveness of our proposed methods. The key discussions in this paper focus on the practical implications of these findings, offering a robust strategy for managing battery-swapping stations under varying operational conditions.
2. Electric Heavy-Duty Truck Battery-Swapping Station Model, Considering Source–Load–Storage Uncertainty
As illustrated in Figure 1, the electric heavy-duty truck battery-swapping station model developed in this paper includes wind turbines, PVs, energy-storage equipment, loads, and battery charging/discharging equipment. The outputs from wind turbines and PVs are assumed to be fully utilized by the battery-swapping station. The energy-storage systems mitigate the impact of renewable energy fluctuations on the station, while the battery charging/discharging equipment is responsible for recharging the depleted batteries removed during the swapping process [14]. Additionally, the battery-swapping station can interact with the power grid to purchase supplementary electricity as needed [15]. The station replaces the depleted batteries of arriving electric heavy-duty trucks with fully charged ones and manages the charging of the depleted batteries. It also supplies power to internal loads such as lighting, monitoring, control, and cooling equipment. This paper divides the overall optimization period into T time slots, denoted as set , with each slot having a consistent length of .
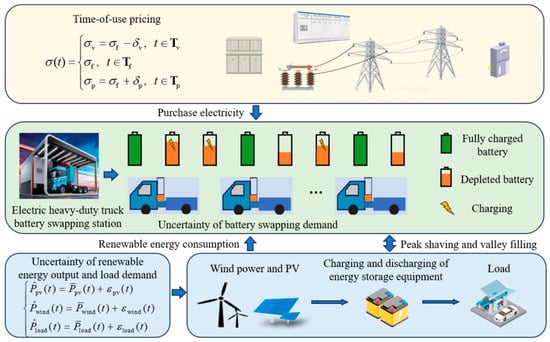
Figure 1.
Electric heavy-duty truck battery-swapping station model, considering the source–load–storage uncertainty.
2.1. Uncertainty Model of Renewable Energy Output and Load Demand
Renewable energy can supply clean and efficient energy to battery-exchange stations for electric heavy-duty trucks while also providing peak shaving, inertia control, and other services, thus ensuring the safe and stable operation of the distribution network [16]. However, wind power and PV power are significantly affected by weather conditions and environmental factors, leading to their intermittent and variable nature [17]. The load within the battery-swapping station is uncertain due to variations in the climate and the different electricity consumption behaviors of users. During slot t, the actual output values of wind and PV power, as well as the load power supplied by the battery-swapping station, are equal to the predicted values plus the prediction error, which can be expressed as
where and represent the actual output of PV and wind power during slot . and represent the predicted output values for PV power, wind power, and load during slot . and represent the forecast errors for the output of PV and wind power during slot . , , and represent the actual power, the predicted power, and the power forecast error supplied to the load by the battery-swapping station during slot , respectively. and represent the upper and lower limits of photovoltaic power generation, respectively; and represent the upper and lower limits of wind power generation during slot , respectively.
2.1.1. Energy-Storage Model
Energy-storage equipment is crucial for regulating the output of renewable energy in electric heavy-duty truck battery-swapping stations [18]. Specifically, the output from renewable sources like wind power and PV power exhibits uncertainty and variability, leading to situations where the load and depleted batteries of the electric heavy-duty truck battery-swapping station cannot fully consume the renewable energy output during certain time periods. Energy-storage equipment can store the excess energy that the battery-swapping station is unable to consume and to release it during periods of high electricity prices or increased energy demand, thereby supplying energy to the station. When storing and releasing energy, energy-storage equipment experiences energy losses due to factors such as internal resistance, energy conversion, and operation losses in the equipment. If the energy-storage equipment is charged during time slot , the additional energy stored in the equipment can be expressed as
where represents the charging efficiency of the energy-storage equipment. represents the charging power of the energy-storage equipment.
If the energy-storage equipment discharges during slot , the amount of energy lost by the energy-storage equipment can be expressed as
where represents the discharge efficiency of the energy-storage equipment. represents the discharge power of the equipment.
The amount of energy stored by the energy-storage equipment during slot can be expressed as
where represents the energy stored by the energy-storage equipment during slot . and represent the charging and discharging indicators, respectively. When the energy-storage equipment is in charging mode, and ; when the equipment is in discharging mode, and .
2.1.2. Interaction Model Between Electric Heavy-Duty Truck Battery-Swapping Stations and Power Grids
The power generated by PV and wind power is characterized by uncertainty and significant fluctuations over time. During certain periods, the combined output from PV power, wind power, and energy storage is insufficient to meet the demands of the battery-swapping station. As a result, these battery-swapping stations must purchase electricity from the power grid. Under the time-of-use pricing mechanism, the optimization periods are categorized into valley, flat, and peak periods. The electricity purchasing cost of the battery-swapping station during time slot can be expressed as
where represents the power purchased by the battery-swapping station during slot . represents the time-of-use pricing during slot , which can be expressed as
where , , and represent the electricity prices during valley, flat, and peak periods, respectively. and denote the fluctuations in electricity prices during valley and peak periods, respectively. , , and represent sets of the valley, flat, and peak periods, respectively.
2.1.3. Battery-Charging Model
The battery charging and discharging equipment is responsible for recharging depleted batteries swapped from electric heavy-duty trucks, with the capability to charge up to batteries simultaneously. In the battery-swapping station, there are a total of batteries, which include those that are either being charged or already fully charged. At the beginning of slot , the state of charge (SoC) of the -th battery is denoted as , where . The SoC of the batteries is categorized into levels, with batteries at the -th level considered to be fully charged. The SoC corresponding to the -th level battery is represented as . and are given by
and , respectively, represent the number of batteries at the -th energy level at the start of slot t and those at the -th energy level in a charging state at the same time. The big method is a widely used mathematical approach in linear programming that introduces additional constraints to ensure that certain logical relationships or priorities are satisfied within the model. To ensure that the battery-swapping station meets its demand during peak swapping periods, we construct constraints based on the SoC of the batteries. This allows batteries with higher charging levels to be prioritized for charging, thereby accelerating the process of having more fully charged batteries. The constraints developed using the big method can be expressed as
where represents the introduced continuous variable, denotes the introduced binary variable, and is a large constant.
As the battery charging and discharging equipment can provide charging services for up to batteries simultaneously, we have
2.1.4. Uncertainty Model of Battery-Swapping Demand
By forecasting the battery-swapping demand at stations, we can effectively optimize battery-charging schedules to ensure that the battery supply aligns with the swapping demands. Based on the actual operation conditions faced by battery-swapping stations, we selected relevant historical data within a reasonable range to calculate the number of battery swaps during each slot, allowing us to predict the number of battery swaps . During slot , the actual number of battery swaps for electric heavy-duty trucks is equivalent to the predicted value plus the prediction error, which can be expressed as
where represents the actual number of battery swaps. represents the forecasting error.
2.1.5. Constraints
Due to limitations in the interaction power between electric heavy-duty truck battery-swapping stations and the grid, along with limitations on the charging and discharging power of energy-storage equipment, it is crucial to account for various constraints when optimizing the battery-charging strategy.
- (1)
- Electricity Purchase Constraints
The electricity purchase constraint of the battery-swapping station can be expressed as
where represents the maximum purchasing power during slot .
- (2)
- Charging Power Constraints
The charging power of a single battery should satisfy
where represents the charging power of the -th battery at level during slot . denotes the maximum charging power for each battery.
The total charging power of all batteries should satisfy
where represents the maximum allowable charging power.
- (3)
- Battery-swapping Demand Constraints
At the beginning of slot , the number of fully charged batteries at the battery-swapping station should be greater than or equal to the swapping demand during that period, which can be expressed as
- (4)
- Energy-storage Charging and Discharging Constraints
The charging and discharging power of the energy-storage equipment should satisfy
where and represent the maximum charging and discharging power of the energy-storage equipment, respectively.
The energy stored in the energy-storage equipment should satisfy [19]
where represents the maximum capacity of the energy-storage equipment. and represent the maximum and minimum values of the SoC of the energy-storage equipment, respectively.
- (5)
- Power Balance Constraints
The charging and discharging power of the battery-swapping station during each slot should be balanced to satisfy
2.1.6. Problem Formulation of Multi-Timescale Battery-Charging Optimization
To minimize the costs of electric heavy-duty truck battery-swapping stations, we optimize the battery-charging strategy at both the day-ahead and intra-day timescales. The optimization objectives for both the day-ahead and intra-day optimizations are to minimize the weighted difference between the electricity purchasing cost and the subsidy revenue for PV and wind power consumption. First, the battery-charging power is allocated efficiently by the day-ahead optimization based on long-term forecast information, and these allocations are provided to the intra-day optimization. Second, the day-ahead scheduling strategy is adjusted by the intra-day optimization based on the latest short-term forecast information. Finally, the results of the intra-day optimization are evaluated, and the evaluation outcomes are used to update the day-ahead optimization parameters through real-time feedback.
Based on both the day-ahead and intra-day optimization timescales, we decompose the battery-charging optimization problem for battery-swapping stations into day-ahead and intra-day optimization subproblems.
- (1)
- Day-Ahead Optimization Objective Function
- (2)
- Intra-Day Optimization Objective Function
2.2. Multi-Timescale Battery-Charging Optimization Model for Electric Heavy-Duty Truck Battery-Swapping Stations
2.2.1. Day-Ahead Battery-Charging Optimization Algorithm for Electric Heavy-Duty Truck Battery-Swapping Stations Based on Intra-Day Optimization Feedback IGDT
IGDT is a decision-making method designed for situations with high uncertainty. Unlike traditional stochastic programming and robust optimization approaches, IGDT does not require knowledge of the exact probability distribution or uncertainty ranges of the variables, making it ideal for scenarios involving significant uncertainty [20]. IGDT seeks to determine the allowable fluctuation range of uncertain parameters, known as the uncertainty radius, based on the target expectation values established based on the decision-maker’s changing risk preferences. Considering the diverse decision-making styles in practice, IGDT can be classified into robust and opportunistic models. The former regards uncertainty as an unfavorable factor and provides corresponding risk-avoidance strategies, while the latter treats uncertainty as a favorable condition and optimizes decisions to pursue higher returns. To enhance the accuracy of the day-ahead battery-charging strategy for the battery-swapping station, the results of intra-day optimization are used to inform the day-ahead optimization. This feedback is then used to adjust the parameters of the robust and opportunistic models.
Primary methods for establishing uncertain parameter models based on IGDT include energy constraint models, change rate constraint models, and envelope constraint models. The envelope constraint model is adopted to represent the uncertain parameters , , , and . The uncertainty variable is defined. Fluctuations in the battery-swapping number, the actual output of PV and wind power, and the actual power supplied to the load by the battery-swapping station around their predicted values can be expressed as
where represents the fluctuation range of the uncertain variable , i.e., the uncertain radius. represents all sets of with deviations no greater than .
The decision-making problem of the IGDT model mainly consists of four parts: the objective function, uncertainty modeling, the opportunistic model, and the robust model. The battery-charging model for battery-swapping stations can be expressed in vector form as
where represents the objective function. represents the equality constraints of the model. represents the inequality constraints.
Using the aforementioned envelope constraint model, we establish uncertainty models of the PV and wind power outputs, as well as the supply load power of the battery-swapping station, i.e.,
Taking into account the risk preferences of the battery-swapping station operators, robust and opportunistic models for battery scheduling in battery-swapping stations are established, respectively. The robust model can be expressed as
where represents the determined profit threshold, which is typically the optimal value of the objective function from a deterministic model based on forecasted values. is the robust factor, representing the extent of deviation from the expected profit target above , indicating the operator’s tolerance for risk in the profit target. Through the robust model, the deterministic model is converted into a problem of maximizing the variability of uncertain parameters under the condition that the target cost does not exceed . The goal is to determine the decision value such that when the uncertain variable fluctuates within the set , the target value can be guaranteed to be less than or equal to the preset target expectation of the decision-maker. A larger indicates that the corresponding decision-making scheme is less sensitive to uncertainties, i.e., the better the robustness.
Correspondingly, the opportunistic model can be expressed as
where represents the opportunistic factor, which is the degree of deviation of the expected revenue target below , indicating the operator’s risk preference for the revenue target. Through the opportunistic model, the deterministic model is converted into a problem of minimizing the variability of uncertain parameters while ensuring that the target cost does not exceed . The goal is to determine the decision value in the opportunistic model such that when the uncertain variable fluctuates within the set , there is an opportunity for the target value to be less than or equal to the preset target expectation of the decision-maker. A smaller value suggests that the corresponding decision-making approach is more likely to yield positive results.
Therefore, we propose an improved IGDT algorithm to make it applicable to the electric heavy-duty truck battery-swapping stations model developed in this paper. The robust factor and the opportunistic factor are adjusted in real time based on the intra-day optimization results, and their values are updated as follows:
where represents the intra-day real-time optimization evaluation result, which will be further introduced in Section 2.2. When the real-time battery-swapping station cost obtained from intra-day optimization is lower than the predicted cost from day-ahead optimization, is positive; otherwise, it is negative. and are the adjustment steps for the robust factor and the opportunistic factor, respectively. When the real-time battery-swapping station cost is lower than the predicted cost, the opportunistic factor is increased and the robust factor is decreased to seek greater revenue. Conversely, when the real-time cost is higher than the predicted cost, the opportunistic factor is decreased and the robust factor is increased to avoid revenue deterioration.
Based on the above model, the bi-level structure is challenging to solve directly. In the lower-level model, can be treated as a constant. The battery-charging cost at the battery-swapping station is positively associated with the number of battery swaps and the power supplied, while negatively correlates with the outputs of PV and wind power. Therefore, the optimal outcome of the lower-level model in the robust model must be obtained at the upper bounds of the information-gap region for the battery-swapping number and the power supplied by the battery-swapping station, as well as by the lower bounds of the information-gap region for PV and wind power outputs, to ensure acceptable performance even in the worst-case scenario. By equivalent transformation of the bi-level model, Equation (30) is converted into
Similarly, in the opportunistic model, the optimal solution of the lower-level model is determined at specific bounds of the information-gap regions. It is obtained at the lower bounds for the battery-swapping number and the power supplied by the battery-swapping station. For the PV and wind power outputs, it is obtained at the upper bounds of their respective information-gap regions. This ensures better performance under the most optimistic scenario. Equation (31) is converted into
Due to the presence of nonlinear terms in the battery scheduling model for battery-swapping stations based on IGDT, represented by Equations (33) and (34), the big M method is employed to introduce auxiliary constraints for equivalent linearization of the product terms between the continuous variables and the Boolean variables. Subsequently, a mathematical programming solver is used to solve the problem.
2.2.2. Intra-Day Battery-Charging Optimization Algorithm for Electric Heavy-Duty Truck Battery-Swapping Stations Based on an Improved Grasshopper Algorithm
In Section 2.1.6 an optimization problem for the intra-day battery-charging strategy for electric heavy-duty truck battery-swapping stations is formulated. By optimizing the intra-day battery-charging power adjustment values, the charging cost of the battery-swapping stations is minimized. This optimization problem can be solved using swarm intelligence algorithms such as the grasshopper algorithm [21]. However, traditional algorithms suffer from issues such as slow convergence speed, being easily trapped in the local optima, and instability in optimization ability. To address these issues, we propose an improved grasshopper algorithm to solve the optimization problem. The intra-day optimization variable is abstracted as the position information of the optimal individual of the grasshopper population in each dimension for optimization. The steps to using the improved grasshopper algorithm to solve the battery-charging strategy optimization problem are introduced as follows:
- (1)
- Initialization
Set the algorithm parameters, including the number of individuals in the grasshopper population, the dimension of the grasshopper population, and the number of iterations of the algorithm. Additionally, set the constraint conditions of the algorithm according to (20).
Initialize the positions of the grasshopper population within the feasible space using a chaotic sequence method. First, generate a -dimensional vector , where each component value is a random number within the interval . Then, map vector iteratively through a mapping function into the chaotic space to obtain vectors: . We select the commonly used complete logistic chaotic iteration formula, i.e.,
Second, transform each component in the chaotic variable into the search feasible domain to obtain the initialized grasshopper population, i.e.,
where represents the value of the -th grasshopper individual on the -th dimension. and are, respectively, the lower and upper bounds of the -dimensional search space of the algorithm.
Finally, all the grasshopper individuals transformed into the search feasible domain are combined to form the grasshopper population .
- (2)
- Calculate Fitness Values, Nonlinear Convergence Parameters, and Lévy Flight Lengths
Each individual in the current population is substituted into Equation (20), and the result is used as the fitness value of the individual in the current population. We adopt a nonlinear convergence strategy to strike a balance between exploration and exploitation in the algorithm, which accelerates the convergence speed of the algorithm while increasing the precision of the local search. The nonlinear convergence parameter is calculated as
where represents the current iteration number of the grasshopper algorithm. and are the preset maximum and minimum values of the nonlinear convergence parameter, respectively.
Additionally, we incorporate a random perturbation mechanism based on Lévy flight into the grasshopper position update. The Lévy distribution, a non-Gaussian random process, aptly simulates the ideal state of animals moving over long and short distances during predation. The distribution formula is given by
where the parameters , , and are defined as
where represents the standard gamma function.
- (3)
- Elite Opposition-Based Learning Decision-Making Mechanism
Elite decision-making refers to taking the best part of the individuals in the current population according to the ranking order of the fitness value and then guiding the updating of the positions of other individuals in the population through negotiation decision-making. By using the elite opposition-based learning decision-making mechanism to guide the grasshopper population to update, the population can better seek the optimal solution in the search space, which enhances the algorithm’s ability to find the optimal solution. The elite set is defined as
where is the elite set containing the top grasshopper individuals selected by sorting the individual fitness values on merit.
Generate an elite set of the elite set based on the opposing-point mechanism, denoted as
where is the opposing point of the -th elite grasshopper . represents the position of the -th elite grasshopper in the -th dimension.
The final elite set is identified by comparing with through a reverse-learning strategy, and a merit selection is performed by comparing the fitness values as
where is the set of new elite grasshoppers generated after the reverse-learning strategy. is the -th new elite grasshopper.
The weight size of the fitness value for each elite grasshopper is calculated, and new elite grasshoppers are generated to guide the population update. The weights of the elite grasshoppers are defined in terms of the size of the fitness value. Since the elite grasshoppers are sorted from the smallest to the largest fitness values, the smaller the fitness value, the larger the weight of the elite individual. The fitness value of the -th elite individual is used as the weight of the -th elite individual, denoted as
where is the set of elite grasshopper fitness value weights. represents the weight of the i-th grasshopper elite. After each elite grasshopper individual has its own fitness value weight, a new individual is decided by negotiation to be used to guide the grasshopper population position update, i.e.,
where is the new individual decided by negotiation among elites.
- (4)
- Updating the Population Position
The population position is updated according to the nonlinear convergence parameter and the Lévy flight length, which can be expressed as
where represents the -th individual after updating. and represent the upper and lower bounds of the search space domain, respectively. and represent the -th and -th individuals in the current population, respectively. represents the spatial vectors between the -th and -th individuals. is the optimal individual in the current population.
Subsequently, fitness values are calculated for the updated populations, which are ranked in order of fitness value superiority.
- (5)
- For each grasshopper individual, determine whether the constraints of the optimization problem are satisfied. If satisfied, go to step (6); if not, regenerate a grasshopper individual in the search interval instead.
- (6)
- Determine whether to meet the iteration termination conditions, i.e., to reach the preset maximum number of iterations. If the iteration termination conditions are met, the algorithm outputs the position information of the current optimal individual and its fitness value and then terminates. Otherwise, it proceeds to step (2) to continue the iteration.
- (7)
- Evaluate the intra-day real-time optimization results.
Based on the intra-day real-time optimization results, an intra-day real-time optimization evaluation is carried out, and the evaluation result is fed back to the day-ahead optimization and used to adjust the parameters. is denoted as
where is the result of the intra-day real-time optimization assessment. is the intra-day real-time charging cost of the station in slot . is the expected day-ahead charging cost.
3. Numerical Experiment Analysis
3.1. Numerical Experiment Setup
The battery-charging simulation scene of the electric heavy-duty truck battery-swapping station is constructed by using the relevant parameters of the actual battery-swapping station in a certain province, and the simulation verification is carried out by using MATLAB software R2023a. The scene contains 700 batteries, and the charging equipment is used to charge, at most, 300 batteries at the same time. The battery state is divided into seven grades, and the specific simulation parameters are shown in Table 1 [22]. To assess the performance of the proposed algorithm, two algorithms are selected for comparison. Baseline 1 is the battery-charging optimization algorithm based on the integrated algorithm [6], which takes into account the time-of-use pricing model. An integrated approach is proposed to solve the optimization problem, merging genetic algorithms, differential evolution, and particle swarm optimization techniques. Baseline 2 is the dual-timescale battery-charging optimization algorithm based on a genetic algorithm [23]. The algorithm constructs the battery-swapping station model with multi-functions such as charging, discharging, and idleness, and optimizes the scheduling strategy by the genetic algorithm. The optimization objectives of the two comparison algorithms are the same as those of the proposed algorithm. Baseline 2 does not consider the impact of time-of-use pricing, and the two comparison algorithms do not take into account the day-ahead and intra-day two-stage optimization.

Table 1.
Simulation parameters [24].
3.2. Analysis of Simulation Results
Figure 2 illustrates how the intra-day charging cost varies with the number of iterations. The intra-day charging costs for all three algorithms decrease as the number of iterations increases, with the proposed algorithm having the best convergence effect and the fastest convergence speed. When the number of iterations is 200, the intra-day charging cost of the proposed algorithm is reduced by 4.26% and 6.03% compared with that of Baseline 1 and Baseline 2, respectively. This is because the proposed algorithm uses a chaotic sequence to initialize the population, which generates a better population at the beginning of the iteration of the algorithm and speeds up the convergence speed. In addition, the proposed algorithm adopts an elite opposition-based learning strategy to update the grasshopper position, and it increases the disturbance to the grasshopper population through the Lévy flight disturbance mechanism, which avoids falling into the local optima and increases the accuracy of the solution.
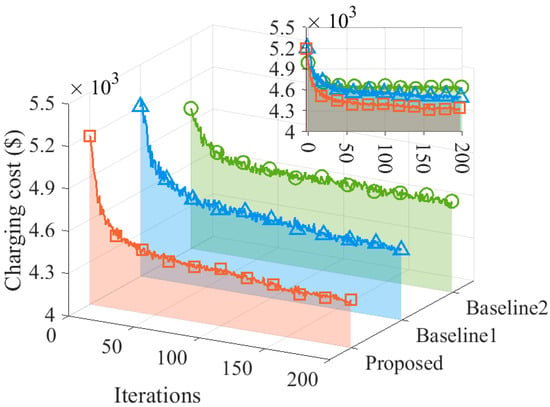
Figure 2.
The intra-day charging cost varies with the number of iterations.
Figure 3 illustrates the variation in the number of batteries at different SoC levels over time. It can be seen that although the battery-swapping station provides a battery-swapping service from 9:00 to 16:00, due to the larger output from PV generation, more batteries are charged to consume excess power. As a result, the number of fully charged batteries continues to increase, corresponding to the SoC level of . From 18:00 to 24:00 in the evening, due to the peak of the load demand and replacement demand, more batteries are discharged, and the number of fully charged batteries decreases. In contrast, the number of depleted batteries continues to increase, corresponding to an SoC level of .
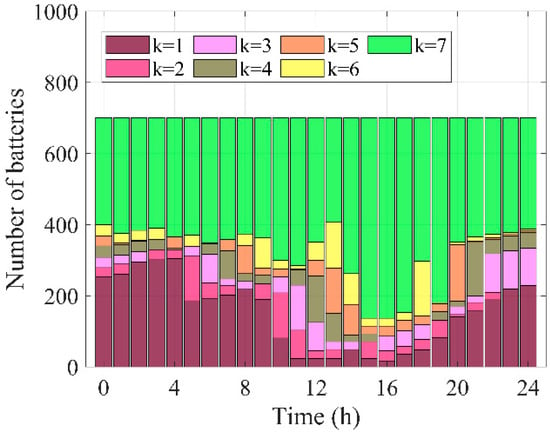
Figure 3.
The variation in the number of batteries at different SoC levels over time.
Figure 4 illustrates the variation in the total charging power of the energy-storage equipment and batteries over time. It can be observed that from 9:00 to 16:00, due to the large PV output, the energy-storage equipment and batteries are charged during this period to absorb the excess power generated by PVs in the battery-swapping station. From 0:00 to 6:00 and 22:00 to 23:00, due to insufficient PV generation, the battery-swapping station experiences a power deficit. During these periods, the energy-storage equipment and batteries are discharged to ensure the smooth operation of the battery-swapping station. From 17:00 to 21:00 in the evening, when load demand reaches its peak, even with the discharging of the energy-storage equipment and batteries, the demand cannot be fully met, requiring the battery-swapping station to purchase electricity from the grid at a premium to cover the shortfall.
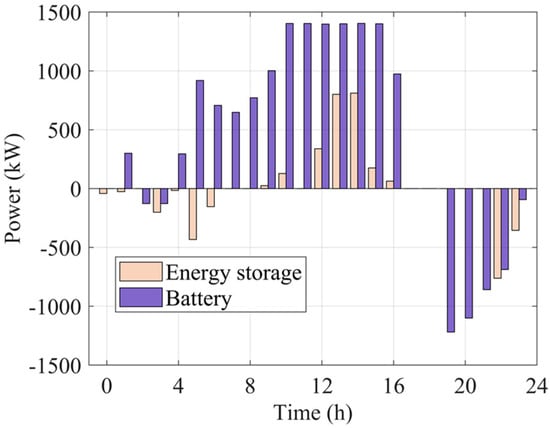
Figure 4.
The variations in total charging power of the energy-storage equipment and batteries over time.
Figure 5 illustrates how and the charging cost vary with robust and opportunistic factors. In the robust model, as increases, the expected target value gradually rises, and the total operation cost obtained through model optimization increases, and the radius of uncertainty increases. This is because in the robust model, decision-makers assume that uncertainty will have negative effects. The larger the value of is, the greater the risk of uncertainty, which may lead to additional operation costs and result in greater total operation costs. In the opportunistic model, as increases, the expected target value gradually decreases, and the total operation cost obtained through the model optimization decreases, while the radius of uncertainty increases. This is because in the opportunistic model, decision-makers assume that uncertainty will have positive effects. The larger the value of is, the greater the possible benefits of uncertainty, which may lead to additional benefits and result in lower total operation costs.
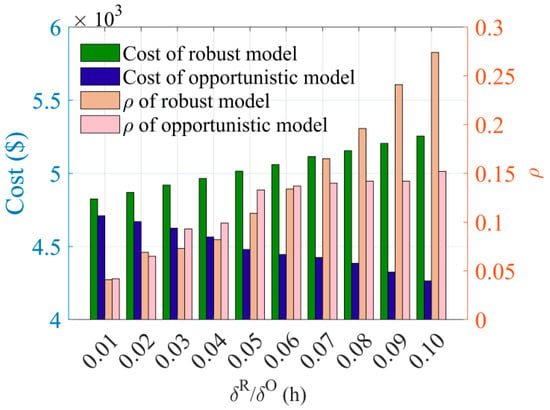
Figure 5.
Variations in the charging costs due to robust and opportunistic factors.
Figure 6 illustrates the load curves before and after the battery-charging strategy optimization for the electric heavy-duty truck battery-swapping station from 17:00 to 23:00. After optimization, the peak load of the battery-swapping station decreases from 41.4 kW to 39.2 kW, corresponding to a reduction of 5.31%. The proposed algorithm significantly reduces the total charging power during peak periods, thereby lowering the maximum load of the battery-swapping station and enabling its effective participation in grid peak-shaving.
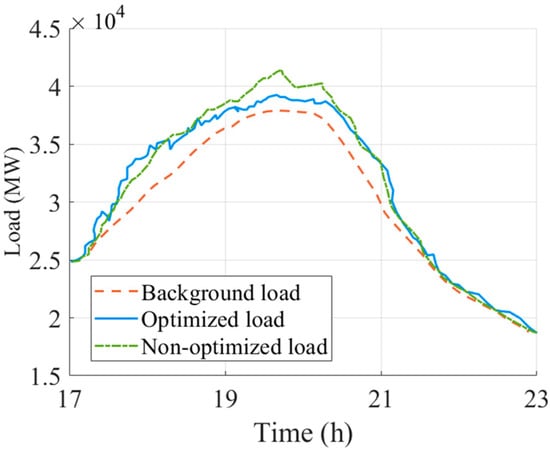
Figure 6.
Load curves before and after battery-charging strategy optimization for the electric heavy-duty truck battery-swapping station.
4. Conclusions
This study aimed to address the challenges of optimizing battery-charging management in electric heavy-duty truck battery-swapping stations, considering the uncertainties in renewable energy outputs, such as wind and photovoltaic power, and the fluctuations in battery-swapping demand. We proposed a multi-timescale battery-charging optimization algorithm that accounts for source–load–storage uncertainty, with the primary objectives being to enhance the economic efficiency of battery-swapping stations and to improve grid stability.
Methodologically, we developed a comprehensive model for the electric heavy-duty truck battery-swapping station under the time-of-use pricing mechanism, incorporating uncertainties in renewable energy sources, grid-load fluctuations, and battery-swapping demand. Our approach leveraged both day-ahead and intra-day optimization timescales, decomposing the complex optimization problem into manageable subproblems. The day-ahead optimization was formulated using information-gap decision theory (IGDT) to handle uncertainties, while the intra-day optimization was addressed with an improved grasshopper optimization algorithm to fine-tune the charging strategies based on real-time data.
Our findings demonstrated the effectiveness of the proposed approach. Simulation results showed that the algorithm reduced intra-day charging costs by 4.26% and 6.03%compared with the two baseline algorithms, respectively. Moreover, the optimized battery-charging strategy led to a 5.31% decrease in peak load, contributing to grid peak-shaving and stability. The proposed method’s ability to dynamically adjust risk preferences based on intra-day optimization results and its robustness against uncertainties in the renewable energy output and grid-load fluctuations were particularly noteworthy.
In conclusion, the multi-timescale battery-charging optimization algorithm presented in this study not only offers a cost-effective solution for managing battery-swapping stations under uncertainty but also enhances grid stability. Future research should focus on integrating user behavior models into the charging strategy optimization to provide more personalized and efficient battery-swapping services, further improving the resilience and economic viability of electric heavy-duty truck operations.
Author Contributions
Conceptualization, P.S., R.J. and J.W.; Investigation, P.S., G.N., H.W. and G.Q.; Methodology, P.S. and G.N.; Software, P.S., G.N. and J.W.; Visualization, P.S. and Z.S.; Writing—original draft, P.S., G.N. and G.Q.; Formal analysis, G.N. and Z.S.; Validation, G.N. and H.W.; Funding acquisition, R.J.; Project administration, R.J. and J.W.; Supervision, R.J.; Writing—review and editing, R.J., Z.S. and G.Q.; Data curation, H.W.; Resources, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to restrictions.
Acknowledgments
We thank Jin Rifeng for providing technical guidance for this research. We thank Zhongwei Sun for building the framework of the paper, proposing innovative points, and making contributions to the writing.
Conflicts of Interest
Authors Peijun Shi and Haibo Wang were employed by the Datang Beijing Tianjin Hebei Energy Marketing Co., Ltd. Author Rifeng Jin was employed by the Datang Henan Power Generation Co., Ltd. Authors Jinsong Wang and Guizhi Qiu were employed by the China Datang Corporation Science and Technology General Research Institute North China Electric Power Test and Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interests.
References
- Ghandriz, T.; Jacobson, B.; Murgovski, N.; Nilsson, P.; Laine, L. Real-Time Predictive Energy Management of Hybrid Electric Heavy Vehicles by Sequential Programming. IEEE Trans. Veh. Technol. 2021, 70, 4113–4128. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wang, P.; Xiao, G. Coordinated preparation and recovery of a post-disaster multi-energy distribution system considering thermal inertia and diverse uncertainties. Appl. Energ. 2023, 336, 120736. [Google Scholar] [CrossRef]
- Tarar, M.O.; Hassan, N.U.; Naqvi, I.H.; Pecht, M. Techno-Economic Framework for Electric Vehicle Battery Swapping Stations. IEEE Trans. Transp. Electrif. 2023, 9, 4458–4473. [Google Scholar] [CrossRef]
- Wang, R.; Ju, Y.; Allybokus, Z.; Zeng, W.; Obrecht, N.; Moura, S. Optimal Sizing, Operation, and Efficiency Evaluation of Battery Swapping Stations for Electric Heavy-Duty Trucks. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024. [Google Scholar]
- Li, Z.; Wu, L.; Xu, Y.; Moazeni, S.; Tang, Z. Multi-Stage Real-Time Operation of a Multi-Energy Microgrid With Electrical and Thermal Energy Storage Assets: A Data-Driven MPC-ADP Approach. IEEE Trans. Smart Grid. 2022, 13, 213–226. [Google Scholar] [CrossRef]
- Wu, H.; Pang, G.K.H.; Choy, K.L.; Lam, H.Y. An Optimization Model for Electric Vehicle Battery Charging at a Battery Swapping Station. IEEE Trans. Veh. Technol. 2018, 67, 881–895. [Google Scholar] [CrossRef]
- Ko, H.; Pack, S. An Optimal Battery Charging Algorithm in Electric Vehicle-Assisted Battery Swapping Environments. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3985–3994. [Google Scholar] [CrossRef]
- Esmaeili, S.; Anvari-Moghaddam, A. Optimal Operation Scheduling of a Microgrid Incorporating Battery Swapping Stations. IEEE Trans. Power Syst. 2019, 34, 5063–5072. [Google Scholar] [CrossRef]
- Jin, J.; Mao, S. Optimal Priority Rule-Enhanced Deep Reinforcement Learning for Charging Scheduling in an Electric Vehicle Battery Swapping Station. IEEE Trans. Smart Grid. 2023, 14, 4581–4593. [Google Scholar] [CrossRef]
- Davari, M.; Nafisi, H.; Nasr, M.-A.; Blaabjerg, F. A Novel IGDT-Based Method to Find the Most Susceptible Points of Cyberattack Impacting Operating Costs of VSC-Based Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3695–3714. [Google Scholar] [CrossRef]
- Gazijahani, F.; Salehi, J. IGDT-Based Complementarity Approach for Dealing With Strategic Decision Making of Price-Maker VPP Considering Demand Flexibility. IEEE Trans. Ind. Inf. 2020, 16, 2212–2220. [Google Scholar] [CrossRef]
- Jamian, J.J.; Mustafa, M.W.; Mokhlis, H.; Baharudin, M.A. Simulation Study on Optimal Placement and Sizing of Battery Switching Station Units Using Artificial Bee Colony Algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 592–601. [Google Scholar] [CrossRef]
- Fang, S.-C.; Ke, B.-R.; Chung, C.-Y. Minimization of Construction Costs for an All Battery-Swapping Electric-Bus Transportation System: Comparison with an All Plug-In System. Energies 2017, 10, 890. [Google Scholar] [CrossRef]
- Singh, S.; More, V.; Batheri, R. Driving Electric Vehicles Into the Future With Battery Management Systems. IEEE Eng. Manag. Rev. 2022, 50, 157–161. [Google Scholar] [CrossRef]
- González-Romera, E.; Roncero-Clemente, C.; Barrero-González, F.; Milanés-Montero, M.I.; Romero-Cadaval, E. A Comprehensive Control Strategy for Multibus Nanogrids With Power Exchange Between Prosumers. IEEE Access 2021, 9, 104281–104293. [Google Scholar] [CrossRef]
- Zhang, H.; Zhai, X.; Zhang, J.; Bai, X.; Li, Z. Mechanism Analysis of the Effect of the Equivalent Proportional Coefficient of Inertia Control for a Doubly Fed Wind Generator on Frequency Stability in Extreme Environments. Sustainability 2024, 16, 4965. [Google Scholar] [CrossRef]
- Ahmed, H.M.A.; Sindi, H.F.; Azzouz, M.A.; Awad, A.S.A. Optimal Sizing and Scheduling of Mobile Energy Storage Toward High Penetration Levels of Renewable Energy and Fast Charging Stations. IEEE Trans. Energy Convers. 2022, 37, 1075–1086. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, D.; Ma, Y.; Sui, Q.; Lin, X.; Wei, F. Restoration Enhancement for Distribution Systems Based on Multiple Battery Swapping Stations. IEEE Trans. Ind. Appl. 2024, 60, 2025–2036. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Wang, P. A Stochastic Bi-Level Optimal Allocation Approach of Intelligent Buildings Considering Energy Storage Sharing Services. IEEE Trans. Consum. Electron. 2024, 70, 5142–5153. [Google Scholar] [CrossRef]
- Nojavan, S.; Zare, K.; Feyzi, M.R. Optimal Bidding Strategy of Generation Station in Power Market Using Information Gap Decision Theory (IGDT). Electr. Power Syst. Res. 2013, 96, 56–63. [Google Scholar] [CrossRef]
- Ghaleb, S. Feature Selection by Multiobjective Optimization: Application to Spam Detection System by Neural Networks and Grasshopper Optimization Algorithm. IEEE Access 2022, 10, 98475–98489. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Y.; Xu, Q. Day-ahead Robust Optimal Dispatch of Integrated Energy Station Considering Battery Exchange Service. J. Energy Storage 2022, 50, 104228. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Ma, K.; Yang, B. Optimal Dispatching Strategy for Shared Battery Station of Electric Vehicle by Divisional Battery Control. IEEE Access 2019, 1, 1. [Google Scholar] [CrossRef]
- Zhang, W. Multi-Objective Optimization of Charging Dispatching for Electric Vehicle Battery Swapping Station. Master’s thesis, Jilin University, Changchun, China, 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).