Advanced Single-Phase Non-Isolated Microinverter with Time-Sharing Maximum Power Point Tracking Control Strategy
Abstract
1. Introduction
- This work addresses the challenge of performing MPPT for multiple PV panels with distinct I–V characteristics using a single shared microinverter, maintaining performance without degradation.
- It eliminates the need for additional active switches by integrating a multi-input boost converter directly into an H-bridge structure, reducing cost and complexity.
- The proposed control strategy leverages the slow-varying nature of PV panel characteristics, enabling efficient low speed control without requiring high-frequency updates.
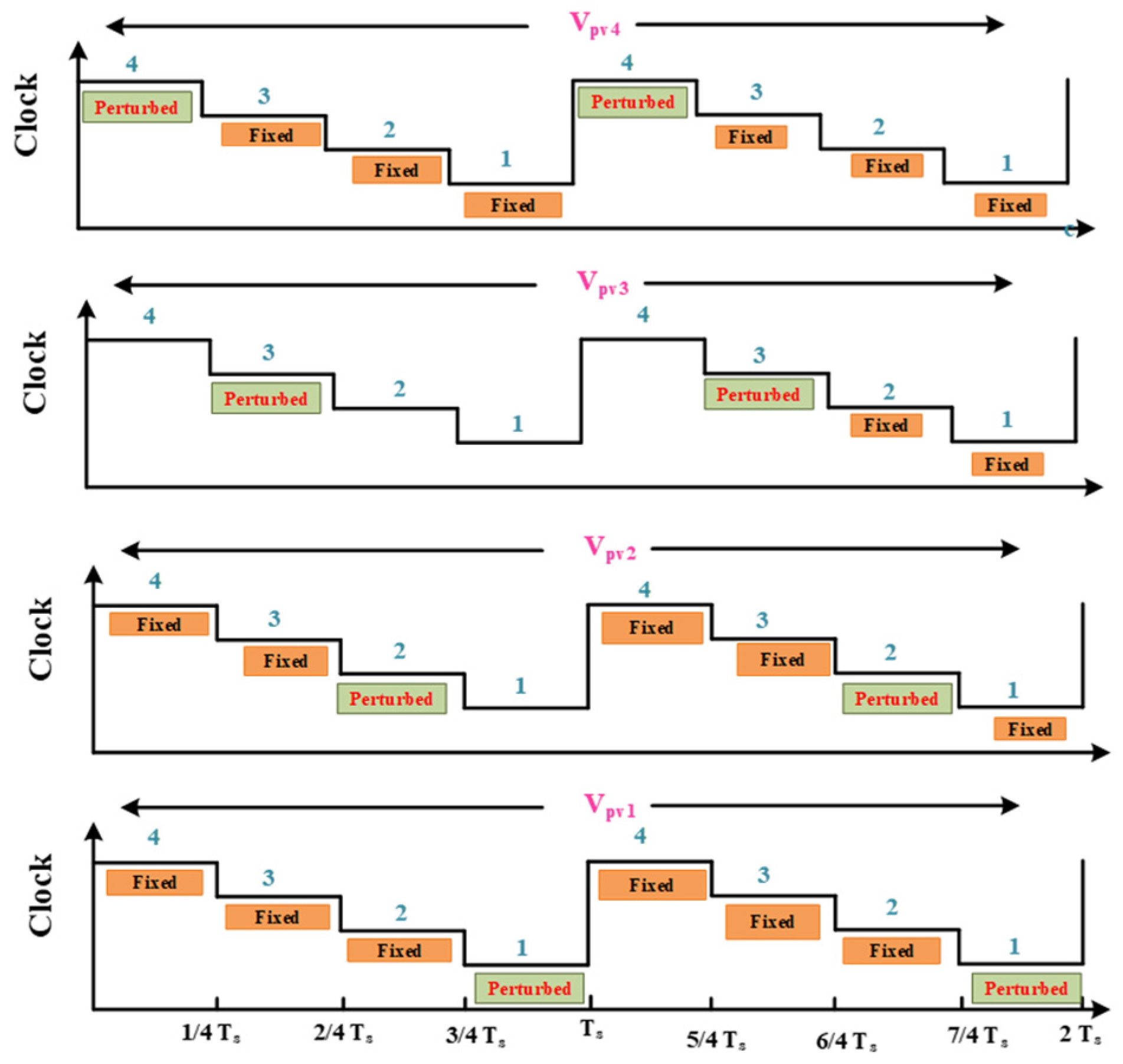
- A time-shared MPPT scheme is introduced, updating the tracking and modulation variables of each PV module once every half-cycle of the AC output, allowing coordinated operation across multiple inputs.
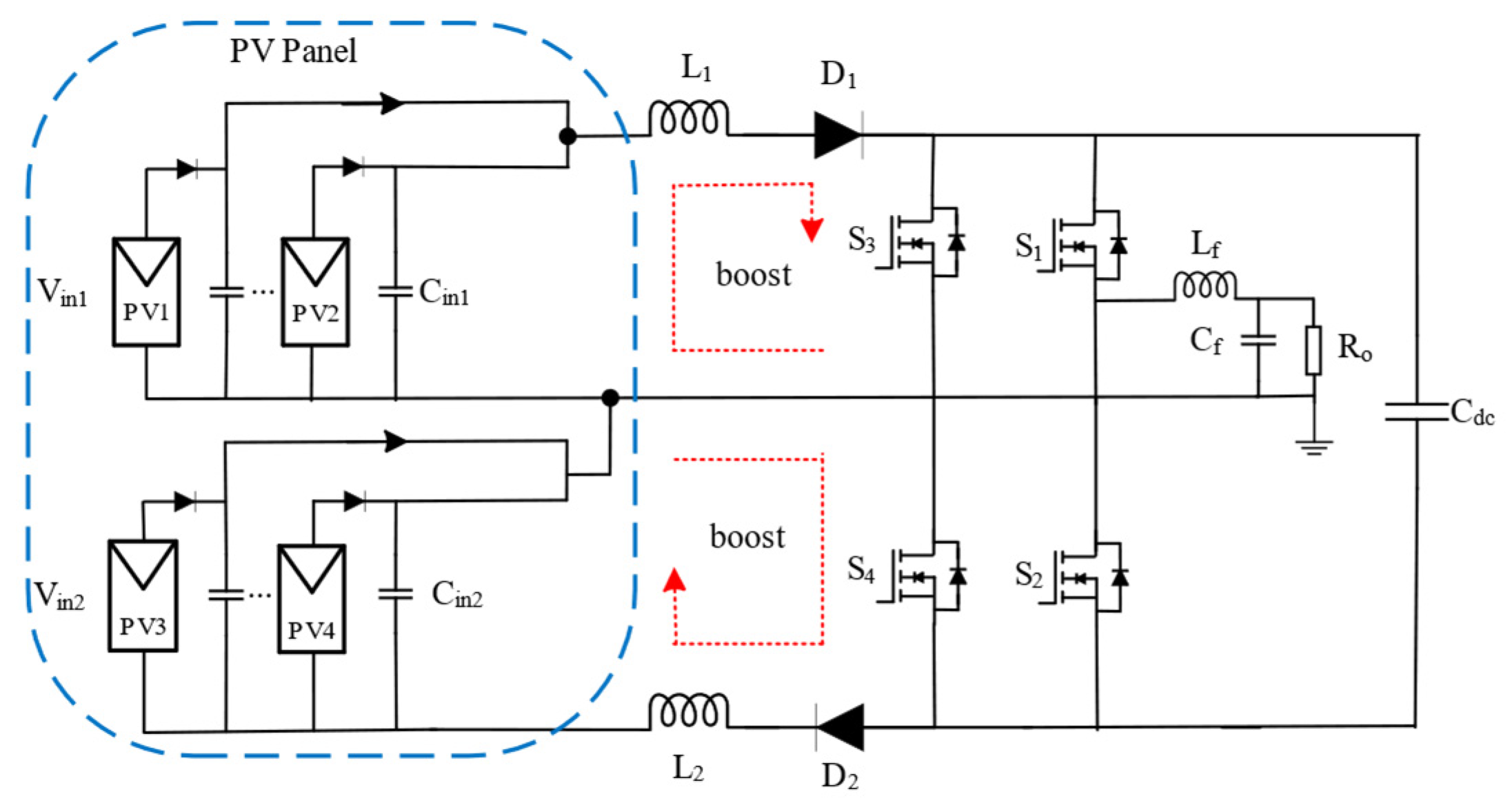
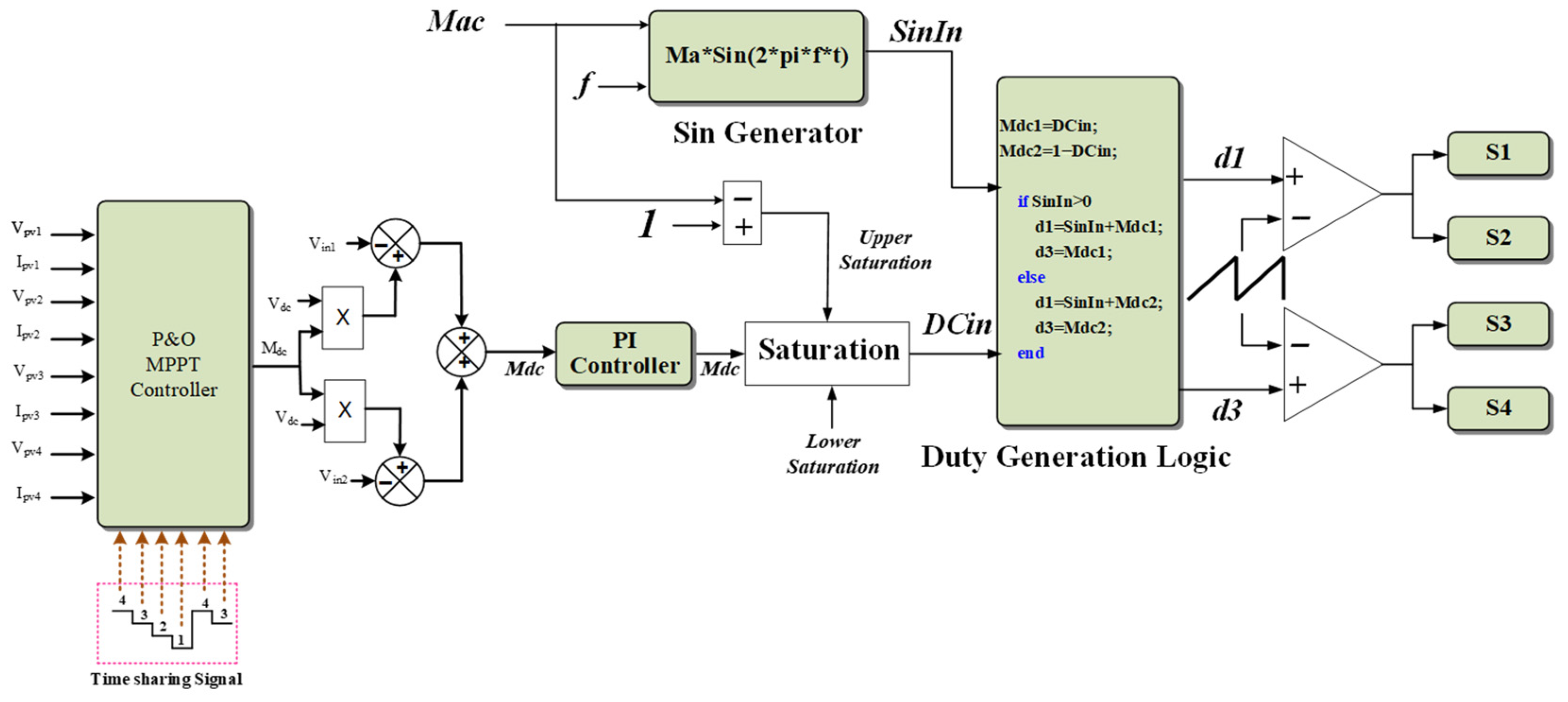
2. Proposed Microinverter Topology and Its Operation
- A reduced number of power switches of only four switches is required to interface four PV sources.
- Built-in active power decoupling capability to enhance power quality.
- Elimination of leakage current due to the common ground between the AC and DC sides.
- Low current stress on switches and diodes, as they handle only the input current from each PV source.
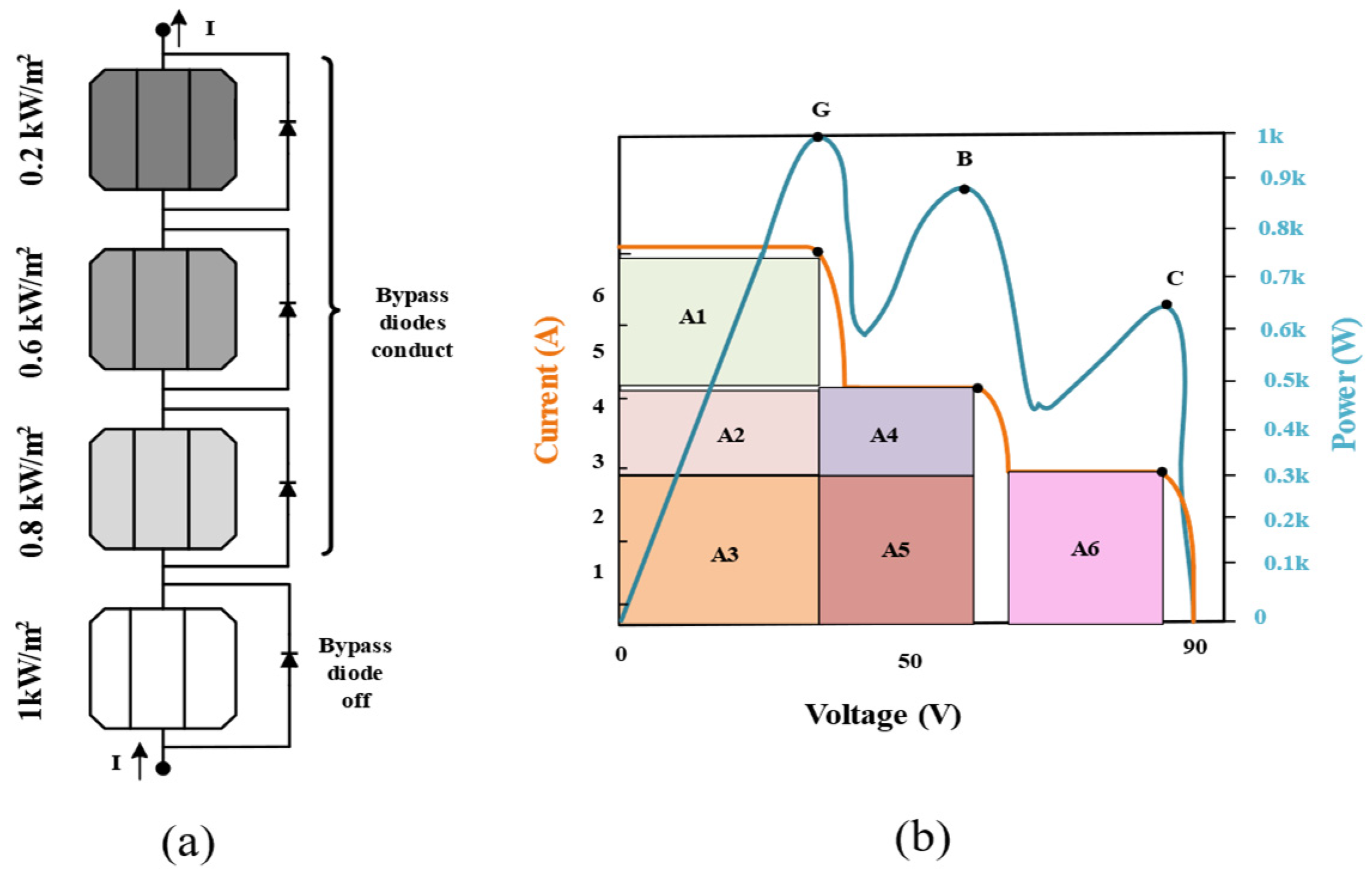
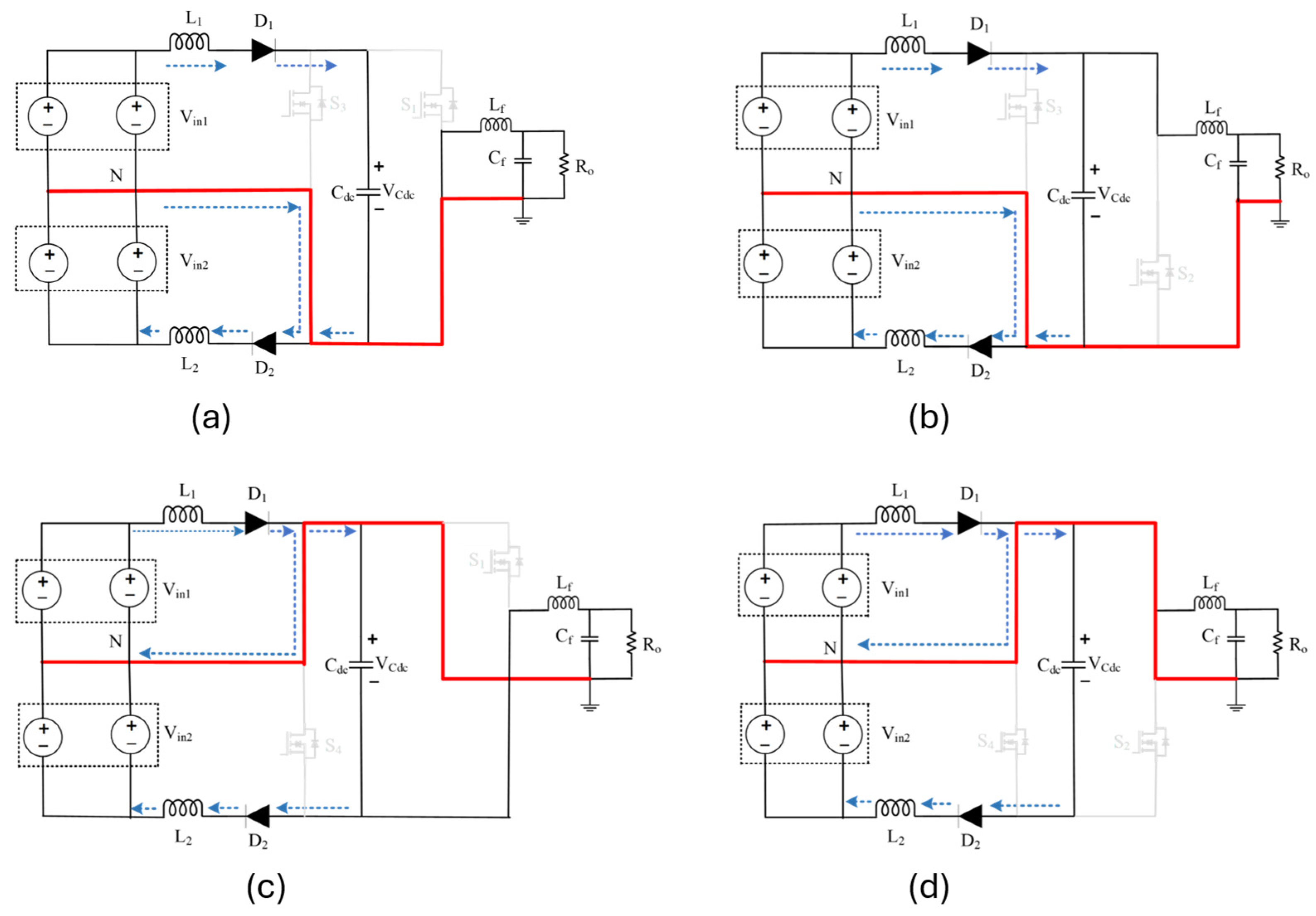
2.1. Operation and Power Loss Analysis
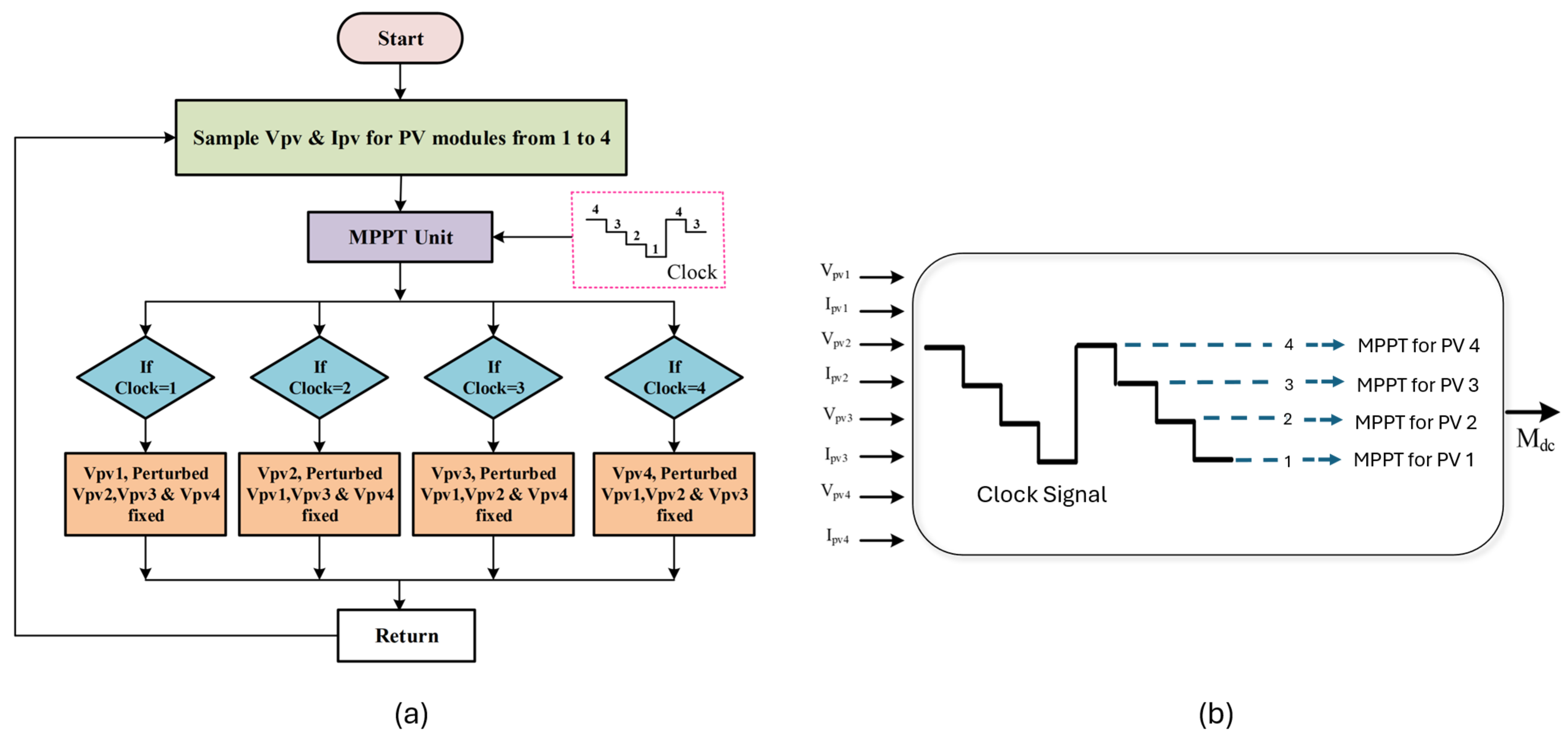
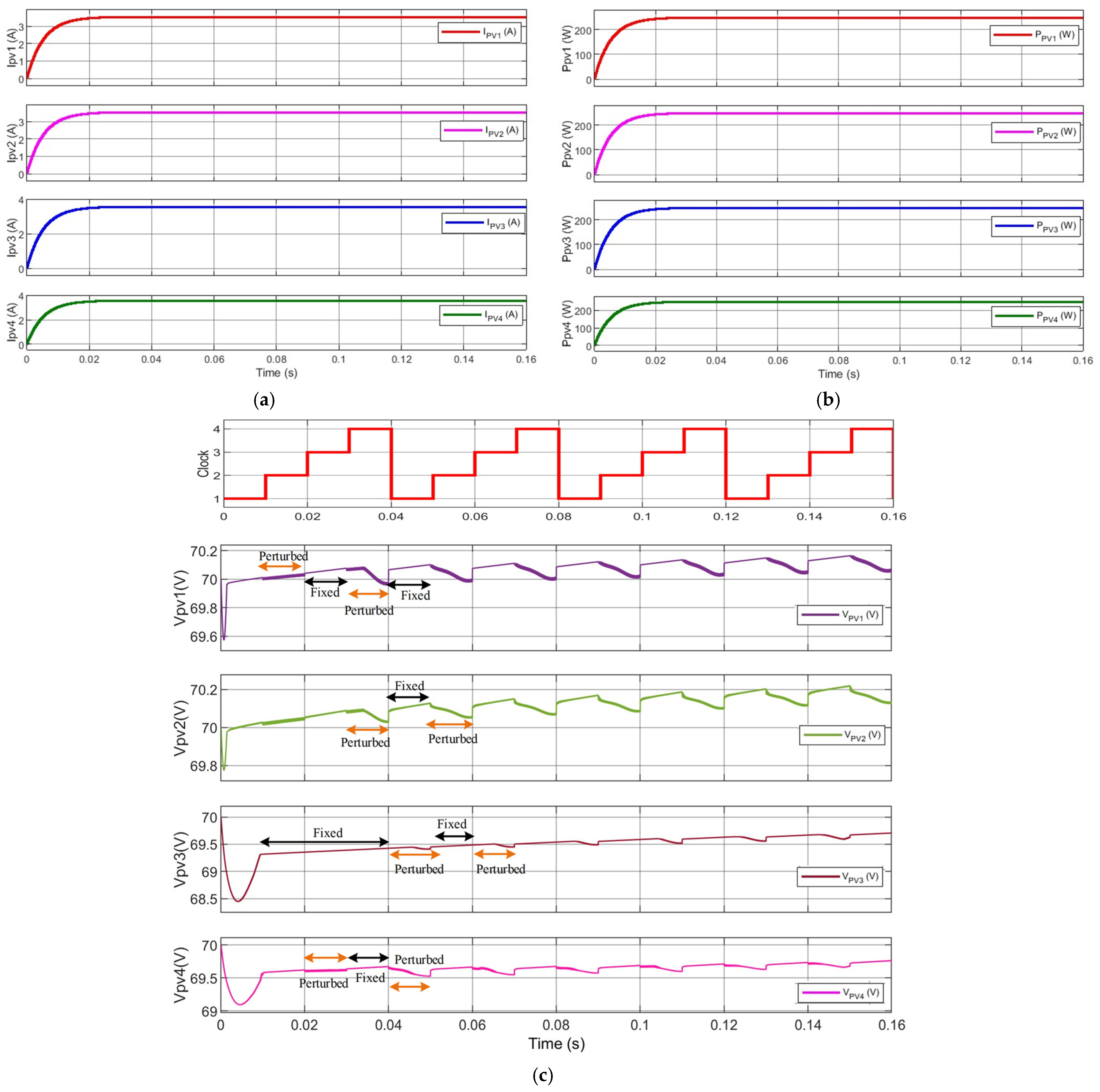
2.2. MI Time-Sharing Algorithm and MPPT Control Strategy
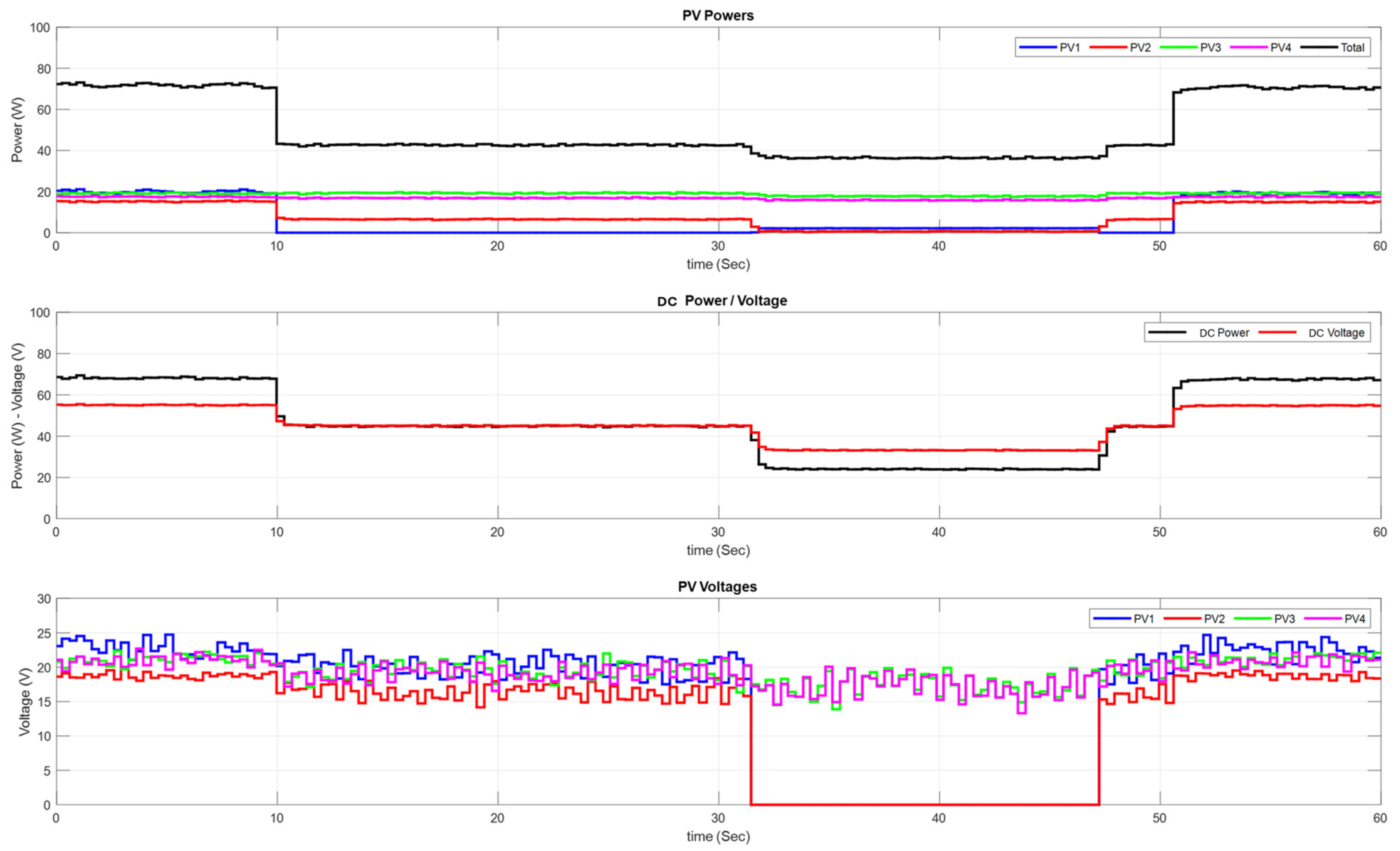
3. Simulation Evaluation with PV Sources
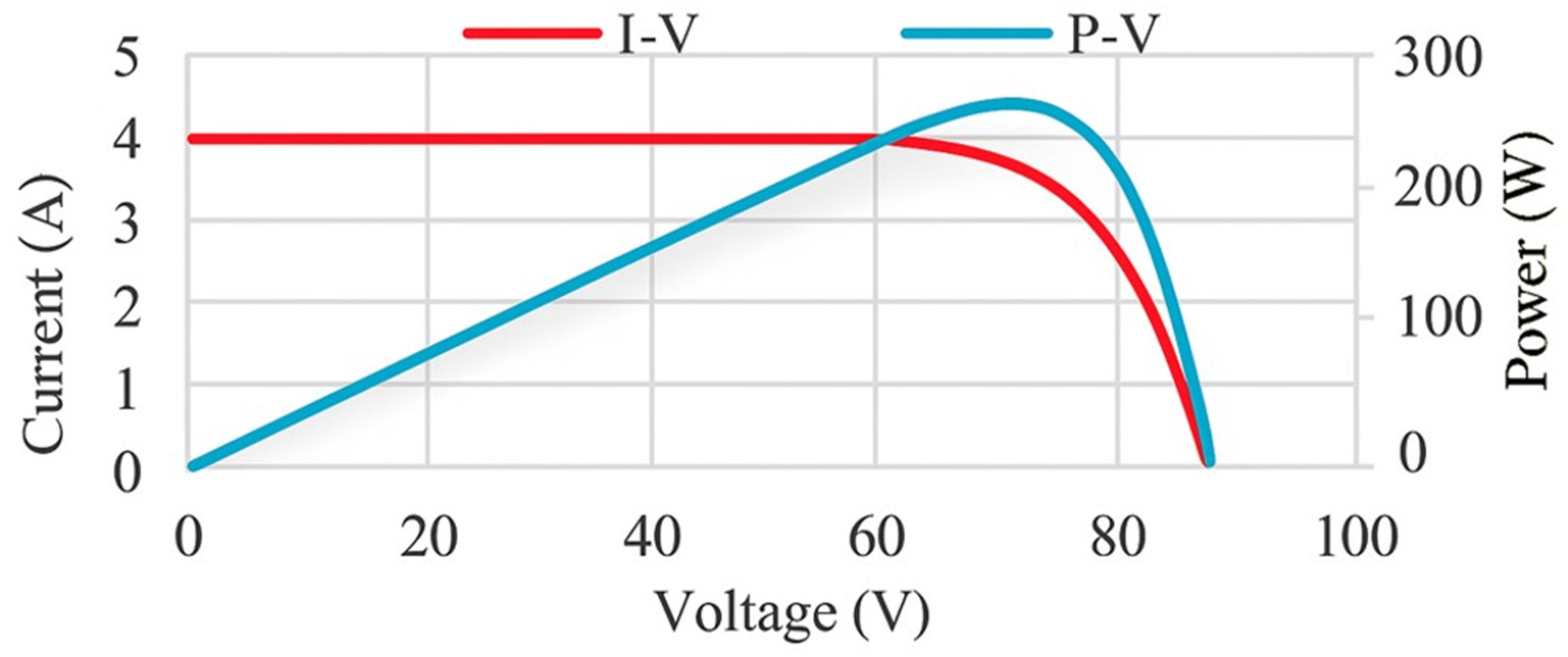
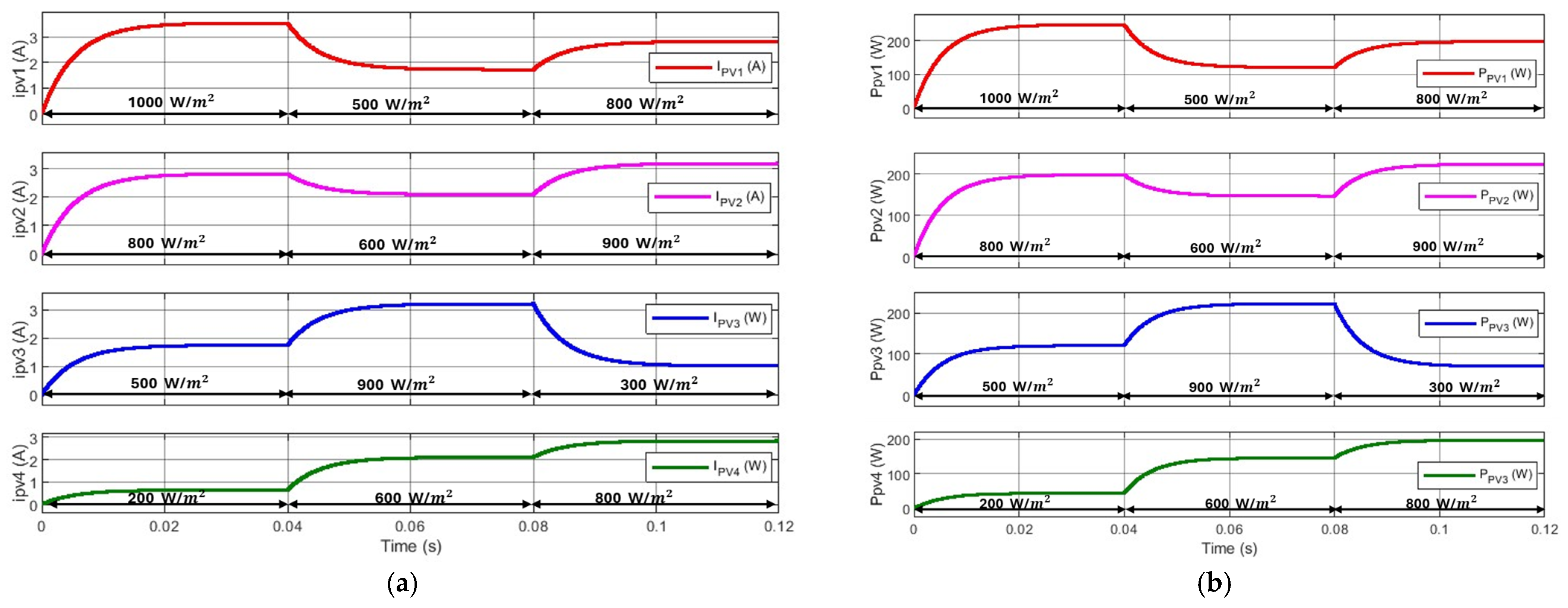
3.1. Fixed Irradiance Conditions
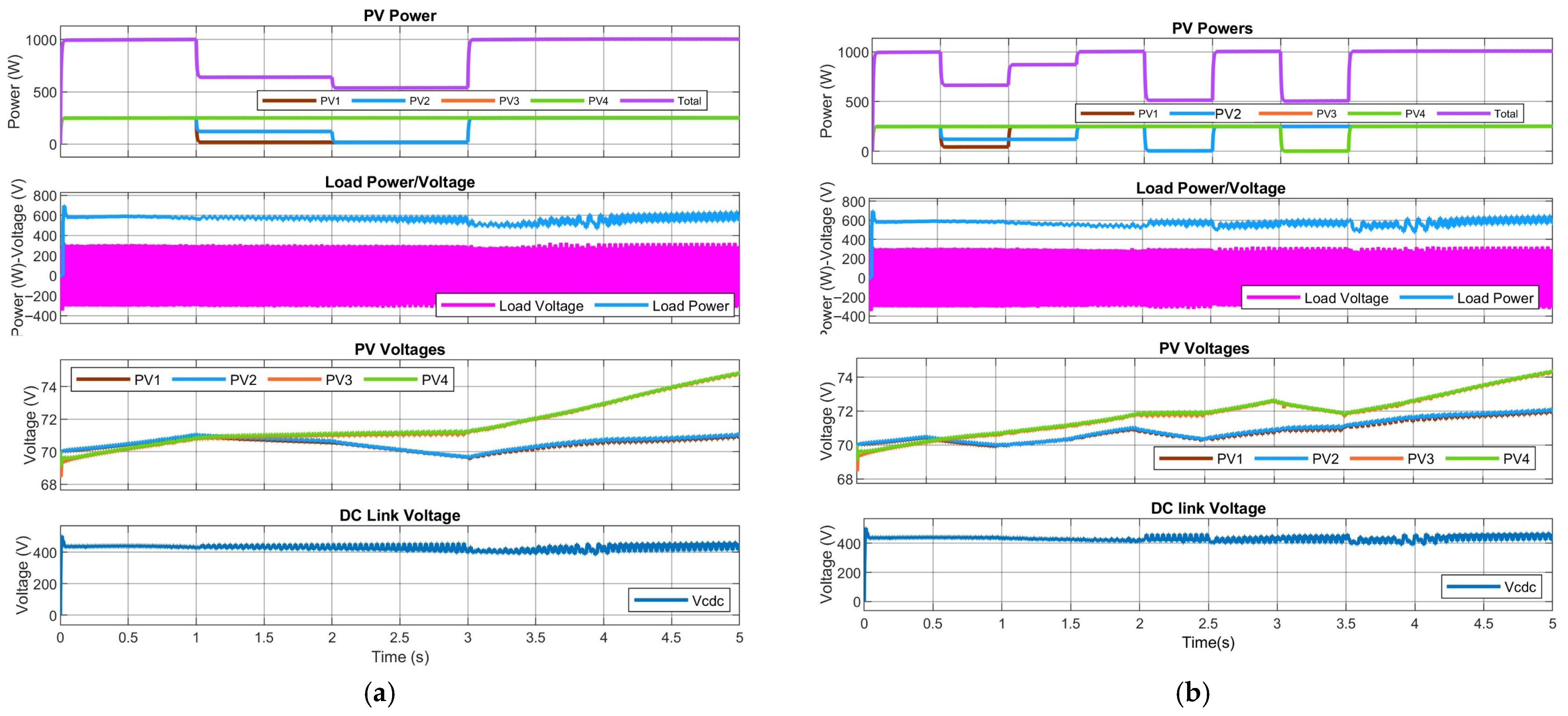
3.2. Dynamic Irradiance Conditions
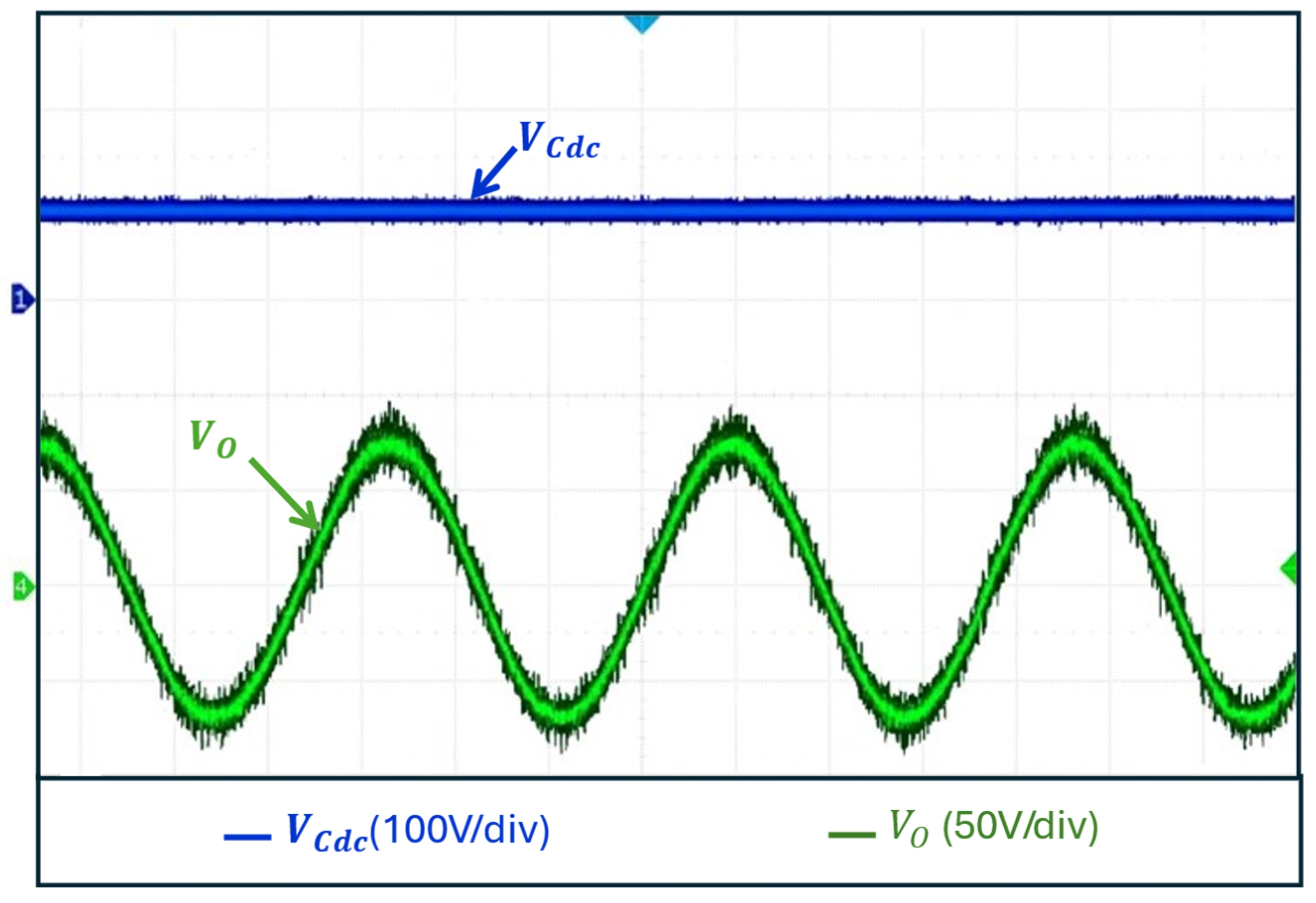
4. Experimental Results
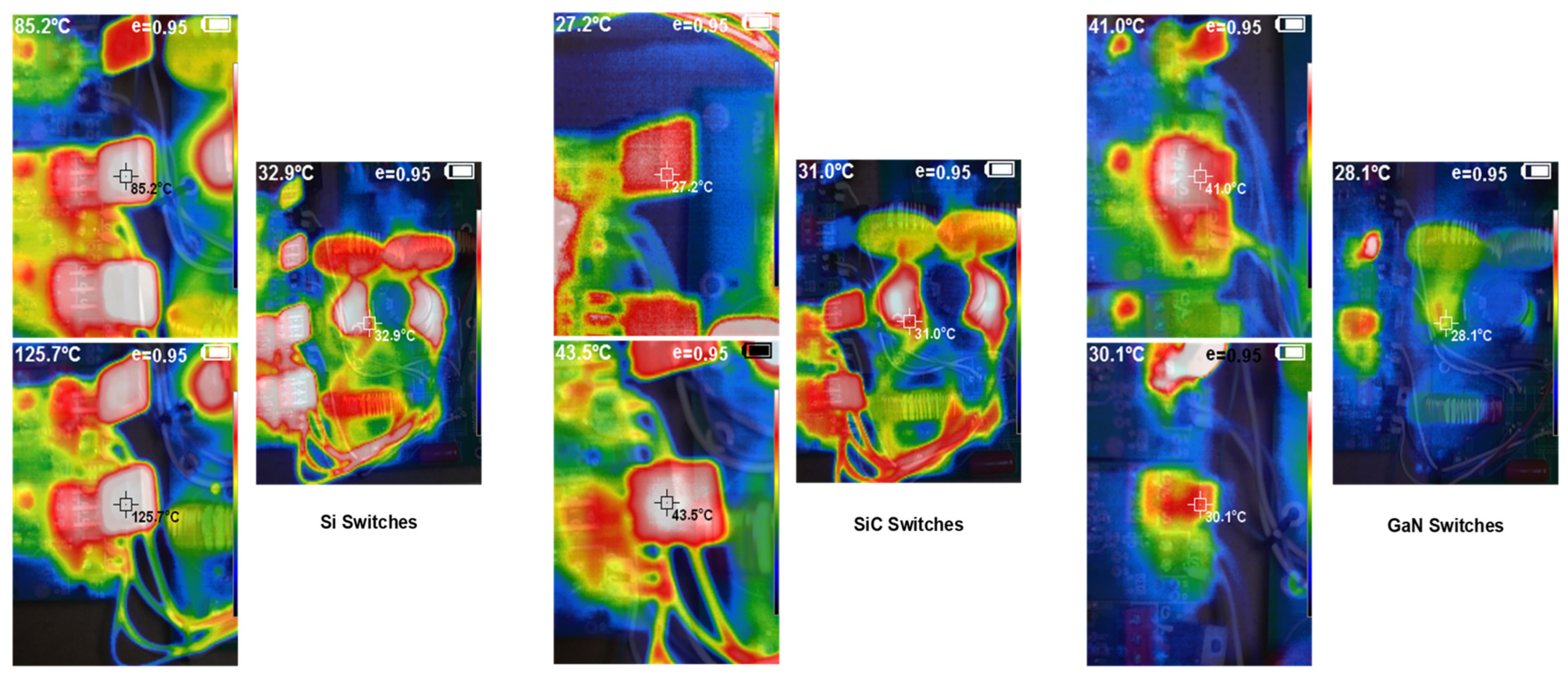
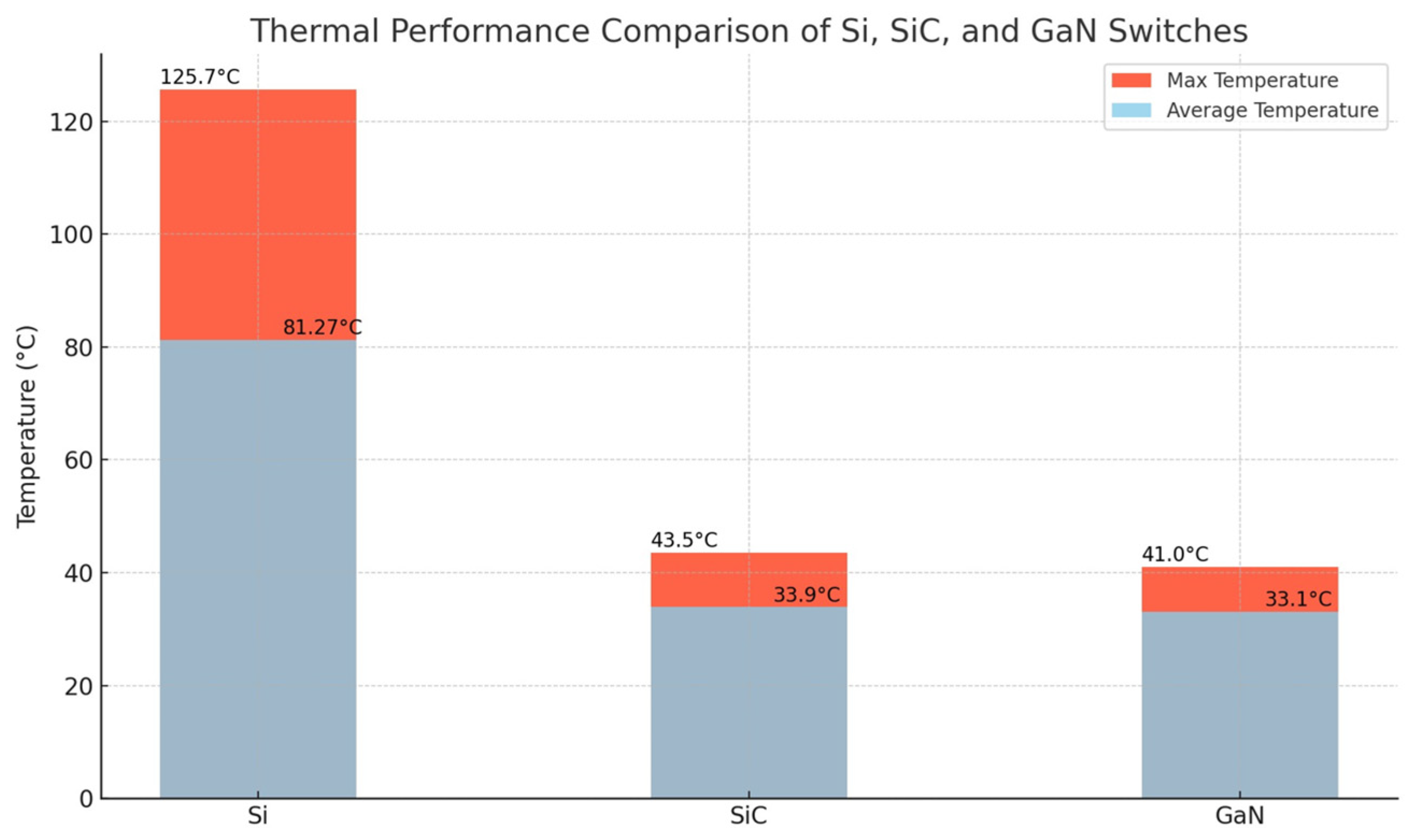
4.1. Thermal Analysis
4.2. Comparison with Current DMPPT Control Strategies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PV | Photovoltaic |
| PGS | PV Generation Systems |
| FPP | Full Power Processing |
| DPP | Differential Power Processing |
| MPPT | Maximum Power Point Tracking |
| CMPPT | Centralized Maximum Power Point Tracking |
| DMPPT | Distributed Maximum Power Point Tracking |
| GMPP | Global Maximum Power Point |
| GMPPT | Global Maximum Power Point Tracking |
| LMPPs | Local Maximum Power Points |
| TS-MPPT | Time-Sharing Maximum Power Point Tracking |
| CCM | Continuous Conduction Mode |
| DC | Direct Current |
| DCM | Discontinuous Conduction Mode |
References
- Ruchira; Tamrakar, E.; Patel, R.N.; Choudekar, P. Customized Design of Microinverter Based Solar Photovoltaic System for Small Houses in Developing Nations. Renew. Energy Focus 2022, 42, 178–189. [Google Scholar] [CrossRef]
- Mehta, H.K.; Panchal, A.K. A Novel Exponent I–V Relation Based Maximum Power Point Algorithm for Photovoltaic Panel. Renew. Energy Focus 2021, 36, 56–64. [Google Scholar] [CrossRef]
- Husain, M.A.; Pingale, S.B.; Bakar Khan, A.; Faiz Minai, A.; Pandey, Y.; Shyam Dwivedi, R. Performance Analysis of the Global Maximum Power Point Tracking Based on Spider Monkey Optimization for PV System. Renew. Energy Focus 2023, 47, 100503. [Google Scholar] [CrossRef]
- Satapathy, P.; Dhar, S.; Dash, P.K. An Evolutionary Online Sequential Extreme Learning Machine for Maximum Power Point Tracking and Control in Multi-Photovoltaic Microgrid System. Renew. Energy Focus 2017, 21, 33–53. [Google Scholar] [CrossRef]
- Alenezi, A.; Hussain, H.A. A New Control Approach for Least Processed Power Tracking Under Mismatch Conditions in PV Systems Using Differential Power Processing. IEEE Trans. Ind. Appl. 2024, 60, 532–543. [Google Scholar] [CrossRef]
- Mäki, A.; Valkealahti, S. Power Losses in Long String and Parallel-Connected Short Strings of Series-Connected Silicon-Based Photovoltaic Modules Due to Partial Shading Conditions. IEEE Trans. Energy Convers. 2012, 27, 173–183. [Google Scholar] [CrossRef]
- Sameera; Tariq, M.; Rihan, M.; Ayan, M. A Comprehensive Review on the Application of Recently Introduced Optimization Techniques Obtaining Maximum Power in the Solar PV System. Renew. Energy Focus 2024, 49, 100564. [Google Scholar] [CrossRef]
- Kim, K.A.; Krein, P.T. Hot Spotting and Second Breakdown Effects on Reverse I-V Characteristics for Mono-Crystalline Si Photovoltaics. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition (ECCE 2013), Denver, CO, USA, 15–19 September 2013. [Google Scholar]
- Ko, S.W.; Ju, Y.C.; Hwang, H.M.; So, J.H.; Jung, Y.S.; Song, H.J.; Song, H.-e.; Kim, S.H.; Kang, G.H. Electric and Thermal Characteristics of Photovoltaic Modules under Partial Shading and with a Damaged Bypass Diode. Energy 2017, 128, 232–243. [Google Scholar] [CrossRef]
- Guiver, C.; Opmeer, M.R. The Energy-Balance Method for Optimal Control in Renewable Energy Applications. Renew. Energy Focus 2024, 50, 100582. [Google Scholar] [CrossRef]
- Ziar, H.; Nouri, M.; Asaei, B.; Farhangi, S. Analysis of Overcurrent Occurrence in Photovoltaic Modules with Overlapped By-Pass Diodes at Partial Shading. IEEE J. Photovolt. 2014, 4, 713–721. [Google Scholar] [CrossRef]
- Abudulimu, A.; Wenner, S.L.; Philips, A.B.; Lee, C.; Li, D.B.; Jamarkkatel, M.K.; Zawisza, Z.W.; Neupane, S.; Katakumbura, N.P.; Brau, T.; et al. Bias-Dependent Quantum Efficiency Reveals Recombination Pathways in Thin Film Solar Cells. Adv. Energy Mater. 2025, 15, e01709. [Google Scholar] [CrossRef]
- Ncir, N.; El Akchioui, N.; El Fathi, A. Enhancing Photovoltaic System Modeling and Control under Partial and Complex Shading Conditions Using a Robust Hybrid DE-FFNN MPPT Strategy. Renew. Energy Focus 2023, 47, 100504. [Google Scholar] [CrossRef]
- Khan, O.; Xiao, W.; Zeineldin, H.H. Gallium-Nitride-Based Submodule Integrated Converters for High-Efficiency Distributed Maximum Power Point Tracking PV Applications. IEEE Trans. Ind. Electron. 2016, 63, 966–975. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, T.; Zhuo, F.; Yi, H. An Improved Submodule Differential Power Processing-Based PV System with Flexible Multi-MPPT Control. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 94–102. [Google Scholar] [CrossRef]
- Chu, G.; Wen, H.; Jiang, L.; Hu, Y.; Li, X. Bidirectional Flyback Based Isolated-Port Submodule Differential Power Processing Optimizer for Photovoltaic Applications. Sol. Energy 2017, 158, 929–940. [Google Scholar] [CrossRef]
- Qin, S.; Barth, C.B.; Pilawa-Podgurski, R.C.N. Enhancing Microinverter Energy Capture with Submodule Differential Power Processing. IEEE Trans. Power Electron. 2016, 31, 3575–3585. [Google Scholar] [CrossRef]
- Chu, G.; Wen, H.; Yang, Y.; Wang, Y. Elimination of Photovoltaic Mismatching with Improved Submodule Differential Power Processing. IEEE Trans. Ind. Electron. 2020, 67, 2822–2833. [Google Scholar] [CrossRef]
- Khan, O.; Xiao, W. An Efficient Modeling Technique to Simulate and Control Submodule-Integrated PV System for Single-Phase Grid Connection. IEEE Trans. Sustain. Energy 2016, 7, 96–107. [Google Scholar] [CrossRef]
- Poshtkouhi, S.; Palaniappan, V.; Fard, M.; Trescases, O. A General Approach for Quantifying the Benefit of Distributed Power Electronics for Fine Grained MPPT in Photovoltaic Applications Using 3-D Modeling. IEEE Trans. Power Electron. 2012, 27, 4656–4666. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, F.; Fan, Y.; Zhuo, F. Subpanel Level Time-Sharing Maximum Power Point Tracking System with Self-Adaptively Adjusted Control Strategy. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC 2015), Taipei, Taiwan, 1–4 November 2015. [Google Scholar]
- Cao, Z.; Li, Q.; Lee, F.C. Multi-Phase Smart Converter for PV System. In Proceedings of the Conference Proceedings—IEEE Applied Power Electronics Conference and Exposition (APEC 2015), Charlotte, NC, USA, 15–19 March 2015; Volume 2015. [Google Scholar]
- Madeti, S.R.K. A Monitoring System for Online Fault Detection in Multiple Photovoltaic Arrays. Renew. Energy Focus 2022, 41, 160–178. [Google Scholar] [CrossRef]
- Mazumdar, D.; Biswas, P.K.; Sain, C.; Ahmad, F.; Ustun, T.S.; Kalam, A. Performance Analysis of Drone Sqadron Optimisation Based MPPT Controller for Grid Implemented PV Battery System under Partially Shaded Conditions. Renew. Energy Focus 2024, 49, 100577. [Google Scholar] [CrossRef]




| Characteristic Comparison | DPP | FPP |
|---|---|---|
| PV cell group coupling | High | Low |
| DC-DC converter coupling | High | Low |
| Priority of bidirectional converter | High | Low |
| Cable demand | High | Low |
| Communication | Yes | No |
| Ease of system expansion | Moderate | Flexible |
| Number of converters | n × m | n |
| Control design | Multiple | MPPT |
| MPPT granularity (no modification of PV panel) | High | Low |
| States | Positive FHC (Vo > 0) | Negative FHC (Vo < 0) | ||||
|---|---|---|---|---|---|---|
| Null-1 (00) | Active-1 (10) | Null-2 (11) | Null-1 (00) | Active-2 (01) | Null-2 (11) | |
| L1 | Non-active | Non-active | Active | Non-active | Active | Active |
| L2 | Active | Active | Non-active | Active | Non-active | Non-active |
| Cdc (Ic) | Active (IL1+) | Non-active (iO − iL1+) | Active (IL2+) | Active (IL1−) | Non-active (iO − iL1+) | Active (IL2−) |
| Duration | Mdc1, Ts | (d1 − Mdc1) Ts | (1 − d1) Ts | d1 Ts | (Mdc2 − d1) Ts | (1 − Mdc2) Ts |
| Parameter | Specification |
|---|---|
| 4 input PV panels (Vmpp) | 70 v |
| Output AC (Vo) | 220 Vrms, |
| Modulation indexes | Mac = 0.8; Mdc1 = 0.17 |
| Carrier frequency (kHz) | 30 |
| Inductors L1, L2 (µH) | 450 |
| DC-link capacitor Cdc (µF) | 440 |
| Parameter | Specification |
|---|---|
| Open circuit voltage (Voc) | 23 V |
| Short circuit current (Isc) | 2 A |
| Carrier frequency (kHz) | 30 |
| Inductors L1, L2 (µH) | 450 |
| DC-link capacitor Cdc (µF) | 440 |
| Diodes D1, D2 | FFSH1665A |
| Power switches S1-S4 | TP65H150G4PS (650 V, Ron = 180 mΩ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhasi, A.; Luk, P.C.-K.; Ibrahim, K.A.; Luo, Z. Advanced Single-Phase Non-Isolated Microinverter with Time-Sharing Maximum Power Point Tracking Control Strategy. Energies 2025, 18, 4925. https://doi.org/10.3390/en18184925
Alhasi A, Luk PC-K, Ibrahim KA, Luo Z. Advanced Single-Phase Non-Isolated Microinverter with Time-Sharing Maximum Power Point Tracking Control Strategy. Energies. 2025; 18(18):4925. https://doi.org/10.3390/en18184925
Chicago/Turabian StyleAlhasi, Anees, Patrick Chi-Kwong Luk, Khalifa Aliyu Ibrahim, and Zhenhua Luo. 2025. "Advanced Single-Phase Non-Isolated Microinverter with Time-Sharing Maximum Power Point Tracking Control Strategy" Energies 18, no. 18: 4925. https://doi.org/10.3390/en18184925
APA StyleAlhasi, A., Luk, P. C.-K., Ibrahim, K. A., & Luo, Z. (2025). Advanced Single-Phase Non-Isolated Microinverter with Time-Sharing Maximum Power Point Tracking Control Strategy. Energies, 18(18), 4925. https://doi.org/10.3390/en18184925







