A Novel Nonlinear Droop Function for Flexible Operation of Grid-Forming Inverters
Abstract
1. Introduction
2. Exponent Droop Function (EDF) Control Strategy
- The proposed EDF control dynamically adjusts the loading of DGs to ensure optimal stabilization of both frequency and voltage even under varying load conditions. This adaptive capability ensures more balanced power distribution which leads to enhanced system resilience.
- EDF control supports the generation of multiple nonlinear droop characteristics by tuning one parameter which allows the control to adapt to diverse operational requirements. This flexibility ensures efficient power management in microgrids with complex configurations.
- The novel EDF approach introduces simultaneous horizontal and vertical shifts in droop characteristics which allows DGs to meet complex technical and economic constraints. This generalization provides a higher degree of operational flexibility which, in turn, ensures that DGs can adjust to a wider range of conditions and setpoints.
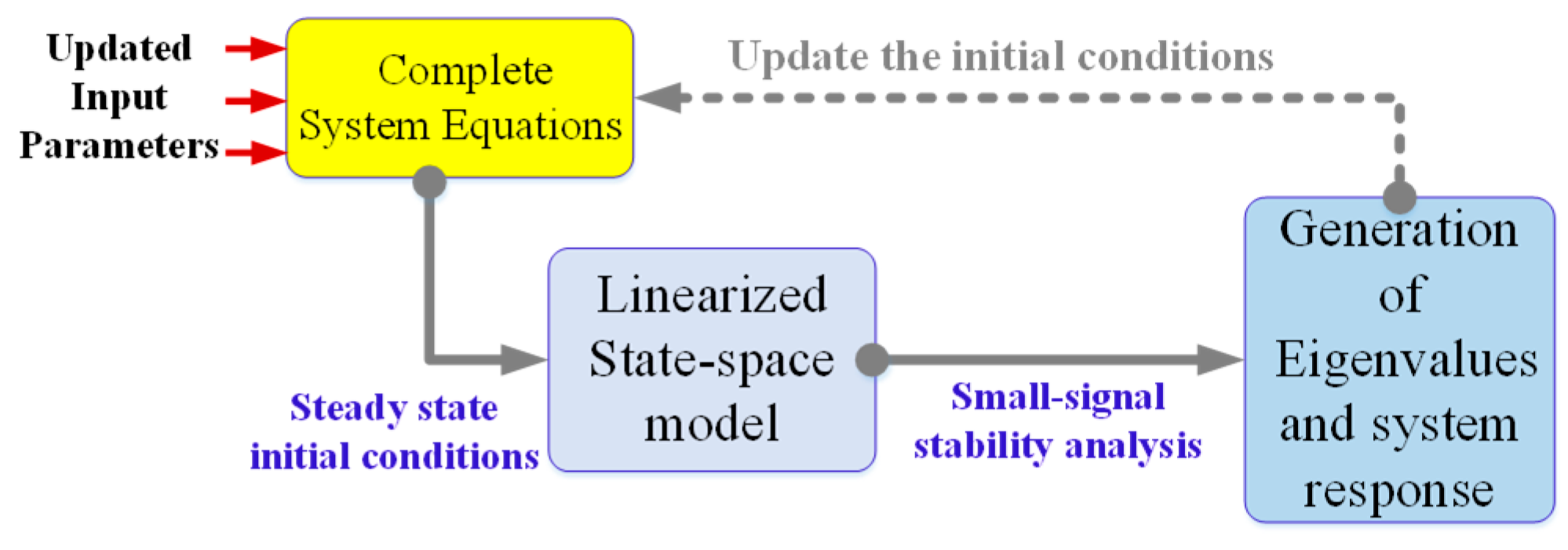
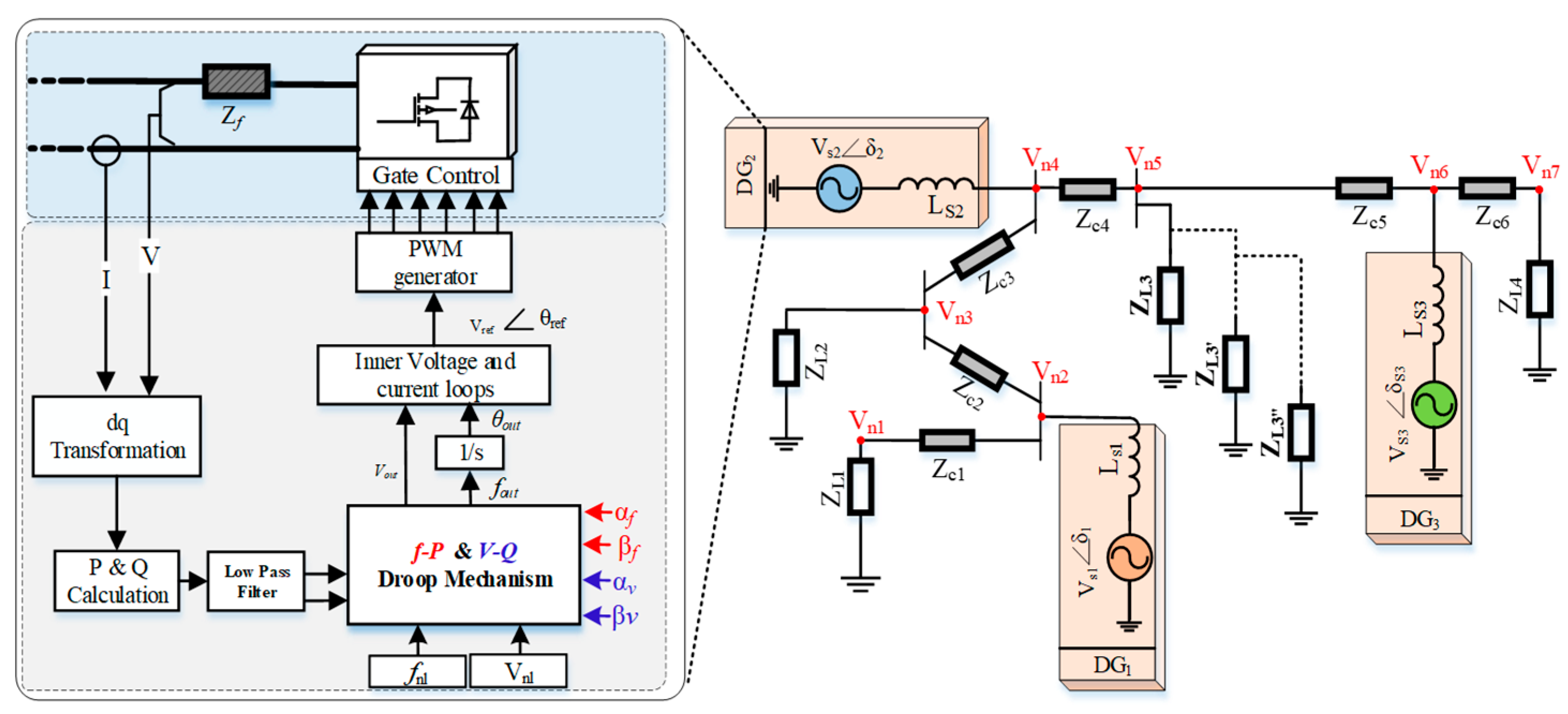
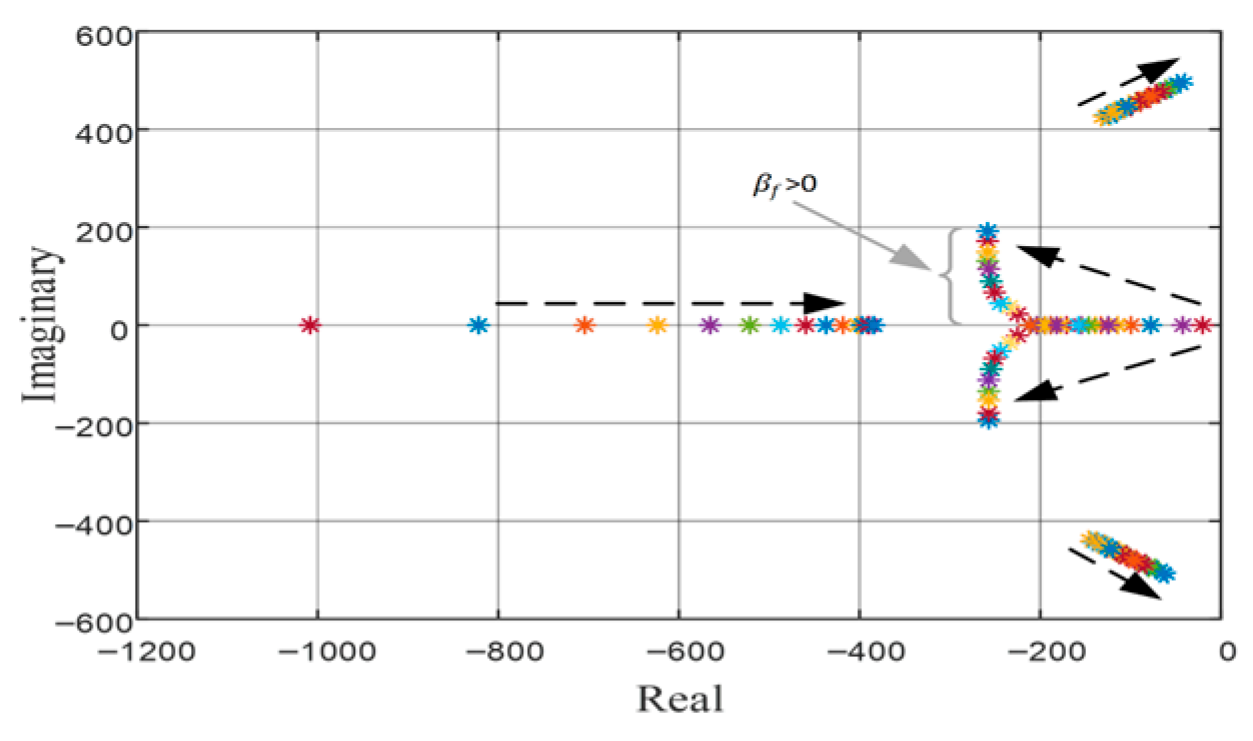
- A variable load-variable control (VLVC) small-signal stability analysis is performed to rigorously evaluate the system stability under EDF control. This analysis provides a deeper understanding of the control method’s dynamic behavior across various operating conditions (The proposed technique is visualized in Figure 2).
- The paper identifies the feasible range of coefficients for maintaining stable microgrid operation under EDF control.
- A complete and adaptive procedure is developed to evaluate the dynamics and stability of a microgrid equipped with EDF under variable load conditions. This procedure ensures that EDF control can be reliably deployed under variable loading conditions.
- Several time-domain simulations are performed to validate the effectiveness of EDF as an advanced GFM control strategy. These simulations demonstrate the control’s ability to handle variable power-sharing and system stability under various load profiles, supporting its practical application.
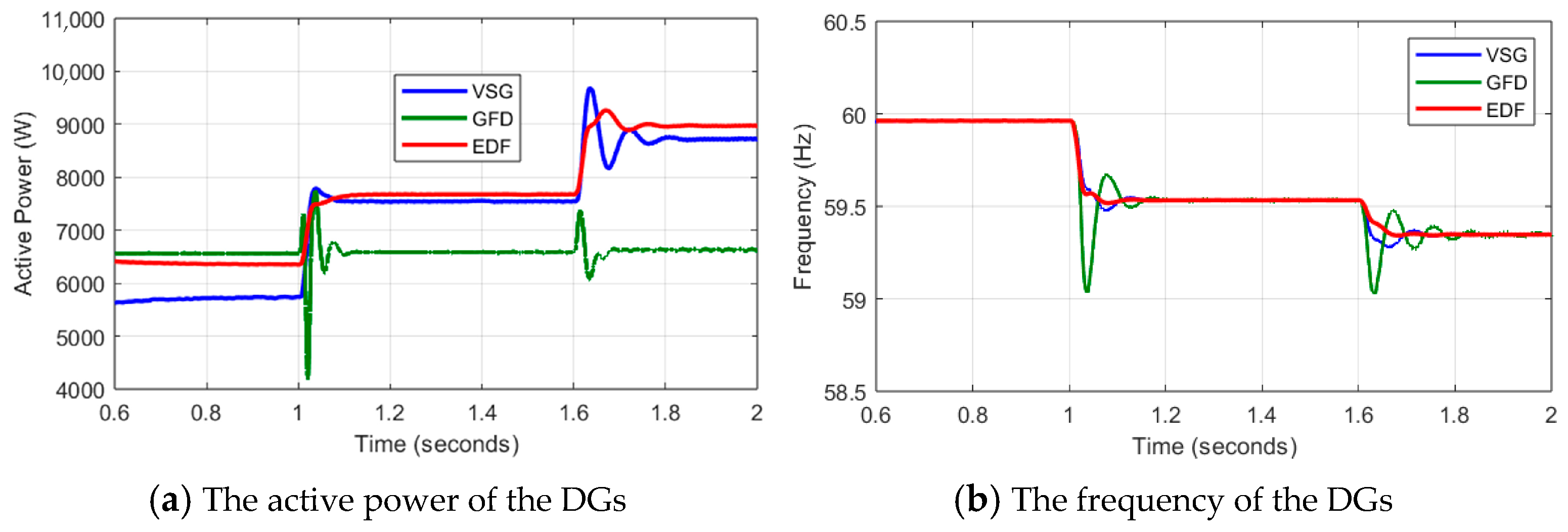
- In addition, EDF is compared with other GFM (e.g., VSG) and GFD (e.g., MPPT) control strategies. This comparison confirms the superior dynamic performance, adaptability, and enhanced stability of EDF which emphasizes its effectiveness as an optimal replacement of the conventional droop control.
- 1-
- By changing the exponent droop coefficient (i.e., ) (considering as a “variable” with a predetermined fixed ), the relation can be flexibly shaped. The obtained relation is equivalent to a high-order polynomial that requires several terms to construct. An example is given in Figure 3 where the droop relation is reconstructed using a 3rd order polynomial (equivalent to ) and 7th order polynomial (equivalent to ).
- 2-
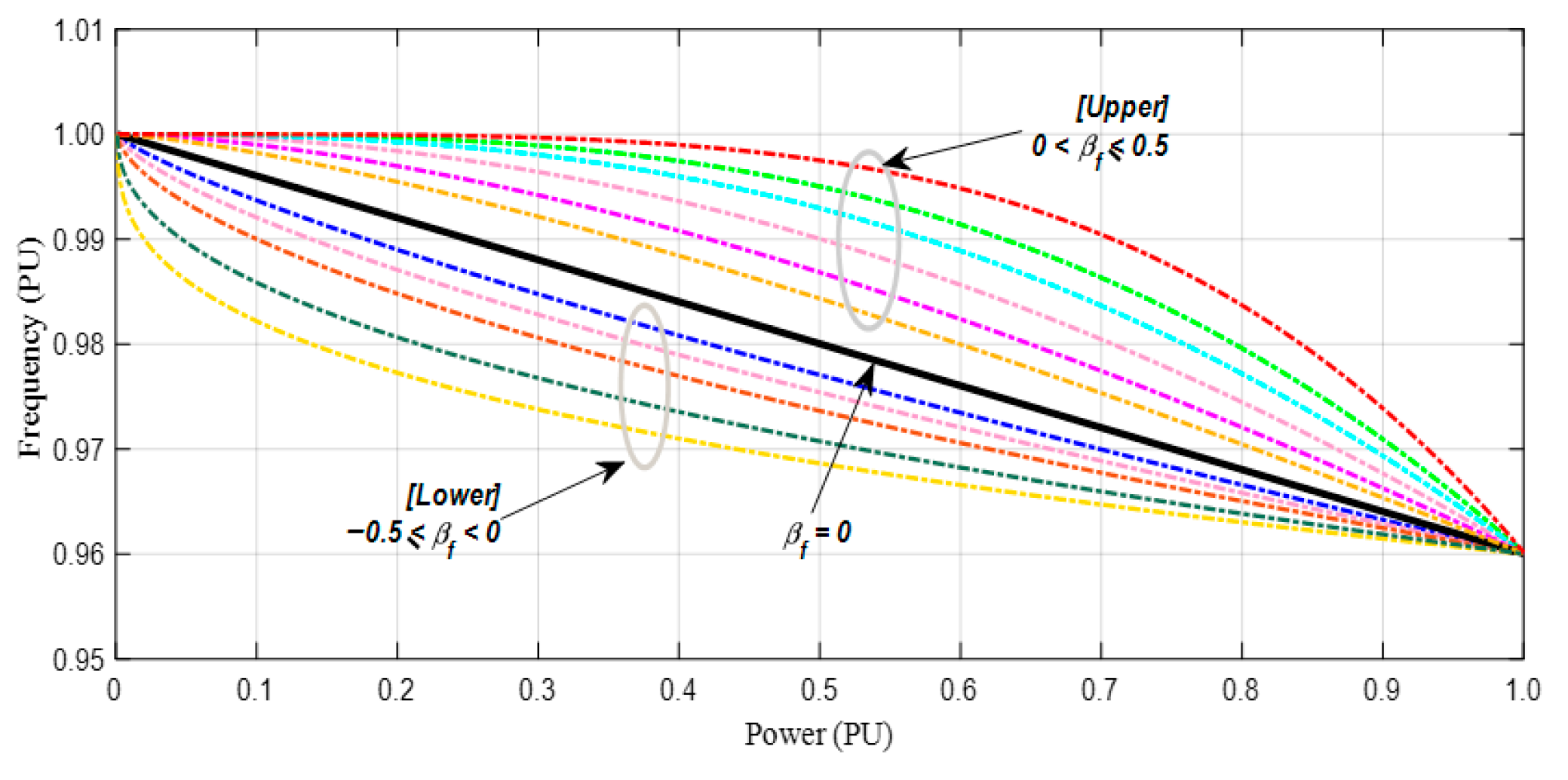
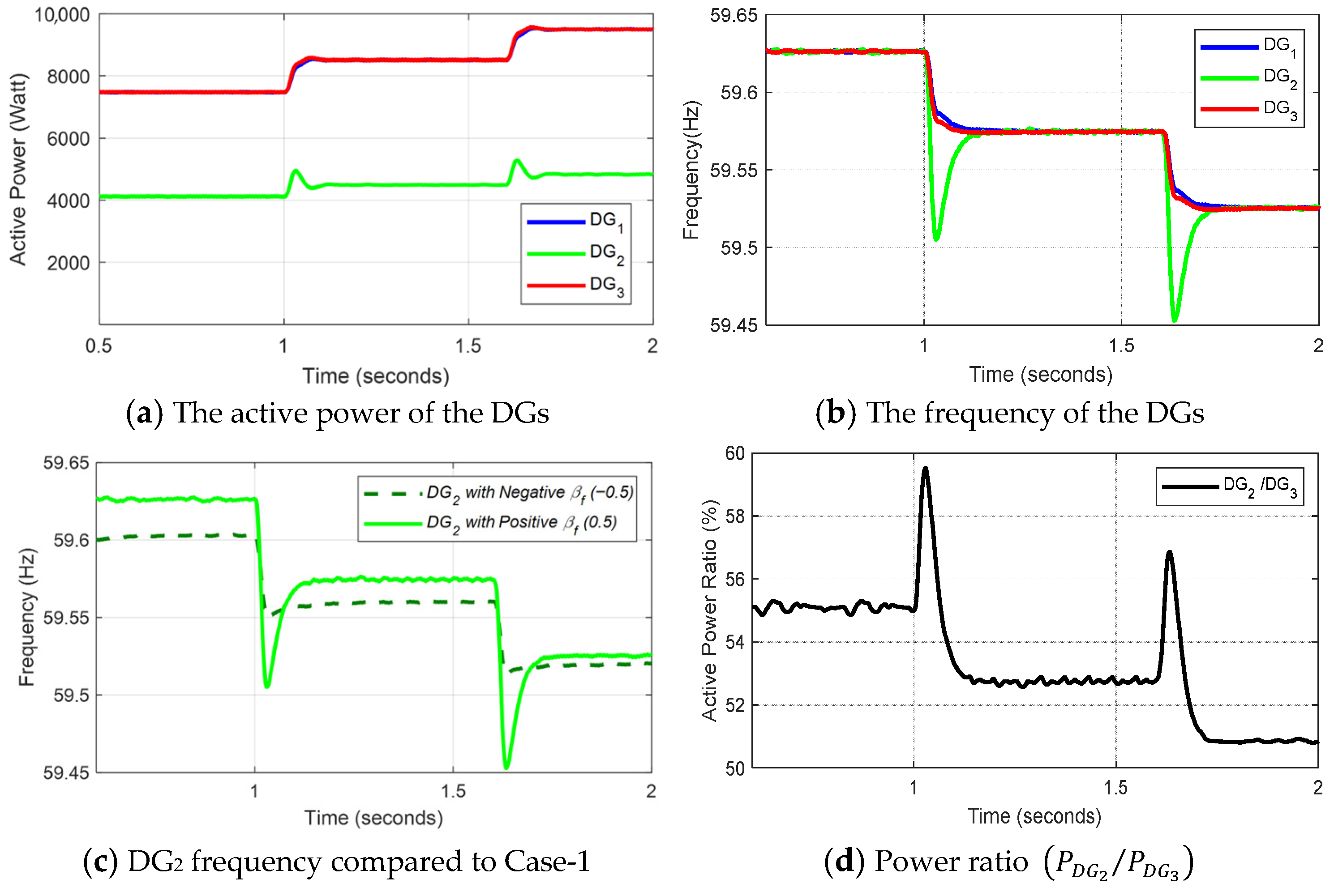
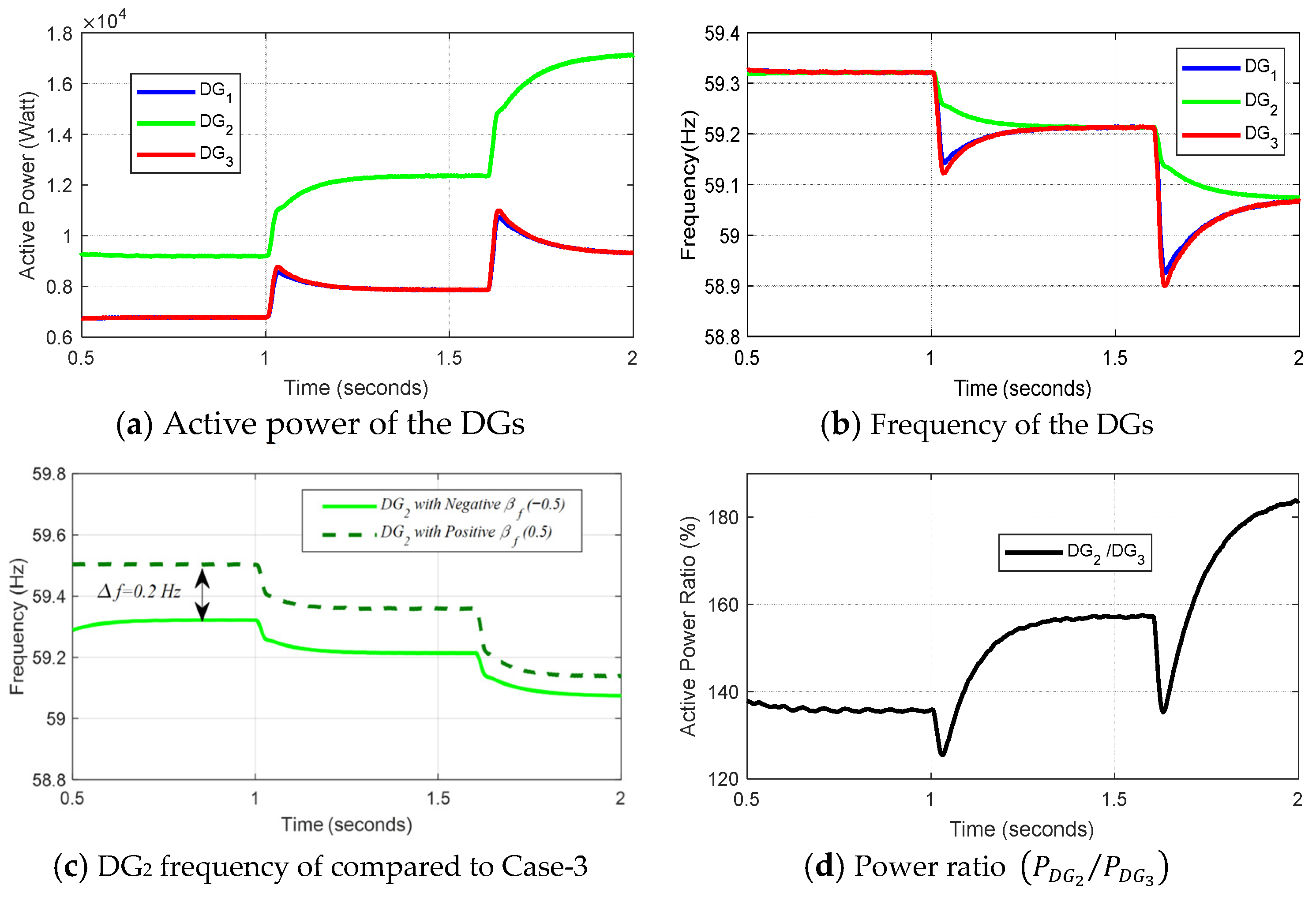
- The droop relation with can be effectively applied to large DGs due to the high utilization levels of the existing reserve compared to linear droop. This is because, as increases, more power can be processed from the source with minimal frequency deviation. This can be visualized from the upper characteristics depicted in Figure 4.
- 3-
- The droop relation with can be effectively implemented on small DGs. The small equivalent droop coefficient at high loadings, where the relation relaxes, helps stabilize a small DG under disturbances. This increases the stability margins at high loadings in the presence of disturbances. This can be visualized from the lower characteristics depicted in Figure 4.
3. Dynamic Modeling of EDF-Controlled Microgrid
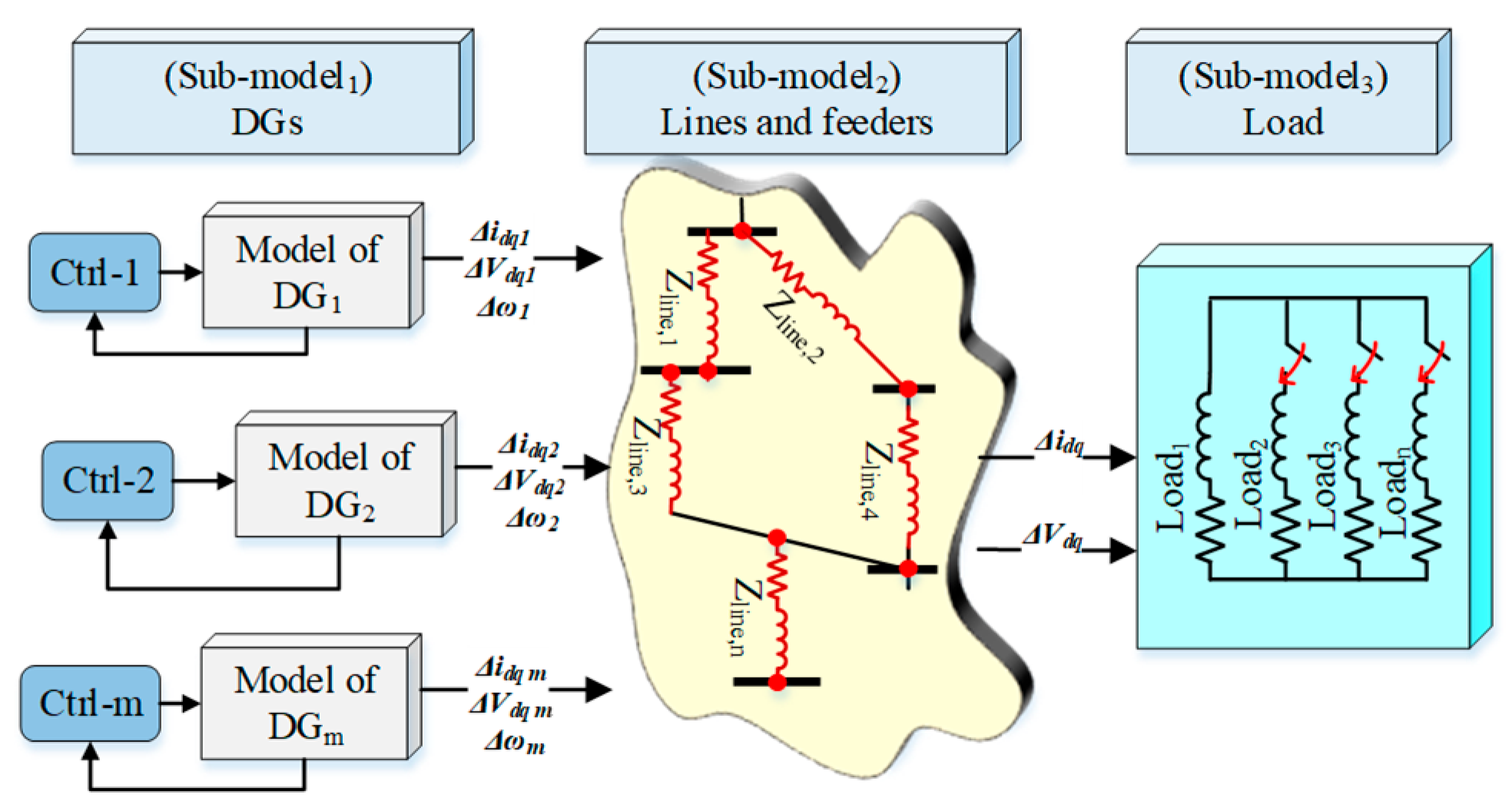
3.1. Constructing EDF Controlled DG Model
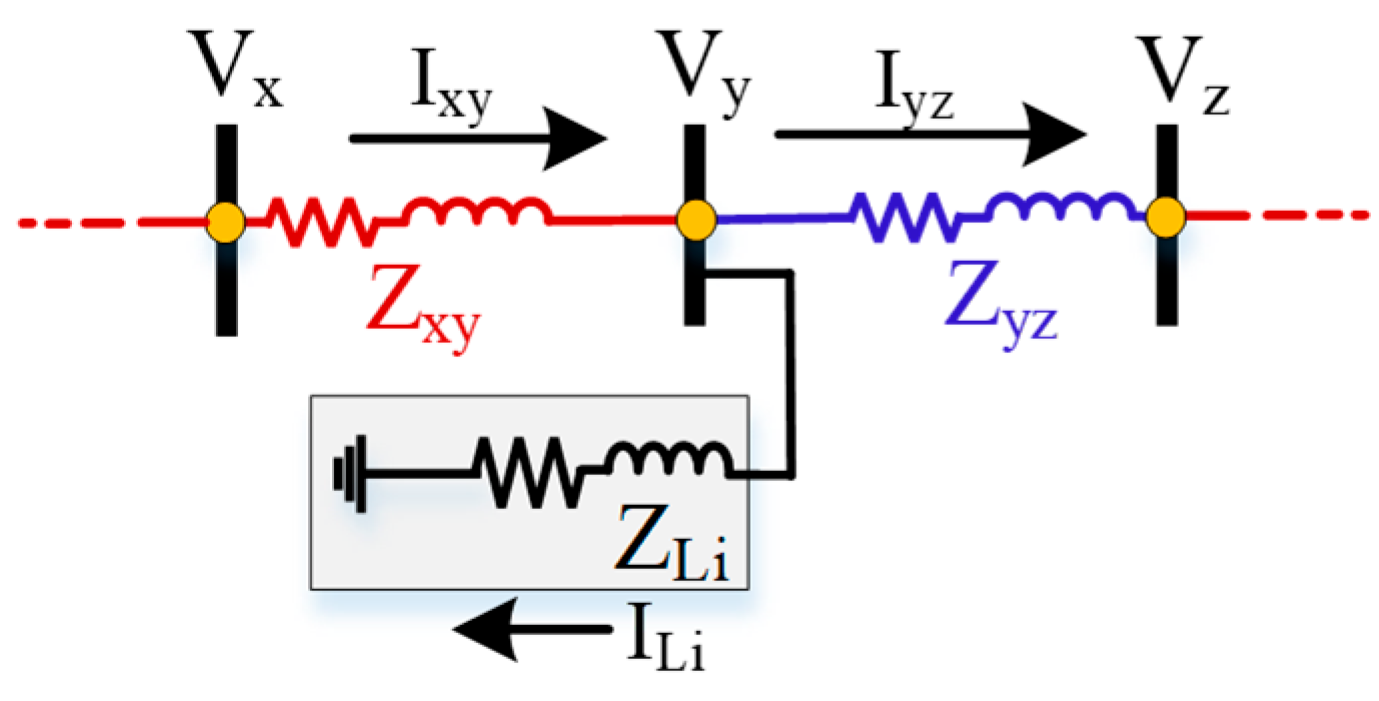
3.2. Constructing Distribution Lines and Load Models
3.3. The Entire Model of the System
4. EDF Control Implementation
- Changing the load indicates horizontal scanning of the droop characteristic.
- Changing βf indicates vertical scanning of the droop characteristic at the same loading conditions (see Figure 4).
4.1. Frequency Domain Analysis
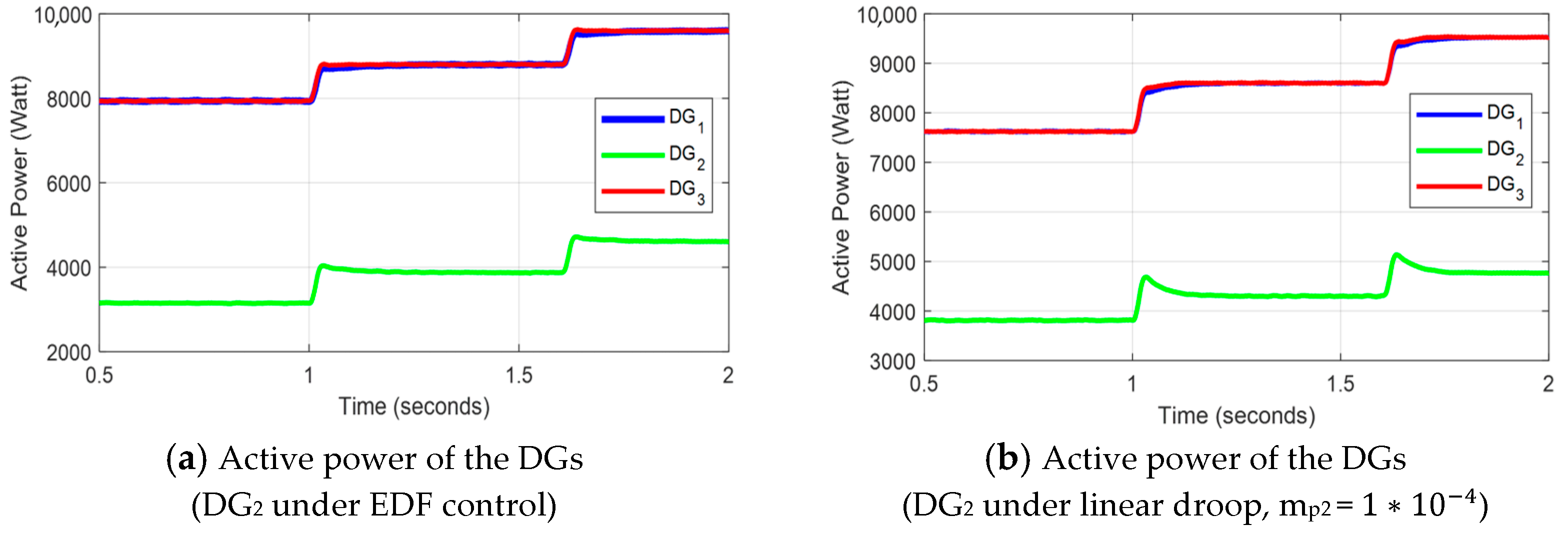
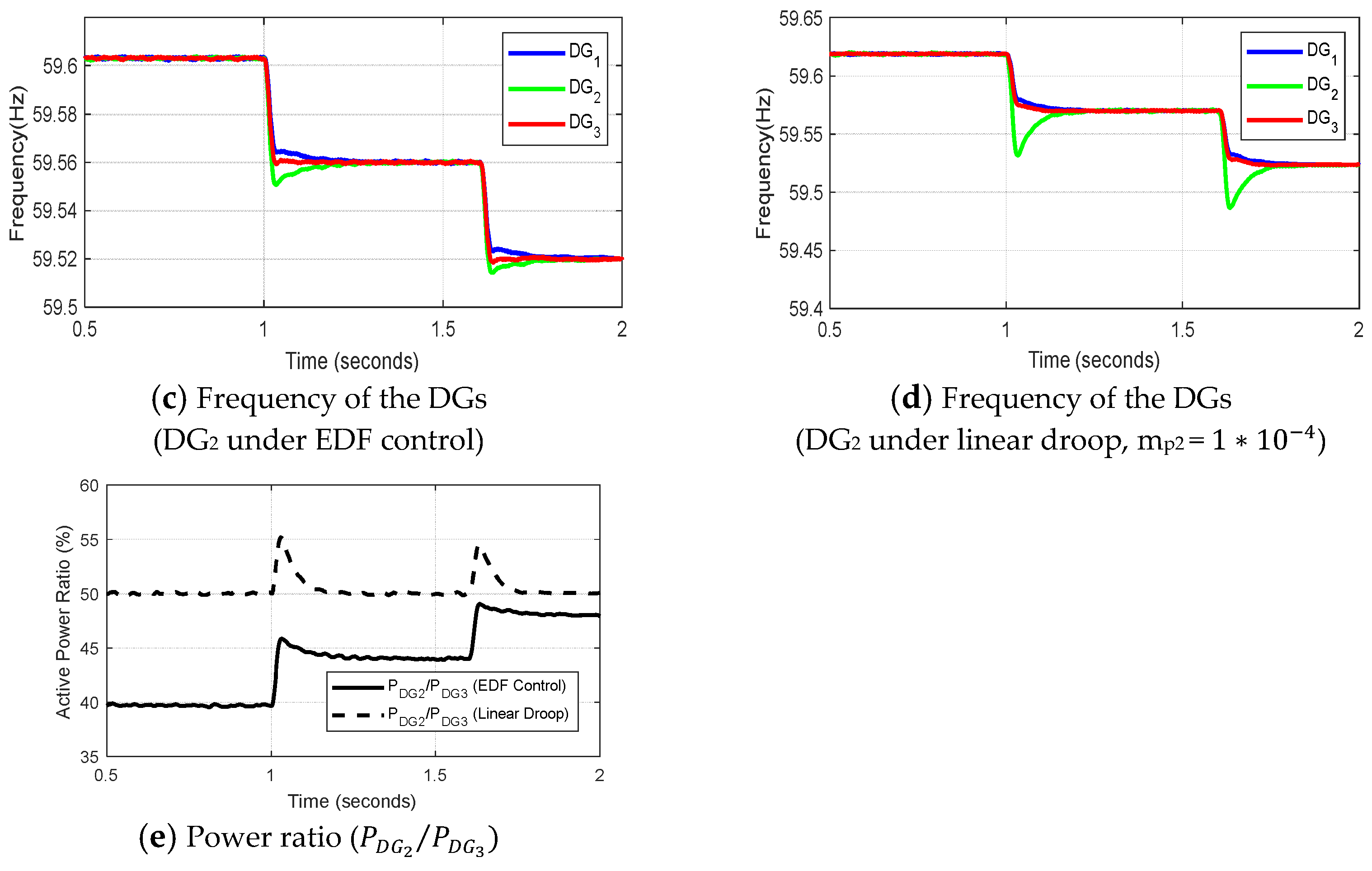
4.2. Time Domain Analyses
4.2.1. Desirable Dynamic Performance
- i.
- ii.
- iii.
- iv.
4.2.2. Undesirable Dynamic Performance
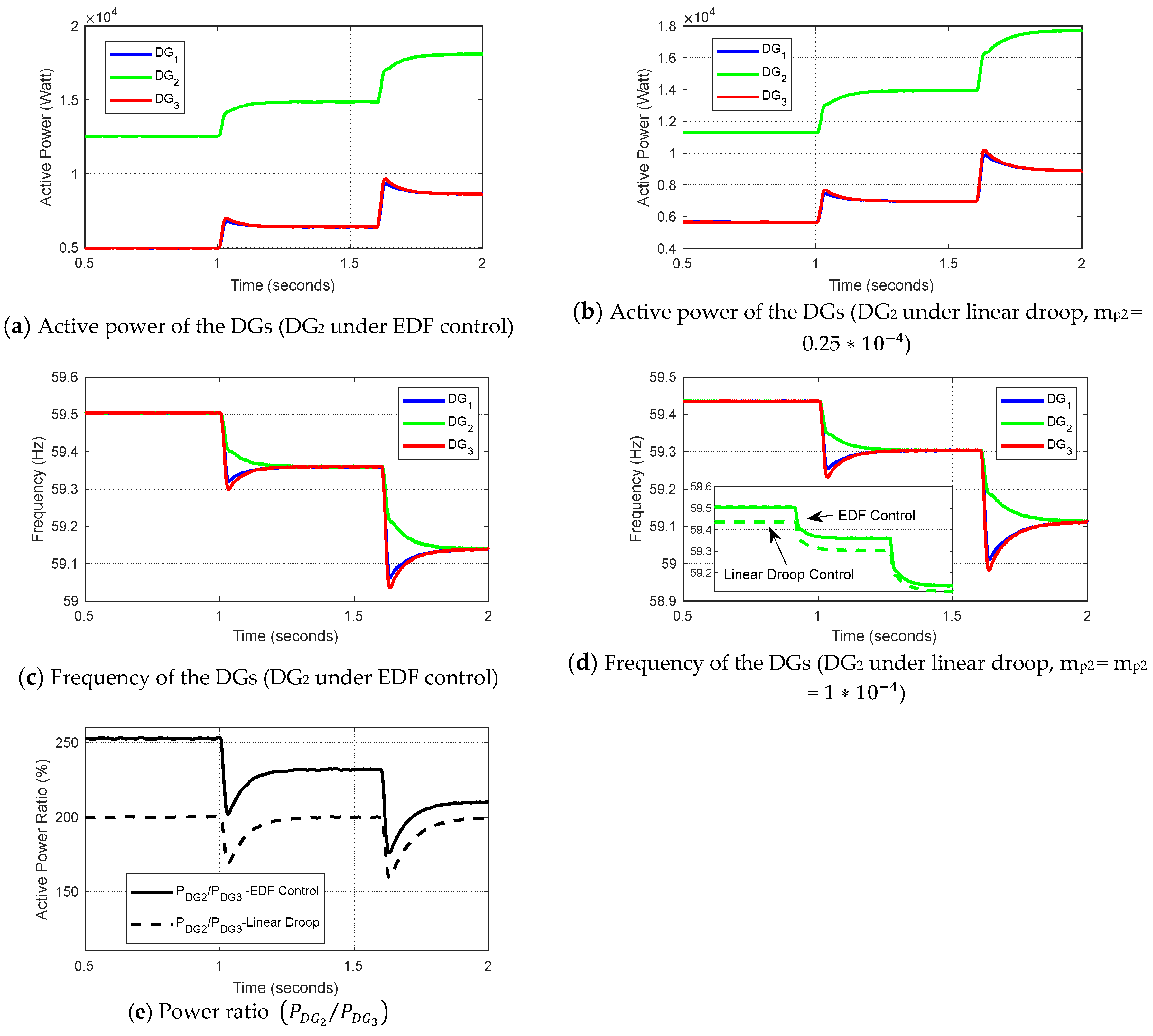
5. Dynamic Performance of EDF-Based Microgrid
6. Discussion
7. Conclusions and Future Work
- -
- The proposed droop control exhibits distinctive advantages, including its simplicity in construction, minimal coefficient requirements, variable adaptability, and ease of implementation, making it a viable alternative to conventional droop control for inverterbased DGs.
- -
- The pivotal role of the coefficient in influencing DG dynamics was confirmed through case studies. This coefficient can be tuned to shape the dynamics according to the design requirements.
- -
- Small DGs demonstrate stability and reliable performance across a wide operating range when working under negative values.
- -
- On the other side, larger DGs with positive values lead and maximize the power sharing in microgrids.
- -
- During disturbances, large fully loaded DGs exhibited fast response capabilities, effectively protecting smaller DGs from transient overloads.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Implication of EDF Control in Realizing the State Matrix of the DG
Appendix B. A Summary of the Carried-Out Cases
| Case # | Case Description and Objective |
|---|---|
| Case-1 | To investigate the impact of the negative droop coefficient ( on a small DG size |
| Case-2 | To investigate the impact of positive and negative droop coefficient ( on a DG that works with other similar-sized DGs |
| Case-3 | To investigate the impact of positive droop coefficient ( on a large DG size |
| Case-4 (opposite to Case-1) | To investigate the impact of positive droop coefficient ( on a small DG size |
| Case-5 (opposite to Case-3) | To investigate the impact of the negative droop coefficient ( on a large DG size |
| Case-6 | To demonstrate the impact of all EDF-controlled microgrid on power sharing, dynamics, and stability |
| Case-7 | To demonstrate the superiority of EDF as an advanced GFM control works against state-of-the-art control strategies |
References
- Antunes, H.M.A.; Piero, R.R.D.; Silva, S.M. Application of Repetitive Control to Grid-Forming Converters in Centralized AC Microgrids. Energies 2025, 18, 3427. [Google Scholar] [CrossRef]
- Rios, M.A.; Pérez-Londoño, S.; Garcés, A. Dynamic Performance Evaluation of the Secondary Control in Islanded Microgrids Considering Frequency-Dependent Load Models. Energies 2022, 15, 3976. [Google Scholar] [CrossRef]
- Liu, C.; Li, B.; Zhang, Y.; Jiang, Q.; Liu, T. The LCC Type DC Grids Forming Method and Fault Ride-Through Strategy Based on Fault Current Limiters. Int. J. Electr. Power Energy Syst. 2025, 170, 110843. [Google Scholar] [CrossRef]
- Harasis, S. Controllable transient power sharing of inverter-based droop controlled microgrid. Int. J. Electr. Power Energy Syst. 2024, 155, 109565. [Google Scholar] [CrossRef]
- Bragin, M.A.; Yan, B.; Kumar, A.; Yu, N.; Zhang, P. Efficient Operations of Micro-Grids with Meshed Topology and Under Uncertainty through Exact Satisfaction of AC-PF, Droop Control and Tap-Changer Constraints. Energies 2022, 15, 3662. [Google Scholar] [CrossRef]
- Harasis, S. Development of a droop control strategy for flexible operation of distributed generators. Jordan J. Electr. Eng. 2022, 8, 179–194. [Google Scholar] [CrossRef]
- Huang, X.; Chen, D.; Xu, L. Microgrid design using folded P-f droop and new grid interface unit to minimize the need for communication. Int. J. Electr. Power Energy Syst. 2021, 130, 106949. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M. Impact of converter control strategy on low- and high-frequency resonance interactions in power electronic dominated systems. Int. J. Electr. Power Energy Syst. 2020, 120, 105978. [Google Scholar] [CrossRef]
- Tavakoli, S.; Araujo, E.; Sanchez, E.; Bellmunt, O. Interaction assessment and stability analysis of the MMC-based VSC-HVDC link. Energies 2020, 13, 2075. [Google Scholar] [CrossRef]
- Kabalan, M.; Singh, P.; Niebur, D. Large signal Lyapunov-based stability studies in microgrids: A review. IEEE Trans. Smart Grid 2017, 8, 2287–2295. [Google Scholar] [CrossRef]
- Agundis-Tinajero, G.D.; Vasquez, J.C.; Guerrero, J.M. Stability Boundary Analysis of Islanded Droop-Based Microgrids Using an Autonomous Shooting Method. Energies 2022, 15, 2120. [Google Scholar] [CrossRef]
- Khanabdal, S.; Banejad, M.; Blaabjerg, F.; Hosseinzadeh, N. A Novel Power Sharing Strategy Based on Virtual Flux Droop and Model Predictive Control for Islanded Low-Voltage AC Microgrids. Energies 2021, 14, 4893. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Robust tuning of transient droop gains based on Kharitonov’s stability theorem in droop-controlled microgrids. IET Gener. Transm. Distrib. 2018, 12, 3495–3501. [Google Scholar] [CrossRef]
- Zhong, Q.; Zeng, Y. Universal droop control of inverters with different types of output impedance. IEEE Access 2016, 4, 702–712. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Yazdaninejadi, A.; Golshannavaz, S. Transient stability enhancement in multiple-microgrid networks by cloud energy storage system alongside considering protection system limitations. IET Gener. Transm. Distrib. 2023, 17, 1816–1826. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Nurdin, H.I.; Fletcher, J.E. Transient response comparison of virtual oscillator controlled and droop controlled three-phase inverters under load changes. IET Gener. Transm. Distrib. 2020, 14, 1138–1147. [Google Scholar] [CrossRef]
- Cingoz, F.; Elrayyah, A.; Sozer, Y. Plug-and-play nonlinear droop construction scheme to optimize islanded microgrid operations. IEEE Trans. Power Electron. 2017, 32, 2743–2756. [Google Scholar] [CrossRef]
- Ouederni, R.; Davidson, I.E. Co-Optimized Design of Islanded Hybrid Microgrids Using Synergistic AI Techniques: A Case Study for Remote Electrification. Energies 2025, 18, 3456. [Google Scholar] [CrossRef]
- Yang, M.; Wang, C.; Han, Y.; Xiong, J.; Yang, P. Small-signal stability analysis of the standalone single-phase parallel inverter with BPF-based droop control scheme. In Proceedings of the IEEE 4th Southern Power Electronics Conference, Singapore, 10–13 December 2018. [Google Scholar]
- Long, B.; Li, X.; Rodriguez, J.; Guerrero, J.M.; Chong, K.T. Frequency stability enhancement of an islanded microgrid: A fractional-order virtual synchronous generator. Int. J. Electr. Power Energy Syst. 2023, 147, 108896. [Google Scholar] [CrossRef]
- Eskandari, M.; Savkin, A.V. A critical aspect of dynamic stability in autonomous microgrids: Interaction of droop controllers through the power network. IEEE Trans. Ind. Inform. 2022, 18, 5. [Google Scholar] [CrossRef]
- Dheer, D.K.; Vijay, A.S.; Kulkarni, O.V.; Doolla, S. Improvement of stability margin of droop-based islanded microgrids by cascading of lead compensators. IEEE Trans. Ind. Appl. 2019, 55, 3241–3251. [Google Scholar] [CrossRef]
- Mestriner, D.; Labella, A.; Brignone, M.; Bonfiglio, A.; Procopio, R. A transient stability approach for the analysis of droop-controlled islanded microgrids. Electr. Power Syst. Res. 2020, 187, 106509. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Gui, Y.; Ma, D. Exponential-function-based droop control for islanded microgrids. J. Mod. Power Syst. Clean Energy 2019, 7, 899–912. [Google Scholar] [CrossRef]
- Rowe, C.N.; Summers, T.J.; Betz, R.E.; Cornforth, D.J.; Moore, T.G. Arctan power–frequency droop for improved microgrid stability. IEEE Trans. Power Electron. 2013, 28, 8. [Google Scholar] [CrossRef]
- Khan, M.Z.; Ahmed, E.M.; Habib, S.; Ali, Z.M. Multiobjective optimization technique for droop controlled distributed generators in AC islanded microgrid. Electr. Power Syst. Res. 2022, 213, 108671. [Google Scholar] [CrossRef]
- Nutkani, U.; Loh, P.C.; Blaabjerg, F. Droop scheme with consideration of operating costs. IEEE Trans. Power Electron. 2014, 29, 1047–1052. [Google Scholar] [CrossRef]
- Li, C.; Huang, Y.; Wang, Y.; Monti, A.; Wang, Z.; Zhong, W. Modelling and small signal stability for islanded microgrids with hybrid grid-forming sources based on converters and synchronous machines. Int. J. Electr. Power Energy Syst. 2024, 157, 109831. [Google Scholar] [CrossRef]
- Isakov, I.; Vekić, M.; Rapaić, M.; Todorović, I.; Grabić, S. Decentralized self-stabilizing primary control of microgrids. Int. J. Electr. Power Energy Syst. 2023, 155, 109477. [Google Scholar] [CrossRef]
- Kweon, J.; Jing, H.; Li, Y.; Monga, V. Small-signal stability enhancement of islanded microgrids via domain-enriched optimization. Appl. Energy 2023, 353, 122172. [Google Scholar] [CrossRef]
- Kenyon, R.; Sajadi, A.; Hodge, B. Droop-e: Exponential droop as a function of power output for grid-forming inverters with autonomous power sharing. arXiv 2022, arXiv:2207.03564. [Google Scholar]
- Elrayyah, A.; Cingoz, F.; Sozer, Y. Construction of nonlinear droop relations to optimize islanded microgrid operation. IEEE Trans. Ind. Appl. 2015, 51, 3404–3413. [Google Scholar] [CrossRef]



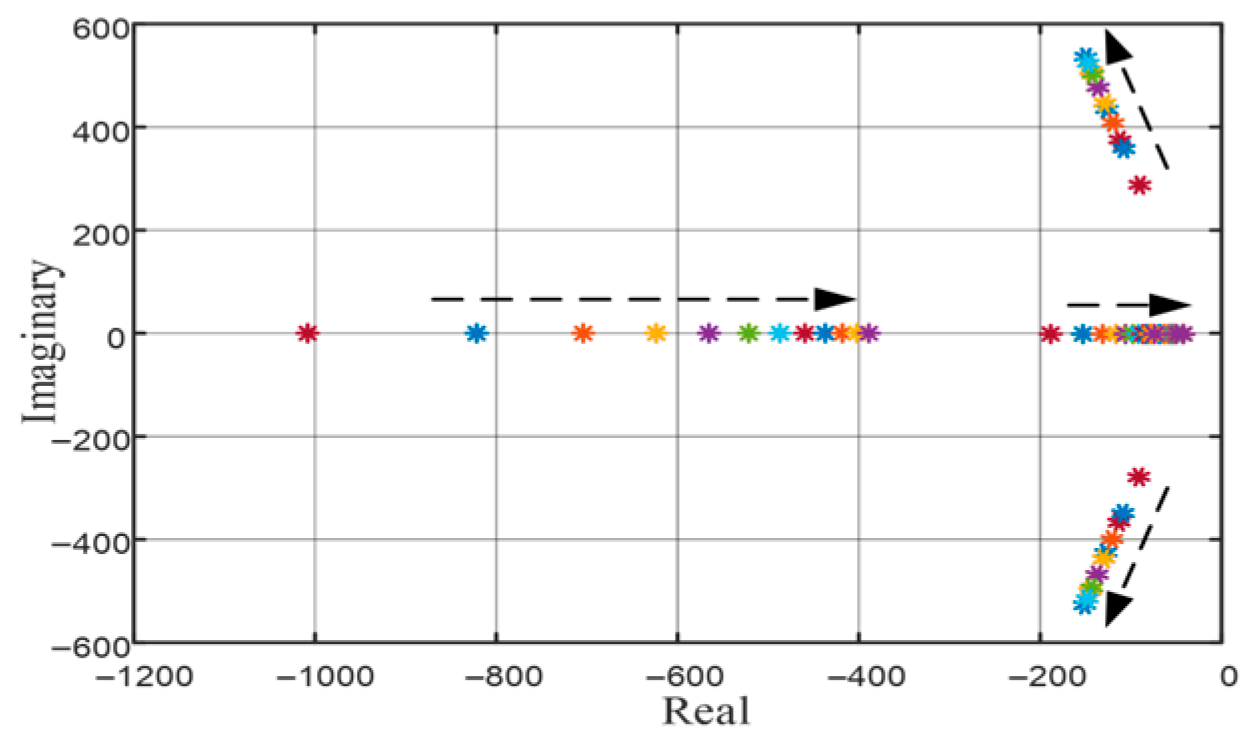
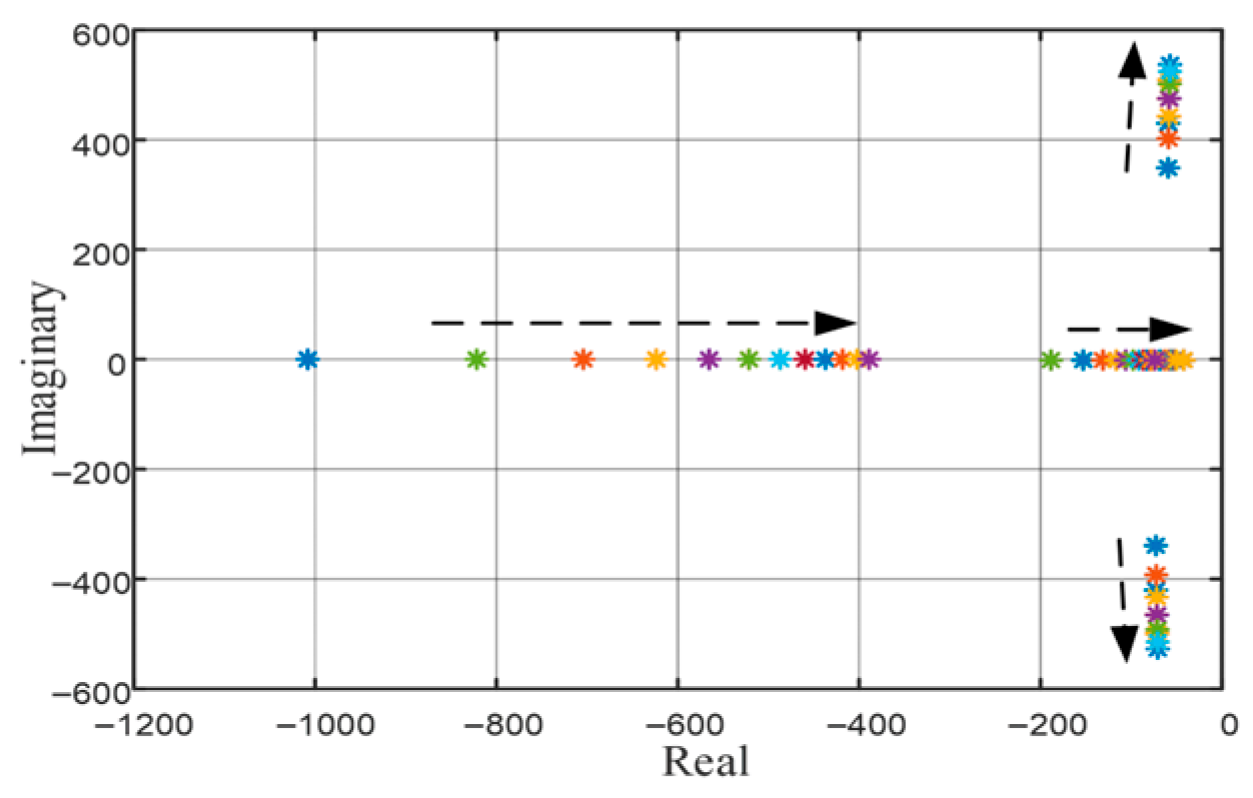
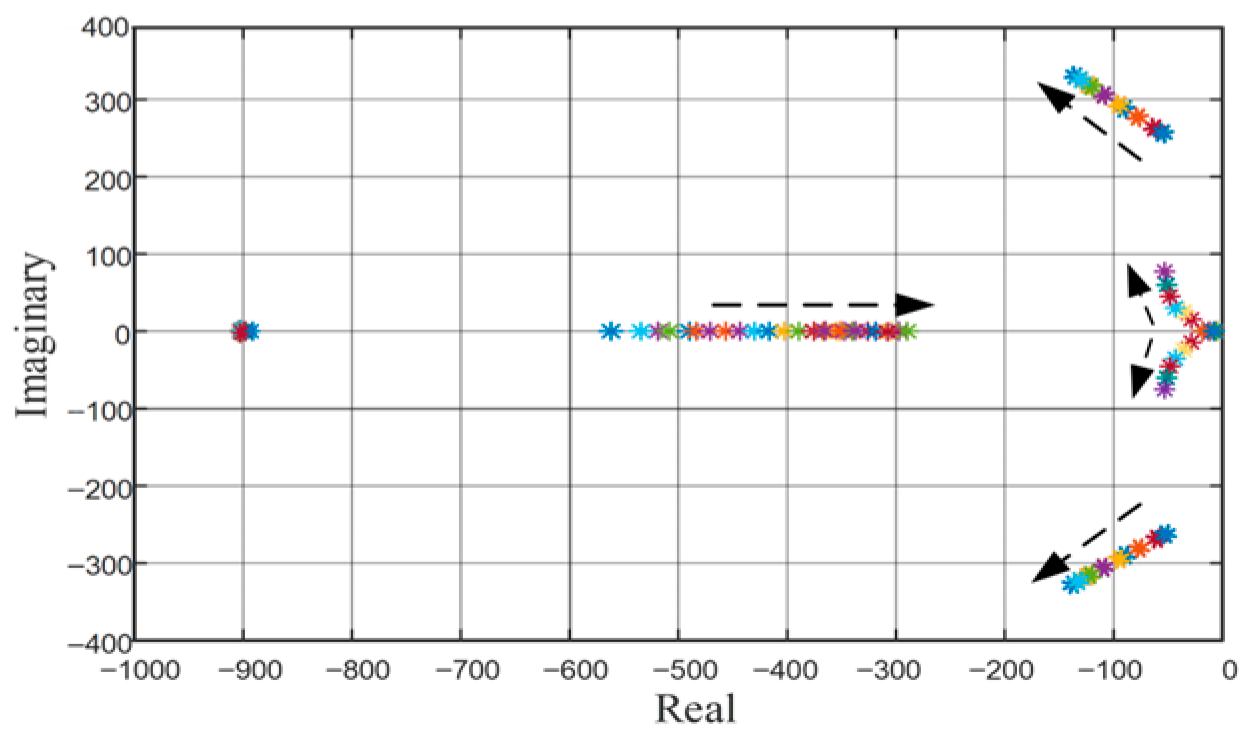


| Ref | Droop Function Type | Droop Coefficients | Mathematical Representation | Ease of Implementation | Purpose (Application) | Function Flexibility | Remark |
|---|---|---|---|---|---|---|---|
| [24] | Natural Exponential Function | 2 | Moderate | To reduce the reactive power-sharing deviation | ✕ | Unwanted variable offset appears with each coefficient | |
| [25] | Arctan Droop Function | 4 | Easy | To relax the slope of the relation as the power increases | ✕ | Unwanted variable offset appears with each coefficient | |
| [26,27] | Cost-based Nonlinear Function (Quadratic Functions) | >3 | Moderate/Offline optimization is required | To minimize operating costs in microgrids | ✕ | At each characteristic, the Min/Max frequency/voltage should be updated | |
| [31] | Power Exponent Droop | 2 | Easy | To minimize the power reserve | ✕ | Unwanted variable offset appears with each coefficient | |
| [32] | Combination of Integer and Fractional Terms | >3 | Difficult | To minimize operating costs in microgrids | ✕ | Requires several terms to increase flexibility | |
| Proposed | Exponent Droop Function | 2 | Easy | To flexibly share the power at minimum frequency deviation and forms a general droop function | ✓ | Can realize any point on planes by tuning one coefficient |
| Parameter | Value |
|---|---|
| 157 d/s |
| Parameter | Case-1 | Case-4 |
| Graphical Representation |  |  |
| Microgrid Capacity | 25.0 kW microgrid | 25.0 kW microgrid |
| Control Type | (DG1/DG3): Linear Droop, (DG2): EDF | (DG1/DG3): Linear Droop, (DG2): EDF |
| DG Capacity | (DG1/DG3): 10.0 kW, (DG2): 5.0 kW | (DG1/DG3): 10.0 kW, (DG2): 5.0 kW |
| Droop Parameters | (DG1/DG3): (DG2): | (DG1/DG3): , (DG2): |
| Parameter | Case-2 | Case-5 |
| Graphical Representation |  | 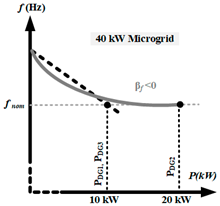 |
| Microgrid Capacity | 30.0 kW microgrid | 40.0 kW microgrid |
| Control Type | (DG1/DG3): Linear Droop, (DG2): EDF | (DG1/DG3): Linear Droop, (DG2): EDF |
| DG Capacity | (DG1/DG2/DG3): 10.0 kW | (DG1/DG3): 10.0 kW, (DG2): 20.0 kW |
| Droop Parameters | (DG1/DG3): (DG2): | (DG1/DG3): , (DG2): |
| Parameter | Case-3 | Case-6 (EDF Controlled DGs) |
| Graphical Representation | 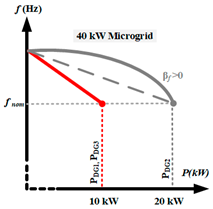 | 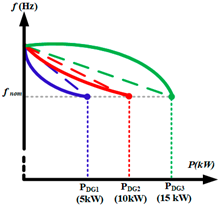 |
| Microgrid Capacity | 40.0 kW microgrid | 30.0 kW microgrid |
| Control Type | (DG1/DG3): Linear Droop, (DG2): EDF | (DG1/DG2/DG3): EDF Control |
| DG Capacity | (DG1/DG3): 10.0 kW, (DG2): 20.0 kW | (DG1): 5.0 kW, (DG2): 10.0 kW, (DG3): 15.0 kW |
| Droop Parameters | (DG1/DG3): (DG2): | (DG1): (DG3): (DG2): |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harasis, S. A Novel Nonlinear Droop Function for Flexible Operation of Grid-Forming Inverters. Energies 2025, 18, 4885. https://doi.org/10.3390/en18184885
Harasis S. A Novel Nonlinear Droop Function for Flexible Operation of Grid-Forming Inverters. Energies. 2025; 18(18):4885. https://doi.org/10.3390/en18184885
Chicago/Turabian StyleHarasis, Salman. 2025. "A Novel Nonlinear Droop Function for Flexible Operation of Grid-Forming Inverters" Energies 18, no. 18: 4885. https://doi.org/10.3390/en18184885
APA StyleHarasis, S. (2025). A Novel Nonlinear Droop Function for Flexible Operation of Grid-Forming Inverters. Energies, 18(18), 4885. https://doi.org/10.3390/en18184885






