Synergizing Metaheuristic Optimization and Model Predictive Control: A Comprehensive Review for Advanced Motor Drives

Abstract

Model predictive control (MPC) is a prominent research focus in motor drives, offering advantages in dynamic response, steady-state accuracy, robustness, and multi-objective handling. However, increasing performance demands in modern systems, coupled with power-electronic device constraints (switching frequency, saturation), impose stringent requirements: high torque response, minimal power loss, torque ripple suppression, switching frequency minimization, high real-time performance, and strong robustness. Meeting these demands requires overcoming challenges like prediction-model errors, random disturbances, coupled parameter tuning, and reconciling real-time execution with global optimality in high-dimensional nonconvex optimization. Metaheuristic optimization algorithms (MOAs) present a viable alternative to traditional methods. Requiring no explicit model and offering global search capabilities with versatile mechanisms, MOAs efficiently identify model parameters, tune cost weights, and rapidly generate multi-constraint control strategies in complex spaces. This significantly accelerates MPC’s online computation and enhances disturbance rejection. This paper systematically reviews the combined application of MOAs and MPC in modern motor-drive systems, evaluating their optimization effectiveness and engineering potential across operating conditions to provide theoretical guidance and practical insights for future research.

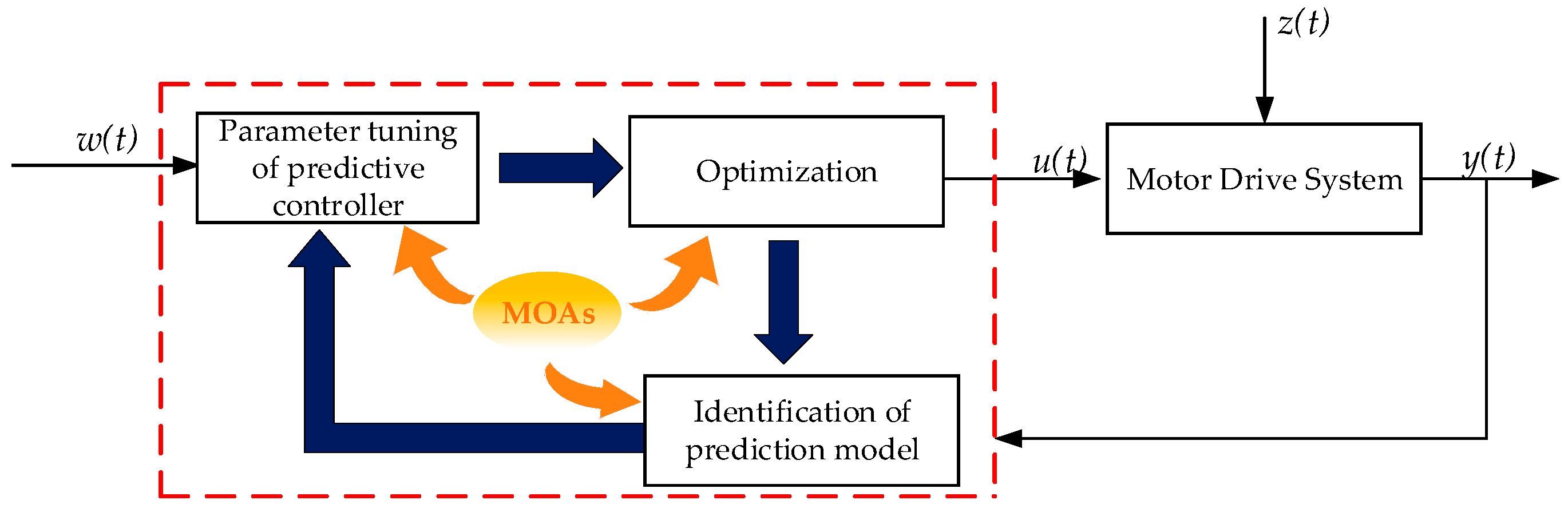
1. Introduction

Modern motor drive systems, widely employed in industrial automation, electric vehicles, and aerospace, face increasingly complex operating environments with strong nonlinearities and coupling effects. Under multiple constraints of current, speed, and temperature, and limitations from power electronic device switching frequencies and saturation effects, achieving high performance and efficiency requires control algorithms that deliver rapid torque response and minimized power consumption while simultaneously ensuring torque ripple suppression, switching frequency reduction, high real-time capability, and strong robustness [1,2,3].

Classical control methods, such as field-oriented control (FOC) and direct torque control (DTC), often struggle to simultaneously achieve both dynamic performance and steady-state accuracy when addressing these challenges [4,5,6,7,8]. MPC as an advanced control strategy, utilizes a dynamic model to predict future states over a specified time horizon. At each control interval, it executes an optimization process to determine the optimal control actions. This optimization incorporates the dynamic process model, predicted future states, constraints, and an objective function, minimizing deviations from the reference signal to achieve optimal control [9,10,11]. Owing to its superior ability to effectively handle system constraints and optimize multiple performance objectives while maintaining excellent dynamic response and steady-state characteristics, MPC has become a significant research focus in the field of motor control [12].

The increasingly complex operating environments and strong coupling characteristics of modern motor drive systems pose new challenges for establishing accurate dynamic models in MPC. These challenges include model uncertainties [13], time-varying characteristics of internal and external disturbances [14], system nonlinearities, and time delays in parameter optimization [15]. To address the issue of model parameter uncertainty, an adaptive model predictive current control method was proposed for permanent magnet synchronous motor (PMSM) drives based on Bayesian inference (BI) [16]. This approach integrates artificial intelligence (AI) with MPC through the application of Bayesian inference, enabling precise control without requiring prior knowledge of motor parameters. The impact of inverter nonlinearities and DC-link voltage uncertainty disturbances on MPC performance was evaluated [17]. They effectively compensated for voltage errors caused by internal disturbances by combining DC-link voltage identification with candidate voltage vectors. A refined model for induction motor direct starting was proposed [18]. In this model, current displacement in slots was considered. As a result, dynamic representation accuracy was improved, and MPC prediction became more reliable. To address the parameter sensitivity of flexible joint permanent magnet synchronous motors (FJ-PMSMs), a Lyapunov function-based predictive model was introduced [19]. In this method, the finite control set MPC formulation was combined with adaptive laws. Robustness was ensured, and current quality was shown to be superior to that of conventional strategies. A systematic review of weighting factor design in finite-control-set MPC for AC drives was provided [20]. It was emphasized that proper weighting factor selection plays a critical role. This role includes balancing current ripple suppression, torque dynamics, and switching losses.

The selection and optimization of parameters within the MPC algorithm, specifically the prediction horizon, control horizon, weighting coefficients, and system constraint parameters, directly determine the control system’s dynamic response speed, steady-state accuracy, robustness, and prediction precision. Consequently, systematic parameter tuning is crucial for enhancing MPC quality and balancing system performance with computational cost [21,22]. Although manual parameter adjustment is the simplest tuning method, it relies heavily on extensive expertise and experience, and suffers from being cumbersome, time-consuming, and prone to significant errors. To efficiently utilize limited processor resources and enhance control performance, an MPC method with adaptive prediction and control horizons and online selection of weighting factors was proposed [23], in which the hysteresis principle is applied to assess the motor operating state and the adaptive horizons are adjusted online within normal time ranges. In addition, a real-time branch-and-bound algorithm is employed to select suitable weighting factors, addressing timeout issues caused by long prediction horizons. Robust boundaries and a penalty weight adjustment mechanism were introduced into the MPC cost function [24], through which analytical tuning of the weighting and incremental weighting parameters is achieved, thereby enhancing system robustness against parameter deviations and load variations.

The rapid development of modern motor drive systems in electric vehicles and aerospace applications has led to increased demands on MPC, which must achieve multi-objective optimization under multiple constraints, including current, voltage, torque, and hardware limits, while also providing enhanced real-time performance, robustness, and global optimality. Consequently, the efficacy of the optimization solver in MPC is paramount for attaining optimal control states in modern motor drive systems.

This context reveals three critical challenges for MPC optimization algorithms in motor drive control.

(1) Real-time performance and computational efficiency: Modern motor drive systems impose stringent requirements on dynamic performance, response speed, and reliability. Consequently, the MPC optimization process must be guaranteed to complete within the control interval [25].

(2) Multi-objective optimization and constraint-handling capability: Modern motor drives operate in increasingly complex environments with extensive inputs and outputs. These conditions require optimization algorithms capable of effectively handling system nonlinearities and strong coupling effects [26].

(3) Robustness and prediction accuracy: Insufficient prediction accuracy leads to deviations in the estimated future states during the prediction horizon. These deviations result in suboptimal control sequences that fail to rapidly counteract errors. Inadequate robustness can cause systems to miss optimal compensation opportunities, even with minor prediction deviations, inducing overshoot or undershoot. To prevent control inputs from causing limit violations or instability while minimizing current and torque transients, and suppressing speed fluctuations and torque ripple, MPC optimization algorithms must possess enhanced robustness and high prediction accuracy. Specifically, they must be capable of rapidly adjusting control actions before disturbances occur, thereby minimizing system impact [27].

These challenges are discussed in detail in the subsequent sections: Challenge 1 in Section 3.3, Challenge 2 in Section 3.2 and Section 3.3, and Challenge 3 in Section 3.1 and Section 3.3.

Modern motor drive systems frequently require large-range speed/torque switching within milliseconds or even microseconds. It demands controllers capable of “seeing accurately” (precisely predicting future behavior over a time horizon) and “acting swiftly” (computing and outputting control signals in real-time). Fundamentally, addressing these challenges requires that MPC adopt efficient multi-objective optimization algorithms. These algorithms must satisfy system constraints. They should achieve convergence to the global optimum with minimal iterations. However, common optimization algorithms such as interior-point methods [28,29,30,31], sequential quadratic programming [32,33,34], or gradient descent [35,36,37,38], which are gradient-based solvers, often trap systems in local minima. Moreover, they become computationally prohibitive when handling models with complex constraints.

In recent years, with the continuous advancement of research in the control field, metaheuristic optimization algorithms (MOAs) have emerged and rapidly given rise to hundreds of advanced algorithms with distinct characteristics [39]. With ongoing research on MOAs, it has been observed that these algorithms offer significant advantages in solving large-scale, nonlinear, multimodal, and highly constrained optimization problems [40]. This enables the realization of MPC algorithms that meet the demands of modern motor drive systems for high performance, high efficiency, ultra-fast response, and strong robustness.

MOAs do not rely on explicit mathematical models of the system. They can perform data-driven dynamic modeling for systems with strong nonlinearity, parameter uncertainty, or black-box characteristics. Operators of MOAs have been widely applied to parameter identification in physical process modeling. Although many of these studies originated in agriculture or materials engineering [41,42,43,44,45,46], the same approach is applicable to motor drive modeling. In this case, the global search capability of MOAs is used to refine parameters of dynamic equations.

By incorporating uncertainty variables, MOAs can optimize both the structure and parameters of motor models. This enhances system robustness against disturbances and modeling errors. The approach is particularly useful for constructing nonlinear models of flux linkage, inductance, and back electromotive force, which are difficult to describe analytically in modern motor drive systems.

To avoid modeling errors in traditional physical models, a hybrid identification method was proposed [47,48]. The method combined data-driven modeling with recursive least squares (RLS). A particle swarm optimization algorithm was used to compensate for flux linkage and voltage harmonic errors. In this way, parasitic effects and parameter deviation issues of conventional predictive models were mitigated. This cross-domain study demonstrated the potential of MOAs in reducing modeling errors and enhancing the robustness of MPC prediction models.

MPC cost functions typically contain multiple weighting parameters, including current tracking error, torque ripple suppression, and switching frequency penalties. Leveraging MOAs’ superior global search capabilities [49], optimal combinations of prediction horizons, control intervals, weighting coefficients, and constraint penalty factors can be efficiently identified. This process is effective even in high-dimensional non-convex spaces. It eliminates inaccuracies that arise from experience-dependent manual tuning.

Under specified vehicle conditions and motor loads, a PSO was employed offline to identify optimal horizon parameters, obtaining ideal datasets across speeds and adhesion coefficients [50]. Subsequent online optimization via adaptive neuro-fuzzy inference systems enhanced MPC adaptability across operating conditions, maintaining robust dynamic performance and steady-state accuracy.

During MPC optimization, MOAs do not require explicit gradient information of the objective function. Instead, they perform global search in the solution space by introducing random perturbations and leveraging population-based collaboration mechanisms. This makes them less likely to be trapped in local minima and provides both flexibility and versatility, enabling more efficient exploration of complex and diverse control strategy spaces [51]. In model predictive current control of permanent magnet synchronous motors, PSO was applied to train the echo state network (ESN) model [52]. This training improved speed prediction, making it more stable and accurate. The ESN–MPC was then combined with a fast gradient method. PSO was employed to search the ESN without requiring gradient information. Through population-based collaboration and random perturbations, the accuracy of nonlinear model prediction was significantly improved. In addition, the online solving speed of MPC was enhanced. To address the conflict between current ripple and switching frequency in doubly fed induction generators, the convergence performance of several MOAs under different weighting factors was compared in detail [53]. It was verified that algorithms such as PSO, NSGA-II, and Gorilla Troops Optimizer possess the ability to avoid local optima. This capability is achieved through population-based cooperation during weight adjustment.

In addition, when faults such as winding open/short circuits or sensor failures occur, MOAs can be used to optimize the voltage allocation of the remaining phases [54]. This enables the rapid reconfiguration of feasible MPC strategies, allowing optimal or suboptimal control under fault conditions and enhancing system fault tolerance. These advantages demonstrate that MOAs are capable of effectively addressing engineering problems in modern motor drive systems [55].

In summary, modern motor drive systems are increasingly nonlinear and complex. Traditional gradient-based optimization algorithms are often constrained by local minima.

They also face high computational complexity when solving MPC problems. As a result, it becomes difficult to balance dynamic response, steady-state accuracy, and robustness under multiple constraints and strict real-time requirements. By contrast, MOAs do not rely on explicit mathematical models, possess global search capability and flexibility. They can efficiently identify model parameters, optimize cost function weights, and rapidly generate control strategies that satisfy multi-objective constraints in high-dimensional non-convex parameter spaces. Consequently, MPC online computation speed and disturbance rejection performance can be significantly enhanced. Researchers have validated the superiority of MOAs, including PSO, genetic algorithms (GA), and GTO, across diverse applications such as PMSM, induction motor, and fault-reconfiguration control. In recent years, several reviews have been published on predictive control for motor drives. These works have summarized classical MPC schemes, optimization methods, robustness strategies, and emerging model-free approaches, as well as advances in power converters and hybrid control methods [56,57,58,59,60,61,62]. However, none of these reviews has systematically discussed the integration of MOAs into MPC for motor drives, which leaves a gap that this paper aims to address.

By comparing with the existing reviews on MPC for motor drives, the contributions of this paper can be presented as follows.

(1) MOAs-enhanced modeling: A comprehensive analysis is provided on how MOAs improve MPC modeling accuracy, robustness, and adaptability, covering white-box, gray-box, and black-box modeling approaches.

(2) MOAs-based parameter tuning: A systematic review is presented on parameter tuning methods, with comparisons between offline and online MOA-based strategies, highlighting their capability to replace or complement manual tuning and conventional solvers.

(3) MOAs-optimized solvers: A detailed study is carried out on MOA-based optimization solvers, with particular attention to engineering concerns such as computational cost, triggering mechanisms, and embedded hardware implementation.

Therefore, this paper aims to systematically review the integration of MOAs with MPC, providing an in-depth analysis of their specific implementations and performance comparisons in motor control. Furthermore, the optimization effects under different operating conditions and the engineering potential of MOAs are discussed, with the expectation of offering theoretical guidance and practical insights for future research on the application of MOAs in MPC.

The rest of this paper is organized as follows. Section 2 introduces the fundamentals of MPC in motor-drive systems, including modeling approaches, control objectives, and typical challenges. Section 3 reviews MOAs and their common operators, systematically discusses the integration of MOAs with MPC, focusing on three main areas: dynamic model, parameter tuning, and optimization. Section 4 concludes the paper and presents potential directions for future research.

2. Principles of Model Predictive Control

MPC is essentially an advanced process control strategy. MPC explicitly incorporates the physical constraints of inputs and outputs. It considers the dynamic relationships among multiple input and output variables. MPC performs real-time rolling optimization on the prediction model. Based on these steps, MPC determines the system’s optimal control actions. These characteristics grant MPC a natural advantage in handling nonlinear, strongly coupled, and constrained motor drive systems. However, MPC still faces inherent theoretical limitations, such as high computational complexity in optimization, strict dependence on model accuracy, and stringent requirements for real-time implementation. This paper focuses on three key aspects—model formulation, parameter tuning, and optimization algorithms—to analyze both the strengths of MPC in motor drive systems and the challenges that remain to be addressed.

MPC operates through an iterative cycle of three core steps: Prediction, optimization, and feedback, as shown in Figure 1.

Prediction: at each sampling instant, MPC predicts the system’s future response over a finite horizon using the system’s state variables and mathematical model.

Optimization: an optimal control sequence is computed by minimizing the objective function subject to predefined constraints.

Feedback: the optimal control action from the optimized sequence is applied to the system. The process repeats at the next sampling instant, with actual measurements refining subsequent predictions and optimizations.

As indicated by the foregoing analysis, the core of MPC lies in its capability to perform optimizations based on predictions of future system behavior. This allows it to proactively address potential issues and constraints, thereby enhancing control quality. Concurrently, MPC’s online optimization capability enables adaptation to variations in system dynamics, improving the robustness of the control strategy. These attributes establish MPC as a powerful tool for addressing complex control problems. Nevertheless, they also render MPC strategies critically dependent on the parameters of the prediction model. Due to inaccurate measurements and the uncontrollable nature of operational environments, the parameters of the prediction model employed in control often deviate from their counterparts. This mismatch commonly degrades the control performance of the algorithm and may even induce system instability. Commonly encountered plant models can be described by linear discrete-time systems.

$$\begin{array}{l}\widehat{x}(k+1)=Ax(k)+Bu(k)\\ y(k)=Cx(k)+Du(k)\end{array}$$

(1)

where x, u, and y denote the state vector, input vector, and output vector of the system, respectively. The matrices A, B, C, and D correspond to the state matrix, input matrix, output matrix, and feedthrough matrix, respectively. The indices k and k + 1 represent the information at the current and next discrete time steps.

The essence of the MPC cost function lies in its reliance on prediction errors. Short-term prediction errors are smaller than long-term prediction errors. This characteristic enables MPC to perform continuous rolling optimization. By iteratively optimizing short-term predictions (over a prediction horizon of N steps) at each sampling instant, it accomplishes long-term optimal tracking of the system output y relative to the given reference y*, as illustrated in Figure 2.

Unlike traditional pre-designed control laws, MPC integrates model prediction with online optimization, enabling it to explicitly handle system constraints and support multi-objective optimization. Its cost function typically consists of a tracking error term and several weighted objective terms (e.g., weights a, b, …, n). By adjusting these weighting coefficients, a comprehensive balance can be achieved among performance metrics such as dynamic response, steady-state accuracy, control increments, energy consumption, or switching frequency. The cost function J for a common controlled object model is shown as

$$J=f(x(k),u(k))=a{j}_1+b{j}_2+,\cdots ,+n{j}_n$$

(2)

where j₁, j₂, …, j_n represent sub-objective terms, each corresponding to a distinct performance metric.

As illustrated in Figure 2 and Equation (2), the parameters of the MPC algorithm exhibit mutually constraining relationships across performance optimization, real-time feasibility, robustness and safety, and multi-objective balancing. Specifically, the selection of the prediction horizon and control horizon determines the system’s computational cost and the accuracy of prediction outcomes. Meanwhile, the weighting factors in the cost function, including tracking error, control increments, energy consumption, and oscillation suppression, directly govern the system’s control performance. Traditional manual parameter tuning inevitably leads to performance compromises. Only through systematic parameter optimization can MPC simultaneously satisfy high-performance requirements and ensure stable/reliable operation within computational constraints.

From the preceding analysis, it is evident that the optimal input values for the future system can be selected by evaluating the objective function J. For simple systems, all possible values of the objective function J can be assessed using an enumeration method, as follows:

$$J_{opt}=\min \left\{J_1,J_2,\cdots ,J_n\right\}$$

(3)

where J_out denotes the optimal cost function value, while J₁, J₂, …, J_n represent the cost function values corresponding to different control inputs.

However, in increasingly complex operating environments, such as electric vehicles and aerospace applications, the multi-objective and high-performance requirements of modern motor drive systems render conventional enumeration methods inadequate. Therefore, an optimization algorithm with high cost-effectiveness is urgently needed, one that can simultaneously account for system prediction accuracy, control performance, and computational cost.

In summary, while MPC demonstrates superior dynamic performance and robustness in complex motor drive scenarios by leveraging future behavior prediction and online multi-objective optimization with explicit constraint handling, it still faces three critical limitations.

(1)

Model inaccuracies and stochastic disturbances degrading prediction efficacy;

(2)

Empirical parameter tuning struggling to balance performance against computational efficiency;

(3)

Traditional gradient-based or enumerative solvers often fail in high-dimensional, non-convex constrained spaces. They struggle to simultaneously achieve real-time feasibility and global optimality.

To overcome these limitations, numerous studies have integrated MOAs with MPC, conducting in-depth research on key aspects such as dynamic model development, parameter tuning, and optimization algorithms. Therefore, the next section focuses on reviewing the introduction and application of MOAs in modern motor drive MPC systems. It explores how MOAs, through global search capabilities and adaptive strategies, collaboratively support model formulation, parameter tuning, and optimization. In this way, they provide new theoretical and methodological support for achieving efficient, robust, and real-time control in motor MPC.

3. Applications of MOA in MPC

The integration of MOAs with MPC in motor-drive systems is discussed in this chapter, organized into three key aspects: dynamic modeling, parameter tuning and optimization algorithms. Figure 3 provides a high-level overview of the MOAs-MPC framework, illustrating the interactions between the motor model, predictive controller, and optimization algorithms through iterative feedback loops. This schematic highlights the data flow from system measurements to control actions, as well as the role of MOAs in adaptively optimizing controller parameters to balance real-time performance, robustness, and tracking accuracy. The subsequent sections explore each of these aspects in detail, providing theoretical foundations and representative studies from recent literature.

3.1. Dynamic Models

In MPC, the optimal control actions are derived through optimization based on predictive models. Consequently, a high-fidelity prediction model is critical to ensure MPC’s effectiveness, efficiency, constraint handling and stability [63]. In practical motor drive systems, electromagnetic and mechanical parameters often vary with operating conditions. Non-ideal factors, such as external load disturbances, can introduce additional nonlinear interference terms [64]. Thus, conventional prediction models often fail to achieve perfect consistency with the actual system. As a result, modeling inaccuracies and disturbance coupling effects cause deviations in MPC predictions, degrading the dynamic responsiveness and stability margin of the control system. Therefore, constructing a predictive model that accurately captures the nonlinear behavior and uncertainties of the motor is a pressing theoretical challenge. At the same time, the model must maintain real-time solvability.

3.1.1. Studies Discussion

In research on predictive model development for motor MPC, three typical approaches have gradually emerged to better capture the dynamic characteristics of motor systems while balancing interpretability and adaptability: white-box models based on physical mechanisms, black-box models driven primarily by data, and gray-box models that integrate the advantages of both. Meanwhile, MOAs have been widely applied in the construction and calibration of these models due to their efficiency in global search, parameter identification, and structural optimization. Depending on the modeling paradigm, MOAs can be used for precise identification of physical parameters in white-box models, automatic optimization of neural network structures in black-box models, and efficient coordination of physical priors with data-driven corrections in gray-box models. The following sections review representative studies and key advances in the application of MOAs to white-box, black-box, and gray-box predictive model development for motor MPC.

White-box models focus on the physical mechanisms of the motor and explicitly describe its dynamic characteristics through equivalent magnetic circuits, parameter equations, and other formulations. These models offer a high degree of interpretability, as shown in Figure 4. In Figure 4, the white-box model utilizes standard nomenclature for electric motor modeling: u_d represents the d-axis voltage, i_d represents the d-axis current, L_d represents the d-axis inductance, L_q represents the q-axis inductance and R represents the stator resistance. The symbol p_n denotes the number of pole pairs, ω_e represents the electrical angular velocity, ω_m is the mechanical angular velocity, while ψ_f signifies the permanent magnet flux linkage. The electromagnetic torque produced by the motor is represented by T_e, and T_L is the load torque applied to it. The model’s mechanical dynamics are defined by J, the moment of inertia, and B, the viscous damping coefficient. The outputs of the model are the electromagnetic torque and the rotor speed, plotted against time.

Taking the state-space modeling of a PMSM as an example, white-box models are directly derived from physical laws. For a PMSM, the electrical and mechanical equations define the state vector as

$$\begin{array}{c}\widehat{x}(k+1) = \left[\begin{array}{c}{\omega }_m(k+1)\\ i_d(k+1)\\ i_q(k+1)\end{array}\right]=\left[\begin{array}{ccc}-{\displaystyle \frac{B}{J}}& {\displaystyle \frac{3p{\psi }_f}{2J{L}_d}}& -{\displaystyle \frac{3p{\psi }_f}{2J{L}_q}}\\ {\displaystyle \frac{R}{L_d}}& -{\displaystyle \frac{R}{L_d}}\tau & {\displaystyle \frac{p{\psi }_f}{L_d}}{\omega }_m(k)\\ -{\displaystyle \frac{R}{L_q}}& -{\displaystyle \frac{p{\psi }_f}{L_q}}{\omega }_m(k)& -{\displaystyle \frac{R}{L_q}}{\displaystyle \frac{J}{B}}\end{array}\right]\left[\begin{array}{c}{\omega }_m(k)\\ i_d(k)\\ i_q(k)\end{array}\right]+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{L_d}}\\ 0\end{array}\right]u_d(k)+\left[\begin{array}{c}0\\ 0\\ {\displaystyle \frac{1}{L_q}}\end{array}\right]u_q(k)\\ y(k)=\left[\begin{array}{c}{i}_d(k)\\ i_q(k)\\ {\omega }_m(k)\end{array}\right]\end{array}$$

(4)

where $x(k)={[i_d,i_q,{\omega }_m]}^T,u(k)={[u_d,u_q]}^T$. The matrices A, B, C, D are determined by parameters such as R, L_d, L_q, J, B, ψ_f. MOAs can be applied for online identification of time-varying parameters (e.g., R, L), compensating model mismatches caused by temperature and load variations.

PSO was applied to the parameter identification of the equivalent magnetic circuit in PMSMs [65]. A cost function was constructed to evaluate the identification accuracy, which was defined as the weighted squared error between measured and predicted phase currents and rotor speed. The dataset contained 1000 samples, collected with a sampling period of 10 µs, corresponding to a 0.1 s measurement window. Experiments were performed on a 19.8 kW PMSM at a rotor speed of 1700 rpm and a load torque of 3 N·m. Both constant and time-varying stator resistance and load torque scenarios were considered. Compared to the RLS, PSO reduced the cost function value by approximately 25%. This demonstrated the superior robustness of PSO in nonlinear and time-varying operating conditions. However, the method also exposed a trade-off between convergence speed and computational cost under high sampling rates.

Subsequently, to better balance the exploration capability and computational efficiency of PSO, the PSO operators were enhanced through a tolerance-based search direction adjustment mechanism [66]. A variable neighborhood search was employed to strengthen global search capability. Adaptive inertia weights were applied to accelerate the optimization of MPC predictive model parameters, achieving satisfactory experimental results. Differential evolution (DE) was combined with the least-squares method for the identification of rotor reactance and stator resistance in induction motors [67]. Initial parameters were provided through the global exploration capability of DE and then fine-tuned by the least-squares method, resulting in a reduction in predictive model errors by approximately 15%.

The successful application of conventional metaheuristic algorithms (e g., PSO and DE) in the modeling of motor drive systems has sparked increased research interest. Gray wolf optimizer (GWO) was applied to the identification of friction parameters in motor drive systems [68]. By simulating social hierarchy and prey-encircling mechanisms, robustness of the system model under high-torque impact conditions was improved. However, the convergence performance of GWO is highly sensitive to parameters in the encircling and attacking phases, such as search step size and cooperation weights [69,70]. Without returning for different motor types or load ranges, slow convergence or trapping in local optima may occur. To address this issue, genetic algorithm was combined with adaptive RLS methods [71]. Mixed online correction of motor magnetic saturation inductance was performed, allowing inductance errors across different motors within a temperature range of ±40 °C to be controlled below 5%. Nevertheless, the fixed cascade structure of this hybrid parameter identification strategy lacks an adaptive mechanism for random disturbances, resulting in high computational costs for global search under small-disturbance scenarios.

Meanwhile, black-box data-driven models have attracted attention due to their low dependence on physical priors and capability to autonomously learn nonlinear mappings from data, as shown in Figure 5. In black-box modeling, MOAs have been widely applied to improve the training of neural networks and kernel-based models. Examples include radial basis function (RBF) networks optimized by genetic algorithms [72,73], long short-term memory (LSTM) architectures enhanced by gray wolf optimization [74,75], and hybrid MOAs–support vector machine (SVM) frameworks [76,77]. Although these studies originated in different domains, their methodological principle remains consistent. Global optimization is used to overcome local minima and to improve generalization ability. The same principle is applicable to black-box model predictive control of motor drives.

Take the load disturbance prediction model based on LSTM as an example, the black-box approach replaces explicit physical equations with LSTM to capture nonlinear dynamics. In this case, the model learns the mapping from inputs

$$u(k)={[i_d,i_q,{\omega }_m]}^T$$

(5)

to the disturbance-related output, namely the estimated load torque ${\widehat{T}}_L(k)$. The internal dynamics of the LSTM can be expressed as

$$\begin{array}{c}{f}_t=\sigma \left(W_f\left[h_{t-1},u(k)\right]+b_f\right)\\ i_t=\sigma \left(W_i\left[h_{t-1},u(k)\right]+b_i\right)\\ o_t=\sigma \left(W_o\left[h_{t-1},u(k)\right]+b_o\right)\\ {\tilde{c}}_t=\tanh \left(W_c\left[h_{t-1},u(k)\right]+b_c\right)\\ c_t=f_t\odot c_{t-1}+i_t\odot {\tilde{c}}_t\\ h_t=o_t\odot \tanh \left(c_t\right) \\ {\widehat{T}}_L(k)=W_y{h}_t+b_y\end{array}$$

(6)

MOAs can optimize the hyperparameters of neural networks (such as the number of hidden layer nodes, learning rate, etc.). The definitions of the variables in Formula (6) can be explained as follows:

h_t: hidden state vector of the LSTM at time step t, representing dynamic features learned from data.

c_t: cell state vector of the LSTM at time step ttt, storing long-term memory.

f_t, i_t, o_t: forget gate, input gate, and output gate activation vectors, respectively.

${\tilde{c}}_t$: candidate cell state.

W_f, W_i, W_o, W_c, W_y: weight matrices for the forget gate, input gate, output gate, candidate cell state, and output layer.

b_f, b_i, b_o, b_c, b_y: corresponding bias vectors.

σ(⋅): sigmoid activation function.

⊙: element-wise (Hadamard) product.

In the dynamic modeling of PMSM, PSO was applied to jointly optimize network structure and learning rate, reducing root mean squared error (RMSE) on simulation datasets and improving predictive model accuracy [78]. In multi-condition tests of screw compressor drive motors, GA was used to optimize the number of hidden nodes and basis function widths in RBF networks. The dataset was divided into 80% training and 20% testing, and the GA-based MPC predictive model reduced RMSE by approximately 15% compared with physics-based models with fixed parameters [72,73,79]. For high-power-density motor parameter prediction, GWO was combined with LSTM networks. The dataset was again split 80/20 for training and testing, and model accuracy was evaluated by mean absolute error (MAE) and RMSE. The optimized GWO–LSTM reduced both MAE and RMSE by approximately 50% relative to the baseline LSTM, and decreased RMSE by about 25% compared with PSO–LSTM [77,78]. Comparative studies further showed that GWO–LSTM achieved faster convergence and stronger ability to escape local optima when the model scale was relatively small, while its search efficiency decreased with increasing model complexity [80]. Collectively, these studies demonstrate the capability of MOAs in black-box neural network modeling for motor drives. However, the lack of physical interpretability in such models constrains optimization to error reduction and makes it difficult to guarantee system stability [81].

Gray-box models provide a compromise between interpretability, data efficiency, and adaptability by introducing data-driven online correction or optimization for nonlinear or time-varying components, such as friction, magnetic saturation, or temperature drift, which are difficult to precisely describe in physical models, while maintaining a framework of physical interpretability, as shown in Figure 6.

Taking the hybrid model with magnetic saturation compensation as an example, the gray-box approach combines physical equations with data-driven corrections. Performing online compensation for the d-axis inductance parameters

$$\begin{array}{l}\widehat{x}(k+1)=[A+\Delta A(k)]x(k)+[B+\Delta B(k)]u(k)+w(k)\\ y(k)=Cx(k)+v(k)\end{array}$$

(7)

where $x(k)={[i_d,i_q,{\omega }_m]}^T$ is the state vector, $u(k)={[u_d,u_q]}^T$ is the input vector, and y(k) is the measured output; A, B, C are the nominal system matrices derived from physical laws; ΔA(k), ΔB(k) are data-driven correction matrices, typically obtained via neural networks or regression models:

$$\Delta A(k)={\mathrm{MLP}}_A\left(i_d,i_q,{\omega }_m\right), \Delta B(k)=\mathrm{ML}{\mathrm{P}}_B\left(i_d,i_q,{\omega }_m\right)$$

(8)

where w(k), v(k) denotes process and measurement noise, respectively. This formulation allows the gray-box model to retain physical interpretability while capturing unmodeled nonlinearities and parameter variations.

GA–PSO was applied to jointly search for submodules of gray-box models, such as motor friction coefficients and flux linkage parameters. This approach combines the advantage of GA in reducing premature convergence with the capability of PSO to accelerate convergence using local information [82]. Data-driven corrections were performed while retaining the main structure of the physical model, demonstrating for the first time the complementary advantages of MOAs in gray-box parameter identification. This coordinated algorithm-controlled tracking errors within 3% under both high- and low-speed extreme conditions, and reduced iteration numbers by approximately 20% compared with conventional parameter identification methods. This highlights the necessity of parallel structured search and local fine-tuning in gray-box model identification [83].

Gray-box models also benefit from the integration of MOAs. In applications such as quality assessment and agricultural process monitoring [84,85,86,87], cuckoo search (CS) and its variants have been employed to optimize SVM and artificial neural networks (ANN). Although the application domains differ, MOAs can fine-tune data-driven components within a physics-based framework. This capability, which can capture the nonlinearity and uncertainty of system, is analogous to gray-box modeling in motor drives and has inspired the proposal of CS-identified gray-box models. For discrete-segment magnetic saturation characteristics of switched reluctance motors, the nonlinear flux–current relationship was divided into several continuous submodels while preserving the original physical model [88]. An error metric function was constructed for each subinterval. Subsequently, to perform a global search for the optimal parameter combination of all submodels, CS was employed with pheromone updating and heuristic transfer rules. This method effectively avoids local optima caused by nonconvexity and discontinuities. Under high-current transient conditions, the CS-identified model reduced the average energy estimation error by 15% compared with the conventional gray wolf algorithm. These results indicate that precise characterization of predictive models can significantly reduce the negative impact of energy-weighting on steady-state performance, enabling lower power losses under comparable dynamic response conditions [89].

In gray-box predictive model development for motor MPC, the whale optimization algorithm (WOA) was applied. WOA automatically selects candidate subnets for flux saturation and friction models, targeting nonlinear components that are difficult to describe precisely in physical models [90,91,92]. This approach reduced parameter identification time by approximately 40%. The impact of different subnet structures on prediction error and computational cost was analyzed. It was observed that subnets with mild nonlinear compensation increase computational burden. The increase is roughly linear once the marginal error reduction becomes negligible.

Based on this finding, an adaptive structure selection criterion based on curve inflection points was proposed [93], providing guidance for subsequent adaptive modeling. The criterion emphasizes not only minimizing error but also balancing the trade-off between error reduction and computational cost. Building upon traditional physical models, a disturbance-based adaptive cascade gray-box model identification strategy was proposed [94].

Under small system disturbances, a low-computational-cost PSO–RLS structure search was employed. During large operational transients, the algorithm switched to DE–RLS to leverage stronger global search capability. The adaptive switching was realized via an online disturbance detection mechanism [95]. This approach reduced the average online computation time by approximately 35%. It maintained identification accuracy comparable to pure DE–RLS under severe disturbances. This “on-demand” switching approach provides a new perspective for dynamically balancing MPC real-time performance and control accuracy. It is particularly useful for systems with mixed slow and fast dynamics.

3.1.2. Research Comparison and Prospects

After reviewing the aforementioned studies, a comprehensive comparison of various MOAs in motor dynamic model development was conducted. The comparison considered model accuracy versus algorithm convergence efficiency. It also examined algorithm real-time performance versus computational cost, and model robustness versus sensitivity to algorithm hyperparameters.

This comparison aims to provide guidance for subsequent research on MOAs simplification, online hyperparameter adjustment, and adaptive switching strategies in MPC dynamic modeling.

Hybrid MOAs, such as PSO-RLS, offer clear advantages over traditional least squares methods by significantly reducing MPC prediction errors, measured as RMSE, typically achieving reductions of 15–30% under standard operating conditions [95]. This improvement stems from their ability to perform global parameter searches and avoid local minima, enhancing model accuracy. However, this global search incurs a notable trade-off in high-frequency sampling scenarios: the initial iterations introduce response delays of several milliseconds, which can be critical in fast-dynamics motor control applications. Enhanced variants, such as PSO-VNS with adaptive inertia weights, partially mitigate this issue by accelerating parameter convergence [67], yet they still struggle to meet the requirements demanded by motor drive systems. These observations suggest that while hybrid MOAs improve RMSE, their practical deployment in high-speed MPC requires careful tuning of population size, iteration number, and inertia weight to balance convergence speed and prediction fidelity. Moreover, these methods are sensitive to hyperparameter selection, which may limit robustness under varying operating conditions.

Regarding the trade-off between algorithm real-time performance and computational cost, multi-objective MOAs frameworks (e.g., GA-PSO, NSGA-II) can generate Pareto-optimal solution sets covering prediction RMSE, response latency, and model complexity in each operation cycle [82,83]. This allows designers to select configurations that balance accuracy and efficiency. However, internal operations, such as non-dominated sorting and multi-dimensional crowding distance evaluation, significantly increase computational load. This prolongs response times by tens to hundreds of milliseconds, depending on population size and iteration number. Meanwhile, online adaptive gray-box MOAs for model identification (e.g., PSO–RLS, DE–RLS) can quickly update parameters. They maintain low RMSE under minor disturbance scenarios [93,94,95]. Yet, because most strategies lack disturbance-intensity-adaptive switching mechanisms, even weak disturbances trigger full iteration searches, resulting in unnecessary computational effort and potential delays in high-frequency control loops.

From the perspective of model robustness and hyperparameter sensitivity, black-box MOAs network training methods (e.g., PSO-LSTM) demonstrate strong RMSE convergence under limited samples or noisy conditions, highlighting their ability to capture complex nonlinear behaviors [90]. However, due to the absence of physical mechanism constraints, these models often struggle with multi-condition generalization and validation of predicted outputs. In contrast, gray-box MOAs structure search strategies (e.g., WOA subnet screening, firefly algorithm polynomial compensation optimization) retain physical prior equations while adaptively pruning redundant sub-models, improving nonlinear compensation and reducing model degrees of freedom [90,91,92]. Nevertheless, the determination of the benefit–cost inflection point heavily depends on offline statistical distributions. When online sample distributions shift, the previously optimal “RMSE–computational cost” trade-off may fail, revealing a vulnerability in adaptive deployment under real-world, non-stationary conditions.

In summary, various MOAs exhibit distinct strengths and limitations in MPC dynamic modeling for motors. Single-population algorithms deliver high precision in targeted scenarios but suffer from compromised real-time performance. Multi-objective and hybrid MOA frameworks provide comprehensive Pareto-optimal solutions for model parameters, yet their high iteration costs introduce real-time latency in online parameter identification. Black-box MOAs training methods enhance model robustness against noise but lack physical interpretability due to unconstrained data-driven mechanisms. Gray-box MOAs structure search strategies balance model interpretability and efficiency but heavily rely on static sample distributions, leading to failure under online sample drift. Hybrid switching algorithms reduce redundant computational costs yet require more flexible adaptive mechanisms to avoid resource wastage in weak-disturbance scenarios. The advantages and disadvantages of the three modeling paradigms—white-box, black-box, and gray-box models—are summarized in

Table 1. Comparison of advantages and disadvantages among the three modeling paradigms.

Type	Algorithms	Advantages	Limitations	References
White-box	PSO, DE, GWO	High interpretability	Slow convergence	[64,65,66,67,68,69,70,71]
Black-box	PSO, GA, GWO-LSTM	Capable of capturing complex nonlinearities	Poorly interpretable	[73,74,75,76,77,78,79,80]
Gray-box	GA-PSO, CS, WOA	Balances interpretability and adaptability	High computational costs	[90,91,92,93]

.

Based on the above analysis, future research could focus on several directions. On one hand, more lightweight swarm intelligence operators should be developed to significantly reduce the cost per iteration. Hierarchical optimization frameworks should also be implemented to maintain global search capability.

Online disturbance-adaptive mechanisms can be implemented to switch operators according to disturbance intensity. Performance-feedback mechanisms can enable hyperparameter self-tuning in response to system changes. This approach helps avoid redundant computations under weak disturbance scenarios. Moreover, in gray-box modeling, deep physical constraints and uncertainty quantification methods could be leveraged to enhance the reliability of “benefit–cost” trade-off strategies when online sample distributions drift.

The analysis above indicates that MOAs with different characteristics exhibit distinct strengths in motor predictive model development. The performance of these algorithms is highly sensitive to hyperparameters such as population size, iteration number, and learning factors. Without systematic hyperparameter tuning, stable performance across varying operating conditions is difficult to achieve.

3.2. Parameter Tuning

In MPC, the selection and optimization of prediction and control horizons, weighting coefficients, and system constraint parameters directly determine the dynamic response, steady-state accuracy, robustness, and predictive performance of the control system. Therefore, parameter tuning is critical for improving MPC performance and balancing control quality with computational cost. In modern motor drive systems, system load, speed, and environmental disturbances often vary dynamically. Offline static parameter settings are usually unable to track the optimal operating point in real time, which degrades the system performance and dynamic response under MPC. Moreover, the coupling between prediction and control horizons, the multi-objective trade-offs in weighting matrices, and the real-time requirements of the control algorithm make online adaptive parameter adjustment highly challenging. Consequently, there is an urgent need for efficient algorithms capable of automatically determining optimal parameter combinations while satisfying embedded real-time constraints. These factors together constitute the key research bottleneck in motor MPC parameter tuning.

3.2.1. Studies Discussion

At the forefront of motor MPC parameter tuning research, offline metaheuristic optimization strategies have been widely adopted due to their excellent global search capabilities. In model predictive torque control, PSO was applied to the offline tuning of cost function weights [96], where the prediction and control horizons were encoded as particle position vectors, and dynamic adjustments of inertia weight and learning factors were employed. As a result, the MPC’s adaptability to load disturbances and frequent speed fluctuations was enhanced, and torque ripple was significantly reduced, demonstrating the rapid optimization potential of metaheuristic algorithms in high-dimensional MPC parameter spaces. Similarly, a novel hybrid offline MPC parameter tuning strategy has been applied in other fields [97,98], which combines GA and PSO. In this strategy, GA exploits its global search capability to generate multiple candidate solutions in the parameter space. PSO is then applied to refine these solutions and accelerate convergence, producing a set of Pareto-optimal solutions. This hybrid approach was shown to maintain system dynamic response speed, reduce torque ripple by approximately 30% compared with standard GA, and decrease the average switching frequency by nearly 15% relative to a PSO-only approach.

Following the aforementioned single-objective or bi-objective swarm intelligence parameter tuning strategies, multi-objective weight joint optimization has further expanded the scope of MPC parameter tuning, aiming to simultaneously balance multiple performance indices in the MPC cost function, such as tracking accuracy, control smoothness, switching frequency, and computational latency, thereby comprehensively enhancing overall system performance. NSGA-II was applied for offline tuning of multi-objective cost function weights in model predictive torque control (MPTC), where the pareto front was searched in parallel for torque tracking error, flux linkage tracking error, and switching frequency [99]. An evaluation criterion based on multi-attribute decision theory was subsequently used to select the optimal weight configuration from the set of non-dominated solutions. This method effectively suppressed current harmonics and reduced system energy consumption. The multi-objective framework prevented performance bias caused by single-weight tuning, demonstrating the advantages of multi-objective optimization in MPC parameter tuning. However, NSGA-II is sensitive to population size and the computational overhead of non-dominated sorting; when the number of objectives or candidate weights increases, the evaluation time in high-dimensional parameter space rises sharply.

Based on this, multi-objective particle swarm optimization (MOPSO) was applied to MPC parameter tuning of sensorless vector-controlled induction motor systems. The weights of tracking error, flux oscillation suppression, and switching frequency were optimized in parallel. This achieved dynamic coordination between control accuracy and energy efficiency. It also verified the engineering adaptability of MOPSO for managing multi-performance trade-offs in motor drives [100]. Compared with NSGA-II, MOPSO was observed to converge more rapidly to a well-distributed solution set during collaborative weight iteration, and the maintenance of solution diversity during iteration was more natural, without reliance on complex sorting or crowding calculations [101]. Nevertheless, MOPSO also requires careful selection of particle swarm size and neighborhood update rules; otherwise, premature convergence or sparsity in multi-peak objective space may occur.

Furthermore, multi-objective bee algorithm was applied for joint optimization of multiple indices, including tracking error, control increment, and energy consumption weights in the MPC of PMSM, generating a pareto front covering a wide performance spectrum [102]. This method was based on the artificial bee colony (ABC) algorithm. Parallelized sampling and update strategies were employed to balance dynamic response and energy consumption. These strategies provided diversified parameter tuning solutions for engineering applications.

Although offline metaheuristic optimization strategies have achieved effective synergy between global and local search, highlighting their tuning advantages in high-dimensional MPC parameter spaces, they generally suffer from reliance on large-scale offline computations, lack of online adaptability, and insufficient hardware validation. To enhance system responsiveness and robustness, online adaptive MPC parameter tuning strategies combining swarm intelligence and classical estimation algorithms have been developed [103].

Firstly, μ-synthesis techniques were integrated with PSO to obtain initial weight configurations by solving linear matrix inequalities (LMI), ensuring offline feasibility in the first stage. This was followed by PSO-based fine-tuning of MPC parameters in the local search space. This approach demonstrated the feasibility of online parameter gain adjustment under MPC real-time constraints. It combined complex swarm intelligence search with rapidly solvable convex optimization, thereby meeting the real-time requirements of modern motor drive systems [104].

PSO was embedded within the MPC loop. It enabled online automatic tuning of prediction and control horizon weights across multiple operating conditions. This implementation resulted in significant improvements in torque and speed performance [105]. An event-triggered mechanism was adopted, activating global search only when control performance indices exceeded predefined thresholds, which mitigated high computational load but introduced a secondary tuning problem for threshold selection.

Q-learning was combined with PSO to dynamically adjust MPC prediction horizon, control horizon, and weight coefficients online through a reinforcement learning reward function [106], allowing rapid convergence and low steady-state error under complex and varying operating conditions. The reward function was updated iteratively based on environmental feedback, enhancing adaptability and scalability, though its performance remained highly sensitive to threshold and reward design, potentially leading to “ineffective exploration” in high-noise scenarios.

K-means clustering was integrated with PSO to partition typical operating condition clusters. PSO searches were then conducted within each cluster, effectively reducing the parameter update range per iteration and alleviating computational load, while improving tracking accuracy and power balance under multiple operating conditions [107,108,109,110,111]. However, this method required high clustering accuracy, and dynamic clustering or incremental learning was needed when the online distribution of operating conditions drifted to maintain continuous tuning performance.

Overall, these studies have provided diverse feasible approaches for online automatic MPC parameter tuning from the perspectives of global search, reinforcement learning enhancement, hardware-in-the-loop validation, and cluster-assisted strategies. While these online adaptive strategies can respond to changing operating conditions in real time, most still rely on preset trigger thresholds or reward criteria, lacking adaptive triggering based on disturbance intensity or system state, and frequent global iterations remain challenging to sustain on resource-constrained embedded platforms.

3.2.2. Research Comparison and Prospects

Based on the analysis of the above literature, the research progress of MOAs in MPC parameter tuning shows a gradual evolution. Three mainstream strategies have emerged: offline single- or double-objective MOAs, offline multi-objective MOAs, and online adaptive MOAs. This evolution has expanded from initial single-performance improvement to multidimensional performance balancing, continuously enhancing responsiveness to real-time requirements and system robustness, thereby driving MPC parameter tuning toward more intelligent and engineering-oriented approaches. A comparison of the three mainstream MOAs in MPC parameter tuning is presented in

Table 2. Comparison of MOAs in MPC parameter tuning.

Type	Algorithms	Advantages	Limitations	References
Offline single-objective	PSO, GA, GA-PSO	Strong global search capability	Limited to simple conditions	[95,96,97,98]
Offline multi-objective	NSGA-II, MOPSO, ABC	Multi-objective parallel optimization	Poor generalization and robustness	[99,101,103]
Online adaptive	Q-learning, K-means	Rapid response, high robustness	High computational cost	[104,105,106,107,108,109,110,111]

.

Early studies primarily focused on offline single-objective or double-objective MOAs parameter tuning strategies. Algorithms such as PSO and DE were applied to optimize specific performance indicators, such as tracking error or torque ripple [96,97,98]. In these methods, swarm intelligence generated fixed optimal parameter configurations through offline global search. This approach indeed improved MPC performance under specific operating conditions. However, its simplicity comes at a cost. While computationally stable, these strategies lack flexibility to adapt to varying operating scenarios. Their robustness and stability under system disturbances or parameter drift are limited. Moreover, these studies rarely quantify trade-offs between convergence speed, error reduction (e.g., RMSE), and computational burden. Therefore, although effective in controlled settings, offline single- or double-objective MOAs may fail to maintain multi-dimensional performance coordination in more complex motor control tasks. These limitations motivate the development of optimization methods with stronger structural constraints and feasibility guarantees, which aim to enhance performance while preserving practical applicability.

Building on this, multi-objective MOAs extended research toward parallel optimization of multiple performance indicators [99,101,103]. These strategies typically construct a cost function set encompassing tracking accuracy, energy efficiency, dynamic response, and switching frequency. Algorithms such as NSGA-II, MOPSO, or GWO are then applied to solve the Pareto front, yielding diverse parameter configurations that aim to balance system performance in motor control. This approach effectively avoids performance bias caused by single-weight tuning. It also demonstrates strong adaptability across different hardware platforms and load conditions.

However, these benefits come with trade-offs. Internal operations, including non-dominated sorting and crowding distance evaluation, significantly increase computational cost. In practice, this can prolong online parameter identification by tens to hundreds of milliseconds depending on population size and iteration number. Moreover, while these methods provide a set of Pareto-optimal solutions, they do not explicitly quantify the trade-offs between convergence speed, error reduction (e.g., RMSE), and computational burden. As a result, although multi-objective MOAs enhance performance flexibility, their high computational demand poses substantial challenges for real-time deployment in high-sampling-rate motor control applications.

Online adaptive MOAs represent the latest direction in MPC parameter tuning research. These methods aim to integrate the global search capability of MOAs directly into the MPC loop. Real-time parameter adjustment is achieved through event-triggered mechanisms, reinforcement learning-based dynamic rewards, or clustering-assisted approaches [107,108,109,110,111]. Compared with conventional offline strategies, online adaptive algorithms respond more effectively to dynamic factors such as load disturbances, model drift, and system degradation. This allows flexible adaptation under varying operating conditions.

However, the high computational complexity of swarm intelligence algorithms remains a major limitation. If there is no effective resource management, frequent iterations can overwhelm the computational resources of embedded control platforms. Moreover, while online adaptive MOAs improve real-time responsiveness and robustness, they may still exhibit trade-offs between convergence speed, parameter accuracy (e.g., RMSE or torque ripple reduction), and computational load. For example, faster adaptation can increase computation time, whereas reducing iterations to save resources may compromise model precision. Therefore, reducing computational costs and enhancing the intelligence of triggering mechanisms are critical challenges. Quantitative evaluation of these trade-offs remains necessary to fully assess algorithm effectiveness in practical motor drive applications.

The comparative performance of the three mainstream MOAs in MPC parameter tuning is shown in Figure 7, which summarizes their trade-offs across five key dimensions.

It presents a qualitative radar chart comparison of four parameter tuning strategies for MPC: online adaptive MOAs, offline single-objective MOAs, offline multi-objective MOAs, and offline multi-objective MOAs. The evaluation spans five performance dimensions: real-time capability, tracking accuracy, robustness, computational complexity, and multi-objective balance. The radial score (distance from center) indicates performance level, with a higher score representing better performance for all axes. For the computational complexity axis specifically, a higher score indicates a simpler and more favorable algorithm (lower computational burden). From Figure 7, we can observe that online adaptive strategies excel in real-time capability and robustness but exhibit the highest computational complexity (lowest score on that axis). Offline single-objective methods prioritize low computational complexity (high score) but sacrifice performance in other domains. Offline multi-objective approaches demonstrate strong tracking accuracy and balanced performance, though with increased complexity compared to single-objective methods.

In summary, MPC parameter tuning strategies will continue to evolve toward “intelligence, real-time capability, and engineering applicability.” First, lightweight multi-objective MOA designs deserve further attention. Incremental non-dominated sorting can reduce the computational burden of multi-objective optimization. Approximate crowding distance updates further help lower computation costs. Second, adaptive triggering mechanisms should rely more on disturbance intensity estimation and system state assessment rather than static thresholds, thereby enhancing the flexibility of control strategies under non-stationary conditions. Third, automatic hyperparameter configuration will become a key aspect of future tuning strategies; integrating meta-learning or Bayesian optimization can enable adaptive evolution of algorithm structures, improving generality and robustness. Additionally, parallel acceleration techniques will be crucial for enhancing the practical deploy ability of these algorithms, particularly in high-sampling-rate, low-latency motor control scenarios, where distributed computing using multi-core DSPs, FPGAs, or neural processors may satisfy industrial requirements for microsecond-level response times.

3.3. Optimization Algorithms

The rapid development of MPC in modern motor drive systems relies on the construction of predictive models, parameter tuning, and optimization algorithm solving, all of which jointly determine the ultimate performance of MPC. Although high-precision predictive models and adaptive parameter configurations provide a solid foundation for MPC engineering practice, the key to meeting multi-constraint requirements and achieving multi-objective trade-offs in modern motor drive systems lies in the MPC optimization process. In industrial automation, electric vehicles, and aerospace applications, MPC optimization problems are typically highly non-convex, multi-modal, and time-varying. The pursuit of multiple objectives—such as tracking accuracy, torque ripple, switching losses, efficiency losses, and temperature rise—often formulated as weighted sums with penalty functions, further increases solution complexity in this context, MPC optimization algorithms for modern motor drives must possess global search capability. This enables them to escape local minima effectively. They must also compute feasible solutions within extremely short control cycles. This ensures real-time response under high dynamic loads. Robustness must be maintained even under fault scenarios. MOAs do not rely on gradient information, can flexibly integrate physical constraints with engineering requirements, achieving parallel search through population intelligence and evolutionary mechanisms for global “coarse tuning” and local “fine tuning”. Moreover, with the development of hybrid operator architectures and the emergence of high-performance parallel computing platforms such as multi-core DSPs, the iteration cost of MOAs has been significantly reduced, making it possible to complete MPC optimization within kilohertz-level control cycles in modern motor drive systems. Based on this, this section systematically reviews the application status of MOAs in MPC optimization for motor drives. It analyzes the optimization characteristics and performance of various MOAs operators. The analysis considers real-time performance and computational efficiency. It also examines optimization solving and constraint handling capability. Furthermore, robustness and prediction accuracy are evaluated. The performance of MOAs is compared with traditional MPC optimization algorithms. This review provides theoretical support for the development of high-performance MPC controllers. It also offers practical guidance for their application in motor drive systems.

3.3.1. Studies Discussion

In the implementation of MPC for motor drives, efficient optimization algorithms are key to combining model prediction with real-time control, as they directly determine whether the system can output optimal control actions within each control cycle. Among traditional optimization strategies, due to their simple computational structure and ease of hardware implementation, gradient-based methods have been widely applied in early motor MPC solvers. However, they are highly sensitive to problem condition numbers and active constraints. Encountering ill-conditioned matrices can significantly increase iteration counts. Tightly bound inequalities can also substantially slow down convergence. To address this, adaptive step-size strategies have been proposed to mitigate oscillation caused by abrupt changes in condition numbers [112]. Relaxation strategies have been introduced to reduce stagnation under similar conditions [113], yet convergence delays remain a bottleneck under severe disturbances or large operating-point jumps.

To improve constraint handling and parallelization, operator splitting methods, exemplified by alternating direction method of multipliers (ADMM), decompose large-scale quadratic programs into several quickly projectable subproblems, facilitating parallel implementation and faster response to active-set changes, thus demonstrating good online iterative performance under high sampling rates. Regarding penalty factor sensitivity, improvements such as adaptive updates based on primal/dual residual ratios and continuous relaxation factor adjustments have been proposed, which enhances the algorithm’s robustness and reduce iteration numbers [114,115,116]. However, these enhancements often increase per-iteration cost or rely on offline parameter estimation.

Another approach is explicit MPC, which partitions the feasible region offline and generates lookup tables, replacing online optimization with table lookup or polynomial evaluation to achieve extremely low latency (e.g., microsecond-level lookup delays). The effectiveness of delineating feasible regions under nonlinear constraints has been validated in other fields [117,118,119]. However, with increasing state dimensions and constraint numbers, feasible region partitioning grows exponentially, leading to prohibitive storage and retrieval costs. Semi-explicit or hybrid strategies have thus emerged, storing critical boundaries or high-frequency active regions offline while retaining lightweight online iterations for the remaining regions, seeking a compromise between memory usage and speed [120,121,122,123,124].

Overall, these classical optimization algorithms each have advantages and limitations. Yet, in meeting the “kilohertz-level” real-time requirements, complex multi-objective trade-offs, and strongly nonlinear/multi-constraint coupling of modern motor drives, traditional methods often struggle to simultaneously satisfy global search capability, real-time performance, and constraint robustness. Consequently, MOAs, with their intrinsic global search capability and ease of parallelization, have emerged as a promising solution. A comparison of the advantages and limitations of traditional MPC optimization algorithms and MOAs is shown in

Table 3. Comparison of traditional MPC optimization algorithms and MOAs.

Category	Advantages	Disadvantages	Application	References
Gradient-based	Low computational cost	Prone to local optima	Simple	[112,113]
Operator splitting	Good parallelism	High iteration cost	High sampling-rate	[114,115,116]
Explicit MPC	Extremely low latency	Large memory requirement	Few variables and constraints	[120,121,122,123,124]
MOAs	Strong global search capability	Sensitive to hyperparameters	High-dimensional, multi-objective	[125,126,127,128,129]

.

The operators of MOAs, which are characterized by population-based iteration acceleration and heuristic sequence search, were applied to improve MPC online solving efficiency while maintaining global search capability. PSO was applied to the model predictive current control solver of PMSM [125]. According to hardware experimental results reported in [125], subgroup updates and parallel motor kinematics simulation were implemented on a dSPACE DS1006 multi-core platform, which reduced the single-step optimization delay to approximately 120 μs. High tracking accuracy was maintained under ±15% load disturbances, demonstrating that MOAs can balance real-time performance and global search capability in MPC when parallel computing resources are available. GA was employed to heuristically screen an enumerated set of voltage vector candidates [126]. The number of online evaluations was reduced, lowering MPC computational delay and improving harmonic content and switching losses. Ant colony optimization (ACO) was applied to the discrete voltage vector sequence search in MPC [127]. Pheromone-guided and path-based candidate updates were used to accelerate convergence in large search spaces. Torque ripple and current harmonics were significantly reduced, and global search and dynamic adaptation performance were improved under load step changes.

MOAs are regarded as more suitable for multi-objective optimization, because global search ability in non-convex and multimodal spaces can be preserved, and adaptability to complex constraints can be ensured. A priority-aware simulated annealing (SA) strategy was proposed in [128], where the multi-objective cost function of MPC was constructed in lexicographic or dynamic weighted form. In this strategy, high-priority objectives were satisfied first during annealing, while low-priority objectives were gradually improved. For neighborhood generation, local perturbations of control sequences were applied to maintain feasibility, and a hybrid mechanism combining feasibility repair and constraint penalties was introduced to avoid infeasible solutions. To improve online efficiency, a long annealing process was executed offline to obtain a high-quality initial solution, and an event-triggered restart of local annealing was conducted when disturbances occurred or performance indices exceeded limits, so that optimization updates could be completed in few iterations. This priority-based SA method preserved robustness of high-priority objectives, significantly improved low-priority performance, and achieved more stable convergence than traditional weighting methods under conflicting objectives. ABC was introduced in [129], where the fitness function was defined by state prediction error and input magnitude. Global exploration and local exploitation were balanced through the cooperation of employed, onlooker, and scout bees, so that performance degradation under model mismatch and sudden disturbances was reduced. Real-time feasibility was improved by constraining neighborhood search in the employed bee phase and by dynamically adjusting the number of foraging attempts to suppress redundant computation. In low-frequency control, ABC–MPC demonstrated strong disturbance rejection and fast dynamic recovery. In addition, steady-state error under large disturbances was significantly lower than that of traditional fixed-parameter MPC.

The inherent characteristics of different MOAs’ operators themselves also significantly influence their suitability for MPC. A qualitative comparison of common algorithms (PSO, GA, ACO, SA, ABC) based on their typical performance in the literature [130,131,132,133,134] is summarized in the radar chart of Figure 8.

It illustrates a radar chart comparing five MOAs’ operators across five attributes: convergence accuracy, global search capability, computational complexity, robustness, and convergence speed. The radial score (distance from center) represents performance level, where a higher score is generally better. For the computational complexity axis only, a higher score indicates a simpler and more favorable algorithm (lower computational burden). Each algorithm’s performance is visualized with colored bars and error bars indicating variability. As we can see from Figure 8, PSO achieves the highest score in convergence speed, SA leads in robustness, GA excels in convergence accuracy, and ACO shows superior global search capability. ABC demonstrates moderate but balanced performance across all metrics. Computational complexity analysis reveals that PSO and GA receive higher scores on this axis, indicating relatively lower complexity compared to other algorithms.

To further improve the efficiency of MPC optimization while ensuring system robustness, a dual-optimization strategy combining convex optimization and MOAs has been gradually developed, whose structural framework is illustrated in Figure 9. Modern motor drive systems require high real-time performance and robustness. In response, a customized improvement of the PSO operator was proposed in [135]. This improvement introduced adaptive inertia weights, local search acceleration operators, and hierarchical optimization procedures. A feasible solution was first obtained by conventional convex optimization, after which a refined global adjustment was performed within its neighborhood using the modified PSO. The improved MOAs–MPC demonstrated significant advantages in suppressing current ripple and reducing steady-state speed oscillations, while maintaining low computational cost and strong adaptability across operating conditions. A set of initial solutions satisfying robustness constraints for the MPC quadratic programming problem was generated using μ-synthesis and LMI [136]. These initial solutions were iteratively refined by an embedded PSO operator, and convergence was accelerated through information sharing among particles. Significant improvements in system tracking accuracy and disturbance rejection were achieved. The search space for initial solutions was greatly reduced through convex optimization, which consequently lowered the computational cost of the MPC optimization algorithm. In induction motor MPC, LMI feasible set analysis was combined with the DE. The feasible region of objective function weights ensuring closed-loop stability and disturbance robustness was defined offline via LMIs [137]. Within this feasible region, prediction horizons, control horizons, and multi-objective cost weights were simultaneously optimized by the DE algorithm, with candidate solutions projected back into the LMI feasible set before each iteration to avoid infeasible solutions. Compared with pure DE-based tuning, the two-stage hybrid optimization strategy allowed the maximum tracking error to be reduced by approximately 18%, while closed-loop stability was maintained under ±20% parameter perturbations. Meanwhile, the pre-reduction in the search space resulted in an average iteration number decrease of approximately 25%, which significantly enhanced the online convergence speed.

In recent years, event-triggered and hybrid optimization strategies based on MOAs have gradually been developed. These strategies employ performance feedback to drive the start-stop logic of the optimization process, balancing response speed and computational resource usage. An event-triggered hybrid optimization strategy was proposed [138]. In this strategy, the initialization of the MOAs population is controlled by real-time monitoring of key performance indicators, such as tracking error and dynamic response. When any performance indicator exceeds a predefined threshold, PSO is immediately reset near the current operating point, and a new round of global search is initiated. This allows MPC to rapidly compensate for random disturbances or sudden load changes. Building on this, an adaptive relaxation and restart mechanism was further introduced based on a Gaussian process regression model [139]. In this strategy, the trigger thresholds are adaptively adjusted according to the online estimation of disturbance amplitude and frequency. As a result, the system can remain in a dormant state during stable periods, while only one or two iterations are required to rapidly respond and restore the system to its optimal state under severe disturbances. Although event-triggered and hybrid MOAs have demonstrated significant improvements in system response speed and computational efficiency, the trigger logic, disturbance modeling, and clustering mapping also introduce new hyperparameter tuning requirements and potential error propagation risks. Therefore, further optimization is needed to enhance their generalization capability and adaptability.

3.3.2. Research Comparison and Prospects

As the requirements for control accuracy, response speed, and multi-objective coordination in motor drive systems continue to increase, the optimization algorithms of MPC have gradually been recognized as a key bottleneck limiting system performance. Through the coordinated advancement of these technical pathways, future MPC systems for motor drives are expected to reach new heights in real-time performance, robustness, scalability, and safety—delivering more efficient and reliable solutions for high-performance control applications in electric vehicles, industrial automation, and rail transit.

In terms of real-time performance and computational efficiency, MOAs have achieved notable progress in accelerating MPC optimization. For instance, the application of PSO in MPC optimization has demonstrated the feasibility of parallel subpopulation update strategies within MOAs [125]. Similarly, heuristic candidate sequence search has been proposed to reduce online computational load. For example, pre-screening enumerated candidates with GA can significantly decrease the number of control sequences that need evaluation. This approach effectively lowers the computational cost of the objective function [126]. These approaches show that, when sufficient parallel computing resources (e.g., multi-core DSP, FPGA, or GPU) are available, MOAs can maintain a balance between global search capability and real-time performance.

However, these results are often reported in a descriptive manner without consistent quantification of performance trade-offs. For example, some studies report that computation cycles can be reduced to several hundred microseconds. However, the corresponding gains in error reduction are seldom quantified. Similarly, improvements in convergence stability are rarely compared across different algorithms. Moreover, the efficiency of MOAs is highly sensitive to hyperparameters such as population size, inertia weight, and crossover/mutation rates. While large populations and more iterations may enhance robustness, they also increase computational cost and introduce cycle-time unpredictability. Conversely, smaller configurations improve real-time feasibility but risk premature convergence and degraded accuracy. These trade-offs—between speed, error performance, and computational burden—remain insufficiently quantified, making it difficult to establish fair benchmarks for algorithm suitability across different operating conditions.

The simple setting reference for the robust parameters of MOAs is shown in

Table 4. Reference for Robust Parameter Settings of Metaheuristic Algorithms.

Category	Common Ranges or Strategies	Key Notes and Considerations
Population Size (N)	Small-scale: 20–50 Medium-scale: 50–100 Large-scale: 100–200+	Population size affects exploration ability. Larger sizes enhance global search but increase cost [135].
Iterations (T)	Typical range: 500–5000+ T = (Max function evaluations FEₘₐₓ)/(N)	Jointly determined with population size. In CEC2017 benchmarks, FEₘₐₓ = 10,000 × dimension.
Adaptive Mechanisms	Dynamically adjust parameters	Enhances robustness, reduces manual tuning [136].
Termination Criteria	Max iterations or evaluations Stagnation threshold Target solution quality	Often combined. Stagnation-based thresholds avoid wasted computation [135].
Algorithm-Specific Parameters	GA: Crossover rate Pc = 0.6–0.9, Mutation rate Pm = 0.001–0.1 PSO: Inertia weight ω = 0.4–0.9, Cognitive factor c1 = c2 = 1.5–2.0 SA: Initial temperature T0, Cooling rate α = 0.8–0.99	Each algorithm has unique core parameters [137,138,139]. Strong impact on performance, usually tuned experimentally or via auto-configuration.

.

In terms of multi-objective and constraint-handling capability, MOAs are well-suited for non-convex, multi-peak, and multi-objective problems. By employing fitness functions and multi-objective operators, MOAs can explore the multi-dimensional objective space in parallel. This approach avoids priority conflicts that typically arise from linear weighting of objectives. The combination of various MOA operators with hierarchical multi-objective processing offers significant advantages. It can satisfy strict requirements, such as hard constraints. It also addresses high-priority objectives under scenarios with demanding real-time performance. Some studies further incorporate convex-theory tools, such as LMI or convex feasible sets, as a priori constraints. These guide the MOAs search to feasible subdomains, ensuring system stability and engineering applicability [132].

However, several challenges remain. If all objectives and constraints are collapsed into a single scalar fitness, the algorithms become highly sensitive to the chosen weight parameters. This can lead to suboptimal performance or biased solutions. Furthermore, maintaining an accurate Pareto front within extremely short control cycles imposes a significant computational burden. In practice, there is a trade-off between achieving a high-quality Pareto front, minimizing computational cost, and ensuring real-time feasibility. Quantitative evaluation of these trade-offs—such as convergence speed, solution diversity, and computation time—remains limited in existing studies, which makes it difficult to determine the most effective MOA configuration for online motor control applications.

Against this background, hybrid dual-optimization strategies that combine convex optimization with MOAs have gradually attracted attention. Typically, these hybrid strategies operate in two steps. First, convex optimization methods (e.g., LMI solving, μ-synthesis, or quadratic programming relaxation) are used to generate initial solutions. These solutions define parameter regions that satisfy stability and constraint requirements. Second, MOAs operators (e.g., PSO, DE, or GA) perform global search or local improvement to further refine solutions [133,134].

This dual-stage approach leverages the fast convergence of convex optimization and the global search capability of metaheuristics. It effectively narrows the search space and enhances system disturbance rejection. However, its performance comes with trade-offs. The initial convex optimization step may limit solution diversity, while the MOAs stage can introduce additional computational cost and latency, especially for large population sizes or high-dimensional systems. Moreover, the overall convergence speed and the quality of final solutions are sensitive to hyperparameters such as population size, iteration number, and crossover/mutation rates, which can vary significantly across different motor operating conditions. Quantifying these trade-offs, for instance in terms of iteration time versus RMSE reduction or constraint violation rate, is necessary to fully assess the practical benefits of hybrid dual-optimization strategies.

The advantages of this hybrid strategy are threefold. First, the convex optimization phase reduces the search space to feasible regions, thereby minimizing the blind exploration of the metaheuristic. Second, the global optimization stage prevents entrapment in local minima or non-convex regions, a limitation often observed in purely gradient-based methods. Third, the hybrid design can be integrated with event-triggered mechanisms, so the metaheuristic is activated only when required by performance indicators, which enables dynamic allocation and reduces unnecessary computational cost.

However, a deeper examination reveals several challenges. The computation flow of hybrid algorithms becomes more complex, typically involving multiple optimization stages, which makes cycle predictability difficult. Moreover, while metaheuristics such as PSO, DE, or GA improve robustness, their hyperparameter tuning (e.g., population size, mutation rate, crossover rate) directly influences convergence speed and error reduction. For instance, PSO generally converges faster but is prone to premature stagnation, DE achieves lower RMSE but at the cost of longer iterations, and GA offers flexibility yet introduces heavy computational overhead. These trade-offs are often described only in qualitative terms. They are rarely quantified by metrics such as convergence time, error reduction, or computational load. As a result, it is difficult to make a fair comparison of algorithm suitability.

To mitigate these limitations, event-triggered and adaptive restart mechanisms have been proposed [135,136]. Specifically, metaheuristic search is activated only when system performance indicators exceed preset thresholds. The triggering conditions are dynamically adjusted according to disturbance characteristics. Full-power computation is executed only under severe disturbances. During nominal conditions, the algorithm maintains lightweight operation. This design helps preserve the global search advantage of MOAs while reducing average computational load. Nevertheless, unresolved issues remain regarding cycle-time predictability, reliability, and error performance under extreme disturbances, highlighting the need for more systematic and quantitative evaluation of these hybrid approaches.

In summary, research on MPC optimization for motor drives has evolved from a “single lightweight” approach to an “intelligent adaptive plus parallel-coordinated” framework. The algorithmic complexity of MOAs and the challenges of embedded parallelization cannot be overlooked. Future MPC optimization algorithms can focus on several directions. On one hand, data-driven and online learning techniques could be integrated to identify system nonlinearities in real time using neural networks or manifold learning, enabling adaptive tuning of algorithm parameters. On the other hand, resource-aware, multi-metric event-triggered mechanisms could be developed to optimize algorithm execution timing based on tracking errors, energy consumption, temperature rise, and hardware utilization. Meanwhile, MPC could be integrated with system-level optimizations, including energy management, fault diagnosis, and power electronics control, to establish a joint scheduling framework targeting multiple objectives such as efficiency, lifetime, and reliability. By advancing these technical pathways collaboratively, future motor drive MPC is expected to achieve a new level of real-time performance, robustness, scalability, and safety, offering more efficient and reliable solutions for high-performance control applications in electric vehicles, industrial automation, and rail transit.

4. Conclusions

This paper systematically reviews the application status and research advances of MOAs in three critical aspects of MPC for modern motor drive systems: dynamic model identification, parameter adaptation, and optimization solution. In dynamic model establishment, MOAs significantly enhance the identification accuracy of white-box, gray-box, and black-box models through synergistic global-local search, overcoming the limitations of traditional least squares or gradient methods, which are susceptible to local optima. However, convergence delays under high sampling frequencies and embedded resource constraints necessitate further optimization via lightweight operators or online adaptive hyperparameter strategies.

For MPC parameter adaptation, offline MOAs, hybrid swarm-convex methods, and multi-objective Pareto techniques collectively deliver balanced solutions for tuning control/prediction horizons and cost weights. Concurrently, online strategies (event-triggered, reinforcement learning, clustering-assisted) enable real-time adjustment, enhancing robustness against disturbances and model drift, though challenges remain in trigger thresholds, computational overhead, and clustering generalization.

Regarding MPC optimization, solution strategies balance computational cost, optimality, and latency. Fast gradient methods and operator splitting offer low overhead via fixed-size matrix-vector operations. Explicit/semi-explicit MPC achieves microsecond latency using offline partitioning and lookup. Hybrid MOAs-convex solvers ensure feasibility by first solving a convex region, then using metaheuristics to escape local optima. Event-triggered and adaptive restart mechanisms further reduce computational burden on embedded platforms.

To address the urgent demands of modern motor drive systems for high precision, robustness, and real-time performance, and building on the proposed MOAs-MPC integrated framework, future research should focus on the following four specific directions to advance technology deployment and tackle practical engineering challenges:

1.

Lightweight Swarm Intelligence Operators and Hierarchical Optimization Strategies: Breakthroughs in computational efficiency for embedded platforms

Given the constraints of limited computational resources (e.g., processing power and memory) in embedded systems (e.g., DSPs/FPGAs), future work should develop lightweight MOA operators and adopt hierarchical global-local optimization strategies to reduce search overhead. Key approaches include:

• Operator Simplification: Designing adaptive MOAs variants (e.g., “adaptive PSO” with dynamically adjusted inertia weights and crossover probabilities) or incorporating “pruning mechanisms” (e.g., early termination of ineffective particle searches) to reduce per-iteration computation while preserving global exploration capabilities.
• Hierarchical Optimization: Decomposing the optimization process into “global coarse-tuning” and “local fine-tuning” stages. The global stage uses low-complexity MOAs (e.g., simplified PSO) to rapidly locate feasible solution regions, while the local stage employs gradient-based methods (e.g., fast gradient descent in MPC) for precise adjustments, balancing search efficiency and solution quality.
• Hardware Adaptation: Optimizing the parallel computing architecture of MOAs (e.g., grouped parallel evaluation of particles) to align with edge computing hardware (e.g., low-power DSPs, specialized AI chips), enabling online optimization within 100 μs time windows to meet the high-frequency control requirements of motors (e.g., switching frequencies above 10 kHz).

2.

Online Hyperparameter Adaptation: Data-driven dynamic tuning and robustness enhancement

To address uncertainties such as load disturbances and time-varying parameters (e.g., stator resistance changes with temperature), future research should investigate online hyperparameter adaptation mechanisms to dynamically optimize MPC parameters (e.g., prediction horizons, weight matrices). Specific pathways include:

• Meta-Learning-Driven Parameter Tuning: Training meta-learning models (e.g., MAML) on historical operational data (e.g., optimal prediction horizons and weight configurations under different loads) to enable rapid adaptation to new operating conditions, mitigating the lag of offline tuning.
• Bayesian Optimization for Online Tuning: Treating MPC performance (e.g., tracking error, switching losses) as the objective function, gaussian process regression models can map parameter-performance relationships to online select optimal parameter combinations, balancing exploration and exploitation.
• Reinforcement Learning for Robustness: Designing reinforcement learning agents with hyperparameter adjustments as the action space and “minimizing long-term control costs” as the reward function to online learn robust parameter configurations adaptable to extreme disturbances (e.g., ±20% load abrupt changes).

3.

Dynamic Multi-Objective Strategies: Online weight reconstruction and rapid pareto frontier updates

Motor drive systems often involve dynamic multi-objectives (e.g., maximizing efficiency, improving torque precision, accelerating response) that evolve with operating conditions (e.g., transitioning from steady-state to rapid acceleration). Future work should develop dynamic multi-objective optimization strategies for online weight reconstruction and rapid Pareto frontier updates. Key methods include:

• Operating Condition-Aware Weight Adjustment: Using real-time monitoring of load torque, speed fluctuations, and other features, fuzzy rules or neural networks can dynamically allocate objective weights (e.g., prioritizing response speed during acceleration, efficiency at steady-state).
• Rapid Pareto Frontier Updates: Adopting incremental multi-objective optimization algorithms (e.g., dynamic MOEA/D) allows retaining only current non-dominated solutions, thereby reducing Pareto update time from seconds to milliseconds.
• Disturbance-Integrated Decision-Making: Incorporating load disturbance predictions into multi-objective optimization to generate “disturbance-resilient” pareto frontiers, ensuring control strategies remain optimal during disturbances.

4.

Objective-Structure-Guided Optimization: Intelligent search scope limitation based on problem characteristics

Given the strong nonlinearity and complex constraints (e.g., current limits, voltage saturation) in motor control, future research should explore objective-structure-guided search strategies to narrow optimization scopes and reduce ineffective computations via problem feature analysis. Specific approaches include:

• Feature-Driven Search Space Reduction: Online identification of key motor parameters (e.g., inductance, flux linkage) and combining them with control objectives (e.g., torque tracking) to dynamically define feasible regions for optimization variables (e.g., limiting inductance variations to ±10%), avoiding unstructured global searches.
• Structure-Adaptive MOAs Design: Automatically selecting MOA types based on problem structure (e.g., continuous/discrete control variables, convex/non-convex objectives)—e.g., improved PSO for continuous variables, ant colony optimization (ACO) for discrete voltage vector selection, and simulated annealing (SA) for non-convex objectives to enhance global escape.
• Constraint-Aware Heuristic Search: Translating hard constraints (e.g., current limits) into penalty functions or boundary constraints, and combining them with MOA heuristic rules (e.g., particle “obstacle avoidance”), can guide the search toward feasible regions and improve optimization efficiency.

Advancing hardware, online learning, and MOAs’ operators will enable MPC for motor drives to achieve breakthroughs in high-precision, robustness, and real-time performance under demanding conditions, benefiting applications like EVs, industrial robots, and aerospace propulsion.