Numerical Modeling of Potential CO2-Fed Enhanced Geothermal System (CO2-EGS) in the Gorzów Block, Poland
Abstract
1. Introduction
2. Materials and Methods
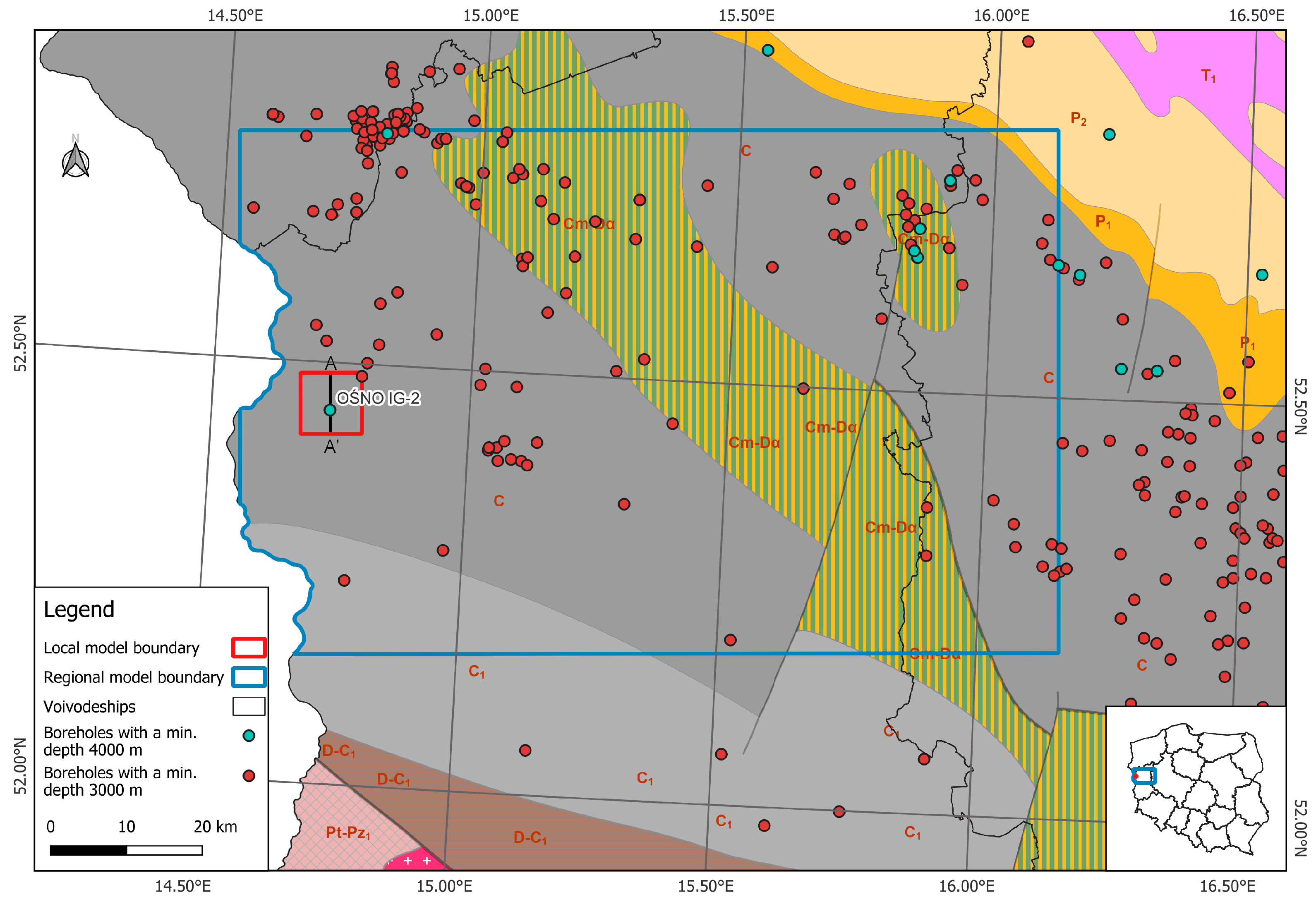
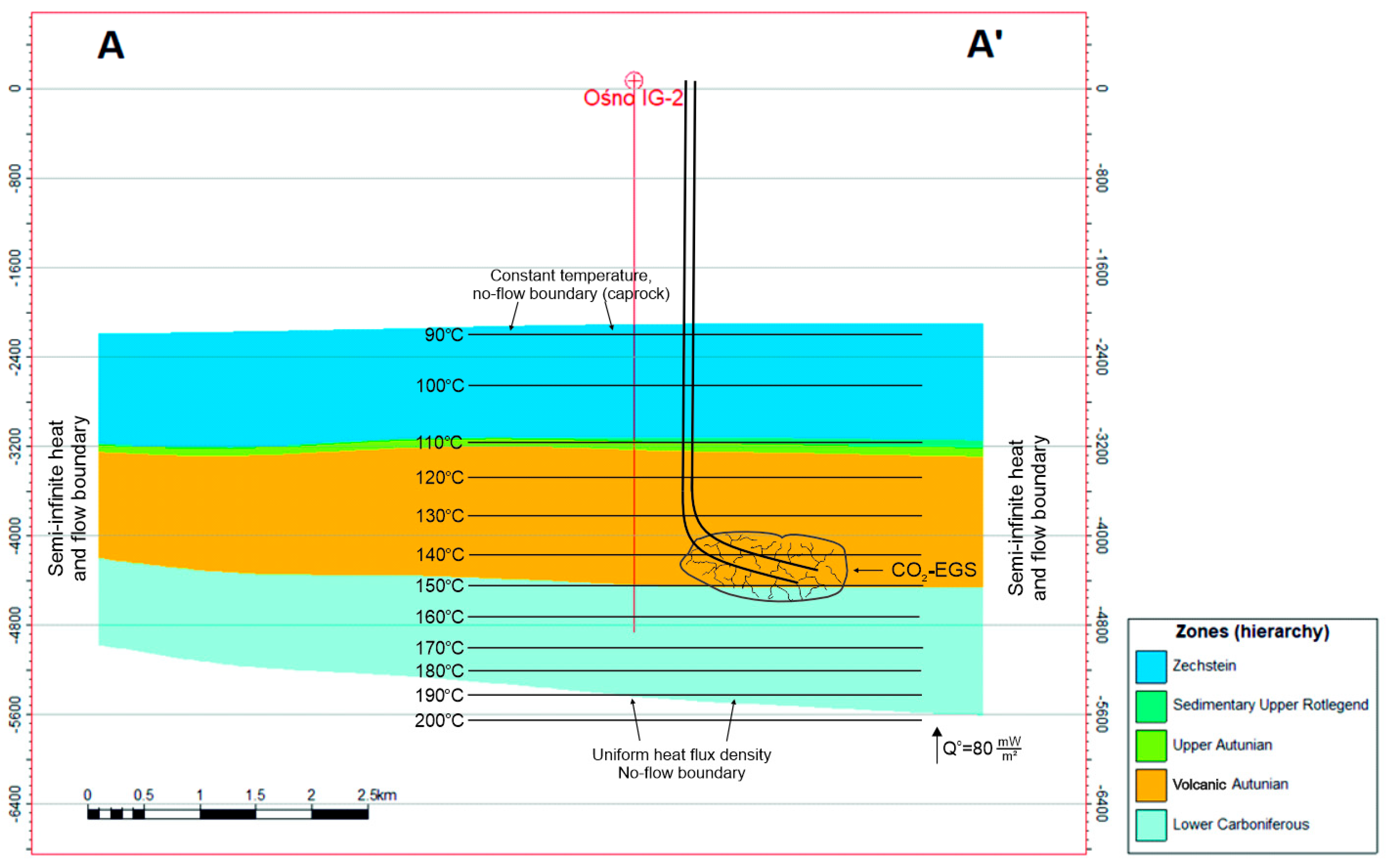
2.1. Geological Setting and the Conceptual Model of the Gorzów Block
2.2. Model Workflow
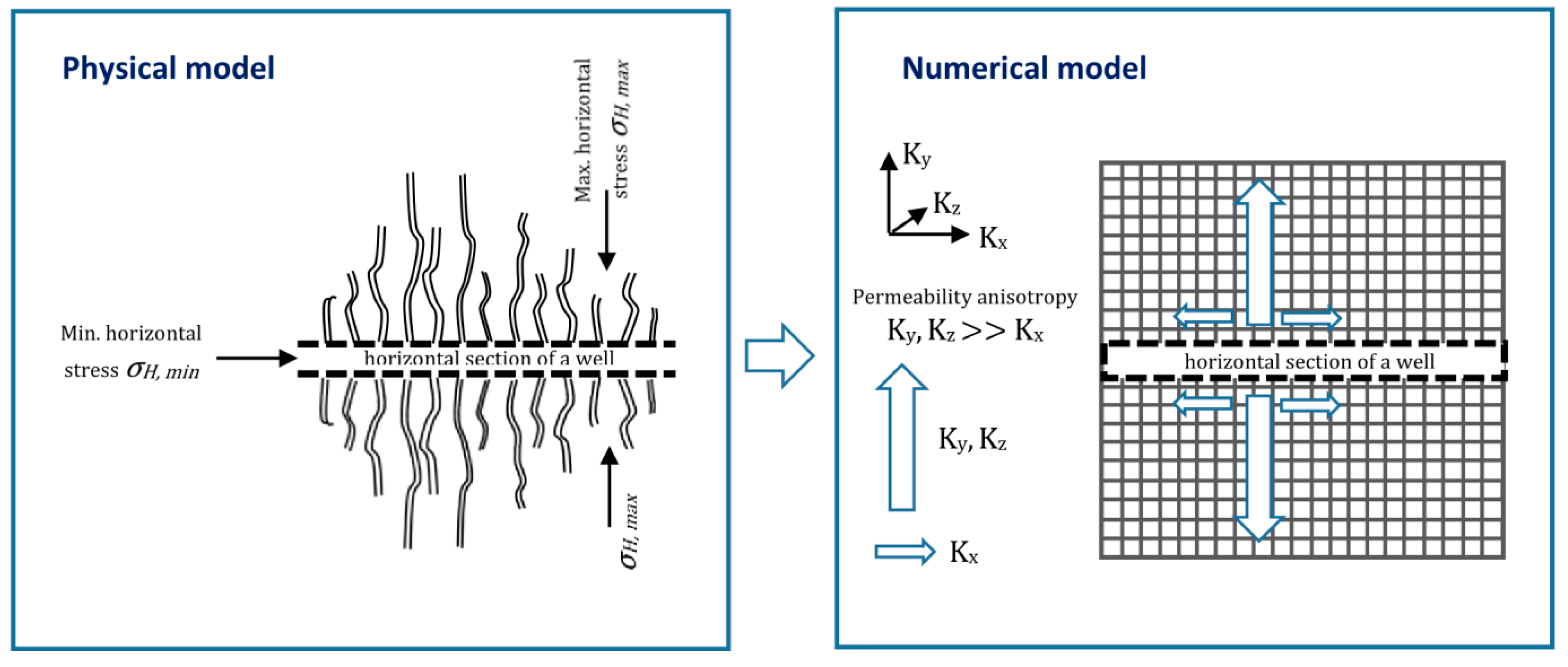
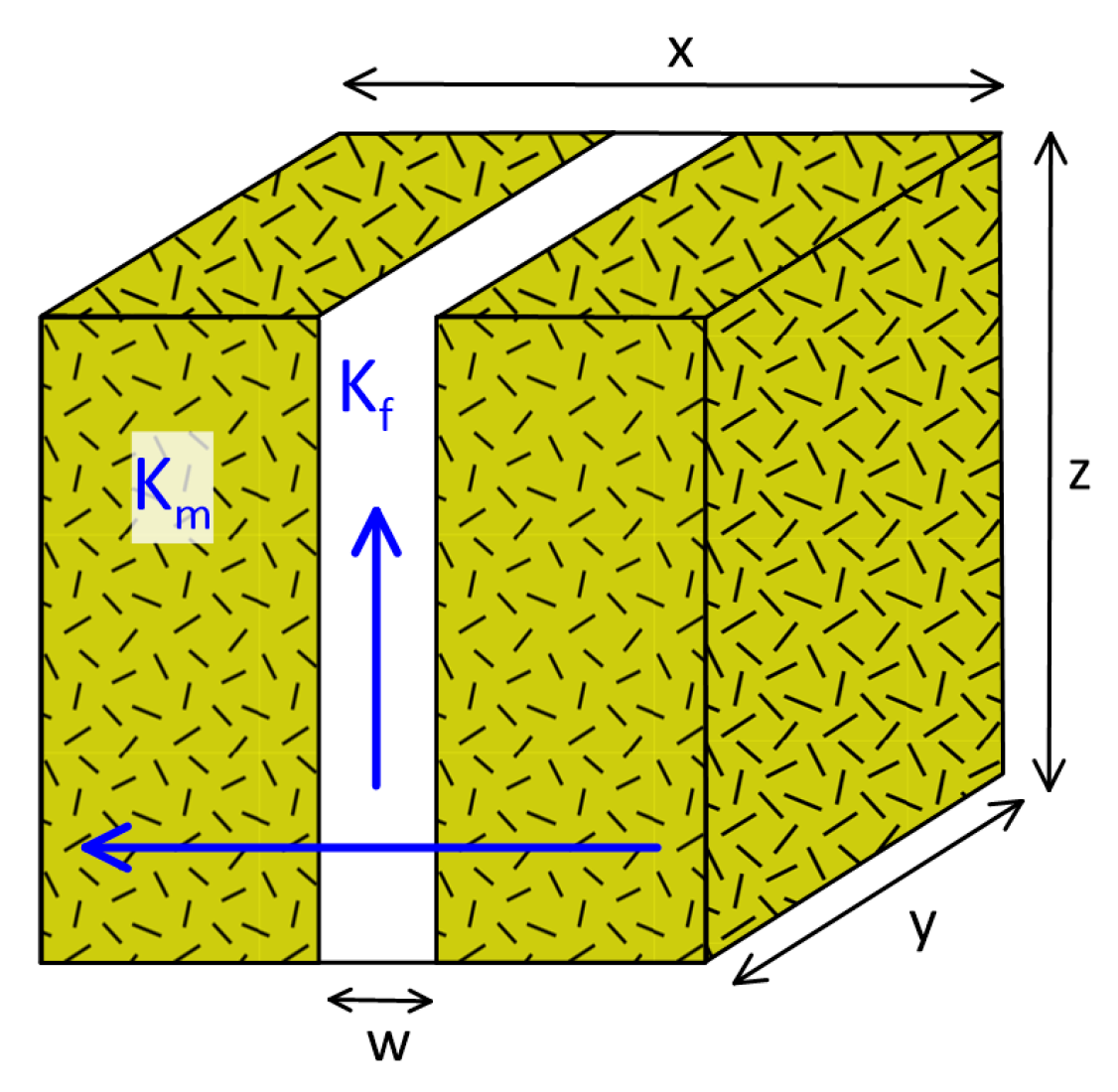
2.3. Model Setup
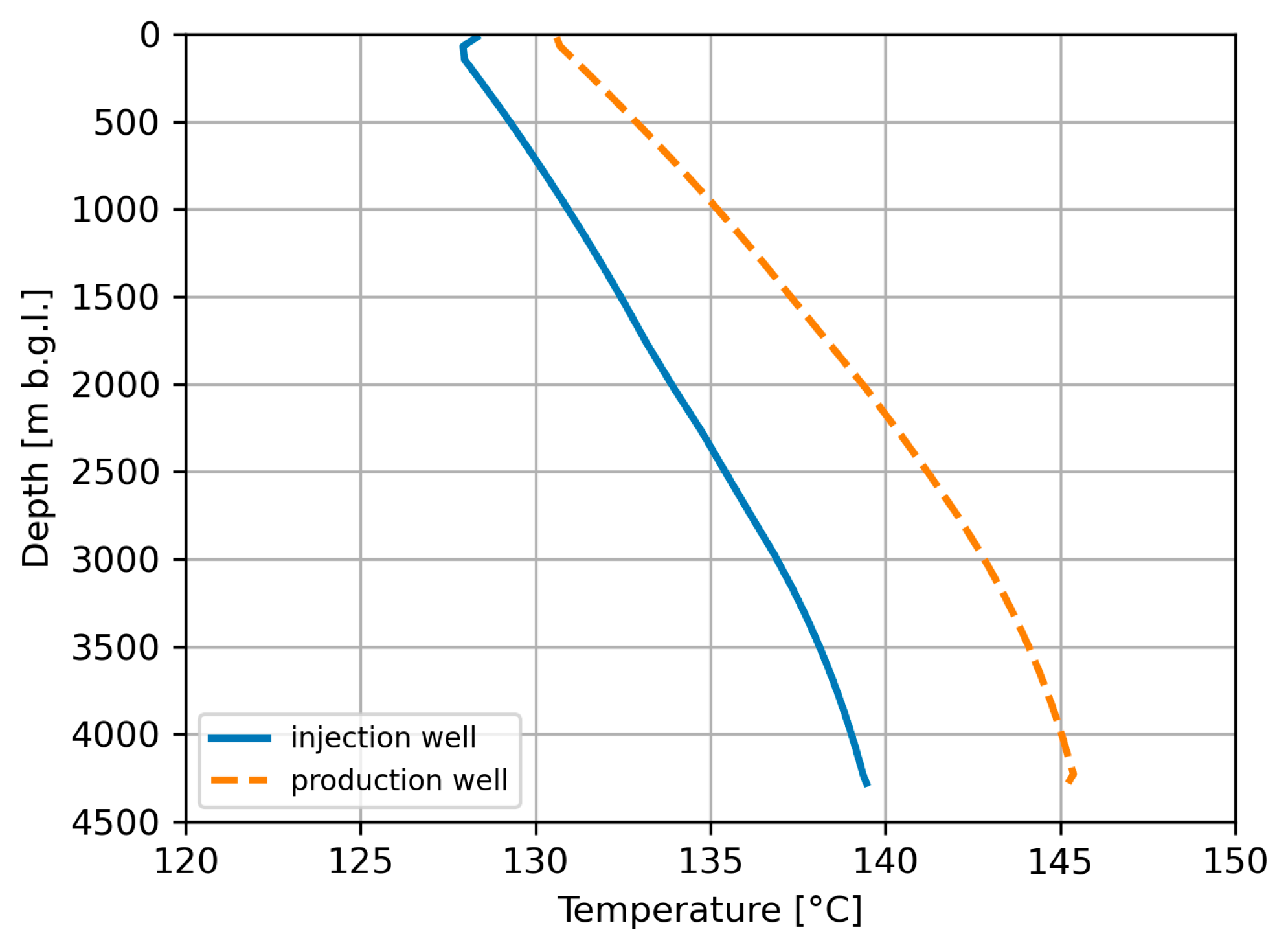
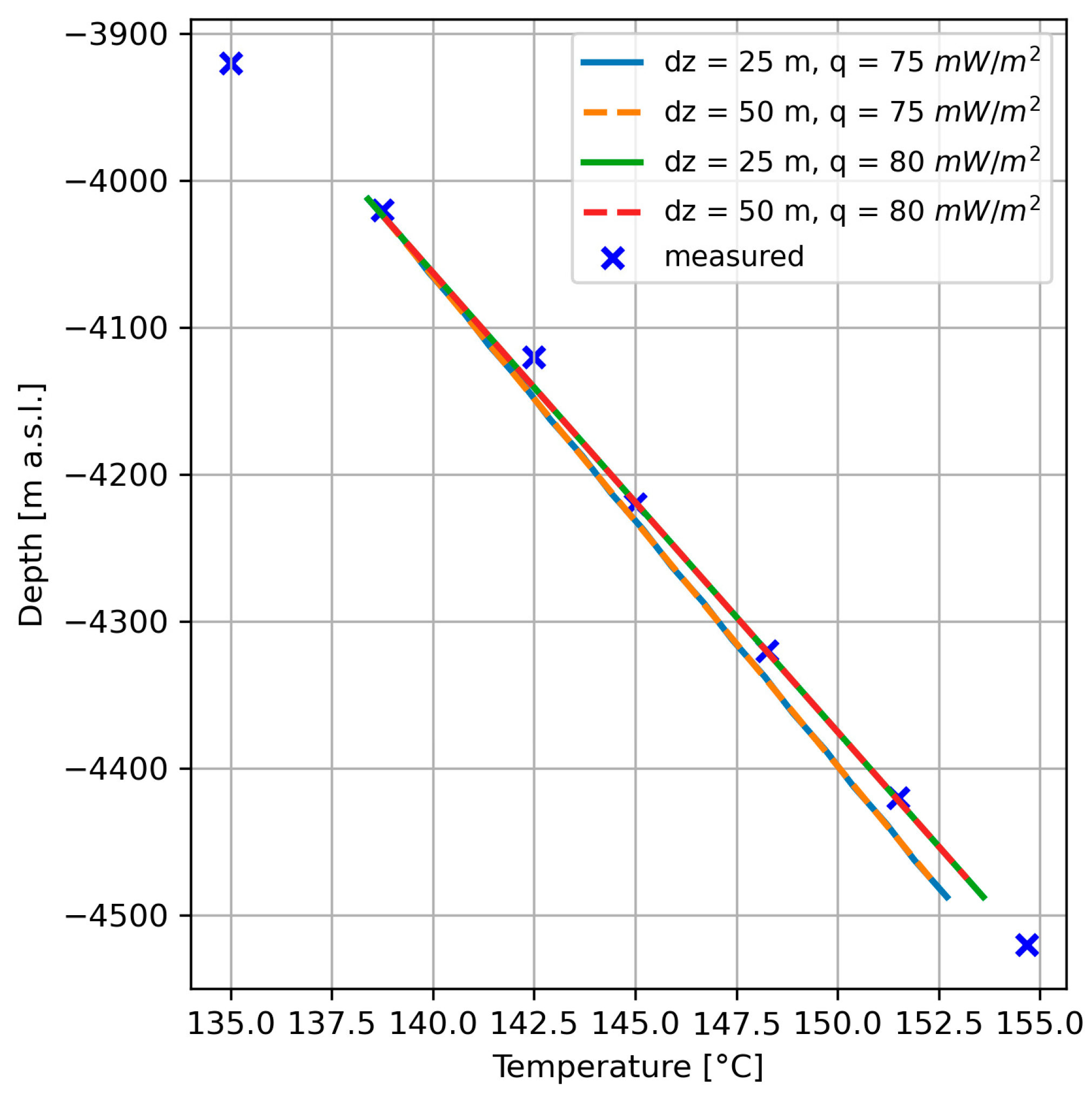
2.3.1. Temperature Calibration of Natural State
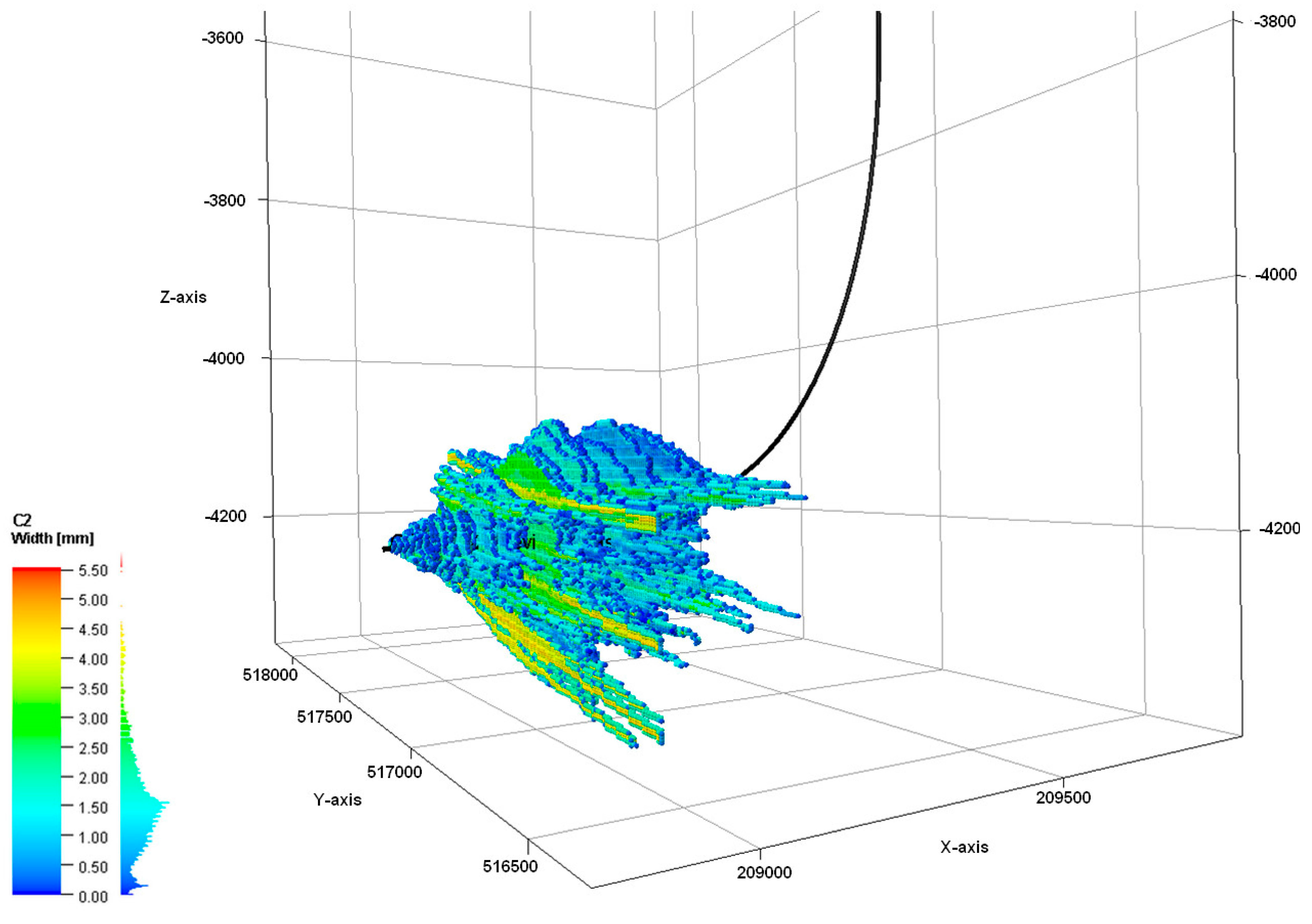
2.3.2. Phase 0—Fracturing the Target Interval
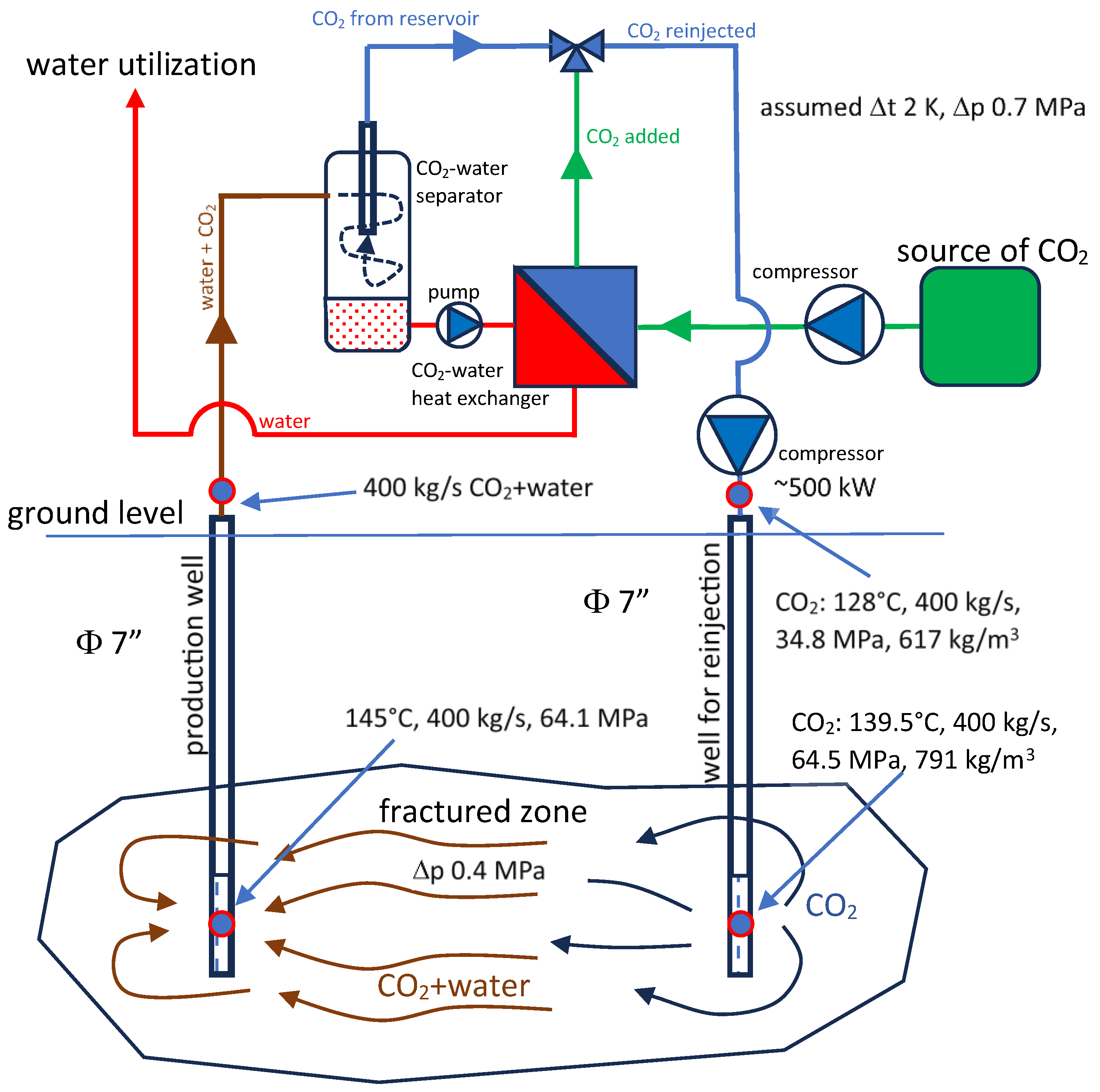
2.4. Phase 1—Saturation of the Fractured Zone with CO2
2.5. Phase 2—Continous Operation of CO2-EGS
3. Results
- Average flow rate in the production well:
- Production-to-injection flow rate ratio:
- Total CO2 injected:
- Total CO2 extracted:
- Total CO2 stored:
- Cumulative CO2 storage ratio:
4. Discussion
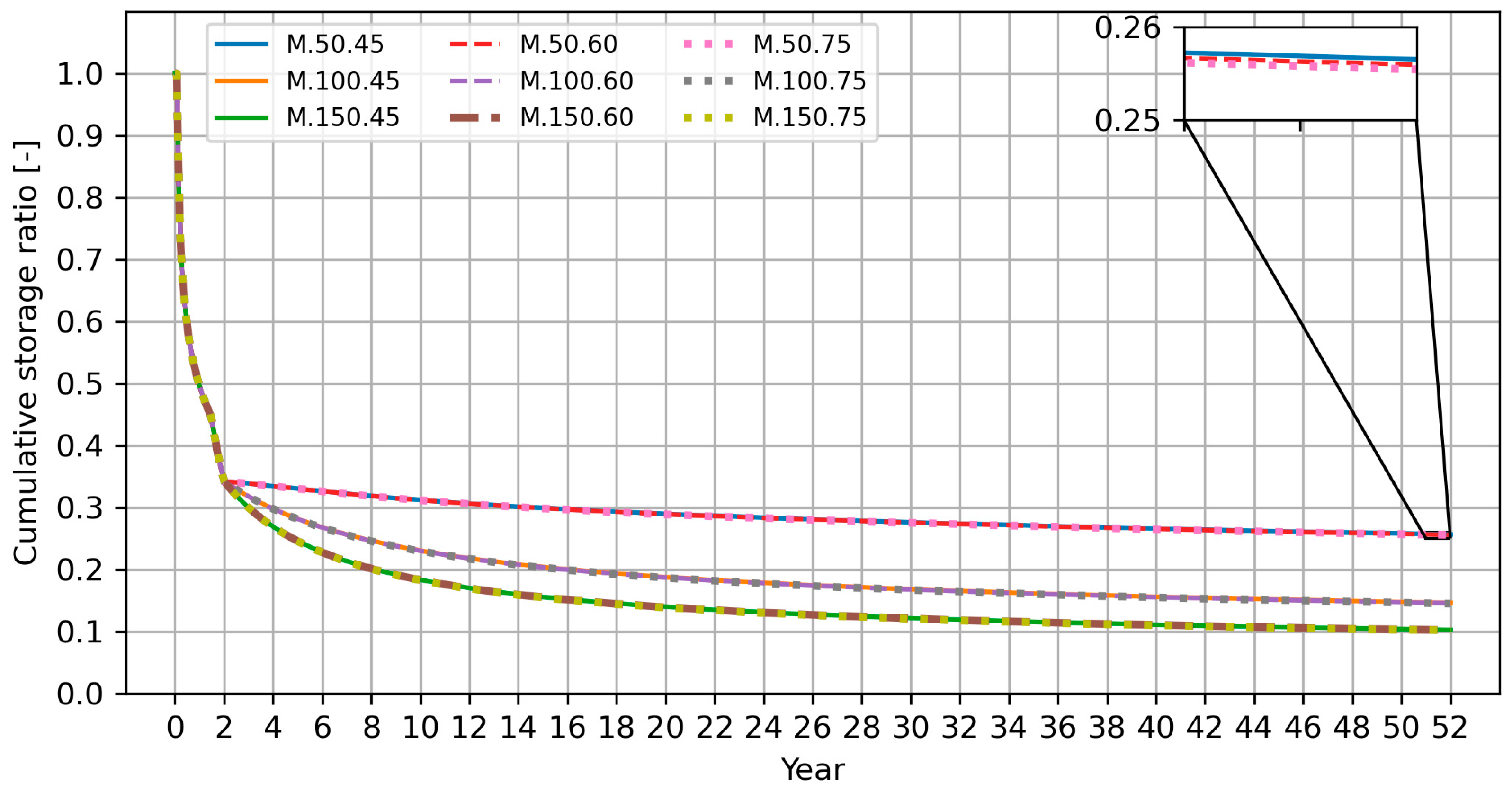
- The cumulative CO2 storage ratio is the ratio of the total mass of CO2 permanently stored in the formation to the total mass of CO2 injected over a period of time. This ratio appeared to be inversely proportional to the injection rate of CO2.
- The production to injection ratio is the greater, the higher the mass flow rate of injected CO2. This is due to the fact that a higher injection flow rate prevents the rapid release of pressure from the fractured zone into the host rock, and thus allows preserving a relatively high flow between the injection and production wells, while maintaining the pressure above the threshold of 64 MPa, below which fractures may close.
- In order for CO2 to become the only component flowing into the production well within a reasonable time period, it must be injected with a sufficiently high intensity. The simulation results indicate that there is a certain breakthrough point below which flow such an effect may never be achieved because it will not be possible to completely displace the water remaining after fracturing the rocks.
- 4.
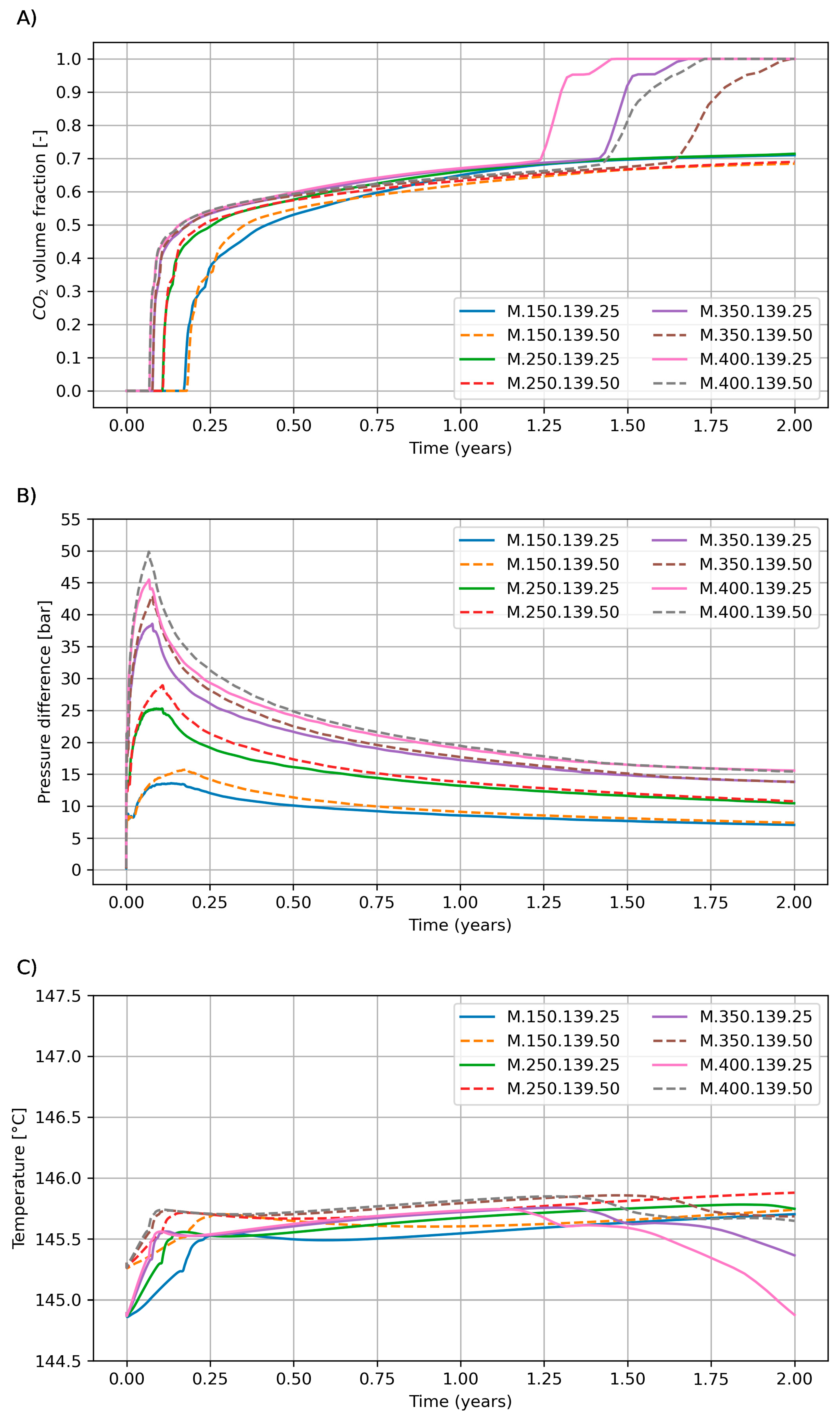
- The injection rate has a greater impact on the production temperature than the injection temperature, if we consider reasonable limits for both of these parameters.
- 5.
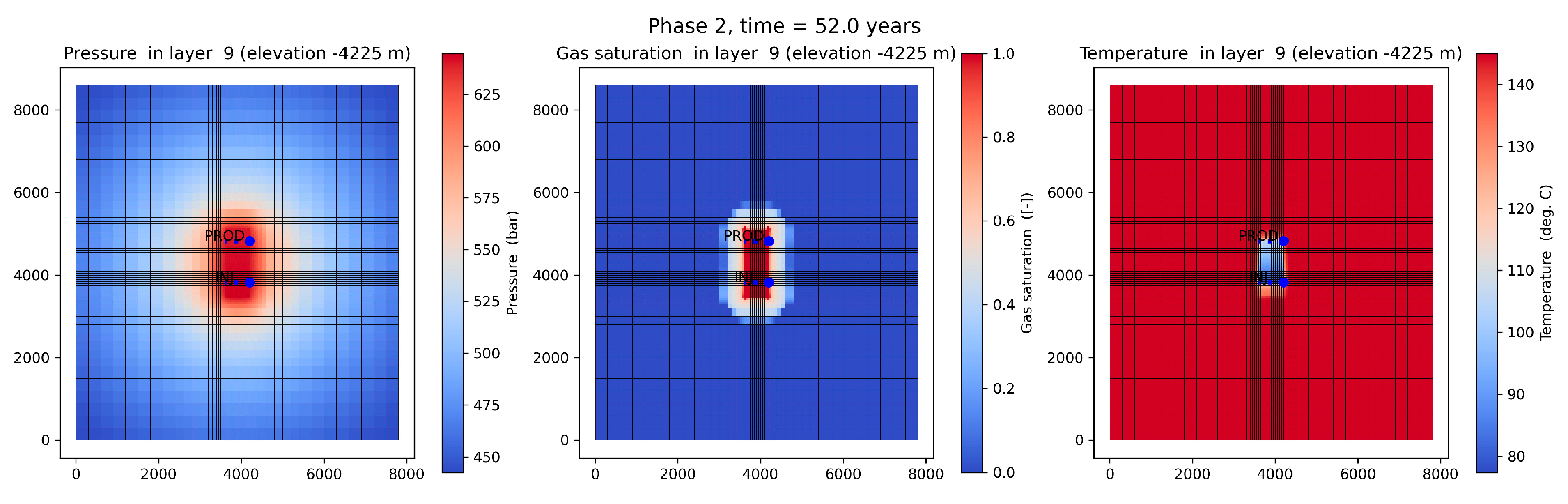
- In the Gorzów Block case, the cold front approaches the production well after 10 years in the worst case (models M.150.X) and after approx. 30 years in the best-case scenario (models M.50.X; Figure 12, where X is the injection temperature in °C at the injection depth).
- 6.
- After achieving 100% saturation of the fractured zone with CO2, most of the injected CO2 during phase 2 will be extracted, not stored, assuming very low permeability of rocks outside of the fractured volume. As can be seen in Table 5, the ratio of CO2 extracted to injected, considering phase 2 only, is increasing with the increasing injection rate, from 77% for the injection rate of 50 kg/s up to 92% for the injection rate of 150 kg/s. Therefore, the CO2 storage process in EGS-like formations, after reaching the initial saturation, becomes much less efficient in phase 2 and is decreasing with increasing injection rate.
- 7.
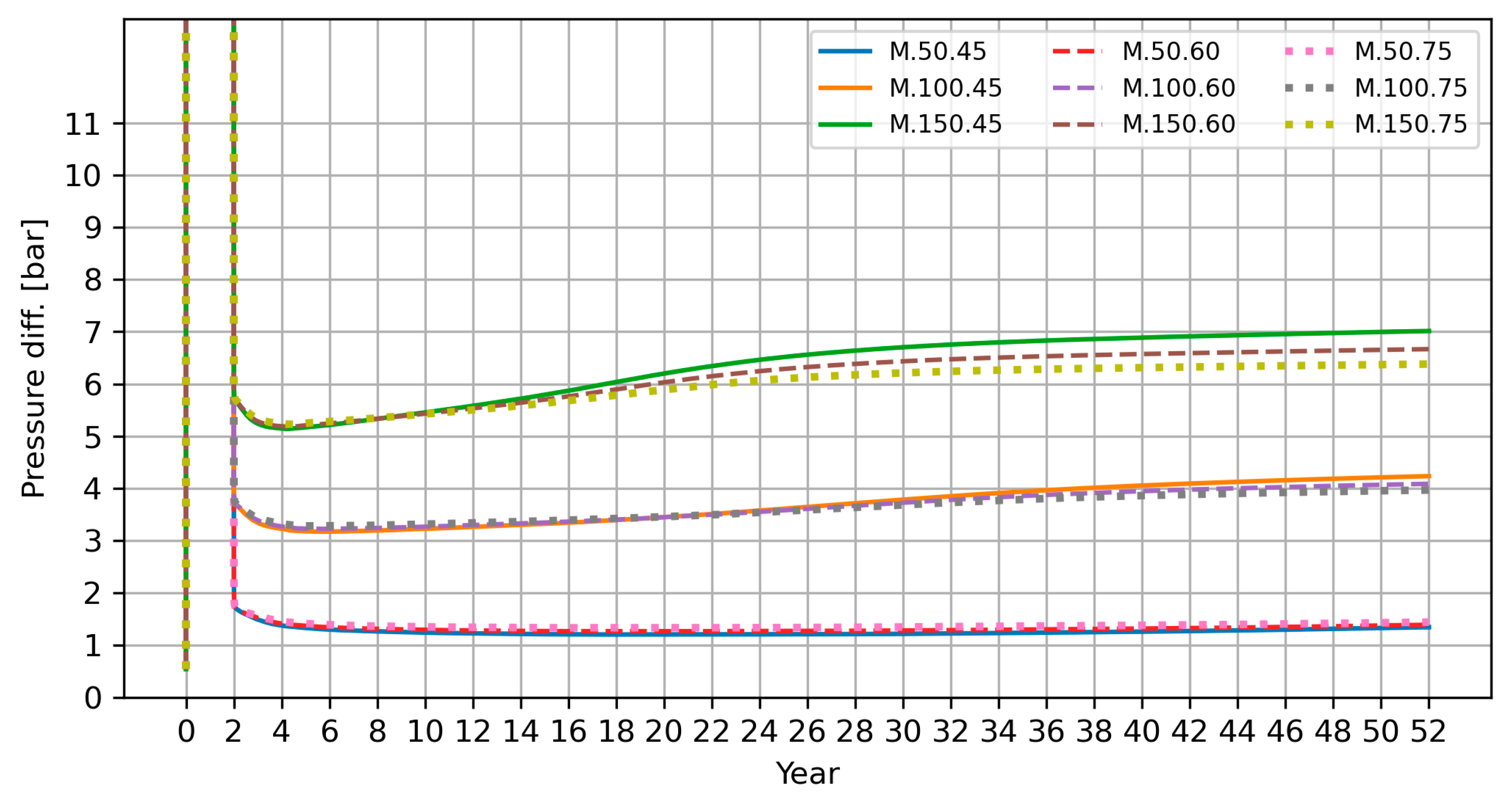
- The pressure difference between the injection and production wells is highly sensitive to the injection rate and depends only to a small extent on the injection temperature (Figure 13). In all cases, the pressure difference is slightly increasing with time as a result of increasing injection pressure (reservoir pressure around the production well is set to a fixed value of 64 MPa in this study).
- 8.
- The cumulative CO2 storage ratio after 52 years, considering phases 1 and 2 combined, is highly dependent on the injection rate, but completely independent of the injection temperature. It declines with time for all cases, as proven on Figure 14.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| b.s.l. | Below sea level |
| CCS | Carbon capture and storage |
| CO2-EGS | CO2-fed enhanced geothermal system |
| EGS | Enhanced geothermal system |
| EOR | Enhanced oil recovery |
| EOS | Equation of state |
| GCS | Geological carbon storage |
| HDR | Hot dry rock |
| JT | Joule–Thompson effect |
| kt | 1000 tons |
| MD | Measured depth |
| Mt | 1,000,000 tons |
| sCO2 | Supercritical carbon dioxide |
| TVD | True vertical depth |
Appendix A. Determination of the Parameters of the Injected CO2 in Phase 1
- qfr—Unit heat flux exchanged between the fluid and the rock mass [W/m].
- λ—Rock thermal conductivity [W/(m∙K)].
- tf—Fluid temperature [K].
- t∞—Temperature of the rock mass in natural conditions or at a distance outside the zone of thermal impact of the borehole [K].
- c—Rock specific heat [J/(kg∙K)].
- ρ—Rock density [kg/m3].
- τ—Time for which the qfr value is determined [s]. The model assumes one year of continuous well exploitation.
- rw—Well radius.
- γ—Euler’s gamma function.
- Δp—Flow resistance [Pa].
- φ—Pipe roughness coefficient, which usually takes the following values:
- 1—for smooth and new pipes made of brass, copper, lead,
- 1.1—for steel and cast-iron pipes, new,
- 1.56—for cast iron and riveted steel,
- 1.78—for old steel pipes (this value was assumed in the model as typical for boreholes),
- 2.22—for old riveted steel pipes.
- σ—Coefficient of linear resistances.
- Re—Reynolds number .
- —Mass flow rate [kg/s].
- π—Pi number [-].
- d—Well’s inner diameter [m].
- μ—Dynamic viscosity coefficient [Pa∙s].
- w—Fluid velocity [m/s].
- ρ—Fluid density [kg/m3].
- L—Length of the section where the fluid flow occurs [m].
- Δt(n)JT—Temperature drop in n-th zone caused by the Joule–Thomson effect [K].
- h(n − 1)—Specific enthalpy of CO2 in n − 1 zone [J/kg].
- p(n)—Pressure in n-th zone after subtracting the dynamic pressure () flow resistance [Pa].
- t(n)m—Mean temperature of CO2 in n-th zone [K].
- t[h(n − 1),p(n)]—Temperature of CO2 corresponding to the enthalpy of CO2 in the n − 1 zone under pressure in n-th zone, after subtracting the dynamic pressure and flow resistance [K].
References
- Wetzel, M.; Otto, C.; Chen, M.; Masum, S.; Thomas, H.; Urych, T.; Bezak, B.; Kempka, T. Hydromechanical Impacts of CO2 Storage in Coal Seams of the Upper Silesian Coal Basin (Poland). Energies 2023, 16, 3279. [Google Scholar] [CrossRef]
- Gładysz, P.; Pająk, L.; Andresen, T.; Strojny, M.; Sowiżdżał, A. Process Modeling and Optimization of Supercritical Carbon Dioxide-Enhanced Geothermal Systems in Poland. Energies 2024, 17, 3769. [Google Scholar] [CrossRef]
- Song, Y.; Jun, S.; Na, K.; Kim, K.; Jang, Y.; Wang, J. Geomechanical challenges during geological CO2 storage: A review. Chem. Eng. J. 2023, 456, 140968. [Google Scholar] [CrossRef]
- Brown, D. A hot dry rock geothermal energy concept utilizing supercritical CO2 instead of water. In Proceedings of the Twenty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 24–26 January 2000; pp. 233–238. [Google Scholar]
- Pruess, K. On production behavior of enhanced geothermal systems with CO2 as working fluid. Energy Convers. Manag. 2008, 49, 1446–1454. [Google Scholar] [CrossRef]
- Avanti Isaka, B.L.; Ranjith, P.G.; Rathnaweera, T.D. The use of super-critical carbon dioxide as the working fluid in enhances geothermal systems (EGSs): A review study. Sustain. Energy Technol. Assess. 2019, 36, 100547. [Google Scholar] [CrossRef]
- Wu, Y.; Li, P. The potential of coupled carbon storage and geothermal extraction in a CO2-enhanced geothermal system: A review. Geotherm. Energy 2020, 8, 19. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, P.; Xu, R. System thermodynamic performance comparison of CO2-EGS and water-EGS systems. Appl. Therm. Eng. 2013, 61, 236–244. [Google Scholar] [CrossRef]
- Zhao, W.; Yuan, Y.; Jing, T.; Zhong, C.; Wei, S.; Yin, Y.; Zhao, D.; Yuan, H.; Zheng, J.; Wang, S. Heat Production Performance from an Enhanced Geothermal System (EGS) Using CO2 as the Working Fluid. Energies 2023, 16, 7202. [Google Scholar] [CrossRef]
- Potter, R.; Robinson, E.; Smith, M. Method of Extracting Heat from Dry Geothermal Reservoirs. US Patent No. 3,786,858, 22 January 1974. [Google Scholar]
- Breede, K.; Dzebisashvili, K.; Liu, X.; Falcone, G. A systematic review of enhanced (or engineered) geothermal systems: Past, present and future. Geotherm. Energy 2013, 1, 4. [Google Scholar] [CrossRef]
- Huang, G.; Hu, X.; Ma, H.; Liu, L.; Yang, J.; Zhou, W.; Liao, W.; Ningbo, B. Optimized geothermal energy extraction from hot dry rocks using a horizontal well with different exploitation schemes. Geotherm. Energy 2024, 11, 5. [Google Scholar] [CrossRef]
- Duchane, D. The history of HDR research and development. In Proceedings of the Draft Proceedings of the 4th International HDR Forum, Strasbourg, France, 28–30 September 1998. [Google Scholar]
- Bujakowski, W.; Barbacki, A.; Skrzypczak, R. New directions of research in the Polish part of the Sudetic area in the aspect of HDR and EGS technologies. Przegl. Geol. 2013, 61, 706–711. [Google Scholar]
- Busby, J.; Terrington, R. Assessment of the resource base for engineered geothermal systems in Great Britain. Geotherm. Energy 2017, 5, 7. [Google Scholar] [CrossRef]
- Hori, Y.; Kitano, K.; Kaieda, H.; Kiho, K. Present status of the Ogachi HDR project, Japan, and future plans. Geothermics 1999, 28, 637–645. [Google Scholar] [CrossRef]
- Kitano, K.; Hori, Y.; Kaieda, H. Outrline of the Ogachi HDR Project and character of the reservoirs. In Proceedings of the World Geothermal Congress 2000, Tohoku, Japan, 28 May–10 June 2010. [Google Scholar]
- Ueda, A.; Yamada, T.; Yajima, T.; Sugiyama, K.; Odashima, Y.; Ito, H.; Todaka, N.; Sato, T.; Ohsumi, S.; Mito, S.; et al. CO2 sequestration into hydrothermal system at Ogachi HDR site. Jpn. Mag. Mineral. Petrol. Sci. 2009, 38, 220–231. [Google Scholar] [CrossRef]
- Sowiżdżał, A.; Starczewska, M.; Papiernik, B. Future Technology Mix—Enhanced Geothermal System (EGS) and Carbon Capture, Utilization, and Storage (CCUS)—An Overview of Selected Projects as an Example for Future Investments in Poland. Energies 2022, 15, 3505. [Google Scholar] [CrossRef]
- Bujakowski, W.; Barbacki, A.; Skrzypczak, R.; Kasztelewicz, A. Planowane wiercenie badawcze w Karkonoszach dla potrzeb modelowania termicznego systemów gorących suchych skał (HDR). Przegl. Geol. 2012, 60, 199–205. [Google Scholar]
- Uliasz-Misiak, B.; Lewandowska-Śmierzchalska, J.; Matuła, R. Criteria for selecting sites for integrated CO2 storage and geothermal energy recovery. J. Clear. Prod. 2021, 285, 124822. [Google Scholar] [CrossRef]
- Pruess, K. Enhanced geothermal systems (EGS) using CO2 as working fluid—A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Plaksina, T.; White, C. Modeling coupled convection and carbon dioxide injection for improved heat harvesting in geopressured geothermal reservoirs. Geotherm. Energy 2016, 4, 2. [Google Scholar] [CrossRef]
- Liu, H.; Qi, L.; Gou, Y.; Zhang, L.; Feng, W.; Liao, J.; Zhu, Z.; Wang, H.; Zhou, L. Numerical modelling of the cooling effect in geothermal reservoirs induced by injection of CO2 and cooled geothermal water. Oil Gas Sci. Technol. Rev. D’ifp Energ. Nouv. 2020, 75, 15. [Google Scholar] [CrossRef]
- Miecznik, M.; Tyszer, M.; Sowiżdżał, A.; Andresen, T.; Frengstad, B.S.; Stenvik, L.A.; Pierzchała, K.; Gładysz, P. Numerical modeling of the potential CO2-supplied enhanced geothermal system (CO2-EGS) in the Åsgard field, Norway. Geol. Geophys. Environ. 2024, 50, 175–190. [Google Scholar] [CrossRef]
- Wójcicki, A.; Sowiżdżał, A.; Bujakowski, W. Ocena Potencjału, Bilansu Cieplnego i Perspektywicznych Struktur Geologicznych dla Potrzeb Zamkniętych Systemów Geotermicznych (Hot Dry Rocks) w Polsce; Ministry of Environment: Warsaw, Poland; Krakow, Poland, 2013; ISBN 978-83-7863-263-4. [Google Scholar]
- Bujakowski, W.; Barbacki, A.; Miecznik, M.; Pająk, L.; Skrzypczak, R.; Sowiżdżał, A. Modelling geothermal and operating parameters of EGS installations in the lower triassic sedimentary formations of the central Poland area. Renew. Energy 2015, 80, 441–453. [Google Scholar] [CrossRef]
- Tarkowski, R.; Uliasz-Misiak, B. Prospects for the use of carbon dioxide in enhanced geothermal systems in Poland. J. Clean. Prod. 2019, 229, 1189–1197. [Google Scholar] [CrossRef]
- Starczewska, M.; Strojny, M.; Sowiżdżał, A.; Gładysz, P.; Pająk, L. Life cycle assessment of enhanced geothermal systems with CO2 as a working fluid—Polish case study. Clean Technol. Environ. Policy 2025, 27, 1863–1875. [Google Scholar] [CrossRef]
- Dadlez, R. Types of local tectonic structures in the Zechstein-Mesozoic complex of northwestern Poland. Biul. Inst. Geol. 1974, 274, 149–177. [Google Scholar]
- Narkiewicz, M.; Dadlez, R. Geologiczna regionalizacja Polski—Zasady ogólne i schemat podziału w planie podkenozoicznym i podpermskim. Przegl. Geol. 2008, 56, 391–397. [Google Scholar]
- Karnkowski, P.H. Regionalizacja tektoniczna Polski—Niż Polsk. Przegl. Geol. 2008, 56, 895–903. [Google Scholar]
- Karnkowski, P.H. Geology, origin and evolution of the Gorzów Block (NW Poland). Przegl. Geol. 2010, 56, 680–688. [Google Scholar]
- Moska, R.; Labus, K.; Kasza, P.; Moska, A. Geothermal potential of the Hot Dry Rock in south-east Baltic Basin countries—A review. Energies 2023, 16, 1662. [Google Scholar] [CrossRef]
- Sowiżdżał, A.; Machowski, G.; Krzyżak, A.; Puskarczyk, E.; Krakowska-Madejska, P.; Chmielowska, A. Petrophysical evaluation of the Lower Permian formation as a potential reservoir for CO2-EGS—Case study from NW Poland. J. Clean. Prod. 2022, 373, 134768. [Google Scholar] [CrossRef]
- Szewczyk, J.; Gientka, D. Terrestrial heat flow density in Poland—A new approach. Geol. Q. 2009, 53, 125–140. [Google Scholar]
- Plewa, S. Rozkład Parametrów Geotermalnych na Obszarze Polski; CPPGSMiE PAN: Krakow, Poland, 1994; ISBN 83-86286-15-6. [Google Scholar]
- Majorowicz, J.; Wybraniec, S. New terrestrial heat flow map of Europe after regional paleoclimatic correction application. Int. J. Earth Sci. 2011, 100, 881–887. [Google Scholar] [CrossRef]
- Majorowicz, J.; Polkowski, M.; Grad, M. Thermal properties of the crust and the lithosphere–asthenosphere boundary in the area of Poland from the heat flow variability and seismic data. Int. J. Earth Sci. 2019, 108, 649–672. [Google Scholar] [CrossRef]
- Majorowicz, J.; Grad, M. Differences Between Recent Heat Flow Maps of Poland and Deep Thermo-Seismic and Tectonic Age Constraints. Int. J. Terr. Heat Flow Appl. 2020, 3, 11–19. [Google Scholar] [CrossRef]
- Popov, Y.A.; Chekhonin, E.M.; Savelev, E.G.; Ostrizhniy, D.A.; Shakirov, A.B.; Romushkevich, R.A.; Babich, E.A.; Andreyev, B.E.; Spasennykh, M.Y.; Sannikova, I.A. Technique and results of determination of vertical variations in rock thermal properties, temperature gradient and heat flow. Geothermics 2024, 116, 102864. [Google Scholar] [CrossRef]
- Jung, Y.; Pau, G.S.H.; Finsterle, S.; Pollyea, R.M. TOUGH3: A new efficient version of the TOUGH suite of multiphase flow and transport simulators. Comput. Geosci. 2017, 108, 2–7. [Google Scholar] [CrossRef]
- Jung, Y.; Pau, G.S.H.; Finsterle, S.; Doughty, C. TOUGH3 User’s Guid, Version 1.0; Report no. LBNL-2001093; Lawrence Berkeley National Laboratory, University of California: Berkeley, CA, USA, 2018. [Google Scholar]
- Pan, L.; Spycher, N.; Doughty, C.; Pruess, K. ECO2N V2.0: A TOUGH2 Fluid Property Module for Mixtures of Water, NaCl, and CO2; Report no. LBNL-6930E; Lawrence Berkeley National Laboratory, University of California: Berkeley, CA, USA, 2015. [Google Scholar]
- Croucher, A. PyTOUGH: A Python scripting library for automating TOUGH2 simulations. In Proceedings of the 33rd New Zealand Geothermal Workshop, Auckland, New Zealand, 21–23 November 2011. [Google Scholar]
- Croucher, A. PyTOUGH User’s Guide, Version 1.6.5; University of Auckland: Auckland, New Zealand, 2025. [Google Scholar]
- Wojnarowski, P.; Janiga, D. Study of the Effectiveness of the EGS/HDR Fracturing Process with the Application of a 3d Planar Fracture Propagation Model. SSRN 2024, preprint. [CrossRef]
- Ahmed, T. Reservoir Engineering Handbook, 5th ed.; Gulf Professional Publishing: Cambridge, MA, USA, 2019; ISBN 978-0128136508. [Google Scholar]
- Diamond, L.W.; Akinfiew, N.N. Solubility of CO2 in water from −1.5 to 100 °C and from 0.1 to 100 MPa: Evaluation of literature data and thermodynamic modelling. Fluid Phase Equilibria 2003, 208, 265–290. [Google Scholar] [CrossRef]
- Steyn, M.; Oglesby, J.; Turan, G.; Zapantis, A.; Gebremedhin, R. Global status of CCS 2022; Global CCS Institute: Melbourne, Australia, 2022. [Google Scholar]
- CoolProp Thermophysical Fluid Properties Library, Ver. 6.1.1. Available online: http://www.coolprop.org (accessed on 24 January 2025).
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1956. [Google Scholar]
- Recknagel, H.; Sprenger, E.; Schramek, E.H. Heating, Air-Conditioning, Hot Water, Cooling—Hand Book (Polish: Ogrzewanie, Klimatyzacja, Ciepła Woda, Chłodnictwo—Poradnik); OMNI SCALA: Wroclaw, Poland, 2008. [Google Scholar]


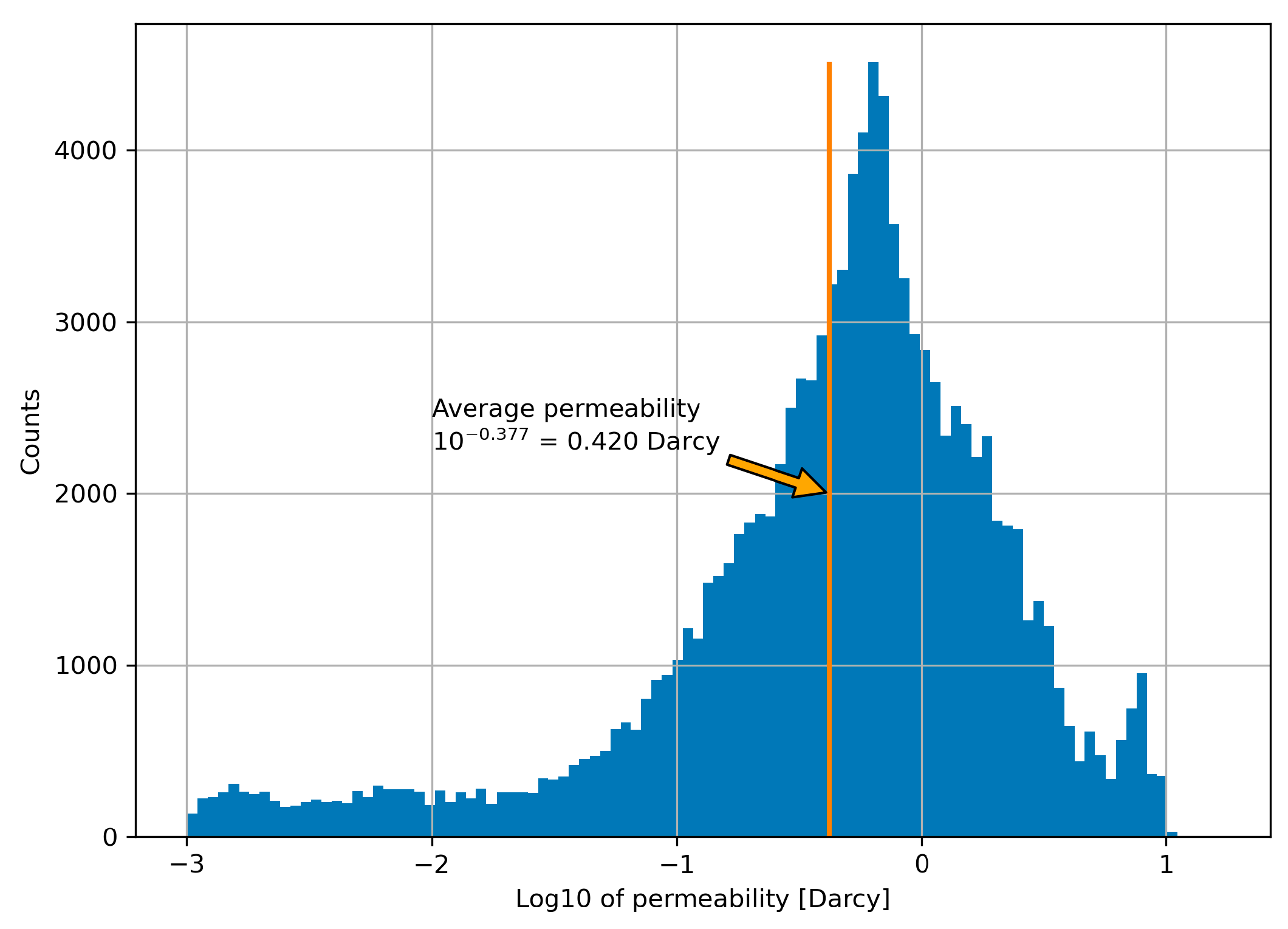
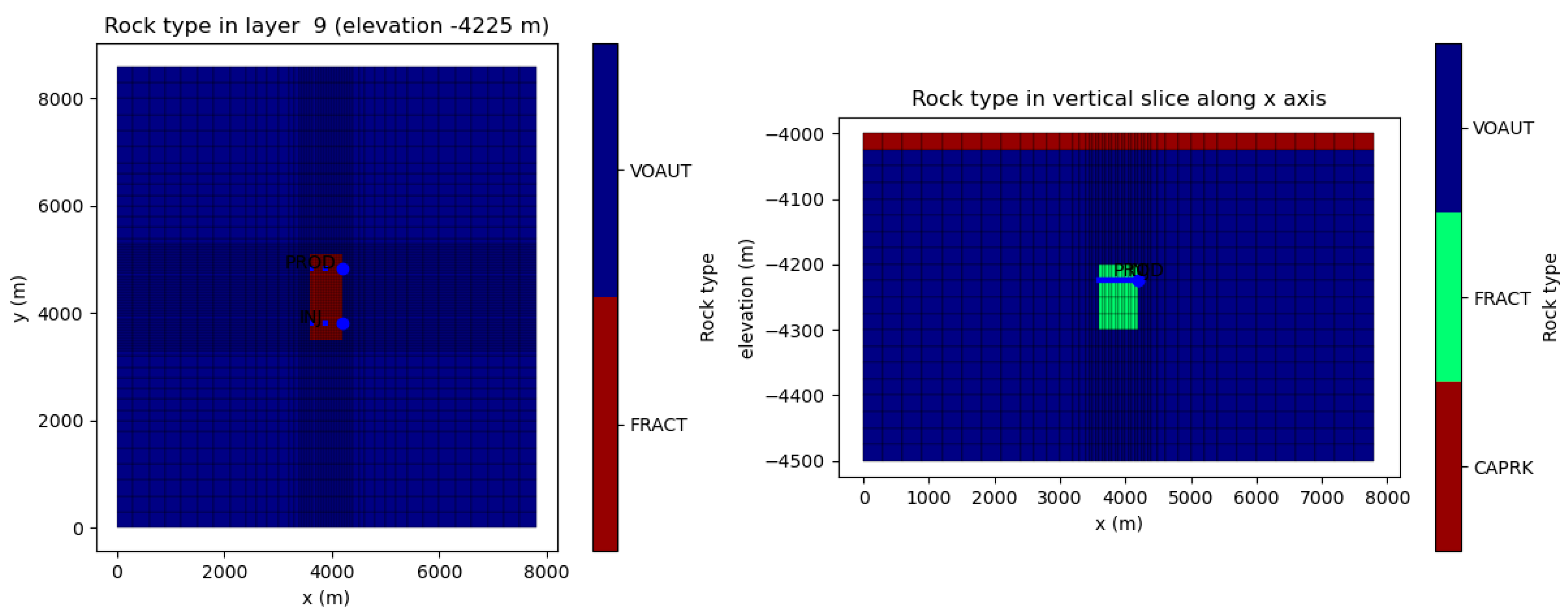

| Rock Name | VOAUT | FRACT | CAPRK |
|---|---|---|---|
| Description | Volcanic Autunian | Fractured zone | Top boundary |
| Density [kg/m3] | 2564.0 | 2564.0 | 1.0 × 1020 |
| Porosity [-] | 0.03 | ||
| Permeability X, Y, Z [m2] | 9.87 × 10−17 (X, Y, Z) | 9.87 × 10−17 (X) 4.2 × 10−13 (Y, Z) | 9.87 × 10−17 (X, Y, Z) |
| Thermal conduct. [W/(m∙K)] | 2.5 | ||
| Specific heat [J/kg] | 900.0 | ||
| General Model Setup | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model size [m] | 7800 (X) × 8600 (Y) × 500 (Z) | |||||||
| Top layer boundary condition | Dirichlet B.C. (fixed temperature) + no-flow boundary | |||||||
| Bottom layer boundary condition | Uniform heat flow density of 80 mW/m2 + no-flow boundary | |||||||
| Lateral boundary conditions | Semi-infinite heat and flow boundaries (volume of lateral elements increased 100 times) | |||||||
| Initial conditions | Temperature and pressure taken from the natural (steady-state) model; no NaCl and CO2 concentration at the start of phase 1 | |||||||
| Relative permeability model | Correy’s curves: Slr = 0.2, Sgr = 0.1 | |||||||
| Capillary pressure model | Linear function; saturation limits [0, 1] | |||||||
| Fractured zone size [m] | 600 (X) × 1600 (Y) × 100 (Z) | |||||||
| Fractured zone volume [km3] | 0.096 | |||||||
| Fractured zone permeability [m2] | X: 9.87 × 10−17, Y and Z: 4.2 × 10−13 | |||||||
| Fractured zone porosity [-] | 0.03 | |||||||
| Depth of the working interval of injection and production wells [m a.s.l.] | From −4200 to −4300 m a.s.l. | |||||||
| Distance between wells [m] | 1000 | |||||||
| Working length of injection and production wells [m] | 600 | |||||||
| Orientation of the working length of injection and production wells | Horizontal | |||||||
| Natural temperature prior to the exploitation phase at injection/production depth [°C] | 145.3 | |||||||
| Natural reservoir pressure outside of the fractured zone, depth = −4225 m a.s.l. [MPa] | 43.6 | |||||||
| Fractured zone pressure prior to the exploitation phase, but after fracturing; depth = −4225 m a.s.l. [MPa] | 64.89 | |||||||
| Phase 1 setup | ||||||||
| Model ID | M.150.139.25 | M.150.139.50 | M.250.139.25 | M.250.139.50 | M.350.139.25 | M.350.139.50 | M.400.139.25 | M.400.139.50 |
| Simulation time [yrs] | 2.0 | |||||||
| Injection mass flowrate [kg/s] | 150 | 250 | 350 | 400 | ||||
| Injection temperature at the reservoir depth [°C] | 139.5 | |||||||
| Δz—layer thickness [m] | 25 | 50 | 25 | 50 | 25 | 50 | 25 | 50 |
| Model ID | M.150.139.25 | M.150.139.50 | M.250.139.25 | M.250.139.50 | M.350.139.25 | M.350.139.50 | M.400.139.25 | M.400.139.50 |
|---|---|---|---|---|---|---|---|---|
| Average flow rate in the production well during phase 1 [kg/s] | 127.78 | 126.59 | 227.35 | 225.91 | 327.38 | 325.61 | 377.01 | 375.68 |
| Production-to-injection flow rate ratio [-] | 0.85 | 0.84 | 0.91 | 0.90 | 0.94 | 0.93 | 0.94 | 0.94 |
| Production temperature after 2 years of phase 1 [°C] | 145.70 | 145.74 | 145.75 | 145.88 | 145.36 | 145.69 | 144.88 | 145.65 |
| Maximum pressure difference between injection and production blocks during phase 1 [bar] | 13.59 | 15.82 | 25.30 | 28.94 | 38.56 | 42.95 | 45.50 | 49.88 |
| Total CO2 injected to reach full CO2 saturation in production blocks [tons] | full saturation not achieved | full saturation not achieved | full saturation not achieved | full saturation not achieved | 1.86 × 107 | 2.20 × 107 | 1.85 × 107 | 2.18 × 107 |
| Time passed to reach full CO2 saturation in production well [yrs] | full saturation not achieved | full saturation not achieved | full saturation not achieved | full saturation not achieved | 1.68 | 1.99 | 1.47 | 1.73 |
| Total CO2 injected in phase 1 [tons] | 9.46 × 106 | 9.46 × 106 | 1.58 × 107 | 1.58 × 107 | 2.21 × 107 | 2.21 × 107 | 2.52 × 107 | 2.52 × 107 |
| Total CO2 extracted in phase 1 [tons] | 4.68 × 106 | 4.54 × 106 | 8.77 × 106 | 8.49 × 106 | 1.45 × 107 | 1.34 × 107 | 1.75 × 107 | 1.64 × 107 |
| Total CO2 stored at the end of phase 1 [tons] | 4.78 × 106 | 4.92 × 106 | 7.00 × 106 | 7.28 × 106 | 7.58 × 106 | 8.70 × 106 | 7.72 × 106 | 8.84 × 106 |
| Cumulative CO2 storage ratio after phase 1 [-] | 0.51 | 0.52 | 0.46 | 0.46 | 0.34 | 0.39 | 0.31 | 0.35 |
| Rock Type\Model ID | M.150.139.25 | M.150.139.50 | M.250.139.25 | M.250.139.50 | M.350.139.25 | M.350.139.50 | M.400.139.25 | M.400.139.50 |
|---|---|---|---|---|---|---|---|---|
| CAPRK gas [-] | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| CAPRK aqueous [-] | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| CAPRK total [-] | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| FRACT gas [-] | 64.9% | 63.4% | 65.6% | 64.3% | 66.0% | 64.9% | 66.0% | 65.0% |
| FRACT aqueous [-] | 2.8% | 3.1% | 1.9% | 2.2% | 1.4% | 1.5% | 1.3% | 1.3% |
| FRACT total [-] | 67.6% | 66.5% | 67.5% | 66.4% | 67.5% | 66.4% | 67.3% | 66.3% |
| VOAUT gas [-] | 22.0% | 20.5% | 22.2% | 20.7% | 22.3% | 20.9% | 22.5% | 21.0% |
| VOAUT aqueous [-] | 10.4% | 13.0% | 10.3% | 12.9% | 10.2% | 12.7% | 10.2% | 12.7% |
| VOAUT total [-] | 32.4% | 33.5% | 32.5% | 33.6% | 32.5% | 33.6% | 32.7% | 33.7% |
| Model ID | M.50.45 | M.100.45 | M.150.45 | M.50.60 | M.100.60 | M.150.60 | M.50.75 | M.100.75 | M.150.75 |
|---|---|---|---|---|---|---|---|---|---|
| Average flow rate in the production well during phase 2 [kg/s] | 38.39 | 88.13 | 137.97 | 38.43 | 88.20 | 138.05 | 38.46 | 88.26 | 138.13 |
| Production-to-injection flow rate ratio during phase 2 [-] | 0.77 | 0.88 | 0.92 | 0.77 | 0.88 | 0.92 | 0.77 | 0.88 | 0.92 |
| Production temperature after 32 years [°C] | 144.49 | 122.27 | 91.17 | 144.52 | 125.10 | 98.20 | 144.61 | 127.80 | 104.90 |
| Production temperature after 52 years [°C] | 136.94 | 96.23 | 76.18 | 138.04 | 102.60 | 86.17 | 139.15 | 109.11 | 96.13 |
| Pressure difference between injection and production well after 52 years [bar] | 1.34 | 4.23 | 7.01 | 1.39 | 4.08 | 6.67 | 1.44 | 3.96 | 6.38 |
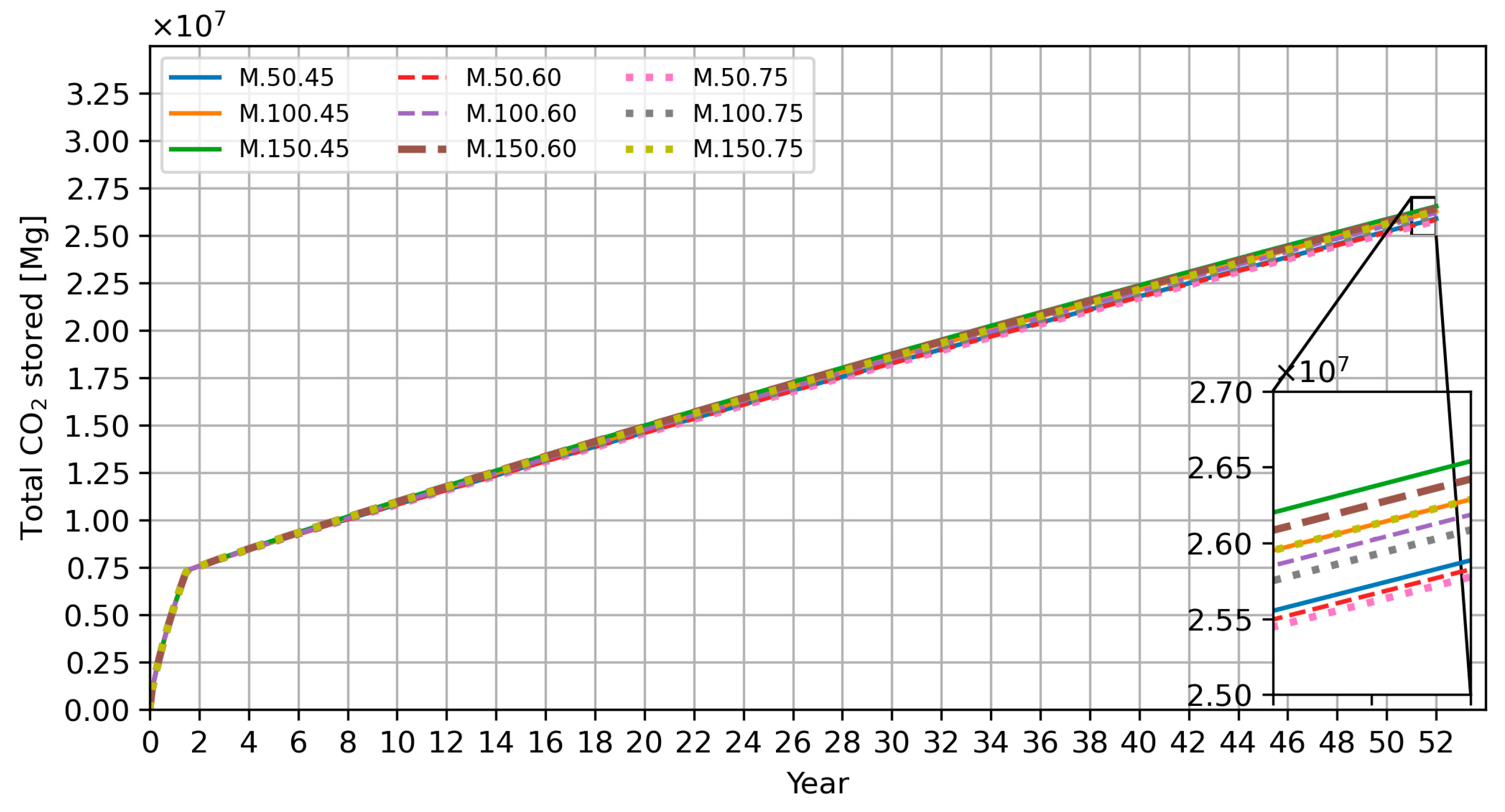
| Total CO2 injected in 52 years [tons] | 1.01 × 108 | 1.80 × 108 | 2.59 × 108 | 1.01 × 108 | 1.80 × 108 | 2.59 × 108 | 1.01 × 108 | 1.80 × 108 | 2.59 × 108 |
| Total CO2 extracted in 52 years [tons] | 7.50 × 107 | 1.53 × 108 | 2.32 × 108 | 7.51 × 107 | 1.54 × 108 | 2.32 × 108 | 7.51 × 107 | 1.54 × 108 | 2.32 × 108 |
| Total CO2 stored in rocks in 52 years [tons] | 2.59 × 107 | 2.63 × 107 | 2.65 × 107 | 2.58 × 107 | 2.62 × 107 | 2.64 × 107 | 2.58 × 107 | 2.61 × 107 | 2.63 × 107 |
| Ratio of CO2 extracted to injected in phase 2 only [-] | 0.77 | 0.88 | 0.92 | 0.77 | 0.88 | 0.92 | 0.77 | 0.88 | 0.92 |
| Cumulative CO2 storage ratio after 52 years [-] | 0.257 | 0.146 | 0.103 | 0.256 | 0.146 | 0.102 | 0.255 | 0.145 | 0.102 |
| Average annual CO2 storage in phase 2 [tons] | 3.66 × 105 | 3.74 × 105 | 3.79 × 105 | 3.65 × 105 | 3.72 × 105 | 3.77 × 105 | 3.64 × 105 | 3.70 × 105 | 3.74 × 105 |
| Average daily replenishment of CO2 from the pipeline as a result of geological storage [tons] | 1003.4 | 1025.4 | 1039.2 | 1000.1 | 1019.8 | 1032.7 | 997.4 | 1014.4 | 1025.3 |
| Model ID | M.50.45 | M.100.45 | M.150.45 | M.50.60 | M.100.60 | M.150.60 | M.50.75 | M.100.75 | M.150.75 |
|---|---|---|---|---|---|---|---|---|---|
| CAPRK gas [-] | 1.1% | 1.1% | 1.1% | 1.1% | 1.1% | 1.1% | 1.1% | 1.1% | 1.1% |
| CAPRK aqueous [-] | 1.0% | 0.9% | 0.9% | 1.0% | 0.9% | 0.9% | 1.0% | 0.9% | 1.0% |
| CAPRK total [-] | 2.0% | 2.0% | 2.0% | 2.1% | 2.0% | 2.1% | 2.1% | 2.0% | 2.1% |
| FRACT gas [-] | 11.7% | 12.3% | 12.4% | 11.5% | 12.0% | 12.1% | 11.4% | 11.8% | 11.8% |
| FRACT aqueous [-] | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| FRACT total [-] | 11.7% | 12.3% | 12.4% | 11.5% | 12.0% | 12.1% | 11.4% | 11.8% | 11.8% |
| VOAUT gas [-] | 70.6% | 70.3% | 70.2% | 70.7% | 70.5% | 70.4% | 70.9% | 70.6% | 70.6% |
| VOAUT aqueous [-] | 15.6% | 15.4% | 15.4% | 15.7% | 15.5% | 15.4% | 15.7% | 15.5% | 15.5% |
| VOAUT total [-] | 86.3% | 85.7% | 85.6% | 86.4% | 86.0% | 85.8% | 86.5% | 86.2% | 86.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miecznik, M.; Tyszer, M.; Sowiżdżał, A.; Pierzchała, K.; Pająk, L.; Gładysz, P. Numerical Modeling of Potential CO2-Fed Enhanced Geothermal System (CO2-EGS) in the Gorzów Block, Poland. Energies 2025, 18, 4825. https://doi.org/10.3390/en18184825
Miecznik M, Tyszer M, Sowiżdżał A, Pierzchała K, Pająk L, Gładysz P. Numerical Modeling of Potential CO2-Fed Enhanced Geothermal System (CO2-EGS) in the Gorzów Block, Poland. Energies. 2025; 18(18):4825. https://doi.org/10.3390/en18184825
Chicago/Turabian StyleMiecznik, Maciej, Magdalena Tyszer, Anna Sowiżdżał, Karol Pierzchała, Leszek Pająk, and Paweł Gładysz. 2025. "Numerical Modeling of Potential CO2-Fed Enhanced Geothermal System (CO2-EGS) in the Gorzów Block, Poland" Energies 18, no. 18: 4825. https://doi.org/10.3390/en18184825
APA StyleMiecznik, M., Tyszer, M., Sowiżdżał, A., Pierzchała, K., Pająk, L., & Gładysz, P. (2025). Numerical Modeling of Potential CO2-Fed Enhanced Geothermal System (CO2-EGS) in the Gorzów Block, Poland. Energies, 18(18), 4825. https://doi.org/10.3390/en18184825










