Machine Learning Approaches for Predicting Lithological and Petrophysical Parameters in Hydrocarbon Exploration: A Case Study from the Carpathian Foredeep
Abstract
1. Introduction
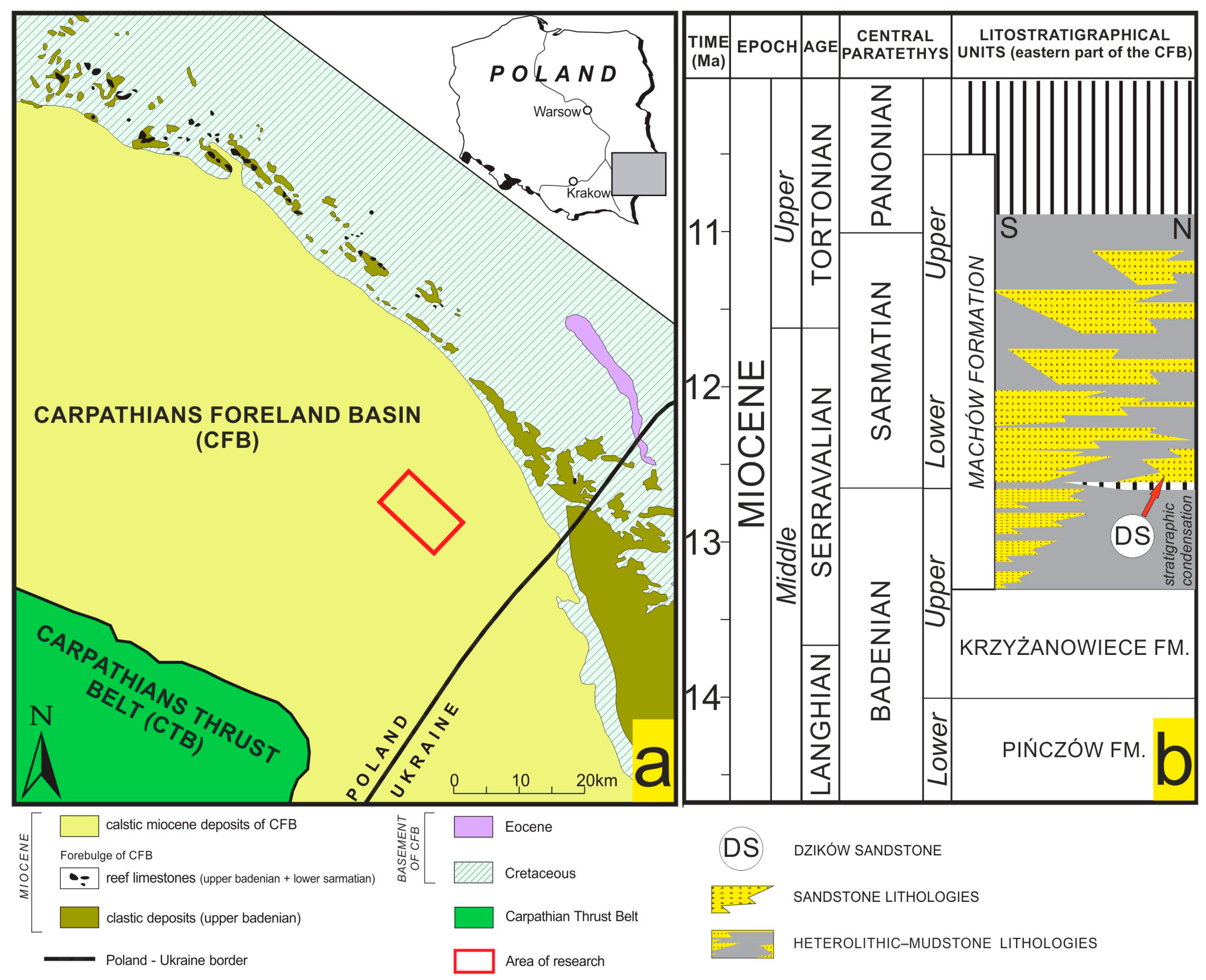
2. Location and Description of the Study Area
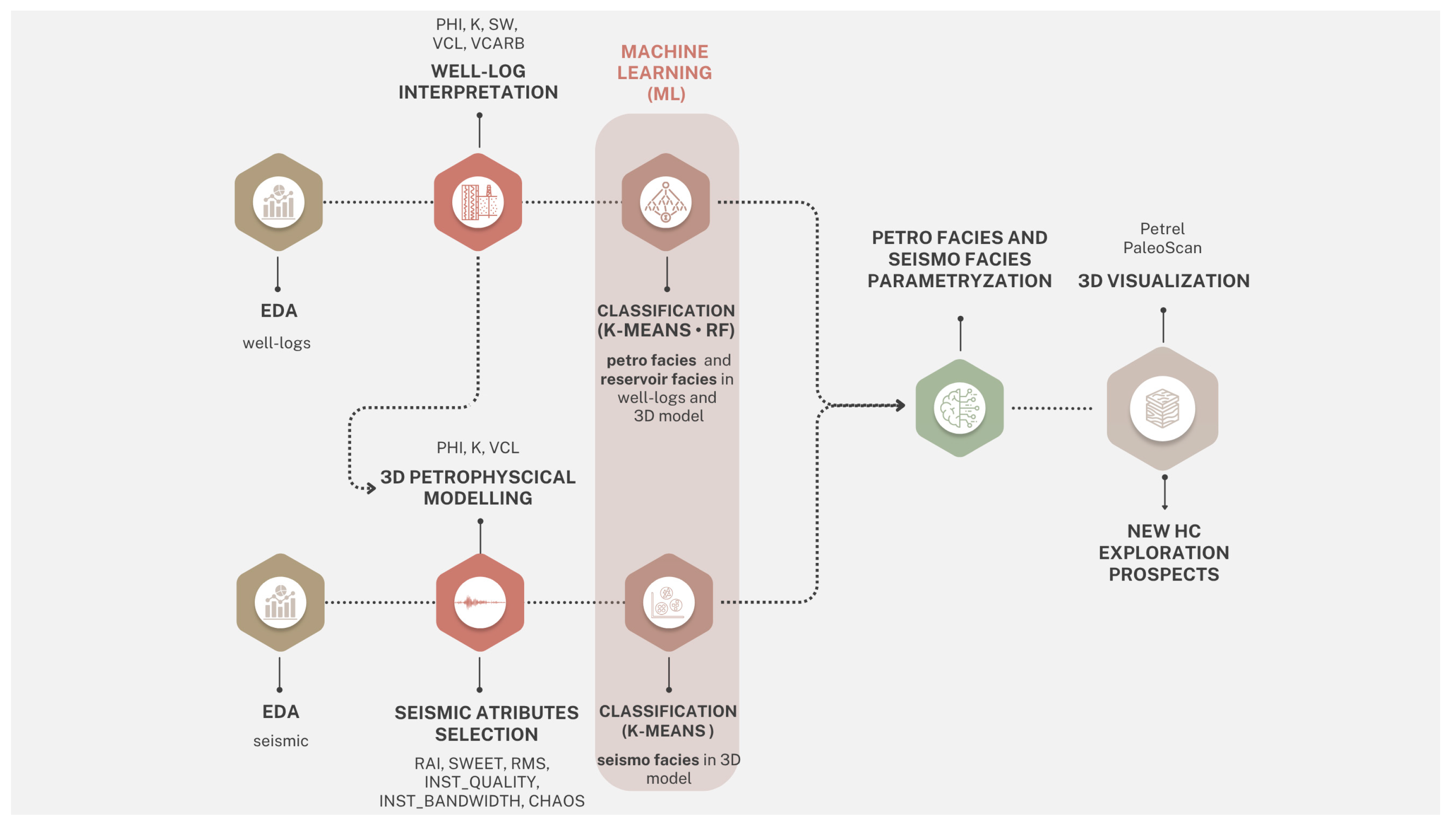
3. Methodology
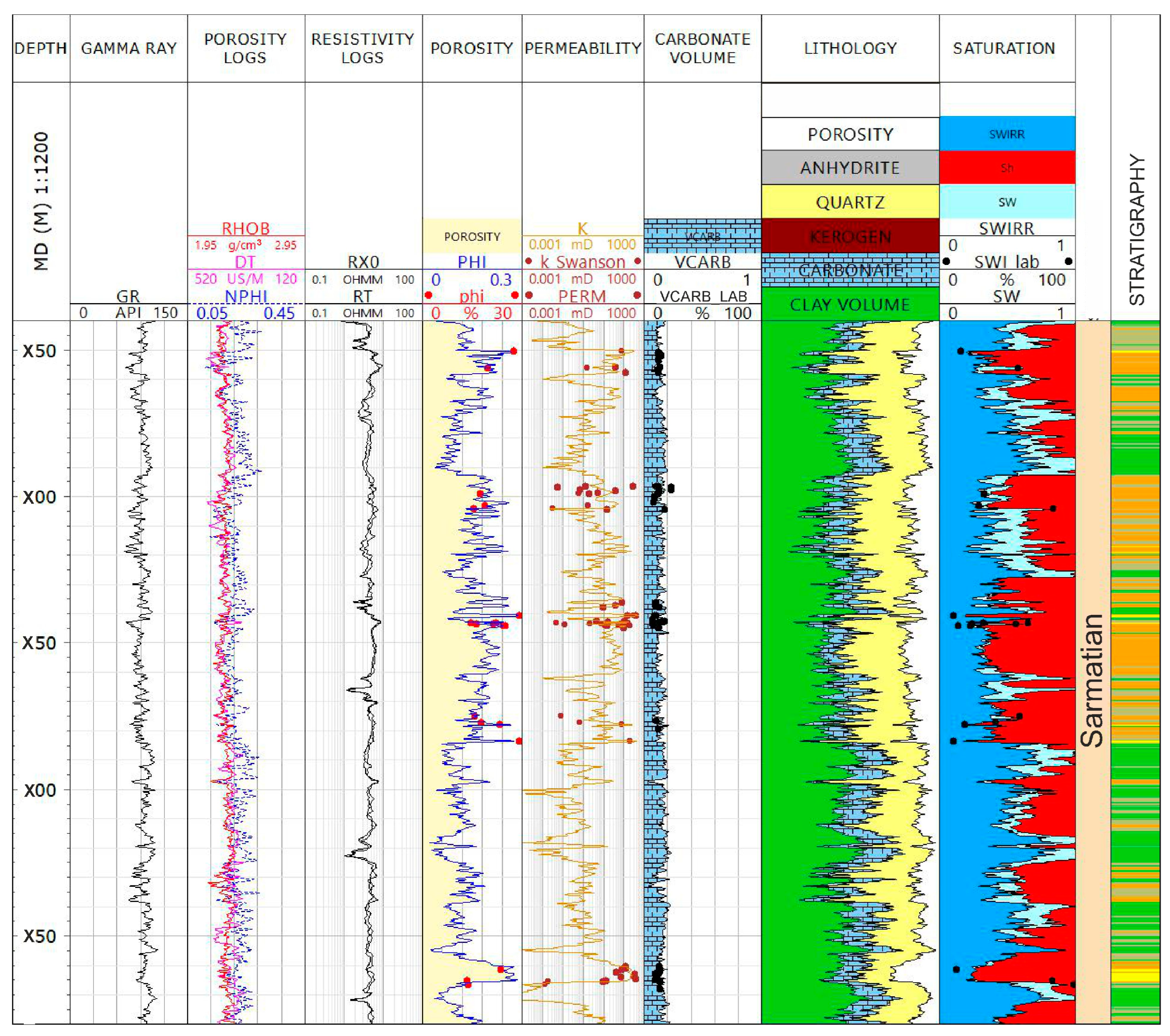
3.1. Data Preparation—Interpretation of Well Log Data
- Clay + Quartz + Carbonates + PHI—for Sarmatian, Upper Badenian, and Lower Badenian formations.
- Clay + Anhydrite + Gypsum + PHI—for Middle Badenian formations.
3.2. Data Preparation—Seismic Analysis
3.3. Structural Model Construction
3.4. Seismic Attribute Calculations
3.5. Construction of the Seismo-Geological Model
3.6. Prediction of Petro Facies and Hydrocarbon Saturated Zones in Bereholes
3.7. Parametric Modeling
3.8. Three-Dimensional Seismic Facies Prediction
4. Results and Discussion
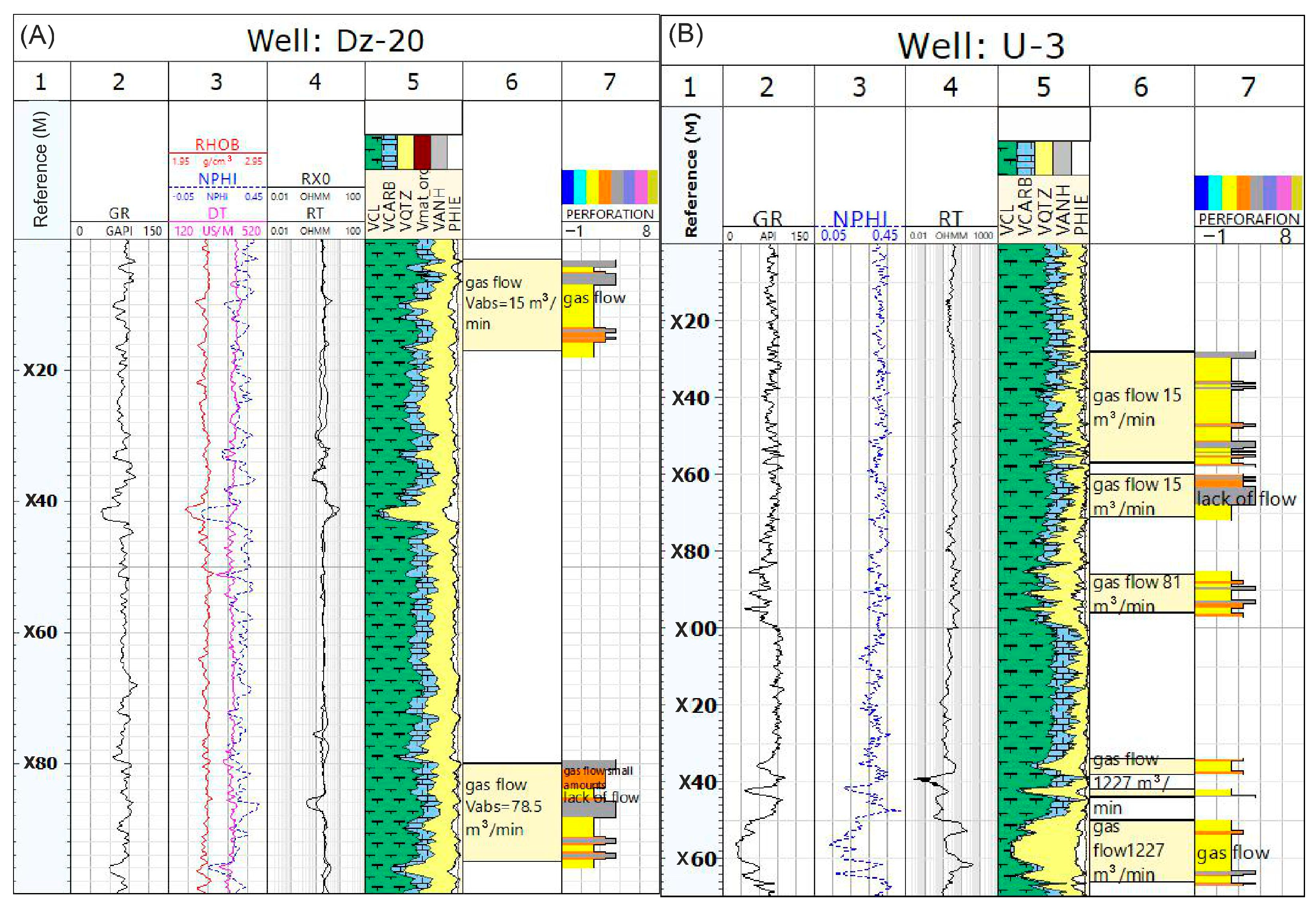
4.1. Prediction of PETRO FACIES and RESERVOIR FACIES in Well Logs
4.2. Prediction of PETRO FACIES in the 3D Model
4.3. Prediction of RESERVOIR FACIES in the 3D Model
4.4. Seismic Facies Parametrization
4.5. Spatial Results Analysis
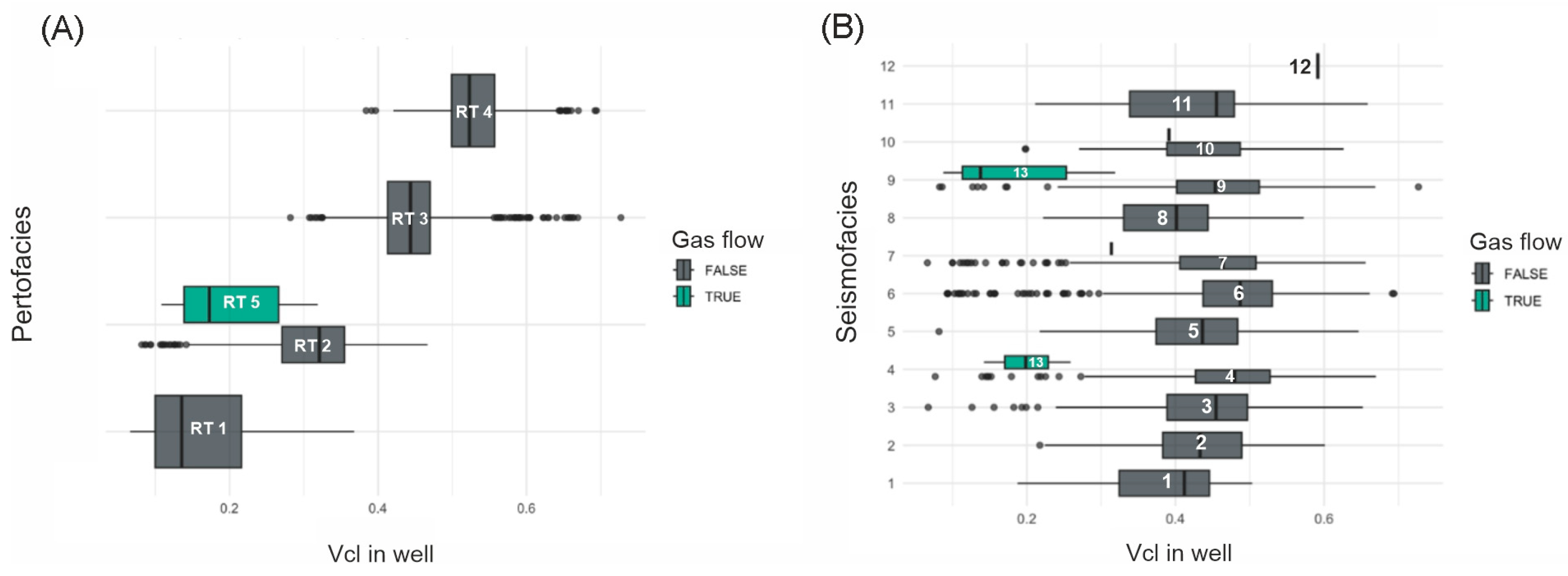
- Unsupervised SEISMO FACIES, 13 classes, class No. 13—Gas-Saturated Sandstones;
- Supervised PETRO FACIES, 5 classes: RT1—Clean Sandstones; RT2—Heteroliths with Sandstone Dominance; RT3—Heteroliths Dominated by Mudstones; RT4—Mudstones and Claystones; RT5—Gas-Saturated Sandstones.
- a—result of spectral decomposition with a visible course of the seismic profile from panels B, D, and F (blue line);
- b—seismic profile with a visible position of the seismic horizon presented in panels a, c, e (yellow line);
- c—result of the SEISMO FACIES model;
- d—profile (analogous position as in b and f) representing the result of the SEISMO FACIES model;
- e—result of the PETRO FACIES model;
- f—profile (analogous position as in b and d) representing the result of the PETRO FACIES model.
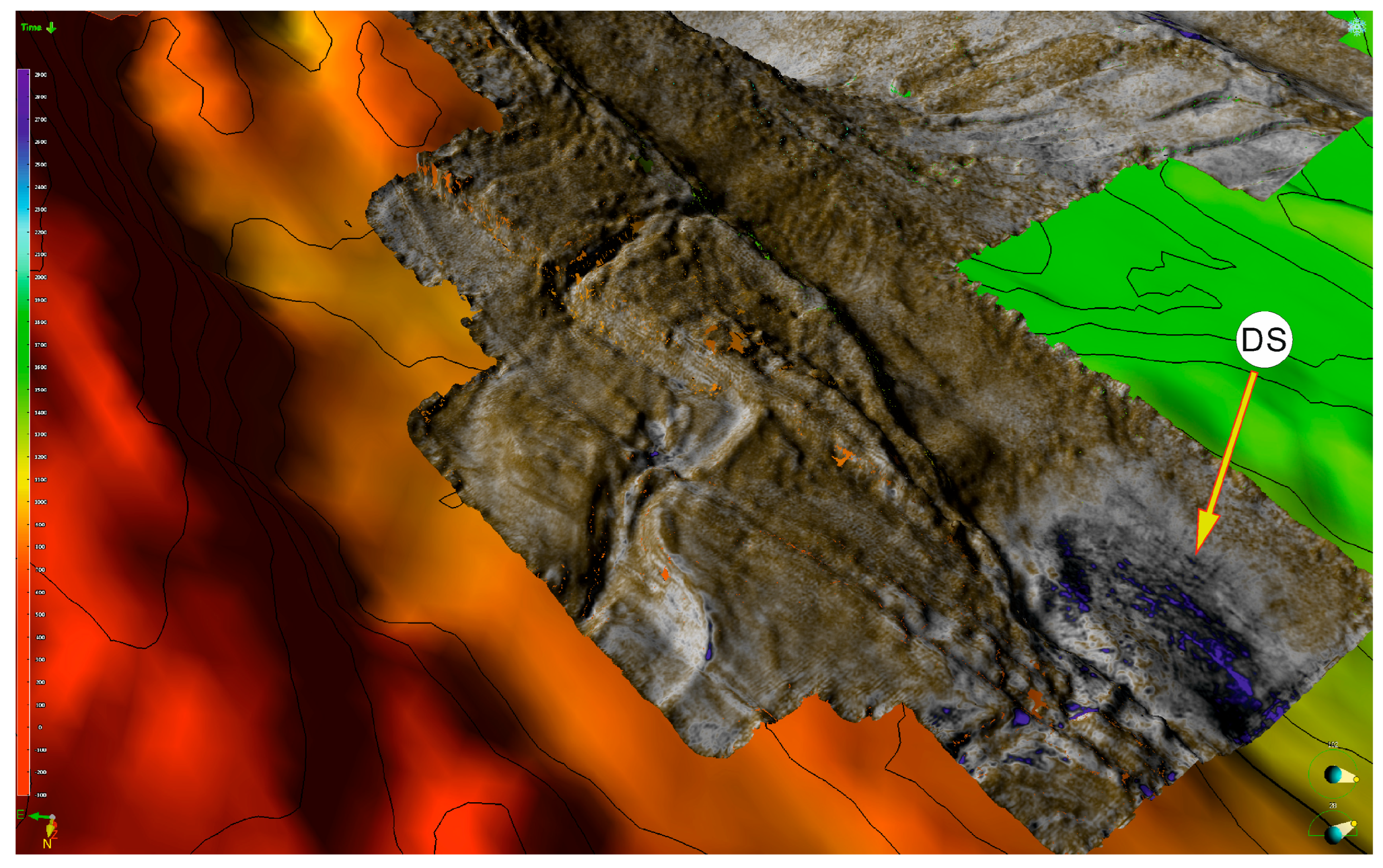
- A positive correlation was obtained for gas-saturated zones in both the Dz-24 and U-14 boreholes in the SEISMO and PETRO FACIES models. Classes 13 (SEISMO FACIES—dark navy blue) and 5 (PETRO FACIES–black) are observed around U-14, while they are absent near Dz-24.
- A strong correlation was observed between the spectral decomposition image and the results of the SEISMO and PETRO FACIES models. The compiled dataset accurately reflects the depositional architecture in the form of depositional lobes with varying spatial extent.
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dziadzio, P. Sekwencje depozycyjne w utworach badenu i sarmatu w SE części zapadliska przedkarpackiego. Prz. Geol. 2000, 48, 1124–1138. [Google Scholar]
- Dziadzio, P.; Maksym, A.; Olszewska, B. Sedymentacja utworów miocenu we wschodniej części zapadliska przedkarpackiego. Prz. Geol. 2006, 54, 413–420. [Google Scholar]
- Antariksa, G.; Muammar, R.; Lee, J. Performance evaluation of machine learning-based classification with rock-physics analysisof geological lithofacies in Tarakan Basin, Indonesia. J. Pet. Sci. Eng. 2022, 208, 109250. [Google Scholar] [CrossRef]
- Feng, R. Improving uncertainty analysis in well log classification by machine learning with a scaling algorithm. J. Pet. Sci. Eng. 2021, 196, 107995. [Google Scholar] [CrossRef]
- Wang, P.; Chen, X.; Wang, B.; Li, J.; Dai, H. An improved method for lithology identification based on a hidden Markov model and random forests. Geophysics 2020, 85, IM27–IM36. [Google Scholar] [CrossRef]
- Okpoli, C.C.; Arogunyo, D.I. Integration of Well Logs and Seismic Attribute Analysis in Reservoir Identification on PGS Field Onshore Niger Delta, Nigeria. Pak. J. Geol. 2020, 4, 12–22. [Google Scholar] [CrossRef]
- Pietsch, K.; Jarzyna, J. Identification of Miocene gas deposits from seismic data in the southeastern part of the Carpathian Foredeep. Geol. Q. 2002, 46, 449–461. [Google Scholar]
- Łukaszewski, M. The application of volume texture extraction to three-dimensional seismic data—Lithofacies structures exploration within the Miocene deposits of the Carpathian Foredeep. Geol. Geophys. Environ. 2020, 46, 301–313. [Google Scholar] [CrossRef]
- Myśliwiec, M. Traps for gas accumulations and the resulting zonation of the gas fields in the Miocene strata of the eastern part of the Carpathian Foredeep (SE Poland). Przegląd Geol. 2004, 52, 657–664. [Google Scholar]
- Oszczypko, N.; Ślączka, A. The evolution of the Miocene Basin in the Polish Outer Carpathian and their foreland. Geol. Carpathica 1989, 40, 23–36. [Google Scholar]
- Ney, R.; Burzewski, W.; Bachleda, T.; Górecki, W.; Jakóbczak, K.; Słupczyński, K. Outline of paleogeography and evolution of lithology and facies of Miocene layers on the Carpathian Foredeep. Pr. Geol. 1974, 82, 1–65. [Google Scholar]
- Porębski, S.J.; Warchoł, M. Znaczenie przepływów hiperpyknalnych i klinoform deltowych dla interpretacji sedymentologicznych formacji z Machowa (miocen zapadliska przedkarpackiego. Przegląd Geol. 2006, 54, 421–429. [Google Scholar]
- Zawisza, L.; Nowak, J. Metodyka określania parametrów filtracyjnych skał na podstawie kompleksowej analizy danych geofizyki otworowej; Wydawnictwa AGH: Kraków, Poland, 2012; pp. 106–115. ISBN 978-83-7464-497-6. [Google Scholar]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Hill, H.J.; Milburn, J.D. Effect of clay and water salinity on electrochemical behavior of reservoir rocks. Trans. AIME 1956, 207, 65e72. [Google Scholar] [CrossRef]
- Simandoux, P. Mesures Dielectriques en Milieu Poreux, Application à la Mesure des Saturations en Eau, Etude du Comportement des Massifs Argileux. Rev. L’institut Français Pétrole 1963, 18, 193–215. [Google Scholar]
- Poupon, A.; Leveaux, J. Evaluation of Water Saturation in Shaly Formations. In Proceedings of the 12th Annual SPWLA Symposium, Dallas, TX, USA, 2–5 May 1971. Society of Petrophysicists and Well Log Analysts. [Google Scholar]
- Worthington, P.F. Recognition and development of low-resistivity pay. In Proceedings of the SPE, Asia Pacific Oil and Gas Conference and Exhibition, Kuala Lumpur, Malaysia, 14–16 April 1997. [Google Scholar]
- Li, C.; Shi, Y.; Zhou, C.; Li, X.; Liu, B.; Tang, L.; Li, S. Evaluation of low amplitude and low resistivity pay zones under the fresh drilling mud invasion condition. Pet. Explor. Dev. 2010, 37, 696–702. [Google Scholar] [CrossRef]
- Pratama, E.; Mohd, S.I.; Syahrir, R. An integrated workflow to characterize and evaluate low resistivity pay and its phenomenon in a sandstone reservoir. J. Geophys. Eng. 2017, 14, 513–519. [Google Scholar] [CrossRef]
- Mashaba, V.; Altermann, W. Calculation of water saturation in low resistivity gas reservoirs and pay-zones of the Cretaceous Grudja formation, onshore Mozambique basin. Mar. Pet. Geol. 2015, 67, 249–261. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B. Hands-On Machine Learning with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020; Available online: https://bradleyboehmke.github.io/HOML/ (accessed on 1 November 2024).
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Louppe, G. Understanding Random Forests: From Theory to Practice. Ph.D. Thesis, University of Liège, Wallonia, Belgium, 2014. [Google Scholar] [CrossRef]
- Kuhn, M.; Silge, J. Tidy Modeling with R: A Framework for Modeling in the Tidyverse. O’Reilly Media. 2022. Available online: https://www.tmwr.org/ (accessed on 1 January 2023).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 1 November 2024).
- Kuhn, M. Futility analysis in the cross-validation of machine learning models. arXiv 2014. [Google Scholar] [CrossRef]
- Owusu, B.A.; Boateng, C.D.; Asare, V.-D.S.; Danuor, S.K.; Adenutsi, C.D.; Quaye, J.A. Seismic facies analysis using machine learning techniques: A review and case study. Earth Sci. Inform. 2024, 17, 3899–3924. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Lance, G.N.; Williams, W.T. A general theory of classificatory sorting strategies, I. Hierarchical systems. Comput. J. 1967, 9, 373–380. [Google Scholar] [CrossRef]
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement Ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Yeo, I.-K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]








| Laboratory Data | |||||
|---|---|---|---|---|---|
| Well Name | Available Logs | PHI | PERM | XRD | NMR |
| C-6 | CALI, BS, GR, NPHI, DT, RX0, RT | % | mD | % | % |
| DA-1 | CALI, BS, GR, NPHI, RX0, RT | ||||
| DA-2 | CALI, BS, GR, NPHI, RX0, RT | 3 | |||
| DS-2 | CALI, BS, GR, NPHI, RX0, RT | 44 | 6 | 10 | |
| D-12 | CALI, BS, GR, NPHI, DT, RX0, RT | 14 | 14 | 14 | |
| D-13 | CALI, BS, GR, NPHI, DT, RX0, RT | 19 | 19 | 19 | |
| D-15 | CALI, BS, GR, NPHI, RHOB, DT, RX0, RT | 13 | 13 | 13 | |
| D-16 | CALI, BS, GR, NPHI, RHOB, DT, RX0, RT | 5 | |||
| D-17 | CALI, BS, GR, NPHI, DT, RHOB, RX0,RT | 26 | 22 | ||
| D-18 | CALI, BS, GR, NPHI, DT, RHOB, RX0,RT | 31 | |||
| D-19 | CALI, BS, GR, NPHI, DT, RX0, RT | 17 | 13 | ||
| D-20 | CALI, BS, GR, NPHI, DT, RX0, RT | 5 | |||
| D-21 | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | 12 | |||
| D-24 * | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | ||||
| L-3 | CALI, BS, GR, NPHI, RX0, RT | ||||
| N-1 * | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | 8 | 9 | 18 | 9 |
| O-1 | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | ||||
| SW-1 | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | ||||
| U-3 | CALI, BS, GR, NPHI, RX0, RT | ||||
| U-4 | CALI, BS, GR, NPHI, RX0, RT | ||||
| U-12 | CALI, BS, GR, NPHI, RX0, RT | ||||
| U-14 | CALI, BS, GR, NPHI, RX0, RT | ||||
| U-19 | CALI, BS, GR, NPHI, RX0, RT | ||||
| U-22 | CALI, BS, GR, NPHI, RX0, RT | 7 | 5 | ||
| U-25 | CALI, BS, GR, NPHI, RX0, RT | 4 | 2 | ||
| WC-1 | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | ||||
| Z-1 | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | 8 | |||
| Z-2 | CALI, BS, GR, NPHI, DT, RHOB, RX0, RT | ||||
| Method | Target Classes | Input Variables | Pre-Processing Steps | Tuning Strategy | Verification | Comments |
|---|---|---|---|---|---|---|
| K-means | PETRO FACIES (RT1–RT4) | PHIE, PERM, VCL, VCARB | Scaling and centering (step_normalize) | - | - | Large datasets (~100,000 observations) |
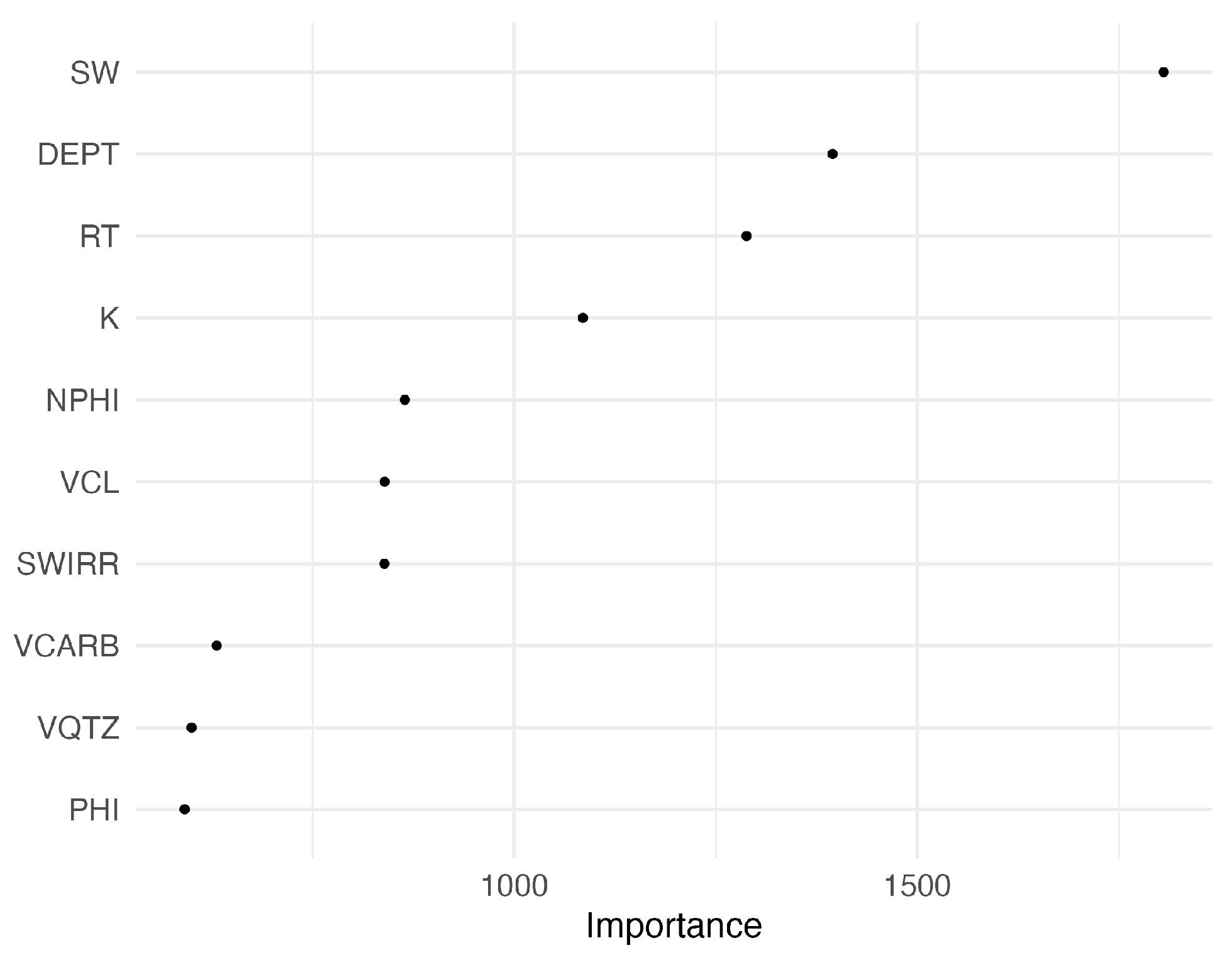
| Random Forest | RESERVOIR FACIES in well logs (HWS, HWGS, HGS, HNCG, HNF, BSWGS, BSGS) | DEPTH, PERM, NPHI, PHI, PHIE, PHIT, RT, SW, SWIRR, VCARB, VCL, VQRTZ, PETRO FACIES | step_dummy (PETRO FACIES), step_normalize, step_smote (RESERVOIR FACIES) | Default: mtry = √(num predictors), trees = 500, min_n = 1 | Train/test split (80/20%) | - |
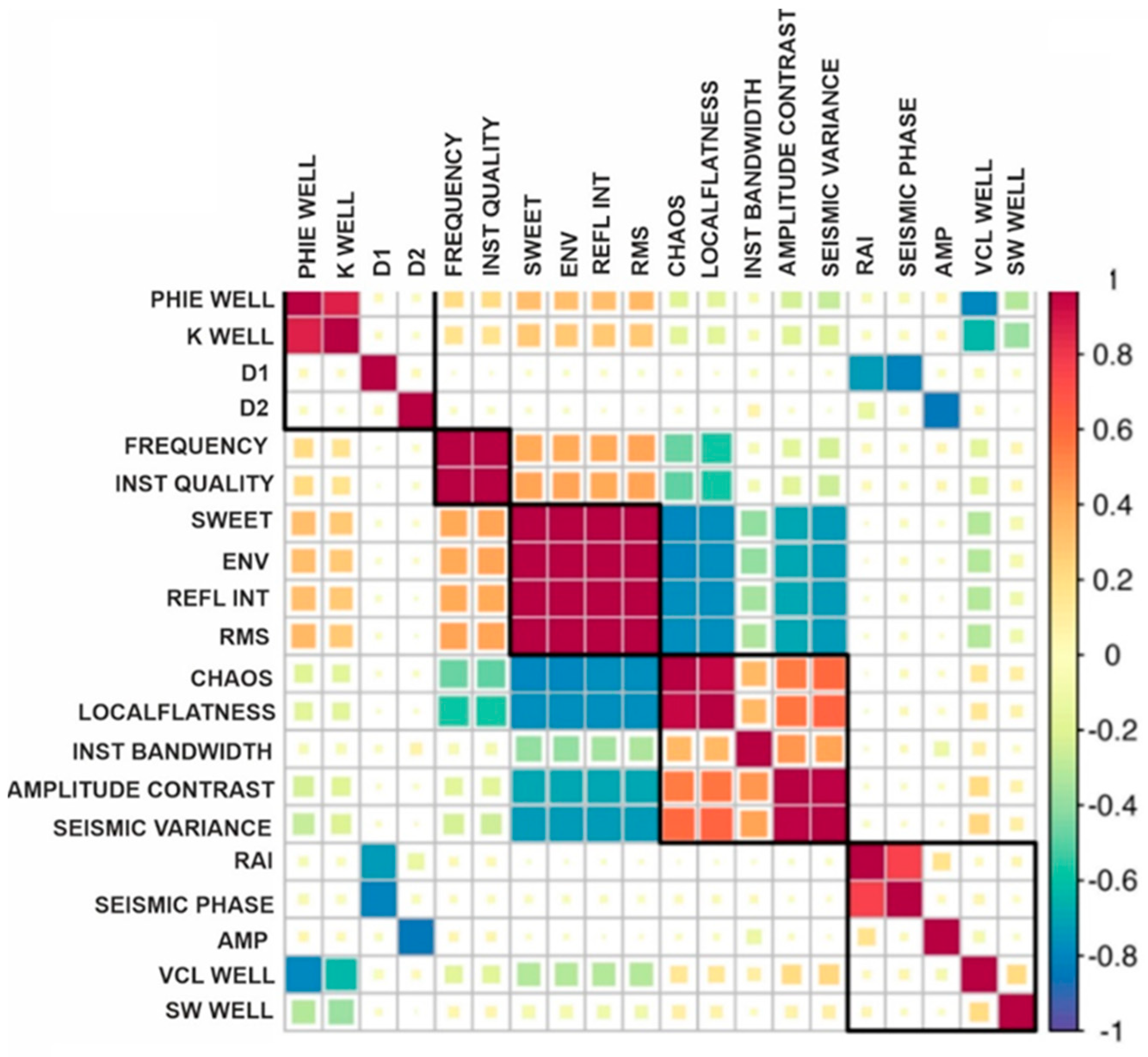
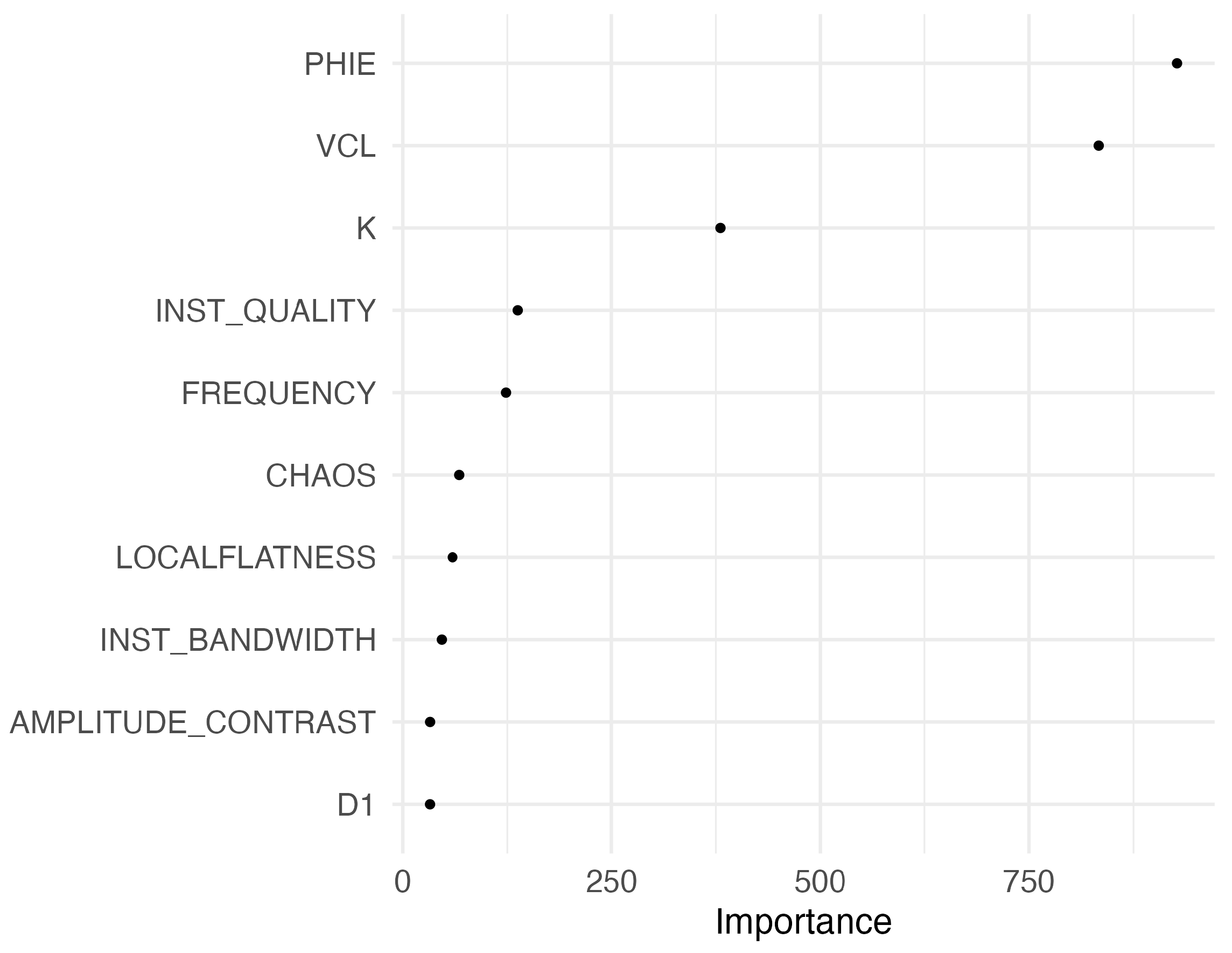
| Random Forest | PETRO FACIES in 3D seismic (RT1–RT4, plus RT5) | AMP, SEISMIC_PHASE, RAI, SEISMIC_VARIANCE, AMPLITUDE_CONTRAST, INST_BANDWIDTH, LOCAL_FLATNESS, CHAOS, RMS, REFL_INT, ENV, SWEET, INSTANT_QUALITY, FREQUENCY, D1, D2, PHIE, K, VCL | step_normalize (all_numeric), step_smote (PETRO FACIES) | RACES ANOVA (200 models, 20 combinations), mtry = 6, trees = 1000, min_n = 35 | Validation via bootstrapping (200 subsets), tested on 2 blind wells | Limited observations after upscaling to seismic grid |
| Random Forest | RESERVOIR FACIES in 3D seismic (HWS, HWGS, HGS, HNCG, HNF, BSWGS, BSGS) | Same as above plus PETRO FACIES | step_dummy (PETRO FACIES), step_normalize (all_numeric), step_smote (RESERVOIR FACIES) | RACES ANOVA (200 models, 20 combinations), mtry = 9, trees = 1000, min_n = 11 | Validation via bootstrapping (200 subsets), tested on 2 blind wells | Limited observations after upscaling to seismic grid |
| K-means | SEISMO FACIES (1–12, plus 13) | RAI, SWEET, RMS, INST_QUALITY, INST_BANDWIDTH, CHAOS | Yeo–Johnson transformation, scaling and centering (step_normalize) | - | - | Large seismic datasets (~10 mln observations) |
| Class | Precision | Recall | F1 Score |
|---|---|---|---|
| HNF | 0.92 | 0.91 | 0.92 |
| BSGS | 0.92 | 0.97 | 0.95 |
| HGS | 0.95 | 0.90 | 0.92 |
| HNCG | 0.60 | 0.80 | 0.69 |
| HWS | 0.99 | 0.99 | 0.99 |
| HWGS | 0.99 | 0.99 | 0.99 |
| BSWGS | 1.00 | 1.00 | 1.00 |
| Class | Precision (Mean) | SD | Recall (Mean) | SD | F1 Score (Mean) | SD |
|---|---|---|---|---|---|---|
| RT1 | 0.70 | 0.16 | 0.65 | 0.18 | 0.65 | 0.13 |
| RT2 | 0.82 | 0.04 | 0.88 | 0.03 | 0.85 | 0.02 |
| RT3 | 0.82 | 0.02 | 0.78 | 0.02 | 0.80 | 0.01 |
| RT4 | 0.78 | 0.02 | 0.80 | 0.02 | 0.79 | 0.01 |
| Class | Precision (Mean) | SD | Recall (Mean) | SD | F1 Score (Mean) | SD |
|---|---|---|---|---|---|---|
| BSGS | 0.11 | 0.24 | 0.05 | 0.14 | 0.08 | 0.15 |
| BSWGS | 0.81 | 0.09 | 0.81 | 0.07 | 0.81 | 0.06 |
| HGS | 0.40 | 0.14 | 0.07 | 0.03 | 0.12 | 0.04 |
| HNCG | 0.09 | 0.28 | 0.00 | 0.02 | 0.03 | 0.07 |
| HNF | 0.82 | 0.02 | 0.84 | 0.02 | 0.83 | 0.01 |
| HWGS | 0.70 | 0.02 | 0.78 | 0.03 | 0.74 | 0.02 |
| HWS | 0.55 | 0.03 | 0.68 | 0.04 | 0.60 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arkadiusz, D.; Tomasz, T.; Anita, L.-Ś.; Krzysztof, S. Machine Learning Approaches for Predicting Lithological and Petrophysical Parameters in Hydrocarbon Exploration: A Case Study from the Carpathian Foredeep. Energies 2025, 18, 4521. https://doi.org/10.3390/en18174521
Arkadiusz D, Tomasz T, Anita L-Ś, Krzysztof S. Machine Learning Approaches for Predicting Lithological and Petrophysical Parameters in Hydrocarbon Exploration: A Case Study from the Carpathian Foredeep. Energies. 2025; 18(17):4521. https://doi.org/10.3390/en18174521
Chicago/Turabian StyleArkadiusz, Drozd, Topór Tomasz, Lis-Śledziona Anita, and Sowiżdżał Krzysztof. 2025. "Machine Learning Approaches for Predicting Lithological and Petrophysical Parameters in Hydrocarbon Exploration: A Case Study from the Carpathian Foredeep" Energies 18, no. 17: 4521. https://doi.org/10.3390/en18174521
APA StyleArkadiusz, D., Tomasz, T., Anita, L.-Ś., & Krzysztof, S. (2025). Machine Learning Approaches for Predicting Lithological and Petrophysical Parameters in Hydrocarbon Exploration: A Case Study from the Carpathian Foredeep. Energies, 18(17), 4521. https://doi.org/10.3390/en18174521






