Deep Reinforcement Learning Approaches the MILP Optimum of a Multi-Energy Optimization in Energy Communities
Abstract
1. Introduction
1.1. Related Works
1.2. Contribution
- Side-by-side comparison of MILP and RL, for the economic optimization of an existing EC using real-world input data and real-time electricity prices.
- Development of an RL-based control strategy for economic demand response, leveraging price signals to shift grid usage toward low-price periods by optimizing the operation of thermal storage and PV flexibility, aiming to approach the MILP-derived optimum.
- Comprehensive benchmark of RL and MILP optimization in a direct comparison and compared with a no-flexibility reference scenario. Within the benchmark cost savings and operational strategies under realistic conditions, including PV variability and demand patterns, are assessed.
2. Methods
2.1. System
2.2. Data
2.3. Physical Model
- The specific heat capacity of water is equal to , irrespective of the TES temperature.
- Spatial temperature variations in the TES are neglected, making it a single-node model.
- The mass balance is always fulfilled for the TES. Due to the narrow operating temperature range of only 20 °C, the volume of the storage is assumed to remain constant, as thermal expansion effects are negligible.
- The electric power of the heating element is equivalent to its heating power ().
- The COP of the heat pump is equal to . This is in accordance with Walden and Pedulla [39].
2.4. Reinforcement Learning
- At the start of each episode, a day index was randomly sampled from the training dataset.
- For the selected day, the corresponding normalized profiles were loaded, including electricity prices , thermal load demand , electrical load , and feed-in tariffs .
- Seasonal indicators such as winter (), spring (), summer (), and autumn () flags were extracted for the selected day. This approach ensures diversity across episodes and captures a wide range of operational conditions.
- The agent was trained over a total of 5000 episodes.
2.5. Mixed Integer Linear Programming
3. Results and Discussion
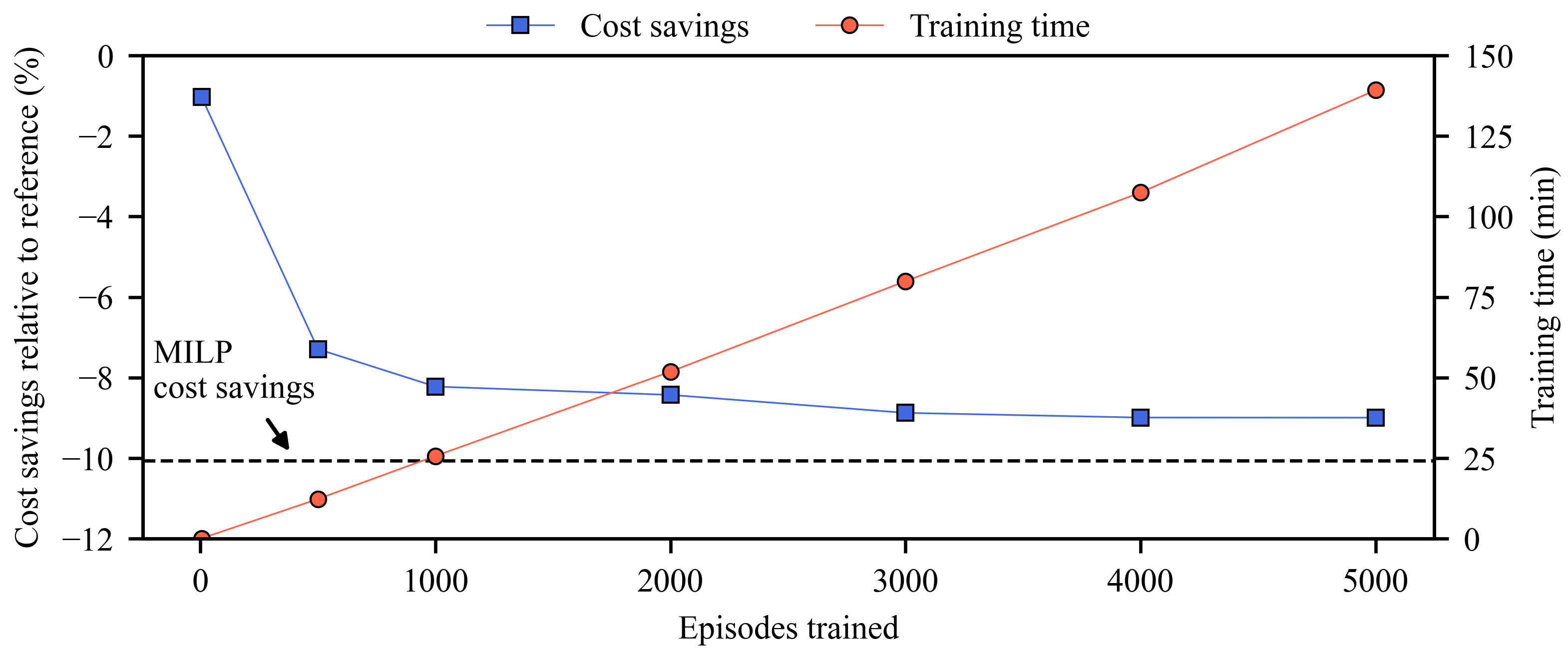
3.1. Preliminary Results
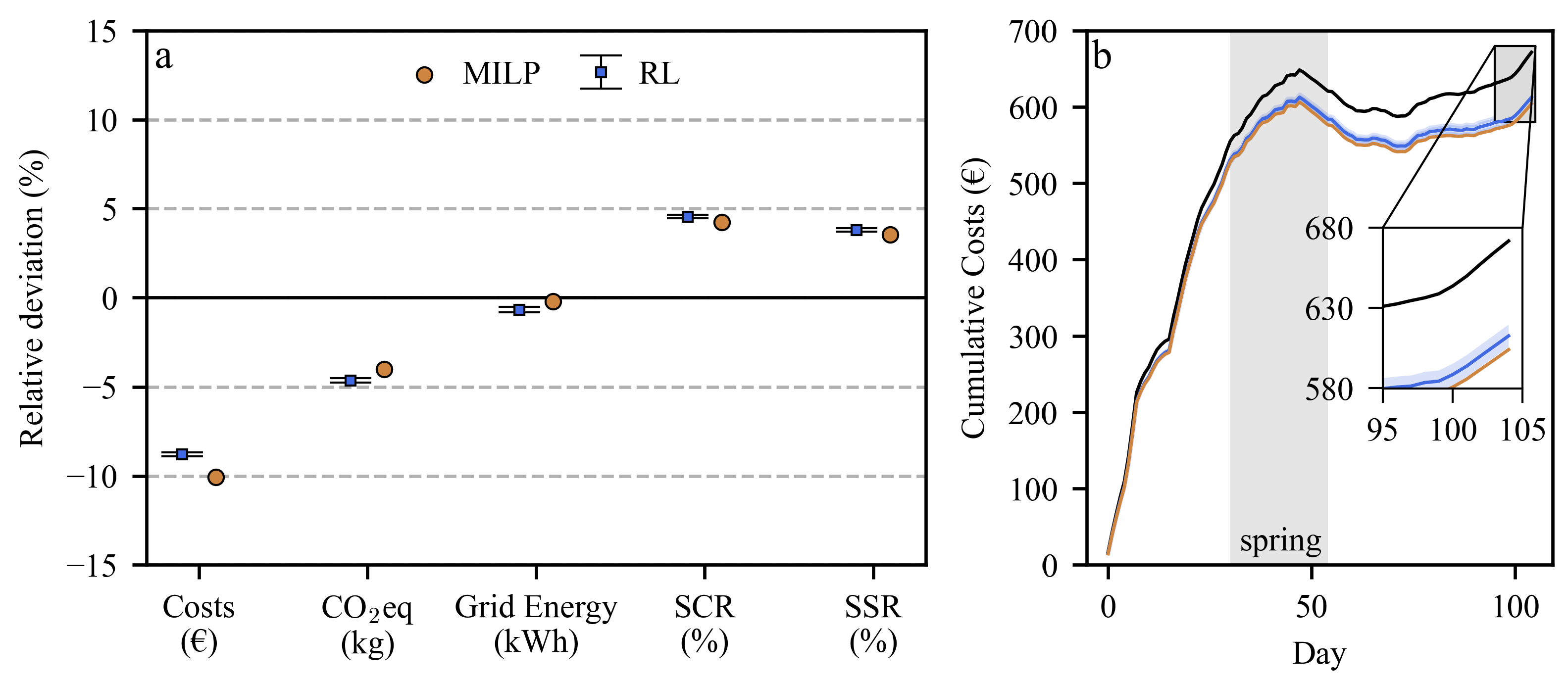
3.2. Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Configurations
| Algorithm A1 P-controller with saturation and auxiliary heater logic |
|
| Parameter | Value |
|---|---|
| Training episodes | 5000 |
| Batch size | 1250 |
| Memory buffer size | 10,000 |
| Update rate | 0.005 |
| Adam learning rate | 0.0001 |
| Initial exploration rate | 0.9 |
| End exploration rate | 0.05 |
| Exploration decay rate | 5000 |
| Discount factor | 0.999 |
| Neural network layers | 3 |
| Layer 1 | (input, 512), ReLU activation |
| Layer 2 | (512, 512), ReLU activation |
| Layer 3 | (512, 101), linear activation |
| Loss function | Huber Loss |
References
- Seiler, V.; Moosbrugger, L.; Huber, G.; Kepplinger, P. Assessing Model Predictive Control for Energy Communities’ Flexibilities. In Intelligente Energie- und Klimastrategien: Energie–Gebäude–Umwelt; Science Research Pannonia; Holzhausen: Wien, Austria, 2024; pp. 1–22. ISBN 978-3-903207-89-9. [Google Scholar] [CrossRef]
- Jaysawal, R.K.; Chakraborty, S.; Elangovan, D.; Padmanaban, S. Concept of net zero energy buildings (NZEB)—A literature review. Clean. Eng. Technol. 2022, 11, 100582. [Google Scholar] [CrossRef]
- Riechel, R. Zwischen Gebäude und Gesamtstadt: Das Quartier als Handlungsraum in der lokalen Wärmewende. Vierteljahrsh. Wirtsch. 2016, 85, 89–101. [Google Scholar] [CrossRef]
- Kannengießer, T. Bewertung Zukünftiger Urbaner Energieversorgungskonzepte für Quartiere. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 2023. [Google Scholar]
- Zhang, Q.; Grossmann, I.E. Enterprise-wide optimization for industrial demand side management: Fundamentals, advances, and perspectives. Chem. Eng. Res. Des. 2016, 116, 114–131. [Google Scholar] [CrossRef]
- Ren, H.; Gao, W. A MILP model for integrated plan and evaluation of distributed energy systems. Appl. Energy 2010, 87, 1001–1014. [Google Scholar] [CrossRef]
- Lindholm, O.; Weiss, R.; Hasan, A.; Pettersson, F.; Shemeikka, J. A MILP Optimization Method for Building Seasonal Energy Storage: A Case Study for a Reversible Solid Oxide Cell and Hydrogen Storage System. Buildings 2020, 10, 123. [Google Scholar] [CrossRef]
- Wohlgenannt, P.; Huber, G.; Rheinberger, K.; Kolhe, M.; Kepplinger, P. Comparison of demand response strategies using active and passive thermal energy storage in a food processing plant. Energy Rep. 2024, 12, 226–236. [Google Scholar] [CrossRef]
- Costa, T.; Nogueira, T.; Bomtempo, G.; de Souza, E.; Pimentel, B.; Alves, F.; Alves, J.; Ravetti, M. A Hybrid Mixed-Integer Linear Programming and Reinforcement Learning Framework for Integrated Mineral Supply Chain Optimization. SSRN Electron. J. 2025; preprint. ISSN 1876–6102. [Google Scholar] [CrossRef]
- Urbanucci, L. Limits and potentials of Mixed Integer Linear Programming methods for optimization of polygeneration energy systems. Energy Procedia 2018, 148, 1199–1205. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T. Reinforcement learning for building controls: The opportunities and challenges. Appl. Energy 2020, 269, 115036. [Google Scholar] [CrossRef]
- Charbonnier, F.; Peng, B.; Vienne, J.; Stai, E.; Morstyn, T.; McCulloch, M. Centralised rehearsal of decentralised cooperation: Multi-agent reinforcement learning for the scalable coordination of residential energy flexibility. Appl. Energy 2025, 377, 124406. [Google Scholar] [CrossRef]
- Palma, G.; Guiducci, L.; Stentati, M.; Rizzo, A.; Paoletti, S. Reinforcement Learning for Energy Community Management: A European-Scale Study. Energies 2024, 17, 1249. [Google Scholar] [CrossRef]
- Guiducci, L.; Palma, G.; Stentati, M.; Rizzo, A.; Paoletti, S. A Reinforcement Learning Approach to the Management of Renewable Energy Communities. In Proceedings of the 2023 12th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 6–10 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Pereira, H.; Gomes, L.; Vale, Z. Peer-to-peer energy trading optimization in energy communities using multi-agent deep reinforcement learning. Energy Inform. 2022, 5, 44. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Zhang, R.; Gu, W.; Cao, G. N-1 Evaluation of Integrated Electricity and Gas System Considering Cyber-Physical Interdependence. In IEEE Transactions on Smart Grid; IEEE: Piscataway, NJ, USA, 2025; p. 1. [Google Scholar] [CrossRef]
- Gaggero, G.B.; Piserà, D.; Girdinio, P.; Silvestro, F.; Marchese, M. Novel Cybersecurity Issues in Smart Energy Communities. In Proceedings of the 2023 1st International Conference on Advanced Innovations in Smart Cities (ICAISC), Jeddah, Saudi Arabia, 23–25 January 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gaggero, G.B.; Armellin, A.; Girdinio, P.; Marchese, M. An IEC 62443-Based Framework for Secure-by-Design Energy Communities. IEEE Access 2024, 12, 166320–166332. [Google Scholar] [CrossRef]
- Baumann, C.; Wohlgenannt, P.; Streicher, W.; Kepplinger, P. Optimizing heat pump control in an NZEB via model predictive control and building simulation. Energies 2025, 18, 100. [Google Scholar] [CrossRef]
- Aguilera, J.J.; Padullés, R.; Meesenburg, W.; Markussen, W.B.; Zühlsdorf, B.; Elmegaard, B. Operation optimization in large-scale heat pump systems: A scheduling framework integrating digital twin modelling, demand forecasting, and MILP. Appl. Energy 2024, 376, 124259. [Google Scholar] [CrossRef]
- Kepplinger, P.; Huber, G.; Petrasch, J. Autonomous optimal control for demand side management with resistive domestic hot water heaters using linear optimization. Energy Build. 2015, 100, 50–55. [Google Scholar] [CrossRef]
- Kepplinger, P.; Huber, G.; Petrasch, J. Field testing of demand side management via autonomous optimal control of a domestic hot water heater. Energy Build. 2016, 127, 730–735. [Google Scholar] [CrossRef]
- Cosic, A.; Stadler, M.; Mansoor, M.; Zellinger, M. Mixed-integer linear programming based optimization strategies for renewable energy communities. Energy 2021, 237, 121559. [Google Scholar] [CrossRef]
- Bachseitz, M.; Sheryar, M.; Schmitt, D.; Summ, T.; Trinkl, C.; Zörner, W. PV-Optimized Heat Pump Control in Multi-Family Buildings Using a Reinforcement Learning Approach. Energies 2024, 17, 1908. [Google Scholar] [CrossRef]
- Lissa, P.; Deane, C.; Schukat, M.; Seri, F.; Keane, M.; Barrett, E. Deep reinforcement learning for home energy management system control. Energy AI 2021, 3, 100043. [Google Scholar] [CrossRef]
- Rohrer, T.; Frison, L.; Kaupenjohann, L.; Scharf, K.; Hergenröther, E. Deep Reinforcement Learning for Heat Pump Control. arXiv 2022, arXiv:2212.12716. [Google Scholar] [CrossRef]
- Franzoso, A.; Fambri, G.; Badami, M. Deep reinforcement learning as a tool for the analysis and optimization of energy flows in multi-energy systems. Energy Convers. Manag. 2025, 341, 120095. [Google Scholar] [CrossRef]
- Guo, C.; Wang, X.; Zheng, Y.; Zhang, F. Real-Time Optimal Energy Management of Microgrid with Uncertainties Based on Deep Reinforcement Learning. Energy 2022, 238, 121873. [Google Scholar] [CrossRef]
- Cui, Y.; Xu, Y.; Li, Y.; Wang, Y.; Zou, X. Deep Reinforcement Learning Based Optimal Energy Management of Multi-Energy Microgrids with Uncertainties. arXiv 2023, arXiv:2311.18327. [Google Scholar] [CrossRef]
- Langer, L.; Volling, T. A reinforcement learning approach to home energy management for modulating heat pumps and photovoltaic systems. Appl. Energy 2022, 327, 120020. [Google Scholar] [CrossRef]
- Langer, L.; Volling, T. An optimal home energy management system for modulating heat pumps and photovoltaic systems. Appl. Energy 2020, 278, 115661. [Google Scholar] [CrossRef]
- EXAA Energy Exchange Austria. Spot Market Prices for Austria: 19.10.2022–19.10.2023. 2023. Hourly Spot Electricity Prices from EXAA for the Austrian Market Covering the Period 19 October 2022 to 19 October 2023. Available online: https://markt.apg.at/transparenz/uebertragung/day-ahead-preise/ (accessed on 22 March 2025).
- Illwerke vkw AG. PV-Einspeisetarife Vorarlberg 2025; Illwerke vkw AG: Bregenz, Austria, 2024; Available online: https://www.vkw.at/media/Infoblatt_Photovoltaikanlagen_Einspeisung.pdf (accessed on 22 July 2025).
- Ökostrom-Einspeisetarifverordnung 2018 (ÖSET-VO 2018). Bundesgesetzblatt für die Republik Österreich. Version: 2018.–BGBl. II Nr. 408/2017, § 6. Available online: https://www.ris.bka.gv.at/eli/bgbl/II/2017/408 (accessed on 22 July 2025).
- Electricity Maps. Austria 19.10.2022–19.10.2023 Carbon Intensity Data (Version 27 January 2025). 2025. Available online: https://www.electricitymaps.com (accessed on 22 July 2025).
- GGV Stadtwerke Groß-Gerau Versorgungs GmbH. Standard Load Profiles (SLP)—File: GGV_SLP_1000_MWh_2021_01.xlsx. Standard Load Profile Data Provided by GGV Stadtwerke Groß-Gerau. File version: 2020-09-24. 2021. Available online: https://www.ggv-energie.de/cms/netz/allgemeine-daten/netzbilanzierung-download-aller-profile.php (accessed on 22 October 2024).
- GeoSphere Austria. Messstationen Stundendaten v2—ID 1115 Feldkirch Global Radiation Data (10-Minute Resolution), Version: 2024. 2024. Available online: https://data.hub.geosphere.at/dataset/klima-v2-1h (accessed on 22 March 2025). [CrossRef]
- Walden, J.V.; Padullés, R. An analytical solution to optimal heat pump integration. Energy Convers. Manag. 2024, 320, 118983. [Google Scholar] [CrossRef]
- Towers, M.; Kwiatkowski, A.; Terry, J.; Balis, J.U.; Cola, G.D.; Deleu, T.; Goulão, M.; Kallinteris, A.; Krimmel, M.; KG, A.; et al. Gymnasium: A Standard Interface for Reinforcement Learning Environments. arXiv 2024, arXiv:2407.17032. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. Version: 2025. Available online: https://www.gurobi.com (accessed on 30 April 2025).
- Wohlgenannt, P.; Hegenbart, S.; Eder, E.; Kolhe, M.; Kepplinger, P. Energy Demand Response in a Food-Processing Plant: A Deep Reinforcement Learning Approach. Energies 2024, 17, 6430. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-learning. arXiv 2015, arXiv:1509.06461. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar] [PubMed]
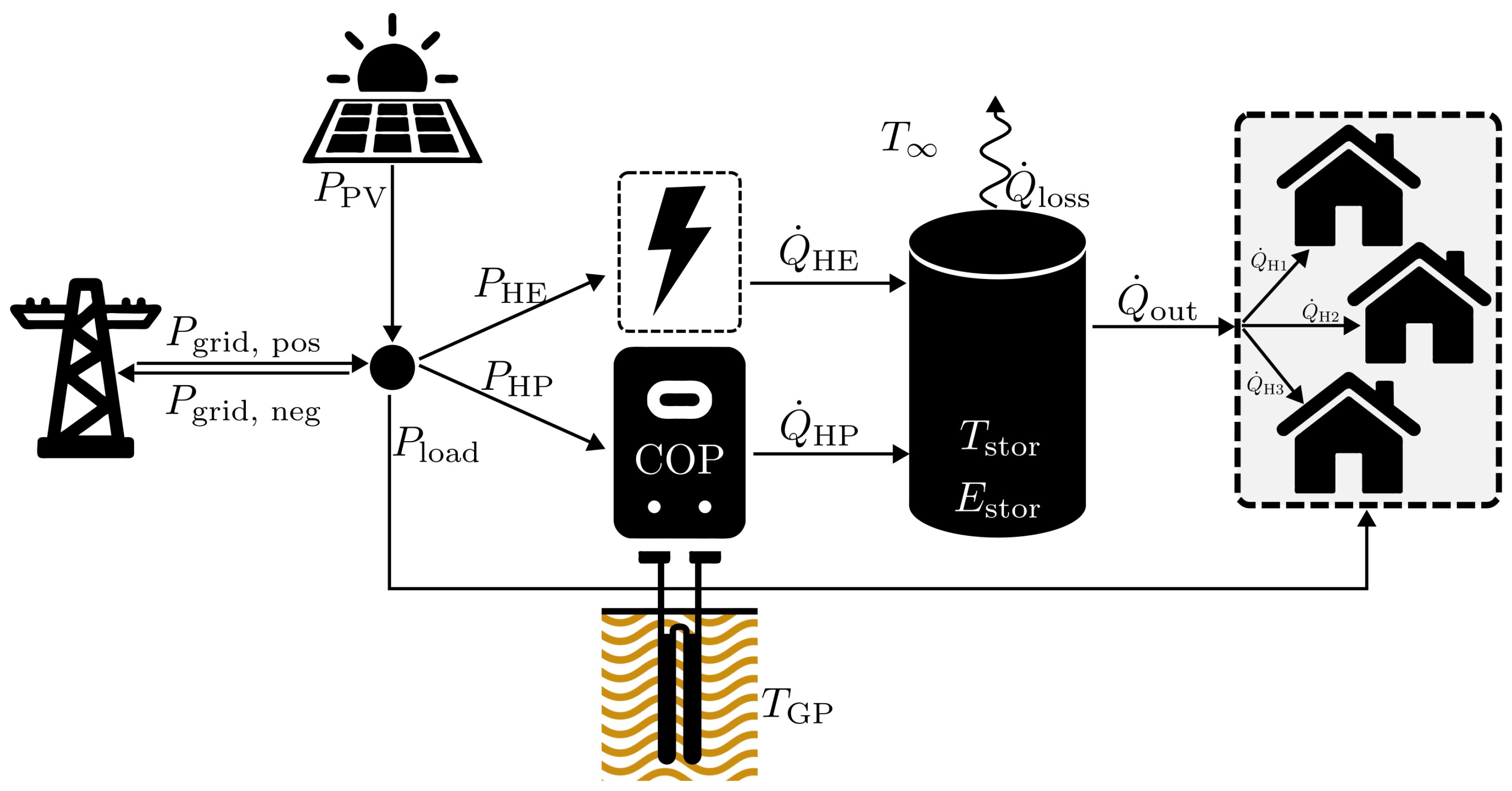




| Variable | Data Type | Source |
|---|---|---|
| Geothermal probe temperatures () | on-site | Measured locally |
| Heat requirements () | on-site | Measured locally |
| Electricity prices () | historical | EXAA market spot prices [33] |
| Feed-in tariffs (f) | historical | Local feed in tariffs [34,35] |
| Carbon intensity | historical | Electricity Maps [36] |
| Electrical load (non-heating) () | synthetic | Standard load profiles [37] |
| Photovoltaic power output () | synthetic | Geosphere Austria [38] |
| Seasonal classification () | synthetic | One hot encoding |
| Binary Indicator | Season | Active Months |
|---|---|---|
| Spring | March, April, May | |
| Summer | June, July, August | |
| Autumn | September, October, November | |
| Winter | December, January, February |
| Description | Parameter | Value | Unit |
|---|---|---|---|
| Resolution | 0.25 | h | |
| Storage capacity | 1.298 | kWh/K | |
| Storage lower temperature bound | 35 | °C | |
| Storage upper temperature bound | 55 | °C | |
| Ambient temperature | 20 | °C | |
| Min. heating power heat pump | 0 | kW | |
| Max. heating power heat pump | 12 | kW | |
| Max. heating power heating element | 6 | kW | |
| Proportional gain | 12 | – | |
| Equivalent CO2 emissions | CO2eq (Solar) | 0 | kg CO2eq/kWh |
| Heat transfer coefficient | h | 0.287 | W/m2K |
| TES surface area | A | 6 | m2 |
| KPI | REF | RL | MILP |
|---|---|---|---|
| Costs (€) | 671.71 | 604.13 | |
| CO2eq (kg) | 929.88 | 892.58 | |
| Grid Energy (kWh) | 1491.63 | 1488.23 | |
| SCR (%) | 28.76 | 33.01 | |
| SSR (%) | 19.58 | 23.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vetter, V.; Wohlgenannt, P.; Kepplinger, P.; Eder, E. Deep Reinforcement Learning Approaches the MILP Optimum of a Multi-Energy Optimization in Energy Communities. Energies 2025, 18, 4489. https://doi.org/10.3390/en18174489
Vetter V, Wohlgenannt P, Kepplinger P, Eder E. Deep Reinforcement Learning Approaches the MILP Optimum of a Multi-Energy Optimization in Energy Communities. Energies. 2025; 18(17):4489. https://doi.org/10.3390/en18174489
Chicago/Turabian StyleVetter, Vinzent, Philipp Wohlgenannt, Peter Kepplinger, and Elias Eder. 2025. "Deep Reinforcement Learning Approaches the MILP Optimum of a Multi-Energy Optimization in Energy Communities" Energies 18, no. 17: 4489. https://doi.org/10.3390/en18174489
APA StyleVetter, V., Wohlgenannt, P., Kepplinger, P., & Eder, E. (2025). Deep Reinforcement Learning Approaches the MILP Optimum of a Multi-Energy Optimization in Energy Communities. Energies, 18(17), 4489. https://doi.org/10.3390/en18174489









