Evaluation of XGBoost and ANN as Surrogates for Power Flow Predictions with Dynamic Energy Storage Scenarios
Abstract
1. Introduction
1.1. Background
1.2. Load Flow Analysis
1.3. Data and Machine Learning in Distribution Networks
- A per-component ML framework is created to predict transformer/line loadings and bus voltages using several different ML models working simultaneously. We hypothesize that training individual models for each state parameter would lend us benefits in accuracy despite the high computational cost of training hundreds of ML models.
- A case study on the Norwegian CINELDI grid with dynamic scenarios generated via randomized DER placement and BESS operation was used to prove the effectiveness of the aforementioned framework.
- A comparative study of XGBoost and ANN models is conducted, with evaluation of speed, error (MAE, RMSE, and MSE), max error, and inference time to comment on the benefits of using individual models to predict unique state parameters per component as well as the impact of increasing the number of scenarios used to train the models.
2. Materials and Methods
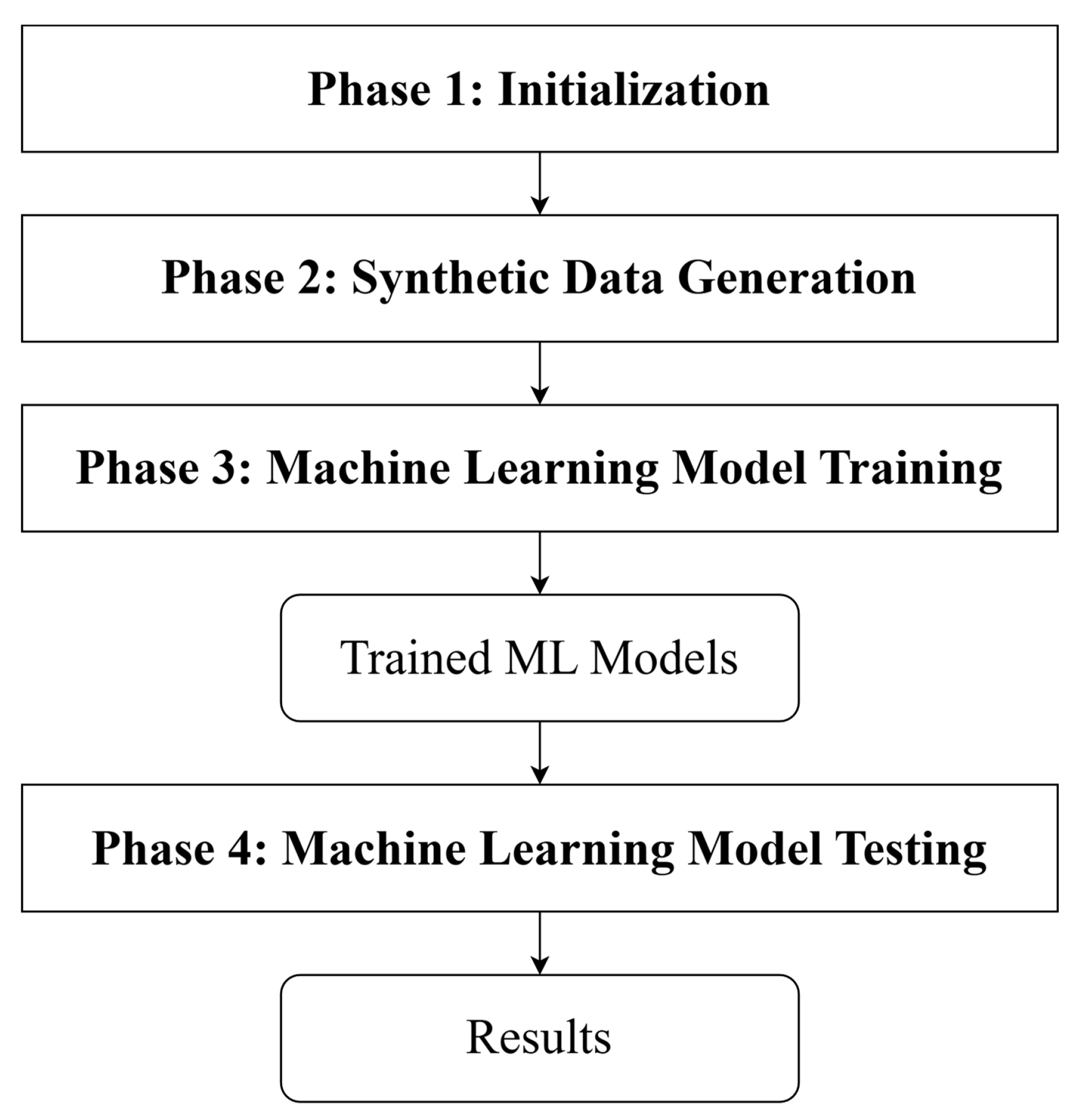
2.1. Overview
2.2. Phase 1: Initialization
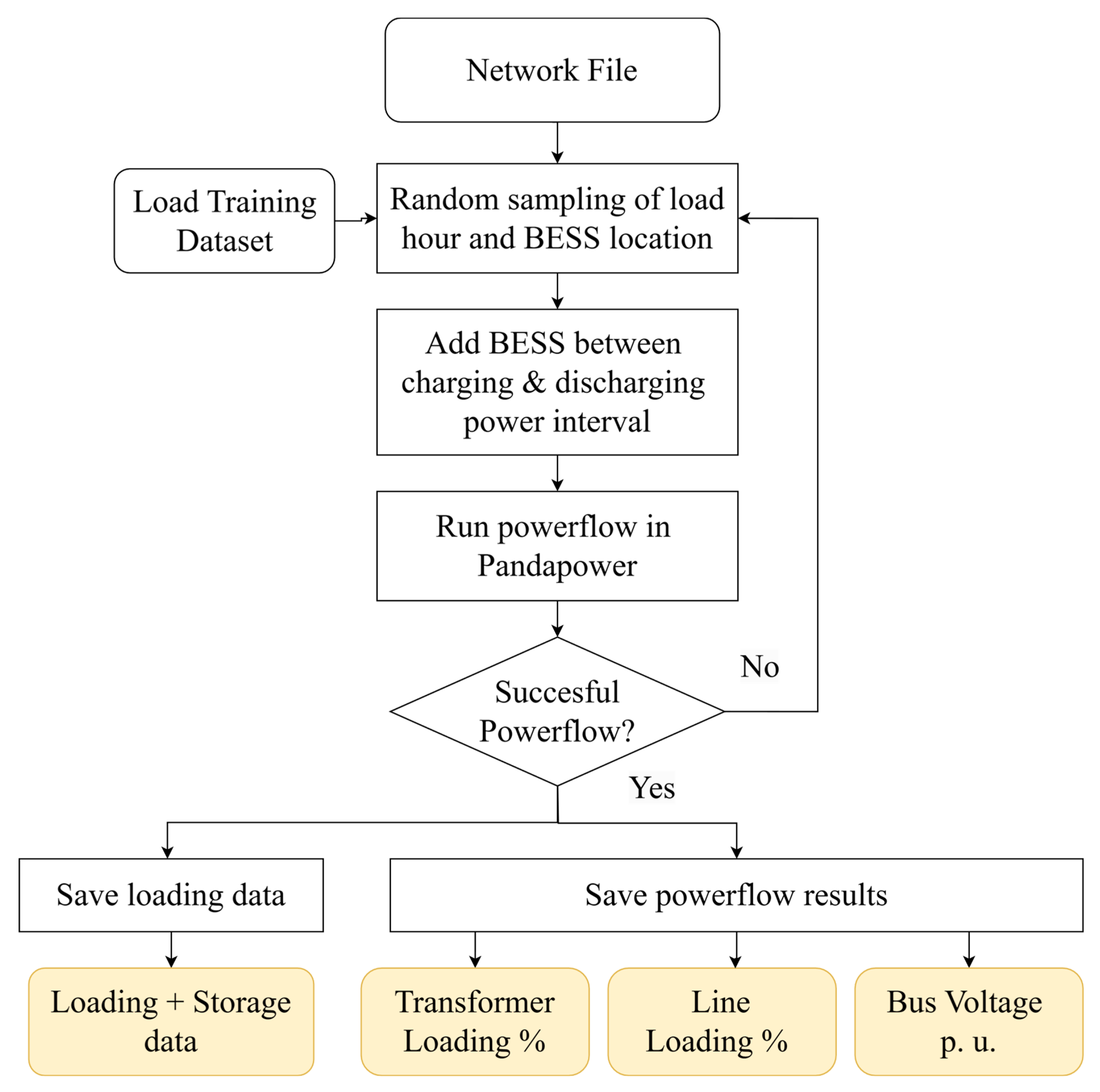
2.3. Phase 2: Synthetic Data Generation
2.4. Phase 3: Machine Learning Model Training
2.5. Phase 4: Testing Machine Learning Models
2.6. Selection of Machine Learning Models
3. Case Study
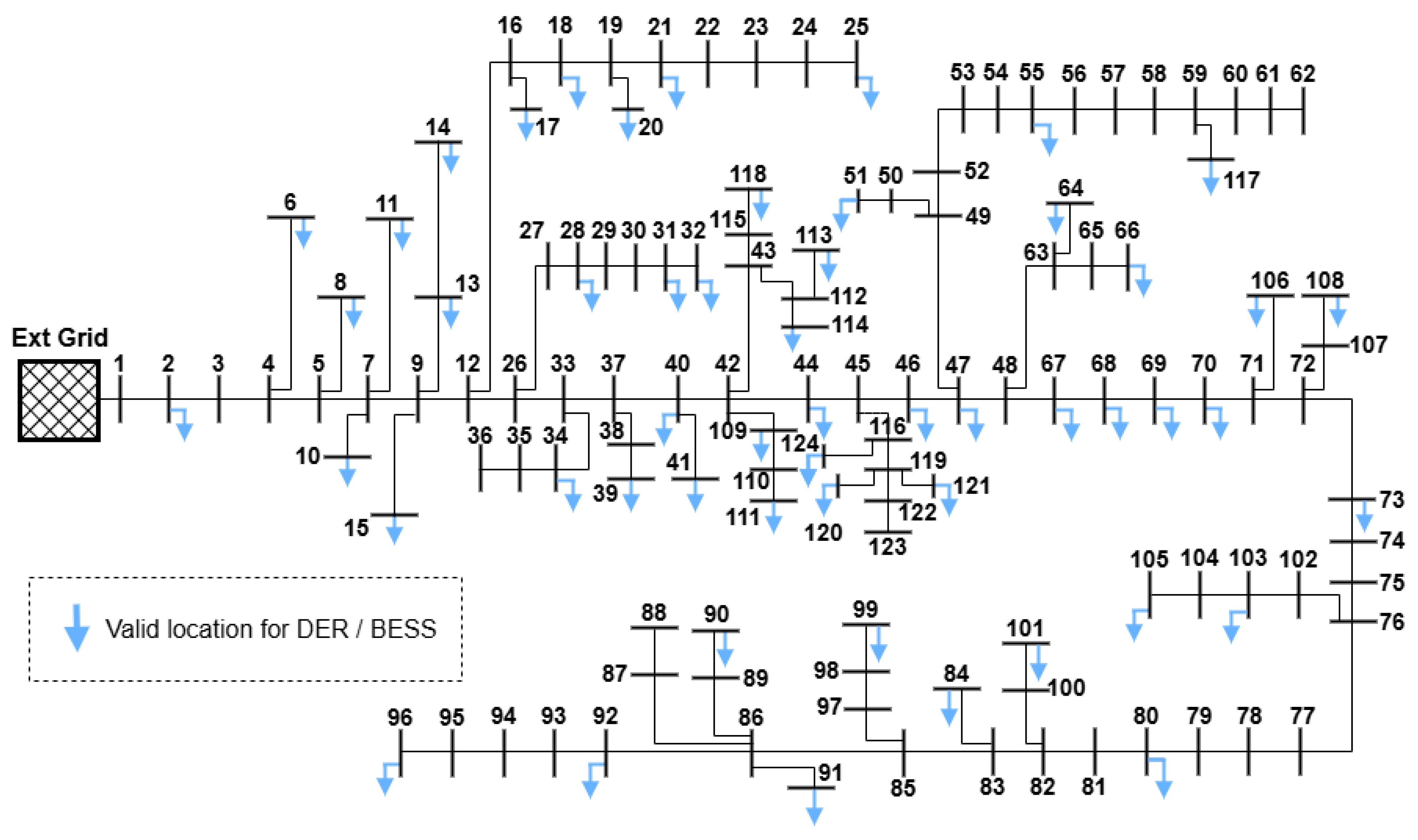
3.1. Reference Grid
3.2. Experimental Parameters
Machine Learning Model Details
4. Results
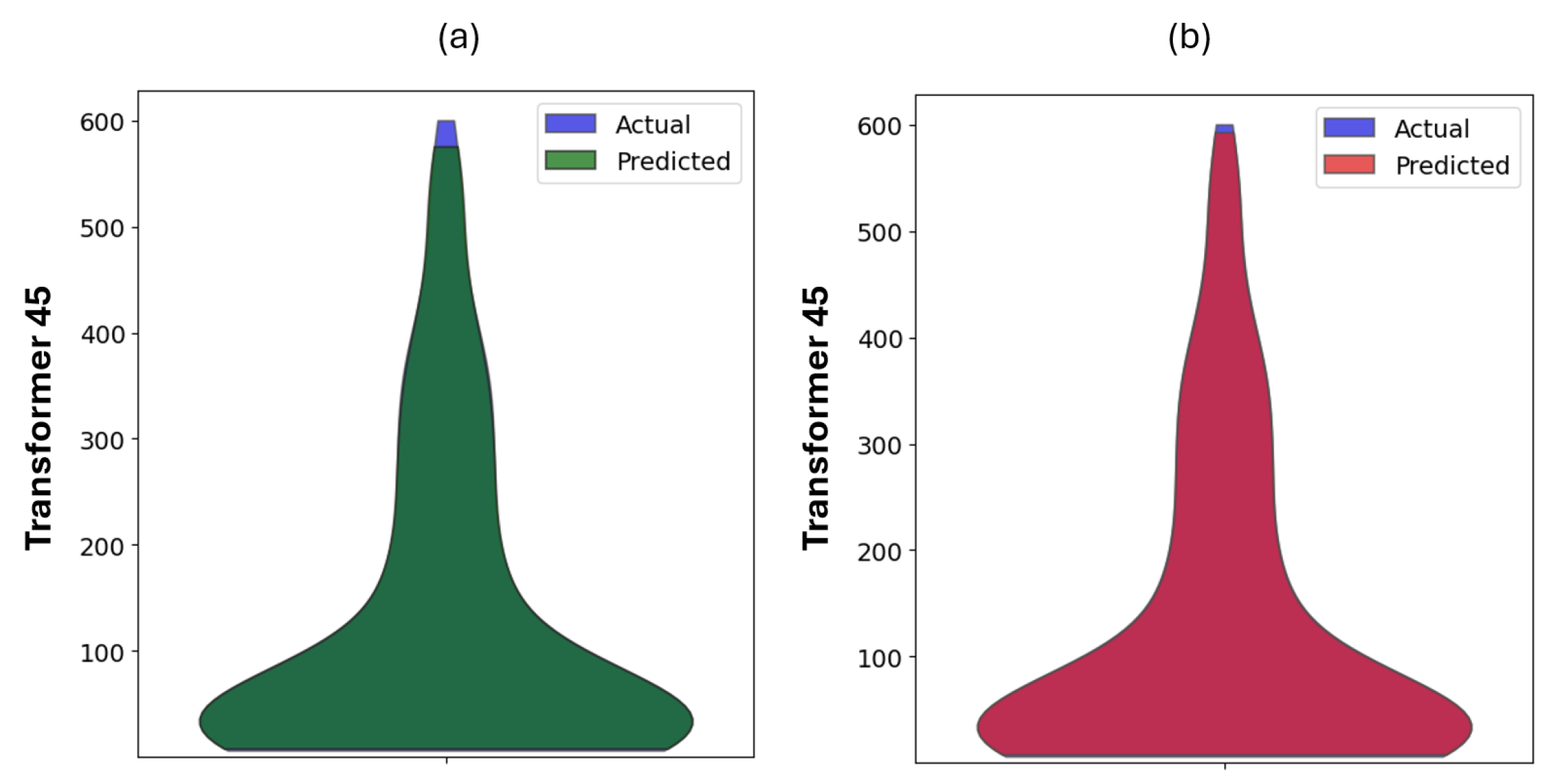
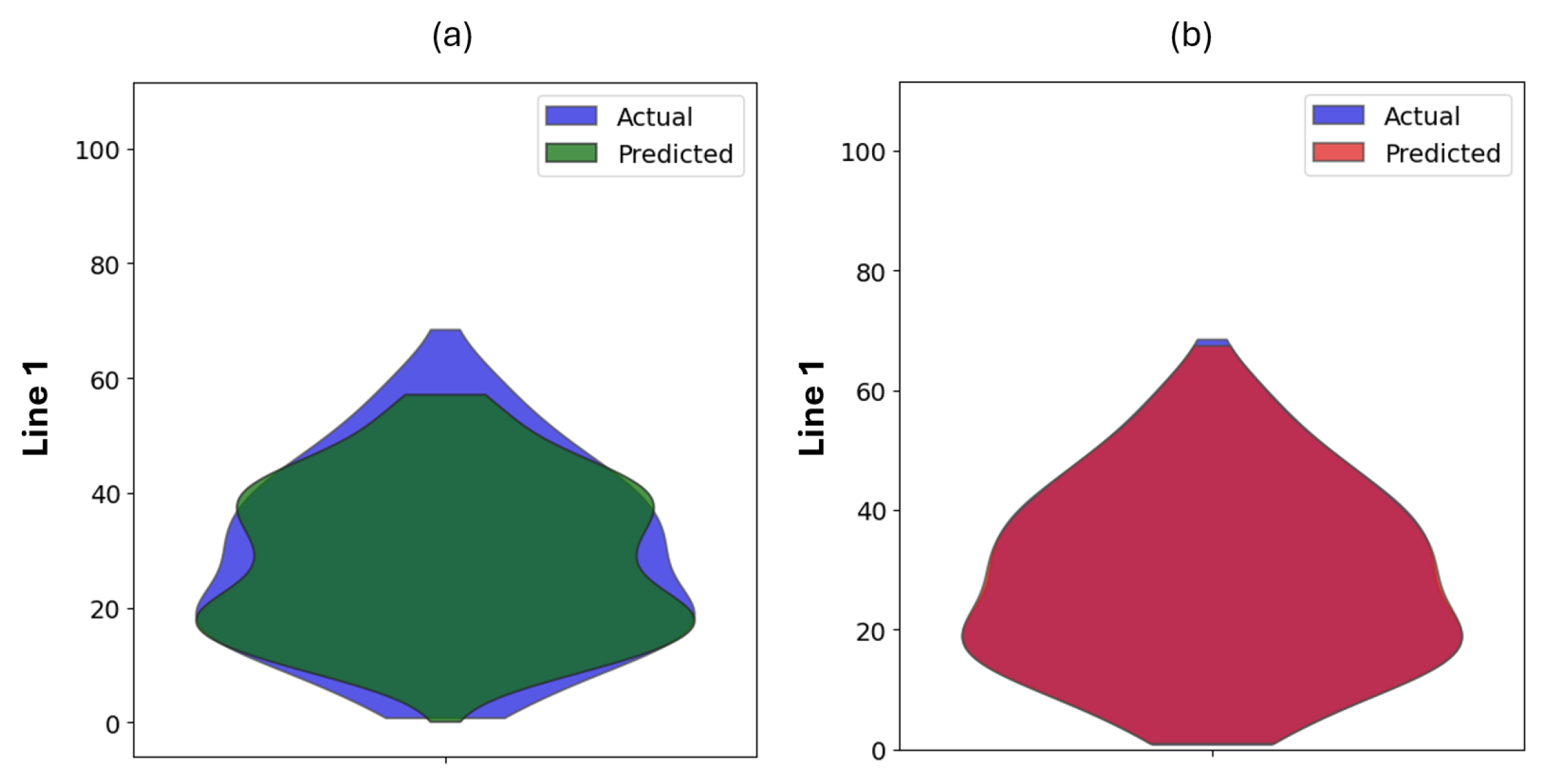
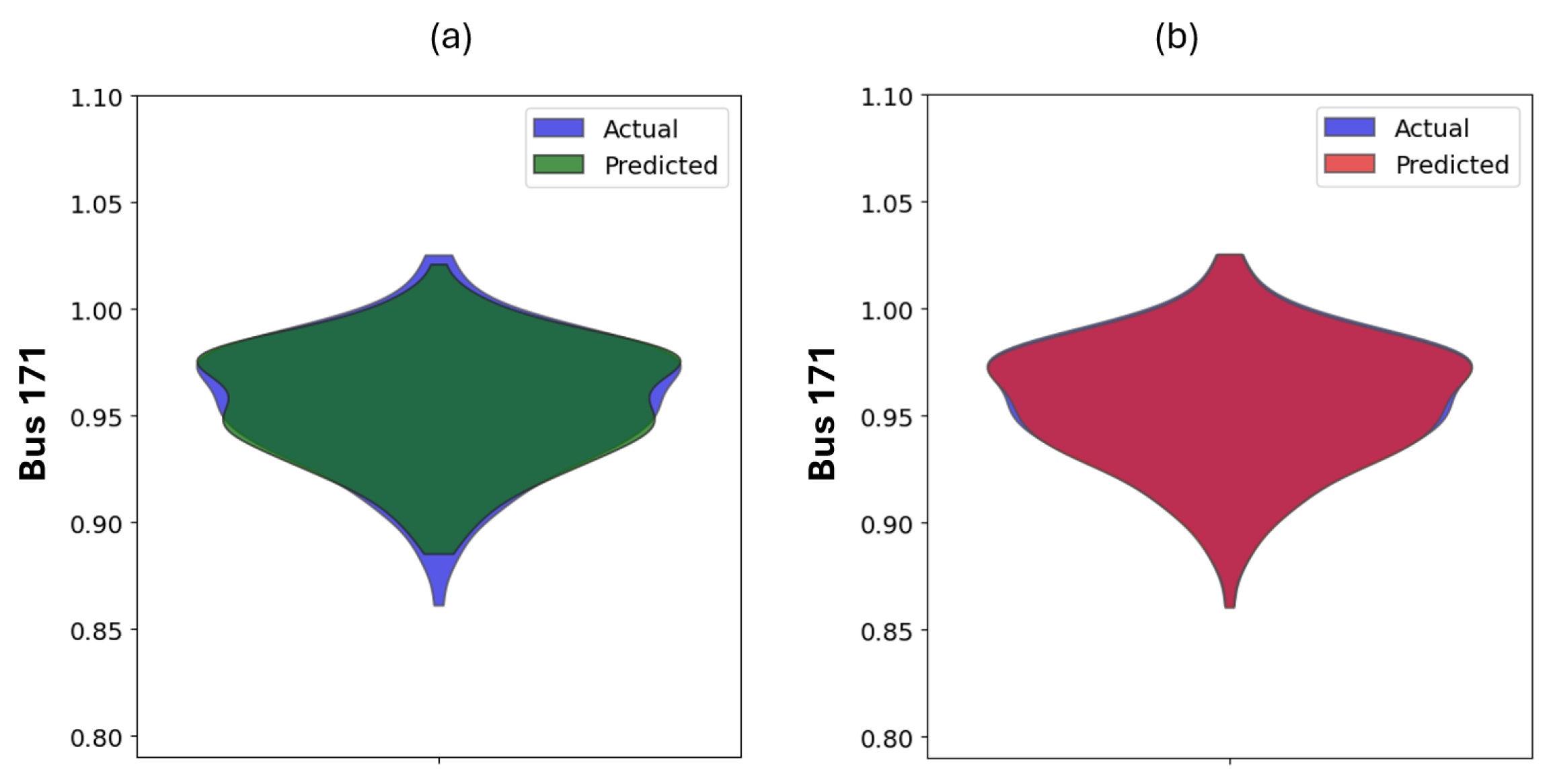
4.1. Predicting Grid Performance with a Single BESS
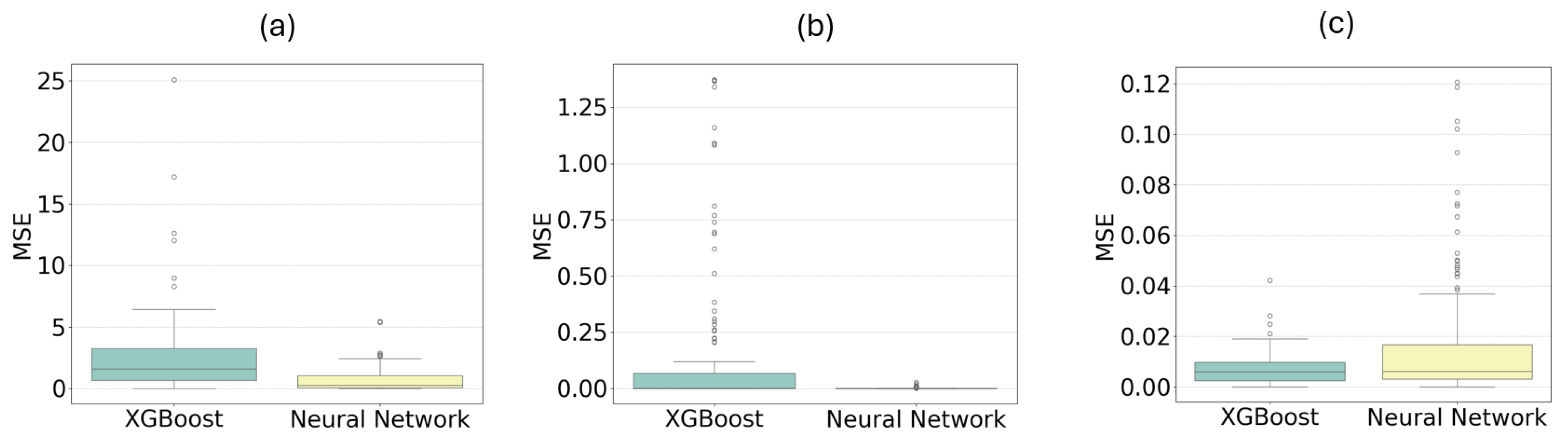
4.2. Distribution of Mean Square Errors for All Models with a Single BESS
4.3. Predicting Grid Performance with Multiple BESSs
4.4. Compilation of Results
5. Discussion
5.1. Inspection of Individual Models
5.2. Comparison Against Traditional Power Flow
6. Conclusions
6.1. Technical Results
6.2. Potential Challenges
6.3. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. Global Installed Grid-Scale Battery Storage Capacity in the Net Zero Scenario, 2015–2030. Available online: https://www.iea.org/data-and-statistics/charts/global-installed-grid-scale-battery-storage-capacity-in-the-net-zero-scenario-2015-2030 (accessed on 5 August 2025).
- International Energy Agency. Unlocking the Potential of Distributed Energy Resources; IEA: Paris, France, 2022; Available online: https://www.iea.org/reports/unlocking-the-potential-of-distributed-energy-resources (accessed on 5 August 2025).
- Ramos, A.F.; Ahmad, I.; Habibi, D.; Mahmoud, T.S. Placement and sizing of utility-size battery energy storage systems to improve the stability of weak grids. Int. J. Electr. Power Energy Syst. 2023, 144, 108427. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J. Smart control of BESS in PV integrated EV charging station for reducing transformer overloading and providing battery-to-grid service. J. Energy Storage 2020, 28, 101224. [Google Scholar] [CrossRef]
- Wei, R.; Chen, Z.; Wang, Q.; Duan, Y.; Wang, H.; Jiang, F.; Liu, D.; Wang, X. A Mechanical Fault Diagnosis Method for On-Load Tap Changers Based on GOA-Optimized FMD and Transformer. Energies 2025, 18, 3848. [Google Scholar] [CrossRef]
- Del Rosso, A.D.; Eckroad, S.W. Energy Storage for Relief of Transmission Congestion. IEEE Trans. Smart Grid 2014, 5, 1138–1146. [Google Scholar] [CrossRef]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M.; Rueda, J.L. PowerFactory applications for power system analysis. In PowerFactory Applications for Power System Analysis; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Zhang, D.; Li, S.; Zeng, P.; Zang, C. Optimal Microgrid Control and Power-Flow Study with Different Bidding Policies by Using PowerWorld Simulator. IEEE Trans. Sustain. Energy 2014, 5, 282–292. [Google Scholar] [CrossRef]
- Cetinay, H.; Soltan, S.; Kuipers, F.A.; Zussman, G.; Van Mieghem, P. Analyzing Cascading Failures in Power Grids under the AC and DC Power Flow Models. SIGMETRICS Perform. Eval. Rev. 2018, 45, 198–203. [Google Scholar] [CrossRef]
- Ding, L.; Bao, Z. Analysis on the Self-Organized Critical State with Power Flow Entropy in Power Grids. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; IEEE: Changsha, China, 2009; Volume 3, pp. 18–21. [Google Scholar] [CrossRef]
- Lukashevich, A.; Maximov, Y. Power Grid Reliability Estimation via Adaptive Importance Sampling. IEEE Control Syst. Lett. 2022, 6, 1010–1015. [Google Scholar] [CrossRef]
- Dagle, J. System Operations, Power Flow and Control; PNNL-SA-125328; Pacific Northwest National Laboratory, U.S. Department of Energy: Arlington, VA, USA, 2017. [Google Scholar]
- Chow, J.H.; Sanchez-Gasca, J.J. Steady-State Power Flow. In Power System Modeling, Computation, and Control; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2019; pp. 9–46. [Google Scholar] [CrossRef]
- Čepin, M. Methods for Power Flow Analysis. In Assessment of Power System Reliability: Methods and Applications; Čepin, M., Ed.; Springer: London, UK, 2011; pp. 141–168. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power Flow Analysis. In Power System Analysis; McGraw-Hill: New York, NY, USA, 1994; pp. 330–355. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2012, 26, 12–19. [Google Scholar] [CrossRef]
- About Pandapower. Available online: https://www.pandapower.org/about/ (accessed on 5 August 2025).
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Azmy, A.M. Optimal Power Flow to Manage Voltage Profiles in Interconnected Networks Using Expert Systems. IEEE Trans. Power Syst. 2007, 22, 1622–1628. [Google Scholar] [CrossRef]
- Rau, N. Issues in the path toward an RTO and standard markets. IEEE Trans. Power Syst. 2003, 18, 435–443. [Google Scholar] [CrossRef]
- Barja-Martinez, S.; Aragüés-Peñalba, M.; Munné-Collado, Í.; Lloret-Gallego, P.; Bullich-Massagué, E.; Villafafila-Robles, R. Artificial intelligence techniques for enabling Big Data services in distribution networks: A review. Renew. Sustain. Energy Rev. 2021, 150, 111459. [Google Scholar] [CrossRef]
- Lu, D.; Hu, D.; Wang, J.; Wei, W.; Zhang, X. A Data-Driven Vehicle Speed Prediction Transfer Learning Method with Improved Adaptability across Working Conditions for Intelligent Fuel Cell Vehicle. IEEE Trans. Intell. Transp. Syst. 2025, 26, 10881–10891. [Google Scholar] [CrossRef]
- Utama, C.; Meske, C.; Schneider, J.; Ulbrich, C. Reactive power control in photovoltaic systems through (explainable) artificial intelligence. Appl. Energy 2022, 328, 120004. [Google Scholar] [CrossRef]
- Crozier, C.; Baker, K. Data-Driven Probabilistic Constraint Elimination for Accelerated Optimal Power Flow. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; IEEE: Denver, CO, USA, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Hasan, F.; Kargarian, A.; Mohammadi, A. A Survey on Applications of Machine Learning for Optimal Power Flow. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; IEEE: College Station, TX, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Saldaña-González, A.E.; Aragüés-Peñalba, M.; Sumper, A. Distribution network planning method: Integration of a recurrent neural network model for the prediction of scenarios. Electr. Power Syst. Res. 2024, 229, 110125. [Google Scholar] [CrossRef]
- Bernadić, A.; Kujundžić, G.; Primorac, I. Reinforcement Learning in Power System Control and Optimization. B&H Electr. Eng. 2023, 17, 26–34. [Google Scholar] [CrossRef]
- Guha, N.; Wang, Z.; Wytock, M.; Majumdar, A. Machine Learning for AC Optimal Power Flow. arXiv 2019. [Google Scholar] [CrossRef]
- Lei, X.; Yang, Z.; Yu, J.; Zhao, J.; Gao, Q.; Yu, H. Data-Driven Optimal Power Flow: A Physics-Informed Machine Learning Approach. IEEE Trans. Power Syst. 2021, 36, 346–354. [Google Scholar] [CrossRef]
- Nellikkath, R.; Chatzivasileiadis, S. Physics-Informed Neural Networks for AC Optimal Power Flow. Electr. Power Syst. Res. 2022, 212, 108412. [Google Scholar] [CrossRef]
- Pagnier, L.; Chertkov, M. Physics-Informed Graphical Neural Network for Parameter & State Estimations in Power Systems. arXiv 2021. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, C.; Liu, C. Model-Informed Generative Adversarial Network for Learning Optimal Power Flow. IISE Trans. 2024, 57, 30–43. [Google Scholar] [CrossRef]
- Zhen, H.; Zhai, H.; Ma, W.; Zhao, L.; Weng, Y.; Xu, Y.; Shi, J.; He, X. Design and Tests of Reinforcement-Learning-Based Optimal Power Flow Solution Generator. Energy Rep. 2022, 8 (Suppl. 1), 43–50. [Google Scholar] [CrossRef]
- Pu, T.; Wang, X.; Cao, Y.; Liu, Z.; Qiu, C.; Qiao, J.; Zhang, S. Power flow adjustment for smart microgrid based on edge computing and multi-agent deep reinforcement learning. J. Cloud Comput. 2021, 10, 48. [Google Scholar] [CrossRef]
- Balduin, S.; Tröschel, M.; Lehnhoff, S. Towards domain-specific surrogate models for smart grid co-simulation. Energy Inform. 2019, 2, 27. [Google Scholar] [CrossRef]
- Junior, J.; Pinto, T.; Morais, H. Hybrid classification-regression metric for the prediction of constraint violations in distribution networks. Electr. Power Syst. Res. 2023, 221, 109401. [Google Scholar] [CrossRef]
- Balduin, S.; Westermann, T.; Puiutta, E. Evaluating different machine learning techniques as surrogate for low voltage grids. Energy Inform. 2020, 3, 24. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Z.; Yu, J.; Zhang, B.; Zhang, Y.; Yu, H. Fast Calculation of Probabilistic Power Flow: A Model-Based Deep Learning Approach. IEEE Trans. Smart Grid 2020, 11, 2235–2244. [Google Scholar] [CrossRef]
- Li, S.; Pan, Z.; Li, H.; Xiao, Y.; Liu, M.; Wang, X. Convergence criterion of power flow calculation based on graph neural network. J. Phys. Conf. Ser. 2024, 2703, 012042. [Google Scholar] [CrossRef]
- Chen, Y.; Lakshminarayana, S.; Maple, C.; Poor, H.V. A Meta-Learning Approach to the Optimal Power Flow Problem Under Topology Reconfigurations. arXiv 2021. [Google Scholar] [CrossRef]
- Menke, J.-H.; Bornhorst, N.; Braun, M. Distribution System Monitoring for Smart Power Grids with Distributed Generation Using Artificial Neural Networks. arXiv 2019. [Google Scholar] [CrossRef]
- Zamzam, A.; Baker, K. Learning Optimal Solutions for Extremely Fast AC Optimal Power Flow. arXiv 2019, arXiv:1910.01213. [Google Scholar] [CrossRef]
- Talebi, S.; Zhou, K. Graph Neural Networks for Efficient AC Power Flow Prediction in Power Grids. arXiv 2025, arXiv:2502.05702. [Google Scholar]
- Jadhav, S.; Sevak, B.; Das, S.; Su, W.; Bui, V.-H. Enhancing Power Flow Estimation with Topology-Aware Gated Graph Neural Networks. arXiv 2025, arXiv:2507.02078. [Google Scholar] [CrossRef]
- Xia, X.; Xiao, L.; Ye, H. Deep Learning-Based Correlation Analysis for Probabilistic Power Flow Considering Renewable Energy and Energy Storage. Front. Energy Res. 2024, 12, 1365885. [Google Scholar] [CrossRef]
- Menke, J.-H.; Dipp, M.; Liu, Z.; Ma, C.; Schäfer, F.; Braun, M. Applications of Artificial Neural Networks in the Context of Power Systems. In Artificial Intelligence Techniques for a Scalable Energy Transition: Advanced Methods, Digital Technologies, Decision Support Tools, and Applications; Springer International Publishing: Cham, Switzerland, 2020; pp. 345–373. [Google Scholar] [CrossRef]
- Jia, J.; Yuan, S.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. Improved Sparrow Search Algorithm Optimization Deep Extreme Learning Machine for Lithium-Ion Battery State-of-Health Prediction. iScience 2022, 25, 103988. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Watson, M.; Chollet, F.; Sreepathihalli, D.; Saadat, S.; Sampath, R.; Rasskin, G.; Zhu, S.; Singh, V.; Wood, L.; Tan, Z.; et al. Keras. Available online: https://keras.io (accessed on 5 August 2025).
- Centre for Intelligent Electricity Distribution. Available online: https://www.sintef.no/projectweb/cineldi/ (accessed on 5 August 2025).
- Sperstad, I.B.; Fosso, O.B.; Jakobsen, S.H.; Eggen, A.O.; Evenstuen, J.H.; Kjølle, G. Reference data set for a Norwegian medium voltage power distribution system [dataset]. Data Brief 2023, 47, 109025. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Matheus, A.; Berg, K.; Gadelha, V.; Aragüés-Peñalba, M.; Bullich-Massagué, E.; Galceran-Arellano, S. Congestion forecast framework based on probabilistic power flow and machine learning for smart distribution grids. Int. J. Electr. Power Energy Syst. 2024, 156, 109695. [Google Scholar] [CrossRef]
- Kazmi, H.; Munné-Collado, Í.; Mehmood, F.; Syed, T.A.; Driesen, J. Towards data-driven energy communities: A review of open-source datasets, models and tools. Renew. Sustain. Energy Rev. 2021, 148, 111290. [Google Scholar] [CrossRef]
- Athay, T.; Podmore, R.; Virmani, S. A Practical Method for the Direct Analysis of Transient Stability. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 573–584. [Google Scholar] [CrossRef]
- Peña, I.; Martinez-Anido, C.B.; Hodge, B.-M. An Extended IEEE 118-Bus Test System with High Renewable Penetration. IEEE Trans. Power Syst. 2018, 33, 281–289. [Google Scholar] [CrossRef]






| Literature | Approach | Conclusion | Drawbacks/Limitations |
|---|---|---|---|
| [36] | Deep Neural Network used to predict bus voltages on the CIGRE LV network | Avg. speed-up factor 2.65; normalized RMSE 7.5%; precision in critical cases 18% | Incompatible with critical grid situations; fixed topology only |
| [37] | LR, SVM, SVR, GB, XGBoost, and ANN models to predict bus voltage constraint violations | Accuracy 94–98%; precision 37–52% | Incompatible with critical grid situations; fixed topology only; no cross-model comparison |
| [38] | LR, RF, KNN, LSTM, and ANN on CIGRE LV and LV-rural3 networks assessing PV and phase-angle effects | RMSE < 0.001 (LR & ANN best); speed-up factor 0.69–9.5× depending on model/topology | Incompatible with critical grid situations; other state parameters omitted; fixed topology only |
| [39] | DNN to approximate power flow on IEEE test systems | Errors < 8.1%; speed-up factor 1234–2040× depending on topology | Incompatible with critical grid situations; single-topology models only |
| [40] | Graph Neural Network to classify convergence of power flow on the IEEE 14-bus system | Accuracy 99.3%; F1 Score 99.3% | Does not compute power flow; only predicts convergence |
| [41] | Meta-learning DNNs pretrained across IEEE 14-, 30-, and 118-bus systems for topology-agnostic initialization | Accuracy 97%; pretrained models train faster on new topologies | No maximum error bounds or critical-case handling; needs many topologies for effective MTL |
| [42] | ANN vs. state estimation using partial measurements in dynamic CIGRE MV network | >99% accuracy for ANN with ample measurements; higher errors under sparse measurements | Incompatible with critical grid situations; high errors with minimal measurement sets |
| [43] | DNN to speed up AC OPF calculations on IEEE test systems | Speed-up factor 6–22× | Restricted to single topology; accuracy metrics and training time missing; requires post-processing to retrieve state parameters |
| [44] | Graph Neural Network used to solve AC OPF on various IEEE test systems | Normalized RMSE < 0.05; R2 scores near 1 | No insight into maximum error or critical-case performance; fixed topology only |
| [45] | Graph Neural Network to solve AC OPF with topology changes on IEEE test systems | RMSE < 0.17; MAE < 0.084; voltage angle error mostly <0.002 rad | No reported speed-up metrics; limited variation; training time 7 h for large networks |
| [46] | DNN to predict power flow fluctuations due to energy storage operations on IEEE test systems vs. probabilistic power flow | Substantial speed-up >700× vs. Latin Hypercube Sampling; max error 6.59% | Restricted to single topology; storage modeling needs improvement |
| Hyperparameter(s) | Value |
|---|---|
| XGBoost | |
| Loss function | Squared Error |
| Number of Estimators | 314 |
| Neural Network | |
| Loss function | Squared Error |
| Activation function | ReLU |
| Number of layers | 3 |
| Neurons per layer | 64, 64, 64 |
| Epochs | 100 |
| Batch Size | 32 |
| Model Type | MSE | RMSE | MAE (%) | Max Error (%) | Speed-Up Factor |
|---|---|---|---|---|---|
| Transformer Loading % | |||||
| XGBoost Single Storage | 2.93 | 1.4 | 0.26 | 16.49 | 45.85 |
| XGBoost Multi Storage | 7.09 | 2.44 | 1.54 | 11.52 | 32.96 |
| ANN Single Storage | 0.81 | 0.71 | 0.43 | 5.43 | 2.87 |
| ANN Multi Storage | 3.13 | 1.54 | 1.09 | 6.89 | 3.67 |
| Line Loading % | |||||
| XGBoost Single Storage | 0.15 | 0.22 | 0.13 | 1.22 | 27.46 |
| XGBoost Multi Storage | 8.09 | 1.42 | 1.04 | 4.95 | 38.10 |
| ANN Single Storage | 0 | 0.02 | 0.02 | 0.12 | 1.43 |
| ANN Multi Storage | 0.05 | 0.13 | 0.09 | 0.69 | 2.49 |
| Bus Voltage p.u. | |||||
| XGBoost Single Storage | 0.01 | 0.08 | 0.05 | 0.37 | 14.11 |
| XGBoost Multi Storage | 0.23 | 0.44 | 0.33 | 1.57 | 19.69 |
| ANN Single Storage | 0.02 | 0.1 | 0.09 | 0.36 | 0.89 |
| ANN Multi Storage | 0.02 | 0.14 | 0.11 | 0.64 | 1.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeptho, P.; Saldaña-González, A.E.; Aragüés-Peñalba, M.; Barja-Martínez, S. Evaluation of XGBoost and ANN as Surrogates for Power Flow Predictions with Dynamic Energy Storage Scenarios. Energies 2025, 18, 4416. https://doi.org/10.3390/en18164416
Yeptho P, Saldaña-González AE, Aragüés-Peñalba M, Barja-Martínez S. Evaluation of XGBoost and ANN as Surrogates for Power Flow Predictions with Dynamic Energy Storage Scenarios. Energies. 2025; 18(16):4416. https://doi.org/10.3390/en18164416
Chicago/Turabian StyleYeptho, Perez, Antonio E. Saldaña-González, Mònica Aragüés-Peñalba, and Sara Barja-Martínez. 2025. "Evaluation of XGBoost and ANN as Surrogates for Power Flow Predictions with Dynamic Energy Storage Scenarios" Energies 18, no. 16: 4416. https://doi.org/10.3390/en18164416
APA StyleYeptho, P., Saldaña-González, A. E., Aragüés-Peñalba, M., & Barja-Martínez, S. (2025). Evaluation of XGBoost and ANN as Surrogates for Power Flow Predictions with Dynamic Energy Storage Scenarios. Energies, 18(16), 4416. https://doi.org/10.3390/en18164416








