Wellhead Choke Performance for Multiphase Flowback: A Data-Driven Investigation on Shale Gas Wells

Abstract

Wellhead choke performance is critical for flowback choke-size managements in unconventional gas wells. Most existing empirical correlations were originally developed for oil and gas flow, and their accuracy for gas/water multiphase flowback remains uncertain. This study presents a data-driven approach to examine the choke–performance relationship during multiphase flowback. We compiled a flowback dataset containing 18,660 surface measurements from 37 shale gas wells in the Horn River Basin. Using machine learning, we modeled choke performance based on flowback features including water rate, gas/water ratio, wellhead and separator pressures and temperatures, and choke size. The models achieved strong predictive accuracy. Based on the machine learning results, we developed a new choke–performance correlation tailored to multiphase flowback. This model was validated against field data and showed reliable performance. The findings provide a useful tool for optimizing choke-size strategies during flowback in hydraulically fractured gas wells, especially in unconventional reservoirs.

1. Introduction

Gas production from shale/tight gas reservoirs has advanced significantly in recent decades. Hydraulic fracturing is one of the primary techniques to unlocking resources from the low-permeability reservoirs. After hydraulic fracturing, wells undergo a flowback process for fracture cleanup, facilitating gas production [1,2,3,4,5,6,7,8]. Flowback operations commonly involve frequent choke-size adjustments, and flowback rates and pressure are highly sensitive to choke-size adjustments [4,5,9]. Recent studies have demonstrated that flowback choke-size managements are critical for preventing proppant return [10,11,12] and securing long-term production from unconventional gas wells [13,14,15,16,17,18]. However, effective choke-size managements thus requires a reliable performance model to capture the relationships between rates, pressure, and choke size.

Theoretically modeling the choke flow is challenging for multiphase flowback due to the rapid and significant changes in rates and pressure, which can change dramatically within hours to days. Also, the flow regime transits quickly from water-dominated flow in the early stages to gas-dominated flow later [4,5,9,11]. Multiphase flow through choke is theoretically linked to the Reynolds number, which depends on fluid density, viscosity, and flow velocity [19,20,21,22]. However, the critical Reynolds number for multiphase flowback through chokes remains unclear. Also, studies have reported large variations in flowback water salinity and temperature [23,24], which cause large fluctuations in fluid density and Reynolds number, adding complexity to choke-performance modeling.

Empirical correlations have traditionally been developed to describe the multiphase flow through choke, particularly for gas and oil production [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Flowback studies have employed these empirical correlations to describe water and gas flow through choke [41,42,43]. However, these empirical correlations were originally developed for steady-state oil and gas flow. The accuracy of empirical correlation and coefficients in capturing the multiphase flow of water and gas through choke for flowback remains uncertain.

Empirical correlations of multiphase flow through choke apply within certain ranges of gas/liquid ratio and flow conditions [21,26,28]. For example, the Gilbert-type correlation assumes critical flow, where flow velocity at the choke exceeds the speed of sound [44]. The multiphase flow rates are independent of downstream pressure, and only upstream pressure is thus required for the Gilbert-type correlation. However, it remains uncertain whether the sonic velocity conditions are met during flowback, and how downstream pressure affects the accuracy of choke-performance predictions.

A recent flowback study [42] employed Perkins correlation [34], which incorporates the upstream and downstream pressure to describe multiphase flowback through chokes. However, the robustness of Perkins correlation for multiphase flowback is limited by the small datasets for calibration. Also, the measurements of downstream pressure are often unavailable during flowback, restricting the broader applications of the Perkins model in flowback choke-size managements. Beyond pressure, factors such as variations in water salinity and wellhead temperature further complicate accurate choke–performance correlation.

Machine learning (ML) provides an alternative to tackling engineering problems where physical models are incomplete and relationships between variables are highly nonlinear. Numerous studies have applied ML algorithms to model the multiphase flow through chokes [45,46,47,48,49,50,51,52], primarily targeting for oil and gas flow. ML techniques have been applied to predict gas and condensate flow behavior through chokes [48]. However, limited work has explored the usage of ML to model the multiphase flowback of water and gas through chokes, leaving a gap in understanding flowback dynamics.

In this study, we present an ML investigation to establish the choke–performance correlation for multiphase flowback. We compiled a dataset containing 18,660 flowback records of 37 shale gas wells from the Horn River Basin. We trained and tested ML algorithms on the flowback dataset to capture the relationship between choke size, pressure, and flow rates. We also evaluated the contribution of variables to choke performance. Based on our findings, we developed a simplified empirical correlation to describe gas/water multiphase flow during flowback.

2. Methodology

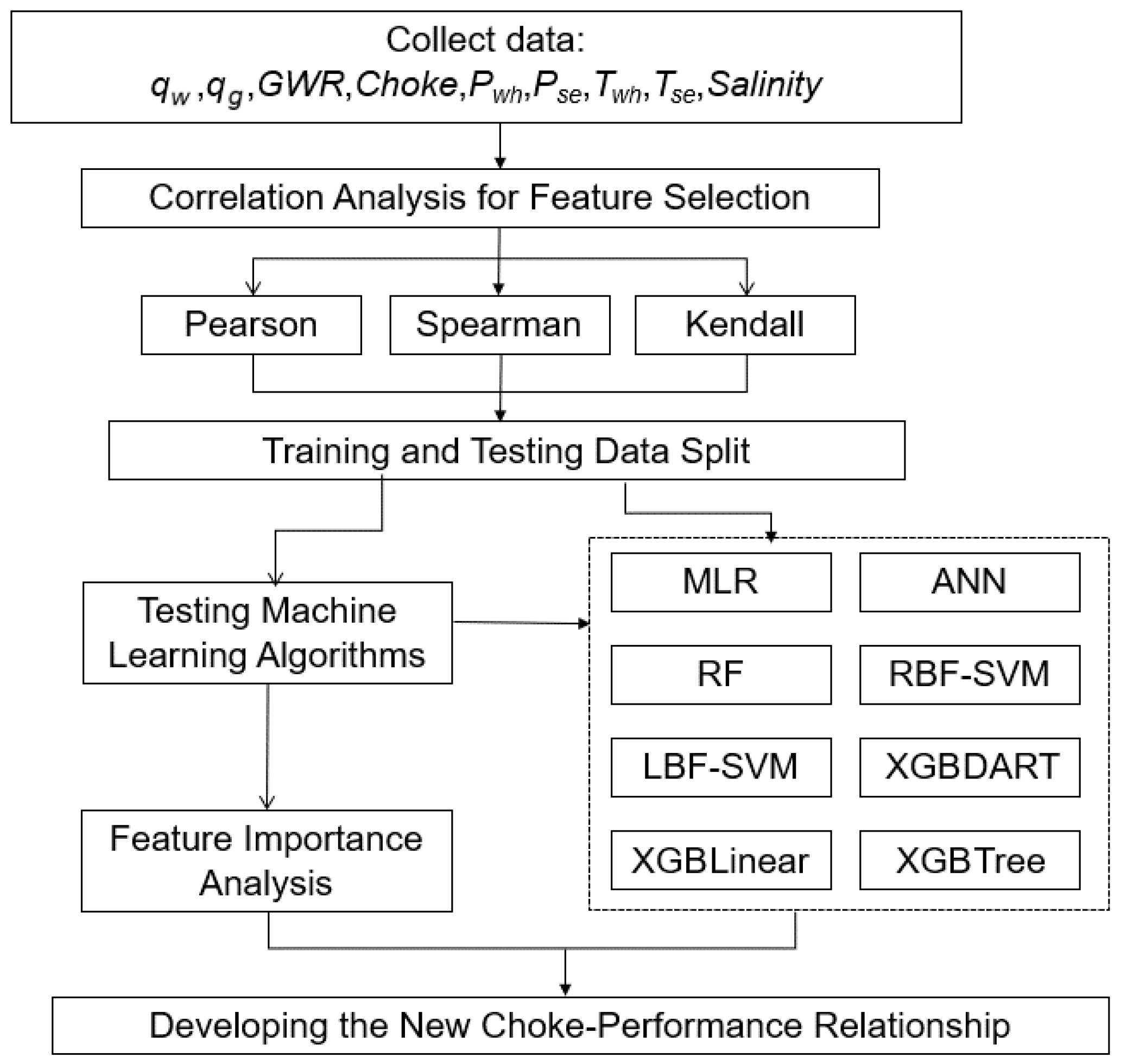
We conducted this work mainly through the following 5 key steps: (a) We collected and preprocessed multiphase flowback data from shale gas wells. (b) We assessed the traditional empirical correlations by fitting to collected flowback data. (c) We conducted correlation analysis of flowback features to identify potential patterns. (d) We implemented machine learning (ML) algorithms on flowback data to link flowback measurements with choke size, and identified the most important features for choke–performance relationship. (e) We developed four new choke–performance relationships for multiphase flowback data through multivariate correlation of key features.

2.1. Data Collection and Preprocessing

In this study, we compiled a flowback dataset from 37 shale gas wells in the Horn River Basin. The flowback dataset includes 18,660 surface measurements of water rate ($q_w$), gas rate ($q_g$), choke size ($Choke$), wellhead pressure ($P_{wh}$), separator pressure ($P_{se}$), wellhead temperature ($T_{wh}$), separator temperature ($T_{se}$), and salinity. We preprocessed the data to ensure quality and consistency. A percentile-based method was used to identify and remove outliers (the threshold of $5th$ and $95th$ percentiles is employed for outlier removal). Records with missing values were excluded to prevent bias in the analysis of choke performance.

2.2. Empirical Choke–Performance Correlations

In this study, we examined the accuracy of traditional empirical choke–performance correlations for multiphase flowback data by linear regression fitting.

Table 1. Empirical correlations and coefficients for multiphase flow through chokes [53].

References	Equation	Empirical Formula	Coefficient
Gilbert [26]	(1)	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.1$, $b=1$,
			$c=1.89$, $d=0.546$
Baxendell [27]	(2)	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.1046$, $b=1$,
			$c=1.93$, $d=0.546$
Ros [28]	(3)	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.05747$, $b=1$,
			$c=2.00$, $d=0.500$
Achong [54]	(4)	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.26178$, $b=1$,
			$c=1.88$, $d=0.650$
Pilehvari [55]	(5)	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.021427$, $b=1$,
			$c=2.11$, $d=0.313$

Note that $Q_l$ represents the liquid rate, STB/day; $D_{64}$ denotes the choke size in 1/64 inch; $P_{\mathit{wh}}^{*}$ indicates the wellhead pressure, psig; ${\mathit{GWR}}^{*}$ is the gas/liquid ratio, Scf/STB; a, b, c, and d are empirical coefficients. All the parameters are in field units.

lists the traditional empirical correlations, together with coefficients for each correlation. We tested empirical choke–performance correlations on flowback data via the following steps: first, we converted the flowback measurements to field units; second, we input the converted wellhead pressure, gas/water ratio, and choke size into empirical formulas, and calculated the water rate using the coefficients listed in Table 1; and third, we conducted linear fitting on the calculated and measured water rate.

2.3. Data-Driven Investigation of Multiphase Flowback Through Choke

As illustrated in Figure 1, we investigate the multiphase flowback through choke via the following key procedures:

(1) Correlation Analysis for Feature Selection: We began by analyzing the relationships among flowback variables to select the most relevant features for machine learning. Pearson, Spearman, and Kendall correlation coefficients [56,57,58] were used to evaluate the strength and consistency of these relationships.

(2) Training and Testing Data Split: Next, we split the dataset into training and testing sets. To determine the optimal ratio, we evaluated five scenarios with training-to-testing splits ranging from 50% to 90%.

(3) Testing Machine Learning Algorithms: We implemented 8 ML algorithms using Python 3.10.7 in the flowback dataset, and assessed the performance of ML algorithms in describing the choke performance. The ML algorithms include Multiple Linear Regression (MLR), Artificial Neural Network (ANN), Random Forest (RF), Support Vector Machines with both linear and radial basis functions (SVM-Linear and SVM-Radial), and 3 versions of Extreme Gradient Boosting (XGBDART, XGBLinear, and XGBTree) [59,60]. We employed these ML algorithms mainly considering their wide applications in data-driven studies of oil and gas industry. Each ML algorithm was run 100 times to eliminate the effects of randomness in training/testing splits.

In this study, we employed the performance metrics of Mean Absolute Error ($MAE$), Root Mean Squared Error ($RMSE$), and the Coefficient of Determination ($R^2$) [61] to evaluate the predictive performance of 8 ML algorithms. $MAE$, $RMSE$, and $R^2$ are defined by

$$MAE={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|y_{i,\mathrm{measured}}-y_{i,\mathrm{predicted}}\right|$$

(1)

where N represents the number of recorded data; $y_{i,\mathrm{measured}}$ is the actual measured value of the wellhead data recorded during flowback; and $y_{i,\mathrm{predicted}}$ is the predicted value.

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(y_{i,\mathrm{measured}}-y_{i,\mathrm{predicted}}\right)}^2}$$

(2)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^N}{(y_{i,\mathrm{measured}}-y_{i,\mathrm{predicted}})}^2}{{\displaystyle \sum _{i=1}^N}{(y_{i,\mathrm{measured}}-y_{i,\mathrm{average}})}^2}}$$

(3)

where $y_{i,\mathrm{average}}$ is the mean of the data recorded.

(4) Feature Importance Analysis: We determined the feature importance of flowback measurements using the outputs from ML algorithms. Also, we designed 5 scenarios with different combinations of flowback features to determine the optimum set of flowback features for describing the choke–performance relationship.

(5) Developing the New Choke–Performance Relationship: We established the new choke–performance relationship by considering the key features determined by the feature importance analysis. We also obtained the coefficients for the choke–performance relationship by fitting the relationship to real flowback measurement data. We further conducted a comparative analysis to obtain the recommended choke-size ranges for the new choke–performance relationship.

3. Field Application with Well/Flowback Information

In this section, we describe the field and well information for application. We report the flowback behaviors of typical shale gas wells, and the statistic results of flowback features of target wells.

3.1. Field and Well Information

In this study, we collected flowback data from 37 shale gas wells completed in the Horn River Basin (more details about the field and target wells can be found in our previous studies [13,62]). The shale gas wells are multi-fractured horizontal wells. After hydraulic fracturing, the shale gas wells remain shut for several months before flowback. Tubing string were placed at the end of flowback, and thus water and gas mainly flowed through the casing during flowback. In this study, we treat the casing pressure data as the wellhead pressure for flowback.

3.2. Flowback Operations and Surface Measurements of Typical Well

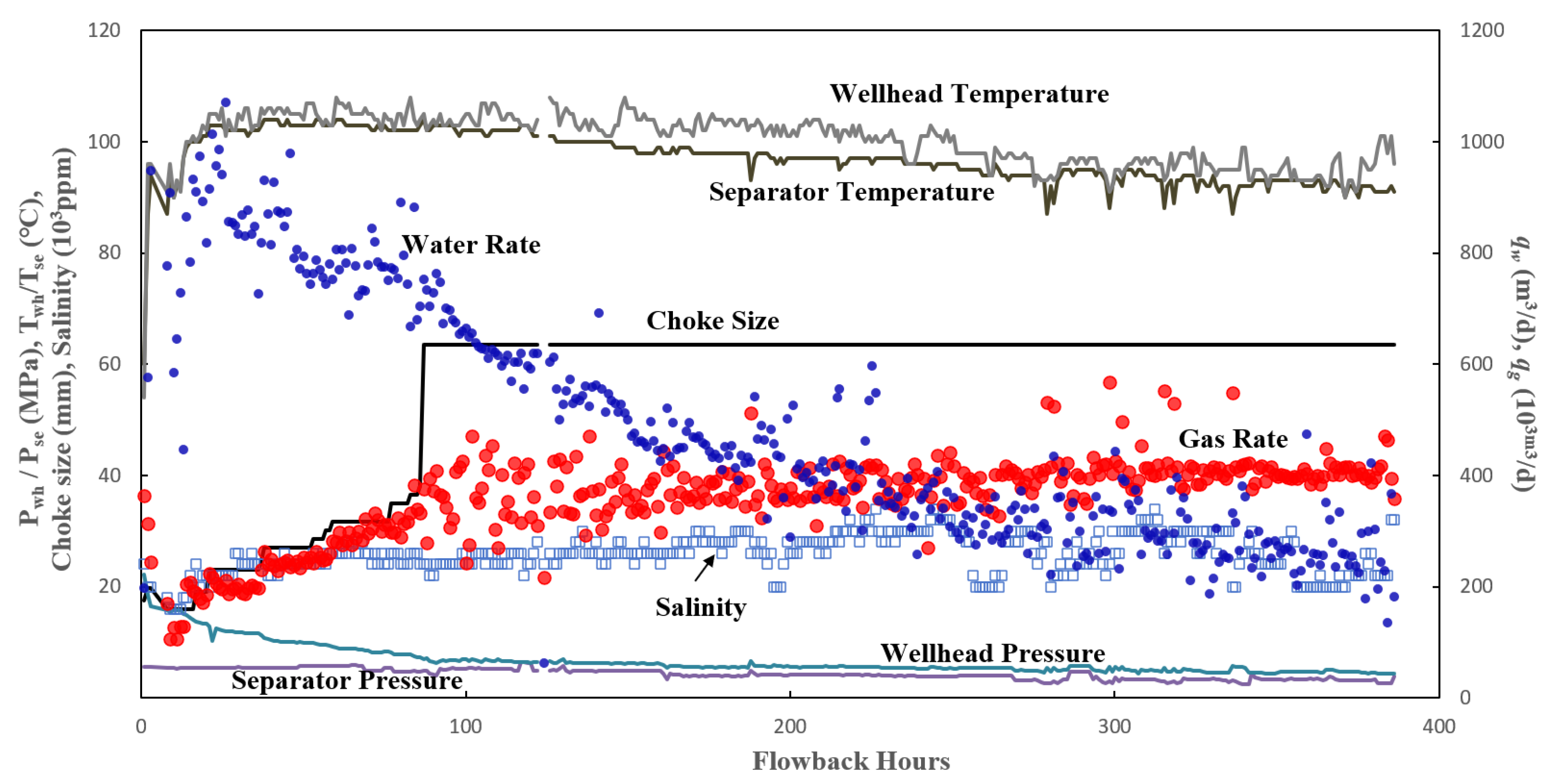
Figure 2 shows the typical flowback profiles of rates, pressure, choke size, and salinity data for a multi-fractured horizontal well completed in the Horn River Shale. The flowback data were reported hourly for target wells over a period of 7–30 days (more details on the flowback measurements can be found in previous studies [9,13,63,64,65]). Flowback generally begins with a relatively small size of choke, and the choke is gradually opened up to accelerate fracture cleanup. Each choke setting typically lasts for several hours to a few days. Most changes in choke size occur early in the flowback period, with the choke eventually stabilizing at a larger size during later stages.

Overall, the flowback profiles show declining trends in wellhead and separator pressure. Water rate initially increases with enlarging choke size, and then gradually decreases over flowback hours. The decreasing water rate is attributed to pressure depletion and multiphase flow effects within fractures [13,66]. Gas rate follows a similar pattern with water rate. Fluctuations in rates and pressure are primarily linked to the choke-size adjustments during flowback. Previous studies [5,67] have reported a “V-shape” behavior in flowback gas/water ratio.

The flowback profiles show pronounced responses of pressure and rates to the change in choke size during early flowback. As shown in Figure 2, a slight increase in choke size leads to a dramatic drop in pressure and increase in rates at early flowback. Comparatively, the flowback rates and pressure become less sensitive to choke-size changes when flowback profiles are stabilized.

Wellhead temperature initially increases, and then declines slightly during flowback. The increase in wellhead temperature is mainly caused by thermal recovery, which is described by the fracturing water being warmed by the formation rock during the extended shut-in periods after hydraulic fracturing [24]. The subsequent decline in wellhead temperature is mainly related to decreasing pressure.

The results of flowback salinity show a steady increase over time, and generally stabilizes after several hundred hours. The trend of flowback salinity reflects an increase in fluid density, and is thought to result from the mixing of injected fracturing fluid with in situ formation water. This trend has also been used as an indicator of fracture complexity in previous studies [23,68].

3.3. Statistical Analysis of Flowback Surface Measurements

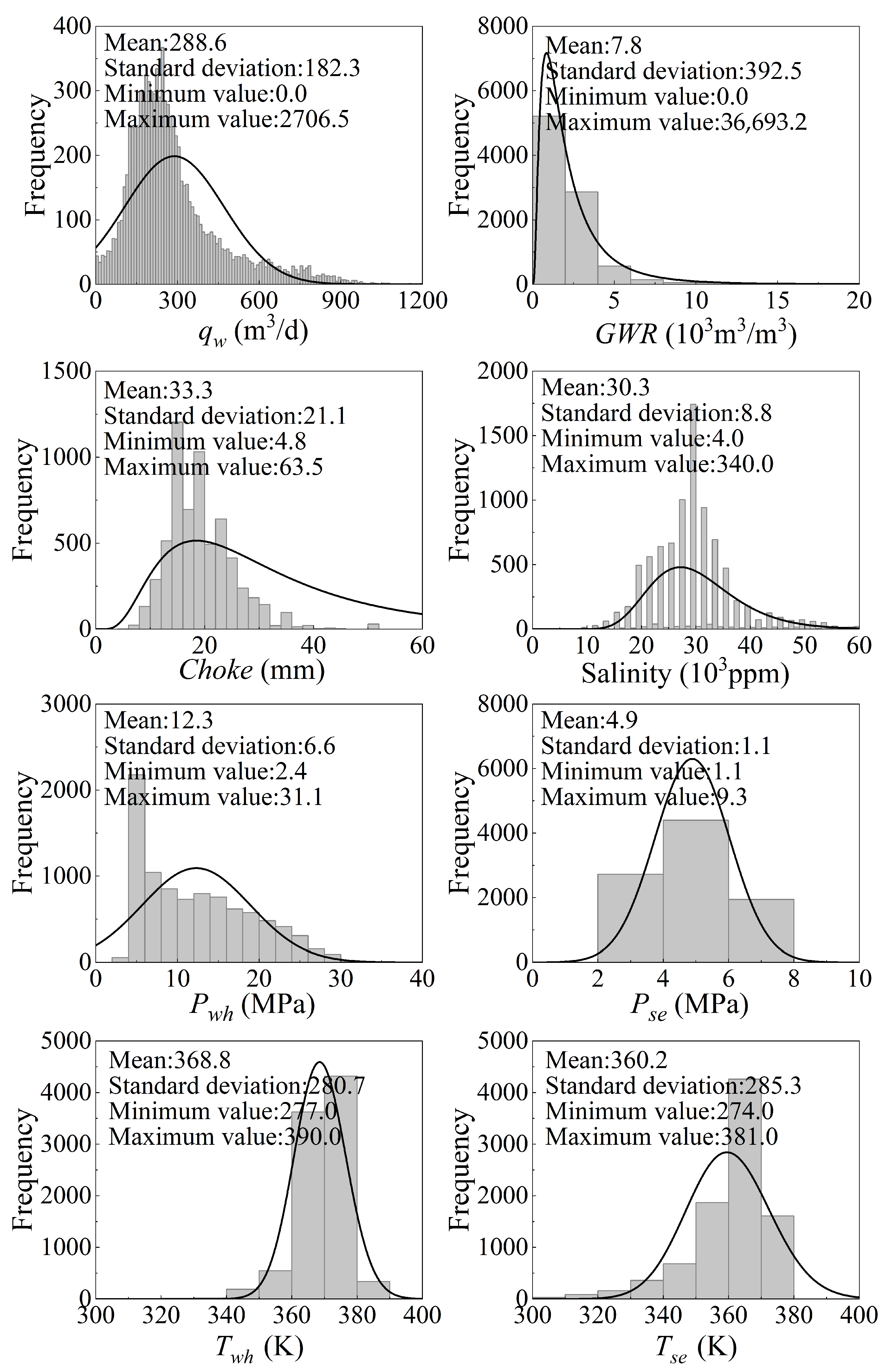
Figure 3 shows the histograms of 18,660 flowback measurements, including $q_w$, $GWR$, $Choke$, $P_{wh}$, $P_{se}$, $T_{wh}$, $T_{se}$, and salinity data (see

Table 2. Statistics of 18,660 flowback surface measurements from 37 Horn River Shale gas wells.

Flowback Features	Abbreviations	Maximum Value	Minimum Value	Average Value
Gas Rate (${\mathrm{m}}^3/\mathrm{d}$)	$q_g$	1,087,000	71,830	429,803
Water Rate (${\mathrm{m}}^3/\mathrm{d}$)	$q_w$	2706	0	288.6
Gas/Water Ratio (${\mathrm{m}}^3/{\mathrm{m}}^3$)	$GWR$	36,693,222	33.1	7800
Choke Size (mm)	$Choke$	63.5	4.8	33.3
Wellhead Pressure (MPa)	$P_{wh}$	31.1	2.4	12.3
Separator Pressure (MPa)	$P_{se}$	9.3	1.1	4.9
Wellhead Temperature (K)	$T_{wh}$	390.0	277.0	368.8
Separator Temperature (K)	$T_{se}$	381.0	274.0	360.2
Salinity (ppm)	$Salinity$	340,000	4000	30,266

for the statistic results of each flowback measurement).

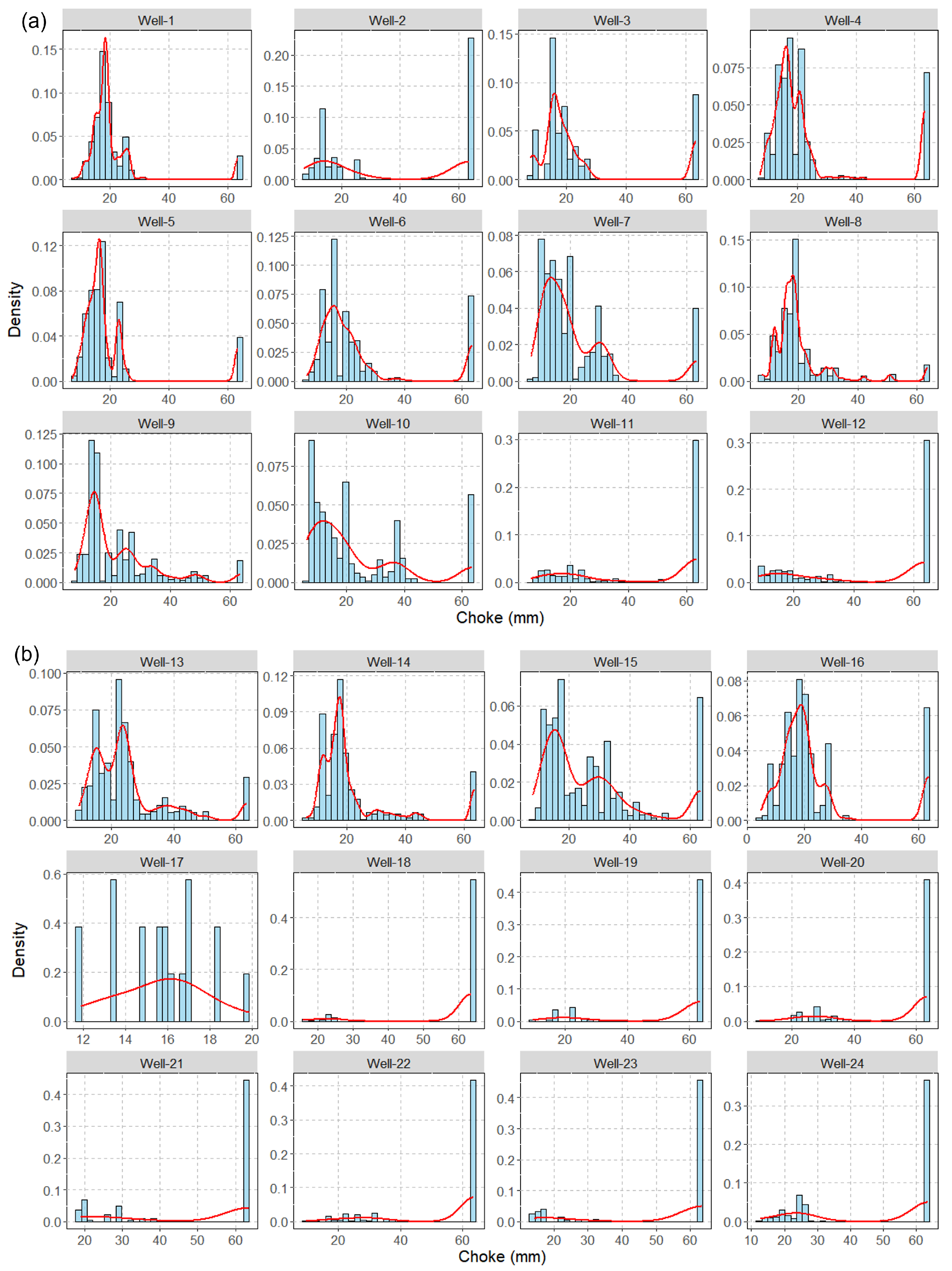
Most wells undergo hundreds of choke-size adjustments over flowback. The wells started flowback with a small-sized choke at 4.762 to 7.938 mm, and ended at the choke of 63.5 mm within 20 days of flowback (see

Table A1. Statistical analysis of choke size for each well (17,646 records of measurements after being preprocessed).

Well Name	First Value (mm)	Maximum (mm)	Minimum (mm)	Average (mm)	Standard Deviation (mm)	Time Range (d)	Number of Choke
Well-1	11.906	63.500	7.144	20.869	10.814	5	638
Well-2	9.525	63.500	7.144	36.677	24.241	21	544
Well-3	7.938	63.500	7.938	24.962	17.890	20	489
Well-4	11.112	63.500	7.144	23.792	16.616	5	546
Well-5	11.906	63.500	7.144	19.866	13.043	1	571
Well-6	12.700	63.500	6.350	24.168	16.943	19	464
Well-7	11.906	63.500	6.350	21.512	14.120	16	482
Well-8	7.938	63.500	7.938	20.524	10.378	20	488
Well-9	7.938	63.500	7.938	22.353	12.428	39	927
Well-10	10.319	63.500	6.350	23.056	17.249	1	422
Well-11	12.700	63.500	6.350	45.317	22.477	29	1176
Well-12	12.700	63.500	8.731	44.418	22.729	31	789
Well-13	9.525	63.500	9.525	25.133	12.531	26	622
Well-14	12.700	63.500	6.350	22.159	14.038	18	455
Well-15	11.906	63.500	7.938	27.021	16.310	36	868
Well-16	12.700	63.500	4.762	23.933	16.255	13	335
Well-17	11.906	19.844	11.906	15.624	2.142	1	19
Well-18	19.050	63.500	15.875	59.231	12.638	14	378
Well-19	9.525	63.500	9.525	55.544	17.029	7	176
Well-20	20.638	63.500	9.525	54.721	15.928	10	399
Well-21	19.050	63.500	19.050	50.989	18.615	5	122
Well-22	17.462	63.500	9.525	55.049	15.967	11	385
Well-23	14.288	63.500	14.288	53.382	18.926	6	146
Well-24	14.288	63.500	12.700	48.814	19.773	17	506
Well-25	12.700	63.500	12.700	38.216	20.391	4	89
Well-26	19.050	63.500	19.050	56.599	14.649	12	301
Well-27	19.050	63.500	9.525	23.918	14.932	9	701
Well-28	11.112	63.500	11.112	26.477	17.861	14	376
Well-29	11.112	63.500	9.525	27.281	17.060	18	695
Well-30	11.112	63.500	11.112	29.753	16.742	7	186
Well-31	9.525	63.500	7.144	19.437	13.563	14	779
Well-32	12.700	63.500	9.525	21.150	10.096	23	842
Well-33	11.112	63.500	9.525	26.286	15.694	11	344
Well-34	12.700	63.500	4.762	20.536	11.549	20	781
Well-35	11.112	63.500	7.938	26.496	17.535	4	281
Well-36	12.700	63.500	11.112	27.953	15.952	7	324

Note: The time range refers to the time spent to reach the maximum choke size.

and Figure A1 in Appendix A). Figure 3 plots the distribution of choke size for flowback. The choke size generally varies from 4.762 mm to 50.8 mm (choke sizes greater than 50.8 mm were excluded from analysis due to the limited number of corresponding measurements). The choke-size data generally follow a normal distribution with a mean value of 19.3 mm (standard deviation: 6.2 mm).

Figure 3 shows asymmetric histograms for water rate, gas rate, and wellhead pressure. Water rate data follow a lognormal distribution with a long tail, suggesting a wide range across the dataset. Most wells were opened for flowback with a water rate of hundreds of cubic meters per day, which declined to just a few cubic meters per day within one to two weeks. A harmonic trend has been reported on water rate decline for shale gas wells [13,66]. The large variation in water rate is largely attributed to differences in fracturing treatment size and choke settings during early flowback.

4. Results and Discussions

4.1. Empirical Formula Fitting

Table 3. Fitting results for five empirical formulas and coefficients (note that the parameters and coefficients were developed based on field units).

Empirical Model	Formulas	Coefficients	${\mathit{R}}^2$
Gilbert [26]	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.1,b=1$, $c=1.89,d=0.546$	0.287
Baxendell [27]	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.1046,b=1$, $c=1.93,d=0.546$	0.277
Ros [28]	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.05747,b=1$, $c=2.00,d=0.500$	0.241
Achong [54]	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.26178,b=1$, $c=1.88,d=0.650$	0.333
Pilehvari [55]	$Q_l=a{\displaystyle \frac{P_{wh}^{\ast b}{D}_{64}^c}{GW{R}^{\ast d}}}$	$a=0.021427,b=1$, $c=2.11,d=0.313$	0.145

summarizes the fitting performance ($R^2$) of five empirical formulas [26,27,28,54,55] applied to the flowback dataset. The five empirical formulas were originally developed to model gas and oil flow through chokes. Each formula was fitted to the flowback measurements, and the corresponding coefficients (a, b, c, and d) are also reported in Table 3.

Overall, the results show an $R^2$ below 0.333, indicating that the empirical formulas are not suitable for capturing the complex relationship between flow rates, pressure, and choke size during multiphase flowback of water and gas.

4.2. Engineering Characteristics

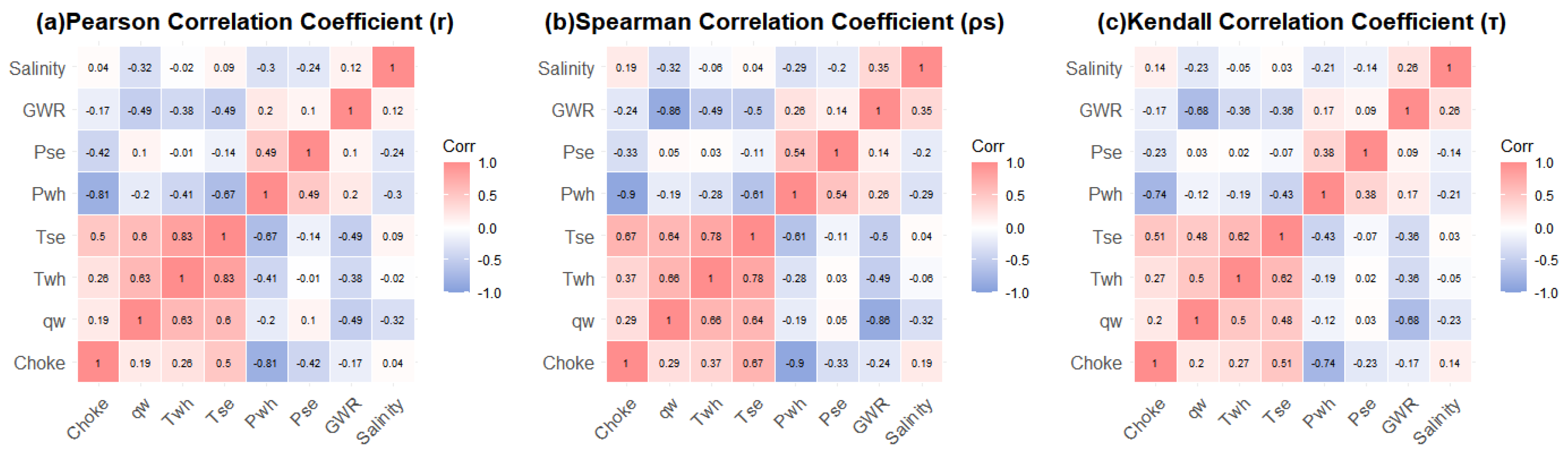
In Figure 4, we plot the correlation matrix between flowback parameters ($N=$ 18,660), including $q_w$, $GWR$, $Choke$, $P_{wh}$, $P_{se}$, $T_{wh}$,$T_{se}$, and $Salinity$. We employed the Pearson, Spearman, and Kendall coefficient (r, ${\rho }_s$, and $\tau$) correlations to measure the correlation between flowback parameters.

Table 4. Correlation coefficients of water rate with 7 flowback parameters.

Features	Correlation
	Pearson Coefficient ($\mathit{r}$)	Spearman Coefficient (${\mathit{\rho }}_{\mathit{s}}$)	Kendall Coefficient ($\mathit{\tau }$)
$Choke$	0.19	0.29	0.20
$GWR$	−0.49	−0.86	−0.68
$P_{wh}$	−0.20	−0.19	−0.12
$P_{se}$	0.10	0.05	0.03
$T_{wh}$	0.63	0.66	0.50
$T_{se}$	0.60	0.64	0.48
$Salinity$	−0.32	−0.32	−0.23

lists the correlation coefficients between $q_w$ and the remaining seven flowback features.

The positive and negative values of r, ${\rho }_s$, and $\tau$ for rates, pressure, and choke generally align with the trends described by empirical formulas (as listed in Table 4). Water rate shows a positive correlation with choke size and a negative correlation with gas/water ratio. As shown in Table 3, the results indicate a strong dependence of water rate on $GWR$, $T_{wh}$, $T_{se}$, and $Salinity$.

Overall, the results highlight strong correlations between choke size and several flowback variables, including $P_{wh}$, $T_{wh}$, $T_{se}$, and $GWR$. High inter-correlation among flowback measurements suggests strong interdependence between these parameters. Based on this analysis, we selected $Choke$, $P_{wh}$, $P_{se}$, $T_{wh}$, $T_{se}$, $Salinity$, and $GWR$ as input features for machine learning.

4.3. Comparing the Machine Learning Algorithms

Figure 5 compares the ML-predicted and measured water rates during flowback. We evaluated eight ML algorithms: MLR, ANN, RF, RBF-SVM, LBF-SVM, XGBDART, XGBLinear, and XGBTree (refer to Appendix C for the settings of hyperparameters of each ML algorithm). We split the flowback data into training and testing data at a 70:30 ratio. We ran each algorithm 100 times to reduce the impact of random variation in data splitting.

Overall, RF, XGBTree, XGBDART, and ANN achieve higher prediction accuracy than the other four algorithms. Among them, RF consistently outperforms all the others on both training and testing datasets. Comparatively, RBF-SVM, MLR, LBF-SVM, and XGBLinear produce lower accuracy. MLR and LBF-SVM may be limited in capturing the nonlinear relationships between water rate, pressure, and choke size.

In Figure 6, we compare the performance metrics ($R^2$, $MAE$, and $RMSE$) of eight ML algorithms on the testing data. Among the eight algorithms, RF achieves the highest $R^2$ and lowest $MAE$ and $RMSE$. Also, the boxplots show a relatively small variation in $R^2$, $MAE$, and $RMSE$ across 100 runs. We thus recommend RF as a reliable ML algorithm for characterizing multiphase flowback behaviors through chokes.

4.4. Feature Selection for Choke Performance

4.4.1. Feature Importance Analysis from Machine Learning

Figure 7 compares the feature importance for predicting $q_w$ using RF, XGBTree, XGBDART, and ANN algorithms. Consistently, GWR is the most influential input across the four algorithms. Also, RF, XGBTree, and XGBDART assign high importance to wellhead/separator temperature, followed by wellhead/separator pressure. The results of ANN suggest that choke size shows a notable contribution to water rate prediction. XGBTree and XGBDART further suggest that salinity may slightly affect water rate prediction, although its influence is minor compared with other variables. These findings indicate that GWR, wellhead temperature, wellhead pressure, and choke size are key parameters influencing multiphase flowback of water and gas.

In Figure 7d, the results of ANN exhibit greater variability in feature importance across runs compared with RF, XGBTree, and XGBDART algorithms. One may expect that feature importance estimates may be more sensitive to random data splits in ANN models than in ensemble-based approaches.

4.4.2. Optimal Feature Combinations

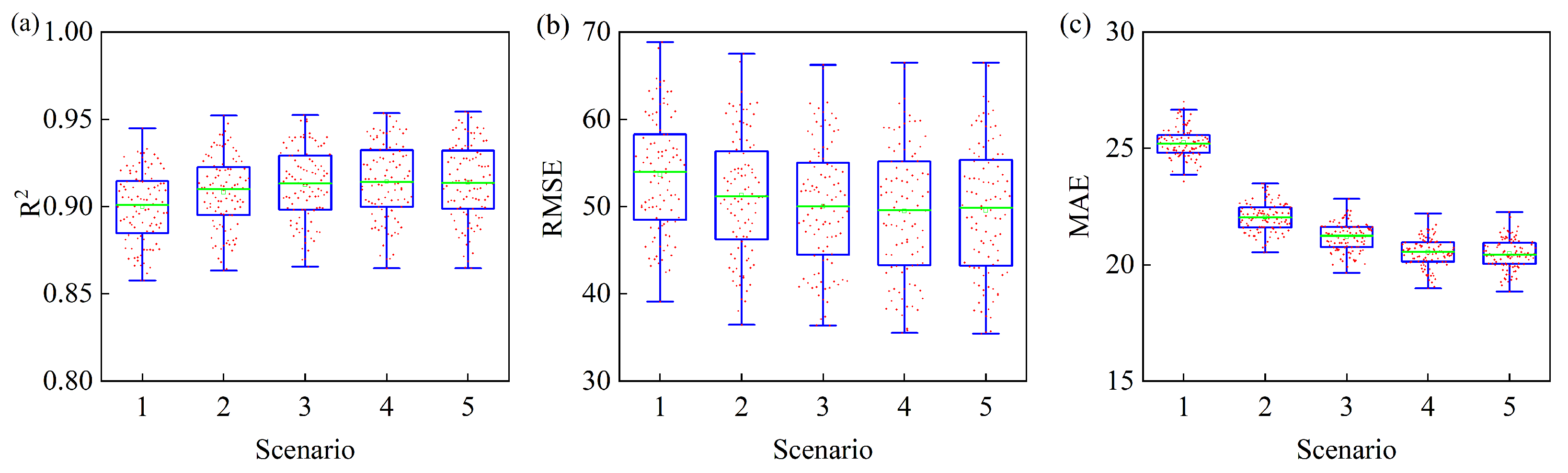
Figure 8 compares the performance metrics for five scenarios using the RF algorithm with different combinations of input features (refer to

Table 5. Statistics of RF models’ performance metrics for 5 scenarios with different combinations of input features.

Scenarios	Input Features	Performance Metrics	Maximum Value	Minimum Value	Average Value
		$R^2$	0.945	0.858	0.900
1	$Choke$, $GWR$, $P_{wh}$	$RMSE$	68.871	39.108	53.641
		$MAE$	27.013	23.581	25.251
		$R^2$	0.952	0.863	0.908
2	$Choke$, $GWR$, $P_{wh}$, $P_{se}$	$RMSE$	67.508	36.481	51.313
		$MAE$	23.489	20.532	22.045
	$Choke$, $GWR$, $P_{wh}$, $P_{se}$	$R^2$	0.952	0.866	0.912
3		$RMSE$	66.235	36.399	50.055
	$T_{wh}$	$MAE$	22.832	19.662	21.192
		$R^2$	0.953	0.865	0.914
4	$Choke$, $GWR$, $P_{wh}$, $P_{se}$	$RMSE$	66.503	35.533	49.466
	$T_{wh}$, $T_{se}$	$MAE$	22.213	18.993	20.542
		$R^2$	0.954	0.865	0.914
5	$Choke$, $GWR$, $P_{wh}$, $P_{se}$	$RMSE$	66.490	35.465	49.575
	$T_{wh}$, $T_{se}$, $Salinity$	$MAE$	22.271	18.851	20.474

for the combination of features for each scenario). Each scenario was run 100 times to reduce the impact of randomness in training and testing splits (see Figure 9 for the corresponding results of the RF algorithm for five scenarios with average $R^2$ values for testing data).

As shown in Figure 8, the average $R^2$ generally increases from Scenario 1 to Scenario 5, while $RMSE$ and $MAE$ generally decrease. The addition of separator pressure in Scenario 2 led to a notable reduction in prediction errors, highlighting its importance in characterizing choke performance. These findings support the use of wellhead and separator pressures as practical substitutes for upstream and downstream pressures in flowback analysis.

Comparing Scenarios 2, 3, and 4 highlights that including wellhead and separator temperatures further enhanced model accuracy. However, Scenario 4 achieved the highest average $R^2$ and lowest $RMSE$ and $MAE$ among the five scenarios, suggesting that the effects of salinity are insignificant for describing choke–performance relationship during flowback. Therefore, we selected $choke$, $GWR$, $P_{wh}$, $P_{se}$, $T_{wh}$, $T_{se}$, and $q_w$ for establishing choke–performance relationship.

4.5. The Effects of Training/Testing Split Ratio

Figure 10 compares the boxplots of $R^2$, $RMSE$, and $MAE$ for 10 runs using training/testing split ratios ranging from 50% to 90%. RF algorithm and features from Scenario 4 were used for the comparative analysis.

Table 6. Statistics of performance metrics of 100 runs of RF model for varying training/testing split ratio.

Training/Testing Split Ratio	Performance Metrics	Maximum Value	Minimum Value	Average Value
	$R^2$	0.945	0.878	0.913
5:5	$RMSE$	60.963	39.349	50.161
	$MAE$	22.745	20.389	21.386
	$R^2$	0.952	0.874	0.916
6:4	$RMSE$	61.166	36.388	49.154
	$MAE$	22.049	19.394	20.873
	$R^2$	0.953	0.865	0.914
7:3	$RMSE$	66.512	35.542	49.470
	$MAE$	22.215	18.999	20.543
	$R^2$	0.962	0.865	0.922
8:2	$RMSE$	66.996	32.576	46.925
	$MAE$	21.877	18.372	20.093
	$R^2$	0.963	0.780	0.922
9:1	$RMSE$	82.405	30.325	46.219
	$MAE$	22.850	17.769	19.855

lists the statistical results of 100 runs for each split ratio.

We observe a general improvement in predictive performance with a higher training/split ratio. As the split ratio increases, the average $R^2$ rises slightly, while $RMSE$ and $MAE$ decline. The highest accuracy was achieved at a 90% split, suggesting that a larger training set enhances model performance. However, the benefits became marginal as the ratio increases further.

Figure 10 shows that the variability of prediction results increases with the split ratio. As shown by the widening boxplots in Figure 10, the range of $R^2$, $RMSE$, and $MAE$ grows from a 50% to 90% split. Table 6 confirms this trend through the corresponding maximum and minimum values. The greater spread implies a reduced model stability at a higher split ratio, which may result from increased noise in the training data or limited sample size in the test set. To balance accuracy and stability, we select a 70/30 training/testing split for the subsequent machine learning investigations.

5. Establishing the New Choke–Performance Relationship

In this section, we introduce four new choke–performance relationships and compare their fitting accuracy against the traditional Gilbert-type formula.

5.1. Choke–Performance Relationships

Equation (4) describes the Gilbert-type choke–performance relationship, which requires four coefficients (a, b, c, and d). As described by Equations (5)–(7), we propose three new types of choke–performance relationships by incorporating the effects of separator pressure and temperatures at both the wellhead and separator (see the results of feature analysis in Section 4.4). The new choke–performance relationships require six coefficients (a, b, c, d, e, and f), and the coefficients are determined by multivariate least squares fitting.

$$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c}{GW{R}^d}}$$

(4)

$$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c{(P_{\mathrm{wh}}-P_{\mathrm{se}})}^e}{GW{R}^d}}$$

(5)

$$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c{\left(\frac{T_{wh}}{T_{se}}\right)}^e}{GW{R}^d}}$$

(6)

$$q_w=a{\displaystyle \frac{P_{wh}^b{Choke}^c{(P_{\mathrm{wh}}-P_{\mathrm{se}})}^e{\left(\frac{T_{\mathrm{wh}}}{T_{\mathrm{se}}}\right)}^f}{{GWR}^d}}$$

(7)

Here, $q_w$ represents the water production volume, m³/d; Choke denotes the size of the choke valve, mm; $P_{wh}$ indicates the wellhead pressure, MPa; $P_{se}$ represents the pressure in the separator, MPa; $T_{wh}$ signifies the wellhead temperature, K; $T_{se}$ is the temperature in the separator, K; $GWR$ is the gas/water ratio, m³/m³; and a, b, c, d, e, and f are empirical coefficients obtained by multivariate least squares fitting to flowback measurements.

In

Table 7. Fitting results of four choke-performance relationships with and without the condition of ${\displaystyle \frac{P_{se}}{P_{wh}}}<0.5$, respectively (the relationships and coefficients are described in SI units).

Formula	All Flowback Data		Flowback Data with $\frac{{\mathit{P}}_{\mathit{se}}}{{\mathit{P}}_{\mathit{wh}}}<0.5$
	${\mathit{R}}^{\mathbf{2}}$ ($\mathit{N}$ = 10,623)	Coefficients	${\mathit{R}}^{\mathbf{2}}$($\mathit{N}$ = 9512)	Coefficients
$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c}{GW{R}^d}}$	0.919	a = 292.1303; b = 0.7344; c = 1.2602; d = 0.7921	0.921	a = 480.5830; b = 1.0008; c = 1.3178; d = 0.8091
$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c{(P_{wh}-P_{se})}^e}{GW{R}^d}}$	0.930	a = 231.0883; b = 0.8067; c = 1.0591; d = 0.7723; e = −0.3309	0.933	a = 375.1778; b = 1.1307; c = 1.1563; d = 0.7905; e = −0.4238
$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c{\left(\frac{T_{wh}}{T_{se}}\right)}^e}{GW{R}^d}}$	0.932	a = 633.9690; b = 0.5943; c = 1.0874; d = 0.7662; e = −0.8210	0.933	a = 469.2333; b = 0.6581; c = 1.1816; d = 0.7851; e = −0.7563
$q_w=a{\displaystyle \frac{P_{wh}^{b}Chok{e}^c{(P_{wh}-P_{se})}^e{\left(\frac{T_{wh}}{T_{se}}\right)}^f}{GW{R}^d}}$	0.932	a = 616.4024; b = 0.6647; c = 1.0757; d = 0.7664; e = −0.0615; f = −0.6988	0.933	a = 396.6285; b = 1.0439; c = 1.1577; d = 0.7890; e = −0.3490; f = −0.1506

, we compare $R^2$ and the coefficients for four types of choke–performance relationships with and without the conditions of $P_{se}/P_{wh}<0.5$, respectively (we excluded the choke size which has less than 100 measurements for the fitting). Overall, we observe an improved fitting accuracy by including $T_{wh}$, suggesting the positive influence of $T_{wh}$ on the model.

Incorporating temperature and separator pressure slightly increases $R^2$ by comparing the fitting results of Equations (4)–(7). Comparatively, the inclusion of separator pressure alone shows limited benefit by comparing the fitting results of Equations (6) and (7). Also, a high fitting accuracy is reached by Equation (6). Consequently, we employ Equation (6) for subsequent analyses, considering the fitting accuracy under the two pressure ratio conditions.

Interestingly, we reach a relatively higher fitting accuracy after screening the flowback data by $P_{se}/P_{wh}<0.5$. The results generally align with earlier studies which suggest that the Gilbert-type model performs best under critical flow conditions (i.e., when downstream-to-upstream pressure ratio is below 0.5). However, we recognize the mismatch between actual downstream pressure and the separator pressure used in our model. Future studies should examine the critical ratio of $P_{se}/P_{wh}$ for the choke-performance relationships.

5.2. The Effects of Choke-Size Range

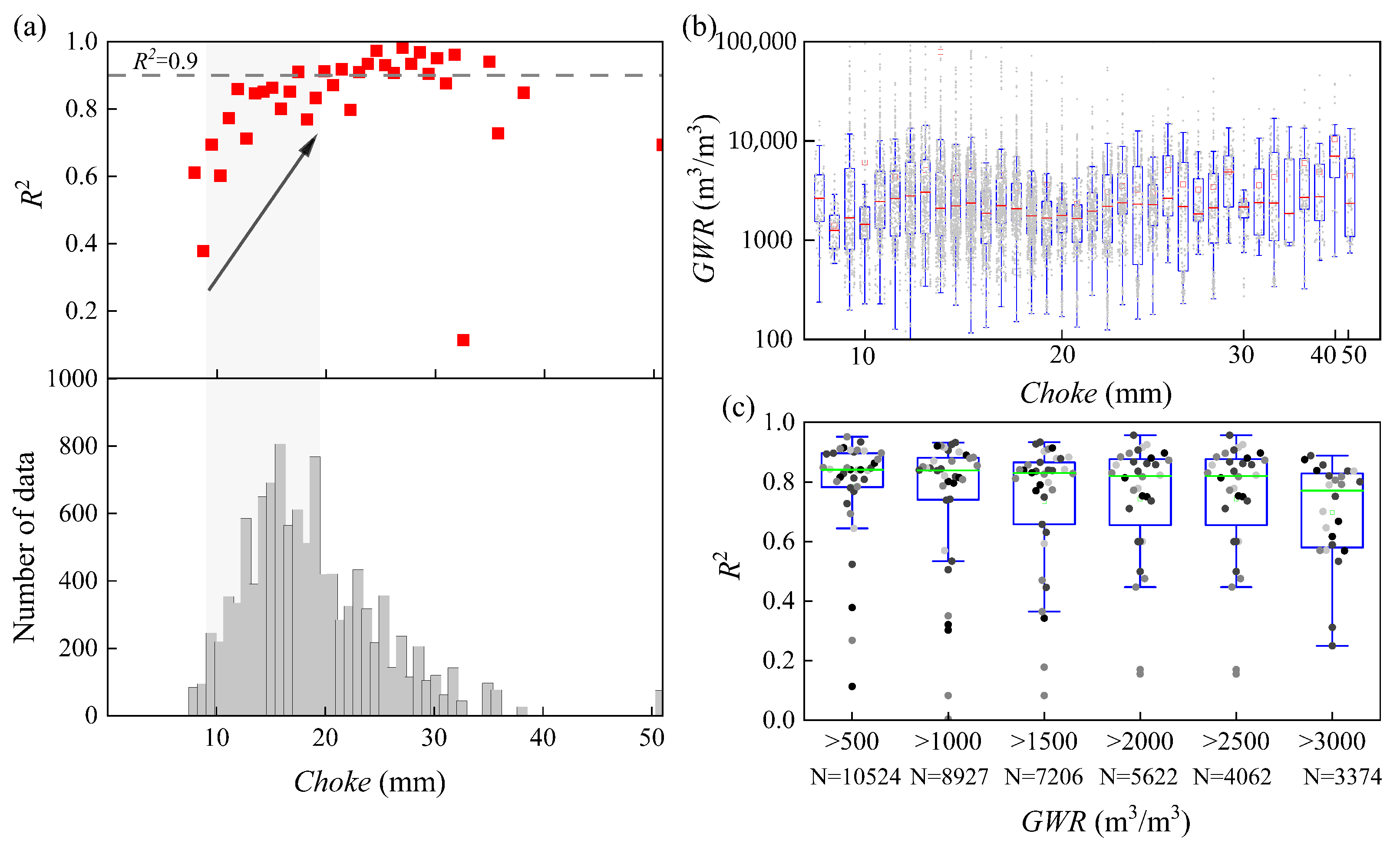
In Figure 11a, we plot the fitting results of $R^2$ for each choke size (7.938 to 50.800 mm) based on the proposed choke-performance model (Equation (6)). We excluded the choke size with fewer than 20 data points, and also excluded the choke size of 63.5 mm due to high variation in $GWR$ for the comparative analysis.

As shown in Figure 11a, $R^2$ generally increases with choke size increasing from 7.938 to 19.844 mm, aligning with the increasing number of measurements (see Figure 11a below). The results indicate that larger datasets improve the reliability of the fitted coefficients.

In general, the proposed model performs best for choke sizes between 17.462 and 34.925 mm. In this range, $R^2$ values typically exceed 0.9 (Figure 12). However, exceptions exist in choke sizes of 30 mm and 32.544 mm, which show a lower accuracy (see Figure A2 in Appendix B) primarily due to smaller datasets ($N=64$ and $N=444$, respectively). We therefore recommend applying the proposed model and coefficients specifically within the 17.462–34.925 mm range.

In Figure 11a, the results show a decreasing trend in $R^2$ for a choke size greater than 30.162 mm. The reduced accuracy at large choke sizes is partially attributed to fewer available measurements. Also, Figure 11b shows a relatively larger variation in $GWR$ for a choke size bigger than 30.162 mm, which may further reduce model accuracy.

By applying a natural logarithm to Equation (6), the proposed model becomes conceptually similar to a multiple linear regression. However, the results of the multiple linear regression indicate limited predictive performance at extremely high water rates (refer to Figure 5). The proposed model is thus expected to perform more reliably under stabilized water rate conditions during flowback.

Figure 11c compares $R^2$ with $GWR$ across all the choke sizes. Excluding low $GWR$ values from the dataset generally reduces $R^2$, suggesting the proposed model is more effective under low-$GWR$ conditions. However, the limited data for large choke sizes also contributes to reduced accuracy. Therefore, the proposed choke-performance model shows satisfying performance in characterizing multiphase flowback. Future work is encouraged to validate the model with more flowback data, particularly for larger choke sizes and a wider range of $GWR$ conditions.

6. Significance, Limitations, and Future Works

Our data-driven study demonstrated that ML models were a valuable tool for characterizing multiphase flowback through chokes at wellhead. Also, a simplified version of an empirical choke-performance model we proposed provides reliable predictions under multiphase conditions for flowback. The ML and empirical models offer tools that help monitor the choke conditions [69] during flowback. The models also offer a practical way to estimate flared gas volumes [70,71,72,73] during early flowback, using common field data such as water rate, choke size, and wellhead pressure. While the results are promising, this study is subject to several limitations that suggest opportunities for future research, as outlined below.

We selected the flowback data from 37 Horn River wells mainly because of the abundance of hourly flowback measurements. We also clarify that the findings of this study should not be constrained by a specific field or basin, and further validation is needed wherever flowback data from other fields are available.

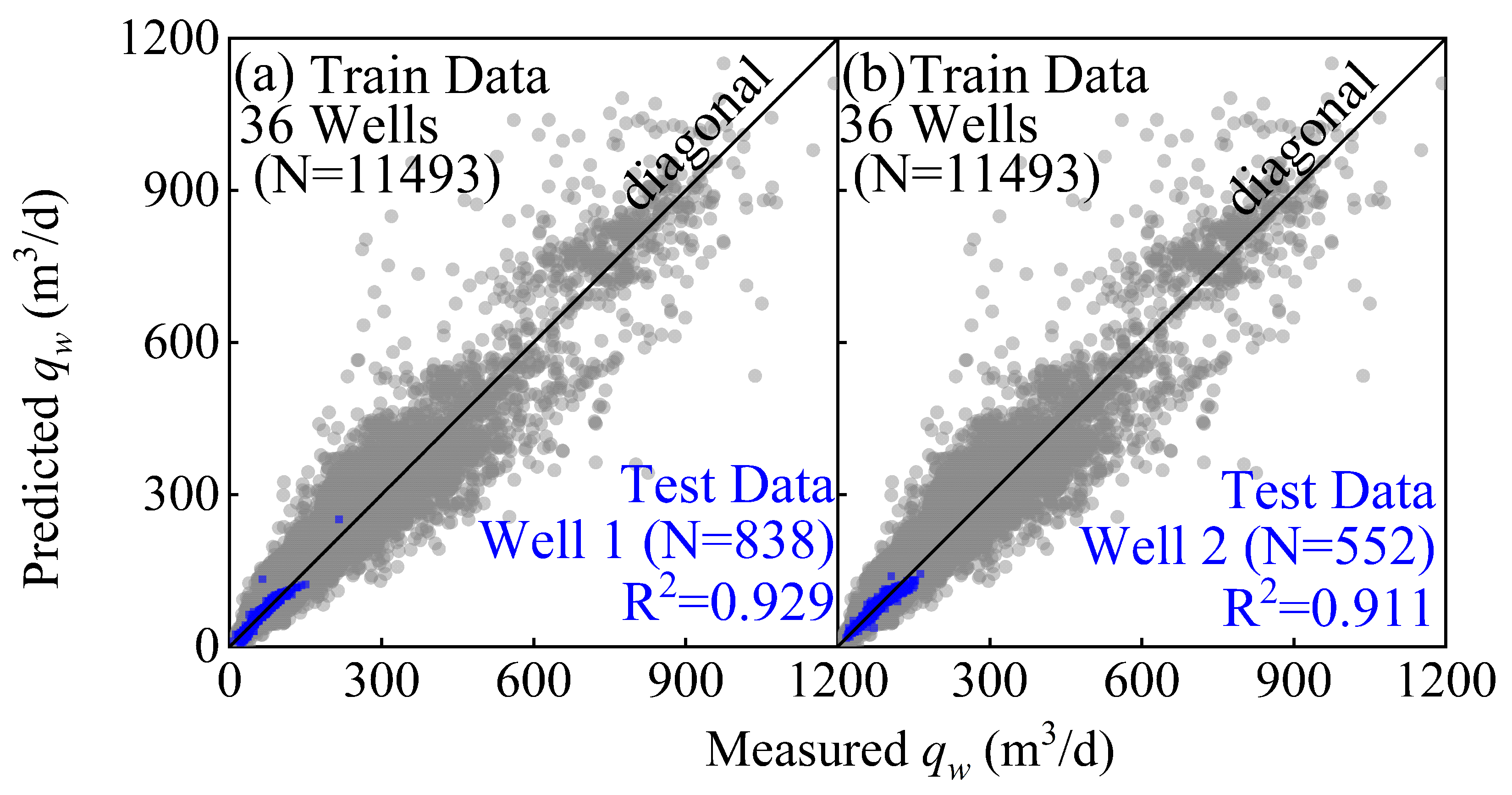
We acknowledge the potential for data leakage due to the random sampling approach used to split the training and testing datasets across 37 wells. The random sampling method may allow neighboring data points from the same well and day to appear in both training and testing sets, which may artificially boost model performance. To address this concern, we conducted an additional test using a well-by-well data split. Specifically, we used flowback data from 36 wells for training and reserved one well for testing, and the results suggested that the model maintained a high predictive accuracy (see two case studies in Appendix D). The results suggest that the data-leakage effects are likely minimal. Future studies are recommended to employ time-series ML methods for multiphase choke flowback data, which may better capture temporal patterns and reduce the risk of data leakage related to sampling across time.

This study used a standard set of ML algorithms for data-driven investigation on the problem of multiphase flowback through chokes. We chose these algorithms based on their proven effectiveness in petroleum-engineering applications. Using multiple algorithms also allowed us to identify the most suitable one for our flowback data and ensure strong predictive performance. Future studies are recommended to explore more advanced ML techniques to further enhance model accuracy and generalization.

7. Summary and Conclusions

In this study, we collected a total of 18,660 measurements of a multiphase flowback dataset from 37 shale gas wells from the Horn River Basin. We performed eight machine learning algorithms on the flowback dataset to predict the choke performance, and identified the key features for describing choke–performance relationship. We further established a new choke–performance relationship for multiphase flowback based on the results of machine learning. A set of coefficients for the new choke–performance relationship is recommended for certain ranges of choke size during flowback. The key conclusions are summarized as follows:

(1) In this study, the empirical choke–performance correlations and coefficients traditionally developed for oil and gas flow are inadequate for modeling gas and water flowback data.

(2) Applying the machine learning algorithms of Random Forest, XGBTree, XGBDART, and ANN on the flowback data leads to a high prediction accuracy in choke performance. The prediction accuracy of Random Forest is improved by including the separator pressure and temperature into the inputs of choke size, gas/water ratio, and wellhead pressure and temperature.

(3) This study developed a new choke–performance relationship which links the flowback rate with choke size, gas/water ratio, wellhead pressure/temperature, and separator temperature. The accuracy of new choke–performance relationships and coefficients has been validated for choke sizes ranging from 17.462 to 34.925 mm. The new choke–performance relationship presented in this study needs further validation in other fields wherever more flowback data are available.