Cost Implications for Collaborative Microgrids: A Case Study of Lean—Heijunka Microgrid Operations Mitigating Renewable Energy Volatility
Abstract
1. Introduction
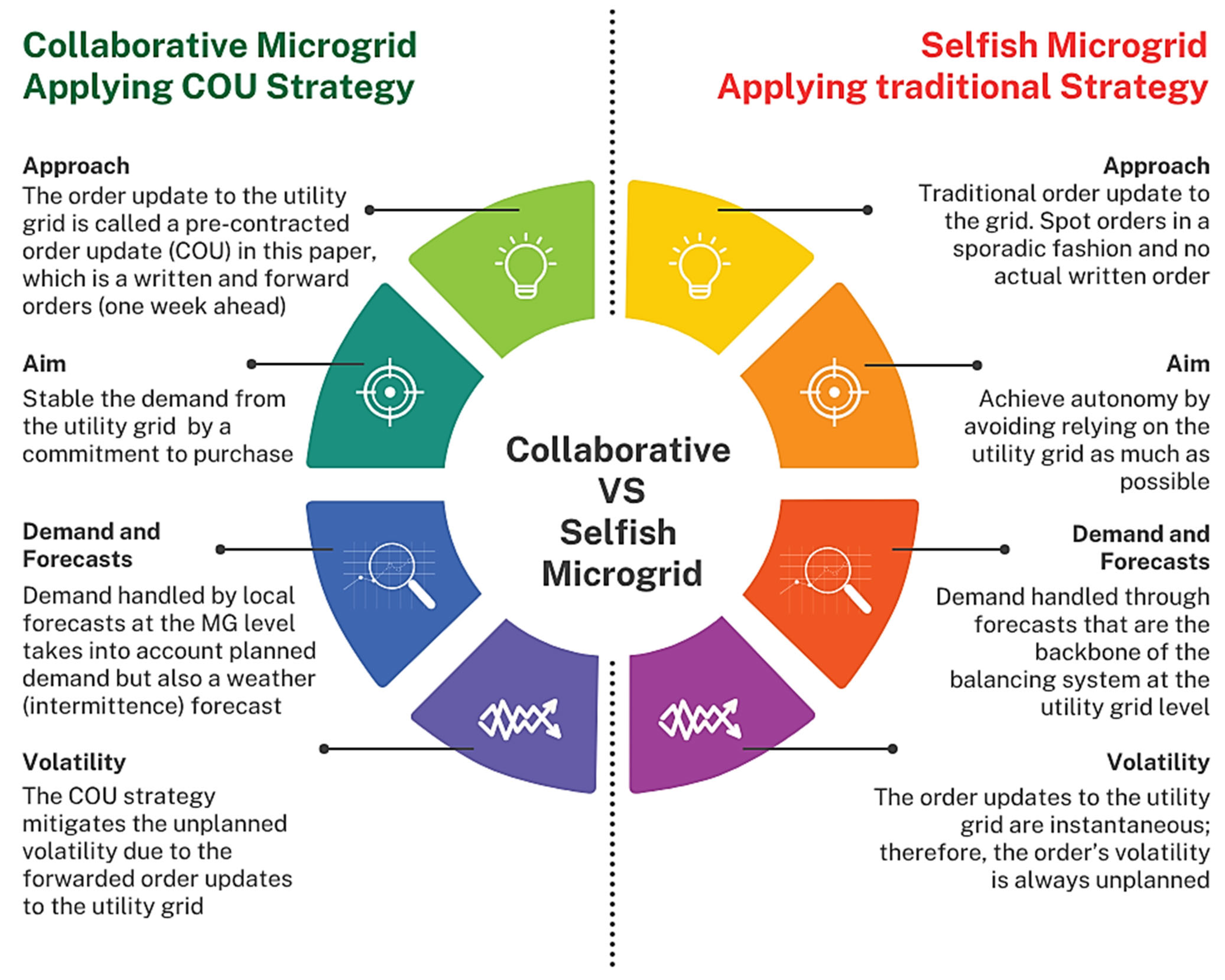
1.1. Collaborative Versus Selfish MG
1.2. Utility Grid Versus Diesel Generator as a Backup Generation Solution
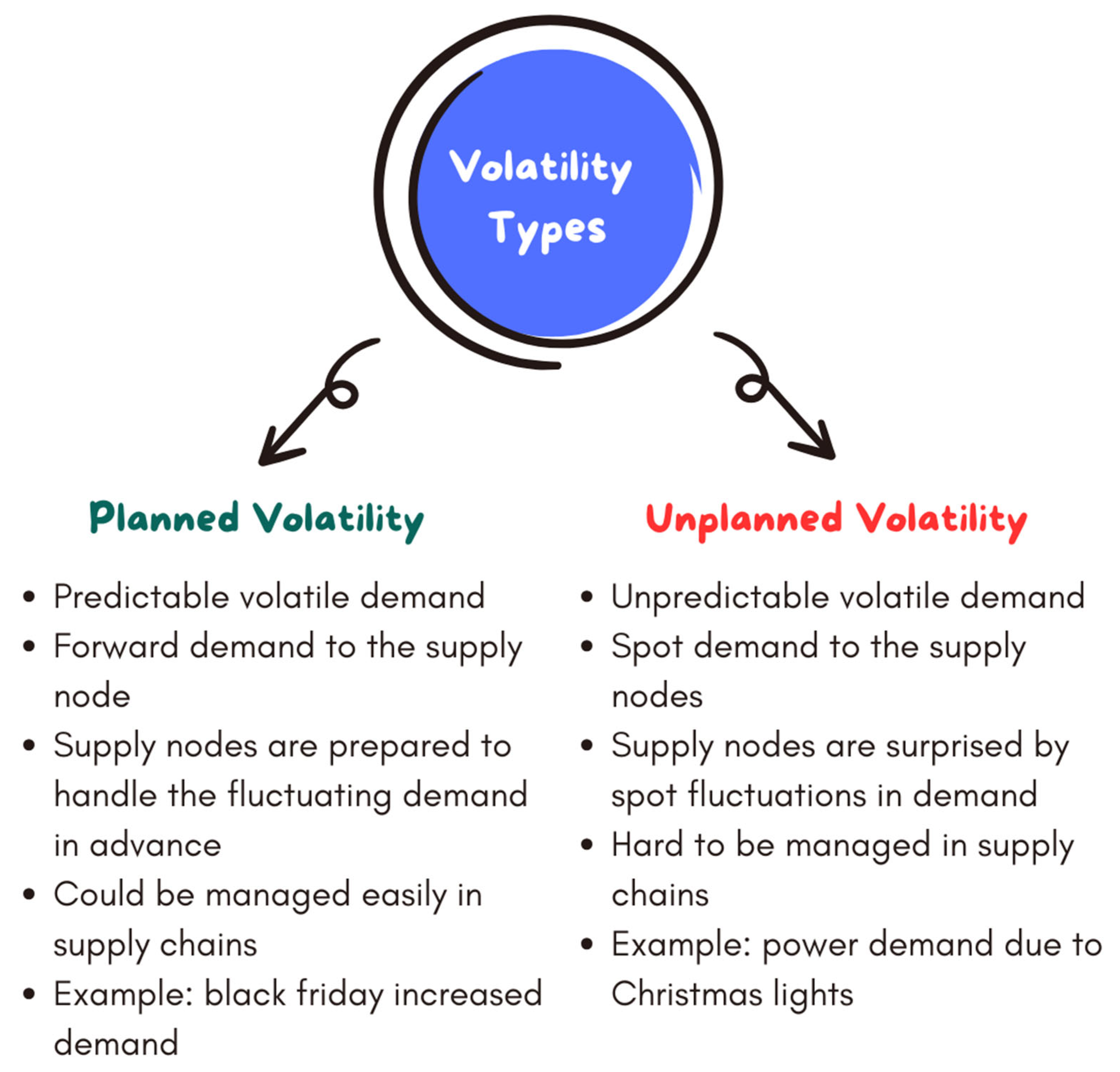
1.3. Heijunka Versus Planned Volatile Orders to the Utility Grid
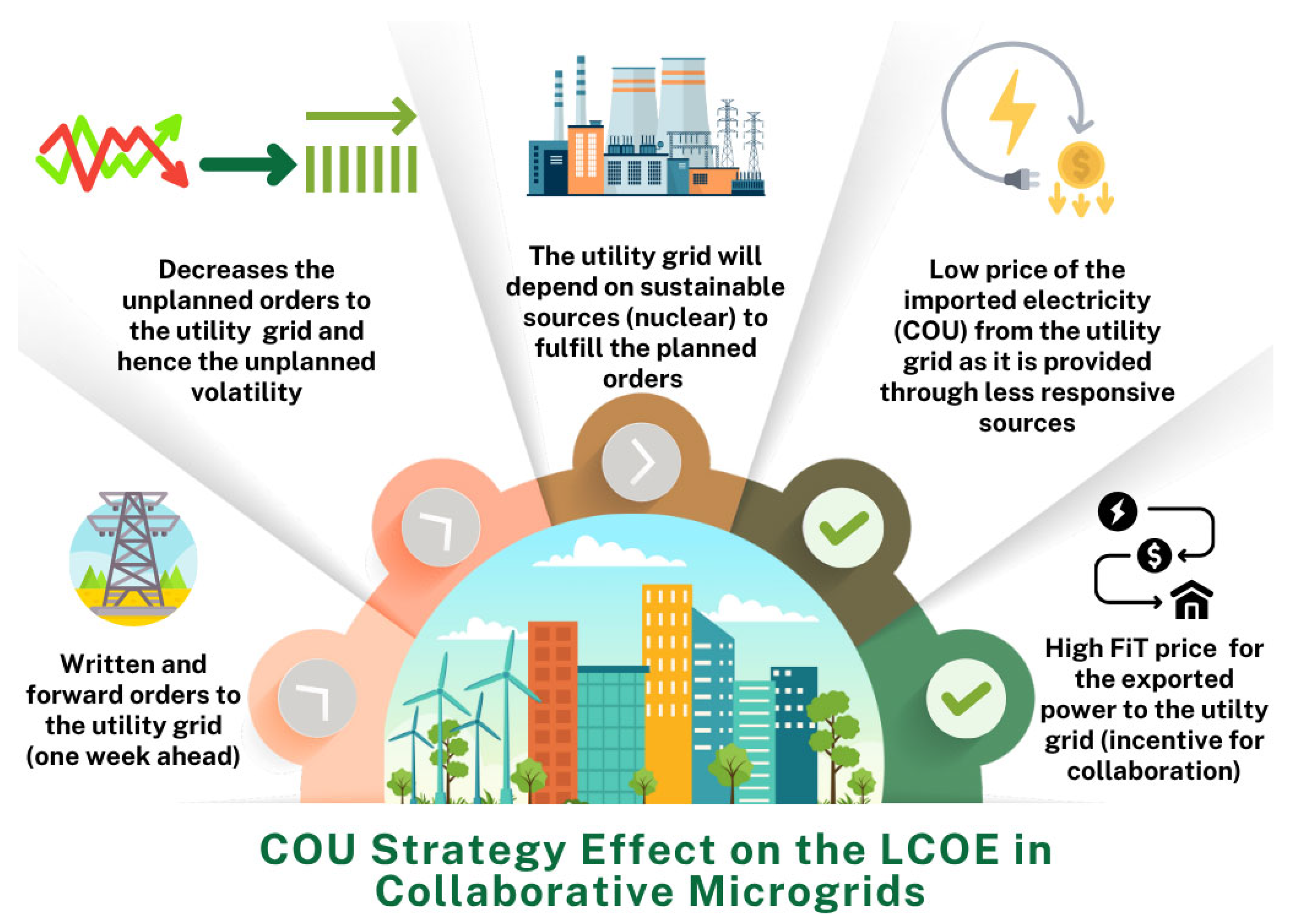
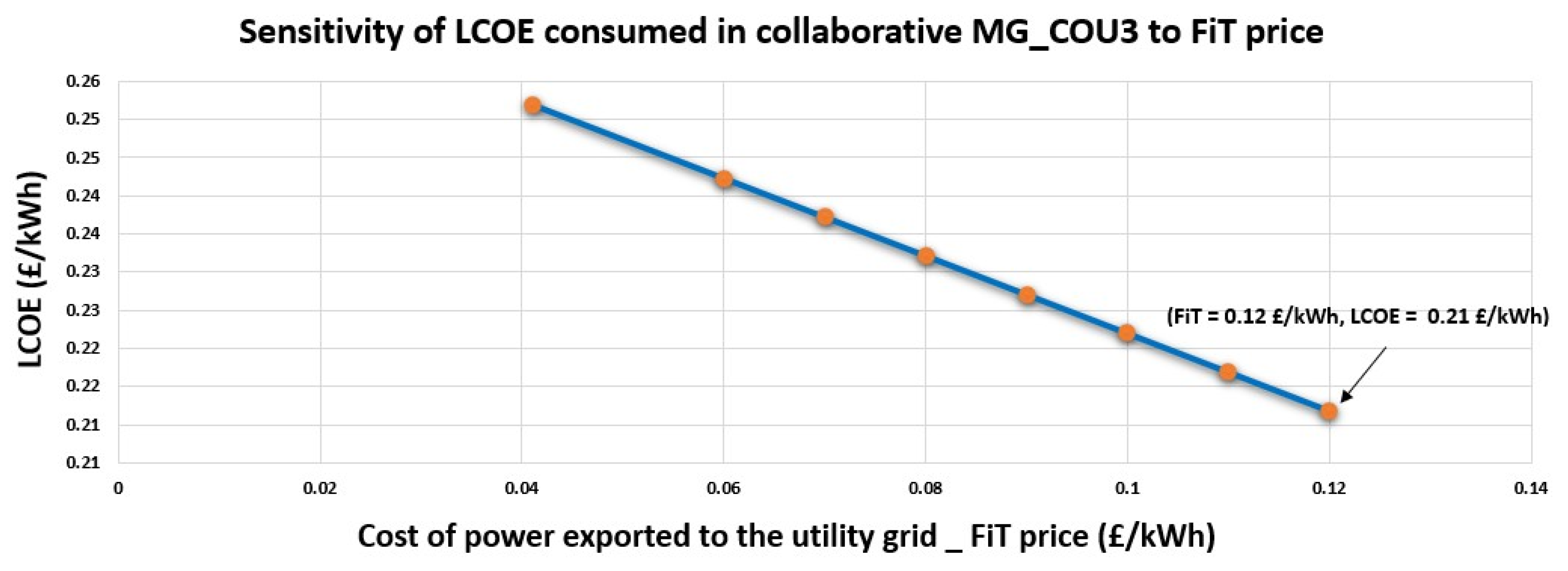
1.4. Potential Impact of the COU Strategy on the LCOE
2. Method
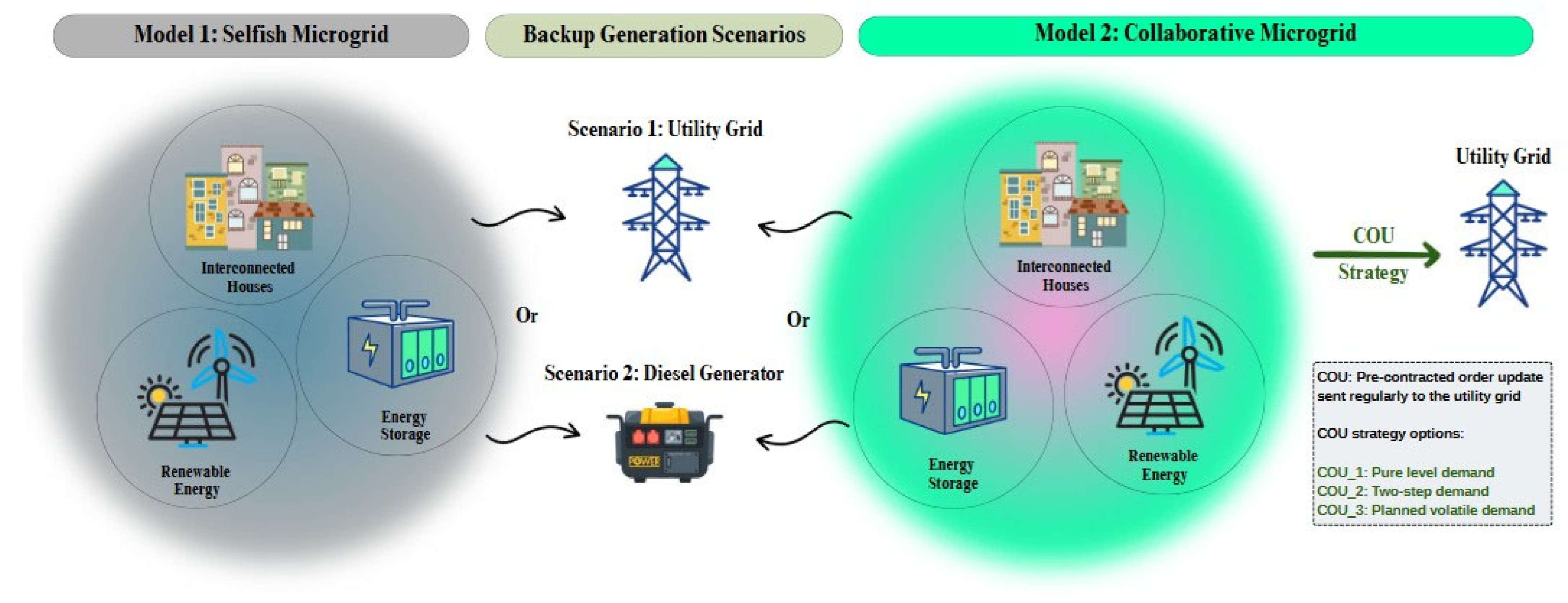
2.1. Models and Scenarios Description
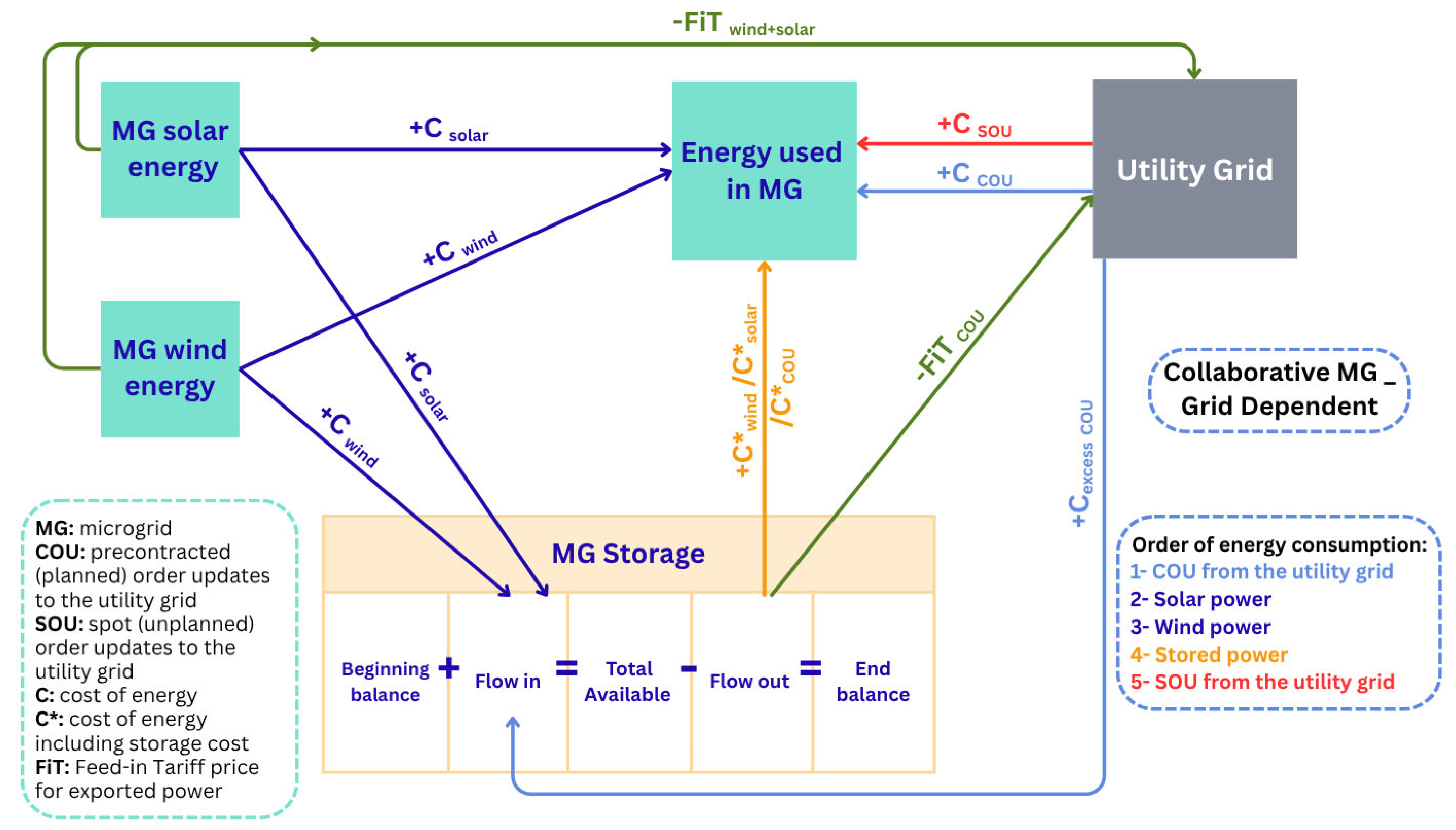
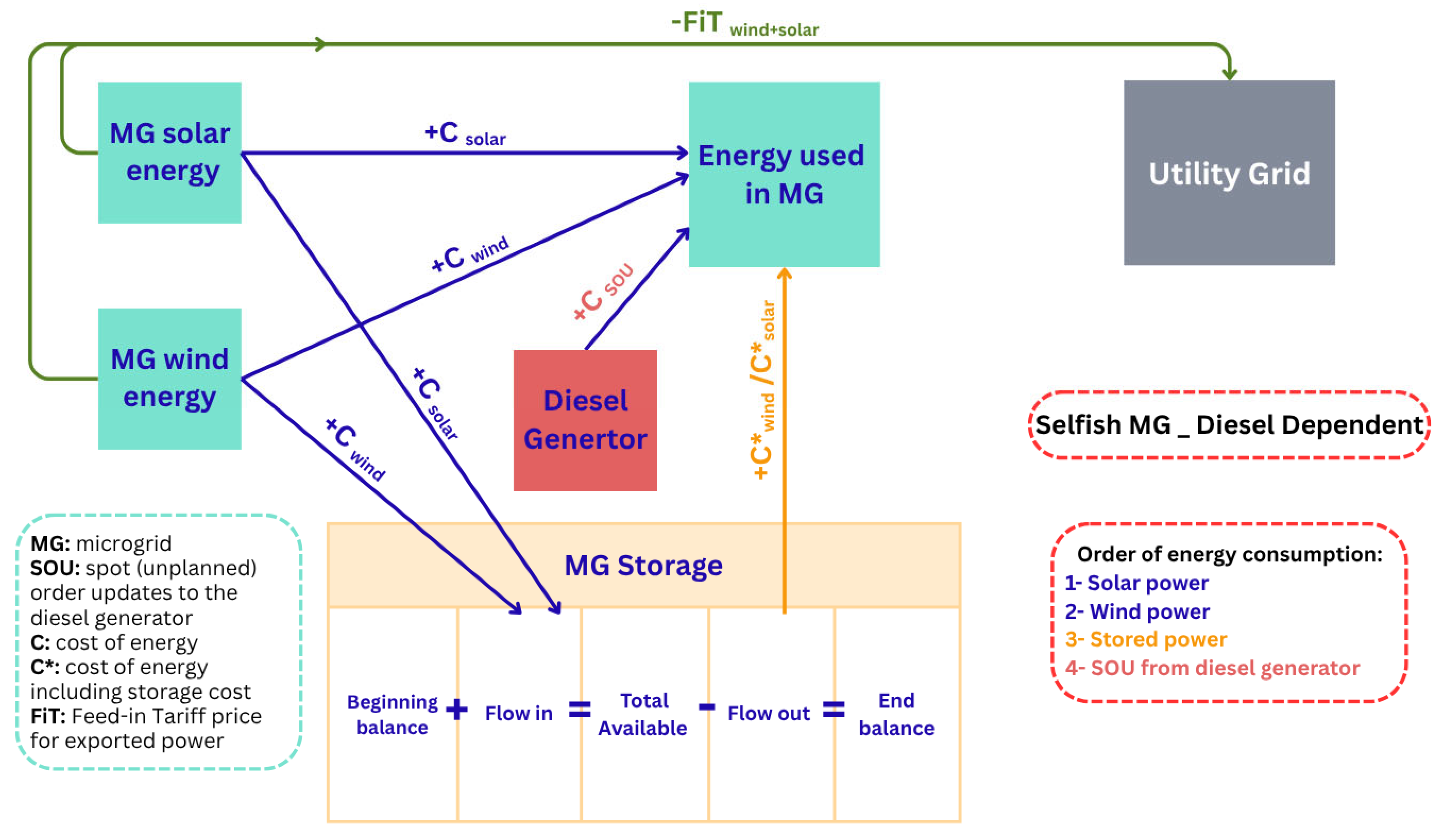
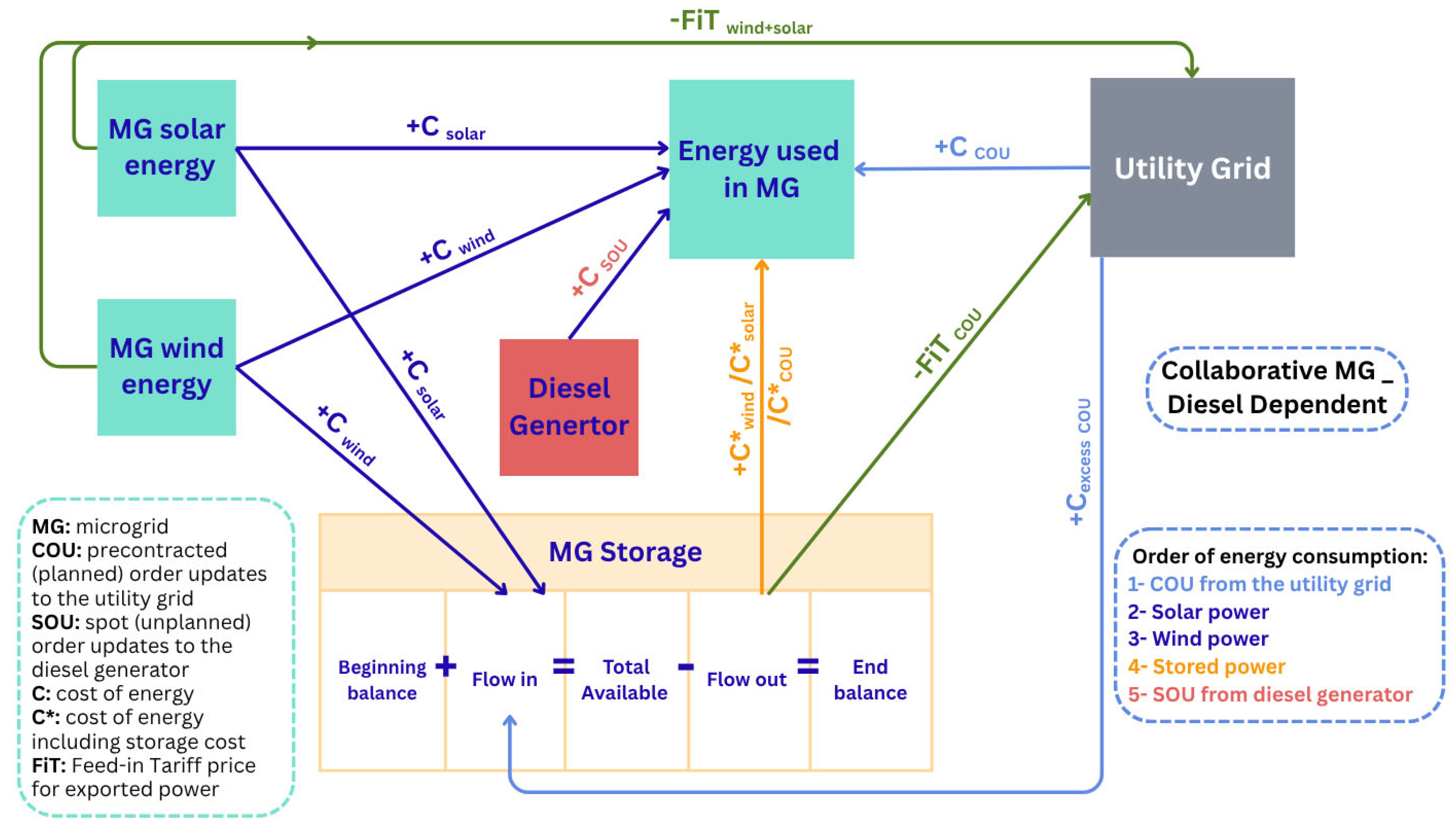
2.2. Cost Flows in the Studied Backup Generation Scenarios
2.2.1. Scenario 1: Utility Grid-Dependent MG
2.2.2. Scenario 2: Diesel Generator-Dependent MG
2.3. Cost Model for the Power Consumed in the MG Systems
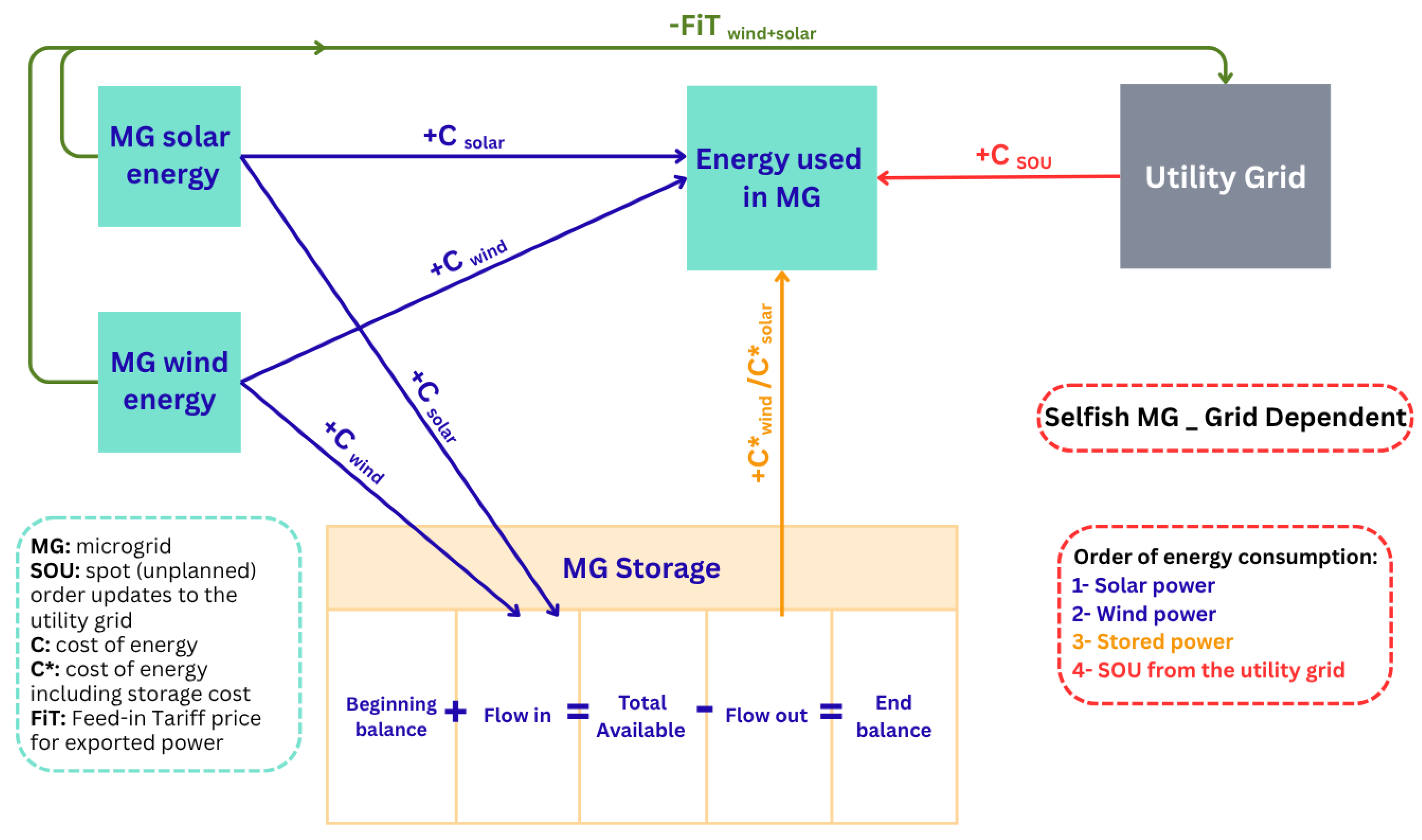
2.3.1. Modelling the Energy Consumed in the MG
- Power consumed from utility grid as COU
- 2.
- Power consumed from solar
- 3.
- Power consumed from wind
- 4.
- Power consumed from storage
- 5.
- Power consumed from backup generation options
2.3.2. The Unit Cost for Each Power Source
| Power Source | Study Ref. | Unit Cost in Literature (GBP/kWh) | Installation Capacity (kW) | Unit Cost in This Study (GBP/kWh) |
|---|---|---|---|---|
| Solar | [18] | 0.02 | Utility scale PV | 0.09 |
| [22] | 0.09 | Residential | ||
| [20] | 0.30 | __ | ||
| Wind | [24] | 0.027 | 1500 | 0.06 |
| [19] | 0.06 | 414 | ||
| [20] | 0.21 | __ | ||
| Storage | [18] | 0.023 | Utility scale | 0.20 |
| [21] | 0.20 | Residential | ||
| Power from grid | [25,26] | 0.26 | __ | 0.27 |
| [27] | 0.27 | __ | ||
| Diesel generator | [19] | 0.19 | 536 | 0.40 |
| [23] | 0.40 | 15 |
2.3.3. The Exported Power from the Microgrid to the Utility Grid
3. Results
3.1. Models’ Parameters
3.2. LCOE Consumed in Collaborative and Selfish MG Models
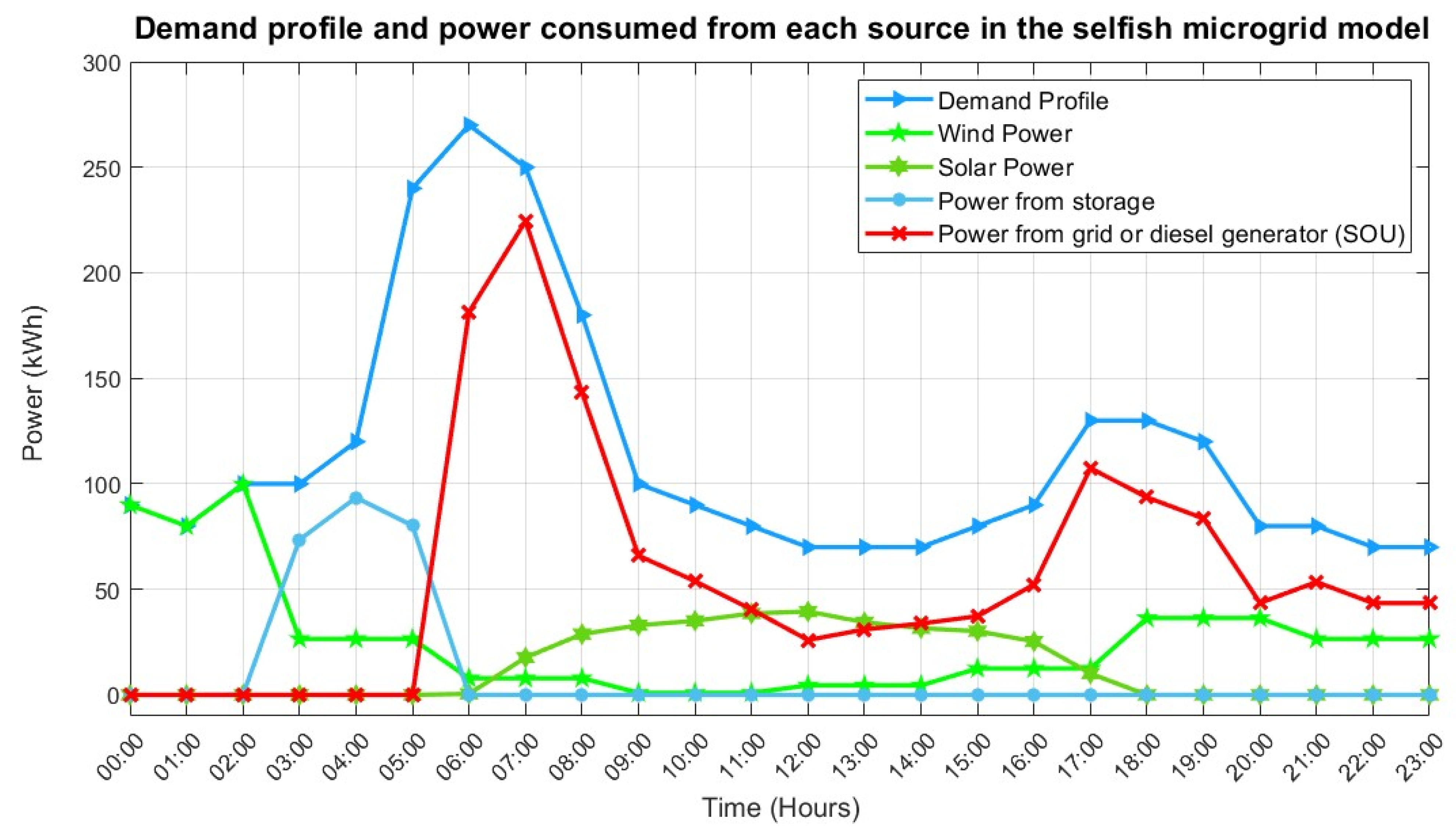
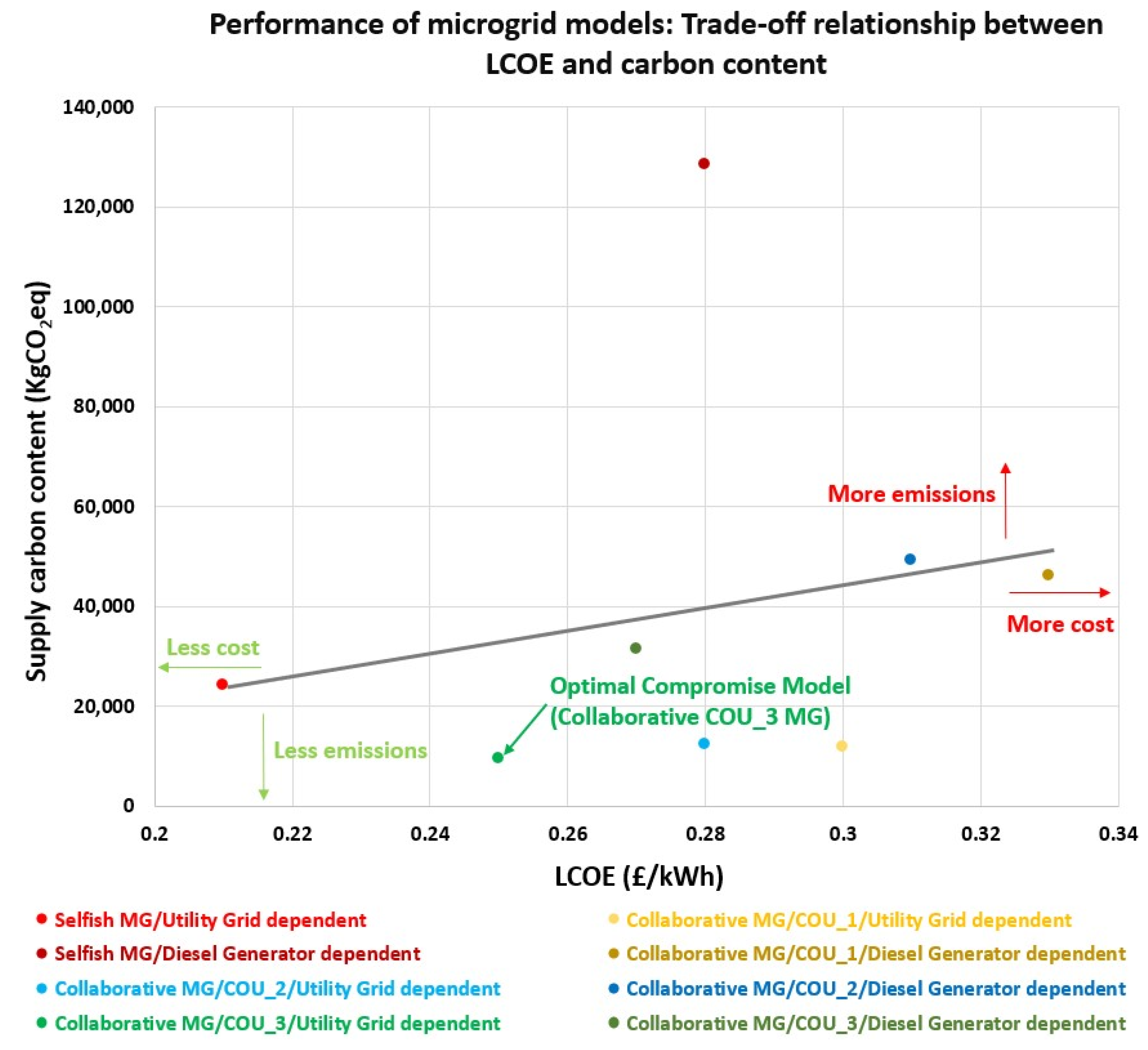
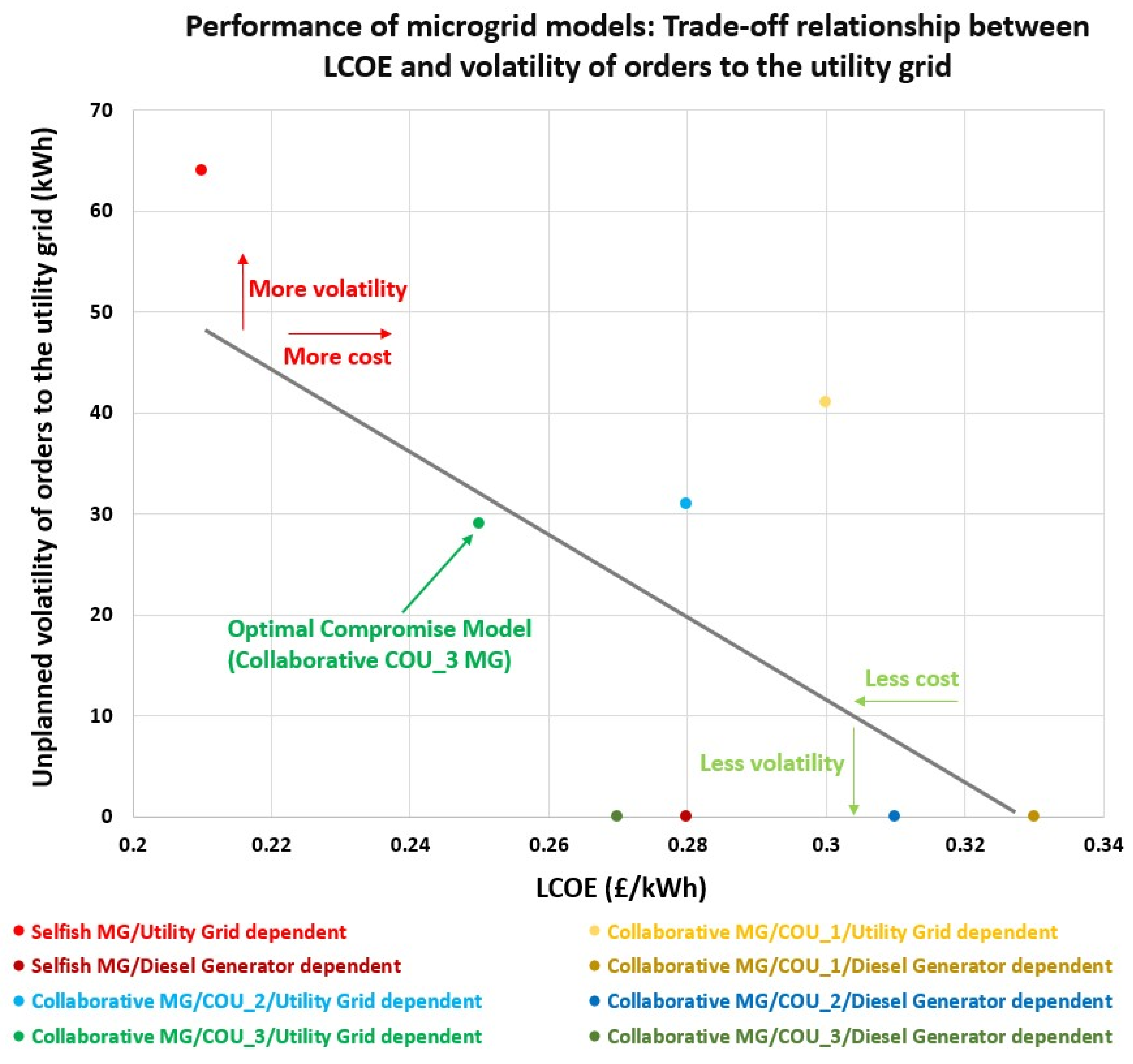
3.3. MG Models Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MG | Microgrid |
| LCOE | Levelized cost of energy |
| COU | Pre-contracted order update |
| FiT | Feed-in tariff |
| T | Time (UK standard time) |
| D(t) | The aggregate demand for the interconnected households at time t |
| Ppv(t) | The power output from PV at time t |
| Pw(t) | The power output from wind turbine at time t, kilowatts |
| LCOEMG | The levelized cost of energy consumed in the MG in GBP/kWh |
| CMG | The cost of total energy consumed in the MG in GBP |
| PEexp | The price of the total exported power from the MG to the utility grid in GBP |
| EMG | The total energy consumed in the MG in kW |
| Ei(t) | The energy consumed from each energy sources at each hour |
| ci | The unit cost of each energy source in GBP/kWh |
| ECOU | The power consumed from the utility grid at the MG level as COU in kWh |
| Epv(t) | The power consumed from the solar output at the MG level in kWh |
| Ew(t) | The power consumed from the wind output at the MG level in kWh |
| Est(t) | The power consumed from the storage at the MG level in kWh |
| ESOU(t) | The power supply (spot order update) from the backup option (utility grid or diesel) in kWh |
| Eexp(t) | The exported energy to the utility grid at each hour in kWh |
| PFiT | The price of the feed-in tariff in GBP/kWh |
| Pst(t) | The power available in storage system at time t, kilowatts |
| PCOU(t) | Precontracted grid order update at time t |
References
- Gudde, P.; Oakes, J.; Cochrane, P.; Caldwell, N.; Bury, N. The Role of UK Local Government in Delivering on Net Zero Carbon Commitments: You’ve Declared a Climate Emergency, so What’s the Plan? Energy Policy 2021, 154, 112245. [Google Scholar] [CrossRef]
- Ejuh Che, E.; Roland Abeng, K.; Iweh, C.D.; Tsekouras, G.J.; Fopah-Lele, A. The Impact of Integrating Variable Renewable Energy Sources into Grid-Connected Power Systems: Challenges, Mitigation Strategies, and Prospects. Energies 2025, 18, 689. [Google Scholar] [CrossRef]
- Feleafel, H.; Radulovic, J.; Leseure, M. Should We Have Selfish Microgrids? Energies 2024, 17, 3969. [Google Scholar] [CrossRef]
- Sato, T.; Murata, K.; Katayama, H. On Stability of Supply Performance by Work-in-Progress Management: A Case Analysis of Photovoltaics-Based Electricity Supply System with Storage Batteries. Procedia Manuf. 2017, 11, 1077–1084. [Google Scholar] [CrossRef]
- Feleafel, H.; Radulovic, J.; Leseure, M. Facilitating the Shift to More Collaborative Microgrids by Alleviating Demand Volatility Using a Precontracted Order Updates Strategy. Next Energy 2025, 8, 100269. [Google Scholar] [CrossRef]
- Feleafel, H.; Leseure, M.; Radulovic, J. Shifting Towards Greener and More Collaborative Microgrids by Applying Lean-Heijunka Strategy. Eng 2025, 6, 69. [Google Scholar] [CrossRef]
- Feleafel, H.; Leseure, M. Feed-in Tariff Policy for Microgrids: Past and Future a Case Study of the Option Value of Complementary Energy Assets in Turbulent Conditions. Int. J. Energy Sect. Manag. 2025; ahead-of-print. [Google Scholar] [CrossRef]
- Manandhar, U.; Zhang, X.; Beng, G.H.; Subramanian, L.; Lu, H.H.C.; Fernando, T. Enhanced Energy Management System for Isolated Microgrid with Diesel Generators, Renewable Generation, and Energy Storages. Appl. Energy 2023, 350, 121624. [Google Scholar] [CrossRef]
- Martinez-Bolanos, J.R.; Manito, A.R.A.; Almeida, M.P.; Almeida, J.C.; Torres, P.F.; Pinho, J.T.; Zilles, R. Improved Dynamic Model of Small Stand-Alone Diesel Generators to Assess the Stability of Autonomous Microgrids. AIP Adv. 2025, 15, 25118. [Google Scholar] [CrossRef]
- Singh, B.; Pathak, G.; Panigrahi, B.K. Seamless Transfer of Renewable-Based Microgrid Between Utility Grid and Diesel Generator. IEEE Trans. Power Electron. 2018, 33, 8427–8437. [Google Scholar] [CrossRef]
- Sanni, S.O.; Oricha, J.Y.; Oyewole, T.O.; Bawonda, F.I. Analysis of Backup Power Supply for Unreliable Grid Using Hybrid Solar PV/Diesel/Biogas System. Energy 2021, 227, 120506. [Google Scholar] [CrossRef]
- Cavalcanti, M.H.C.; Pappalardo, J.R.; Barbosa, L.T.; Brasileiro, P.P.F.; Roque, B.A.C.; da Rocha e Silva, N.M.P.; Silva, M.F.d.; Converti, A.; Barbosa, C.M.B.d.M.; Sarubbo, L.A. Hydrogen in Burners: Economic and Environmental Implications. Processes 2024, 12, 2434. [Google Scholar] [CrossRef]
- Aoki, R.; Katayama, H. Heijunka Operation Management of Agri-Products Manufacturing by Yield Improvement and Cropping Policy. In Lecture Notes on Multidisciplinary Industrial Engineering; Springer: Cham, Switzerland, 2018; Part. F43; pp. 1407–1416. [Google Scholar] [CrossRef]
- Helleno, A.L.; de Moraes, A.J.I.; Simon, A.T. Integrating Sustainability Indicators and Lean Manufacturing to Assess Manufacturing Processes: Application Case Studies in Brazilian Industry. J. Clean. Prod. 2017, 153, 405–416. [Google Scholar] [CrossRef]
- Shetty, D.K.; Abakari, G.; Rodrigues, D.L.L.R.; Oommen Mathew, A.; Motlagh, F.G. To Develop Lean Systems in Electronic Automotive Parts Manufacturing Industry: A System Dynamics Modelling Approach. In Proceedings of the 2019 International Conference on Automation, Computational and Technology Management, ICACTM, London, UK, 24–26 April 2019; pp. 277–283. [Google Scholar] [CrossRef]
- Alvarez, L.; Avella, L.; Martinez, R. Impact and Critical Factors in Heijunka Implementation an Action Research Study. J. Ind. Eng. Manag. 2024, 17, 753–776. [Google Scholar] [CrossRef]
- Kabeyi, M.J.B.; Olanrewaju, O.A. The Levelized Cost of Energy and Modifications for Use in Electricity Generation Planning. Energy Rep. 2023, 9, 495–534. [Google Scholar] [CrossRef]
- Veronese, E.; Manzolini, G.; Moser, D. Improving the Traditional Levelized Cost of Electricity Approach by Including the Integration Costs in the Techno-Economic Evaluation of Future Photovoltaic Plants. Int. J. Energy Res. 2021, 45, 9252–9269. [Google Scholar] [CrossRef]
- Graça Gomes, J.; Xu, H.J.; Yang, Q.; Zhao, C.Y. An Optimization Study on a Typical Renewable Microgrid Energy System with Energy Storage. Energy 2021, 234, 121210. [Google Scholar] [CrossRef]
- Idel, R. Levelized Full System Costs of Electricity. Energy 2022, 259, 124905. [Google Scholar] [CrossRef]
- Residential Battery Economics-Spirit Energy. Available online: https://www.spiritenergy.co.uk/kb-battery-storage-for-solar-residential-economics (accessed on 17 July 2025).
- Lifetime Cost of Solar Electricity vs the Grid. Available online: https://www.spiritenergy.co.uk/lifetime-cost-electricity (accessed on 17 July 2025).
- Rangel, N.; Li, H.; Aristidou, P. An Optimisation Tool for Minimising Fuel Consumption, Costs and Emissions from Diesel-PV-Battery Hybrid Microgrids. Appl. Energy 2023, 335, 120748. [Google Scholar] [CrossRef]
- Dong, M.; Li, Y.; Song, D.; Yang, J.; Su, M.; Deng, X.; Huang, L.; Elkholy, M.H.; Joo, Y.H. Uncertainty and Global Sensitivity Analysis of Levelized Cost of Energy in Wind Power Generation. Energy Convers. Manag. 2021, 229, 113781. [Google Scholar] [CrossRef]
- Average Cost of Electricity Per KWh in the UK. 2025. Available online: https://www.greenmatch.co.uk/average-electricity-cost-uk (accessed on 10 April 2025).
- Energy Prices by Region in 2025-Uswitch. Available online: https://www.uswitch.com/gas-electricity/guides/regional-energy-prices/ (accessed on 13 June 2025).
- What Are the Best SEG Rates?|All 28 Tariffs Ranked. 2025. Available online: https://www.sunsave.energy/solar-panels-advice/exporting-to-the-grid/best-seg-rates (accessed on 13 June 2025).
- Smart Export Guarantee|Octopus Energy. Available online: https://octopus.energy/smart/smart-export-guarantee/ (accessed on 13 June 2025).
- The Feed-in Tariff: Past & Current Rates. 2025. Available online: https://www.sunsave.energy/solar-panels-advice/exporting-to-the-grid/feed-in-tariff (accessed on 13 June 2025).
- Leseure, M.; Feleafel, H.; Radulovic, J. Collaborative Microgrids as Power Quality Improvement Nodes in Electricity Networks. Energies 2025, 18, 4197. [Google Scholar] [CrossRef]
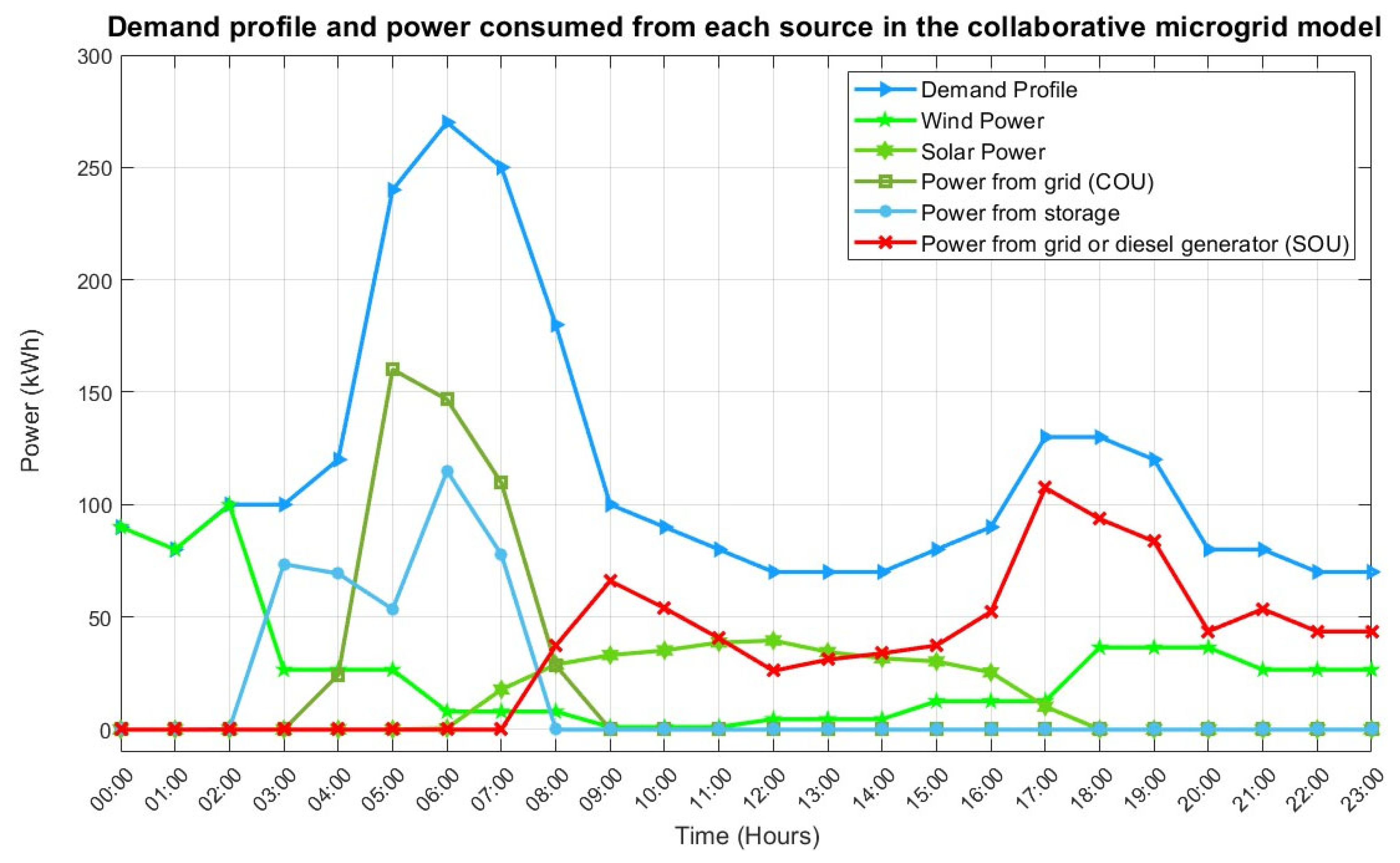
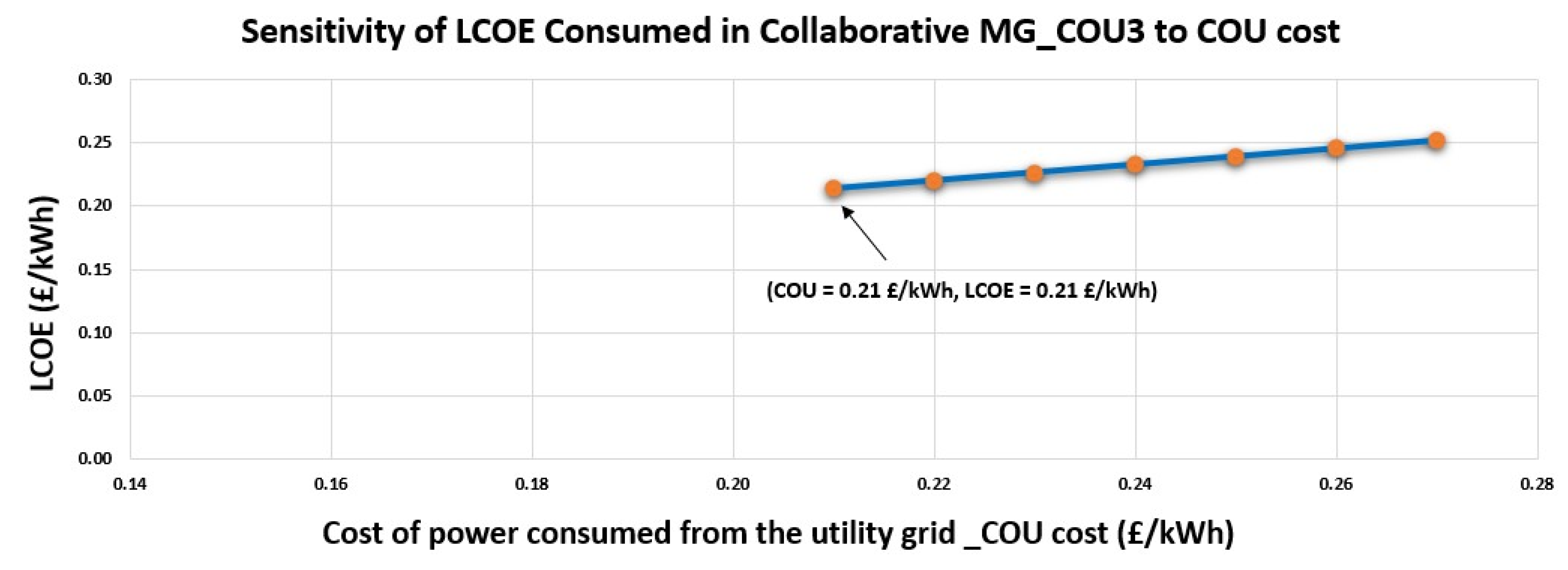
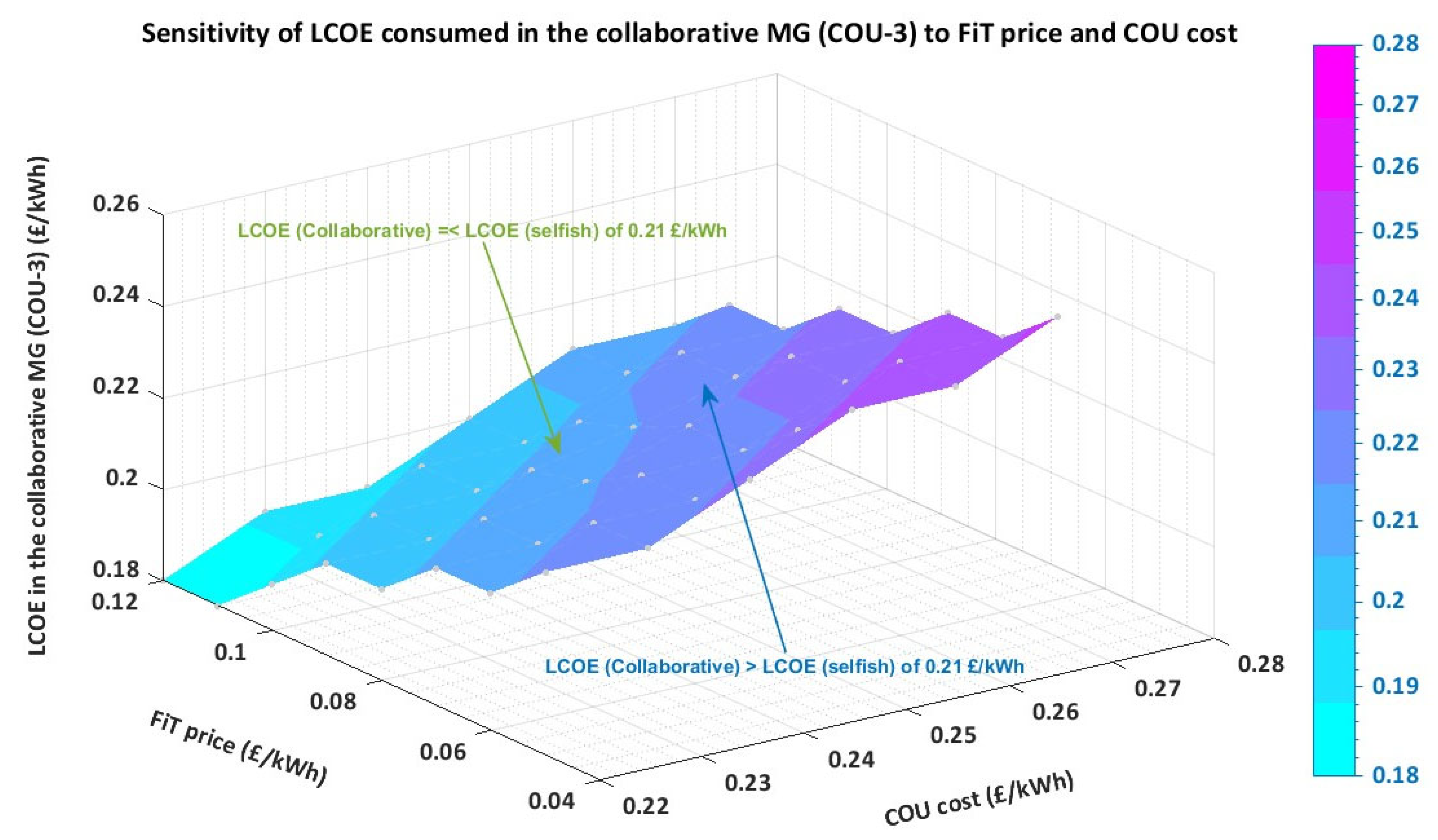
| Time Horizon | Storage Capacity | Storage Efficiency |
|---|---|---|
| 90 days in spring | 1500 kWh | 95% |
| Microgrid Model | Backup Generation Scenario | LCOE (GBP/kWh) | Unplanned Volatility of Orders to the Utility Grid (kWh) | Supply Carbon Content (kgco2eq) |
|---|---|---|---|---|
| Selfish MG | Utility grid | 0.21 | 64 | 24,209 |
| Diesel generator | 0.28 | 0 | 128,594 | |
| Collaborative MG (COU_1: pure level demand) | Utility grid | 0.30 | 41 | 11,978 |
| Diesel generator | 0.33 | 0 | 46,176 | |
| Collaborative MG (COU_2: two-step demand) | Utility grid | 0.28 | 31 | 12,363 |
| Diesel generator | 0.31 | 0 | 49,379 | |
| Collaborative MG (COU_3: planned volatile demand) | Utility grid | 0.25 | 29 | 9583 |
| Diesel generator | 0.27 | 0 | 31,472 |
| FiT price | 0.12 | 0.11 | 0.10 | 0.09 | 0.08 | 0.07 |
| COU cost | 0.27 | 0.26 | 0.25 | 0.24 | 0.23 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feleafel, H.; Leseure, M.; Radulovic, J. Cost Implications for Collaborative Microgrids: A Case Study of Lean—Heijunka Microgrid Operations Mitigating Renewable Energy Volatility. Energies 2025, 18, 4320. https://doi.org/10.3390/en18164320
Feleafel H, Leseure M, Radulovic J. Cost Implications for Collaborative Microgrids: A Case Study of Lean—Heijunka Microgrid Operations Mitigating Renewable Energy Volatility. Energies. 2025; 18(16):4320. https://doi.org/10.3390/en18164320
Chicago/Turabian StyleFeleafel, Hanaa, Michel Leseure, and Jovana Radulovic. 2025. "Cost Implications for Collaborative Microgrids: A Case Study of Lean—Heijunka Microgrid Operations Mitigating Renewable Energy Volatility" Energies 18, no. 16: 4320. https://doi.org/10.3390/en18164320
APA StyleFeleafel, H., Leseure, M., & Radulovic, J. (2025). Cost Implications for Collaborative Microgrids: A Case Study of Lean—Heijunka Microgrid Operations Mitigating Renewable Energy Volatility. Energies, 18(16), 4320. https://doi.org/10.3390/en18164320









