Hybrid Adaptive Learning-Based Control for Grid-Forming Inverters: Real-Time Adaptive Voltage Regulation, Multi-Level Disturbance Rejection, and Lyapunov-Based Stability
Abstract
1. Introduction
- A control strategy diagram for inverter regulation utilizing a feedback control mechanism designed whereby the voltage controller uses the integration of RL and MPC in a single framework is a major breakthrough since each control technique works in concert to give short, long, and rapid reactions to disturbances.
- A control law for MPC has been formulated using Lyapunov-based stability analysis, ensuring that the Lyapunov function continuously decreases over time, thereby guaranteeing system stability.
- RL is modeled based on dynamic optimal control using a system based on a Markov Decision Process (MDP) to describe the dynamic behavior for disturbance rejection and error reduction by minimizing time. To ensure the system is stable even under disturbances, constraints are set. Starting with the fastest, these constraints are divided into three rejection levels: slow, probabilistic, and fast rejection constraints. The ability of the system to respond to disturbances with different levels of certainty and response speed is specified at each level. By rejecting disturbances according to their intensity and dynamically modifying control techniques, the system’s adaptive nature improves the grid’s overall stability and resilience.
- Different timeframes are used by the suggested system: milliseconds for instantaneous voltage adjustments, seconds for short-term optimization, and minutes to hours for long-term learning. The inverter’s ability to manage disruptions of different sizes and durations is guaranteed by this multi-stage system.
2. Problem Formation
2.1. Problem Statement
2.2. Model Predictive Control for Short-Term Optimization
2.3. Reinforcement Learning for Long-Term Learning
2.3.1. MDP Formulation of the GFI RL Problem
2.3.2. Learning Mechanism and Policy Update
- 1.
- Observation: The agent records system states () from real-time measurements and state estimators.
- 2.
- Action selection: An action is chosen according to the current policy , with a balance between exploration (testing new control strategies) and exploitation (applying known optimal actions).
- 3.
- Environment transition: The inverter–grid system evolves to a new state following the applied action and external disturbances.
- 4.
- Reward evaluation: The immediate reward is computed using the performance metrics in (6).
- 5.
- Policy update: The policy parameters are adjusted using collected experience, e.g., via Q-learning, policy gradient methods, or actor–critic architectures.
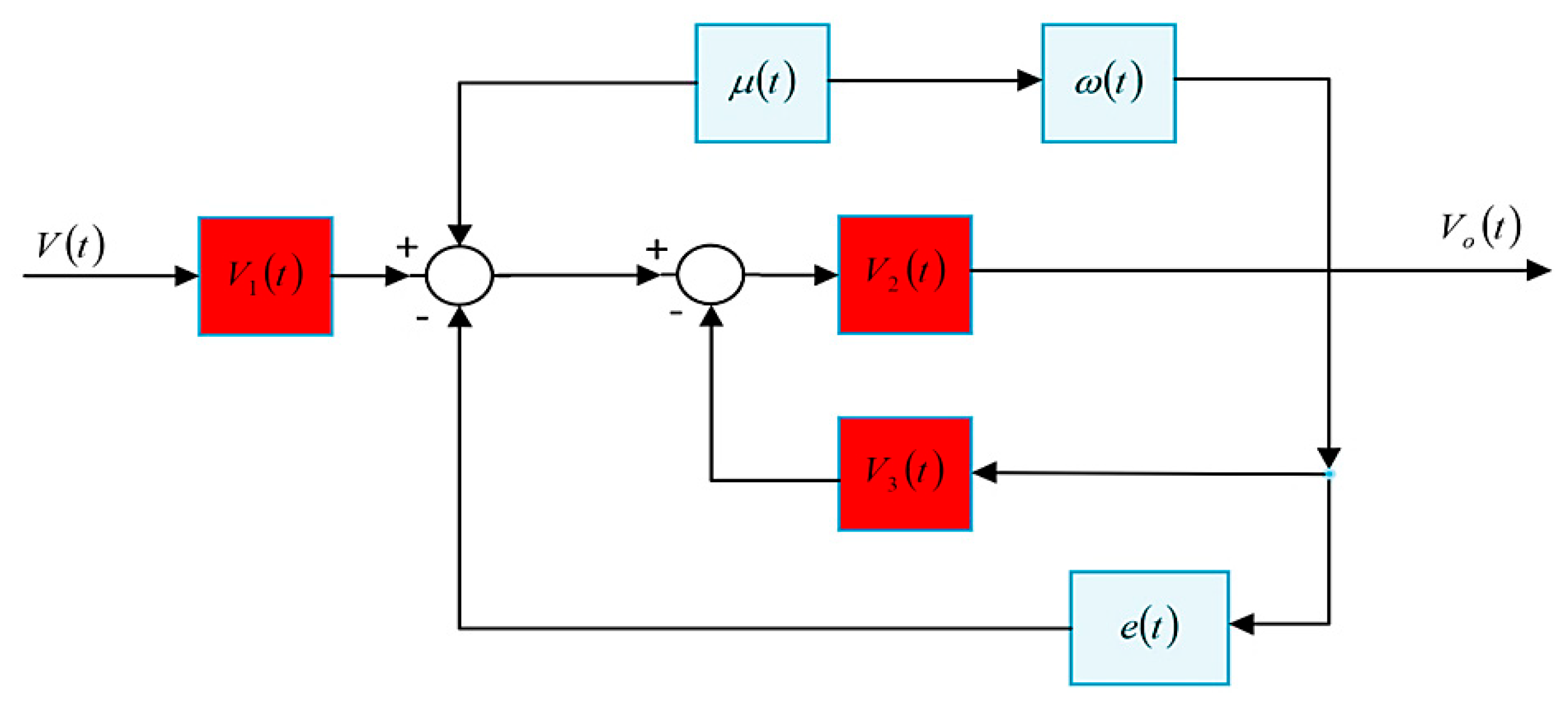
3. Modeling of Voltage Control Feedback Loop of Grid Forming Inverters
4. Methodology
4.1. Mathematical Model for Lyapunov-Based Stability in MPC
4.2. Reinforcement Learning
4.3. Dynamic Optimal Control with Reinforcement Learning
4.4. Dynamic Optimal Control with Reinforcement Learning for Disturbance Rejection
4.5. Dynamic Optimal Control with Reinforcement Learning for Stability Analysis
4.6. Analytical Stability and Optimality for HALC Algorithm
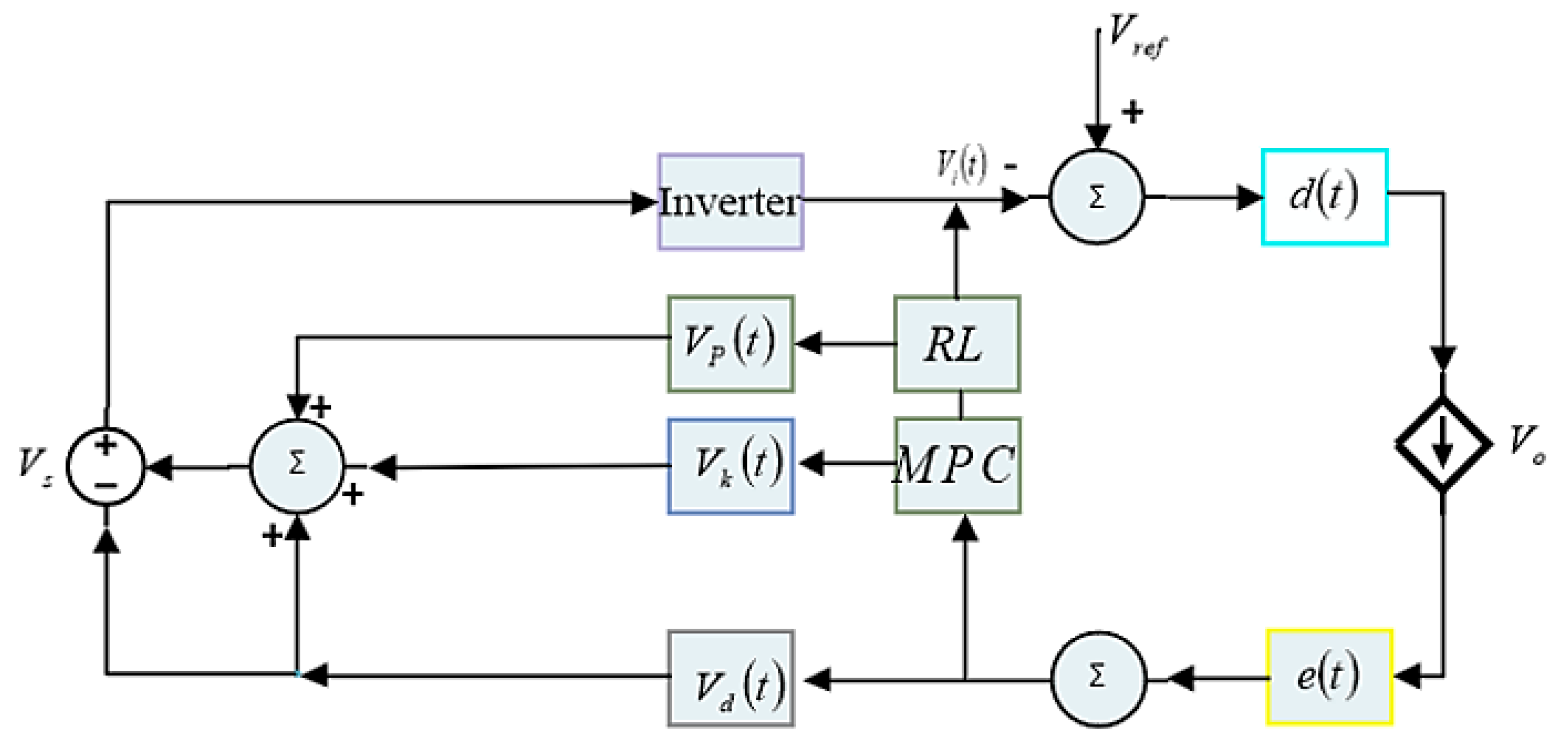
4.7. Proposed Control System Diagram
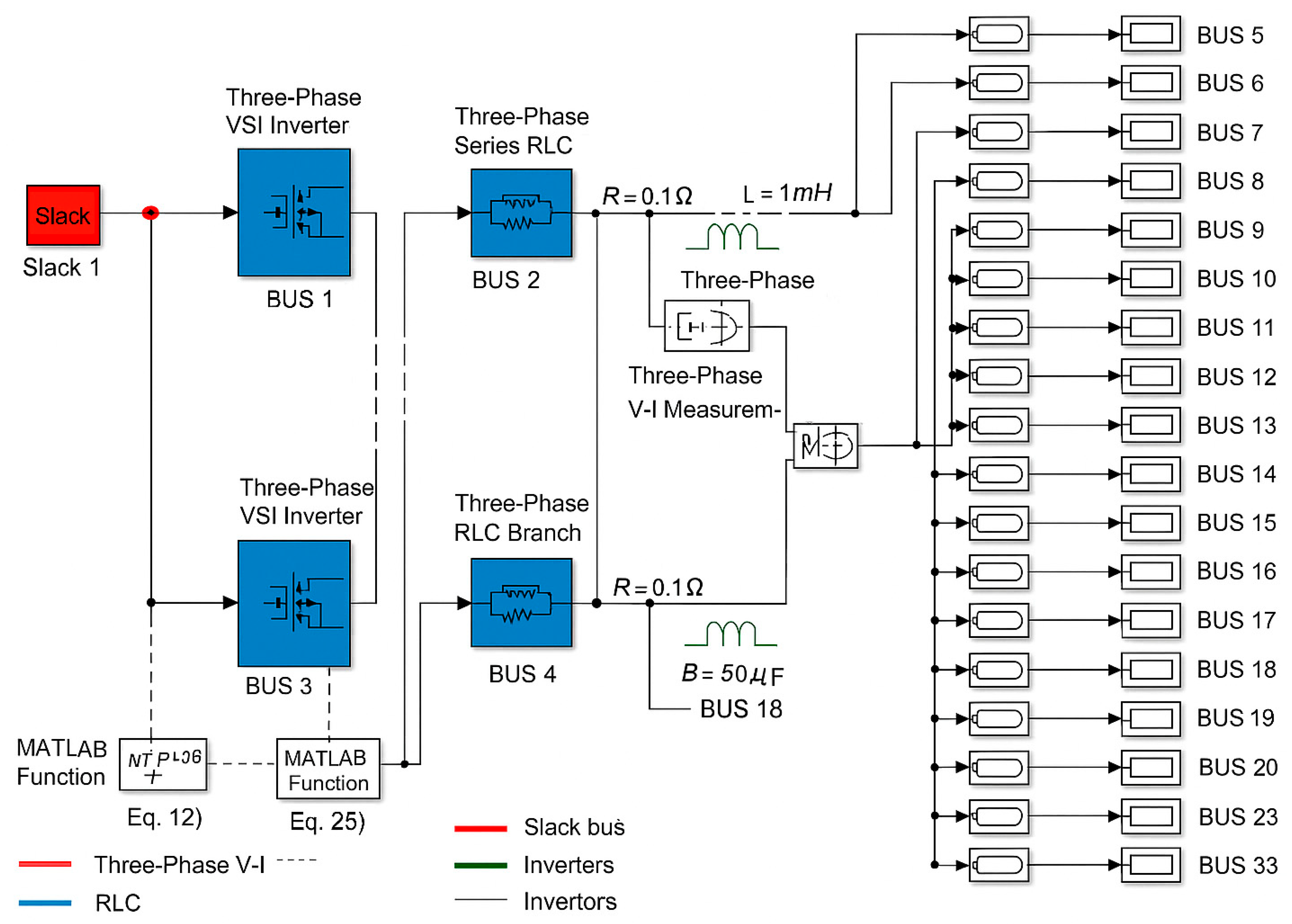
5. Simulation Results and Discussion
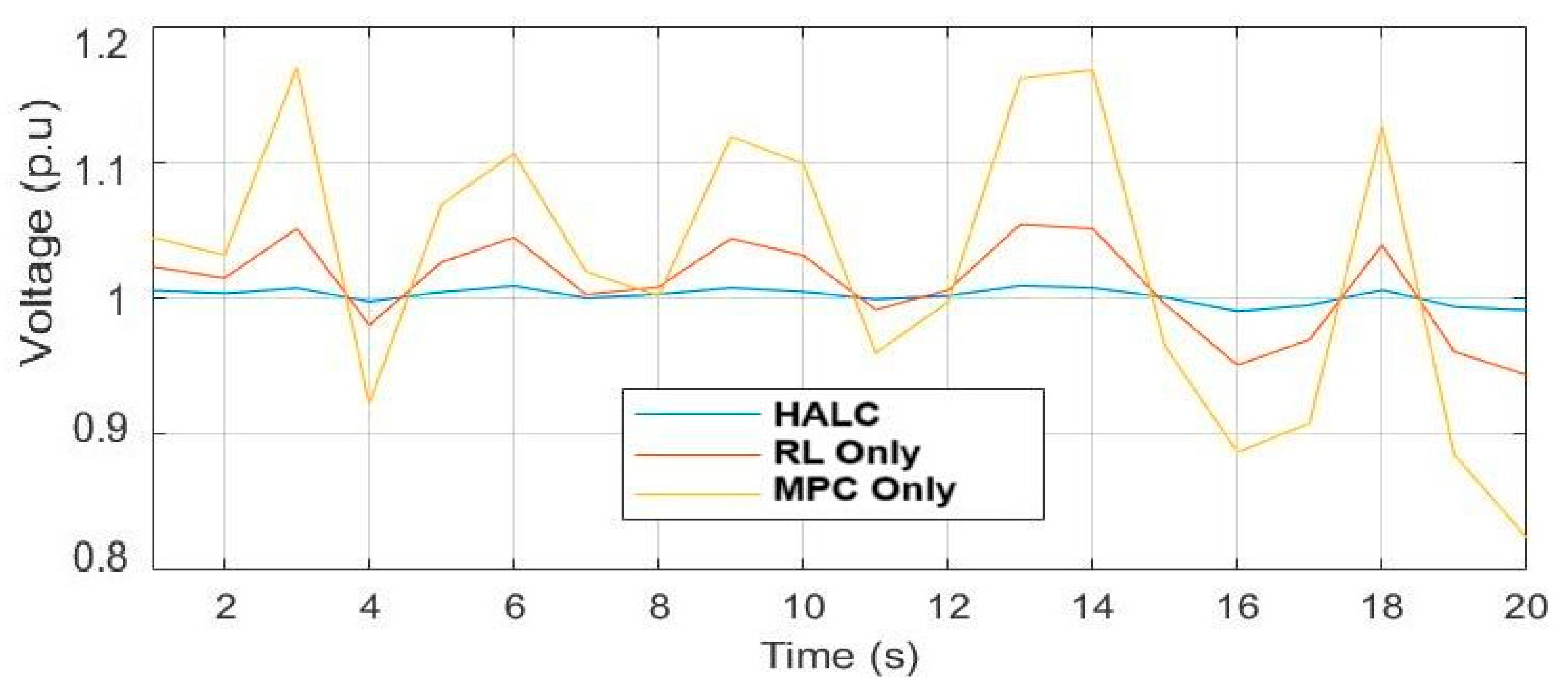
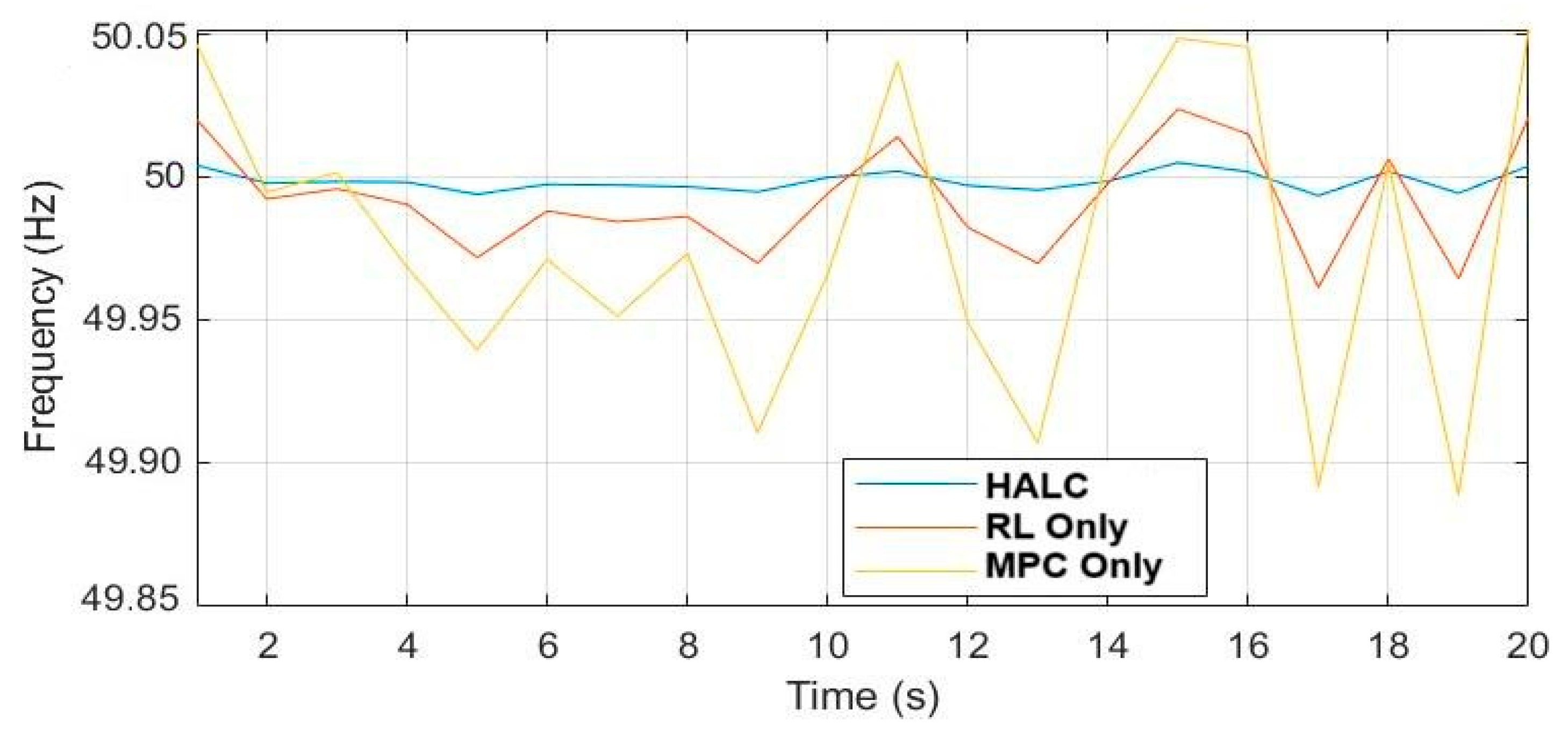
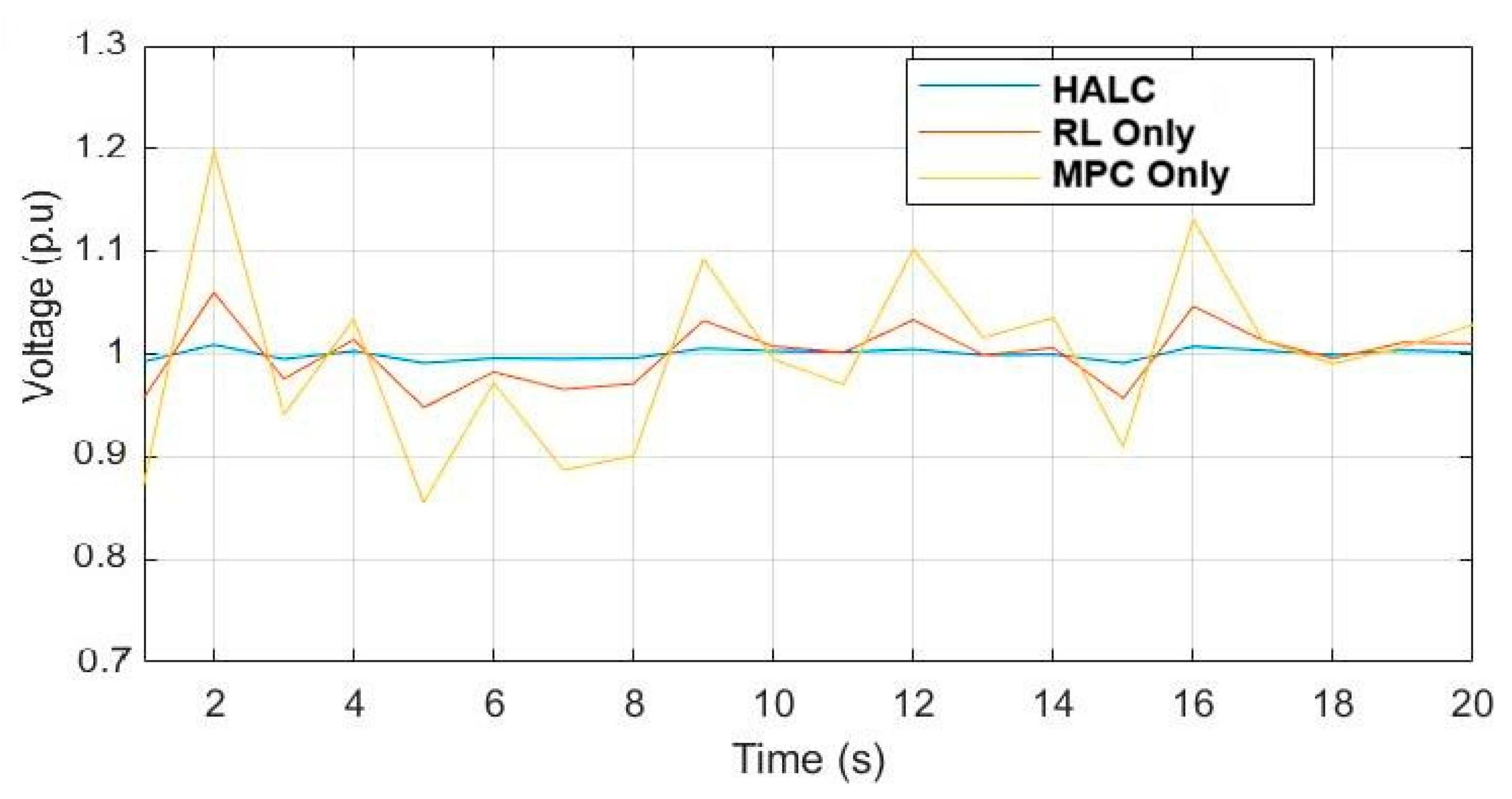
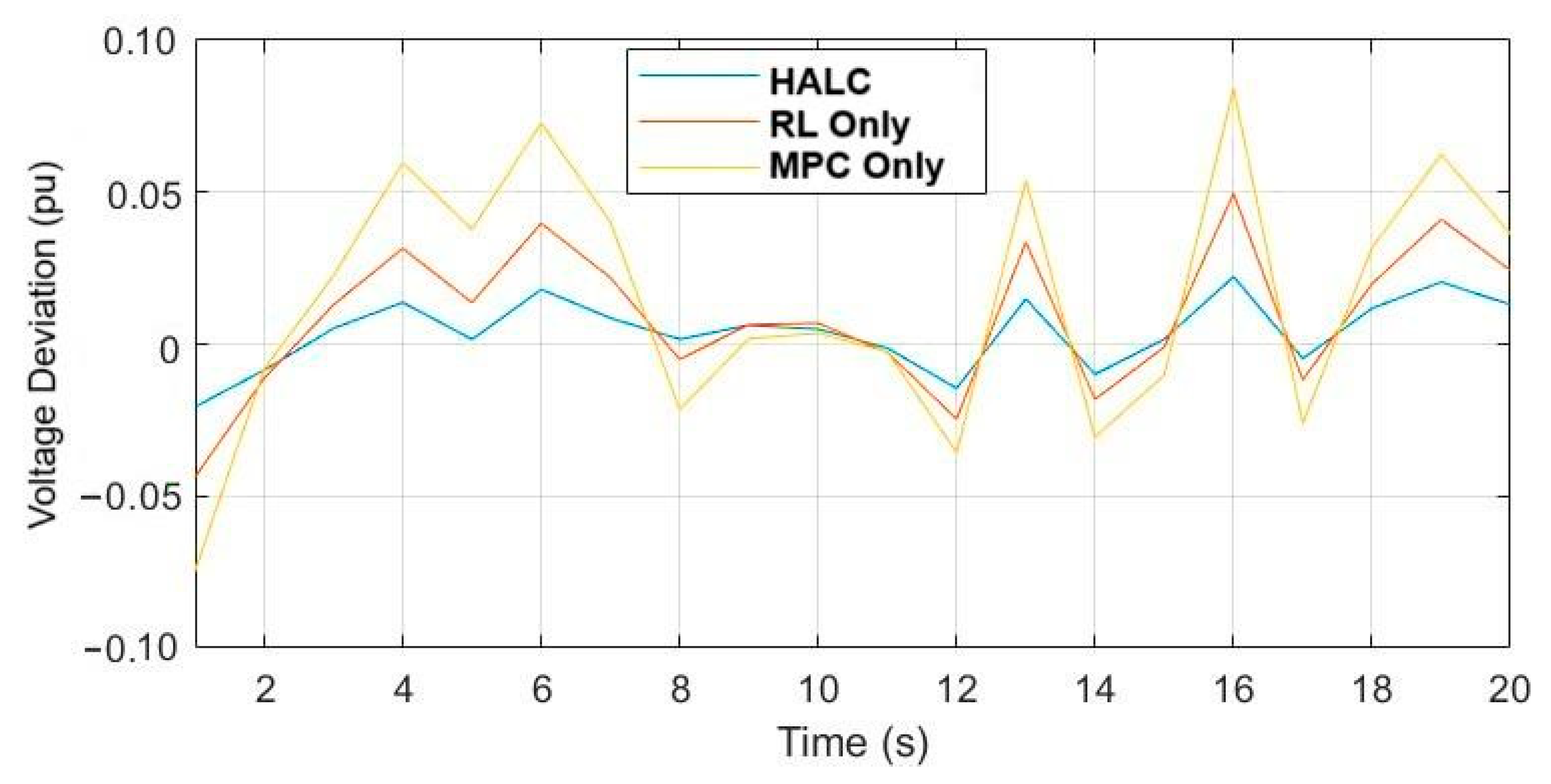
5.1. Scenario 1: Steady-State Performance
5.2. Scenario 2: Voltage Sag and Swell Response
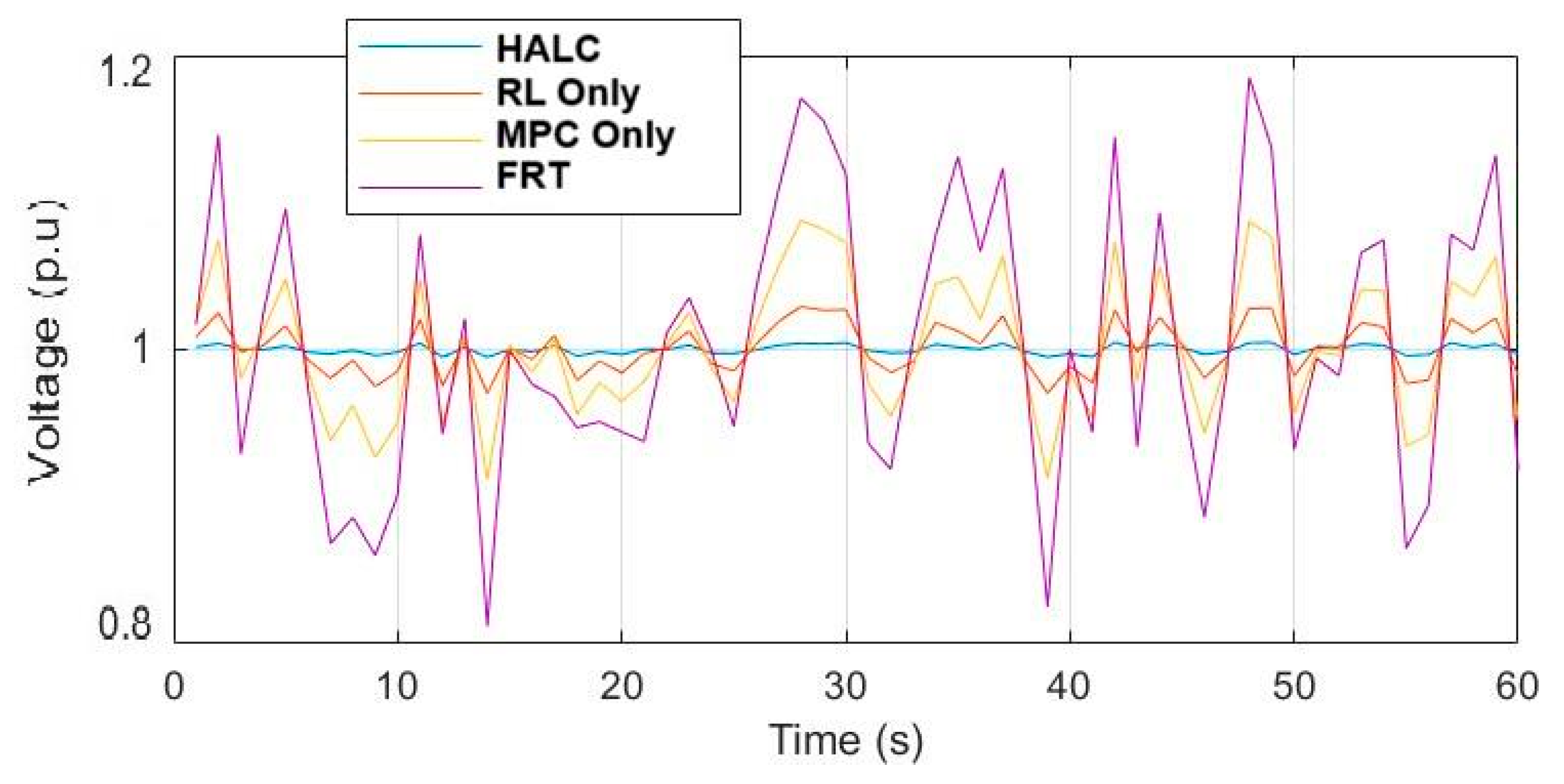
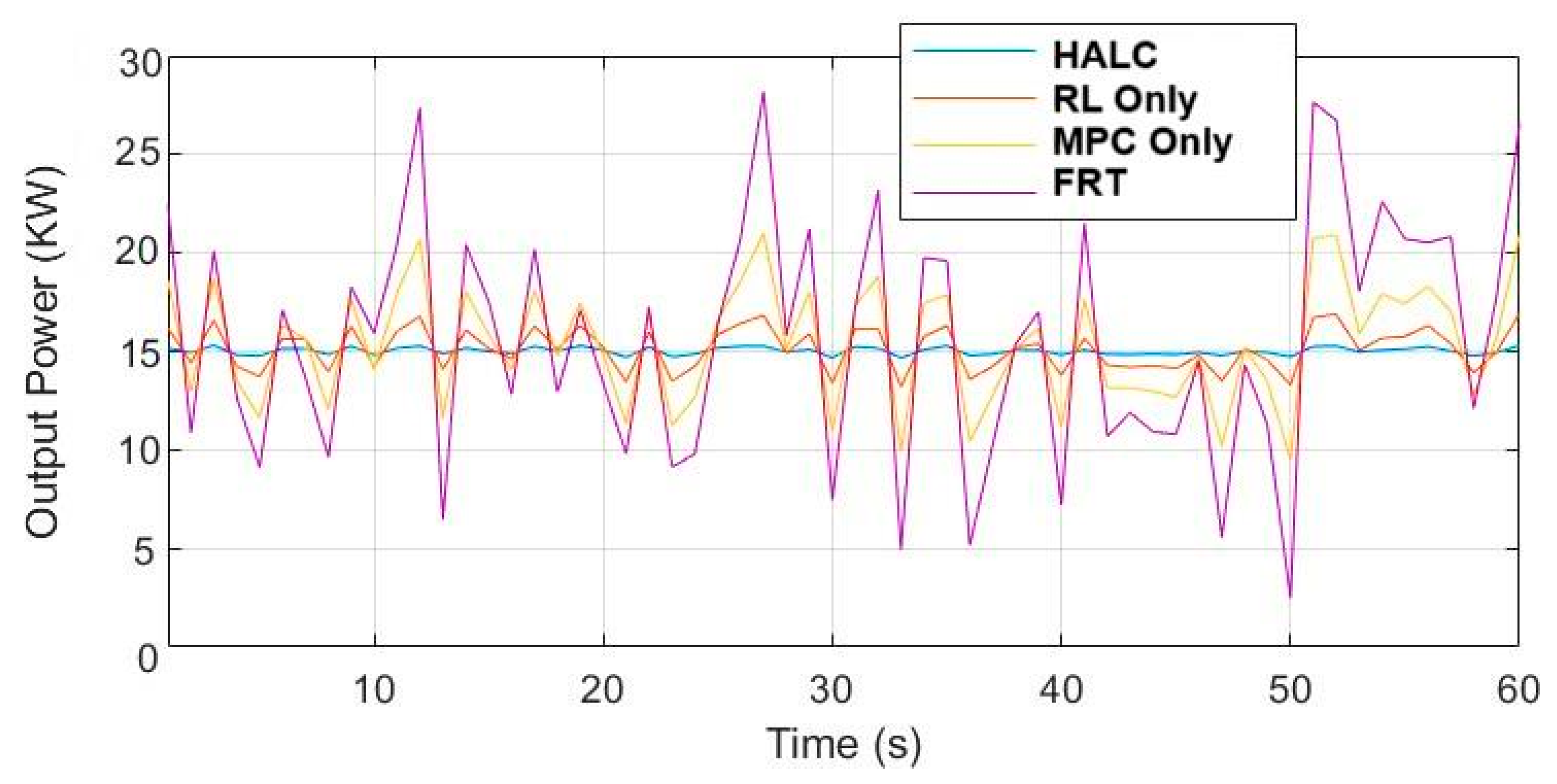
5.3. Scenario 3: Grid Fault Ride-Through (FRT)
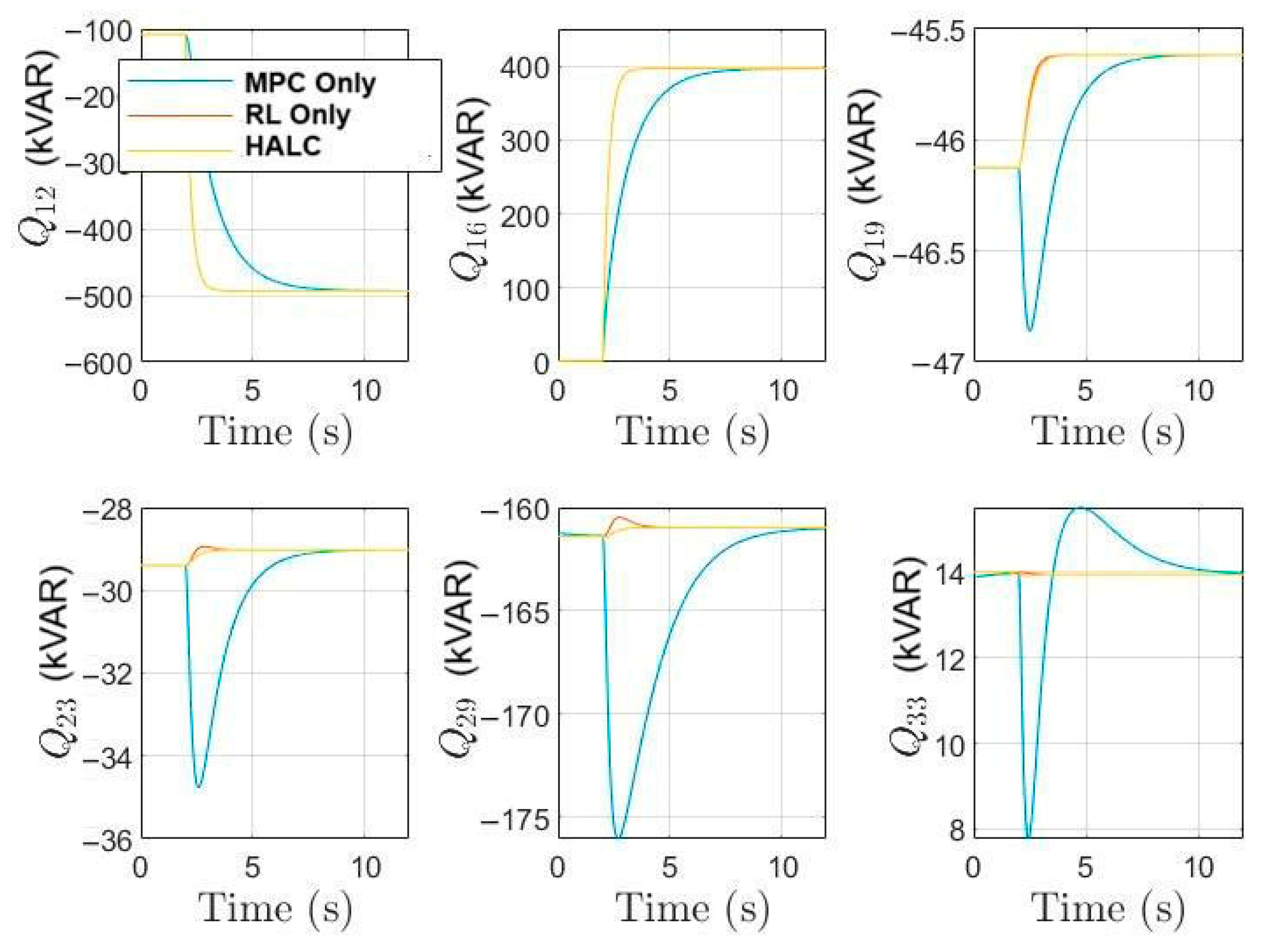
5.4. Scenario 4: Load Variability and Sudden Load Changes
5.5. Scenario 5: Renewable Energy Integration (Solar PV Variability)
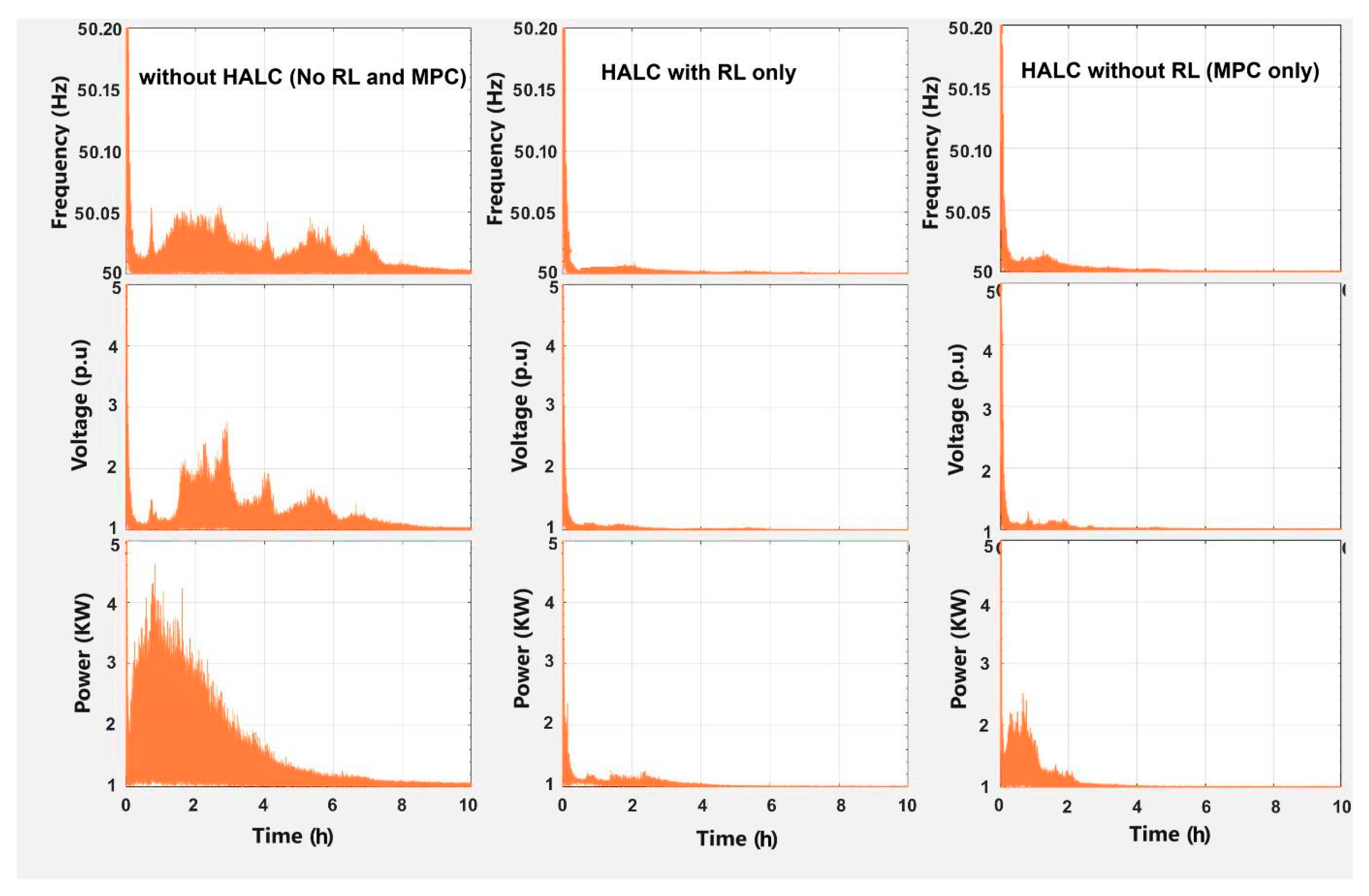
5.6. Scenario 6: Long-Term Learning Efficiency of RL in HALC
5.7. Comparison and Analysis of Control Strategies
- 1.
- Superior Voltage Regulation and Robustness: The HALC strategy achieves a voltage regulation accuracy of 97% and a robustness to voltage disturbances (5/5) because MPC provides immediate corrective action while RL fine-tunes control policies over time based on grid behavior.
- 2.
- Fast Response with Delay Compensation: With a response time of 20 ms, the HALC algorithm outperforms both MPC and RL. This is achieved by incorporating delay compensation mechanisms in both voltage and current control loops, ensuring stability even in the presence of computational or hardware delays.
- 3.
- Improved Fault Ride-Through Capability: The HALC algorithm achieves a fault ride-through score of 5/5, outperforming MPC’s 3/5. MPC alone may react optimally in short-term fault conditions, but it struggles under sustained grid disturbances. By contrast, the HALC methodology leverages RL’s accumulated experience to handle unforeseen grid faults effectively.
- 4.
- Balanced Computational Load: The HALC algorithm maintains moderate computational complexity (2/5) compared to MPC (4/5) and RL (5/5), making it feasible for real-time implementation on standard embedded hardware. This is due to offloading high-complexity tasks (e.g., RL training) to offline phases, while the online control relies on lightweight MPC-based predictions.
- 5.
- Energy Efficiency and Long-Term Adaptation: The HALC algorithm achieves energy efficiency of 95%, reflecting its ability to minimize losses during both steady-state and transient operations. The continuous self-improvement enabled by RL allows the HALC algorithm to refine its control policy for varying grid topologies and renewable integration challenges.
5.8. Practical Implications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Von Jouanne, A.; Agamloh, E.; Yokochi, A. Power hardware-in-the-loop (PHIL): A review to advance smart inverter-based grid-edge solutions. Energies 2023, 16, 916. [Google Scholar] [CrossRef]
- Meysam, Y.; Seyed, F.Z.; Nader, M.; Ahmed, M. An adaptive voltage control compensator for converters in DC microgrids under fault conditions. Int. J. Electr. Power Energy Syst. 2024, 156, 109697. [Google Scholar]
- Ali, M.; Rasoul, G.; Feifei, B.; Josep, M.G.; Mirsaeed, M.; Junwei, L. Adaptive power-sharing strategy in hybrid AC/DC microgrid for enhancing voltage and frequency regulation. Int. J. Electr. Power Energy Syst. 2024, 156, 109696. [Google Scholar]
- Chen, R.; Ling, Q.; Fang, J.; Fei, X.; Wang, D. A bit rate condition for feedback stabilization of uncertain switched systems with external disturbances based on event triggering. IET Control Theory Appl. 2024, 18, 1136–1151. [Google Scholar] [CrossRef]
- Luo, C.; Ma, X.; Liu, T.; Wang, X. Adaptive-output-voltage-regulation-based solution for the DC-link undervoltage of grid-forming inverters. IEEE Trans. Power Electron. 2023, 38, 12559–12569. [Google Scholar] [CrossRef]
- Qiu, L.; Gu, M.; Chen, Z.; Du, Z.; Zhang, L.; Li, W.; Huang, J.; Fang, J. Oscillation Suppression of Grid-Following Converters by Grid-Forming Converters with Adaptive Droop Control. Energies 2024, 17, 5230. [Google Scholar] [CrossRef]
- Muhammad, A.Q.; Salvatore, M.; Francesco, T.; Alberto, R.; Andrea, M.; Gianfranco, C. A novel model reference adaptive control approach investigation for power electronic converter applications. Int. J. Electr. Power Energy Syst. 2024, 156, 109722. [Google Scholar]
- Kumar, K.J.; Kumar, R.S. Fault ride through of solar photovoltaic based three phase utility interactive central inverter. Iran. J. Sci. Technol. Trans. Electr. Eng. 2024, 48, 945–961. [Google Scholar] [CrossRef]
- Tripathi, P.M.; Mishra, A.; Chatterjee, K. Fault ride through/low voltage ride through capability of doubly fed induction generator–based wind energy conversion system: A comprehensive review. Model. Control Dyn. Microgrid Syst. Renew. Energy Resour. 2024, 275–311. [Google Scholar] [CrossRef]
- Khan, K.R.; Kumar, S.; Srinivas, V.L.; Saket, R.K.; Jana, K.C.; Shankar, G. Voltage Stabilization Control with Hybrid Renewable Power Sources in DC Microgrid. IEEE Trans. Ind. Appl. 2024, 61, 2057–2069. [Google Scholar] [CrossRef]
- Lu, R.; Wu, J.; Zhan, X.S.; Yan, H. Practical Finite-Time and Fixed-Time Guaranteed Cost Consensus for Second-Order Nonlinear Multi-Agent Systems with Switching Topology and Actuator Faults. Int. J. Robust Nonlinear Control 2025, 35, 3572–3583. [Google Scholar] [CrossRef]
- Jiao, Z.; Wang, Z.; Luo, Y.; Wang, F. H∞ PID Control for Singularly Perturbed Systems With Randomly Switching Nonlinearities Under Dynamic Event-Triggered Mechanism. Int. J. Robust Nonlinear Control 2025, 35, 3584–3597. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, H.; Liang, X.; Deng, S. Model Predictive Control for Three-Phase, Four-Leg Dynamic Voltage Restorer. Energies 2024, 17, 5622. [Google Scholar] [CrossRef]
- Jabbarnejad, A.; Vaez-Zadeh, S.; Khalilzadehz, M.; Eslahi, M.S. Model-free predictive control for grid-connected converters with flexibility in power regulation: A Solution for Unbalanced Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2130–2140. [Google Scholar] [CrossRef]
- Arjomandi-Nezhad, A.; Guo, Y.; Pal, B.C.; Varagnolo, D. A model predictive approach for enhancing transient stability of grid-forming converters. IEEE Trans. Power Syst. 2024, 39, 6675–6688. [Google Scholar] [CrossRef]
- Ikram, M.; Habibi, D.; Aziz, A. Networked Multi-Agent Deep Reinforcement Learning Framework for the Provision of Ancillary Services in Hybrid Power Plants. Energies 2025, 18, 2666. [Google Scholar] [CrossRef]
- Mai, V.; Maisonneuve, P.; Zhang, T.; Nekoei, H.; Paull, L.; Lesage-Landry, A. Multi-agent reinforcement learning for fast-timescale demand response of residential loads. Mach. Learn. 2024, 113, 5203–5234. [Google Scholar] [CrossRef]
- Xu, N.; Tang, Z.; Si, C.; Bian, J.; Mu, C. A Review of Smart Grid Evolution and Reinforcement Learning: Applications, Challenges and Future Directions. Energies 2025, 18, 1837. [Google Scholar] [CrossRef]
- Lee, W.G.; Kim, H.M. Deep reinforcement learning-based dynamic droop control strategy for real-time optimal operation and frequency regulation. IEEE Trans. Sustain. Energy 2024, 16, 284–294. [Google Scholar] [CrossRef]
- Mukherjee, S.; Hossain, R.R.; Mohiuddin, S.M.; Liu, Y.; Du, W.; Adetola, V.; Jinsiwale, R.A.; Huang, Q.; Yin, T.; Singhal, A. Resilient control of networked microgrids using vertical federated reinforcement learning: Designs and real-time test-bed validations. IEEE Trans. Smart Grid 2024, 16, 1897–1910. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, C.; Chai, Q.; Meng, K.; Guo, Q.; Dong, Z.Y. Robust regional coordination of inverter-based volt/var control via multi-agent deep reinforcement learning. IEEE Trans. Smart Grid 2021, 12, 5420–5433. [Google Scholar] [CrossRef]
- Li, Q.; Lin, T.; Yu, Q.; Du, H.; Li, J.; Fu, X. Review of deep reinforcement learning and its application in modern renewable power system control. Energies 2023, 16, 4143. [Google Scholar] [CrossRef]
- Adhau, S.; Gros, S.; Skogestad, S. Reinforcement learning based MPC with neural dynamical models. Eur. J. Control 2024, 80, 101048. [Google Scholar] [CrossRef]
- Alshahrani, S.; Khan, K.; Abido, M.; Khalid, M. Grid-forming converter and stability aspects of renewable-based low-inertia power networks: Modern trends and challenges. Arab. J. Sci. Eng. 2024, 49, 6187–6216. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M.; Rossi, M.; Abdelrahem, M.; Trabelsi, M.; Ahmed, M.; et al. Model-predictive control of multilevel inverters: Challenges, recent advances, and trends. IEEE Trans. Power Electron. 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Massaoudi, M.S.; Abu-Rub, H.; Ghrayeb, A. Navigating the landscape of deep reinforcement learning for power system stability control: A review. IEEE Access 2023, 11, 134298–134317. [Google Scholar] [CrossRef]
- Al-Saadi, M.; Al-Greer, M.; Short, M. Reinforcement learning-based intelligent control strategies for optimal power management in advanced power distribution systems: A survey. Energies 2023, 16, 1608. [Google Scholar] [CrossRef]
- Marko, Č.B.; Tomislav, B.Š.; Djordje, M.S.; Milan, R.R. Novel tuning rules for PIDC controllers in automatic voltage regulation systems under constraints on robustness and sensitivity to measurement noise. Int. J. Electr. Power Energy Syst. 2024, 157, 109791. [Google Scholar] [CrossRef]
- Afshari, A.; Davari, M.; Karrari, M.; Gao, W.; Blaabjerg, F. A multivariable, adaptive, robust, primary control enforcing predetermined dynamics of interest in islanded microgrids based on grid-forming inverter-based resources. IEEE Trans. Autom. Sci. Eng. 2023, 21, 2494–2506. [Google Scholar] [CrossRef]
- Ebinyu, E.; Abdel-Rahim, O.; Mansour, D.E.A.; Shoyama, M.; Abdelkader, S.M. Grid-forming control: Advancements towards 100% inverter-based grids—A review. Energies 2023, 16, 7579. [Google Scholar] [CrossRef]
- Safamehr, H.; Izadi, I.; Ghaisari, J. Robust VI droop control of grid-forming inverters in the presence of feeder impedance variations and nonlinear loads. IEEE Trans. Ind. Electron. 2023, 71, 504–512. [Google Scholar] [CrossRef]
- Samanta, S.; Lagoa, C.M.; Chaudhuri, N.R. Nonlinear model predictive control for droop-based grid forming converters providing fast frequency support. IEEE Trans. Power Deliv. 2023, 39, 790–800. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, Z.; Zhang, G.; Ye, T.; Zhao, P.; Wang, Y.; Yang, J.; Yu, J. Adaptive model predictive control for grid-forming converters to achieve smooth transition from islanded to grid-connected mode. IET Gener. Transm. Distrib. 2023, 17, 2833–2845. [Google Scholar] [CrossRef]
- Khan, I.; Vijay, A.S.; Doolla, S. A power-derived virtual impedance scheme with hybrid PI-MPC based grid forming control for improved transient and steady state power sharing. IEEE Trans. Sustain. Energy 2025, 1–12. [Google Scholar] [CrossRef]
- Joshal, K.S.; Gupta, N. Microgrids with model predictive control: A critical review. Energies 2023, 16, 4851. [Google Scholar] [CrossRef]
- Chowdhury, I.J.; Yusoff, S.H.; Gunawan, T.S.; Zabidi, S.A.; Hanifah, M.S.B.A.; Sapihie, S.N.M.; Pranggono, B. Analysis of model predictive control-based energy management system performance to enhance energy transmission. Energies 2024, 17, 2595. [Google Scholar] [CrossRef]
- Balouji, E.; Bäckstrüm, K.; McKelvey, T. Deep reinforcement learning based grid-forming inverter. In Proceedings of the 2023 IEEE Industry Applications Society Annual Meeting (IAS), Nashville, TN, USA, 29 October 2023–2 November 2023; pp. 1–9. [Google Scholar]
- Rajamallaiah, A.; Karri, S.P.K.; Alghaythi, M.L.; Alshammari, M.S. Deep reinforcement learning based control of a grid connected inverter with LCL-filter for renewable solar applications. IEEE Access 2024, 12, 22278–22295. [Google Scholar] [CrossRef]
- Hossain, R.R.; Yin, T.; Du, Y.; Huang, R.; Tan, J.; Yu, W.; Liu, Y.; Huang, Q. Efficient learning of power grid voltage control strategies via model-based deep reinforcement learning. Mach. Learn. 2024, 113, 2675–2700. [Google Scholar] [CrossRef]





| Symbol | Definition |
|---|---|
| State vector (includes ,,: inductor current, capacitor voltage, grid current) | |
| Control input vector (inverter voltage commands) | |
| External disturbances (load variations, renewable fluctuations) | |
| Output vector (grid voltage/current measurements) | |
| Continuous-time state-space matrices | |
| Discrete-time state-space matrices (zero-order hold) | |
| Lyapunov function (proves stability via ) | |
| ) | System transition function (nonlinear dynamics) |
| ) | State and control cost terms in MPC objective |
| γ | Discount factor (RL reward weighting) |
| System error over horizon | |
| Reward function (RL) | |
| Constraint function for disturbance rejection (levels: fast/probabilistic/slow) | |
| Tolerance bound for slow disturbance rejection | |
| True dynamics, nominal model, and uncertain model components | |
| RL policy (control law) | |
| RL state observation | |
| RL adaptive parameters | |
| Composite Lyapunov function (HALC stability) | |
| MPC-controlled instantaneous voltage, DC-link voltage; RL-controlled peak voltage |
| Parameter | Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Rated Power | 100 | kVA | Inverter apparent power rating | |
| Nominal Voltage (Line-to-Line RMS) | 400 | V | Grid voltage level | |
| Nominal Frequency | 50 | Hz | Grid frequency (depends on region) | |
| DC Link Voltage | 700 | V | DC bus voltage | |
| Switching Frequency | 10 | kHz | PWM switching frequency | |
| Filter Inductance | 2.5 | mH | Output filter inductor | |
| Filter Capacitance | 100 | μF | Output filter capacitor | |
| Grid Impedance (L) | 5 | mH | Grid side inductor | |
| Grid Resistance (R) | 0.1 | Ω | Grid side resistance | |
| Short Circuit Ratio (SCR) | 3–5 | - | Ratio defining grid strength | |
| Harmonic Limits (THD) | ≤ 3 | % | Total harmonic distortion threshold |
| Parameter | Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Prediction Horizon | 10 | steps | Number of future steps considered | |
| Control Horizon | 3 | steps | Number of steps MPC optimizes at each iteration | |
| Sampling Time | 50 | μs | Time step for MPC calculations | |
| Weight on Voltage Tracking | 10 | - | Higher weight ensures accurate voltage regulation | |
| Weight on Control Effort | 0.1 | - | Limits excessive control action | |
| Voltage Constraint | 0.9–1.1 | pu | Voltage operating range | |
| Current Limit | 1.2 | pu | Maximum allowable current | |
| Solver Type | Quadratic Programming (QP) | - | Optimization algorithm for MPC |
| Parameter | Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Learning Rate | 0.01–0.05 | - | Defines how quickly RL updates its policy | |
| Discount Factor | 0.9 | - | Prioritizes long-term rewards | |
| Exploration Rate (Initial/Decay) | 1 | - | Controls balance between exploration and exploitation | |
| State Variables | - | - | RL observes voltage, frequency, and power variations | |
| Action Space | MPC Adjustments | - | RL can fine-tune droop coefficients and MPC gains | |
| Reward Function | - | - | Penalizes voltage deviations and power losses |
| Parameter | Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Grid Voltage | 1 | pu | Nominal grid voltage | |
| Grid Frequency | 50 | Hz | Grid frequency | |
| Grid Strength (SCR) | 3–5 | - | Weak (<3), Medium (3–5), Strong (>5) | |
| Load Step Increase | +50% | - | Instantaneous load jump | |
| Load Step Decrease | −50% | - | Instantaneous load reduction | |
| Voltage Sag Event | 0.7 | pu | Temporary voltage dip | |
| Voltage Swell Event | 1.2 | pu | Temporary voltage rise | |
| Renewable Power Fluctuation | 50–100 | kW | Solar/wind power variation |
| Criteria | PID Control [28,29,30] | Droop Control [6,31,32] | Model Predictive Control (MPC) [33,34,35,36] | Reinforcement Learning (RL) [37,38] | Proposed HALC (MPC + RL) |
|---|---|---|---|---|---|
| Voltage Regulation Accuracy (%) | 80 | 85 | 88 | 92 | 97 |
| Response Time (ms) | 80 | 60 | 30 | 50 | 20 |
| Computational Complexity (1 = Low, 5 = High) | 1 | 3 | 4 | 5 | 2 |
| Adaptability to Grid Changes (1–5 Scale) | 2 | 2 | 3 | 5 | 5 |
| Robustness to Voltage Disturbances (1–5 Scale) | 3 | 2 | 4 | 4 | 5 |
| Learning and Self-Improvement (1–5 Scale) | 1 | 1 | 2 | 5 | 5 |
| Stability Guarantee (1–5 Scale) | 3 | 2 | 4 | 3 | 5 |
| Energy Efficiency (%) | 80 | 78 | 85 | 87 | 95 |
| Fault Ride-Through Capability (1–5 Scale) | 2 | 2 | 3 | 4 | 5 |
| Computational Time per Control Action (ms) | 5 | 8 | 20 | 25 | 10 |
| Comparison Criteria | Model Predictive Control (MPC) [36] | Reinforcement Learning (RL) [39] | Proposed HALC (MPC + RL) |
|---|---|---|---|
| Control Approach | Predictive, optimization-based | Data-driven, self-learning | Hybrid (predictive + learning) |
| Response Time | Fast short-term optimization | Slower, requires training | Fast response with continuous learning |
| Adaptability to Grid Changes | Limited to model accuracy | Adapts over time | Immediate and long-term adaptation |
| Computational Complexity | High due to optimization | High due to training | Moderate (balanced approach) |
| Real-Time Implementation | Challenging due to solver time | Requires pre-training | Feasible with adaptive control |
| Handling of Voltage Sags and Swells | Effective in short-term | Learns from past disturbances | Immediate correction and long-term adaptation |
| Stability Guarantee | Ensured by constraints | No explicit stability guarantee | Stability ensured via Lyapunov analysis |
| Robustness to Disturbances | Moderate, depends on model accuracy | Improves with training | High, due to multi-stage control |
| Learning and Self-Improvement | No learning, fixed optimization | Learns over time | Continuous learning and optimization |
| Energy Efficiency | Moderate | Can be inefficient initially | Optimized efficiency through learning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mensah Akwasi, A.; Chen, H.; Liu, J.; Duku, O.-A. Hybrid Adaptive Learning-Based Control for Grid-Forming Inverters: Real-Time Adaptive Voltage Regulation, Multi-Level Disturbance Rejection, and Lyapunov-Based Stability. Energies 2025, 18, 4296. https://doi.org/10.3390/en18164296
Mensah Akwasi A, Chen H, Liu J, Duku O-A. Hybrid Adaptive Learning-Based Control for Grid-Forming Inverters: Real-Time Adaptive Voltage Regulation, Multi-Level Disturbance Rejection, and Lyapunov-Based Stability. Energies. 2025; 18(16):4296. https://doi.org/10.3390/en18164296
Chicago/Turabian StyleMensah Akwasi, Amoh, Haoyong Chen, Junfeng Liu, and Otuo-Acheampong Duku. 2025. "Hybrid Adaptive Learning-Based Control for Grid-Forming Inverters: Real-Time Adaptive Voltage Regulation, Multi-Level Disturbance Rejection, and Lyapunov-Based Stability" Energies 18, no. 16: 4296. https://doi.org/10.3390/en18164296
APA StyleMensah Akwasi, A., Chen, H., Liu, J., & Duku, O.-A. (2025). Hybrid Adaptive Learning-Based Control for Grid-Forming Inverters: Real-Time Adaptive Voltage Regulation, Multi-Level Disturbance Rejection, and Lyapunov-Based Stability. Energies, 18(16), 4296. https://doi.org/10.3390/en18164296







