Abstract
The industrial sector is a major contributor to energy-related CO2 emissions in Europe, making the transition to renewable energy solutions essential. Decarbonization strategies integrate renewable energy sources, power-to-heat technologies, and energy storage systems into existing production sites to enhance sustainability and flexibility. However, a key challenge lies in designing energy systems that remain robust under long-term operational uncertainties. Usually the design of each energy system component is discrete, as it is manufactured in a predetermined size. Classical state-of-the-art coupled design and operational optimization methods are based on continuous design variables, which might give sub-optimal solutions. This study overcomes this limitation by employing novel, computationally efficient robust quantum-classical discrete-design methods. Traditional approaches often optimize operations for a single year due to the computational limitations of operational optimization algorithms, leading to designs that lack robustness. By incorporating long-term operational uncertainties, this approach ensures that selected energy-system configurations minimize both CO2 emissions and costs while maintaining resilience to variations in weather conditions and demand fluctuations. Robust discrete designs which consider operational uncertainties show 12% less global warming impact (GWI) with 27% higher total annualized cost (TAC) compared to designs based on operational optimization without uncertainty. A novel quantum-assisted non-dominated sorting genetic algorithm (QANSGA-II) shows accuracy up to 90%, which leads to 27% less computational effort than the NSGA-II algorithm. This novel method can help industries to search larger and more optimal robust discrete-design spaces for making decarbonization decisions.
1. Introduction
The intensifying climate crisis has elevated the urgency to decarbonize all sectors of the global economy. Among these, the industrial sector stands out as one of the largest consumers of energy and sources of greenhouse gas (GHG) emissions, particularly carbon dioxide (CO2). Globally, industry accounts for nearly 24% of total direct CO2 emissions from fuel combustion [1]. The imperative to address these emissions is enshrined in major international frameworks such as the Paris Agreement, which aims to limit global temperature rise to well below 2 °C, and preferably 1.5 °C, above pre-industrial levels [2]. Achieving this goal requires rapid and deep reductions in emissions from industry through electrification, efficiency improvements, and integration of low-carbon energy technologies. In the European context, the industrial sector represents approximately one-quarter of the EU’s final energy consumption and is responsible for a significant share of energy-related CO2 emissions [3]. Much of this energy use is concentrated in energy-intensive industries, such as chemicals, paper, steel, manufacturing and food processing.
The European Green Deal and the Fit for 55 package reinforce the region’s commitment to climate neutrality by 2050, imposing stricter CO2 emission standards, increasing carbon pricing mechanisms, and pushing for integration of renewable energy technologies in industrial sectors [4]. However, these shifts pose challenges for existing energy infrastructures, which are heavily reliant on fossil fuels and centralized energy-supply systems.
Smart energy utility systems offer a promising pathway for industrial decarbonization. These systems are characterized by the integration of renewable energy sources (e.g., solar photovoltaic, wind), power-to-heat technologies (e.g., heat pumps, electric boilers), and multi-modal energy storage solutions (thermal and electrical) within industrial facilities [5,6]. Their benefits include reduced dependency on fossil fuels, improved energy flexibility, and enhanced energy efficiency through local generation and optimized demand–response strategies. These technologies enable the electrification of heat demand, a significant step toward decarbonization, given that industrial heat accounts for more than 50% of final industrial energy use in the EU [7]. Additionally, energy storage and smart controls allow these systems to respond dynamically to fluctuating electricity prices and renewable availability, increasing overall system resilience and process efficiency.
1.1. The Design Problem: Discreteness and Uncertainty
Designing smart energy supply systems for industrial environments is non-trivial. A core challenge lies in the discrete nature of component sizing. Technologies like heat pumps, batteries, and PV modules are available in pre-manufactured, discrete sizes, requiring formulation of the design as a Mixed-Integer Nonlinear Programming (MINLP) problem. Unlike continuous models, discrete decision-making restricts the solution space and introduces non-convexities.
Adding to this complexity is the presence of long-term operational uncertainties. Key uncertainties include the following:
- Variability in renewable energy availability due to weather fluctuations.
- Changes in industrial demand profiles, often driven by market cycles, process changes, or scheduling.
- Volatility in energy prices, influenced by regulatory, geopolitical, and market dynamics.
These uncertainties can drastically affect the performance of a given system design. Therefore, robustness, defined as the ability of a system to maintain near-optimal performance across a wide range of future conditions, is a critical design requirement [8,9].
1.2. Limitations of Classical Optimization Approaches
Traditional energy system design approaches often use coupled design and operational optimization models, typically formulated as Nonlinear Programming (NLP) or Mixed-Integer Linear Programming (MILP) problems. While these models can generate feasible system configurations, they suffer from three major limitations:
- Local optima and suboptimality: MILP and NLP models are especially susceptible to local optima instead of finding the global one, particularly in high-dimensional, non-convex design spaces.
- Computational constraints: Coupled design–operation optimization is computationally intensive. As a result, most studies limit the operational optimization to a single representative year [10], which fails to capture multi-year variability in renewable energy and demand profiles.
- Lack of robustness: Designs optimized for a single scenario often perform poorly when subjected to real-world uncertainties. This lack of robustness can lead to higher operational costs or emissions when actual conditions deviate from modeled ones [11].
1.3. Robust Design and Hybrid Optimization
To address the previously mentioned shortcomings, robust optimization and scenario-based stochastic programming have emerged as promising alternatives [12]. Robust optimization seeks solutions that perform well across all plausible realizations of uncertainties, not just in average conditions. However, these approaches further increase the complexity and dimensionality of the optimization problem. State-of-the-art robust optimization methods in energy systems solve linear problems to avoid large complexities [13,14].
In this context, multi-objective evolutionary algorithms (MOEAs) such as NSGA-II have been widely adopted due to their ability to handle complex, nonlinear, multi-modal search spaces and simultaneously optimize competing objectives (e.g., cost and CO2 emissions) [15]. Yet, even these advanced heuristics face challenges in efficiently exploring the vast, discrete-design space.
1.4. Novel Contributions of This Study
This study introduces a novel hybrid optimization framework to design robust smart energy utility systems under long-term uncertainties. Key contributions include:
- Quantum-classical MINLP design method: At the design level, the discrete-design space is explored using an NSGA-II multi-objective genetic algorithm enhanced with QA. Specifically, QA is integrated into the mutation operator to escape local optima and accelerate exploration of high-quality, discrete-design solutions—a novel method in energy systems research [16,17].
- Explicit handling of long-term uncertainties: The methodology incorporates multi-year operational scenarios derived from historical and future predicted weather and demand data, ensuring robustness to variability.
- Application to a real-world industrial case in Germany: The framework is demonstrated on a case study involving a food and cosmetic industry site in Germany, offering insights into practical decarbonization strategies for mid-sized European manufacturers.
This study reports the robust quantum-assisted discrete design of industrial smart energy utility systems with long-term operational uncertainties for a food and cosmetic industry in Germany. The following sections include the materials and methods, results and conclusion. Section 2 first explains the uncertainty scenarios used for the robust optimization. Then, it considers the basic fundamentals of quantum computing for combinatorial optimization followed by presentation of the novel Quantum-Assisted Non-dominated Sorting Algorithm (QANSGA). Section 3 discusses in detail the effects of uncertainty on optimal designs. It also provides a comparison between NSGA and QANSGA in terms of computational time and accuracy. Section 4 summarizes the methods used, briefly describes the outcomes and considers the scope for future work.
2. Materials and Methods
2.1. Energy System Design Under Uncertainty
The field of energy system design has evolved to incorporate various uncertainties, ranging from techno-economic parameters to environmental and operational variables. Pfenninger and Keirstead [18] emphasize the importance of using long-term historical and synthetic time series for demand and weather modeling to avoid over fitting to a single-year profile. Several studies have attempted to incorporate uncertainty via scenario-based approaches [19,20], while others use robust optimization frameworks, particularly in distributed energy systems and micro-grids [21,22]. However, these methods often rely on linear approximations or limit the problem scale to maintain tractability.
To address the uncertainty in design process, we generated a 4-year random profile with Monte Carlo simulation based on historical data for the region of Herzberg, Germany. We took 2023 as the base year, as the preliminary investigation of the case study started in 2023, and step-by-step, all the changes in the particular food industry have been carried out. The reference historical profile for the food and cosmetic industry we have used as the case study in Herzberg, Germany, is shown in blue in Figure 1. Solar radiation of a particular location generally is quite predictable compared to other renewable sources such as wind. According to DWD (German Meteorological Service), Global Horizontal Irradiance (GHI) in Germany is increasing by 3.4 kw/m2 [23]. By taking 2023 as the base year, we additionally created a 4-year long solar radiation profile. The electricity price profile is shown in Figure 2. We have not considered uncertainties in demand profiles and investment costs. It is advisable to include those uncertainties in future work due to their implications for design decisions.
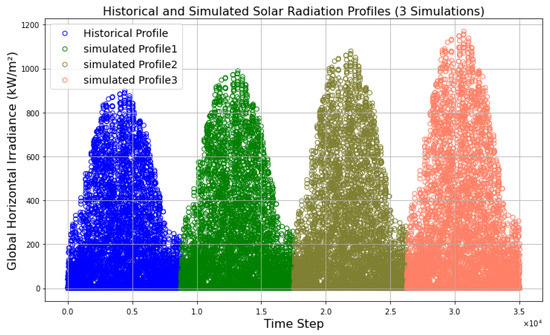
Figure 1.
Solar radiation in Herzberg, Germany.
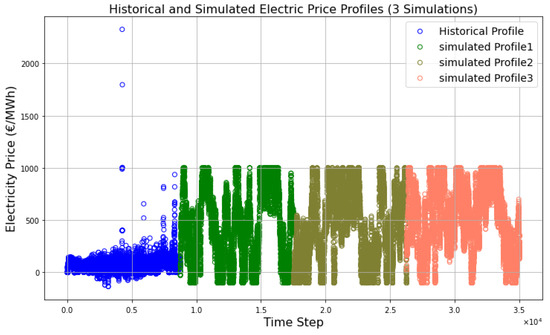
Figure 2.
Electricity prices with uncertainty.
Discrete component sizing is often addressed through MILP or MINLP formulations. For example, Dhariwal et al. (2017) [24] explore MILP-based optimizations for building energy systems, but scalability becomes a bottleneck. The inclusion of nonlinear performance curves (e.g., for heat pumps or batteries) makes MILP insufficient, necessitating MINLP formulations, which are harder to solve to global optimality. Recent reviews (e.g., [25]) stress the trade-off between model realism and computational tractability, with most large-scale design studies opting for reduced model complexity to ensure solvability. Figure 3 shows the superstructure of the energy system components which are considered for the energy system design of the food industry. Kansara et al. (2024) [26] presented a coupled design and operation optimization with nonlinear thermal interaction. We consider the same superstructure for this study with the component sizes included in Table 1.
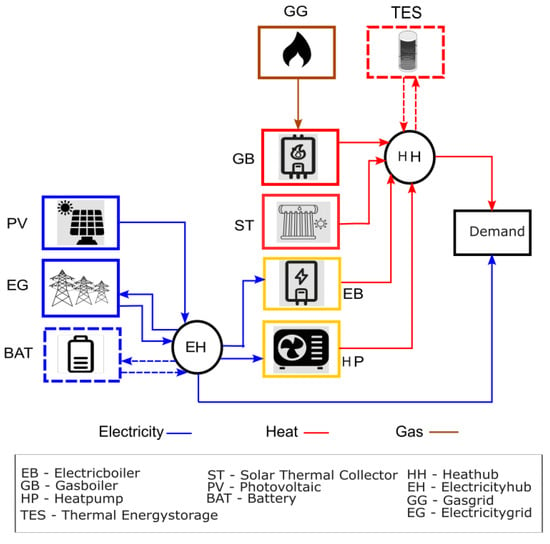
Figure 3.
Energy system components in a superstructure [27].

Table 1.
Discrete designs of energy components.
Kansara et al. (2023) [27] described coupled optimization with continuous capacity sizes of energy components. As explained previously, in this study, we focused on solving coupled optimization for discrete designs.
Evolutionary algorithms like the non-dominated sorting genetic algorithm NSGA-II have been widely adopted for multi-objective energy optimization [26,28]. Their ability to find Pareto-optimal solutions makes them suitable for balancing cost, emissions, and other performance metrics. However, performance depends heavily on the efficiency of genetic operators and diversity of the population. To address stagnation in local optima, several studies have proposed hybridization with local search methods, surrogate models, or even data-driven heuristics [29]. The integration of quantum optimization techniques into NSGA-II still remains under-explored, particularly in the energy system context. This study explores quantum-enhanced NSGA-II for optimizing designs of integrated energy system components.
2.2. Quantum Computing for Combinatorial Optimization
2.2.1. Fundamentals of Quadratic Unconstrained Binary Optimization
Quantum annealing (QA), implemented in systems such as D-Wave, has emerged as a viable tool for solving Quadratic Unconstrained Binary Optimization (QUBO) problems. Applications in logistics, finance, and molecular biology have demonstrated its potential in escaping local optima in large combinatorial spaces [30]. Initial studies in energy systems have shown its feasibility in unit commitment problems and transmission network design. However, its integration into evolutionary design algorithms, especially as a mutation accelerator in discrete multi-objective settings, remains a novel frontier, one that this study explores and demonstrates in an applied industrial context.
To tackle discrete optimization problems with QA, one generally needs access to specialized quantum hardware, like the systems offered by D-Wave. D-Wave’s approach to QA centers is based on finding the lowest energy state of a system, which can be mathematically represented as a Quadratic Unconstrained Binary Optimization (QUBO) problem [31].
A QUBO problem is mathematically defined by the following objective function:
where is an N-dimensional vector of binary decision variables and is a real-valued coefficient matrix representing the interactions between these variables. For a QUBO problem (1) characterized by a quadratic form , an equivalent Hamiltonian is constructed. QA is then used to identify the ground state of this Hamiltonian, which corresponds to the optimal solution of (1). For this reason, expressing a discrete optimization problem in QUBO form is suitable for execution on D-Wave’s QA hardware.
When solving QUBO problems on a D-Wave quantum computer, each binary variable in the given problem needs to be mapped to a qubit, the basic computational unit of the quantum annealer. However, current quantum annealers have a limited number of available qubits, which restricts the size and complexity of the QUBO problems they can handle. This means that, to ensure computational feasibility for large-scale optimization problems, it is essential to minimize the number of variables in the QUBO formulation. This can be achieved through careful discretization of any continuous variables and by avoiding redundant penalty terms in the QUBO. Ultimately, creating compact and efficient QUBO formulations is crucial for successfully leveraging quantum annealers in complex optimization challenges.
2.2.2. Methodology for Robust Optimization with the Quantum-Assisted Genetic Algorithm
As explained in Section 2.1, this study tries to solve discrete-design decisions under uncertainty of renewable sources and energy prices. As explained in Section 2.2.1, quantum annealing is capable of solving binary decisions efficiently and computationally faster compared to classical computing in particular conditions. We developed a novel quantum-enhanced classical NSGA-II algorithm which can be used to find robust discrete decisions of coupled design–operation energy optimization problems.
This section details the iterative process of the robust discrete design algorithm, focusing on how candidate energy-system designs are evaluated and refined across generations using a hybrid optimization approach. It is shown in Algorithm 1.
| Algorithm 1 Robust discrete design with quantum-assisted NSGA-II algorithm |
|
The core of the algorithm operates within a loop, iterating for a predefined number of generations, , in each generation G:
- Candidate Design Evaluation (cf. lines 3–9): In Algorithm 1, for every candidate design currently in the population , the performance is rigorously assessed through a lower-level operational optimization.
- Operational Optimization (cf. lines 6–7): To evaluate ’s robustness, its operational performance is simulated across each long-term uncertainty scenario s from the set S. For a given and s, a Nonlinear Programming (NLP) problem is solved. This NLP aims to minimize the operational cost , where d represents the operational dispatch variables (e.g., hourly energy flows, storage charging/discharging). This minimization is subject to a set of constraints (inequality constraints) and (equality constraints), which model the energy balance, component operational limits, and other system requirements. From the solution of this NLP problem, the annual cost and CO2 emissions for design under scenario s are determined.
- Robust Fitness Calculation (cf. lines 10–12): After evaluating the operational performance across all scenarios, the robust fitness values for are calculated. Two objective functions, and , represent the robust total annualized cost and robust CO2 emissions, respectively. These are obtained by aggregating the scenario-specific and over all scenarios . Common aggregation methods include taking the expected value () or the worst-case () performance across scenarios, depending on the desired level of robustness.
- Application of NSGA-II Genetic Operators (cf. lines 14–21): Once all candidate designs in the current population are evaluated, NSGA-II applies its core genetic operators to evolve the population:
- Selection (cf. line 15): Parents for the next generation, , are selected from . This selection process prioritizes individuals that are on non-dominated fronts (i.e., not inferior to any other solution in all objectives) and those that contribute to a diverse Pareto front (achieved through crowding distance calculation).
- Crossover (cf. line 16): Offspring designs, , are generated by combining the genetic material of selected parents through a crossover operator.
- Mutation (Quantum-Assisted) (cf. lines 17–21): A crucial step for exploring the discrete-design space efficiently is the quantum-assisted mutation. For selected offspring designs , a sub-problem involving the modification of discrete-design variables is formulated as a QUBO problem, represented as . QUBO formulation for discrete design follows the representation shown in [32]. This QUBO problem is then submitted to a QA. The solution returned by the quantum annealer is decoded to yield new, mutated discrete-design variables , which are then incorporated back into the offspring population. This quantum assistance aims to facilitate more effective exploration of the discrete-design space, potentially discovering novel and improved solutions that might be difficult for classical mutation operators to find.
- Population Update (cf. lines 22–25): After applying genetic operators, the parent population and the newly generated offspring population are combined to form . Non-dominated sorting and crowding distance calculations are performed on this combined population. Finally, individuals are selected from the resulting non-dominated fronts to form the next generation’s population, , ensuring that the population always maintains its size and prioritizes better, diverse solutions.
This iterative process continues until the maximum number of generations () is reached, at which point the algorithm returns the final set of Pareto-optimal robust discrete designs. These designs represent the optimal trade-offs between minimizing TAC and CO2 emissions while demonstrating resilience to long-term operational uncertainties.
A detailed explanation of the optimization problem, component modeling, objective functions and constraints is given in [27].
2.3. Scenario Selections for Optimization
As explained in Section 2.1, we considered original and simulated profiles to ensure optimized design under uncertainties over a longer period of time. The profiles generated are 4-years long, which is quite long when operational optimization is considered, as the time-step of the operational optimization is 1 h. This means that the operation has to be optimized for each design population for 35,040 time-steps, which is computationally very expensive. The scenarios must be selected in a way that captures the different uncertainties and provides robust designs through optimization.
The algorithm is fully implemented in Python 3.10, leveraging the ‘tsam’ package for effective time-series aggregation [33]. For this aggregation, we selected a period size of 15 days (Nd = 15) and a total of four representative periods (Np = 4). This relatively large period size was chosen specifically to minimize the overall number of periods, thereby reducing the impact of circular conditions at the boundaries of each representative period. Furthermore, these aggregated values are set to correspond to the minimum storage capacities for Thermal Energy Storage (TES) (200 kWh) and Battery Energy Storage (BAT) (200 kWh) systems to prevent inefficient or unnecessary charging cycles.
The clustered data represent four scenarios (periods) with 15 days’ data in each scenario. This clustering follows the K-medoids method [33]. K-medoids is a partitioning clustering algorithm that selects actual data points, called medoids, to represent the center of each cluster. The algorithm iteratively assigns each data point to its closest medoid based on a chosen distance metric. Subsequently, it updates the medoids by selecting new data points that minimize the sum of dissimilarities within their respective clusters. This approach makes K-medoids particularly robust to outliers and allows for its application with any arbitrary distance function.The clustering centers are chosen in a way that also includes extreme events to make the optimization robust. Each scenario (S1, S2, S3, S4) has 360 time-steps which considers possible uncertainties. With this approach, we can reduce the time-steps from 35,040 to 1440, as shown in Figure 4.
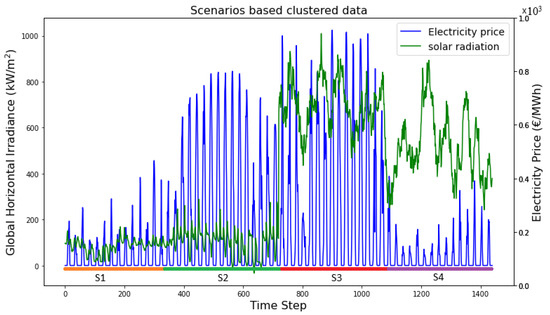
Figure 4.
Different scenarios clustered for computational relaxation.
3. Results
The coupled design and operation optimization was performed for 1440 time-steps, including the four different scenarios described in Section 2.3. As explained in Section 2.2.2, the novel quantum-assisted NSGA-II (QANSGA-II) is applied on the design level to optimize discrete decisions. The results are compared with those obtained from NSGA-II on the design level. This section is divided into four subsections. First, Section 3.1 explains the original optimized continuous designs of the integrated energy system of the industrial site. Then, the continuous designs are compared with the discrete designs optimized with the same original coupled optimization using NSGA-II on a design level. Section 3.2 compares the discrete designs for the reference year and uncertain scenarios. This subsection follows a detailed analysis for comparison of the different results. Considering the discrete sizes of the design variables, there are a total of 66 discrete variables. This also includes the size 0 for all design variables, which relates to the existence of the component in the decarbonization concept. Each discrete variable is embedded as a binary variable in QUBO for solving it on the quantum annealer [31]. Finally, Section 3.3 compares the discrete-design Pareto fronts solved with NSGA-II and QANSGA-II.
3.1. Objective Comparison of Continuous and Discrete Designs
Figure 5 shows the integrated energy system of the industrial site, whose sizes have been optimized with coupled design and operation optimization, as explained in [26], using continuous design variables. In this paper, we optimized designs with discrete sizes. A comparison of the optimized discrete sizes of the components with original continuous designs can be seen in Figure 6.
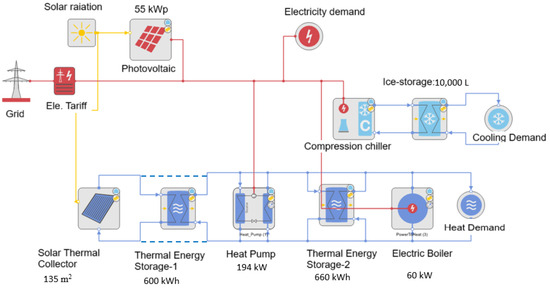
Figure 5.
Integrated optimized energy system of the case study [26].
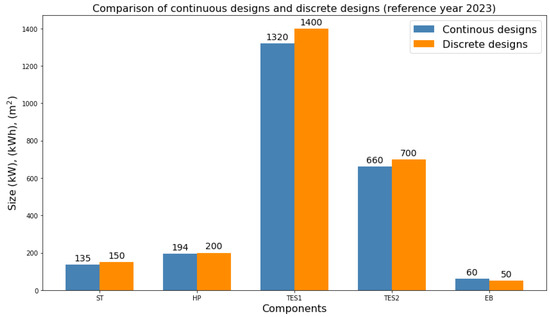
Figure 6.
Comparison of continuous and discrete designs for a reference year.
It can be seen that the discrete designs are larger than the continuous designs as the algorithm seeks to select the nearest available discrete designs from the optimal continuous designs. This is reflected in the larger sizes of ST, TES-1, TES-2 and HP. PV remains the same as it is fixed by the industrial stakeholder. The optimal discrete design of EB is reduced compared to the optimal continuous design. The reason for this reduction in EB size is increase in the size of all the other heat-supplying components. This decreases the backup demand of EB in case of peak loads.
Table 2 shows the objective values for optimal continuous and discrete designs. It can be seen that discrete designs have higher TAC and lower GWI compared to continuous designs due to large energy components. TAC is increased by 5% whereas GWI is decreased by 3.7%.

Table 2.
Objective comparison of continuous and discrete designs.
3.2. Discrete Design Comparison for a Reference Year and Uncertain Scenarios
Figure 7 shows the discrete design comparison for the operation optimized for the reference year and the operation optimized considering four uncertain scenarios. It can be seen that due to inclusion of uncertainties while optimizing the design and operation of the energy system, the optimized design for renewable energy-based components turns out to be more conservative compared to the case when uncertainties over a longer period of time are not considered.
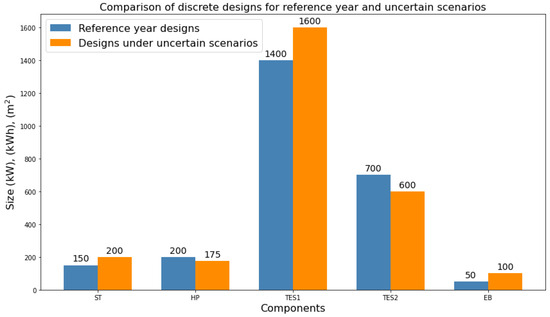
Figure 7.
Comparison of discrete designs for a reference year and uncertain scenarios.
The reason for this larger design is the increase in solar radiation by 3.4%; additionally, the average electricity price of the uncertainty scenarios is 120% higher than in the reference year. Both higher electricity price and higher available solar radiation force the renewable energy components to be larger and consume more renewable energy sources. That leads to larger ST and TES-1. Due to increase in the electricity price, the HP size reduces as the HP operation will be more expensive. Smaller HP size causes the size of the back-up EB to be larger. This increases the TAC by 27% due to the increase in electricity prices and larger components. Because of larger renewable components and storage capacity, GWI is decreased by 12%, as shown in Table 3.

Table 3.
Objective comparison of reference year and uncertain scenarios.
3.3. Pareto Comparison with Original NSGA-II and Quantum-Assisted NSGA-II
Figure 8a shows a comparison of the Pareto fronts for TAC and GWI using NSGA-II and QANSGA-II for the uncertain scenarios with 1440 operational time-steps. It can be seen that NSGA-II performs better in terms of lower objective values. QANSGA-II converges to suboptimal solutions and QANSGA-II uses quantum mutation at every generation G of NSGA-II during design optimization. Figure 8b shows the same comparison but with uncertain scenarios trimmed to 360 time-steps. The reduction in operational time-steps results in similar QANSGA-II performance as NSGA-II. Quantum-assisted mutation uses surrogate QUBO which is solved on D-Wave QA. For state-of-the-art QA, it is very difficult to handle a large number of variables due to the limited number of qubits available on a quantum computer. That is why QANSGA-II performs better with fewer operational time-steps. A higher number of time-steps makes surrogate QUBO very large and gives suboptimal solutions from QA, and, eventually, the hybrid mutation leads to overall suboptimal solutions. However, with fewer operational time-steps, QUBO is efficiently solved on QA and gives better results in whole optimization.
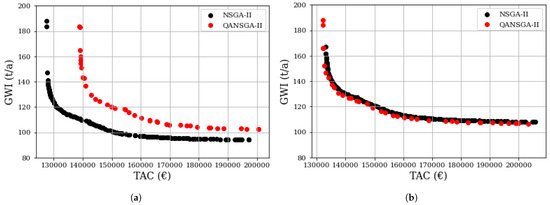
Figure 8.
(a) Comparison of Pareto fronts of NSGA-II (black dots) and QANSGA-II (red dots) (1440 time-steps), and (b) comparison of Pareto fronts of NSGA-II (black dots) and QANSGA-II (red dots) (360 time-steps); both the Pareto fronts show multi-objective designs for Total Annualized Cost (TAC) and Global Warming Impact (GWI).
Figure 9 shows the Pareto fronts for different mutation strategies. The black Pareto front represents design solutions with only NSGA-II on the design level. The red Pareto front shows QANSGA-II design points with quantum solutions injected to NSGA-II solutions in every generation G. The blue Pareto front shows QANSGA-II design points with quantum solutions injected to NSGA-II solutions in every second generation. This relaxes the quantum part of the problem. Thus, it does not need to optimize surrogate QUBO in every mutation step but in every second mutation step, which allows QUBO to be solved efficiently and search a wider discrete-design space. At the same time, it contains more information from the NSGA-II mutation, which results in solutions which are near to the optimum. However, NSGA-II alone performs better in terms of minimum objective values compared to QANSGA-II, as depicted in Figure 9.
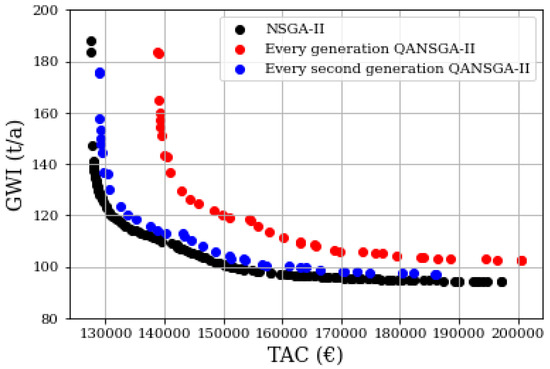
Figure 9.
Comparison of Pareto fronts of NSGA-II (black dots) and QANSGA-II (red dots) and (blue dots) with different mutation strategies; all the Pareto fronts show multi-objective designs for Total Annualized Cost (TAC) and Global Warming Impact (GWI).
Table 4 shows a computational time comparison between NSGA-II and QANSGA-II with different mutation strategies. QANSGA-II-1 (red dots in Figure 9) injects quantum solutions in the mutation step at every generation, whereas QANSGA-II-2 (red dots in Figure 8) does it every second generation. The classical part of the optimization is solved on an 11th Gen Intel(R) Core(TM) i7-1185G7 with 16 GB RAM and the quantum approach is solved on a D-Wave Advantage-4 System and NSGA-II (50 ) shows the highest computational effort. QANSGA-II-1 (red dots in Figure 9) is 47% faster than NSGA-II. Overall, QANSGA-II reduces the number of NSGA-II generations required to reach the optimal solution due to quantum solutions injection, which reduces the overall computational time of any QANSGA-II version. Additionally, QANSGA-II-2 is 27% faster than NSGA-II. Every second generation, quantum mutation injection increases the total number of required generations to 41 to reach the optimal solution compared to QANSGA-II-1, which requires only 32 generations . Following Figure 9 and Table 4, the best trade-off between accuracy of results and computational effort is provided by QANSGA-II-2, which allows quantum mutation injection at every second generation of NSGA-II.

Table 4.
Computational time comparison NSGA-II vs. QANSGA-II.
4. Conclusions
This study introduces a robust, quantum-assisted optimization framework for the decarbonization of industrial energy systems, addressing the critical challenge of designing systems that perform optimally under long-term operational uncertainties. The proposed approach departs from traditional methods that typically rely on continuous design variables and optimize operations for only a single representative year. Such simplifications often result in designs that are either sub-optimal or lack robustness in real-world fluctuating conditions.
To overcome these limitations, we developed and implemented a mixed-integer nonlinear programming (MINLP) framework using discrete sizing of components, reflecting actual manufacturing constraints, and integrated it with a novel quantum-assisted non-dominated sorting genetic algorithm (QANSGA-II). This method enables the exploration of robust design solutions that account for multi-year operational variability in weather and energy prices. A comparative analysis was performed between continuous and discrete sizing methods under operational uncertainty using the classical NSGA-II algorithm. The results show that switching from continuous to discrete-design sizing increases the total annualized cost (TAC) by approximately 5%, while delivering a 3.7% reduction in global warming impact (GWI). This highlights the environmental advantage of discrete, realistic designs even when incurring a moderate cost penalty.
Discrete robust designs resulted in 12% lower GWI and 27% higher TAC compared to reference year designs, emphasizing the trade-off between sustainability and economic performance when uncertainty is accounted for. Importantly, QANSGA-II-2 achieved up to 90% accuracy based on the root mean squared error (RMSE) with 27% less computational effort than the conventional NSGA-II, demonstrating its potential.
In summary, the study demonstrates that robust discrete design under uncertainty not only provides more resilient and sustainable solutions, but also when paired with efficient quantum-classical optimization techniques, becomes computationally tractable. These findings contribute a practical and forward-looking method to support the transition of industrial systems toward low-carbon operations and are applicable to optimization modelers exploring hybrid quantum-classical methods. The state-of-the-art quantum annealers have a limited number of qubits (ca. 5000) [31], which restricts the size of problem to be solved on the state-of-the-art quantum annealers. The quantum computer is on its way to becoming scalable by adding more qubits and more robust by decreasing errors. In future work, QANSGA-II can be improved to search a larger discrete-design space and increase performance of the coupled optimization.
Author Contributions
R.K.: conceptualization, methodology, validation, investigation, data curation, software, writing—original draft, visualization; L.K.: conceptualization, review; M.I.R.S.: project administration, supervision, review. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union’s Horizon Europe project SINNO GENES (Storage innovations for green energy systems), under Grant Agreement No. 101096992.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from the industrial site in Herzberg and are available from the authors with the permission of the owner.
Acknowledgments
We would like to thank Martin Brylka, Herzberg, Germany, for providing data and his continuous support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MILP | Mixed-Integer Linear Problem |
| MINLP | Mixed-Integer Nonlinear Problem |
| NLP | Nonlinear Problem |
| TAC | Total Annualized Cost |
| GWI | Global Warming Impact |
| NSGA | Non-dominated Sorting Genetic Algorithm |
| QANSGA | Quantum-Assisted Non-dominated Sorting Genetic Algorithm |
| GHG | Greenhouse Gas |
| MOEA | Multi-Objective Evolutionary Algorithm |
| DWD | Deutsche Wetterdienst |
| GHI | Global Horizontal Irradiance |
| GB | Gas Boiler |
| EB | Electric Boiler |
| HP | Heat Pump |
| PV | Photovoltaic |
| ST | Solar Thermal |
| TES | Thermal Energy Storage |
| BAT | Battery |
| QUBO | Quadratic Unconstrained Binary Optimization |
| QA | Quantum Annealing |
References
- Intergovernmental Panel on Climate Change (IPCC). AR6 Synthesis Report: Climate Change 2023. Available online: https://www.ipcc.ch/report/ar6/syr/ (accessed on 20 May 2025).
- UNFCCC. Paris Agreement. 2015. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 20 May 2025).
- European Environment Agency (EEA). Primary and Final Energy Consumption in the European Union. 2024. Available online: https://www.eea.europa.eu/en/analysis/indicators/primary-and-final-energy-consumption (accessed on 20 May 2025).
- The European Green Deal. Fit for 55 Policy Package and Upcoming Milestones. 2021. Available online: https://www.corporateleadersgroup.com/ (accessed on 20 May 2025).
- International Renewable Energy Agency (IRENA). Sector Coupling in Cities: Facilitating Integration of Variable Renewable Energy. 2021. Available online: https://www.irena.org/Publications/2021/Oct/Sector-Coupling-in-Cities (accessed on 22 May 2025).
- Pisciotta, M.; Pilorge, H.; Feldmann, J.; Jacobson, R.; Davids, J.; Swett, S.; Sasso, Z.; Wilcox, J. Current state of industrial heating and opportunities for decarbonization. Prog. Energy Combust. Sci. 2022, 91, 100982. [Google Scholar] [CrossRef]
- Eurostat. Final Energy Consumption in Industry—Detailed Statistics. 2023. Available online: https://ec.europa.eu/eurostat/statistics-explained/ (accessed on 22 May 2025).
- Bertsimas, D.; Sim, M. The Price of Robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making Under Uncertainty in Electricity Markets; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lin, X.; Zhang, N.; Zhong, W.; Kong, F.; Cong, F. Regional integrated energy system long-term planning optimization based on multi-energy complementarity quantification. J. Build. Eng. 2023, 68, 106046. [Google Scholar] [CrossRef]
- Domínguez-Muñoz, F.; Cejudo-López, J.M.; Carrillo-Andrés, A.; Ruivo, C.R. Design of solar thermal systems under uncertainty. Energy Build. 2012, 47, 474–484. [Google Scholar] [CrossRef]
- Zakaria, A.; Ismail, F.B.; Lipu, M.H.; Hannan, M.A. Uncertainty models for stochastic optimization in renewable energy applications. Renew. Energy 2020, 145, 1543–1571. [Google Scholar] [CrossRef]
- Wedemeyer, M.; Cramer, E.; Mitsos, A.; Dahmen, M. Robust Energy System Design via Semi-infinite Programming. arXiv 2025, arXiv:2411.14320. [Google Scholar]
- Yang, X.; Chen, Z.; Huang, X.; Li, R.; Xu, S.; Yang, C. Robust capacity optimization methods for integrated energy systems considering demand response and thermal comfort. Energy 2021, 221, 119771. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Venturelli, D.; March, D.J.; Rojo, G. Quantum Annealing Implementation of Job-Shop Scheduling. arXiv 2016, arXiv:1506.08479. [Google Scholar]
- Kim, S.; Ahn, S.W.; Suh, I.S.; Dowling, A.W.; Lee, E.; Luo, T. Quantum Annealing for Combinatorial Optimization: A Benchmarking Study. npj Quantum Inf. 2025, 11, 77. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Palensky, P.; Widl, E.; Stifter, M.; Elsheikh, A. Modeling Intelligent Energy Systems: Co-Simulation Platform for Validating Flexible-Demand EV Charging Management. IEEE Trans. Smart Grid 2013, 4, 1939–1947. [Google Scholar] [CrossRef]
- Kaleta, M. Robust Co-Optimization of Medium- and Short-Term Electrical Energy and Flexibility in Electricity Clusters. Enegries 2025, 18, 479. [Google Scholar] [CrossRef]
- Oropallo, E.; Piscopo, P.; Centobelli, P.; Cerchione, R.; Nuevo, E.; Rodríguez-Prieto, A. A decision support system to assess the operational safety and economic benefits of risk-based inspection implementation strategies. Saf. Sci. 2024, 177, 106570. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, İ.; Den Hertog, D. A practical guide to robust optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef]
- DWD. Deutscher Wetter Dienst. 2025. Available online: https://www.dwd.de/DE/leistungen/solarenergie/ (accessed on 30 May 2025).
- Dhariwal, J.; Banerjee, R. An approach for building design optimization using design of experiments. Build. Simul. 2017, 10, 323–336. [Google Scholar] [CrossRef]
- Bracco, S.; Cancemi, C.; Causa, F.; Longo, M.; Siri, S. Optimization model for the design of a smart energy infrastructure with electric mobility. IFAC-PapersOnLine 2018, 51, 200–205. [Google Scholar] [CrossRef]
- Kansara, R.; Roldán Serrano, M.I. Coupled Design and Operation Optimization for Decarbonization of Industrial Energy Systems Using an Open-Source In-House Tool. Eng 2024, 5, 3033–3048. [Google Scholar] [CrossRef]
- Kansara, R.A.; Lockan, M. Combined Physics-Data Driven Modeling for Design and Operation Optimization of an Energy Concept. In Proceedings of the 36th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, ECOS 2023, Las Palmas de Gran Canaria, Spain, 25–30 June 2023. [Google Scholar]
- Rawat, T.; Niazi, K.R.; Gupta, N.; Sharma, S. Multi-objective techno-economic operation of smart distribution network integrated with reactive power support of battery storage systems. Sustain. Cities Soc. 2021, 75, 103359. [Google Scholar] [CrossRef]
- Gabrielli, P.; Fürer, F.; Mavromatidis, G.; Mazzotti, M. Robust and optimal design of multi-energy systems with seasonal storage through uncertainty analysis. Appl. Energy 2019, 238, 1192–1210. [Google Scholar] [CrossRef]
- Denchev, V.S.; Boixo, S.; Isakov, S.V.; Ding, N.; Babbush, R.; Smelyanskiy, V.; Martinis, J.; Neven, H. What is the Computational Value of Finite-Range Tunneling? Phys. Rev. J. 2016, 6, 031015. [Google Scholar] [CrossRef]
- D-Wave Systems. What Is Quantum Annealing? 2024. Available online: https://docs.dwavequantum.com/ (accessed on 26 May 2025).
- Ajagekar, A.; You, F. Quantum Computing for Energy Systems Optimization: Challenges and opportunities. Energy 2019, 179, 76–87. [Google Scholar] [CrossRef]
- Kotzur, L.; Markewitz, P.; Robinius, M.; Stolten, D. Impact of different time series aggregation methods on optimal energy system design. Renew. Energy 2024, 117, 474–487. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).