Transient Stability Assessment of Power Systems Built upon Attention-Based Spatial–Temporal Graph Convolutional Networks
Abstract
1. Introduction
- To tackle the issue of sample imbalance, we propose an improved adaptive focal loss function that mitigates the underfitting of unstable samples caused by imbalanced datasets while effectively identifying hard-to-classify samples that contribute to better parameter updates.
- To address the limitation of existing models in feature extraction, we introduce attention mechanisms in both temporal and spatial dimensions to accurately capture dynamic correlations across different times and locations. The spatiotemporal attention module enhances the model’s feature extraction capability, followed by spatial and temporal convolutional layers, which extract spatial features and capture temporal dependencies, respectively. Finally, the residual network and fully connected layers process these features to produce accurate TSA results. The proposed algorithm offers distinct advantages: The integration of spatiotemporal attention mechanisms significantly improves the model’s ability to focus on critical features, while the combination of convolutional layers and residual networks ensures efficient feature extraction and prevents overfitting, leading to better generalization performance. Additionally, the overall architecture is designed to handle complex spatiotemporal data effectively, making it highly adaptable to various power system scenarios.
- Comprehensive case studies performed on the New England 10-machine 39-bus system and the NPCC 48-machine 140-bus system validate the effectiveness of the proposed methodology.
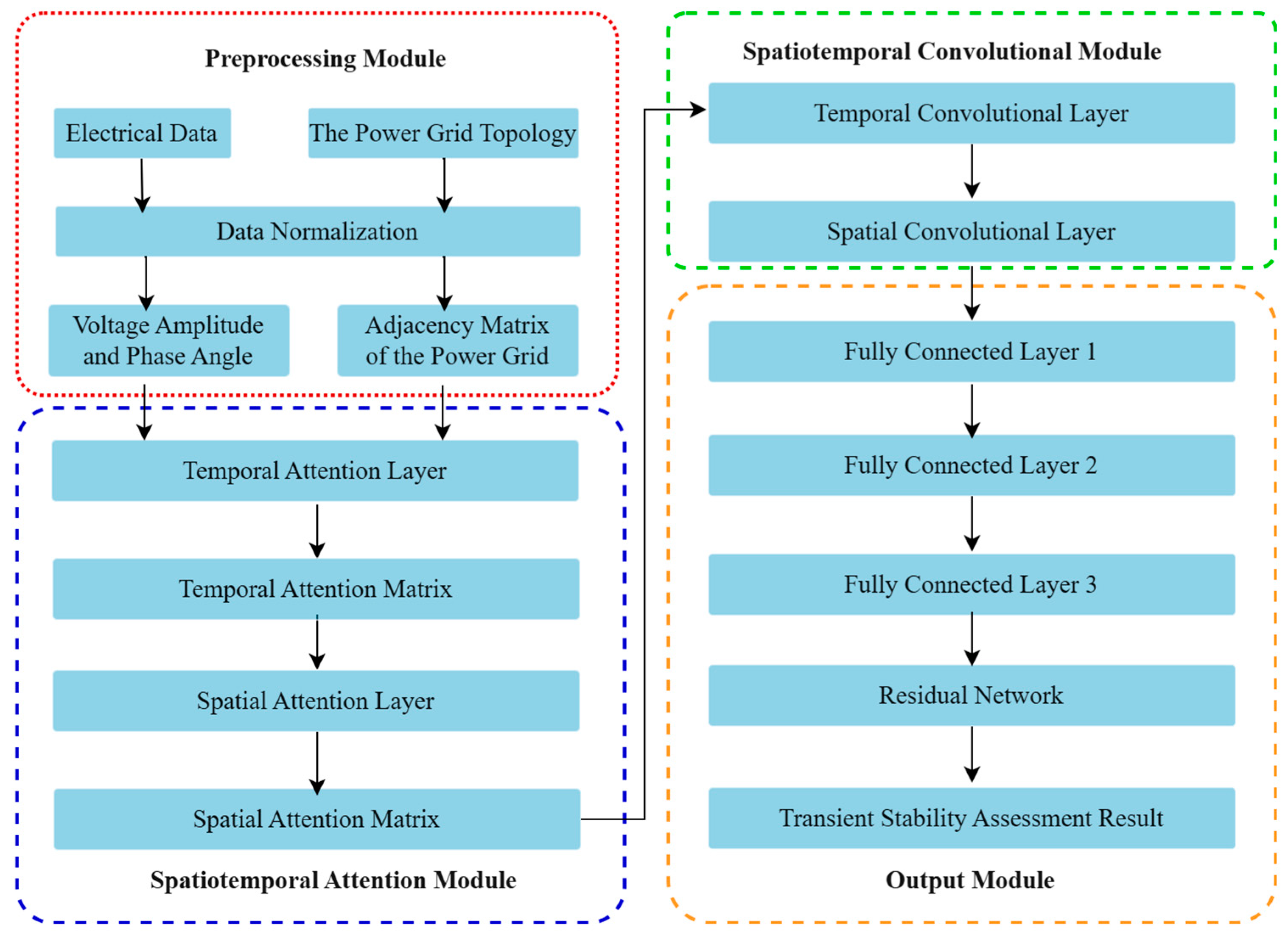
2. Attention-Based Spatial–Temporal Graph Convolutional Network (ASTGCN)
2.1. Spatiotemporal Attention Module
- spatial attention layer
- temporal attention layer
2.2. Spatiotemporal Convolutional Module
- Spatial Convolutional Layer
- Temporal Convolutional Layer
3. The TSA Method Based on the ASTGCN
3.1. Model Input and Output
3.2. Adaptive Focal Loss Function
- Adaptive Weight Factor
- Adaptive Focusing Factor
- Adaptive Focal Loss Function
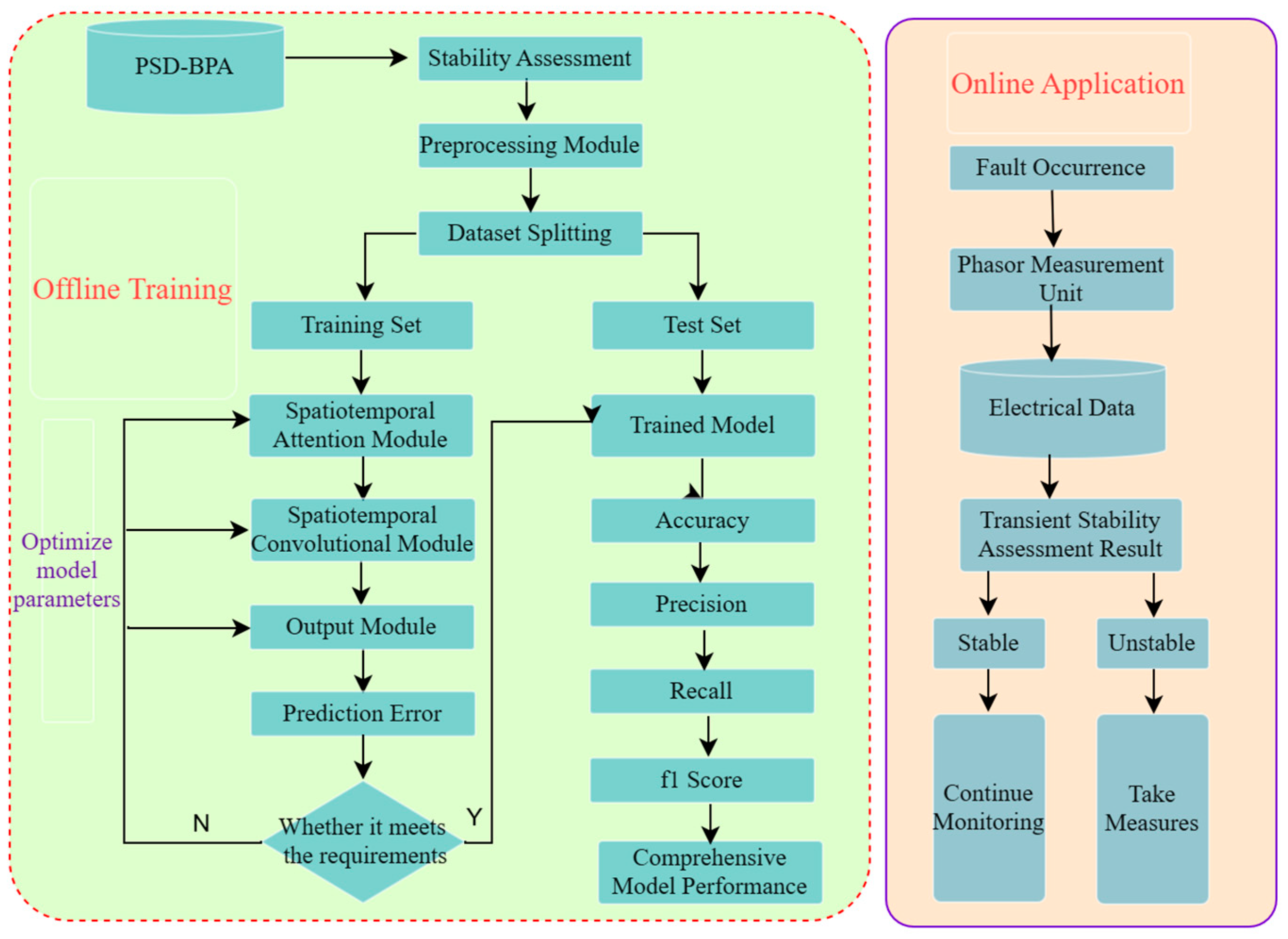
3.3. The TSA Process
- Simulation Data Generation: A large amount of simulation data is generated using the PSD-BPA 4.5.3 time-domain simulation software, with the richness and diversity of the sample data improved by varying load levels, fault locations, and load compositions.
- Transient Stability Classification of Samples: Based on the transient stability evaluation criteria for power systems and combined with the simulation data, the transient stability status of the samples is classified.
- Input Feature Processing: Voltage magnitudes and phase angles of each node are extracted from the generated simulation data to construct the input features.
- Model Training: The ASTGCN model is trained in a forward manner using the training set, and its parameters are optimized in reverse based on the adaptive focal loss function.
- Model Testing: The test set is fed into the trained ASTGCN model for evaluation, and the model’s assessment performance is comprehensively evaluated based on the test results.
- Online Application: Online operational data is collected and processed, and by utilizing the trained ASTGCN model, fast and accurate assessment of transient stability is achieved. If the assessment indicates that the system is unstable, immediate emergency control measures must be taken to prevent further deterioration of the system. For instance, generator tripping can be implemented to rapidly reduce the system’s generation power, thereby balancing the power imbalance. Additionally, load shedding can be carried out to alleviate the system’s load pressure and swiftly restore system stability.
3.4. Evaluation Metrics
4. Case Study
4.1. The New England 10-Machine 39-Bus System
4.1.1. Sample Generation
4.1.2. Performance Analysis of the Adaptive Focal Loss Function
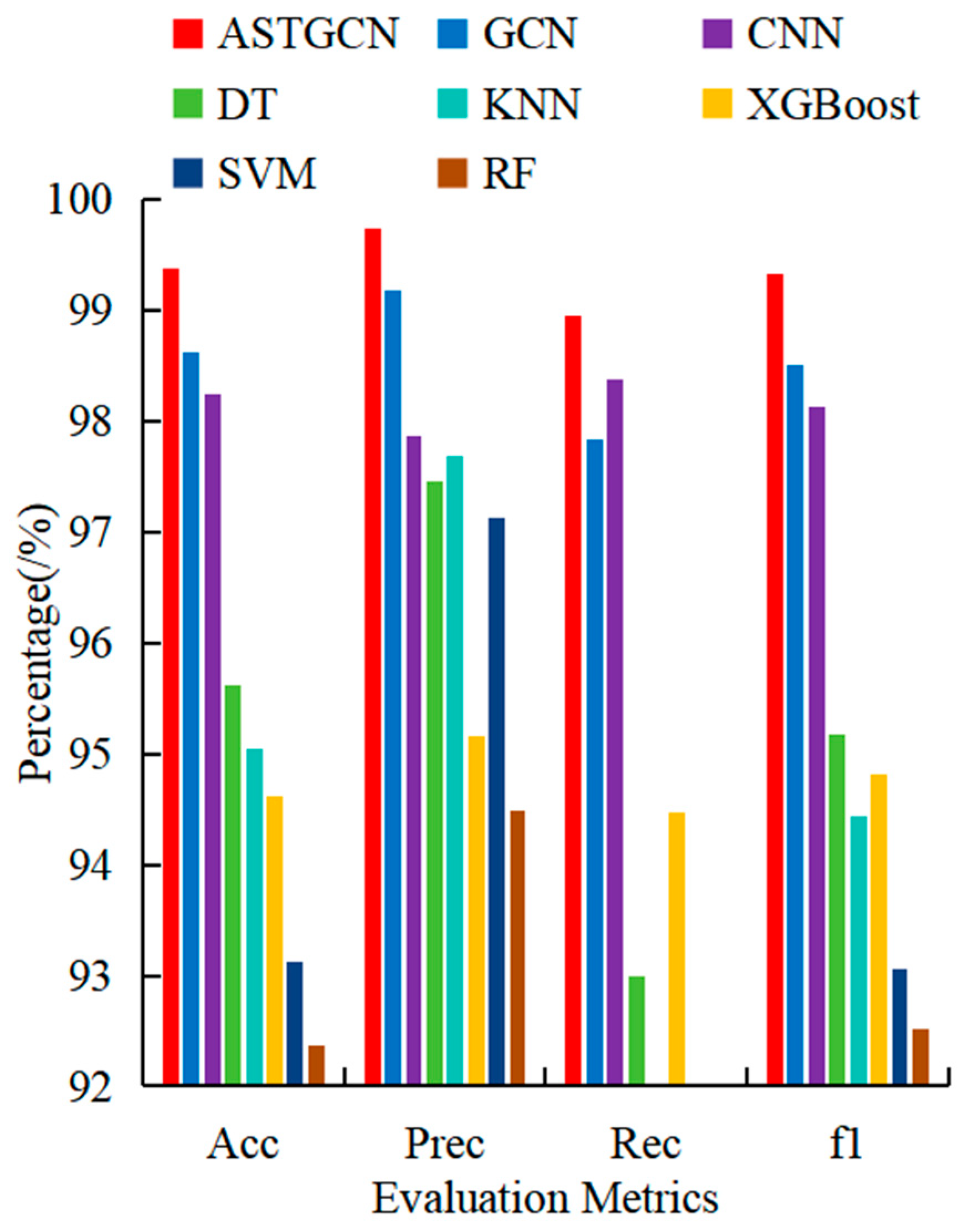
4.1.3. Comparative Evaluation of Model Performance
4.1.4. Ablation Studies on ASTGCN
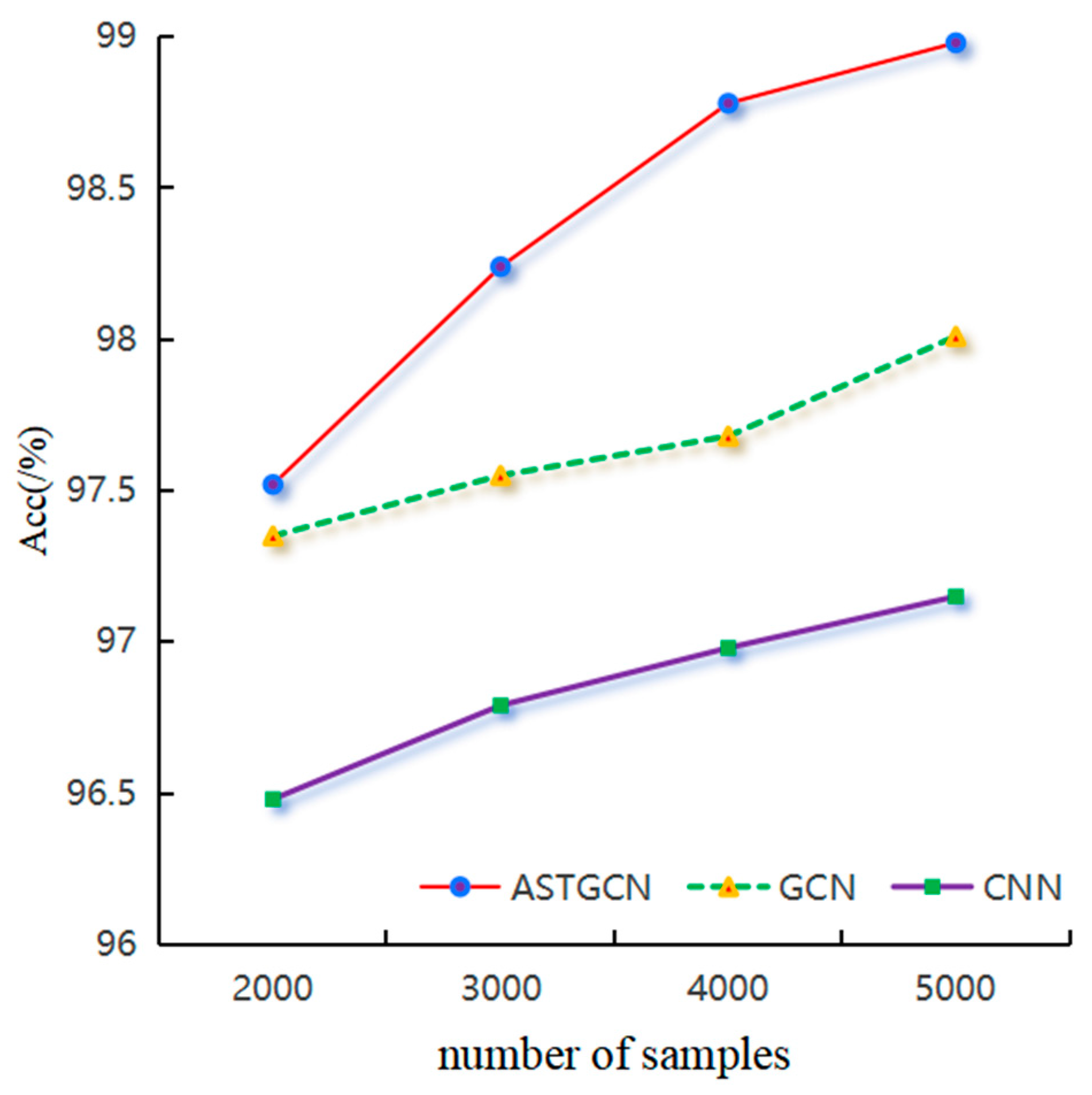
4.1.5. Analysis of the Impact of Sample Size on Model Performance
4.1.6. Robustness of the Model to Noise
4.1.7. Generalization Performance Under Unknown Topologies
4.2. Large-Scale Power Grid Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, H.; Wang, K.; Wang, Y.; Gao, M.; Zhang, Y. Energy big data: A survey. IEEE Access 2016, 4, 3844–3861. [Google Scholar] [CrossRef]
- Zadkhast, P.; Jatskevich, J.; Vaahedi, E. A Multi-Decomposition Approach for Accelerated Time-Domain Simulation of Transient Stability Problems. IEEE Trans. Power Syst. 2015, 30, 2301–2311. [Google Scholar] [CrossRef]
- Vu, T.L.; Turitsyn, K. Lyapunov Functions Family Approach to Transient Stability Assessment. IEEE Trans. Power Syst. 2016, 31, 1269–1277. [Google Scholar] [CrossRef]
- Ashraf, S.M.; Gupta, A.; Choudhary, D.K.; Chakrabarti, S. Voltage stability monitoring of power systems using reduced network and artificial neural network. Int. J. Electr. Power Energy Syst. 2017, 87, 43–51. [Google Scholar] [CrossRef]
- Guo, T.; Milanović, J.V. Probabilistic Framework for Assessing the Accuracy of Data Mining Tool for Online Prediction of Transient Stability. IEEE Trans. Power Syst. 2014, 29, 377–385. [Google Scholar] [CrossRef]
- Gomez, F.R.; Rajapakse, A.D.; Annakkage, U.D.; Fernando, I.T. Support Vector Machine-Based Algorithm for Post-Fault Transient Stability Status Prediction Using Synchronized Measurements. IEEE Trans. Power Syst. 2011, 26, 1474–1483. [Google Scholar] [CrossRef]
- Kamwa, I.; Samantaray, S.R.; Joos, G. Catastrophe predictors from ensemble decision-tree learning of wide-area severity indices. IEEE Trans. Smart Grid 2010, 1, 144–158. [Google Scholar] [CrossRef]
- Wang, L.; Lyu, F.; Su, Y.; Yue, J. Kernel Entropy-Based Classification Approach for Super buck Converter Circuit Fault Diagnosis. IEEE Access 2018, 6, 45504–45514. [Google Scholar] [CrossRef]
- Pannell, Z.; Ramachandran, B.; Snider, D. Machine learning approach to solving the transient stability assessment problem. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 14–17 January 2018; pp. 1–6. [Google Scholar]
- Wang, N.; Ma, Z.; Huo, P.; Liu, X. Predicting Crop Yield Using 3D Convolutional Neural Network with Dimension Reduction and Metric Learning. In Proceedings of the 2023 IEEE 6th International Conference on Pattern Recognition and Artificial Intelligence (PRAI), Haikou, China, 18–20 August 2023; pp. 1004–1008. [Google Scholar]
- Dong, Q.; Ge, F.; Ning, Q.; Zhao, Y.; Lv, J.; Huang, H.; Yuan, J.; Jiang, X.; Shen, D.; Liu, T. Modeling Hierarchical Brain Networks via Volumetric Sparse Deep Belief Network. IEEE Trans. Biomed. Eng. 2020, 67, 1739–1748. [Google Scholar] [CrossRef] [PubMed]
- Bang, S.S.; Kwon, G.-Y. Anomaly Detection for HTS Cable Using Stacked Autoencoder and Reflectometry. IEEE Trans. Appl. Supercond. 2023, 33, 1–5. [Google Scholar] [CrossRef]
- Quan, Z.; Zeng, W.; Li, X.; Liu, Y.; Yu, Y.; Yang, W. Recurrent Neural Networks with External Addressable Long-Term and Working Memory for Learning Long-Term Dependences. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 813–826. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Yao, W.; Zeng, L.; Wen, J.; Fang, J.; Ai, X.; Wen, J. Convolutional neural network-based power system transient stability assessment and instability mode prediction. Appl. Energy 2020, 263, 114586. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Hill, D.J.; Lam, A.Y.S.; Gu, J.; Li, V.O.K. Intelligent time-adaptive transient stability assessment system. IEEE Trans. Power Syst. 2018, 33, 1049–1058. [Google Scholar] [CrossRef]
- Lu, Z.; Shi, X.; He, C.; Wang, X.; Zhou, B. Transient Stability Assessment Based on Two-Step Improved One-Dimensional Convolutional Neural Networks with Long and Short Time-Series Input. In Proceedings of the 2023 International Conference on Power System Technology (PowerCon), Jinan, China, 21–22 September 2023; pp. 1–5. [Google Scholar]
- Wu, S.; Zheng, L.; Hu, W.; Yu, R.; Liu, B. Improved Deep Belief Network and Model Interpretation Method for Power System Transient Stability Assessment. J. Mod. Power Syst. Clean Energy 2020, 8, 27–37. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Q.; Huang, C.; Liao, S.; Jiang, Y.; Ge, Y. A Transient Stability Assessment Method Using LSTM Network with Attention Mechanism. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 21–24 October 2019; pp. 120–124. [Google Scholar]
- Ramirez-Gonzalez, M.; Sevilla, F.R.S.; Korba, P.; Castellanos, R. CNN with squeeze and excitation attention module for power system transient stability assessment. In Proceedings of the 2024 12th International Conference on Smart Grid (icSmartGrid), Setubal, Portugal, 27–29 May 2024; pp. 475–479. [Google Scholar]
- Hu, W.; Li, X.; Zhao, Y.; Zhang, Y.; Chen, L.; Wang, Z.; Zhou, H. An Updated Method of Transient Stability Assessment Rules for Power Systems in Variable Topology Scenarios Based on Double-Layer Heterogeneous Graph Attention Network. In Proceedings of the 2023 6th Asia Conference on Energy and Electrical Engineering (ACEEE), Chengdu, China, 21–23 July 2023; pp. 222–228. [Google Scholar]
- Xia, S.; Zhang, C.; Li, Y.; Li, G.; Ma, L.; Zhou, N.; Zhu, Z.; Ma, H. GCN-LSTM Based Transient Angle Stability Assessment Method for Future Power Systems Considering Spatial-Temporal Disturbance Response Characteristics. Prot. Control Mod. Power Syst. 2024, 9, 108–121. [Google Scholar] [CrossRef]
- Huang, J.; Guan, L.; Su, Y.; Yao, H.; Guo, M.; Zhong, Z. A topology adaptive high-speed transient stability assessment scheme based on multigraph attention network with residual structure. Int. J. Electr. Power Energy Syst. 2021, 130, 106948. [Google Scholar] [CrossRef]
- Shao, C.; He, X.; Ma, L.; Wang, H.; Zhou, C.; Dong, H. Transient Assessment of Power Systems Based on Graph Attention Networks. In Proceedings of the 2024 IEEE 5th International Conference on Advanced Electrical and Energy Systems (AEES), Lanzhou, China, 29 November–1 December 2024; pp. 525–530. [Google Scholar]
- Huangfu, H.; Wang, Y.; Lin, H. Power System Transient Stability Assessment Method Based on Optimized Time-Spectral Graphical Neural Network. In Proceedings of the 2024 Boao New Power System International Forum—Power System and New Energy Technology Innovation Forum (NPSIF), Qionghai, China, 8–10 December 2024; pp. 763–767. [Google Scholar]
- Huang, J.; Guan, L.; Cai, Z.; Chen, L.; Chen, H.; Chen, Z. A Global Attention Pooling-Based Graph Learning Scheme for Generator-Level Transient Stability Assessment. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 42, 2999–3007. [Google Scholar]

| Sample Set | Total Numbers | Stable Samples | Unstable Samples |
|---|---|---|---|
| Total Samples | 24,276 | 15,030 | 9246 |
| Training Set | 19,420 | 12,024 | 7397 |
| Test Set | 4856 | 3006 | 1849 |
| Function | /% | /% | /% | /% |
|---|---|---|---|---|
| 98.52 | 98.91 | 97.84 | 98.37 | |
| 99.10 | 99.45 | 98.65 | 99.05 | |
| 99.38 | 99.73 | 98.94 | 99.32 |
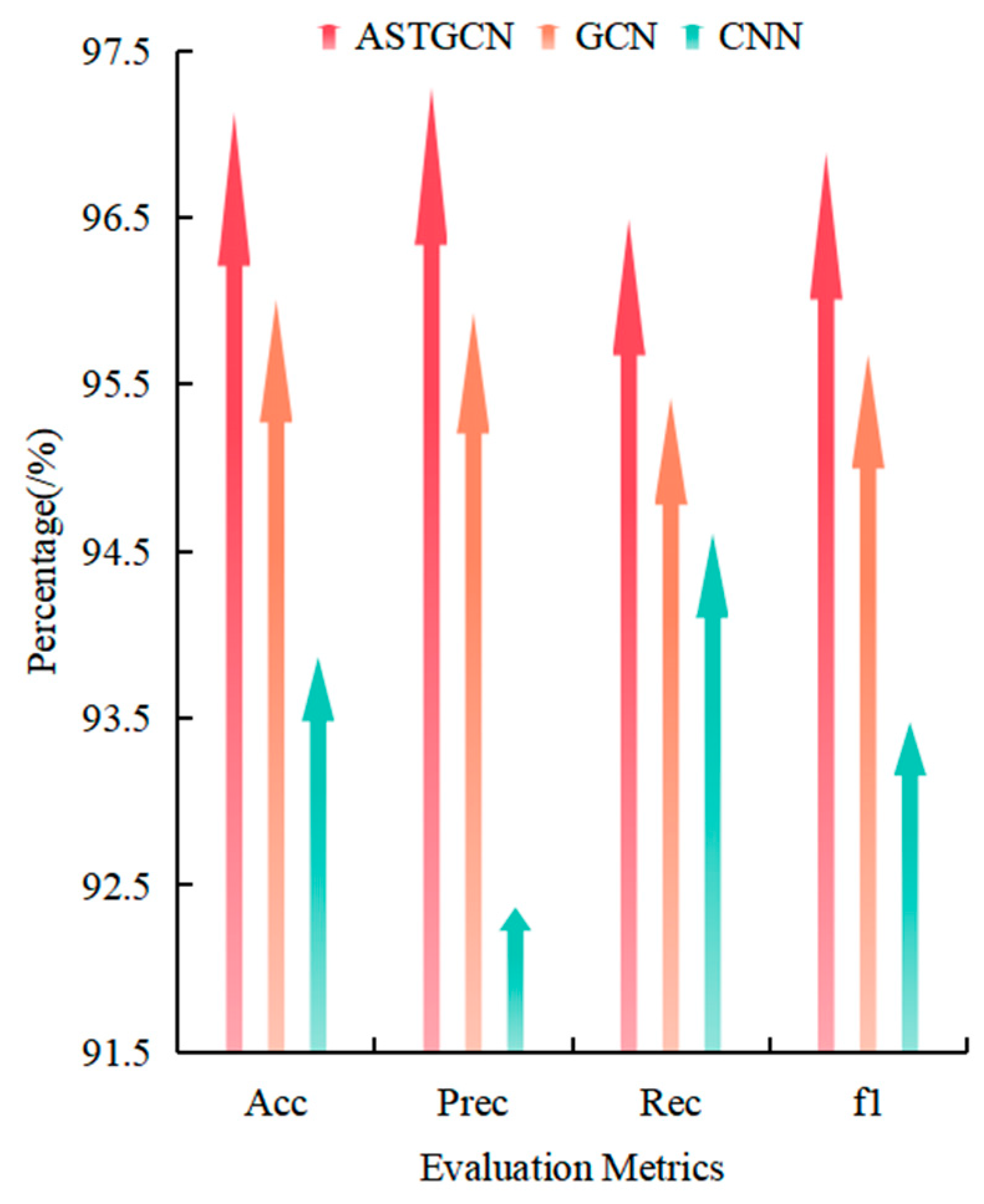
| Model | /% | /% | /% | /% |
|---|---|---|---|---|
| ASTGCN | 99.38 | 99.73 | 98.94 | 99.32 |
| GCN | 98.62 | 99.18 | 97.83 | 98.51 |
| CNN | 98.25 | 97.86 | 98.38 | 98.12 |
| DT | 95.62 | 97.45 | 92.99 | 95.17 |
| KNN | 95.04 | 97.69 | 91.37 | 94.43 |
| XGBoost | 94.62 | 95.15 | 94.47 | 94.81 |
| SVM | 93.12 | 97.13 | 88.71 | 93.06 |
| RF | 92.37 | 94.48 | 90.63 | 92.51 |
| Model | /% | /% | /% | /% |
|---|---|---|---|---|
| Ablation Model 1 | 99.02 | 99.18 | 98.65 | 98.91 |
| Ablation Model 2 | 99.13 | 99.45 | 98.64 | 99.05 |
| Model | /% | /% | /% | |
|---|---|---|---|---|
| ASTGCN | 99.00 | 99.72 | 98.11 | 98.93 |
| GCN | 98.36 | 98.91 | 97.57 | 98.24 |
| CNN | 98.11 | 98.63 | 97.30 | 97.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, Y.; Niu, W.; Chang, Y.; Kong, Z.; Zhao, H. Transient Stability Assessment of Power Systems Built upon Attention-Based Spatial–Temporal Graph Convolutional Networks. Energies 2025, 18, 3824. https://doi.org/10.3390/en18143824
Nan Y, Niu W, Chang Y, Kong Z, Zhao H. Transient Stability Assessment of Power Systems Built upon Attention-Based Spatial–Temporal Graph Convolutional Networks. Energies. 2025; 18(14):3824. https://doi.org/10.3390/en18143824
Chicago/Turabian StyleNan, Yu, Weiping Niu, Yong Chang, Zhenzhen Kong, and Huichao Zhao. 2025. "Transient Stability Assessment of Power Systems Built upon Attention-Based Spatial–Temporal Graph Convolutional Networks" Energies 18, no. 14: 3824. https://doi.org/10.3390/en18143824
APA StyleNan, Y., Niu, W., Chang, Y., Kong, Z., & Zhao, H. (2025). Transient Stability Assessment of Power Systems Built upon Attention-Based Spatial–Temporal Graph Convolutional Networks. Energies, 18(14), 3824. https://doi.org/10.3390/en18143824





