Incorporating a Deep Neural Network into Moving Horizon Estimation for Embedded Thermal Torque Derating of an Electric Machine
Abstract
1. Introduction
- Integration of DNN with MHE: This work represents one of the first attempts to directly integrate a DNN-based model within MHE, offering a novel framework for state estimation. Instead of relying on DNNs externally to provide Supplementary Information, the MHE leverages the DNN’s learned dynamics directly within the optimization.
- Deployment and validation on embedded systems: The feasibility of implementing a DNN-based MHE framework in real time is demonstrated. This research is also one of the first to test and validate the deployment of DNN-based state estimation on real-time hardware using the acados optimal control framework [37].
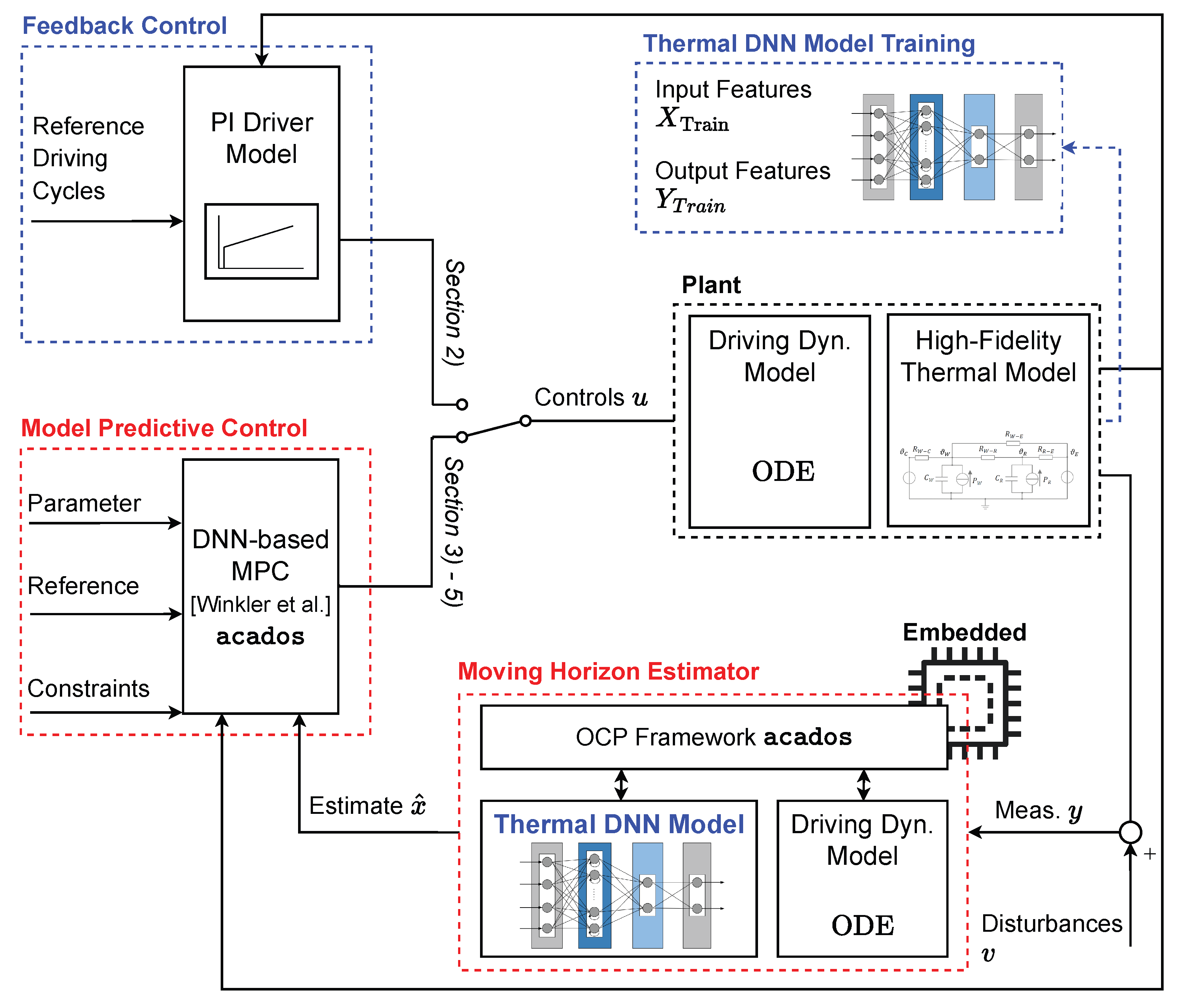
2. Materials and Methods
2.1. Deep Neural Network Modeling
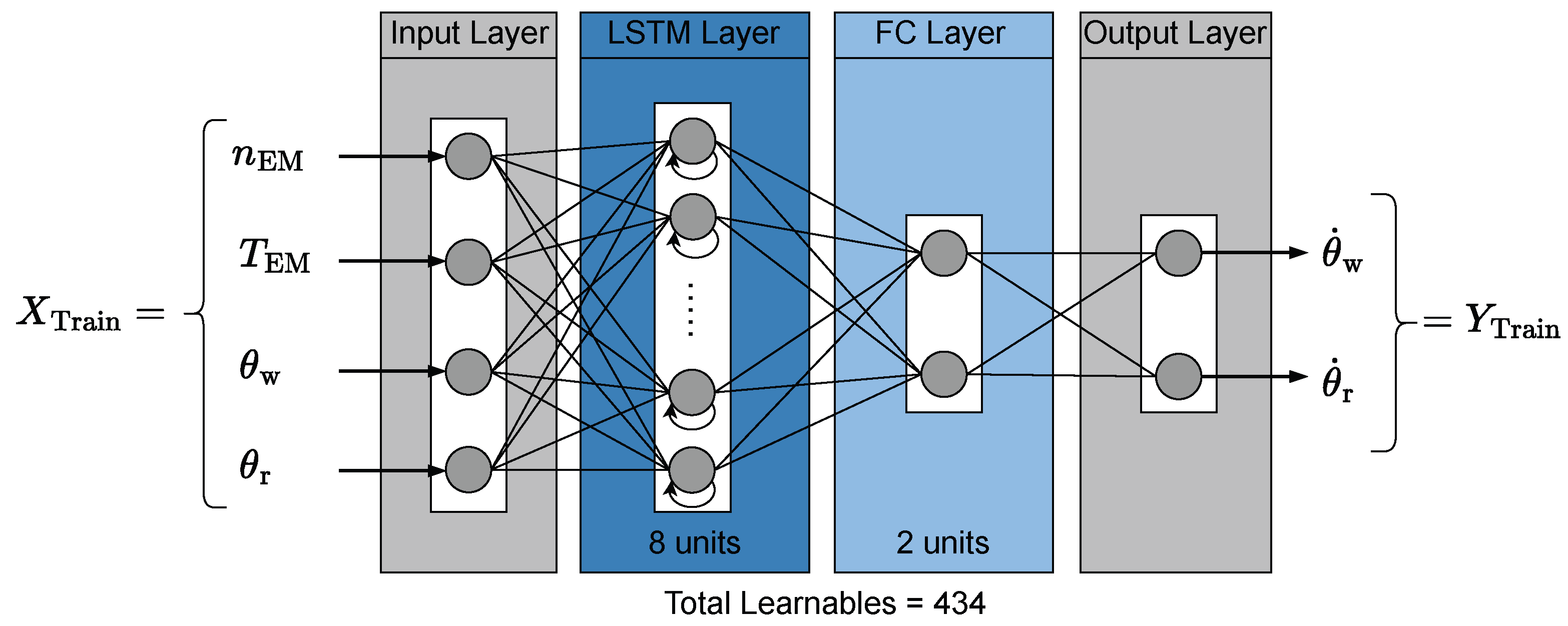
2.1.1. Long Short-Term Memory Network
- hyperbolic tangent activation function:
- sigmoid activation function:
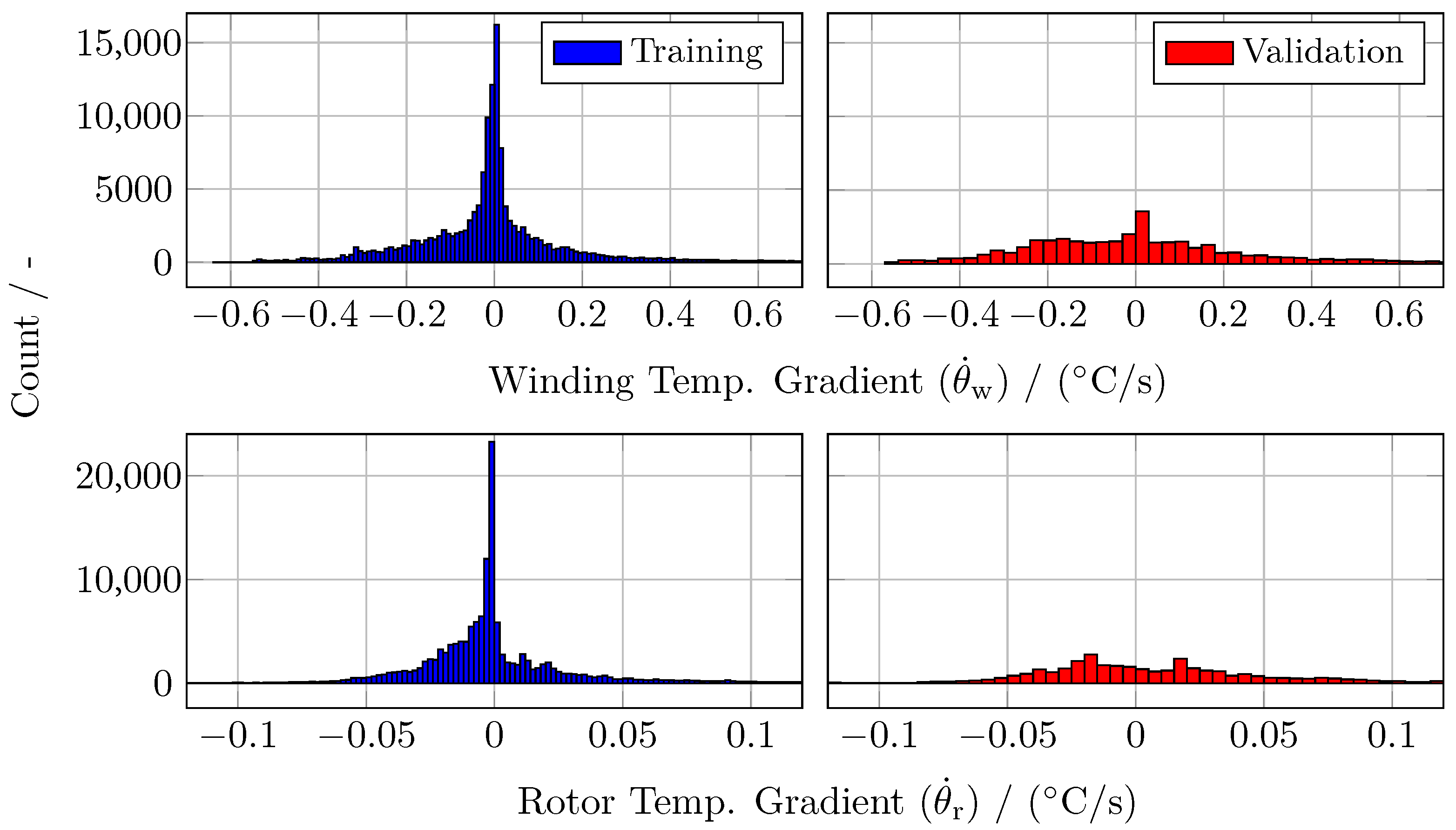
2.1.2. Experimental Setup and Data Generation
2.1.3. Neural Network Training
| Algorithm 1:Pseudo-code: LSTM network training procedure using Adam optimizer. |
|
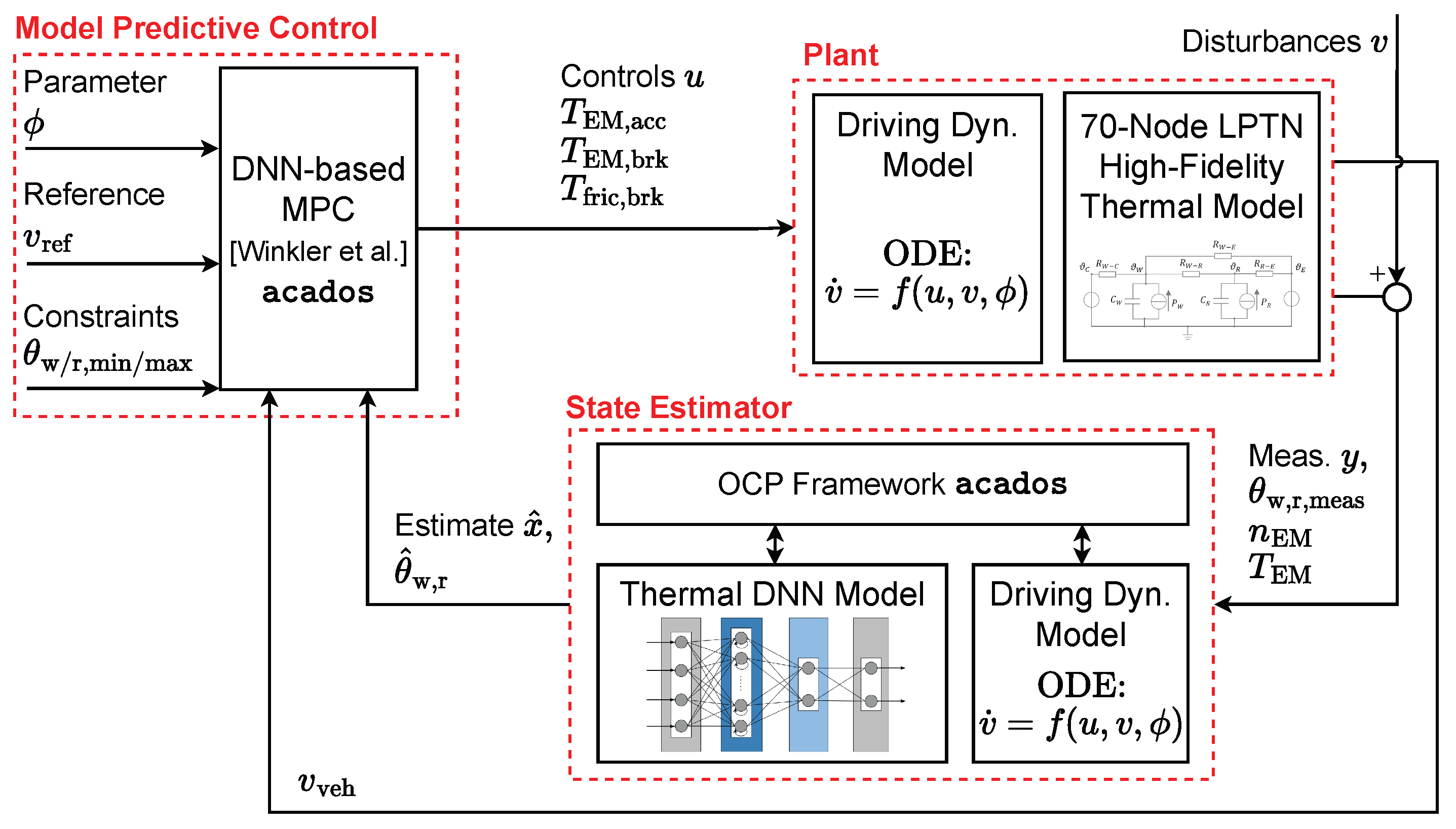
2.2. Estimator Formulation
2.2.1. MHE Problem Formulation
2.2.2. Implementation in Acados
3. Results and Discussion
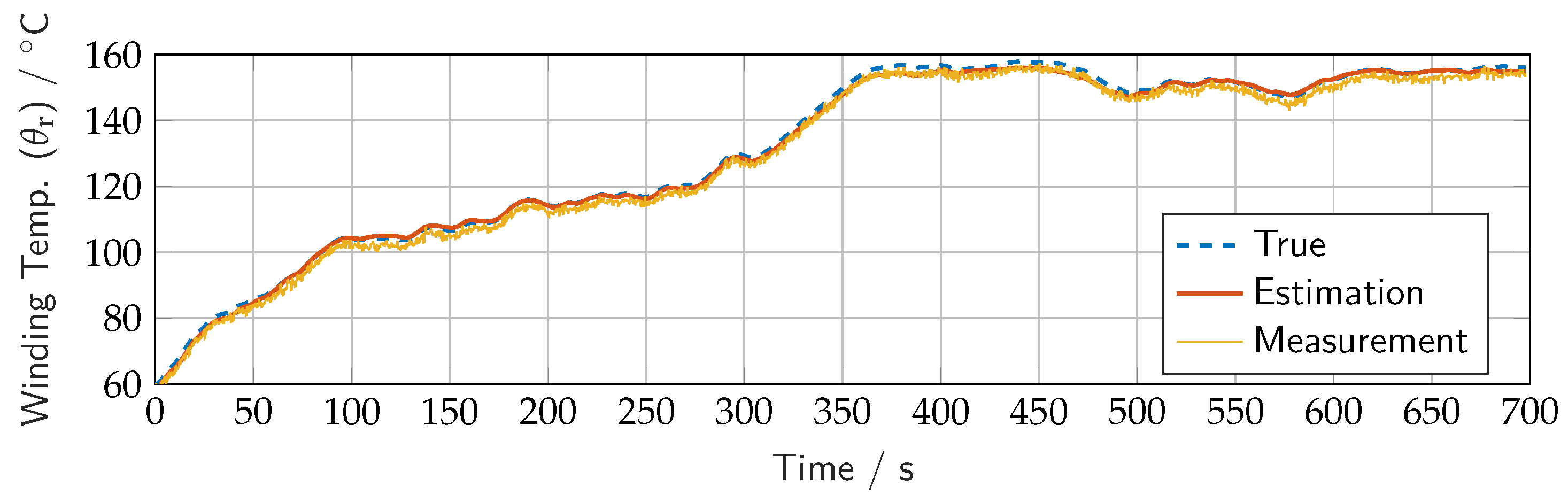
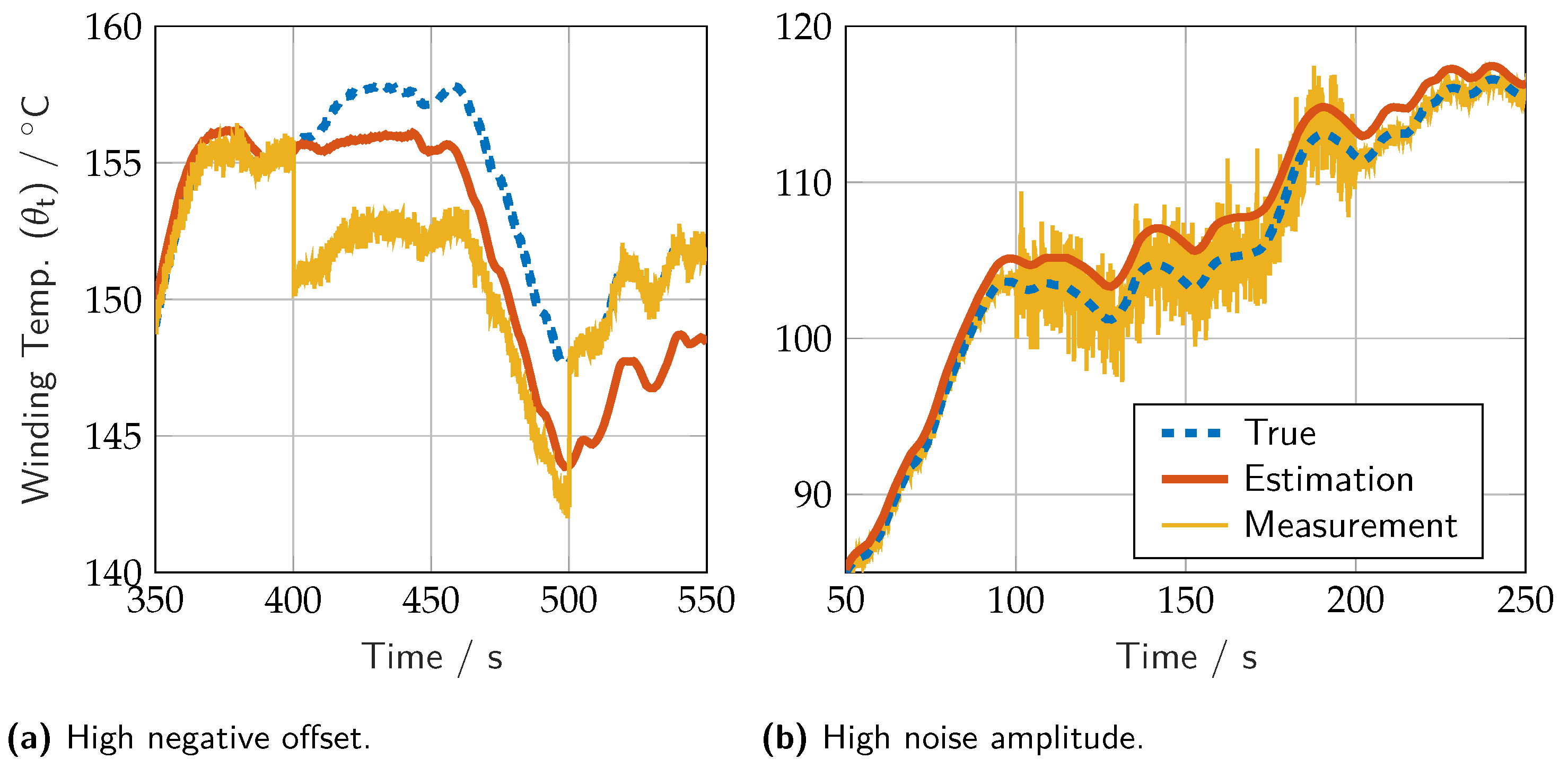
3.1. Model-in-Loop Simulation
3.2. Embedded Integration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Aldrich, J.R.A. Fisher and the making of maximum likelihood 1912–1922. Stat. Sci. 1997, 12, 162–176. [Google Scholar] [CrossRef]
- Janacek, G.J. Estimation of the minimum mean square error of prediction. Biometrika 1975, 62, 175. [Google Scholar] [CrossRef]
- Ribeiro, M. Isabel, Kalman and Extended Kalman Filters: Concept, Derivation and Properties; Technical Report; Instituto de Sistemas e Robótica, Instituto Superior Técnico: Lisbon, Portugal, 2004; Available online: https://www.researchgate.net/publication/2888846_Kalman_and_Extended_Kalman_Filters_Concept_Derivation_and_Properties (accessed on 19 March 2025).
- Julier, S.; Uhlmann, J. New extension of the Kalman filter to nonlinear systems. In Proceedings of the SPIE 3068, Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 28 July 1997. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B.; Lee, J.H. Constrained linear state estimation—A moving horizon approach. Automatica 2001, 37, 1619–1628. [Google Scholar] [CrossRef]
- Vandersteen, J.; Diehl, M.; Aerts, C.; Swevers, J. Spacecraft Attitude Estimation and Sensor Calibration Using Moving Horizon Estimation. J. Guid. Control Dyn. 2013, 36, 734–742. [Google Scholar] [CrossRef]
- Bae, H.; Oh, J.H. Humanoid state estimation using a moving horizon estimator. Adv. Robot. 2017, 31, 695–705. [Google Scholar] [CrossRef]
- Baumgärtner, K.; Zanelli, A.; Diehl, M. Zero-Order Moving Horizon Estimation. In Proceedings of the IEEE Conference on Decision and Control, Nice, France, 11–13 December 2019. [Google Scholar]
- Baumgärtner, K.; Frey, J.; Hashemi, R.; Diehl, M. Zero-order moving horizon estimation for large-scale nonlinear processes. Comput. Chem. Eng. 2021, 154, 107433. [Google Scholar] [CrossRef]
- Girrbach, F. Moving Horizon Estimation for Inertial Motion Tracking: Algorithms and Industrial Applications. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2021. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Allan, D.A. Moving Horizon Estimation. In Encyclopedia of Systems and Control; Springer International Publishing: Cham, Switzerland, 2021; pp. 1352–1358. [Google Scholar] [CrossRef]
- Asch, M.; Bocquet, M.; Nodet, M. Data Assimilation: Methods, Algorithms, and Applications. Volume 11 of Fundamentals of Algorithms; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2016; ISBN 978-1-61197-453-9. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hewing, L.; Wabersich, K.P.; Menner, M.; Zeilinger, M.N. Learning-based model predictive control: Toward safe learning in control. Annu. Rev. Control. Robot. Auton. Syst. 2020, 3, 269–296. [Google Scholar] [CrossRef]
- Salzmann, T.; Arrizabalaga, J.; Andersson, J.; Pavone, M.; Ryll, M. Learning for CasADi: Data-driven models in numerical optimization. In Proceedings of the 6th Annual Learning for Dynamics and Control Conference, Oxford, UK, 15–17 July, 2024, Volume 242 of Proceedings of Machine Learning Research; pp. 541–553.
- Lahr, A.; Näf, J.; Wabersich, K.P.; Frey, J.; Siehl, P.; Carron, A.; Diehl, M.; Zeilinger, M.N. L4acados: Learning-based models for acados, applied to Gaussian process-based predictive control. arXiv 2025, arXiv:2411.19258. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sarker, I.H. Deep Learning: A comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bragantini, A.; Baroli, D.; Posada-Moreno, A.F.; Benigni, A. Neural-network-based state estimation: The effect of pseudo- measurements. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021. [Google Scholar] [CrossRef]
- Suykens, J.a.K.; De Moor, B.L.R.; Vandewalle, J. Nonlinear system identification using neural state space models, applicable to robust control design. Int. J. Control 1995, 62, 129–152. [Google Scholar] [CrossRef]
- Pan, Y.; Sung, S.W.; Lee, J.H. Nonlinear dynamic trend modeling using feedback neural networks and prediction error minimization. IFAC Proc. Vol. 2000, 33, 827–832. [Google Scholar] [CrossRef]
- Mobeen, S.; Cristobal, J.; Singoji, S.; Rassas, B.; Izadi, M.; Shayan, Z.; Yazdanshenas, A.; Sohi, H.K.; Barnsley, R.; Elliott, L.; et al. Neural Moving Horizon Estimation: A Systematic Literature Review. Electronics 2025, 14, 1954. [Google Scholar] [CrossRef]
- Song, R.; Fang, Y.; Huang, H. Reliable Estimation of Automotive States Based on Optimized Neural Networks and Moving Horizon Estimator. IEEE/ASME Trans. Mechatron. 2023, 28, 3238–3249. [Google Scholar] [CrossRef]
- Mostafavi, S.; Doddi, H.; Kalyanam, K.; Schwartz, D. Nonlinear Moving Horizon Estimation and Model Predictive Control for Buildings with Unknown HVAC Dynamics. IFAC-PapersOnLine 2022, 55, 71–76. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.; Chen, S.; Ren, H.; Gao, Z. A Combined Robust Approach Based on Auto-Regressive Long Short-Term Memory Network and Moving Horizon Estimation for State-of-Charge Estimation of Lithium-Ion Batteries. Int. J. Energy Res. 2021, 45, 12838–12853. [Google Scholar] [CrossRef]
- Alessandri, A.; Baglietto, M.; Battistelli, G.; Zoppoli, R. Moving-horizon state estimation for nonlinear systems using neural networks. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2557–2562. [Google Scholar] [CrossRef]
- Norouzi, A.; Shahpouri, S.; Gordon, D.; Winkler, A.; Nuss, E.; Abel, D.; Andert, J.; Shahbakhti, M.; Koch, C.R. Deep learning based model predictive control for compression ignition engines. Control Eng. Pract. 2022, 127, 105299. [Google Scholar] [CrossRef]
- Gordon, D.C.; Winkler, A.; Bedei, J.; Schaber, P.; Pischinger, S.; Andert, J.; Koch, C.R. Introducing a Deep Neural Network-Based Model Predictive Control Framework for Rapid Controller Implementation. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; pp. 5232–5237. [Google Scholar] [CrossRef]
- Winkler, A.; Wang, W.; Norouzi, A.; Gordon, D.; Koch, C.; Andert, J. Integrating Recurrent Neural Networks into Model Predictive Control for Thermal Torque Derating of Electric Machines. IFAC-PapersOnLine 2023, 56, 8254–8259. [Google Scholar] [CrossRef]
- Engelhardt, T. Derating-Strategien für elektrisch angetriebene Sportwagen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017. [Google Scholar] [CrossRef]
- Etzold, K.; Fahrbach, T.; Klein, S.; Scheer, R.; Guse, D.; Klawitter, M.; Pischinger, S.; Andert, J. Function Development with an Electric-Machine-in-the-Loop Setup: A Case Study. IEEE Trans. Transp. Electrif. 2019, 5, 1419–1429. [Google Scholar] [CrossRef]
- Wallscheid, O.; Böcker, J. (Eds.) Derating of Automotive Drive Systems Using Model Predictive Control. In Proceedings of the 2017 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Pilsen, Czech Republic, 4–6 September 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Verschueren, R.; Frison, G.; Kouzoupis, D.; Frey, J.; van Duijkeren, N.; Zanelli, A.; Novoselnik, B.; Albin, T.; Quirynen, R.; Diehl, M. acados—A modular open-source framework for fast embedded optimal control. Math. Program. Comput. 2021, 14, 147–183. [Google Scholar] [CrossRef]
- Brownlee, J. Long Short-Term Memory Networks with Python; Machine Learning Mastery: Vermont, Victoria, VIC, Australia, 2017. [Google Scholar]
- Winkler, A.; Frey, J.; Fahrbach, T.; Frison, G.; Scheer, R.; Diehl, M.; Andert, J. Embedded Real-Time Nonlinear Model Predictive Control for the Thermal Torque Derating of an Electric Vehicle. IFAC-PapersOnLine 2021, 54, 359–364. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. Conference Track Proceedings. [Google Scholar]
- Rawlings, J.; Mayne, D.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Haykin, S.; Moher, M. Communication Systems, 5th ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Frison, G.; Diehl, M. HPIPM: A high-performance quadratic programming framework for model predictive control. IFAC-PapersOnLine 2020, 53, 6563–6569. [Google Scholar] [CrossRef]
- Frey, J.; Hänggi, S.; Winkler, A.; Diehl, M. Embedded Workflow—acados Documentation. Available online: https://docs.acados.org/embedded_workflow/index.html (accessed on 5 March 2025).
- Winkler, A. Deep Neural Network Based Moving Horizon Estimation: Data, Models, Scripts (feat. acados). 2025. Zenodo Repository. Available online: https://zenodo.org/records/15056784 (accessed on 10 June 2025).








| Hyperparameter | Value |
|---|---|
| Max epoch | 10,000 |
| Performance metric | MSE |
| Optimizer | Adam [40] |
| Mini-batch size | 512 |
| Initial learning rate | 0.02 |
| Learn rate schedule | Piecewise drop by 25% every 500 epochs |
| L2 regularization | 0.1 |
| Validation frequency | 10 |
| Metric | ||
|---|---|---|
| MAE/(° C/s) | 0.0288 | 0.0210 |
| RMSE/(°C/s) | 0.0373 | 0.0282 |
| NRMSE/- | 2.77% | 9.39% |
| Symbol | Parameter | Value |
|---|---|---|
| Minimum winding and rotor temperature | 0 °C | |
| Maximum winding and rotor temperature | 155 °C | |
| Weighting matrix of the arrival cost | diag(1, 1) | |
| Q | Weighting matrix of mapped states | |
| R | Weighting matrix of controls | |
| N | Estimation horizon | 15 |
| Timestep size | 100 ms | |
| T | Horizon length | 1.5 s |
| Parameter | Value |
|---|---|
| Timestep | 100 ms |
| Horizon length (nodes) | 15, condensed to 5 |
| Maximum number of SQP iterations | 20 |
| Maximum number of iterations within the QP solver | 100 |
| Maximum computation time per timestep | 28 ms |
| Average computation time per timestep | 5.7 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winkler, A.; Shah, P.; Baumgärtner, K.; Sharma, V.; Gordon, D.; Andert, J. Incorporating a Deep Neural Network into Moving Horizon Estimation for Embedded Thermal Torque Derating of an Electric Machine. Energies 2025, 18, 3813. https://doi.org/10.3390/en18143813
Winkler A, Shah P, Baumgärtner K, Sharma V, Gordon D, Andert J. Incorporating a Deep Neural Network into Moving Horizon Estimation for Embedded Thermal Torque Derating of an Electric Machine. Energies. 2025; 18(14):3813. https://doi.org/10.3390/en18143813
Chicago/Turabian StyleWinkler, Alexander, Pranav Shah, Katrin Baumgärtner, Vasu Sharma, David Gordon, and Jakob Andert. 2025. "Incorporating a Deep Neural Network into Moving Horizon Estimation for Embedded Thermal Torque Derating of an Electric Machine" Energies 18, no. 14: 3813. https://doi.org/10.3390/en18143813
APA StyleWinkler, A., Shah, P., Baumgärtner, K., Sharma, V., Gordon, D., & Andert, J. (2025). Incorporating a Deep Neural Network into Moving Horizon Estimation for Embedded Thermal Torque Derating of an Electric Machine. Energies, 18(14), 3813. https://doi.org/10.3390/en18143813









