Periodic Power Fluctuation Smoothing Control Using Blade Inertia and DC-Link Capacitor in Variable-Speed Wind Turbine
Abstract
1. Introduction
2. Modeling of PMSM-Based Wind Turbine Systems
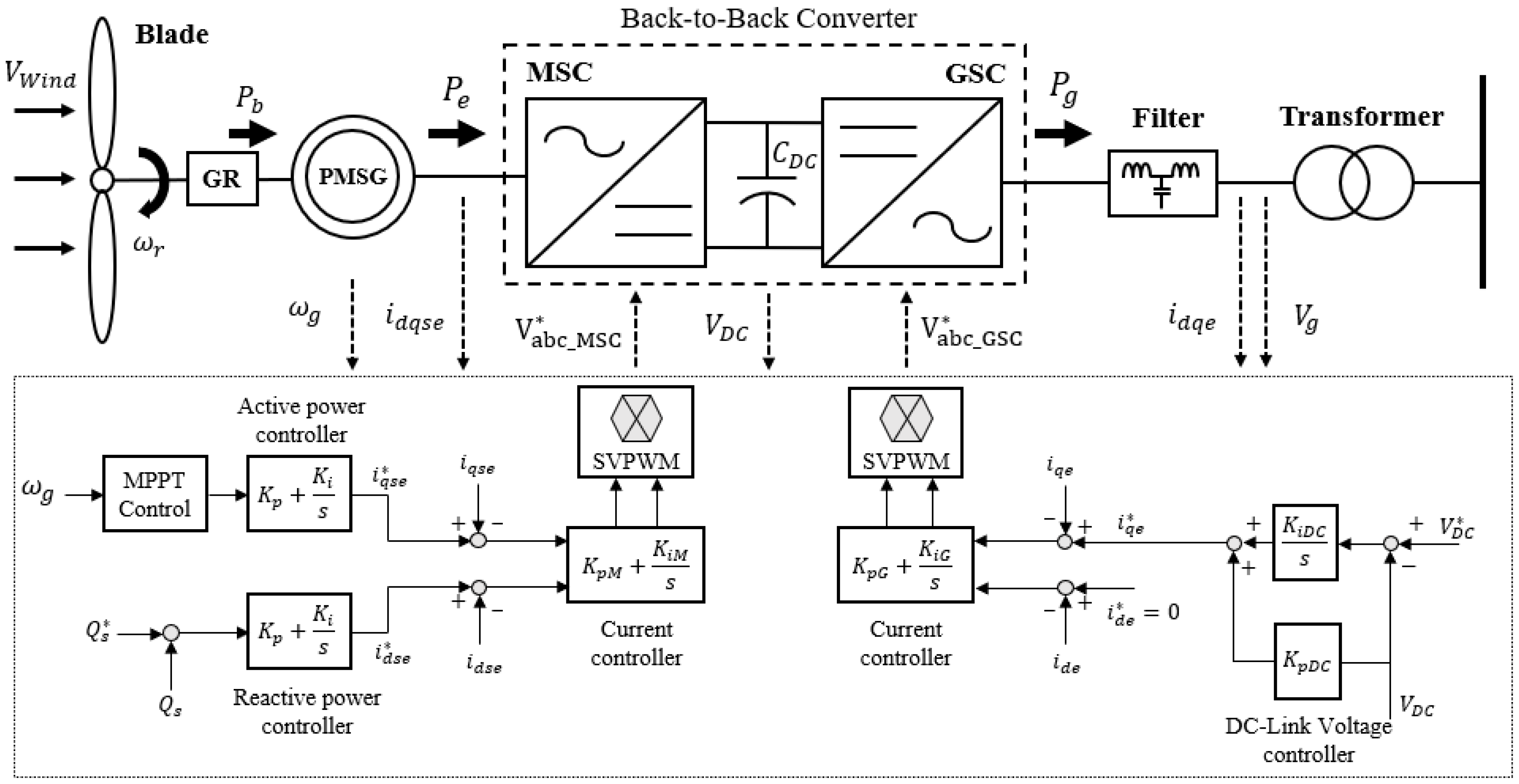
2.1. System Modeling and Configuration
2.2. Controller of Back-to-Back Converter
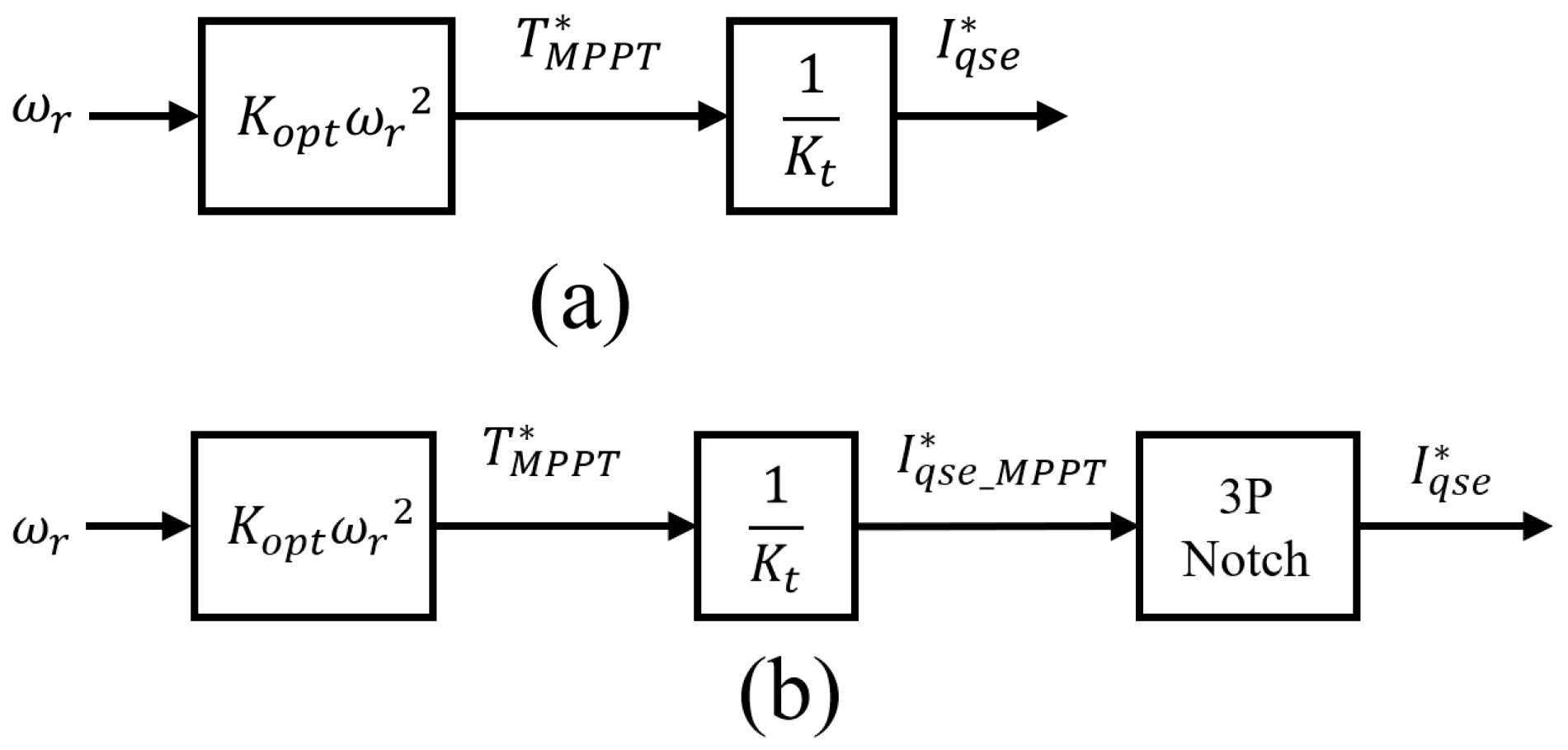
2.2.1. Controller of Machine-Side Converter
2.2.2. Controller of Grid-Side Converter
2.3. Modeling and Analysis of Periodic Power Fluctuations
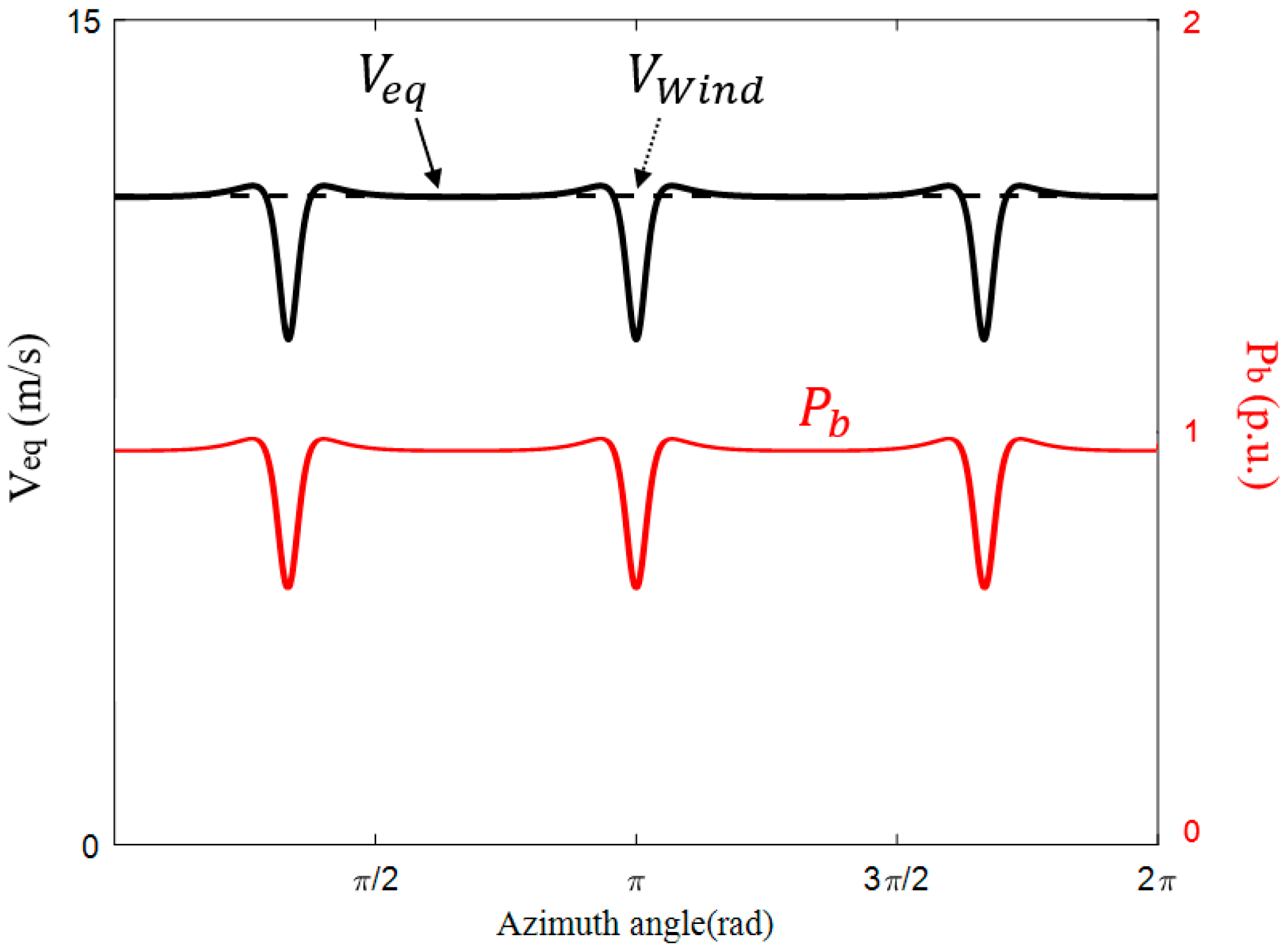
2.3.1. Aerodynamic Aspects of Wind Turbine
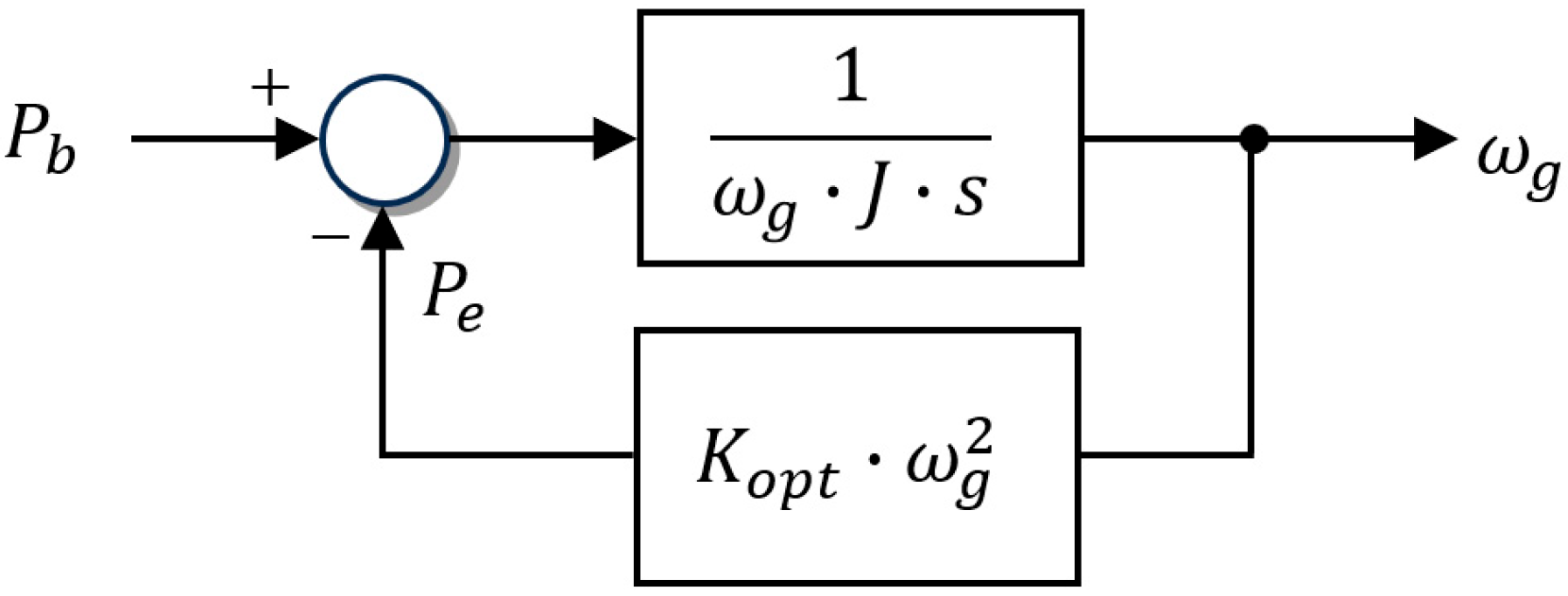
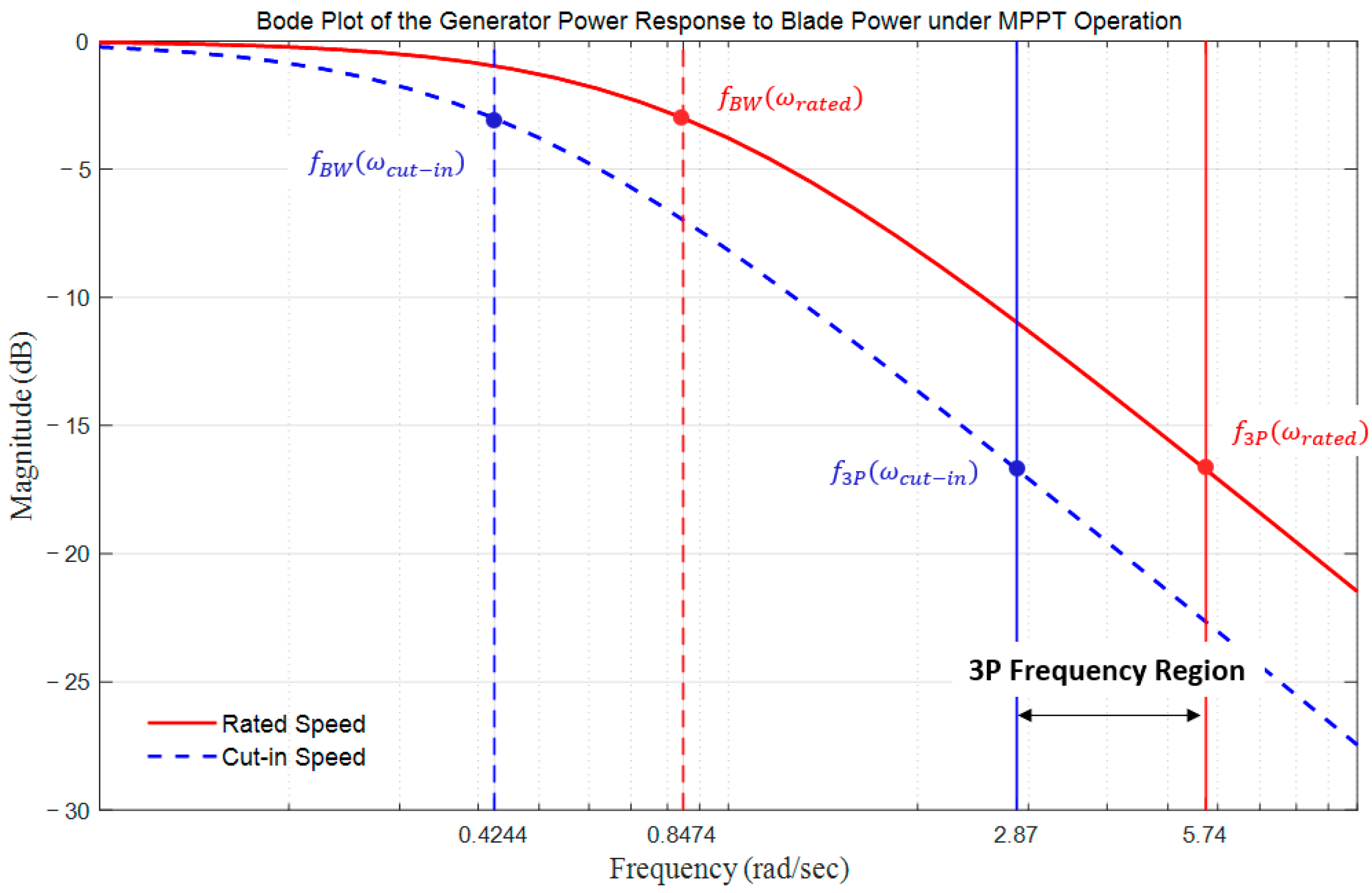
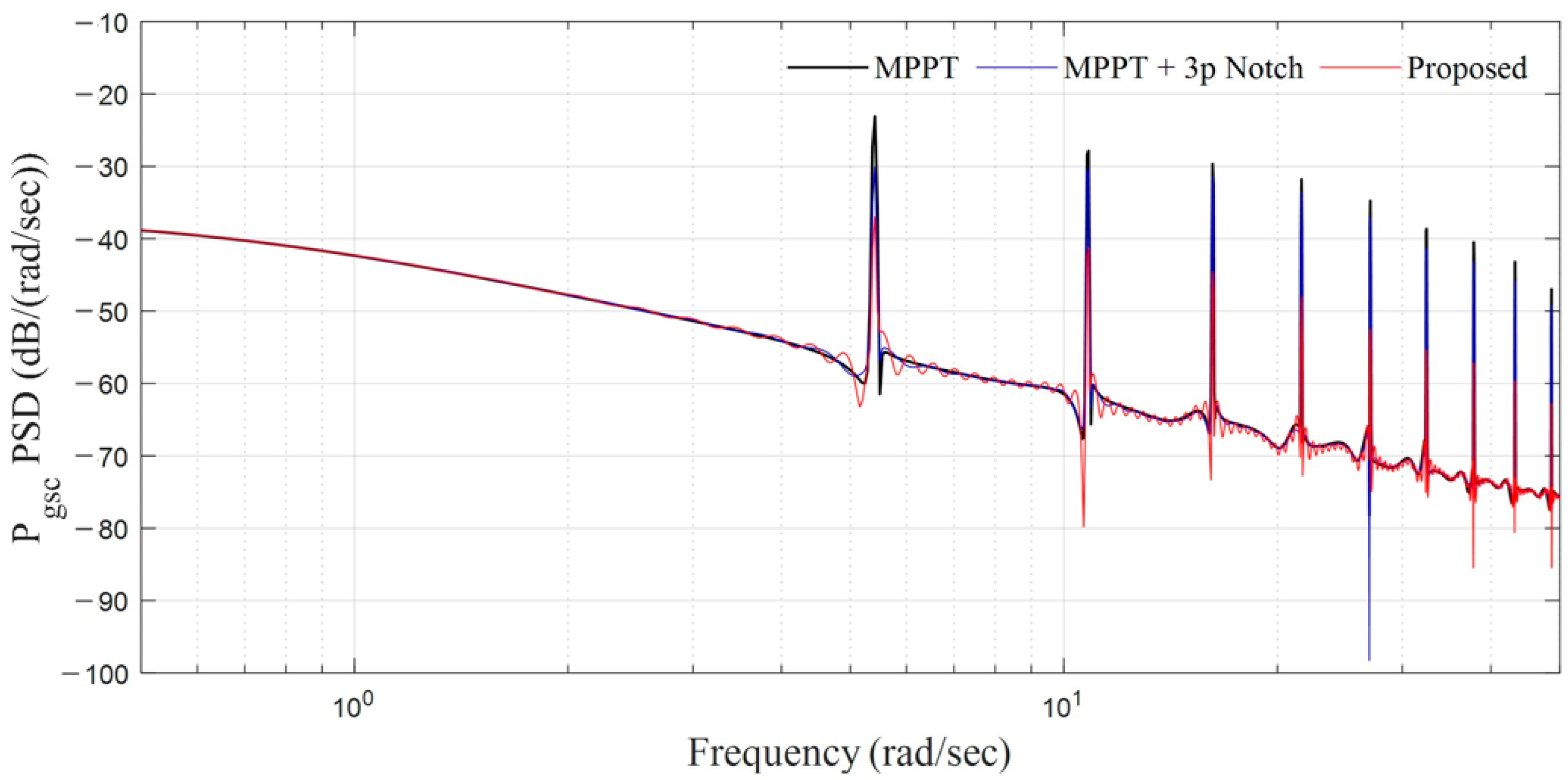
2.3.2. Frequency-Domain Analysis of 3P Oscillations in the MPPT Control System
3. Periodic Power Fluctuation Smoothing Controller
3.1. Energy Storage Analysis for Rotor Inertia and DC-Link Capacitor
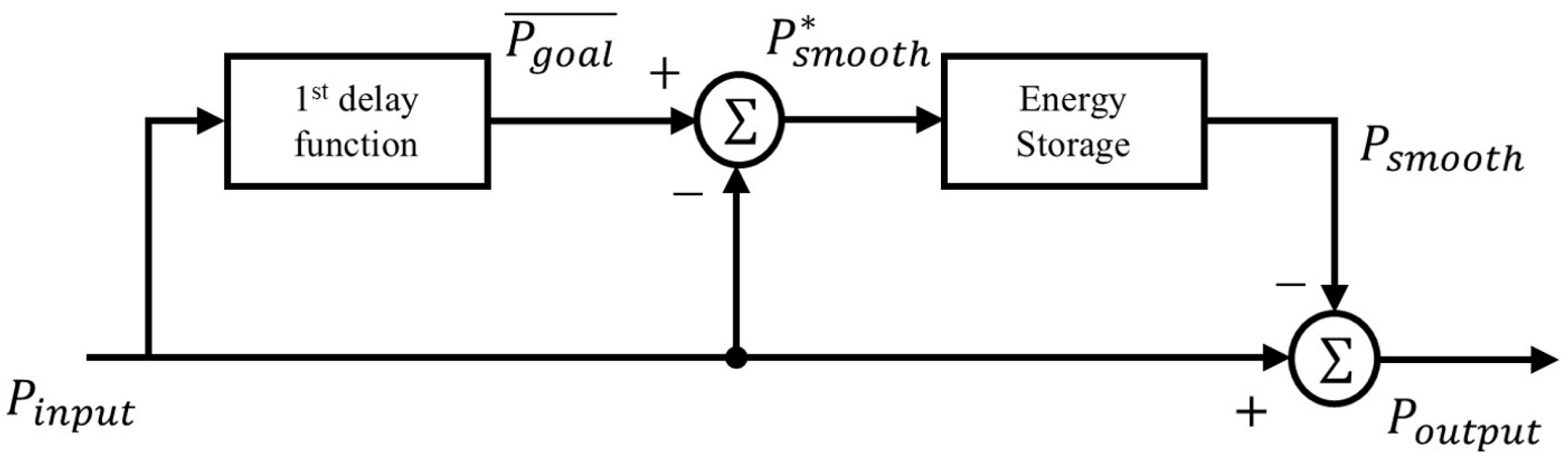
3.2. The Concept of Utilizing ESS Smoothing Method for Power Fluctuation Smoothing Algorithm
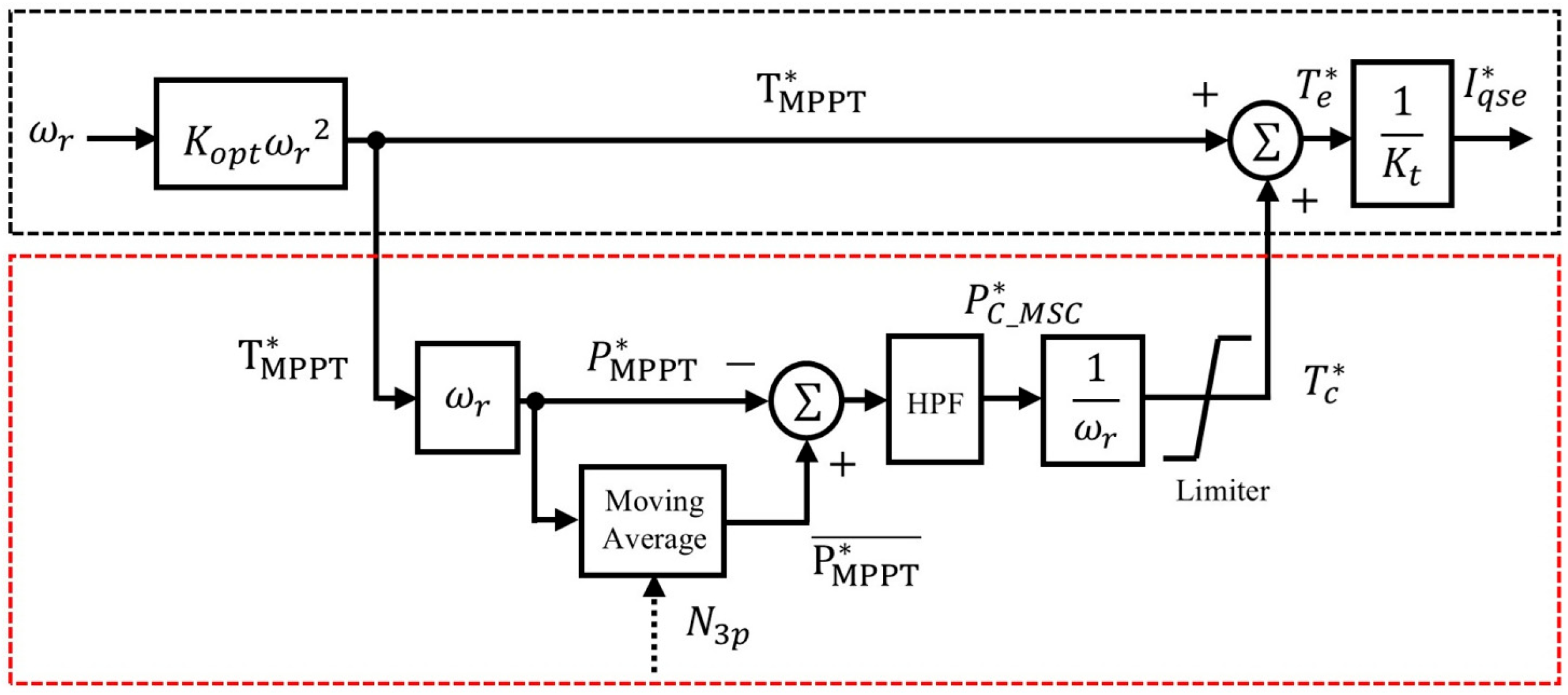
3.2.1. Periodic Power Fluctuation Smoothing Control of Machine-Side Controller (MSC)
3.2.2. Periodic Power Fluctuation Smoothing Control of GSC
4. Controller Verifying Simulation Through MATLAB/Simulink
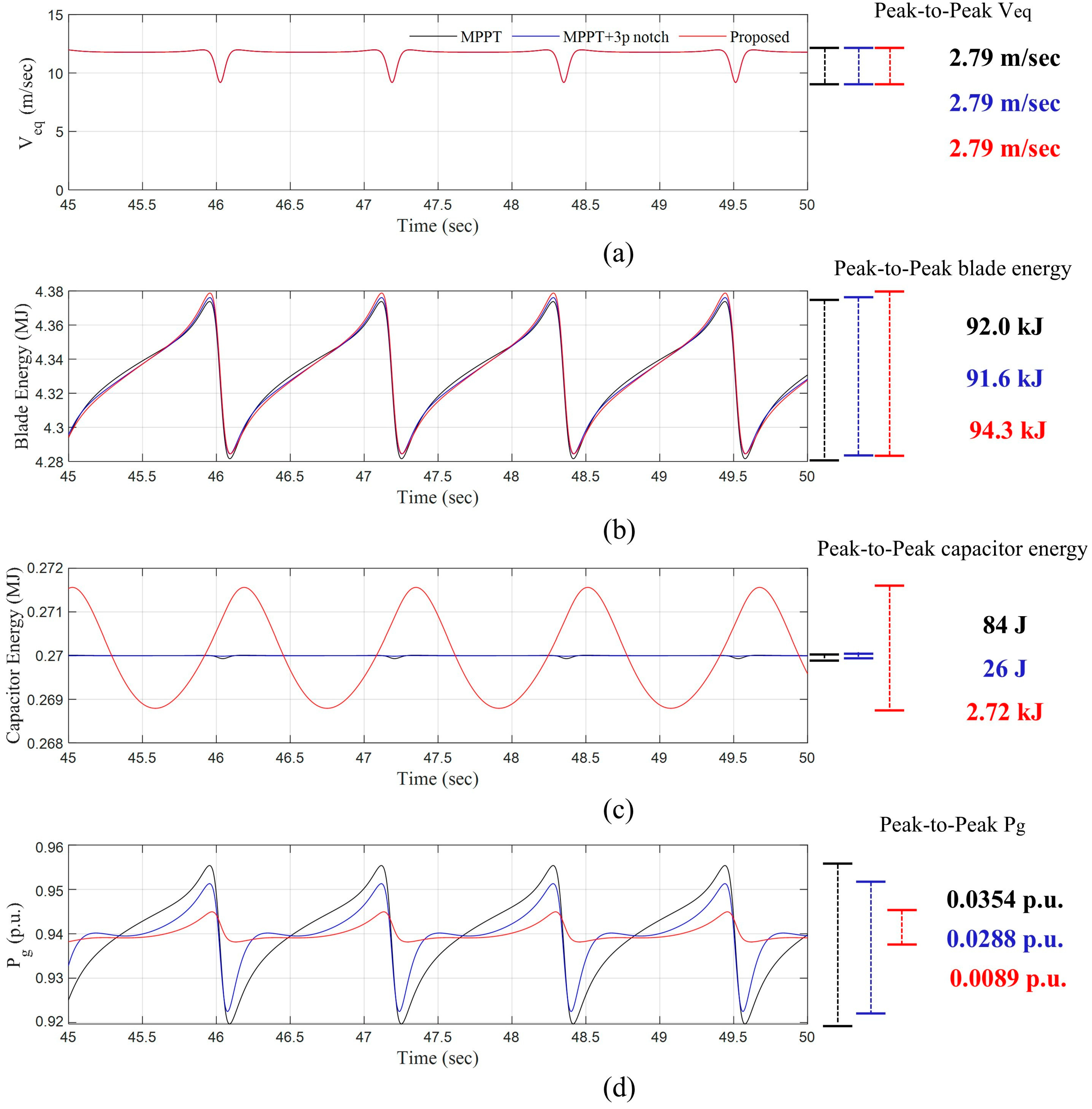
4.1. Case 1: Average Wind Velocity = 12 m/s Constant Wind Speed Condition
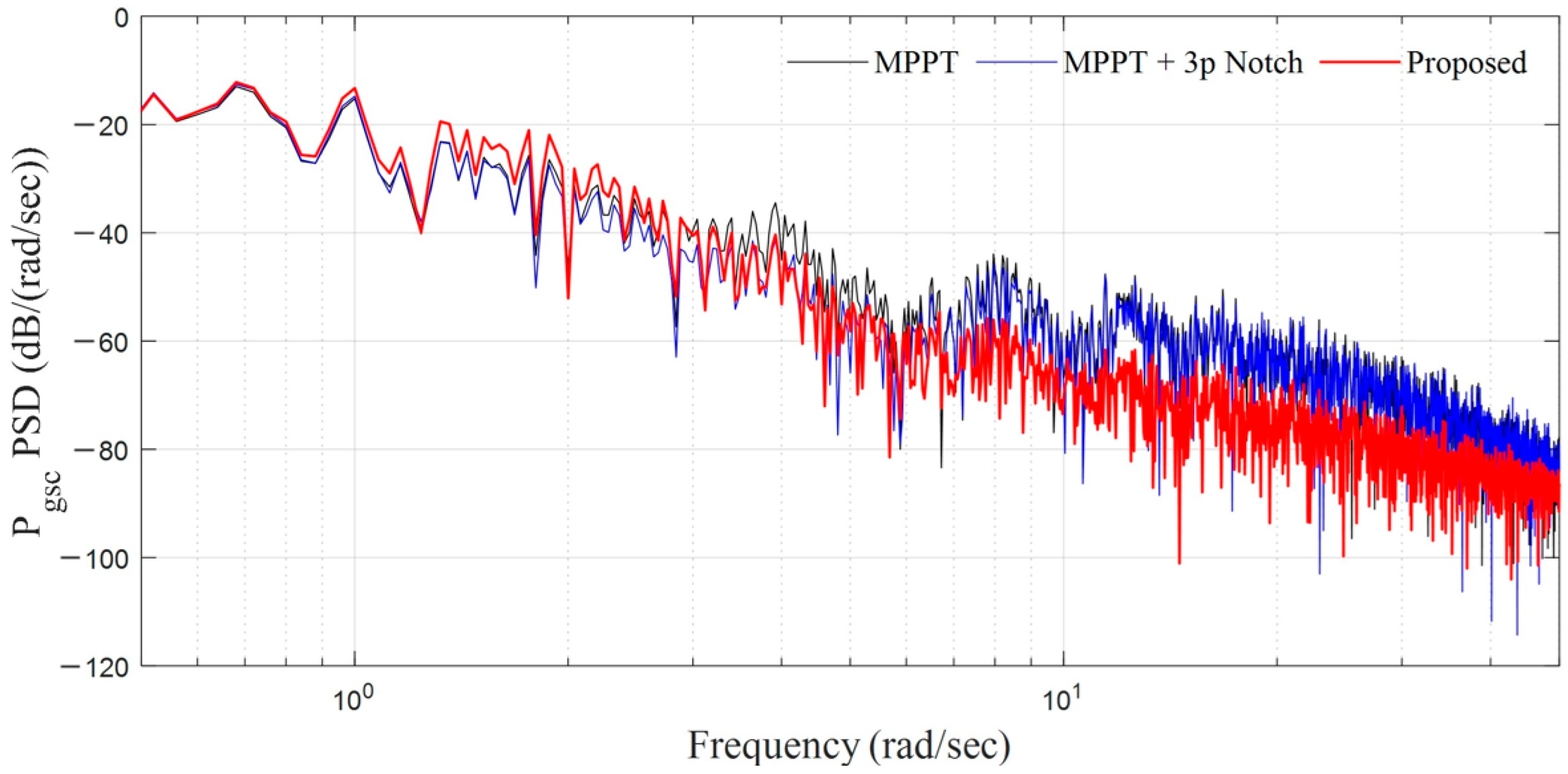
4.2. Case 2: Average Wind Velocity = 9 m/s Time-Varying Wind Speed with Turbulence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Global Wind Energy Council (GWEC). Global Wind Report 2025; GWEC: Brussels, Belgium, 2025; Available online: https://www.gwec.net/reports/globalwindreport (accessed on 21 June 2025).
- Das, S.; Karnik, N.; Santoso, S. Time-domain modeling of tower shadow and wind shear in wind turbines. ISRN Renew. Energy 2011, 2011, 890582. [Google Scholar] [CrossRef]
- Dolan, D.S.L.; Lehn, P.W. Simulation model of wind turbine 3p torque oscillations due to wind shear and tower shadow. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 2050–2057. [Google Scholar] [CrossRef]
- Ketabipour, S.; Samet, H.; Mohammadi, M.; Li, Q.; Terzija, V. Modeling of extremely short-time power variations of wound rotor induction machines wind farms for flicker studies. IEEE Access 2023, 11, 135556–135567. [Google Scholar] [CrossRef]
- Yin, L.; Zhu, R.; Gu, Y. Impacts of multi-physical domain coupling of wind turbine on power grid performances. In Proceedings of the 2023 8th IEEE Workshop on the Electronic Grid (eGRID), Karlsruhe, Germany, 16–18 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, W.L.; Chan, C.C. Periodic pulsation mitigation and operation speed extension in wind-driven squirrel-cage induction generators through voltage injection. J. Power Electron. 2025. [Google Scholar] [CrossRef]
- Esmaeilian, H.R.; Fadaeinedjad, R. Resolving power quality issues raised by aerodynamic aspects of wind turbine in isolated microgrids using fuel cell/electrolyzer system. IEEE Trans. Sustain. Energy 2016, 7, 1274–1283. [Google Scholar] [CrossRef]
- Liao, K.; Xu, Y.; Yin, M.; Chen, Z. A virtual filter approach for wind energy conversion systems for mitigating power system frequency fluctuations. IEEE Trans. Sustain. Energy 2020, 11, 1268–1277. [Google Scholar] [CrossRef]
- Su, C.; Hu, W.; Chen, Z.; Hu, Y. Mitigation of power system oscillation caused by wind power fluctuation. IET Renew. Power Gener. 2013, 7, 639–651. [Google Scholar] [CrossRef]
- Ammar, M.; Joós, G. A short-term energy storage system for voltage quality improvement in distributed wind power. IEEE Trans. Energy Convers. 2014, 29, 997–1007. [Google Scholar] [CrossRef]
- Díaz-González, F.; Bianchi, F.D.; Sumper, A.; Gomis-Bellmunt, O. Control of a flywheel energy storage system for power smoothing in wind power plants. IEEE Trans. Energy Convers. 2014, 29, 204–214. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Hu, W.; Cheng, M. Flicker mitigation by individual pitch control of variable speed wind turbines with DFIG. IEEE Trans. Energy Convers. 2014, 29, 20–28. [Google Scholar] [CrossRef]
- Yang, G.; Chen, L.; Cai, P.; Gao, W.; Ai, C. Adaptive Disturbance Rejection and Power Smoothing Control for Offshore Hydraulic Wind Turbines Based on Pitch and Motor Tilt Angles. Energies 2024, 17, 6244. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, W.; Chen, Z.; Cheng, M.; Hu, Y. Flicker mitigation strategy for a doubly fed induction generator by torque control. IET Renew. Power Gener. 2014, 8, 91–99. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z.; Wang, Y.; Wang, Z. Flicker mitigation by active power control of variable-speed wind turbines with full-scale back-to-back power converters. IEEE Trans. Energy Convers. 2009, 24, 640–649. [Google Scholar] [CrossRef]
- Uehara, A.; Pratap, A.; Goya, T.; Senjyu, T.; Yona, A.; Urasaki, N.; Funabashi, T. A coordinated control method to smooth wind power fluctuations of a PMSG-based WECS. IEEE Trans. Energy Convers. 2011, 26, 550–558. [Google Scholar] [CrossRef]
- Lyu, X.; Zhao, J.; Jia, Y.; Xu, Z.; Wong, K.P. Coordinated control strategies of PMSG-based wind turbine for smoothing power fluctuations. IEEE Trans. Power Syst. 2019, 34, 391–401. [Google Scholar] [CrossRef]
- Kim, J.-J.; Song, S.-H. PSCAD/EMTDC simulation model of variable speed wind power generation system using permanent magnet synchronous machine. Trans. Korean Inst. Power Electron. 2005, 10, 253–256. [Google Scholar]
- Nam, Y.-S. Wind Turbine System Control; GS Intervision: Seoul, Republic of Korea, 2013; pp. 28–37. [Google Scholar]
- Yue, H.; Zhang, H.; Zhu, Q.; Ai, Y.; Tang, H.; Zhou, L. Wake dynamics of a wind turbine under real-time varying inflow turbulence: A coherence mode perspective. Energy Convers. Manag. 2025, 332, 119729. [Google Scholar] [CrossRef]
- Elkinton, M.R.; Rogers, A.L.; McGowan, J.G. An investigation of wind-shear models and experimental data trends for different terrains. Wind Eng. 2006, 30, 341–350. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef]
- Grid Code Frequency Response Working Group. System Inertia. Available online: https://www.nationalgrid.com/sites/default/files/documents/16890-Meeting%208%20-%20Inertia%20presentation.pdf (accessed on 22 May 2025).
- Rajendran, S.; Diaz, M.; Cárdenas, R.; Espina, E.; Contreras, E.; Rodriguez, J. A review of generators and power converters for multi-MW wind energy conversion systems. Processes 2022, 10, 2302. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Seok, B. Analysis on smoothing algorithms performance and battery capacity for intermittent and variable wind power mitigation. J. Korean Inst. Electr. Eng. Power Eng. 2021, 70, 63–69. [Google Scholar] [CrossRef]
- Yoo, M.-S.; Kim, S.-B.; Song, S.-H.; Choy, Y.-D.; Yoon, G.-G. Periodic Pulsation of Wind Turbine Output Power due to Wind Shear and Tower Effect. In Proceedings of the KIEE Summer Conference, Gwangju, Republic of Korea, 12 October 2015; pp. 262–264. [Google Scholar]
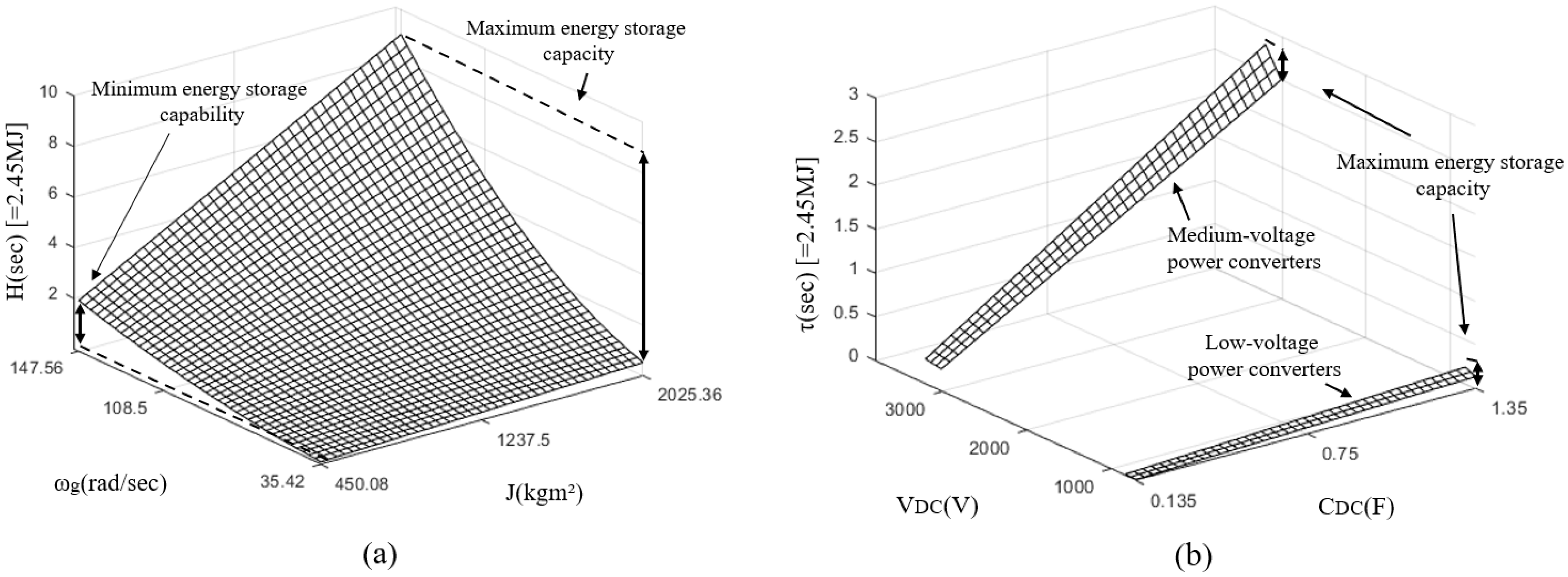



| Category | Roter Inertia | Low Voltage Power Converters | Medium Voltage Power Converters |
|---|---|---|---|
| Energy Storage Capacity (s) | 2~9 s | 0.005~0.05 s | 0.04~0.31 s |
| Parameter | Value | Unit |
|---|---|---|
| Rated power | 2.45 | MW |
| Gear ratio | 77 | |
| Generator type | PMSG | |
| Rated generator speed | 1409.1 | rpm |
| Cut-in generator speed | 704.55 | rpm |
| Rated wind speed | 12.12 | m/s |
| Cut-in wind speed | 3 | m/s |
| 10 | rad/s | |
| 200 | rad/s | |
| 2 | ||
| 450.08 | ||
| 0.3 | ||
| 3 | m | |
| 5 | m |
| Harmonic Components | MPPT (dB) | MPPT with 3P Notch (dB) | Proposed (dB) | Mitigation by Proposed (vs. MPPT) |
|---|---|---|---|---|
| 3P | −23 | −30 | −37 | −14 dB |
| 6P | −27 | −30 | −41 | −14 dB |
| 9P | −29 | −31 | −44 | −15 dB |
| 12P | −31 | −33 | −48 | −17 dB |
| Category | MPPT | MPPT + 3P Notch | Proposed |
|---|---|---|---|
| Total energy Yield (MW·s) | 144.790 | 144.861 | 144.865 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, J.-H.; Kim, Y.-C.; Song, S.-H. Periodic Power Fluctuation Smoothing Control Using Blade Inertia and DC-Link Capacitor in Variable-Speed Wind Turbine. Energies 2025, 18, 3763. https://doi.org/10.3390/en18143763
Do J-H, Kim Y-C, Song S-H. Periodic Power Fluctuation Smoothing Control Using Blade Inertia and DC-Link Capacitor in Variable-Speed Wind Turbine. Energies. 2025; 18(14):3763. https://doi.org/10.3390/en18143763
Chicago/Turabian StyleDo, Jin-Ho, Ye-Chan Kim, and Seung-Ho Song. 2025. "Periodic Power Fluctuation Smoothing Control Using Blade Inertia and DC-Link Capacitor in Variable-Speed Wind Turbine" Energies 18, no. 14: 3763. https://doi.org/10.3390/en18143763
APA StyleDo, J.-H., Kim, Y.-C., & Song, S.-H. (2025). Periodic Power Fluctuation Smoothing Control Using Blade Inertia and DC-Link Capacitor in Variable-Speed Wind Turbine. Energies, 18(14), 3763. https://doi.org/10.3390/en18143763






