Hybrid Prediction Model of Burn-Through Point Temperature with Color Temperature Information from Cross-Sectional Frame at Discharge End
Abstract
1. Introduction
- (1)
- By combining image information with time-series data, traditional data-driven approaches are supplemented to help the model predict BTP temperature.
- (2)
- Combining the strengths of ensemble learning helps to mitigate the impact of non-stationary sequences.
2. Description of Sintering Process and Design of Hybrid Prediction Model of Burn-Through Point Temperature
2.1. Sintering Process
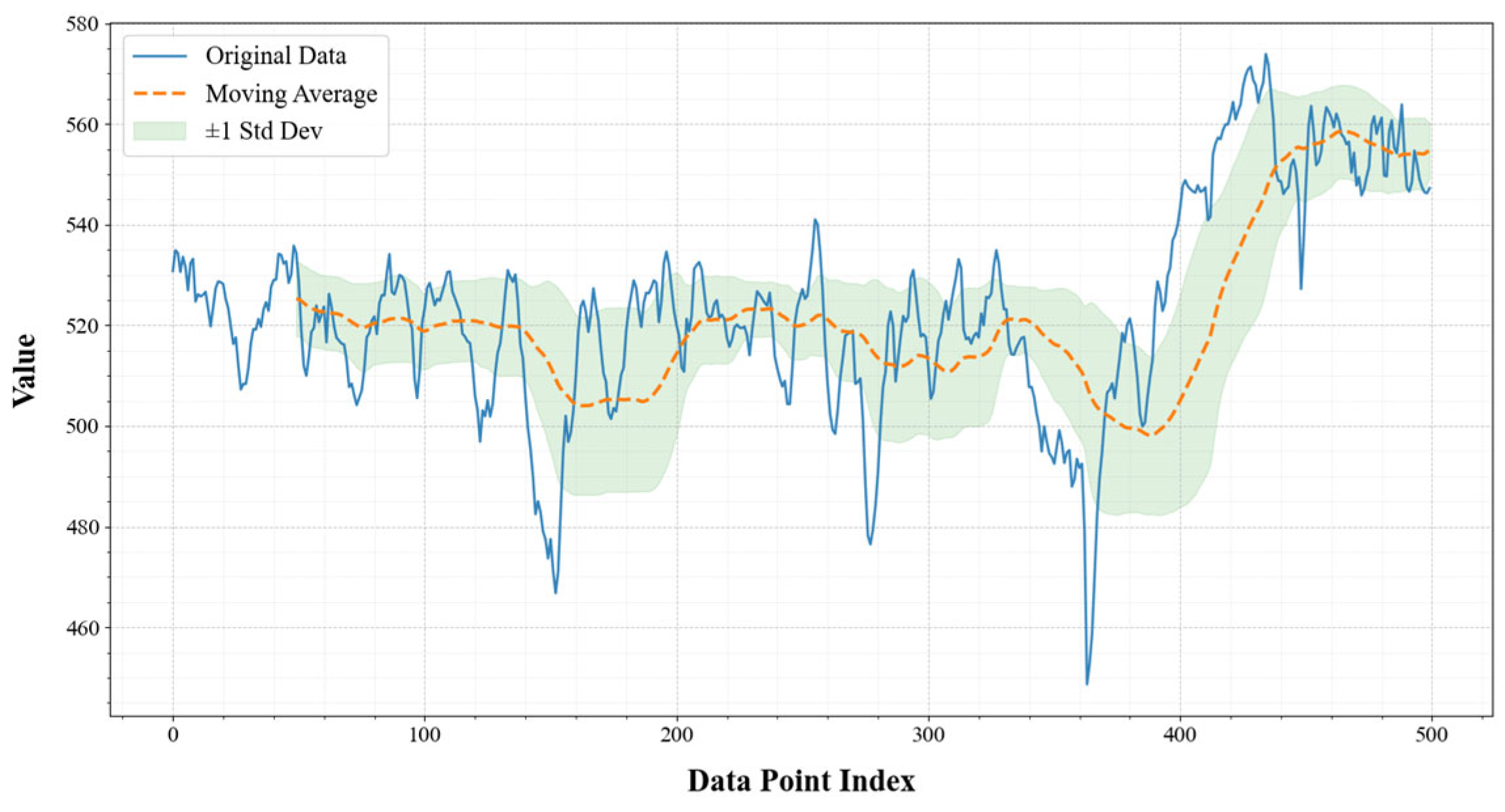
2.2. Analysis of Influencing Factors on BTP Temperature and Data Stationarity
2.3. Structure Design of Hybrid Prediction Model of BTP Temperature
3. Hybrid Prediction Model of BTP Temperature
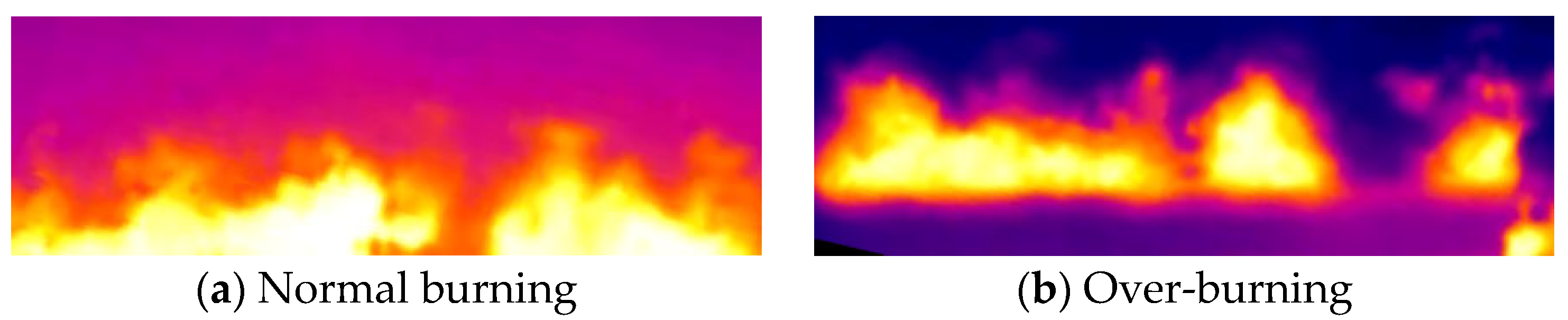
3.1. Color Temperature Information Calibration
3.2. Analysis and Selection of Feature Variables
- (1)
- The two temperature features with the largest mutual information values (temperature of exhaust gas in the 23rd bellow and 22nd bellow), which cover the key thermal areas of the sinter ore layer;
- (2)
- The exhaust gas pressure in the 24th bellow with the largest mutual information value in the exhaust gas pressure category, supplementing the information in the air permeability dimension.
3.3. Construction of Hybrid Prediction Model for BTP Temperature
4. Experimental Study and Analysis
4.1. Ablation Experiments
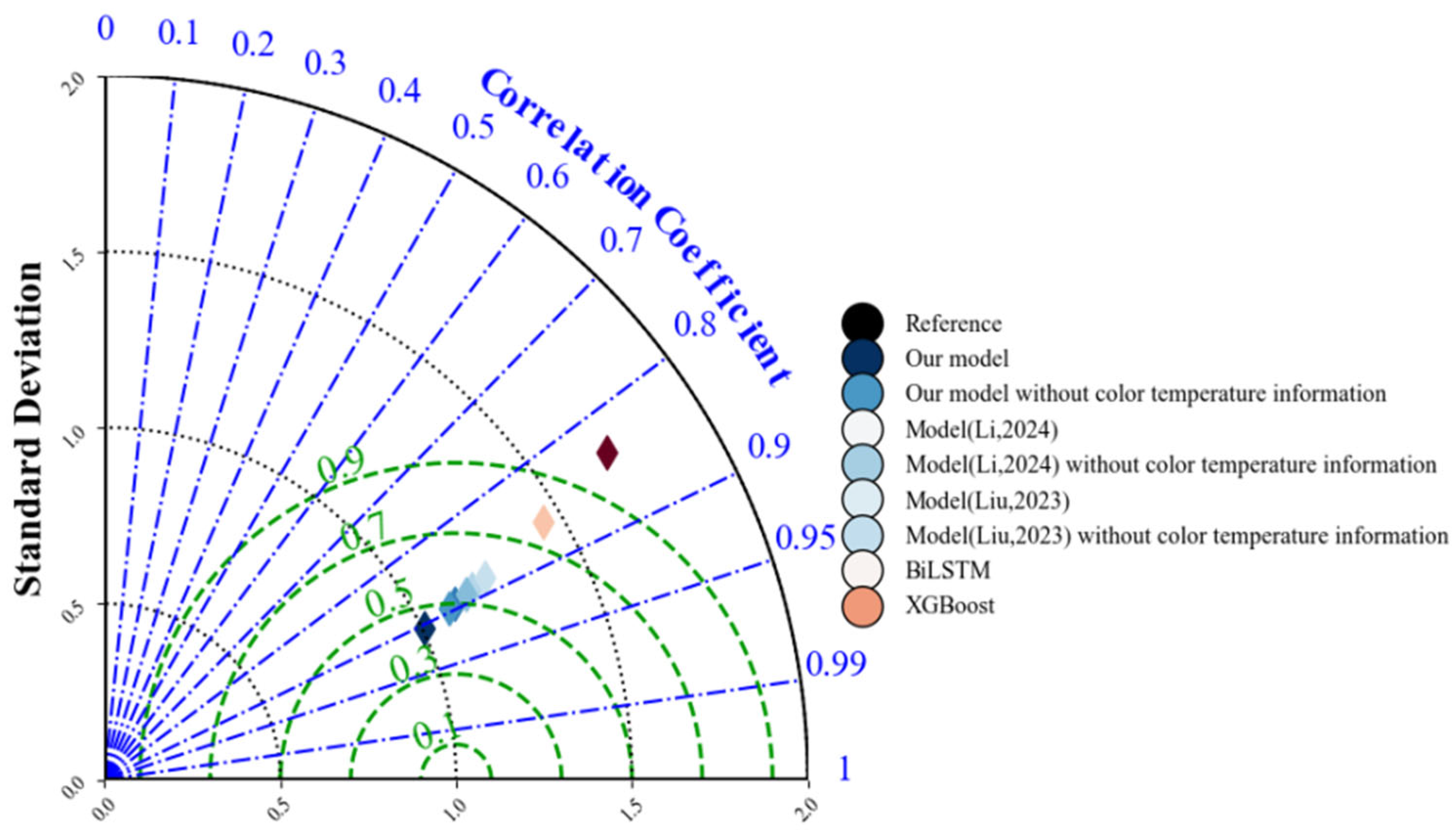
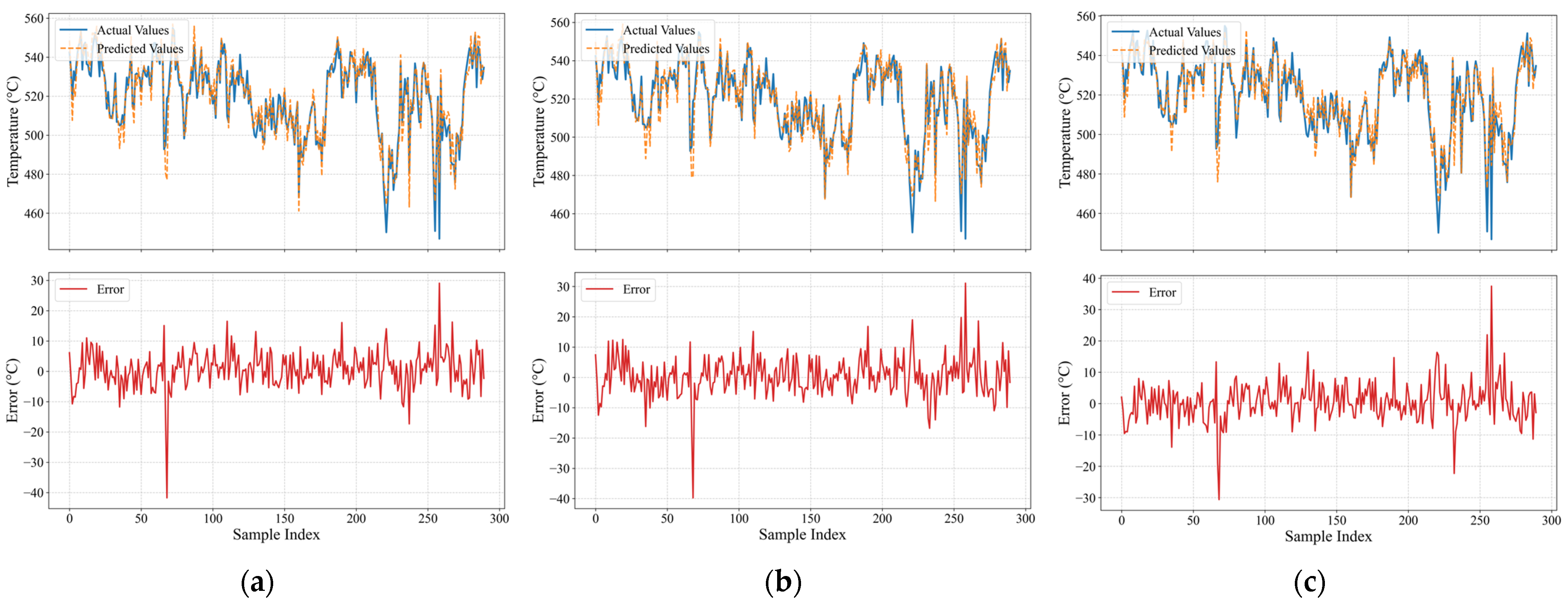
4.2. Comparison Experiments
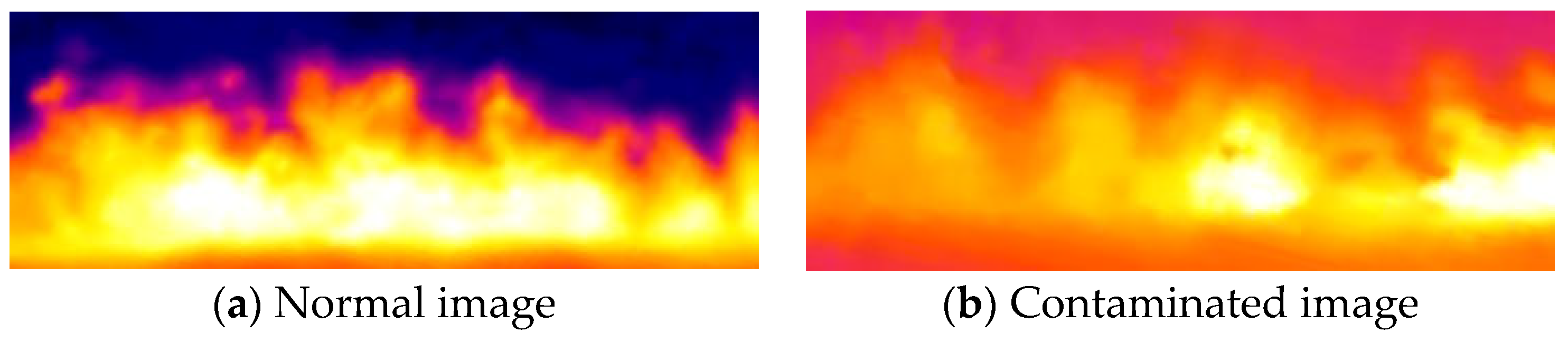
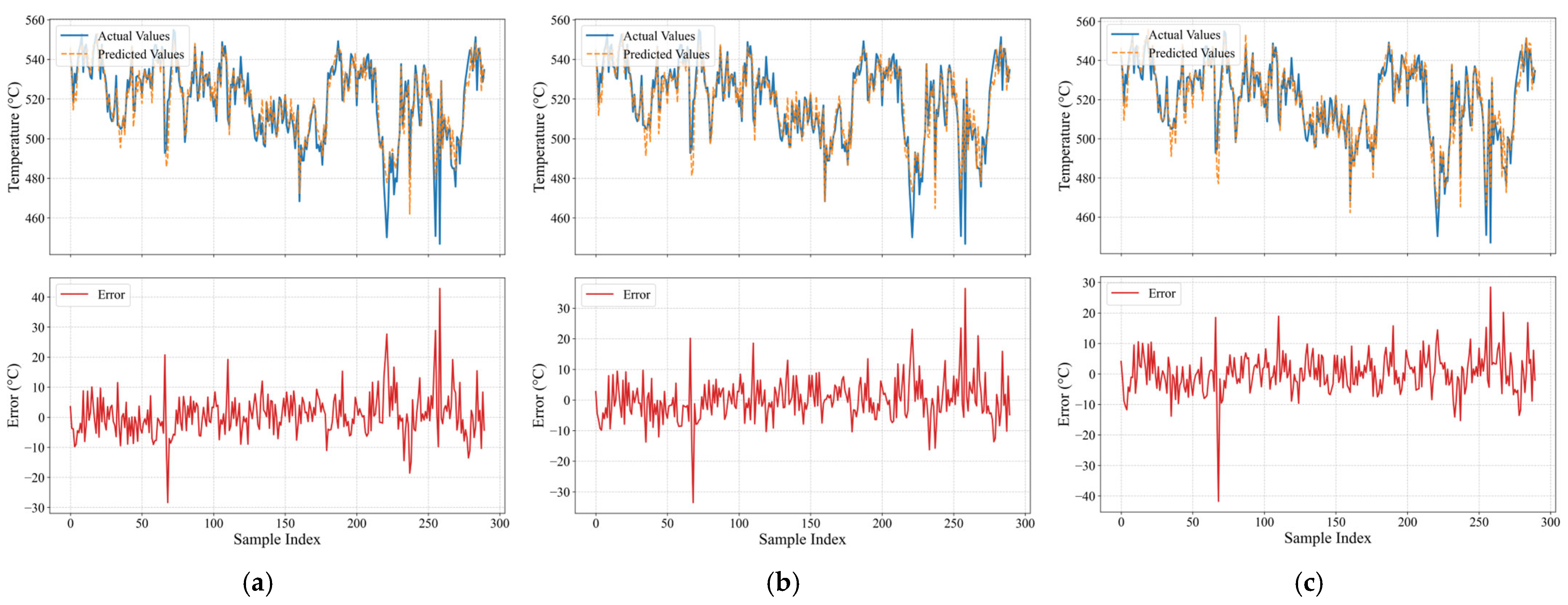
4.3. Analysis of Model Robustness and Limitations
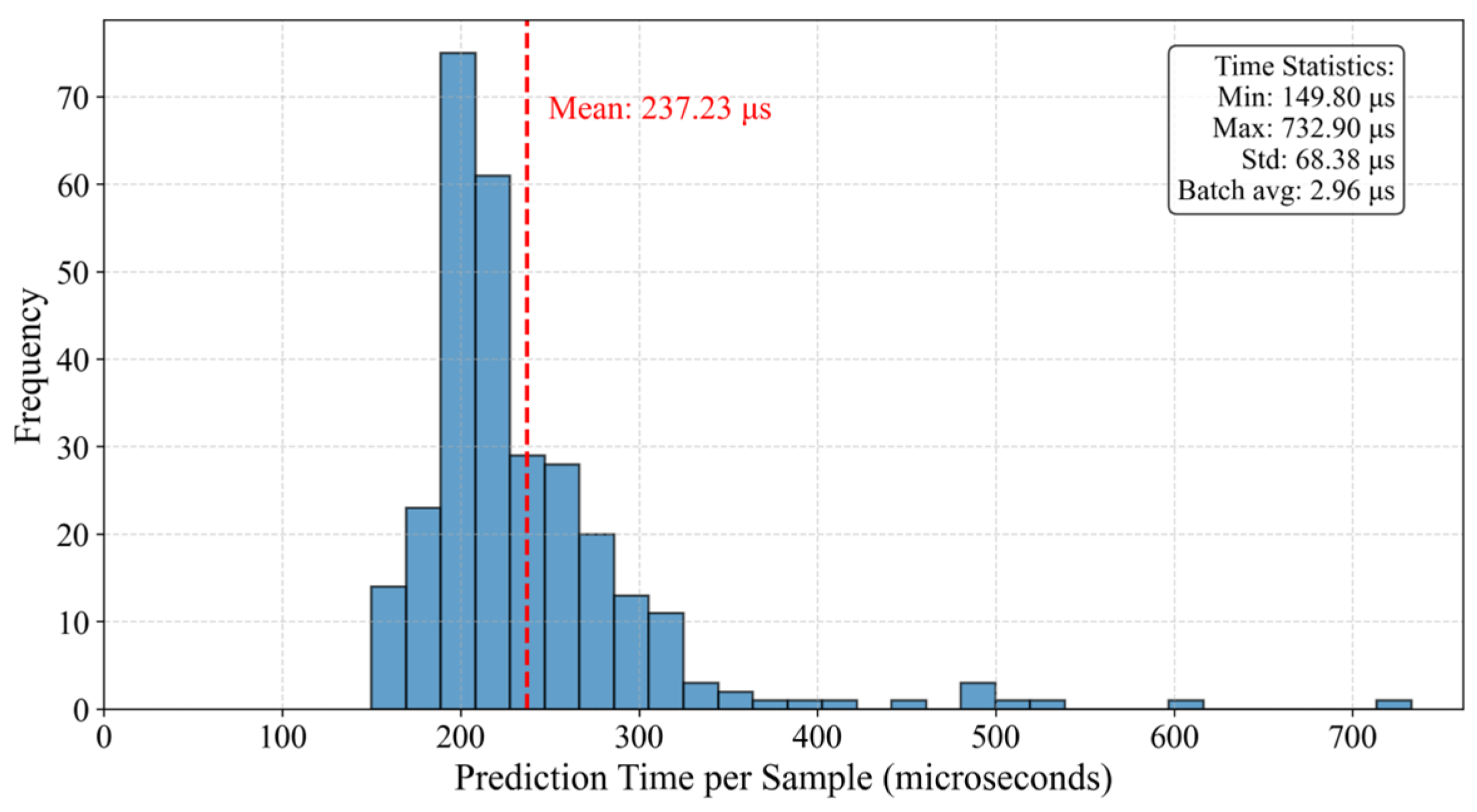
4.4. Analysis of Model Real-Time Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, J.; Li, H.; Li, H.; Wu, M.; Cao, W.; Pedrycz, W. Relevance vector machine with hybrid kernel-based soft sensor via data augmentation for incomplete output data in sintering process. Control Eng. Pract. 2024, 145, 105850. [Google Scholar] [CrossRef]
- Hu, J.; Wu, M.; Chen, L.; Cao, W.; Pedrycz, W. Real-time dynamic prediction model of carbon efficiency with working condition identification in sintering process. J. Process Control 2022, 111, 97–105. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, J.; Li, M. Prediction of sinter yield and strength in iron ore sintering process by numerical simulation. Appl. Therm. Eng. 2018, 131, 70–79. [Google Scholar] [CrossRef]
- Ding, C.; Jiang, F.; Xue, S.; Chang, R.; Long, H.; Yu, Z.; Ding, X. Prediction model of sintering bed temperature based on lognormal distribution function: Construction and application. J. Mater. Res. Technol. 2023, 26, 5478–5487. [Google Scholar] [CrossRef]
- Xu, B.; Ye, N. BP-PID Temperature Controlling System for Selective Laser Sintering Based on Fiber Bragg Grating Temperature Sensors. Instrum. Technol. Sens. 2022, 2, 61–64. [Google Scholar]
- Wu, M.; Duan, P.; Cao, W.; She, J.; Xiang, J. An intelligent control system based on prediction of the burn-through point for the sintering process of an iron and steel plant. Expert Syst. Appl. 2012, 39, 5971–5981. [Google Scholar] [CrossRef]
- Du, S.; Wu, M.; Chen, X.; Cao, W. An intelligent control strategy for iron ore sintering ignition process based on the prediction of ignition temperature. IEEE Trans. Ind. Electron. 2020, 67, 1233–1241. [Google Scholar] [CrossRef]
- Du, S.; Wu, M.; Chen, L.; Pedrycz, W. Prediction model of burn-through point with fuzzy time series for iron ore sintering process. Eng. Appl. Artif. Intell. 2021, 102, 104259. [Google Scholar] [CrossRef]
- Wu, M.; Xu, C.; She, J.; Cao, W. Neural-network-based integrated model for predicting burn-through point in lead–zinc sintering process. J. Process Control 2012, 22, 925–934. [Google Scholar] [CrossRef]
- Chi, Z.; Chen, X.; Xia, H.; Liu, C.; Wang, Z. An adaptive control system based on spatial–temporal graph convolutional and disentangled baseline-volatility prediction of bellows temperature for iron ore sintering process. J. Process Control 2024, 140, 103254. [Google Scholar] [CrossRef]
- Li, H.; Wu, M.; Du, S.; Hu, J.; Zhang, W.; Chen, L.; Ma, X.; Li, H. Prediction model of burn-through point with data correction based on feature matching of cross-section frame at discharge end. J. Process Control 2024, 140, 103265. [Google Scholar] [CrossRef]
- Chen, X.; Shi, X.; Lan, T. A semi-supervised linear-nonlinear prediction system for tumbler strength of iron ore sintering process with imbalanced data in multiple working modes. Control Eng. Pract. 2021, 110, 104766. [Google Scholar] [CrossRef]
- Chen, X.; Hu, Y.; Liu, C.; Chen, A.; Chi, Z. Dynamic spatio-temporal graph network based on multi-level feature interaction for sinter TFe prediction. J. Process Control 2025, 148, 103401. [Google Scholar] [CrossRef]
- Anisimov, S.V.; Galichenko, S.V.; Prokhorchuk, A.A.; Klimanova, E.V.; Kozmina, A.S.; Aphinogenov, K.V. Estimation of autocorrelation functions of atmospheric electric field variations using a Golomb array of sensors. Atmos. Res. 2025, 315, 107847. [Google Scholar] [CrossRef]
- Averty, T.; Boudraa, A.O.; Daré-Emzivat, D. Hurst exponent estimation using natural visibility graph embedding in Fisher–Shannon plane. Signal Process. 2025, 230, 109884. [Google Scholar] [CrossRef]
- Du, S.; Wu, M.; Chen, L.; Jin, L.; Cao, W.; Pedrycz, W. Operating Performance Improvement Based on Prediction and Grade Assessment for Sintering Process. IEEE Trans. Cybern. 2022, 52, 10529–10541. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Yang, C.; Zhang, X. DSTED: A Denoising Spatial–Temporal Encoder–Decoder Framework for Multistep Prediction of Burn-Through Point in Sintering Process. IEEE Trans. Ind. Electron. 2022, 69, 10735–10744. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Y.; He, H.; Xiao, H.; Wang, S.; Zhang, Y.; Li, H.; Qian, X. Time series prediction of the chemical components of PM2.5 based on a deep learning model. Chemosphere 2023, 342, 1040153. [Google Scholar] [CrossRef] [PubMed]
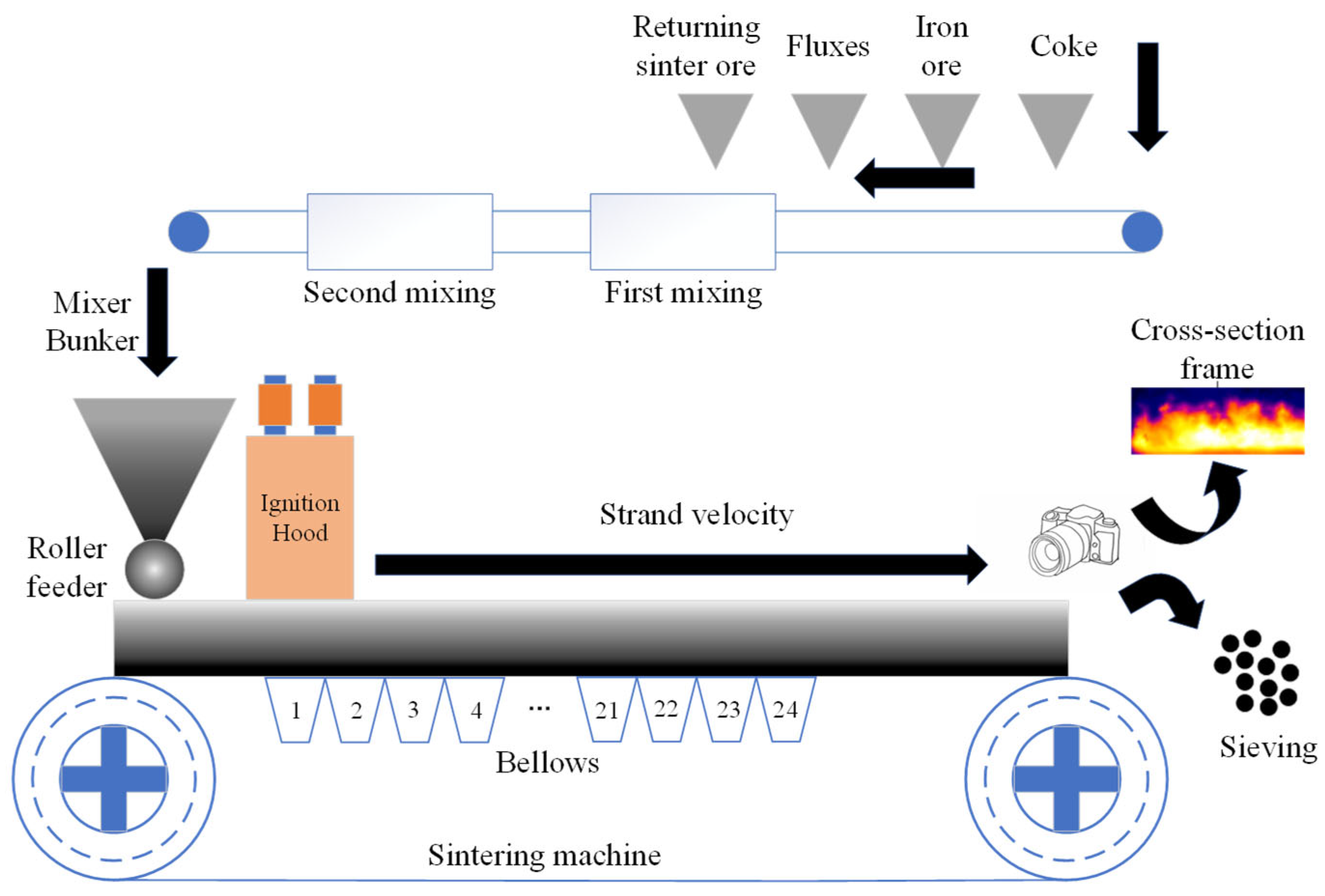






| Physical Variable | Meaning | Unit |
|---|---|---|
| Burn-through point temperature | °C | |
| Burn-through point position | / | |
| Temperature of exhaust gas in bellows | The temperature of exhaust gas in the sintering machine bellows | °C |
| Exhaust gas pressure in bellows | The pressure of exhaust gas in the bellows | Pa |
| Strand velocity | The moving speed of the sintering trolley | m/min |
| Ignition temperature | The temperature in the ignition hood, used to ignite coke in the sinter mixture | °C |
| Material layer thickness | The thickness of the material layer on the sintering trolley | mm |
| Ambient temperature | The environmental temperature at the sintering site | °C |
| Pixel value | A value representing the brightness of pixels in an image | / |
| Feature | Mutual Information |
|---|---|
| Temperature of exhaust gas in the 23rd bellows | 2.410 |
| Temperature of exhaust gas in the 22nd bellows | 1.166 |
| Exhaust gas pressure in the 24th bellows | 0.734 |
| Temperature of exhaust gas in the 24th bellows | 0.705 |
| Exhaust gas pressure in the 23rd bellows | 0.698 |
| Temperature of exhaust gas in the 21st bellows | 0.646 |
| Exhaust gas pressure in the 17th–19th bellows | 0.633 |
| Exhaust gas pressure in the 5th bellows | 0.630 |
| Exhaust gas pressure in the 4th bellows | 0.629 |
| Exhaust gas pressure in the 13rd–15th bellows | 0.628 |
| Method | |||||
|---|---|---|---|---|---|
| Hybrid Prediction Model | 6.1031 | 4.3542 | 37.2479 | 0.8490% | 0.9049 |
| BiLSTM | 7.3168 | 5.2079 | 53.5352 | 1.0222% | 0.8633 |
| XGBoost | 7.9415 | 5.6836 | 63.0671 | 1.1096% | 0.8389 |
| Information | Model | |||||
|---|---|---|---|---|---|---|
| With color temperature information | Our model | 6.1031 | 4.3542 | 37.2479 | 0.8490% | 0.9049 |
| Model in [11] | 6.4229 | 4.5534 | 41.2534 | 0.8890% | 0.8946 | |
| Model in [18] | 6.3644 | 4.6344 | 40.5008 | 0.9011% | 0.8965 | |
| Without color temperature information | Our model | 6.5995 | 4.8254 | 43.5536 | 0.9408% | 0.8887 |
| Model in [11] | 6.5399 | 4.7292 | 42.7697 | 0.9208% | 0.8908 | |
| Model in [18] | 6.7326 | 4.8651 | 45.3278 | 0.9500% | 0.8842 |
| Metric | Original | With 10% Noise | Change (%) |
|---|---|---|---|
| 6.1207 | 6.4688 | 5.3% | |
| 4.4441 | 4.6202 | 3.8% | |
| 0.9043 | 0.8931 | 1.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Fan, Y.; Ge, J.; Hao, X.; Wu, C.; Ma, X.; Du, S. Hybrid Prediction Model of Burn-Through Point Temperature with Color Temperature Information from Cross-Sectional Frame at Discharge End. Energies 2025, 18, 3595. https://doi.org/10.3390/en18143595
Zhao M, Fan Y, Ge J, Hao X, Wu C, Ma X, Du S. Hybrid Prediction Model of Burn-Through Point Temperature with Color Temperature Information from Cross-Sectional Frame at Discharge End. Energies. 2025; 18(14):3595. https://doi.org/10.3390/en18143595
Chicago/Turabian StyleZhao, Mengxin, Yinghua Fan, Jing Ge, Xinzhe Hao, Caili Wu, Xian Ma, and Sheng Du. 2025. "Hybrid Prediction Model of Burn-Through Point Temperature with Color Temperature Information from Cross-Sectional Frame at Discharge End" Energies 18, no. 14: 3595. https://doi.org/10.3390/en18143595
APA StyleZhao, M., Fan, Y., Ge, J., Hao, X., Wu, C., Ma, X., & Du, S. (2025). Hybrid Prediction Model of Burn-Through Point Temperature with Color Temperature Information from Cross-Sectional Frame at Discharge End. Energies, 18(14), 3595. https://doi.org/10.3390/en18143595