Equivalent Modeling of Temperature Field for Amorphous Alloy 3D Wound Core Transformer for New Energy
Abstract
1. Introduction
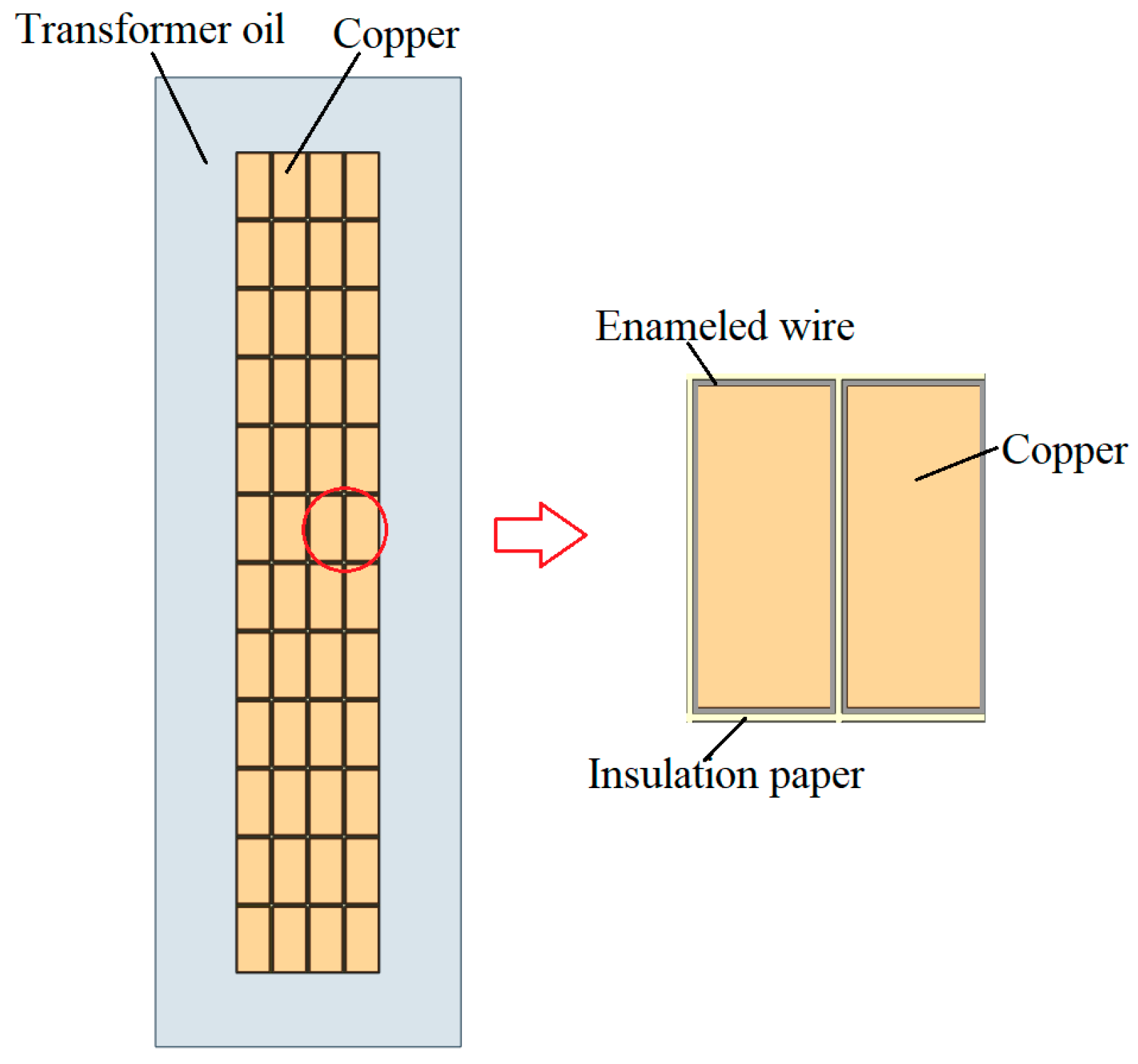
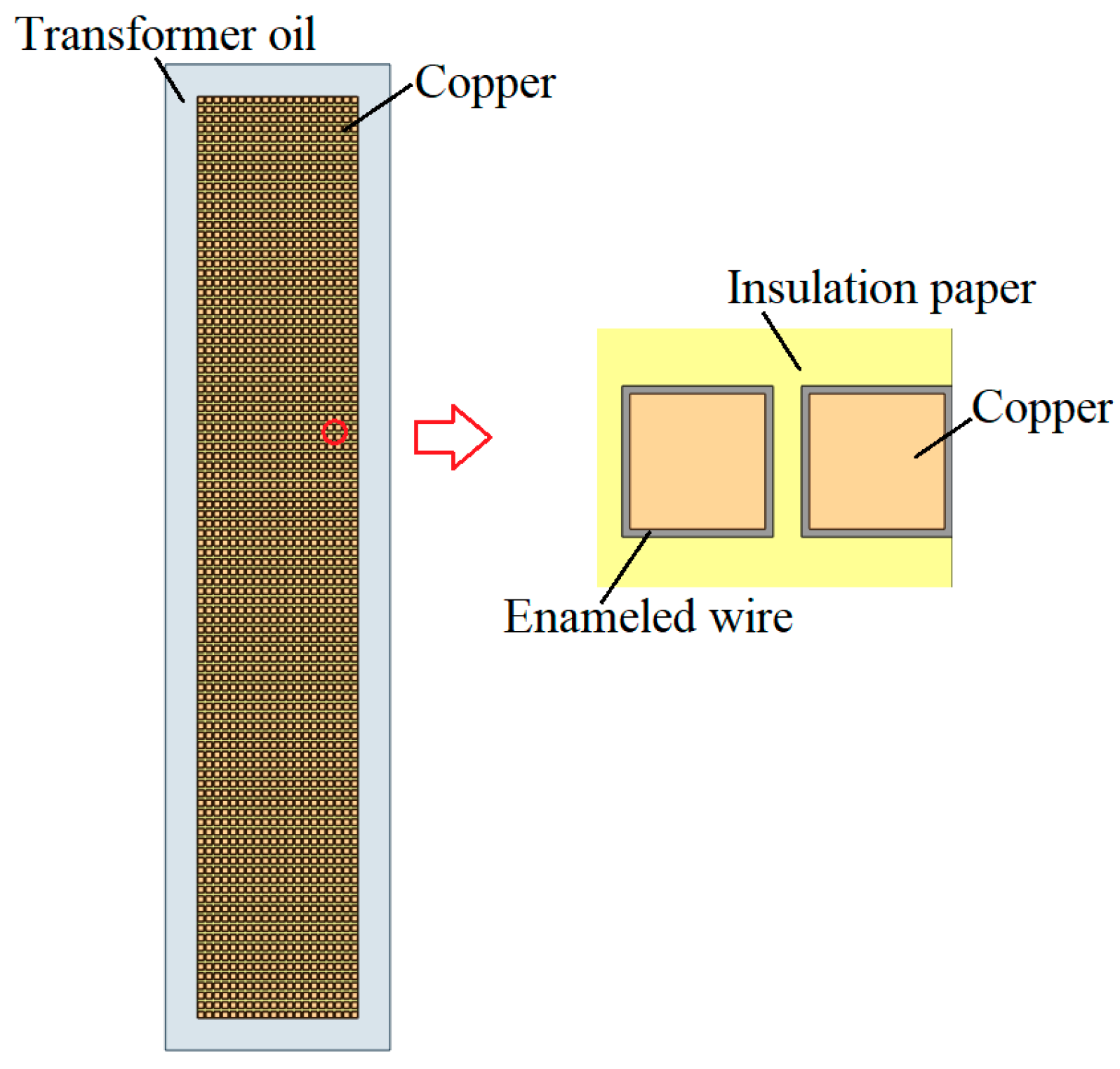
2. Equivalent Treatment Modeling
- A.
- The model of low-voltage winding
- B.
- The model of high-voltage winding
- C.
- Calculation method of equivalent thermal conductivity of winding
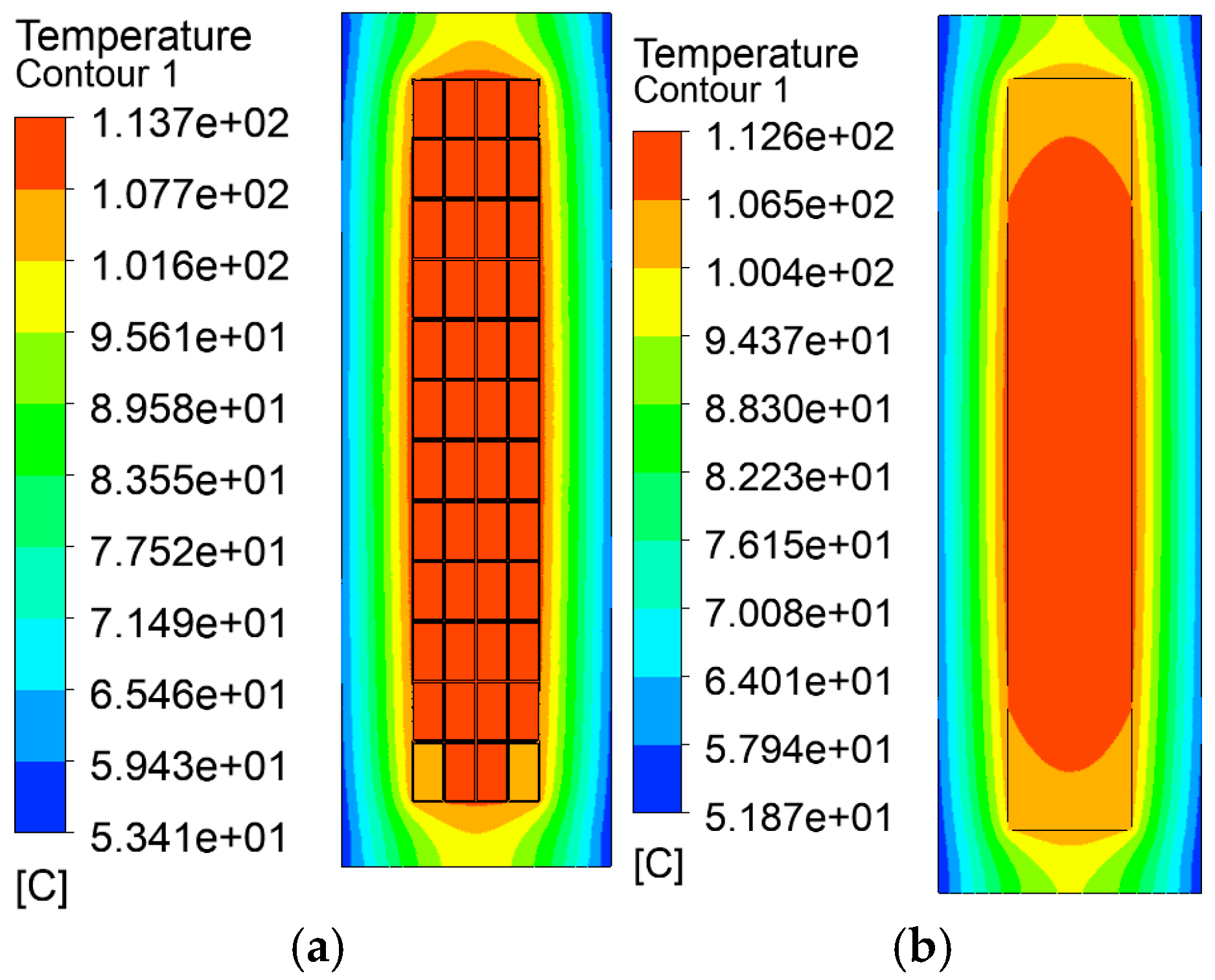
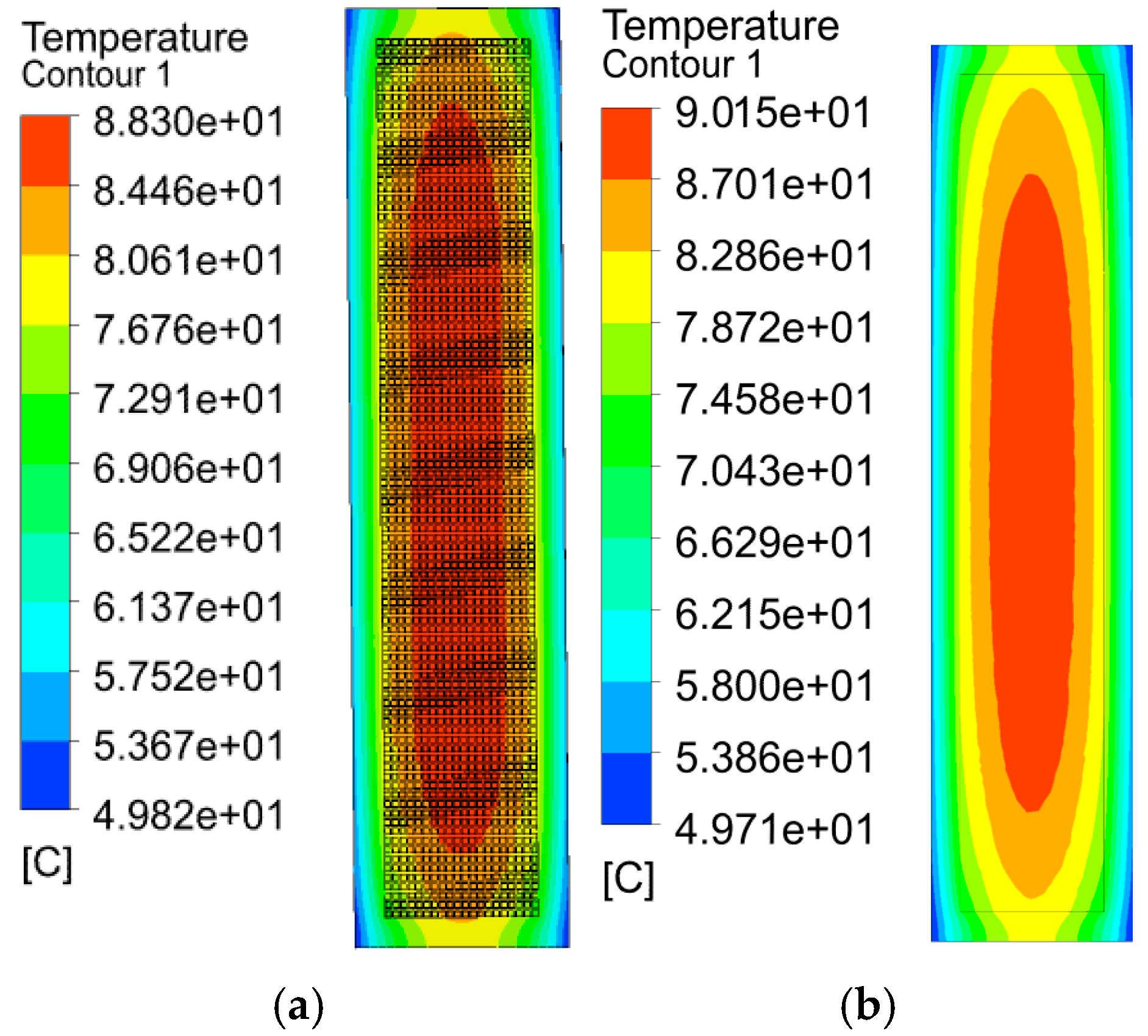
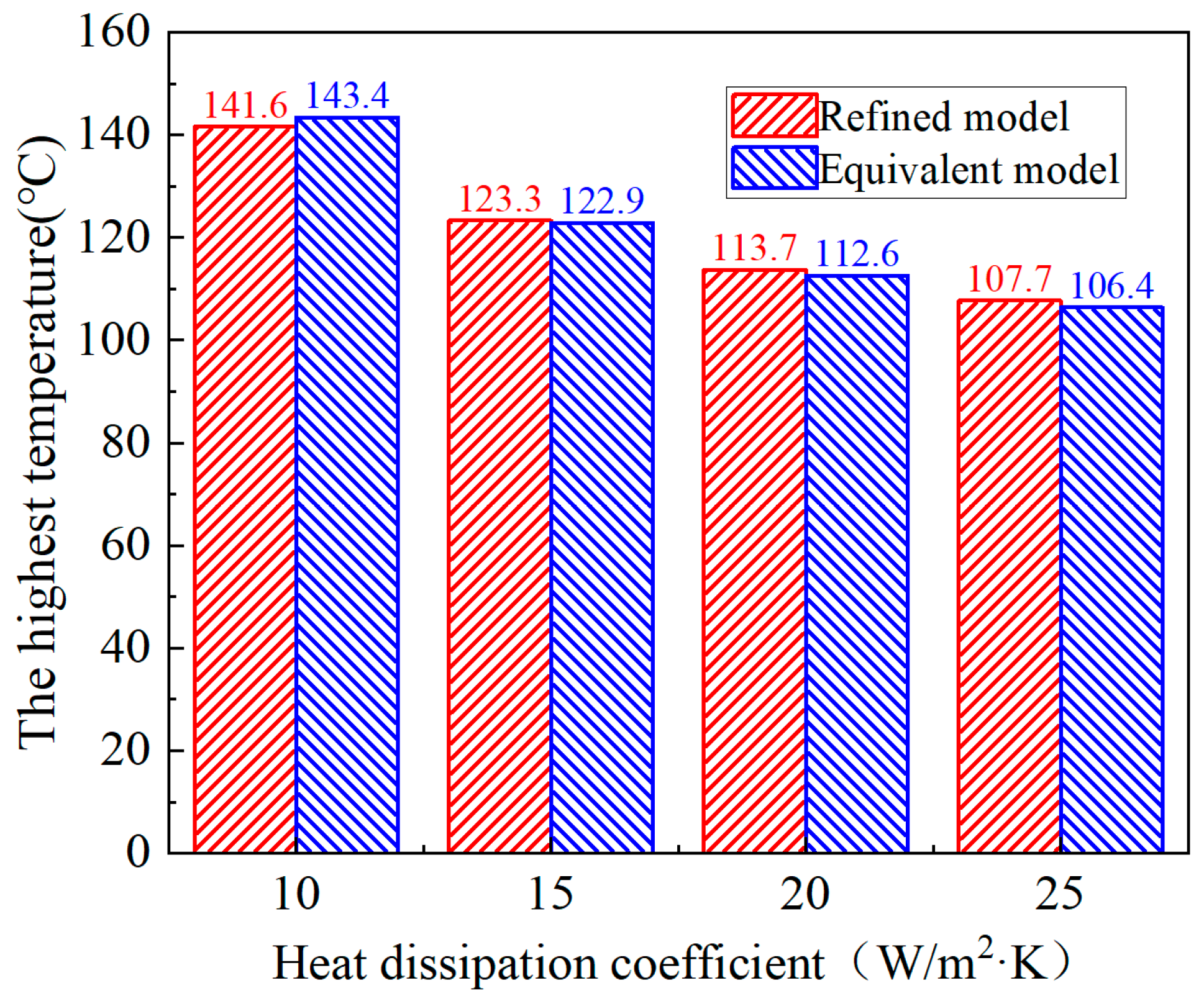
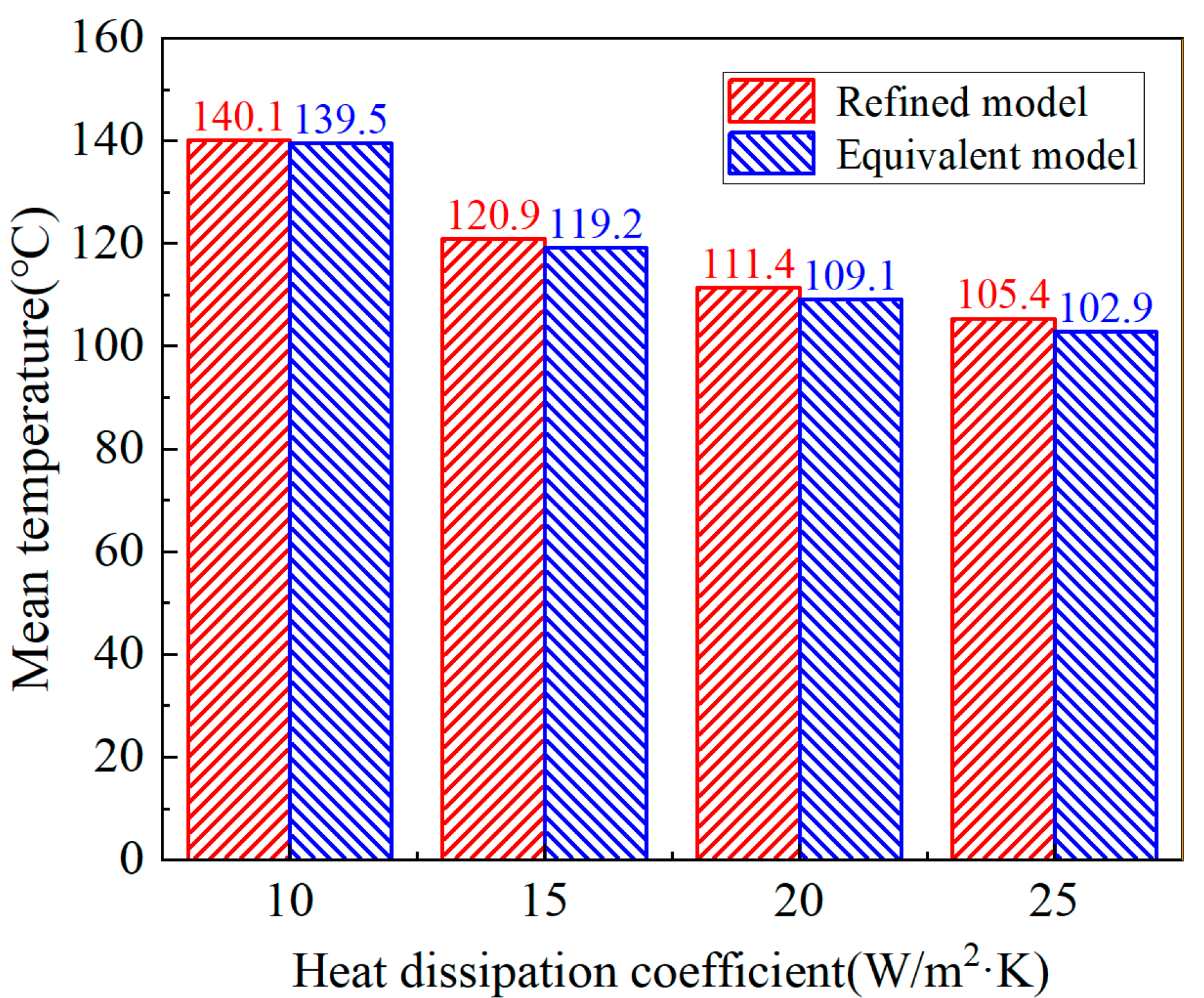
3. 2-D Simulation Validation
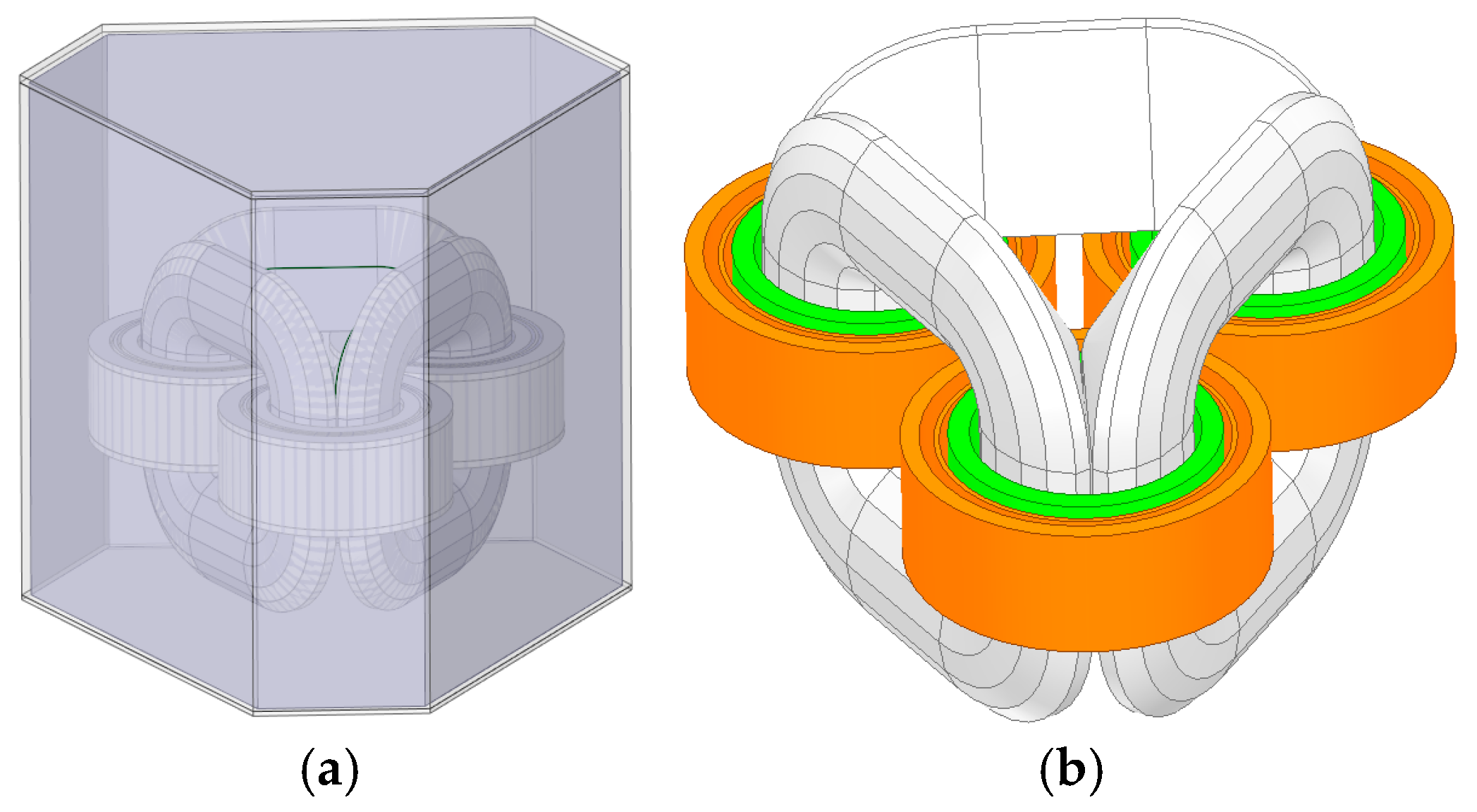
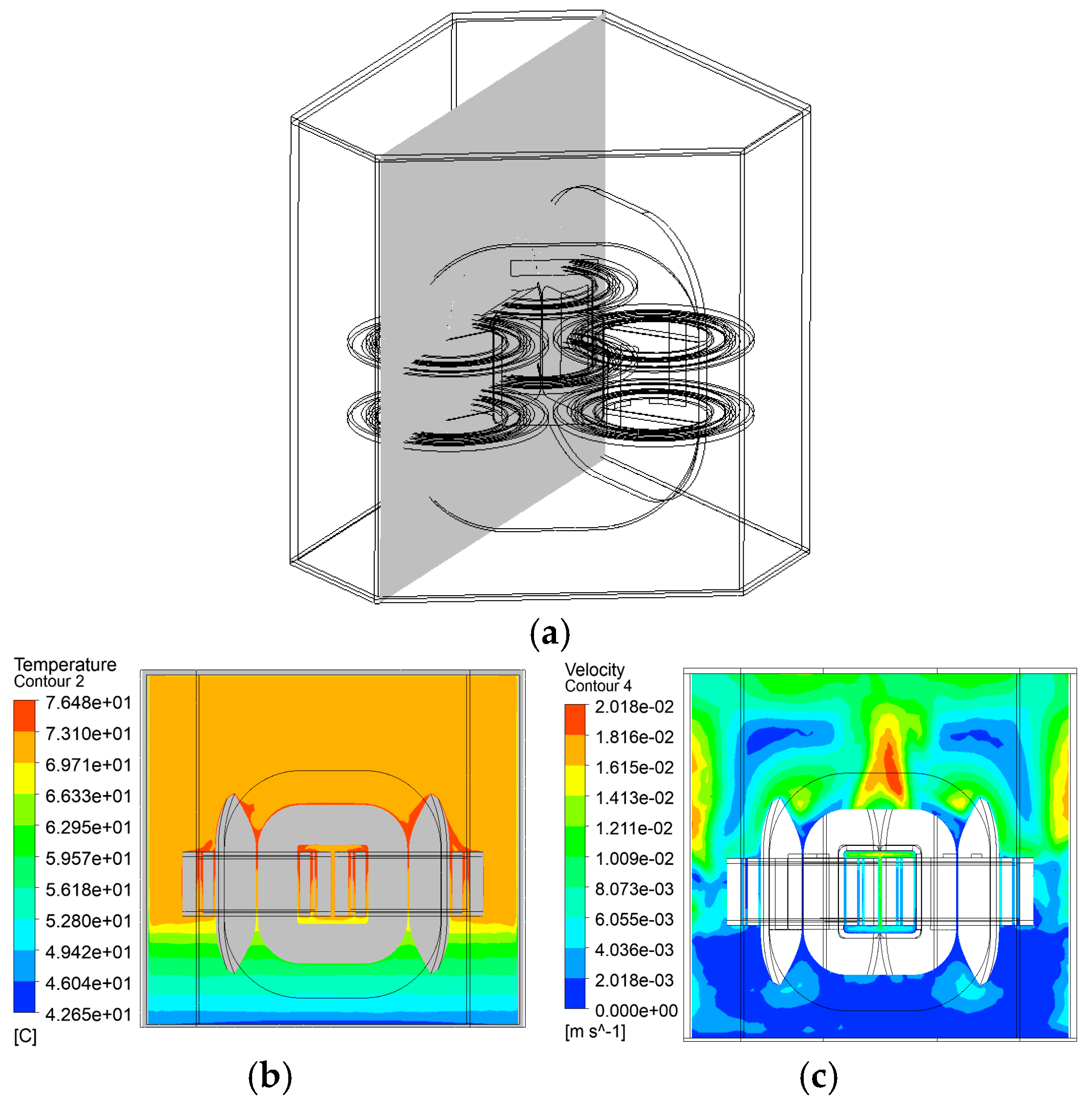
4. 3D Global Temperature Field Solution
- A.
- Temperature field modeling
- B. Transformer loss
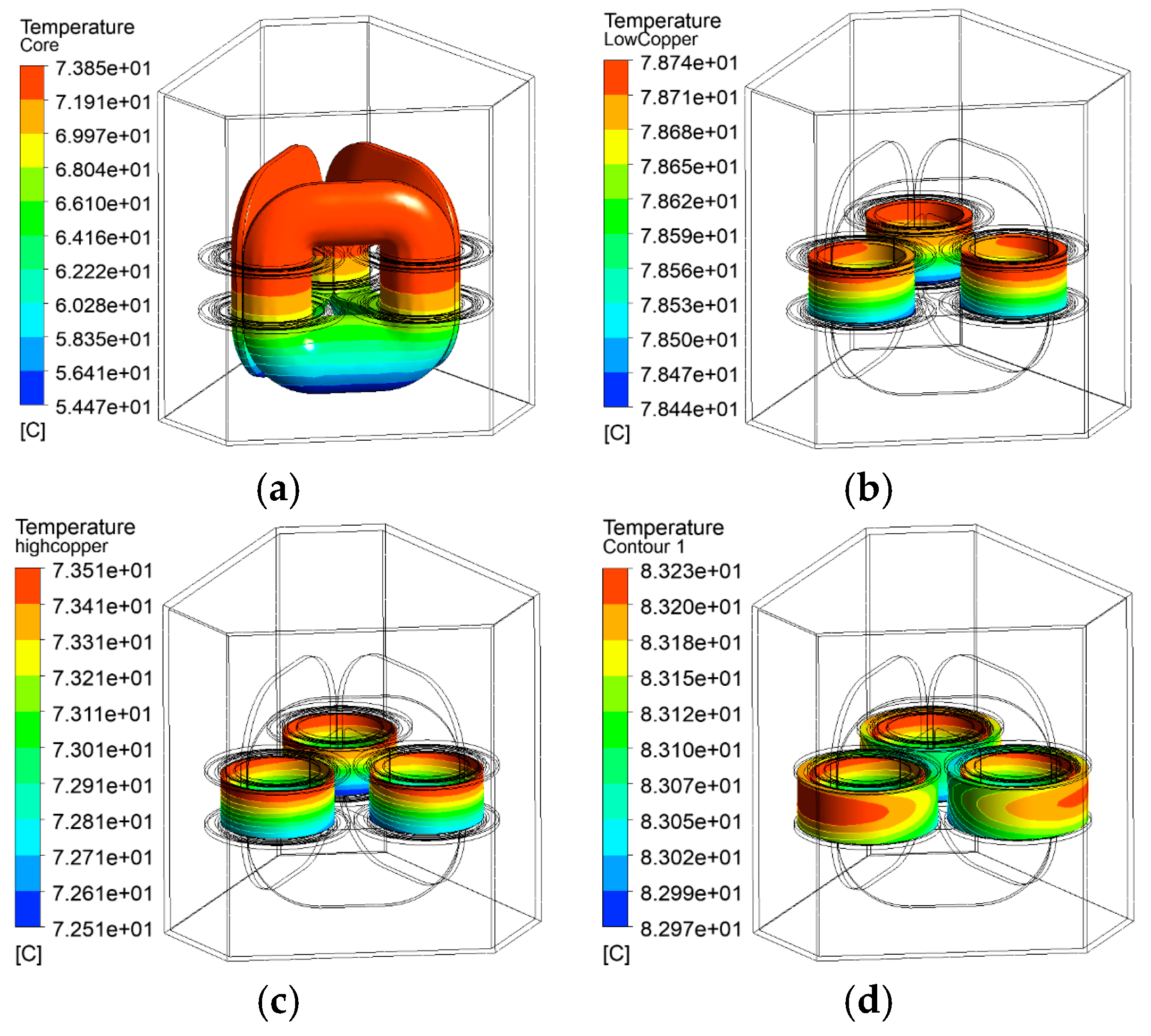
- C. Temperature field simulation results
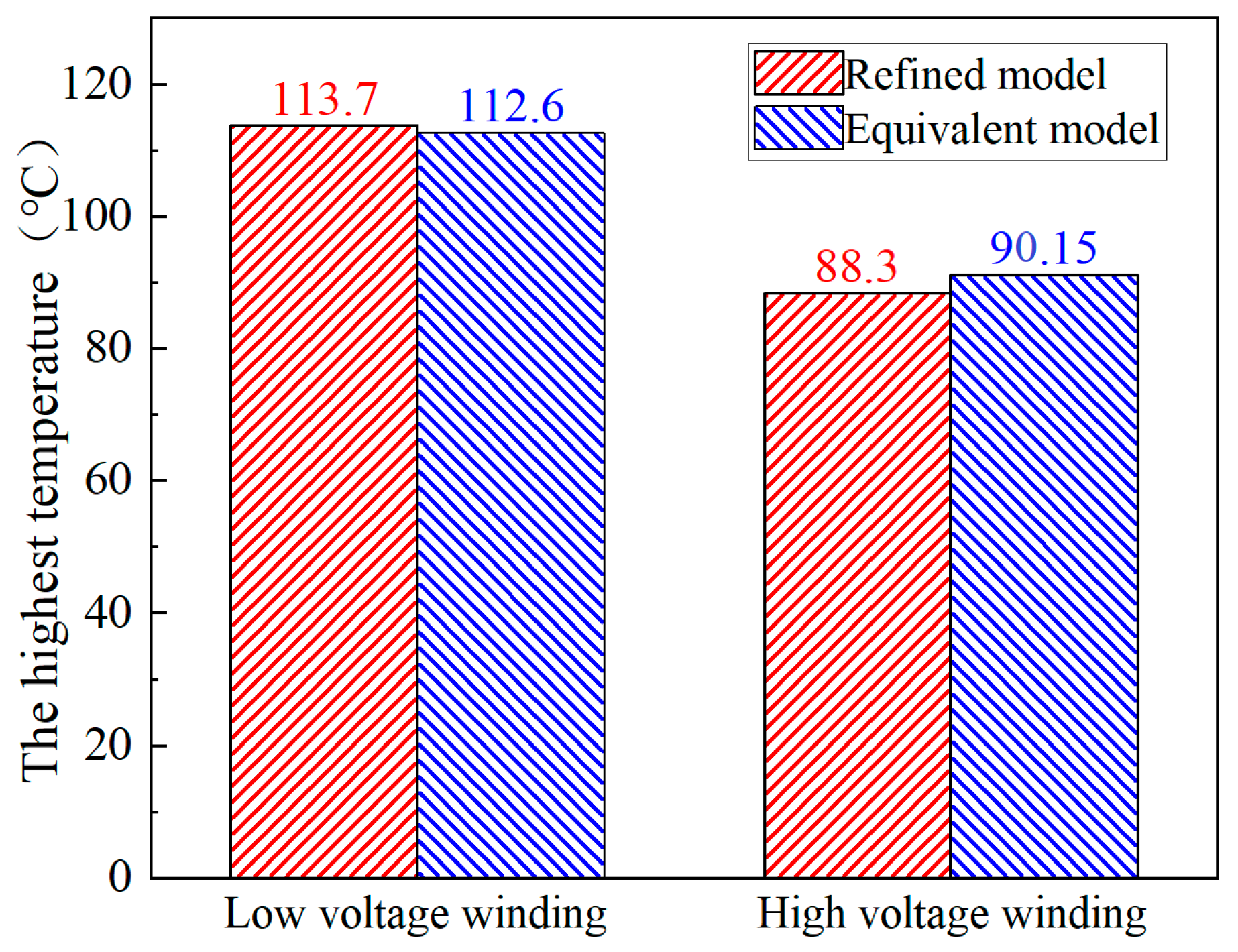
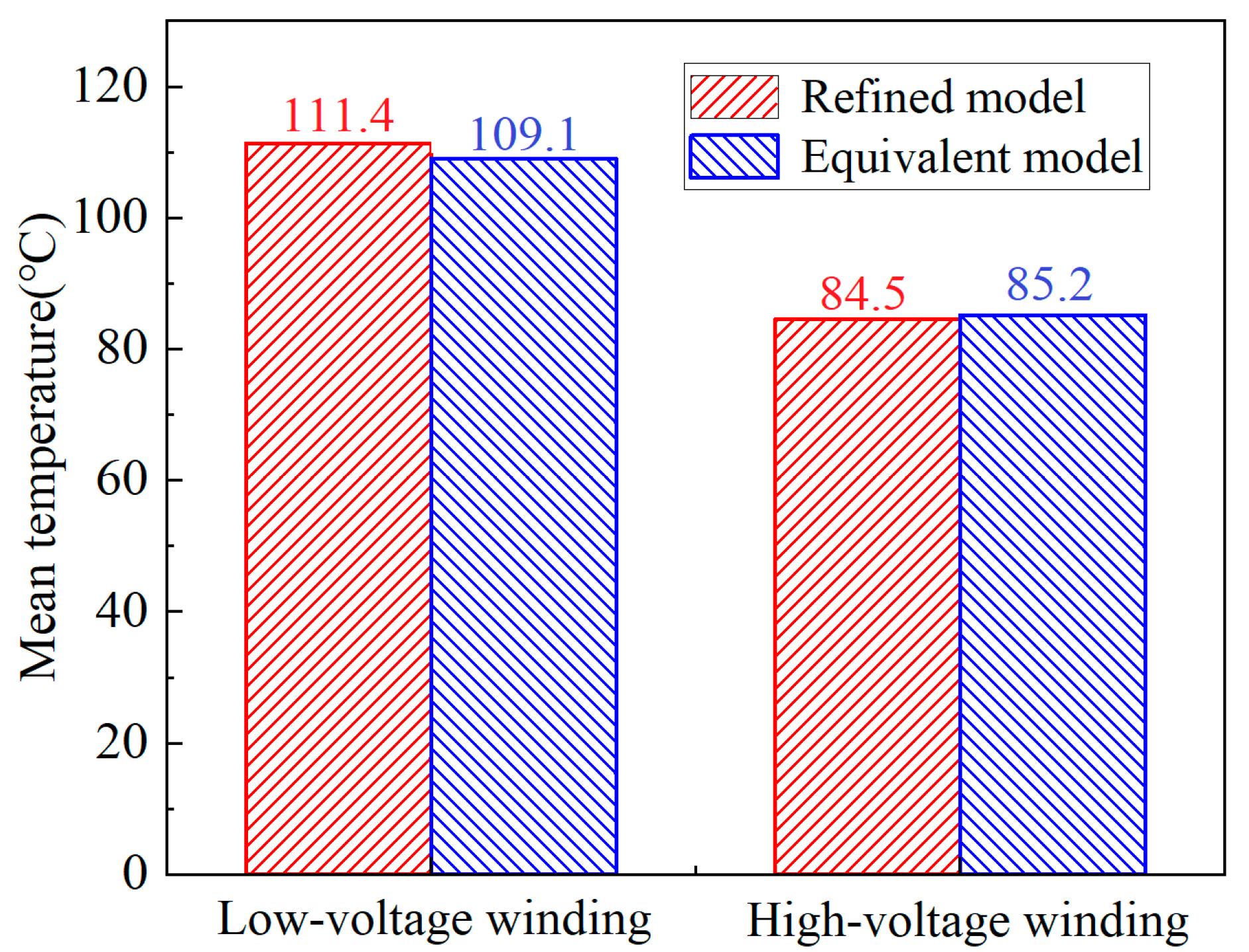
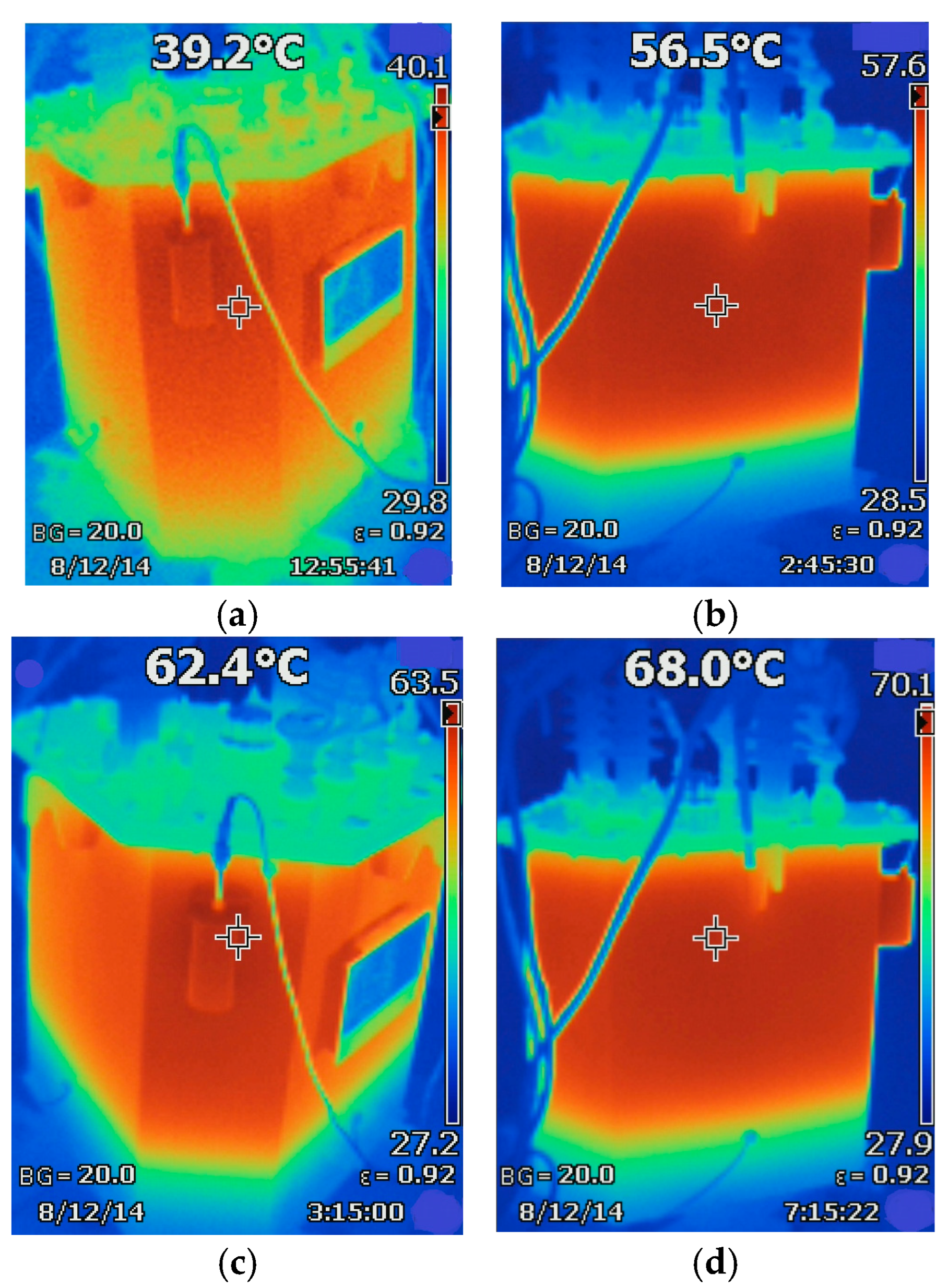
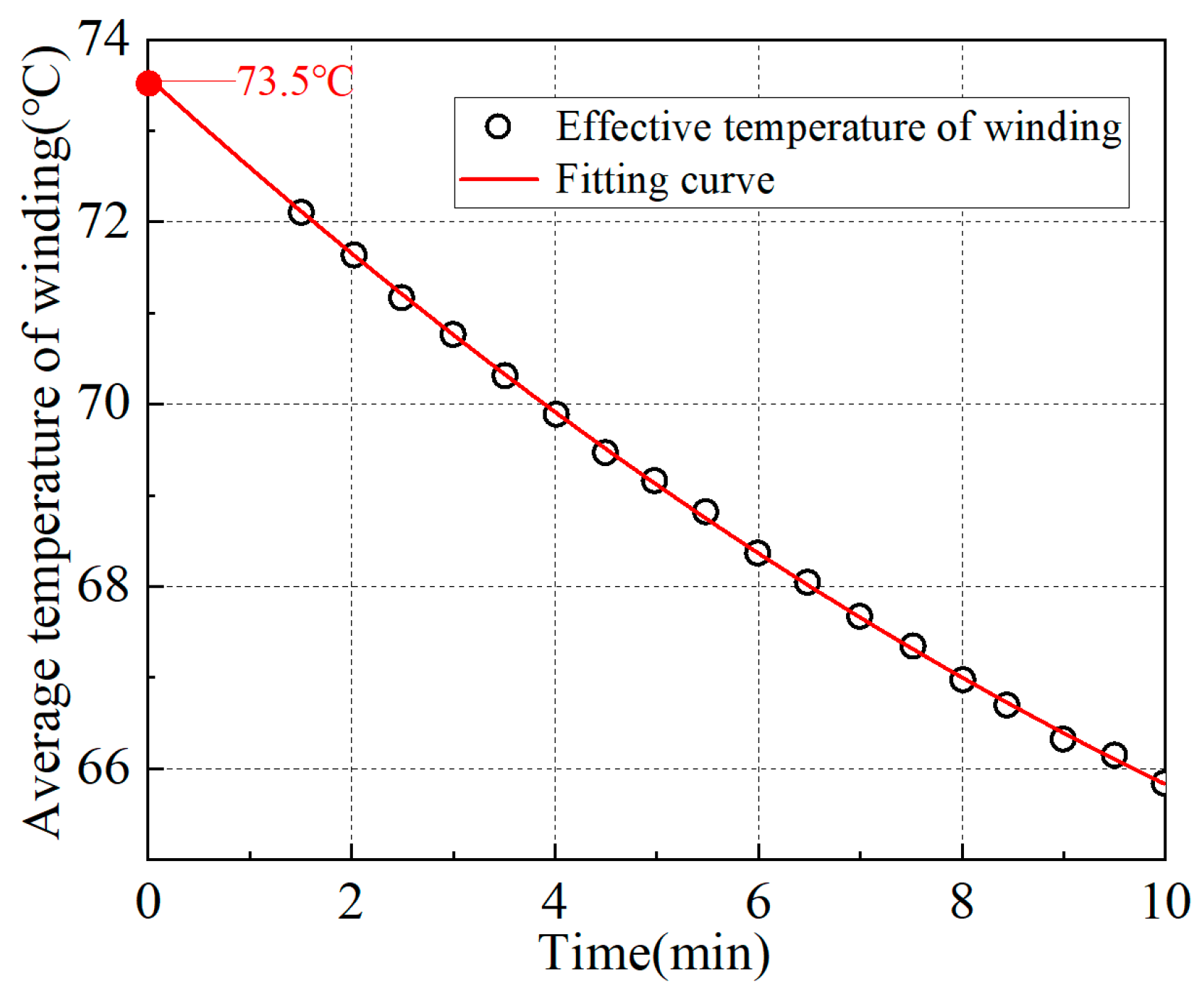
5. Experimental Measurement
6. Conclusions
- (1)
- An equivalent modeling approach for the winding of amorphous alloy 3D wound core transformer is proposed. By homogenizing the high- and low-voltage windings into an equivalent bulk conductor, this method remarkably enhances the temperature field simulation speed while maintaining high calculation accuracy.
- (2)
- Based on the principle of unchanged equivalent thermal resistance, the influence of winding size parameters, arrangement characteristics, and other factors on the equivalent thermal conductivity is analyzed, and the equivalent thermal conductivities of and the high- and low-voltage windings are accurately obtained.
- (3)
- Through two-dimensional temperature field simulation analysis, it is shown that the maximum temperature and average temperature calculation errors of the equivalent model and the refined model are controlled within 1.0% and 2.0%, and the equivalent thermal conductivity still has high reliability under different boundary conditions.
- (4)
- The temperature field experiment tests the prototype, and the test results show that the error between high- and low-voltage winding simulation and experiment results is less than 3 K, which proves the effectiveness of this method in practical application.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Liu, N.; Liang, Y.; Xu, Y.-Y.; Lin, D.; Mu, H.-B.; Zhang, G.-J. A model of load capacity assessment for oil-immersed transformer by using temperature rise characteristics. Proc. CSEE 2018, 38, 6737–6746. [Google Scholar]
- Yuan, S.; Zhou, L.; Gou, X.; Zhu, Q.; Ding, S.; Wang, L.; Wang, D. Modeling method for thermal field of turbulent cooling dry-type on-board traction transformer in EMUs. IEEE Trans. Transp. Electrif. 2022, 8, 298–311. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Q.; Zhang, C.; Li, Y.; Li, X. Thermal network model of high-power dry-type transformer coupled with electromagnetic loss. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Niu, S.Y.; Yu, H.; Niu, S.X.; Jian, L. Power loss analysis and thermal assessment on wireless electric vehicle charging technology: The over-temperature risk of ground assembly needs attention. Appl. Energy 2020, 275, 115344. [Google Scholar] [CrossRef]
- Ortiz, C.; Skorek, A.W.; Lavoie, M.; Benard, P. Parallel CFD analysis of conjugate heat transfer in a dry-type transformer. IEEE Trans. Ind. Appl. 2009, 45, 1530–1534. [Google Scholar] [CrossRef]
- Niu, S.; Yu, H.; Jian, L. Thermal Behavior Analysis of Wireless Electric Vehicle Charging System under Various Misalignment Conditions. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 607–612. [Google Scholar]
- Zhao, Y.; Zhang, X.; Ho, S.L.; Fu, W.N. An adaptive mesh method in transient finite element analysis of magnetic field using a novel error estimator. IEEE Trans. Magn. 2012, 48, 4160–4163. [Google Scholar] [CrossRef]
- Gu, H.; Luo, Y.; Qiu, Y.; Hou, J. A fast solution method for large scale linear sparse equations based on parallelism. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), Chengdu, China, 13–16 May 2022; pp. 1337–1340. [Google Scholar]
- Liu, G.; Hu, W.; Hao, S.; Gao, C.; Liu, Y.; Wu, W.; Li, L. A fast computational method for internal temperature field in Oil-Immersed power transformers. Appl. Therm. Eng. 2024, 236, 121558. [Google Scholar] [CrossRef]
- Kiradjiev, K.B.; Halvorsen, S.A.; Van Gorder, R.A.; Howison, S.D. Maxwell-type models for the effective thermal conductivity of a porous material with radiative transfer in the voids. Int. J. Therm. Sci. 2019, 145, 106009. [Google Scholar] [CrossRef]
- Liu, X.; Gerada, D.; Xu, Z.; Corfield, M.; Gerada, C.; Yu, H. Effective thermal conductivity calculation and measurement of litz wire based on the porous metal materials structure. IEEE Trans. Ind. Electron. 2019, 67, 2667–2677. [Google Scholar] [CrossRef]
- Yi, X.; Yang, T.; Xiao, J.; Miljkovic, N.; King, W.P.; Haran, K.S. Equivalent thermal conductivity prediction of form-wound windings with litz wire including transposition effects. IEEE Trans. Ind. Appl. 2021, 57, 1440–1449. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, T.; Zhou, F. Equivalent thermal conductivity estimation for compact electromagnetic windings. IEEE Trans. Ind. Electron. 2018, 66, 6210–6219. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Li, G.; Qian, Z.; Li, W.; Jing, J. A closed-form analytical method for reliable estimation of equivalent thermal conductivity of windings with round-profile conductors. IEEE Trans. Energy Convers. 2020, 36, 1143–1155. [Google Scholar] [CrossRef]
- Simpson, N.; Wrobel, R.; Mellor, P. Estimation of equivalent thermal parameters of impregnated electrical windings. IEEE Trans. Ind. Appl. 2013, 49, 2505–2515. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, D.; Li, S.; Xie, F.; Zhao, J.; Liu, Z.; Liang, J.; Jiang, Y. Heat transfer performance of the solid microencapsulated fuel in light water reactors. Ann. Nucl. Energy 2022, 179, 109420. [Google Scholar] [CrossRef]
- Folsom, C.; Xing, C.; Jensen, C.; Ban, H.; Marshall, D.W. Experimental measurement and numerical modeling of the effective thermal conductivity of TRISO fuel compacts. J. Nucl. Mater. 2015, 458, 198–205. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, Z. A lattice Boltzmann algorithm for fluid–solid conjugate heat transfer. Int. J. Therm. Sci. 2007, 46, 228–234. [Google Scholar] [CrossRef]
- Yang, Y.; Fathidoost, M.; Oyedeji, T.D.; Bondi, P.; Zhou, X.; Egger, H.; Xu, B.-X. A diffuse-interface model of anisotropic interface thermal conductivity and its application in thermal homogenization of composites. Scripta Mater. 2022, 212, 114537. [Google Scholar] [CrossRef]
- Pitchai, P.; Guruprasad, P.J. Determination of the influence of interfacial thermal resistance in a three phase composite using variational asymptotic based homogenization method. Int. J. Heat Mass Transfer 2020, 155, 119889. [Google Scholar] [CrossRef]
- Staton, D.; Boglietti, A.; Cavagnino, A. Solving the more difficult aspects of electric motor thermal analysis in small and medium size industrial induction motors. IEEE Trans. Energy Convers. 2005, 20, 620–628. [Google Scholar] [CrossRef]
- Ahmed, F.; Kar, N.C. Analysis of end-winding thermal effects in a totally enclosed fan-cooled induction motor with a die cast copper rotor. IEEE Trans. Ind. Appl. 2017, 53, 3098–3109. [Google Scholar] [CrossRef]
- Kwon, S.; Zheng, J.L.; Wingert, M.C.; Cui, S.; Chen, R.K. Unusually High and Anisotropic Thermal Conductivity in Amorphous Silicon Nanostructures. ACS Nano 2017, 11, 2470–2476. [Google Scholar] [CrossRef] [PubMed]
- Ishibe, T.; Okuhata, R.; Kaneko, T.; Yoshiya, M.; Nakashima, S.; Ishida, A.; Nakamura, Y. Heat transport through propagon-phonon interaction in epitaxial amorphous-crystalline multilayers. Commun. Phys. 2021, 4, 153. [Google Scholar] [CrossRef]



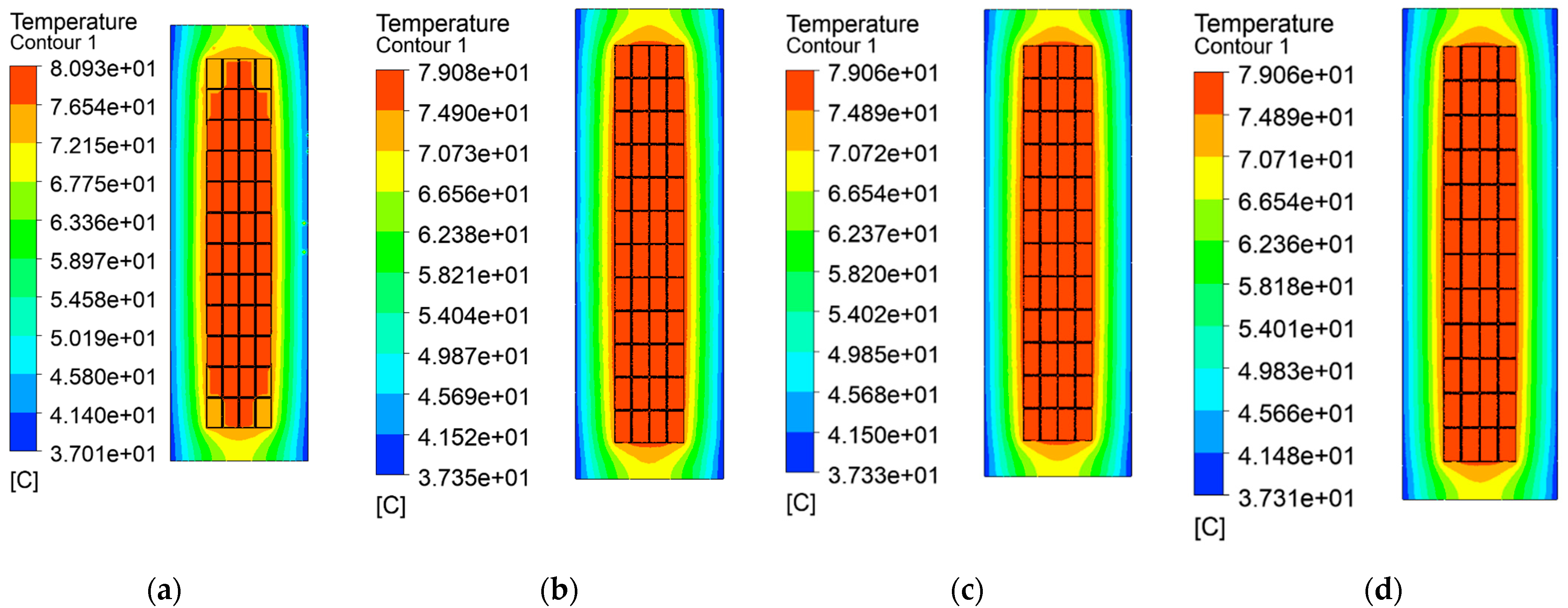



| Case | The Number of Grids | Measure (°C) | |
|---|---|---|---|
| 1 | Default split grid | 32,354 | 80.93 |
| 2 | 3-layer grid | 218,478 | 79.08 |
| 3 | 10-layer grid | 220,952 | 79.06 |
| 4 | 20-layer grid | 235,634 | 79.06 |
| Parameter | Value |
|---|---|
| Rated voltage/kV | 10 × (1 ± 5%)/0.4 |
| Capacity/kVA | 50 |
| Connection mode | Dynl1 |
| Core radius/mm | 80.0 |
| Number of turns | 49 |
| Low-voltage winding height/mm | 109 |
| High-voltage winding height/mm | 104 |
| Low-voltage winding radius/mm | 208/173 |
| High-voltage winding radius/mm | 288/218 |
| Short-circuit impedance/% | 4.0 |
| Parameter | High-Voltage Winding | Low-Voltage Winding | Core |
|---|---|---|---|
| Loss/W | 396.3 | 310.8 | 40 |
| Volume/m3 | 0.0044 | 0.0031 | 0.0276 |
| Loss density (W/m3) | 89,923.1 | 100,045.1 | 1449.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Hou, X.; Yao, X.; Yan, Y.; Dai, Z.; Wang, X.; Zhao, P.; Zhuang, P.; Yu, Z. Equivalent Modeling of Temperature Field for Amorphous Alloy 3D Wound Core Transformer for New Energy. Energies 2025, 18, 3212. https://doi.org/10.3390/en18123212
Han J, Hou X, Yao X, Yan Y, Dai Z, Wang X, Zhao P, Zhuang P, Yu Z. Equivalent Modeling of Temperature Field for Amorphous Alloy 3D Wound Core Transformer for New Energy. Energies. 2025; 18(12):3212. https://doi.org/10.3390/en18123212
Chicago/Turabian StyleHan, Jianwei, Xiaolin Hou, Xinglong Yao, Yunfei Yan, Zonghan Dai, Xiaohui Wang, Peng Zhao, Pengzhe Zhuang, and Zhanyang Yu. 2025. "Equivalent Modeling of Temperature Field for Amorphous Alloy 3D Wound Core Transformer for New Energy" Energies 18, no. 12: 3212. https://doi.org/10.3390/en18123212
APA StyleHan, J., Hou, X., Yao, X., Yan, Y., Dai, Z., Wang, X., Zhao, P., Zhuang, P., & Yu, Z. (2025). Equivalent Modeling of Temperature Field for Amorphous Alloy 3D Wound Core Transformer for New Energy. Energies, 18(12), 3212. https://doi.org/10.3390/en18123212





