Photovoltaic Power Generation Forecasting Based on Secondary Data Decomposition and Hybrid Deep Learning Model
Abstract
1. Introduction
2. Materials and Methods
2.1. CEEMDAN
2.2. VMD
2.3. Sparrow Search Algorithm Enhanced with Multi-Strategy Integration
2.3.1. Circle Chaotic Mapping
2.3.2. Integration of Sine Cosine Algorithm (SCA) and Nonlinear Learning Factor Strategy
2.3.3. Fusion of Cauchy Variation and Variable Spiral Search Strategy
2.4. Bidirectional Long Short-Term Memory Network
2.5. Photovoltaic Forecasting Model
3. Results
3.1. Data Preprocessing
3.2. Evaluation Metrics
3.3. Experimental Environment
3.4. Experimental Analysis
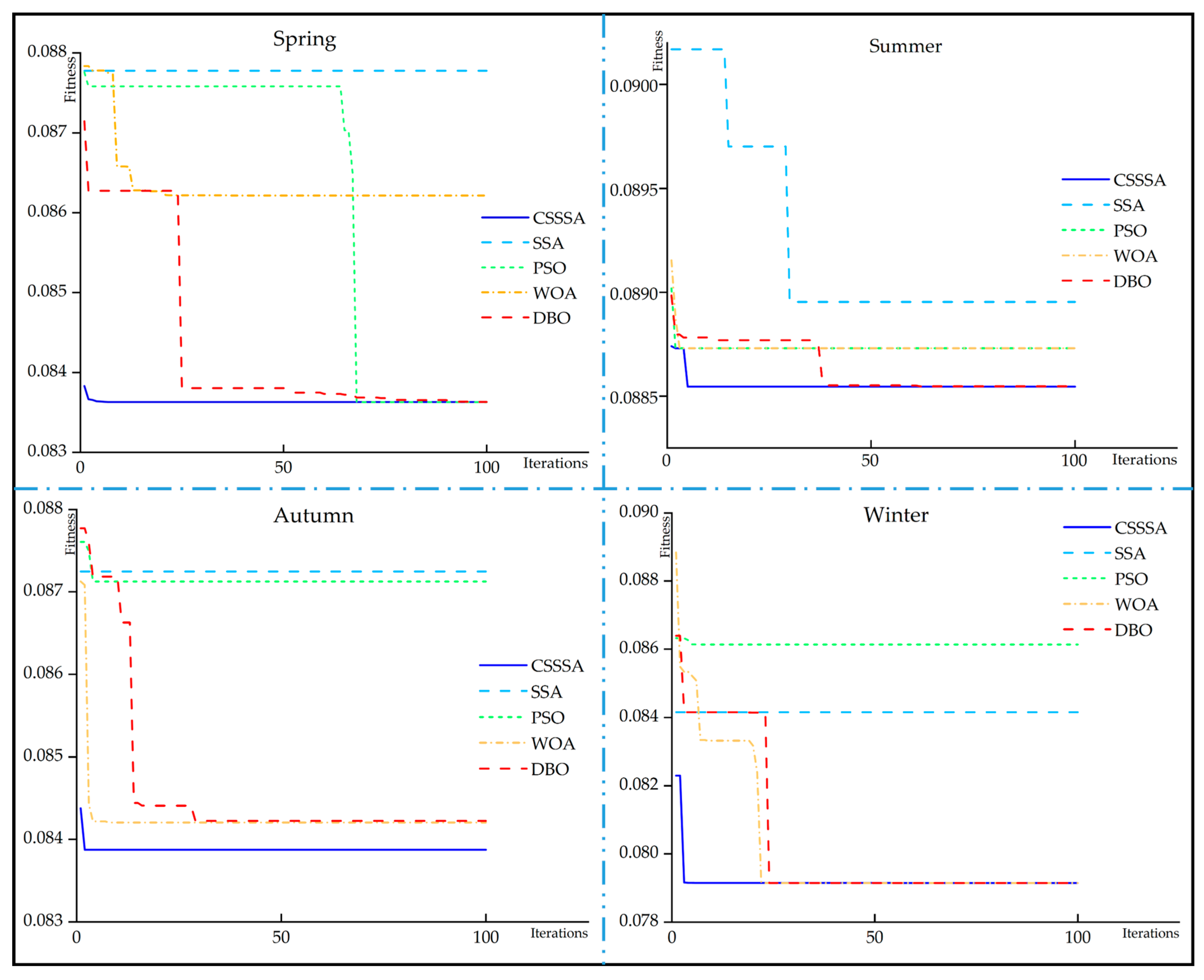
3.4.1. Comparative Results of CSSSA with Different Intelligent Algorithms
3.4.2. Ablation Study
3.4.3. Traditional Single-Model Comparison Experiment
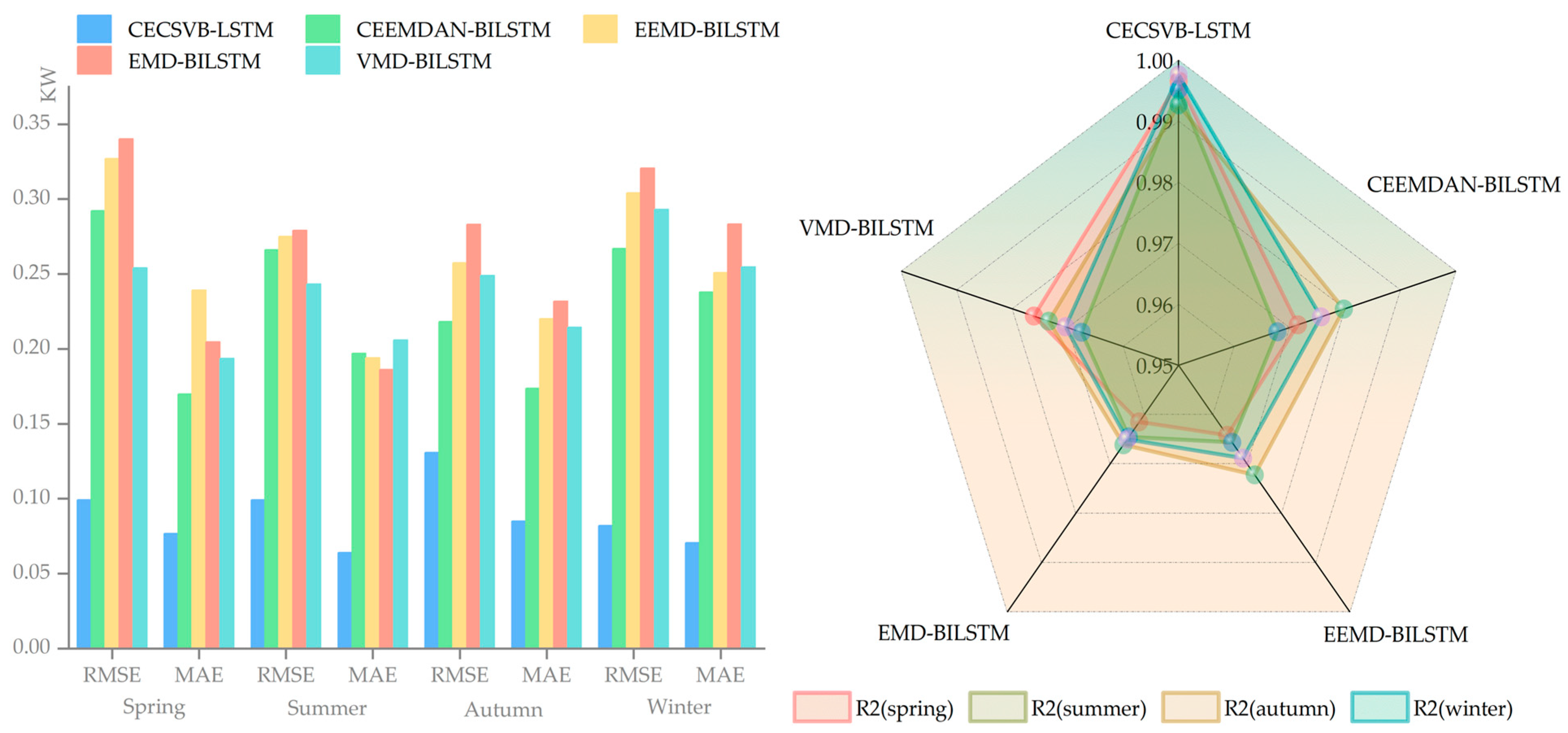
3.4.4. Comparison Experiment of Different Signal Decomposition Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sabadus, A.; Blaga, R.; Hategan, S.M.; Calinoiu, D.; Paulescu, E.; Mares, O.; Boata, R.; Stefu, N.; Paulescu, M.; Badescu, V. A cross-sectional survey of deterministic PV power forecasting: Progress and limitations in current approaches. Renew. Energy 2024, 226, 120385. [Google Scholar] [CrossRef]
- Jebli, I.; Belouadha, F.Z.; Kabbaj, M.I.; Tilioua, A. Prediction of solar energy guided by pearson correlation using machine learning. Energy 2021, 224, 120109. [Google Scholar] [CrossRef]
- Kim, G.G.; Lee, W.; Bhang, B.G.; Choi, J.H.; Ahn, H.K. Fault Detection for Photovoltaic Systems Using Multivariate Analysis With Electrical and Environmental Variables. IEEE J. Photovolt. 2021, 11, 202–212. [Google Scholar] [CrossRef]
- Zhu, T.; Li, Q.; Yu, A. Analysis of the solar spectrum allocation in a spectral-splitting photovoltaic-thermochemical hybrid system. Sol. Energy 2022, 232, 63–72. [Google Scholar] [CrossRef]
- Zhang, H.C.; Zhu, T.T. Stacking Model for Photovoltaic-Power-Generation Prediction. Sustainability 2022, 14, 5669. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Boubakr, G.; Gu, F.S.; Farhan, L.; Ball, A. Enhancing Virtual Real-Time Monitoring of Photovoltaic Power Systems Based on the Internet of Things. Electronics 2022, 11, 2469. [Google Scholar] [CrossRef]
- Rodríguez, F.; Galarza, A.; Vasquez, J.C.; Guerrero, J.M. Using deep learning and meteorological parameters to forecast the photovoltaic generators intra-hour output power interval for smart grid control. Energy 2022, 239, 122116. [Google Scholar] [CrossRef]
- Ye, W.J.; Yang, D.M.; Tang, C.H.; Wang, W.; Liu, G. Combined Prediction of Wind Power in Extreme Weather Based on Time Series Adversarial Generation Networks. IEEE Access 2024, 12, 102660–102669. [Google Scholar] [CrossRef]
- Mayer, M.J.; Gróf, G. Extensive comparison of physical models for photovoltaic power forecasting. Appl. Energy 2021, 283, 116239. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Nam, S.; Hur, J. A hybrid spatio-temporal forecasting of solar generating resources for grid integration. Energy 2019, 177, 503–510. [Google Scholar] [CrossRef]
- Liu, L.S.; Guo, K.Q.; Chen, J.; Guo, L.; Ke, C.Y.; Liang, J.R.; He, D.W. A Photovoltaic Power Prediction Approach Based on Data Decomposition and Stacked Deep Learning Model. Electronics 2023, 12, 2764. [Google Scholar] [CrossRef]
- Pan, M.Z.; Li, C.; Gao, R.; Huang, Y.T.; You, H.; Gu, T.S.; Qin, F.R. Photovoltaic power forecasting based on a support vector machine with improved ant colony optimization. J. Clean. Prod. 2020, 277, 123948. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, N.R.; Gong, L.H.; Jiang, M.L. Prediction of photovoltaic power output based on similar day analysis, genetic algorithm and extreme learning machine. Energy 2020, 204, 117894. [Google Scholar] [CrossRef]
- Behera, M.K.; Majumder, I.; Nayak, N. Solar photovoltaic power forecasting using optimized modified extreme learning machine technique. Eng. Sci. Technol. Int. J. 2018, 21, 428–438. [Google Scholar] [CrossRef]
- Heng, S.Y.; Ridwan, W.M.; Kumar, P.; Ahmed, A.N.; Fai, C.M.; Birima, A.H.; El-Shafie, A. Artificial neural network model with different backpropagation algorithms and meteorological data for solar radiation prediction. Sci. Rep. 2022, 12, 10457. [Google Scholar] [CrossRef]
- Zheng, J.Q.; Zhang, H.R.; Dai, Y.H.; Wang, B.H.; Zheng, T.C.; Liao, Q.; Liang, Y.T.; Zhang, F.W.; Song, X. Time series prediction for output of multi-region solar power plants. Appl. Energy 2020, 257, 114001. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Lughi, V. Deep learning neural networks for short-term photovoltaic power forecasting. Renew. Energy 2021, 172, 276–288. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.F.; Wang, D.J.; Liu, X.J.; Wang, Y.Y. A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 2021, 235, 113960. [Google Scholar] [CrossRef]
- Zhu, H.L.; Li, X.; Sun, Q.; Nie, L.; Yao, J.X.; Zhao, G. A Power Prediction Method for Photovoltaic Power Plant Based on Wavelet Decomposition and Artificial Neural Networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.W.; Li, Y.F. Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short term memory neural network and Elman neural network. Energy Convers. Manag. 2018, 156, 498–514. [Google Scholar] [CrossRef]
- Yang, X.Y.; Yang, L.; Li, Y.K.; Zhao, Z.Y.; Zhang, Y.F. A new method of photovoltaic clusters power prediction based on Informer considering time-frequency analysis and convergence effect. Electr. Power Syst. Res. 2025, 238, 111049. [Google Scholar] [CrossRef]
- Wen, Y.; Pan, S.; Li, X.X.; Li, Z.B. Highly fluctuating short-term load forecasting based on improved secondary decomposition and optimized VMD. Sustain. Energy Grids Netw. 2024, 37, 101270. [Google Scholar] [CrossRef]
- Chen, J.Y.; Liu, L.S.; Guo, K.Q.; Liu, S.R.; He, D.W. Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Appl. Sci. 2024, 14, 5966. [Google Scholar] [CrossRef]
- Wang, S.C.; Huang, Y. Spatio-temporal photovoltaic prediction via a convolutional based hybrid network. Comput. Electr. Eng. 2025, 123, 110021. [Google Scholar] [CrossRef]
- Wang, Y.; Bi, Y.; Guo, Y.; Liu, X.L.; Sun, W.Q.; Yu, Y.; Yang, J.Q. A Wind and Solar Power Prediction Method Based on Temporal Convolutional Network-Attention-Long Short-Term Memory Transfer Learning and Sensitive Meteorological Features. Appl. Sci. 2025, 15, 1636. [Google Scholar] [CrossRef]
- Zhang, J.L.; Tan, Z.F.; Wei, Y.M. An adaptive hybrid model for day-ahead photovoltaic output power prediction. J. Clean. Prod. 2020, 244, 118858. [Google Scholar] [CrossRef]
- Chen, X.; Ding, K.; Zhang, J.W.; Han, W.; Liu, Y.J.; Yang, Z.N.; Weng, S. Online prediction of ultra-short-term photovoltaic power using chaotic characteristic analysis, improved PSO and KELM. Energy 2022, 248, 123574. [Google Scholar] [CrossRef]
- An, G.Q.; Jiang, Z.Y.; Chen, L.B.; Cao, X.; Li, Z.; Zhao, Y.Y.; Sun, H.X. Ultra Short-Term Wind Power Forecasting Based on Sparrow Search Algorithm Optimization Deep Extreme Learning Machine. Sustainability 2021, 13, 10453. [Google Scholar] [CrossRef]
- Jia, P.Y.; Zhang, H.B.; Liu, X.M.; Gong, X.F. Short-Term Photovoltaic Power Forecasting Based on VMD and ISSA-GRU. IEEE Access 2021, 9, 105939–105950. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Li, T.; Xie, X.; Chang, C. Short-term PV power prediction based on optimized VMD and LSTM. IEEE Access 2020, 8, 165849–165862. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B.; Pan, A.Q. A hierarchical sparrow search algorithm to solve numerical optimization and estimate parameters of carbon fiber drawing process. Artif. Intell. Rev. 2023, 56, 1113–1148. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Zheng, Z.W. A Novel Groundwater Burial Depth Prediction Model Based on Two-Stage Modal Decomposition and Deep Learning. Int. J. Environ. Res. Public Health 2023, 20, 345. [Google Scholar] [CrossRef] [PubMed]
- Sepulveda-Oviedo, E.H. Impact of environmental factors on photovoltaic system performance degradation. Energy Strategy Rev. 2025, 59, 101682. [Google Scholar] [CrossRef]
- Gueymard, C.A. A review of validation methodologies and statistical performance indicators for modeled solar radiation data: Towards a better bankability of solar projects. Renew. Sustain. Energy Rev. 2014, 39, 1024–1034. [Google Scholar] [CrossRef]







| K Is Too Large | K Is Small | α Is Too Large | α Is Small |
|---|---|---|---|
| Over-decomposition with overlapping center frequencies | Under-decomposition, loss of information | Useful information is eliminated | Redundant information is retained |
| Season | Data | Number of Data |
|---|---|---|
| Spring | 1 September 2019 to 30 November 2019 | 12,103 |
| Summer | 1 December 2018 to 28 February 2019 | 11,970 |
| Autumn | 1 March 2019 to 31 May 2019 | 12,103 |
| Winter | 1 June 2019 to 31 August 2019 | 12,103 |
| Season | GHI | DHI | RH | WS | Temp |
|---|---|---|---|---|---|
| Spring | 0.996 | 0.582 | −0.384 | −0.504 | 0.507 |
| Summer | 0.994 | 0.670 | −0.376 | −0.568 | 0.586 |
| Autumn | 0.988 | 0.580 | −0.412 | −0.208 | 0.482 |
| Winter | 0.991 | 0.598 | −0.455 | −0.122 | 0.535 |
| Model | Spring | Summer | Autumn | Winter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | ||
| CECSVB-LSTM | 5 min | 0.0992 | 0.0768 | 0.9965 | 0.0993 | 0.0641 | 0.9952 | 0.1309 | 0.0849 | 0.9927 | 0.0821 | 0.0706 | 0.9976 |
| 10 min | 0.1652 | 0.1179 | 0.9903 | 0.1770 | 0.1095 | 0.9850 | 0.1466 | 0.0969 | 0.9909 | 0.1110 | 0.0937 | 0.9957 | |
| CEEMDAN-SSA -VMD-BILSTM | 5 min | 0.5734 | 0.3468 | 0.8997 | 0.5231 | 0.3014 | 0.8830 | 0.3316 | 0.2794 | 0.9536 | 0.2494 | 0.2096 | 0.9784 |
| 10 min | 0.6461 | 0.3977 | 0.8728 | 0.6128 | 0.3708 | 0.8396 | 0.4707 | 0.4058 | 0.9067 | 0.3583 | 0.3039 | 0.9556 | |
| CEEMDAN-WOA -VMD-BILSTM | 5 min | 0.5409 | 0.2972 | 0.9099 | 0.4543 | 0.2545 | 0.9116 | 0.2839 | 0.2337 | 0.9655 | 0.4156 | 0.3732 | 0.9403 |
| 10 min | 0.6580 | 0.3799 | 0.8666 | 0.4866 | 0.2900 | 0.8986 | 0.4127 | 0.3455 | 0.9273 | 0.4604 | 0.3865 | 0.9268 | |
| CEEMDAN-PSO -VMD-BILSTM | 5 min | 0.5546 | 0.3201 | 0.9051 | 0.4757 | 0.2498 | 0.9033 | 0.2211 | 0.1766 | 0.9794 | 0.2702 | 0.2325 | 0.9746 |
| 10 min | 0.6583 | 0.4035 | 0.8661 | 0.5242 | 0.2999 | 0.8828 | 0.3078 | 0.2473 | 0.9602 | 0.3551 | 0.3084 | 0.9562 | |
| CEEMDAN-DBO -VMD-BILSTM | 5 min | 0.5448 | 0.3085 | 0.9081 | 0.5030 | 0.2495 | 0.8921 | 0.2620 | 0.2278 | 0.9708 | 0.2470 | 0.2199 | 0.9788 |
| 10 min | 0.6550 | 0.4020 | 0.8669 | 0.6133 | 0.3223 | 0.8403 | 0.3953 | 0.3405 | 0.9338 | 0.2599 | 0.2265 | 0.9766 | |
| Model | Spring | Summer | Autumn | Winter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | ||
| CECSVB-LSTM | 5 min | 0.0992 | 0.0768 | 0.9965 | 0.0993 | 0.0641 | 0.9952 | 0.1309 | 0.0849 | 0.9927 | 0.0821 | 0.0706 | 0.9976 |
| 10 min | 0.1652 | 0.1179 | 0.9903 | 0.1770 | 0.1095 | 0.9850 | 0.1466 | 0.0969 | 0.9909 | 0.1110 | 0.0937 | 0.9957 | |
| CEEMDAN-VMD-BILSTM | 5 min | 0.1772 | 0.1044 | 0.9887 | 0.1605 | 0.1214 | 0.9846 | 0.1693 | 0.1219 | 0.9878 | 0.1764 | 0.1536 | 0.9894 |
| 10 min | 0.3108 | 0.1882 | 0.9653 | 0.2374 | 0.1788 | 0.9663 | 0.2383 | 0.1732 | 0.9760 | 0.2034 | 0.1811 | 0.9859 | |
| VMD-BILSTM | 5 min | 0.2541 | 0.1935 | 0.9761 | 0.2433 | 0.2058 | 0.9675 | 0.2489 | 0.2143 | 0.9734 | 0.2931 | 0.2547 | 0.9704 |
| 10 min | 0.3156 | 0.2388 | 0.9630 | 0.2865 | 0.2494 | 0.9550 | 0.2931 | 0.2560 | 0.9631 | 0.3775 | 0.3268 | 0.9508 | |
| CEEMDAN-BILSTM | 5 min | 0.2923 | 0.1698 | 0.9715 | 0.2661 | 0.1969 | 0.9678 | 0.2183 | 0.1736 | 0.9798 | 0.2670 | 0.2379 | 0.9757 |
| 10 min | 0.3454 | 0.1960 | 0.9602 | 0.3211 | 0.2411 | 0.9531 | 0.2867 | 0.2332 | 0.9652 | 0.3112 | 0.2789 | 0.9670 | |
| BILSTM | 5 min | 0.5157 | 0.2987 | 0.9117 | 0.3920 | 0.2264 | 0.9302 | 0.4296 | 0.3563 | 0.9221 | 0.4125 | 0.3355 | 0.9421 |
| 10 min | 0.6400 | 0.3658 | 0.8639 | 0.4568 | 0.2654 | 0.9052 | 0.4783 | 0.4045 | 0.9034 | 0.4328 | 0.3749 | 0.9362 | |
| Model | Spring | Summer | Autumn | Winter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | ||
| CECSVB-LSTM | 5 min | 0.0992 | 0.0768 | 0.9965 | 0.0993 | 0.0641 | 0.9952 | 0.1309 | 0.0849 | 0.9927 | 0.0821 | 0.0706 | 0.9976 |
| 10 min | 0.1652 | 0.1179 | 0.9903 | 0.1770 | 0.1095 | 0.9850 | 0.1466 | 0.0969 | 0.9909 | 0.1110 | 0.0937 | 0.9957 | |
| BP | 5 min | 0.5068 | 0.2528 | 0.9146 | 0.3781 | 0.1700 | 0.9350 | 0.3635 | 0.2967 | 0.9442 | 0.4007 | 0.3541 | 0.9454 |
| 10 min | 0.6402 | 0.3648 | 0.8635 | 0.4479 | 0.2050 | 0.9086 | 0.3853 | 0.3194 | 0.9373 | 0.4201 | 0.3675 | 0.9399 | |
| ELM | 5 min | 0.6145 | 0.3811 | 0.8746 | 0.5018 | 0.3327 | 0.8856 | 0.2768 | 0.2011 | 0.9676 | 0.1865 | 0.1421 | 0.9881 |
| 10 min | 0.7263 | 0.4796 | 0.8248 | 0.5709 | 0.4095 | 0.8519 | 0.3251 | 0.2532 | 0.9554 | 0.2072 | 0.1588 | 0.9853 | |
| BILSTM | 5 min | 0.5157 | 0.2987 | 0.9117 | 0.3920 | 0.2264 | 0.9302 | 0.4296 | 0.3563 | 0.9221 | 0.4125 | 0.3355 | 0.9421 |
| 10 min | 0.6400 | 0.3658 | 0.8639 | 0.4568 | 0.2654 | 0.9052 | 0.4783 | 0.4045 | 0.9034 | 0.4328 | 0.3749 | 0.9362 | |
| BIGRU | 5 min | 0.5377 | 0.3001 | 0.9040 | 0.3981 | 0.2469 | 0.9280 | 0.1899 | 0.1380 | 0.9847 | 0.3222 | 0.2799 | 0.9646 |
| 10 min | 0.6613 | 0.3844 | 0.8548 | 0.4987 | 0.3385 | 0.8870 | 0.2420 | 0.1818 | 0.9752 | 0.4322 | 0.3705 | 0.9364 | |
| Model | Spring | Summer | Autumn | Winter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | ||
| CECSVB-LSTM | 5 min | 0.0992 | 0.0768 | 0.9965 | 0.0993 | 0.0641 | 0.9952 | 0.1309 | 0.0849 | 0.9927 | 0.0821 | 0.0706 | 0.9976 |
| 10 min | 0.1652 | 0.1179 | 0.9903 | 0.1770 | 0.1095 | 0.9850 | 0.1466 | 0.0969 | 0.9909 | 0.1110 | 0.0937 | 0.9957 | |
| CEEMDAN-BILSTM | 5 min | 0.2923 | 0.1698 | 0.9715 | 0.2661 | 0.1969 | 0.9678 | 0.2183 | 0.1736 | 0.9798 | 0.2670 | 0.2379 | 0.9757 |
| 10 min | 0.3454 | 0.1960 | 0.9602 | 0.3211 | 0.2411 | 0.9531 | 0.2867 | 0.2332 | 0.9652 | 0.3112 | 0.2789 | 0.9670 | |
| EEMD-BILSTM | 5 min | 0.3270 | 0.2393 | 0.9642 | 0.2751 | 0.1941 | 0.9656 | 0.2574 | 0.2201 | 0.9722 | 0.3040 | 0.2509 | 0.9688 |
| 10 min | 0.4058 | 0.2794 | 0.9449 | 0.3253 | 0.2219 | 0.9518 | 0.3198 | 0.2629 | 0.9571 | 0.3769 | 0.3158 | 0.9521 | |
| EMD-BILSTM | 5 min | 0.3402 | 0.2046 | 0.9615 | 0.2790 | 0.1862 | 0.9645 | 0.2832 | 0.2318 | 0.9661 | 0.3207 | 0.2833 | 0.9650 |
| 10 min | 0.4393 | 0.2046 | 0.9358 | 0.3659 | 0.2622 | 0.9388 | 0.3311 | 0.2555 | 0.9536 | 0.4491 | 0.2833 | 0.9314 | |
| VMD-BILSTM | 5 min | 0.2541 | 0.1935 | 0.9761 | 0.2433 | 0.2058 | 0.9675 | 0.2489 | 0.2143 | 0.9734 | 0.2931 | 0.2547 | 0.9704 |
| 10 min | 0.3156 | 0.2388 | 0.9630 | 0.2865 | 0.2494 | 0.9550 | 0.2931 | 0.2560 | 0.9631 | 0.3775 | 0.3268 | 0.9508 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, L.; Chen, W.; Lin, Z.; He, D.; Chen, J. Photovoltaic Power Generation Forecasting Based on Secondary Data Decomposition and Hybrid Deep Learning Model. Energies 2025, 18, 3136. https://doi.org/10.3390/en18123136
Zhang L, Liu L, Chen W, Lin Z, He D, Chen J. Photovoltaic Power Generation Forecasting Based on Secondary Data Decomposition and Hybrid Deep Learning Model. Energies. 2025; 18(12):3136. https://doi.org/10.3390/en18123136
Chicago/Turabian StyleZhang, Liwei, Lisang Liu, Wenwei Chen, Zhihui Lin, Dongwei He, and Jian Chen. 2025. "Photovoltaic Power Generation Forecasting Based on Secondary Data Decomposition and Hybrid Deep Learning Model" Energies 18, no. 12: 3136. https://doi.org/10.3390/en18123136
APA StyleZhang, L., Liu, L., Chen, W., Lin, Z., He, D., & Chen, J. (2025). Photovoltaic Power Generation Forecasting Based on Secondary Data Decomposition and Hybrid Deep Learning Model. Energies, 18(12), 3136. https://doi.org/10.3390/en18123136






