Thermal-Hydrologic-Mechanical Processes and Effects on Heat Transfer in Enhanced/Engineered Geothermal Systems
Abstract
1. Introduction
2. Mathematical Model for Fluid/Heat Flow and Geomechanics
2.1. Mass Balance Equations
2.2. Energy Balance Equations
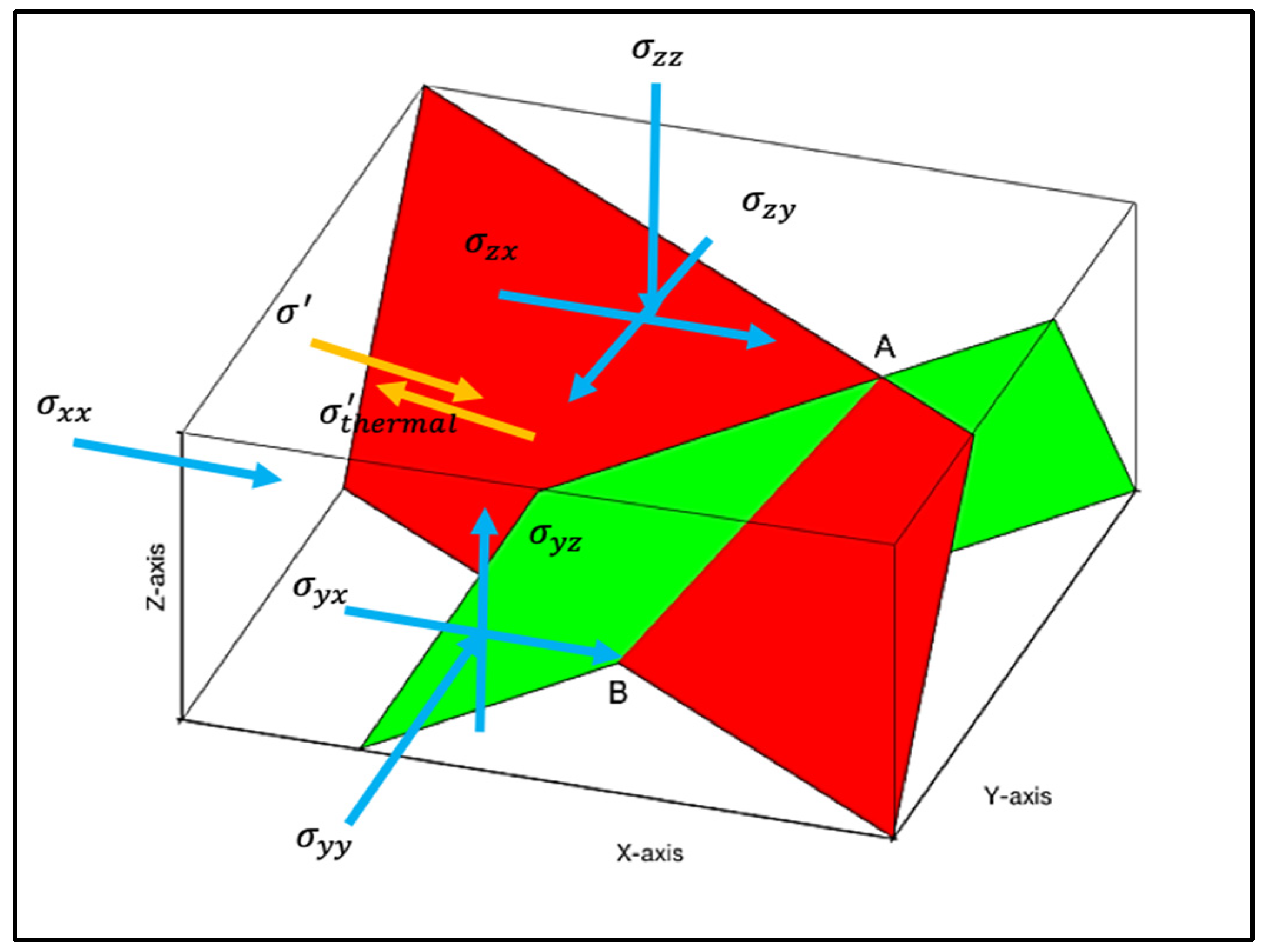
2.3. Momentum Balance Equations
3. Numerical Solution Techniques
3.1. Numerical Discretization of Space and Time
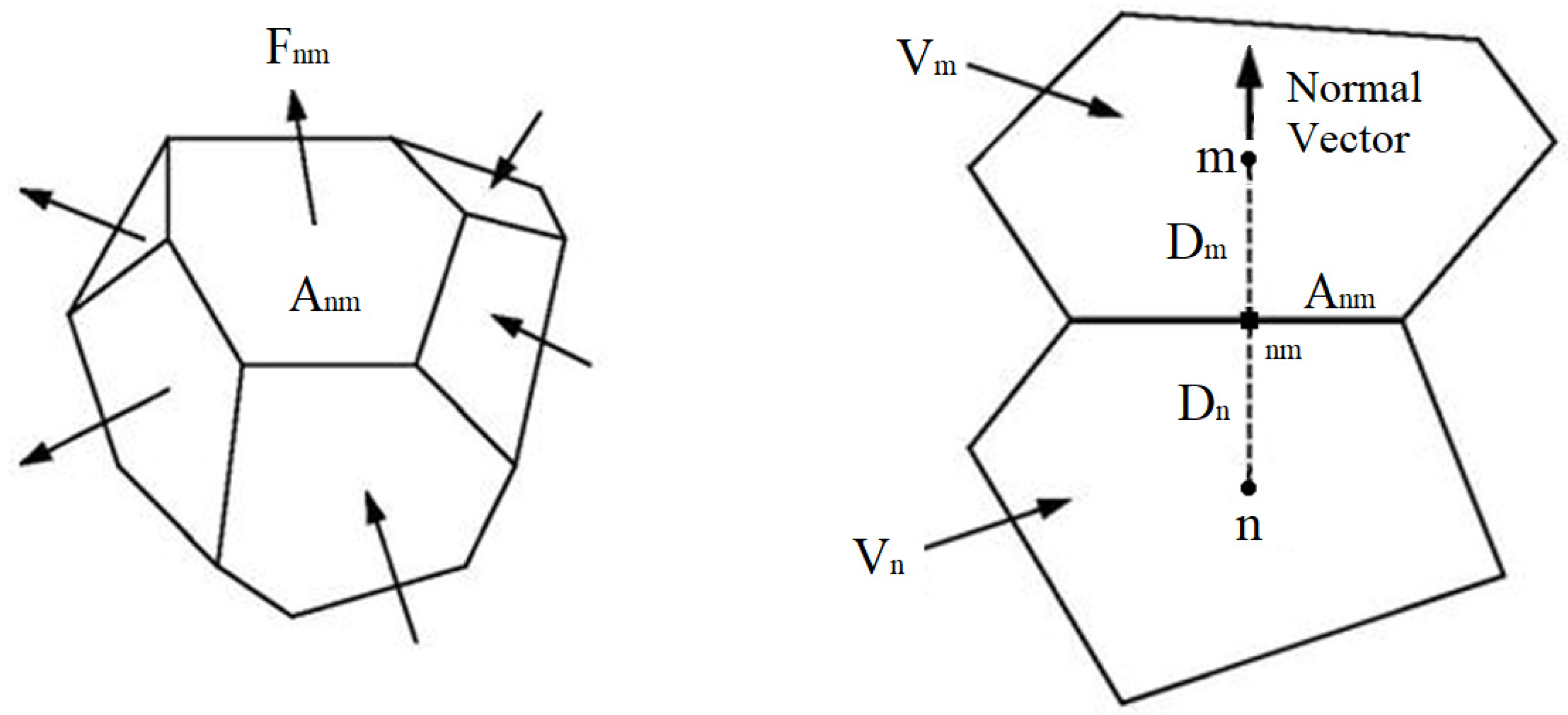
3.1.1. Discretization of Mass and Energy Balance Equations
3.1.2. Discretization of Momentum Balance Equation
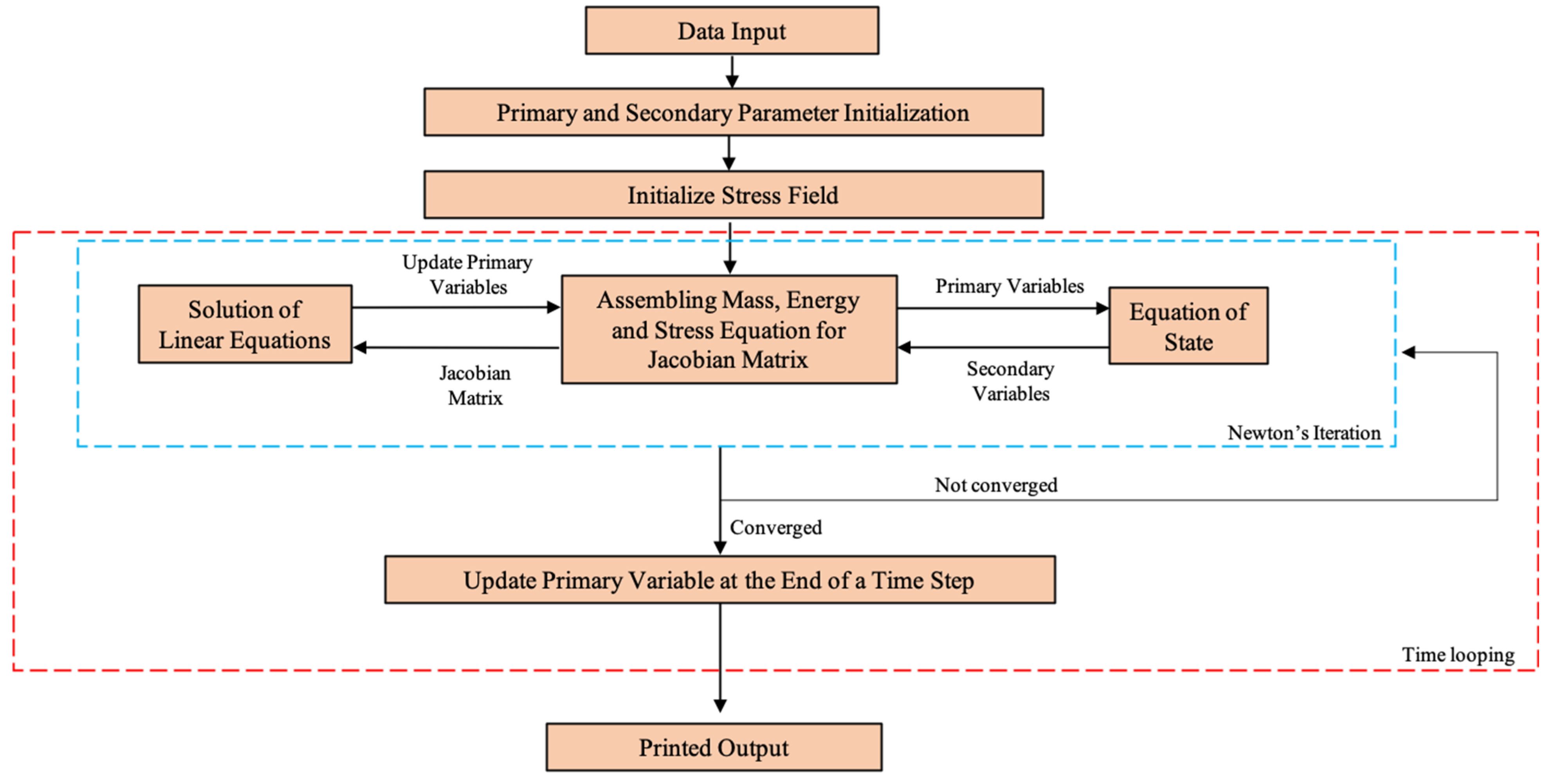
3.2. Numerical Solution Approach
4. Model Validation
4.1. Validation Using an Existing Simulation Case
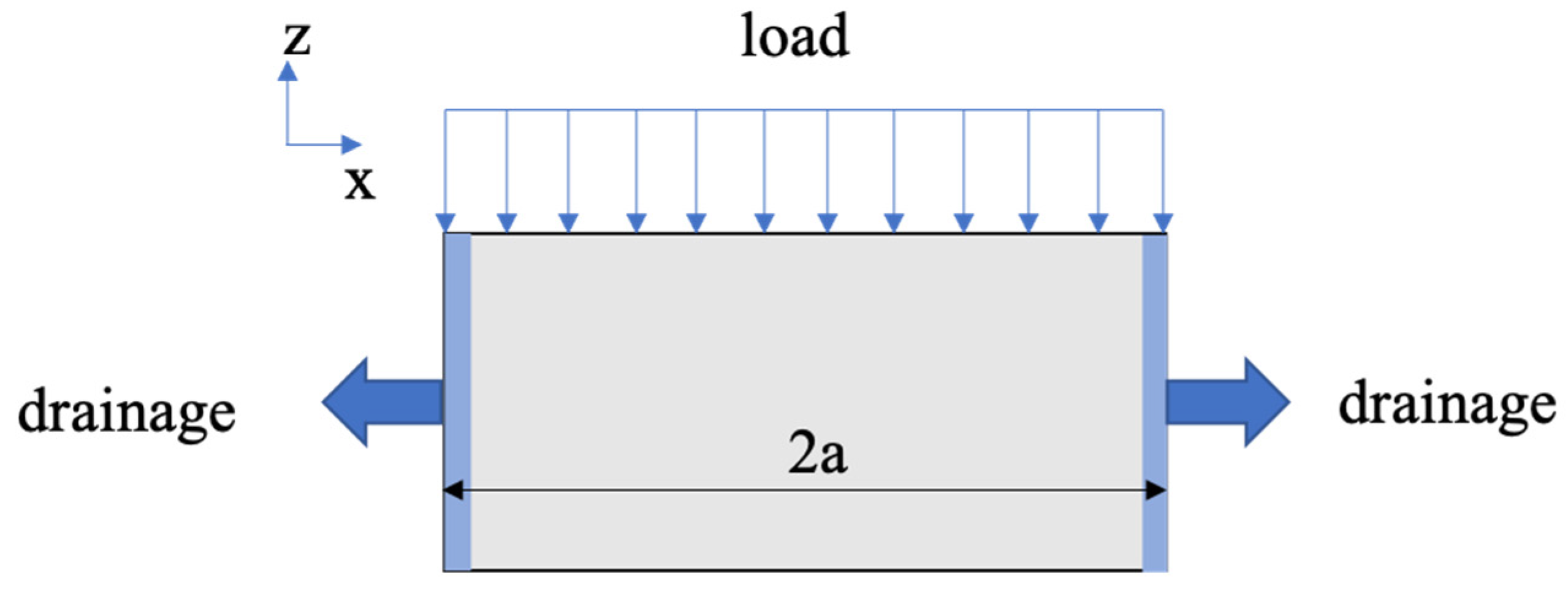
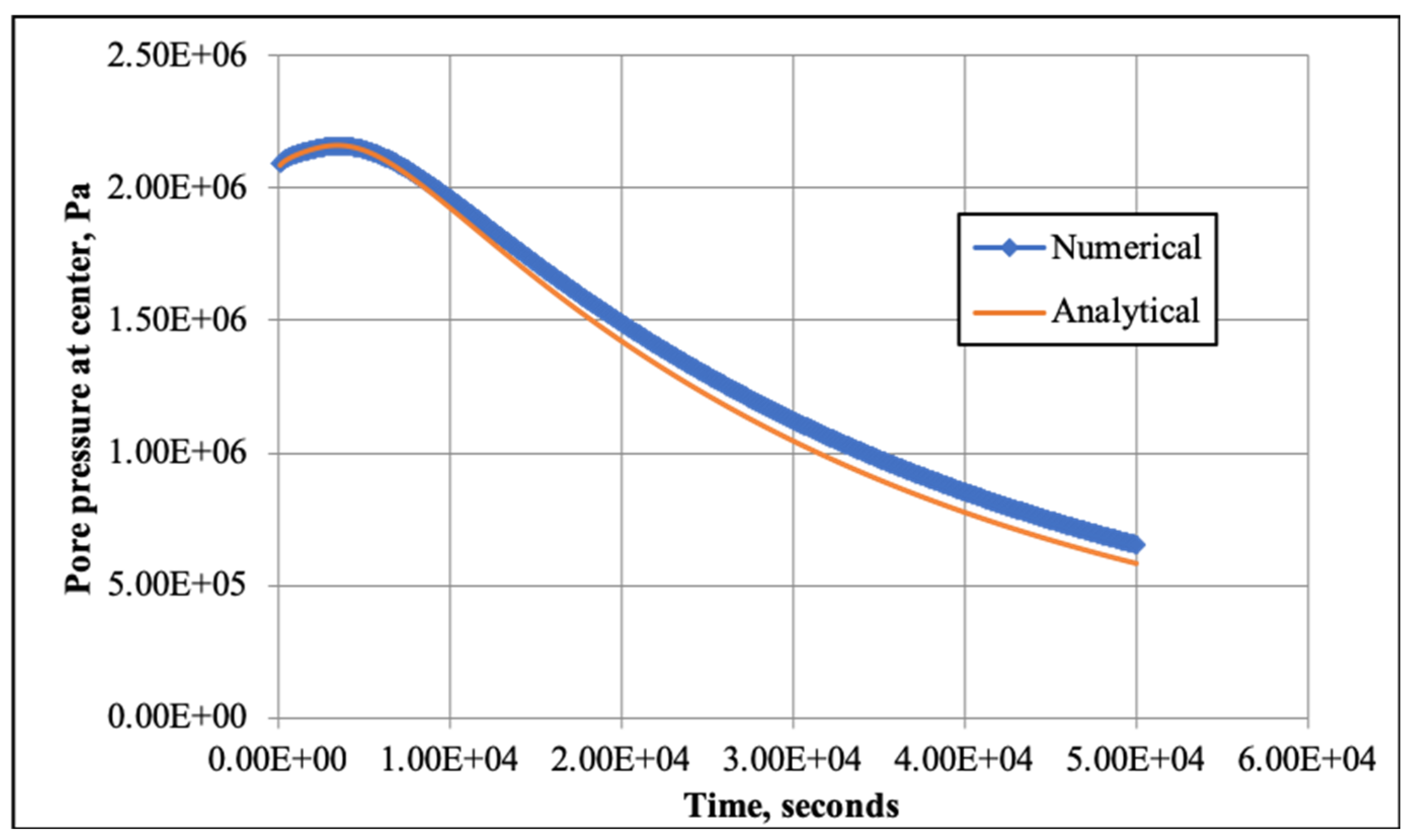
4.2. Validation Using an Analytical Solution
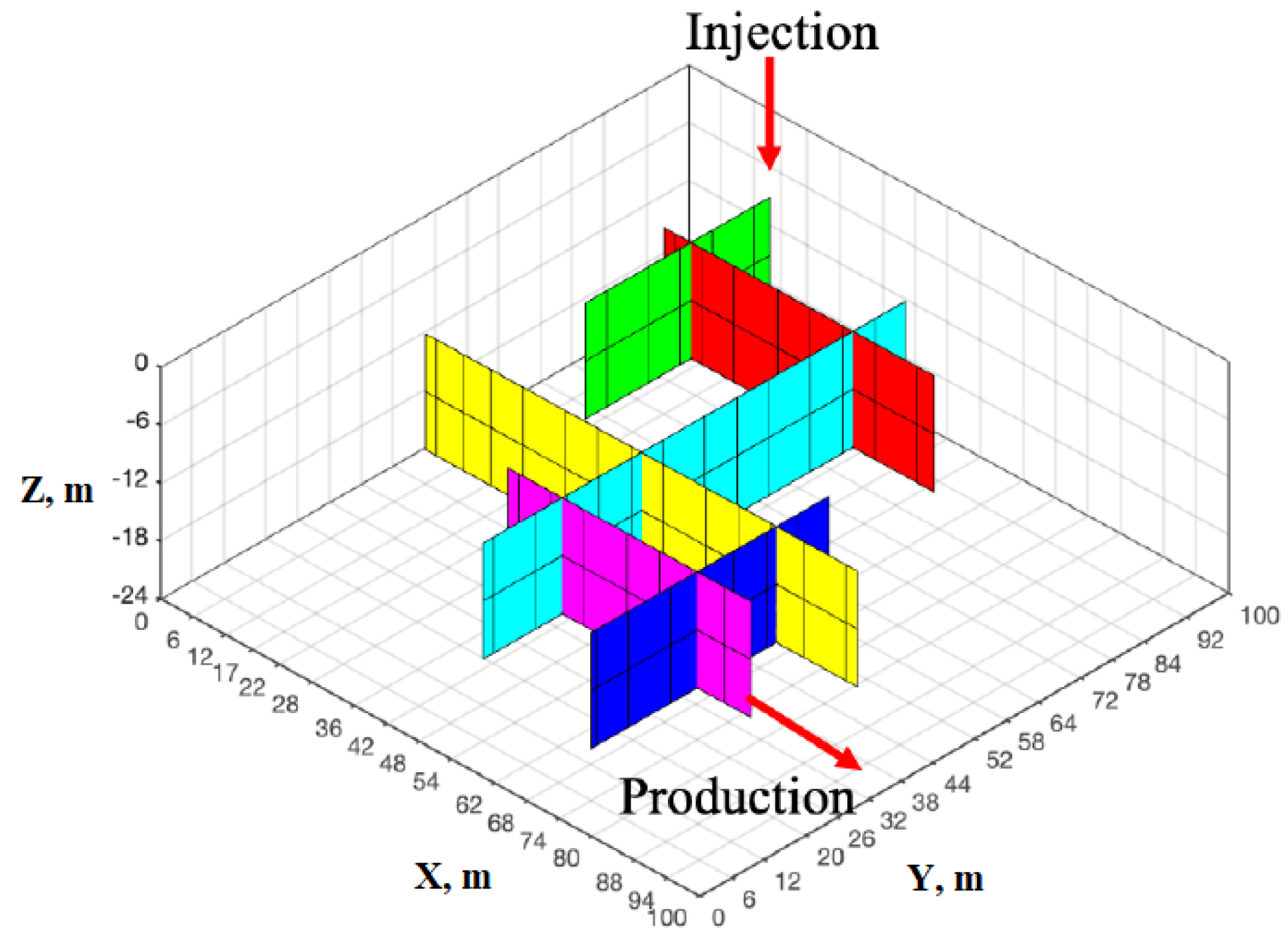
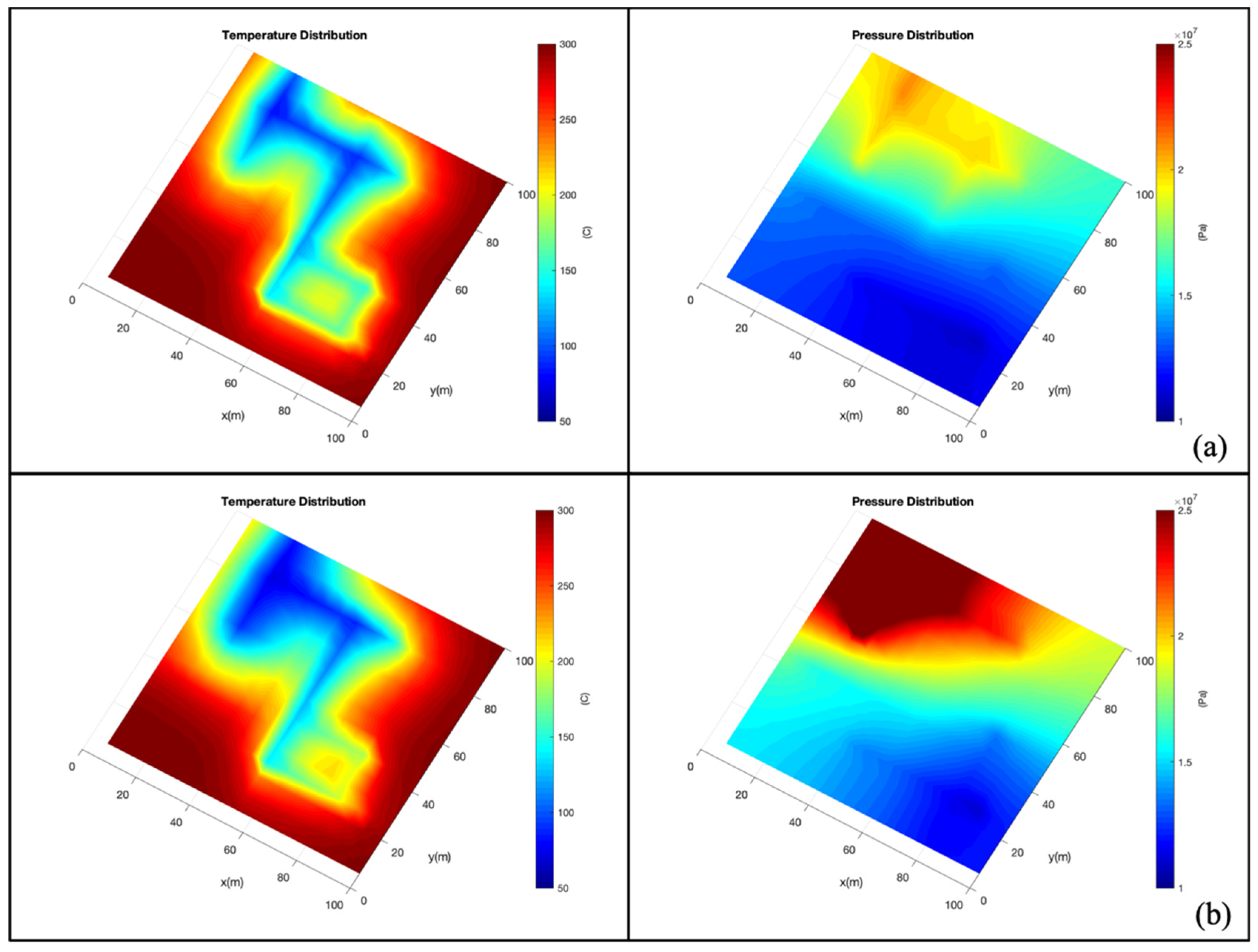
5. Model Application into Geothermal Reservoir Simulation
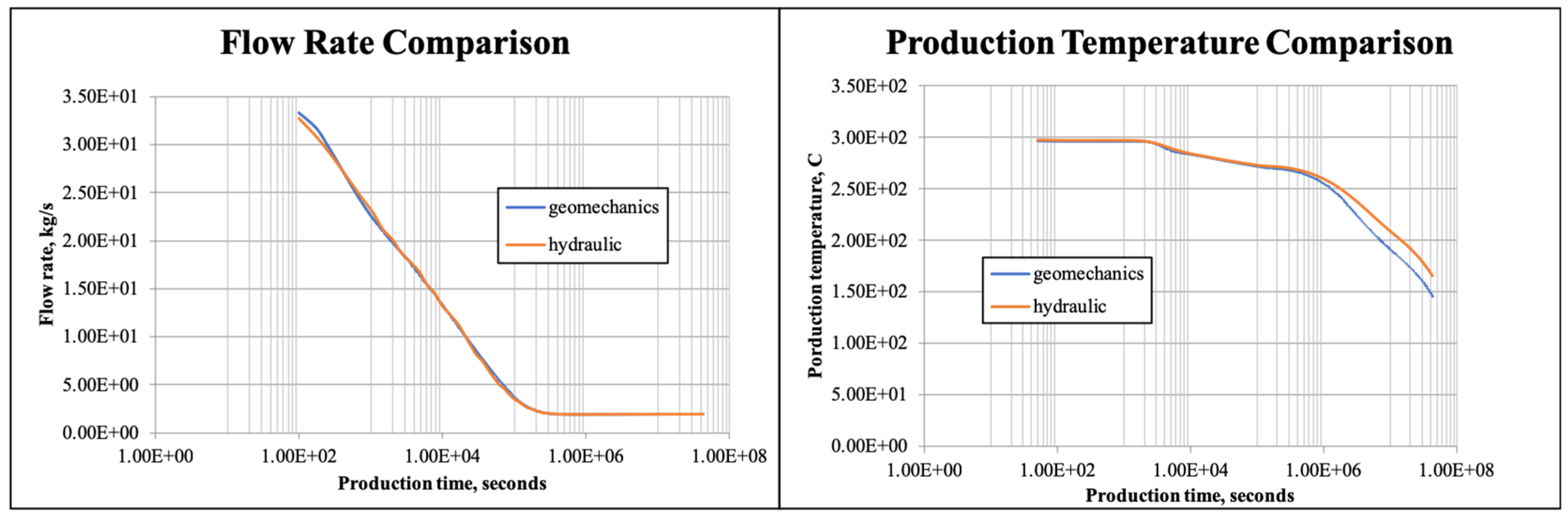
5.1. Coupled THM Model with Double-Porosity Approach
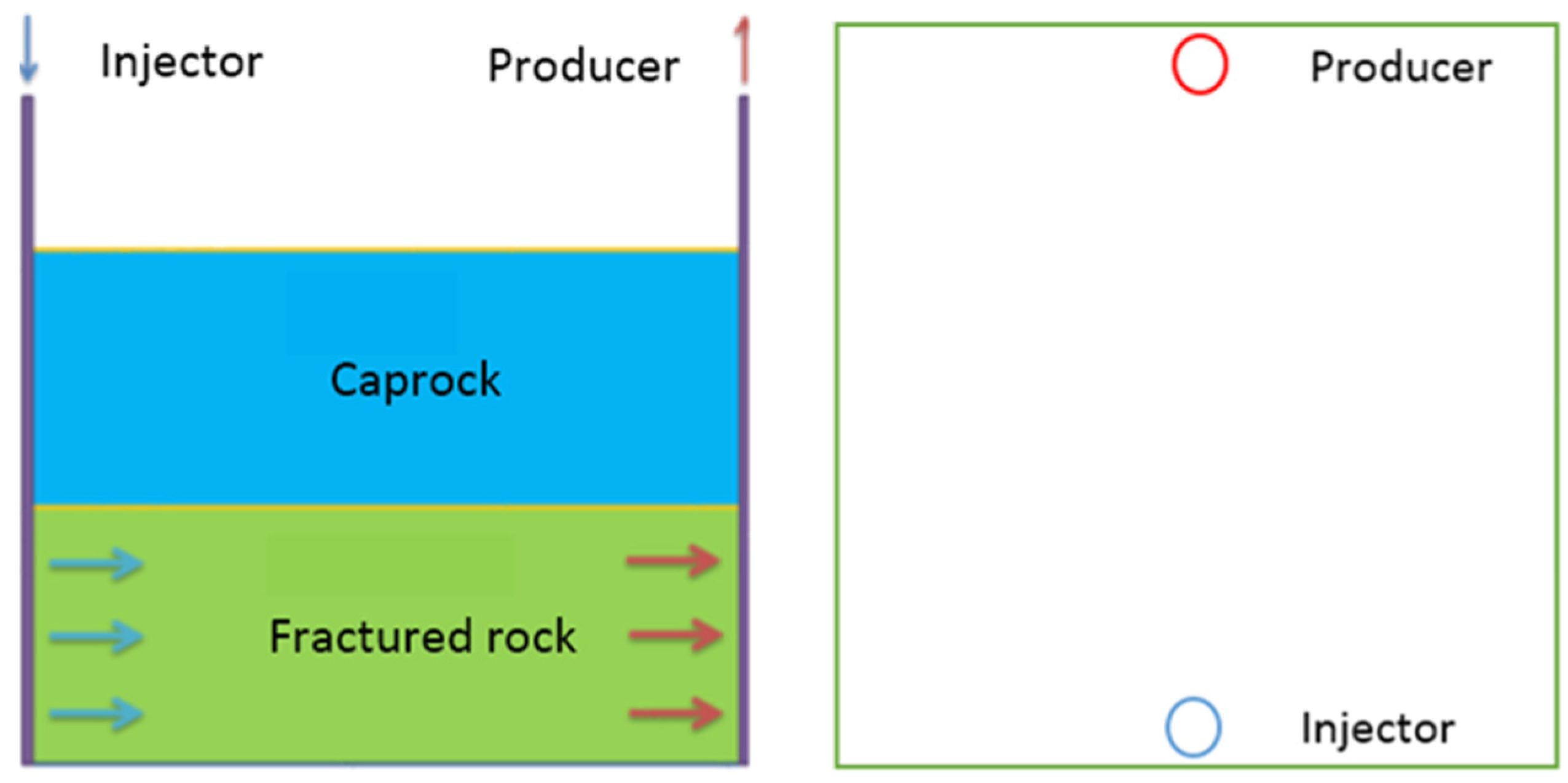
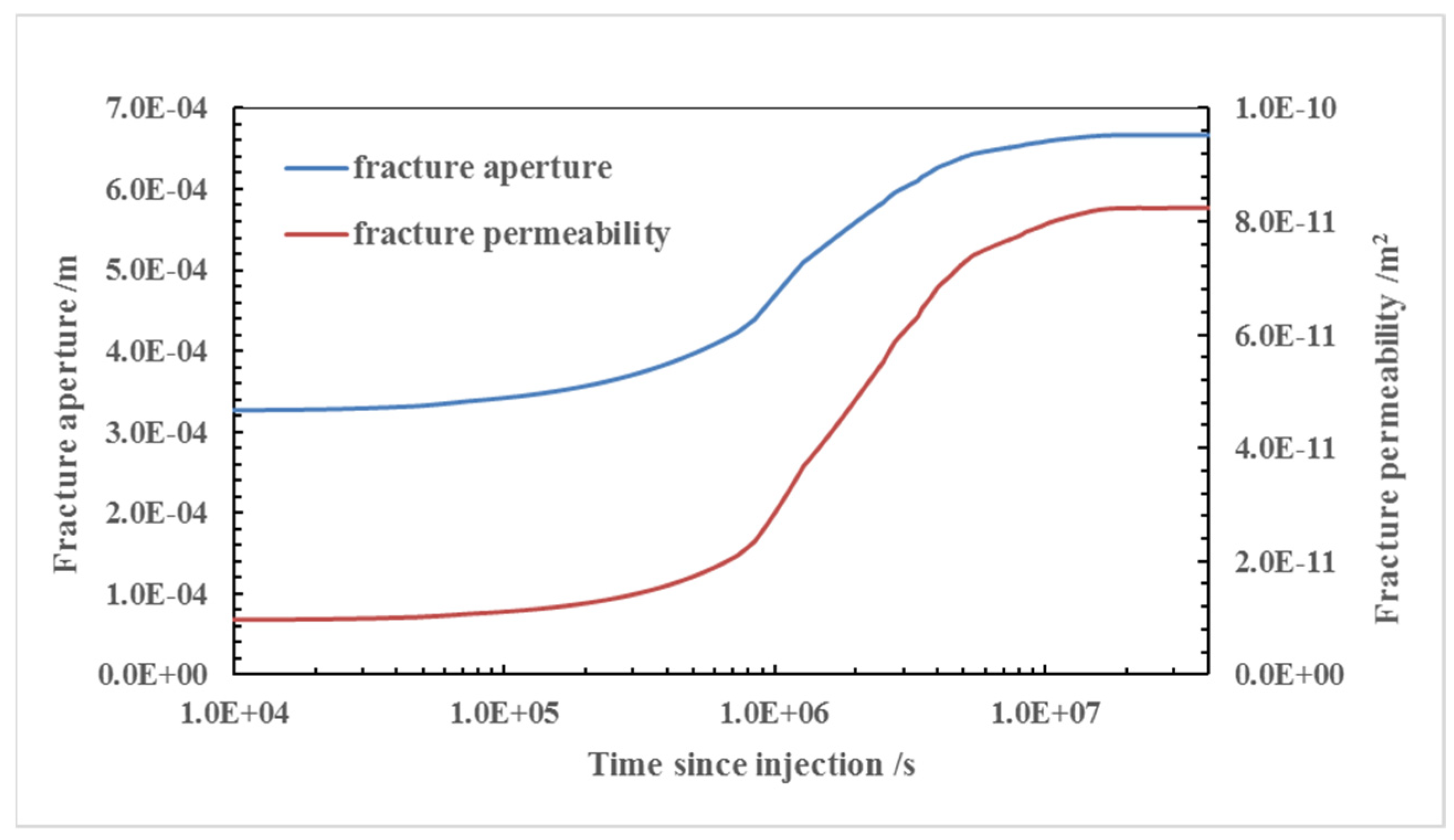
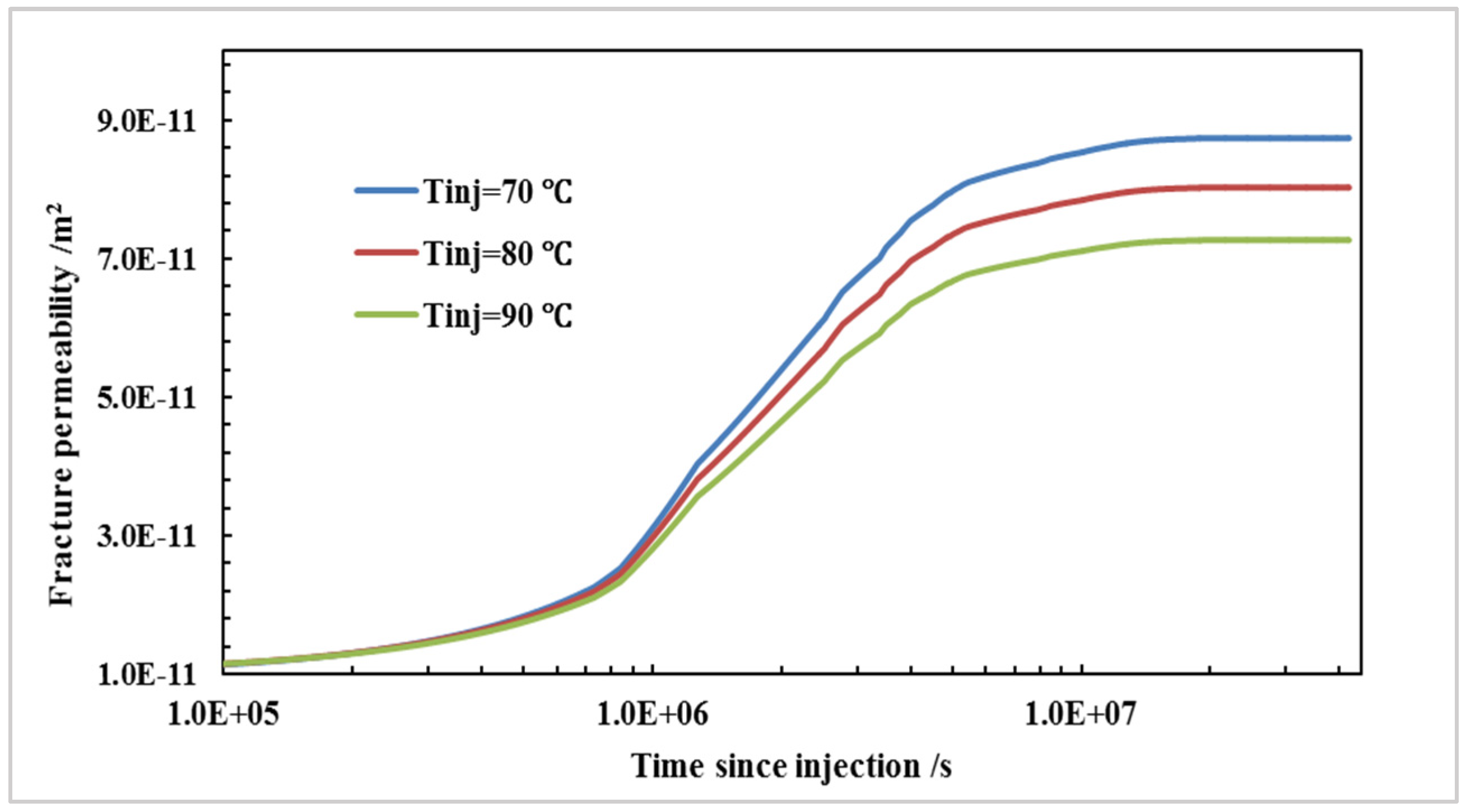
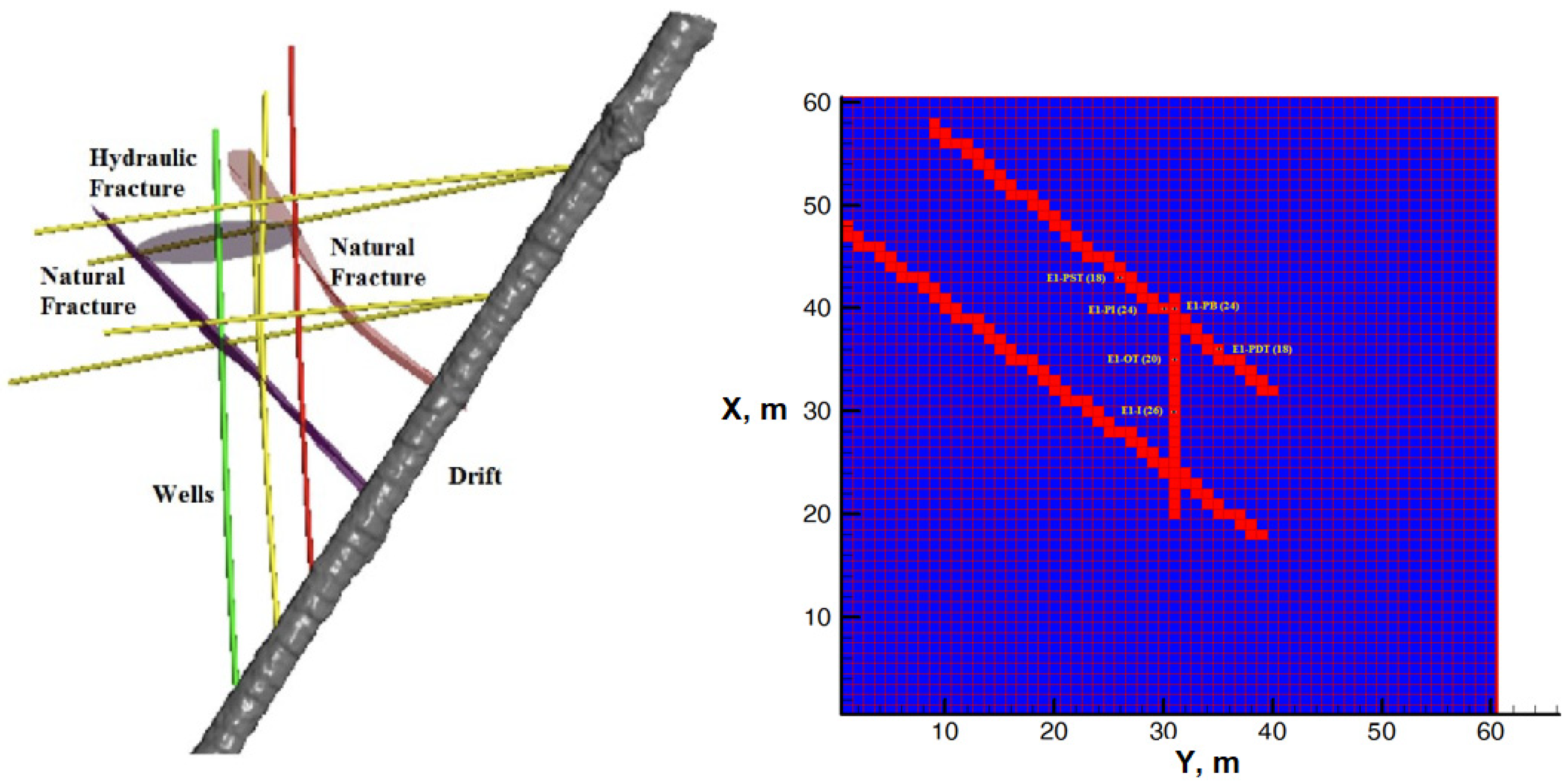
5.2. Coupled THM Model with EDFM for Fracture Mechanics
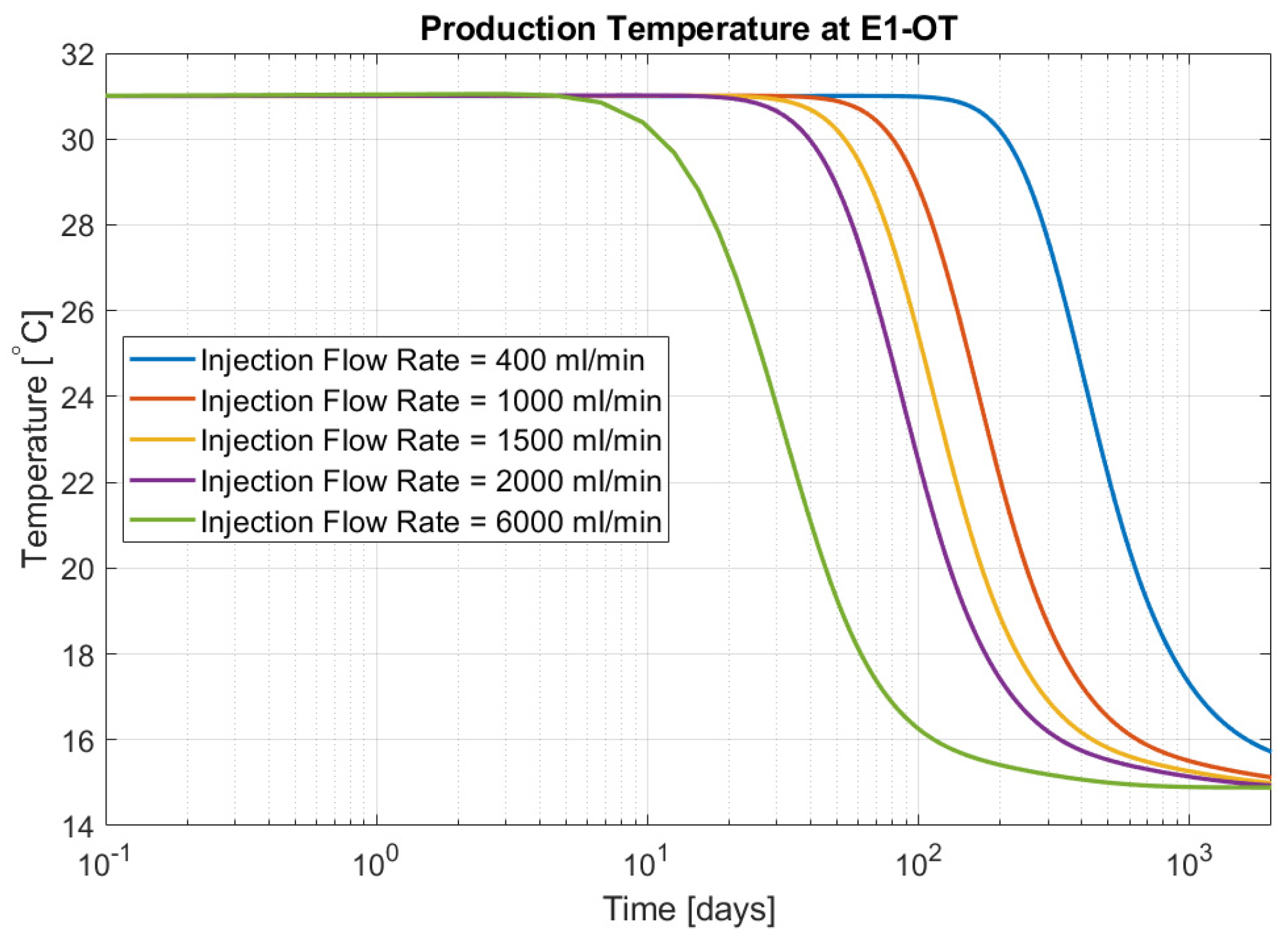
5.3. Coupled TH Model with EDFM for Tracer Transport
6. Summary and Conclusions
Funding
Conflicts of Interest
References
- Gens, A.; Guimaräes, L.D.N.; Olivella, S.; Sánchez, M. Modelling Thermo-Hydro-Mechano-Chemical Interactions for Nuclear Waste Disposal. J. Rock Mech. Geotech. Eng. 2010, 2, 97–102. [Google Scholar] [CrossRef]
- Huang, Z.-Q.; Winterfeld, P.H.; Xiong, Y.; Wu, Y.-S.; Yao, J. Parallel Simulation of Fully-Coupled Thermal-Hydro-Mechanical Processes in CO2 Leakage through Fluid-Driven Fracture Zones. Int. J. Greenh. Gas Control 2015, 34, 39–51. [Google Scholar] [CrossRef]
- Cappa, F.; Rutqvist, J. Modeling of Coupled Deformation and Permeability Evolution during Fault Reactivation Induced by Deep Underground Injection of CO2. Int. J. Greenh. Gas Control 2011, 5, 336–346. [Google Scholar] [CrossRef]
- Lei, H.; Xu, T.; Jin, G. TOUGH2Biot—A Simulator for Coupled Thermal-Hydrodynamic-Mechanical Processes in Subsurface Flow Systems: Application to CO2 Geological Storage and Geothermal Development. Comput. Geosci. 2015, 77, 8–19. [Google Scholar] [CrossRef]
- Rutqvist, J. Status of the TOUGH-FLAC Simulator and Recent Applications Related to Coupled Fluid Flow and Crustal Deformations. Comput. Geosci. 2011, 37, 739–750. [Google Scholar] [CrossRef]
- Taron, J.; Elsworth, D. Thermal-Hydrologic-Mechanical-Chemical Processes in the Evolution of Engineered Geothermal Reservoirs. Int. J. Rock Mech. Min. Sci. 2009, 46, 855–864. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, X.; Sun, Z.; Huang, Z.; Liu, J.; Li, Y.; Xin, Y.; Yan, X.; Liu, W. Numerical Simulation of the Heat Extraction in 3D-EGS with Thermal-Hydraulic-Mechanical Coupling Method Based on Discrete Fractures Model. Geothermics 2018, 74, 19–34. [Google Scholar] [CrossRef]
- Taron, J.; Elsworth, D. Coupled Mechanical and Chemical Processes in Engineered Geothermal Reservoirs with Dynamic Permeability. Int. J. Rock Mech. Min. Sci. 2010, 47, 1339–1348. [Google Scholar] [CrossRef]
- Taron, J.; Elsworth, D.; Min, K.-B. Numerical Simulation of Thermal-Hydrologic-Mechanical-Chemical Processes in Deformable, Fractured Porous Media. Int. J. Rock Mech. Min. Sci. 2009, 46, 842–854. [Google Scholar] [CrossRef]
- Pandey, S.N.; Chaudhuri, A.; Kelkar, S. A Coupled Thermo-Hydro-Mechanical Modeling of Fracture Aperture Alteration and Reservoir Deformation during Heat Extraction from a Geothermal Reservoir. Geothermics 2017, 65, 17–31. [Google Scholar] [CrossRef]
- Hofmann, H.; Babadagli, T.; Yoon, J.S.; Blöcher, G.; Zimmermann, G. A Hybrid Discrete/Finite Element Modeling Study of Complex Hydraulic Fracture Development for Enhanced Geothermal Systems (EGS) in Granitic Basements. Geothermics 2016, 64, 362–381. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Z.; Wu, Y.-S.; Winterfeld, P.H.; Zerpa, L.E. A Semi-Analytical Correlation of Thermal-Hydraulic-Mechanical Behavior of Fractures and Its Application to Modeling Reservoir Scale Cold Water Injection Problems in Enhanced Geothermal Reservoirs. Geothermics 2016, 64, 81–95. [Google Scholar] [CrossRef]
- Cao, W.; Huang, W.; Jiang, F. A Novel Thermal–Hydraulic–Mechanical Model for the Enhanced Geothermal System Heat Extraction. Int. J. Heat Mass Transf. 2016, 100, 661–671. [Google Scholar] [CrossRef]
- Garipov, T.T.; Tomin, P.; Rin, R.; Voskov, D.V.; Tchelepi, H.A. Unified Thermo-Compositional-Mechanical Framework for Reservoir Simulation. Comput. Geosci. 2018, 22, 1039–1057. [Google Scholar] [CrossRef]
- Pandey, S.N.; Vishal, V.; Chaudhuri, A. Geothermal Reservoir Modeling in a Coupled Thermo-Hydro-Mechanical-Chemical Approach: A Review. Earth-Sci. Rev. 2018, 185, 1157–1169. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability, Accuracy and Efficiency of Sequential Methods for Coupled Flow and Geomechanics. In Proceedings of the SPE Reservoir Simulation Symposium: Society of Petroleum Engineers, The Woodlands, TX, USA, 2–4 February 2009. [Google Scholar]
- Jha, B.; Juanes, R. A Locally Conservative Finite Element Framework for the Simulation of Coupled Flow and Reservoir Geomechanics. Acta Geotech. 2007, 2, 139–153. [Google Scholar] [CrossRef]
- Min, K.-B.; Rutqvist, J.; Tsang, C.-F.; Jing, L. Stress-Dependent Permeability of Fractured Rock Masses: A Numerical Study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
- Rutqvist, J.; Wu, Y.-S.; Tsang, C.-F.; Bodvarsson, G. A Modeling Approach for Analysis of Coupled Multiphase Fluid Flow, Heat Transfer, and Deformation in Fractured Porous Rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability and Convergence of Sequential Methods for Coupled Flow and Geomechanics: Fixed-Stress and Fixed-Strain Splits. Comput. Methods Appl. Mech. Eng. 2011, 200, 1591–1606. [Google Scholar] [CrossRef]
- Dean, R.H.; Gai, X.; Stone, C.M.; Minkoff, S.E. A Comparison of Techniques for Coupling Porous Flow and Geomechanics. SPE J. 2006, 11, 132–140. [Google Scholar] [CrossRef]
- Mikelić, A.; Wheeler, M.F. Convergence of Iterative Coupling for Coupled Flow and Geomechanics. Comput. Geosci. 2013, 17, 455–461. [Google Scholar] [CrossRef]
- Wang, W.; Kosakowski, G.; Kolditz, O. A Parallel Finite Element Scheme for Thermo-Hydro-Mechanical (THM) Coupled Problems in Porous Media. Comput. Geosci. 2009, 35, 1631–1641. [Google Scholar] [CrossRef]
- Hu, L.; Winterfeld, P.H.; Fakcharoenphol, P.; Wu, Y.-S. A Novel Fully-Coupled Flow and Geomechanics Model in Enhanced Geothermal Reservoirs. J. Pet. Sci. Eng. 2013, 107, 1–11. [Google Scholar] [CrossRef]
- Winterfeld, P.H.; Wu, Y.-S. Simulation of Coupled Thermal/Hydrological/Mechanical Phenomena in Porous Media. SPE J. 2016, 21, 1041–1049. [Google Scholar] [CrossRef]
- Yu, X.; Wang, S.; Wu, Y.-S. Performance Evaluation of a Physics-Based Multi-Stage Preconditioner in Numerical Simulation of Coupled Fluid and Heat Flow in Porous Media. In Proceedings of the 44th Stanford Geothermal Workshop Proceedings, Stanford, CA, USA, 11–13 February 2019. [Google Scholar]
- Lacroix, S.; Vassilevski, Y.V.; Wheeler, M.F. Decoupling Preconditioners in the Implicit Parallel Accurate Reservoir Simulator (IPARS). Numer. Linear Algebra Appl. 2001, 8, 537–549. [Google Scholar] [CrossRef]
- Cusini, M.; Lukyanov, A.A.; Natvig, J.; Hajibeygi, H. Constrained Pressure Residual Multiscale (CPR-MS) Method for Fully Implicit Simulation of Multiphase Flow in Porous Media. J. Comput. Phys. 2015, 299, 472–486. [Google Scholar] [CrossRef]
- Cao, H.; Tchelepi, H.A.; Wallis, J.R.; Yardumian, H.E. Parallel Scalable Unstructured CPR-Type Linear Solver for Reservoir Simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition: Society of Petroleum Engineers, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Liu, H.; Wang, K.; Chen, Z.; Jordan, K.E. Efficient Multi-Stage Preconditioners for Highly Heterogeneous Reservoir Simulations on Parallel Distributed Systems. In Proceedings of the SPE Reservoir Simulation Symposium: Society of Petroleum Engineers, Houston, TX, USA, 23–25 February 2015. [Google Scholar]
- Winterfeld, P.H.; Wu, Y.-S. A Novel Fully Coupled Geomechanical Model for CO2 Sequestration in Fractured and Porous Brine Aquifers. In Proceedings of the XIX International Conference on Water Resources: University of Illinois at Urbana-Champagne, Urbana, IL, USA, 17–21 June 2012. [Google Scholar]
- Yu, X.; Winterfeld, P.; Wang, S.; Wang, C.; Wang, L.; Wu, Y. A Geomechanics-Coupled Embedded Discrete Fracture Model and Its Application in Geothermal Reservoir Simulation. In Proceedings of the SPE Reservoir Simulation Conference: Society of Petroleum Engineers, Galveston, TX, USA, 10–11 April 2019. [Google Scholar]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Kazemi, H.; Merrill, L.S.; Porterfield, K.L.; Zeman, P.R. Numerical Simulation of Water-Oil Flow in Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1976, 16, 317–326. [Google Scholar] [CrossRef]
- Wu, Y.-S. On the Effective Continuum Method for Modeling Multiphase Flow, Multicomponent Transport, and Heat Transfer in Fractured Rock. Am. Geophys. Union (AGU) 2000, 122, 299–312. [Google Scholar]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of a Coupled Dual Continuum and Discrete Fracture Model for the Simulation of Unconventional Reservoirs. In Proceedings of the SPE Reservoir Simulation Symposium: Society of Petroleum Engineers, The Woodlands, TX, USA, 18–20 February 2013. [Google Scholar]
- Lee, S.H.; Lough, M.F.; Jensen, C.L. Hierarchical Modeling of Flow in Naturally Fractured Formations with Multiple Length Scales. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient Field-Scale Simulation for Black Oil in a Naturally Fractured Reservoir via Discrete Fracture Networks and Homogenized Media. In Proceedings of the International Oil & Gas Conference and Exhibition in China: Society of Petroleum Engineers, Beijing, China, 5–7 December 2006. [Google Scholar]
- Horne, R.N.; Rodriguez, F. Dispersion in Tracer Flow in Fractured Geothermal Systems. Geophys. Res. Lett. 1983, 10, 289–292. [Google Scholar] [CrossRef]
- Kocabas, I. Geothermal Reservoir Characterization via Thermal Injection Backflow and Interwell Tracer Testing. Geothermics 2005, 34, 27–46. [Google Scholar] [CrossRef]
- Shook, G.M. Predicting Thermal Breakthrough in Heterogeneous Media from Tracer Tests. Geothermics 2001, 30, 573–589. [Google Scholar] [CrossRef]
- Winterfeld, P.; Johnston, B.; Beckers, K.; Wu, Y.-S.; The EGS Collab Team. Code Modifications for Modeling Chemical Tracers and Embedded Natural Fractures at EGS Collab. In Proceedings of the 44th Stanford Geothermal Workshop Proceedings, Stanford, CA, USA, 11–13 February 2019. [Google Scholar]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, Version 2; Earth Sciences Division, Lawrence Berkeley National Laboratory University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Zhang, K.; Wu, Y.-S.; Pruess, K. User’s Guide for TOUGH2-MP—A Massively Parallel Version of the TOUGH2 Code. In LBNL-315E, Earth Sciences Division; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2008. [Google Scholar]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R. Fundamentals of Rock Mechanics; Blackwell Publishing: Oxford, UK, 2007; ISBN 1444308912. [Google Scholar]
- Winterfeld, P.H.; Wu, Y.-S. An Overview of Our Coupled Thermal-Hydrological-Mechanical Simulator for Porous and Fractured Media. In Proceedings of the ARMA 20-1252, in 54th US Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 28 June–1 July 2020. [Google Scholar]
- Winterfeld, P.H.; Wu, Y.-S. Parallel Simulation of CO2 Sequestration with Rock Deformation in Saline Aquifers. In Proceedings of the SPE Reservoir Simulation Symposium: Society of Petroleum Engineers, The Woodlands, TX, USA, 21–23 February 2011. [Google Scholar]
- Karypis, G.; Kumar, V. A Parallel Algorithm for Multilevel Graph Partitioning and Sparse Matrix Ordering. J. Parallel Distrib. Comput. 1998, 48, 71–85. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs. Siam J. Sci. Comput. 1999, 20, 359–392. [Google Scholar] [CrossRef]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P. PETSc User’s Manual; Argonne National Laboratory: Argonne, IL, USA, 2019. [Google Scholar]
- Rutqvist, J.; Vasco, D.W.; Myer, L. Coupled Reservoir-Geomechanical Analysis of CO2 Injection and Ground Deformations at In Salah, Algeria. Int. J. Greenh. Gas Control 2010, 4, 225–230. [Google Scholar] [CrossRef]
- Itasca. FLAC3D, Fast Lagrangian Analysis of Continua in 3-Dimensions, Version 4.0; Itasca Consulting Group: Minneapolis, MN, USA, 2009.
- Mandel, J. Consolidation Des Sols (Étude Mathématique). Géotechnique 1953, 3, 287–299. [Google Scholar] [CrossRef]
- Abousleiman, Y.; Cheng, A.H.-D.; Cui, L.; Detournay, E.; Roegiers, J.-C. Mandel’s problem revisited. Géotechnique 1996, 46, 187–195. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.Y.; Iwai, K.; Gale, J.E. Validity of Cubic Law for Fluid Flow in a Deformable Rock Fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases Through Porous Media; Academic Press: Cambridge, MA, USA, 1956. [Google Scholar]
- Gutierrez, M.; Lewis, R.W.; Masters, I. Petroleum Reservoir Simulation Coupling Fluid Flow and Geomechanics. SPE Reserv. Eval. Eng. 2001, 4, 164–172. [Google Scholar] [CrossRef]




| Parameters | Shallow Overburden (0–900 m) | Caprock (900–1800 m) | Injection Zone (1800–1820 m) | Base (>1820 m) |
|---|---|---|---|---|
| Young’s modulus (GPa) | 1.5 | 20.0 | 6.0 | 20.0 |
| Poisson’s ratio | 0.2 | 0.15 | 0.2 | 0.15 |
| Biot’s coefficient | 1.0 | 1.0 | 1.0 | 1.0 |
| Porosity | 0.1 | 0.01 | 0.17 | 0.01 |
| Permeability (m2) | 1.0 × 10−17 | 1.0 × 10−19 | 0.875 × 10−14 | 1.0 × 10−21 |
| Residual CO2 saturation | 0.05 | 0.05 | 0.05 | 0.05 |
| Residual liquid saturation | 0.3 | 0.3 | 0.3 | 0.3 |
| CO2 injection rate (kg/s) | 9.734 | |||
| Initial injection well pressure (MPa) | 18.5 | |||
| Injection time (years) | 3 |
| Parameters | Value | Unit |
|---|---|---|
| Matrix permeability | 1 × 10−13 | m2 |
| Initial pore pressure | 1× 105 | Pa |
| Initial sample temperature | 60 | °C |
| Production (constant pressure) | 1× 105 | Pa |
| Rock/fracture porosity | 0.094 | Unitless |
| Production well index | 1.7 × 10−9 | m3 |
| Rock expansion coefficient | 4 × 10−6 | 1/°C |
| Poisson’s ratio | 0.25 | Unitless |
| Young’s modulus | 5 | GPa |
| Biot’s coefficient | 1 | Unitless |
| Water viscosity (@ 60 °C, analytical) | 0.00046 | Pa-s |
| Water compressibility (analytical) | 4.04 × 10−10 | 1/Pa |
| Water density (analytical) | 983 | kg/m3 |
| Properties | Values | Units |
|---|---|---|
| Initial permeability of the fracture continuum | Kf = 1.0 × 10−11 | m2 |
| Initial permeability of the matrix continuum | Kmx = 1.0 × 10−15 | m2 |
| Porosity of the matrix at zero stress | 0.04 | dimensionless |
| Residual porosity of the matrix | 0.01 | dimensionless |
| Parameter a for porosity | 1 × 10-8 | dimensionless |
| Initial porosity of the fracture | 0.001 | dimensionless |
| Young’s modulus | 66.0 | GPa |
| Fracture spacing | 0.3 | m |
| Poisson’s ratio | 0.25 | dimensionless |
| Biot’s coefficient | 0.7 | dimensionless |
| Linear thermal expansion coefficient | 7.9 | 10−6 m/(m K) |
| Thermal conductivity of dry rock | 1.0 | W/(m K) |
| Heat capacity of rock | 1000 | J/(kg K) |
| Density of rock | 2.5 | 103 kg/m3 |
| Vertical stress | 90 | MPa |
| Maximum horizontal stress | 140 | MPa |
| Minimum horizontal stress | 110 | MPa |
| Fracture stiffness | 4 | GPa/m |
| Parameters | Value | Unit |
|---|---|---|
| Matrix permeability | 2 × 10−16 | m2 |
| Fracture permeability | 2 × 10−11 | m2 |
| Initial reservoir pressure | 4.53 × 107 | Pa |
| Initial reservoir temperature | 300 | °C |
| Production (constant pressure) | 1 × 107 | Pa |
| Injection (constant rate) | 2 | kg/s |
| Injection specific enthalpy | 3 × 105 | J/kg |
| Rock/fracture porosity | 0.05 | Unitless |
| Rock/fracture heat conductivity | 5 | W/(m°C) |
| Rock/fracture specific heat | 1000 | J/(kg°C) |
| Production well index | 4 × 10−11 | m3 |
| Rock expansion coefficient | 4 × 10−6 | 1/°C |
| Matrix/fracture Poisson’s ratio | 0.25 | Unitless |
| Matrix Young’s modulus | 30 | GPa |
| Biot’s coefficient | 1 | Unitless |
| Matrix permeability correlation coefficient, c (in Equation (44)) | 2 | Unitless |
| Initial fracture aperture | 15 × 10−6 | m |
| Maximum mechanical fracture aperture | 2.5 × 10−4 | m |
| Fracture permeability correlation coefficient, d (in Equation (56)) | 4 × 10−7 | 1/Pa |
| Parameter | Value | Unit |
|---|---|---|
| Fracture aperture | 0.0001 | m |
| Initial pressure | 6.895 | MPa |
| Tracer injection rate | 2.91 × 10−4 | |
| Tracer injection time | 360 | s |
| Water injection rate | 6.667 × 10−4 | |
| Matrix permeability | 8.0 × 10−16 | |
| Fracture permeability (layer 1–22) | 2.333 × 10−10 | |
| Fracture permeability (Layer 23–49) | 1.333 × 10−10 | |
| Reservoir temperature | 31 | °C |
| Injected water temperature | 15 | °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.-S.; Winterfeld, P.H. Thermal-Hydrologic-Mechanical Processes and Effects on Heat Transfer in Enhanced/Engineered Geothermal Systems. Energies 2025, 18, 3017. https://doi.org/10.3390/en18123017
Wu Y-S, Winterfeld PH. Thermal-Hydrologic-Mechanical Processes and Effects on Heat Transfer in Enhanced/Engineered Geothermal Systems. Energies. 2025; 18(12):3017. https://doi.org/10.3390/en18123017
Chicago/Turabian StyleWu, Yu-Shu, and Philip H. Winterfeld. 2025. "Thermal-Hydrologic-Mechanical Processes and Effects on Heat Transfer in Enhanced/Engineered Geothermal Systems" Energies 18, no. 12: 3017. https://doi.org/10.3390/en18123017
APA StyleWu, Y.-S., & Winterfeld, P. H. (2025). Thermal-Hydrologic-Mechanical Processes and Effects on Heat Transfer in Enhanced/Engineered Geothermal Systems. Energies, 18(12), 3017. https://doi.org/10.3390/en18123017





