Method of Helicopter Turboshaft Engines’ Protection During Surge in Starting Mode

Abstract

This article proposes a mathematical model for protecting helicopter turboshaft engines from surges, starting with fuel metering supply and maintaining stable compressor operation. The model includes several stages: first, fuel is supplied according to a specified program; second, an unstable compressor operation signal is determined based on the gas temperature in front of the compressor turbine and the gas generator rotor speed derivatives ratio; at the third stage, when the ratios’ threshold value is exceeded, fuel supply is stopped, and the ignition system is turned on. Then, the fuel supply is restored with reduced consumption, and the rotor speed is corrected, followed by a return to regular operation. The neural network model implementing this method consists of several layers, including derivatives calculation, comparison with the threshold, and correction of fuel consumption and rotor speed. The input data for the neural network are the gas temperature in front of the compressor turbine and the rotor speed. A compressor instability signal is generated if the temperature and rotor speed derivatives ratio exceed the threshold value, which leads to fuel consumption adjustment and rotor speed regulation by 28…32%. The backpropagation algorithm with hyperparameter optimization via Bayesian optimization was used to train the network. The computational experiments result with the TV3-117 turboshaft engine on a semi-naturalistic simulation stand showed that the proposed model effectively prevents compressor surge by stabilizing pressure, vibration, and gas temperature and reduces rotor speed by 29.7% under start-up conditions. Neural network quality metrics such as accuracy (0.995), precision (0.989), recall (1.0), and F1-score (0.995) indicate high efficiency of the proposed method.

1. Introduction

Helicopter turboshaft engines (TE) [1] are a crucial element of helicopter technology [2], which has become widespread in both civil [3] and military [4] aviation in many countries around the world. One of the helicopter’s TE operations’ critical tasks is to prevent surges during engine starting modes when turbulent processes in the compressor [5] and disruption of air supply uniformity can significantly decrease engine performance or cause failure [6]. To minimize the risk of surge development, an urgent task is to develop innovative approaches to protecting helicopter TEs, including the modern control technologies and adaptive algorithms used, which will ensure stable engine operation in a wide range of operating conditions [7]. Surges during the helicopter TE starting phase are one of the most dangerous non-stationary dynamic problems [8,9,10] due to the high probability of extreme loads and thermal deformations in the compressor elements. The preventing helicopter TE surge tasks’ complexity in the starting mode [11] is increased by the uncertainty’s presence caused by the engines’ external conditions and the operational status variability. Introducing practical protection methods based on adaptive and intelligent control systems [12,13] is an urgent task aimed at increasing helicopter TE reliability and safety operations [14] under the requirements of modern conditions to ensure helicopter flight safety [15,16].

The surge prevention problem in helicopter TE is widely studied in the helicopter flight safety context [17,18,19]. Traditional surge protection methods [20,21] include design solutions such as bypass valves, rotor angular velocity control systems, and fuel dosing control algorithms. These approaches aim to ensure stable compressor operation, minimize non-stationary processes, and prevent critical deviations in engine operating parameters.

Research [22,23] focuses on intelligent control systems development that integrates data from multichannel sensors and uses machine learning methods [24] to the helicopter TE starting to predict and prevent surges. For example, recurrent neural networks [25] allow the dynamic processes in the compressor modeling and identify precursors to unstable operation. However, most of these solutions focus on engine operation in steady-state modes, while starting modes remain less studied.

The fuel dosage control during helicopter TE starting methods is also being studied in the context of surge risk reduction [26]. Research [26,27] shows that optimizing fuel supply, considering the temperature and rotor speed current values, can significantly reduce the likelihood of unstable processes. However, most existing models are based on fixed control algorithms, which limits their adaptability to changes in the engines’ external conditions and operational status.

The helicopters’ complex dynamic operating conditions, such as exposure to low temperatures, increased loads at high altitudes, and the need for frequent engine starts, create additional difficulties for effective surge prevention. Traditional methods [20,21] do not sufficiently consider the rapidly changing factors and the operating modes’ variability influence. It emphasizes the need to develop adaptive approaches that effectively respond to real-time parameter changes.

Existing studies [17,18] do not fully cover the issues of integrating intelligent control systems [12,13] based on neural network models [24,25] with surge protection algorithms in starting modes. In particular, the following have not been sufficiently studied:

• The fuel dosing adaptive correction methods depend on the engine’s dynamic parameters’ current values [19,20];
• Algorithms for the unstable compressor operation generating signals that take into account not only absolute but also the temperature and rotor speed derivative values [22,23];
• The software-defined influence dependencies of compressor operating parameters on the engines’ starting stabilization [26,27].

Developments in protecting helicopter TE from the surge method with a neural network implementation will eliminate existing limitations through adaptive control use. The proposed method is based on the fuel-metered supply according to a software-defined dependency, the compressor operating parameters correction when unstable operation is detected, and dynamic relations analysis between the gas temperature in front of the compressor turbine and the gas generator rotor speed derivatives. The neural network inclusion implementation ensures the control actions adaptation in real time depending on changes in environmental parameters and engine conditions, which will improve the engines’ operation reliability due to predictive starting control. Thus, the research aim is to develop a method for protecting helicopter TE from surges in the starting mode, based on neural network implementation, providing the metered fuel supply adaptive control and the unstable compressor operation signals formation, considering the engines’ dynamic parameters. The research object is the helicopter TE functioning processes in the starting mode, accompanied by the surge risk. The research subject includes methods for controlling the helicopter TE metered fuel supply to the combustion chamber, algorithms for the unstable compressor operation, and neural network models that generate signals to provide adaptive control in the engine starting mode.

2. Materials and Methods

An analysis of algorithms for protecting helicopter TE during surge in starting mode [17,18] reveals several key points that justify the need for a new approach. The sequential stages of use, including metered fuel supply [20], compressor condition monitoring [21], and rotor speed adjustment [22], allow for a high degree of control over the engine starting process. Each stage is aimed at preventing damage caused by unstable operation, which is especially critical for helicopter TE subject to high loads and sudden changes in operating conditions. Special attention should be paid to algorithms designed to monitor and record the compressor operating condition [23]. This is important since traditional diagnostic methods may not have time to respond to rapidly changing conditions. The temperature and speed derivatives ratio using [21] allows for promptly identifying deviations from the norm and responding to them, which is a significant improvement over simpler threshold algorithms that do not take into account the dynamics of changes. However, such algorithms may struggle with low signal levels, requiring fine-tuning of thresholds and potential use of additional sensors to improve robustness.

Fuel control and ignition unit activation also demonstrate the system’s adaptive capability importance [25,27]. The ability to temporarily stop fuel supply and switch to reduced power helps avoid fuel overruns and possible overheating [26] but can also lead to the system’s excessive sensitivity to changes in operating conditions. If timing parameters are not adapted to specific starting conditions, this can cause delays in system response. However, despite all these advantages, those algorithms that rely on fixed dependent functions and thresholds may not withstand the external factors influence, such as changes in temperature, pressure, and fuel characteristics.

Thus, to simulate the helicopter TE protection during surge in the starting mode [17] with metered fuel supply [23] and the compressor operation stability maintaining [26], a mathematical model is proposed based on the sequential actions and specified dependencies algorithm.

Stage 1. Fuel supply according to the program. In the starting beginning, fuel is supplied to the helicopter TE combustion chamber according to the program with the flow rate $G_T^{prog}$ according to the dependence, calculated as follows:

$$G_T=G_T^{prog}\left(t\right).$$

(1)

Stage 2. The unstable compressor operation signal formation.

At this stage, unstable compressor operation is recorded through the gas temperature in front of the compressor turbine $T_G^{*}$ and the gas generator rotor speed n_TC first derivatives ratio according to the following expression:

$$R={\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}.$$

(2)

If R exceeds a given threshold value, an unstable operation signal is generated, i.e., the following becomes valid:

$$\mathrm{I}\mathrm{f} {\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}>{\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.},\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n} \mathrm{a}\mathrm{n} \mathrm{u}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{i}\mathrm{s} \mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}.$$

(3)

Stage 3. Stopping the fuel supply and turning on the ignition unit. When an unstable operation signal is generated, the fuel supply to the combustion chamber is stopped for a specific time Δt_fuel, and the ignition unit is turned on for a time Δt_ign. After this, the fuel supply is resumed with a reduced flow rate $G_T^{prog \left(1\right)}$, calculated as follows:

$$G_T=G_T^{prog \left(1\right)}\left(t\right).$$

(4)

Remark 1. 

Changing the fuel supply and ignition unit control algorithm when starting helicopter TE, aimed at minimizing voltage surges, can have a positive effect on the overall system performance. Reducing voltage surges reduces the electrical network’s overloading risk, increases the compressor stability, and improves the fuel flammability. This approach helps maintain the gas generator’s stability and reduces its surge likelihood, which ultimately increases the system’s reliability as a whole [28].

Stage 4. The metered fuel supply restoration. After the unstable operation signal is removed, the fuel supply is restored linearly from $G_T^{prog \left(1\right)}$ to $G_T^{prog}$, according to a linear dependence over a specified time Δt_rest. The linear change in fuel consumption is described as follows:

$$G_T\left(t\right)=G_T^{prog \left(1\right)}\left(t\right)+\left({\displaystyle \frac{G_T^{prog}-G_T^{prog \left(1\right)}}{∆t_{rest}}}\right)·t, t\in \left[0,∆t_{rest}\right].$$

(5)

Stage 5. Determining the software dependence ${\dot{n}}_{TC}=f\left(n_{TC}\right)$. Before the compressor’s unstable operation signal appears, the gas generator rotor speed software dependence on its current value is established, calculated as follows:

$${\dot{n}}_{TC}=f\left(n_{TC}\right),$$

(6)

where f is a function that determines the rotor speed change dynamics depending on the current value.

Stage 6. Adjustment when the ignition unit is turned on. When the ignition unit is turned on, the n_TC frequency is adjusted downwards by 28…32%. The adjusted dependence takes the following form:

$${\dot{n}}_{TC}^{cor.}=f\left(n_{TC}^{cor.}\right),$$

(7)

where

$$n_{TC}^{cor.}=n_{TC}·\left(1-∆\right), ∆\in \left[0.28, 0.32\right].$$

(8)

Remark 2. 

The n_TC reduction by 28…32% when the ignition unit is turned on is based on the need to prevent overheating and ensure stable compressor operation under high temperatures and loads at the starting time. This reduction helps control the flow dynamics and temperature conditions, which reduces the unstable compressor operation risk. This practice is supported by research results, for example [29].

Stage 7. The starting modes end. The corrected frequency dependence (8) is maintained until the engine starting mode ends, after which the system switches to normal operation mode.

Thus, the helicopter TE protection algorithm developed a mathematical model determined by analytical expressions (1)–(8), which include dynamic fuel supply, compressor parameter monitoring, and rotor speed adjustment. The helicopter TE developed a mathematical model protection during the surge in the starting mode, which represents an innovative approach that allows dynamic adapting of the fuel supply and compressor rotor speed to prevent unstable operation. The developed mathematical model is implemented with a structural diagram, as shown in Figure 1.

According to Figure 1, unit 1 calculates ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}$ according to (2), unit 2 compares ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}$ with the threshold value ${\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$ according to (3), and when ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}>{\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$, it generates a signal H1 = 1 for unstable compressor operation. Unit 3 is a timer set for t = 0.3…0.4 s. Unit 3 generates a signal H₂ = 1. After 0.3…0.4 s [29], it removes the signal (H₂ = 0). Unit 4 is a logical device “AND” that generates a signal to stop the fuel supply to the engine combustion chamber at H₁ = 1 and H₂ = 1. Unit 5 is a logical device “AND” that generates a signal H₃ = 1 to turn on the ignition unit at H₁ = 1 and H₂ = 0; it initiates the start cyclogram after stopping the fuel supply (cutoff) for a time of t = 0.3…0.4 s [29]. Unit 6 is a device that corrects the fuel consumption reduction program $G_T^{prog \left(1\right)}$ according to (4). Unit 6, based on the signal H₃ = 1, generates an analogue correction signal H₄, which is fed to unit 7, which is a multiplying (multiplicative) device that produces the fuel consumption $G_T^{prog \left(1\right)}$ reduced (corrected) value to the metering needle. Unit 8, based on signal H₃ = 1, generates a corrected dependence ${\dot{n}}_{TC}^{cor.}=f\left(n_{TC}^{cor.}\right)$ according to (7) at starting and sends a signal to the gas generator rotor speed controller.

Unit 1 receives data on the n_TC and $T_G^{*}$ current values, where the ratio ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}$ value is formed according to (2); information about which is sent to the comparison unit 2 first input. At the same time, information about the threshold value ${\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$ is sent to unit 2’s input. When ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}>{\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$, signal H₁ = 1 is formed, characterizing unstable operation of the compressor (“surge”). Signal H₁ is fed to units 4 and 5, the first and timer three inputs. When signal H₁ = 1 appears, timer 3 starts counting down time t = 0.3…0.4 s [29] and generates a control signal, H₂ = 1, fed to the inputs of units 4 and 5. At the end of the periods’ of 0.3…0.4, the timer removes control signal H₂ (H₂ = 0). When H₁ = 1 and H₂ = 0, unit 5 generates signal H₃ = 1 to the control system to perform the starting cyclogram after the fuel cutoff is terminated. In this case, a repeated start occurs with the starting program correction performed by units 6, 7, and 8. Block 6, based on signal H₃ = 1, generates analogue correction signal H₄, changing from a value of 0.9 to 1.0 within ~10 s. The analogue correction signal H₄ from the unit 6 output is fed to the first input of multiplying unit 7. In this case, the data on the standard value $G_T^{prog}$ are fed to unit 7’s input. Unit 7 multiplies the $G_T^{prog}$ value and the correction signal I4, forming the corrected value of the fuel consumption value $G_T^{prog \left(1\right)}$ according to (4). At the same time, using the signal H₃ = 1, unit 8 corrects the software dependence ${\dot{n}}_{TC}^{cor.}=f\left(n_{TC}^{cor.}\right)$ according to (7), towards decreasing the value by 28…32 % [29]. Unit 8 sends a signal to the gas generator rotor speed controller, which maintains the starting mode completion corrected dependence ${\dot{n}}_{TC}^{cor.}=f\left(n_{TC}^{cor.}\right)$.

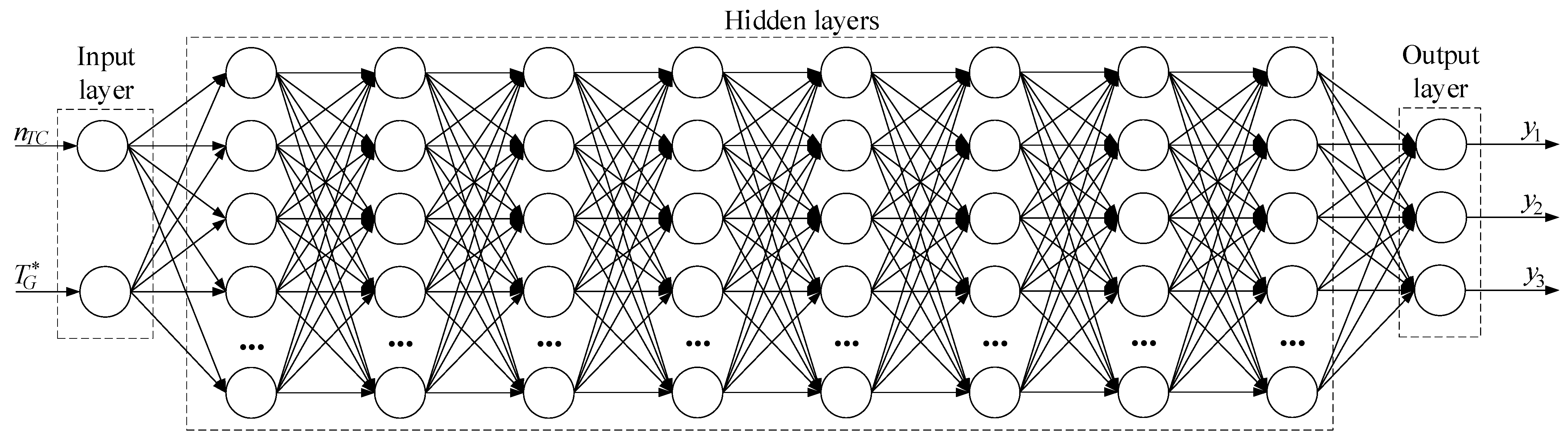
To implement the protecting helicopter TE during a surge-developed method, a neural network is proposed (Figure 2), which performs the control, signal processing and logical control specified functions and consists of several specialized layers simulating the operation of units 1–8 (according to Figure 2).

In the input layer, the gas temperature in front of the compressor turbine $T_G^{*}$ and the gas generator rotor speed n_TC current values are recorded and transmitted to the next layer for processing.

The layer for calculating derivative values ensures unit 1’s operation. In this layer, the ${\dot{T}}_G^{*}$ and ${\dot{n}}_{TC}$ derivatives are calculated based on the input data, as well as their ratio ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}$ according to (2), which value is passed to the next layer. This layer is the recurrent elements (e.g., LSTM [30]) layer since the ${\dot{T}}_G^{*}$ and ${\dot{n}}_{TC}$ derivative values depend on changes in temperature and rotor speed over time.

The threshold comparison layer ensures the operation of unit 2. In this layer, the current value ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}$ is compared with the threshold value ${\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$, based on which the logical signal H₁ = 1 is output if ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}>{\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$. This layer is dense with a sigmoid activation function, representing the threshold function. The sigmoid function transforms the comparison result into a binary value H₁.

The timer layer, which ensures the operation of unit 2, is a time delay layer. In this layer, when the signal H₁ = 1 is received, the time countdown t = 0.3…0.4 s [29] begins, after which the signal H₂ = 1 is formed, and after the specified time, the signal H₂ = 0 is removed. This layer function is to withstand the time delay for the necessary commands’ formation for subsequent blocks.

The logical “AND” layer for stopping the fuel supply (Unit 4) is a logical layer that models the “AND” operation, in which, upon receipt of signals H₁ = 1 and H₂ = 1, a command is generated to stop the fuel supply, that is, the following logical condition is realized:

$$H_{fuel}=H_1˄H_2.$$

(9)

The logical “AND” layer for turning on the ignition unit (Unit 5) is also a logical layer simulating the “AND” operation, in which, when H₁ = 1 and H₂ = 0, the signal H₃ = 1 is activated to start the ignition unit, which initiates the start cyclogram after the fuel cutoff, that is, the following condition for turning on the ignition is realized:

$$H_{ignition}=H_1˄\neg H_2.$$

(10)

In the fuel consumption correction layer (Unit 6), the H₃ = 1 signal generates the H₄ correction signal, changing from 0.9 to 1.0 over 10 s [29], i.e., the fuel consumption correction $G_T^{prog \left(1\right)}$ is performed depending on time. This layer is dense with the SmoothReLU activation function [31], generating an analogue correction signal capable.

The multiplication layer that ensures the unit 7 operation is a multiplying layer in which the corrected fuel consumption value $G_T^{prog \left(1\right)}$ is multiplied by the correction signal H₄, obtaining the final fuel consumption value. Thus, the fuel consumption correction is calculated as follows:

$$G_T^{cor.}=G_T^{prog \left(1\right)}·H_4.$$

(11)

The rotor speed dependence correction layer (Unit 8) is a layer with a dense structure and recurrent elements, in which, based on the signal H₃ = 1, the dependence ${\dot{n}}_{TC}^{cor.}=f\left(n_{TC}^{cor.}\right)$ is corrected downwards by 28…32% [29]. Thus, when the signal H₃ = 1 is activated in this layer, the target frequency value changes dynamically, ensuring the engines’ stable operation in the specified modes.

The proposed neural network architecture (Figure 2) allows helicopter TE protection automation and control under unstable operating conditions, implementing the developed surge protection method in the sequential logical and mathematical control format.

A specialized algorithm is proposed to train the developed neural network (Figure 2), the helicopter TE protection system during surge operation simulating, including the data generation stages, setting up time dependencies, logical conditions, and parameter correction. The developed neural network training includes simulating signals and logical states for the neural network functions’ accurate execution related to fuel cutoff conditions, flow rate adjustment, and starting.

The input data were simulated at the initial stage of neural network training. It is assumed that the input data include the gas temperature in front of the compressor turbine $T_G^{*}$ and the gas generator rotor speed n_TC current values, for which the derivatives are set as follows:

$${\dot{T}}_G^{*}={\displaystyle \frac{d{T}_G^{*}}{dt}}, {\dot{n}}_{TC}={\displaystyle \frac{d{n}_{TC}}{dt}}.$$

(12)

The input data for the model include pairs ($T_G^{*}$ and n_TC) and their derivatives (${\dot{T}}_G^{*}$ and ${\dot{n}}_{TC}$). Next, the surge event is modeled by defining a surge as a situation when ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}>{\left({\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}\right)}^{t.v.}$. After that, the initial weights and thresholds W and b are specified for all the networks’ layers. The initial distribution is specified, for example, as follows:

W∼N(0, σ²), b∼N(0, σ²),

(13)

where σ is the standard deviation.

Backpropagation through time is used to train temporal dependencies in a neural network. For each time step t, an input vector $x_t=\left[T_G^{*}\left(t\right), n_{TC}\left(t\right)\right]$ is formed, with the help of which the neural networks’ hidden states are updated, for example, in the recurrent layer (e.g., LSTM [30]) case as follows:

h_t = f(W_h · h_t−1 + W_x · x_t + b),

(14)

where h_t is the hidden layers’ state at step t.

To generate a signal H₁ = 1 if the surge condition is met, the neural network is trained in such a way that the target error function takes into account the logical condition, which is calculated as follows:

$$L_{log}=-\left(y·\log \left(\widehat{y}\right)+\left(1-y\right)·\log \left(1-\widehat{y}\right)\right),$$

(15)

where y is the real value (0 or 1), and $\widehat{y}$ is neural network prediction value.

When H₁ = 1, the timer is activated and generates a signal H₂ = 1 for t = 0.3…0.4 s [29]. In this case, the time t is set for the timer, written as follows:

t_timer = [0.3…0.4],

(16)

and is controlled by a delay. Next, the neural network is trained to hold H₂ = 1 for the required time.

At the next stage, the correction signal H₄ is formed, which, when H₃ = 1, changes according to a linear law, written as follows:

$$H_4=0.9+{\displaystyle \frac{t}{10}} \mathrm{f}\mathrm{o}\mathrm{r} 0\le t\le 10,$$

(17)

where H₄ → 1.0 after 10 s.

The H₄ signal adjusts the fuel consumption according to (11). The gas generator rotor speed is adjusted as follows:

$${\dot{n}}_{TC}^{cor.}={\dot{n}}_{TC}·\left(1-k\right),$$

(18)

where k = 0.28…0.32 (a reduction by 28…32%).

The overall loss function includes errors for each unit and is defined as:

L_total = L_log + L_timer + L_correction,

(19)

where L_log is the loss for logical conditions, L_timer is the loss for time delays, and L_correction is the loss for correction signals.

The loss function L_log minimizes the error for the logical signals’ operation, corresponding to the required logical conditions. Logical conditions take into account the surge signals’ operation. If the network output ${\widehat{H}}_1$ does not correspond to the required logical value H₁, an error occurs. To minimize the error in signal operation, binary cross-entropy (15) is used, calculated as follows:

$$L_{log}=-\left(H_1·\log \left({\widehat{H}}_1\right)+\left(1-H_1\right)·\log \left(1-{\widehat{H}}_1\right)\right),$$

(20)

where H₁ ∈ {0, 1} is the actual value of the signal (for example, operation during surge), and ${\widehat{H}}_1$ is the signal-predicted value by the neural network.

The loss function L_timer minimizes the actual signal activation time deviation from the target interval [0.3, 0.4], thereby increasing the timer accuracy. The timer function is to hold the signal H₂ = 1 for a given interval t_timer ∈ [0.3, 0.4] seconds [29]. To ensure high accuracy, a penalty for deviation from the target response time is added to the delay. Thus, the following analytical expression for the loss for the timer includes the difference between the actual delay duration tactual and the target duration t_target, as well as the penalty coefficient λ for duration errors:

$$L_{timer}={\left(H_2-{\widehat{H}}_2\right)}^2+{\lambda }_t·{\left(t_{timer}-t_{target}\right)}^2,$$

(21)

where ${\left(H_2-{\widehat{H}}_2\right)}^2$ is the signals’ H₂ activation/deactivation prediction error, t_timer is the timer response actual duration, t_target is the t_timer duration target value, and λ_t is the penalty coefficient for errors in the delay duration.

The correction signals’ loss function helps the neural network to smoothly adjust the correction signal H₄ by the required linear dependence, reaching a value of 1.0 after 10 s. The correction signal H₄ should smoothly change from a 0.9 to a 1.0 value over a 10-second period. We use a quadratic loss function to minimize the ${\widehat{H}}_4$ deviation from the target value H₄ at each time moment, calculated as follows:

$$L_{correction}={\displaystyle \frac{1}{T}}·\sum _{t=0}^T{\left(H_4\left(t\right)-{\widehat{H}}_4\left(t\right)\right)}^2,$$

(22)

where T is the total number of time steps in the correction process, H₄(t) is the correction signals’ target value at time t, and ${\widehat{H}}_4\left(t\right)$ performs the neural network prediction for the correction signals’ value at time t.

To optimize the neural network weights and achieve the required time accuracy, the Adam optimization algorithm [32,33] is used, which is a preferred algorithm compared to RMSprop [34] for a problem involving time and logic conditions, as well as smooth signal adjustments, since its adaptive training rate and moment accounting allow stable weight control, which is critical for fine-tuning time delays and logic conditions. In the Adam algorithm [33], the first moments (average gradients) are updated as follows:

m_t = β₁ · m_t−1 + (1 − β₁) · ∇_θL_t,

(23)

where m_t is the first moment, β₁ is the coefficient for the first moment, and ∇_θL_t is the loss gradient for the weights θ at step t.

The second moment update (the gradients’ direct movement) is as follows:

$$v_t-{\beta }_2·v_{t-1}+\left(1-{\beta }_2\right)·{\left({\nabla }_{\theta }{L}_t\right)}^2,$$

(24)

where v_t is the second moment, and β₂ is the coefficient for the second moment.

The offset correction for moments is defined as follows:

$${\widehat{m}}_t={\displaystyle \frac{m_t}{1-{\beta }_1^t}}, {\widehat{v}}_t={\displaystyle \frac{v_t}{1-{\beta }_2^t}}.$$

(25)

The weights are updated as follows:

$${\theta }_t={\theta }_t-{\displaystyle \frac{\alpha }{\sqrt{{\widehat{v}}_t}+ϵ}}·{\widehat{m}}_t,$$

(26)

where α is the training rate, and ϵ is a small number to prevent division by zero.

To combat overfitting and improve generalization ability, L2 regularization is applied by adding it to the loss function [35], calculated as follows:

$$L_{total}=L_{total}+\lambda ·\sum _i{\theta }_i^2,$$

(27)

where L_total is the original loss function calculated according to (19), and λ is the regularization coefficient, which regulates the penalty strength for large weights.

To optimize hyperparameters, such as the training rate α, moment coefficients β₁, β₂, and regularization coefficient λ, Bayesian optimization is used, which consists of constructing a probabilistic model for the hyperparameters and choosing the next point based on an assessment of its utility, calculated as follows:

$$\mathrm{O}\mathrm{p}\mathrm{t}\left({\theta }^{*}\right)=\arg \underset{\theta }{\max } \mathrm{A}\mathrm{c}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{F}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(\theta \right),$$

(28)

where AcquisitionFunction(θ) is a function that evaluates the hyperparameters θ different combinations effectiveness to improve the model.

To achieve the time delays required accuracy, additional hyperparameters are introduced to control timers and logic units, calculated as follows:

Penalty_t = λ_t · ∣t_timer − t_target∣,

(29)

where t_timer is the delay time, t_target is the target delay, λ is the penalty coefficient for the time error.

Taking into account the above, (19) takes the following form:

$$L_{total}=-\left(H_1·\log \left({\widehat{H}}_1\right)+\left(1-H_1\right)·\log \left(1-{\widehat{H}}_1\right)\right)+{\left(H_2-{\widehat{H}}_2\right)}^2+{\lambda }_t·{\left(t_{timer}-t_{target}\right)}^2+{\displaystyle \frac{1}{T}}·\sum _{t=0}^T{\left(H_4\left(t\right)-{\widehat{H}}_4\left(t\right)\right)}^2+\lambda ·\sum _i{\theta }_i^2.$$

(30)

The developed training algorithm is unique in its adaptability to time and logic constraints, which is critical for helicopter TE control in operational mode. It combines optimization by logical conditions and delay metrics, ensuring accuracy considering operational requirements. Including special losses for time delays and logical conditions allows the algorithm to learn reliably, maintaining stability and accuracy when detecting surges in real time.

3. Results

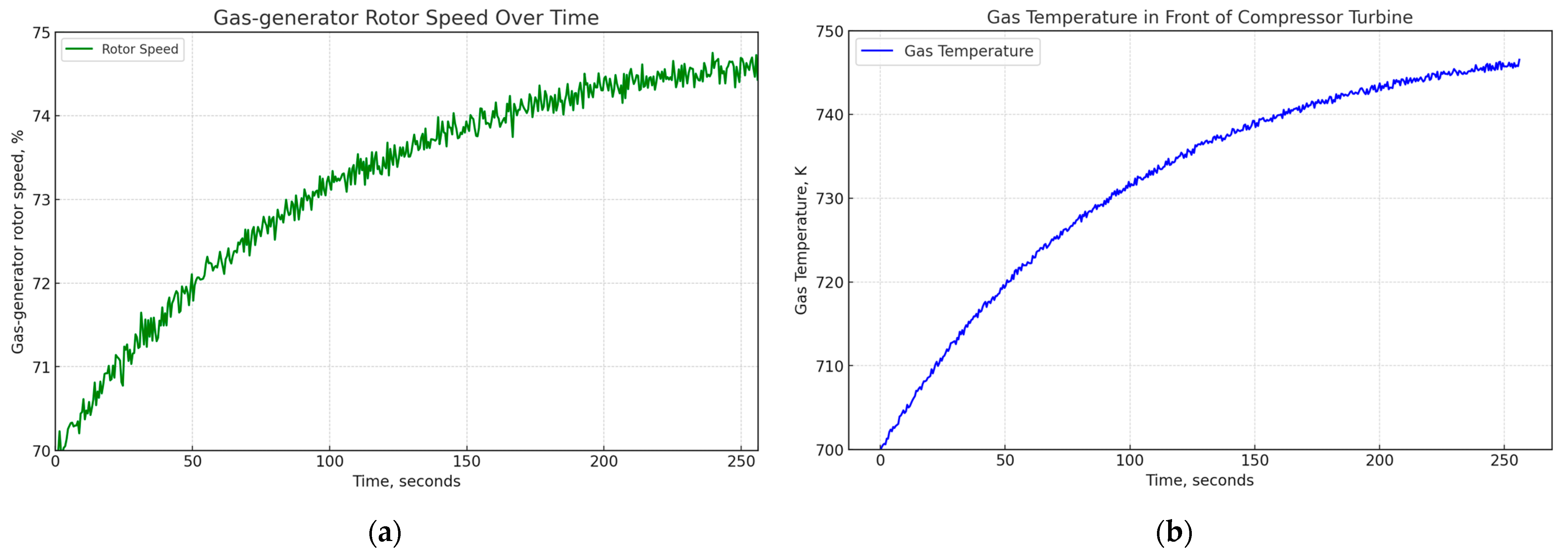
To conduct the computational experiment, the TV3-117 TE [36], which is part of the Mi-8MTV helicopter power plant, was selected as the research object [37]. The TV3-117 TE parameters (n_TC, $T_G^{*}$, etc.) required for the computational experiment were obtained exclusively from the flight data obtained during the Mi-8MTV helicopter engines’ start (Figure 3). Data recording was carried out on board using D-2M sensors and 14 dual T-101 thermocouples [31] (data recording took place for 256 s in actual flight with a sampling period of 1 s). The specified data were provided at the authors’ team’s official request to the Ministry of Internal Affairs of Ukraine and are intended for the project “Theoretical and Applied Aspects of Aviation Sphere” implementation, officially registered in Ukraine under number 0123U104884.

As can be seen in Figure 3, the gas temperature in front of the compressor turbine $T_G^{*}$ ≈ 770 K, and the gas generator rotor speed n_TC ≈ 79%. To form the training dataset (

Table 1. The training dataset fragment.

Value	1	…	41	…	94	…	159	…	209	…	233	…	256
$n_{TC}^{\left(i\right)}$	0.975	…	0.978	…	0.983	…	0.984	…	0.982	…	0.981	…	0.954
$T_G^{*\left(i\right)}$	0.988	…	0.980	…	0.972	…	0.985	…	0.986	…	0.979	…	0.982
${\dot{n}}_{TC}^{\left(i\right)}$	0.983	…	0.992	…	0.990	…	0.993	…	0.983	…	0.986	…	0.988
${\dot{T}}_G^{*\left(i\right)}$	0.984	…	0.985	…	0.981	…	0.988	…	0.985	…	0.987	…	0.983

), z-normalization of the data was carried out, with the help of which each value of the variables n_TC and $T_G^{*}$ was transformed so that they are expressed in standard deviation units from the mean. It allowed us to bring the n_TC and $T_G^{*}$ data to a form with a mean value of 0 and a standard deviation of 1, which is essential for improving the convergence of some machine learning algorithms and for the correct comparison of data with different scales. The n_TC and $T_G^{*}$ z-normalization was carried out according to the following expression:

$$\begin{gathered} {z\left(n_{TC}\right)}_i={\displaystyle \frac{n_{TC}^{\left(i\right)}-\frac{1}{N}·\sum _{i=1}^N{n}_{TC}^{\left(i\right)}}{\sqrt{\frac{1}{N}·\sum _{i=1}^N{\left(n_{TC}^{\left(i\right)}-\frac{1}{N}·\sum _{i=1}^N{n}_{TC}^{\left(i\right)}\right)}^2}}}, \\ {z\left(T_G^{*}\right)}_i={\displaystyle \frac{T_G^{*\left(i\right)}-\frac{1}{N}·\sum _{i=1}^N{T}_G^{*\left(i\right)}}{\sqrt{\frac{1}{N}·\sum _{i=1}^N{\left(T_G^{*\left(i\right)}-\frac{1}{N}·\sum _{i=1}^N{T}_G^{*\left(i\right)}\right)}^2}}}, \end{gathered}$$

(31)

where N = 256.

To calculate the n_TC and $T_G^{*}$ z-normalized values time derivative, given that the data were sampled at a sampling rate of 1 s (i.e., the $n_{TC}^{\left(i\right)}$ and $T_G^{*\left(i\right)}$ of each sample) which occurred at one second, the finite difference method approximates the derivative. Thus, we obtained the following:

$${\displaystyle \frac{d{n}_{TC}^{\left(i\right)}}{dt}}\approx {\displaystyle \frac{{z\left(n_{TC}\right)}_{i+1}-{z\left(n_{TC}\right)}_i}{∆t}}, {\displaystyle \frac{d{T}_G^{*\left(i\right)}}{dt}}\approx {\displaystyle \frac{{z\left(T_G^{*}\right)}_{i+1}-{z\left(T_G^{*}\right)}_i}{∆t}},$$

(32)

where Δt = 1 s, since the sampling frequency is 1 Hz (one sample per second), I = 1, 2, …, 255, since 256 samples were used.

The training dataset homogeneity [38,39] was assessed using the Fisher–Pearson [40] and Fisher–Snedecor [41] criteria at a significance level of α = 0.01 (

Table 2. The training dataset homogeneity evaluates results for the V_i parameter using the Fisher–Pearson and Fisher–Snedecor criteria.

Parameter	The Fisher–Pearson Criterion Meaning		The Fisher–Snedecor Criterion Meaning		Description
	Calculated	Critical	Calculated	Critical
$n_{TC}^{\left(i\right)}$	13.118	13.3	15.736	15.98	The Fisher–Pearson and Fisher–Snedecor criteria calculated values are less than the critical ones. It allowed us to establish the training dataset homogeneity.
$T_G^{*\left(i\right)}$	13.232		15.747
${\dot{n}}_{TC}^{\left(i\right)}$	13.196		15.742
${\dot{T}}_G^{*\left(i\right)}$	13.203		15.749

) [42,43]. The significance level of 0.01 was chosen in the helicopter TE protection during the surge in the starting mode problem to ensure the statistical conclusion of high reliability, which is especially important in helicopter flight safety. This strict criterion minimizes the type I error probability, contributing to more accurate and safe control of helicopter Tes under operating conditions [44] (in the starting mode).

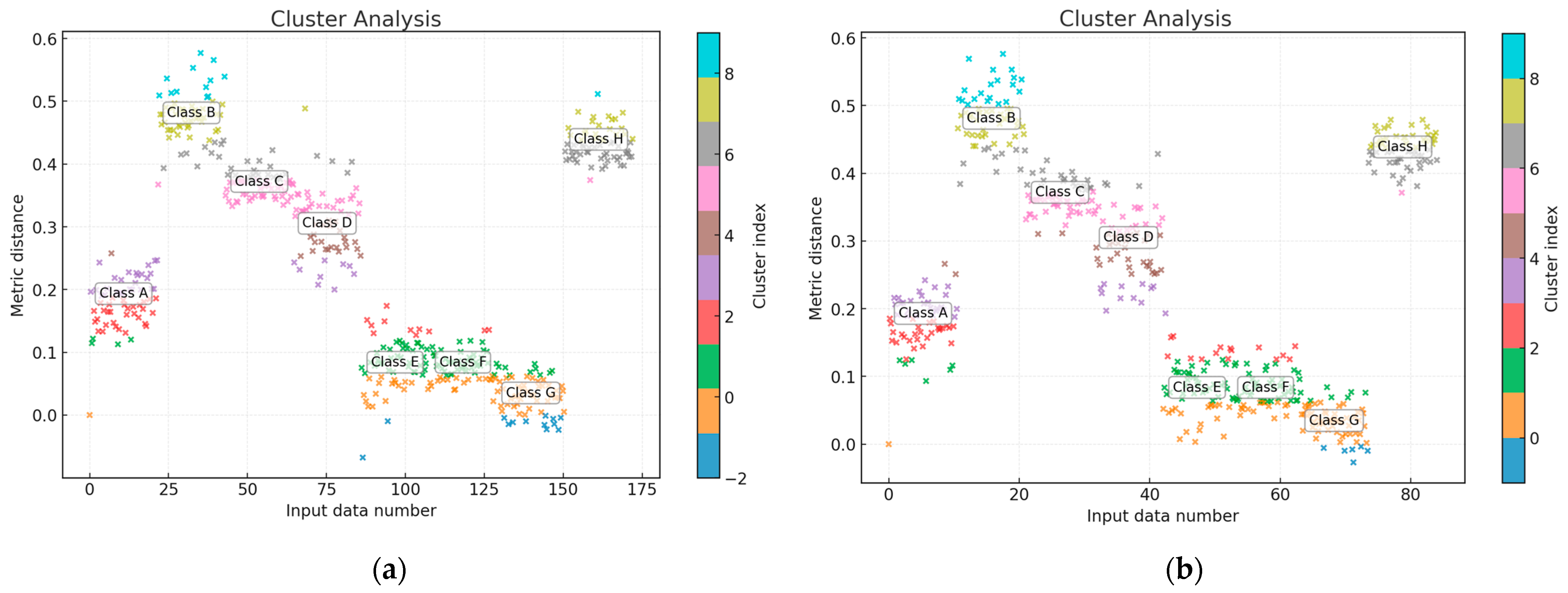
The training and test datasets’ representativeness was assessed using cluster analysis (k-means method) [45], which involved dividing the input dataset $Z=\left({z\left(n_{TC}\right)}_i,{z\left(T_G^{*}\right)}_i, {\displaystyle \frac{d{n}_{TC}^{\left(i\right)}}{dt}}, {\displaystyle \frac{d{T}_G^{*\left(i\right)}}{dt}} \right)$ (Table 1) into k groups (clusters), where each value belongs to the cluster with the nearest mean value [46,47]. The algorithm repeats the point distribution, minimizing the distance between them and their centroids until the clusters stabilize [46]. The training data (Table 1) cluster analysis revealed eight clusters (I…VIII). The training and test datasets were randomly generated in a 2:1 ratio (67% and 33%, respectively), and the same eight clusters were observed in both sets, indicating their structural similarity. The distances between the clusters in the training and test datasets were almost the same, confirming their similarity (Figure 4).

Thus, the training dataset was 256 elements (100%), the control dataset was 172 elements (67% of the training dataset size), and the test dataset was 84 elements (33% of the training dataset size) optimal size.

The research involved a computational experiment (simulation modeling) using the developed neural network method for protecting helicopter TEs during the surge in the TV3-117 TE starting mode on a semi-naturalistic modeling stand (Figure 5), which is designed to reproduce and analyze actual engine operating conditions, including various load, temperature, and pressure modes [48]. It allows for testing control systems, practicing control and diagnostic algorithms, and assessing the stability of helicopter TE operations under various external influences.

The data processing and analysis module is the central element that connects all sensors with connected modules and knowledge bases, ensuring their interaction to improve the helicopter Tes monitoring and control efficiency.

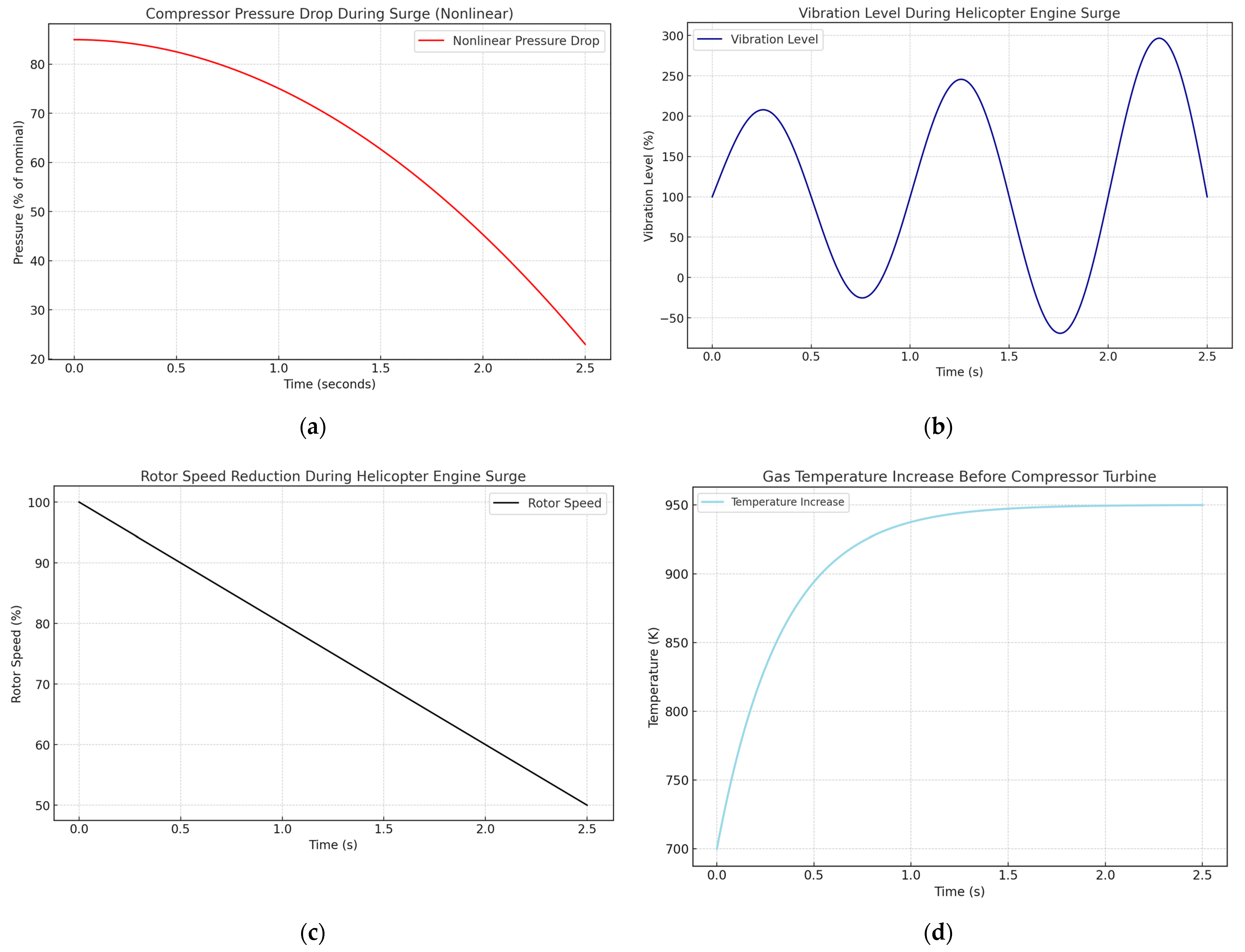
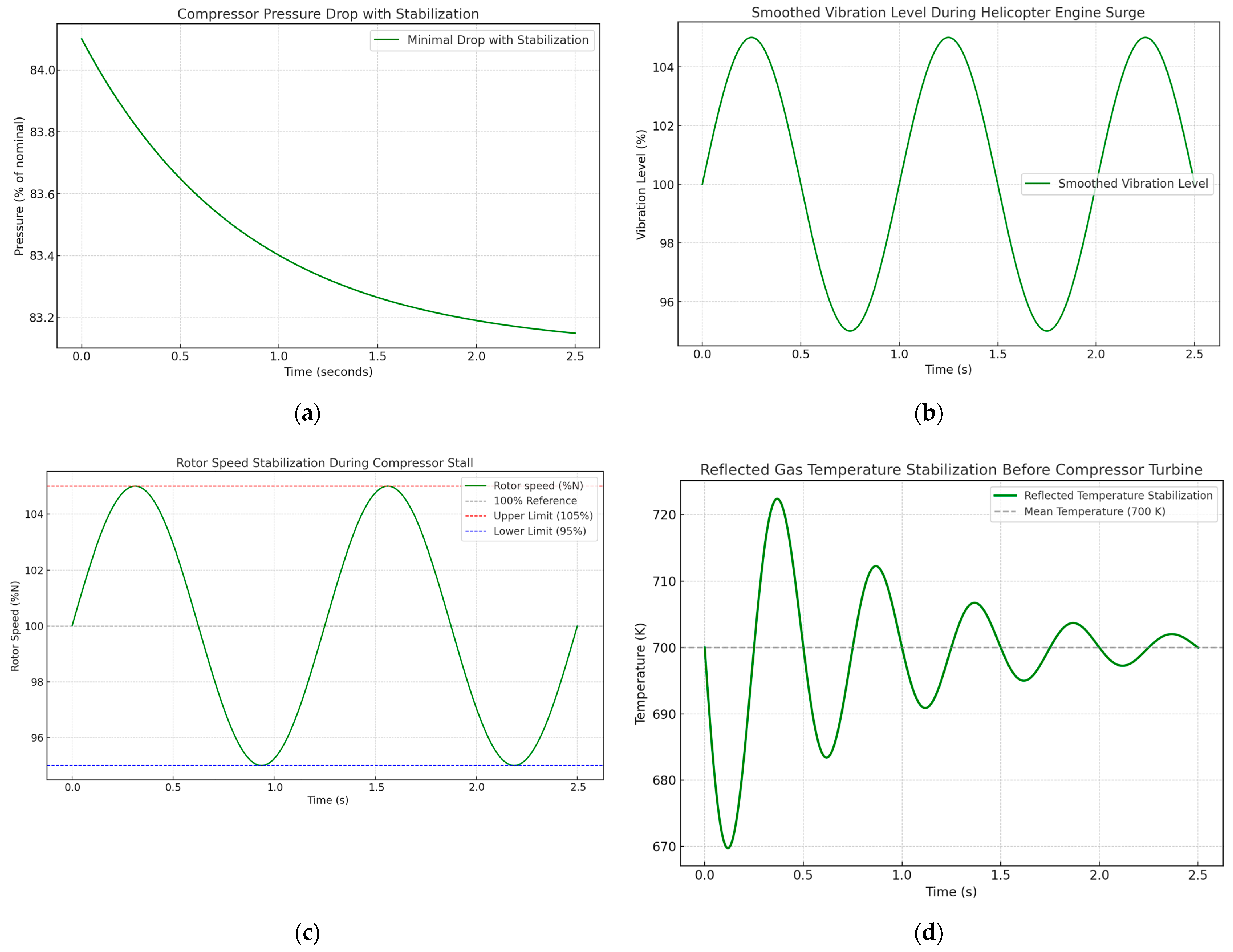
During the simulation modeling, the TV3-117 TE surge condition occurrence in the starting mode was reproduced, and the diagrams of the pressure change behind the compressor during the surge, the change in the vibration level during the surge, the compressor turbine rotor speed dynamics during the surge, and the change in the exhaust units’ temperature during the surge were obtained (Figure 6). It is noted that the following phenomena accompany the surge:

• Fluctuations in pressure, speed, and gas flow rates along the path with a clearly expressed drop in pressure behind the compressor relative to the pressure at its inlet;
• An increase in the vibration level;
• A decrease in the gas generator and the free turbine rotors speed;
• The compressor turbines’ gas temperature increased at the inlet and outlet.

An adjusted gas generator rotor speed diagram was obtained, which shows a 29.7% reduction (Figure 7), which helps prevent surge and stabilize compressor operation under starting conditions, namely:

• No fluctuations in pressure, speeds, and gas flow rates along the tract with a pronounced drop in pressure behind the compressor relative to the pressure at its inlet;
• No increase in vibration levels;
• Stabilization of the gas generator and the free turbine rotor speeds;
• Stabilization of the compressor turbines’ gas temperature at the inlet and outlet.

This adjustment ensures a fuel supply’s smooth restoration, which minimizes the emergency conditions risk.

As shown by the computational experiments series results, stopping the fuel supply to the engine combustion chamber for a set time and resuming the fuel supply with a reduced flow rate $G_T^{prog \left(1\right)}$ leads to repeated compressor instability (diagrams similar to Figure 6 were obtained). The compressor instability repetition prevention is achieved by adjusting the program dependence (6) towards reducing the n_TC value by 28…32% when the ignition unit is turned on again and maintaining the adjusted reliance (7) until the start is complete. Reducing the n_TC value by <28% is undesirable since repeated compressor instability is highly likely. Reducing n_TC by >32% will not solve this problem since this will lead to a shift in fuel consumption to the engines’ static characteristics and, consequently, to a long start time or termination of the start.

To assess the neural network (Figure 2) quality in the helicopter TE surge monitoring task during starting mode, traditional metrics, accuracy, precision, recall, F-measure, and others [49,50], were used. In helicopter TE surge monitoring during starting mode, the applied metrics of neural network quality play a crucial role in assessing its efficiency in classification and regression. Accuracy allows us to determine the correct prediction proportion, providing a general understanding of the models’ quality. Precision and recall give a more detailed assessment of the system’s performance in the unbalanced classes case, for example, when it is essential to minimize false positives and missed critical events. The F-measure (F1-score) is the harmonic mean between accuracy and recall. The determination coefficient (R²) helps to assess how well the model explains the data variability, which is especially important for predicting and detecting abnormal modes during helicopter TE start. The applied metrics together provide a comprehensive assessment of the neural network (Figure 2) quality under conditions of the helicopter TE operational status dynamic monitoring in the starting mode. The applied metrics are determined according to the following expressions:

$$\begin{gathered} Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}, Precision={\displaystyle \frac{TP}{TP+FP}}, \\ Recall={\displaystyle \frac{TP}{TP+FN}}, F1-score=2·{\displaystyle \frac{Precision·Recall}{Precision+Recall}}. \end{gathered}$$

(33)

In the context of the helicopter TE surge monitoring task in the starting mode, TP (true positive) is the correct detection of an anomaly (surge) when the model correctly classifies the malfunction; TN (true negative) is the correct absence of an anomaly when the model correctly identifies the normal operating mode; FP (false positive) is the false positive when the model incorrectly classifies the normal mode as an anomaly; and FN (false negative) is the false negative when the model does not detect an anomaly, although it is present.

Figure 8 and Figure 9 show the accuracy and loss metrics diagrams for 300 epochs of neural network training. In this case, based on [31], the following data were used when deriving the results:

• For the training dataset: accuracy is 99% and loss is 0.05;
• For the validation dataset: accuracy is 98% and loss is 0.08.

The accuracy metric diagram (Figure 8) shows the model’s accuracy on the training and validation datasets increasing during training. Accuracy on the training dataset reaches a value of about 0.995 after 300 epochs, demonstrating that the model almost perfectly matches the target labels. Accuracy on the validation dataset also increases, reaching a value of about 0.993, indicating that the model generalizes well. The difference (about 0.002) between the metrics on the training and validation data suggests that there is no significant overfitting.

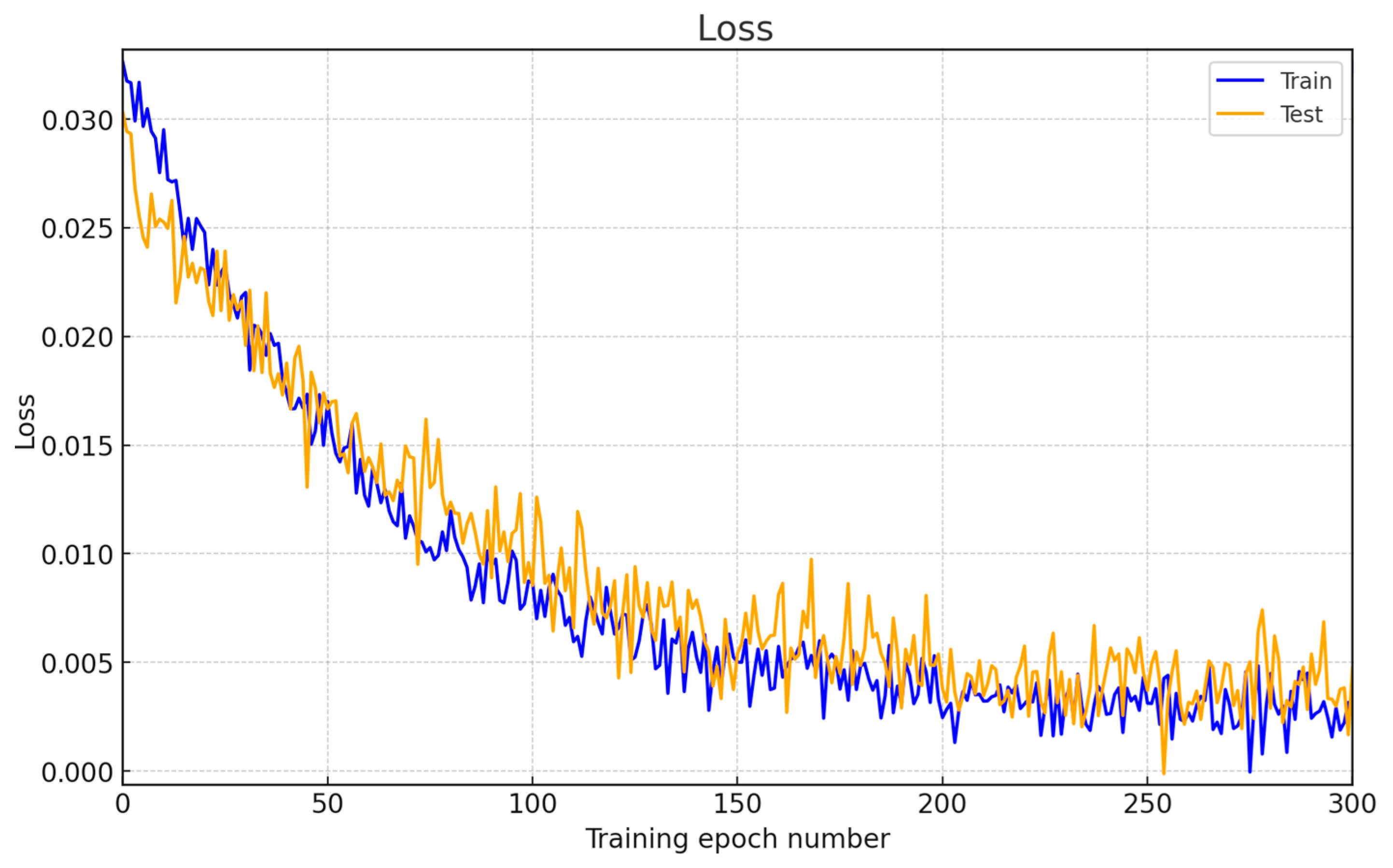
The loss metric diagram (Figure 9) shows a gradual decrease in error during the model training process from 0.025 at the initial epoch to 0.005 by the 300th epoch. The training dataset curve (blue line) decreases error compared to the test dataset (orange line), indicating efficient model training without significant overfitting. The final loss value on the test dataset stabilized around 0.007, indicating the models’ generalization efficiency.

The results of the evaluation of the effectiveness of the developed method compared to the closest analogue [26] are given in

Table 3. The comparative analysis results.

Metric	The Proposed Method	The Closest Analogue [26]
Accuracy	0.995	0.972
Precision	0.989	0.963
Recall	1.0	0.988
F1-score	0.995	0.975
True Positives	119	76
True Negatives	6	31
False Positives	354	319
False Negatives	11	44
True Positive Rate	0.813	0.614
False Positive Rate	0.0105	0.0318
False Negative Rate	0.0092	0.0293
AUC-ROC	0.809	0.605

. For this aim, the research applied the area under the AUC-ROC curve (Figure 10), which evaluates the binary classification models’ quality, showing their ability to distinguish between positive and negative classes [51]. The AUC value reflects the models’ ability to differentiate between normal and surge modes at different decision threshold values [52]. The closer the AUC is to 1, the higher the classification quality. An AUC value of 0.5 indicates random guessing. TPR [51] is the proportion of correctly detected surge cases among all real surge cases. FPR [51] is the proportion of standard operation cases incorrectly classified as surges among all typical operation cases. The area under the AUC-ROC curve is calculated as follows:

$$AUC=\sum _{i=1}^{n-1}\left({FPR}_{i+1}-{FPR}_i\right)·{\displaystyle \frac{{TPR}_{i+1}+{TPR}_i}{2}}.$$

(34)

The proposed method with the closest analogue comparison shows its significant advantage in key metrics. The proposed method demonstrates higher accuracy (accuracy 0.995 vs. 0.972) and a better ratio between precision (0.989 vs. 0.963) and recall (1.0 vs. 0.988), which is confirmed by a higher F1-score value (0.995 vs. 0.975). In addition, the improved TPR (0.813 vs. 0.614) and reduced FPR (0.0105 vs. 0.0318) indicate more efficient detection of target events with fewer false positives. The increase in AUC-ROC from 0.605 to 0.809 confirms the better ability of the proposed method to distinguish between classes and increases its reliability in operational conditions.

4. Discussion

This research proposes a mathematical model based on the actions and specified dependencies of a sequential algorithm for modeling helicopter TE protection against a surge in the starting mode with a metered fuel supply and maintaining compressor stability. In the first stage, fuel is supplied according to a specified program (1). The second stage involves the unstable compressor operation signal formation based on the gas temperature in front of the compressor turbine and the gas generator rotor speed derivatives ratio (2). When this ratio exceeds the threshold value (3), an instability signal is sent, which at the third stage leads to stopping the fuel supply and turning on the ignition system for specified time intervals. Then, the fuel supply is resumed with a reduced flow rate according to (4), and at the fourth stage, it is smoothly restored to its original value according to (5). The fifth and sixth stages include determining the rotor speed change dependence (6) and adjusting it when the ignition is turned on (7). The process (seventh stage) is completed by switching to the ordinary operation mode after the start is complete. The developed model provides dynamic control of fuel supply and rotor speed, preventing the compressor’s unstable operation.

The developed mathematical model is implemented as a method, and the structural diagram is presented in Figure 1. According to this diagram, unit 1 calculates the gas temperature before the compressor turbine and the gas generator rotor speed derivatives ratio. Unit 2 compares it with the threshold value and, if the threshold is exceeded, generates the H₁ signal, indicating the compressors’ unstable operation. Unit 3 starts the timer for 0.3…0.4 s and generates the H₂ signal to temporarily stop the fuel supply. Units 4 and 5 control the fuel supply stop and the ignition system inclusion. Unit 6 adjusts the fuel supply program, block 7 generates the adjusted fuel consumption, and block 8 regulates the gas generator rotor speed, reducing it by 28…32% if necessary. The system provides a restart with program adjustment to stabilize the engine operation.

To implement the helicopter TE protection method under surge conditions, a neural network method is proposed (Figure 2), which performs the functions of control, signal processing, and logical control. The proposed neural network consists of several specialized layers simulating the operation of units 1–8. The input layer receives the gas temperature in front of the compressor turbine $T_G^{*}$, and the current speed of the turbocharger rotor n_TC values are passed to the next layer for processing. The derivative calculation layer calculates the derivatives ${\dot{T}}_G^{*}$ and ${\dot{n}}_{TC}$, as well as their ratio, which are passed to the recurrent layer (e.g., LSTM). The threshold comparison layer performs logical control and generates the H₁ signal if the ${\displaystyle \frac{{\dot{T}}_G^{*}}{{\dot{n}}_{TC}}}$ ratio exceeds the threshold value. The timer layer starts counting down the time upon receiving the H₁ = 1 signal and, after 0.3…0.4 s, generates the H₂ = 1 signal, which is removed after a delay. The AND logic layer for stopping the fuel supply generates a fuel stop command at H₁ = 1 and H₂ = 1 and turns on the ignition—at H₁ = 1 and H₂ = 0. In the fuel consumption correction layer with the H₃ = 1 signal, the H₄ signal is changed from 0.9 to 1.0 in 10 s, adjusting the fuel consumption depending on time. In the multiplying layer, the final value of fuel consumption is calculated. The rotor speed dependence correction layer dynamically adjusts the target frequency by 28…32% depending on the H₃ = 1 signal, ensuring stable engine operation. The proposed neural network architecture allows for the helicopter TE protection automation and control in unstable modes, implementing the anti-surge protection method in the sequential logical and mathematical control format.

To train the developed neural network simulating the helicopter TE protection under surge conditions, a specialized algorithm is proposed, which includes the data generation stages, setting time dependencies, logical conditions, and parameter adjustment. At the initial training stage, input data are simulated, including the gas temperature in front of the compressor turbine $T_G^{*}$ and the gas generator rotor n_TC current speed, for which derivatives are calculated (12). The surge event is simulated when the derivatives ratio exceeds the threshold value, after which the initial weights and thresholds for the network layers are set (13). Training using error backpropagation over time allows for updating the networks’ hidden states and adjusting logical conditions, such as activation of the H₁ signal during the surge. During training, loss functions for logical conditions, time delays, and adjustment signals, such as H₄ for changing the fuel consumption (15)–(18), are considered. To optimize the network weights, the Adam algorithm with L2 regularization is used to combat overfitting and improve the generalization capabilities of the model (23)–(27). To optimize the hyperparameters, Bayesian optimization is used (28). The algorithm is highly adaptive to time and logical constraints, ensuring accuracy when monitoring helicopter TE in real operating conditions, taking into account the requirements for the time delays and logical conditions accuracy (30).

The TV3-117 TE, part of the Mi-8MTV helicopter power plant, was selected as the research object to conduct the computational experiment. The TV3-117 TE parameters (n_TC, $T_G^{*}$, etc.) required for the experiment were obtained exclusively from the flight data during the engine starting of the Mi-8MTV helicopter (Figure 3). Data recording was performed on board using D-2M sensors and 14 T-101 dual-circuit thermocouples [30] (data recording was performed in accurate flight for 256 s with a sampling period of 1 s). The specified data were provided to the authors’ team upon an official request to the Ministry of Internal Affairs of Ukraine and are intended for the projects’ “Theoretical and Applied Aspects of the Aviation Sphere” implementation, officially registered in Ukraine under number 0123U104884. As part of this study, a computational experiment was conducted using the developed neural network method to protect the helicopter TE from surge in the TV3-117 TE starting mode on a semi-naturalistic modeling stand (Figure 5) designed to reproduce and analyze actual engine operating conditions, including various load, temperature, and pressure modes. The stand allows testing control systems, practicing control and diagnostic algorithms, and assessing helicopter TE operation stability under various external influences.

During the simulation, the TV3-117 TE surge occurrence in the starting mode was reproduced, and diagrams of pressure change behind the compressor during the surge, vibration level change, compressor rotor speed dynamics, and gas temperature at the turbine outlet change during the surge were obtained (Figure 6). It was found that the following phenomena accompany surge: fluctuations in pressure, speed, and gas flow rate along the tract with a pronounced pressure drop behind the compressor relative to the pressure at its inlet; an increase in the vibration level; a decrease in the gas generator and free turbine rotors speed; and an increase in the gas temperature at the inlet and outlet of the compressor turbine. A diagram of the gas generator rotor speed change was obtained, showing a decrease of 29.7% (Figure 7), which helps to prevent surge and stabilize compressor operation under starting conditions, namely: no fluctuations in pressure, speed, and gas flow rate along the tract with a pronounced pressure drop behind the compressor; no increase in the vibration level; the gas generator and free turbine rotors speed stabilization; and the gas temperature at the inlet and outlet of the compressor turbine stabilization. This setting ensures the smooth restoration of the fuel supply, minimizing the risks of emergencies. As shown by the computational experiments series results, stopping the fuel supply to the engine combustion chamber for a given time and resuming the fuel supply with a reduced flow rate $G_T^{prog \left(1\right)}$ leads to repeated compressor instability (diagrams similar to Figure 6 were obtained). Repeated compressor instability is prevented by additionally adjusting the software dependence (6) with a decrease in the n_TC value by 28…32% when the ignition device is turned on again and maintaining the adjusted reliance (7) until the start is complete. Decreasing the n_TC value by <28% is undesirable since repeated compressor instability is highly probable. Decreasing n_TC by >32% will not solve this problem since this will lead to a shift in the fuel consumption along the engines’ static characteristic and, as a result, to a long start time or its termination.

The following metrics were used to assess the neural network (Figure 2) quality in the helicopter TE surge monitoring task in the starting mode: accuracy, precision, recall, F-measure, and others. Accuracy reflects the correct predictions proportion; precision and recall are essential for assessing the unbalanced classes’ case model performance. The accuracy diagram (Figure 8) shows an increase in accuracy on the training (0.995) and validation (0.993) datasets, which indicates the models’ good generalizability. The loss diagram (Figure 9) demonstrates a decrease in error from 0.025 to 0.005, which confirms practical training without overfitting. The proposed method outperforms its analogue in the metrics: accuracy 0.995 vs. 0.972, precision 0.989 vs. 0.963, and recall 1.0 vs. 0.988, which is confirmed by a higher F1-score (0.995 vs. 0.975) and improved TPR (0.813 vs. 0.614). The increase in AUC-ROC from 0.605 to 0.809 confirms the better ability of the method to distinguish between classes.

This mathematical model’s main limitations are its dependence on the accuracy of the data obtained, such as the gas temperature in front of the compressor turbine and the gas generator rotor speed, as well as the need for constant adjustment of the models’ parameters in actual operating conditions. The model requires accurate measurements and current data on the engine condition for correct operation, which can be difficult in unstable operating conditions.

Prospects for further research include improving the models’ accuracy by integrating additional sensors [53] for improved gas temperature [54] and rotor speed [55] measurements and developing methods for the models’ automatic adaptation to changing operating conditions [56,57]. An important direction is to improve the algorithms for working with incomplete or noisy data [58], increasing the models’ stability in unstable modes. In addition, it is necessary to study the method of applying the possibility to the engines’ other types with different characteristics [59,60] and develop methods for the neural network model protecting against overfitting when working with limited data. It is also proposed that alternative methods be studied to optimize hyperparameters and expand the models’ functionality for implementation in natural aviation systems with increased reliability and safety requirements.

In addition, prospects for further research in the helicopter TE mathematical model development and improvement field protection include improving the accuracy of models by integrating additional sensors for more accurate measurements of gas temperature and rotor speed, as well as developing methods for automatic adaptation of models to changing operating conditions. The working algorithms optimization with incomplete or noisy data is also a critical task for increasing stability in unstable modes. Conducting case studies in real conditions will help demonstrate the effectiveness of the methods and confirm their relevance, showing how improvements reduce the unstable engine operation risks and increase operational reliability, which is especially important for new aviation systems with high safety requirements.

5. Conclusions

As a result of the research, a mathematical model was developed to protect helicopter turboshaft engines from surges during starting, including metered fuel supply and maintaining stable compressor operation. The developed model is based on the action’s sequential algorithm, including monitoring the gas temperature and the gas generator rotor speed and generating instability signals, which helps prevent engine surge during its starting. The proposed model allows for dynamic regulation of fuel supply and rotor speed adjustment to stabilize compressor operation.

A neural network method was developed to implement this model, simulating the control units and logical control operation. The neural network architecture includes specialized layers for signal processing, calculating derivatives, rational control, and adjusting fuel consumption. The neural network was trained using the backpropagation algorithm and hyperparameter optimization through Bayesian optimization, which made it possible to ensure the models’ adaptability to actual operating conditions.

During the computational experiments conducted on the semi-naturalistic modeling stand basis, the TV3-117 turboshaft engine surge situation was simulated in the starting mode. The results showed that the proposed protection method effectively prevents compressors’ unstable operation, stabilizing their operation and minimizing the risk of emergencies. Changing the rotor speed by 28…32% when re-igniting and adjusting the fuel supply ensured regular engine operation and smooth restoration.

The neural network quality metrics, such as accuracy, precision, recall, and F1-score, showed excellent results, confirming the high efficiency of the model. The models’ accuracy on the training and validation datasets was 0.995 and 0.993, respectively, and the methods’ good generalizability and reliability were indicated. Unlike similar methods, this approach demonstrates better results in quality metrics, confirming its high ability to monitor and protect helicopter turboshaft engines in unstable starting modes.

Although the neural network performance metrics are high (e.g., accuracy above 99%), it is important to consider potential operational issues that may arise in real-world implementations. These external factors influence things such as temperature fluctuations and sensor contamination, which can make predictions and control difficult. Periodic calibration of the model is also necessary to maintain its effectiveness and reliability in the long term.