Optimal Scheduling Strategy for Distribution Network with Mobile Energy Storage System and Offline Control PVs to Minimize the Solar Energy Curtailment
Abstract
1. Introduction
- Day-ahead offline control for PVs is implemented to mitigate the PV trips resulting from uncertainties in renewable energy. This day-ahead offline control is pre-determined based on a probabilistic approach to respond to unexpected voltage rises because offline control units cannot adjust the upper limit in real-time.
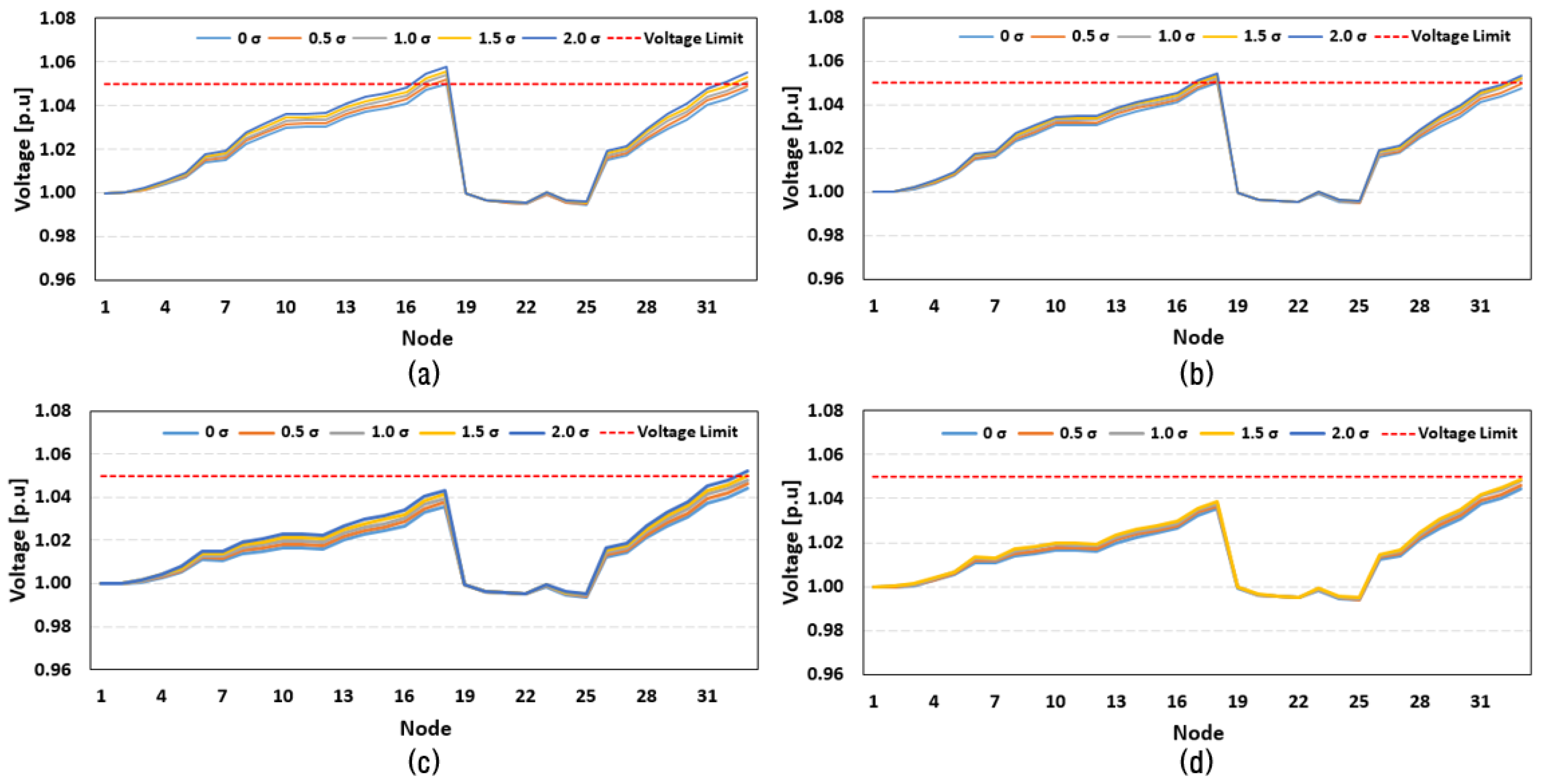
- CC-OPF is used to minimize energy curtailment considering soft chance constraints related to voltage, which can ensure that the system conditions are not below the confidence level. This can lead to moving the MESS to nodes with overvoltage risk to minimize energy curtailment due to overvoltage.
- The energy and transportation scheduling is performed to minimize total operating costs considering the cooperative operation of MESS and offline control PVs. The proposed method can significantly reduce PV production curtailment in forecasting error scenarios, while hardly increasing the operating costs of DSO in the base case scenario without forecasting errors.
2. Mathematical Modeling
2.1. Offline Control PV Model
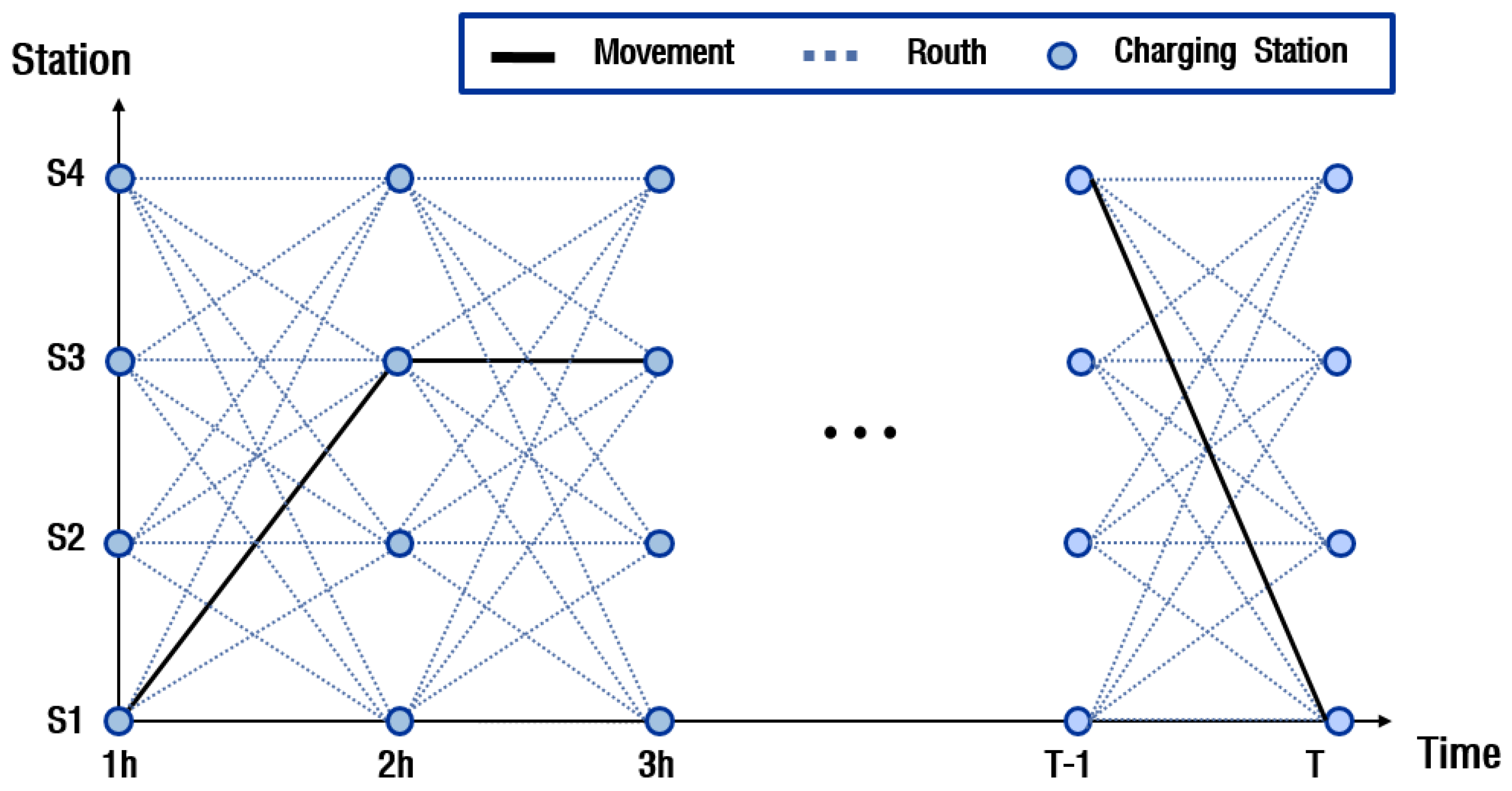
2.2. The MESS Model
3. Problem Formulation
3.1. Objective Function
3.2. Charging and Discharging of the MESS
3.3. The System Constraints
3.4. Chance-Constraints
4. Proposed Algorithm
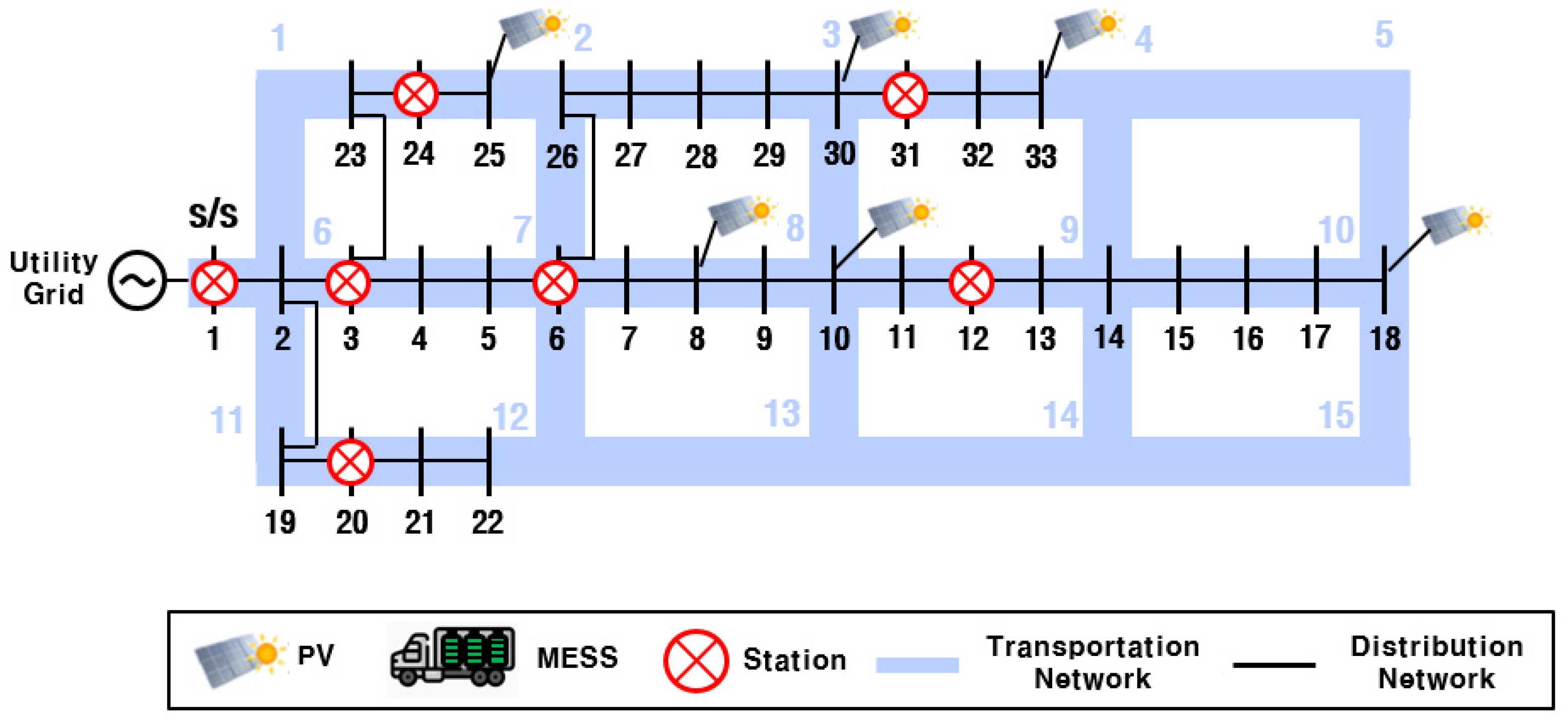
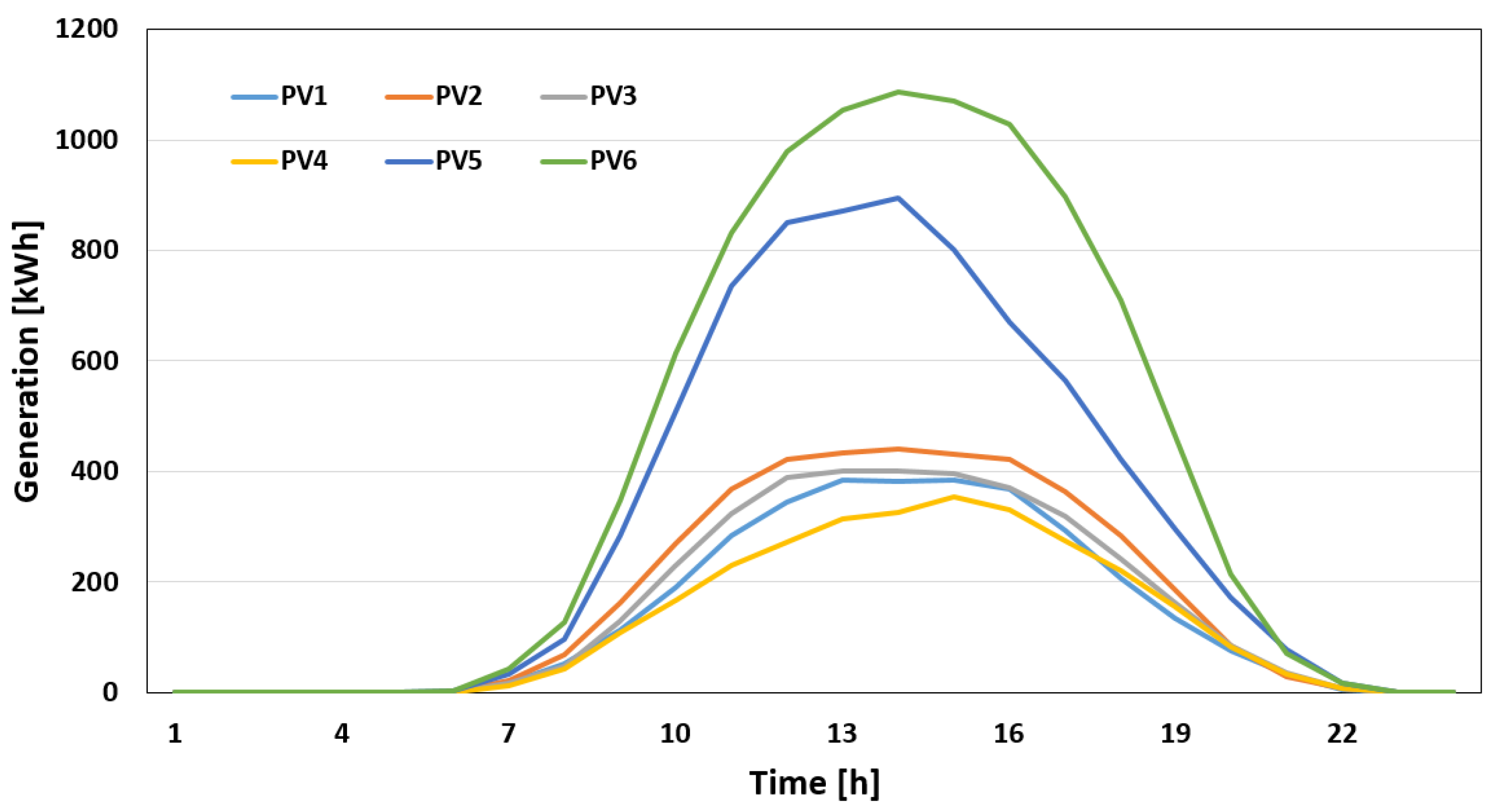
5. Case Study
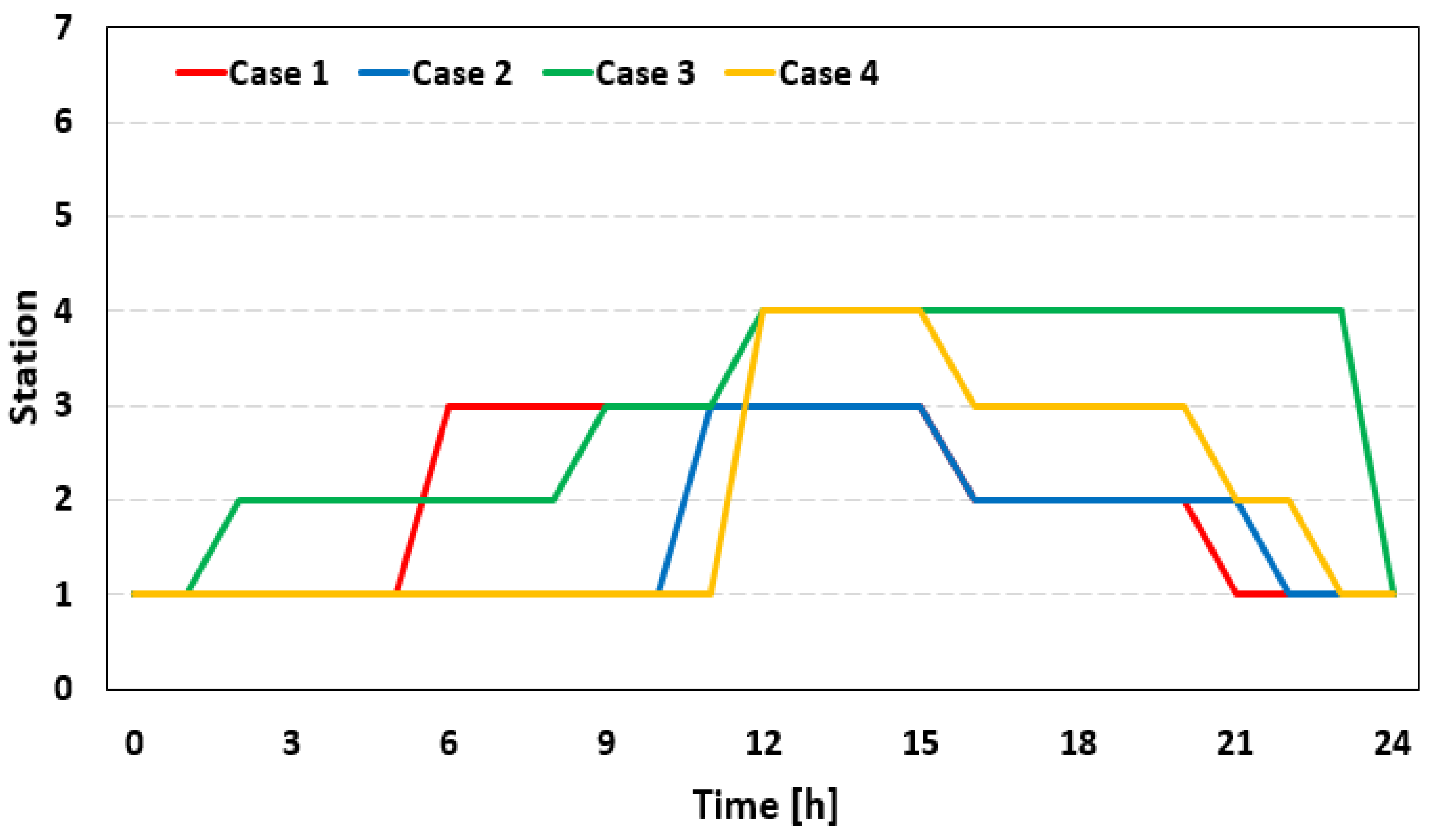
- Case 1: OPF without day-ahead curtailment;
- Case 2: OPF with day-ahead curtailment;
- Case 3: CC-OPF without day-ahead curtailment;
- Case 4: CC-OPF with day-ahead curtailment.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sexauer, J.M.; Mohagheghi, S. Voltage quality assessment in a distribution system with distributed generation—A probabilistic load flow approach. IEEE Trans. Power Deliv. 2013, 28, 1652–1662. [Google Scholar] [CrossRef]
- Kim, D.; Kim, J.-C.; Su, Q.; Joo, S.-K. Electricity blackout and its ripple effects: Examining liquidity and information asymmetry in U.S. financial markets. Energies 2023, 16, 4939. [Google Scholar] [CrossRef]
- Lee, D.; Lee, D.; Jang, H.; Joo, S.-K. Backup capacity planning considering short-term variability of renewable energy resources in a power system. Electronics 2021, 10, 709. [Google Scholar] [CrossRef]
- Kim, S.; Joo, S.K. Transmission pricing incorporating the impact of system fault and renewable energy uncertainty on the transmission margin. IEEE Access 2023, 11, 103779–103789. [Google Scholar] [CrossRef]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Cha, J.-W.; Joo, S.-K. Probabilistic short-term load forecasting incorporating behind-the-meter (BTM) photovoltaic (PV) generation and battery energy storage systems (BESSs). Energies 2021, 14, 7067. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Shahidehpour, M.; Ai, B. Battery-based Energy Storage Transportation for Enhancing Power System Economics and Security Country. IEEE Trans. Smart Grid 2009, 19, 291–312. [Google Scholar]
- Divya, K.C.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 19, 511–520. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Hu, S.; Xu, H.; Rasmussen, C.N. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- Ding, H.; Hu, Z.; Song, Y. Value of the energy storage system in an electric bus fast charging station. Appl. Energy 2015, 157, 630–639. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Shahidehpour, M.; Xu, Z.; Zhou, B.; Cao, Y.; Zeng, L. Optimal planning of islanded integrated energy system with solar-biogas energy supply. IEEE Trans. Sustain. Energy 2020, 11, 2437–2448. [Google Scholar] [CrossRef]
- Jian, L.; Hu, Z.; David, B.; Zhao, Y.; Wang, Z. The future of energy storage shaped by electric vehicles: A perspective from China. Energy 2018, 154, 249–257. [Google Scholar] [CrossRef]
- Mohammad, J.; Behnam, M.-I.; Mousa, M.; Pierluigi, S. Short-term self-scheduling of virtual energy hub plant within thermal energy market. IEEE Trans. Ind. Electron. 2021, 68, 3124–3136. [Google Scholar]
- Xu, D.; Zhou, B.; Wu, Q.; Chung, C.Y.; Li, C.; Huang, S.; Chen, S. Integrated modelling and enhanced utilization of power-to-ammonia for high renewable penetrated multi-energy systems. IEEE Trans. Power Syst. 2020, 35, 4769–4780. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.R.I. Mobile energy storage scheduling and operation in active distribution systems. IEEE Trans. Ind. Electron. 2017, 64, 6828–6840. [Google Scholar] [CrossRef]
- Lei, S.; Wang, J.; Chen, C.; Hou, Y. Mobile emergency generator prepositioning and real-time allocation for resilient response to natural disaster. IEEE Trans. Smart Grid 2018, 9, 2030–2041. [Google Scholar]
- Prabawa, P.; Choi, D.H. Multi-agent framework for service restoration in distribution systems with distributed generators and static/mobile energy storage systems. IEEE Access 2020, 8, 51736–51752. [Google Scholar] [CrossRef]
- Yao, S.; Wang, P.; Zhao, T. Transportable energy storage for more resilient distribution systems with multiple microgrids. IEEE Trans. Smart Grid 2019, 10, 3331–3341. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Y.; Mei, S.; Huang, S.; Xu, Y. Resilience oriented pre-hurricane resource allocation in distribution systems considering electric buses. Proc. IEEE 2017, 105, 1214–1233. [Google Scholar] [CrossRef]
- Lei, S.; Chen, C.; Zhou, H.; Hou, Y. Routing and scheduling of mobile power sources for distribution system resilience enhancement. IEEE Trans. Smart Grid 2019, 10, 5650–5662. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid policy-based reinforcement learning of adaptive energy management for the energy transmission-constrained island group. IEEE Trans. Ind. Inform. 2020, 16, 6423–6432. [Google Scholar] [CrossRef]
- Pulazza, G.; Zhang, N.; Kang, C.; Nucci, C.A. Transmission planning with battery-based energy storage transportation for power systems with high penetration of renewable energy. IEEE Trans. Power Syst. 2021, 36, 4928–4940. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, Y.; Luo, F.; Wen, J.; Xu, Z. Reliability evaluation of distribution systems with mobile energy storage systems. IET Renew. Power Gener. 2009, 3, 783–791. [Google Scholar] [CrossRef]
- Kim, J.; Dvorkin, Y. Enhancing distribution resilience with mobile energy storage: A progressive hedging approach. In Proceedings of the Power & Energy Society General Meeting 2018 IEEE, Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Jeon, S.; Choi, D.H. Optimal energy management framework for truck-mounted mobile charging stations considering power distribution system operating conditions. Sensors 2021, 21, 2798. [Google Scholar] [CrossRef] [PubMed]
- Saboori, H.; Jadid, S.; Savaghebi, M. Spatio-temporal and power–energy scheduling of mobile battery storage for mitigating wind and solar energy curtailment in distribution networks. Energies 2021, 14, 4853. [Google Scholar] [CrossRef]
- Yang, S.N.; Wang, H.W.; Gan, C.H.; Lin, Y.B. Mobile charging station service in smart grid networks. In Proceedings of the International Conference on Smart Grid Communications 2018 IEEE, Tainan, Taiwan, 5–8 November 2012. [Google Scholar]
- Sun, Y.; Zhong, J.; Li, Z.; Tian, W.; Shahidehpour, M. Stochastic scheduling of battery-based energy storage transportation system with the penetration of wind power. IEEE Trans. Sustain. Energy 2017, 8, 135–144. [Google Scholar] [CrossRef]
- Ogimoto, K.; Wani, H. Making renewables work: Operational practices and future challenges for renewable energy as a major power source in Japan. IEEE Power Energy Mag. 2020, 18, 47–63. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Wang, H.; Yan, Z. Routing and scheduling of mobile energy storage system for electricity arbitrage based on two-layer deep reinforcement learning. IEEE Trans. Transp. Electrif. 2023, 9, 1087–1102. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S. A learning and operation planning method for uber energy storage system: Order dispatch. IEEE Trans. Intell. Transp. Syst. 2022, 12, 23070–23083. [Google Scholar] [CrossRef]
- Sun, W.; Qiao, Y.; Liu, W. Economic scheduling of mobile energy storage in distribution networks based on equivalent reconfiguration method. Sustain. Energy Grids Netw. 2022, 32, 100879. [Google Scholar] [CrossRef]
- Samara, S.; Shaaban, M.F.; Osman, A.H. Optimal management of mobile energy generation and storage systems. IEEE Access 2020, 8, 203890–203900. [Google Scholar] [CrossRef]
- Abdeltawab, H.; Mohamed, Y.A.R.I. Mobile energy storage sizing and allocation for multi-services in power distribution systems. IEEE Access 2019, 7, 176613–176623. [Google Scholar] [CrossRef]
- Chen, X.; Wu, W.; Zhang, B. Robust restoration method for active distribution networks. IEEE Trans. Power Syst. 2016, 31, 4005–4015. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Yin, X.; Zhang, B. Preventive security-constrained optimal power flow with probabilistic guarantees. Energies 2020, 13, 2344. [Google Scholar] [CrossRef]
- Schmidli, J.; Roald, L.; Chatzivasileiadis, S.; Andersson, G. Stochastic AC optimal power flow with approximate chance-constraints. In Proceedings of the Power & Energy Society General Meeting 2016 IEEE, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- An, J.; Kim, D.-K.; Lee, J.; Joo, S.-K. Least squares monte carlo simulation-based decision-making method for photovoltaic investment in Korea. Sustainability 2021, 13, 10613. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Wi, Y.-M.I. Impact of revised time of use tariff on variable renewable energy curtailment on Jeju island. Electronics 2021, 10, 135. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Ghorbanian, M.; Siano, P.; Hatziargyriou, N.D. An enhanced IEEE 33 bus benchmark test system for distribution system studies. IEEE Trans. Power Syst. 2021, 36, 2565–2572. [Google Scholar] [CrossRef]




| Case | Reactive Power (MVAR) |
|---|---|
| 6 | 0.3 |
| 14 | 0.3 |
| 18 | 0.4 |
| 33 | 0.6 |
| Hour | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| 1 | Discharging | Discharging | Discharging | Discharging |
| 2 | Idle | Idle | Moving | Idle |
| 3 | Idle | Idle | Idle | Idle |
| 4 | Charging | Charging | Charging | Charging |
| 5 | Charging | Charging | Charging | Charging |
| 6 | Moving | Idle | Idle | Idle |
| 7 | Discharging | Idle | Idle | Moving |
| 8 | Discharging | Discharging | Discharging | Discharging |
| 9 | Idle | Idle | Moving | Idle |
| 10 | Discharging | Discharging | Discharging | Discharging |
| 11 | Idle | Moving | Idle | Idle |
| 12 | Idle | Idle | Moving | Idle |
| 13 | Charging | Charging | Charging | Charging |
| 14 | Charging | Charging | Charging | Charging |
| 15 | Charging | Charging | Charging | Charging |
| 16 | Moving | Moving | Idle | Idle |
| 17 | Charging | Idle | Idle | Idle |
| 18 | Idle | Discharging | Idle | Idle |
| 19 | Idle | Idle | Idle | Discharging |
| 20 | Discharging | Discharging | Discharging | Discharging |
| 21 | Moving | Discharging | Idle | Moving |
| 22 | Charging | Moving | Idle | Idle |
| 23 | Charging | Idle | Idle | Moving |
| 24 | Idle | Idle | Moving | Idle |
| Case | Operating Cost (KRW) |
|---|---|
| Case 1 | 15,811,261 |
| Case 2 | 15,815,593 |
| Case 3 | 15,813,446 |
| Case 4 | 15,817,811 |
| Case | Forecasting Error | Operating Cost (KRW) | Total Curtailment (kW) | Curtailment Due to Upper Limit (kW) | Curtailment Due to Trip (kW) |
|---|---|---|---|---|---|
| Case 1 | 0 σ | 15,811,261 | 0 | 0 | 0 |
| +0.5 σ | 16,044,332 | 1186 | 0 | 1186 | |
| +1.0 σ | 16,054,169 | 1236 | 0 | 1236 | |
| +1.5 σ | 16,059,278 | 1262 | 0 | 1262 | |
| +2.0 σ | 16,213,351 | 2000 | 0 | 2000 | |
| Case 2 | 0 σ | 15,815,593 | 22 | 22 | 0 |
| +0.5 σ | 15,975,341 | 828 | 51 | 778 | |
| +1.0 σ | 16,064,836 | 1290 | 79 | 1211 | |
| +1.5 σ | 16,087,617 | 1406 | 149 | 1258 | |
| +2.0 σ | 16,255,175 | 2212 | 229 | 1983 | |
| Case 3 | 0 σ | 15,813,446 | 0 | 0 | 0 |
| +0.5 σ | 15,813,446 | 0 | 0 | 0 | |
| +1.0 σ | 15,813,446 | 0 | 0 | 0 | |
| +1.5 σ | 16,049,431 | 1201 | 0 | 1201 | |
| +2.0 σ | 16,215,536 | 2000 | 0 | 2000 | |
| Case 4 | 0 σ | 15,817,811 | 22 | 22 | 0 |
| +0.5 σ | 15,823,394 | 51 | 51 | 0 | |
| +1.0 σ | 15,828,976 | 79 | 79 | 0 | |
| +1.5 σ | 15,842,709 | 149 | 149 | 0 | |
| +2.0 σ | 16,084,269 | 1339 | 229 | 1110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Lee, J. Optimal Scheduling Strategy for Distribution Network with Mobile Energy Storage System and Offline Control PVs to Minimize the Solar Energy Curtailment. Energies 2024, 17, 2234. https://doi.org/10.3390/en17092234
Kim S, Lee J. Optimal Scheduling Strategy for Distribution Network with Mobile Energy Storage System and Offline Control PVs to Minimize the Solar Energy Curtailment. Energies. 2024; 17(9):2234. https://doi.org/10.3390/en17092234
Chicago/Turabian StyleKim, San, and Jinyeong Lee. 2024. "Optimal Scheduling Strategy for Distribution Network with Mobile Energy Storage System and Offline Control PVs to Minimize the Solar Energy Curtailment" Energies 17, no. 9: 2234. https://doi.org/10.3390/en17092234
APA StyleKim, S., & Lee, J. (2024). Optimal Scheduling Strategy for Distribution Network with Mobile Energy Storage System and Offline Control PVs to Minimize the Solar Energy Curtailment. Energies, 17(9), 2234. https://doi.org/10.3390/en17092234







