Upsampling Monte Carlo Reactor Simulation Tallies in Depleted Sodium-Cooled Fast Reactor Assemblies Using a Convolutional Neural Network
Abstract
1. Introduction
2. Methods
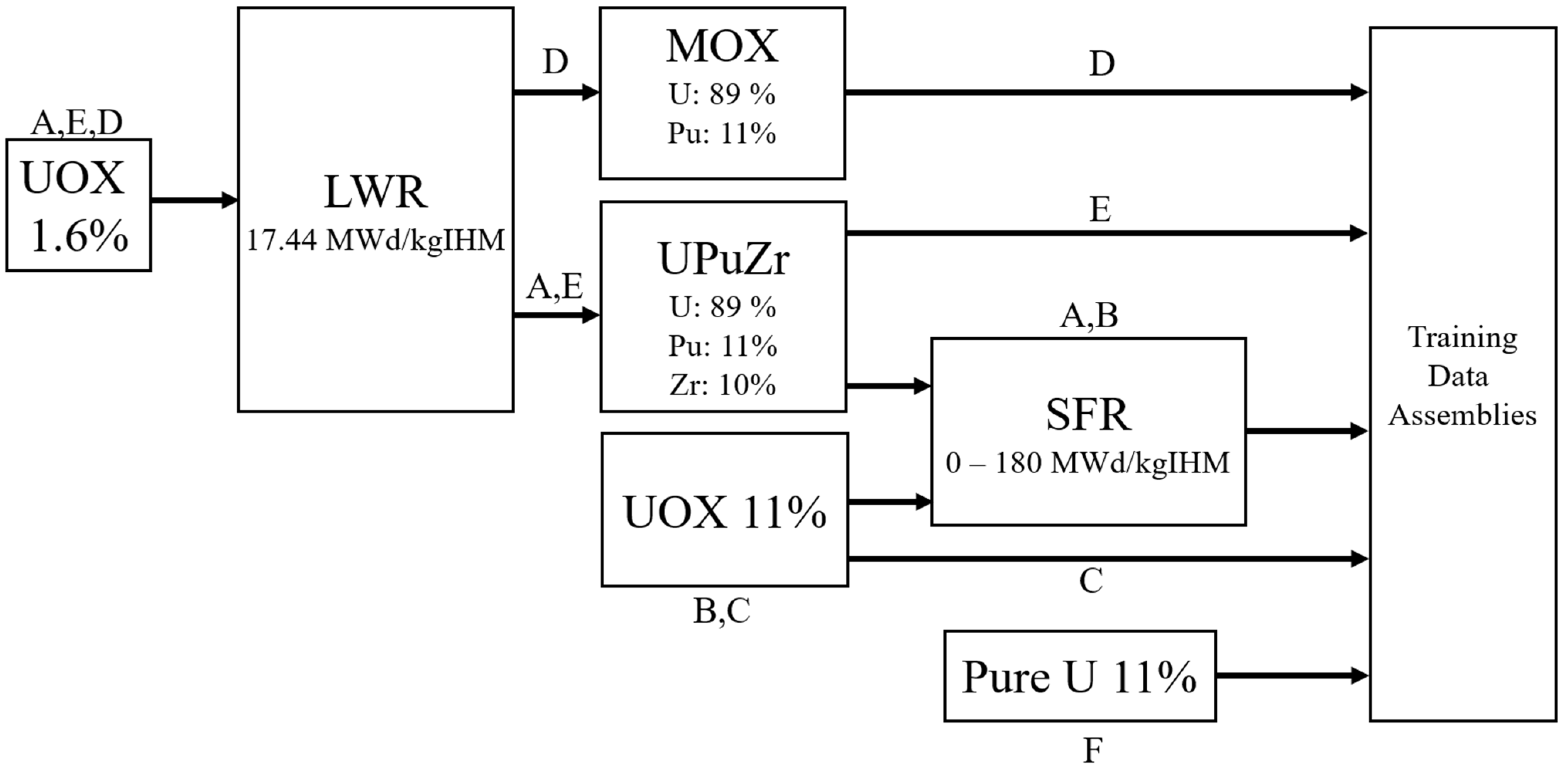
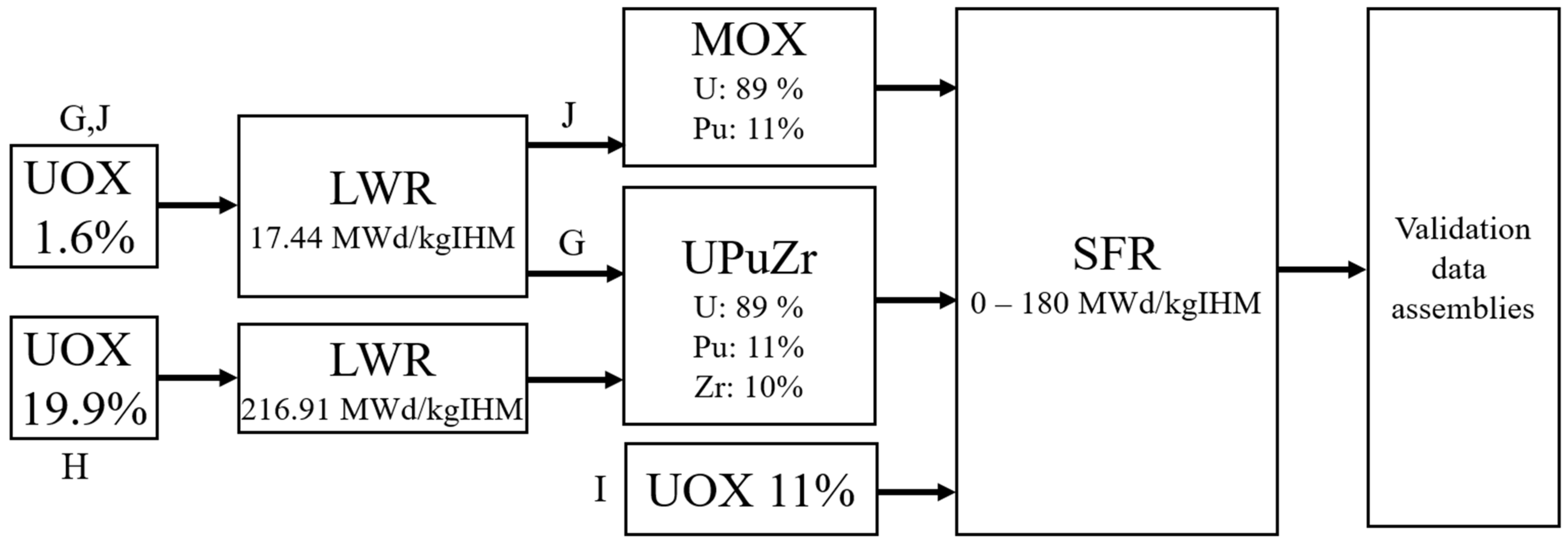
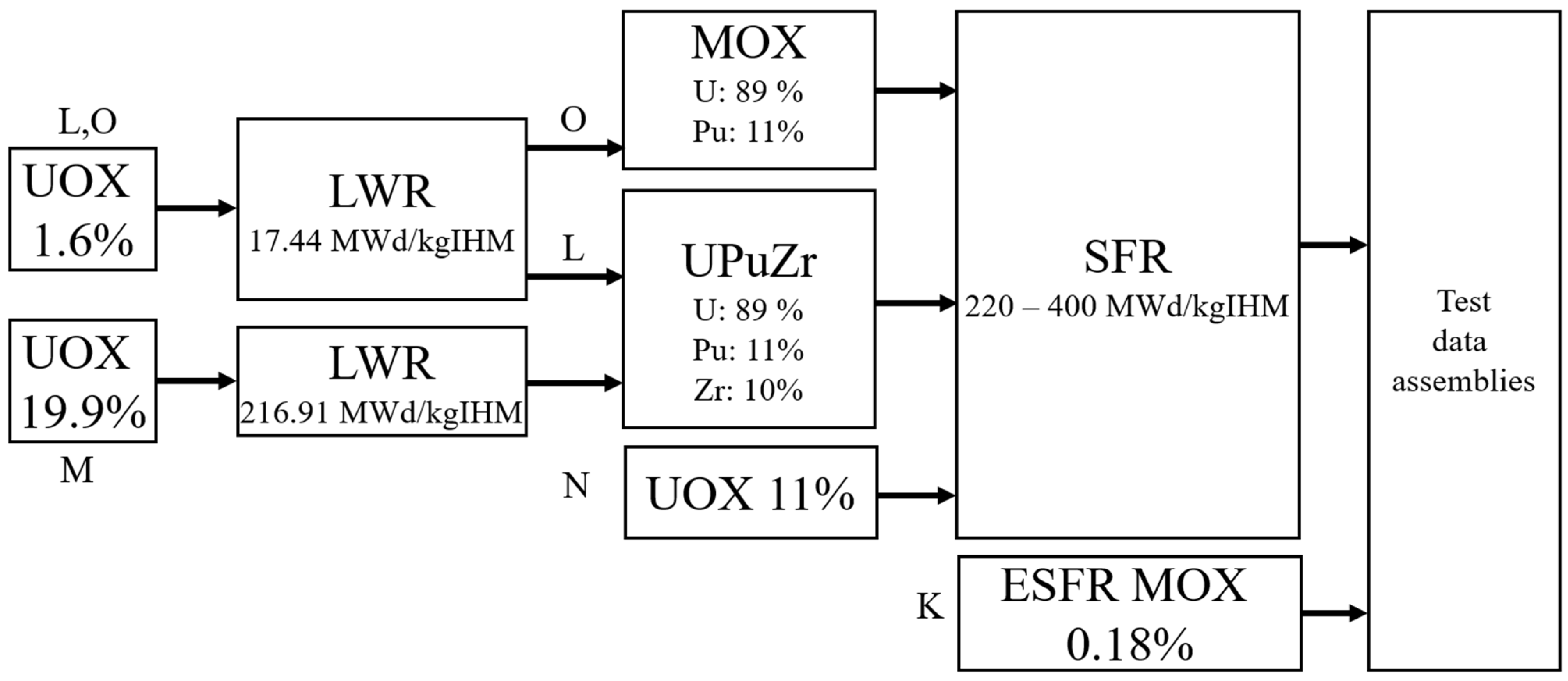
2.1. Data Generation
2.2. Convolutional Neural Network
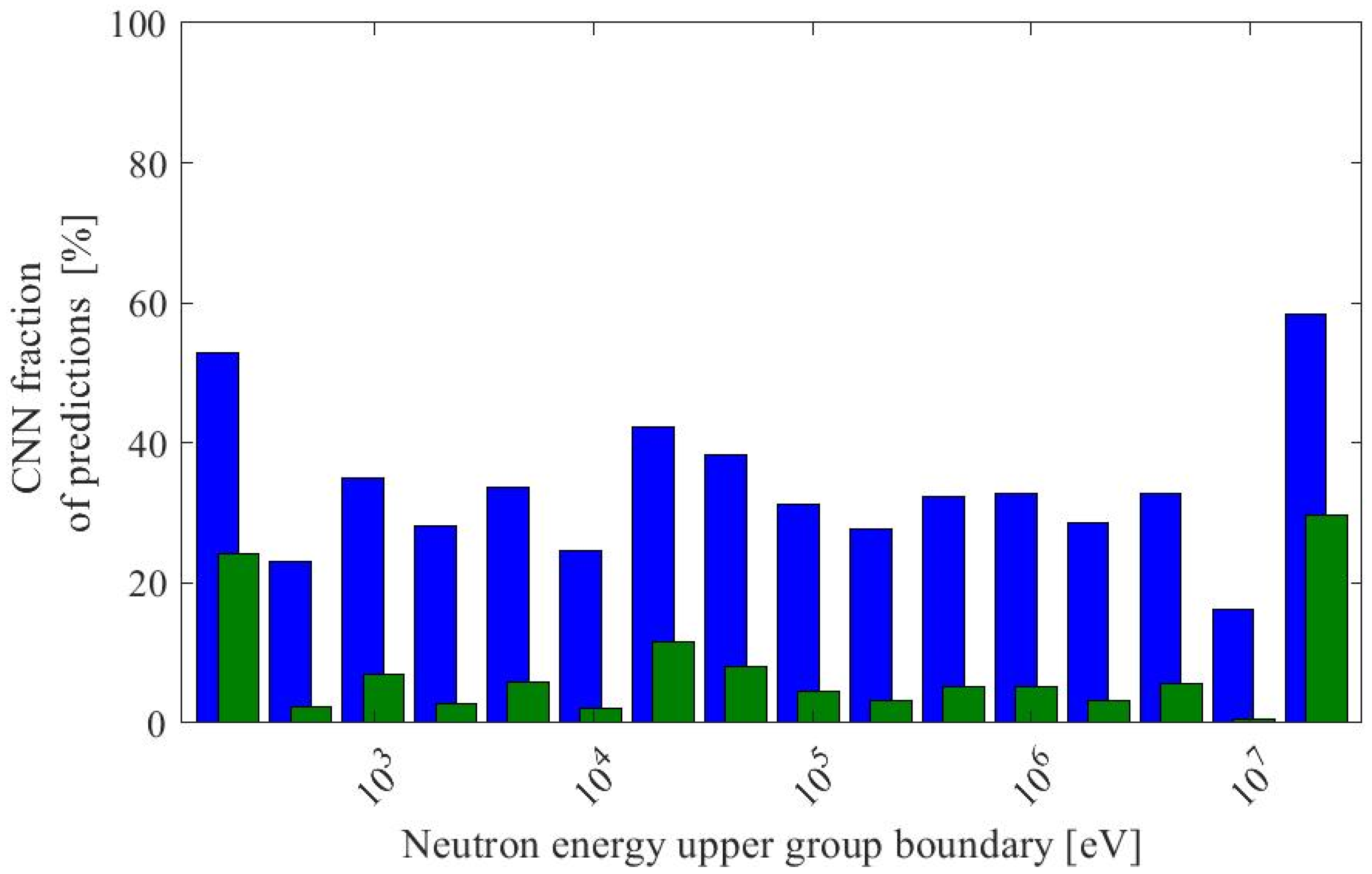
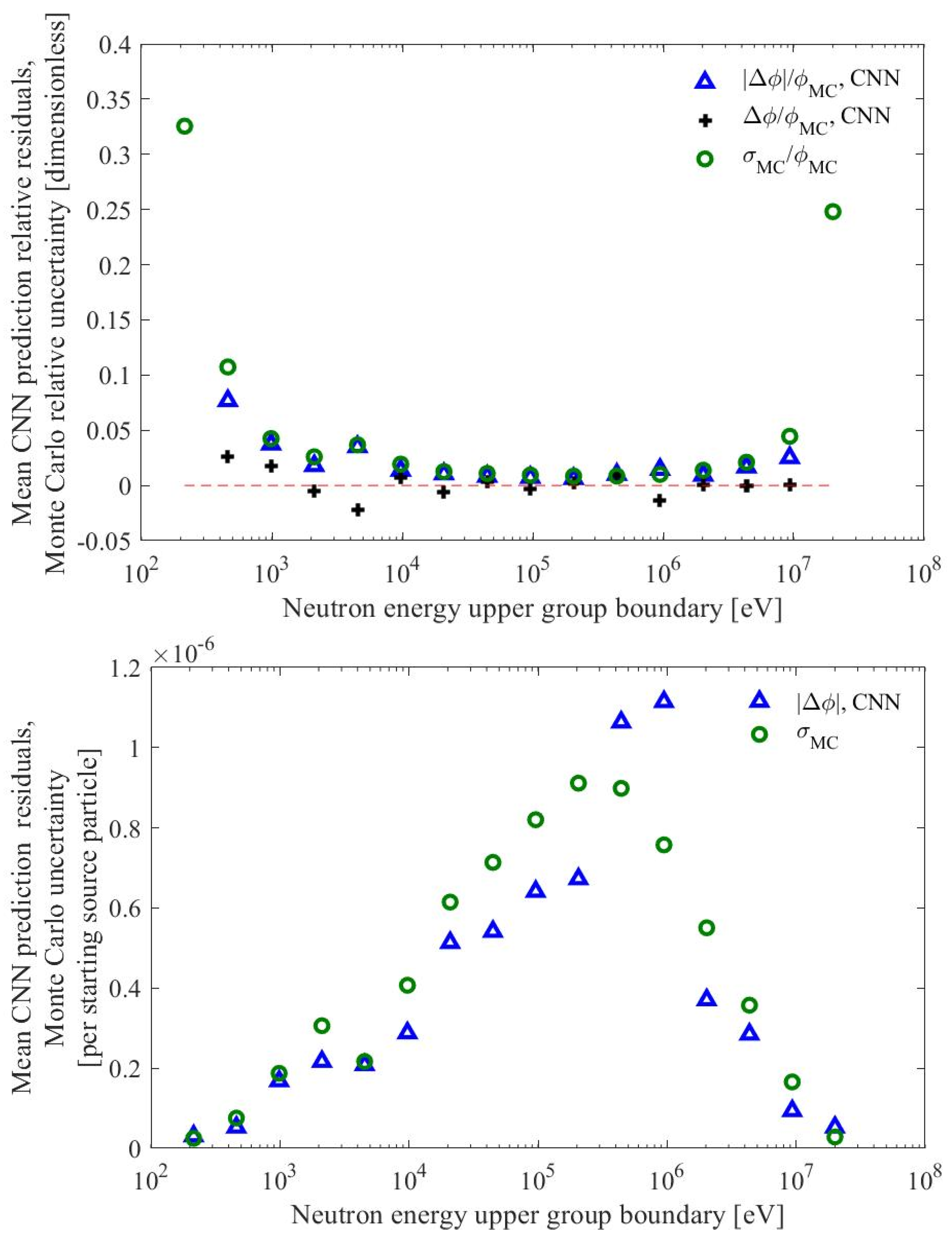
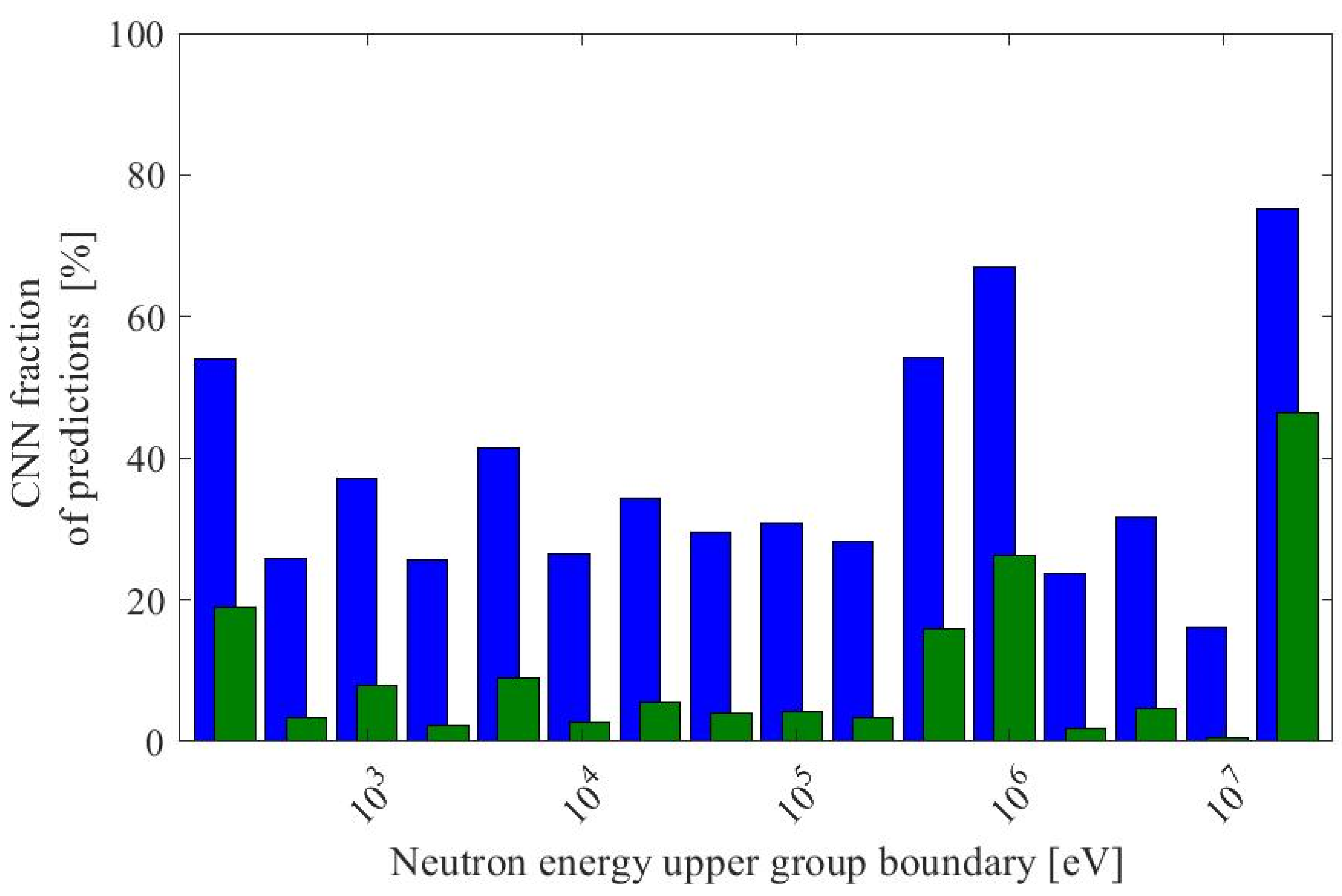
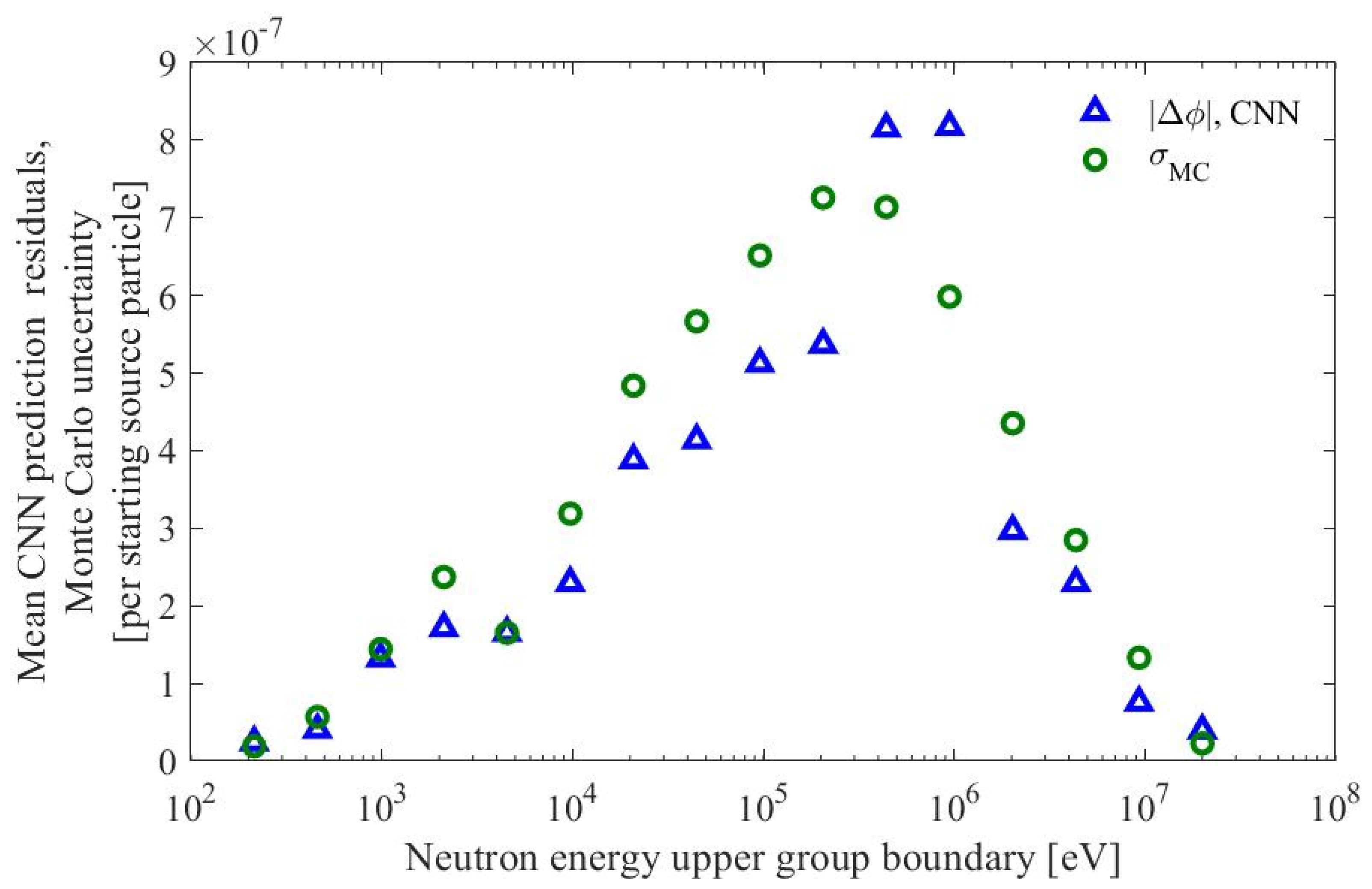
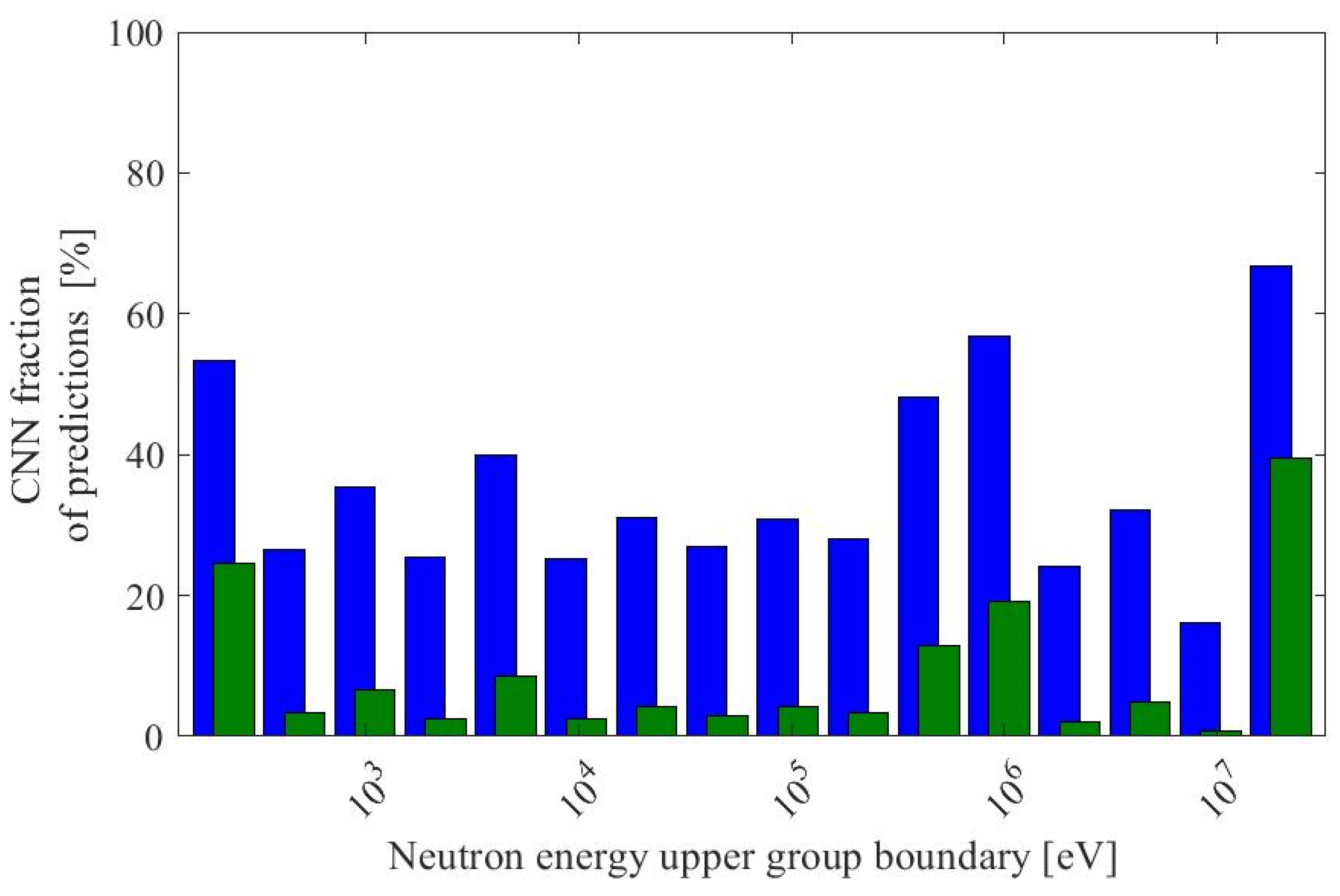
3. Results and Discussion
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
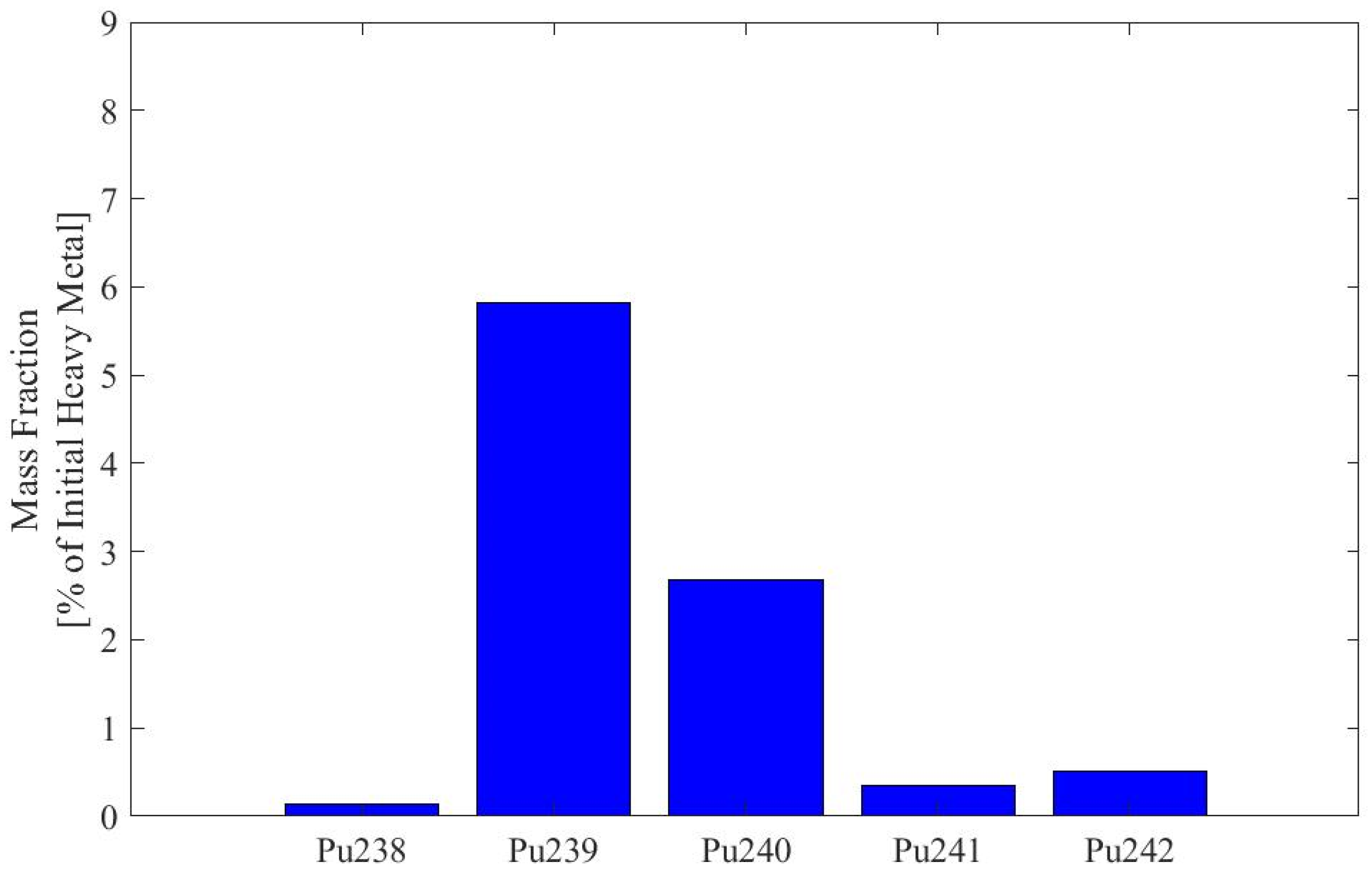
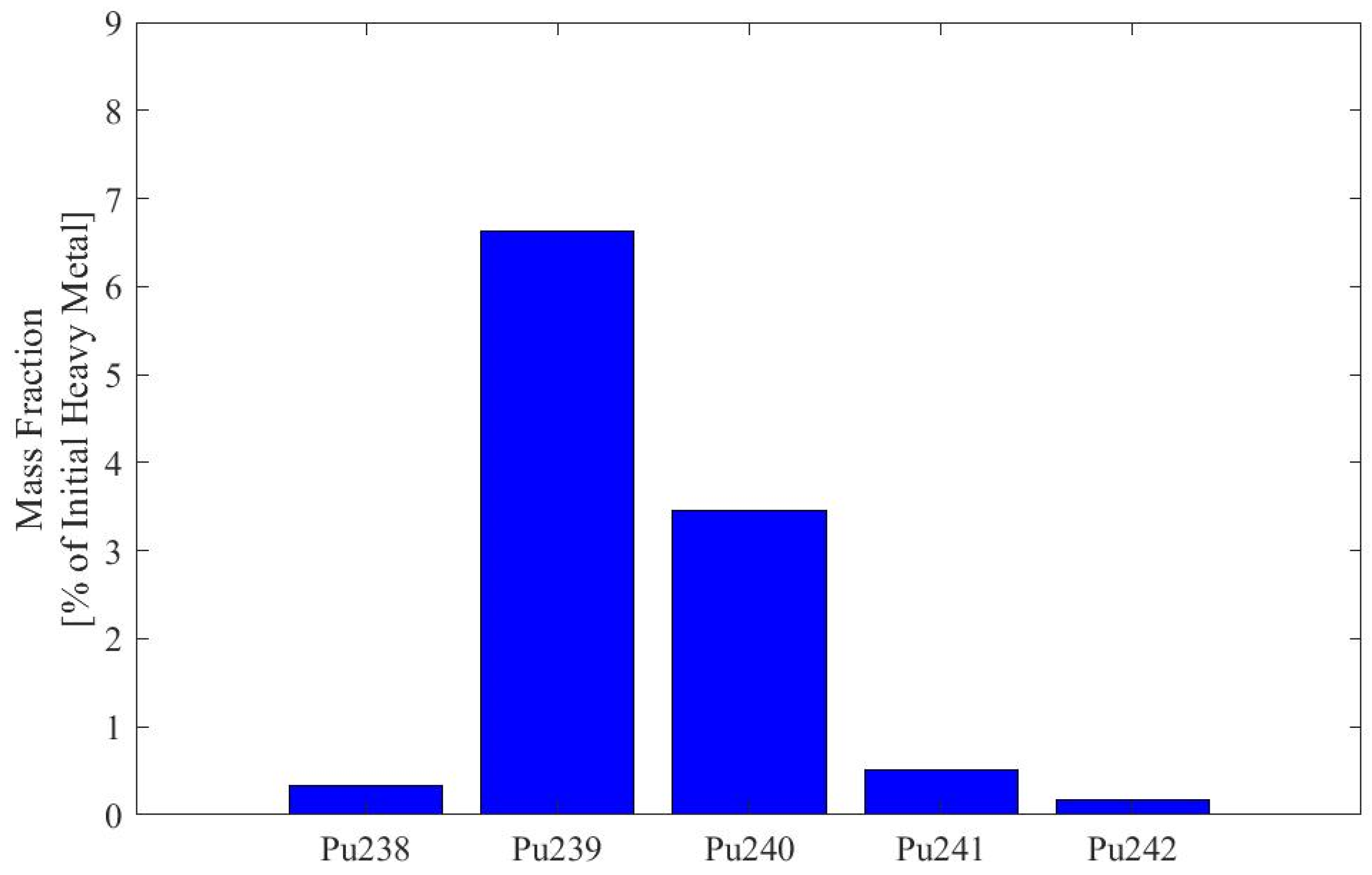
Appendix A. Plutonium Isotopics of Fuel Depleted in SFR Pincell Simulations
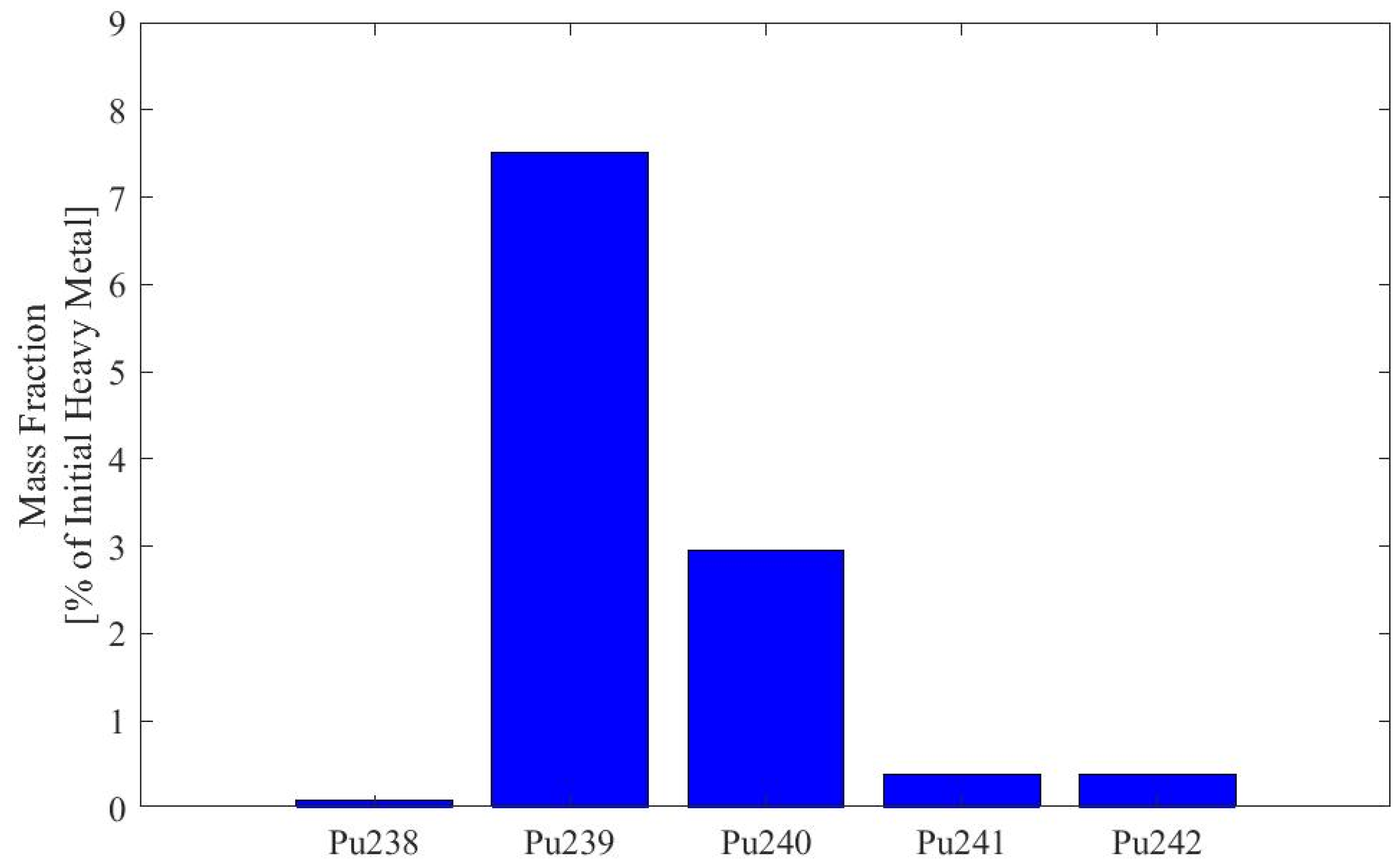

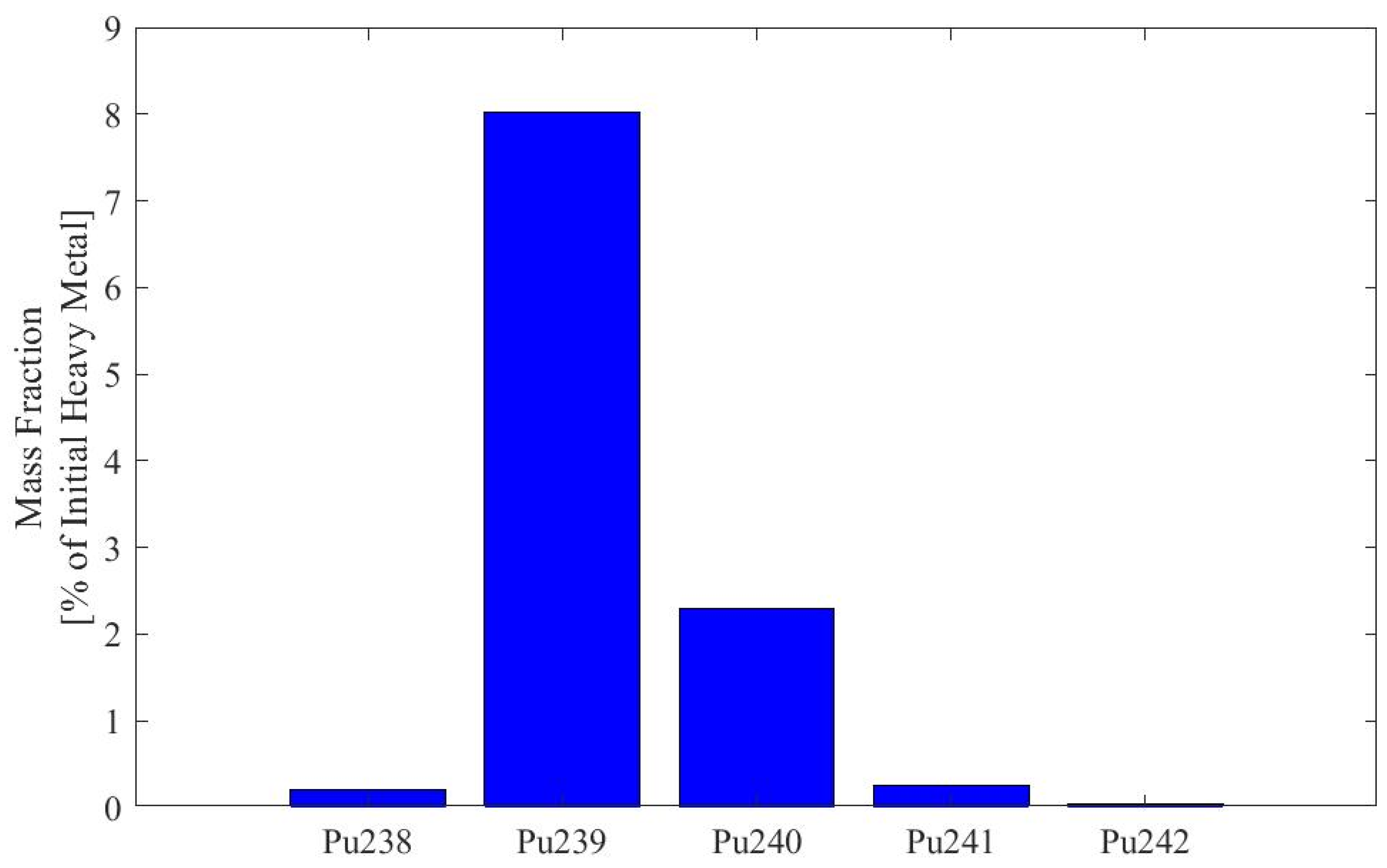
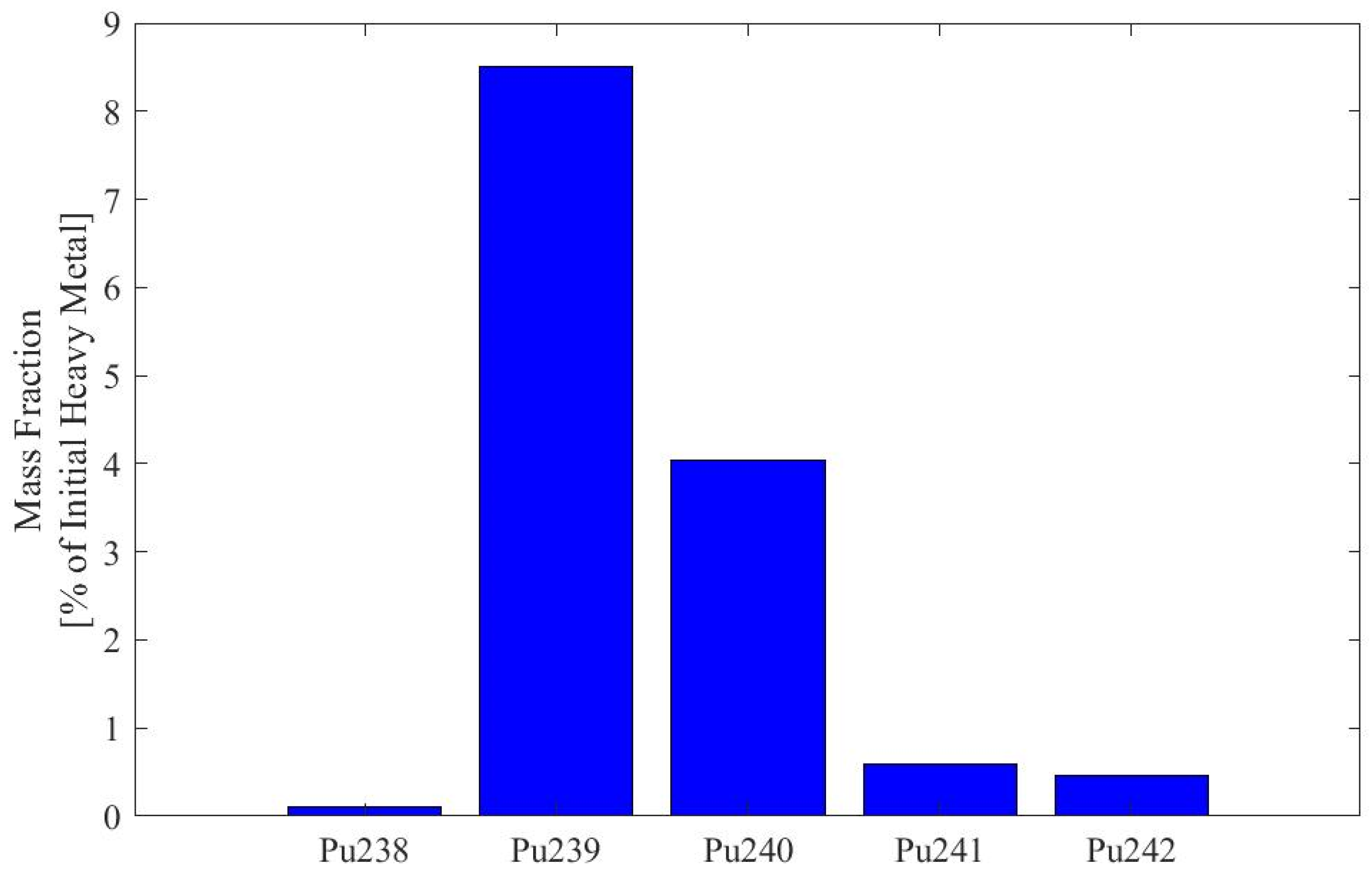
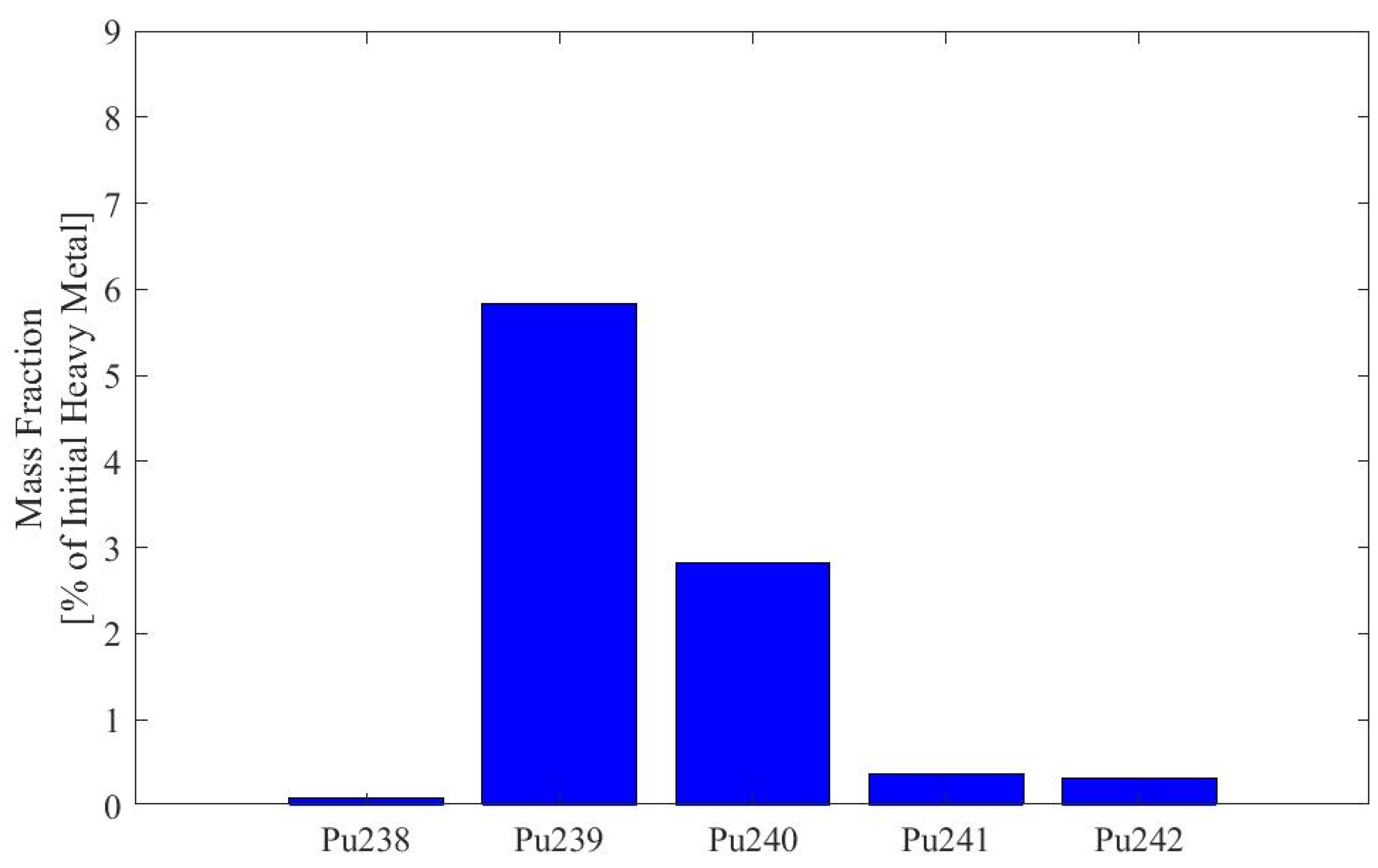

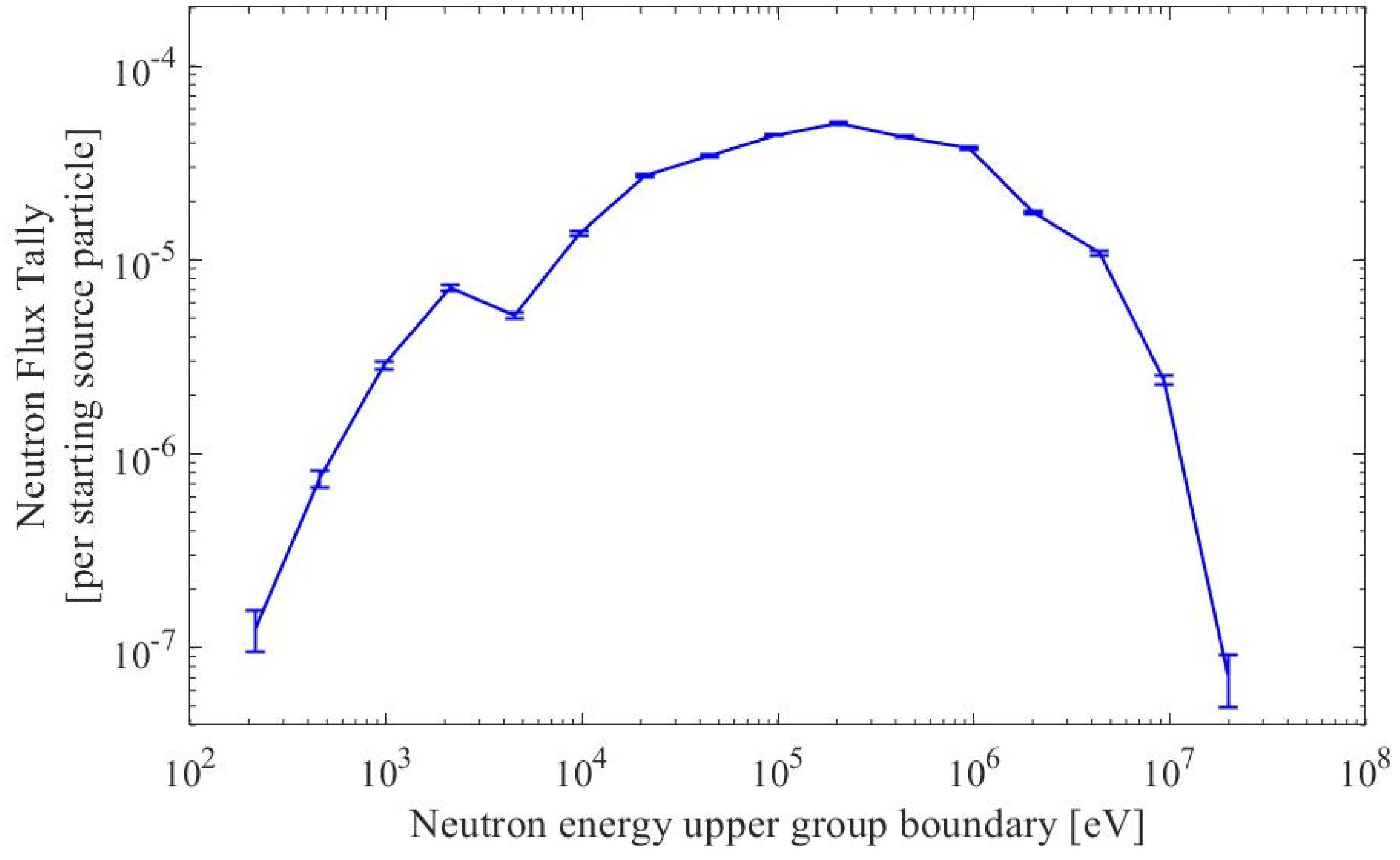
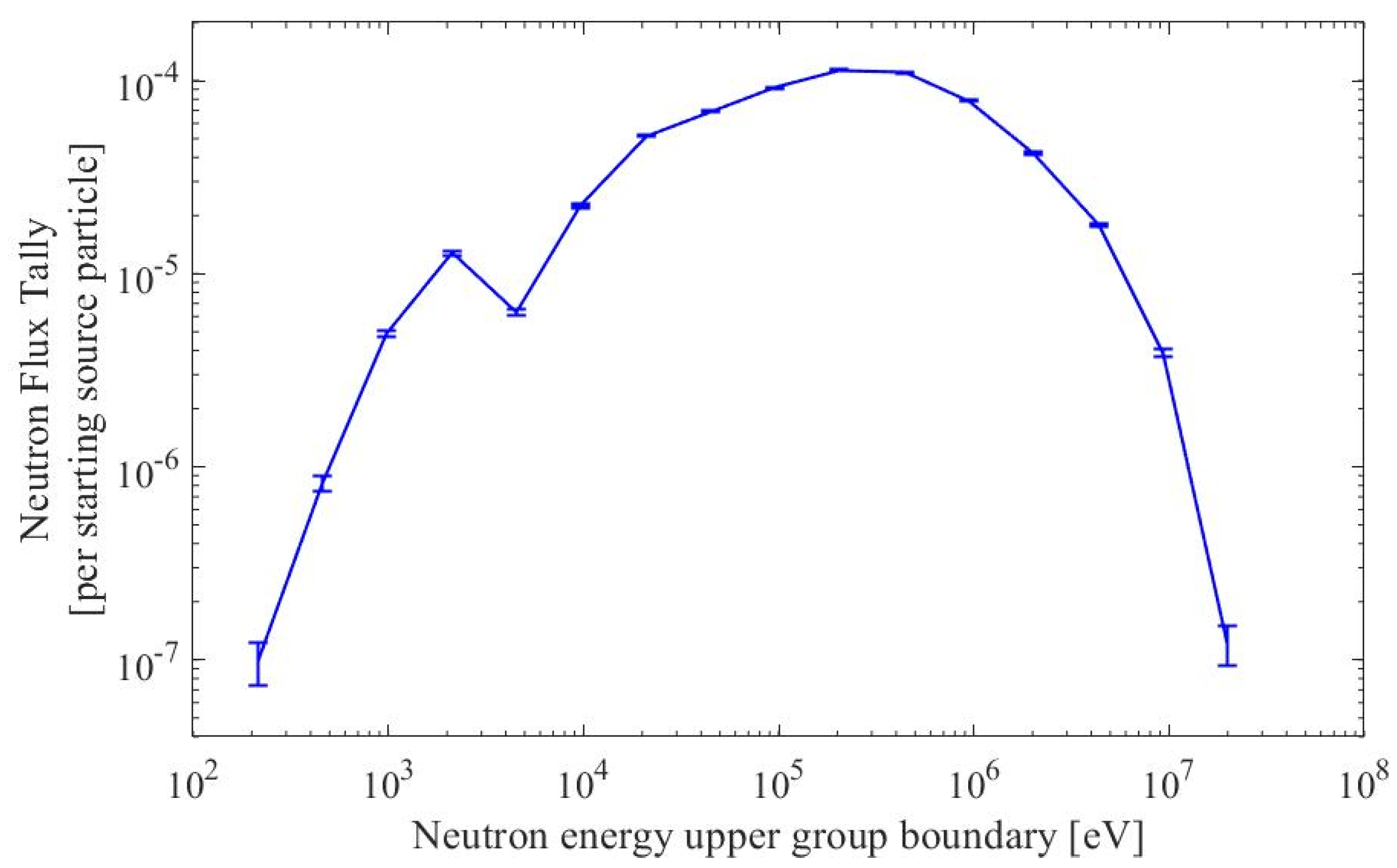
- Neutron Flux Plots: Test Datasets
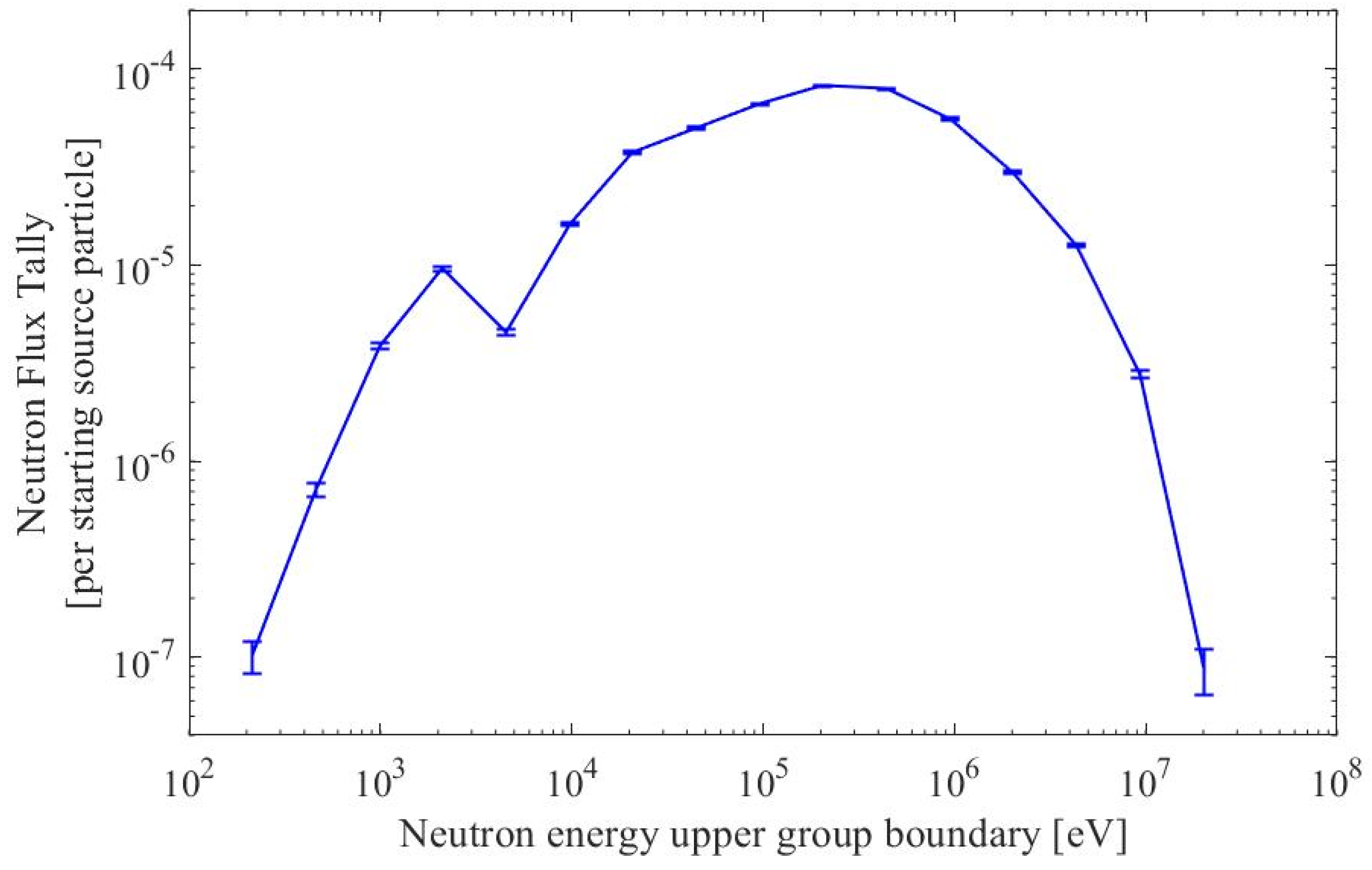
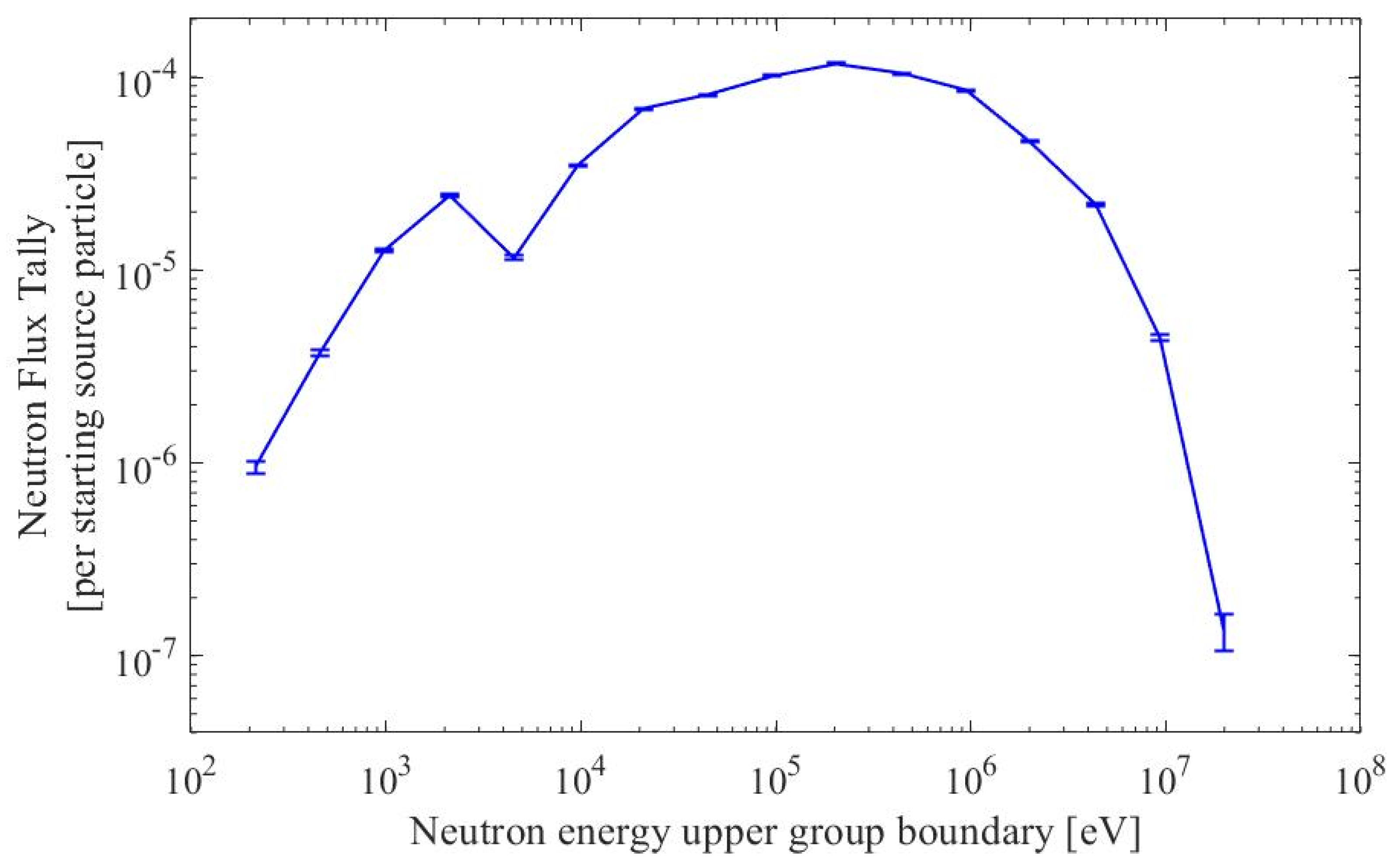
- Tabulated Data: Test Datasets
| Upper Energy Bin [eV] | MC Relative Error [%] | CNN Relative Residual [%] | CNN Relative Residual Bias [%] | MC Absolute Error a | CNN Absolute Residual a | Fraction of Predictions Worse Than MC Uncertainty [%] | |
|---|---|---|---|---|---|---|---|
| 1σ | 2σ | ||||||
| 2.14 × 102 | 24.38 | 34.85 | 29.56 | 2.98 × 10−8 | 3.64 × 10−8 | 52.88 | 24.25 |
| 4.60 × 102 | 10.06 | 6.76 | 1.15 | 7.43 × 10−8 | 4.91 × 10−8 | 23.14 | 2.27 |
| 9.86 × 102 | 5.14 | 4.44 | 2.10 | 1.47 × 10−7 | 1.24 × 10−7 | 35.05 | 7.02 |
| 2.11 × 103 | 3.26 | 2.39 | −1.24 | 2.34 × 10−7 | 1.72 × 10−7 | 28.07 | 2.67 |
| 4.53 × 103 | 3.86 | 3.22 | 0.87 | 1.99 × 10−7 | 1.65 × 10−7 | 33.72 | 5.94 |
| 9.72 × 103 | 2.37 | 1.62 | −0.45 | 3.23 × 10−7 | 2.22 × 10−7 | 24.53 | 2.01 |
| 2.09 × 104 | 1.67 | 1.68 | 1.21 | 4.52 × 10−7 | 4.49 × 10−7 | 42.27 | 11.65 |
| 4.47 × 104 | 1.49 | 1.35 | −0.91 | 5.12 × 10−7 | 4.70 × 10−7 | 38.21 | 8.11 |
| 9.59 × 104 | 1.31 | 1.04 | 0.43 | 5.77 × 10−7 | 4.53 × 10−7 | 31.16 | 4.59 |
| 2.06 × 105 | 1.22 | 0.90 | 0.14 | 6.17 × 10−7 | 4.50 × 10−7 | 27.64 | 3.17 |
| 4.41 × 105 | 1.32 | 1.07 | 0.20 | 5.70 × 10−7 | 4.60 × 10−7 | 32.39 | 5.18 |
| 9.46 × 105 | 1.40 | 1.14 | −0.04 | 5.32 × 10−7 | 4.32 × 10−7 | 32.84 | 5.08 |
| 2.03 × 106 | 2.06 | 1.53 | −0.65 | 3.59 × 10−7 | 2.68 × 10−7 | 28.48 | 3.10 |
| 4.35 × 106 | 2.61 | 2.13 | 0.85 | 2.82 × 10−7 | 2.28 × 10−7 | 32.68 | 5.56 |
| 9.33 × 106 | 5.52 | 3.14 | −0.05 | 1.32 × 10−7 | 7.47 × 10−8 | 16.20 | 0.64 |
| 2.00 × 107 | 31.57 | 53.90 | 50.44 | 2.16 × 10−8 | 2.83 × 10−8 | 58.41 | 29.68 |
| Upper Energy Bin [eV] | MC Relative Error [%] | CNN Relative Residual [%] | CNN Relative Residual Bias [%] | MC Absolute Error a | CNN Absolute Residual a | Fraction of Predictions Worse Than MC Uncertainty [%] | |
|---|---|---|---|---|---|---|---|
| 1σ | 2σ | ||||||
| 2.14 × 102 | 32.55 | 43.74 | −8.21 | 2.48 × 10−8 | 3.08 × 10−8 | 54.07 | 18.94 |
| 4.60 × 102 | 10.73 | 7.68 | 2.65 | 7.54 × 10−8 | 5.27 × 10−8 | 25.88 | 3.39 |
| 9.86 × 102 | 4.25 | 3.74 | 1.78 | 1.87 × 10−7 | 1.68 × 10−7 | 37.05 | 7.95 |
| 2.11 × 103 | 2.59 | 1.79 | −0.49 | 3.06 × 10−7 | 2.17 × 10−7 | 25.55 | 2.23 |
| 4.53 × 103 | 3.68 | 3.51 | −2.22 | 2.17 × 10−7 | 2.08 × 10−7 | 41.35 | 8.98 |
| 9.72 × 103 | 1.93 | 1.37 | 0.74 | 4.07 × 10−7 | 2.88 × 10−7 | 26.48 | 2.78 |
| 2.09 × 104 | 1.26 | 1.05 | −0.56 | 6.15 × 10−7 | 5.14 × 10−7 | 34.30 | 5.45 |
| 4.47 × 104 | 1.08 | 0.83 | 0.36 | 7.14 × 10−7 | 5.41 × 10−7 | 29.62 | 3.90 |
| 9.59 × 104 | 0.94 | 0.73 | −0.31 | 8.21 × 10−7 | 6.42 × 10−7 | 30.86 | 4.13 |
| 2.06 × 105 | 0.84 | 0.62 | 0.22 | 9.12 × 10−7 | 6.73 × 10−7 | 28.22 | 3.35 |
| 4.41 × 105 | 0.85 | 1.00 | 0.90 | 8.99 × 10−7 | 1.06 × 10−6 | 54.15 | 15.94 |
| 9.46 × 105 | 1.01 | 1.45 | −1.39 | 7.58 × 10−7 | 1.11 × 10−6 | 67.00 | 26.27 |
| 2.03 × 106 | 1.38 | 0.93 | 0.02 | 5.51 × 10−7 | 3.71 × 10−7 | 23.74 | 1.93 |
| 4.35 × 106 | 2.10 | 1.67 | −0.03 | 3.57 × 10−7 | 2.85 × 10−7 | 31.72 | 4.75 |
| 9.33 × 106 | 4.45 | 2.52 | 0.07 | 1.66 × 10−7 | 9.37 × 10−8 | 16.06 | 0.64 |
| 2.00 × 107 | 24.81 | 53.11 | 52.09 | 2.84 × 10−8 | 5.25 × 10−8 | 75.21 | 46.35 |
| Upper Energy Bin [eV] | MC Relative Error [%] | CNN Relative Residual [%] | CNN Relative Residual Bias [%] | MC Absolute Error a | CNN Absolute Residual a | Fraction of Predictions Worse Than MC Uncertainty [%] | |
|---|---|---|---|---|---|---|---|
| 1σ | 2σ | ||||||
| 2.14 × 102 | 59.16 | 282.61 | 196.20 | 1.91 × 10−8 | 2.41 × 10−8 | 53.45 | 24.56 |
| 4.60 × 102 | 17.95 | 13.11 | 1.37 | 5.68 × 10−8 | 4.04 × 10−8 | 26.42 | 3.37 |
| 9.86 × 102 | 6.48 | 5.37 | −0.07 | 1.44 × 10−7 | 1.32 × 10−7 | 35.39 | 6.49 |
| 2.11 × 103 | 3.81 | 2.62 | 0.47 | 2.37 × 10−7 | 1.72 × 10−7 | 25.42 | 2.55 |
| 4.53 × 103 | 5.43 | 4.89 | −2.06 | 1.65 × 10−7 | 1.65 × 10−7 | 39.97 | 8.49 |
| 9.72 × 103 | 2.71 | 1.85 | 0.73 | 3.19 × 10−7 | 2.30 × 10−7 | 25.27 | 2.57 |
| 2.09 × 104 | 1.76 | 1.36 | −0.50 | 4.84 × 10−7 | 3.88 × 10−7 | 31.00 | 4.16 |
| 4.47 × 104 | 1.49 | 1.06 | 0.27 | 5.67 × 10−7 | 4.14 × 10−7 | 26.87 | 2.99 |
| 9.59 × 104 | 1.28 | 1.00 | −0.36 | 6.52 × 10−7 | 5.12 × 10−7 | 30.85 | 4.12 |
| 2.06 × 105 | 1.14 | 0.85 | 0.27 | 7.26 × 10−7 | 5.37 × 10−7 | 28.12 | 3.36 |
| 4.41 × 105 | 1.16 | 1.20 | 1.00 | 7.14 × 10−7 | 8.15 × 10−7 | 48.10 | 12.96 |
| 9.46 × 105 | 1.37 | 1.64 | −1.46 | 5.98 × 10−7 | 8.17 × 10−7 | 56.89 | 19.07 |
| 2.03 × 106 | 1.87 | 1.27 | −0.01 | 4.35 × 10−7 | 2.97 × 10−7 | 24.24 | 2.05 |
| 4.35 × 106 | 2.80 | 2.24 | 0.16 | 2.85 × 10−7 | 2.30 × 10−7 | 32.08 | 4.92 |
| 9.33 × 106 | 5.86 | 3.33 | 0.09 | 1.33 × 10−7 | 7.54 × 10−8 | 16.13 | 0.68 |
| 2.00 × 107 | 32.88 | 66.87 | 64.30 | 2.27 × 10−8 | 3.94 × 10−8 | 66.71 | 39.41 |
| Upper Energy Bin [eV] | MC Relative Error [%] | CNN Relative Residual [%] | CNN Relative Residual Bias [%] | MC Absolute Error a | CNN Absolute Residual a | Fraction of Predictions Worse Than MC Uncertainty [%] | |
|---|---|---|---|---|---|---|---|
| 1σ | 2σ | ||||||
| 2.14 × 102 | 13.53 | 13.32 | −7.23 | 6.92 × 10−8 | 6.47 × 10−8 | 42.66 | 9.18 |
| 4.60 × 102 | 5.82 | 4.03 | 1.66 | 1.50 × 10−7 | 1.01 × 10−7 | 24.44 | 2.63 |
| 9.86 × 102 | 2.89 | 2.36 | 1.01 | 2.88 × 10−7 | 2.30 × 10−7 | 32.45 | 5.41 |
| 2.11 × 103 | 2.01 | 1.39 | −0.44 | 4.09 × 10−7 | 2.85 × 10−7 | 25.24 | 2.19 |
| 4.53 × 103 | 2.87 | 2.35 | −0.42 | 2.86 × 10−7 | 2.42 × 10−7 | 33.87 | 5.55 |
| 9.72 × 103 | 1.61 | 1.06 | 0.25 | 4.98 × 10−7 | 3.35 × 10−7 | 23.26 | 1.91 |
| 2.09 × 104 | 1.15 | 0.86 | −0.10 | 6.91 × 10−7 | 5.19 × 10−7 | 28.84 | 3.49 |
| 4.47 × 104 | 1.05 | 0.75 | 0.05 | 7.58 × 10−7 | 5.48 × 10−7 | 26.92 | 2.90 |
| 9.59 × 104 | 0.93 | 0.68 | 0.02 | 8.47 × 10−7 | 6.22 × 10−7 | 27.77 | 3.16 |
| 2.06 × 105 | 0.86 | 0.62 | 0.05 | 9.12 × 10−7 | 6.55 × 10−7 | 26.70 | 2.83 |
| 4.41 × 105 | 0.92 | 0.81 | 0.54 | 8.57 × 10−7 | 7.56 × 10−7 | 37.07 | 7.01 |
| 9.46 × 105 | 1.00 | 0.93 | −0.65 | 7.76 × 10−7 | 7.22 × 10−7 | 39.79 | 7.94 |
| 2.03 × 106 | 1.35 | 1.08 | −0.66 | 5.72 × 10−7 | 4.52 × 10−7 | 32.24 | 4.24 |
| 4.35 × 106 | 1.92 | 1.96 | 1.39 | 3.94 × 10−7 | 3.91 × 10−7 | 43.78 | 11.59 |
| 9.33 × 106 | 4.19 | 2.38 | 0.21 | 1.77 × 10−7 | 1.01 × 10−7 | 16.26 | 0.70 |
| 2.00 × 107 | 23.77 | 43.03 | 41.12 | 2.99 × 10−8 | 4.94 × 10−8 | 66.78 | 37.54 |
References
- Leppänen, J.; Pusa, M.; Viitanen, T.; Valtavirta, V.; Kaltiaisenaho, T. The Serpent Monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 2015, 82, 142–150. [Google Scholar] [CrossRef]
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B.; Smith, K. OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Werner, C.J.; Brown, F.B.; Bull, J.S.; Casswell, L.; Cox, L.J.; Dixon, D.; Forster, R.A. MCNP® User’s Manual, Code Version 6.2; Los Alamos National Laboratory: Los Alamos, NM, USA, 2017. [Google Scholar]
- Wendt, B.; Kerby, L.; Tumulak, A.; Leppänen, J. Advancement of functional expansion capabilities: Implementation and optimization in Serpent 2. Nucl. Eng. Des. 2018, 334, 138–153. [Google Scholar] [CrossRef]
- Horelik, N.; Siegel, A.; Forget, B.; Smith, K. Monte Carlo domain decomposition for robust nuclear reactor analysis. Parallel Comput. 2014, 40, 646–660. [Google Scholar] [CrossRef]
- García, M.; Leppänen, J.; Sanchez-Espinoza, V. A Collision-based Domain Decomposition scheme for large-scale depletion with the Serpent 2 Monte Carlo code. Ann. Nucl. Energy 2021, 152, 108026. [Google Scholar] [CrossRef]
- Vaquer, P.A.; McClarren, R.G.; Ayzman, Y.J. A Compressed Sensing Framework for Monte Carlo Transport Simulations Using Random Disjoint Tallies. J. Comput. Theor. Transp. 2016, 45, 219–229. [Google Scholar] [CrossRef]
- Madsen, J.R. Disjoint Tally Method: A Monte Carlo Scoring Method Using Compressed Sensing to Reduce Statistical Noise and Memory. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2017. [Google Scholar]
- Osborne, A.; Dorville, J.; Romano, P. Upsampling Monte Carlo neutron transport simulation tallies using a convolutional neural network. Energy AI 2023, 13, 100247. [Google Scholar] [CrossRef]
- Berry, J.; Romano, P.; Osborne, A. Upsampling Monte Carlo reactor simulation tallies in depleted LWR assemblies fueled with LEU and HALEU using a convolutional neural network. AIP Adv. 2024, 14, 015004. [Google Scholar] [CrossRef]
- Facchini, A.; Giusti, V.; Ciolini, R.; Tuček, K.; Thomas, D.; D’Agata, E. Detailed neutronic study of the power evolution for the European Sodium Fast Reactor during a positive insertion of reactivity. Nucl. Eng. Des. 2017, 313, 1–9. [Google Scholar] [CrossRef]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nuclear Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Berry, J.; Romano, P.; Osborne, A. Data and Software: Upsampling Monte Carlo Reactor Simulation Tallies in Depleted SFR Assemblies using a Convolutional Neural Network 2024. AIP Adv. 2024, 14, 015004. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1132–1140. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Stengel, K.; Glaws, A.; Hettinger, D.; King, R.N. Adversarial super-resolution of climatological wind and solar data. Proc. Natl. Acad. Sci. USA 2020, 117, 16805–16815. [Google Scholar] [CrossRef]
- Wilkinson, I.M.; Bhattacharjee, R.R.; Shafer, J.C.; Osborne, A.G. Confidence estimation in the prediction of epithermal neutron resonance self-shielding factors in irradiation samples using an ensemble neural network. Energy AI 2022, 7, 100131. [Google Scholar] [CrossRef]
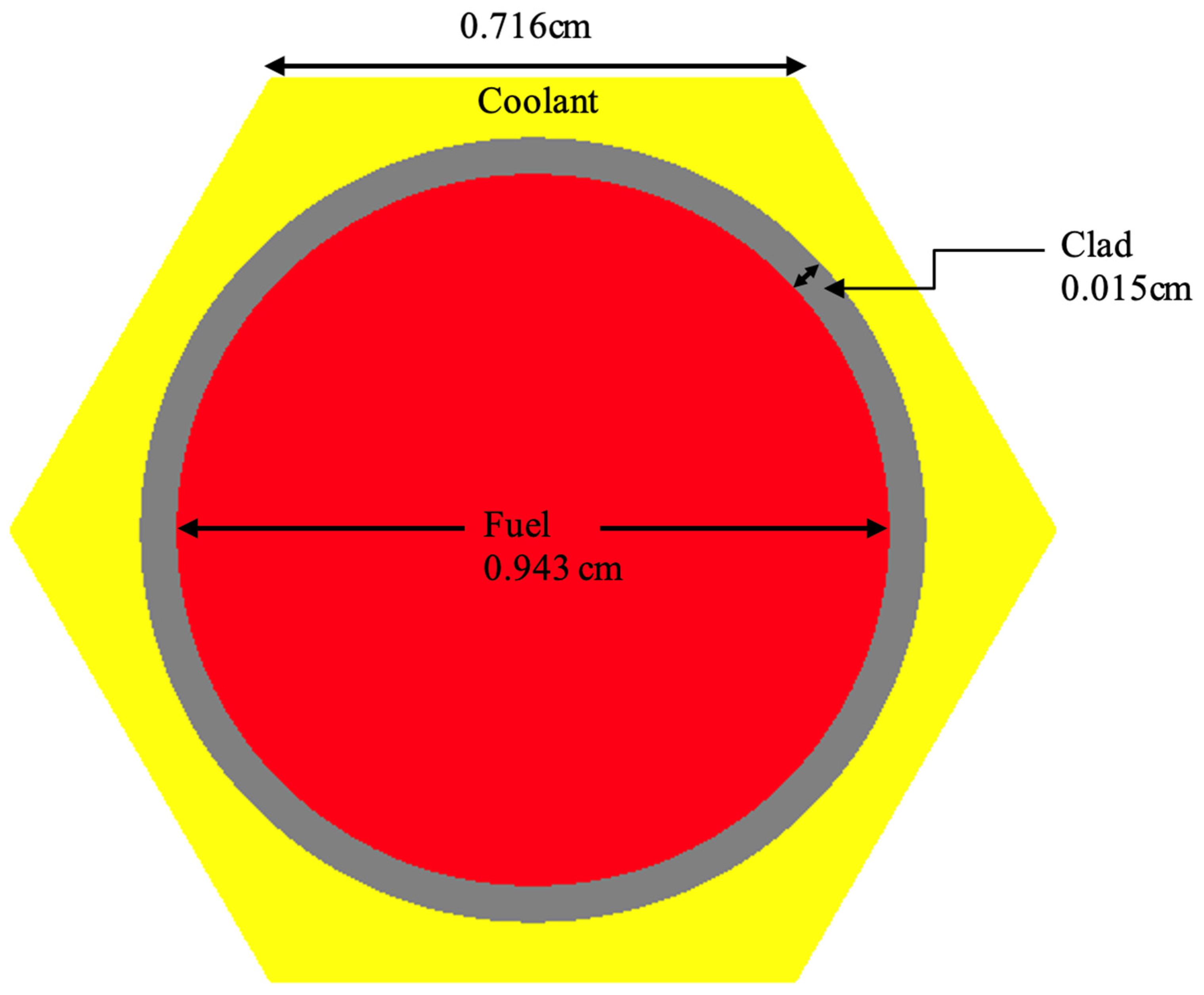



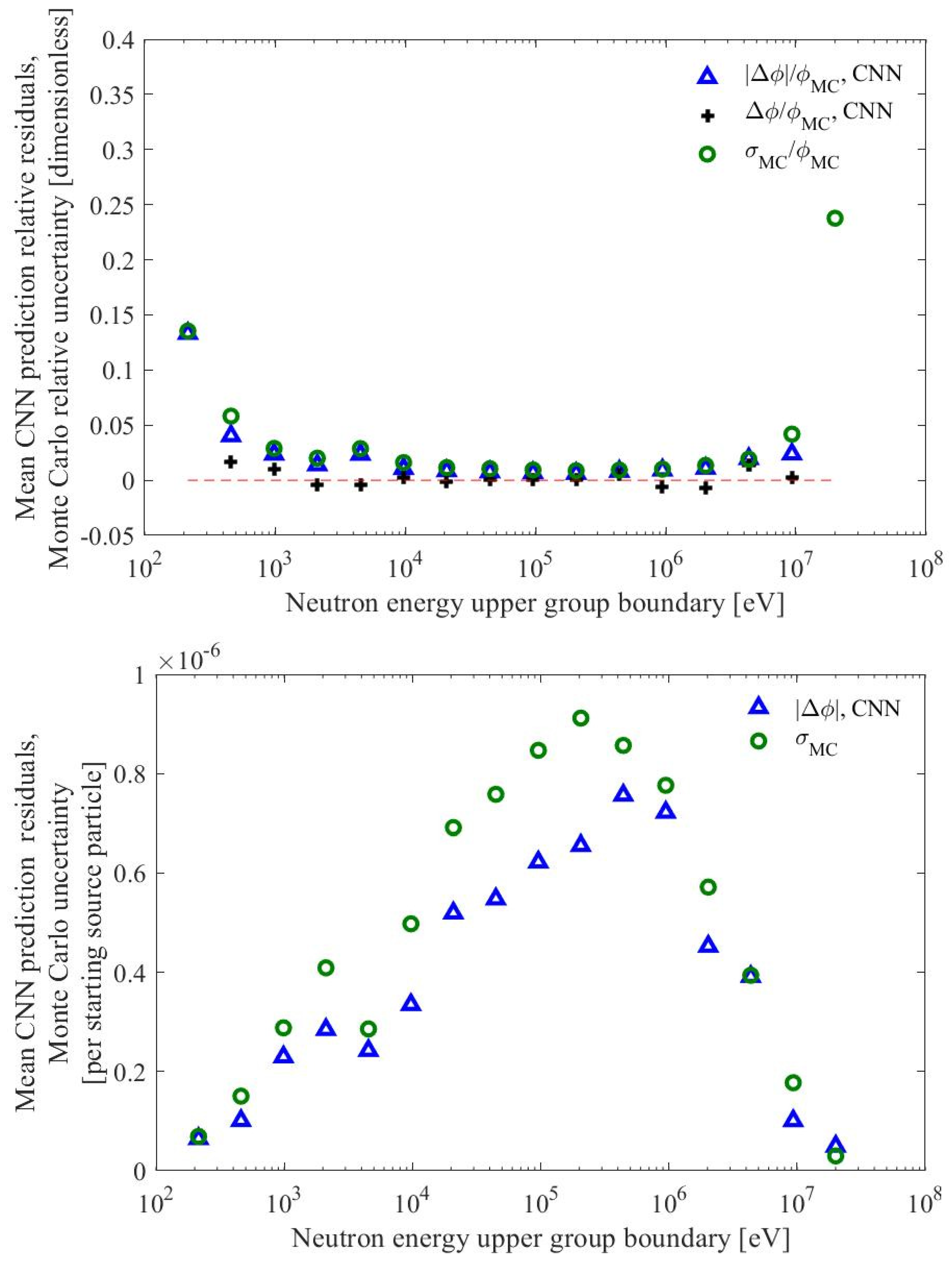
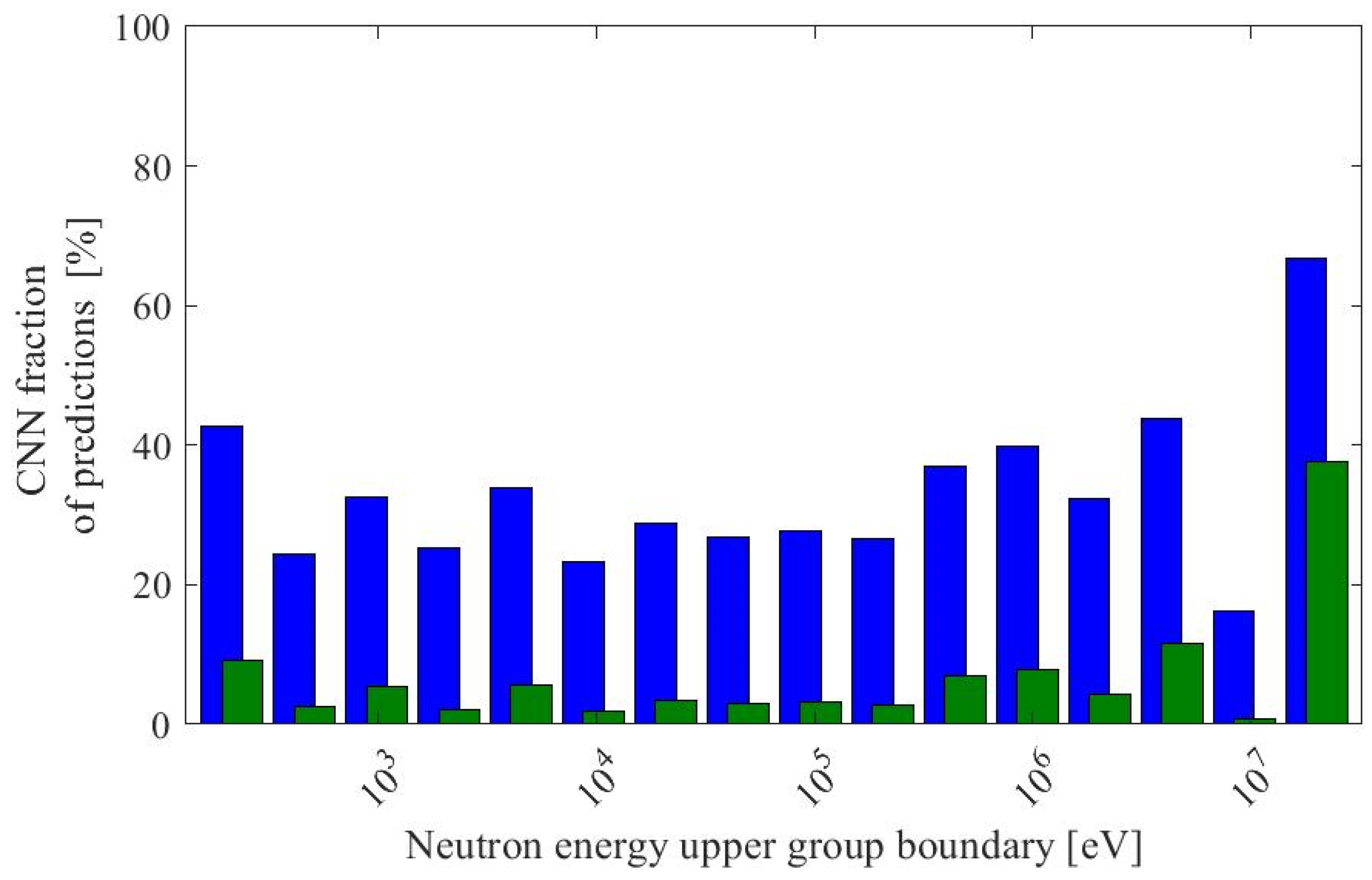
| Parameter | Range (Procedurally Generated Assemblies) | Value (ESFR Test Assembly) |
|---|---|---|
| Pin Diameter a | 0.5 to 1.0 | 0.4715 cm |
| Pin Pitch [cm] | 0.51 to 1.32 | 1.073 cm |
| Clad Thickness a | 0.0633 to 0.0942 | 0.5 mm |
| Duct Thickness [cm] | 0 to 0.24 | 0.45 cm |
| Coolant Temperature [K] | 350 to 800 | 743 |
| Fuel Temperature [K] | 500 to 1428 | 1624 |
| Assembly Rings | 2 to 5 (training) 10 to 11 (validation and testing) | 10 |
| Dataset | Number of Samples | Data Type | Fuel Type | Plutonium Origin | Spectrum | Burnup Range [MWd/kgIHM] | Fraction of B4C, Empty Pin Positions |
|---|---|---|---|---|---|---|---|
| A | 50 | Training | UPuZr a | 1.6% UOX b LWR | SFR | 0 to 180 | 14%, 14% |
| B | 50 | Training | UOX b | N/A (Fresh 11% UOX b in pincell sim) | SFR (Softened, OX Fuel) | 0 to 180 | 14%, 14% |
| C | 50 | Training | UOX b | N/A (Fresh UOX b) | SFR (Softened, OX Fuel) | 0 | [0% or 14%], [14% or 17%] |
| D | 50 | Training | UPuZr a | 1.6% UOX b LWR | LWR d | 0 | [0% or 14%], [0% or 14% or 17%] |
| E | 50 | Training | UPuZr a | 1.6% UOX b LWR | Hard e | 0 | [0% or 14% or 17%], [0% or 14% or 17%] |
| F | 50 | Training | U b | N/A (Fresh 11% U) | Hard f | 0 | 0%, 0% |
| G | 2 | Validation | UPuZr a | 1.6% UOX b LWR | SFR | 0 to 180 | 14%, 14% |
| H | 2 | Validation | UPuZr a | 19.9% UOX b LWR | SFR | 0 to 180 | 14%, 14% |
| I | 2 | Validation | UOX b | N/A (Fresh UOX b) | SFR (Softened, OX Fuel) | 0 to 180 | 14%, 14% |
| J | 2 | Validation | MOX b,c | 1.6% UOX b LWR | SFR (Softened, OX Fuel) | 0 to 180 | 14%, 14% |
| K | 1 | Test | MOX b,c | N/A (Fresh MOX b) | SFR (Softened, OX Fuel) | 0 | 0%, 0% |
| L | 2 | Test | UPuZr a | 1.6% UOXb LWR | SFR | 220 to 400 | 14%, 14% |
| M | 2 | Test | UPuZr a | 19.9% UOX b LWR | SFR | 220 to 400 | 14%, 14% |
| N | 2 | Test | UOX b | N/A (Fresh UOX b) | SFR (Softened, OX Fuel) | 220 to 400 | 14%, 14% |
| O | 2 | Test | MOX b,c | 1.6% UOX b LWR | SFR (Softened, OX Fuel) | 220 to 400 | 14%, 14% |
| Dataset, Pu Origin | |||
|---|---|---|---|
| Pu Isotope | A, D, E, G, J, L, O 1.6% UOX LWR [Atom %] | H, M 19.9% UOX LWR [Atom %] | K Pu from [11] [Weight %] |
| 236Pu | 1.9 × 10−9% | 6.3 × 10−7% | 0% |
| 237Pu | 7.2 × 10−7% | 8.5 × 10−6% | 0% |
| 238Pu | 0.59% | 21.47% | 3.6% |
| 239Pu | 60.0% | 35.8% | 47.7% |
| 240Pu | 23.8% | 17.9% | 29.9% |
| 241Pu | 11.9% | 14.0% | 8.3% |
| 242Pu | 3.7% | 10.9% | 10.5% |
| 243Pu | 0.0014% | 0.0024% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berry, J.; Romano, P.; Osborne, A. Upsampling Monte Carlo Reactor Simulation Tallies in Depleted Sodium-Cooled Fast Reactor Assemblies Using a Convolutional Neural Network. Energies 2024, 17, 2177. https://doi.org/10.3390/en17092177
Berry J, Romano P, Osborne A. Upsampling Monte Carlo Reactor Simulation Tallies in Depleted Sodium-Cooled Fast Reactor Assemblies Using a Convolutional Neural Network. Energies. 2024; 17(9):2177. https://doi.org/10.3390/en17092177
Chicago/Turabian StyleBerry, Jessica, Paul Romano, and Andrew Osborne. 2024. "Upsampling Monte Carlo Reactor Simulation Tallies in Depleted Sodium-Cooled Fast Reactor Assemblies Using a Convolutional Neural Network" Energies 17, no. 9: 2177. https://doi.org/10.3390/en17092177
APA StyleBerry, J., Romano, P., & Osborne, A. (2024). Upsampling Monte Carlo Reactor Simulation Tallies in Depleted Sodium-Cooled Fast Reactor Assemblies Using a Convolutional Neural Network. Energies, 17(9), 2177. https://doi.org/10.3390/en17092177






