Abstract
The development of floating photovoltaic systems (FPV) for coastal and offshore locations requires a solid understanding of a design’s hydrodynamic performance through reliable methods. This study aims to extend insights into the hydrodynamic behavior of a superficial multi-body FPV system in mild and harsh wave conditions through basin tests at scale 1:10, with specific interest in the performance of hinges that interconnect the PV panels. Particular effort is put into correctly scaling the elasticity of the flexible hinges that interconnect the PV modules. Tests of a 5 × 3 FPV matrix are performed, with and without shelter, by external floating breakwater (FBW). The results show that the PV modules move horizontally in the same phase when the wave length exceeds the length of the FPV system, but shorter waves result in relative motions between modules and, for harsh seas, in hinge buckling. Relative motions suggest that axial loads are highest for the hinges that connect the center modules in the system and for normal wave incidence, while shear loads are highest on the outward hinges and for oblique incidence. The FBW reduces hinge loads as it attenuates the high-frequency wave energy that largely drives relative motions between PV modules.
1. Introduction
The acceleration of the energy transition requires the upscaling of energy sources that are more environmentally friendly and more widely distributed than fossil fuels. In this respect, photovoltaic (PV) systems (solar power plants) are a key technology. In many countries, solar energy already constitutes a significant portion of total energy demand and it is anticipated that, with declining production costs, PV technology will become even more widely available [1]. However, large-scale exploitation on land is hampered by land scarcity and resistance among local communities [2]. This has led to the installation of PV systems at water bodies, where space is more abundant. Such floating PV (FPV) systems have been installed across the globe, initially on inland fresh-water bodies such as reservoirs, ports, canals, and lakes [3,4], but recently also in coastal seas [5,6]. Upscaling to offshore sites is considered a next step for FPV.
Several papers summarize the benefits and downsides of floating relative to ground-mounted PV [3,5,7,8]. Benefits include a higher power efficiency due to wind and water cooling and higher irradiation levels, although these factors are very site-specific [9]. Offshore floating PV can be integrated with the power cable infrastructure of offshore wind parks, bringing down its leveled costs of energy [10,11]. The downsides of FPV, in particular in marine environments, are higher installation and maintenance costs, corrosion, biofouling and exposure to bird droppings, and the environmental loads of wind, waves, and current. Nevertheless, offshore deployment of FPV is believed to have large market potential [5,12,13,14].
Various concepts for offshore FPV have been presented (see overviews in [3,5,7,8]). Designs can be classified into pontoon-type (PV modules elevated above the waterline by a supporting floating structure) versus superficial (PV modules resting on the water surface), and into rigid versus flexible structures [8]. The present study focuses on the hydrodynamic behavior of an interconnected multi-body system, with individual modules being rigid and superficial. For such systems, the joints (hinges) between modules can experience considerable wave loads and class rules recommend to evaluate their durability over the design life time prior to installation [15].
Offshore FPV concepts are often lightweight to keep production costs low, but they nevertheless need to withstand fatigue and survive aero-hydrodynamic loading. To assess a floating concept’s survivability at sea, and to improve its design, the hydrodynamic load and motion behavior need to be determined. Complexity arises because FPV systems and other very large floating structures (VLFS) are characterized by a large number of mode shapes, which strongly depend on floater and grid dimensions and on hinge properties [16,17,18]. Wave loads and motions on FPV systems can be calculated through existing numerical methods used in maritime engineering, e.g., boundary element methods, Morison formulations, or computational fluid dynamics (CFD) [8,19]. However, in order to resolve the behavior of FPV systems and other VLFS, new implementations are required to simulate the dynamics of many interconnected bodies (e.g., [8,16,20,21,22,23,24]) or the hydro-elastic behavior of flexible structures (e.g., [25,26,27]). It is still uncertain how one can model the complex multi-body and elastic behavior of FPV systems correctly [28] and the necessity for model validation through physical experiments is stressed [29].
Wave basin tests are an alternative to numerical simulations and can provide an independent means for hydrodynamic design verification and numerical model validation. Wave basin tests of FPV systems have been performed at full scale [25,30,31] and reduced scale [32,33,34,35]. Wave makers in basins can typically simulate waves with periods 1–4 s. At scale 1:1, this corresponds to ship- or wind-generated waves in sheltered or inland conditions. To simulate harsher offshore environments in a basin, a floater design needs to be scaled down from prototype. What is particularly challenging in the scale model testing of FPV systems is that the models become very light and difficult to instrument, and that the elasticity of the structure and/or joints should be properly modeled for a realistic motion behavior.
Due to the novelty of the topic and the uncertainties in numerical and physical modeling, there is still much unknown about the hydrodynamic behavior of multi-body FPV systems, especially in harsh environments. Therefore, the present study aims to extend insights into the motion response and hinge loads of multi-body floating PV systems in mild and harsh waves. This is performed through physical model testing at scale 1:10 for a novel design concept that consists of an FPV system sheltered by an external floating breakwater. To ensure a realistic motion behavior, particular effort is put into the correct modeling of the nonlinear stiffness of floater joints in all degrees of freedom. Specific test objectives are to investigate the floater (relative) motions, occurrences of hinge buckling, and the effectiveness of the FBW in reducing the hydrodynamic loads on the FPV system, for different wave conditions and angles of incidence. Furthermore, challenges in physical modeling of such FPV concepts are identified. The experimental data are made publicly available for numerical model validation.
2. Design of Coupled Floating Breakwater and FPV System
The present study is part of the Horizon Europe project SUREWAVE that aims to upscale FPV concepts to offshore environments. An existing FPV system developed by the Norwegian company Sunlit Sea is adopted. The design, which has passed demonstrations in inland lakes and fjords, consists of 1.88 m × 1.88 m aluminum modules with 0.5 kWp capacity that are interconnected through polyurethane hinges (Figure 1a).
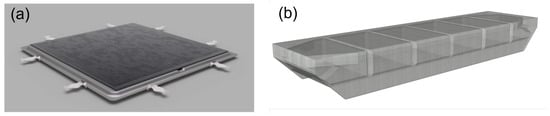
Figure 1.
Design components: (a) floating PV module (courtesy of Sunlit Sea); (b) pontoon-type floating breakwater (courtesy of CLEMENT Germany GmbH).
For upscaling to offshore environments, the FPV system is integrated with an external floating breakwater (FBW) that reduces direct wave loads on the FPV modules. FBWs are floating structures that attenuate the transmitted wave energy through wave reflection and dissipation due to wave overtopping and viscous losses [36,37,38]. Various FBW designs have been developed (see, e.g., [36,38,39]); the present study considers a common pontoon-type FBW built of concrete (Figure 1b).
The effectiveness of a breakwater is commonly expressed in terms of the transmission coefficient , where and are the transmitted and incident wave amplitudes, respectively. For box-type FBWs, assuming 2D conditions and neglecting motions and energy dissipation, can be approximated as function of water depth (h), wave number (k), floater width (W), and floater draft () through the Macagno relation [40]:
means that all wave energy is passed, i.e., the FBW is ineffective, while corresponds to all wave energy being attenuated. For pontoon-type FBWs, an empirical correction to Equation (1) was proposed by Ruol et al. [41]. FBWs are mainly effective when their width exceeds the incident wave length and are therefore more applicable in sites with predominantly short waves (bays, ports, or inland waters) than at offshore locations. Past studies have shown that motions of interconnected smaller modules, such as the present FPV design, are partly governed by the excitation of relatively short waves (e.g., [20,21,30,33]). Hence, it is hypothesized that an FBW, despite its lower effectiveness in offshore environments, may still reduce an FPV system’s (relative) motions and hinge loads.
The full integrated FBW-FPV design consists of a ring of interconnected FBWs, a large matrix (hundreds) of PV modules, and surface and seabed moorings. The present study does not aim to verify the full system; instead, it explores the general wave-frequent hydrodynamic behavior of the PV modules and the effectiveness of the FBW. Therefore, a reduced system is modeled, i.e., the surface and seabed mooring are not considered, the FPV matrix is limited to 5 × 3 modules, and only a section of the FBW ring is modeled.
3. Methods
3.1. Scaling and Sign Convention
The tests were performed at a model scale of 1:10 following Froude’s law of similitude. Throughout this paper, values are presented at full scale unless specified otherwise. A right-handed coordinate system is used, as illustrated for the FPV system in Figure 2. Translations are defined as surge (x), sway (y), and heave (z) motions. Rotations around the x, y, and z axes are termed roll (), pitch (), and yaw (). Figure 2 further indicates the four incident wave headings considered in the present study.
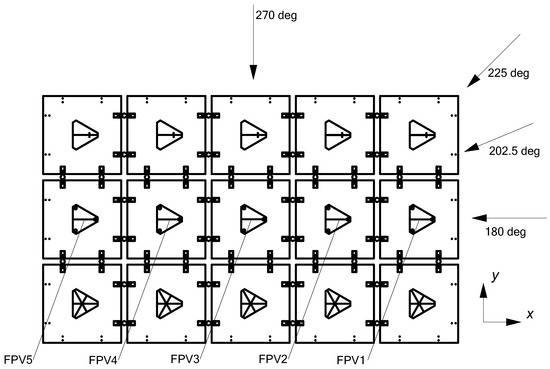
Figure 2.
Sign convention of FPV system, including designation of wave incident headings.
3.2. Facility
The tests were performed in the Concept Basin at the Maritime Research Institute Netherlands (MARIN). The basin measures 220 × 4.0 × 3.6 m (length × width × water depth, model scale) and is equipped with a hinge-type wave maker at one end and a passive absorbing beach at the other end.
3.3. Floater Models
3.3.1. Floating Breakwater
The FBW model was represented through a wooden model and is shown in Figure 3a. The prototype FBW design measures 20 × 5.0 × 2.5 m (length × width × height). For the present tests, the FBW length was increased to 38 m in order to cover 95% of the basin width, leaving 1 m spacing (prototype values) between the model and the walls at each end. The draft and inertial properties of the FBW were matched to prototype using ballast weights. Table 1 presents the weight distribution of the FBW.

Figure 3.
(a) Models of FPV system and FBW; (b) models installed in the basin for 202.5 deg wave incidence heading onto the FPV system.

Table 1.
As-built particulars of FBW, PV modules, and hinges (full scale).
3.3.2. PV Modules
A total of fifteen PV modules were modeled, configured in a 5 × 3 matrix with 0.15 m spacing. The PV modules were represented through solid, rigid polyurethane board plates, the density of which was chosen to obtain a good match with the specified mass (Figure 3). Table 1 presents the weight distribution of the PV modules, including an assumed marine growth layer of 0.06 m (following [15]). Note that the module mass without marine growth equals 65 kg; the assumed marine growth assumption increases the mass and draft by over a factor 5. Uncertainties in the reported total floater mass and draft are estimated to be ±3%. The uncertainty in CoG positions and radii of gyration is estimated to be cm (full scale).
Due to the (dummy) instrumentation on top of the modules (see Section 3.4), the center of gravity (CoG) was raised by 0.06 m compared to prototype. However, in terms of metacentric moment and hydrostatic stiffness, the relative difference between model and prototype is within 2%. Furthermore, the radii of gyration of the model modules were 12–20% lower than for the prototype. This is due to the models being built from one solid material, while the actual PV modules have a lightweight core and a heavier outer shell.
3.3.3. FPV Hinges
The prototype joints between FPV modules are polyurethane rubber hinges mounted with aluminum brackets (Figure 1a). The hinge stiffness has a large effect on the hydrodynamic behavior of multi-body floating structures [16] and should therefore be accurately modeled. In the present design, the hinge material is elastic and has a strongly nonlinear stiffness. In order to accurately model the effect of the nonlinear hinge stiffness on the motion response in each degree of freedom, 1:10 model scale versions of the prototype hinges and brackets were engineered. Froude scaling laws dictate that not only should the hinges be geometrically scaled, bu their elasticity modulus (E) should also be reduced by a scaling factor of 10. This was performed by casting the model scale hinges with a more elastic material.
To select the appropriate material for the model scale hinges, the stiffness properties of the prototype hinges were quantified through tensile load tests (described in Appendix A). Table 1 presents the hinge stiffness in different directions at small deflection. Next, a polyurethane type with the right model scale stiffness (i.e., 10 times lower E) was selected based on database values. In total, 88 hinges were produced to interconnect the 5 × 3 FPV matrix. Due to their small size, the elasticity of the produced hinges could not be verified through tensile tests. Based on available information from the manufacturer, it is estimated that the hinge stiffness is modeled within 20% from the prototype.
The hinges were fixed through scaled brackets that resemble prototype. For pragmatic reasons, it was decided to mount the hinges directly on top of the modules, which is 10 cm higher than for the prototypes. Numerical calculations indicate that this difference has a minor effect (<3%) on the motion response.
3.4. Instrumentation
A Northern Digital Incorporated optical system at 50 Hz sampling frequency (model scale) measured the motions of the FBW and five PV modules. The system logged the six degrees of freedom positions of optical targets placed on the models. For the PV modules, these optical targets were elevated 0.85 m (full scale) above the top side of each module to maintain a clear view during overwash events. Motions were logged for the center array of five PV modules (indicated FPV 1 through FPV 5 in Figure 2). Five other modules were equipped with relative wave probes to measure overwash (not further discussed in this study) and dummy targets were placed on the remaining modules to ensure the same weight distribution for all fifteen modules.
To reduce the effects of the power and acquisition cables on the FPV motions, the cables were made as thin as possible and were given some slack (see Figure 3b). Nevertheless, slight effects of the cables on the FPV system motions cannot be ruled out. For the FBW, which is much heavier than the FPV model, the effects of cables is expected to be negligible.
Water surface elevations were measured through three resistance-type wave probes, sampled at 200 Hz (model scale). In addition, soft-mooring loads, wave overwash on five PV modules, and accelerations of the FBW were measured, but these results are not further discussed herein. All data were logged and synchronized using the same acquisition system.
3.5. Basin Setup
To prevent the FPV and FBW models from drifting off, both type of models were connected to the basin sidewalls through so-called soft-mooring lines that consist of a steel wire and linear spring. The soft-mooring arrangement does not reflect the prototype mooring of the FPV and FBW and was designed to keep the models within the view of the optical measurement system without affecting the wave frequency motions of interest. For the FPV modules, two lines were connected to the outer modules and were orientated to be perpendicular to the basin sidewalls (as can be seen in Figure 3b). The FBW model was connected through four lines, connected to the longitudinal ends of the model. Details of the soft-mooring arrangement are presented in the data report [42] and include line and mooring stiffness properties, realized pretensions, and established natural periods from motion decay tests.
The test campaign involved four different types of basin setups. During wave calibration stage, only the three wave probes (and no models) were installed in the basin. Later, tests were performed with the FPV system only, with the FPV system in combination with the FBW, and with the FBW only. For the tests with FPV system, the FPV system was physically rotated to vary the relative incident wave heading. In total, four incident wave headings onto the FPV system were tested (180, 202.5, 225, and 270 deg; see also heading convention in Figure 2).
One basin setup is illustrated in Figure 4. The measurement area was near the middle of the basin; the distance from the FBW to the wave maker was approximately 1200 m (full scale). The FBW orientation was not varied; waves were always beam on. The distance between FBW and FPV system was 20 m (center to center, full scale). The three wave probes were positioned 15 m downwave of the FPV system, at different transverse locations (at 4, 12, and 20 m from the basin sidewall, the latter corresponding to basin center line).
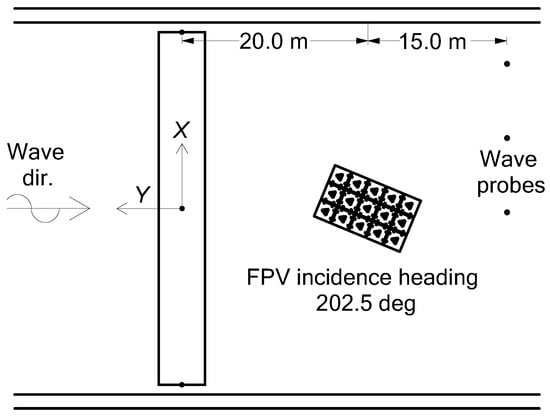
Figure 4.
Basin setup for tests with FBW and FPV system, corresponding to 202.5 deg wave incidence at the PV modules. The distances are at full scale.
3.6. Wave Conditions
For each setup and heading of the FPV system, three irregular wave conditions were simulated (Table 2). One condition was a so-called white noise wave with energy content distributed evenly between periods 2.4 to 11.8 s. This condition is primarily used to quantify the motion response at low amplitude; hence, it has a low significant wave height (. Further, two irregular JONSWAP conditions were simulated. Condition J2 corresponds to a 1 y return period storm condition at a field site in the Baltic Sea, which is one of the locations of interest for the present design. Condition J1 has a peak period close to the natural roll period of the FBW, is close to the steepness limit of wave breaking, and has a higher probability of occurrence than condition J2 (for the Baltic Sea field site). Each irregular wave was simulated for a duration of 1 h (full scale); a longer test duration was not deemed desirable due to increased effects of spurious reflected waves in the basin.

Table 2.
Overview of wave conditions (full-scale values).
For multi-body floating structures in waves, resonant fluid oscillations in the gaps between floats can importantly affect floater motions [43,44]. Therefore, the expected gap resonance frequencies were calculated following Chen et al. [43]. Due to the small draft of the PV floats, the gap natural frequencies are much higher than the incident wave frequencies. Hence, it is anticipated that gap resonance is of minor importance in the present study.
3.7. Data Processing
The optical target motions were translated to CoG and other points of interest of each floater and the earth-fixed motion measurements were transformed to a model-fixed heading convention. For pairs of connected PV modules, the relative motion between CoGs in six degrees of freedom and the distance between the two connection points of the hinges connecting the module pair was derived.
The model tests were time-synchronized with the measurements of the undisturbed wave during wave calibration based on the wave flap position. For selected signals, response amplitude operators (RAOs) were computed as a frequency response function with the undisturbed wave at basin center line as lead signal. Further, signal peaks (maxima and minima) were identified based on zero crossings with a minimum time spacing between peaks of . For each test, the first 15 min. are considered a start-up stage; the last 45 min. were used to compute the RAOs and peak distributions. The latter duration corresponds to 500 to 900 wave cycles, which is considered sufficient for converged RAOs.
During the tests, the optical view on the PV modules was occasionally (typically a few times during a test) lost. This occurred especially at instances of high rotational angles or larger overwash events. As a result, the motions were not continuously recorded. Because the time instants without signal are only a small fraction of the full time trace, it is expected that the motion RAOs are not affected much.
4. Results
4.1. Floating Breakwater Motions
Figure 5 presents the amplitudes of motion RAOs of the FBW, i.e., the amplitude of floater motions normalized by the incident wave amplitude (), as function of the angular frequency . Results are presented for the three relevant degrees of freedom for the FBW orientation in the basin: sway (amplitude ), heave (), and roll (). The roll RAO is normalized with the wave steepness , where is the wave number and is the wave length based on linear wave theory.
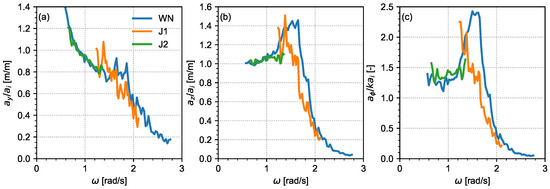
Figure 5.
Motion RAOs of the FBW for the three irregular wave conditions. (a) sway; (b) heave; (c) roll.
The RAOs for all three degrees of freedom show a trend of decreasing motions with increasing wave frequency. Towards the low-frequency limit, the normalized heave and roll RAOs approach a value of 1, which corresponds to the FBW following the water surface. The heave and roll RAOs show a local peak at their natural frequency (1.6 and 1.5 rad/s, respectively). At these natural frequencies, the heave and roll response amplitudes are lower for the higher condition J1 than for WN and J2 due to quadratic damping contributions, as also confirmed by motion decay tests.
4.2. Wave Attenuation by the Floating Breakwater
The performance of a floating breakwater is typically expressed in terms of the wave transmission coefficient (see Section 2). A spatially averaged was calculated for each wave condition as the mean of the RAOs of the three wave probe measurements. The wave attenuation by the FBW was quantified for tests without the FPV modules installed.
Figure 6a shows the resulting , including the FBW natural heave frequency (1.6 rad/s) and the theoretical formulation by Ruol et al. [41] for pontoon-type FBWs for reference. It follows that the breakwater is hardly effective for low-wave frequencies ( for rad/s), becomes increasingly effective for rad/s, and reduces the wave heights by about 50–60% for rad/s. Hence, the FBW is mostly effective for wave frequencies that exceed the FBW’s natural heave frequency.
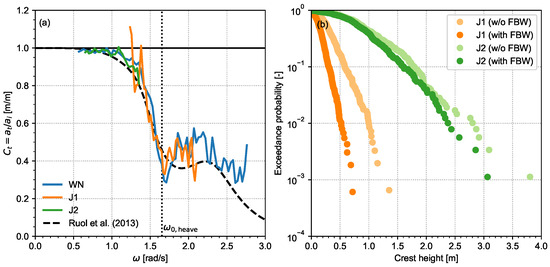
Figure 6.
Wave attenuation by the FBW. Panel (a): transmission coefficients for the three irregular wave conditions, including the theoretical formulation by Ruol et al. [41]. Panel (b): wave crest distributions for conditions J1 and J2 without and with FBW.
The transmission coefficients are highly similar for all irregular and regular wave conditions. This indicates that the attenuation performance by the FBW is approximately linear, despite the nonlinear response in heave and roll motions seen in Figure 5b. Compared to the semi-empirical formulation by Ruol et al. [41], the measured data points are overall in close agreement but appear to be slightly shifted towards higher frequencies and yield higher for rad/s.
Because the FBW does not cover the entire basin width, the wave diffraction pattern around the FBW ends was assessed through numerical diffraction calculations that included the moving FBW and the basin sidewalls. The results (not shown for brevity) indicated that the wave field at the FBW lee side is approximately uniform for wave frequencies up to 2 rad/s, but some transverse wave propagation becomes apparent towards rad/s. The effect on FPV panel motions is small, but is nevertheless apparent for some tested conditions (see Section 4.3.2).
Figure 6b presents the crest distributions for the two JONSWAP conditions, without and with FBW. Note that condition J2 has a higher than J1, hence it also results in considerably higher wave crests. For wave condition J1, the breakwater presence reduces the highest ten wave crests by 40 to 50%. Condition J2 is in a frequency range for which the FBW is hardly effective (see also Figure 6a) and its presence reduces the highest ten wave crests only by 6 to 18%.
4.3. FPV Motions
4.3.1. Motions in FBW Absence
The RAOs of the five instrumented PV modules in white noise waves are presented in Figure 7 (translations) and Figure 8 (rotations). The RAOs for the two JONSWAP conditions are highly similar to the WN condition, suggesting an approximately linear response for the range of wave frequencies tested, and are therefore not shown.
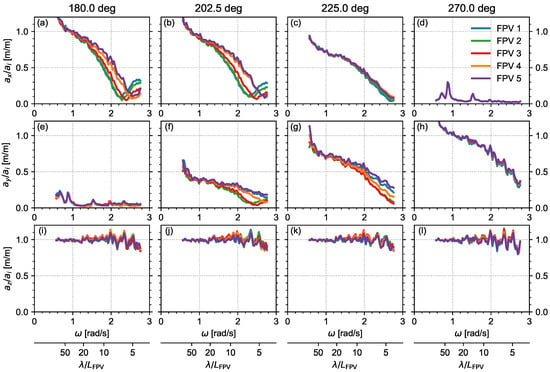
Figure 7.
RAOs of the PV modules for WN waves, in absence of the FBW: surge (a–d), sway (e–h), and heave (i–l) motions. For reference, the horizontal scale at the bottom presents the wave length () normalized by the length of a PV panel ( m).
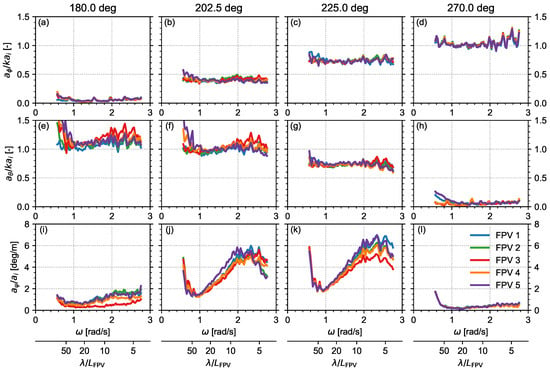
Figure 8.
RAOs of the PV modules for WN waves, in absence of the FBW: roll (a–d), pitch (e–h), and yaw (i–l) motions.
The surge RAOs (top row in Figure 7) are highest for 180 and 202.5 deg, as is to be expected. The surge RAOs are highest for low , decrease towards 2.3–2.5 rad/s, and then increase again for higher frequencies. At = 2.5 rad/s, the wave length equals the longitudinal length of the assembled five-module FPV system ( m), which explains the surge RAOs of near 0. The surge RAOs further suggest a slightly higher response, as well as a shift towards higher frequencies of the local depression where RAOs are , for the aft modules (FPV 4 and 5) compared to the fore modules (1 and 2). These differences in surge response amplitude between modules may relate to the higher buckling occurrence of the hinges connecting the aft modules, as further discussed in Section 4.4.2, but could also relate to the soft-mooring lines that are connected to the middle of the PV system. These explanations are to be further investigated through numerical simulations.
A notable result for sway motions (Figure 7e–h) is that oblique incident waves (202.5 and 225 deg) towards higher frequencies result in a larger response for the outer modules (1 and 5) compared to the modules near the system center. These differences in surge and sway response between modules imply that the 5 × 3 system does not move horizontally as a single body, but instead, relative motions between modules occur due to the elasticity of the hinges.
The heave RAOs (Figure 7i–l) are approximately 1 m/m for the full range of covered wave frequencies. Similarly, roll RAOs for 270 deg incidence (Figure 8d) and pitch RAOs for 180 deg (Figure 8e) show normalized amplitudes of near 1 deg/deg. These results correspond to the floaters following the water surface. Towards the low and high frequency limits, roll and pitch RAOs above 1 were measured, possibly due to wave reflection or hydrodynamic interaction with the basin sidewalls. All five FPV modules result in highly similar heave, roll, and pitch response amplitudes, suggesting that each module experiences a similar incident wave amplitude and that the shielding effect by the upwave modules is minor. This is consistent with results for a lightweight FPV system by Delacroix et al. [30] and Jiang et al. [35], which also found negligible shielding effects when wave lengths are considerably larger than the length of a single module. Note that shielding effects will likely become more significant for FPV farms that are larger than the presently tested matrix.
The yaw motions (Figure 8i–l), finally, show the largest response for incident headings 202.5 and 225 deg and towards higher wave frequencies. Similar to the sway motions, a higher response is observed for the outward modules (FPV 1 and 5). The increase in yaw RAO for < 0.8 rad/s is attributed to influences of the soft-mooring system, which resulted in a yaw natural frequency of around 0.5 rad/s.
For further understanding, Figure 9 presents the phase of motions of FPV 2 through 5 relative to FPV 1 in head seas. Note that the uncertainty in phase increases towards higher frequencies due to smaller motion amplitudes and a resulting loss of coherence in the analysis. It follows that for surge motions (Figure 9a), the phase difference is ≈0 up to rad/s, which means that the five modules move together, despite each individual module experiencing a different phase of the wave cycle. However, for rad/s, phase differences emerge, even leading to modules 4 and 5 being almost in anti-phase (180 deg phase difference) with module 1. This change in behavior occurs around = 2.5 rad/s, at which the wave length equals the length of the FPV system, leading to high compressive loads on the FPV system and on the joints. Such phase difference ≠ 0, in combination with motion amplitudes that are small but >0 (Figure 7a), implies relative surge motions between modules (further addressed in Section 4.4).
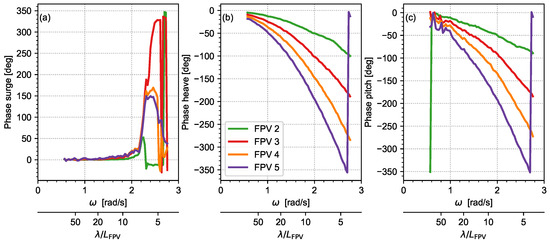
Figure 9.
Phase of surge (a), heave (b), and pitch (c) motions for the WN condition in head seas (180 deg), for PV modules 2–5 relative to the phase of FPV 1.
For heave and pitch motions (Figure 9b,c), a progressive increase in phase difference between modules is observed. This behavior corresponds to the modules moving individually, with phase differences emerging because, at a given time instant, each module encounters a different phase of the incident wave cycle. The phase difference increases with as waves become shorter.
4.3.2. FPV Motions in FBW Shelter
The RAOs of the PV modules in presence of the FBW are shown in Figure 10 (translations) and Figure 11 (rotations). The response without FBW is also plotted to enable a direct comparison. It follows that the FBW effectively reduces the motions of the PV modules, especially towards the highest tested frequencies where a factor 3 reduction is observed, but is less effective for lower frequencies and hardly effective for < 1.0 rad/s. This overall pattern is consistent with the transmission coefficients presented in Section 4.2, including the local reduction in response around the heave natural frequency of the FBW (1.6 rad/s).
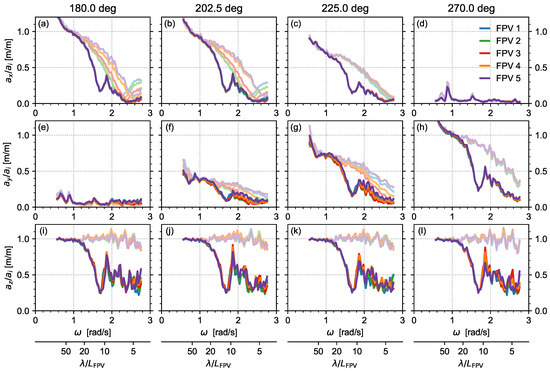
Figure 10.
RAOs of the PV modules in WN waves, with and without the FBW: surge (a–d), sway (e–h), and heave (i–l) motions.
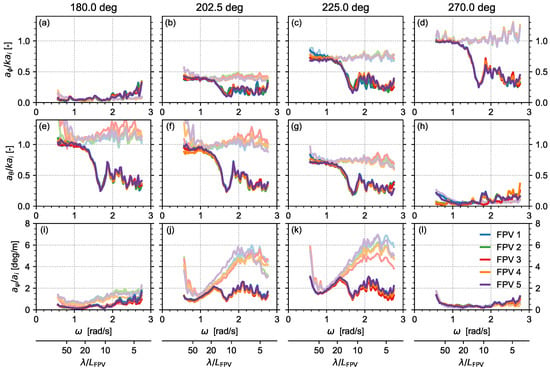
Figure 11.
RAOs of the PV modules in WN waves, with and without the FBW: roll (a–d), pitch (e–h), and yaw (i–l) motions.
The hydrodynamic interaction with the FBW leads to a small increase in response in roll for 180 deg incidence (Figure 11a) and in pitch for 270 deg incidence (Figure 11h), in particular for higher frequencies. This is explained by the formation of transverse waves around the longitudinal ends of the FBW, as described in Section 4.2.
4.4. Relative Motions between PV Modules
Of particular relevance for the integrated FPV design are the loads on the hinges. It is recalled that the hinge geometric and elastic properties are scaled from prototype to obtain a realistic (nonlinear) stiffness at model scale. The hinge loads could not be measured directly because instrumentation would have been too intrusive. Therefore, for a more qualitative insight into the hinge loads and behavior, the relative motions between PV modules (Section 4.4.1) and between hinge connection points (Section 4.4.2) are studied.
4.4.1. Relative Motion RAOs
The relative motions between CoGs of interconnected modules, denoted with (surge) through (yaw), were calculated as time traces and were subsequently used to compute the relative motion RAOs presented in Figure 12 (translations) and Figure 13 (rotations).
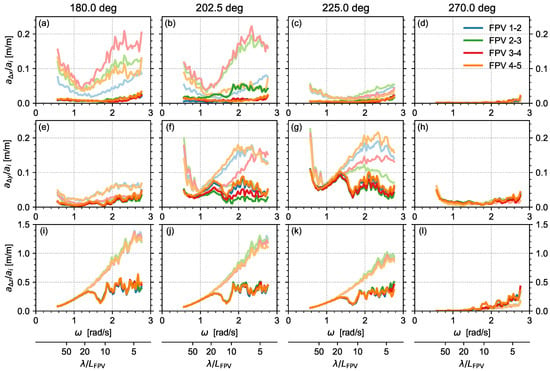
Figure 12.
RAOs of the relative motions of PV modules in WN waves, without and with FBW: surge (a–d), sway (e–h), and heave (i–l) motions.
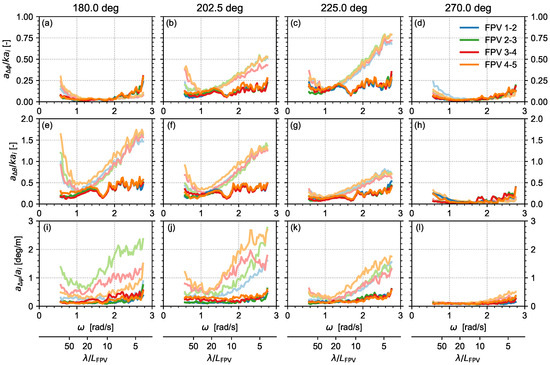
Figure 13.
RAOs of the PV modules for the WN waves, with and without the FBW: roll (a–d), pitch (e–h), and yaw (i–l) motions.
It follows that, in absence of the FBW, the largest relative motions for each degree of freedom occur for the highest wave frequencies. This is explained by the fact that, for low frequencies, the PV system length is small compared to the wave length; consequently, the five PV modules move at a similar phase. In contrast, for high wave frequencies (and short wave lengths), differences in phase and (to lesser extent) amplitude arise between modules, resulting in larger relative motions (see also the phase behavior in Figure 9 and accompanying discussion). The FBW is especially effective towards these high frequencies and can be seen to substantially reduce the relative motion RAOs for rad/s (its heave natural frequency) in all degrees of freedom.
Given the configuration of the FPV system and instrumented modules (see also sign convention in Figure 2), the relative surge () motions are a measure for the axial loads on the hinges. The motion amplitudes are largest for 180 and 202.5 deg and between modules 2–3 and modules 3–4, i.e., the modules near the center of the assembled system (Figure 12b,c). A possible explanation is that when the assembled FPV system is compressed and elongated under wave forcing, the inertia of the modules in line of wave propagation accumulates, leading to largest hinge loads in the system center. This explanation is supported through preliminary wave diffraction calculations, beyond the scope of the present study, which indicate that the horizontal connector loads are dominated by inertial loads and which also result in the highest axial loads for the connectors near the system’s center.
The relative sway () motions between instrumented modules, on the other hand, are a measure for the shear loads on the hinges. Figure 12e–h show that the motion amplitudes are largest for the more outwards modules (module pairs 1–2 and 4–5) and for oblique incident waves (202.5 and 225 deg). These relatively high motions on the outer modules may partly be explained because these modules are more exposed, and partly because these modules are interconnected by fewer hinges, and are therefore less motion-restricted. A qualitatively similar result of high shear loads on the outer hinges was obtained numerically by Li et al. [45].
The relative roll and pitch RAOs are a measure for torsional and bending loads, respectively, on the hinges. Results in (Figure 13a–h) are normalized with the incident wave steepness . When one module exactly follows the rising edge of a wave whilst the connected module exactly follows the falling edge, a normalized amplitude of 2 would be the result. The relative roll and pitch RAOs are much similar for all PV module pairs. In absence of the FBW the highest RAOs are observed towards higher frequencies.
Finally, Figure 13i–l shows the relative yaw RAOs. Because relative yaw motions are generally small (0.1–1 deg), i.e., in a range where the measurement uncertainty becomes significant, these results are not further discussed.
4.4.2. Hinge Buckling Occurrence
The fluctuating spacing (from here denoted s) between the two connection points of each hinge is a measure for the hinge loads and allows insights into hinge buckling occurrence. Each pair of modules is connected through two hinges. For the relevant module pairs, the hinges are at portside (PS, ) and starboard (SB, ) side from center line (see Figure 2). For the present tests, s was calculated for the hinges connecting FPV pairs 1–2 through 4–5 following the methodology described in Section 3.7. The estimated measurement uncertainty of the derived s is 0.01 m.
Figure 14 presents time traces of the fluctuating spacing s for condition J1 at 180 deg wave incidence without and with the floating breakwater. Both plots show asymmetric fluctuations around s = 0.15 m (i.e., the still water equilibrium spacing). This relates to the strongly nonlinear axial stiffness of the hinges. The high tensile stiffness prevents large elongations, which explains the relatively small fluctuations towards s > 0.15 m. In contrast, the higher amplitude oscillations, towards m down to near 0 m, which would correspond to floater collision, are explained by the low compressive stiffness once the critical compressive load for buckling occurrence is exceeded. The loss in compressive stiffness may be driven not only by pure compressive loads, but also partly by bending moments on the hinges due to relative pitching between modules.
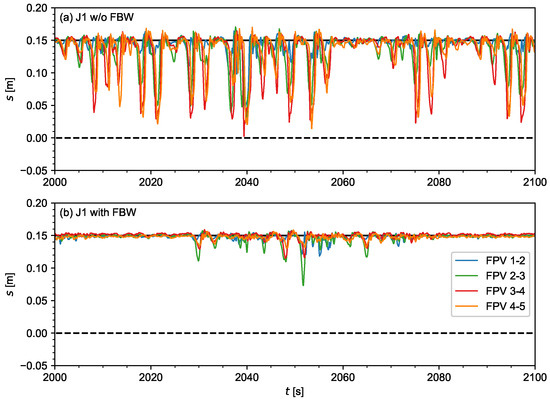
Figure 14.
Time series of spacing between the PS FPV hinge connection points for 180 deg incident waves without FBW, condition J1 without FBW (a) and with FBW (b).
Visual observations confirm hinge buckling during the tests. Hinge buckling occurs during wave crest phases when the FPV system is compressed; during the wave trough phase, the FPV system is elongated and the system restores to s = 0.15 m. Visually, it was observed that this restoring results in snap loads on the hinges. The relatively high buckling occurrence is partly explained by the absence of a surface mooring and the conservative assumption on marine growth, as further discussed in Section 5.
The time traces show that such hinge buckling occurs regularly, but not for each wave cycle. Comparison between Figure 14a,b also shows that the FBW presence significantly reduces the fluctuations in s and the occurrence of hinge buckling. To assess the buckling frequency for varying hinges and test conditions, buckling events were quantified from the time series as occurrences of s < 0.075 m, i.e., half the spacing in still water equilibrium, within a moving time window of . The mentioned threshold is somewhat arbitrary, as the loss of compressive stiffness already occurs at deflections of about 1 cm (see Appendix A). However, such small deflections are within the measurement uncertainty of the derived s. This means that the obtained estimates of buckling events are a rough and non-conservative approximation of the actual buckling occurrence and merely allow a qualitative comparison between the different hinges and test conditions.
Figure 15 presents the number of buckling events for both JONSWAP conditions at varying incidence, both with and without FBW. To compare the wave conditions, the number of events were normalized with the number of undisturbed waves. For each test condition and module pair, a similar buckling occurrence is observed for the SB and PS hinge. Comparison between the top and bottom panels shows that the normalized buckling occurrence is similar for both JONSWAP waves, despite J1 having three times lower than J2. This is explained by the fact that relative (surge) motions between modules are especially driven by excitation at rad/s (see Figure 9 and Figure 12); both JONSWAP conditions have a similar energy content at these high frequencies.
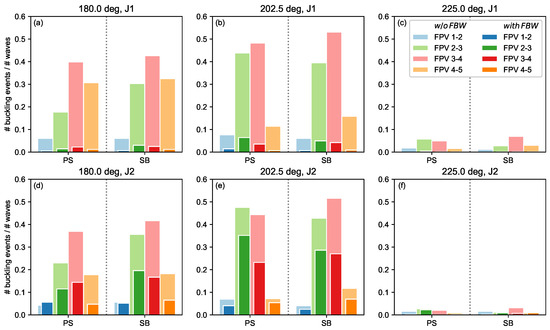
Figure 15.
Number of buckling events, for incidence headings 180 (a,d), 202.5 (b,e), and 225 deg (c,f), wave conditions J1 (a–c) and J2 (d–f).
Comparison between wave headings (left–right panels) shows that buckling of the studied hinges occurs most frequently for heading 202.5 deg, followed by heading 180 deg, and much less frequently for heading 225 deg. For 270 deg incidence heading, corresponding to transverse loads on the studied hinges, no buckling occurred (not shown for this reason). Further, buckling occurs less frequently for the fore hinge pairs (FPV 1–2) than for the pairs near the middle (FPV 2–3 and 3–4) and back (FPV 4–5), which is consistent with the relative motion RAOs for the different module pairs (Section 4.4.1).
Finally, Figure 15 also shows the effect of the FBW on buckling occurrence. For condition J1, the FBW reduces the buckling frequency by a factor 12 on average, which is considerably higher than the approximate factor 2 reduction in wave crests (Section 4.2). Condition J2 is in a range where the FBW is hardly effective, but nevertheless reduces the buckling frequency by a factor or 2 on average. These relatively high differences in buckling occurrence compared to the FBW’s attenuation performance are explained, firstly, because the relative motions between modules are governed by wave excitation at the higher frequencies for which the FBW is most effective, and secondly, because the strongly nonlinear compressive stiffness of the hinges in the buckling regime leads to a relatively large reduction in deflections for a given reduction in loads.
5. Discussion
The present study assesses the hydrodynamic response of an integrated FBW and FPV system in a linear regime as well as in survival wave conditions, with the two tested JONSWAP conditions corresponding to steep storm conditions that include wave breaking. The simulated harsh environments led to frequent buckling of the hinges when the FPV system was compressed, generally followed by snap loads upon system elongation. Although the hinges recovered after buckling, frequent buckling and snap loads contribute to fatigue loading that could ultimately damage the hinges. Given the low compressive stiffness but high tensile strength of the hinges, it is expected that hinge buckling events can be lowered substantially by means of a mooring arrangement that would apply a horizontal pretension to the FPV system, i.e., pulling the modules apart. The absence of such a surface mooring arrangement in the present tests means that the presented number of buckling events is conservative.
It is further noted that the assumption of 0.06 m thick marine growth (see Section 3.3.2) increased the mass of the modules by a factor 5. This high factor is explained by the light weight and large surface area of the tested PV modules. The assumption on marine growth also led to increased inertial loads on the hinges and to increased buckling frequencies. The assumed marine growth thickness was based on general class rules for offshore structures [15]; the actual marine growth thickness will depend on many factors such as field site, materials of the floating structure, and anti-fouling and cleaning measures. The susceptibility of hydrodynamic loads to the assumed marine growth thickness illustrates the relevance of studies that monitor marine growth development at offshore FPV systems (such as [6]).
The present study shows that scale model wave basin testing of FPV systems in harsh conditions is possible, yet not trivial. Firstly, the elastic properties of the system (in this case the hinges) should be carefully scaled. For the present tests, scaled hinges were engineered through a surrogate material with the appropriate scaled elasticity. However, this may not be possible for all FPV designs and the scaling procedure requires profound knowledge of the elastic properties of the prototype. Secondly, their light weight makes the FPV models susceptible to influences of cables, soft-mooring lines, and instrumentation, and restricts direct measurements of key parameters such as the hinge loads. A third and more practical point is that the preparation of models, hinges, and instrumentation rapidly increases with the size of the PV farm. This likely explains why most wave basin tests on FPV [20,30,33,34], as well as the present study, focus on relatively small matrices.
Most of these uncertainties to scale model testing can be resolved by a complimentary numerical study in which the exact basin setup is reproduced and measurements are used for validation. For the present tests, numerical simulations may particularly help to assess the influence of the soft-mooring arrangement in the basin, to explore the sensitivity to assumptions in the experimental modeling (e.g., the marine growth thickness), and to quantify parameters that could not be measured directly (e.g., hinge loads). Numerical modeling may also help to scale up the basin test results to larger farm sizes, although one should be cautious to extrapolate a numerical model to a regime for which it has not been validated.
Ongoing work for the present integrated FBW and FPV system focuses on further improvement of the design of the hinges and the FBW, the design of a surface mooring for the FPV, and a numerical hydrodynamic assessment of the full system including breakwater ring and a larger FPV farm.
6. Conclusions
The wave-frequent behavior of a 5×3 matrix of interconnected superficial floating PV (FPV) modules was studied through wave basin tests at scale 1:10. Of specific interest for the tested design was the hydrodynamic performance of the elastic hinges that interconnect the PV panels. Therefore, particular effort was put into the correct modeling of the hinge elasticity. In addition, the effectiveness of an external floating breakwater (FBW) in reducing FPV motions and loads was assessed. Although a specific FPV design was tested, it is anticipated that the obtained insights can be extended to other multi-body FPV systems and very large floating structures. The results lead to the following conclusions:
- The FBW is effective in terms of wave attenuation for wave frequencies rad/s, which roughly corresponds to the FBW’s natural frequency in heave. This is reflected in the motion RAOs of the FPV modules, which in the sheltering presence of the FBW, reduce by a factor 2 to 3 at high frequencies. However, the FBW is less effective for rad/s and hardly effective for rad/s.
- The five instrumented PV modules generally result in similar-amplitude motion RAOs, suggesting that the hydrodynamic interaction between modules is minor (for the present small PV farm). For vertical motions and roll/pitch rotations, the PV modules tend to move individually and follow the water surface. In surge, the multi-body system moves as a whole (similar amplitude and phase for all modules) when the wave length exceeds the length of the assembled system, but phase differences between modules emerge for waves shorter than the PV farm. This suggests that larger farm sizes will result in higher relative surge motions between panels and in higher axial hige loads.
- Compressive loads on the FPV system, possibly in combination with bending loads due to relative pitching between modules, lead to hinge buckling. Buckling occurs especially for normal and close to normal incident waves, implying that such conditions result in the highest axial hinge loads. The hinges in the center of the FPV system appear to be more susceptible to buckling, which is attributed to an accumulation of inertial loads towards the FPV system center when compressed.
- Quartering seas lead to few buckling events, but do result in relative sway motions between modules. The relative sway motions are a measure for shear loads on the hinges and are largest for the outward PV modules.
- The FBW has the potential to reduce hinge loads in all directions (axial, shear, torsional, and bending), because it is effective at the high wave frequencies that largely drive relative motions between modules. The FBW effectiveness is demonstrated by a significant reduction in hinge buckling events in the tested steep waves conditions.
From a practical (engineering) perspective, the present study provides insights into hinge stresses in multi-body floating structures for varying wave conditions and incident angles. In addition, the applicability of a floating breakwater to reduce these stresses is demonstrated. For the present design, hinge buckling and subsequent snap loads can likely be reduced through a surface mooring that applies an outward pretension to the FPV system, or by increasing the initial compressive strength of the hinges.
A (numerical) verification of the more detailed results such as the relative spacing between PV modules is recommended to assess effects of the soft-mooring arrangement and marine growth assumption. Numerical simulations are also required for upscaling the results to larger FPV farms. The basin test data are made publicly available to validate and advance the development of numerical methods for FPV applications.
Author Contributions
Conceptualization, J.v.d.Z., T.B., A.C., V.D., T.P., G.K. and B.P.; methodology, J.v.d.Z., V.D., G.K., and T.P.; formal analysis, J.v.d.Z. and T.B.; investigation, J.v.d.Z.; resources, T.P., G.K. and V.D.; data curation, J.v.d.Z.; writing—original draft preparation, J.v.d.Z.; writing—review and editing, T.B., A.C., V.D., T.P., G.K. and B.P.; visualization, J.v.d.Z.; supervision, J.v.d.Z.; project administration, J.v.d.Z., A.C. and B.P.; funding acquisition, J.v.d.Z., T.B., A.C., V.D., T.P., G.K. and B.P. All authors have read and agreed to the published version of the manuscript.
Funding
The present study is part of the SUREWAVE project, Funded by the European Union with GA No. 101083342. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the granting authority can be held responsible for them.
Data Availability Statement
The full dataset including an accompanying data report can be accessed through https://zenodo.org/doi/10.5281/zenodo.10960432 (accessed on 19 April 2024).
Acknowledgments
The support of the staff of the Maritime Research Institute Netherlands in model preparation, test execution, and data processing and quality assurance is gratefully acknowledged. In addition, the authors thank the two anonymous reviewers for their suggestions to improve the manuscript.
Conflicts of Interest
Authors Thomas Pehlke and Guillaume Kegelart were employed by the companies CLEMENT GmbH and Sunlit Sea AS, respectively. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CoG | center of gravity |
| FBW | floating breakwater |
| (F)PV | (floating) photovoltaics |
| JONSWAP | Joint North Sea wave project |
| PS | portside |
| RAO | response amplitude operator |
| SB | starboard |
| VLFS | very large floating structure |
| a | amplitude |
| wave transmission coefficient | |
| significant wave height | |
| s | spacing between PV modules |
| wave peak period | |
| x | longitudinal position (surge) |
| y | transverse position (sway) |
| z | vertical position (heave) |
| JONSWAP peak enhancement factor | |
| rotation around x axis (roll) | |
| rotation around y axis (pitch) | |
| rotation around z axis (yaw) | |
| radial wave frequency |
Appendix A. Hinge Tensile Tests
Tensile and compression tests on the full scale hinges were performed to obtain the material stiffness as well as its strength and elongation at failure. This enabled to select the right material candidate for the reduced scale hinges in the basin tests as presented in Section 3.3.3. Three repetitions were performed for each test to verify the repeatability (for both tension and compression). A quasi-static strain rate was applied through an Instron tensile machine with a load cell of 50 kN. Special grips were machined to clamp the hinges during the tests to ensure no slipping. The machine displacement velocity was set to 1.44 mm/s, which corresponds to a nominal strain rate of 0.01 s−1, considering that the initial length between grips was 144 mm. In addition, for each tensile test, a speckled pattern was applied, which enabled DIC measurement using a camera and the software Ecorr [46]. This enabled highly accurate quantification of the full strain field and the displacement during the tests. The DIC results are not presented herein but they were used to calculate the elongation depicted in Figure A1.
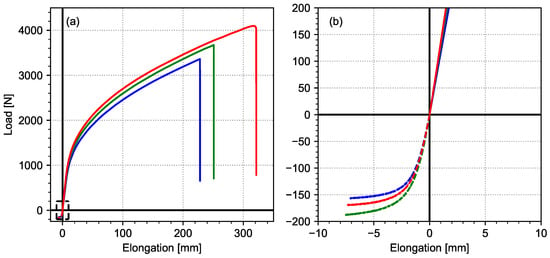
Figure A1.
Load elongation curves for tensile and compression tests of the prototype hinges, with colors distinguishing different samples. Full curve (a) and close-up (b).
The material exhibits a typical elastomeric behavior, as expected for a polyurethane [47], with a very large strain to failure (around 300%). The mean tensile strength of the hinge in tension was 3690 N, with a standard deviation ± 360 N, for a displacement at failure of 265 ± 48 mm. The stiffness at 5% elongation was 114 ± 8 N/mm, while it was 84 ± 4.8 N/mm at 10% elongation. In compression, the max force drops to 171 ± 16 mm for a max displacement of 7.3 ± 0.2 mm. This is explained by the early buckling of the hinges during the tests, leading to an almost immediate loss of structural behavior as shown in Figure A2.

Figure A2.
Buckling of the hinge during compression test.
References
- Melnyk, L.H.; Shaulska, L.V.; Maziin, Y.O.; Matsenko, O.I.; Piven, V.S.; Konoplov, V.V. Modern Trends in the Production of Renewable Energy: The Cost Benefit Approach. Mech. Econ. Regul. 2021, 1, 5–16. [Google Scholar] [CrossRef]
- Cousse, J. Still in love with solar energy? Installation size, affect, and the social acceptance of renewable energy technologies. Renew. Sustain. Energy Rev. 2021, 145, 111107. [Google Scholar] [CrossRef]
- Sahu, A.; Yadav, N.; Sudhakar, K. Floating photovoltaic power plant: A review. Renew. Sustain. Energy Rev. 2016, 66, 815–824. [Google Scholar] [CrossRef]
- Abid, M.; Abid, Z.; Sagin, J.; Murtaza, R.; Sarbassov, D.; Shabbir, M. Prospects of floating photovoltaic technology and its implementation in Central and South Asian Countries. Int. J. Environ. Sci. Tecnol. 2019, 16, 1755–1762. [Google Scholar] [CrossRef]
- Shi, W.; Yan, C.; Ren, Z.; Yuan, Z.; Liu, Y.; Zheng, S.; Li, X.; Han, X. Review on the development of marine floating photovoltaic systems. Ocean Eng. 2023, 286, 115560. [Google Scholar] [CrossRef]
- Mavraki, N.; Bos, O.G.; Vlaswinkel, B.M.; Roos, P.; de Groot, W.; van der Weide, B.; Bittner, O.; Coolen, J.W.P. Fouling community composition on a pilot floating solar-energy installation in the coastal Dutch North Sea. Front. Mar. Sci. 2023, 10. [Google Scholar] [CrossRef]
- Kumar, V.; Shrivastava, R.; Untawale, S. Solar Energy: Review of Potential Green & Clean Energy for Coastal and Offshore Applications. Aquat. Procedia 2015, 4, 473–480. [Google Scholar] [CrossRef]
- Claus, R.; López, M. Key issues in the design of floating photovoltaic structures for the marine environment. Renew. Sustain. Energy Rev. 2022, 164, 112502. [Google Scholar] [CrossRef]
- Golroodbari, S.Z.; Ayyad, A.W.; van Sark, W. Offshore floating photovoltaics system assessment in worldwide perspective. Prog. Photovoltaics Res. Appl. 2023, 31, 1061–1077. [Google Scholar] [CrossRef]
- Golroodbari, S.; Vaartjes, D.; Meit, J.; van Hoeken, A.; Eberveld, M.; Jonker, H.; van Sark, W. Pooling the cable: A techno-economic feasibility study of integrating offshore floating photovoltaic solar technology within an offshore wind park. Sol. Energy 2021, 219, 65–74. [Google Scholar] [CrossRef]
- Solomin, E.; Sirotkin, E.; Cuce, E.; Selvanathan, S.P.; Kumarasamy, S. Hybrid Floating Solar Plant Designs: A Review. Energies 2021, 14, 2751. [Google Scholar] [CrossRef]
- Vo, T.T.E.; Ko, H.; Huh, J.; Park, N. Overview of Possibilities of Solar Floating Photovoltaic Systems in the OffShore Industry. Energies 2021, 14, 6988. [Google Scholar] [CrossRef]
- Cuce, E.; Cuce, P.M.; Saboor, S.; Ghosh, A.; Sheikhnejad, Y. Floating PVs in Terms of Power Generation, Environmental Aspects, Market Potential, and Challenges. Sustainability 2022, 14, 2626. [Google Scholar] [CrossRef]
- Ghosh, A. A comprehensive review of water based PV: Flotavoltaics, under water, offshore & canal top. Ocean Eng. 2023, 281, 115044. [Google Scholar] [CrossRef]
- DNV-GL. Recommended Practice: Environmental Conditions and Environmental Loads (DNVGL-RP-C205, April 2014); Technical Report; DNV GL Group: Baerum, Norway, 2014. [Google Scholar]
- Fu, S.; Moan, T.; Chen, X.; Cui, W. Hydroelastic analysis of flexible floating interconnected structures. Ocean Eng. 2007, 34, 1516–1531. [Google Scholar] [CrossRef]
- Michailides, C.; Loukogeorgaki, E.; Angelides, D.C. Response analysis and optimum configuration of a modular floating structure with flexible connectors. Appl. Ocean Res. 2013, 43, 112–130. [Google Scholar] [CrossRef]
- Li, Y.; Ren, N.; Li, X.; Ou, J. Hydrodynamic Analysis of a Novel Modular Floating Structure System Integrated with Floating Artificial Reefs and Wave Energy Converters. J. Mar. Sci. Eng. 2022, 10, 1091. [Google Scholar] [CrossRef]
- DNV-GL. Recommended Practice: Design, Development and Operation of Floating Solar Photovoltaic Systems (DNVGL-RP-0584, March 2021); Technical Report; DNV GL Group: Baerum, Norway, 2021. [Google Scholar]
- Yoon, J.S.; Cho, S.P.; Jiwinangun, R.G.; Lee, P.S. Hydroelastic analysis of floating plates with multiple hinge connections in regular waves. Mar. Struct. 2014, 36, 65–87. [Google Scholar] [CrossRef]
- Waals, O.J.; Bunnik, T.H.J.; Otto, W.J. Model tests and numerical analysis for a floating mega island. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2018), Madrid, Spain, 17–22 June 2018; ASME: New York, NY, USA, 2018; p. OMAE2018-78589. [Google Scholar]
- Ren, N.; Zhang, C.; Magee, A.R.; Hellan, Ø.; Dai, J.; Ang, K.K. Hydrodynamic analysis of a modular multi-purpose floating structure system with different outermost connector types. Ocean Eng. 2019, 176, 158–168. [Google Scholar] [CrossRef]
- Bispo, I.; Mohapatra, S.; Guedes Soares, C. Numerical analysis of a moored very large floating structure composed by a set of hinged plates. Ocean Eng. 2022, 253, 110785. [Google Scholar] [CrossRef]
- Ikhennicheu, M.; Blanc, A.; Danglade, B.; Gilloteaux, J.C. OrcaFlex modeling of a Multi-Body Floating Solar Island Subjected to Waves. Energies 2022, 15, 9260. [Google Scholar] [CrossRef]
- Otto, W.J.; Bunnik, T.H.J.; Kaydihan, L. Hydro-Elastic Behavior of an Inflatable Mattress in Waves. In Proceedings of the 9th International Conerence on Hydroelasticity in Marine Technology, Rome, Italy, 10–13 July 2022. [Google Scholar]
- Xu, P.; Wellens, P.R. Theoretical analysis of nonlinear fluid–structure interaction between large-scale polymer offshore floating photovoltaics and waves. Ocean Eng. 2022, 249, 110829. [Google Scholar] [CrossRef]
- Zhang, M.; Schreier, S. Review of wave interaction with continuous flexible floating structures. Ocean Eng. 2022, 264, 112404. [Google Scholar] [CrossRef]
- Friel, D.; M, K.; Whittaker, T.; Doran, W.J.; Howlin, E. A review of floating photovoltaic design concepts and installed variations. In Proceedings of the 4th International Conference on Offshore Renewable Energy (CORE2019), Glasgow, UK, 29–30 August 2019; ASRANet Ltd.: Surrey, UK, 2019. [Google Scholar]
- Claus, R.; López, M. A methodology to assess the dynamic response and the structural performance of floating photovoltaic systems. Sol. Energy 2023, 262, 111826. [Google Scholar] [CrossRef]
- Delacroix, S.; Bourdier, S.; Soulard, T.; Elzaabalawy, H.; Vasilenko, P. Experimental modeling of a Floating Solar Power Plant Array under Wave Forcing. Energies 2023, 16, 5198. [Google Scholar] [CrossRef]
- Zhang, C.; Dai, J.; Ang, K.K.; Lim, H.V. Development of compliant modular floating photovoltaic farm for coastal conditions. Renew. Sustain. Energy Rev. 2024, 190, 114084. [Google Scholar] [CrossRef]
- Sree, D.K.; Law, A.W.K.; Pang, D.S.C.; Tan, S.T.; Wang, C.L.; Kew, J.H.; Seow, W.K.; Lim, V.H. Fluid-structural analysis of modular floating solar farms under wave motion. Sol. Energy 2022, 233, 161–181. [Google Scholar] [CrossRef]
- Lee, J.H.; Paik, K.J.; Lee, S.H.; Hwangbo, J.; Ha, T.H. Experimental and Numerical Study on the Characteristics of Motion and Load for a Floating Solar Power Farm under Regular Waves. J. Mar. Sci. Eng. 2022, 10, 565. [Google Scholar] [CrossRef]
- Friel, D.; Karimirad, M.; Whittaker, T.; Doran, J. Experimental hydrodynamic assessment of a cylindrical-type floating solar system exposed to waves. J. Ocean Eng. Sci. 2023, 8, 461–473. [Google Scholar] [CrossRef]
- Jiang, Z.; Dai, J.; Saettone, S.; Tørå, G.; He, Z.; Bashir, M.; Souto-Iglesias, A. Design and model test of a soft-connected lattice-structured floating solar photovoltaic concept for harsh offshore conditions. Mar. Struct. 2023, 90, 103426. [Google Scholar] [CrossRef]
- McCartney, B.L. Floating breakwater design. J. Waterw. Port, Coastal, Ocean Eng. 1985, 111, 304–318. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Zanuttigh, B.; Andersen, T.L.; Lara, J.L.; Steendam, G.J.; Ruol, P.; Sergent, P.; Ostrowski, R.; Silva, R.; Martinelli, L.; et al. Chapter 3—Innovative Engineering Solutions and Best Practices to Mitigate Coastal Risk. In Coastal Risk Management in a Changing Climate; Zanuttigh, B., Nicholls, R., Vanderlinden, J.P., Burcharth, H.F., Thompson, R.C., Eds.; Butterworth-Heinemann: Boston, MA, USA, 2015; pp. 55–170. [Google Scholar]
- van der Zanden, J.; van der Hout, A.; Otto, W.; Spaargaren, F.; Walles, B.; de Wilde, J. Experimental study on a breaking-enforcing floating breakwater. J. Coast. Hydraul. Struct. 2022, 2, 1–28. [Google Scholar] [CrossRef]
- Dai, J.; Ming, C.; Utsunomiya, T.; Duan, W. Review of recent research and developments on floating breakwaters. Ocean Eng. 2018, 158, 132–151. [Google Scholar] [CrossRef]
- Macagno, E.O. Fluid mechanics—Experimental study of the effects of the passage of a wave beneath an obstacle. In Proceedings of the Academic des Sciences, Paris, France, 13 July 1953. [Google Scholar]
- Ruol, P.; Martinelli, L.; Pezzutto, P. Formula to Predict Transmission for π-Type Floating Breakwaters. J. Waterw. Port Coastal Ocean Eng. 2013, 139, 1–8. [Google Scholar] [CrossRef]
- van der Zanden, J.; Heijmen, R.; van Engelenburg, R. Data Report SUREWAVE WP6.4: Early Stage Model Tests of Integrated Floating Breakwater-FPV Design. 2024. Available online: https://zenodo.org/doi/10.5281/zenodo.10960432 (accessed on 19 April 2024).
- Chen, M.; Guo, H.; Wang, R.; Tao, R.; Cheng, N. Effects of Gap Resonance on the Hydrodynamics and Dynamics of a Multi-Module Floating System with Narrow Gaps. J. Mar. Sci. Eng. 2021, 9, 1256. [Google Scholar] [CrossRef]
- Gao, J.L.; Lyu, J.; Wang, J.H.; Zhang, J.; Liu, Q.; Zang, J.; Zou, T. Study on Transient Gap Resonance with Consideration of the Motion of Floating Body. J. Mar. Sci. Eng. 2022, 36, 994–1006. [Google Scholar] [CrossRef]
- Li, Z.; Chen, D.; Feng, X. Hydroelastic and expansibility analysis of a modular floating photovoltaic system with multi-directional hinge connections. Ocean Eng. 2023, 289, 116218. [Google Scholar] [CrossRef]
- Fagerholt, E. DIC Software, eCorr v4.0, Copyright 2017; NTNU: Trondheim, Norway, 2017. [Google Scholar]
- Somarathna, H.; Raman, S.; Mohotti, D.; Mutalib, A.; Badri, K. Rate dependent tensile behavior of polyurethane under varying strain rates. Constr. Build. Mater. 2020, 254, 119203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).