Inertia Energy-Based Required Capacity Calculation of BESS for Achieving Carbon Neutrality in Korean Power System

Abstract

Frequency response performance in power systems is becoming vulnerable due to the transition toward the higher penetration of renewable energy such as achieving carbon neutrality. In particular, reducing power system inertia energy as the asynchronous generation increases could result in violating the frequency stability constraint when a disturbance occurs in the power systems. In order to control the rapidly fluctuating frequency of the power system with low inertia, it is necessary to introduce fast frequency response resources such as a Battery Energy Storage System (BESS). This paper proposes a method to calculate the required capacity of BESS for compensating the frequency control performance of the power system using inertia energy. For calculating the required capacity of BESS, the inertia energy in the critical power system, where frequency control performance marginally satisfies frequency stability constraint, should be calculated. Also, the inertia energy in the evaluated power system having deficit inertia energy should be calculated. By comparing power systems that respond with different dynamics when the same disturbance occurs, the proposed calculation corresponds to the ratio of inertia energy deficiency based on critical power system inertia energy within the power imbalance. Through various case studies employing Korean power systems, the effectiveness of the inertia energy-based calculation method for the required BESS is verified by the fact that the BESS integrated power system marginally satisfies the frequency stability constraint. In these study cases, it is found that the instant response of BESS is very effective for compensating the frequency control performance of the low inertia power system. By applying the proposed method, it is also found that about 840 MW of BESS can achieve carbon neutrality in the Korean power system.

1. Introduction

Throughout the world, many efforts have been made to reduce greenhouse gas (GHG) emissions under the Paris Agreement. In particular, the power industry has tried to harness the power of Renewable Energy Sources (RESs) to eliminate its dependence on fossil fuels [1,2]. In the case of Korea, RESs are expected to take charge of about 71% of the electric power supply to achieve carbon neutrality [3]. However, the power system with such a high RESs penetration level would need more advanced operation schemes due to the high uncertainty and variability of RESs. In addition, since RESs are based on asynchronous generation and decoupled from the power system, those high penetration levels in the power system result in a low inertia, which might deteriorate the frequency control performance [4,5,6].

In order to control the rapidly fluctuating frequency of the power system with low inertia, it is necessary to introduce fast frequency response resources such as BESS. BESS usually consists of a chemical battery, power converter, power control system, and power management system. It has the advantages of responsiveness and controllability but also has disadvantages such as limited energy capacity and performance degradation. Its price is also still high. Therefore, it is very important to accurately calculate the required amount of BESS.

This paper proposes a method to calculate the required capacity of BESS for compensating the frequency control performance of the power system using inertia energy. The inertial energy has been studied from several perspectives. The method of deriving the required capacity of BESS using the RoCoF for a transient state in a given system has been studied. However, this cannot be applied to systems with different inertial energy, and only to specific systems with critical values [7]. In addition, a study was conducted on a power system consisting only of a synchronous generator. A method was proposed to estimate the amount of trip of the generator according to the change of inertia energy. This has the advantage of being able to estimate the trip amount in real time, but there is a limit that can only be applied to a small and determined system [8]. However, this paper has the advantage of being able to simply estimate the state of the system using inertial energy and can be used to estimate the amount of BESS required in the expected future system in preparation for system operation.

Through various case studies employing Korean power systems, it is verified that the calculated capacity of BESS is appropriate for the low inertia power system to satisfy frequency stability constraints. Also, the capacity of BESS for implementing carbon neutrality in the Korean power system is derived and verified its appropriate. As a result, it was confirmed that the amount of BESS required to equivalently reduce the power imbalance in relation to frequency change was accurately calculated.

2. BESS Application in the Power System with Low Inertia

2.1. Characteristics of the Power System with High Penetration Rate of RESs

The continuous increase in RESs’ penetration rate in order to reduce carbon dioxide emissions and ultimately achieve carbon neutrality brings characteristic changes to the power system. First of all, the resources available for governor response representing a primary frequency control service typically provided by synchronous generators have decreased. The high volatility of RESs has made it difficult to output a predetermined amount during a predetermined period, so it is difficult to secure the governor response amount. Accordingly, in order to secure the promised governor response amount, it is necessary to improve the performance of existing governor response resources [9].

This also reduces the power system inertia energy. Most of the RESs are solar and wind, and they convert the energy based on asynchronous generators, not rotor-based synchronous generators used in conventional coal-fired or nuclear power. Therefore, in the power system the inertia energy, which is a physical characteristic inherent in the rotor, is reduced. The power system inertia energy decreasing reduces the amount of energy that can withstand the immediate change such as a generator trip. This makes it difficult to keep the power system stable until a subsequent frequency response. Reduced power system inertia is an issue that must be solved to maintain frequency response performance. This cannot be solved by improving the performance of existing frequency response resources such as the governor response, and additional compensation is required. Accordingly, the power system Electricity System Operator (ESO) should identify the exact required capacity for compensating the power system vulnerability.

In the power system, the frequency indicates the balance of supply and demand, and the stability of the power system can be evaluated through the Nadir frequency, the Rate of Change of Frequency (RoCoF), or the inertia energy. Regarding the allowable disturbance size, the Nadir frequency can be considered for satisfying the frequency stability constraint. The RoCoF can be used commonly for evaluating the power system inertia state. However, it can only be used when there are predetermined conditions, such as window size. In the European Network of Transmission System Operators for Electricity (ENTSO-e), the RoCoF criteria have a moving average of ±2 Hz/s when the window size is 500 ms, the RoCoF criteria have a moving average of ±1.5 Hz/s when the window size is 1000 ms, the RoCoF criteria have a moving average of ±1.25 Hz/s when the window size is 2000 ms. However, it is derived based on transient states such as generator trips.

The inertia energy can be estimated in a normal state depending on the configuration of the power system source [10]. The inertia energy represents the sum of the potential electrical energy in the power system caused by physical energy. The inertia energy may vary depending on the configuration of the power system source. Under the same power generation output, the more synchronous generators the higher the inertia energy in the power system. In the future, if the capacity of the power generation facility increases without increasing the inertia energy due to the increasing proportion of asynchronous generators, the value of the inertia energy will continue to decrease [11,12].

2.2. Frequency Control of the Power System with Low Inertia

The power system must be satisfied above the frequency stability constraint to secure the power system even in a sudden imbalance of supply and demand caused by an unexpected disturbance. To this end, power system ESOs establish a frequency response plan [13,14,15]. Generators for each frequency response build a mutual cooperation system according to the requirements. To this end, each generator must dispatch a predetermined amount of output to the power system for a predetermined period of time. A frequency response system consisting of primary, secondary, and tertiary frequency response. In particular, a primary frequency response should be activated within a few seconds.

Commonly, the governor’s response has been responsible for this, using the reserve power normally possessed by the generator. The amount of the output power is determined by the Speed Droop (SD), which means the governor sensitivity, the rated power of the generator for governor response (P_rate), the rated frequency in the system (F_rate), and the frequency deviation (Δf) as shown in Equation (1).

$$∆\mathrm{P}=\frac{1}{\mathrm{S}\mathrm{D}}\times {\mathrm{P}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}}\times \frac{∆\mathrm{f}}{{\mathrm{F}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}}}\times 100$$

(1)

Therefore, it is necessary to manage the amount of governor response considering the amount of active power prepared for the governor response and the sensitive performance of the governor according to the frequency change. The increase in the ratio of RESs generation, which are asynchronous generators to achieve carbon neutrality, and the disposal of coal-fired generators, which accounted for a large part of the synchronous generator, made it difficult to secure the governor’s response. Also, due to the nature of renewable power generation with high intermittency, most power systems cannot use renewable power generation for their governor's response. Therefore, the change in the power generation mix directly affects the frequency response, especially the reduction in the amount of governor response that requires rapid response within a few seconds. Nevertheless, the reduction in the response of the governor can be solved by adjusting the SD of the remaining generators, which have a fast response performance such as LNG and increasing the reserve power capacity of the generator used for the governor response. It is necessary to keep the same governor response capacity among the cooperative systems for frequency response performance in order to verify the inertia energy compensation effect through BESS.

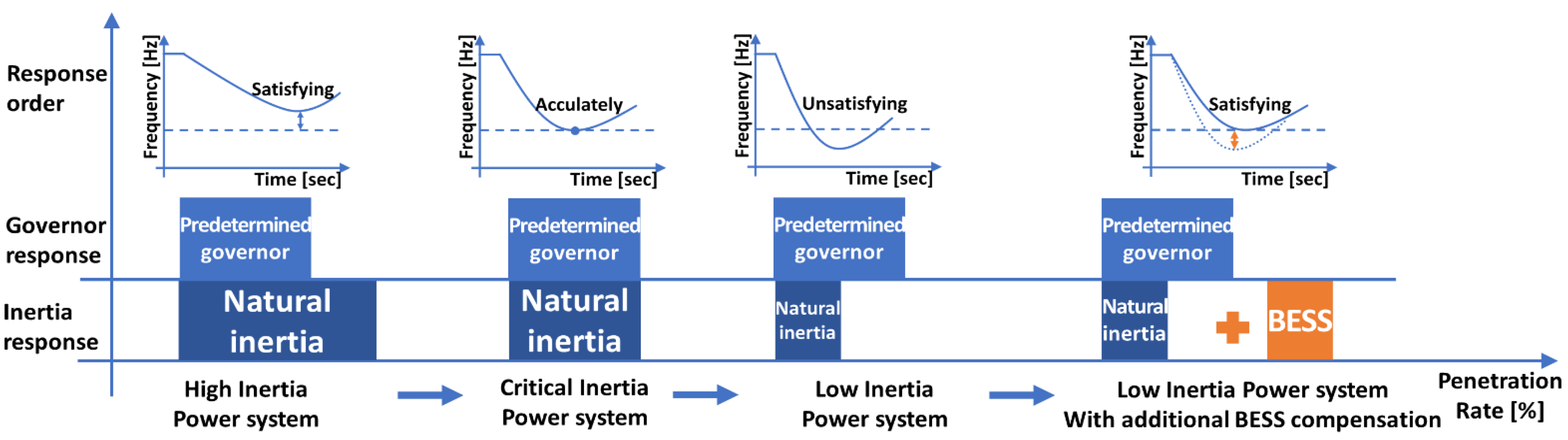
In addition, before the governor response, the kinetic energy of the synchronous generators instantaneously responds to the frequency drop, which is an inertia response. Accordingly, the primary frequency response is combined with the inertia response and governor response. This can respond to the frequency fluctuation primarily and can keep the frequency above the frequency stability constraint at all times. However, as shown in Figure 1, if the predetermined capacity in the mutual cooperation system is not satisfied, the subsequent frequency response resources cannot be sufficiently ready to dispatch the predetermined amount of output, and thus the frequency stability constraint cannot be satisfied. Therefore, the momentary active power should be provided and managed like BESS in order to maintain the power system securely [16,17].

The inertia response has the characteristic that effective power can be produced before the governor response produces the rated power. It can be divided into a natural inertia response and a synthetic inertia response. The natural inertia response is the release of the physical characteristics of the rotating synchronizer as an electrical output, and the resulting inertia energy (IE_i) is stored when the synchronous generator rotor rotates at a constant speed (ω_sm) with an inertia moment (J_i), as shown in Equation (2) [18,19]. Therefore, the capacity adjustment is impossible because the rotor constant is fixed.

$${\mathrm{I}\mathrm{E}}_{\mathrm{i}}=\frac{1}{2}{\mathrm{J}}_{\mathrm{i}}{\mathsf{\omega }}_{\mathrm{s}\mathrm{m}}^2$$

(2)

The synthetic inertia response can dispatch the effective output power as a predetermined amount of effective power within a pre-planned condition before the governor response dispatches the rated output. The inertia energy can be secured by fast responsive resources within one cycle such as BESS. In order to introduce fast responsive resources such as BESS, it is necessary to calculate the appropriate capacity. To this end, in this paper, a method for calculating the required capacity of BESS to secure the frequency stability constraint is presented. For this purpose, a method for determining the critical inertia energy is presented and a method for calculating the required capacity of BESS based on the inertia energy of the evaluated power system and the critical power system is presented.

Various attempts have been made to stably operate a power system that has become vulnerable due to a decrease in inertia conditions. A methodology for calculating BESS capacity for synthetic inertia is presented, which calculates the BESS capacity through the RoCoF deficiency with the reference RoCoF value. However, it is impossible to use this method without the RoCoF reference value. In addition, since it can only be applied in the same state of inertia, it cannot be used to evaluate the expected low inertia energy power system. Also, a method for calculating the trip amount of a synchronous generator according to a change in inertia energy in the power system is presented. This power system only consists of synchronous generators. Therefore, this approach is difficult to apply in power systems with a mix of synchronous and asynchronous generators [20,21].

As a result, calculating the required capacity of BESS using the inertia energy is effective and simple in order to evaluate the expected low inertia power systems.

2.3. BESS Application for Compensation of the Inertia Energy

As an immediate response method to improve the vulnerability of the power system, it has traditionally relied on a synchronous compensator or “imported” AC connection. Recently, various measures using asynchronous power have also been proposed, and the interest in the use of BESS is increasing. BESS is a resource that can provide instantaneous output in a step format with fast response speed, excluding the dead band period. It is applied for frequency response in many power systems and can also be used for inertia energy compensation due to its instantaneous active power supply characteristics. BESS generally has appropriate dynamic characteristics for frequency support and can apply various control methods, such as variable droop or specially designed energy management systems (EMSs), which utilize inertia energy. Applying these solutions throughout the system can contribute to the reduction in inertia but may not be fully effective in preventing frequency imbalance. Therefore, this should be contributed as a share of the subsequent frequency response coordination system [9,22,23].

3. BESS Required Amount Calculation Method Using the Inertia Energy

3.1. Power System with the Critical Inertia Energy

The inertia energy of the power system (IE_sys) refers to the energy stored in rotating generators and some motor loads, which causes them to remain rotating. This can be determined as a weighted average value of the inertia energies of the synchronous generators as shown in Equation (3) using the MVA rating (S_i) and the inertia constant (H_i) of each generator in the power system [24,25].

$${\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s}}=\sum _{\mathrm{n}=1}^{\mathrm{n}}{\mathrm{H}}_{\mathrm{i}}·{\mathrm{S}}_{\mathrm{i}}$$

(3)

This energy plays a very important role in compensating instantaneous imbalances between the generations and loads in the power system, especially right after the disturbance occurs since there are no responses from the frequency control resources yet. As the penetration level of RESs increases, which does not have an intrinsic inertia response, the frequency control performance of the power system easily deteriorates if the inertia energy is below the required level. The critical inertia energy (IE_critical) can be calculated as the required minimum level of inertia energy for the power system to meet the frequency stability constraint.

In this section, the critical inertia energy is calculated as the inertia energy of the power system when its frequency control performance marginally meets the frequency stability constraint. The following flowchart in Figure 2 shows the process for this calculation.

As shown in the flowchart above, the maximum penetration level of RES is found by increasing its penetration level until just before the frequency stability constraint, which is the Nadir frequency is violated. The inertia energy of the power system with the maximum penetration level of RES is the critical inertia energy.

Moreover, the dynamics of the power system with the critical inertia energy can be represented by the swing equation as shown in Equation (4).

$$\frac{\mathrm{d}∆\mathsf{\omega }}{\mathrm{d}\mathrm{t}}=∆\mathrm{P}·\frac{{\mathrm{f}}_0}{2·{\mathrm{I}\mathrm{E}}_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}$$

(4)

where $\frac{\mathrm{d}∆\mathsf{\omega }}{\mathrm{d}\mathrm{t}}$ is RoCoF, $∆\mathrm{P}$ is the power imbalance size, f₀ is nominal frequency, and IE_critical is the critical inertia energy.

3.2. Required Capacity Calculation of BESS for Compensating the Inertia Energy

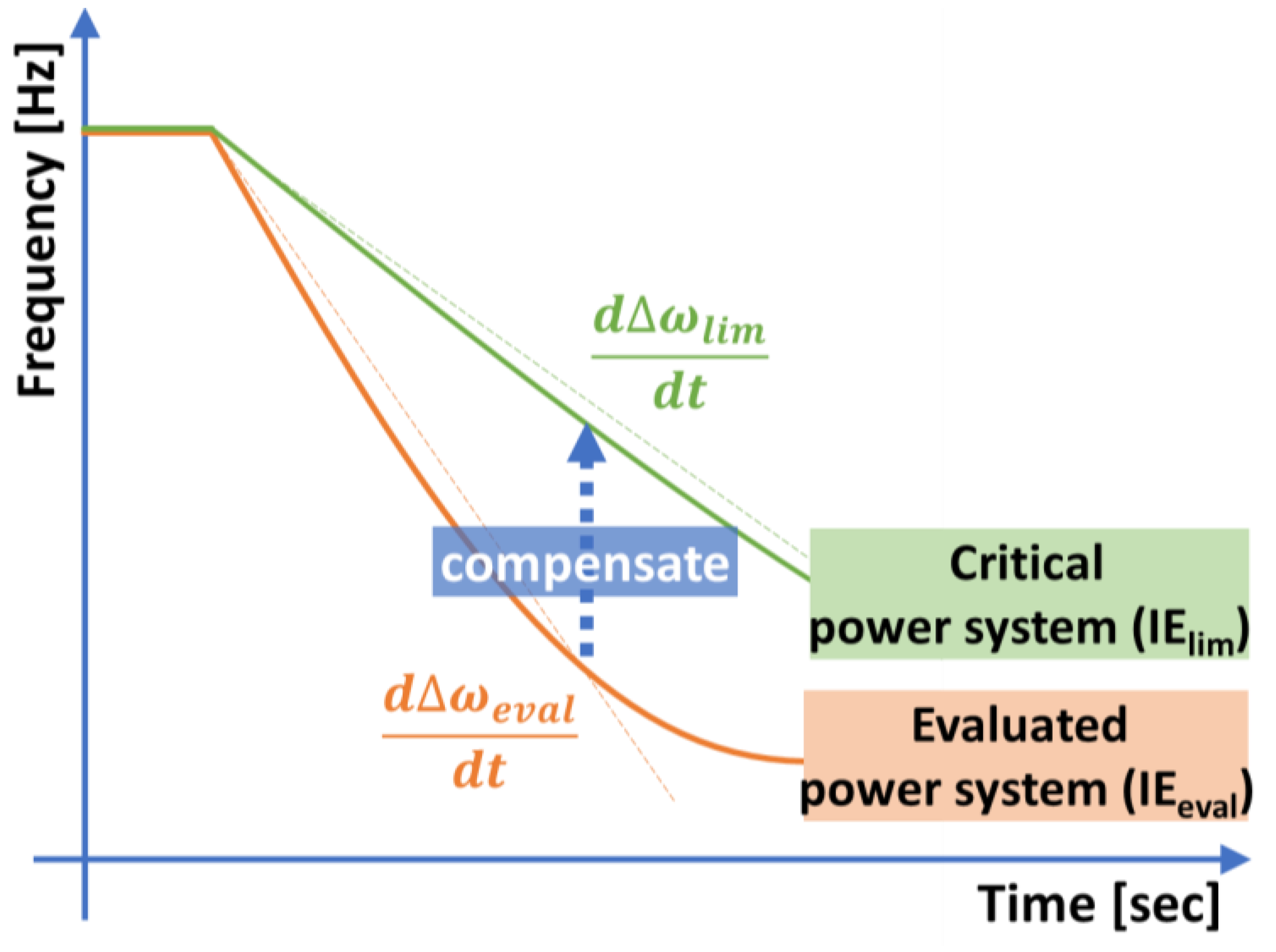
BESS has been proposed to be a good solution to the power system with a low inertia energy due to its fast and accurate response to frequency deterioration. However, BESS should be efficiently installed and controlled since it still costs much more than the typical resources. In this section, a calculation of the required contribution from BESS for compensating the inertia energy is proposed using the difference in RoCoF between the evaluated power system and the critical power system responding to the same disturbance. Since RoCoF mainly depends on the inertia energy of the power system right after a generator trip, the steeper RoCoF at the low inertia energy would be recovered to the RoCoF limit at the critical inertia energy if BESS could compensate for the insufficient inertia energy. Figure 3 shows this concept.

Also, the RoCoF can be derived by the swing equation representing the power system dynamics as shown in Equation (5)

$$\frac{\mathrm{d}∆\mathsf{\omega }}{\mathrm{d}\mathrm{t}}=∆\mathrm{P}·\frac{{\mathrm{f}}_0}{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s}}}$$

(5)

From swing equations about the evaluated power system with a low inertia energy (IE_sys,eval) and the critical power system with a critical inertia energy (IE_sys,critical) to the same disturbance (P_trip), Equations (6) and (7) can be derived.

$${\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}=\frac{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}{{\mathrm{f}}_0}·\frac{\mathrm{d}∆{\mathsf{\omega }}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}{\mathrm{d}\mathrm{t}}$$

(6)

$${\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}=\frac{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{{\mathrm{f}}_0}·\frac{\mathrm{d}∆{\mathsf{\omega }}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{\mathrm{d}\mathrm{t}}$$

(7)

Using the Equations (6) and (7) about the same generator trip, the Equation (8) can be derived.

$${\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}=\frac{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}{{\mathrm{f}}_0}·\frac{\mathrm{d}∆{\mathsf{\omega }}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}{\mathrm{d}\mathrm{t}}=\frac{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{{\mathrm{f}}_0}·\frac{\mathrm{d}∆{\mathsf{\omega }}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{\mathrm{d}\mathrm{t}}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$$

(8)

Equation (8) describes the relationship among trip generator amount, the inertia energy, and RoCoF, which means the RoCoF of the evaluated power system would be steeper than that of the critical power system if the inertia energy is lower than the critical inertia energy. Therefore, the amount of the tripped generator causing the power imbalance in the power grid needs to be equivalently reduced if RoCoF should be maintained the same as that of the critical power system even with the low inertia energy. Since BESS (P_BESS) provides the inertia response using its fast and accurate performance, its contribution equivalently reduces the impact of the generator trip and restores RoCoF at a low inertia energy to that at a critical inertia energy as represented by using Equation (9)

$${\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}-{\mathrm{P}}_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}=\frac{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{{\mathrm{f}}_0}·\frac{\mathrm{d}∆{\mathsf{\omega }}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}{\mathrm{d}\mathrm{t}}$$

(9)

Using Equations (8) and (9), Equation (10) can be derived.

$${\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}-{\mathrm{P}}_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}=\frac{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{{\mathrm{f}}_0}·\left({\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}\frac{{\mathrm{f}}_0}{2·{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}\right)={\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}\frac{{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}$$

(10)

Therefore, the required capacity of BESS can be calculated by using Equation (11).

$${\mathrm{P}}_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}={\mathrm{P}}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}}\left(\frac{{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}-{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}}}{{\mathrm{I}\mathrm{E}}_{\mathrm{s}\mathrm{y}\mathrm{s},\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}}\right)$$

(11)

As shown in Equation (11), the required capacity of BESS for compensating the inertia energy can be calculated by multiplying the ratio of the inertia energy shortfall to the critical inertia energy in the tripped generator amount.

4. Case Studies

Case studies were conducted using the Korean power system to verify the proposed method. The standards and composition of the Korean power system are as follows. In the case of the Korean power system, the government enacted the “Power System Reliability and Electricity Quality Maintenance Criteria” to ensure that the power system frequency is constrained at 59.70 Hz in the event of a disturbance in which one of the maximum unit capacity generators is tripped. These criteria must be maintained by securing frequency response resources and a predetermined operation strategy.

The Korean power system consists of 183 generators, the sum of their rated output power is 79,515 MW. The configuration of the power system source under the condition of a 32% RES generation penetration rate is as follows. There are 103 synchronous generators using coal-fired, nuclear, LNG, and hydro sources, and the sum of the rated output power is 54,400 MW. There are 80 asynchronous generators such as solar and wind power, and the sum of the rated output power is 25,115 MW. The output power of the maximum unit capacity generator is 1460 MW. The governor response amount, which can affect the frequency response, sets output power to 1000 MW when the power system frequency decreases by 0.2 Hz.

The simulation was conducted to evaluate the calculation capacity of BESS by using the power system simulator for engineering (PSS/E 33.12.2) from Siemens PTI (Schenectady, NY, USA), which is the most widely used simulation tool for power system analysis.

4.1. The Critical Inertia Energy in Korean Power System

In order to evaluate the expected system, the critical condition when its inertia energy is marginal should be established. The critical power system inertia energy can be derived based on the method proposed in Figure 2. 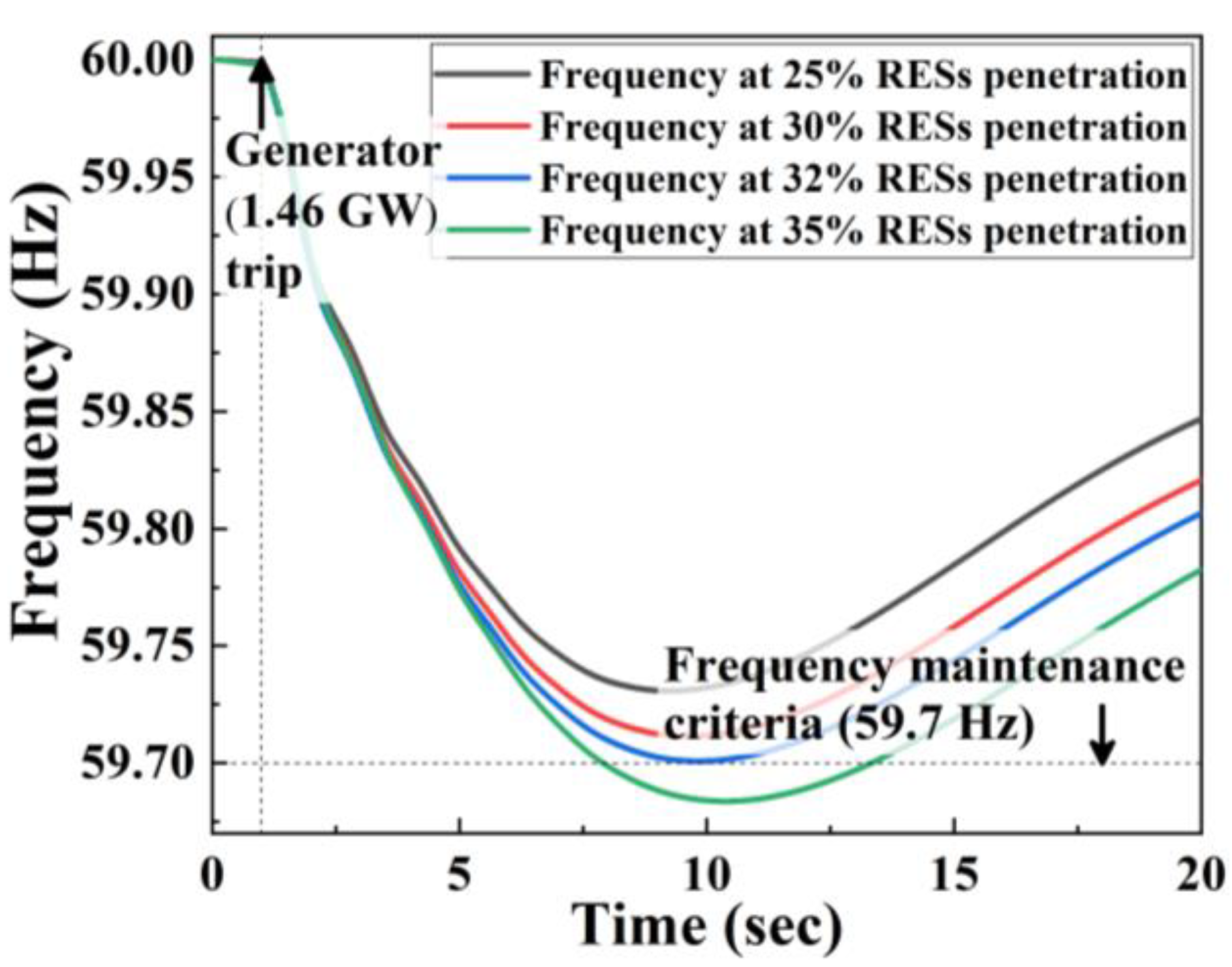Starting with the base power system that can satisfy the frequency stability constraint with the existing frequency response performance, the critical power system can be found by repeatedly increasing the asynchronous generation output power (P_RES) and decreasing the synchronous generation output power (P_SG). We started with an RESs generation penetration rate of 25%, which is a power system that can sufficiently satisfy the frequency stability constraint. By increasing the penetration rate by 5%, it was confirmed that there was a critical condition between 30% and 35%, and finally, it was confirmed that 32% was the critical power system.

The result is as shown in Figure 4, the Nadir frequency of the 25% penetration rate power system is 59.73 Hz, the Nadir frequency of the 30% penetration rate power system is 59.71 Hz, and the Nadir frequency of the 32% penetration rate power system is 59.70 Hz. In the power system with a 35% penetration rate, the Nadir frequency is reduced to 59.68 Hz, so it is out of the critical state.

As a result, it is confirmed that the power system, which is a critical condition, is the power system with a penetration rate of 32%. The inertia energy at this time can be calculated followed by Equation (3). For 103 synchronous generators out of 183 generators, the inertia energy at this time is 308,338 MVA.

4.2. BESS Required Capacity Calculation and Verifying the Compensation Effect

To verify the suitability of the proposed method using inertia energy, it started evaluating from an RESs generation penetration rate of 35% which was beginning to exceed the critical state. It was also verified at lower inertia power systems of 40% and 45%. The frequency response in the disturbance of a 1460 MW generator trip at the low inertia energy in an RESs generation penetration rate of 35%, 40%, and 45% for verification, are shown in Figure 5. As the penetration rate increases, the inertia energy decreases, and the frequency changes rapidly in the same size disturbance. Therefore, the Nadir frequency decreased to 59.68 Hz, 59.64 Hz, and 59.59 Hz, respectively.

Also, in order to maintain the existing frequency response performance consistently, the governor response amount must also be maintained at a similar level.

Table 1. The inertia energy and the governor response amount in Korean power system following the change of penetration rate.

Division	32%	35%	40%	45%
IE (MVAs)	308,388	291,978	274,015	254,180
Nadir Frequency (Hz)	59.70	59.68	59.64	59.59
Gov power (MW) at △F = 0.2 Hz	1067	1089	1053	1090

shows the Nadir frequency, inertia energy, and governor response power in each power system.

The power system that fails to secure the frequency stability constraint with existing frequency response performance requires additional compensation. As BESS has fast and accurate response characteristics, it is suitable for compensating for the power system inertia. The BESS adopted for compensation resources has a dead band of 30 mHz and a control algorithm that maximizes the output power that responds proportionally to the frequency change is applied so that it can effectively contribute to the inertia response of the power system.

4.2.1. RESs Generation Penetration 35% Case

For modeling the power system with 35% penetration of RES, the generator mix of the existing power system is changed as follows. Five coal-fired power generators out of 103 synchronous generators, which have an output of 3060 MW, were switched to renewable power sources. The reduction in coal-fired generators and synchronous generators reduces the inertia energy of the power system. This results in rapid frequency changes and a decrease in the Nadir Frequency for the same disturbance. This power system deteriorates frequency stability constraints under the existing frequency response performance in the disturbance of a 1460 MW generator trip, which is the unit maximum generator capacity. As a result, the Nadir frequency decreased to 59.68 Hz from 59.70 Hz, and the result cannot be satisfied with the frequency stability constraint.

To solve this violation, the required capacity of BESS was calculated according to the proposed method. The inertia energy of the critical power system is 308,388 MVAs, and the inertia energy in the case of an RESs generation penetration rate of 35% is 291,978 MVAs. The inertia energy decreases by 16,410 MVAs and the deficit ratio is 5.3% of the critical inertia energy. Therefore, the required capacity is calculated to be 78 MW according to Equation (11), which is 5.3% of the imbalance output power of 1460 MW. It is calculated as the capacity to compensate for the shortfall of inertia energy.

The frequency characteristics of the same disturbance were verified by adopting the calculated 78 MW of BESS to the low inertia power system, which has less inertia energy than the critical power system. As shown in Figure 6a, the existing frequency response system had a Nadir frequency of 59.68 Hz (red line), which could not satisfy the frequency stability constraint of 59.70 Hz. However, after adopting the calculated capacity of BESS of 78 MW to this power system (blue line), it was confirmed that the frequency stability constraint could be satisfied as 59.711 Hz.

4.2.2. RESs Generation Penetration 40% Case

For modeling the power system, the previously presented Korean power system was changed as follows. Eight coal-fired power generators out of 103 synchronous generators, which have an output of 6670 MW, were switched to renewable power sources. This power system deteriorates frequency stability constraints under the existing frequency response performance in the disturbance of a 1460 MW generator trip, which is the unit maximum generator capacity. As a result, the Nadir frequency decreases to 59.64 Hz from 59.70 Hz. And the result cannot be satisfied with the frequency stability constraint.

To solve this violation, the required capacity of BESS was calculated according to the proposed method. The inertia energy of the critical power system is 308,388 MVAs, and the inertia energy in the case of an RESs generation penetration rate of 40% is 274,015 MVAs. The inertia energy decreases by 34,373 MVAs and the deficit rate is 11.2% of the critical inertia energy. Therefore, the required capacity is calculated to be 163 MW according to Equation (11), which is 11.2% of the unbalanced output power of 1460 MW.

As shown in Figure 6b, the existing frequency response system had a Nadir frequency of 59.64 Hz (red line), which could not satisfy the frequency stability constraint of 59.70 Hz. However, after adopting the calculated capacity of BESS of 163 MW to this power system (blue line), it was confirmed that the frequency stability constraint could be satisfied as 59.712 Hz.

4.2.3. RESs Generation Penetration 45% Case

For modeling the power system, the previously presented Korean power system was changed as follows. Thirteen coal-fired power generators out of 103 synchronous generators, which have an output of 10,726 MW, were switched to renewable power sources. This power system deteriorates frequency stability constraints under the existing frequency response performance in the disturbance of a 1460 MW generator trip, which is the unit maximum generator capacity. As a result, the Nadir frequency decreases to 59.59 Hz from 59.70 Hz. And the result cannot be satisfied with the frequency stability constraint.

To solve this violation, the required capacity of BESS was calculated according to the proposed method. The inertia energy of the critical power system is 308,388 MVAs, and the inertia energy at the case of an RESs generation penetration rate of 45% is 254,180 MVAs. The inertia energy decreases by 54,208 MVAs and the deficit ratio is 17.6% of the critical inertia energy. Therefore, the required capacity is calculated to be 257 MW according to Equation (11), which is 17.6% of the imbalance output power of 1460 MW.

As shown in Figure 6c, the existing frequency response system had a Nadir frequency of 59.59 Hz (red line), which could not satisfy the frequency stability constraint of 59.70 Hz. However, after adopting the calculated capacity of BESS of 257 MW to this power system (blue line), it was confirmed that the frequency stability constraint could be satisfied as 59.709 Hz.

Table 2. Calculation of required BESS using the proposed method.

Penetration Rate	Power System Inertia Energy				Ptrip	PBESS
	Critical	Evaluated	Deficiency Amount	Deficiency Ratio
35%	308,388 MVAs	291,978 MVAs	16,410 MVAs	3%	1460 kW	78 MW
40%		274,015 MVAs	34,373 MVAs	11.2%		163 MW
45%		254,180 MVAs	54,208 MVAs	17.6%		257 MW

summarizes the inertia energy in the power system, deficiency amount and ratio, and the required capacity of P_BESS for each of the penetration rates of 35%, 40%, and 45%, respectively.

Through the proposed method, 78 MW BESS is required for the 35% power system to satisfy the frequency stability constraint, 163 MW BESS is required for the 40% power system, and 257 MW BESS is required for the 45% power system, respectively. In each case, it is verified that the calculated capacity of BESS effectively reduces the power imbalance equivalently, prevents the deterioration of the frequency stability constraint, and even approximately meets the constrained level.

4.3. BESS Required Capacity Calculation and Experimental Validation in Carbon Neutrality Case

To achieve carbon neutrality, the Korean government presents a scenario. The main characteristic is that the ratio of coal-fired generation is 0%, the ratio of RESs is more than 70% and the other energy source mix is changed to maintain the power system stability. In terms of inertia energy, the ratio of power generation using synchronous machines, such as nuclear power, coal-fired, nuclear, LNG, and hydro source, is 29%, and the ratio of power generation using asynchronous machines, such as renewable power, fuel cells, northeast-grid, and by-product gas, is 71%.

For modeling the power system, the previously presented Korean power system was changed as follows. All coal-fired generators were converted into renewable power generation or carbon-free gas power plants. This makes it difficult to secure the governor response amount due to the decrease in the synchronizer, and the inertia was also reduced. The nuclear power source will also decrease, but it does not affect the governor response as it does not participate in the governor response, but it has a significant effect on the reduction in inertia. In order to simulate the carbon-neutral situation, the system was constructed as shown in

Table 3. Comparison of energy mix between critical power system and carbon neutral model.

Mix	Critical Power System Generators			Carbon Neutral Power System Generators
	Number	Power		Number	Power
		MW	%		MW	%
RES	80	25,115	32	119	56,456	71
Nu	18	21,390	27	4	4771	6
Coal-fired	43	27,993	35	0	0	0
LNG	19	4034	5	37	17,493	22
HY	23	983	1	23	795	1
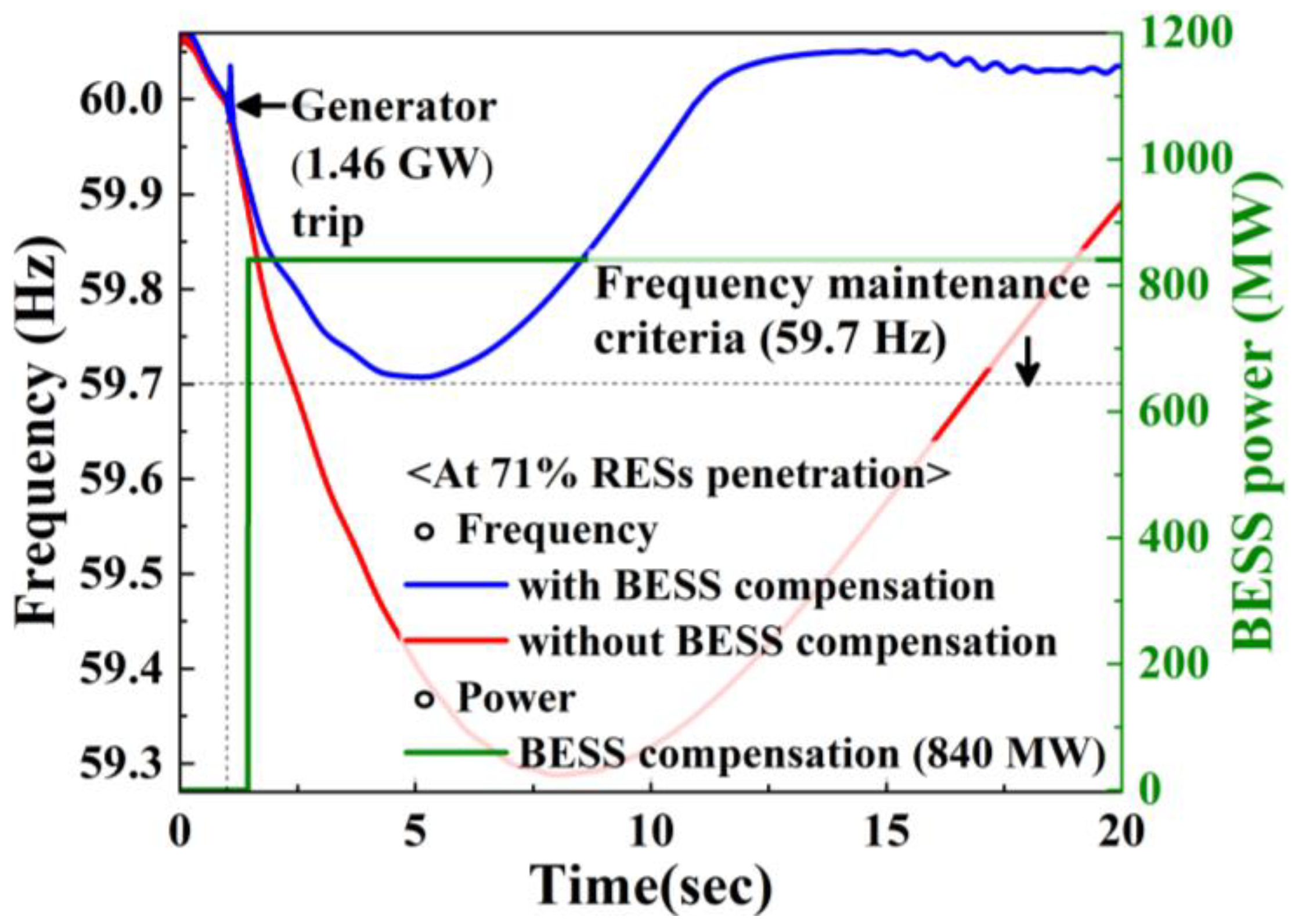
Total	183	79,515	100	183	79,515	100

according to Scenario A with reference to the ‘Carbon Neutrality Scenarios’. Based on the 2031-year DB, 43 coal-fired generators were converted to 25 renewable generators and 18 carbon-free LNG power plants to eliminate all carbon sources. The number of 18 nuclear power plants was reduced to 4, meeting the 6% ratio suggested in the scenario. In the case of a penetration rate of 71%, which is an output of 31,341 MW, they were switched to renewable power sources. This power system deteriorates frequency stability constraints under the existing frequency response performance in the disturbance of a 1460 MW generator trip, which is the unit maximum generator capacity. As a result, the Nadir frequency decreases to 59.27 Hz from 59.70 Hz. And the result cannot be satisfied with the frequency stability constraint.

To solve this violation, the required capacity of BESS was calculated according to the proposed method. The inertia energy of the critical power system is 308,388 MVAs, and the inertia energy in the case of an RESs generation penetration rate of 71% is 136,053 MVAs. The inertia energy decreases by 172,283 MVAs and the deficit ratio is 57.3% of the critical inertia energy. Therefore, the required capacity is calculated to be 840 MW according to Equation (11), which is 57.3% of the imbalance output power of 1460 MW.

As shown in Figure 7, the existing frequency response system had a Nadir frequency of 59.27 Hz (red line), which could not satisfy the frequency stability constraint of 59.70 Hz. However, after adopting the calculated capacity of BESS of 840 MW to this power system (blue line), it was confirmed that the frequency stability constraint could be satisfied as 59.701 Hz.

5. Conclusions

RESs are actively introduced in the power system to solve problems such as sustainable development and response to the climate crisis. RESs use an asynchronous power generator and do not have the inertia energy that naturally exists in the existing synchronous power generator. So, if an asynchronous generator is replaced by a synchronous generator in the power system, the inertia energy decreases. And in the event of a disturbance, it would not be possible to secure the frequency stability with the existing frequency response performance.

Therefore, additional compensation is required, the BESS having fast and accurate characteristics is considered to secure the frequency stability in the reduced inertia energy power system. In terms of future system operation planning, it is necessary to calculate the appropriate amount of the BESS required for this purpose. A method of using the inertia energy was proposed so that it can be applied even when there is no RoCoF standard. We derived the inertia energy of the power system at the critical power system and compared it with the evaluated power system. The insufficient inertia energy was calculated, and the BESS capacity was calculated using the relational equation derived from the Swing equation. As a result, to maintain frequency stability constraint in the evaluated power system, the power imbalance was equivalently reduced using the fast and accurate BESS. Through the proposed method, it is possible to calculate the required capacity of BESS by multiplying the ratio of the inertia energy shortfall to the critical inertia energy in the tripped generator amount.

For verification, the Korean power system is simulated, and by increasing the RES generation penetration rate, the state of the power system becomes vulnerable due to decreasing the inertia energy. The critical power system is confirmed at the 32% RES generation penetration rate, and the 78 MW BESS compensation power is needed to maintain the power system stable at 35% case. The 163 MW BESS compensation power at 40% case and the 257 MW BESS compensation power at 45% case are necessary to secure power system frequency stability. It was confirmed that all of these satisfy the frequency stability constraint as the target level when applying the proposed BESS capacity to the power system. Finally, it is verified whether the proposed method is effective even in the carbon-neutral scenario. The frequency is reduced to 59.27 Hz at a 71% renewable generation penetration ratio when the 1460 MW generation trip. Additional 840 MW BESS compensation could satisfy the frequency stability constraint. Even in extreme cases such as carbon neutrality, it was confirmed that the proposed method resulted in an accurate amount to satisfy the criteria.