Dynamic Comprehensive Evaluation of a 660 MW Ultra-Supercritical Coal-Fired Unit Based on Improved Criteria Importance through Inter-Criteria Correlation and Entropy Weight Method

Abstract

To address the issue of traditional static evaluation models being unable to comprehensively analyze the performance of ultra-supercritical coal-fired units under varying loads, we propose a dynamic comprehensive evaluation model based on the improved Criteria Importance Through Inter-criteria Correlation (CRITIC) method and entropy weight method (EWM). The comprehensive performance evaluation index system of ultra-supercritical coal fired units is constructed by examining the boiler performance, turbine performance, plant power performance, environmental performance, and flexible performance of coal-powered units. The CRITIC and EWM methods are used to calculate the weights of the indicators, which are then combined with the static evaluation results. Using a dynamic comprehensive evaluation model, we analyze ultra-supercritical coal-fired units, taking into account time weight. This allows us to obtain the comprehensive dynamic real-time evaluation value of the units under different loads. The research indicates that the weight of the evaluation index is changed when using the dynamic comprehensive evaluation model of the improved CRITIC and EWM. The index with lower weight is increased by 6.2%, while the index with higher weight is decreased by 0.22%. This alteration in weight range can provide a more objective reflection of the relationship between evaluation indicators. This model offers significant advantages in improving evaluation accuracy, weight balance distribution, and generality.

1. Introduction

As global climate change and environmental pollution continue to intensify, countries have established carbon-neutral and dual-carbon targets to promote a more sustainable direction for the energy industry. Therefore, it is particularly urgent to comprehensively evaluate and analyze coal-fired units [1]. As an important part of traditional energy, the development and reform of coal-fired units under the background of dual carbon is particularly important [2]. The evaluation of coal-fired units encompasses not only the efficiency and quality of power production but also factors such as energy utilization efficiency, environmental emissions, and safe and stable operation [3]. Therefore, the comprehensive evaluation and analysis of coal-fired units holds significant theoretical and practical importance [4].

In recent years, the comprehensive performance evaluation methods of coal-fired power plants have emerged, and many scholars at home and abroad have proposed a variety of comprehensive evaluation methods, such as the analytical hierarchy process, entropy weight method, rank-sum ratio comprehensive evaluation method and fuzzy comprehensive evaluation method [5].

To date, numerous scholars have conducted extensive research on the comprehensive evaluation of coal-fired power plants. This research covers evaluation methods, index systems, and model establishment, among other aspects. Ma et al. [6] proposed a comprehensive dynamic performance evaluation method to comprehensively understand the overall performance of coal-fired units under load changes, and to provide a basis for future optimization and improvement. Filonchyk et al. [7] conducted a comprehensive analysis of air pollution emissions from coal-fired power plants by using modeling techniques, and proposed the importance of coal power plants moving to sustainable energy systems. Tabassum et al. [8] conducted a study on Bangladesh using remote sensing technology and geographic information system analysis and proposed policies to enhance sustainable development and improve environmental quality. Filonchyk et al. [9] employed remote sensing technology and model analysis methods to monitor and evaluate NO₂ emissions in order to better understand the impact of NO₂ emissions on the environment and human health. Chen et al. [10] used the fuzzy analytical hierarchy process and improved criteria importance through intercriteria correlation (CRITIC) to empower evaluation indicators, which reflect the rationality of comprehensive evaluation indicators and the effectiveness of the evaluation methods. Wang et al. [11] determined the weights of the evaluation indicators by combining the entropy weighting method (EWM) and the subjective weighting method to achieve a comprehensive evaluation of the flexibility of coal-fired units. Huang et al. [12] analyzed the distribution characteristics of carbon emissions from buildings across six aspects and provided recommendations for development. Abulude et al. [13] evaluated the air quality in different Nigerian cities and towns and proposed measures to enhance it. Wang et al. [14] assessed the long-term operational status of near-zero emission coal-fired units. Ma et al. [15] established the assessment framework of the source–network–load interaction to provide a set of systematic indicators and methods for the low-carbon development of coal-fired units and a more sustainable development path for coal-fired power plants. Wu et al. [16] proposed a comprehensive multi-criteria decision model and weight uncertainty analysis of the analytic hierarchy process to assess the sustainability assessment of coal-fired units in many aspects, and introduced grey correlation analysis and other methods to address the weight uncertainty of analytic hierarchy process, improving the reliability and robustness of the evaluation results. Wu et al. [17] used the grey correlation analysis method and mixed entropy weight method to determine the weights of different indicators, improving the accuracy and objectivity of the evaluation results.

Comprehensive evaluation can be divided into static comprehensive evaluation and dynamic comprehensive evaluation [18]. In the static comprehensive evaluation, the evaluation object is evaluated comprehensively in a single period based on the information of each index of the evaluation object [18]. Dynamic comprehensive evaluation uses the same evaluation method to perform static comprehensive evaluation of evaluation objects at different time periods, and integrates with information aggregation operators to obtain the dynamic comprehensive evaluation value of evaluation objects [19]. At present, many scholars are paying attention to dynamic comprehensive evaluation. In 2007, Guo et al. [20] first proposed two types of information aggregation operators that can be used for dynamic comprehensive evaluation. On this basis, Li et al. [21] proposed a series of dynamic comprehensive evaluation methods based on the technique for order preference by similarity to ideal solution. Wang et al. [22] built an evaluation index system of the basic emergency response capability of the power grid based on the analysis of time and space dimensions, in order to achieve a dynamic and comprehensive evaluation of the emergency response capability of the power grid. Zhang et al. [23] proposed a new dynamic comprehensive evaluation model of multi-source uncertainty indicators based on the generalized grey incentive factors, and proved the effectiveness and feasibility of the model in combination with practical cases.

Currently, research on the performance evaluation of coal-fired units is diverse and innovative both domestically and internationally. This provides a scientific basis and technical support for the operation, management, and optimization of coal-fired units. However, there are still challenges and problems that require solutions, such as improving the evaluation index system, standardizing the weight determination method, and enhancing the accuracy of the comprehensive evaluation model. Further research and exploration are necessary.

However, for the comprehensive performance evaluation of coal-fired units, the traditional static evaluation model cannot analyze the comprehensive performance of ultra-supercritical coal-fired units under load. This paper presents a dynamic evaluation model for coal-fired units that comprehensively assesses their performance. The model uses a combination of the improved CRITIC and EWM methods to calculate the weights, and then combines them with time weights to obtain the comprehensive evaluation results. Furthermore, a comprehensive evaluation of ultra-supercritical coal-fired units is conducted using a constructed set of evaluation indices. The system considers five indexes: boiler performance, steam turbine performance, power consumption rate performance, environmental performance, and flexibility performance. Sub-indexes are set under each index. This paper presents research on the key factors affecting the comprehensive performance of coal-fired units. It provides valuable references for power plant operation departments.

2. The Construction of Index System

2.1. Principle of Index System Construction

Coal-fired units are an extremely complex energy consumption system, combined with the economic and environmental benefits of the development of coal-fired units; the index system includes all aspects of the characteristics of the development of coal-fired units under the dual-carbon target, and can reflect the development characteristics of coal-fired units under the low-carbon target. Therefore, the index system should be based on the following construction principles [24]:

The principle of independence: the degree of coupling between the primary index and the secondary index of the index system should be chosen to be low, and redundancy, cross-information and noise between indicators should be reduced.

Operability principle: the selection of indicators should be easy to quantify, the data source should be reliable and easy to measure, collect and obtain, and it should ensure that the indicator data can be processed in a standardized way.

Completeness principle: the selection of evaluation indicators should be able to reflect the characteristics and connotation of the overall performance of coal-fired units in a comprehensive, multifaceted and accurate manner. When selecting evaluation indicators, special attention should be paid to the selection of qualitative and quantitative indicators.

Objectivity principle: in the selection of indicators, the selected indicators can truly and accurately reflect the objectivity of the evaluation object, without complicating subjective factors so as to make a fair and impartial comprehensive evaluation of the evaluation object.

Dynamic principle: the index system is a dynamically changing process in the selection process. Therefore, the dynamic change of indicators over time should be fully considered in the selection of indicators. Horizontal comparison indicators should be selected with a clear trend of change in order to differentiate so as to avoid the selection of no change or small changes in the data.

2.2. Index System of Coal-Fired Units

The evaluation criteria for coal-fired units are based on current national standards, relevant industry regulations, current management standards and methods of various group companies, and local processes [25]. According to the selection principle of the evaluation index system, through the feasibility analysis of the initial index, combined with the actual situation of the site, the main factors of the coal-fired power plant are decomposed layer by layer, and the evaluation index system of the comprehensive performance of the coal-fired power plant is constructed, including 5 first-level evaluation indicators and 23 second-level evaluation indicators. Figure 1 shows the comprehensive evaluation index system of coal-fired units.

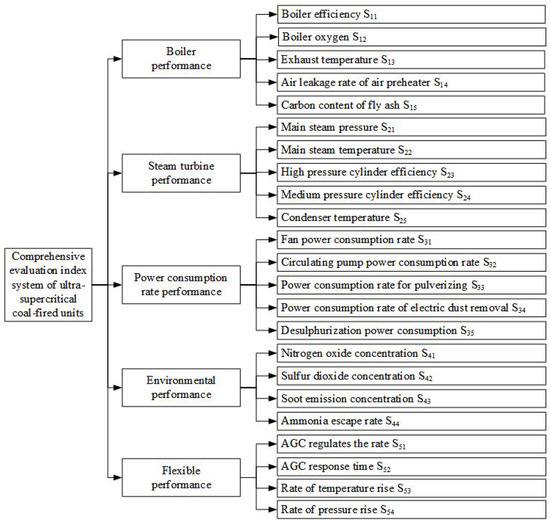
Figure 1. Comprehensive evaluation index system of coal-fired units.

3. Methods

3.1. Improve CRITIC Method

Criteria Importance Through Intercrieria Correlation (CRITIC) [10] is an objective weighting method proposed by Diakoulaki. It comprehensively measures the comparison intensity of evaluation indicators and the conflict between indicators. It takes into account both the variability of evaluation indicators and the correlation between evaluation indicators. Thus, it comprehensively considers the variability of evaluation indicators and their correlation, utilizing the objective attributes of data for scientific evaluation.

The standard deviation expresses the intensity of the contrast. The weight increases as the standard deviation increases, indicating greater fluctuation. The correlation coefficient expresses the presence of a conflict. If there is a strong positive correlation between the two indicators, a smaller conflict will result in a lower weight.

To address issues with determining evaluation index weights in the original CRITIC, this paper introduces the concept of information entropy to improve the method, resulting in the improved criteria importance though intererieria correlation (ICRITIC). The original CRITIC method has problems in calculating indicator weights, mainly due to the excessive weight of indicators caused by direct attribute assignment and correlation between indicators. This issue affects the accuracy and fairness of the evaluation results.

ICRITIC is highly objective and versatile, allowing for a comprehensive reflection of the relationship between evaluation indicators. It also avoids any potential bias towards certain indicators that may be present in other methods. In practical applications, the ICRITIC method proposed in this paper provides a more accurate, reasonable, and reliable way to determine the weight of evaluation indicators.

Step 1: Select m evaluation indications for n evaluation objects, establish the evaluation indicator system, construct the level matrix, and standardize the processing.

Step 2: The variability of the evaluation index

$$\left\{\begin{array}{c}\hfill {\overline{x}}_j=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{x}_{ij}\hfill \\ \hfill S_j=\sqrt{\frac{{\displaystyle \sum _{i=1}^m}{\left(x_{ij}-{\overline{x}}_j\right)}^2}{m-1}}\hfill \end{array}\right.,\left(1\le i\le m,1\le j\le n\right),$$

(1)

In the formula, $x_{ij}$ is the evaluation matrix of each index, and $S_j$ is the standard deviation of the evaluation index.

Step 3: The conflict of evaluation indicators

$$R_j=\sum _{i=1}^m\left(1-\left|r_{ij}\right|\right),\left(1\le i\le m,1\le j\le n\right)$$

(2)

In the formula, $R_j$ is the conflict of evaluation index.

Step 4: Information of evaluation indicators

$$\left\{\begin{array}{c}{p}_{ij}=\frac{{x^{\prime }}_{ij}}{{\displaystyle \sum _{j=1}^n}{x^{\prime }}_{ij}}\hfill \\ \hfill E_j=-\frac{1}{lnm}{\displaystyle \sum _{i=1}^m}{p}_{ij}ln{p}_{ij}\hfill \\ \hfill C_j=\left(E_j+\frac{S_j}{{\overline{x}}_j}\right)\times R_j\hfill \end{array}\right.,\left(1\le i\le m,1\le j\le n\right),$$

(3)

In the formula, $p_{ij}$ is the characteristic of evaluation index, $E_j$ is the information entropy of evaluation index, and $C_j$ is the information content of evaluation index.

Step 5: Objective weights of evaluation indicators

$$w_j^{\prime }=\frac{C_j}{{\displaystyle \sum _{j=1}^n}{C}_j},\left(1\le j\le n\right)$$

(4)

In the formula, $w_j^{\prime }$ is the weight of the evaluation index.

3.2. Entropy Weight Method

The entropy weight method (EWM) [25,26] is a weighting method that is objective. Entropy is a physical concept from thermodynamics that was later introduced into information theory by Shannon. Entropy is a measure of the degree of disorder in a system. The higher the entropy, the more chaotic the system, and the lower the entropy, the more ordered the system. According to the definition of information entropy, entropy is used to evaluate indicators by judging the degree of their dispersion. The degree of dispersion of the index increases as the information entropy decreases, resulting in a greater impact of the index on the comprehensive evaluation. If the evaluation indicators have equal values, they will not affect the comprehensive evaluation results.

Step 1: The original data matrix composed of m evaluation objects and n evaluation indicators is denoted as $X={\left(x_{ij}\right)}_{m\times n}$.

Step 2: Data normalization processing

$$\left\{\begin{array}{c}\hfill {x^{\prime }}_{ij}=\frac{x_{ij}-min\left(x_{ij}\right)}{max\left(x_{ij}\right)-min\left(x_{ij}\right)}\hfill \\ \hfill {x^{\prime }}_{ij}=\frac{max\left(x_{ij}\right)-x_{ij}}{max\left(x_{ij}\right)-min\left(x_{ij}\right)}\hfill \end{array}\right.,\left(1\le i\le m,1\le j\le n\right),$$

(5)

In the formula, ${x^{\prime }}_{ij}$ is the standardized value of the evaluation indicators (without negative indicators).

Step 3: Characteristic proportion of evaluation index

$$f_{ij}={x^{\prime }}_{ij}/\phantom{{x^{\prime }}_{ij}\sum _{j=1}^n{x^{\prime }}_{ij}}\sum _{j=1}^n{x^{\prime }}_{ij},\left(1\le i\le m,1\le j\le n\right)$$

(6)

In the formula, $f_{ij}$ is the characteristic of evaluation index.

Step 4: The information entropy of evaluation index

$$H_j=-\frac{1}{lnm}\sum _{i=1}^m{f}_{ij}ln{f}_{ij},\left(1\le i\le m,1\le j\le n\right)$$

(7)

In the formula, $H_j$ is the information entropy of the evaluation index.

Step 5: Objective weights of evaluation indicators

$$w_j=\frac{1-H_j}{{\displaystyle \sum _{j=1}^n}\left(1-H_j\right)},\left(1\le j\le n\right)$$

(8)

In the formula, $w_j$ is the weight of evaluation index.

3.3. Combinatorial Weighting

In order to avoid an accident in the calculation process and the neglect of indicators by objective assignment, the overall weight is as close as possible to the objective weight, taking into account the advantages of each objective weight assignment. This paper adopts the minimum information entropy principle to synthesize the index weights obtained by ICRITIC and EWM. The Lagrange multiplier method is then used to optimize and obtain the comprehensive weights [27,28]:

$${W_j}^{CW}=\frac{\sqrt{W_j^{CRITIC}\ast W_j^{EWM}}}{{\displaystyle \sum _{j=1}^n}\sqrt{W_j^{CRITIC}\ast W_j^{EWM}}}$$

(9)

In the formula, ${W_j}^{CW}$ is the combined weight of the evaluation index, $W_j^{CRITIC}$ is the weight of the evaluation index calculated by CRITIC, and $W_j^{EWM}$ is the weight of the evaluation index calculated by EWM.

3.4. Aggregation Operator

In 1998, Yager proposed the ordered weighted average (OWA) operator [29,30], which is an aggregation method of multi-attribute decision information between the maximum and minimum operators. Later, Guo et al. [20] proposed the time-ordered weighted averaging (TOWA) operator and the time-ordered weighted geometric averaging (TOWGA) operator.

3.4.1. TOWA Operator

Let $N=\left\{1,2,\cdots ,n\right\}$, $⟨u_i,a_i⟩$ be a TOWA pair, where $u_i$ is the time-induced component and $a_i$ is the data component:

$$F\left(⟨u_1,a_1⟩,\cdots ,⟨u_p,a_p⟩\right)=\sum _{j=1}^p{\lambda }_j{b}_j$$

(10)

In the formula, vectors $\lambda ={\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_p\right)}^T$ and vectors $\overrightarrow{F}$ are related weighted vectors, ${\lambda }_j\in \left[0,1\right]$ and ${\displaystyle \sum _{j=1}^n}{\lambda }_j=1$. $b_j$ represents the second component of the TOWA operator corresponding to time j, so the function is called an n-dimensional TOWA operator.

3.4.2. TOWGA Operator

Let $N=\left\{1,2,\cdots ,n\right\}$, $⟨v_i,c_i⟩$ be a TOWA pair, where $v_i$ is the time-induced component and $c_i$ is the data component:

$$G\left(⟨v_1,c_1⟩,\cdots ,⟨v_p,c_p⟩\right)=\prod _{j=1}^p{d}_j^{{{\lambda }^{\prime }}_j}$$

(11)

In the formula, vectors ${\lambda }^{\prime }={\left({{\lambda }^{\prime }}_1,{{\lambda }^{\prime }}_2,\cdots ,{{\lambda }^{\prime }}_p\right)}^T$ and vectors $\overrightarrow{G}$ are related weighted vectors, ${\lambda }_j^{\prime }\in \left[0,1\right]$ and ${\displaystyle \sum _{j=1}^n}{{\lambda }^{\prime }}_j=1$. $d_j$ represents the second component of the TOWA operator corresponding to time j, so the function is called an n-dimensional TOWA operator.

3.4.3. TOWA-TOWGA Hybrid Model

According to the definition of aggregation operators, TOWA operators care about functionality and TOWGA operators care about balance; both have advantages and disadvantages [31]. Therefore, based on the static evaluation results and considering the influence of the time factor, the TOWA-TOWGA hybrid model is used to perform a dynamic comprehensive evaluation of the performance of ultra-supercritical coal-fired units:

$$Y_i={\alpha }_{1}F\left({\lambda }_t\right)+{\alpha }_{2}G\left({\lambda }_t\right)$$

(12)

In the formula, ${\alpha }_1$ and ${\alpha }_2$ are the proportion of TOWA and TOWGA operators, respectively, $0\le {\alpha }_1\le 1$, $0\le {\alpha }_2\le 1$, ${\alpha }_1+{\alpha }_2=1$.

3.5. Determination of Time Weight

In dynamic comprehensive evaluation, time weighting reflects the relative importance of the evaluation object in different time periods in the process of information aggregation. Therefore, both subjective and objective factors need to be fully considered when determining time weights. On the one hand, the knowledge and experts experience should be taken into account, and on the other hand, objective information from time samples should be taken into account [20]. For the solution of the time weight, it is necessary to have a definition of the “time degree”:

$$\theta =\sum _{t=1}^p\frac{p-t}{p-1}{\lambda }_t$$

(13)

In the formula, $\theta$ is the time degree, ${\lambda }_t$ is the time weight vector.

Table 1 shows the value of the “time degree” reflecting the importance of time series to operators in the process of aggregation. When $\theta$ approaches 0, it indicates that the decision maker is paying more attention to the data in the most recent period. When $\theta$ approaches 1, it indicates that the decision maker pays more attention to data in the distant time period. When $\theta$ is the tent threshold with a value of 0.5, it indicates that the decision maker attaches the same importance to the sample information in each time period.

Table 1. Scale reference table for “time degree”.

$\mathit{\theta }$	Significance
0.1	Great emphasis on recent data
0.3	Pay more attention to recent data
0.5	Also focus on period data
0.7	Pay more attention to the forward data
0.9	Great emphasis on forward data
0.2, 0.4, 0.6, 0.8	The intermediate case corresponding to the above two adjacent judgments

Under the condition of determining the “time degree”, the programming method is used to determine the time weight. Through in-depth mining of sample information and comprehensive consideration of the relative importance of the evaluation object in different time periods, the time weight vector of the sample is clarified. We calculate the weight coefficient according to the variance formula [13]:

$$D^2\left(\lambda \right)=\sum _{i=1}^p\frac{1}{p}{\left[{\lambda }_t-E\left(\lambda \right)\right]}^2=\frac{1}{p}\sum _{i=1}^p{\lambda }_t^2-\frac{1}{p^2}$$

(14)

In the formula, $D^2\left(\lambda \right)$ is the variance, and $E\left(\lambda \right)$ is the mean value of the time weight coefficient. Therefore, the least variance method is used to solve the nonlinear programming problem [20]:

$$\left\{\begin{array}{c}\hfill min\left(\frac{1}{p}{\displaystyle \sum _{i=1}^p}{\lambda }_t^2-\frac{1}{p^2}\right)\hfill \\ \hfill st.\left\{\begin{array}{c}\hfill \theta ={\displaystyle \sum _{=1}^n}\frac{p-t}{p-1}{\lambda }_t\hfill \\ \hfill {\displaystyle \sum _{t=1}^p}{\lambda }_t=1\hfill \end{array}\right.\hfill \\ \hfill {\lambda }_t\in \left[0,1\right]\hfill \\ \hfill t=1,2,\cdots ,n\hfill \end{array}\right.$$

(15)

4. Results and Discussion

4.1. Unit Introduction

This paper focuses on a 660 MW ultra-supercritical boiler located in Xinjiang, China. The boiler has a single furnace, balanced ventilation, solid state slag discharge, all steel frame, and all-suspension structure. The boiler adopts an atmospheric expansion start-up system without a recirculation pump and a positive pressure direct blowing cold primary air powder system. The primary burner is positioned in the four corners of the water wall, with each layer having four burners that correspond to a coal mill. Additionally, the SOFA burner is located in the four corners of the water wall above the primary burner area. The steam turbine is a reaction type with one intermediate reheating, three cylinders, and two rows of steam. It is ultra-supercritical and features a single shaft and indirect air cooling. Table 2 displays the primary technical parameters of coal-fired units.

Table 2. Technical parameters of coal-fired units.

Name	Unit	BMCR
Initial steam flow rate	t/h	2030
Main steam pressure	MPa.g	28.25
Main steam temperature	℃	605
Feed water temperature	℃	303.0
Reheat steam flow	t/h	1637.22
Reheat steam pressure	MPa.g	27.00
Reheat steam temperature	℃	600
Exhaust gas temperature	℃	130
Boiler efficiency	%	94.05

4.2. Determination of Combinatorial Weights

Based on the consultation of experts and the combination of the actual situation of the site, this paper takes the operating data of a 660 MW coal-fired unit in Xinjiang from February 2023 to August 2023 as the research object. The operating data with a stable operating time of more than 1 h and a load variation range within ±2% have been selected for the analysis.

At the same time, the variable working condition data with load variation range between 25% and 98%, excluding the selected stable operation data, is analyzed based on the three sets of data selected in this paper. Due to the influence of environmental factors in the summer, turbine heat acceptance (THA) does not operate at 100% heat consumption during operation. Therefore, this paper selects data from summer 90%THA coal-fired units for comparative analysis.

The combined weights of evaluation indicators were obtained based on the objective weight data obtained by ICRITIC and EWM. Table 3 and Table 4 respectively show the combined weights of different evaluation indicators for the coal-fired units in different environments, where $T_1$ to $T_6$ represent February, March, April, June, July and August, respectively.

Table 3. Static evaluation results in winter.

Index	100%THA (±2%)			50%THA (±2%)			Variable Load (25–98%)
	${\mathit{T}}_{\mathbf{1}}$	${\mathit{T}}_{\mathbf{2}}$	${\mathit{T}}_{\mathbf{3}}$	${\mathit{T}}_{\mathbf{1}}$	${\mathit{T}}_{\mathbf{2}}$	${\mathit{T}}_{\mathbf{3}}$	${\mathit{T}}_{\mathbf{1}}$	${\mathit{T}}_{\mathbf{2}}$	${\mathit{T}}_{\mathbf{3}}$
$S_{11}$	0.0080	0.0122	0.0111	0.0226	0.0254	0.0161	0.0205	0.0144	0.0099
$S_{12}$	0.6344	0.6577	0.6244	0.6474	0.6134	0.5613	0.7631	0.7522	0.7143
$S_{13}$	0.1462	0.1058	0.1195	0.1131	0.1376	0.1803	0.0908	0.0915	0.0943
$S_{14}$	0.2113	0.2243	0.2449	0.2169	0.2236	0.2423	0.1256	0.1420	0.1816
$S_{15}$	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
$S_{21}$	0.2178	0.1807	0.0830	0.3461	0.3281	0.2949	0.6262	0.5593	0.6110
$S_{22}$	0.1716	0.1429	0.0471	0.2073	0.1359	0.1073	0.0524	0.0474	0.0302
$S_{23}$	0.1518	0.1213	0.0710	0.1932	0.1636	0.1493	0.0882	0.0859	0.0708
$S_{24}$	0.0350	0.0256	0.0168	0.0417	0.0249	0.0240	0.0781	0.0662	0.0632
$S_{25}$	0.4237	0.5295	0.7821	0.2117	0.3475	0.4244	0.1552	0.2412	0.2248
$S_{31}$	0.0976	0.0713	0.0870	0.0472	0.0231	0.0264	0.1275	0.1198	0.1096
$S_{32}$	0.0292	0.0240	0.2759	0.0282	0.6038	0.5370	0.2553	0.3535	0.4052
$S_{33}$	0.1199	0.0725	0.0982	0.2486	0.0969	0.0953	0.1034	0.0862	0.0782
$S_{34}$	0.2855	0.2772	0.2270	0.3037	0.1224	0.1547	0.2230	0.1937	0.1885
$S_{35}$	0.4677	0.5551	0.3119	0.3723	0.1537	0.1866	0.2908	0.2468	0.2185
$S_{41}$	0.1166	0.1037	0.1366	0.2312	0.1556	0.1950	0.1580	0.1775	0.1903
$S_{42}$	0.4714	0.4768	0.3200	0.2962	0.3261	0.2028	0.4656	0.3767	0.2849
$S_{43}$	0.1274	0.2200	0.2714	0.0740	0.1633	0.1767	0.0983	0.1230	0.1615
$S_{44}$	0.2846	0.1995	0.2720	0.3986	0.3550	0.4255	0.2780	0.3228	0.3634
$S_{51}$	0.0715	0.2632	0.1142	0.2029	0.2231	0.1665	0.1055	0.1226	0.1252
$S_{52}$	0.8677	0.6324	0.7506	0.5780	0.6750	0.6754	0.7611	0.7779	0.7718
$S_{53}$	0.0280	0.0375	0.0718	0.0921	0.0392	0.0613	0.0452	0.0359	0.0384
$S_{54}$	0.0328	0.0669	0.0635	0.1270	0.0628	0.0968	0.0882	0.0635	0.0646

Table 4. Static evaluation results in summer.

Index	90%THA (±2%)			50%THA (±2%)			Variable Load (25–98%)
	${\mathit{T}}_{\mathbf{4}}$	${\mathit{T}}_{\mathbf{5}}$	${\mathit{T}}_{\mathbf{6}}$	${\mathit{T}}_{\mathbf{4}}$	${\mathit{T}}_{\mathbf{5}}$	${\mathit{T}}_{\mathbf{6}}$	${\mathit{T}}_{\mathbf{4}}$	${\mathit{T}}_{\mathbf{5}}$	${\mathit{T}}_{\mathbf{6}}$
$S_{11}$	0.0094	0.0063	0.0094	0.0124	0.0130	0.0142	0.0126	0.0071	0.0073
$S_{12}$	0.5838	0.6621	0.5509	0.4771	0.5025	0.5046	0.8002	0.7027	0.6911
$S_{13}$	0.1255	0.1180	0.1371	0.1695	0.1651	0.1645	0.0701	0.0813	0.0848
$S_{14}$	0.2813	0.2135	0.3026	0.3410	0.3194	0.3167	0.1170	0.2089	0.2169
$S_{15}$	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
$S_{21}$	0.1477	0.1583	0.1712	0.2646	0.1734	0.2239	0.5009	0.4394	0.4787
$S_{22}$	0.0388	0.1104	0.0909	0.0519	0.0640	0.0488	0.0365	0.0485	0.0332
$S_{23}$	0.1113	0.1569	0.1253	0.1448	0.1203	0.1415	0.0920	0.0957	0.0921
$S_{24}$	0.0183	0.0174	0.0229	0.0216	0.0285	0.0276	0.0717	0.0432	0.0495
$S_{25}$	0.6839	0.5571	0.5897	0.5171	0.6138	0.5582	0.2988	0.3732	0.3464
$S_{31}$	0.0920	0.1074	0.0135	0.0501	0.0741	0.0054	0.1269	0.0853	0.0138
$S_{32}$	0.2497	0.1461	0.3647	0.4825	0.2762	0.4340	0.2992	0.3067	0.4155
$S_{33}$	0.1117	0.1728	0.3859	0.1700	0.2238	0.4969	0.0704	0.1087	0.4496
$S_{34}$	0.2487	0.3178	0.1110	0.0833	0.1474	0.0298	0.1841	0.2189	0.0549
$S_{35}$	0.2979	0.2558	0.1249	0.2142	0.2785	0.0340	0.3194	0.2803	0.0662
$S_{41}$	0.1127	0.0819	0.0767	0.1517	0.1315	0.1628	0.1354	0.1211	0.2295
$S_{42}$	0.3424	0.3073	0.3340	0.2378	0.1697	0.2359	0.3122	0.2631	0.2521
$S_{43}$	0.3108	0.4462	0.3592	0.2205	0.3837	0.2845	0.2837	0.3846	0.2985
$S_{44}$	0.2342	0.1647	0.2300	0.3900	0.3151	0.3168	0.2687	0.2312	0.2199
$S_{51}$	0.1622	0.2897	0.1186	0.2748	0.1181	0.0921	0.1380	0.0795	0.0795
$S_{52}$	0.7328	0.5992	0.6849	0.6139	0.7710	0.7752	0.7646	0.7977	0.8362
$S_{53}$	0.0522	0.0420	0.0965	0.0445	0.0331	0.0411	0.0295	0.0294	0.0211
$S_{54}$	0.0528	0.0691	0.1001	0.0669	0.0777	0.0915	0.0680	0.0935	0.0632

According to Table 3 and Table 4, the weight of the evaluation index may vary depending on the unit load changes in different environments. Therefore, this paper holds significance for the comprehensive evaluation of coal-fired units under varying loads.

According to Figure 2 and Figure 3, to evaluate the effectiveness of ICRITIC, we tested and calculated the weight of evaluation indicators and compared it with CRITIC before the improvement. The comparison results indicate that the improved ICRITIC can eliminate any unjustified weight bias present in the original method. This leads to a more accurate evaluation of index weight and a more objective and comprehensive assessment.

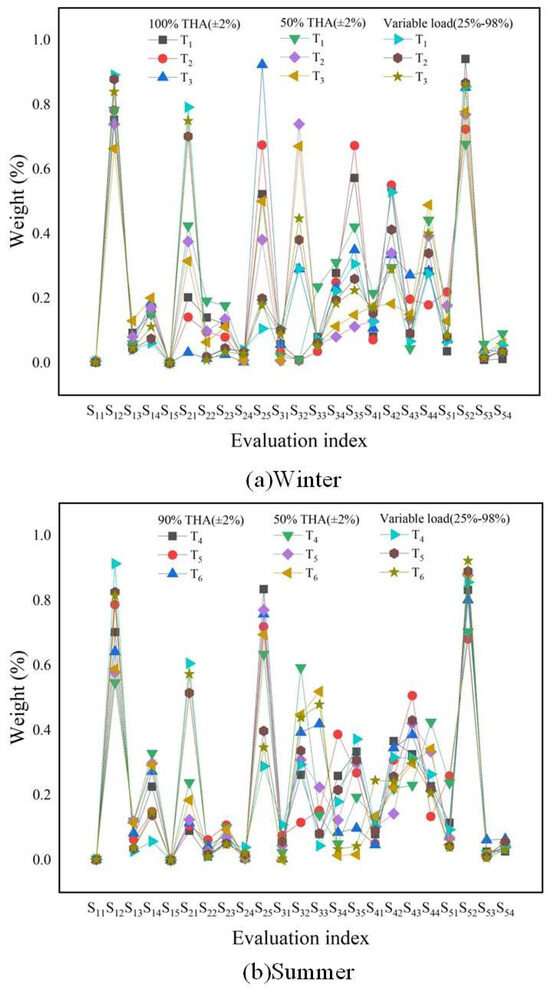
Figure 2. The indicators’ combined weights are determined using the CRITIC in various environments.

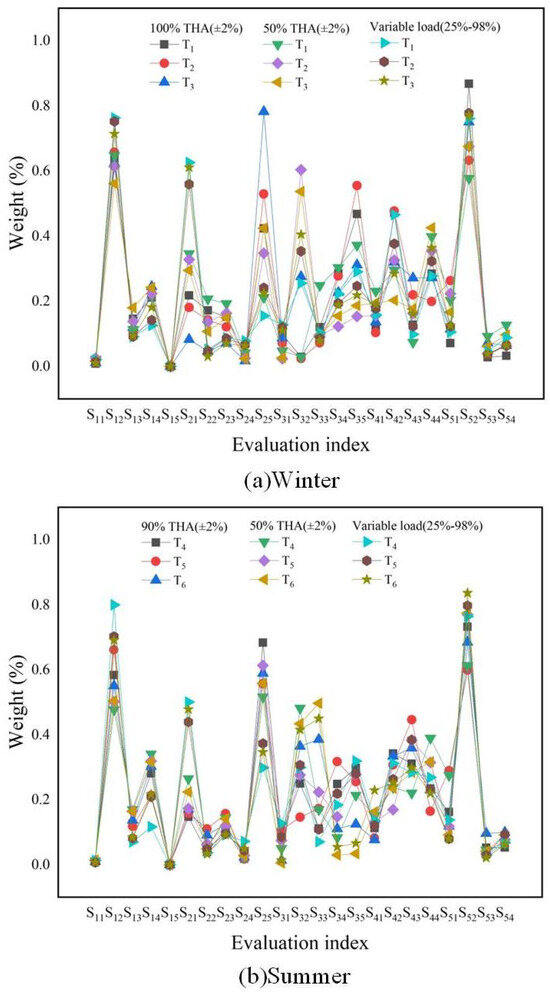
Figure 3. The indicators’ combined weights are determined using the ICRITIC in various environments.

4.3. Determination of Comprehensive Evaluation Results

According to the advice of relevant experts, when $\theta$ is the tent threshold with a value of 0.3, solve the programming equation with minimum variance to obtain the time weight vector:

$$\lambda =\left[\begin{array}{ccc}0.1333& 0.3333& 0.5333\end{array}\right]$$

The static assessment results of each index are aggregated over time to produce the dynamic comprehensive assessment of the index, where ${\alpha }_1$ and ${\alpha }_2$ are the tent threshold with a value of 0.5. Table 5 shows the final evaluation results of each indicator.

Table 5. Results of dynamic comprehensive evaluation.

Index	Winter			Summer
	100%THA (±2%)	50%THA (±2%)	Variable Load (25–98%)	90%THA (±2%)	50%THA (±2%)	Variable Load (25–98%)
$S_{11}$	0.0110	0.0198	0.0126	0.0083	0.0136	0.0079
$S_{12}$	0.6367	0.5897	0.7333	0.5913	0.5002	0.7091
$S_{13}$	0.1182	0.1560	0.0929	0.1290	0.1654	0.0816
$S_{14}$	0.2334	0.2326	0.1601	0.2684	0.3208	0.1991
$S_{15}$	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
$S_{21}$	0.1279	0.3125	0.5955	0.1637	0.2114	0.4683
$S_{22}$	0.0883	0.1285	0.0383	0.0885	0.0541	0.0384
$S_{23}$	0.0962	0.1596	0.0780	0.1335	0.1347	0.0933
$S_{24}$	0.0217	0.0264	0.0661	0.0204	0.0270	0.0500
$S_{25}$	0.6415	0.3661	0.2200	0.5908	0.5708	0.3486
$S_{31}$	0.0829	0.0277	0.1153	0.0450	0.0258	0.0434
$S_{32}$	0.1248	0.4342	0.3660	0.2661	0.3832	0.3616
$S_{33}$	0.0918	0.1126	0.0840	0.2643	0.3462	0.2521
$S_{34}$	0.2508	0.1602	0.1947	0.1869	0.0672	0.1145
$S_{35}$	0.4063	0.1961	0.2370	0.1849	0.1136	0.1517
$S_{41}$	0.1225	0.1859	0.1816	0.0829	0.1505	0.1768
$S_{42}$	0.3887	0.2531	0.3367	0.3261	0.2128	0.2634
$S_{43}$	0.2319	0.1559	0.1391	0.3802	0.3064	0.3239
$S_{44}$	0.2481	0.3978	0.3378	0.2075	0.3256	0.2299
$S_{51}$	0.1499	0.1893	0.1216	0.1740	0.1204	0.0864
$S_{52}$	0.7248	0.6618	0.7724	0.6619	0.7512	0.8136
$S_{53}$	0.0528	0.0569	0.0384	0.0699	0.0388	0.0248
$S_{54}$	0.0599	0.0882	0.0672	0.0823	0.0834	0.0733

According to Table 5 and Figure 4, analysis of evaluation results under different circumstances:

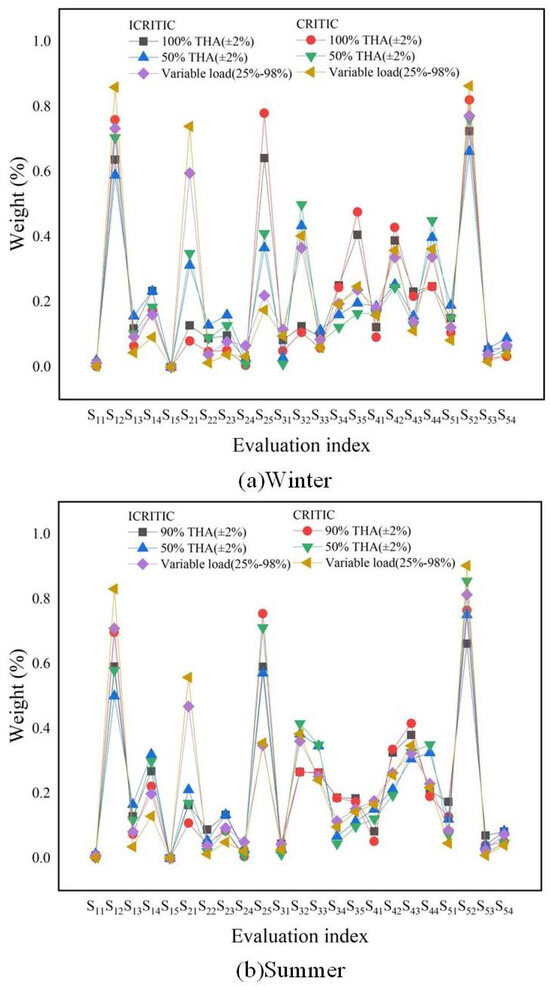
Figure 4. Evaluation results of different loads in different environments.

Under varying load conditions, the oxygen and air leakage rate of the boiler’s air preheater fluctuate significantly. It is important to note that the boiler’s oxygen levels have the most significant impact. The adjustment of system parameters is caused by a change in load, which in turn affects the air leakage rate of the air preheater. Under different working conditions in summer and winter, the weight of main steam pressure increases, and the temperature of the condenser decreases slightly in terms of turbine index. The reason for this is that the alteration in load results in a modification of the characteristics of the steam that is released from the turbine, which subsequently impacts the operational condition of the condenser. Regarding plant power consumption, circulating pumps may operate off-design, which can lead to reduced efficiency and increased power consumption. Regarding environmental protection, the stability of the combustion system is decreased, the performance of the desulfurization system is reduced, and there is an increase in incomplete combustion of pulverized coal and particulate matter. The increase in environmental indicators, such as SO₂ concentration, ammonia escape rate, and soot emission concentration, is observed. Finally, from the perspective of flexible indicators, coal-fired units must quickly adjust their load to meet the power system’s demand, ensuring the quality, reliability, and stability of the power supply’s frequency.

According to Figure 4, it shows that the improved CRITIC adjusts the weight of evaluation indicators. Under the improved method, the less heavily weighted indicators increase by approximately 6.2%, while the more heavily weighted indicators decrease by approximately 0.22%. This alteration ensures that the weight accurately reflects the relationship between the evaluation indicators, thus avoiding any potential bias issues. The results indicate that the revised method enhances the balance and stability of the weights, leading to improved accuracy in index weighting.

5. Conclusions

In order to analyze the change in overall performance of a 660 MW ultra-supercritical coal-fired unit in Xinjiang under varying operating conditions, a dynamic overall evaluation model based on an ICRITIC-EWM is proposed in this paper. The ICRITIC-EWM is used to improve the objective accuracy of static weights, and the TOWA-TOWGA mixed operator model is combined to aggregate the evaluation process of coal-fired units in the time dimension so as to realize the dynamic comprehensive evaluation of coal-fired units under changing operating conditions.

• This paper proposes a dynamic comprehensive evaluation model based on ICRITIC-EWM. The model aims to make the static weights of each evaluation index more objective, enabling efficient and accurate determination of the static weight parameters of coal-fired units.
• Based on the actual running data of the power plant and the power plant performance assessment model in this paper, we analyze the five comprehensive performances of the object power plant. Figure 4 and Table 4 show the different factors that affect the performance level of a power plant. These include the air leakage rate of the air preheater, condenser temperature, desulfurization power consumption rate, circulating pump power consumption rate, SO₂ concentration, dust emission concentration, ammonia escape rate, and AGC response time. It is important for the operator of the power plant to consider these factors when aiming to improve the plant’s performance.
• This paper proposes a dynamic comprehensive evaluation model based on the improved CTITIC-EWM to address the issue of comprehensive performance evaluation of ultra-supercritical coal-fired units under variable load. The revised method adjusts the weight of evaluation indicators, resulting in a 6.2% increase in the index with less weight and a 0.22% decrease in the index with more weight. This model demonstrates improved accuracy, reliability, and applicability, providing a more effective method for researching and practically applying multi-index evaluation problems.